

| {1} |

| {2} |
ACCADEMIA DELLE SCIENZE DELL'URSS
GALILEO GALILEI
OPERE SCELTE
IN DUE VOLUMI
TOMO SECONDO
CASA EDITRICE «NAUKA»
MOSСА
1 9 6 4
| {3} |
АКАДЕМИЯ НАУК СССР
ГАЛИЛЕО ГАЛИЛЕЙ
ИЗБРАННЫЕ ТРУДЫ
В ДВУХ ТОМАХ
ТОМ ВТОРОЙ
МЕХАНИКА
•
О ТЕЛАХ, ПРЕБЫВАЮЩИХ
В ВОДЕ
•
БЕСЕДЫ И МАТЕМАТИЧЕСКИЕ
ДОКАЗАТЕЛЬСТВА

ИЗДАТЕЛЬСТВО «НАУКА»
МОСКВА
1 9 6 4
| {4} |
Редакционная коллегия:
А. Ю. Ишлинский (главный редактор),
А. Т. ГРИГОРЬЯН, М. А. ДЫННИК,
Б. Г. КУЗНЕЦОВ, М. А. ЛАВРЕНТЬЕВ,
И. Б. ПОГРЕБЫССКИЙ, В. Г. ФЕСЕНКОВ
Составитель
У. И. ФРАНКФУРТ
| {5} |
|
МЕХАНИКА |
| {6} |
ПЕРЕВОД
Н. М. ТЕЛЕВНОЙ
| {7} |
О пользе, которая извлекается
из науки механики и ее орудий
Мне думается, что прежде чем переходить к рассуждениям по поводу механических орудий, было бы чрезвычайно важно рассмотреть их в общем и уяснить себе, каковы те выгоды, которые получают от этих орудий; по-моему, это тем более следует сделать потому, что, насколько я наблюдал (если не ошибаюсь), механики часто заблуждаются, желая применить машины ко многим действиям, невозможным по самой своей природе, а в результате и сами оказываются обманутыми и в равной степени обманывают тех, кто исходил в своих надеждах из их обещаний1. Как мне кажется, я понял: главная причина подобных заблуждений — это уверенность, что такими приспособлениями всегда можно поднять и передвинуть при помощи незначительной силы громадные грузы, обманывая таким образом природу, стремление которой, я сказал бы даже: основа ее устройства, состоит в том, что никакое сопротивление нельзя преодолеть силой менее мощной, чем оно само. Я надеюсь, что те точные и необходимые доказательства, которые мы Получим в дальнейшем, сделают очевидным, насколько ошибочна такая уверенность.
Поскольку было отмечено, что польза, извлекаемая из машин, состоит вовсе не в том, чтобы при помощи машины перемещать малой силой такие грузы, которые мы не были бы в состоянии переместить одной только силой, считаю уместным объяснить, какие же собственно выгоды получают {8} от машин, так как, если нет надежды на какую-либо выгоду, то напрасно затрачивать труд на создание самих машин.
И вот, чтобы начать наши рассмотрения, надо принять во внимание четыре предмета2: первый — это груз, который нужно перенести с места на место; второй — это сила или мощь3, которая должна его перенести; третий — это расстояние между начальной и конечной точками перемещения; четвертый — это время, в течение которого должно произойти перемещение; но время сводится к тому же, что и скорость, быстрота (velocita) движения, ибо из двух движений за более быстрое принимается то движение, при котором то же расстояние проходят за меньшее время. Теперь, когда задано любое сопротивление, определена сила и указано любое расстояние, нет сомнения в том, что заданная сила переместит заданный груз на указанное расстояние. Ибо, даже если сила весьма мала, то, разделив груз на множество частей, из которых ни одна не превосходит силу, и, перенося эти части одну за другой, мы переместим в конце концов весь груз на установленное расстояние; но по окончании действия следует сказать, что больший груз был сдвинут и перемещен не силой меньшей, чем он сам, а силон, несколько раз повторившей то движение и прошедшей пространство, которое, один только раз было пройдено всем грузом. Отсюда вытекает, что скорость силы во столько раз превосходит сопротивление груза, во сколько раз сам груз превосходит силу; однако из того, что за время, пока движущая сила несколько раз преодолевала расстояние между крайними точками движения, само перемещаемое тело прошло его только один раз, не следует все-таки делать вывод, что большое сопротивление оказалось преодоленным, вопреки устройству природы, малой силой. О преодолении установления природы можно было бы говорить только в случае, если бы меньшая сила переместила большее сопротивление с той же скоростью движения, с которой перемещается она сама; чего, кто это мы с полной уверенностью утверждаем, невозможно добиться при помощи какой бы то ни было машины, как изобретенной, так и такой, какую вообще возможно изобрести4. Но поскольку иногда бывает необходимо, имея малую силу, переместить большой груз целиком, не разделяя его на части, то в таком случае приходится прибегать к машине, с помощью которой и перемещают предложенный груз на установленное расстояние; но при этом той же самой силе неизбежно придется преодолевать то же самое расстояние или другое, равное ему, столько раз, во сколько раз сам груз превосходит силу; так что в конце действия не получим от машины никакой пользы, кроме того, что она переместит данной силой на данное расстояние зараз весь тот груз, который, будучи разделен на части, был бы перенесен той же самой силой в течение того же самого времени на то же расстояние и без помощи машины. А именно это и должно расцениваться {9} как одна из выгод, получаемая от механики, потому что действительно часто оказывается необходимым при недостатке силы, но не времени, перемещать целиком большие грузы. Но кто понадеется и попытается добиться при помощи машины того же результата, не замедляя движения перемещаемого тела, тот неизбежно окажется обманутым в своих надеждах и обнаружит непонимание как природы механических орудий, так и принципов их действия.
Другая выгода, получаемая от механических орудий, зависит от места, где их применяют, ибо не все механические орудия применяются с одинаковым удобством в любом месте.
Объясним нашу мысль примером: беря воду из колодца, мы пользуемся простой веревкой с привязанным к ней сосудом, который принимает и сохраняет то количество воды, какое мы можем вычерпать за определенное время нашими ограниченными силами; но кто воображает, что можно какой-либо машиной за то же самое время при помощи той же самой силы вычерпать большее количество воды, тот глубочайшим образом заблуждается. И тем чаще и глубже он будет заблуждаться, чем более разнообразные и многочисленные приспособления он будет измышлять. Но тем не менее мы видим, что воду извлекают и другими орудиями: так, например, для высушивания корабельного трюма используют помпы. Но здесь следует заметить, что помпы применяются с той же целью вовсе не потому, что они извлекают больше воды, чем это можно сделать за то же самое время и той же самой силой простым ведром, а только потому, что применение ведра или другого какого-либо подобного сосуда в этом месте не дало бы желаемого результата, т. е. полного освобождения трюма от любого незначительного количества воды. Это вообще невозможно сделать ведром, так как оно погружается и черпает воду только там, где она стоит на достаточно высоком уровне. Мы видим, что при помощи той же помпы высушивают и погреба, откуда воду нельзя вычерпать иначе, как только наклонно, а действовать так обычным ведром, которое поднимается и опускается на своей веревке перпендикулярно, невозможно.
Третья и, вероятно, наибольшая выгода среди других выгод, получаемых от механических орудий, связана с тем, что движет; движение может быть вызвано или какой-либо неодушевленной силой, например течением реки, или же одушевленной силой, расходы на содержание которой окажутся, однако, значительно меньше расходов, необходимых для поддержания силы человека. Так, например, используя для вращения жернова течение реки или силу лошади, добиваются такого же результата, для которого оказалось бы недостаточной мощь (il potere) четырех или шести человек. Именно поэтому и удается нам извлекать выгоду при подъеме воды, а также совершать другие действия, которые {10} люди выполняют и без специальных устройств. Так, ведь уже простым сосудом можно брать воду, поднимать ее и выливать там, где это необходимо; но поскольку лошадь или другой подобный двигатель обладает только избытком сил, но не умеет рассуждать и при нем нет приспособлений, устроенных для того, чтобы подхватывать сосуд, вовремя его опоражнивать, а затем снова возвращать для наполнения, то механику необходимо восполнить этот естественный недостаток двигателя, придумывая такие приспособления, при помощи которых удавалось бы добиться желаемого результата приложением только силы. В этом-то и заключается величайшая выгода: она не в том, что колеса или другие машины меньшей силой и с большей скоростью и на большем пространстве переносят тот самый груз, который могла бы перенести без применения орудий равная, но разумно и хорошо организованная сила, а в том, что падение воды ничего не стоит или стоит очень мало, а содержание лошади или другого какого-либо животного, сила которого превосходит силу восьми, а то и более человек, потребует гораздо меньше расходов, чем те, что необходимы для содержания такого количества людей5.
Итак, вот в чем выгода, которую получают от механических орудий; она не в том вовсе, о чем мечтают неразумные инженеры, думающие обмануть природу и только посрамляющие себя, стремясь применять машины для невыполнимых предприятий.
И из немногого, до сих пор сказанного, и из того, что будет в этом трактате доказано в дальнейшем, мы придем к тому же убеждению, если будем внимательно воспринимать все, что следует.
В нашем трактате мы должны следовать тому, что необходимо во всех точных науках, а именно: предложить определения подходящих терминов и сделать первоначальные допущения, из которых, как из плодоноснейшего семени, возьмут свое начало и последовательно развернутся причины и точные доказательства свойств всех механических орудий. А так как последние используются главным образом в связи с движением тяжелых тел, то прежде всего определим, что такое тяжесть (gravita).
И вот: тяжестью мы называем естественное стремление к движению вниз, вызываемое в тяжелых телах большим или меньшим количеством материи, из которой они состоят.
Момент (momento) — это стремление двигаться вниз, вызванное не столько тяжестью движущегося тела, сколько тем, как различные тяжелые тела размещаются относительно друг друга; при этом часто наблюдается, что благодаря моменту более тяжелые тела перевешиваются более легкими; например, в безмене, где крошечный противовес поднимает {11} огромный груз не из-за избытка тяжести, а из-за удаленности от точки, где безмен поддерживается, из-за удаленности, которая, в сочетании с тяжестью меньшего груза, увеличивает ему момент и импето (impeto) опускаться вниз, которым он может превысить момент другого, более тяжелого тела. Итак, момент — это импето опускаться вниз, состоящее из тяжести, положения и всего остального, что может вызвать такое стремление6.
За центр тяжести в каждом тяжелом теле принимается такая точка, вокруг которой расположены части с одинаковыми моментами; так что, если представим себе, что тяжелое тело подвешено и удерживается за эту точку, то части справа будут уравновешиваться частями слева, части спереди — частями сзади, части снизу — частями сверху, и тяжелое тело, будучи поддерживаемо таким образом, никуда не отклонится, а помещенное в какое угодно положение, будет в нем оставаться, если только оно подвешено за центр. Но это ведь именно та точка, которая стремилась бы соединиться с общим центром всех тяжелых вещей, т. е. с центром Земли, если бы она могла опускаться в какой-либо свободной среде.
На этом основании принимаем такое допущение: тяжелое тело опускается вниз таким образом, чтобы его центр тяжести никогда не сходил с прямой линии, проведенной из центра тела в его начальном положении, к общему центру тяжелых предметов.
Это допущение вполне обосновано, ибо, если отдельный центр должен стремиться соединиться с общим центром, необходимо, чтобы он соединился с ним при отсутствии препятствий по кратчайшей линии, а таковой всегда является прямая. Во-вторых, можем допустить следующее: каждое тело тяготеет больше всего над центром своей тяжести, и в этом центре собственно сосредотачиваются все импето, вся тяжесть и все моменты. И, наконец, допустим, что центр тяжести двух тел с одинаковым весом находится посредине прямой линии, которая соединяет эти центры; или у двух грузов, подвешенных на равных расстояниях, точка равновесия находится на общей, соединяющей их
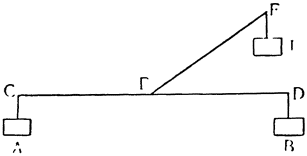 |
После этих определений и допущений перейдем к объяснению самого общего, главнейшего принципа большей части механических орудий и докажем, что неравные грузы, подвешенные на неравных расстояниях, уравновешиваются каждый раз, когда эти расстояния обратно пропорциональны грузам. Убежденные в истинности ранее изложенного принципа, что равные грузы, будучи подвешены на равных расстояниях, уравновешиваются, мы докажем не только то, что неравные грузы, подвешенные на неравных расстояниях, действительно уравновешиваются, если эти расстояния обратно пропорциональны самим грузам, но также и то, что подвешивание неравных грузов на обратно пропорциональных расстояниях является, по существу, тем же самым что и подвешивание равных грузов на равных расстояниях8.
Итак, представим себе однородное по весу и одинаковое по толщине твердое тело CDFE, цилиндрической или другой, сходной формы,
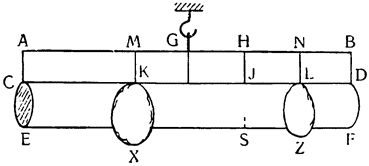 |
Мне думается, что из всего сказанного становится совершенно ясно каким образом два неравных тяжелых тела CS и SD, будучи подвешены на расстояниях, обратно пропорциональных их тяжестям, не только уравновешиваются но, более того, in rei natura* это оказывается тем же, что подвесить на равных расстояниях два равных груза, поскольку тяжесть {14} груза CS некоторым образом, мы скажем — виртуально распространяется за опору G, а тяжесть груза SD от той же самой опоры G оттягивается, что может понять любой рассуждающий человек, внимательно изучив все сказанное по поводу данной фигуры. И если тяжести грузов и расстояния, на которых они подвешены, остаются теми же, пусть даже изменятся формы фигур, став сферическими, подобными X и Z, нет сомнения в том, что равновесие сохранится, потому что форма — случайное качество, не могущее изменить тяжесть, которая проистекает скорее от количества. Отсюда делаем общий вывод: оказывается совершенно верным то, что неравные грузы уравновешиваются, будучи подвешены на неравных расстояниях, обратно пропорциональных самим грузам.
Показав, как уравниваются моменты неравных грузов, подвешенных на расстояниях, обратно пропорциональных отношению их весов, мне кажется, не следует обходить молчанием и другое сходное и вероятное положение, из которого логически вытекает подтверждение той же истины9.
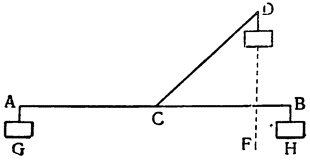
Рассмотрим весы АВ, разделенные на неравные части в точке С, и грузы, подвешенные к точкам А и В, и относящиеся друг к другу, как расстояния ВС и АС; из уже сказанного очевидно, что один груз уравновесит другой, но если к одному из грузов добавить минимальный момент тяжести, он станет опускаться вниз, поднимая второй груз; так, например, если мы
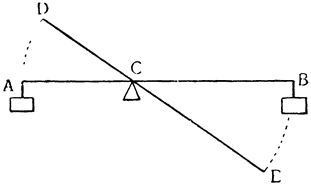 |
Но прежде, чем пойти дальше, необходимо рассмотреть еще один вопрос, касающийся расстояний, на которых подвешиваются грузы, поскольку чрезвычайно важно знать, как согласовываются равные и неравные расстояния, и, вообще как следует их измерять. Представим себе, что к концам прямой линии АВ подвешены два равных груза; если посередине этой линии взять точку С, то над ней установится равновесие, так как расстояние АС равно расстоянию СВ. Но если поднять
 |
| {16} |
Поняв из доказанного один из основных принципов, откуда, как из плодотворнейшего источника, берут начало многие механические орудия, мы можем без труда перейти к изучению природы последних.
И сразу же, говоря о безмене, этом весьма распространенном орудии, которым взвешивают различные грузы, удерживая их, даже самые
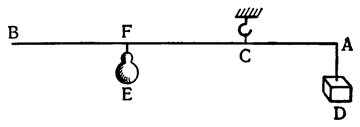 |
Это орудие ничем не отличается от так называемой ваги (в просторечье ее называют рычагом, lieve), при помощи которой перемещают, прикладывая малую силу, огромные камни и другие грузы. Способ применения можно понять по приложенному здесь рисунку, где рычагом является палка BCD из дерева или какого-либо другого твердого материала; А — это груз, который нужно поднять, Е — твердая опора, на которую рычаг
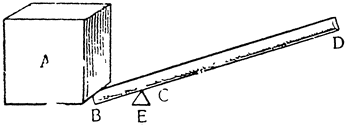 |
Здесь остается заметить (то же самое в своем месте будет сказано по поводу всех других механических орудий), что польза, извлекаемая из рычага, состоит вовсе не в том, как в этом убеждают себя большинство {17} механиков, чтобы победить и определенным образом обмануть природу, преодолевая при его помощи малой силой огромнейшее сопротивление, так как мы докажем, что и без помощи рычага можно той же силой и в течение того же самого времени добиться того же результата. Возьмем снова тот же самый рычаг BCD, где С —
 |
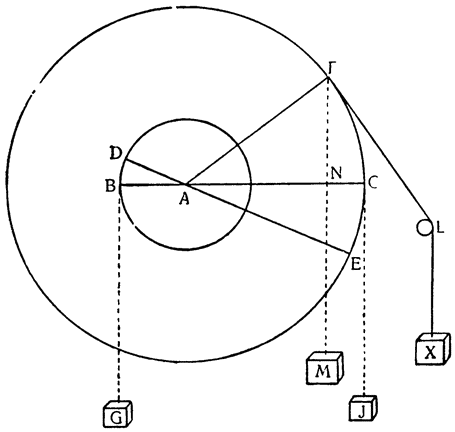
Два орудия, природу которых мы собираемся объяснить, прямо связаны с рычагом; больше того, они являются не чем иным, как рычагом непрерывного действия (vette perpetue). Итак, представим себе рычаг ВАС с опорой в точке A и с грузом G, подвешенным в точке В; если в {18} точке С приложить силу, то очевидно, что при перемещении рычага в положение DAE груз поднимется по расстоянию BD, но дальше этот подъем продолжать нельзя и если хотят поднять груз выше, его необходимо закрепить какой-либо другой опорой, перевести рычаг в
 |
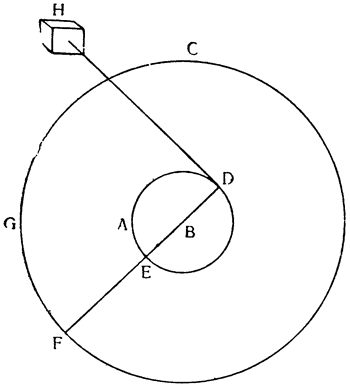
От рассмотренного орудия, которое мы объяснили, по форме мало чем отличается другое, которое назовем воротом; собственно говоря, различие между ними заключается только в способе применения: колесо лебедки установлено и перемещается в вертикальной плоскости, а ворот работает своим приводом параллельно горизонту. Предположим, что над кругом DAE установлена ось цилиндрической формы, вращающаяся около центра В, а вокруг оси обернута веревка DH, привязанная к грузу, чтобы тащить его за собой; если вставить в эту ось жердь FEBD, а к концу F приложить силу, то ли человека, то ли лошади или какого-либо другого животного, способного перемещать грузы, которое будет ходить по кругу FGE, то окажется, что мы сконструировали и построили ворот; так как при круговом движении жердь будет вращать также ось, или ствол (барабан) ворота EAD, то веревка, наматываясь на ось, заставит перемещаться тяжелое тело Н. А так как точка опоры, вокруг которой происходит движение,—это центр В и движущее тело удалено от него на расстояние BF, а оказывающее сопротивление — на расстояние BD, то {20} у нас образуется рычаг FBD, в результате чего сила получает момент, равный сопротивлению, всякий раз, когда между силой и сопротивлением устанавливается то же отношение, что и между линиями DB и BF, т. е. между радиусом оси и радиусом окружности, по которой движется
 |
| {21} |
Нами были уже объяснены орудия, сущность которых можно свести к весам, а наряду с ними и другие, мало чем от них отличающиеся. Теперь же для понимания того, что следует сказать о природе полиспаста (taglia), оказывается необходимым несколько задуматься над другим способом употребления ваги, что во многом поможет как исследовать полиспаст, так и понять другие механические действия.
Объясненный ранее способ употребления рычага заключается в следующем: к одному концу прилагают груз, а к другому силу, опору же помещают где-нибудь между концами рычага. Но мы можем пользоваться рычагом еще и другим способом,
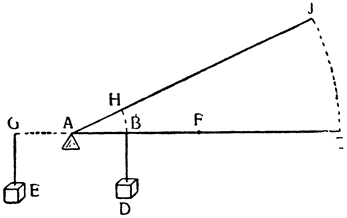 |
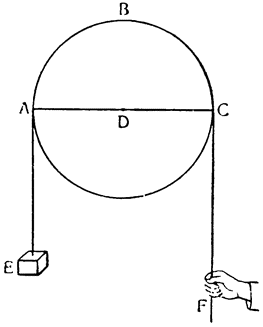
Объяснив эти принципы, перейдем к рассмотрению полиспаста, действие и устройство которого будут объяснены вместе со способом его употребления. Сначала представим себе блок ABC, сделанный из металла или твердого дерева, вращающийся вокруг оси, которая проходит через его центр D, и веревку EABCF, обмотанную вокруг этого блока, к одному концу которой подвешен груз, а к другому приложена сила. Утверждаю, что груз будет удерживаться равной ему силой, а блок
 |
Но если пользоваться подобной машиной другим способом, как это мы собираемся сейчас объяснить, то мы сможем поднять груз с уменьшением силы.
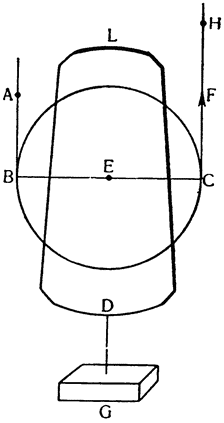 |
На основании доказанного ранее, сила будет так же относиться к весу, как расстояние ЕВ относится к расстоянию ВС, т. е. она будет равна половине груза, и, хотя при подъеме силы в направлении Н блок вращается, никогда не меняется соотношение между опорой В и центром Е, от которых зависит груз, и конечной точкой, на которую действует сила: ведь при вращении точки В и C, не изменяя своих свойств, меняются местами, замещая все время одна другую, от чего рычаг ВС и оказывается рычагом постоянного действия. И здесь, как это делалось, когда речь шла о других орудиях, {24} и как в дальнейшем всегда будет делаться, нельзя не рассмотреть, каким образом путь, совершаемый силой, оказывается двойным перемещением груза. А именно, когда груз переместится так, что линия ВС попадет своими точками В и С на точки А и F, две равные веревки АВ и FC
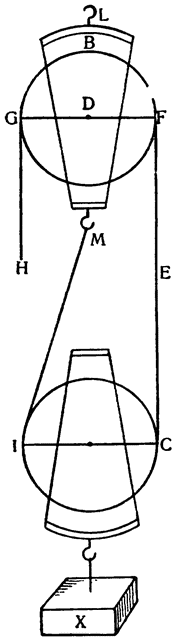 |
Учтем теперь, что сила, приложенная в F, для того чтобы поднять груз, должна перемещаться снизу вверх, что для неодушевленного движущего тела, как более тяжелого, оказывается вообще невозможным, а для одушевленного, если не невозможно, то, во всяком случае, затруднительнее, чем действовать силой сверху вниз. Во избежание этого неудобства найдено, однако, средство, а именно: добавляют второй верхний блок, где, как это видно по приложенному рисунку, веревка CEGF проходит вокруг верхнего блока CF, удерживаемого крюком L, таким образом, что, переводя веревку в Н и перенося, следовательно, силу в Е, окажется возможным, потянув вниз, переместить груз Н. Но сила не должна быть меньше той силы, которая была в Е, поскольку моменты сил Е и H, зависящие от равных расстояний FD и DC от опоры верхнего блока, остаются все время равными, и верхний блок, как это уже было доказано, не дает никакого уменьшения труда. Кроме того, так как после добавления верхнего блока потребовалось ввести крючок В, чтобы удерживать блок, то оказалось удобным удалить другой крючок А, а конец веревки, который к нему прикреплялся, перевести на крючок или кольцо М, приделанное к нижней части обоймы верхнего блока, что, как мы видим, и было сделано. И вот, наконец, перед нами машина, составленная из верхних и нижних блоков, которую греки называли trochlea, а мы по-тоскански называем taglia.
Мы объяснили, как можно при помощи полиспаста удваивать силу. Теперь остается только, как можно более кратко, показать способ увеличивать ее в любое число раз, но сначала поговорим об увеличении в четное число, а потом уже в нечетное число раз. Чтобы показать, как можно увеличить силу четырехкратно, предпошлем последующему, как лемму, такое рассуждение.
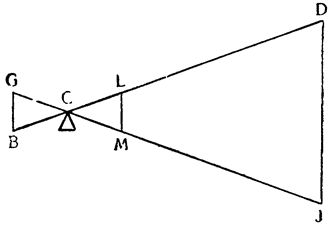
Примем АВ и CD за два рычага с опорами на концах А и С и с подвешенным посередине, к точкам Е и F, грузом G, который удерживается {25} силами равных моментов, приложенными в В и D. Утверждаю, что момент каждой из них уравнивает момент четвертой части груза G. Если предположить, что груз удерживается обеими силами В и D равномерно, то очевидно, что силе D противостоит только половина
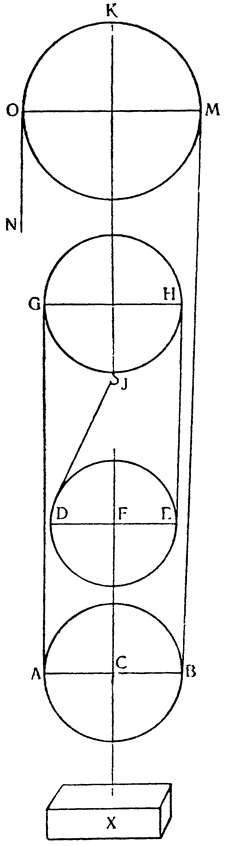
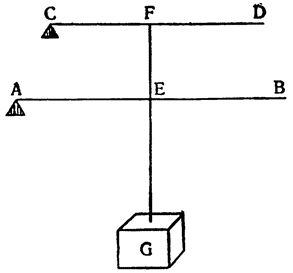
груза G: но если сила D удерживает с помощью рычага DC половину груза C, подвешенного в точке F, то, как это уже было доказано, сама сила D так же относится к удерживаемому ею грузу, как расстояние FC к расстоянию CD, а это отношение равно отношению одного к двум. Отсюда: момент D вдвое меньше момента половины груза, удерживаемого им; из этого вытекает, что он является четвертой частью момента всего груза. Таким же образом то же самое доказывается относительно момента В. И вполне обосновано то, что если груз G удерживается равномерно четырьмя точками A, B, C и D, то каждая из них воспринимает только четвертую часть труда.
Теперь посмотрим, как применить это рассуждение к полиспасту. Представим себе, что груз X подвешен к двум нижним блокам АВ и DE; чтобы удержать всю машину в точке К, обмотаем веревку и вокруг них и вокруг верхнего блока Н по линии IDEHGAB. Утверждаю, что приложив силу в М, можно будет удержать груз X, если сила окажется равна четвертой части груза. Теперь, если мы представим себе два диаметра DE и АВ и груз, подвешенный к средним точкам F и С, то {26} получим два рычага, подобные тем, что были уже объяснены, с опорами, соответствующими точкам D и А, поэтому сила, приложенная в точке В, или, если угодно, в М, сможет удержать груз X, будучи четвертой частью последнего. А если прибавим еще один верхний блок, то, переводя веревку в MON и перенося силу М в N, сможем удерживать тот груз силою тяжести, направленной вниз, так как верхний блок, что было уже доказано, не увеличивает и не уменьшает силу. Заметим себе также, что, для того чтобы поднять груз, силе надо пройти четыре веревки ВМ, EH, DJ и AG; итак: пока движущее тело будет проходить длину четырех веревок, груз при этом переместится на длину только одной из них. Все это говорится в подтверждение того, что уже много раз говорилось, а именно: труд по перемещению уменьшается в том же отношении, в котором увеличивается длина пути.
Но если мы захотим увеличить силу в шестикратной пропорции, окажется необходимо к нижнему полиспасту добавить еще один блок. Чтобы в этом лучше разобраться, начнем со следующего рассуждения. Предположим, что АВ, CD и EF — три рычага, к срединам которых, к точкам Н и J, подвешен общий груз H, а к конечным точкам В, D и F приложены три равные силы (potenze), которые удерживают груз К; таким образом, каждая из них будет удерживать третью часть груза К. Поэтому
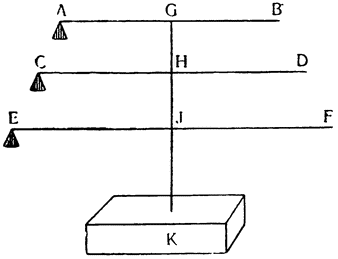 |
Следовательно, момент силы В равен половине третьей части груза К, т. е. одной шестой его. То же самое докажем для других сил D и F. Теперь легко понять, каким образом, поместив в нижнем полиспасте три блока, а в верхнем два или три других, можем увеличить силу шестикратно. Если же хотят увеличить ее в какое-либо четное число раз, то увеличивают количество блоков нижнего полиспаста на половину того числа, пропорционально которому должна расти сила, и привязывают к полиспасту веревку, один конец которой прикрепляют к верхнему полиспасту, а к другому прикладывают силу, как это понятно из приложенного рисунка.
Переходя теперь к объяснению способа увеличения силы в нечетное число раз, начнем с трехкратного увеличения, и сперва изложим следующие соображения, на которых основано понимание всего дальнейшего. Пусть АВ — это рычаг с опорой в точке A, к середине его в точке С {27} подвешен груз D, удерживаемый двумя равными силами, одна из которых приложена в точке С, а другая к концу В; утверждаю, что момент каждой из этих сил равен третьей части груза D.
 |
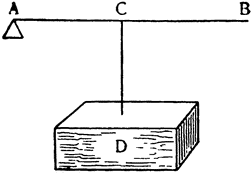 |
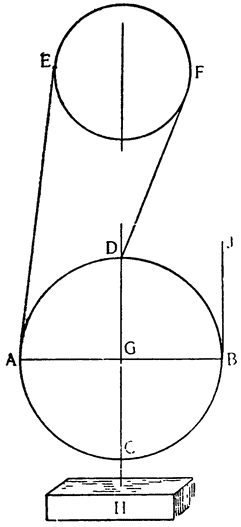
Доказав это, перейдем к полиспасту и, описав нижний блок АСВ, вращающийся вокруг центра G, с подвешенным к нему грузом H, отметим второй, верхний блок. Обернем вокруг обоих веревку DFEACBJ, закрепив один конец ее D за нижний полиспаст, а к другому концу J, приложив силу, которая, я утверждаю это, удерживая и перемещая груз H, будет ощущать только третью часть его тяжести. И вот, рассматривая устройство такой машины, увидим, что диаметр АВ заменяет рычаг, к одному концу которого приложена сила J, а другой конец А служит опорой, посредине же находится тяжелое тело H, и здесь же приложена другая сила D; таким образом, сам груз закреплен тремя веревками JB, FD и ЕА, которые {28} удерживают его равным трудом (con eguale fatica). Теперь из всего того, что было рассмотрено, вытекает: поскольку две силы — одна, приложенная к середине рычага АВ, а другая — к концу его В, оказались равны,
 |
Мне думается, что из всех орудий, созданных для равных целей человеческой изобретательностью, первое место по замыслу и по полезности должно принадлежать винту; он искусно приспособлен не только для того, чтобы перемещать, но и для того, чтобы удерживать и с огромной силой сжимать; к тому же винт устроен так, что, занимая ничтожнейшее место, он совершает действия, возможные для других орудий только в том случае, если они превращены в большие машины. Итак, являясь великолепнейшим и полезнейшим изобретением, винт заслуживает того, чтобы мы потрудились над наиболее ясным объяснением его происхождения и природы; а для этого начнем с рассуждения, которое хотя и покажется, на первый взгляд, несколько далеким от рассматриваемого орудия, тем не менее является его основанием.
Нет ни малейшего сомнения, что основное естественное свойство движения тяжелых тел состоит в том, что любое тяжелое тело, будучи свободным, стремится двигаться по направлению к центру не только по перпендикулярной линии (к горизонту), но, если иначе невозможно, то и по любой другой, которая, имея небольшой наклон к центру, идет постепенно опускаясь. Так, например, мы видим, что вода, находящаяся на какой-либо возвышенности, не только падает по перпендикуляру вниз, но и растекается по поверхности земли вдоль линий, имеющих хотя бы самый незначительный наклон; как это и наблюдается стечением рек, воды которых, поскольку ложа их несколько наклонны, свободно стекают вниз. То же самое явление, как оно наблюдается у жидких тел, также проявлялось бы и у твердых, если бы только их формы и другие случайные {29} и внешние помехи не препятствовали бы этому. Так что имей мы очень чистую и отполированную поверхность, такую, скажем, как поверхность зеркала или абсолютно круглого и гладкого шара из мрамора, стекла или из какого-либо другого подобного им, пригодного для полирования материала, то твердое тело, помещенное на эту поверхность, если только у нее есть небольшой, даже минимальный уклон, пришло бы в движение и остановилось бы только у такой поверхности, которая оказалась бы точнейшим образом выравненной и равноотстоящей от плоскости горизонта. Такой поверхностью могла бы быть, например, поверхность замерзшего озера или пруда, на котором сферическое тело оставалось бы неподвижным, но со склонностью быть приведенным в движение любой малейшей силой. Итак, мы поняли, что имей эта плоскость (piano) уклон, хотя бы даже на волос, шар самопроизвольно устремился бы в сторону уклона, а с другой стороны, наоборот, обладай он сопротивлением, его нельзя было бы сдвинуть с места в сторону отлогой или наклонной части, не применяя усилия; отсюда с необходимостью следует, что на тщательно выравненной поверхности этот шар будет оставаться как бы безразличным и как бы в сомнении между покоем и движением, но любой малейшей силы может оказаться достаточно, чтобы привести его в движение, и, наоборот, малейшее сопротивление, даже сопротивление воздуха, сможет удержать его в неподвижном состоянии.
Теперь, как заключение, вытекает следующая, не подлежащая сомнению, аксиома: тяжелые тела, если удалить все внешние и случайные помехи, могут быть перемещаемы в плоскости горизонта любой самой незначительной силой15. Но когда то же самое тяжелое тело нужно втолкнуть
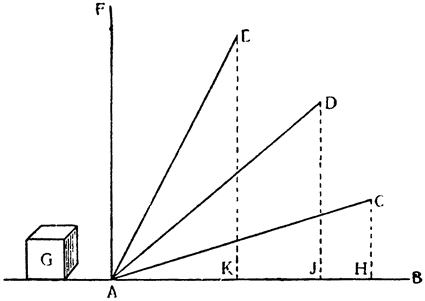 |
Итак, опустив перпендикуляры СН, DJ и ЕК из точек С, D и Е на горизонтальную линию АВ, докажем, что тот же самый груз перемещается по наклонной плоскости АС, движимый меньшей силой, чем по перпендикуляру AF (где он оказывается поднятым силой, равной ему самому), и сила эта меньше в том соотношении, в каком сама линия АС меньше перпендикуляра AFJ; а на плоскости AD сила так же относится к грузу, как перпендикуляр JD к DA, и, наконец, на плоскости АЕ сила и груз сохраняют между собой то же отношение, которое имеется между линиями ЕК и АЕ.
Рассуждать таким образом пытался еще Папп Александрийский в 8-й книге своих «Математических собраний»; но, по моему мнению, он не достиг цели, а запутался в им же выдвинутом положении, когда допустил, что груз должен перемещаться в горизонтальной плоскости при помощи определенной силы16, а это неверно, поскольку не требуется ощутимой силы (если отбросить случайные помехи, которые теоретически не принимаются в расчет) для перемещения данного груза в горизонтальном направлении; так что напрасно было затем искать, какой силой груз перемещается по наклонной плоскости. Поэтому вернее будет искать, какой должна быть сила, которая перемещает груз по наклонной плоскости, если дана сила, которая перемещает груз по перпендикуляру вверх и которая равна его тяжести; именно это мы и попытаемся сделать, но наш подход отличен от подхода Паппа.
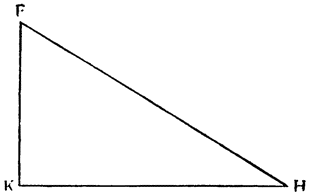
Итак, допустим, что у нас имеется круг AJC, в нем диаметр ABC и центр В, а на концах А и С два груза с одинаковыми моментами. Поскольку линия АС является как бы рычагом или весами, вращающимися вокруг центра В, груз С будет удерживаться грузом А. Но если мы представим себе, что плечо весов ВС наклонено вниз по линии ВР таким образом, что обе линии АВ и BF устойчиво соединяются в точке В, то момент груза С не будет равен моменту груза А, так как уменьшилось расстояние точки F от линии направления, которая проходит от опоры В, вдоль ВJ, к центру Земли. Но если мы опустим из точки F перпендикуляр {31} на ВС, а таковым перпендикуляром является FK, то момент груза в точке F будет таким, каким он был бы, если бы груз был подвешен по линии KB, и насколько уменьшится расстояние KB по сравнению с расстоянием ВА, настолько же уменьшится момент груза в F по сравнению с моментом груза в А. Таким же образом, если груз наклонить еще больше, по линии BL, его момент начнет уменьшаться и станет таким, словно груз подвешен на расстоянии ВМ по линии ML; груз же в точке L можно удерживать грузом, помещенным в А, который настолько меньше его, насколько расстояние ВА больше, чем расстояние ВМ. Итак, видим, как у груза, находящегося на конце наклоненной вниз по окружности CFLJ линии ВС, момент и импето падать постепенно уменьшаются, будучи все больше и больше удерживаемы линиями BF и BL. Но, рассмотрев это тяжелое тело, которое, опускаясь то больше, то меньше, поддерживается радиусами BF и BL и принуждается к перемещению по окружности CFLJ, увидим, что это то же, что представить себе поверхность, также выгнутую, как окружность CFLJ, и подложенную под то же самое движущееся тело таким образом, чтобы, опираясь на нее, оно (тело) было бы вынуждено спускаться по ней. Словом, если движущееся тело должно тем или иным способом совершать тот же путь, то совершенно неважно, будет ли оно подвешено в центре В и удерживаемо радиусом круга, или же эта опора будет удалена, и оно будет опираться и перемещаться по окружности CFLJ. Теперь можем, не сомневаясь, утверждать, что, когда тяжелое тело опускается вниз из точки С по окружности CFLJ, то в начальной точке С его момент опускаться является полным и цельным, так как оно нисколько не удерживается окружностью и не имеет никакого стремления к движению, отличному от того, которое оно свободно совершало бы по перпендикуляру и касательной DCE. Но если движущееся тело будет помещено в точку F, то из-за кругового пути, по которому оно движется, его тяжесть окажется отчасти удержанной, а его момент опускаться вниз уменьшится в том же отношении, в котором линия ВС превосходит линию ВК. Но когда движущееся тело находится в начальной точке своего движения, в точке F17, то оно как бы {32} находится на плоскости, наклоненной по касательной линии GFH, так как наклон окружности в точке F отличается от наклона касательной FG разве только неощутимым углом соприкасания. Таким же образом найдем, что в точке L момент движущегося тела во столько раз уменьшится, во сколько раз линия ВМ уменьшится по сравнению с линией
 |
 |
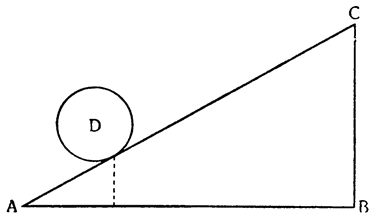
Вернувшись теперь к нашему первому заданию — к исследованию природы винта, рассмотрим треугольник АСВ, в котором линия АВ горизонтальная, ВС — перпендикуляр к ней, а АС — наклонная плоскость, по которой движущееся тело тащат силой настолько меньшей, чем оно само, насколько линия ВС короче, чем линия СА. Но поднять тот же самый груз на ту же самую плоскость
 |
 |
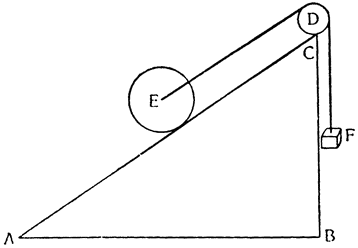
Насколько понятно все то, что мы до сих пор объясняли относительно природы этого орудия, настолько же, я совершенно не сомневаюсь в этом, будут понятны и все другие обстоятельства: как, например, почему вместо того, чтобы заставить груз подниматься на винте, к последнему для удобства приспособили гайку с выдолбленной спиралью, входя в которую болт, т. е. червяк винта, будучи повернутым вокруг оси, перемещает и поднимает гайку вместе с прикрепленным к ней грузом. Наконец, не следует обходить молчанием и то соображение, которое мы предпослали с самого начала как необходимое для всех механических орудий: т. е. насколько посредством их выигрывают в силе, настолько же проигрывают во времени и в быстроте. Возможно, что кто-нибудь решит на основании настоящего рассуждения, что это положение не верно и не очевидно, так как может показаться, что здесь имеет место увеличение силы, а двигатель совершает тот же путь, который проделало движущееся тело. Поэтому давайте примем в треугольнике ABC линию АВ за плоскость горизонта, а линию АС за наклонную плоскость, высота которой измеряется перпендикуляром СВ; находящееся в движении тело помещено на плоскость АС и к нему привязана веревка EDF и к точке F приложена сила или груз, который так относится к тяжести
 |
Мне думается, что именно здесь не следует обходить молчанием изобретение Архимеда, применившего винт для подъема воды, что не только великолепно, но просто чудесно, поскольку мы увидим, что вода поднимается в винте, беспрерывно опускаясь. Но прежде чем переходить к другому,
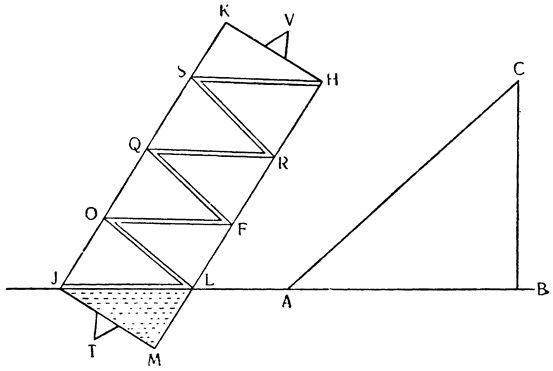 |
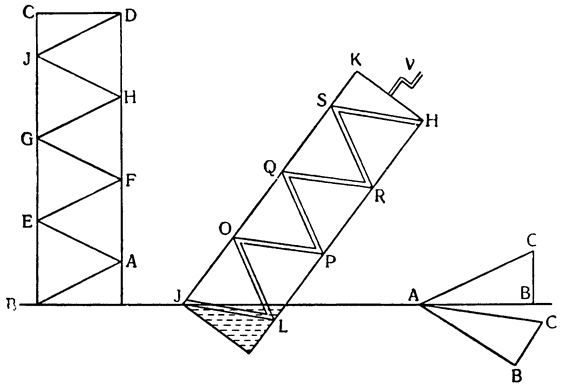
третьей частью прямого, то подъем канала АС оказывается сведенным на нет в том случае, когда часть С опускают на третью часть прямого угла.
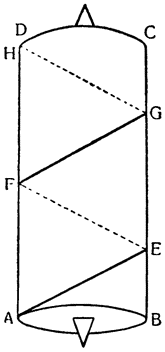
Теперь, когда все это понятно, обернем треугольник вокруг колонны и сделаем винт BAEFGHJD, который, если его поставить вертикально с концом В, опущенным в воду, и повернуть вокруг оси, не будет поднимать воду, потому что канал, идущий вокруг колонны, приподнят, как это видно по части ВА. Но если колонна стоит вертикально, подъем вдоль винта, который обернут вокруг колонны, не будет из-за этого больше одной трети прямого угла, поскольку он вызывается подъемом канала АС. Если же колонну наклонить на одну третью этого прямого угла и еще немного (см. JKHM), то перегонка и движение (воды) будут происходить по каналу не на подъеме, а на спуске, как это видно уже в случае с каналом JL. Итак, вода из точки J в точку L перемещается, опускаясь, а при вращении винта вокруг оси различные части его, последовательно замещая одна другую, будут находиться по отношению к воде все время в таком же положении, в каком находится участок JL; поэтому вода начнет постепенно {37} опускаться, но в конце концов окажется, что она поднялась из точки J в точку Н. Насколько это великолепно, предоставлю решать тем, кто это до конца поймет. А из сказанного мы видим, что для того, чтобы при помощи винта поднимать воду, необходимо наклонять его немного больше, чем на величину угла треугольника, которым описывается сам винт.
Исследовать, в чем причина силы удара, оказывается крайне необходимо по многим поводам. А прежде всего потому, что при ударе проявляется гораздо больше удивительного, чем это заметно в каком-либо другом механическом орудии. Ведь ударяя по гвоздю, чтобы загнать его в крепчайшее дерево, или по колу, который должен войти в достаточно твердую землю, видим, как силой только удара и первый и второй продвигаются вперед, а без удара, если просто поместить на них молот, они не будут перемещаться даже в том случае, если сверху положить еще груз во много раз более тяжелый, чем сам молот: явление поистине чудесное, и оно еще более заслуживает размышлений потому, что, по моему мнению, из всех тех, кто до сих пор философствовал по этому поводу, никто не сказал ничего, что достигло бы цели, а это мы и можем принять за бесспорнейший довод и доказательство сложности и трудности таких умозрений. Что до Аристотеля и других, которым хотелось причину этого чудесного явления свести к длине ручки или рукоятки молота, то, как мне кажется, слабость их умозрений можно открыть без долгих слов, если исходить из действия инструментов, которые, не имея ручки, наносят удар, падая сверху вниз или же будучи быстро загоняемы поперечным толчком. Поэтому, желая найти истину касательно этого явления, следует прибегнуть к другому принципу. И, хотя само явление по своей природе еще настолько темно и трудно для объяснения, попытаемся сделать его очевидным и понятным, доказав, наконец, что первопричина и начало его происходят из того же источника, из которого проистекают причины других механических действий.
Мы достигнем этого, если выявим здесь то, что было обнаружено и при других механических действиях, т. е. что сила, сопротивление и пространство, па котором происходит движение, взаимно зависят друг от друга по закону, что сопротивление, равное силе, будет этой силой перемещено на такое пространство и с такой быстротой, которые равны пространству и быстроте, с которыми перемещается сама сила. Сила же, наполовину меньшая своего сопротивления, сможет его переместить, но будет перемещать его с удвоенной быстротой или же по пути, вдвое большем, чем путь, пройденный сопротивлением. В результате, как это мы {38} видели и во всех других орудиях, оказывается возможным перемещать сопротивление любой величины любой заданной малой силой, лишь бы пространство, по которому эта сила перемещается, так бы относилось к пространству, по которому перемещается сопротивление, как большое сопротивление относится к малой силе, а так и должно быть по необходимому устройству природы. И вот, рассуждая и аргументируя от обратного, подумаем, в чем же будет заключаться чудо, если та же сила, которая перемещает на большой промежуток малое сопротивление, протолкнет на сотую часть этого промежутка сопротивление в сто раз большее? Ни в чем, конечно; наоборот, если бы было иначе, это было бы не только абсурдно, но и невозможно.
Итак, рассмотрим, каково сопротивление перемещению у молота в точке, откуда он ударяет, и как далеко он был бы отброшен полученной силой, если бы не ударил, а кроме этого, чему равно сопротивление к перемещению у того (тела), по которому молот ударяет, и как далеко оно перемещается при одном ударе. А когда мы найдем, что это большое сопротивление окажется перемещенным при одном ударе настолько меньше, чем переместился бы сам молот, движимый импето, насколько это большое сопротивление больше сопротивления молота, то мы перестанем удивляться по поводу действия, которое ни в чем не выходит за пределы естественного устройства и того, что говорилось. Добавим еще для большего понимания частный пример. Пусть молот, имеющий четыре доли сопротивления, окажется перемещенным такой силой, что если освободиться от нее в пределах, где происходит удар, то он (молот) отлетит, в случае отсутствия препятствий, на расстояние десяти шагов. А если в этих пределах положить бревно, сопротивление движению у которого равна четырем тысячам, т. е. в тысячу раз больше сопротивления молота, [но оно (бревно) не несдвигаемо, так как его сопротивление превосходит сопротивление молота не беспредельно], то при ударе по бревну, оно окажется перемещенным, но только на тысячную часть десяти шагов, на которые бы переместился сам молот. Итак, ведя рассуждение в порядке, обратном тому, как мы рассуждали по поводу других механических действий, мы сможем исследовать причину силы удара.
Знаю, что для некоторых здесь родятся трудности и помехи, которые, однако, устранимы малым усилием, и которые мы охотно отнесем к тем механическим проблемам, что добавятся к концу этого рассуждения20.
| {39} |
|
Светлейшему дону Козимо II РАССУЖДЕНИЕ ГАЛИЛЕО ГАЛИЛЕЯ, философа и математика |
| {40} |
ПЕРЕВОД
А. Н. ДОЛГОВОЙ и С. Н. ДОЛГОВА
| {41} |
Т |
Что касается астрономии, то не столько последние открытия, касающиеся состоящего из трех тел Сатурна2 и изменений фигуры Венеры, подобных тем, которые наблюдаются с Луною, вместе с последствиями, отсюда вытекающими, задержали меня, сколько определение времени обращения каждой из четырех планет Медичи вокруг Юпитера, чем я занимался в апреле прошлого, 1611 года, находясь в Риме. Здесь я окончательно убедился, что планета, ближайшая к Юпитеру, проходит в час 8 градусов 29 минут своей орбиты, совершая полное обращение в один день и 181/2 часов, приблизительно; вторая проходит в час около 4 градусов 13 минут своей орбиты и совершает полное обращение в 3 дня и 131/2 часов, приблизительно; третья проходит в час около 2 градусов 6 минут своей орбиты и полный круг — в 7 дней и 4 часа, приблизительно; наконец, четвертая и самая {42} отдаленная проходит в каждый час 0 градусов 541/2 минуты, приблизительно, и делает полный круг в 16 дней и 18 часов, приблизительно.
Так как большая скорость обращения планет требует строжайшей точности для вычисления положения их в прошлом и будущем, особенно, если дело идет о многих месяцах и годах, то мне пришлось посредством других более тщательных наблюдений, относящихся к большим промежуткам времени, исправить таблицы движений и привести их к кратчайшим периодам. Моих первоначальных наблюдений было недостаточно для получения надлежащей точности как вследствие их кратковременности, так и потому, что я тогда еще не нашел способа измерять посредством инструмента расстояние между этими планетами и отмечал эти промежутки простым отношением к диаметру тела Юпитера, как говорится, на глаз. Такой способ хотя и не допускает ошибки, превышающей одну минуту, недостаточно точен для вычислений при значительной величине сфер этих звезд. Но теперь, когда я нашел способ производить измерения без ошибки и на единую секунду, я буду продолжать свои наблюдения до кончания видимости Юпитера. Эти наблюдения должны будут иметь большое значение для наших познаний о движении этих планет, размерах их орбит и некоторых вытекающих отсюда следствиях. Попутно с этим я обратил внимание на темные пятна, появляющиеся на солнечном диске; они, меняя свое положение на нем, указывают или на то, что Солнце обращается вокруг своей оси, или что другие звезды, подобные Венере и Меркурию, обращаются вокруг него, видимые по своим малым, менее Меркурия, размерам, только в том положении, когда они становятся между Солнцем и нашим глазом. Разрешение вопроса, какое из этих предположений является истинным, не может не иметь значения, и им не следует пренебрегать.
Продолжительные наблюдения убедили меня в том, что эти пятна суть вещество, связанное с поверхностью солнечного тела; они то появляются на ней в большом количестве, то расплываются, одни — быстрее, другие — медленнее, перемещаясь вместе с обращением Солнца вокруг своей оси, что совершается приблизительно в один лунный месяц,— явление, само по себе весьма значительное и еще более важное по своим последствиям3.
Что касается предлагаемого трактата, поводом для которого послужил происходивший несколько времени назад диспут с некоторыми учеными нашего города, и последовавшие затем, как известно вашей светлости, неоднократные споры, то написать его побудили меня многие причины. Самой главной было указание вашей светлости на то, что письменное изложение представляет единственный способ научить различать истинное от ложного, действительные причины от кажущихся; способ несравненно лучший, нежели словесный спор, при котором тот или другой, а чаще оба диспутанта, чрезмерно увлекаясь и от увлечения возвышая голос, не слушают друг друга, упорно не желая ни в чем уступить один другому и переходят к {43} новым вопросам, отдаляясь от первоначальных положений и ставя в тупик как себя, так и слушателей.
Притом я полагал, что мне надлежит осведомить вашу светлость о том, как обсуждался данный вопрос во всей полноте, и как до того он трактовался другими, а также — почему доктрина, которой я следую в своем рассуждении, отличается от учения Аристотеля и его принципов; я полагаю, что лучше пером, нежели устно высказать свое мнение, противное авторитету этого великого мужа, авторитету, который многих заставляет относиться с недоверием ко всему, что выходит не из школы перипатетиков; поэтому я и решился написать настоящее рассуждение, в котором надеюсь показать, что я часто расхожусь с Аристотелем во взглядах и не по прихоти и не потому, что я не читал или не понял его, но в силу убедительных доказательств. Сам Аристотель научил меня удовлетворять свой разум только тем, в чем убеждают меня рассуждения, а не только авторитет учителя; совершенно правильно изречение Алкиноя4, что философствование хочет быть свободным. По моему мнению, правильное разрешение вопроса, зависит ли от формы предметов то, что одни из них погружаются в воду а другие нет, было бы небесполезно и для постройки мостов или иных сооружений над водами.
Итак, я говорю: прошлым летом на собеседовании с учеными было высказано положение, что сжатие есть свойство охлаждения, и, как пример этому, приводится лед. Тогда я сказал, что лед можно считать скорее разреженной, чем сгущенной водой, так как сжатие или конденсация подразумевают уменьшение объема и увеличение тяжести, а разрежение вызывает большую легкость и увеличение объема, вода же именно при замерзании увеличивается в объеме, и образовавшийся лед легче воды и держится на ее поверхности. Сказанное согласуется с тем, что доказал Архимед в своей книге I о телах, находящихся в воде, т. е. что при вычитании веса объема среды из общего веса тела, чем более увеличивается объем тела, тем более увеличивается и вычитаемый вес среды, взятой в том же объеме, и, наоборот, последний становится тем меньше, чем более тело при конденсации сжимается, принимая меньший объем.
Мне возражали, что это происходит не от большей легкости, но от широкой и плоской формы образующегося льда, который не может преодолеть сопротивления воды и потому плавает. Я отвечал, что всякий кусок льда какой угодно формы остается над водой — видимое доказательство того, что плоскость и ширина не играют никакой роли в его нахождении на поверхности; я прибавил, что еще более яркое доказательство этому — немедленное всплывание на поверхность льда, какой бы плоской формы кусок его мы ни опустили на дно; это было бы невозможно, если бы лед действительно был тяжелее воды, и его нахождение на поверхности обусловливалось формою, неспособной преодолеть сопротивление воды. Из сего {44} заключаю, что нахождение тела на поверхности или на дне никоим образом не зависит от формы, но от большей или меньшей тяжести относительно воды, почему все тела тяжелее воды, безразличия формы, опускаются на дно, а более легкие, также всякой формы, непременно остаются на поверхности. Полагаю, что те, кто думают иначе, вывели свое заключение из того, что различие в форме весьма влияет на быстроту или медленность движения, так что тела формы широкой и плоской погружаются значительно медленнее, чем тела того же вещества, но формы более сжатой; отсюда кто-нибудь может заключить, что расширение формы может быть доведено до такой степени, что не только замедлит, но и совсем прекратит движение; это я признаю ложным. Споры относительно этого положения велись в продолжение многих дней, причем были произведены различные опыты, некоторые из которых ваша светлость видели.
В этом трактате будет воспроизведено все, что было выдвинуто против моих заключений, а также все, что мне пришло на мысль в защиту и подтверждение их. Если этого будет достаточно, чтобы рассеять указанное утверждение, по моему мнению — ложное, то я сочту, что недаром потратил труд и время; если же мне это не удастся, то я все-таки извлеку из этого пользу для самого себя, познавая истину из опровержения моих ошибок и приведения верных доказательств теми, кто думает иначе. Чтобы выполнить это с большей убедительностью и ясностью, мне кажется необходимым прежде всего установить истинную, внутреннюю и общую причину всплывания некоторых тел из воды и нахождения их на поверхности ее, а также погружения других тел на дно, тем более, что меня совсем не удовлетворяет написанное по этому поводу Аристотелем5.
Итак, я говорю, что причиной погружения некоторых тел на дно является превышение их тяжести над тяжестью воды; обратно, большая тяжесть воды по сравнению с тяжестью других тел является той причиной, которая заставляет их не погружаться, а, наоборот, подниматься со дна и всплывать на поверхность. Это было искусно доказано Архимедом в книгах о плавающих телах и было неверно понято весьма серьезным автором, что я и попытаюсь доказать в защиту мнения Архимеда6.
Выводы последнего я постараюсь подтвердить иным методом и иными средствами, приведя причины указанных явлений к внутренним и непосредственным принципам, причем выяснится и причина того изумительного и почти невероятного явления, когда ничтожное количество воды своим легким весом поднимает и поддерживает твердое тело, которое в сто и тысячу раз тяжелее этого количества воды. А так как это требует последовательного доказательства, то я прежде всего определю некоторые термины и установлю некоторые положения, как истинные и известные, которыми я воспользуюсь для своих целей7.
| {45} |
 |
титульный лист трактата «о телах, пребывающих в воде» |
| {46} |
Я называю равными по удельному весу те вещества, которые имеют равный вес при равном объеме; так, например, если два шарика из воска и из какого-нибудь дерева, будучи равными по объему, имеют равный вес, то мы говорим, что такое дерево и воск одинаковы по удельному весу8.
Но я буду называть равными по абсолютному весу такие два твердых тела, которые весят одинаково, хотя и разнятся по объему; так, например, если кусок свинца и кусок дерева весят каждый десять фунтов, то мы говорим, что они имеют одинаковый абсолютный вес, хотя объем дерева гораздо больше объема свинца, и дерево, следовательно, меньшего удельного веса.
Более тяжелым по удельному весу я называю такое вещество, которое при равном объеме с другим телом весит более последнего; таким образом, я говорю, что свинец по удельному весу тяжелее, чем олово, так как, если взять их в равном объеме, то свинец будет весить больше. Но более тяжелым абсолютно я называю такое тело, которое по сравнению с другим весит более последнего, независимо от соотношения их объемов; так, большое бревно весит абсолютно больше малого куска свинца хотя по удельному весу свинец тяжелее дерева. Аналогично будем говорить о телах, менее тяжелых по удельному весу и менее тяжелых абсолютно.
Определив эти термины, я позаимствую из науки механики два принципа. Первый,— что два абсолютно равных груза, двигающихся с равными скоростями, действуют с одинаковой силой или одинаковым моментом.
Под моментом в механике разумеется та сила, то качество, то действие, с которым двигатель двигает и движимое сопротивляется; эта сила зависит не только от простой тяжести, но и от скорости движения и от различного наклонения путей, по которым совершается движение, потому что тяжесть производит большее действие при опускании по более наклонному пути, чем по менее наклонному. В общем, какова бы ни была причина этого качества она сохраняет название момента; мне казалось, что это слово не является новостью в нашем языке, так как, если не ошибаюсь, часто говорят: «Это важное дело, а то имеет меньше значения», или — «Мы ценим пустые вещи и пренебрегаем имеющими значение». Эти метафоры, по моему мнению, взяты из механики9.
Так, например, два груза, равные по абсолютному весу и помещенные на двух равных плечах коромысла весов, остаются в равновесии и не опускаются, поднимая один другой; в самом деле, равенство расстояний их от центра, в котором укреплено коромысло и около которого они вращаются, заставляет эти грузы проходить при движении коромысла в данное время равные пространства, так как они движутся с одинаковой скоростью; следовательно, нет причины, почему бы один груз опустился более другого; поэтому они сохраняют равновесие, и моменты сил их остаются подобными и равными. {47}
Второй принцип заключается в том, что момент и сила тяжести возрастают вместе со скоростью движения, так что грузы абсолютно равные, но движимые с разной скоростью, обладают различными качествами, моментами и силами; при этом более мощным оказывается более быстрый груз в той мере, в какой скорость его больше скорости другого тела. Прекрасным примером этого служат весы с неравноплечим коромыслом; если на них положить абсолютно равные грузы, то последние будут давить неравно и развивать неравные усилия; груз, находящийся в большем расстоянии от центра, около которого вращается коромысло, опустится, подняв другой груз, причем движение поднимающегося груза будет медленным, а движение опускающегося — быстрым; такова сила или качество, которое скорость движения придает движущемуся телу и которое может быть восполнено соответствующим грузом, приданным медленнее движущемуся телу. Если, таким образом, одно плечо коромысла в десять раз длиннее другого, вследствие чего при вращении коромысла около центра конец его проходит в десять раз большее пространство, чем конец короткого плеча, то груз, помещенный на длинном плече, сможет поддержать и уравновесить другой груз, который в десять раз больше него по абсолютному весу; это происходит оттого, что при вращении коромысла меньший груз движется со скоростью в десять раз большей, чем скорость большего груза. При этом надо всегда понимать, что оба движения происходят при одинаковом наклоне, так что, если одно движущееся тело движется перпендикулярно к горизонту, то и другое движется по тому же направлению, если же движение одного происходит в горизонтальной плоскости, то и другое движется в той же плоскости; вообще оба движения имеют одинаковый наклон. Такое соотношение между тяжестью и скоростью существует у всех механических инструментов и принимается Аристотелем как принцип в его «Проблемах механики», почему мы можем принять за достоверное то положение, что неравные по абсолютной величине грузы могут взаимно уравновешиваться и приобретать равные моменты всякий раз, когда их вес будет обратно пропорционален скорости их движения, т. е. когда один груз будет во столько же раз легче другого, во сколько раз скорость его движения будет больше скорости другого10.
Установив это, мы можем уже начать исследовать, каковы те твердые тела, которые совсем погружаются в воду и идут ко дну, и каковы те тела, которые неизбежно всплывают, так что, будучи силой погружены в воду, возвращаются на поверхность ее и возвышаются над нею частью своего объема. Это мы сделаем, рассмотрев взаимодействие тел и воды, происходящее при погружении. Тело, увлекаемое вниз своей собственной тяжестью, вытесняет при погружении воду из тех мест, которые оно, идя вниз, последовательно занимает; вытесненная вода при этом поднимается и возвышается над своим прежним уровнем; но, будучи по природе своей телом {48} тяжелым, она противится этому подъему; и так как по мере погружения твердого тела поднимается все большее и большее количество воды, пока все тело не погрузится, то момент сопротивления воды подъему следует сравнить с моментом давящей тяжести твердого тела; если при этом момент сопротивления воды сравняется с моментом давящего твердого тела ранее его полного погружения, то, без сомнения, наступит равновесие, и тело перестанет погружаться; если же момент твердого тела будет постоянно превосходить момент сопротивления последовательно вытесняемой воды, то оно не только погрузится в воду, но под конец опустится до самого дна; если же, наконец, при погружении установится равновесие между моментами давящего твердого тела и сопротивления воды, то наступит покой, и тело сможет оставаться в воде неподвижным в любом месте.
Отсюда ясна необходимость сравнивать тяжесть воды и твердых тел; на первый взгляд может даже показаться, что такого сравнения достаточно, чтобы заключить и определить, какие тела будут всплывать и какие пойдут на дно, и заявить, что плавать будут те тела, которые по удельному весу легче воды, и пойдут на дно те, которые по удельному весу тяжелее воды; в самом деле, погружающееся тело вытесняет такой же объем воды, какой занимает его погруженная часть, так что кажется невозможным, чтобы тело, которое по удельному весу легче воды, совсем ушло в воду: оно не в состоянии поднять тяжесть большую, чем его собственная, а таковой несомненно обладает равный ему объем воды. Точно так же кажется неизбежным, что тяжелое тело падает на дно, так как оно обладает достаточной силой, чтобы вытеснить равный ему объем воды, который легче его по весу. Однако на деле происходит иначе, и хотя выводы эти верны, но основания, приведенные здесь, не без изъяна; иногда объем вытесняемой воды меньше объема погружающейся части тела, и тем меньше, чем уже наполненный ею сосуд; таким образом, может случиться, что тело совсем погрузится в воду, подняв воды одну десятую или двадцатую часть своего объема; и наоборот, ничтожное количество воды в состоянии поднять тело громадного объема, хотя бы это твердое тело было абсолютно тяжелее воды в сто или более раз, если только вещество его по удельному весу легче воды; таким образом, громадное бревно, которое весит, скажем, 1000 фунтов, может быть поднято и поддержано водой, которая не весит и 50 фунтов, и это непременно произойдет, если момент воды усилится быстротой движения.
Но так как подобные явления, излагаемые отвлеченно, нелегки для понимания, то следует подтвердить их особыми примерами. Для облегчения доказательства условимся, что сосуды, содержащие воду и предназначенные для помещения в них твердых тел, будут цилиндрическими или призматическими со стенками, перпендикулярными к плоскости горизонта, а твердые тела будут представлять собою прямые цилиндры или призмы и ничто иное. {49}
Условившись в этом, начнем доказывать истину вышеизложенного, опираясь на следующую теорему.
Объем воды, который поднимается при погружении призмы или цилиндра или опускается, вытесняя их назад, меньше объема погружающегося или вытесняемого тела, причем отношение первого объема ко второму равно отношению поверхности воды, окружающей тело, к сумме той же поверхности с площадью основания тела. Пусть ABCD — данный сосуд,
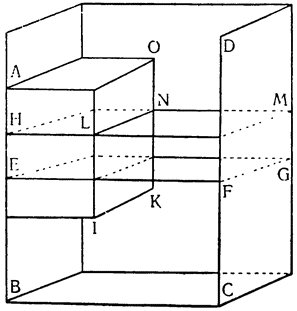 |
Отсюда явствует, что объем воды, поднимающейся при погружении твердого тела или опускающейся при извлечении его, равен не всему объему тела, которое погружается или извлекается, а только некоторой части его, которая при погружении остается под первоначальным уровнем воды, а при извлечении — над соответствующим первоначальным уровнем, что и требовалось доказать.— Перейдем теперь к другим явлениям.
Прежде всего покажем, что если в один из сосудов условленной выше формы и какой угодно величины, безразлично — широкий или узкий, поместить
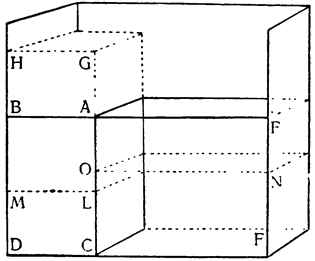 |
Пусть в сосуд помещена призма ABCD, а остальное пространство заполнено водой, достигающей уровня ЕА, и пусть при поднятии тела AD и перемещении его в положение GM вода понижается с уровня ЕА до NO. Утверждаю, что понижение уровня воды, измеренное по линии АО, так относится к поднятию призмы по линии GA, как основание тела GH к поверхности воды NO. В самом деле, объем тела GABH, выступающий над первоначальным уровнем ЕАВ, равен объему опустившейся воды ENOA; мы имеем здесь, следовательно, две равновеликих призмы ENOA и GABH. Но у равновеликих призм отношение оснований равно обратному отношению высот; поэтому высота ОА так относится к высоте AG, Как площадь основания GH к поверхности воды NO12. Таким образом, если поставить, например, колонну в обширный резервуар, полный воды, или в колодец, содержащий воды в объеме немного большем, чем объем колонны, то при подъеме и извлечении колонны из воды окружающая вода опустится, и опускание это будет так относиться к поднятию колонны, как площадь основания колонны к превышению площади основания резервуара или колодца над площадью основания колонны; если поэтому отверстие колодца будет только на одну восьмую больше основания колонны, а основание резервуара будет в двадцать пять раз больше основания колонны, то при поднятии колонны на один фут вода в колодце опустится на семь футов, а в резервуаре — только на одну двадцать четвертую часть фута.
Убедившись в этом, нетрудно будет понять и то, что призма или прямой цилиндр, состоящие из вещества, которое по удельному весу легче воды, будучи окружены со всех сторон водою, не остаются внизу, но поднимаются, хотя бы окружающей воды было очень мало, и абсолютный вес {51} ее уступал абсолютному весу тела. Пусть в сосуд CDFВ помещена призма AEFB, которая по удельному весу легче воды, и налита вода до уровня верхнего основания призмы; утверждаю, что если предоставить эту призму самой себе, то она поднимется, будучи вытеснена окружающей водой CDEA. В самом деле, вода СЕ по удельному весу тяжелее тела AF; поэтому отношение ее абсолютного веса к абсолютному весу призмы AF будет
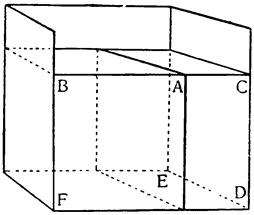 |
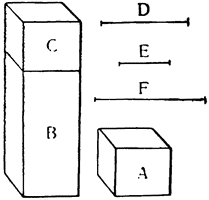
Вслед за этим покажем подробно, насколько поднимаются тела, которые легче воды, т. е. какая часть их остается под водой и какая над поверхностью воды; но прежде докажем следующую лемму: отношение абсолютных весов твердых тел равно сложному отношению их удельных весов и их объемов.
Пусть имеем два тела А и В. Утверждаю, что отношение абсолютного веса тела А к абсолютному весу тела В равно сложному отношению удельного веса
 |
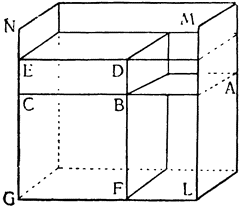 |
Перейдем теперь к доказательству того, что цилиндр и призма, которые по удельному весу легче воды, будучи помещены в сосуд любой величины, не поднимаются при наполнении его водою до тех пор, пока вода не доходит до такого уровня, что отношение высоты тела к высоте стояния воды становится равным отношению удельного веса воды к удельному весу этого тела, и что при дальнейшем прибавлении воды тело поднимается.
Возьмем сосуд MLGN любой величины, поместим в него призму DFGE, которая по удельному весу легче воды, и предположим, что отношение удельного веса воды к удельному весу призмы равно отношению высоты DF к высоте FB. Утверждаю, что при наполнении сосуда водою до высоты FВ тело DG не поднимется и будет пребывать в равновесии, но что прибавление еще малого количества воды непременно его поднимет. Нальем в сосуд воды до уровня ABC; так как удельный вес тела DG относится к удельному, весу воды, как высота BF к высоте FD, т. е. как объем BG к объему GD, а отношение объема BG к объему GD, вместе с отношением объема GD к объему AF, дает отношение объема BG к объему AF, то отношение объема BG к объему AF равно сложному отношению удельного веса тела GD к удельному весу воды и объема GD к объему AF. Но такое сложное отношение удельного веса тела GD к удельному весу воды и объема GD к объему AF выражает, по предыдущей лемме, отношение абсолютного веса тела DG к абсолютному весу объема воды AF. Следовательно, отношение объема BG к объему AF равно отношению абсолютного веса тела GD к абсолютному весу объема воды AF; но объем BG относится к объему AF, как основание призмы DE к поверхности воды АВ, или как опускание воды АВ к поднятию тела DG; следовательно, отношение опускания воды к поднятию призмы равно отношению абсолютного веса призмы к абсолютному весу воды. Поэтому момент, составляющийся из абсолютного веса воды AF и скорости ее движения при понижении уровня, с которым она стремится вытолкнуть и поднять призму DG, равен моменту, составленному из абсолютного веса призмы DG и скорости движения, которым она обладала бы, будучи поднята; этим моментом она и {53} противится поднятию. Так как эти моменты равны, то между водою и твердым телом устанавливается равновесие. Ясно, что прибавление даже небольшого количества воды к имеющейся уже AF увеличивает ее вес и момент; поэтому призма DG будет вытолкнута и поднята, и только часть ее BF останется под водою, что и требовалось доказать15.
Из доказанного следует, что тела, которые по удельному весу легче воды, погружаются в воду только до тех пор, пока вес воды, взятой в объеме погруженной части тела, не становится равным весу всего тела. В самом деле, зная, что отношение удельного веса воды к удельному весу призмы DG равно отношению высоты DF к высоте FB, или тела DG к телу GB, легко доказать, что абсолютный вес воды, взятой в объеме тела BG, равен абсолютному весу тела DG. Действительно, по предыдущей лемме отношение абсолютного веса объема воды, равного объему BG, к абсолютному весу призмы DG равно сложному отношению объема BG к объему GD и удельного веса воды к удельному весу призмы; но отношение удельного веса воды к удельному весу призмы равно отношению объема DG к объему GB; следовательно, отношение абсолютного веса воды в объеме BG к абсолютному весу тела GD равно сложному отношению объема BG к объему GD и объема DG к объему GB, т. е. единице. Следовательно, абсолютный вес воды, взятой в объеме погруженной части призмы BG, равен абсолютному весу всего тела DG16.
Таким образом, если поместить твердое тело, которое по удельному весу легче воды, в сосуд любой величины и налить кругом воды до такой высоты, чтобы объем воды, равный объему погруженной части тела, весил столько же, сколько все тело, то это тело будет поддерживаться водою, независимо от того, будет ли количество ее огромным или ничтожным. Так, если поместить призму или цилиндр М, удельный вес которого составлял бы только три четверти удельного веса воды, в большой сосуд ABCD

и налить воды на три четверти его вышины, т. е. до уровня DA, то он будет поддерживаться водой и пребывать в равновесии; то же случится, если его поместить в сосуд ENSF, который был бы до того мал, что между сосудом и телом М оставалось только узкое пространство, способное вместить объем воды, составляющий лишь сотую часть объема М: он одинаково будет поднят и удержан водою, если налить последней, как и прежде, на три четверти вышины тела. Многим это покажется на первый взгляд совершенным парадоксом, и они подумают, что доказательство подобных явлений — {54} только софистика и обман; однако в справедливости изложенного они могут убедиться опытом. Тот же, кто вспомнит, как много значит скорость движения и как точно она возмещает недостаток или отсутствие тяжести, перестанет изумляться; в самом деле, поднятие тела М лишь в малой мере понижает большой объём воды ABCD; но оно сильно и в одно мгновенье опускает малый объем воды ENSF, хотя бы тело М было поднято на самую незначительную величину. Вследствие этого момент, слагающийся из небольшого абсолютного веса воды ENSF и большой скорости опускания, сравнивается с силой и моментом, слагающимся из огромной тяжести воды ABCD и крайней медленности ее опускания; при подъеме же тела М опускание малого количества воды ES происходит во столько раз быстрее, чем опускание большого объема воды АС, во сколько раз этот последний объем больше первого; это мы докажем следующим образом.
При подъеме тела М отношение его поднятия к опусканию окружающей воды ENSF равно отношению поверхности этой воды к поверхности или основанию тела М, а отношение этого последнего к поверхности AD равно отношению опускания воды АС к поднятию тела М; соединяя эти пропорции, получаем, что при подъеме тела М опускание воды ABCD так относится к опусканию воды ENSF, как поверхность воды EF к поверхности воды AD, или как весь объем воды ENSF ко всему объему ABCD, которые имеют одинаковые высоты; отсюда ясно, что при захвате и подъеме тела М вода ENSF превосходит по скорости движения воду ABCD
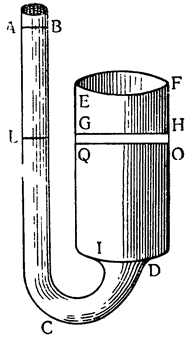 |
А для полного подтверждения и ясного объяснения этого явления рассмотрим прилагаемую фигуру, которая, если не ошибаюсь, может предохранить от о заблуждения некоторых механиков-практиков, строящих иногда свои изобретения на ложных основаниях. Здесь от широкого сосуда EIDF отходит узкая трубка ICAB; если налить в них воду до уровня LGH, то она в этом положении успокоится к удивлению того, кто не может сразу понять, почему тяжелый вес большого объема воды GD, давя вниз, не поднимает и не выталкивает малого количества воды, содержащегося в трубке CL, которое противится и препятствует этому подъему. Но мы перестанем изумляться, если представим себе, что вода GD опустилась до QO, и посмотрим, что сделалось с водою CL. Чтобы дать место воде, понизившейся с уровня GH до уровня QO, вода в трубке должна была бы подняться с уровня L до АВ, причем поднятие LB было бы во столько раз больше опускания GQ, во сколько раз ширина сосуда GD больше ширины {55} трубки LC, или, что то же самое, во сколько раз количество воды GD больше количества LC; но так как момент скорости движения одного движущегося тела возмещает момент тяжести другого, то что же удивительного в том, что быстрое поднятие малого количества воды CL сопротивляется медленному опусканию большого количества GD?
Здесь происходит, следовательно, точно то же, что в весах, где груз в 2 фунта уравновешивает груз в 200 фунтов всякий раз, когда пространство, проходимое первым грузом, в 100 раз больше пространства, проходимого вторым; а это бывает, когда одно коромысло весов в 100 раз длиннее другого. Пусть отпадет ложное мнение, что корабль держится лучше и легче в большом пространстве воды, чем в малом (как утверждает Аристотель в «Проблемах», отд. 23, предл. 11); напротив, верно и непреложно то, что корабль так же хорошо плавает в 10 бочках воды, как в океане.
Продолжая рассуждение, говорю, что из всего здесь до сих пор доказанного можно заключить, что тела, удельный вес коих более веса воды, не могут поддерживаться водою, в каком бы количестве ее ни взять. Мы видели, что момент, с которым твердое тело равного с водою удельного веса противодействует моменту некоторого давящего объема воды, может удержать тело в состоянии равновесия; тем менее, следовательно, вода может поднять тело, если оно тяжелее ее по удельному своему весу. Залитое водою до полного его погружения, такое тело останется на дне и будет сопротивляться поднятию с силою, равною излишку его абсолютного веса над абсолютным весом равного объема воды или другого вещества, равного воде по удельному весу. Какое бы большое количество воды мы ни прибавили сверх уровня, определяемого высотою погруженного тела, мы этим не сможем получить такого давления на погруженные части твердого тела, которое могло бы вытолкнуть тело из воды, так как сопротивление погружению тела получается только от тех частей воды, которые при движении тела сами приходят в движение, а таковыми являются только те, которые заключены между двумя горизонтальными параллельными плоскостями, заключающими высоту погруженного в воду тела.
Мне кажется, что предыдущим я достаточно наметил и пояснил путь к рассмотрению истинной, действительной, внутренней причины движения и покоя разных твердых тел в разных средах, в особенности в воде, показав, что на деле все зависит от перевеса тяжестей движущегося тела и среды. Что особенно важно, я разобрал пример, который для многих мог бы быть причиною сомнения и помешать признать за истину мои утверждения, а именно, каким образом, если причиною плавания и поднимания тела со дна на поверхность является перевес тяжести воды над тяжестью данного тела, количество воды, весом менее десяти фунтов, может поднять тело, весящее более ста фунтов; я доказал, что достаточно наличия разницы в удельном весе между средою и телом, отдельные же и абсолютные веса {56} могут быть какими угодно; таким образом, любое тело, будь только оно по удельному весу легче воды, может быть поднято десятью и менее фунтами воды, хотя бы оно само весило тысячу фунтов, и, наоборот, другое тело, если оно по удельному весу тяжелее воды, не может быть поднято и поддержано целым морем, хотя бы абсолютный вес его не превышал и одного фунта. Приведенные выше объяснения и примеры в достаточной мере выяснили и доказали все, относящееся к настоящему вопросу, чтобы стоило распространяться о нем в длинном трактате; если бы не необходимость рассеять указанное выше сомнение, то я остановился бы даже только на том, что доказывается Архимедом в первой книге о плавающих телах, где в общем устанавливаются те же самые положения, а именно: что тела легче воды всплывают, тяжелее воды — идут на дно, а равные по весу — остаются безразлично в любом месте, хотя и под водою17.
Но так как эта доктрина Архимеда, изложенная и рассмотренная синьором Франческо Буонамико в книге V О движении, гл. 29, им же опровергалась, а это в силу авторитета столь знаменитого и славного философа, могло бы возбудить сомнения в ее истинности, то я счел необходимым выступить на ее защиту, если только смогу, и снять с имени Архимеда те ошибки, которые ему приписывают. Буонамико отказывается от доктрины Архимеда прежде всего потому, что она не согласуется с мнением Аристотеля; при этом он прибавляет, что ему кажется удивительным, что вода должна превосходить весом землю, тогда как, наоборот, мы видим, что тяжесть в воде возрастает через прибавление земли. Далее, его совсем не удовлетворяют доводы Архимеда, так как на основании его доктрины нельзя понять причину, по которой судно или сосуд, плавающие на поверхности, опускаются на дно при наполнении водою; так как вес воды в сосуде равен весу всякой другой воды, то он должен был бы остаться на поверхности, а между тем он тонет. Он прибавляет далее, что Аристотель определенно опровергает древних, которые говорили, что легкие тела поднимаются, будучи подталкиваемы давлением более тяжелой окружающей среды: что, если бы это было так, необходимо было бы заключить, что все тела в природе тяжелы, и нет легких, так как подобное должно было бы случиться и с воздухом, и с огнем, помещенными в глубь воды. И хотя Аристотель допускает пульсацию стихий18, благодаря чему Земля принимает сферическую форму, но, по его мнению, это не может сдвинуть тяжелые тела с присущего им места, а скорее направляет их к центру, к которому (как он довольно туманно говорит далее) особенно стремится вода, если только она не встречает препятствия, и тяжестью его не вытесняется со своего места; но и в таком случае, если не прямо, вода все же по возможности направляется к центру. Вообще, если случается, что легкие тела от таких ударов идут вверх, то это, равно как и нахождение на поверхности, происходит в силу их природы. В заключение Буонамико говорит, что {57} согласен с Архимедом в его выводах, но не признает указанных им причин, которые он и пытается свести к легкому или трудному разделению сред и к действию стихий, так что когда движущееся тело превосходит мощностью среду, как, например, свинец воду, то он будет двигаться в ней, в противном же случае — нет.
Вот и все, что, насколько я мог собрать, выдвинуто синьором Буонамико против Архимеда. Он не взял на себя труда опровергнуть принципы и положения Архимеда, которые ведь ложны, если ложна самая доктрина, от которой они зависят, и удовольствовался приведением некоторых затруднений и указанием некоторых противоречий мнению и доктрине Аристотеля. Отвечая на эти возражения, скажу прежде всего: никто не может подвергать сомнению доктрину Архимеда только потому, что она отличается от аристотелевой, так как нет какого-либо основания противополагать авторитет одного философа другому. Там, где перед нами веления природы, одинаково доступные очам рассудка каждого человека, тот или другой авторитет теряет силу убедительности, уступая место силе разума.
Теперь перейду ко второму пункту, где приводится как абсурдное следствие из доктрины Архимеда, что вода должна быть тяжелее земли. На самом деле я не знаю, где Архимед сказал такую вещь, или как можно подобное утверждение извлечь из его положений; если бы мне это было доказано, то я, наверное, оставил бы его доктрину как совершенно ложную. Может быть, такой вывод был сделан Буонамико из приведенного им примера пустого сосуда, плавающего на поверхности, который идет ко дну, будучи наполнен водою. Подразумевая, что сосуд сделан из земли, он аргументирует против Архимеда следующим образом: ты говоришь, что тела, которые плавают, легче воды; этот сосуд из земли плавает, следовательно, он легче воды; значит, земля легче воды. Если таково его рассуждение, то на него нетрудно ответить, соглашаясь с тем, что сосуд легче воды, но отрицая второе следствие, т. е. что и земля легче воды. Плавающий сосуд занимает в воде место, равное не только объему земли, из которой он сделан, но равное объему земли и воздуха, наполняющего его пустоту. И если такое тело, составленное из земли и воздуха, легче соответственного объема воды, то оно будет плавать, что совершенно согласно с доктриною Архимеда; если теперь мы удалим воздух и наполним сосуд водою, так что, будучи помещен в воду, он останется только землею, т. е. будет занимать только тот объем, который имеет земля, послужившая для него материалом, то он пойдет ко дну, так как земля тяжелее воды, и это прекрасно согласуется с мнением Архимеда. Тот же результат получается при другом подобном опыте. При погружении на дно стеклянной бутылки, пока в ней есть воздух, чувствуется сильное сопротивление, так как не только стекло погружается в воду, но вместе с ним и большой объем воздуха, так что если взять такой же объем воды, какой составляется из стекла и {58} содержащегося в нем воздуха, то получается вес гораздо больший; поэтому бутылка погружается только значительным усилием; но если поместить в воду только одно стекло, т. е. бутылку, наполненную водою, то тогда стекло само опустится на дно, как превосходящее по тяжести воду.
Возвращаясь к первоначальному предложению, скажу, что земля тяжелее воды, почему тело из земли идет на дно; но можно сделать состав из земли и воздуха, который будет легче соответственного объема воды и останется на поверхности; и тот, и другой опыты отлично согласуются с доктриною Архимеда. Не встречая здесь никаких затруднений, я не хочу определенно утверждать, что синьор Буонамико из подобного вопроса вывел и приписал Архимеду нелепую доктрину, будто земля легче воды; хотя, по правде сказать, я не могу представить, какое другое обстоятельство навело его на ту мысль.
Возможно, что эта проблема (по моему убеждению, вымышленная) была вычитана синьором Буонамико у какого-либо другого автора, приписавшего такое странное свойство какой-то особой воде, и пущена им в ход для опровержения Архимеда вдвойне неправильно, так как Архимед подобной вещи не говорил, а тот, кто подобное говорил, не имел в виду обыкновенную воду.
Третьим затруднением в доктрине Архимеда является невозможность дать объяснение, почему судно или сосуд из дерева, которые в ином случае плавают, идут ко дну, будучи наполнены водою. Синьор Буонамико полагает, что деревянный сосуд, который по природе своей держится на поверхности, идет ко дну, наполненный водою, о чем он пространно рассуждает в следующей 30-й главе книги V; но я, не умаляя его странной доктрины, осмеливаюсь, защищая Архимеда, отрицать такой факт в уверенности, что дерево, которое по природе своей не тонет, не пойдет ко дну и выдолбленное и обделанное в форме какого угодно сосуда, а затем наполненное водою. Кто хочет произвести подобный опыт с другим удобным материалом, легко принимающим любую форму, может взять чистого воска и сделать из него шарик или другую плотную фигуру и затем прибавить к воску свинца в таком количестве, чтобы эти фигуры с трудом тонули, т. е. чтобы свинца на одно зернышко менее было бы уже недостаточно для их погружения. Придав тому же воску форму сосуда и наполнив его водою, найдем, что без свинца он не пойдет ко дну, а со свинцом опустится с медленностью; в общем налитая вода не внесет никакого изменения.
Я не отрицаю, что из дерева, по природе своей плавающего, могут быть сделаны суда, которые по заполнении водою тонут; но это происходит не от увеличения их веса водою, а от тяжести гвоздей или других железных частей; через соединение дерева и железа здесь получается тело, которое не легче, но тяжелее соответственного объема воды. Пусть уже синьор Буонамико перестанет отыскивать причины явления, которое не существует; {59} если он полагает, что опускание на дно наполненного водою деревянного сосуда подвергает сомнению доктрину Архимеда, по которой он не должен опускаться, и согласуется с доктриною перипатетиков, объясняющей, почему такой сосуд должен потонуть, то я выскажусь в совершенно обратном смысле: доктрина Архимеда истинна, так как вполне согласуется с опытами, сомнительна же другая, выводы из которой приспособляются к ложным заключениям. Что касается другого пункта, относящегося к тому же примеру, из которого видно, что синьор Буонамико подразумевает не только дерево в форме сосуда, но и массивные куски его, которые будучи наполнены, т. е., я полагаю, он хочет сказать — насыщены и пропитаны водою, опускаются в конце концов на дно, то это объясняется следующим образом. Пористое дерево, пока пустоты в нем наполнены воздухом или иной материей легче воды, представляет объем по удельному весу легче воды, как стеклянная бутылка, пока в ней есть воздух; но когда место легкой материи в порах и пустотах дерева займет вода, то может легко получиться тело, тяжелее воды, подобно тому как, заменив в стеклянной бутылке воздух водою, мы получаем соединение воды и стекла более тяжелое, нежели соответственный объем воды. Однако перевес тяжести заключается в самом веществе стекла, а не в воде, которая не может быть тяжелее самой себя; равным образом, когда из дерева после отнятия воздуха и заполнения его пор водою образуется соединение дерева и воды, тяжелее воды, то это происходит не в силу воды, проникшей в поры, но в силу вещества самого дерева, остающегося по удалении воздуха. Такое тело, согласно с доктриною Архимеда, пойдет ко дну, тогда как первоначальное, в согласии с ней же, плавало на поверхности.
Перехожу, наконец, к тому, что приведено как четвертое возражение Архимеду, а именно, что уже Аристотель опроверг древних, отрицавших положительную и абсолютную легкость, признававших на самом деле все тела тяжелыми и приписывавших всякое движение толчкам окружающей среды; и так как доктрина Архимеда примыкает к этому мнению, то должна быть осуждена и отвергнута. Во-первых, мне думается, синьор Буонамико приписывает Архимеду или выводит из его слов более того, что тот говорил или что можно извлечь из его положений; Архимед нигде не отрицает и не признает положительной легкости и даже не касается этого вопроса, почему и не следовало бы обвинять его в отрицании ее как причины или принципа самостоятельного движения огня и других легких тел. Архимед, показав, как тела тяжелее воды опускаются в ней, вследствие перевеса их тяжести над тяжестью воды, показал равным образом, как менее тяжелые тела идут вверх в той же воде вследствие перевеса тяжести последней; отсюда, самое большее, можно сделать заключение: как перевес тяжести движущегося тела над тяжестью воды есть причина его опускания, так перевеса тяжести воды над тяжестью тела достаточно, {60} чтобы оно не тонуло, а поднималось на поверхность. Архимед не рассматривает, существует ли еще какая-либо причина самопроизвольного движения, противная силе тяжести. Если полуденный ветер уносит барку с большею силою, чем течение реки, которое увлекает ее к югу, то движение ее будет направлено к северу; но если сила течения воды преодолевает силу ветра, то движение будет к югу; такое рассуждение справедливо, и напрасно стали бы опровергать его, говоря: ты неправильно приводишь нам как причину движения барки к югу течение воды, превосходящее силу полуденного ветра; неправильно потому, что и сила северного ветра, противоположного южному, может уносить барку к югу. Такие возражения излишни, так как тот, кто приводит как причину движения течение воды, вовсе не отрицает, что и ветер, дующий в том же направлении, может иметь то же действие, но лишь утверждает, что в случае преобладания силы течения воды над силою южного ветра барка будет двигаться к югу,— и говорит истину. Совершенно так же, когда Архимед говорит, что перевес тяжести воды над той, с какой движущееся тело идет вниз, заставляет тело подниматься со дна на поверхность, то он приводит истинную причину этого явления, но не утверждает и не отрицает существования иного свойства, противоположного тяжести называемой некоторыми легкостью, которая может быть в состоянии заставить некоторые тела двигаться вверх-Оружие синьора Буонамико должно быть направлено против Платона и других древних, которые совершенно отрицали легкость и, признавая все тела тяжелыми, говорили, что движение тела вверх происходит не от присущего ему внутреннего принципа, а единственно от воздействия среды; Архимед же со своей доктриною пусть останется незатронутым, так как он не дает повода к нападкам. Если это выступление мое в защиту Архимеда покажется кому-либо недостаточным, чтобы освободить его от возражений и доводов, выставляемых Аристотелем против Платона и других древних, могущих быть направленными и против Архимеда, видевшего в выталкивании водою причину возвращения на поверхность тел, которые легче нее, то я не отказался бы и от поддержки признаваемого мною истинным положения Платона и других, совершенно отрицающих легкость и утверждающих, что в элементарных телах нет другого внутреннего принципа движения, кроме как к центру Земли, и другой причины движения вверх (подразумевая такое, которое имеет подобие естественного движения), кроме выталкивания жидкой средой, более тяжелой, чем движущееся тело. Все противные доводы Аристотеля, думается, я мог бы полностью опровергнуть и постарался бы это сделать, если бы то было необходимо при обсуждении настоящего вопроса и не заняло бы слишком много места в этом кратком трактате. Скажу только, что если бы каким-либо из наших элементарных тел были присущи внутренний принцип и естественная наклонность стремиться от центра Земли и направляться к Луне, {61} то такие тела, без сомнения, шли бы вверх быстрее в среде, менее сопротивляющейся движению тела, т. е. более легкой и тонкой, какою, например, является по сравнению с водою воздух, в чем каждый может убедиться, вращая руку или доску,— в воздухе гораздо быстрее и легче, нежели в воде. Между тем не найдется ни одного тела, которое поднималось бы в воздухе быстрее, чем в воде; мы видим даже, что все тела, постоянно поднимающиеся в воде, совершенно утрачивают движение, достигнув пределов воздуха, не исключая и самого воздуха, который, быстро восходя в воде, останавливается в самом движении, как только достигает своей области, и медленно расходится в ней. Так как опыт показывает нам, что тела, последовательно менее и менее тяжелые, поднимаются в воде все быстрее, нельзя сомневаться, что и вещество огня быстрее поднимается в воде, чем в воздухе, каковой воздух, по наблюдениям, поднимается в воде быстрее, чем вещество огня в воздухе; отсюда приходим к неизбежному заключению, что то же вещество гораздо скорее поднимется в воде, нежели в воздухе, и что, следовательно, оно движется воздействием окружающей среды, а не внутренним принципом, заставляющим его удаляться от центра, к которому тяготеют другие тяжелые тела.
По поводу последнего заключения синьора Буонамико, в котором то явление, что одни тела опускаются, а другие нет, объясняется легкостью или трудностью разделения среды и соотношением элементов, я отвечу сначала на первую часть: ни в каком случае выставляемая причина не является действительной, так как в жидкой среде, как-то: воздухе, воде и других жидкостях нет противодействия разделению, но все они малейшей силою разделяются и проникаются, как я покажу ниже; таким образом, из сопротивления разделению не может возникнуть никакого действия, и его не существует. Что касается второго положения, то я скажу, что действие элементов в движущихся телах обнаруживается лишь в излишке или недостатке тяжести их по отношению к среде, ибо в своем действии элементы играют роль только как более тяжелые или как более легкие; поэтому все равно сказать, что еловое дерево не идет ко дну, потому что в нем преобладает воздух, или сказать, что оно легче воды. Непосредственная причина — его сравнительная легкость, а преобладание воздуха — причина меньшей тяжести, поэтому тот, кто приводит как причину преобладание определенного элемента, приводит причину причины, а не причину ближайшую и непосредственную. А кто же не знает, что истинная причина есть именно непосредственная, а не та, которая действует через посредство других?! Кроме того, тот, кто ссылается на тяжесть, приводит причину, осязательную для чувства, и нам весьма просто понять, что эбеновое или еловое дерево тяжелее или легче воды; но как наглядно доказать нам, что в них преобладает земля или воздух? — Для этого нет иного средства, как убедиться на опыте, плавают они или идут ко дну. {62} Таким образом, тот, кто не знает, что такое-то тело плавает, пока не узнает, что в нем преобладает воздух, не узнает, будет ли оно плавать, пока не увидит его плавающим, потому что нельзя узнать, преобладает ли в теле воздух иначе, как увидав, что оно плавает; итак, следовательно, нельзя узнать, что тело плавает иначе, как увидав его пребывающим на поверхности воды. Не будем поэтому отвергать того, хотя бы и небольшого облегчения, которое предлагает нашему разуму рассуждение, и примем за истину положения Архимеда: всякое твердое тело, которое тяжелее воды, пойдет ко дну, если оно легче нее, то обязательно будет плавать; тело остановится безразлично в любом месте внутри воды, если его тяжесть будет совершенно равна тяжести воды.
Установив и разъяснив эти положения, я хочу рассмотреть теперь, какое значение имеет различие в форме данного тела, по отношению к упомянутым движениям или покою, и возвращаюсь к утверждению: различие формы, придаваемой тому или другому телу, не может быть ни в коем случае причиною его опускания на дно или поднятия на поверхность; так что, если тело, которому придана, например, сферическая форма, идет в жидкости ко дну или к поверхности, то утверждаю, что и при всякой иной форме оно в той же жидкости опустится или поднимется, и такое его движение не может быть отнято или уничтожено большей шириной или другими изменениями формы.
Возможно, что ширина фигуры замедлит быстроту опускания или подъема в тем большей степени, чем более широкой и тонкой будет сделана фигура; но довести подобное изменение до такой степени, чтобы устранить дальнейшее движение того же вещества в той же воде,— это я признаю совершенно невозможным. В этом пункте я нашел много возражающих, которые произвели несколько опытов, между прочим, один с тонкой дощечкою и шариком из эбенового дерева, показав, как шарик в воде опускался на дно, а дощечка, тихонько положенная на воду, не тонула, но оставалась на поверхности, из чего заключили, подкрепив свое мнение авторитетом Аристотеля, что настоящей причиной покоя была ширина фигуры, неспособной по своему малому весу разделить и преодолеть противодействующую густоту воды, какое противодействие быстро преодолевается другой — круглой фигурой.
Это главный пункт настоящего вопроса, в котором я постараюсь доказать, что отстаиваю правильное воззрение. Начну с попытки исследовать при помощи точного опыта, действительно ли фигура не изменяет опускания или неопускания на дно одних и тех же тел, после того как я уже доказал, что большая или меньшая тяжесть тела по отношению к тяжести среды есть причина опускания и подъема. Когда мы хотим испробовать, какое влияние на это движение может иметь различие фигуры, то необходимо производить опыты с веществами, в которых не может иметь места {63} разница в тяжести; иначе, употребляя вещества, тела из которых могут быть разного удельного веса, мы останемся всегда при сомнительных выводах, встречаясь с разницей эффекта опускания или подъема, — происходит ли такая разница действительно от одной формы или же еще и от разницы в тяжести. Устраним это неудобство, взяв вещество, которому можно легко и удобно придать любой вид и форму. Затем, в высшей степени удобно брать вещество, наиболее близкое по тяжести к воде, потому что такое вещество является безразличным в отношении тяжести к опусканию или поднятию; следовательно, на нем всего быстрее обнаружится каждое малое различие, происходящее от изменения фигуры.
Чтобы достигнуть этого, всего пригоднее воск, который, не испытывая особого изменения от пропитывания водою, удобен также тем, что один и тот же кусок его легко превращается в любую фигуру; к тому же он па удельному весу немного легче воды и с прибавлением малой доли свинцовых опилок становится совершенно равным с нею по весу.
Приготовим из воска шарик величиною с апельсин или более, сделав его таким тяжелым, чтобы он оставался на дне, но настолько незначительно более тяжелым, чем вода, чтобы при отнятии небольшой частицы свинца он поднимался на поверхность, при прибавлении же ее возвращался на дно. Превратив затем тот же воск в тончайшую и широкую пластинку и проделав тот же опыт, увидим, как она, положенная на дно, с прибавлением крупинки свинца останется внизу, при отнятии свинца поднимается на поверхность, а при прибавлении снова опустится на дно. Подобное же произойдет с фигурами всех видов как правильными, так и неправильными, и среди них не встретится ни одной, которая поднималась бы, пока мы не отнимем от нее крупинки свинца, или пошла бы на дно, пока мы не прибавим его. В результате увидим, что вообще в движении не обнаружится никакой разницы, кроме увеличения или уменьшения быстроты; тела более широкие и плоские будут двигаться медленнее как при опускании на дно, так и при поднятии; другие тела, более узкие и плотные, будут двигаться быстрее. После этого я не могу понять, какое значение можно приписывать разнице фигур, если разнообразнейшие формы сами по себе не могут произвести того действия, какое производит отнятие или прибавление малейшей частицы свинца.
Представляя себе, что кто-нибудь из противников может подвергнуть сомнению произведенный мною опыт, обращаю внимание прежде всего на то, что фигура сама по себе, только как таковая, отдельно от вещества, ничего не производит; необходимо, чтобы она была соединена с веществом, и притом не со всяким веществом, а только с таким, с которым она может произвести желаемое действие. По опыту мы знаем, что острый и тонкий угол более пригоден для резания, чем тупой; однако это свойство обнаруживается лишь по отношению к веществу, способному резать, например {64} железу, ибо нож с острым и тонким лезвием режет хлеб и дерево лучше, чем нож с острием тупым и грубым; но кто вздумал бы взамен железа взять воск и сделать из него нож, конечно, не мог бы при таком веществе узнать, какое действие производит лезвие острое и лезвие тупое, потому что ни то, ни другое в данном случае не будет резать, ибо воск по своей мягкости не способен преодолеть твердость дерева или хлеба. Прилагая подобное рассуждение к нашему примеру, скажем, что разность фигур выкажет различие в эффекте опускания или неопускания лишь в соединении с веществом, но ни каким угодно, а только таким, которое по своей тяжести способно преодолеть сопротивление воды; но, если бы кто-нибудь взял пробковое или иное легчайшее дерево, неспособное по своей легкости преодолеть сопротивления плотности воды, и из такого материала сделал бы тела разной формы, то он напрасно стал бы наблюдать, как влияет форма на опускание тел, ибо все тела останутся на поверхности, и это не в силу свойства той или иной фигуры, но вследствие легкости вещества, лишенного того веса, который требуется, чтобы превзойти и преодолеть плотность воды.
Следовательно, если мы хотим видеть, как влияет различие в форме тела, то необходимо выбрать прежде всего вещество, способное преодолеть плотность воды; для этого необходимо взять материал, который, будучи обделан в форму шара, идет ко дну; выбрав для этой цели эбеновое дерево, сделали из него маленькую тонкую дощечку и показали, что, положенная на поверхность воды, она остается, не опускаясь на дно; сделав из того же дерева шарик не более ореха величиною, нашли, что он не остается на поверхности, но тонет. Из этого опыта, по-видимому, можно заключить, что ширина фигуры в плоской дощечке и есть причина того, что она не опускается вниз, ибо шарик из того же материала, отличающийся от дощечки только фигурою, в той же воде идет ко дну. Это рассуждение и этот опыт представляются весьма вероятными и правдоподобными, и не удивительно, что многие, убежденные тем, что сами видели, согласятся со сделанными отсюда выводами; однако же, думается, я в состоянии установить, что тут допускается погрешность.
Начиная рассматривать по частям все приведенное, скажу, что фигуры, просто как фигуры, не только не оказывают влияния на тела в природе, но и не существуют отдельно от субстанции тел, и я ни в коем случае не предполагал их в отвлечении от материи; я свободно допускаю, что если мы хотим испробовать, какова будет разница результатов в зависимости от разницы фигур, то их надо прилагать к веществам, которые не препятствовали бы проявлению действия этих разных фигур; признаю и заявляю, что поступил бы неправильно, если бы захотел исследовать, какое значение может иметь острота лезвия ножика из воска в применении к разрезыванию им дуба, ибо не существует остроты, соединенной с {65} воском, которая могла бы разрезать твердейшее дерево. Но нелишним может оказаться произвести опыт с подобным ножом, разрезая им простоквашу или другую подобную, легко поддающуюся воздействию материю; для такого вещества, напротив, чтобы узнать разницу, происходящую от более или менее острых углов, гораздо пригоднее воск, нежели сталь, ибо простокваша одинаково легко разрезывается и острой бритвой и тупым ножом. Поэтому необходимо принимать во внимание не только твердость, плотность и тяжесть тел, которые в виде разных фигур должны разделять другие вещества и проникать в них, но учитывать и сопротивление этих последних веществ разделению и проникновению в их среду. Так как я для опыта по предмету нашего разногласия выбрал вещество, которое преодолевает сопротивление воды и при всех формах опускается на дно, то мои противники не могут представить мне никакого возражения, тем более, что я предложил способ более утонченный, чем они, при котором устранены все иные причины опускания или неопускания на дно и сохранено единственное и простое различие фигур, и показал, как все эти фигуры опускаются единственно от увеличения этого веса на один гран, по отнятии же добавочного веса возвращаются на поверхность. Неправильно было бы поэтому возражение (возвращаясь к приведенному примеру), что я пожелал исследовать влияние остроты на разрезывание при помощи веществ, не способных резать; напротив, я выбрал вещества, вполне отвечающие нашей задаче, и не подвергал их никаким изменениям, кроме тех, которые относятся к фигуре тела, то более тупой, то более острой.
Но будем продолжать дальше и отметим, что в рассуждение было действительно без особой надобности введено соображение относительно необходимости выбирать вещество, пригодное для нашего опыта, именно соображение, что как острота достаточна для резания только в соединении с веществом твердым и способным преодолеть сопротивление дерева или чего-либо иного, что мы намереваемся резать, точно так же и движение в воде должно и может познаваться на веществах, способных превзойти сопротивление воды и преодолеть ее плотность. Если я и говорю, что крайне необходимо делать различие между веществами при выборе того, из которого предполагают делать разные фигуры для разрезания того или иного тела, в соответствии с большей или меньшей плотностью и твердостью этих тел, то затем прибавлю, что такое различие, выбор и предосторожность представляются бесполезными и излишними, если разрезываемое или разделяемое тело не представляет никакого сопротивления и совсем не противится разрезыванию и разделению; если бы, например, предполагалось резать ножами туман или дым, то мы могли бы одинаково пользоваться как картоном, так и дамасской сталью. Так как вода не представляет никакого сопротивления для проникновения в нее любого твердого {66} тела, всякий выбор вещества является излишним и ненужным; и когда я говорил выше о том, что хорошо избирать вещество, схожее по плотности с водою, то это потому, чтобы было необходимо преодолевать не плотность воды, но ее тяжесть, в силу которой она единственно противится погружению твердых тел. Тому, кто видит причину сопротивления в плотности, скажу, что при внимательном рассмотрении мы найдем, что все твердые тела, как те, которые идут на дно, так и другие, которые плавают, одинаково пригодны и способны привести нас к познанию истины в нашем споре. От веры в такой вывод меня не отвратят опыты, могущие еще быть выставленными против меня над разными сортами дерева и пробки или тонкими пластинами из разного рода камня, металла и вообще вещества, стремящегося по своей природной тяжести к центру Земли, хотя бы все они и были неспособны, вследствие ли фигуры (как полагают мои противники) или по своей легкости, проникнуть в среду водяных частиц, разрушив их соединение между собою, и остаются, не погружаясь в воду, на ее поверхности; не убедит меня и авторитет Аристотеля, который во многих местах утверждает противное тому, что показывает мне опыт.
Итак, возвращаюсь к утверждению, что нет твердого тела, ни такой легкости, ни такой фигуры, чтобы, будучи положено на воду, оно не разделяло частиц и не проникало в нее; напротив, тот, кто внимательным взглядом станет наблюдать тонкие деревянные дощечки, увидит, что частью своей толщины они находятся под водою, а не только соприкасаются своей нижней поверхностью с поверхностью воды, что было бы неизбежно, если признать правильным мнение тех, которые говорят, что такие дощечки не тонут, ибо не способны преодолеть сцепление частиц воды; они увидят затем, что тончайшие пластинки эбена, камня или металла, оставаясь на поверхности, не только разрушают сплошность воды, но всей своей толщиной остаются ниже поверхности воды и тем ниже, чем тяжелее их вещества, так что тонкий лист свинца остается ниже поверхности окружающей воды приблизительно на двенадцатикратную свою толщину, а золото опускается в воду на глубину почти в двадцать раз большую, чем толщина его пластинки, как это я и покажу ниже.
Но продолжим доказательство того, что вода уступает и позволяет проникнуть в нее каждому легчайшему твердому телу, а вместе с тем покажем, как и на веществах, которые не тонут, можно убедиться, что фигура тела не оказывает влияния на опускание или неопускание его на дно, так как вода свободно проникается любою фигурою.
Сделаем конус или пирамиду из кипариса, ели или иного дерева подобного веса, или же из чистого воска; пусть эта фигура будет достаточной высоты, например в пядь или более; поместим ее в воду основанием книзу. Мы увидим, во-первых, что пирамида проникнет в воду, чему совсем не помешает ширина основания; однако она не вся погрузится, а будет {67} выставлять из воды вершину, откуда ясно, что такое твердое тело останавливается в погружении не по невозможности разделить сцепление частиц воды, так как оно уже разделило водяные частицы своей широкой стороной, по мнению наших противников, наименее способной разделять. Когда пирамида установится, заметим, какая часть ее находится над водою; обратив ее затем острым концом вниз, увидим, что она проникает в воду не более, чем прежде; напротив, если отметим, до какой черты она погрузилась, каждое лицо, знакомое с геометрией, будет в состоянии вычислить, что части, остающиеся над водой и в том и в другом опыте совершенно равны по объему, откуда вытекает, что острая фигура, казавшаяся более приспособленной для разделения воды и проникновения в нее, разделяет ее не более, чем фигура широкая и плоская.
Кто захочет произвести еще более наглядный опыт, пусть сделает из того же материала два цилиндра — один длинный и тонкий, а другой короткий, но более широкий, и опустит их в воду не боком, но прямо, основанием вниз; измерив тщательно части того и другого, он увидит, что в каждом из цилиндров погруженная часть по отношению к той, которая остается вне воды, сохраняет в точности ту же пропорцию и что у длинного и легкого цилиндра погружается не большая часть, чем у более объемистого и широкого, хотя последний и опирается на большее пространство поверхности воды, чем первый; итак, различие фигуры не облегчает и не затрудняет опускания и проникновения в воду, а следовательно, не может быть и причиною опускания или неопускания на дно. Подобное же отсутствие влияния разности фигур при подъеме тел со дна на поверхность обнаруживается, если возьмем воск, прибавим к нему достаточное количество свинца, чтобы он сделался определенно тяжелее воды, сделаем из него шарик и опустим его на дно; после того привяжем к нему столько пробки или другого легкого вещества, чтобы последнего было как раз достаточно для всплывания воска на поверхность; при раскатывании затем воска в широкую пластинку и при любом ином изменении его формы найдем, что та же пробка таким же образом поднимает его вверх.
Но мои противники не удовлетворяются этим, говоря, что для них мало значат все мои приведенные до сих пор рассуждения. Основываясь на одном своем примере, в котором вещество и фигуры, избранные ими, были плоская дощечка и шарик эбенового дерева, причем, как они показали, последний идет ко дну, а первая остается на поверхности, они утверждают, что так как вещество одно и то же, различие же заключается лишь в фигурах тел, то они и достигли своей цели, наглядно и окончательно доказав то, что им требовалось. Тем не менее я верю и, надеюсь, в состоянии показать, что такой опыт не заключаете себе ничего, противного моим выводам.
Во-первых, неверно, что шарик идет ко дну, а дощечка нет, потому что дощечка так же тонет, как и всякая иная фигура, если с ней поступить {68} так, как то требуется по условиям нашей задачи, т. е. если она будет положена в воду.
Существо нашего спора таково: противники полагают, что фигура вносит изменение в способность твердых тел подниматься или не подниматься, опускаться или не опускаться в жидкой среде, например в простой воде, таким образом, что, например, твердое тело сферической формы пойдет ко дну, а при придании ему иной фигуры — не пойдет; я, полагая противное, утверждаю, что твердое тело, которое, имея сферическую форму, упадет на дно, упадет туда и при всякой иной форме. Но быть в воде — это значит быть помещенным в воду; а, по определению понятия места тем же Аристотелем, быть помещенным — значит быть окруженным поверхностью объемлющего тела; следовательно, обе фигуры тогда только будут в воде, когда поверхность воды их окружает и объемлет. Но, когда противники показывают эбеновую дощечку, не опускающуюся на дно, они кладут ее не в воду, а сверх воды, где она, удерживаемая некоторым препятствием (как это выяснится ниже), и остается окруженная частью водою, частью же воздухом, каковое обстоятельство противно нашему условию, согласно которому тела должны быть в воде, а не частью в воде, частью в воздухе.
А что это именно так, видно из самой постановки вопроса, касающегося как тел, которые должны тонуть, так и тех, которые со дна должны подниматься на поверхность; а кто же не признает, что вещи, помещенные на дно, должны быть окружены водою?
Заметим, далее, что эбеновая дощечка и шарик, положенные в воду, оба пойдут ко дну, но шарик быстрее, а дощечка медленнее, и тем медленнее, чем она шире и тоньше; и причиной такого замедления является действительно ширина фигуры. Но дощечки, которые медленно опускаются, те же самые, которые, легко положенные на воду, плавают; следовательно, если бы утверждение противников было правдою, то одна и та же фигура в одной и той же воде была бы причиною то покоя, то медленности движения, что невозможно, потому что каждая особая фигура, опускающаяся на дно, необходимо имеет собственную и присущую ей от природы медленность, в соответствии с которой она опускается; увеличенная или уменьшенная медленность движения не свойственна ее природе; поэтому, если дощечка, скажем, в квадратную пядь, опускается естественно с медленностью, которую мы обозначим семью градусами, то невозможно, чтобы она опускалась с десятью или двадцатью градусами медленности, если только какое-нибудь новое препятствие не будет тому причиною. Еще менее может она по причине той же фигуры успокоиться и остаться совершенно лишенной движения; каждый раз, когда она останавливается, необходимо искать какое-либо встретившееся препятствие, независимое от ширины фигуры. Итак, что-то иное, чем форма, удерживает эбеновую {69} дощечку над водой, потому что форма влияет единственно на замедление движения, почему дощечка и опускается медленнее шарика. Поэтому в рассуждении своем я и говорю, что истинная и единственная причина опускания на дно эбена — это перевес его тяжести над весом воды, большей же или меньшей медленности движения — более широкая или более сжатая фигура; но об остановке движения никоим образом нельзя сказать, чтобы причиною ее было свойство фигуры, потому что, если и будем достигать большой медленности, по мере того как расширяется и утончается фигура, то все же нельзя представить себе такого огромного расширения, которому не соответствовала бы чрезвычайная медленность, не достигающая, однако, полного отсутствия движения; фигуры, выставляемые противниками для доказательства покоя, на самом деле идут ко дну.
Я не могу умолчать о другом доказательстве, основанном также на опыте, из которого, если я не ошибаюсь, можно определенно заключить, что ширина фигуры и сопротивление воды разделению не производят никакого действия на движение или покой тела в воде. Выберем дерево или другой материал, шарик из которого поднимается со дна на поверхность медленнее, нежели опускается на дно шарик эбенового дерева, из чего заключаем, что эбеновый шарик быстрее разделяет воду при погружении, чем другой при подъеме; пусть выбранное вещество будет ореховое дерево. Сделаем теперь из ореха дощечку, совершенно сходную и одинаковую с остающейся на поверхности эбеновой дощечкой наших противников; если правда, что она остается там благодаря неспособности своей фигуры по ее ширине разделить водяные частицы, то ореховая дощечка, будучи помещена на дно, без всякого сомнения, должна будет остаться там, как неспособная в силу той же особенности фигуры преодолеть ту же плотность воды. Но, если мы найдем и на опыте увидим (а оно так и будет), что не только дощечка, но и всякая иная фигура из того же ореха будет подниматься на поверхность, пусть мои противники перестанут приписывать плавание эбена форме дощечки, так как сопротивление воды одинаково наверху и внизу, а сила подъема орехового дерева на поверхность менее силы опускания эбенового дерева ко дну.
Сверх того, замечу следующее: сравнив золото с водою, найдем, что оно превосходит ее по весу в 20 раз; отсюда сила и импульс, с которыми золотой шарик идет ко дну, очень велики.
С другой стороны, нет недостатка в веществах, как-то: простой воск и дерево разного рода, которые по тяжести разнятся едва на два процента от воды; поэтому они поднимаются в воде очень медленно: стремление их к подъему раз в тысячу слабее, нежели стремление золота опуститься; и все же тонкая золотая пластинка плавает, не опускаясь на дно, в то время как мы не можем сделать из воска или дерева пластинки, которая, будучи положена на дно, осталась бы там без движения. Теперь, если фигура {70} может воспрепятствовать разделению воды и помешать опусканию золота, имеющего большое стремление тонуть, то почему ее не будет достаточно, чтобы воспрепятствовать разделению воды другим веществом при его подъеме, хотя оно при этом обладает едва ли одной тысячной силы стремления золота ко дну?
Необходимо, следовательно, признать, что поддерживает тонкую пластинку золота и эбеновую дощечку что-то такое, чего недостает другим пластинкам и дощечкам из веществ легче воды, ибо они, будучи помещены на дно и оставлены на свободе, беспрепятственно всплывают на поверхность; но они обладают плоской и широкой фигурой; следовательно, не фигура удерживает золото и эбен на поверхности. Какая же здесь действует причина? Я сказал бы, что это нечто противоположное причине, по которой тело опускается на дно, так как опускание на дно и нахождение на поверхности суть явления противоположные, а причины противоположных явлений также должны быть противоположными.
Но, так как причиною опускания на дно эбеновой дощечки и тонкой золотой пластинки, когда они тонут, является, без всякого сомнения, их большая по сравнению с водою тяжесть, то необходимо признать, что причиною их нахождения на поверхности, когда они плавают, является легкость, которая в этом случае, каким-то до сих пор незамеченным образом присоединяется к дощечке, делая ее не такой, какой она была ранее, когда тонула, т. е. не более тяжелой, чем вода, а более легкой. Но эта новая легкость не может зависеть от фигуры, как потому, что фигуры не прибавляют и не отнимают веса, так и потому, что в дощечке не происходит никакого изменения в фигуре, когда она идет на дно и когда плавает на поверхности.
Возьмем теперь опять тонкую золотую или серебряную пластинку или дощечку из эбенового дерева и положим их легонько на воду так, чтобы они остались там, не погружаясь, и будем наблюдать, что при этом происходит. Прежде всего увидим, насколько неосновательны слова Аристотеля и моих противников, что они останутся на поверхности по неспособности разделить противодействующую плотность воды и проникнуть в нее, ибо наглядно выяснится, что эти пластинки не только проникнут в воду, но будут значительно ниже ее поверхности; вода кругом этих пластинок возвышается, образуя нечто вроде вала, в глубине которого те плавают, и сообразно тому, во сколько раз вещество этих пластинок будет тяжелее воды — в два, четыре, десять или двадцать раз,— и поверхность их будет ниже общей поверхности окружающей воды на величину, во столько-то и столько-то раз превосходящую их собственную толщину, как то впоследствии будет показано.
Пока для лучшего усвоения сказанного рассмотрим прилагаемый чертеж, на котором поверхность воды обозначена линией BDLF; если положим {71} на нее дощечку из вещества тяжелее воды так осторожно, чтобы она не потонула, то она не только не останется сверху, но всей своей толщиной войдет в воду и опустится еще, как то показано на чертеже для дощечки OIAI, которая всей своей толщиной погружается в воду, а вокруг нее остаются валики LA, DO воды, поверхность которой значительно выше поверхности дощечки. Теперь мы видим, насколько справедливо мнение, будто пластинка не идет ко дну по причине неспособности ее фигуры преодолеть плотность воды! Но, если она уже преодолела сплошность воды и
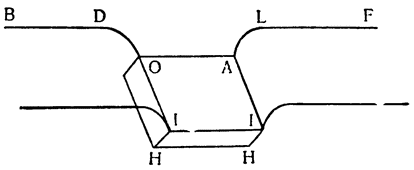 |
Но я уже предчувствую, как кто-нибудь из противников возражает, что они и не ожидали ничего иного, раз дощечка была смочена, так как {72} прибавленный вес воды делает пластинку более тяжелой, чем прежде, и тянет ее на дно, но что добавление веса противно нашему условию, согласно которому вещество должно оставаться тем же самым.
На это отвечу, во-первых, что, рассматривая вопрос относительно влияния формы на тела, помещенные в воду, никто не должен ставить условием помещение их в воду без смачивания; со своей стороны, я не требую ничего иного, кроме того, чтобы с дощечкою поступали так же, как с шариком. Сверх того, неверно, что дощечка идет ко дну в силу прибавления новой тяжести только от того, что она слегка смочена водою, потому что я могу налить на дощечку, пока она находится на поверхности, десять или двадцать капель воды, и эти капли, если они не соединятся с окружающей водой, не отягчат ее настолько, чтобы она потонула; но, если вынуть дощечку и, стряхнув с нее всю налитую на нее воду, одной только мельчайшей каплею смочить ее поверхность и опять положить дощечку на воду, то она, без сомнения, потонет, так как окружающая вода притечет и покроет ее, не задерживаемая более воздухом, каковой, вследствие введения легкого покрова воды, мешающего его непосредственному соприкосновению с эбеном, беспрепятственно отделяется и совсем не противится притоку воды. Иначе говоря, пластинка опустится свободно потому, что вся окажется окруженной и покрытой водою, как только ее верхняя часть, уже смоченная водой, коснется уровня общей поверхности воды. Говорить, что вода может увеличить тяжесть тел, в ней помещающихся, совершенно нелепо, так как вода в воде не имеет никакой тяжести, ибо она в ней не опускается. Поэтому, если захотим хорошенько рассудить, какое действие оказывает некоторое огромное количество воды, расположенное над находящимся в ней тяжелым телом, то найдем по опыту, что она, наоборот, скорее уменьшает, и в значительной мере, его вес; мы можем поднять в воде со дна тяжелый камень, а, удалив воду, не сможем сделать этого. На это мне возразят, что хотя расположенная поверх находящихся в ней тел вода не прибавляет им тяжести, но она прибавляет тяжесть тем, которые плавают и находятся частью в воде, частью в воздухе, как то видим на примере медного сосуда, который, пока не содержит воды и наполнен воздухом, остается на поверхности, но налитый водою становится таким тяжелым, что опускается на дно,— и это по причине прибавления новой тяжести. На это я отвечу, как и ранее, что не тяжесть воды, содержащейся в сосуде, тянет его на дно, но собственная тяжесть меди, превосходящая по удельному весу воду, и что если бы сосуд был сделан из вещества легче воды, то океана было бы недостаточно, чтобы его потопить. Да позволено мне будет вновь подчеркнуть как основной и главный пункт нашего вопроса, что воздух, содержавшийся внутри сосуда до заполнения его водою, и поддерживал его на поверхности, ибо из него и меди образовалось соединение, более легкое, чем соответственный объем воды; место {73} же, занимаемое сосудом, пока он плавает, равно не одной меди, но вместе и меди и воздуху, заполняющему часть сосуда, находящуюся ниже уровня воды. Когда затем наливается вода, то воздух вытесняется и получается соединение меди и воды по удельному весу тяжелее простой воды, но вовсе не в силу налитой воды, которая не имеет большего удельного веса, чем всякая другая вода, а вследствие собственной тяжести меди и удаления воздуха. Если бы кто-нибудь утверждал, что медь, по природе своей тонущая, которой придана форма сосуда, приобретает поэтому способность оставаться на воде, не опускаясь, я скажу, что это неверно, потому что медь, которой придана любая форма, всегда тонет, лишь бы то, что опускается в воду, было простой медью; что не фигура сосуда заставляет плавать медь, но то обстоятельство, что опускается в воду непросто медь, но агрегат меди и воздуха. Так же не менее ложно и то, что тонкая пластинка из меди или эбена плавает в силу широкой и плоской фигуры, но вполне верно, что она остается, не погружаясь, потому что опускается в воду не чистая медь или простой эбен, но агрегат меди и воздуха или эбена и воздуха. И это нисколько не противно моим заключениям, когда я, тысячу раз наблюдая металлические сосуды и тонкие пластинки тяжелых веществ, плавающие в силу связанного с ними воздуха, утверждаю, что не фигура является причиною опускания или неопускания на дно тел, помещенных в воду. Не могу умолчать, но прямо скажу противникам, что их новое требование — не допускать, чтобы поверхность дощечки была смочена,— может навести лиц сторонних на мысль, что их аргументы в защиту своего мнения весьма скудны, тем более, что такое смачивание, по существу нашего вопроса, не должно бы огорчать их или вообще иметь какое-либо значение, так как спор возник относительно плавания льдин, сухость поверхности которых легко может быть оспариваема; к тому же, суха поверхность льда или смочена, льдины все же плавают и, как утверждают противники, в силу их фигуры.
Может быть, кто-нибудь вздумает сказать, что после смачивания верхней поверхности эбеновой дощечки она, сама по себе неспособная разделить воду и проникнуть в нее, увлекается книзу, если и не тяжестью смачивающей воды, то, по крайней мере, тем стремлением и склонностью, которые верхние части воды имеют к воссоединению и слиянию, и стремлением этих частей дощечка как бы увлекается книзу.
Но и такое слабое обоснование совсем отпадет, если принять во внимание, что, какова склонность верхних частей воды к соединению, таково же противодействие нижних частей их разъединению; ни верхние не могут соединиться с нижними, не надавив книзу дощечку, ни последняя не может опуститься, не разделив частей находящейся ниже воды, откуда вытекает, как необходимое следствие, что по подобным причинам дощечка не должна опуститься. Притом же все только что сказанное о верхних {74} частях воды с таким же правом может быть отнесено и к нижним, которые, стремясь к соединению, выталкивают дощечку кверху.
Может быть, кто-нибудь из синьоров, не согласных со мною, удивится моему утверждению, что прилегающий сверху воздух в состоянии поддержать пластинку меди или серебра, которая держится на воде; выходит, что я хочу приписать воздуху как бы свойство магнита — поддерживать тяжелые тела, с которыми он соприкасается19. Желая; насколько это мне возможно, разрешить все затруднения, я думал, каким бы иным наглядным опытом показать, что действительно малое количество прилегающего сверху воздуха поддерживает тела, которые, будучи по природе своей склонными опускаться на дно, положенные легко на воду, не тонут, если ранее не смочены водою; и я нашел, что, если такое тело опустилось на дно, то, ничем не трогая его, но прибавив к нему в небольшом количестве воздух, который бы прикоснулся к его вершине, можно добиться не только того, что, как мы видели ранее, воздух будет поддерживать тело, но даже поднимет и поведет его вверх, где оно остановится и будет пребывать в покое, пока не отнимется помощь соприкасающегося с ним воздуха. Для этого опыта я взял восковой шарик с чистой и гладкой поверхностью и сделал его путем прибавления свинца настолько тяжелым, чтобы он очень медленно опускался на дно; осторожно положенный в воду, он погружается почти весь, оставляя видной только верхушку, которая, пока соприкасается с воздухом, поддерживает шарик наверху; но если отнять этот воздух, смочив шарик, то последний опускается на дно и там остается. Постараемся теперь той же силой воздуха, которая поддерживала шарик, привести его обратно наверх и там задержать. Для этого опустим в воду отверстием вниз опрокинутый стакан, который захватит с собою заключающийся в нем воздух; направляя его сперва к шарику и опуская до тех пор, пока не заметим через прозрачное стекло, что содержащийся в стакане воздух достиг верхушки шарика, медленно вынем затем стакан; при этом мы увидим, что и шарик поднимется и остановится наверху, если отделим стакан от воды так осторожно, чтобы она не взволновалась. Следовательно, между воздухом и другими телами существует известная связь, которая держит их в некотором соединении, так что они отделяются друг от друга только с некоторым усилием. Подобное же явление наблюдается и с водою: если погрузим в нее какое-нибудь тело так, чтобы оно омылось кругом водою, то, вынимая его осторожно обратно, увидим, как вода последует за ним и поднимется заметно над своей поверхностью, прежде чем отделится от тела. Точно так же и твердые тела, имеющие совершенно одинаковую поверхность и столь плотно прилегающие одно к другому, что между ними не остается воздуха, который, рассеиваясь при их разделении, позволяет окружающей среде заполнять образующееся между телами пространство,— крепко {75} соединяются и отделяются друг от друга только с большим усилием. Но так как воздух, вода и другие жидкости при прикосновении к твердым телам весьма легко облекают их, причем их поверхность в совершенстве уподобляется поверхности облекаемого твердого тела, то поэтому на них чаще и нагляднее обнаруживается действие такого соединения и прилегания, чем на телах твердых, поверхности которых редко прилегают одна к другой надлежащим образом. Такова, следовательно, та магнетическая сила, которая плотно соединяет все тела, соприкасающиеся при отсутствии между их поверхностями податливых жидкостей; и, кто знает, не это ли теснейшее соприкосновение является достаточной причиной цельности и сплошности частей тел в природе?
Теперь, продолжая мое рассуждение, скажу: не следует ссылаться на связность частей воды между собою, благодаря которой они сопротивляются и противодействуют разделению и рассеиванию, потому что такой связности и противодействия не существует; если бы они существовали, то во внутренних слоях воды они сказывались бы не в меньшей степени, нежели в ближайших к поверхности, так что та же дощечка, встречая всюду одинаковое противодействие и задержку, могла бы останавливаться равно хорошо среди воды, как и на поверхности, чего не бывает на самом деле. К тому же, какое сопротивление разделению можно приписать воде, если мы видим, что невозможно найти такое тело, какого бы то ни было состава, формы и величины, которое, помещенное в воду, осталось бы неподвижным благодаря связности частей воды между собою, а не двигалось вверх и вниз сообразно имеющей в данном случае место причине движения? И какого лучшего опыта в подтверждение сказанного будем искать, когда ежедневно видим, как мутная вода, налитая в сосуды для питья, в течение нескольких часов, как говорят, еще беловата, а по прошествии четырех — шести дней становится совершенно чистой и прозрачной? Ее сопротивление не может задержать даже тончайших неосязаемых атомов песка, которые по ничтожности своей силы употребляют шесть дней, для того чтобы опуститься вниз на пространство в поллоктя.
Кто-нибудь может сказать, что ясным доказательством сопротивления воды разделению и является то, что такие легкие тельца употребляют шесть дней, чтобы опуститься на такое короткое пространство; но это не противодействие разделению, а лишь замедление движения, и было бы наивно говорить, что какое-нибудь тело противится разделению и в то же время допускает себя разделить. Для противников недостаточно приводить случаи замедленного движения, им необходимо найти пример, где движение совершенно устраняется, и наступает покой; необходимо, следовательно, найти такие тела, которые останавливались бы в воде, указывая тем на ее сопротивление разделению, а не только такие, которые {76} движутся с замедлением. Какова же эта плотность воды, в силу которой она противится разделению? Какое суждение будем мы иметь о ней (о чем я говорил и раньше) после того, как, стараясь со всей тщательностью привести вещество настолько близко по весу к воде, чтобы оно, хотя бы в форме широкой пластинки, осталось подвешенным между водяными слоями,— не можем достигнуть этого, хотя и подойдем к тождеству веса настолько близко, что количество свинца с четвертую часть зернышка проса, прибавленное к этой широкой пластинке, весящей на воздухе от четырех до шести фунтов, заставляет его тонуть, а отнятое — подниматься на поверхность? Я не знаю (если правильно то, что мною сказано, а это несомненная истина), какую ничтожную способность или силу надо отыскать или вообразить, чтобы противодействие воды разделению и рассеянию ее частиц было не меньше этой силы, из чего необходимо заключить, что противодействие это равно нулю. Если бы оно действительно было сколько-нибудь осязательным, то мы могли бы сделать из вещества, по тяжести равного воде, такую широкую пластинку, которая не только оставалась бы между водяными слоями, но и не могла бы без значительного усилия опуститься или подняться. Ту же истину мы можем извлечь из другого опыта, показав, как вода подобным же образом поддается разделению поперек. Если в спокойную стоячую воду поместим какое-нибудь плавающее тело огромного объема и потянем его осторожно, с помощью хотя бы одного женского волоса, то мы сможем перевести его с одного места на другое без всякого препятствия, хотя бы фигура его была любая, захватывающая большое пространство воды (например, большое бревно, положенное поперек). Кто-нибудь может возразить мне, что если бы сопротивление воды разделению равнялось, как я утверждаю, нулю, то кораблям не требовалось бы столько силы весел и парусов, чтобы передвигаться с места на место даже в спокойном море или в стоячих озерах. Тому, кто сделал бы подобное возражение, я отвечу, что вода противится и противодействует не просто разделению, но быстрому разделению, с тем большею силою, чем больше скорость. Причина такого противодействия заключается вовсе не в плотности или другом свойстве, абсолютно противящемся разделению, но в том, что разделяемые части воды, чтобы дать место телу, которое в ней движется, должны перемещаться отчасти направо, отчасти налево и еще отчасти вниз, и это делается не только с водой впереди корабля или другого тела, плывущего по воде, но и с водой, находящейся позади корабля и следующей за ним, потому что корабль в своем движении вперед, чтобы освободить место, способное вместить его объем, должен носовой частью оттеснить ближайшие части воды направо и налево, передвигая их в этом направлении на пространстве до половины своего корпуса; и такой же обратный путь должны пройти части воды, которые, следуя за кормою, устремляются от наружных {77} частей судна к середине, чтобы последовательно заполнять места, которые корабль освобождает при движении вперед. Теперь, так как все движения совершаются во времени и более длинное пространство тело проходит и в более продолжительный срок, так как, далее, признано за истину, что тело, движущееся с определенною силою и проходящее в некоторое время определенное пространство, может пройти такое же пространство в более краткий срок лишь при условии приложения большей силы, то понятно, почему более широкие суда движутся медленнее, чем узкие, если движущая сила одинакова, и почему судно требует тем большей силы весел или ветра, чем быстрее оно должно двигаться.
И не существует плавающего в воде тела такого большого размера, чтобы оно не могло быть приведено в движение помощью ничтожной силы; верно лишь то, что меньшая сила движет его медленнее, но, если бы сопротивление воды разделению было хотя в какой-нибудь мере ощутительно, следствием было бы то, что этот объем при известной ощутительной силе сопротивления остался бы совершенно неподвижным, чего не случается. Скажу более, когда мы займемся более внимательным исследованием природы воды и других жидкостей, то мы, быть может, откроем, что строение их таково, что они не только не противятся разделению, но что в них нет ничего, что подлежало бы разделению; сопротивление, ощущаемое при движении в воде, может быть уподоблено тому затруднению, какое мы испытываем, продвигаясь через большую толпу народа, где встречаем препятствие не вследствие трудности разделения, так как мы не разделяем никого из составляющих толпу, но вследствие необходимости раздвигать в стороны отдельных и не связанных друг с другом людей; такое же сопротивление мы испытываем, вытаскивая дерево из песчаной кучи, не потому, что надо разделять части песка, а потому, что надо поднимать и передвигать их. Существуют два рода проникновения одних тел через другие: одно — через тела, части коих связаны, и тут разделение представляется необходимым, другое — через тела, представляющие собрание частиц, не связанных, а только прилегающих друг к другу; здесь требуется не разделение, но лишь передвижение. Пока я еще не решил окончательно, следует ли считать воду и другие жидкости состоящими из частиц, связных или только прилегающих друг к другу; скорее я склонен признать частицы их только прилегающими друг к другу (если в природе нет других родов соединения, кроме связности и тесного соприкосновения), к чему приводит меня нахождение большого различия между соединением частей твердого тела и соединением этих же частей, когда то же самое тело сделано жидким и текучим. Если, например, я возьму кусок серебра или другого металла в холодном и твердом виде, то, разделяя его на две части, я почувствую сопротивление не только такое, {78} какое чувствовалось бы при передвижении их, но несравненно большее, зависящее от величины той силы, — каково бы ни было ее существо, — которая держит частицы связными; если захотим разделить обе половины на две части и так последовательно далее, то постоянно будем встречать подобное же сопротивление, но тем меньшее, чем мельче разделяемые части; когда же, наконец, мы прибегнем к тончайшим и острейшим инструментам, каковы тончайшие частицы огня, и посредством их расплавим металл до последних его мельчайших частиц, то в них не останется более не только сопротивления разделению, но даже и возможности к дальнейшему разделению, по крайней мере, орудиями более грубыми, чем частицы огня; какая пила или нож, погружаемые в хорошо расплавленное серебро, найдут что-либо для деления после участия огня? Все вещество уже будет приведено к тончайшим неделимым частицам; если при этом все же останутся части, способные к дальнейшему делению, то достигнуть его мы можем не иначе, как через посредство делительных инструментов еще более острых, чем огонь; но не таковы железные прутики и пластинки, которыми мы мешаем расплавленный металл. Я признаю в воде и других жидкостях такое же строение и расположение частиц и неспособность последних к разделению по причине их тончайшей сущности; если они и не окончательно неделимы, то, по крайней мере, не могут быть разделены доскою или другим твердым телом, служащим орудием в наших руках, так как режущее орудие должно быть тоньше разделяемого твердого тела. Итак, твердые дела, плавающие в воде, только движутся в ней, но не разделяют ее частей, которые уже разделены до крайних пределов и лишь в силу тесного прилегания держатся вместе; эти мельчайшие частицы дают место каждому малому телу, которое опускается в воду, ибо как бы мало и легко оно ни было, спустившись из воздуха и достигнув поверхности воды, оно находит еще более мелкие частицы воды с еще меньшим сопротивлением движению и вытеснению их, чем его собственная давящая и вытесняющая сила, почему оно и погружается и приводит в движение соответствующую своей силе часть воды. Таким образом, в воде нет никакого сопротивления разделению, так как нет частиц, которые могли бы быть разделяемы. Теперь добавлю, что если бы мы нашли какое-либо малейшее сопротивление (что совершенно ложно), желая при помощи волоса привести в движение большое плавающее тело или прибавлением ничтожной части свинца опустить на дно и, обратно, отнятием свинца заставить подняться на поверхность большую пластинку вещества, вполне сходного с водою по тяжести (чего также не случится, если действовать осторожно), то необходимо заметить, что это сопротивление есть нечто совсем отличное от того, которое противники приводят как причину плавания полосок свинца или эбеновых дощечек, потому что можно сделать эбеновую доску, которая, будучи положена на воду, {79} станет плавать, и чтобы потопить ее, недостаточно будет и ста гран свинца; но если потом смочить эту доску водою, то она не только опустится без всякого свинца, но и никакая пробка или другое легкое тело, прикрепленное к ней, не сможет удержать ее от погружения на дно. Отсюда видно, что если мы даже допустим наличность в субстанции воды какого-то малого сопротивления разделению, то оно совершенно ничтожно по сравнению с причиной, удерживающей на воде дощечку и обладающей силою в сто тысяч раз большей той, какую можно предположить в частицах воды. Пусть также не говорят мне, что только поверхность воды обладает свойством сопротивления, а не внутренние части, или что такое сопротивление, вероятно, больше при начале разделения, как то, по-видимому, имеет место при движении, когда тело оказывает более сопротивления при начале движения, нежели при продолжении его, потому что, во-первых, я предложу привести воду в движение и перемешать верхние слои со средними и нижними, или, устранив верхние слои, воспользоваться только средними — все равно, результат получится одинаковый. Волос, тянущий по воде бревно, должен разделять именно верхние ее части, а также начать движение, и все же он начинает его и разделяет воду; наконец, поместив дощечку среди воды, продержим ее там в покое некоторое время, а затем опустим; она тотчас же начнет движение вниз и продолжит его до самого дна; но и дощечка, остающаяся поверх воды, не должна начинать движения или разделения водяных частиц, так как на известную глубину она уже погрузилась.
Итак, признаем правильным и несомненным тот вывод, что вода не оказывает никакого сопротивления простому разделению и что невозможно найти такое твердое тело, какой бы то ни было формы, которое, будучи помещено в воду, было бы лишено возможности благодаря плотности последней двигаться вниз и вверх сообразно тому, превосходит ли оно воду по весу или уступает ей, хотя бы такой излишек или разница были неощутимы. Когда же мы видим, как доска из эбена или другого вещества тяжелее воды останавливается на границе воды и воздуха, не погружаясь, то, чтобы открыть причину такого явления, мы должны будем прибегнуть к чему-либо другому, а не к ширине фигуры, неспособной преодолеть сопротивления, оказываемого водою разделению, ибо такого сопротивления не существует, а тому, что не существует, нельзя приписывать никакого действия.
Итак, остается признать вполне правильным то, что уже было сказано выше, а именно: указанное явление происходит по той причине, что помещается в воду не то тело, которое тонет, ибо тонет чистая эбеновая доска, которая, будучи тяжелее воды, идет ко дну,— кладется же на воду соединение эбена и некоторого количества воздуха, которое по удельному весу легче воды и потому не опускается. {80}
Подтверждаю еще более то, что сказано. Мы согласились, синьоры противники, что тяжесть твердого тела, большая или меньшая по отношению к тяжести воды, есть истинная и действительная причина его движения в воде вниз и вверх. Теперь, если вы желаете показать, что кроме названной причины существует еще другая, настолько сильная, что может помешать движению ко дну опускающегося из-за своей тяжести тела или даже изменить это движение, и выставляете как такую причину ширину фигуры тела, вы обязаны каждый раз, как хотите показать опыт, сначала удостовериться, что тело, помещаемое вами в воду, действительно по удельному весу не легче воды, ибо, если вы этого не сделаете, каждый с основанием может сказать, что не фигура, а легкость тела есть причина его плавания. Но я говорю вам, что когда вы показываете, как кладете в воду эбеновую дощечку, в действительности вы кладете тело по удельному весу не большее, но меньшее воды, ибо вместе с эбеном идет в воду некоторый объем воздуха в соединении с дощечкою, который настолько легок, что из обоих образуется соединение легче воды; отнимите теперь воздух и положите в воду один эбен, т. е. тело тяжелее воды, и если оно не пойдет ко дну, то вы рассуждаете правильно, я же ошибался.
Теперь, после того как найдена истинная причина плавания тел, которые как более тяжелые должны бы были идти ко дну, мне кажется, что для полного и ясного познания этого вопроса было бы хорошо на опыте раскрыть те особые условия, с которыми связаны подобные явления, рассмотрев, какие пропорции должны иметь разные фигуры из разных веществ в соответствии с тяжестью воды, чтобы в силу пристающего к телу воздуха удерживаться на поверхности.
Для большей ясности, пусть имеем сосуд DENE, содержащий воду, и пластинку или дощечку, толщина которой определяется линиями IС, OS; пусть она сделана из вещества тяжелее воды, так что при помещении на поверхность воды она опускается ниже уровня воды в сосуде, оставляя по сторонам валики АI, ВС предельной величины, т. е. такой, что если пластинка опустится еще хотя на самое ничтожное расстояние, то валики не удержатся, но, вытеснив воздух AICB, растекутся над поверхностью IС и затопят пластинку. Величина AI или ВС есть, следовательно, наибольшая глубина, которую допускают валики воды. Теперь я говорю, что на основании этой величины и отношения веса веществ к весу воды мы легко можем найти, какой предельной толщины могут достигать названные пластинки из разного материала, чтобы продолжать удерживаться на воде. Положим, что вещество пластинки IS будет вдвое тяжелее воды; в таком случае пластинка из этого вещества может иметь толщину, приблизительно равную высоте AI, что докажем следующим образом. Пусть тело IS по удельному весу вдвое тяжелее воды и имеет форму правильной призмы или цилиндра, т. е. имеет две плоских поверхности, {81} верхнюю и нижнюю, совершенно сходные, равные и перпендикулярные к боковым поверхностям; пусть, далее, толщина его —IO равна максимальной высоте валиков воды. Утверждаю, что, будучи положено на воду, тело это не потонет, ибо, если высота AI равна высоте IO, то объем воздуха ABCI будет равен объему тела CIOS, и весь объем AOSB —
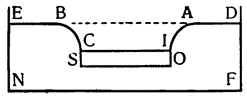 |
Если тело IS будет превосходить воду по удельному весу в полтора раза, то оно останется наверху все время, пока его толщина не превысит двойной предельной высоты валиков, т. е. AI. Так как вес тела IS равен полуторному весу воды, а высота OI равна двойной высоте IA, то погрузившееся тело AOSB будет по объему в полтора раза более тела IS. А так как воздух АС не увеличивает и не уменьшает веса тела IS, то количество воды, занимающее пространство погрузившегося объема AOSB, весит столько же, сколько этот погрузившийся объем; следовательно, объем этот остановится. И вообще всякий раз, когда отношение излишка удельного веса тел над весом воды к весу воды будет равно отношению высоты водяного валика к толщине тела, последнее не пойдет ко дну, при несколько же большей толщине — потонет.
Если тело IS тяжелее воды и имеет такую толщину, что отношение высоты валика AI к толщине тела 10 равно отношению излишка веса этого тела IS над весом объема воды, равного объему IS, к общему весу объема воды, равного объему IS, то утверждаю, что тело IS не потонет, при всякой же большей толщине пойдет ко дну. Как AI относится к IO, так и излишек веса тела IS над весом объема воды, равного объему IS, относится к такому же объему воды, откуда вытекает, что как AO относится к OI, так и вес тела IS относится к весу воды, взятой в объеме, равном IS; обратно, отношение веса воды в объеме IS к весу тела IS будет равняться отношению IO к ОА, но как IO относится к ОА, так относится и объем воды IS к объему воды, равному объему ABSO, или вес объема воды IS к весу объема воды AS; следовательно, вес тела IS равен весу объема воды, равного объему AS; но вес тела IS тот же, что и вес тела AS, составленного из тела IS и воздуха {82} ABCI; с другой стороны, все составное тело AOSB весит столько же, сколько весит вода, которая занимала бы место этого соединенного тела AOSB; а посему получится равновесие и покой, и тело IOSC более не погрузится20. Если бы толщина тела увеличилась, то следовало бы увеличить и высоту валиков AI, чтобы сохранить требуемое отношение; но, согласно условию, высота валика AI есть наибольшая, какую только допускает природа воды и воздуха; при увеличении ее вода вытеснит воздух, прилегающий к поверхности тела IС, и заполнит пространство AICB. Следовательно, тело большей толщины, чем IO, и того же вещества, как тело IS, не останется наверху, но опустится на дно, что и требовалось доказать. Из только что мною доказанного могут быть сделаны многие выводы, подтверждающие истинность моего основного положения, которые также покажут, насколько несовершенны были до сего времени суждения по данному вопросу.
Прежде всего из доказанного вытекает, что все вещества, даже самые тяжелые, могут удерживаться на воде, не исключая и золота, самого тяжелого из всех известных нам тел. Приняв во внимание, что вес золота в двадцать раз больше воды, и определив максимальную высоту валика, который может образовать вода, не разрушая воздушного покрова, одевающего поверхность помещаемого на воду тела, сделаем золотую пластинку такой толщины, чтобы последняя не превышала девятнадцатой части высоты названного валика; пластинка, положенная осторожно на воду, останется на поверхности, не опускаясь на дно. Если, например, взять эбен, удельный вес которого относительно воды равен одной и одной седьмой, то наибольшая толщина, какую можно придать эбеновой дощечке, чтобы она оставалась, не погружаясь, будет в семь раз больше высоты валика; медь же, которая в восемь раз тяжелее воды, будет плавать всякий раз, когда толщина ее пластинки не превысит одной седьмой части высоты валика.
Не хочу обойти молчанием и не отметить, как второй вывод из доказанного, что размеры поверхности не только не являются причиною плавания тяжелых тел, которые в ином виде погружаются, но и не влияют нисколько на определение того, каковы должны быть те пластинки из эбена, железа или золота, которые могут оставаться на поверхности; при таком определении следует принимать во внимание одну лишь толщину фигур из эбена, золота и т. д., оставляя совершенно в стороне соображения о длине и ширине, как не оказывающих никакого влияния на данное явление. Уже было выявлено, что причиною плавания таких пластинок служит единственно уменьшение их веса по отношению к весу воды благодаря присоединению воздуха, который вместе с ними опускается и занимает место в воде; когда это место, занятое в воде ранее, чем окружающая вода разольется и заполнит его, вытесняет столько воды, сколько весит {83} пластинка, то она остается подвешенной на воде и не тонет. Теперь видно, от которого из трех измерений тела зависит решение вопроса — каков должен быть объем тела, дабы помощи присоединенного к нему воздуха было достаточно, чтобы сделать его по удельному весу легче воды, отчего оно и останется непогруженным; мы нашли, что длина и ширина несомненно не принимают никакого участия в этом определении, но единственно высота или, если угодно, толщина, так что если взять пластинку или дощечку, например из эбена, толщина которой находилась бы в определенной нами пропорции к предельной высоте водяного валика, то она будет плавать, чего не случится при увеличении ее толщины; скажу, далее, что, сохраняя ее прежнюю толщину, мы можем увеличить ее поверхность в два, четыре, десять раз или уменьшить ее разделением на четыре, шесть, двадцать или даже сто частей — и все же она останется таким же образом на поверхности. Но если хотя на один волос увеличится ее толщина, то она потонет, хотя бы поверхность ее увеличилась в сотни и тысячи раз. Итак, истинная причина есть та, присутствие которой производит данное действие, а отсутствие прекращает его; увеличение же или уменьшение каким бы то ни было способом ширины и длины тела не производит и не задерживает опускания на дно; следовательно, увеличение или уменьшение поверхности не оказывает никакого влияния на то, пойдет ли тело ко дну или нет. Тот факт, что при сохранении указанным выше способом найден-ной пропорции между высотою валика воды и высотою тела большая или меньшая поверхность не вносит никакой разницы, вытекает из доказанного выше, а также из того, что объемы призм и цилиндров с одинаковым основанием относятся друг к другу, как их высоты; поэтому все цилиндры и призмы, большие и малые дощечки, если только все они имеют одинаковую толщину, сохраняют одно и то же отношение к прилегающему воздуху, имеющему основанием поверхность дощечки, а высотою — высоту водяного валика, так что из дощечки и воздуха постоянно получаются тела, одинаковые по весу с весом воды, взятой в объеме этих тел, составленных из воздуха и дощечки; поэтому-то все такие тела и остаются на поверхности. Заметим, в-третьих, что всякая фигура из какого угодно вещества, даже тяжелее воды, может благодаря валику удержаться от погружения на дно, но некоторые фигуры, хотя бы из тяжелейшего вещества, могут даже оставаться целиком над водой, смочив только нижнюю свою поверхность, соприкасающуюся с водой; такими именно будут все фигуры, которые от основания идут вверх суживаясь, чему в пример приведем теперь пирамиды и конусы, имеющие между собою много общего. Итак, покажем, как можно сделать пирамиду или конус какого угодно предложенного вещества, которые, будучи опущены основанием на воду, не только не тонут, но смачивают водою только свое основание. Для объяснения этого необходимо сначала доказать следующую лемму, а именно: {84} тела, объемы которых обратно пропорциональны их удельному весу, равны по абсолютному весу.
Пусть даны два тела АС и В, причем объем АС так относится к объему В, как удельный вес тела В к удельному весу тела АС. Утверждаю,
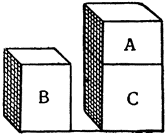 |
Доказав это, утверждаю, далее, что из любого предложенного вещества возможно сделать пирамиду или конус с любым основанием, которые, будучи
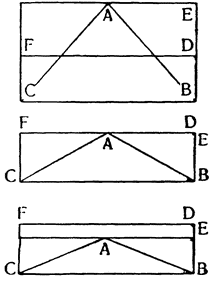 |
Ясно также, как могут быть построены конусы и пирамиды из любого вещества тяжелее воды, которые, будучи помещены в воду вершиною или острием вниз, остановятся, не погружаясь на дно. Припомним все то, что было доказано выше относительно призм и цилиндров, и построим на основаниях, одинаковых с основанием этих цилиндров, конусы из того же вещества, но в три раза выше; они останутся наверху, так как по весу и объему они будут равны цилиндрам, а имея одинаковое с ними основание, захватят наверху одинаковые объемы воздуха, содержащегося между валиками. То, что в виде примера доказано относительно призм, цилиндров, конусов или пирамид, может быть доказано и относительно тел всякой иной формы, но для этого пришлось бы написать целый том, если пожелать включить туда специальные доказательства для всех тел и их сегментов — так велико их число и разнообразие свойств и признаков. Чтобы не растягивать настоящего трактата до бесконечности, я хотел бы ограничиться тем, что сказано выше, полагая, что каждый, обладающий хотя бы средним развитием, понял, что нет такого тяжелого вещества, вплоть до самого золота включительно, из которого нельзя было бы сделать разнообразных фигур, которые поддерживаются и не опускаются на дно в силу пристающего к ним верхнего воздуха, но отнюдь не
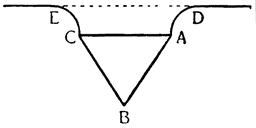 |
Для того чтобы доказать это, возьмем конус ABC по удельному весу в два раза больше воды, и пусть высота его будет равна тройной высоте валика DACE. Утверждаю, во-первых, что помещенный осторожно в воду вершиной вниз конус не опустится на дно: воздушный цилиндр, заключающийся между валиками DACE, равен по объему конусу ABC, так что весь объем тела, составленного из воздуха DACE и конуса ABC, будет вдвое более конуса ABC; так как конус ABC сделан из вещества вдвое тяжелее воды, то вода в объеме, занимаемом всем телом DABCE, помещающимся ниже уровня воды, весит столько же, сколько конус ABC; отсюда установится равновесие, и конус ABC не потонет.
Далее, утверждаю, что тот же конус, помещенный основанием в воду, упадет на дно, и невозможно, чтобы он каким бы то ни было образом остался на поверхности. Так, пусть конус ABD будет по удельному весу вдвое тяжелее воды, а высота его — втрое более высоты валика LB. Как уже было выяснено выше, то, что тяжелее воды, не остается на ее поверхности; но так как цилиндр, заключающийся между валиками LBDP, равен конусу ABD, а вещество конуса вдвое тяжелее воды, то ясно, что вес этого конуса будет в два раза больше, чем вес объема воды, равного цилиндру LBDP, почему конус не останется в прежнем положении, но потонет.
Говорю, далее, что во многих случаях конус остановится, погрузившись частью в воду, что можно понять путем сравнения с водою как
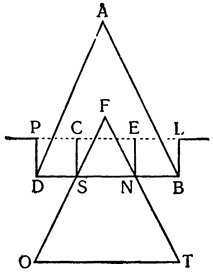 |
Перехожу теперь, в-четвертых, к установлению и доказательству моим противникам следующего предложения, а именно, что возможно сделать твердые тела любой фигуры и любой величины, которые по природе своей идут на дно, но с помощью воздуха, содержащегося между валиками, остаются наверху, не погружаясь.
Истина этого предложения достаточно обнаруживается на примере всех твердых фигур, оканчивающихся в своей верхней части плоской поверхностью.
Если мы сделаем такие фигуры из какого-нибудь вещества, равного воде по удельному весу, и поместим их в воду, так что ею покроется весь объем, то ясно, что такие тела могут оставаться в покое во всяком месте при условии, что удельный вес материала в точности соответствует весу воды; вследствие этого они могут остаться и на поверхности воды, не образуя даже никакого валика. Теперь, если такие фигуры благодаря веществу, из коего они сделаны, способны оставаться на поверхности, хотя и лишены помощи валиков, то ясно, что можно настолько увеличить вес тел, не увеличивая их объема, насколько велик вес воды, содержащейся внутри валиков, образующихся вокруг их верхней плоской поверхности; с помощью валика они задержатся на поверхности, но, будучи смочены, пойдут на дно, сделавшись более тяжелыми, чем вода. Относительно фигур, кончающихся наверху плоскостью, вполне понятно, как приданный им или отнятый валик может устранить или вызвать опускание, но что касается {88} тел, которые идут кверху, утончаясь, то кто-нибудь может, и, по-видимому, не без основания, усумниться, чтобы с ними можно было сделать то же самое, в особенности, если они оканчиваются острою вершиною, как, например, узкие конусы или пирамиды. Относительно этих последних как более сомнительных, чем все другие, я постараюсь доказать, что и они подчинены тому же условию опускания или неопускания на дно вне зависимости от величины.
Пусть ABD будет конус из вещества, равного воде по удельному весу; ясно, что помещенный весь в воду он останется в покое во всяком месте (предполагая, что он весит ровно столько же, сколько вода, чего на самом деле почти невозможно достигнуть), при добавлении же самой малой тяжести — пойдет ко дну. Но если он будет опускаться вниз тихо, то утверждаю, что образуется валик ESTO, и вне воды останется верхушка конуса AST тройной высоты по сравнению с высотой валика ES; это следует из того, что при весе вещества конуса, равном воде, затонувшая часть SBDT остается безразличной к движению вверх или вниз, конус же AST, будучи по объему равным воде, помещающейся внутри валика ESTO, будет равен ей также и повесу; посему во всем наступит равновесие, а следовательно, и покой. Теперь возникает сомнение в том, можно ли сделать конус ABD более тяжелым, так, чтобы, помещенный в воду, он стремился
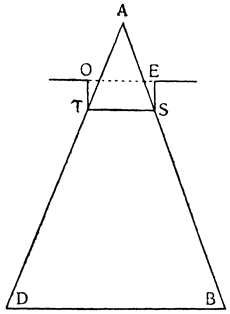 |
Пусть ABD будет конус любой величины из материала, по удельному весу равного воде. Ясно, что опущенный осторожно в воду он остановится, не утонув, и вне воды останется его верхушка AST тройной высоты по сравнению с высотою валика ES. Предположим теперь, что конус ABD
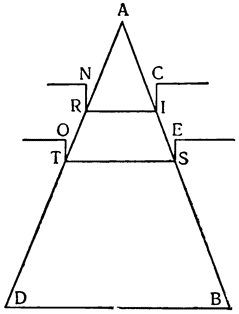 |
Если бы высота конуса AIQ составляла две трети высоты конуса ASTy то объемы конусов AST и AIR относились бы друг к другу, как 27:8, {90} а объемы цилиндров ESTO и CIRN, как 9:4 или 27:12, следовательно, объем цилиндра CIRN относился бы к объему конуса AIR, как 12:8, излишек же объема цилиндра CIRN над объемом конуса AIR к объему конуса AST, как 4:27; таким образом, если к конусу ABD прибавить такую тяжесть, которая бы равнялась 4/27 веса конуса AST, что составит немного более 1/7 части, то он останется на поверхности, и высота выступающей из воды верхушки будет равна двойной высоте валика. То, что здесь доказано относительно конусов, может быть применено и к пирамидам, хотя бы те и другие были весьма остры; отсюда можно заключить, что совершенно то же самое еще легче произойдет со всякими иными фигурами, которые оканчиваются менее острыми вершинами и поддерживаются валиками большого объема.
Следовательно, фигуры любой величины могут опускаться или не опускаться на дно в зависимости от того, будут ли их вершины смочены водою или нет; а так как это явление общее для всех видов фигур без всяких исключений, то, значит, фигура не оказывает никакого влияния на явление опускания в одном случае и неопускания в другом, которое происходит единственно от присоединения или отнятия прилегающего сверху воздуха. Всякий, кто рассмотрит внимательно и, как говорится, непредубежденным глазом это дело, признает указанную выше причину за истинную, естественную и первичную причину нахождения тел на поверхности или их опускания, каковая сводится к избытку или недостатку тяжести воды над тяжестью тела, помещаемого в воду. Как полоса свинца толщиною в ручку ножа, будучи помещена в воду одна, идет ко дну, но с привязанной к ней сверху пробкою пальца в четыре толщиной остается на поверхности, потому что теперь тело, помещаемое в воду, будет уже не тяжелее, но легче воды, так и эбеновая дощечка, по природе своей более тяжелая, чем вода, опускается, если кладется в воду одна; если же она помещается на воду в соединении со слоем воздуха, опускающегося вместе с эбеном, и притом в таком количестве, что образовавшееся соединение легче объема воды, соответствующего объему части тела, уже опустившейся и находящейся ниже уровня воды, то она не пойдет ко дну, но остановится и не по какой иной причине, кроме универсальной и всеобщей, а именно: тела, которые по удельному весу легче воды, не идут ко дну.
Отсюда тот, кто взял бы свинцовую пластинку, примерно в палец толщиной и в ладонь в других направлениях, и пытался заставить ее остаться на поверхности, осторожно опуская на воду, напрасно потерял бы свой труд, потому что как только она углубится на волос более возможной высоты валиков воды, так покроется водою и затонет; но если бы, пока пластинка опускается, вокруг нее могли образоваться валики, которые задержали бы распространение воды поверх пластинки, и борты которых поднимались бы настолько высоко, чтобы вместить внутри себя столько {91} воды, сколько весит пластинка, то она, без сомнения, не потонула бы, но осталась, поддержанная силою воздуха, заключенного внутри названных бортов, так что в результате образовался бы сосуд со свинцовым дном. Если же свинец будет настолько тонок, что ничтожная высота бортов достаточна, чтобы вместить столько воздуха, сколько является необходимым для поддержания его на поверхности, то он останется наверху и без бортов, но не без воздуха, потому что воздух сам по себе образует борты, достаточные при их малой высоте, чтобы задержать распространение воды; отсюда и то, что плавает в настоящем случае, есть также сосуд, наполненный воздухом, силою которого он и держится, не утопая.
В заключение постараюсь другим опытом устранить всякие сомнения, если только осталось еще какое-нибудь место для них, относительно воздействия на тонкую плавающую пластинку соприкасающегося с нею воздуха, и затем закончу эту часть моего рассуждения.
Представляю себе, что вместе с кем-нибудь из противников я рассматриваю вопрос, не оказывает ли фигура влияния на увеличение или уменьшение сопротивления какого-либо веса при поднятии его в воздухе; и я, защищая положительное решение, утверждаю, что объем свинца в форме шарика может быть поднят с меньшим усилием, чем тот же свинец в виде тонкой и широкой пластинки, потому что широкая фигура должна прорезать большее количество воздуха, а более сжатая и плотная — меньшее; чтобы доказать то, что кажется мне верным, подвешиваю к тонкой нитке сначала шарик и кладу его в воду, прикрепив поддерживающую его нитку к одному из концов коромысла весов, которые держу в воздухе; к другому концу прибавляю такой вес, который оказывается достаточным, чтобы поднять шарик и извлечь его из воды, для чего понадобится, предположим, вес в 30 унций. Превращаю потом тот же свинец в плоскую легкую пластинку, которую также кладу на воду, подвесив на трех нитях, чтобы удержать ее параллельно поверхности воды, прибавляю на чашку весов гири до тех пор, пока пластинка не поднимется и не извлечется из воды, и показываю, что и 36 унций недостаточно, чтобы отделить ее от воды и поднять на воздух. Основываясь на этом опыте, утверждаю, что во всей полноте доказал правильность моего предложения.
Тогда выступает мой противник, заставляя меня на некоторое время поникнуть головою, и обращает мое внимание на явления, которых я ранее не замечал, показывая мне, что пластинка, выходя из воды, тянет за собой другую водяную пластинку, которая, прежде чем отделиться и отстать от нижней поверхности свинца, поднимается над общим уровнем воды более, чем на лезвие ножа. Возвращаясь к повторению опыта с шариком, он показывает мне, что к плотной и сжатой фигуре прилегает ничтожное количество воды; это внушает мне мысль, что не удивительно, если при отделении от воды тонкой и широкой пластинки чувствуется гораздо {92} большее сопротивление, чем при отделении шарика, ибо вместе с пластинкой поднимается и большее количество воды, что не имеет места при опыте с шариком, и заставляет обратить внимание на то, что вопрос наш теперь свелся к тому, существует ли большее сопротивление подъему широкой свинцовой пластинки с большим количеством воды, чем шарику с малым. Наконец, он указывает мне, что класть сначала пластинку и шарик в воду, чтобы затем доказывать их сопротивление в воздухе, не соответствует предмету нашего спора, так как мы рассуждаем о подъеме предметов в воздухе и вещах, находящихся в воздухе, а не о сопротивлении, проявляющемся на границе воздуха и воды, или о вещах, находящихся частью в воде, частью в воздухе. Тот же опыт показывает осязательно, что, когда пластинка находится в воздухе и свободна от тяжести воды, она поднимается совершенно тою же силою, как и шарик. Видя и поняв все это, я могу только признать себя убежденным и благодарить друга за то, что он научил меня тому, чего я ранее не заметил. Наученный таким случаем, говорю противникам: у нас идет вопрос о том, одинаково ли опускаются на дно шарик и дощечка из эбена, а не эбеновый шарик и эбеновая дощечка, связанные с воздушным слоем; что мы говорим об опускании и неопускании в воде, а не о том, что происходит на границе воды и воздуха с телами, находящимися частью в воде, частью в воздухе; что мы не рассуждаем о большей или меньшей силе, потребной для отделения того или иного тела от воздуха. Не могу напоследок умолчать, что совершенно так же сопротивляется воздух, отягчая, так сказать, движение вниз к воде, как сопротивляется вода и отягчает движение вверх в воздух; одинаково затруднительно как опустить в воду ведро, полное воздуха, так и поднять в воздух ведро, полное воды, не принимая в соображение веса сосуда, а рассматривая только воду и воздух. Равным образом верно, что нам одинаково трудно как в том случае, когда вводим вниз под воду стакан или другой сосуд, полный воздуха, так и в том, когда поднимаем этот стакан, пока он полон водой, держа его отверстием книзу, над поверхностью воды; вода принуждена следовать за стаканом, содержащим ее, и подняться над общим уровнем воды в пределах воздуха таким же образом, как воздух принужден сопровождать сосуд вниз в пределы воды до тех пор, пока в последнем случае вода, перейдя за край стакана, не устремится туда, вытесняя воздух, а в первом — пока края не выйдут из воды и не достигнут пределов воздуха, после чего вода падает вниз, а воздух проскальзывает и заполняет внутренность сосуда. Отсюда следует, что тот, кто берет дощечку, соединенную с воздухом, чтобы выяснить, опустится ли она на дно, нарушает поставленные условия в не меньшей мере, чем тот, кто доказывает наличие сопротивления подъему в воздухе, пользуясь свинцовой пластинкой, соединенной с некоторым количеством воды.
Я говорил то, что пришло мне на мысль для доказательства {93} истины того положения, которое я взялся защищать. Мне остается теперь рассмотреть, что по этому предмету пишет Аристотель в конце книги «О небе», причем отмечу по этому поводу два пункта. Верно то, как мною доказано, что фигура не имеет отношения к причине простого движения вверх или вниз, и, кажется, Аристотель при первоначальном обсуждении этой проблемы держался такого же мнения, что, как мне думается, можно вывести из его же слов. Однако верно и то, что, желая затем объяснить причину явления, к которому он, как и другие, по моему мнению, подошел неправильно (что рассмотрю в другом месте). Аристотель пришел к признанию участия в этом явлении и ширины фигуры.
Что касается первого пункта, — вот точные слова Аристотеля: «Фигуры не суть причины, производящие простое движение вниз или вверх, но лишь причины медленности или быстроты движения, а по каким причинам это происходит — не трудно видеть».
Здесь, во-первых, я отмечаю, что в данном рассуждении встречаются четыре понятия: движение, покой, медленность и быстрота; и так как Аристотель указывает на фигуры как причину медленности или быстроты, исключая их из категории причин абсолютного и простого движения, то он по необходимости должен исключить их и из причин покоя, так что его мысль можно было бы выразить точнее следующим образом: фигуры не суть причины, производящие абсолютное движение или покой, но лишь причины медленности или быстроты. Если кто-нибудь скажет, что, по мнению Аристотеля, фигуры исключаются, как причина движения, но никак не покоя, и что его мыслью было отрицание за фигурами свойства являться причинами простого движения, но не покоя, то я спрошу его, не должно ли вместе с Аристотелем признать, что все фигуры вообще в известной мере являются причиною покоя в тех телах, которые иначе двигались бы, или же этим свойством обладают только некоторые особые фигуры, как, например, широкие и тонкие; если все без различия, то значит всякое тело придет в состояние покоя, потому что всякое имеет какую-нибудь фигуру, что неверно; если же только какие-нибудь особенные фигуры, например широкие, могут быть в известной мере причиной покоя, то, значит, другие будут в некоторой мере причиною движения. В самом деле, видя, что некоторые тела при сжатой фигуре движутся, а затем, расширенные в виде пластинки, останавливаются, я могу заключить, что обширность фигуры имеет отношение к причине такого покоя; видя, с другой стороны, что такие пластинки остаются в покое, а затем, будучи сжаты, движутся, могу с одинаковым основанием утверждать, что сжатость и плотность фигуры имеют отношение к причине движения, а это прямо противоположно тому, что говорит Аристотель, т. е. что фигуры не суть причина движения. Притом, если бы Аристотель признавал, а не исключал фигуру как причину покоя в некоторых телах, которые, будучи сведены {94} к другим фигурам, пришли бы в движение, то этому совершенно не соответствовали бы непосредственно следующие его слова, в которых он выражает недоумение относительно того, откуда происходит, что широкие и тонкие пластинки из железа и свинца останавливаются в воде; это была бы непонятно, если бы имелась налицо готовая причина — обширность фигуры. Итак, заключаю, что мыслью Аристотеля в данном месте было утверждение, что фигуры не являются причиною абсолютного движения или покоя, но лишь быстроты или медленности движения; этому можно поверить, тем более, что в действительности такая мысль и такое выражение совершенно правильны. Теперь, если мысль Аристотеля была такова, то по своим следствиям она на первый же взгляд скорее противоположна, нежели благоприятна мнению моих противников; но их толкование не совсем таково, причем одними это место понимается так, другими толкуется иначе. Что это действительно имеет место, можно судить по объяснению его смысла, даваемому знаменитыми комментаторами, согласно которому прилагательные «простой» или «абсолютный» в тексте Аристотеля относятся не к слову «движение», а к существительному «причина»; так что смысл слов Аристотеля заключается в утверждении, что фигуры не суть абсолютно причины движения или покоя, но суть причины второстепенные23, т. е. имеют к нему лишь некоторое отношение, почему и носят название причин вспомогательных и сопутствующих. Такое положение принимается и выдается за правильное синьором Буонамико в книге V, гл. 28, где он пишет следующее: «Существуют другие причины, сопутствующие, благодаря которым некоторые тела плавают, другие же тонут; между ними первое место принадлежит фигуре тел» и т. д.
Относительно такого толкования у меня возникают разные сомнения и затруднения, почему мне и кажется, что словам Аристотеля нельзя придавать такое расположение и смысл. Затруднения эти следующие. Во-первых, по порядку и расположению слов у Аристотеля прилагательные «простой» или, скажем, «абсолютный» отнесены к понятию движения и отделены от слова «причина», что дает мне большое преимущество, ибо текст гласит: «фигуры не суть причины простого движения вверх или вниз, но причины более медленного или быстрого движения», а не так, например: «фигуры не суть простые причины движения вверх или вниз...». А когда слова текста при перестановке получают смысл, отличный от того, какой они имеют при сохранении того порядка, в котором они расположены у автора, то не подобает их переставлять. И кто же станет утверждать, что Аристотель, желая изложить свои положения, расположил слова таким образом, чтобы они могли иметь другой и даже противоположный смысл? Говорю «противоположный», потому что понятые так, как они написаны, они гласят, что фигуры не суть причины движения, переставленные же — гласят, что фигуры являются причинами движения и т. д. {95}
Более того, если бы намерением Аристотеля было сказать, что фигуры не суть простые причины движения вверх и вниз, но только причины второстепенные, то он не прибавил бы следующих слов: «но суть причины более быстрого и более медленного»; прибавление это было бы не только излишне, но и ложно, так как тогда все предложение полностью гласило бы так: фигуры не суть абсолютная причина движения вверх или вниз, но суть абсолютная причина медленности или быстроты движения, что неверно. Первичные причины большей или меньшей быстроты рассматриваются Аристотелем в книге IV «Физики», в отделе 71, с отнесением их к большей или меньшей тяжести движущихся тел относительно друг друга и к большему или меньшему сопротивлению сред, зависящему от их большей или меньшей плотности; эти причины устанавливаются Аристотелем как первичные, и только они две упоминаются в этом месте; фигура же рассматривается потом в отделе 74 скорее как посредствующая причина силы тяжести, которая разделяет среду или фигурою или импульсом; и действительно, фигура сама по себе, без силы тяжести или легкости, не производит ничего
Прибавлю, что если бы Аристотель решил, будто фигура каким-либо образом является причиною движения или покоя, то странным было бы замечание, которое он делает тут же немедленно в форме недоумения, отчего происходит то, что свинцовая пластинка плавает; ибо если бы он тогда же сказал, что фигура некоторым образом есть причина движения или покоя, не приходилось бы недоумевать, по какой причине плавает свинцовая пластинка, приписывая затем причину фигуре и составляя рассуждение в таком виде: фигура есть второстепенная причина неопускания на дно, но теперь возникает сомнение, по какой причине тонкая пластинка свинца не идет на дно; отвечаю, что это происходит от фигуры, — рассуждение, которое не приличествовало бы даже ребенку, а не только Аристотелю. И где же повод для недоумения? И кто не согласится, что если бы Аристотель установил, что фигуры есть некоторым образом причины плавания, то он написал бы прямо в положительной форме: фигура является некоторым образом причиною плавания, посему и свинцовая пластинка, благодаря обширной и широкой фигуре, плавает. Но если мы возьмем предложение Аристотеля так, как я его беру, как оно написано и как на самом деле правильно, то рассуждение его идет превосходно и логично, когда после введения быстроты и медленности весьма кстати высказывается недоумение, и сформулировано так: «фигуры не суть причины простого движения или недвижения вверх или вниз, но суть причины большей быстроты или медленности движения. Если же это так, то недоумеваю относительно причины, по которой происходит, что широкая и тонкая пластинка из железа или свинца плавает». Тут повод для недоумения налицо, так как на первый взгляд кажется, что причиной такого плавания является {96} фигура, ибо тот же свинец и даже в меньшем количестве, но другой формы, идет ко дну; а мы уже выше утверждали, что фигура не оказывает влияния на это явление.
Наконец, если бы намерением Аристотеля было сказать в этом месте, что фигуры, хотя не абсолютно, но по крайней мере некоторым образом являются причиною движения или покоя, то я обращаю внимание, что он упоминает не только движение вниз, но и вверх, а затем приводит как пример лишь опыт со свинцовой пластинкой и эбеновой дощечкой — вещами, которые по своей природе стремятся ко дну, но в силу фигуры (как утверждают некоторые) остаются на поверхности; следовало бы, чтобы кто-нибудь произвел другой опыт с такими вещами, которые по своей природе стремятся на поверхность, но, задержанные фигурою, остаются на дне. Но так как сделать этого невозможно, то заключаем, что Аристотель в данном месте не имел намерения присваивать фигуре никакого действия на абсолютное движение или покой.
Я не решился бы утверждать, что Аристотель далее тонко рассуждает, отыскивая решение возникшего у него сомнения; наоборот, разные представляющиеся мне затруднения позволяют мне усомниться в том, что он здесь вполне выяснил действительную причину; эти затруднения я устраню, готовый изменить свое мнение, как только мне будет доказано, что в высказанном мною нет истины, ибо я гораздо более склонен к признанию ее, нежели к противоречию.
Вопрос, поставленный Аристотелем, таков: отчего происходит то, что широкие пластинки железа, свинца и т. д. плавают, особенно если принять во внимание (как бы укрепляя повод к сомнению), что другие предметы меньшей величины и веса, будучи круглыми или длинными, как, например, игла, — идут ко дну? В этом, наоборот, я не только сомневаюсь, но даже уверен, что игла, осторожно положенная на воду, останется на поверхности так же, как тонкая пластинка железа и свинца. Я не могу поверить, как бы мне это ни объясняли, тому, кто, защищая Аристотеля, скажет, что он подразумевал здесь иглу, помещенную не вдоль, но прямо, острием вниз. Все же, чтобы не оставить и такого выхода, весьма слабого, и от которого, конечно, по моему мнению, отказался бы сам Аристотель, скажу: должно понимать, что игла положена согласно измерению, только что упомянутому Аристотелем, а именно — по длине, и что если бы можно и должно было придать телу другое положение, кроме обозначенного, то я сказал бы, что и железная или свинцовая пластинки также идут на дно, если положить их не плашмя, а на ребро. Но так как Аристотель говорит, что широкие фигуры не идут на дно, то должно понимать, что фигуры положены плашмя; когда же он говорит, что фигуры длинные, как игла, хотя и легки, но не остаются на поверхности, следует понимать, что они положены по длине. {97}
При том же утверждать, что Аристотель подразумевал иглу, поставленную на острие, значит заставлять его сказать большую глупость, потому, что в этом же месте он говорит, что малые частицы свинца или железа, если будут круглы или длинны, как игла, идут на дно; значит, по его мнению, и крупинка железа не может остаться на поверхности; если же он так думал, то какой наивностью было бы добавлять, что и игла, поставленная на острый конец, также не останется наверху? А что же такое самая игла, как не ряд многих крупинок, поставленных одна на другую? Слишком недостойно такого человека было бы сказать, что одна крупинка железа не может плавать, и что она не станет плавать, если на нее наложить еще сотню таких же частиц.
В конце концов либо Аристотель думал, что игла, положенная на воду вдоль, останется на поверхности, либо он думал, что она не останется на поверхности; если он думал, что не останется, то прекрасно мог сказать то, что он действительно и сказал; но если он полагал и знал, что игла будет плавать, то почему же вместе с сомнительной проблемою плавания широких фигур, хотя бы сделанных из тяжелых веществ, не высказал он также недоумение относительно того, почему плавают также и длинные и тонкие фигуры, хотя бы из железа или свинца? И это тем знаменательнее, что повод для недоумения кажется большим относительно фигур длинных и сжатых, чем относительно широких и тонких. Отсюда явствует, что никакого сомнения по этому поводу у Аристотеля не возникало.
Не меньшую нелепость приписал бы Аристотелю тот, кто в защиту его сказал бы, что он подразумевал иглу довольно толстую, а не тонкую, потому что я тотчас же спрошу: а что же он думал о тонкой? Придется ответить: он думал, что она будет плавать, — и тогда я снова обвиню его в том, что он уклонился от более замечательной и трудной проблемы и ввел более легкую и менее замечательную.
Итак, скажем откровенно: Аристотель полагал, что только широкие фигуры остаются на поверхности, длинные же и тонкие —нет. Это, однако, неверно, как неверно и положение относительно круглых тел, потому что, как можно было вывести из всего сказанного выше, и малые шарики из железа и даже свинца таким же образом могут плавать.
Далее, он предлагает другое заключение, которое тоже представляется далеким от истины, а именно, что некоторые предметы по своей малости плавают в воздухе, как-то: мельчайшие пылинки земли и тончайшие листки расплющенного золота; но, мне кажется, опыт показывает нам, что этого не случается не только в воздухе, но даже в воде, в которой опускаются даже мутящие ее мельчайшие частицы земли, малость коих такова, что они могут быть видимы только собранные сотнями. Итак, земляная пыль и листочки золота не держатся в воздухе, но опускаются книзу и носятся только вздымаемые сильным ветром или движимые иным возмущением {98} воздуха, что происходит также и при возмущении воды, которое поднимает отложения со дна и крутит их. Но Аристотель не может подразумевать действия такого возмущения, о котором он вовсе не упоминает, и называет лишь легкость этих частиц и сопротивление плотности воды и воздуха, из чего видно, что он говорит о воздухе спокойном, а не взволнованном или возмущенном; но в таком случае ни золото, ни земля, как бы они ни были измельчены, не держатся, но быстро опускаются.
Затем он переходит к опровержению Демокрита, который, по его свидетельству, предполагал, что некие атомы огня, непрестанно восходящие в воде, толкают вверх и поддерживают такие тяжелые тела, которые довольно широки, в то время как тела узкие опускаются вниз, так как им противодействует и толкает их малое количество названных атомов.
Аристотель выступает против этого положения, говоря, что подобное должно было бы скорее происходить в воздухе, что и сам Демокрит приводит против себя же; коснувшись затем этого вопроса, он легко решает его, говоря, что эти тельца, восходящие в воздухе, стремятся вверх несплоченно. Я не скажу здесь, чтобы признанная Демокритом причина была истинной; скажу только, что она, как мне кажется, недостаточно опровергается Аристотелем, когда он говорит, что если бы было правильно, будто восходящие горячие атомы поддерживают тяжелые, но достаточно широкие тела, то они должны были бы проявлять себя более в воздухе, нежели в воде, потому что, быть может, по мнению Аристотеля, эти горячие тельца с большею силою и быстротою восходят в воздухе, нежели в воде. Если постановка вопроса Аристотелем именно такова, как мне кажется, то я полагаю, что он дает повод заподозрить его в заблуждении, и даже не одном. Во-первых, едва ли правильно, что горячие тельца, будь они частицами огня или его парами, или вообще каким-либо легким веществом, восходящим вверх даже в воздухе, будут подниматься вверх в воздухе быстрее, чем в воде; совершенно обратно, они должны двигаться более стремительно в воде, чем в воздухе, как я уже доказывал выше. И тут я не могу уразуметь причину, по которой Аристотель, видя, что движение вниз одного и того же тела совершается в воздухе с большей быстротою, чем в воде, не обратил нашего внимания на то, что при обратном движении по необходимости должно происходить противоположное, т. е. что оно будет быстрее в воде, чем в воздухе; взяв тело, опускающееся вниз с большею быстротою в воздухе, чем в воде, представим себе, что тяжесть его постепенно уменьшается; сначала оно станет таким, что, опускаясь быстро в воздухе, будет медленно опускаться в воде; затем оно сможет стать таким, что, все же опускаясь в воздухе, в воде будет подниматься; сделанное еще легче, в воде поднимается быстро, в воздухе же будет опускаться; и вообще, ранее чем получить способность подняться в воздухе хотя бы самым медленным движением, оно в воде будет подниматься самым быстрым {99} образом. Если это так, то как же может быть верно, будто то, что самопроизвольно движется вверх, будет быстрее двигаться в воздухе, чем в воде?
То, что заставило Аристотеля полагать, будто движение вверх совершается быстрее в воздухе, чем в воде, было, во-первых, признание им причинами медленности и быстроты движения как вверх, так и вниз только разницы в фигуре движущегося тела и большего или меньшего сопротивления среды, обладающей большей или меньшей степенью плотности или легкости, и непринятие им в расчет относительной тяжести движущегося тела и среды, что, однако, как раз и является главным пунктом в настоящем вопросе. Если бы возрастание или уменьшение медленности или быстроты зависело только от плотности или легкости сред, то всякое движущееся тело, опускающееся в воздухе, опускалось бы и в воде, потому что, какая бы разница ни существовала между плотностью воды и плотностью воздуха, соответственная разница всегда может быть найдена между быстротою движения того же тела в воздухе и какою-либо другой быстротою,, которая и должна быть его естественной быстротой при движении в воде; это между тем совершенно ложно. Другой причиной было его предположение, что подобно тому как существует положительное и природное свойство, в силу которого элементарные тела имеют склонность движения по направлению к центру Земли, то не что иное, как такое же внутреннее свойство некоторых тел, дает им стремление убегать от центра Земли и двигаться вверх; в силу такого внутреннего принципа, называемого им легкостью, тела при таком движении легче разделяют среду более тонкую, чем плотную. Но такое положение одинаково не кажется мне верным, как я частью указывал и раньше, и как рассуждениями и опытом мог бы доказать, если бы настоящий вопрос не представлял такой большой важности, и я мог ограничиться немногими словами.
Итак, положение, выдвигаемое Аристотелем против Демокрита, что если восходящие атомы огня поддерживают тяжелые тела, имеющие широкую фигуру, то это действие их должно проявляться более в воздухе, чем в воде, потому что такие тельца быстрее движутся в воздухе, нежели в воде, нехорошо, ибо должно происходить как раз обратное, так как частицы эти в воздухе поднимаются медленно и, кроме того, что движутся медленнее, идут не сплоченно, как в воде, но разъединяются и, как говорится, рассеиваются, а потому, как хорошо выражается Демокрит в заключение своего предложения, не толкают и не оказывают воздействия совокупно.
Во-вторых, заблуждается Аристотель, когда полагает, что названные тяжелые тела должны легче поддерживаться восходящими горячими частицами в воздухе, нежели в воде, не принимая во внимание, что тела эти в воздухе тяжелее, чем в воде, так что, например, если какое-либо тело {100} весит 10 фунтов в воздухе, то в воде оно, может быть, не весит и 1/2 унции; как же может быть, что его легче поддержать в воздухе, чем в воде? Из этого заключаю, что в данном случае Демокрит рассуждал лучше, нежели Аристотель, Но я вовсе не хочу сказать, что рассуждения Демокрита правильны; напротив, есть наглядный опыт, опровергающий его положение, а именно: если бы было правильно, что восходящие в воде горячие атомы поддерживают тело, которое без их воздействия пошло бы на дно, то из этого вытекало бы, что мы можем найти вещество, по тяжести едва превосходящее воду, которое в форме шарика или другой плотной фигуры шло бы ко дну, встречая на пути малое число атомов огня, а потом, расширенное в широкую и тонкую пластинку, вытеснялось бы вверх действием множества этих телец и поддерживалось ими на поверхности воды. На самом деле этого не случается, и, как показывает нам опыт, тело фигуры, скажем, сферической, которое едва-едва с большой медленностью идет ко дну, опустится и останется там и приведенное к виду какой-угодно иной обширнейшей фигуры. Необходимо поэтому сказать или что в воде вовсе нет таких восходящих атомов огня, или что если они там и есть, то они не обладают силою, достаточной для поднятия и выталкивания на поверхность пластинки из того же вещества, которая без их помощи пошла бы ко дну. Из этих двух предположений я признаю правильным второе, подразумевая, что вода сохраняет свою природную холодность. Но если мы возьмем сосуд из стекла, меди или другого твердого вещества, наполненный холодной водой, и положим в него тело плоской или вогнутой фигуры, настолько мало превосходящее воду по удельному весу, что оно идет ко дну медленно, то, подложив под названный сосуд несколько горячих углей, заметим, как новые огневые тельца, проникая через субстанцию сосуда, поднимутся в субстанции воды и, ударяясь о вышеупомянутое тело, вытолкнут его на поверхность и будут поддерживать его там, пока будет продолжаться поток названных телец; когда же после отнятия огня поток их прекратится, тело вернется на дно, лишенное своей опоры.
Но Демокрит отмечает, что это явление имеет место только тогда, когда дело идет о поднятии и поддержании пластинок из вещества немного тяжелее воды или же очень легких; по отношению же к веществам тяжелым или телам некоторой толщины, как пластинки из свинца или из других металлов, такое явление совершенно отсутствует; в подтверждение этого можно наблюдать, что такие пластинки, поднимаемые атомами огня, восходят через всю глубину воды и останавливаются у пределов воздуха, оставаясь все же под водою; пластинки же противников не останавливаются, если не имеют верхней сухой поверхности, и нет способа сделать так, чтобы они не упали на дно, когда они находятся в воде. Иная, следовательно, причина плавания существует в тех случаях, о которых говорил {101} Демокрит, отличная от причины, действующей в таких случаях, о которых говорим мы.
Возвращаясь к Аристотелю, скажу: мне кажется, что он тем менее основательно опровергает Демокрита, что тот же Демокрит, по словам самого Аристотеля, не приводит тех положений, против которых последний выступает; возражать Демокриту, утверждая, что если бы восходящие горячие тельца были тем, что поднимает тонкие пластинки, то тем более такое тело должно было бы выталкиваться и подниматься ими в воздухе, значит, выказать желание сразить Демокрита, несовместимое с тонкостью основательного рассуждения. То же желание Аристотеля проявляется и в других случаях, чтобы не идти далеко — в отделе, предшествующем тому, который мы разбираем, где он пытается опровергнуть того же Демокрита, когда тот, не удовлетворяясь одним названием, желает подробнее определить, что такое тяжесть и легкость, т. е. причина опускания вниз и восхождения кверху, и вводит понятия полного и пустого, придавая последнее свойство огню, почему он движется кверху, а первое — земле, почему она опускается, и присваивает затем воздуху более огня, а воде более земли. Аристотель, желая найти для движения вверх причину положительную, а не просто, как Платон или другие древние, отрицание или отсутствие свойства, в каком отношении находится пустое к полному, — аргументирует против Демокрита, говоря: если верно то, что ты полагаешь, то, следовательно, найдется такой объем воды, который будет содержать более огня, чем малый объем воздуха, и большой объем воздуха, который будет иметь больше земли, чем малый объем воды, вследствие чего следовало бы ожидать, что большой объем воздуха быстрее будет опускаться вниз, нежели малое количество воды; этого, однако, никогда не случается, и, следовательно, рассуждения Демокрита ошибочны.
Но, по моему мнению, доктрина Демокрита остается не опровергнутой таким рассуждением; напротив, если я не ошибаюсь, манера Аристотеля выводить заключения мало убедительна; если же признать ее убедительной, то можно направить ее и против него самого. Допустим, что Демокрит соглашается с Аристотелем, будто можно взять такой большой объем воздуха, что он будет содержать более земли, нежели некоторое количество воды; но он совершенно отрицает, что такой объем воздуха будет опускаться вниз быстрее, чем малое количество воды, и это по многим причинам. Во-первых, если количество земли, содержащееся в большом объеме воздуха, большее по сравнению с количеством земли, содержащимся в малом объеме воды, должно быть причиною большей быстроты, то прежде всего следовало бы признать, что больший объем простой земли должен двигаться быстрее, чем меньший; это, однако, неверно, хотя Аристотель во многих местах и утверждает это как истину; не большая абсолютная тяжесть, но больший удельный вес есть причина большей быстроты; {102} деревянный шар весом в 10 фунтов опускается не быстрее, чем тот, который весит 10 унций, если оба они из одного вещества, но утверждаю, что свинцовый шарик весом в 4 унции опускается быстрее деревянного весом в 20 фунтов, так как свинец по удельному весу тяжелее дерева. Следовательно, вовсе нет необходимости, чтобы большой объем воздуха, благодаря большому количеству содержащейся в нем земли, опускался быстрее, чем малый объем воды; напротив, каждый объем воды должен будет двигаться быстрее всякого объема воздуха, благодаря относительно большему содержанию земных частиц в воде сравнительно с воздухом. Замечу, во-вторых, что при увеличении объема воздуха увеличивается не только то, что принадлежит в нем земле, но и то, что принадлежит огню; поэтому не в меньшей мере возрастает причина поднятия вверх в силу огня, чем причина опускания вниз, благодаря увеличению земли. Надлежало бы при увеличении количества воздуха увеличить только то, что есть в нем земного, оставляя первоначальный огонь в прежнем состоянии так, чтобы земное увеличенного количества воздуха в каждой части его превосходило земное малого количества воды; только тогда можно было бы с достаточным правдоподобием заявлять, что большое количество воздуха должно опускаться вниз с большим стремлением, чем малое количество воды. В рассуждении Аристотеля, таким образом, более ошибок, чем в рассуждении Демокрита, который с таким же правом мог бы опровергнуть Аристотеля и сказать: если верно, что крайние элементы суть — один абсолютно легкий, а другой — абсолютно тяжелый, а средние элементы причастны в разной степени природе того или другого, причем воздуху более свойственна легкость, а воде тяжесть, то, следовательно, можно найти такой объем воздуха, тяжесть которого будет более тяжести малого количества воды, а потому такой объем воздуха опустится быстрее, чем малый объем воды; но подобного никогда не случается, и, следовательно, неверно, что средние элементы причастны тому или другому свойству. Такой довод неправилен, но не более, чем рассуждение Аристотеля против Демокрита.
В заключение, когда Аристотель говорит, что, если бы учение Демокрита было правильно, то следовало бы ожидать, что большой объем воздуха будет двигаться быстрее малого количества воды, а затем прибавляет, что этого никогда не случается, — мне кажется, было бы желательно услышать от него, где должно было бы происходить то, что он выводит против Демокрита, или какой опыт показывает, что этого не случается. Думать, что это можно увидать в элементе — воде или воздухе — напрасно, потому что ни вода в воде, ни воздух в воздухе не движутся и никогда не стали бы двигаться, какую бы ни приписывать им причастность к земле или огню: земля, не будучи телом жидким, поддающимся движению других тел, является средою, не подходящей для подобного опыта; пустоты, по {103} словам Аристотеля, не существует, а если бы она даже существовала, ничто в ней не двигалось бы; остается область огня, но при ее огромной от нас удаленности какой опыт может убедить нас и дать Аристотелю, опровергающему Демокрита, необходимую уверенность утверждать, как нечто совершенно доступное нашим чувствам, что большой объем воздуха не движется быстрее, чем малое количество воды? Но я не хочу более останавливаться на этом вопросе, хотя мог бы сказать еще многое, и, оставляя в стороне Демокрита, возвращаюсь к тому месту Аристотеля, где последний делает попытку выяснить истинную причину того, почему тонкие пластинки железа и свинца плавают на поверхности воды, и даже само золото, обращенное в тончайшие листки, и мельчайшая пыль носятся не только в воде, но и в воздухе. Он полагает, что из связанных тел одни разделяемы, а другие нет, и из разделяемых одни разделяются легче, а другие труднее, и это-то, утверждает он, — и должно считаться причиною. Потом он добавляет, что легко разделяется то, что хорошо принимает любую форму, и тем легче, чем лучше ее принимает, и что таков, т. е. легче разделяем, воздух сравнительно с водою, и вода сравнительно с землею. Напоследок он высказывает положение, что в каждом веществе легче разделяется и рассеивается меньшее количество,» чем большее.
Здесь я замечу, что заключения Аристотеля в общем все верны, но мне кажется, что он прилагает их к частным случаям, где они не имеют места, в то время как вполне приложимы к другим случаям; так, скажем, воск легче разделяется, чем свинец, а свинец — чем серебро, так же как воск легче принимает всякие формы, чем свинец, а свинец — легче, чем серебро.
Правильно, кроме того, что легче разделяется малое количество серебра, чем большая его масса; и все эти положения верны, потому что правильно, что в серебре, свинце и воске попросту существует сопротивление разделению, а там, где есть абсолютное, там есть и относительное. Но так как ни в воде, ни в воздухе нет никакого сопротивления простому разделению, то как мы можем сказать, что вода труднее разделяется, чем воздух? Выражаясь таким образом, мы не избежим двусмысленности, а потому я повторяю, что сопротивление абсолютному разделению — это одно, сопротивление же разделению, производимому с такой-то скоростью, — — совершенно другое. Чтобы установить покой и задержать движение, необходимо сопротивление абсолютному разделению, сопротивление же быстрому разделению является причиною не покоя, но лишь медленности движения. Но как в воздухе, так и в воде нет сопротивления простому разделению; это ясно из того, что не найдется ни одного твердого тела, которое не разделяло бы и воздух, и воду; утверждение, что сусальное золото и мелкая пыль не способны преодолеть сопротивление воздуха, противно тому, что показывает нам опыт, так как мы видим, что носящиеся {104} в воздухе пыль и золото, в конце концов, оседают вниз и делают это также и в воде, если только помещены в нее и отделены от воздуха. А так как, согласно моему утверждению, ни воздух, ни вода совсем не противодействуют простому разделению, то нельзя сказать, что вода сопротивляется больше, чем воздух. Пусть никто не приводит мне в виде возражения пример легких тел, как-то: пера, кусочка сердцевины маиса и тростника, которые прорезывают воздух, но не воду, желая из этого примера вывести, что воздух разделяется легче воды; я скажу ему, что если он будет хорошо наблюдать, то увидит, как это самое тело разделит связность воды и опустится в нее частью, именно настолько, что занимаемый ею объем воды будет весить столько же, сколько все тело; если все же он будет оставаться в сомнении — не потому ли тело не погружается, что оно не способно разделить воду, — я предложу, чтобы он опустил его под воду, тогда он сам увидит, как оставленное на свободе, оно, поднимаясь, разделит воду не менее быстро, чем разделяло бы воздух, опускаясь. Говорить, что если такое-то тело опускается в воздухе, но, достигнув воды, перестает двигаться, и, следовательно, вода разделяется труднее, — не имеет смысла, потому что я предложу сделать обратное: взять кусок дерева или воска, который поднимется со дна воды, легко разделит и преодолеет ее сопротивление и затем, достигнув воздуха, остановится, едва прикоснувшись к нему; отсюда я с таким же основанием могу заключить, что вода разделяется легче, чем воздух.
Обсуждая этот вопрос, я не хочу умолчать и о другой ошибке того, кто приписывает причину опускания или неопускания на дно меньшему или большему сопротивлению плотности воды ее разделению и, пользуясь примером яйца, которое в пресной воде тонет, в соленой же плавает, видит причину этого в малом сопротивлении разделению пресной воды и в большем сопротивлении воды соленой. Если я не ошибаюсь, из того же опыта может быть сделан совершенно обратный вывод, а именно, что пресная вода более плотна, соленая же реже и легче, ибо яйцо со дна соленой воды быстро восходит на поверхность, разделяя ее сопротивление, чего не может сделать в воде пресной, в которой и остается лежать на дне, не поднимаясь кверху. Вот к каким затруднениям приводят нас ложные принципы; но тот, кто, рассуждая правильно, признает причиною таких явлений разность тяжести движущихся тел и среды, тот скажет, что яйцо идет ко дну в пресной воде, так как оно тяжелее ее, и идет к поверхности в воде соленой, так как легче ее, и без всякого затруднения подтвердит свои заключения.
Итак, совершенно отпадает причина, которую выставляет Аристотель, говоря: «следовательно, предметы, имеющие большую ширину, остаются наверху потому, что много покрывают, а то, что больше, не разделяется». Утверждаю, что такое рассуждение отпадает, ибо неверно, что в воде или {105} в воздухе существует какое-либо сопротивление разделению; к тому же свинцовая пластинка, когда она покоится, уже разделила плотность воды, проникла в нее и погрузилась на глубину в 10 или в 12 раз больше собственной толщины; кроме того, если бы и существовало в воде подобное сопротивление разделению, странно было бы говорить, что оно больше в верхних частях, чем в средних или нижних; если бы даже могло быть какое-либо различие, то более плотными должны были бы быть нижние слои воды, так что пластинка была бы скорее не способна проникнуть через нижние части воды, чем через верхние; а все же мы видим, что как только смачивается верхняя поверхность пластинки, так она тотчас же и без всякой задержки опускается на дно.
Я не думаю, чтобы кто-нибудь (считая, что может таким способом защитить Аристотеля) сказал, что, приняв за верное, будто большее количество воды оказывает большее сопротивление, чем количество малое, мы можем объяснить, почему пластинка, помещенная ниже, опускается на дно, — ибо ей теперь остается разделить меньший объем воды; наблюдая, как пластинка плавает, а затем и тонет в пригоршне воды, испробуем тот же опыт при глубине воды в 10 и 20 локтей и увидим, что последует точное повторение того же явления. Чтобы устранить довольно распространенное заблуждение, упомяну здесь, что судно или другое какое-либо тело, плавающее над глубиною в 100 или 1000 локтей при погружении своего тела в воду на глубину 6 локтей, совершенно таким же образом будет плавать в воде, глубина которой не превосходит 6 локтей и 1/2 дюйма.
Не думаю также, чтобы можно было говорить будто верхние слои воды более плотны, хотя весьма почтенный автор и признавал таковыми верхние воды моря, находя основание этому в том, что они более солоны, нежели более близкие ко дну; но я усомнился бы в этом опыте, разве только при извлечении воды со дна встретился пробивающийся там источник пресной воды; напротив, мы видим, что пресные воды простираются на несколько миль от своего устья над соленой водою моря, не опускаясь в нее и не смешиваясь с нею, если только не происходит какого-либо возмущения или волнения из-за ветров.
Но, возвращаясь к Аристотелю, скажу ему, что ширина фигуры не играет никакой роли в этом явлении, потому что та же пластинка из свинца или другого вещества, обделанная в форме тонких, но длинных полосок, плавает не лучше и не хуже; то же самое будет происходить с этими полосками, если снова разрезать их на малые квадраты, ибо не ширина, но толщина оказывает в этом случае влияние на явление. Скажу ему, далее, что если бы было верно то, что сопротивление разделению есть настоящая причина плавания, много и много лучше плавали бы фигуры более сжатые и короткие, чем обширные и широкие, потому что при увеличении {106} размера фигуры уменьшалась бы легкость плавания, а при ее уменьшении увеличивалась бы. Для выяснения того, что я говорю, необходимо принять во внимание, что, когда тонкая пластинка опускается, разделяя воду, разделение и нарушение связности воды происходят в тех частях, которые находятся вокруг обвода или окружности этой пластинки, и что,
 |
Наконец, по поводу того, что сказано в последней части отдела, т. е. что надлежит сравнивать тяжесть движущегося тела с сопротивлением среды разделению, ибо если сила тяжести превосходит сопротивляемость среды, то тело опускается, если же нет, то оно плавает, нельзя возразить ничего иного, кроме того, что было уже сказано, именно, что в данном случае проявляется не абсолютное сопротивление разделению, которого не существует ни в воде, ни в воздухе, но тяжесть среды по сравнению с тяжестью движущегося тела; если среда обладает большим весом, нежели тело, то последнее не опустится и не погрузится полностью, а только частично, ибо место, которое оно заняло бы в воде, не может быть заполнено телом, имеющим вес меньший, чем соответствующий объем воды; но если тело будет тяжелее воды, то оно опустится на дно, чтобы занять место, пребывать в котором согласно природе ему подобает более, чем другому менее тяжелому телу. И то есть единственная, истинная, присущая телам и абсолютная причина, в силу которой они плавают или опускаются на дно, ибо никакие иные причины не принимают в этом участия; и дощечка моих противников плавает лишь тогда, когда она связана с таким количеством воздуха, что вместе с ним образует тело, которое легче воды в объеме, занятом этим сложным телом; но когда помещается в воду простой эбен, как то и должно быть по сути нашего вопроса, то он всегда идет ко дну, хотя бы был тонок, как бумага.
| {108} |
 |
ТИТУЛЬНЫЙ ЛИСТ ПЕРВОГО ИЗДАНИЯ «БЕСЕД» |
| {109} |
|
БЕСЕДЫ и МАТЕМАТИЧЕСКИЕ ДОКАЗАТЕЛЬСТВА, касающиеся двух новых ОТРАСЛЕЙ НАУКИ, относящихся к МЕХАНИКЕ и МЕСТНОМУ ДВИЖЕНИЮ, синьора С ПРИЛОЖЕНИЕМ |
| {110} |
ПЕРЕВОД
С. Я. ДОЛГОВА
| {111} |
Знаменитейшему синьору
графу ди Ноайль
Советнику его христианскою величества,
кавалеру ордена святою духа, фельдмаршалу эссерцитийскому,
сенешалю и губернатору Роерга,
наместнику его величества в Оверни,
моему глубокоуважаемому синьору и патрону1
С |
ВАШ, ЗНАМЕНИТЕЙШИЙ СИНЬОР, ПРЕДАННЫЙ СЛУГА
ГАЛИЛЕО ГАЛИЛЕЙ
Арчетри, 6 марта 1638 года.
| {113} |
Г |
| {115} |
ПЕРЕЧЕНЬ ГЛАВНЫХ ТЕМ,
излагаемых в настоящем
сочинении
Первая новая наука, касающаяся сопротивления
твердых тел разрушению
ДЕНЬ ПЕРВЫЙ
Какова может быть причина такой связности тел
ДЕНЬ ВТОРОЙ
Другая новая наука, касающаяся местного движения
ДЕНЬ ТРЕТИЙ
О равномерном движении
О естественно ускоренном движении
О принужденном движении или движении бросаемых тел
ДЕНЬ ЧЕТВЕРТЫЙ4
Приложение, содержащее некоторые предложения
и доказательства, касающиеся центра тяжести твердых тел
Об эвклидовых определениях пропорциональности величин
ДЕНЬ ПЯТЫЙ
О силе удара
ДЕНЬ ШЕСТОЙ
| {116} |
Собеседники: Сальвиати, Сагредо, Симпличио
С |
Сагредо. Вы нисколько не ошибаетесь, синьор. Я, будучи по природе любознательным, часто ради удовольствия посещаю это место, наблюдая за деятельностью тех, которых по причине их превосходства над остальными мастерами мы называем «первыми»; беседы с ними не один раз помогли мне разобраться в причинах явлений не только изумительных, но и казавшихся сперва совершенно невероятными. Правда, не раз приходил я при этом в смущение и отчаяние от невозможности постичь то, что выходило из круга моего понимания, но справедливость чего показывал мне наглядный опыт. Что тут мало помогает сказанное кем-либо из древних, — достаточно распространенное мнение и утверждение; но я, более того, считаю такие ссылки совершенно бесполезными, как и многое другое, исходящее из уст людей мало ученых, и полагаю, что все такие объяснения {117} имеют только одну цель — показать, что можешь сказать что-нибудь о том, чего не понимаешь6.
Сальвиати. Вы, синьор, может быть, имеете в виду мой вопрос, заданный тогда, когда мы старались понять причину устройства множества снарядов, подпорок, креплений и иных сооружений для поддержки, пользуясь которыми должны были спустить на воду большую галеру и которых не делают при спуске менее значительных судов; вы ответили мне, что это делается во избежание опасности поломки судна под давлением его собственного громадного веса — опасности, не существующей для малых масс дерева.
Сагредо. Этот факт и в особенности последнее ваше замечание приводят к заключению, которое я всегда считал распространенным, но ошибочным — что относительно этих и других механизмов нельзя делать заключения от малого к большому, так как многие изобретения в машинах удаются в малом, но не применимы в большом. Однако вся механика имеет своею основою геометрию; и мы знаем, что круги, треугольники, а также цилиндры, конусы и другие формы твердых тел не только отличаются друг от друга большей или меньшей величиной, но и изменяются одни по одним, а другие по другим законам. Если поэтому большая машина сделана во всех своих частях пропорционально малой, оказавшейся прочною и пригодной для употребления, то я не вижу, почему мы все же не можем считать себя обеспеченными от какого-либо несчастия или опасности.
Сальвиати. Общераспространенное мнение совершенно ложно, настолько ложно, что скорее можно было бы утверждать как истину противное, а именно, что многие машины можно сделать более совершенными большего размера, нежели меньшего; так, например, часы, показывающие и отбивающие время, легче сделать точными такой-то определенной величины, нежели меньшей. Большей основательностью отличается сходное мнение людей образованных, которые причину различной успешности таких машин, не находящую себе объяснения в чистых и абстрактных положениях геометрии, видят в несовершенстве материи, подверженной многим изменениям и недостаткам. Но, думается, я могу, не навлекая на себя обвинения в дерзости, сказать, что одного несовершенства материи, могущего извратить все выводы чистейшей математики, недостаточно для объяснения несоответствия построенных машин машинам отвлеченным и идеальным. Смею утверждать, что если мы, отвлекшись от всякого несовершенства материи и предположив таковую неизменяемой и лишенной всяких случайных недостатков, построим большую машину из того же самого материала и точно сохраним все пропорции меньшей, то в силу самого свойства материи мы получим машину, соответствующую меньшей во всех отношениях, кроме прочности и сопротивляемости внешнему воздействию; чем больше будет она по размерам, тем менее будет она прочна. Так как я {118} предполагаю, что материя неизменяема, т. е. постоянно остается одинаковой, то ясно, что такое вечное и необходимое свойство может вполне быть основой для чисто математических рассуждений. Поэтому, синьор Сагредо, откажитесь от вашего прежнего мнения, разделяемого также многими механиками, будто машины или приборы, построенные из того же самого материала с точным соблюдением пропорциональности во всех частях, должны одинаково или, лучше сказать, пропорционально своему размеру сопротивляться или уступать внешним воздействиям, потому что геометрически может быть доказано, что большие машины всегда будут менее способны к противодействию. Это справедливо не только по отношению к искусственно сделанным машинам, но и по отношению к натуральным предметам, для которых также имеется неизбежный предел, который не может быть превзойден ни искусством, ни природою; оговариваюсь — не может быть превзойден при соблюдении строгой пропорциональности и тождества материала7.
Сагредо. Я уже чувствую, как меняются мои мысли; подобно тому, как облако озаряется мгновенно молнией, так и мой ум озарился внезапным и необычным светом, который затем опять погас, показав только издали странные и непривычные представления. Из того, что вы только что сказали, я должен, кажется, заключить, что из одного и того же материала невозможно построить двух машин, подобных одна другой, но имеющих различную величину, так, чтобы они были пропорциональны по сопротивляемости; но, если это верно, то невозможно будет найти и двух брусков из одного и того же дерева, сходных по крепости и качеству, но разнящихся по величине.
Сальвиати. Совершенно верно, синьор Сагредо; а чтобы лучше убедиться, что мы пришли с вами к одинаковому заключению, скажу следующее: если мы возьмем деревянное бревно такой-то длины и толщины, вделанное, скажем, в стену под прямым углом так, что оно располагается параллельно горизонту, и предположим, что длина его достигает крайнего предела, при котором оно может еще держаться, т. е. что при увеличении длины его еще на волос оно ломается от собственной тяжести, то бревно это явится единственным в своем роде на свете. Если длина его, предположим, превышает его толщину во сто раз, то мы не сможем найти ни одного бревна из того же дерева, которое при длине, превышающей его толщину во сто раз, было бы способно выдержать ровно столько же, сколько взятое для примера: все бревна большего размера сломаются, меньшего же — будут способны помимо собственной тяжести выдержать и еще некоторую нагрузку. То, что сказано мною о способности выдержать свой собственный вес, применимо и к другим сооружениям; если деревянный брус выдерживает тяжесть, скажем, десяти равных ему брусьев, то подобная ему, но больших размеров балка не сможет выдержать веса десяти {119} одинаковых с нею балок. Обратите внимание, синьор Сагредо, и вы также, синьор Симпличио, сколь правильно наше заключение, которое с первого взгляда кажется таким невероятным; потребовалось лишь немного размышления, чтобы снять с истины скрывающий ее покров и увидеть неприкрытым ее прекрасный лик. Кто не знает, что лошадь, упав с высоты трех-четырех локтей, ломает себе ноги, тогда как собака при этом не страдает, а кошка остается невредимой, будучи брошенной с высоты восьми-десяти локтей, точно так же, как сверчок, упавший с верхушки башни, или муравей, упавший на Землю, хотя бы из лунной сферы; малые дети также остаются здоровыми после таких падений, при которых взрослые ломают себе члены и разбивают головы. Подобно тому, как меньшие животные оказываются относительно более сильными и выносливыми, нежели большие, и меньшие растения держатся лучше; вы оба признаете теперь, я уверен, что дуб в двести локтей вышиной не сможет поддерживать свои ветви совершенно так же, как дуб средней величины, и что природа не могла бы создать лошадь, величиной в двадцать лошадей, или гиганта, в десять раз превышающего обычный человеческий рост, иначе, как чудесным образом, или изменив в достаточной мере пропорцию членов, в особенности костей, весьма и весьма усилив их по сравнению с пропорциями обычного скелета. Равным образом явную ошибку представляет мнение, что искусственные машины, как большие, так и малые, одинаково мощны и прочны. С маленькими обелисками, колоннами и другими твердыми телами мы можем, например, обращаться свободно, наклоняя и поднимая их без риска сломать, в то время как в большом виде эти фигуры разлетелись бы при этом в куски и ни от чего иного, как от собственного своего веса. По этому поводу я могу вам рассказать случай, достойный внимания, как все случаи, которые происходят против ожидания и при которых меры, принимаемые для устранения несчастия, могут оказаться причиною последнего. Большая мраморная колонна была положена двумя своими концами на две массивных деревянных балки; через некоторое время одному механику показалось полезным, дабы предупредить излом колонны посредине, поставить в этом месте третью опору; такая мысль была всеми одобрена, но в действительности случилось нечто совсем обратное: не прошло и нескольких месяцев, как колонна переломилась и притом как раз в середине над новой опорой.
Симпличио. Случай поистине удивительный и действительно «praeter spem».* Как же это могло случиться по причине того, что поставили новую среднюю опору?
Сальвиати. Несчастие произошло именно от этого, и расследование причины устранило элемент чудесного. Когда обе части колонны {120} сложили прямо на землю, то оказалось, что из двух балок, поддерживающих колонну по концам, одна от долгого времени подгнила и опустилась; а так как средняя опора была крепка и прочна, то она и стала причиною того, что половина колонны осталась на весу в воздухе, лишенная поддержки на конце. Таким образом колонна эта переломилась от действия собственного тяжелого веса, чего не случилось бы, если бы она оставалась по-прежнему положенной на две первоначальные опоры; если бы последние и оседали, то колонна следовала бы за ними. Нет никакого сомнения в том, что такого случая не могло бы произойти с маленькой колонной, хотя бы из того же самого материала, если бы длина и толщина ее были пропорциональны размерам большей колонны8.
Сагредо. В справедливости явления я теперь совершенно убежден; но я не могу понять, почему при соответственном увеличении материала не возрастает в той же мере и способность сопротивления. Это смущает меня тем более, что я часто вижу противное в других случаях, когда прочность и сопротивление излому усиливаются в большей степени, чем возрастает толщина материала. Так, например, если в стену вбито два гвоздя, причем один из них вдвое толще другого, то последний может выдержать не только вдвое, но втрое или вчетверо больший груз8a.
Сальвиати. Скажите — в восемь раз больший, и вы будете недалеки от истины; но этот факт не противоречит тому, что было сказано ранее, несмотря на то, что так может показаться вначале.
Сагредо. В таком случае, синьор Сальвиати, не сгладите ли вы, если только можете, эти ухабы и не осветите ли вы эти темные места? Мне кажется, что вопрос о сопротивлении представляет прекрасное поле для исследования и, если вы согласитесь избрать эту тему предметом нашей сегодняшней беседы, то я, а также, полагаю, и синьор Симпличио, будем вам весьма признательны.
Сальвиати. Я всегда готов к вашим услугам, поскольку память поможет мне привести все то, что я слышал от нашего Академика. Последний много поработал над этим предметом, стараясь, по своему обычаю, всему найти геометрическое обоснование, так что не напрасно его учение может претендовать на название новой науки. Если некоторые положения и были уже выдвинуты другими и, прежде всего, Аристотелем, они, однако, не из числа наиболее удачных и, что самое важное, они не выведены с помощью необходимых доказательств из их первоначальных и бесспорных основ. Поэтому я постараюсь, если можно так выразиться, неоспоримо доказать вам все мои положения, а не только убедить вас правдоподобными рассуждениями; при этом я предполагаю, что вы настолько знакомы с основаниями механики, насколько это необходимо для нашей цели9.
Прежде всего, нам надлежит рассмотреть, что собственно происходит, когда ломается кусок дерева или другого тела, части которого прочно {121} связаны между собою. Это есть первичное явление, из которого выводится первый и простейший принцип, лежащий в основе всего остального. Для лучшего объяснения представим себе цилиндр или призму АВ из дерева
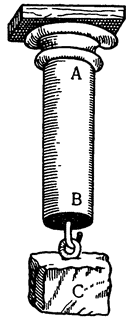 |
Симпличио. Если дело обстоит так, как вы говорите, то я прекрасно понимаю, что волокна дерева, имеющие одинаковую длину с куском его, могут оказывать сопротивление и большой силе, стремящейся его сломить; но, ведь, веревка состоит из нитей пеньки, длиною каждая от двух до трех локтей; каким же образом эти нити могут придавать прочность веревке, длиною в сто локтей? Кроме того, мне хотелось бы знать ваше мнение о сцеплении частей в металлах, камнях и других веществах, лишенных волокон, которые все же обладают, если я не ошибаюсь, еще большей связностью.
Сальвиати. Этих новых вопросов, не стоящих в необходимой связи с поставленной мною задачей, мы можем коснуться позже, когда сумеем разрешить уже указанные выше затруднения.
Сагредо. Но если уклонения могут привести нас к познанию новых истин, то что мешает нам, не связанным строгим и жестким методом и ведущим беседы по собственному своему желанию, сделать отклонение в сторону для выяснения такого вопроса, коснуться которого в другой раз, может быть, и не представится подходящего случая; а затем, кто знает, не откроем ли мы таким путем вещей еще более удивительных, нежели наши первоначальные положения? Поэтому я также прошу вас разрешить предложенный синьором Симпличио вопрос, интересующий и меня; мне очень хотелось бы знать, какой причине приписывается связность частей твердых тел, благодаря которой они представляются цельными; познание этого кажется мне необходимым также для того, чтобы уяснить причину сцепления и тех нитей, из которых состоят некоторые твердые тела10. {122}
Сальвиати. Готов служить вам так, как вы того желаете. Первое затруднение — это: каким образом веревка, длиною в сто и более локтей, состоящая из сплетения нитей (не превышающих двух-трех локтей в длину), может с такою силою сопротивляться их разделению? Но, скажите мне, синьор Симпличио, разве вы не можете держать отдельное волокно пеньки, зажав один конец его между пальцами, так крепко, что я, потянув его за другой конец, скорее разорву волокно, нежели выдерну его из ваших рук? Конечно, можете. Но волокна пеньки держатся в веревке не только концом, но всей своей поверхностью, будучи плотно прижаты друг к другу; не ясно ли поэтому, что освободить их отсюда труднее, нежели разорвать? Скрученность нитей в веревке связывает их между собою так прочно, что когда мы тянем за веревку с большой силой, то пряди ее разрываются, а не отделяются одна от другой; в этом легко убедиться, так как при разрыве остаются короткие концы, а не длинные — в локоть и 'более, какие должны были бы получиться, если бы разрыв веревки происходил не вследствие разрыва нитей, а вследствие взаимного их скольжения.
Сагредо. В подтверждение этого я прибавлю, что веревка часто разрывается не только от вытягивания в длину, но и от сильного скручивания, — аргумент, имеющий, по моему мнению, решающее значение. Здесь нити так прижаты друг к другу, что нажимающие не позволяют нажимаемым соскользнуть даже на самую малую величину, необходимую для того, чтобы описать спираль, обвиваясь вокруг веревки, которая вследствие скручивания укорачивается и становится несколько толще.
Сальвиати. Вы совершенно правы. И заметьте при этом, как одна истина влечет за собою другую. Нить, зажатая между пальцами, которая не выдергивается с какой бы силою мы ее ни тянули, оказывает сопротивление потому, что удерживается двойным давлением: насколько верхний палец нажимает на нижний, настолько же и последний давит на первый. Не подлежит сомнению, что если бы из двух этих давлений мы могли сохранить только одно, то осталась бы половина сопротивляемости, от них зависящей; но сделать этого непосредственно невозможно, так как невозможно поднять верхний палец и устранить его давление, не прекратив давления нижнего. Необходимо поэтому придумать искусственное приспособление для сохранения одностороннего давления, т. е. такое устройство, при котором нить сама прижималась бы к пальцу или другому твердому телу, на которое она положена, и достигнуть того, чтобы сила, стремящаяся оборвать нить, прижимала ее тем плотнее, чем более она становится. Этого можно достигнуть, обвивая нить спирально вокруг твердого тела, для лучшего понимания чего воспользуемся рисунком. Пусть АВ и CD два цилиндра, между которыми находится нить EF; для большей наглядности представим ее себе в виде шнура. Несомненно, что если тянуть {123} шнур EF за конец F, то при сильном прижимании одного цилиндра к другому он окажет немалое сопротивление, прежде чем проскользнет между зажимающими его цилиндрами; если же мы отнимем один из последних,
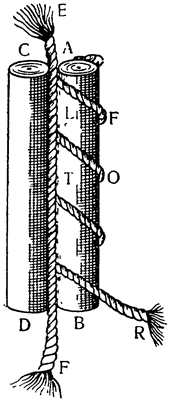 |
 |
Сагредо. Ваши объяснения рассеивают то чудесное, что я видел в двух явлениях, остававшихся для меня ранее непонятными. Первое явление заключалось в том, что двух или трех оборотов каната вокруг вала было достаточно, чтобы он держался и не соскальзывал, несмотря на большую привязанную к нему тяжесть; более того, при вращении ворота этот вал через посредство каната, который только прилегал к нему, мог тащить и поднимать огромные камни, в то время как другой конец каната держал маленький слабый мальчик. Другое — это простое, но остроумное приспособление, изобретенное одним мальчиком — моим родственником — для того, чтобы спускаться из окна по веревке, не натирая себе ладоней, что незадолго до того причинило ему большие мучения. Для лучшего уяснения я набросаю вам рисунок этого приспособления. Вокруг деревянного цилиндра АВ, толщиною с обыкновенную трость и длиной в ладонь, он сделал спиральную выемку, не более чем в полтора оборота, такой глубины, чтобы туда входила веревка, по которой хотят спускаться; веревка входила в конец нарезки А и выходила с другого конца В. Затем он вставлял цилиндр вместе с веревкою {124} в деревянную или, еще лучше, жестяную трубку, разрезанную по длине и могущую удобно раскрываться и закрываться. Крепко привязав верхний конец веревки, он брал затем трубку обеими руками и повисал в воздухе; от нажима трубки на веревку и цилиндр получалось давление, которое он по желанию мог увеличивать и уменьшать; когда он сильно сжимал трубку руками, то оставался висеть в воздухе, когда же он несколько ослаблял давление, то начинал медленно скользить и опускаться вниз.
Сальвиати. Действительно остроумное изобретение. Для полного объяснения его природы, мне кажется, можно было бы высказать еще некоторые соображения. Но я не хочу сейчас делать дальнейших отступлений по поводу этого частного случая, так как вы желали знать мое мнение относительно сопротивления разрыву других тел, состоящих не из волокон, как веревки или большая часть древесных пород, почему и связность частей их должна иметь другие причины. По моему мнению, связность эта может быть сведена к двум основаниям: одно — это пресловутая боязнь пустоты у природы; в качестве другого (не считая достаточной боязнь пустоты) приходится допустить что-либо связующее, вроде клея, что плотно соединяет частицы, из которых составлено тело. Поговорим сперва о пустоте и покажем на опыте природу и величину ее мощи. Возьмем, прежде всего, две пластинки из мрамора, металла или стекла, — плоские, гладкие и тщательно отполированные; положенные одна на другую, они легко передвигаются в стороны (ясное доказательства того, что их не соединяет какое-либо клейкое вещество); но если мы захотим их разделить, держа друг над другом, то проявится такое сопротивление разделению, что верхняя поднимет и подтянет нижнюю и долгое время будет удерживать ее на весу, хотя бы последняя была достаточно велика и тяжела. Этот опыт ясно доказывает нежелание природы допустить хотя бы. на краткий промежуток времени то пустое пространство, которое образовалось бы между пластинками до того момента, как окружающий воздух заполнил бы его. Так же можно видеть, что когда поверхности пластинок отполированы недостаточно хорошо, так что соприкосновение их не столь совершенно, то при медленном разъединении не получается никакого сопротивления, кроме обусловленного собственным весом пластинки; при быстром же подъеме верхней пластинки нижняя также поднимается, на тотчас же отпадает, следуя за верхней в течение весьма краткого промежутка времени, необходимого лишь для того, чтобы рассеялись малые частицы воздуха, находившиеся между не совсем плотно прилегавшими одна к другой поверхностями, и в промежуток между ними вошел новый, окружающий воздух. Сопротивление образованию пустоты, подобное тому, которое обнаруживается на примере двух прилегающих друг к другу пластинок, несомненно существует между частями твердого тела и является по крайней мере одной из причин их сцепления12. {125}
Сагредо. Остановитесь, пожалуйста, и разрешите мне сделать одно замечание, которое только что пришло мне в голову, и вот оно: поскольку мы видели, что нижняя пластинка следует за верхней и поднимается при быстром движении, необходимо признать, что движение в пустоте совершается не мгновенно, в противоположность учению многих философов и в том числе самого Аристотеля; в самом деле, если бы было так, как они утверждают, то обе упомянутые пластинки разделились бы сразу и без всякого сопротивления, ибо уже малейшего промежутка времени было бы достаточно для их разделения и для того, чтобы окружающий воздух заполнил могущую образоваться между ними пустоту. Из того, что нижняя пластинка следует за верхней, необходимо заключить, что движение в пустоте не совершается мгновенно; кроме того, заключаю, что между пластинками остается пустое пространство, хотя бы и на самое короткое время, в течение которого совершается движение окружающей среды, направленное к заполнению пустоты, и что если бы пустоты не образовалось, то не было бы надобности ни в доступе, ни в движении окружающей среды. Приходится, таким образом, сказать, что пустое пространство может образоваться насильственно или вопреки природе (хотя я того мнения, что ничто не может происходить вопреки природе, кроме невозможного, которое поэтому никогда и не случается)13. Но у меня возникают другие затруднения; в то время как опыт доказывает мне справедливость заключения, мой ум остается не совсем удовлетворенным теми причинами, которым мы приписали данное явление. Так как явление разделения обеих пластинок предшествует образованию пустоты, которое следует по времени за разделением, а причина, как мне кажется, если не по времени, то по существу, должна предшествовать действию, всякому же положительному действию должна соответствовать и положительная причина, то я не могу уяснить себе, каким образом причиною прилипания друг к другу двух пластинок и их сопротивления разделению — явлений уже существующих — может быть пустота, которой еще нет и которая еще должна образоваться. А вещи, которых еще нет, не могут проявляться в действии, согласно общепризнанному утверждению философа.
Симпличио. Если вы ссылаетесь на это утверждение Аристотеля, то я надеюсь, что вы не станете отрицать и другого его прекрасного и верного положения, а именно, что природа не стремится творить ничего такого, что сопротивлялось бы ее творению; это положение, кажется мне, дает ключ к разрешению вашего сомнения. Пустое пространство противится само своему образованию, почему природа и препятствует сделать то, что необходимо влечет за собою образование пустоты и чем в данном случае является разделение двух пластинок.
Сагредо. Прекрасно. Принимаю как достаточное разъяснение моих сомнений то, что сказано сейчас синьором Симпличио14. Возвращаясь к {126} началу нашей беседы, замечу, что подобное противодействие образованию пустоты кажется мне достаточной причиной сцепления частиц твердого тела из камня, металла или какого угодно другого вещества, еще более прочного и еще сильнее противящегося разделению. Теперь, если каждое единичное явление, как я слышал и полагал, имеет одну причину — или, если последних и несколько, то все их можно свести к одной, — то почему же нельзя считать достаточной причиной всех явлений сопротивления именно пустоту, которая, как уже доказано, имеет здесь место?
Сальвиати. Сейчас я не хотел бы входить в обсуждение вопроса, является ли одна пустота без добавления какого-либо другого средства достаточной, чтобы держать частицы твердого тела связанными между собою; могу вас уверить, однако, что первая причина, которая действительно имеет место и объясняет явление с пластинками, недостаточна для объяснения прочности частей цилиндра из мрамора или металла, которые под влиянием большой силы, их растягивающей, в конце концов разрываются и разделяются. Если я найду средство отличить известное уже нам сопротивление, вызываемое пустотою, от другого, происходящего от иной причины, какова бы она ни была, также способствующей сцеплению частиц, и если я смогу показать вам, что первая причина недостаточна одна для объяснения явления, то не скажете ли вы сами, что необходимо введение и другой причины. Помогите ему, синьор Симпличио; он молчит, не зная, что ответить.
Симпличио. Быть может, молчание синьора Сагредо и представляет собою ответ, так как такие ясные и необходимые следствия не оставляют места для возражений.
Сагредо. Вы угадали, синьор Симпличио. Я подумал, что если миллиона золотом, получаемого ежегодно из Испании для оплаты военных расходов, недостаточно, то придется искать других источников для того, чтобы платить жалование солдатам. Но продолжайте, синьор Сальвиати, и в предположении, что я принял ваши заключения, покажите нам способ отделить действие пустоты от других причин или, если вы можете его измерить, то покажите, почему его недостаточно для объяснения тех явлений, о которых вы говорите.
Сальвиати. Да поможет вам ваш демон!15 Я покажу вам способ, каким можно отделить противодействие образованию пустоты от действия других причин, и прием, каким его можно измерить. Для этого постараемся отыскать такое сплошное вещество, части которого не оказывали бы иного сопротивления разделению, кроме вызываемого боязнью пустоты. Таким веществом, как уже давно доказал наш Академик, является вода16. Если мы возьмем цилиндр воды и обнаружим в нем сопротивление его частиц разделению, то оно не может происходить от иной причины, кроме стремления не допустить образования пустоты. Чтобы произвести {127} подобный опыт, я придумал прибор, устройство которого я вам объясню при помощи этого рисунка лучше, нежели просто словами. Пусть CABD разрез полого цилиндра, сделанного очень аккуратно из металла или стекла, смотря по желанию, внутрь которого помещен деревянный цилиндр, находящийся в тесном соприкосновении со стенками первого; разрез этого цилиндра обозначен буквами EGHF. Этот цилиндр может перемещаться вверх и вниз; посредине он просверлен, и через него пропущен железный
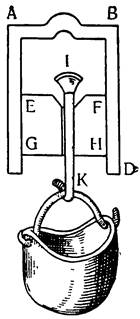 |
Симпличио. Не могу отрицать, что ваше изобретение очень остроумно; но мне думается, что существуют некоторые затруднения, которые делают для меня этот опыт сомнительным. Кто знает, не может ли воздух пройти между стеклом и поршнем, хотя бы таковой и был обернут тканью или другой мягкой материей? И хотя конус хорошо пригнан к отверстию, быть может, не мешало бы смазать его воском или скипидаром для лучшей непроницаемости. Кроме того, почему не допустить, что частицы воды могут разделяться и разрежаться, или что воздух, пар или другие легкие субстанции могут проходить через пористое дерево и даже через самое стекло?
Сальвиати. С большим умением излагаете вы, синьор Симпличио, возникающие затруднения, давая отчасти и средства уничтожить их, поскольку дело касается проникновения воздуха через дерево или между деревом и стеклом. В ответ на ваши возражения замечу, что посредством новых наблюдений мы можем убедиться, имеют ли место упомянутые затруднения. Предположим, что вода способна рассеиваться по своей природе хотя бы под влиянием силы, как это наблюдается с воздухом; тогда поршень должен был бы опуститься; далее, если мы сделаем в верхней части стеклянного цилиндра небольшую выпуклость, наподобие отмеченной на рисунке буквою V, то, проникая через дерево или стекло, воздух или другая тонкая материя должны были бы собраться (пройдя через воду) под выпуклостью V. Так как ни того, ни другого не случается, то мы должны считать опыт произведенным со всеми необходимыми предосторожностями и признать, что вода неспособна к рассеиванию и что стекло непроницаемо ни для какой, даже самой тонкой материи.
Сагредо. Меня очень радует, что в ваших рассуждениях я нашел, наконец, разъяснение причины одного явления, долгое время поражавшего мой ум как нечто чудесное и непонятное. Я видел однажды колодец, в который был помещен насос для накачивания воды кем-то, кто думал, но напрасно, что таким образом можно доставать воду с меньшим трудом или в большем количестве, нежели просто ведрами. Этот насос имел поршень с верхним клапаном, так что вода поднималась всасыванием, а не давлением, как то делается в насосах с нижним клапаном. Пока колодец был наполнен водою до определенной высоты, насос всасывал и подавал ее прекрасно, но как только вода опускалась ниже этого уровня — насос переставал работать. Заметив первый раз такой случай, я подумал, что насос испорчен, и позвал мастера для починки; последний заявил, однако, что все было исправно, но что вода опустилась до той глубины, с которой она не может быть поднята насосом вверх; при этом он прибавил, что ни насосами, ни другими машинами, поднимающими воду всасыванием, невозможно поднять воду и на волос выше восемнадцати локтей; будут ли насосы широкими или узкими — предельная высота остается той же {129} самой. Мне до сего времени не приходило в голову, что если мы можем представить себе веревку, древесную массу или железный стержень удлиненными настолько, что они разрываются наконец от собственного веса, то то же самое и еще гораздо легче может произойти со столбиком или колонною воды. Ибо что же иное представляет собою содержимое всасывающего насоса, как не водяной столб, прикрепленный сверху, все более и более удлиняющийся и достигающий, наконец, предела, при переходе за который он разрывается от собственной тяжести совершенно так же, как это произошло бы с веревкой?
Сальвиати. Дело обстоит именно так. А так как одна и та же высота в восемнадцать локтей является предельной, на которую может быть поднята вода насосами всякой величины по трубам широким, узким и даже толщиною не более соломинки, то мы можем утверждать, что, определяя вес воды, заключающейся в восемнадцати локтях трубы насоса, какого бы диаметра последняя ни была, мы можем определить и величину сопротивления образованию пустоты в прочном цилиндре из любого материала, диаметр которого одинаков с внутренним поперечником трубы. И хотя мы об этом уже много говорили, все же покажем еще раз, как можно легко найти для всех металлов, камня, дерева, стекла и т. д. ту предельную длину цилиндров, которые можно сделать из них в виде нитей или стержней любой толщины, сверх которой они уже не могут держаться и разрываются от собственного веса. Возьмем для примера медную проволоку произвольной толщины и длины и, прикрепив ее за один конец, будем привешивать к другому все больший груз, пока она, наконец, не порвется; предположим, что наибольший вес, который она выдерживает, равняется пятидесяти фунтам; отсюда ясно, что пятьдесят фунтов меди, прибавленные к собственному весу проволоки, равняющемуся, скажем, восьмушке унции, и вытянутые в проволоку той же толщины, дадут проволоку предельной длины, которая только в состоянии держаться. Измерим длину той проволоки, которая оборвалась, и пусть эта длина будет равна одному локтю; так как она сама весила одну восьмую унции и выдерживала сверх своего веса еще пятьдесят фунтов, составляющих 4800 восьмушек унции, то мы вправе сказать: всякая медная проволока, какова бы ни была ее толщина, может держаться, если длина ее не превышает 4801 локтя. Поэтому медный стержень, могущий держаться до предельной длины в 4801 локоть, имеет прочность во столько раз большую по сравнению с той, которая обусловливается сопротивлением пустоте, во сколько развес такого медного стержня более веса столба воды того же диаметра длиною в восемнадцать локтей. Так как медь в девять раз тяжелее воды, то сопротивление разрыву медного стержня, обусловленное боязнью пустоты, равняется весу двух локтей стержня той же толщины. Путем подобных же рассуждений и измерений мы можем найти для нитей и стержней из всяких {130} твердых веществ ту длину, которую они выдерживают, а также и то, какую часть их способности к сопротивлению составляет боязнь пустоты18.
Сагредо. Теперь остается только, чтобы вы сказали нам, в чем заключается причина остальной части прочности тел, а именно, каково то склеивающее или связывающее вещество, которое, помимо боязни пустоты, держит частицы твердого тела в соединении. Я не могу себе представить, каков должен быть этот клей, не сгорающий и не разрушающийся в раскаленной печи в течение двух, трех или четырех месяцев и даже десяти или ста; ведь золото, серебро или стекло, находившиеся в расплавленном состоянии даже столь долгое время, по охлаждении снова собирают свои части и становятся такими же прочными, как раньше. Сверх того то же самое затруднение, которое возникает относительно сцепления хотя бы частиц стекла, возникает и относительно сцепления самого склеивающего вещества: какова же причина, благодаря которой его частицы держатся в таком прочном соединении друг с другом?
Сальвиати. Незадолго перед тем я пожелал, чтобы вам помог ваш добрый демон; теперь мне снова приходится повторить это пожелание. Ощущая собственными руками сопротивление разделению двух пластинок, обусловливаемое, несомненно, пустотою, видя, что разделение их происходит лишь с большим трудом, и находя еще большее сопротивление разрыву надвое мраморной или бронзовой колонны, я не вижу в последнем случае, почему бы именно та же причина не присутствовала и здесь и не имела своим следствием сцепления частей материи, вплоть до самых мелких. А так как каждое действие должно иметь только одну истинную и ясную причину, я же не нахожу другого связующего средства, то не удовлетвориться ли нам одной найденной причиной — пустотою, признав ее достаточность?
Симпличио. После того как вы сами показали, что сопротивление образованию большой пустоты при разъединении двух больших частей твердого тела значительно меньше, чем то, которое держит в связанном состоянии мельчайшие частицы последнего, как же вы не хотите более утверждать, что сопротивление одного рода отлично от другого?
Сальвиати. На это уже ответил синьор Сагредо; он сказал, что подобным же образом платят жалование каждому отдельному солдату из суммы налога, собираемого по сольди и лиардам, хотя требуется более чем на миллион золота для оплаты всего войска19. Кто знает, не действуют ли в мельчайших частях также и мельчайшие пустоты, и не они ли держат в связном состоянии части твердого тела, подобно тому как отдельные монеты образуют совокупность? Скажу вам то, что сейчас пришло мне в голову; выдаю это не за окончательную истину, но за домысел, связанный с немалыми затруднениями и требующий исследования. Посмотрите, не {131} найдете ли вы тут чего-нибудь, что вам понравится; об остальном судите, как вздумается. Много раз я наблюдал, как огонь, проникая между частицами того или иного металла, столь крепко связанными между собою, в конце концов, разделял и разъединял их, и как затем по устранении огня частицы возвращались в прежнее состояние связности, причем не замечалось ни малейшего уменьшения количества золота и очень небольшое уменьшение количества других металлов, если они оставались в расплавленном виде долгое время. Я думал, что это можно объяснить тем, что тончайшие частицы огня, проникая в мельчайшие поры металла (через которые благодаря их ничтожной величине не могут проходить более грубые частицы воздуха или иных жидкостей), заполняют существующие между ними мельчайшие пустоты и освобождают частицы от действия той силы, которая держала их связанными друг с другом, и тем способствуют их разъединению. Получив, таким образом, свободу движения, частицы образуют жидкую массу и остаются в таком состоянии, пока между ними находятся частицы огня; после же того как последние отнимаются, образуются первоначальные пустоты и восстанавливается первоначальное притяжение,, а вместе с тем и связность частиц. На замечание синьора Симпличио, мне кажется, можно ответить, что хотя эти пустоты имеют ничтожную величину и, следовательно, сопротивление каждой из них легко превозмогаемо, но неисчислимость их количества неисчислимо увеличивает сопротивляемость (если можно так выразиться). Какова и сколь велика может быть сила, получающаяся от соединения огромного количества ничтожнейших моментов, мы ясно можем представить себе, видя, как огромная тяжесть, весом в миллион фунтов, поддерживаемая толстым канатом, уступает и дает себя победить и поднять бесчисленным атомам воды. Принесенные южным ветром или рассеянные в виде тончайшего тумана эти атомы носятся по воздуху, проходят между волокнами толстейшего каната, чему не может помешать даже натягивающая его огромная тяжесть, проникают в малейшие щели, заставляя канат разбухать и укорачиваться, и таким образом, поднимают тяжесть20.
Сагредо. Вы не сомневаетесь в том, что если сопротивление не бесконечно велико, то оно может быть преодолено множеством весьма малых сил, так что большое количество муравьев могло бы вытащить на землю судно, нагруженное зерном; в самом деле, мы ежедневно наблюдаем, как муравей тащит зерно, а так как зерен в судне не бесконечное множество, но некоторое ограниченное число, то, увеличив это число даже в четыре или в шесть раз, мы все же найдем, что соответственно большое количество муравьев, принявшись за работу, может вытащить на землю и зерно и корабль. Конечно, для того чтобы это было возможно, необходимо, чтобы и число их было велико; мне кажется, что именно тай обстоит дело и с пустотами, держащими связными частицы металла. {132}
Сальвиати. Но если бы понадобилось, чтобы число их было бесконечным, то сочли бы вы это невозможным?
Сагредо. Нет, не счел бы, если бы масса металла была бесконечной; в противном случае...
Сальвиати. В противном случае — что же? Раз мы уже дошли до парадоксов, то попробуем, нельзя ли каким-либо образом доказать, что в некоторой конечной непрерывной величине может существовать бесконечное множество пустот. Попутно с этим мы найдем, если не что-либо иное,
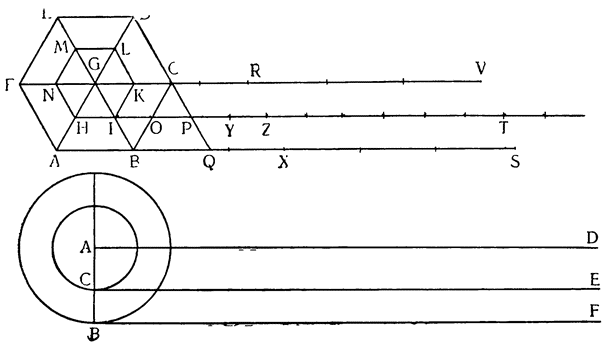
то, по крайней мере, решение проблемы, которую сам Аристотель причислял к наиболее изумительным в области механики. Решение это будет не менее ясным и доказательным, нежели его собственное, а вместе с тем и отличным от глубокомысленных соображений ученейшего монсиньора ди Гуевара21. Однако сперва необходимо рассмотреть одно предложение, не связанное с другими, но от которого зависит решение данного вопроса, а последнее, если не ошибаюсь, приведет ко многим новым и удивительным понятиям. Для пояснения начертим аккуратно следующую фигуру. Дан равносторонний и равноугольный многоугольник с любым числом сторон, центром которого является точка G; предположим, что это будет шестиугольник ABCDEF. Впишем в него подобный же, но меньший концентрический многоугольник HIKZMN. Продолжим одну из сторон АВ большего многоугольника в направлении S, в соответствии с чем продолжим в том же самом направлении в сторону меньшего шестиугольника HI, так что линии НТ и AS будут параллельными, а затем проведем еще третью параллельную эквидистантную линию GV через центр G. Проделав это построение, представим себе, что больший многоугольник {133} катится по линии AS, увлекая с собою и меньший многоугольник. Ясно, что при начале движения В — конечная точка стороны АВ — останется на месте, точка А поднимется, а точка С опустится, описав дугу CQ, так что сторона ВС, достигнув линии AS, образует линию BQ, равную ей. При этом вращении вершина угла I меньшего многоугольника поднимается над линией IT, так как линия IB наклонна по отношению к AS, и точка I достигнет параллели IT, но не ранее, чем точка С придет в положение Q. Тогда I перейдет в О, описав предварительно дугу IO вне линии НТ, и линия IK отложится на параллели, как ОР. При этом центр G также поднимется над линией GV и достигнет ее вновь после того, как опишет дугу GC. После этого первого поворота больший многоугольник окажется поставленным на сторону ВС, занявшую положение BQ, а меньший — на сторону IK, переместившуюся в положение ОР, причем пространство IO останется незатронутым; центр G перейдет в С, также не затронув линии GV. В конце концов вся фигура придет в положение, аналогичное первоначальному. Если продолжать катить многоугольник и сделать второй поворот, то сторона DC большего многоугольника займет положение QX, сторона KL меньшего придет в YZ, перескочив пространство PY, а центр, двигаясь все время над линией GV, достигнет последней в точке R, сделав скачок CR. В результате полного оборота больший многоугольник отложит на линии AS подряд без каких-либо промежутков шесть равных линий, составляющих в сумме его периметр; меньший многоугольник также отложит шесть отрезков, равных его сторонам, но разделенных пятью дугами, хорды которых — части линии НТ — остаются незатронутыми многоугольником; наконец, центр G прикоснется к линии GV только в шести точках. Отсюда вы можете заключить, что пространство, пройденное малым многоугольником, почти равно пройденному большим, так как линия НТ почти равняется линии AS, будучи менее последней лишь на величину хорды одной из дуг, если рассматривать линию НТ сполна, т. е. вместе с отрезками под дугами. Теперь я хотел бы, чтобы, пользуясь показанным и объясненным мною на примере данного шестиугольника, вы представили себе то же в отношении всяких других многоугольников, сколько бы сторон они ни имели, лишь бы они были подобны, концентричны и связаны между собою. При качении большего многоугольника должен также двигаться и произвольно избранный меньший; при этом, повторяю, следует иметь в виду, что пути, проходимые тем и другим, будут почти равны, если включить в пространство, пройденное меньшим, также и интервалы под дугами, не затронутые на самом деле никакой частью периметра меньшего многоугольника. Таким образом, когда больший многоугольник с тысячью сторон, постепенно вращаясь, пройдет прямую линию, равную своему периметру, меньший многоугольник пройдет в то же самое время приблизительно такой же путь, составленный из {134} тысячи отрезков, равных его сторонам, и тысячи пустых пространств между ними, как мы можем назвать эти промежутки, в противоположность отрезкам, отмеченным наложением сторон многоугольника. В том, что было пока сказано, нет ничего сомнительного или возбуждающего какие-либо затруднения. Но теперь скажите мне: если из какого-либо центра, например из точки А, мы опишем две концентрические окружности, представим себе круги связанными между собою, через концы их радиусов С и В проведем касательные СЕ и BF, а через центр А — параллельную им линию AD, и покатим большой круг по линии BF (отмерив последнюю так, чтобы она равнялась длине окружности, равно как и другие линии СЕ, AD), то что произойдет с меньшим кругом и центром после того, как большой круг сделает полный оборот? Центр, конечно, пройдет всю линию AD, а окружность малого круга своим прикосновением пройдет всю линию СЕ так же, как это имело место ранее с малым многоугольником, с той только разницей, что линия НТ не во всех своих частях затрагивалась периметром многоугольника и содержала столько же пустых промежутков, сколько было отрезков, отмеченных наложением сторон многоугольника; что же касается кругов, то окружность меньшего не может оторваться от линии СЕ так, чтобы не соприкасаться с нею в одной точке, и всегда одна из точек окружности лежит на прямой. Каким же образом меньший круг может пройти линию, настолько превышающую его окружность, без скачков и промежутков?
Сагредо. Мне кажется, можно сказать, что как центр круга, рассматриваемый отдельно и являющийся только одной точкой, передвигается по линии AD, соприкасаясь с нею на всем протяжении, так и точки окружности меньшего круга, увлекаемые движением большего, могут двигаться, скользя по частям линии СЕ,
Сальвиати. Этого не может быть по двум причинам. Во-первых, нет никаких оснований для того, чтобы соприкосновение, подобное существующему в точке C, проходило одну часть линии СЕ скользя, а другую иначе; если бы это происходило так, то должно было бы существовать бесконечное множество таких прикосновений (ибо это точки); и следы таких скользящих прикосновений к линии СЕ были бы бесчисленными, а будучи конечно образовали бы бесконечную линию; но линия СЕ конечна. Другая причина та, что когда больший круг при своем вращении меняет точки Касания с прямой, то меньший круг не. может не делать того же, так как ни из какой другой точки, кроме точки В, нельзя провести прямой линии к центру А, которая проходила бы в то же время и через точку С; поэтому как только большая окружность меняет точку касания, так тотчас же меняет таковую и меньшая окружность, и только одна точка малой окружности может соприкасаться с одной точкой соответствующей прямой линии СЕ, Кроме того, было выяснено, что при качении многоугольников каждая точка периметра меньшего многоугольника соприкасается не {135} более чем с одной точкой линии, на которую накладывается его периметр. Это можно легко понять, имея в виду, что линии IK и ВС параллельны: пока ВС еще не наложена на BQ, линия IK остается приподнятой над IP и достигает последней лишь в тот момент, когда ВС совпадает с BQ; тогда и IK совпадает с ОР, после чего немедленно же поднимается.
Сагредо. Это случай, действительно, весьма сложный; мне ничего не приходит на ум, и сообщите нам, пожалуйста, свои соображения.
Сальвиати. Я возвращусь к рассмотрению упомянутых выше многоугольников, на которых явление было понято и уяснено нами, и скажу, что как в многоугольнике со ста тысячами сторон путь, пройденный при обороте, измеряется обводом большего многоугольника, т. е. отложением без перерыва всех его сторон, в то время как путь меньшего многоугольника также равен ста тысячам его сторон с прибавлением такого же числа, т. е. ста тысяч пустых промежутков, так и в кругах (представляющих собою многоугольники с бесконечно большим числом сторон) линия, образуемая непрерывным наложением бесконечно большого числа сторон большего круга, приблизительно равна по длине линии, образованной наложением бесконечно большого числа сторон меньшего круга22, если включить в нее и промежутки; а так как число сторон не ограничено, а бесконечно, то и число промежутков между ними также бесконечно; бесчисленные точки в одном случае заняты все, в другом случае часть их занята, а часть пуста. Я хотел бы, чтобы вы заметили себе, что, разделяя линию на некоторые конечные и потому поддающиеся счету части, нельзя получить путем соединения этих частей линии, превышающей по длине первоначальную, не вставляя пустых пространств между ее частями; но представляя себе линию разделенной на неконечные части, т. е. на бесконечно многие ее неделимые, мы можем мыслить ее колоссально растянутой без вставки конечных пустых пространств, а путем вставки бесконечно многих неделимых пустот. То, что я сказал о простых линиях, относится также и к поверхностям твердых тел, если рассматривать их как состоящие из бесконечного множества атомов. Если мы разделим тело на конечное число частей, то, без сомнения, не сможем получить из них тела, которое занимало бы объем, превышающий первоначальный, без того, чтобы между частями не образовалось пустого пространства, т. е. такого, которое не заполнено веществом данного тела; но если допустить предельное и крайнее разложение тела на лишенные величины и бесчисленные первичные составляющие, то можно представить себе такие составляющие растянутыми на огромное пространство путем включения не конечных пустых пространств, а только бесконечно многих пустот, лишенных величины. И таким образом допустимо, например, растянуть маленький золотой шарик на весьма большой объем, не допуская конечных {136} пустот, — во всяком случае, если мы принимаем, что золото состоит из бесконечно многих неделимых.
Симпличио. Мне кажется, что вы тут подходите к тем пустотам, которые признавал один древний философ.
Сальвиати. Надеюсь, что вы не прибавите «отрицавший божественный промысел», как это весьма неуместно сделал в случае, подобном нашему, один из противников нашего Академика.
Симпличио. В этом замечании я не без досады усматриваю злопамятство недоброжелательного противника. Но я не буду касаться подобных вопросов не только для соблюдения правил вежливости, но и потому, что они совершенно не соответствуют вашим умеренным и высокопросвещенным взглядам; я знаю, что вы являетесь не только религиозным и благочестивым человеком, но и правоверным католиком23. Возвращаясь к нашей проблеме, скажу, что в течение нашей беседы во мне родились многие сомнения, от которых я при всем желании не могу освободиться. Прежде всего, следующее: если окружности двух кругов равны двум прямым СЕ и BF, — последней сполна, а второй — с присоединением бесконечного множества пустых промежутков, — то каким образом линия AD, описанная центром, составляющим одну точку, может быть приравнена к этому центру, в то время как состоит из бесконечного числа точек. Кроме того, это составление линии из точек, делимого из неделимого, конечного из неконечного кажется мне нелегко преодолимым препятствием; точно так же и признание существования пустоты, столь решительно отвергаемой Аристотелем, представляет большие затруднения.
Сальвиати. Такие затруднения действительно существуют, равно как и многие другие; но вспомните о том, что мы имеем дело с бесконечными и неделимыми, постичь которые нашим конечным умом невозможно вследствие огромности одних и малости других. Мы убеждаемся здесь, что человеческая речь не приспособлена для выражения таких понятий. Однако я все же позволю себе изложить некоторые свои измышления, которые хотя и не исчерпывают вопроса, но могут представить некоторый интерес благодаря своей новизне. Впрочем, столь длительное уклонение в сторону от начатого пути, быть может, покажется вам неуместным и маложелательным?
Сагредо. Нисколько. Будем пользоваться теми преимуществами и благами, которые дают нам живая дружеская беседа и свободное, непринужденное обсуждение предмета, столь отличные от изучения мертвых книг, которые возбуждают в тебе тысячи сомнений и не разрешают ни одного. Познакомьте же нас с теми соображениями, которые пришли вам на мысль в течение нашего разговора; за отсутствием особо необходимых дел у нас хватит времени на то, чтобы продолжить обсуждение и других вопросов; в особенности же нельзя обойти те затруднения, которых коснулся синьор Симпличио. {137}
Сальвиати. Пусть будет так, как вы желаете. Начнем с того, как может быть, чтобы одна точка приравнивалась к целой линии. Сейчас я не нахожу иного выхода, как постараться устранить или, по крайней мере, смягчить эту несообразность, указав другую подобную или еще большую, как иной раз удивительные вещи бледнеют перед лицом чудесных. То, что я хочу показать вам, заключается в следующем: представим себе две одинаковых поверхности и два одинаковых тела, поставленные на эти поверхности, как на основания, и пусть затем эти тела, оставаясь все время равными одно другому постепенно делаются все меньше и меньше, причем одно из тел вместе со своей поверхностью обращается в предлинную линию, а другое со своей поверхностью — в одну точку; таким образом в одном случае получится лишь единственная точка, а в другом — бесконечное множество их.
Сагредо. Такое предложение представляется мне на самом деле изумительным; пожалуйста, дайте нам пояснения и доказательства.
Сальвиати. Необходимо нарисовать чертеж, так как доказательство будет чисто геометрическим. Начертим полукруг AFB с центром С и описанный около него прямоугольный параллелограмм ADEB и проведем из центра к точкам D и Е прямые линии CD и СЕ. Представим себе, далее, что линия CF, проведенная из центра перпендикулярно к прямым АВ и DE, остается неподвижной, вся же фигура вращается около нее, как около своей оси. Ясно, что прямоугольник ADEB опишет при этом цилиндр, полукруг AFB — полушар, а треугольник СDЕ — конус. Предположим теперь, что мы вынули полушар, но оставили конус и ту часть цилиндра, которая выходила за пределы полушара, —
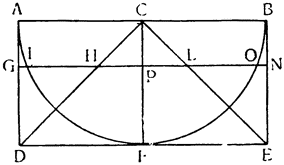 |
Сагредо. Ваше рассуждение кажется мне таким тонким и удивительным, что я, если бы и мог, не хотел бы оспаривать его. Мне представляется почти преступлением разрушать такое прекрасное построение грубыми педантическими нападками. Для полного удовлетворения дайте нам, однако, геометрическое доказательство того, что между упомянутыми телами и их основаниями сохраняется постоянное равенство; я думаю, что оно будет столь же остроумно, как и те философские рассуждения, которые на этом основаны.
Сальвиати. Доказательство очень легко и коротко. Возвращаемся к начерченной нами фигуре. Так как угол IPC прямой, то квадрат радиуса IС равен сумме квадратов сторон IP и PC. Но линия IС, как радиус, равна линии АС, которая, в свою очередь, равна GP, а линия СР {139} равняется РН; таким образом, квадрат линии GP равен сумме квадратов линий IP и РН и, будучи учетверенным, равен учетверенной сумме тех же квадратов; таким образом, квадрат диаметра GN равен сумме квадратов линий IO и HL, а так как площади кругов относятся между собою как квадраты диаметров, то площадь круга с диаметром GN равна сумме площадей двух кругов с диаметрами IO и HL. Вычитая из обеих частей равенства по общему кругу с диаметром IO, получаем в результате, что остаток круга с диаметром GN будет равен кругу с диаметром HL. Вот доказательство первой части; что же касается доказательства второй, то мы опустим его, так как если вы того пожелаете, то можете найти его в предложении XII книги второй «De centro gravitatis solidorum» синьора Луки Валерио, нового Архимеда нашего времени, который пользовался этим предложением, но для другой цели25. Для нас же совершенно достаточно того, что, как мы видели, указанные выше площади равны между собою и что постепенно и в равной степени уменьшаясь, они переходят в конце концов, одна — в простую точку, другая же — в окружность какой угодно величины; в этом именно следствии и заключается все, что тут есть чудесного.
Сагредо. Прекрасное доказательство, вполне соответствующее сделанному выше удивительному выводу. А теперь ответьте что-нибудь и на другой вопрос, затронутый синьором Симпличио, если только вы имеете сказать по тому поводу что-либо особое, хотя, думается мне, это едва ли может иметь место, так как этот вопрос уже столько раз был предметом споров.
Сальвиати. Я хочу высказать свои личные соображения, но сначала повторю то, что было сказано мною незадолго перед этим, а именно, что бесконечное для нас, по существу, непостижимо, равно как и неделимое. Представьте себе, что будет, если соединить и то и другое; однако, если мы хотим составить линию из неделимых точек, их должно быть бесконечно много и таким образом нам приходится изучать одновременно и бесконечное и неделимое. Много разных соображений приходило мне в голову в подобных случаях; некоторые из них и, быть может, наиболее важные я сейчас не могу припомнить, но может случиться, что при продолжении нашей беседы, побуждаемый возражениями и затруднениями, выдвигаемыми вами и в особенности синьором Симпличио, я натолкнусь и на них; без такого побуждения многим фантазиям не суждено было бы родиться на свет. Таким образом, будем с полной свободой вводить в беседу наши человеческие догадки, как мы по совести должны назвать их в сравнении с учением о сверхъестественном, которое одно истинно и надежно разрешает наши споры и вопросы, являясь надежным проводником при блуждании нашем по темным и неверным тропинкам или, вернее, лабиринтам26. {140}
Главное возражение против тех, кто считает возможным составление непрерывного из неделимых, заключается в том, что одно неделимое, при соединенное к другому, не может дать делимой величины, потому что, если бы это было так, то отсюда следовало бы, что и неделимое может быть разделяемо. В самом деле, если два неделимых, например, две точки, будучи соединены вместе, составят некоторую величину — в данном случае делимую линию, — то можно представить себе последнюю состоящей и из трех, пяти, семи или другого числа нечетных частей; разделение такой линии на две равных части повело бы к делению пополам и той неделимой частицы, которая лежит как раз в середине. На это и другие возражения в том же роде можно ответить, что не только два неделимых, но и десять, сто и тысяча их не могут составить конечной делимой величины, ибо для этого их потребуется бесконечное множество.
Симпличио. У меня сейчас рождается сомнение, кажущееся мне неразрешимым. Мы знаем наверное, что одни линии могут быть больше других; представляя их себе составленными из бесконечного множества точек, мы должны признать, что можно найти однородные величины, большие, нежели бесконечность, потому что бесконечность точек большей линии должна превышать бесконечность точек меньшей линии. Такое признание одной бесконечности большей, нежели другая бесконечность, представляется мне совершенно непостижимым.
Сальвиати. Сказанное вами относится к числу затруднений, происходящих вследствие того, что, рассуждая нашим ограниченным разумом о бесконечном, мы приписываем последнему свойства, известные нам? по вещам конечным и ограниченным. Между тем это неправильно, так как такие свойства, как большая или меньшая величина и равенство, неприменимы к бесконечному, относительно которого нельзя сказать, что одна бесконечность больше или меньше другой или равна ей. В подтверждение этого положения мне пришел в голову пример, который я для большей ясности изложу в форме вопросов, обращенных к синьору Симпличио, указавшему на затруднения.
Я полагаю, что вы прекрасно знаете, какие числа являются квадратами и какие нет.
Симпличио. Я прекрасно знаю, что квадратами являются такие числа, которые получаются от умножения какого-либо числа на самого себя; таким образом, числа четыре, девять и т. д. суть квадраты, так как они получаются от умножения двух и соответственно трех на самих себя.
Сальвиати. Великолепно. Вы знаете, конечно, и то, что как произведения чисел называются квадратами, так и образующие их, т. е. перемножаемые числа носят название сторон или корней; другие числа, не являющиеся произведением двух равных множителей, не суть квадраты. Теперь, если я скажу, что количество всех чисел вместе — квадратов и не {141} квадратов — больше, нежели одних только квадратов, то такое утверждение будет правильным; не так ли?
Симпличио. Ничего не могу возразить против этого.
Сальвиати. Если я теперь спрошу вас, сколько квадратов, то можно по справедливости ответить, что их столько же, сколько существует корней, так как каждый квадрат имеет свой корень и каждый корень свой квадрат; ни один квадрат не может иметь более одного корня и ни один корень более одного квадрата.
Симпличио. Совершенно верно.
Сальвиати. Но если я спрошу, далее, сколько корней, то вы не станете отрицать, что их столько, сколько всех чисел вообще, потому что нет ни одного числа, которое не могло бы быть корнем какого-либо квадрата; установив это, приходится сказать, что квадратов столько же, сколько всех чисел, так как столько же корней, а корнями являются все числа. А между тем ранее мы сказали, что всех чисел больше, чем квадратов, так как большая часть их не квадраты. Действительно, число квадратов непрерывно и в весьма большой пропорции убывает по мере того, как мы переходим к большим числам; так, из чисел до ста квадратами являются десять, т. е. одна десятая часть; до десяти тысяч квадратами будет лишь одна сотая часть; до одного миллиона — только одна тысячная часть. А в отношении бесконечного числа, если бы только мы могли постичь его, мы должны были бы сказать, что квадратов столько же, сколько всех чисел.
Сагредо. Что же нужно сделать, чтобы найти выход из такого положения?
Сальвиати. Я не вижу возможности никакого другого решения, как признать, что, поскольку бесконечно много чисел вообще, бесконечно много квадратов, бесконечно много корней, то ни множество квадратов не меньше множества всех чисел, ни последнее не больше первого; в конечном выводе — свойства равенства, а также большей и меньшей величины, не имеют места там, где дело идет о бесконечности, и применимы только к конечным количествам. Поэтому, когда синьор Симпличио предлагает мне неравные линии и спрашивает меня, как может быть, чтобы в боль-тлей из них не содержалось большего количества точек, чем в меньшей, то я отвечаю ему, что их там не больше, не меньше и не одинаковое количество, но бесконечное множество в каждой. В самом деле, если бы я ответил, что число точек одной линии равняется числу квадратных чисел, в другой — большей — их содержится столько, сколько существует чисел вообще, а в какой-нибудь меньшей столько, сколько существует кубов, то был ли бы удовлетворительным мой ответ, приписывающий линиям разное число точек, являющееся в то же самое время в каждом случае бесконечным? Вот что я могу сказать по поводу первого затруднения27. {142}
Сагредо. Обождите немного, пожалуйста, и дайте мне в добавление к сказанному поделиться одной мыслью, которая сейчас пришла мне в голову. На основании изложенного, мне кажется, нельзя утверждать не только того, что одно бесконечное больше другого бесконечного, но даже и того, что оно больше конечного.
В самом деле, если бы, например, бесконечно большое число было больше миллиона, не следовало ли бы из этого, что, переходя за миллион к последовательно большим и большим числам, мы приближаемся к бесконечности? На самом деле этого нет; напротив, может случиться, что, переходя к большим числам, мы удаляемся от бесконечности; так, чем большие числа мы берем, тем меньшее количество квадратных чисел встречаем среди них; при бесконечном же числе квадратов не может быть меньше, чем всех чисел, как это только что было доказано. Таким образом, переходя к большим числам, мы в данном случае удаляемся от бесконечности.
Сальвиати. И таким образом из ваших остроумных соображений необходимо вытекает, что понятия «больший», «меньший», «равный» не имеют места не только между бесконечно большими, но и между бесконечно большим и конечным28.
Перехожу теперь к другому замечанию, а именно: так как линия, как и всякий континуум, может быть разделена на части, также далее делимые, то нельзя избежать заключения, что линия состоит из бесконечного множества неделимых, потому что, предполагая возможность бесконечно продолжать деление, мы получаем и бесконечное множество частей; иначе деление могло бы прийти к концу; а если частей бесконечно много, то нельзя не прийти к заключению, что они не конечны, так как бесконечно много конечных величин дает величину бесконечно большую; таким образом, мы имеем континуум, составленный из бесконечного множества неделимых.
Симпличио. Но если мы можем постоянно производить деление на части конечные, то какая надобность нам вводить здесь не конечные?
Сальвиати. Самая возможность постоянного разделения на конечные части приводит к необходимости признать, что целое состоит из бесконечно многих не конечных частей. Чтобы положить конец спору, ответьте мне определенно: число конечных частей континуума, по вашему мнению, конечно или бесконечно.
Симпличио. Я отвечу вам, что их число и бесконечно и конечно: бесконечно — потенциально, конечна — актуально; бесконечно — потенциально, т. е. ранее, чем произошло разделение, конечно — актуально, т. е. после того, как произошло разделение; в самом деле, нельзя себе представить частей самих по себе, пока они не отделены или, по крайней мере, не обозначены; в противном случае они будут, так сказать, лишь потенциальными. {143}
Сальвиати. Таким образом, про линию, длиною, например, в двадцать локтей, нельзя, по вашему мнению, сказать, что она содержит двадцать линий по одному локтю каждая, до тех пор, пока она не будет разделена на двадцать равных частей; вперед можно лишь сказать, что она содержит их в потенции. Пусть будет по-вашему; но скажите мне, производя действительное деление на части, увеличиваете ли вы первоначальную линию или уменьшаете ее, или же оставляете величину ее без изменения?
Симпличио. Не увеличиваем и не уменьшаем.
Сальвиати. То же самое думаю и я. Таким образом, конечные части континуума, находятся ли они в нем актуально или потенциально, не увеличивают и не уменьшают его величины; но ясное дело, что конечные части, действительно содержащиеся в целом, должны сделать его бесконечно большим, если их бесконечно много; поэтому конечные части, бесчисленные хотя бы только потенциально, могут содержаться лишь в бесконечно большой величине; таким образом, в конечной величине не может содержаться бесчисленного множества частей ни актуально, ни потенциально.
Сагредо. Тогда каким же образом может быть верным, что континуум может быть делим на части, которые всегда можно снова делить?
Сальвиати. Различие между актуальным и потенциальным дает вам, кажется, такие возможности, которых при другой точке зрения не было бы. Я хочу сделать попытку прийти к другому заключению: на предложенный вопрос — конечно или бесконечно число частей ограниченного континуума — я отвечу совершенно иначе, чем синьор Симпличио, а именно, что оно не конечно и не бесконечно.
Симпличио. Подобного ответа я дать, конечно, никогда бы не мог, так как не думаю, что существует нечто среднее между «конечным» и «бесконечным», и утверждение, что какая-либо вещь или конечна или бесконечна, не представляется мне ложным и неправильным.
Сальвиати. А между тем, это так. Если говорить о величине, то между конечным и бесконечным находится еще и третье — среднее, соответствующее любому данному числу; подобным же образом на предложенный выше вопрос, конечно или бесконечно количество частей континуума, самым правильным было бы ответить: оно не конечно и не бесконечно численно, но соответствует любому данному числу; для этого необходимо только, чтобы оно не было ограничено определенным числом, так как в этом случае оно не могло бы соответствовать большему числу; но вовсе нет необходимости, чтобы их было бесконечно много, так как никакое данное число не может быть бесконечно большим. Таким образом, по желанию предлагающего вопрос мы можем приписать данной им линии сто конечных частей, или тысячу, или сто тысяч, соответственно любому {144} желаемому числу. Но деление на бесконечное число частей невозможно. Я готов согласиться с философами, что непрерывное целое содержит столько частей, сколько им будет угодно, и содержит эти части по их желанию актуально или потенциально. Но к этому я добавляю: совершенно так же, как линия в десять сажен содержит в себе одновременно десять линий по одной сажени каждая, сорок линий по локтю каждая, восемьдесят — по полулоктю и т. д., она содержит и бесконечное множество точек, и вы можете сказать — актуально или потенциально, как вам будет угодно; в этом вопросе я, синьор Симпличио, подчиняюсь вашему суждению и решению.
Симпличио. Не могу не отозваться с похвалой о вашей речи, но очень боюсь, что одновременное признание наличия точек (пунктов) наравне с конечными частями не вполне пунктуально и что вам не так легко будет разделить предложенную линию на бесконечное множество точек, как тем философам на десять сажен или десять локтей. Наконец, я считаю совершенно невозможным осуществить на деле такое раздробление, так что оно останется одной из тех возможностей, которые никогда не осуществляются.
Сальвиати. Если какая-нибудь вещь не легка и может быть произведена лишь с большим трудом, напряжением и затратою продолжительного времени, то она не делается от этого невозможной, однако думаю, что и вам не очень-то легко будет произвести разделение линии на тысячу частей или хотя бы на 937, либо какое-нибудь другое большое простое число частей. Но если я сведу это деление, признаваемое вами вовсе невозможным, к такому же короткому процессу, как тот, который требуется другим для разделения линии на сорок частей, то будет ли этого для вас достаточным, чтобы примирительно отнестись к нему в нашей беседе? Симпличио. Мне нравится ваша манера вести разговор, допуская время от времени шутку. На ваш вопрос могу ответить, что легкость деления на точки была бы для меня более чем достаточной, если бы она не была затруднительнее деления даже на 1000 частей.
Сальвиати. Теперь я вам скажу нечто такое, что, вероятно, покажется вам удивительным. Тот, кто, желая разложить линию на бесконечное множество ее точек, предполагает достигнуть своей цели тем же путем, каким пользуются другие для разделения линии на сорок, шестьдесят или сто частей, т. е. сперва делит ее пополам, затем на четыре части и так далее, и надеется получить, таким образом, бесчисленное множество точек, грубо ошибается, потому что такой процесс постепенного деления конечных величин необходимо было бы продолжать вечно; достигнуть же таким путем приближения к неделимым в конечный период времени совершенно невозможно. Я полагаю даже, что, продолжая деление и умножая число частей в предположении приблизиться к бесконечности, мы на {145} самом деле удаляемся от нее, и вот по каким основаниям. Незадолго перед тем мы признали в нашей беседе, что в бесконечном ряде чисел должно иметься столько же квадратов и кубов, сколько вообще чисел, так как число квадратов и кубов равняется числу корней, а последними могут быть все числа вообще. Мы видели, далее, что, чем к большим числам мы переходим, тем реже попадаются в них квадраты и еще реже кубы; отсюда ясно, что, переходя к большим числам, мы все более удаляемся от бесконечного числа; отсюда можно вывести заключение, возвращаясь обратно (ибо избранный путь удаляет нас от искомого предела), что если какое-либо число должно являться бесконечностью, то этим числом должна быть единица: в самом деле, в ней мы находим условия и необходимые признаки, которым должно удовлетворять бесконечно большое число, поскольку она содержит в себе столько же квадратов, сколько кубов и сколько чисел вообще.
Симпличио. Я не совсем постигаю, как следует понимать сказанное вами.
Сальвиати. Сказанное не заключает в себе ничего сомнительного, так как единица является и квадратом, и кубом, и квадратом квадрата и т. д.; точно так же квадраты и кубы и т. д. не имеют никакой существенной особенности, которая не принадлежала бы и единице, как, например, свойство двух квадратных чисел постоянно иметь между собою среднее пропорциональное. Возьмите любое квадратное число, с одной стороны, и единицу, с другой, и вы всегда найдете среднее пропорциональное число. Если возьмем два квадратных числа 9 и 4, то средним пропорциональным между 9 и единицей будет 3; средним пропорциональным между 4 и 1 будет 2; в то же время среднее пропорциональное квадратов 9 и 4 равняется 6. Особенностью кубов является непременное нахождение между ними двух средних пропорциональных чисел. Возьмем 8 и 27; средние пропорциональные между ними равны 12 и 18; средние пропорциональные между единицей и 8 равны 2 и 4; а между единицею и 27 равны 3 и 9. Отсюда заключаем, что нет другого бесконечного числа, кроме единицы. Это представляется столь удивительным, что превосходит способность нашего представления, но в то же время поучает нас, сколь заблуждается тот, кто желает наделить бесконечное теми же атрибутами, которые присущи вещам конечным, в то время как эти две области по природе своей не имеют между собою ничего общего29.
Я не могу не рассказать вам здесь об одном случае, пришедшем мне на память и дающем хороший пример существующей бесконечной разницы и даже противодействия природы, которые встречает конечная величина при переходе в бесконечность. Начертим прямую линию АВ любой длины и возьмем где-нибудь на ней точку C, разделяющую ее на две неравных части. Проведя попарно из конечных точек А и В линии, которые {146} относились бы друг к другу так же, как отрезки АС и ВС, найдем, что все точки пересечения этих линий будут лежать на окружности одного и того же круга; так пусть линии AL и BL, проведенные из точек А и В и сохраняющие между собою то же отношение, что части АС и ВС, пересекаются в точке L, а две другие линии АК и ВК, сохраняющие ту же пропорцию, пересекаются в точке К; дальнейшими линиями пусть будут AI и BI, АН и НВ, AG и GB, АР и FB, АЕ и ЕВ и т. д.; все точки пересечения
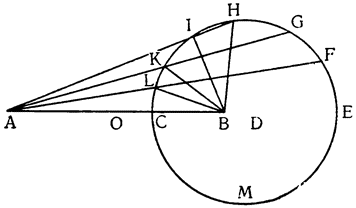 |
Сагредо. Должны ли мы думать, что жидкости таковы, как они есть, потому, что они разложены на бесконечное число первоначальных неделимых частиц, их составляющих?
Сальвиати. Я не нахожу лучшего выхода для объяснения некоторых явлений, и одно из них следующее. Если я беру твердое тело, будь то камень или металл, и молотком или тончайшим напильником превращаю его в возможно тонкий порошок, то ясно, что отдельные частицы его все-таки конечны и имеют форму и число, хотя благодаря своей малой величине они неощутимы и неразличимы нашим глазом; отсюда получается, что сдвинутые вместе, они лежат кучкою; если вырыть в них углубление, то оно таковым и остается и окружающие частицы не стремятся его заполнить; при сотрясении они приходят в движение, но тотчас же останавливаются, как только внешняя движущая причина их покидает. Подобные явления мы можем наблюдать на скоплении телец и большего размера различной, а не только сферической формы, как-то: на кучках проса, пшеницы, свинцовой дроби и всяких других веществ. Но если мы попытаемся усмотреть то же явление, взяв воду, то не увидим ничего похожего: поднимаемая вверх, она тотчас же разливается, если не удерживается сосудом или другой внешней причиной; вырываемое в ней углубление тотчас же заполняется окружающей водою; приведенная в движение, она долгое время сохраняет его, и волны распространяются в ней на большие пространства. Отсюда, кажется мне, можно вполне основательно заключить, что частицы воды, из которых, она, по-видимому, состоит (более тонкие, нежели любой мельчайший порошок, и лишенные всякой устойчивости), весьма отличны от частиц конечных и делимых; и я не {148} могу найти причины различия иначе, как в том, что они неделимы. Кажется мне также, что за то же говорит и ее чрезвычайная прозрачность. Если мы возьмем самый прозрачный кристалл и начнем ломать и толочь его в порошок, то он потеряет прозрачность, и в тем большей степени, чем мельче мы его истолчем; вода же, которая наиболее измельчена, остается совершенно прозрачною. Золото и серебро измельчаются крепкой водкою тоньше, нежели острейшим напильником, под действием которого они все же остаются в порошкообразном состоянии; но они делаются жидкостями и расплавляются лишь тогда, когда неделимые частицы огня или солнечных лучей растворяют и разлагают их, как я думаю, на первоначальные неделимые и бесконечно малые части.
Сагредо. То, что вы сейчас упомянули вскользь относительно солнечного света, я наблюдал несколько раз с удивлением. Я видел, как при помощи вогнутого зеркала около трех ладоней диаметром мгновенно расплавили свинец; поэтому я пришел к заключению, что если бы зеркало было очень велико, хорошо отполировано и имело параболическую форму, то оно в кратчайший срок расплавляло бы и все другие металлы, ибо то зеркало, которое я видел, не было ни большим ни особенно блестящим и обладало сферической формой, а между тем с большой силою расплавляло свинец и зажигало разные горючие материалы. Эти явления заставили меня поверить в чудесное действие зеркал Архимеда.
Сальвиати. Что касается зеркал Архимеда, то я верю всем проявлениям чудесного действия их, о которых можно прочесть у стольких писателей; сочинения самого Архимеда я читал и изучал с бесконечным удивлением; а если бы у меня и оставались какие-либо сомнения, то то, что написал по поводу зажигательных зеркал почтенный Бонавентура Кавальери и что я также с большим удовольствием прочел, окончательно рассеяло их31.
Сагредо. Я также видел этот трактат и прочел его с большим удовлетворением. Будучи ранее знаком с автором, я еще более убедился в справедливости своего мнения о нем, как об одном из значительнейших математиков нашего времени. Но, возвращаясь к чудесному действию солнечных лучей, расплавляющих металлы, спрошу, должны ли мы думать, что действие их, и притом столь энергичное, происходит без участия движения, или же при участии движения, но весьма быстрого?
Сальвиати. Мы видим, что горение и плавление происходят в других случаях при участии движения и притом весьма быстрого: сюда относятся действие молнии, действие пороха в минах и петардах и, наконец, ведь посредством раздувания мехами угольного огня, смешанного с плотными и нечистыми газами усиливается расплавление металла. Поэтому я не думаю, чтобы и действие света, хотя бы и чистейшего, могло происходить без участия движения, и притом быстрейшего. {149}
Сагредо. Но какого рода и какой степени быстроты должно быть это движение света? Должны ли мы считать его мгновенным же или совершающимся во времени, как другие движения? Нельзя ли опытом убедиться, каково оно?
Симпличио. Повседневный опыт показывает, что распространение света совершается мгновенно. Если вы наблюдаете с большого расстояния действие артиллерии, то свет от пламени выстрелов без всякой потери времени запечатлевается в нашем глазу в противоположность звуку, который доходит до уха через значительный промежуток времени.
Сагредо. Ну, синьор Симпличио, из этого общеизвестного опыта я не могу вывести никакого другого заключения, кроме того, что звук доходит до нашего слуха через большие промежутки времени, нежели свет; но это нисколько не убеждает меня в том, что распространение света происходит мгновенно и не требует известного, хотя и малого времени. Не более того дает мне и другое наблюдение, которое выражают так: «Как только Солнце поднимается на горизонте, блеск его тотчас же достигает наших очей». В самом деле, кто же может доказать мне, что лучи его не появились на горизонте ранее, нежели дошли до наших глаз?
Сальвиати. Малая доказательность этих и других подобных же наблюдений заставила меня подумать о каком-либо способе удостовериться безошибочно в том, что освещение, т. е. распространение света, совершается действительно мгновенно, потому что достаточно быстрое движение звука заставляет уже предполагать, что движение света должно быть крайне быстрым. Опыт, который я придумал, заключался в следующем. Два лица держат каждый по огню, заключенному в фонаре или в чем-либо подобном, который можно открывать и закрывать движением руки на виду у компаньона; став друг против друга на расстоянии нескольких локтей, участники начинают упражняться в закрывании и открывании своего огня на виду у компаньона таким образом, что как только один замечает свет другого, так тотчас же открывает и свой. После многократных повторений такого упражнения достигается такое соответствие, что открытию одного огня без чувствительной ошибки немедленно отвечает открытие другого, так как тот, кто открывает свой свет, видит в тот же миг появление света своего компаньона. После подобных упражнений на малом расстоянии два упомянутых компаньона помещаются вместе со своими огнями в расстоянии двух или трех миль друг от друга и, выждав ночи для производства опыта, начинают внимательно наблюдать, получается ли ответ на открытие и закрытие огня с тою же быстротою, что и на близком расстоянии; если это так, то можно с достоверностью заключить, что распространение света происходит мгновенно; если бы для него требовалось время, то расстояние в три мили, пробегаемое {150} светом от одного источника до глаза другого участника и обратно, было бы достаточным, чтобы обнаружить известное запоздание. Если бы пожелали производить наблюдения при еще большем расстоянии, хотя бы в восемь или десять миль, то можно было бы воспользоваться телескопами, поставив лиц, производящих опыт, в таких местах, где ночью зажигались бы огни, хотя и незаметные для простого глаза благодаря малой их величине, но открытие и закрытие которых могло бы быть удобно наблюдаемо при помощи телескопа.
Сагредо. Опыт этот кажется мне столь же надежным, сколь и остроумным. Но, скажите, каков же оказался его результат?
Сальвиати. Мне удалось произвести его лишь на малом расстоянии — менее одной мили — почему я и не мог убедиться, действительно ли появление противоположного света совершается внезапно. Но если оно происходит и не внезапно, то во всяком случае с чрезвычайной быстротой, почти мгновенно; я могу сравнить его с движением света молнии, который мы видим в облаках с расстояния в восемь—десять миль. Здесь мы различаем самый источник, начало и конец света в определенных местах тучи, хотя распространение света на все окружающее следует немедленно же. Это кажется мне доказательством того, что явление совершается с затратою времени, хотя и малою, потому что если бы свет молнии возникал во всех частях сразу, а не постепенно, то, думается, мы не могли бы различить ее источника, центра ее сияния и разветвлений. Но в каком безбрежном океане мы, сами того не замечая, очутились? Мы плаваем среди пустот, бесконечностей, неделимых, мгновенных движений и никак не сможем пристать к берегу и после тысячи рассуждений32.
Сагредо. Положение, действительно не соответствующее нашему намерению. Итак: бесконечное, отыскиваемое среди чисел, как будто находит свое выражение в единице; из неделимого родится постоянно делимое; пустота оказывается неразрывно связанной с телами и рассеянной между их частями; в результате, наши обычные воззрения меняются настолько, что даже окружность круга превращается в бесконечную прямую линию. Это последнее ваше предложение, если память мне не изменяет, вы, синьор Сальвиати, должны были доказать геометрически. Я думаю, что теперь было бы как раз уместно привести его, если вы ничего не имеете против.
Сальвиати. Я к вашим услугам и предложу вашему вниманию следующую задачу: дана прямая линия, разделенная в какой угодно пропорции на две неравных части; требуется описать круг так, чтобы прямые линии, проведенные от концов данной прямой к окружности, и притом к любой точке последней, сохраняли между собою то же отношение, какое существует между частями прямой; так что «гомологичными» будут те линии, которые выходят из одного и того же конца. {151}
Пусть данная прямая линия АВ разделена на две произвольных неравных части точкою С; требуется описать такой круг, чтобы прямые линии, проведенные из точек А и В к любой точке окружности, относились друг к другу как СА к ВС так, чтобы гомологичными были линии, выходящие из одного конца. Опишем из центра С радиусом, равным меньшей части линии или СВ, круг и проведем из точки А касательную к окружности этого круга AD, продолжив ее на неопределенную длину по направлению к Е; пусть точкой касания будет В; проведем линию С, которая будет перпендикулярна к линии АЕ; из точки В восставим перпендикуляр к линии АЕ; из точки В восставим перпендикуляр к линии АВ до пересечения с касательной в точке Е; из точки Е опять восставим перпендикуляр к линии АВ, который пересечет продолжение линии АВ в точке F. Утверждаю, прежде всего, что обе прямые EF и FC равны между собою; действительно, проведя линию ЕС, мы получим два треугольника ВЕС и ВЕС, две стороны одного из коих BE и СЕ соответственно равны двум сторонам другого BE и ЕС, так как линии BE и ЕВ суть касательные к кругу ВВ, линии же ВС и СВ равны как радиусы; следовательно, угол ВЕС равен углу ВЕС. Теперь, так как углу ВСЕ до прямого недостает угла СЕВ, а углу СЕР до прямого недостает угла СЕВ, т. е. равных величин, то углы FCE и FEC будут между собою равны. Треугольник CFE будет, таким образом, равнобедренным, а стороны его FE и FC будут равны между собою; круг, описанный из центра F радиусом FE, пройдет, следовательно, через точку С. Опишем такой круг СEG; утверждаю, что это и есть искомый нами круг, из любой точки окружности коего можно провести к концам А и В прямые линии, которые будут относиться друг к другу как части АС и ВС, соединяющиеся одна с другой в точке С. Относительно двух линий, встречающихся в точке Е, т. е. линий АЕ и BE, это ясно, так как угол Е треугольника АЕВ делится линией СЕ пополам, почему отношение сторон АЕ и BE будет таково же, как и отношение отрезков АС и СВ. То же может быть доказано и относительно линий AG и BG, оканчивающихся в точке G. Из подобия треугольников AFE и EFB вытекает, что отношение AF к FE равно отношению EF к FB; заменяя FE равной ей линией CF, получаем, что отношение AF к CF равно отношению CF к FB; отсюда, вычитая последующие члены из предыдущих, получаем, что АС к CF (или что то же самое — к FG) относится так же, как СВ к BF, а вся линия АВ относится ко всей линии BG, как СВ к BF; отношение AG к GB будет равно отношению CF {152} к FB или EF к FB, или АЕ к ЕВ или АС к СВ, что и требовалось доказать. Возьмем другую произвольную точку на окружности; пусть этой точкой будет Я, а пересекающимися в ней линиями — АН и ВН. Утверждаю, что отношение АН к НВ также равно отношению АС к СВ. Продолжим линию НВ до пересечения с окружностью в точке I и соединим последнюю с точкою F прямой IF; при этом окажется по-прежнему, что отношение АВ к BG будет равно отношению СВ к BF; прямоугольник ABF будет равен прямоугольнику CBG или же IBH33. Так как, далее, отношение АВ к ВН равно отношению IB к BF и углы при В равны, то, следовательно, отношение АН к НВ равняется отношениям IF к FB или EF к FB и АЕ к ЕВ.
Скажу, кроме того, что невозможно, чтобы линии, имеющие указанное выше отношение и исходящие из точек А и В, встречались в какой-либо точке, лежащей внутри или вне окружности CEG. Предположим, действительно, что это возможно и что две такие линии AL и BL встречаются в точке L вне окружности. Продолжим линию LB до пересечения ее с окружностью в точке М и проведем линию MF. Если теперь отношение AL к BL равно отношениям АС к ВС или же MF к FB, то мы будем иметь два треугольника ALB и MFB, у которых стороны, лежащие против равных углов ALB и MFB, будут пропорциональными, углы при вершине в точке В будут равны, а остающиеся углы FMB и LAB будут острыми (ибо угол с вершиной в точке М мог бы быть прямым лишь в том случае, если бы основанием его являлся весь диаметр CG, а не только часть его BF; другой же угол с вершиной в А острый, так как линия AL, гомологичная АС, больше линии BL, гомологичной ВС); следовательно, треугольники ABL и MBF подобны, и отношение АВ к BL равно отношению MB к BF, почему прямоугольник ABF будет равен прямоугольнику MBL; но по доказанному выше прямоугольник ABF равен прямоугольнику CBG; следовательно, выходит, что прямоугольник MBL равен прямоугольнику CBG, что невозможно. Таким образом, пересечение линии вне окружности невозможно; равным образом невозможно оно и внутри круга, что доказывается тем же способом; следовательно, все точки пересечения лежат на самой окружности.
Но нам пора уже вернуться назад и удовлетворить желание синьора Симпличио, показав ему, что разложение линий на бесконечное множество ее точек не только не невозможно, но сопряженно не с большими трудностями, чем разделение на конечные части; для этого необходимо только одно условие, на которое, полагаю, синьор Симпличио согласится. Оно заключается в следующем: вы не должны требовать, чтобы я отделил одну точку от другой и показал их вам в отдельности на этой бумаге; со своей стороны, я не требую действительного разделения линии на четыре или шесть частей и довольствуюсь одним указанием вами точек деления линии {153} или точек ее излома, когда вы хотите образовать из нее квадрат или шестиугольник, это уже убеждает меня в правильности приема.
Симпличио. Согласен.
Сальвиати. Если теперь сгибание линии под углами так, чтобы образовался квадрат или восьмиугольник или многоугольник с сорока, ста или тысячью сторон, представляется вам достаточным для действительного выявления тех четырех, восьми, сорока, ста или тысячи частей, которые, как вы говорите, содержались потенциально в первоначальной прямой линии, то, когда я образую из прямой линии многоугольник с бесконечным числом сторон, т. е. когда я сгибаю ее в окружность, не могу ли я с таким же правом утверждать, что я вызываю к действительности та бесконечное множество частей, которое первоначально, пока линия была прямой, содержалось в ней, по вашему утверждению, в потенции? Вы не можете отрицать, что подобное рассуждение не менее верно в отношении бесконечного множества частей линии, нежели в отношении четырех частей, образующих квадрат, или тысячи частей, образующих тысячеугольник, потому, что в нем не нарушается ни одно из условий, имеющихся для многоугольника с тысячью или ста тысячами сторон. Последний, поставленный на одну из своих сторон и приложенный к прямой линии, соприкасается с ней этой стороной, т. е. одной стотысячной своей частью; круг, который представляет собою многоугольник с бесконечным числом сторон, соприкасается с прямой также одною из своих сторон, т. е. единственной точкой, отличной от других соседних, а потому отделенной и отграниченной от них не в меньшей степени, нежели отделена от соседних сторона любого многоугольника. Подобно тому как многоугольник, вращаемый на плоскости, образует последовательным наложением всех своих сторон прямую линию, равную его периметру, точно так же и круг, катящийся по плоскости, чертит соприкосновением бесчисленного множества точек прямую линию, равную его окружности. Теперь я не знаю, синьор Симпличио, согласятся ли со мною господа перипатетики, которых я поддерживаю, в том, что всякий континуум разложим лишь на делимые части, так что, продолжая подобное деление последовательно, мы никогда не придем к концу, и признают ли они, что ни одно из их делений не будет последним и не может быть таковым, потому что для дальнейшего разложения всегда остаются делимые части, последнее же крайнее деление должно разложить делимое на бесконечное множество неделимых, чего, как я утверждаю, мы не можем достигнуть последовательным раздроблением на большее и большее количество частей. Предложенный же мною метод раздроблять и разделять бесконечность одним разом (прием, в котором мне не следует отказать) должен и их успокоить и заставить принять, что континуум состоит из абсолютно неделимых атомов. Этим дается также путь, более надежный, нежели другие, чтобы выбраться из {154} сложного лабиринта разных вопросов, к которым принадлежит, например, затронутый уже нами вопрос о связности частей твердого тела; приняв, что тела состоят из неделимых частиц, мы можем, как мне кажется, понять и явления разрежения и сгущения тел, не прибегая для объяснения первого к признанию пустых промежутков, а второго — к проникновению одних тел в другие.
Симпличио. Не знаю, что сказали бы вам перипатетики; полагаю, что рассуждения ваши в большей своей части явились бы для них совершенно новыми и как таковые подлежали бы рассмотрению. Возможно, что они нашли бы возражения и ответы на те неясные пункты, которые я за краткостью времени и недостаточностью сообразительности должен был оставить неразрешенными. Но оставим это теперь в стороне; мне очень хотелось бы узнать, каким образом введение таких неделимых облегчает понимание явления сгущения и разрежения, делая излишним в то же время признание пустоты или взаимного проникновения тел.
Сагредо. Я также с большим интересом занялся бы этим вопросом, для меня пока совершенно неясным; мне хотелось бы познакомиться с доводами Аристотеля в опровержение существования пустоты, о чем
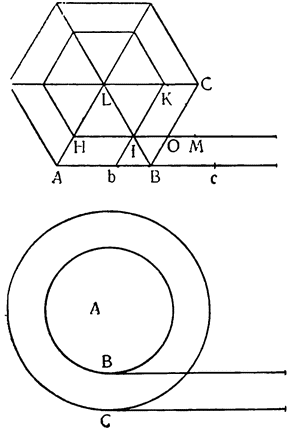 |
Сальвиати. Сделаем и то и другое. Что касается первого, то для понимания разрежения необходимо воспользоваться линией, описываемой малым кругом при вращении большого круга, которая оказалась больше, чем окружность этого малого круга; для понимания же сгущения мы покажем, как при вращении малого круга больший круг описывает прямую линию, меньшую по длине, чем его окружность; для более наглядного пояснения рассмотрим сперва, что происходит с соответствующими многоугольниками. На чертеже, сходном с тем, которым мы пользовались раньше, изображены два шестиугольника с общим центром L, именно АВС и HIК, и параллельные прямые НОМ и АВс, по которым будут катиться многоугольники. Удерживая вершину I малого многоугольника, повернем этот многоугольник так, чтобы сторона его IK совпала с прямой линией, при каковом движении точка К опишет дугу КМ, а сторона IK совпадет с отрезком IM прямой. Теперь посмотрим, что сделается при этом со стороною СВ большого многоугольника. Так как вращение совершается {155} около точки I, то линия IB опишет своим концом В, двигающимся обратно, дугу Вb под параллельной линией cA, так что когда сторона KI совпадает с линией MI, то сторона ВС совпадает с линией bс, продвинувшись вперед лишь на отрезок Вс и отстав на отрезок, соответствующий дуге Вb, который отложится на линии ВА. При продолжении вращения подобным же образом меньший многоугольник опишет и пройдет по своей параллели линию, равную своему периметру; больший же многоугольник пройдет в то же время линию меньшую, чем его периметр, на величину bВ, повторенную столько раз, сколько у него сторон; линия эта будет приблизительно равна пройденной меньшим многоугольником, превышая последнюю лишь на величину bВ. Здесь обнаруживается, таким образом, причина, благодаря которой больший многоугольник (управляемый меньшим) не описывает своими сторонами линии большей, нежели описанная меньшим многоугольником; она заключается в том, что каждая сторона многоугольника покрывает часть пространства, уже пройденного предшествующей стороной.
Рассмотрим теперь два концентрических круга, описанных из центра А и покоящихся на двух параллельных линиях, соприкасаясь с ними — меньший в точке В, а больший — в точке С. При вращении меньшего круга точка В не будет оставаться некоторое время неподвижною, а линия BG не будет перемещать назад точку С, как то имело место в многоугольнике, где точка I оставалась без движения, пока сторона KI не накладывалась на линию IM, а линия IB переносила точку В, т. е. конец стороны СВ, назад в точку b, так что сторона ВС принимала положение be, откладывая часть Вb на линии ВА и подвигаясь вперед только на часть Вс, равную IM или стороне меньшего многоугольника; накладывание на пространство, занимаемое предшествующей стороной, излишков сверх величины стороны меньшего многоугольника и продвижение вперед лишь на остальную часть, равную стороне меньшего многоугольника, объясняло то явление, что линия, откладываемая большим многоугольником, равнялась линии, откладываемой меньшим. Но здесь, если мы пожелаем применить то же рассуждение к явлению качения кругов, то должны будем сказать, что в то время как число сторон любого многоугольника выражается некоторой конечной величиной,— число сторон круга бесконечно; первые конечны и делимы, вторые жене конечны и неделимы; концы сторон многоугольника при вращении остаются некоторый промежуток времени неподвижными, и промежуток этот равен времени полного обращения многоугольника, разделенному на число его сторон; в круге пребывание в покое концов бесчисленных его сторон продолжается одно мгновение, которое так же относится к конечному промежутку времени, как точка к линии, содержащей бесконечно много точек. Обратное движение большего многоугольника происходит не на величину {156} всей его стороны, но лишь на величину излишка большей стороны над меньшей, движение же вперед происходит на величину, равную стороне меньшего многоугольника; при движении кругов точка или сторона С при остановке на мгновение точки В также переносится назад на величину, равную излишку ее над стороною В, и продвигается вперед на величину, равную последней. В результате бесконечное множество неделимых сторон большего круга со своим бесконечным множеством неделимых обратных движений, совершаемых во время бесконечно кратких остановок бесконечно большого числа сторон меньшего круга, и с бесконечным множеством продвижений вперед, равных бесконечному числу сторон меньшего круга, описывает линию, равную описываемой меньшим кругом и содержащую бесконечное множество бесконечно малых наложений, образующих утолщение или, лучше сказать, уплотнение без проникновения одних конечных частей в другие, чего нельзя сделать с разделенной на конечные части линией, равной периметру какого-либо многоугольника; выпрямленный, он не может сократиться без того, чтобы стороны его частью не налегли одна на другую или не проникли одна в другую. Такое уплотнение бесконечного множества бесконечно малых частиц без взаимного проникновения конечных частей и расхождение бесконечного множества бесконечно малых частиц с образованием неделимых пустот представляет собою все, что можно сказать об уплотнении и разрежении тел, не прибегая к допущению взаимного проникновения частей тела или к образованию пустот конечной величины. Если это вам нравится, то примите мои выводы; если же нет, то считайте их ложными так же, как и мои рассуждения, и поищите других объяснений, более удовлетворительных. Я только напомню вам при этом два слова: мы находимся в области бесконечных и неделимых33.
Сагредо. Признаюсь откровенно, что ваши соображения весьма остроумны и звучат для моих ушей, как нечто новое и чуждое; если, однако, природа на самом деле и следует таким законам, я все же не знал бы, на что решиться. Но верно то, что если я не услышу что-либо более меня удовлетворяющего, я остановлюсь на сказанном, чтобы не оставаться совсем безгласным. Но, быть может, синьор Симпличио сможет осветить нам (с чем до сих пор я еще никогда не встречался) те объяснения, которые давали этому столь темному предмету философы. По правде сказать, все то, что мне довелось читать относительно уплотнения, было столь плотным, а относительно разрежения — столь тонким, что моя слабая голова не могла того понять, а в это — проникнуть.
Симпличио. Я нахожусь в полном смущении, встречая серьезные затруднения и на том и на другом пути, в особенности же на новом. Согласно предложенному взгляду, унция золота может разредиться и образовать тело, объемом более земного шара, а с другой стороны, Земля {157} может уплотниться и сжаться до размера ореха. Таким вещам я не верю, и полагаю, что вы сами тоже этому не верите. Ваши рассуждения и доказательства суть чисто математические, отвлеченные и оторванные от всякой ощущаемой материи: я полагаю, что по отношению к физической материи и предметам, встречающимся в природе, выведенные законы не могут иметь приложения.
Сальвиати. Сделать для вас видимым невидимое — это, конечно, не в моих силах, и думаю, что вы не станете этого от меня и требовать. Но, насколько это доступно нашим чувствам, разве мы не можем убедиться в способности сильного разрежения хотя бы золота, которое вы только что назвали? Не знаю, случалось ли вам видеть, как мастера вытягивают золотую проволоку, у которой золото покрывает лишь поверхность, вся же внутренняя часть состоит из серебра. Вытягивают ее следующим образом: берут цилиндр или, проще сказать, стержень из серебра, длиною приблизительно в поллоктя и толщиною в три-четыре пальца, и покрывают его позолотою, накладывая листки сусального золота, которое, как вы знаете, настолько тонко, что от дуновения поднимается в воздухе; таких листков накладывается восемь-десять, не более того. Позолоченный таким образом стержень начинают затем с большой силой вытягивать, заставляя его проходить через отверстия в железной доске; пропуская его много и много раз через отверстия все меньшего диаметра, продолжают этот процесс до тех пор, пока не получают нити столь же тонкой, как женский волос; и вся она остается с поверхности позолоченной. Предоставляю вам судить, сколь велика способность золота к утончению и расширению.
Симпличио. Я не вижу, чтобы из этой операции проистекало столь удивительное утончение вещества золота, как вы того желаете. Во-первых, уже первоначальная позолота состояла из десяти золотых листков, что составляет значительную толщину; во-вторых, хотя серебро при вытягивании и утончении и прибавляется в длине, но зато уменьшается в толщине, так что изменение одного размера компенсируется изменением другого, и поверхность серебра увеличивается лишь настолько, что для покрытия ее золоту достаточно утончиться, может быть, лишь до пределов первоначального листка.
Сальвиати. Вы в достаточной мере ошибаетесь, синьор Симпличио, так как увеличение поверхности составляет квадратный корень из увеличения длины, как я могу это геометрически доказать.
Сагредо. И от себя и от лица синьора Симпличио я прошу вас дать нам это доказательство, если, конечно, оно таково, что может быть нами понято.
Сальвиати. Попробую изложить его так, как оно приходит мне на память без подготовки. Само собою ясно, что первоначальный толстый {158} серебряный стержень и длиннейшая вытянутая нить суть два равных по объему цилиндра, так как содержат то же количество серебра; поэтому если я покажу, какое отношение существует между поверхностями двух равных по объему цилиндров, то я докажу требуемое. Утверждаю, что отношение поверхностей двух равновеликих цилиндров, не считая площадей их оснований, равно корню квадратному из отношения их длин.
Возьмем два равновеликих цилиндра, высота одного из коих равна АВ, а другого CD, и пусть линия Е будет средней пропорциональной между ними. Утверждаю, что поверхность цилиндра АВ, не считая
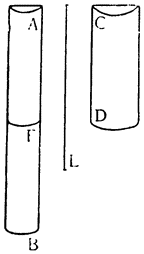 |
Применим теперь то, что сейчас нами доказано, к нашему примеру, предположив, что позолоченный серебряный цилиндр имел не более поллоктя длины и три или четыре пальца толщины и, доведенный до тонкости волоса, образовал нить длиною в двадцать тысяч локтей (что вполне {159} может быть достигнуто). Мы найдем, что поверхность его увеличилась в двести раз против первоначальной, вследствие чего золотые листочки, наложенные первоначально в числе десяти, должны теперь покрыть поверхность в двести раз большую, так что толщина золотого слоя, покрывающего нить, будет составлять всего одну двадцатую часть толщины одного листка сусального золота. Подумайте, какова тонкость этого слоя, и можно ли представить себе таковую без огромного расхождения частей? Вместе с тем не доказывает ли этот опыт, что физическая материя состоит из бесконечного множества малых частиц? Впрочем, этому можно привести и другие, еще более веские и убедительные примеры.
Сагредо. Доказательство кажется мне столь прекрасным, что если бы даже оно и не имело силы убедить нас в том, для чего оно было приведено (и чего, как мне кажется, оно в значительной мере достигает), то оно все же вполне вознаградило нас за то краткое время, которое мы потратили, чтобы его выслушать35.
Сальвиати. Раз я вижу, что вы столь высоко цените геометрические доказательства, дающие нам надежную опору, то я познакомлю вас с другим предложением, дающим ответ на довольно интересный вопрос. Ранее мы рассматривали цилиндры равного объема, но разной высоты или длины; теперь мы займемся цилиндрами, имеющими равную поверхность, но различную длину; отмечу, что речь будет идти лишь о боковых поверхностях,
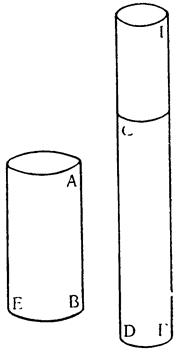 |
Пусть АЕ и CF будут два цилиндра с равными боковыми поверхностями, причем высота второго CD больше высоты первого АВ. Утверждаю, что объем цилиндра АЕ так относится к объему цилиндра CF, как высота CD к высоте АВ. Так как поверхность CF равна поверхности АЕ, то объем цилиндра CF будет меньше объема цилиндра АЕ. В самом деле, если бы они были равны, то по доказанному ранее положению его поверхность превосходила бы поверхность цилиндра АЕ; то же имело бы место в еще большей степени, если бы цилиндр CF был более цилиндра АЕ. Предположим теперь, что имеется цилиндр ID, равновеликий цилиндру АЕ; согласно доказанному выше, поверхность этого цилиндра ID относится к поверхности АЕ, как высота его IF к средней пропорциональной между IF и АВ. Так как, однако, поверхность цилиндра АЕ равна поверхности CF и так как поверхность цилиндра ID относится к поверхности CF, как высота IF к высоте CD, то высота {160} CD есть также среднее пропорциональное между IF и АВ. Так как сверх того цилиндр ID равен цилиндру АЕ, то они имеют одно и то же отношение к цилиндру CF; но ID относится к CF, как высота IF к CD; следовательно, отношение цилиндра АЕ к цилиндру CF будет равно отношению линии IF к CD, т. е. отношению CD к АВ, что и требовалось доказать.
Отсюда можно вывести объяснение одного явления, которое люди часто наблюдают не без удивления. Если из куска холста, у которого длина больше ширины, делается мешок для зерна с дном из деревянной доски, как это обычно принято, то спрашивается, почему мешок будет более вместимым, если короткую сторону направить вверх, а более длинной охватить деревянное дно, нежели если сделать наоборот. Предположим, что холст имеет в ширину шесть и в длину двенадцать локтей; если длинная сторона холста в двенадцать локтей будет охватывать дно, а высота мешка будет равняться шести локтям, то мешок будет более емким, нежели в том случае, когда охватывать дно будет короткая сторона в шесть локтей, а высота мешка будет составлять двенадцать локтей. То, что было ранее доказано, позволяет не только составить общее суждение о том, в каком случае объем будет больше, но и показать, насколько один объем будет больше или меньше другого; он будет во столько раз больше, во сколько высота его ниже, и во столько раз меньше, во сколько она выше. В приведенном нами примере кусок холста имеет длину, в два раза превышающую его ширину; вместимость мешка, обращенного к основанию короткой стороной и сшитого по длине, будет в два раза меньше вместимости мешка, сшитого по ширине. Точно так же, если имеем подобие плетеной циновки, длиною в двадцать пять локтей и шириною в семь локтей, и хотим сделать из нее корзину, то объемы корзин, сшитых по длине и по ширине циновки, будут относиться друг к другу, как семь к двадцати пяти.
Сагредо. Таким путем мы с особым удовлетворением постепенно приобретаем новые познания, не лишенные и практической пользы. В отношении только что затронутого положения я полагаю, что среди лиц, мало знакомых с геометрией, едва ли найдется четыре процента таких, которые сразу же не сделают ошибки и не скажут, что тела, имеющие равные поверхности, равны и во всем прочем. В подобную же ошибку впадают и при определении площадей, сравнивая, как то часто случается, величину различных городов на основании длины их обводов и полагая, что об их сравнительной величине можно судить, зная, во сколько раз обвод одного более обвода другого. При этом упускается из виду, что хотя обвод одного может равняться обводу другого, но пространство, ограниченное равными линиями, может быть в одном случае значительно больше, нежели в другом. Это имеет место в отношении не только неправильных {161} фигур, но и правильных, из коих те, которые имеют большее число сторон, имеют и большую площадь, так что, в конце концов, круг как многоугольник с бесконечным числом сторон охватывает площадь большую, чем все остальные многоугольники, равного с ним обвода. Я с особым удовольствием вспоминаю доказательство этого положения, которое я нашел при изучении «Сферы» Сакробоско и приложенных к ней ученейших комментариев36.
Сальвиати. Совершенно верно. Как раз читая это место, я нашел очень простой способ доказать, что из всех правильных фигур с равным периметром круг имеет наибольшую площадь, которая у многоугольников вообще тем более, чем больше число их сторон.
Сагредо. Так как я очень люблю доказательства известных положений, тонкие и далекие от обычных, то я очень прошу вас познакомить меня с вашим доказательством.
Сальвиати. Это можно сделать в нескольких словах на основании следующей теоремы:
Круг есть среднее пропорциональное между двумя любыми правильными подобными многоугольниками, один из которых описан вокруг него, а другой — изопериметричен кругу. Будучи меньше всех описанных многоугольников, круг в го же время больше всех изопериметричных ему многоугольников. Далее, из описанных многоугольников те, которые имеют большее число углов, меньше тех, которые имеют их меньшее число; наоборот, из изопериметричных кругу многоугольников больше те, число углов у которых больше.
Пусть из двух подобных многоугольников А и В первый — А — описан около круга А, другой же — В — изопериметричен кругу; утверждаю, что круг является средним пропорциональным между ними. Круг этот равен
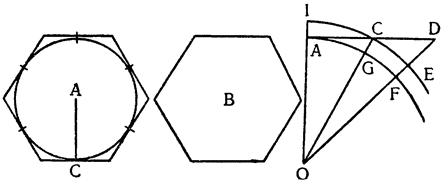 |
Что касается другой части предложения, т. е. что из многоугольников, описанных вокруг данного круга, имеющие меньшее число сторон больше тех, число сторон коих больше, и что, наоборот, из изопериметричных многоугольников больше те, число сторон коих больше, то она доказывается следующим образом. К кругу, имеющему центр в точке О и радиус ОА, проведем касательную АВ, на которой отложим отрезок AD, равный, например, половине стороны описанного пятиугольника, и отрезок АС, равный половине стороны такого же семиугольника. Проведем прямые OGC, OFD и опишем из центра О радиусом, равным линии ОС, дугу ECI. Так как треугольник DOC больше сектора ЕОС, а сектор COI больше треугольника СОА, то отношение треугольника DOC к треугольнику СОА будет больше отношения сектора ЕОС к сектору COI, или сектора FOG к сектору GOА. Сочетая и переставляя37, получим, что отношение треугольника BOA к сектору FOA будет больше отношения треугольника СОА к сектору GOА и отношение десяти треугольников DOА к десяти секторам FOA будет больше отношения четырнадцати треугольников СОА к четырнадцати секторам GOА; таким образом, отношение к кругу описанного пятиугольника будет больше отношения к тому же кругу описанного семиугольника и, следовательно, пятиугольник будет больше семиугольника. Представим себе теперь семиугольник и пятиугольник, имеющие периметры, равные окружности данного круга; утверждаю, что семиугольник больше пятиугольника. Так как круг является средним пропорциональным между пятиугольником, описанным около него, и пятиугольником, имеющим равный с окружностью периметр, а также и средним пропорциональным между описанным и изопериметричным семиугольником, и так как доказано уже, что описанный пятиугольник больше описанного семиугольника, то отношение пятиугольника к кругу будет больше отношения к нему же семиугольника; поэтому отношение круга к изопериметричному с ним пятиугольнику будет больше отношения его к такому же семиугольнику; следовательно, пятиугольник меньше изопериметричного семиугольника, что нам и требовалось доказать.
Сагредо. Прекрасное доказательство, и весьма тонкое38. Но мы, кажется, слишком углубились в область геометрии. Мы собирались рассмотреть затруднения, выдвинутые синьором Симпличио и заслуживающие большого внимания. В особенности затруднительной представляется мне проблема сгущения. {163}
Сальвиати. Если сгущение и разрежение представляют собою явления противоположные, то, видя чрезвычайное разрежение, нельзя отрицать возможности столь же большого сгущения. А чрезвычайное разрежение, совершающееся к тому же почти мгновенно, что делает его еще более удивительным, мы можем наблюдать ежедневно. Не представляется ли примером чрезвычайного разрежения превращение малого количества артиллерийского пороха в огромный объем огня? И как велико к тому же, даже почти безгранично, распространение возникающего при этом света? И если бы этот огонь и этот свет опять соединились, что не представляется невозможным, так как перед тем они заключались в столь малом объеме, то как велико было бы сгущение? Подумав, вы найдете тысячи случаев разрежения, которые гораздо легче наблюдать, нежели случаи сгущения, так как плотное вещество легче поддается нашему воздействию и доступнее нашим чувствам. Если мы возьмем дерево, то мы можем превратить его в огонь и свет, но мы бессильны сгустить эти огонь и свет и обратить их в дерево; мы наблюдаем как плоды, цветы и тысячи других плотных тел частью превращаются в запах, но мы не видим, как атомы, производящие запах, сгущаются в благоухающие тела. Там, где недостает чувственного наблюдения, его надо дополнить размышлением, которое дает нам возможность не только понять явление разрежения и растворения твердых тел, но и сгущения веществ нетвердых и даже самых тонких.
Приступим же к рассмотрению того, как могут происходить сгущение и разрежение таких тел, которые способны к сгущению и разрежению, не прибегая при этом к помощи предположения пустоты и проницаемости тел. При этом не исключена возможность, что в природе существуют такие вещества, с которыми такие явления не происходят, и поэтому с ними не происходит того, что вы называете затруднительным и невозможным. Итак, синьор Симпличио, я много потрудился над тем, чтобы угодить вам, господам философам, представить, каким образом могут происходить сгущение и разрежение без допущения проницаемости тел или существования пустых пространств — допущений, которые вы отрицаете и отклоняете, тогда как, если бы вы пожелали их признать, вы не нашли бы во мне столь упорного противника. Поэтому или примите эти затруднительные допущения, или согласитесь с моими объяснениями, или найдите более удовлетворительные.
Сагредо. Взаимное проникновение тел я совершенно отрицаю, сходясь в этом с философами-перипатетиками. Что же касается пустоты, мне хотелось бы внимательно рассмотреть как доводы Аристотеля против ее допущения, так и ваши, синьор Сальвиати, с ним несогласные; синьор Симличио будет добр точно изложить доводы философа, а вы, синьор Сальвиати, свои возражения. {164}
Симпличио. Аристотель, насколько я помню, оспаривает мнение некоторых древних философов, которые вводили пустоту как необходимое условие движения, говоря, что последнее невозможно без первой. Оспаривая такое положение, Аристотель доказывает, наоборот, что существование движения (как можно видеть) противоречит допущению пустоты. Его доказательство таково. Он рассматривает два случая: один — движение тел различного веса в одинаковой среде; другой — движение одного и того же тела в различных средах. Относительно первого случая он утверждает, что тела различного веса движутся в одной и той же среде с различными скоростями, которые относятся между собою, как веса тел, так что, например, если одно тело в десять раз тяжелее другого, то и движется оно в десять раз быстрее. Относительно второго случая он принимает, что скорость движения одного и того же тела в различных средах различна и обратно пропорциональна степени густоты или плотности среды; таким образом, если предположить, что степень плотности воды равна десятикратной плотности воздуха, то движение в воздухе должно совершаться в десять раз быстрее, чем в воде. Из этого второго положения он выводит дальнейшее доказательство в следующей форме. Так как разреженность пустоты бесконечно отличается от плотности среды, заполненной хотя бы тончайшим веществом, то движущиеся тела, проходящие определенное расстояние в заполненном пространстве в некоторый промежуток времени, должны были бы передвигаться в пустоте мгновенно; но мгновенное движение невозможно; поэтому вследствие движения невозможна пустота.
Сальвиати. Аргумент, как видите, приводится «ad hominem»39, т. е. против тех, кто полагал, что пустота необходима для движения. Поэтому, если я сочту аргумент доказательным, но вместе с тем признаю, что в пустоте движение не совершается, то существование пустоты в абсолютном смысле — без отношения к движению — этим не будет опровергнуто. Но рассуждая в духе этих древних и рассматривая, насколько убедительны доводы Аристотеля, следует, как мне кажется, возражать против его положений, отрицая оба. Во-первых, я сильно сомневаюсь, чтобы Аристотель видел на опыте справедливость того, что два камня, из которых один в десять раз тяжелее другого, начавшие одновременно падать с высоты, предположим, ста локтей, двигались со столь различной скоростью, что в то время как более тяжелый достиг бы земли, более легкий прошел бы всего 10 локтей.
Симпличио. Из ваших слов выходит, что вы производили подобные опыты, потому что вы говорите: «видел более тяжелый», а видеть можно только тогда, когда производишь опыты.
Сагредо. Но я, синьор Симпличио, не производивший никаких опытов, уверяю вас, что пушечное ядро весом в сто, двести и более фунтов {165} не опередит и на одну пядь мушкетной пули весом меньше полфунта при падении на землю с высоты двухсот локтей.
Сальвиати. Да и без дальнейших опытов путем краткого, но убедительного рассуждения мы можем ясно показать неправильность утверждения, будто тела, более тяжелые, движутся быстрее, нежели более легкие, подразумевая тела из одного и того же вещества, т. е. такие, о которых говорит Аристотель. В самом деле, скажите мне, синьор Симпличио, признаете ли вы, что каждому падающему твердому телу присуща от природы определенная скорость, увеличить или уменьшить которую возможно, только применив усилие или противопоставив какое-либо препятствие?
Симпличио. Я не сомневаюсь в том, что одно и то же тело в одной и той же среде имеет постоянную скорость, определенную природой, которая не может увеличиться иначе, как от приложения нового импульса, или уменьшиться иначе, как от замедляющего препятствия.
Сальвиати. Таким образом, если мы имеем два падающих тела, естественные скорости которых различны, и соединим движущееся быстрее с движущимся медленнее, то ясно, что движение тела, падающего быстрее, несколько задержится, а движение другого несколько ускорится. Вы не возражаете против такого положения?
Симпличио. Думаю, что это вполне правильно.
Сальвиати. Но если это так и если вместе с тем верно, что большой камень движется, скажем, со скоростью в восемь градусов, тогда как другой, меньший,— со скоростью в четыре градуса, то соединяя их вместе, мы должны получить скорость, меньшую восьми градусов; однако два камня, соединенные вместе, составляют тело большее первоначального, которое имело скорость в восемь градусов, следовательно, выходит, что более тяжелое тело движется с меньшей скоростью, чем более легкое40; а это противно вашему предположению. Вы видите теперь, как из положения, что более тяжелые тела движутся с большей скоростью, чем легкие, я мог вывести заключение, что более тяжелые тела движутся менее быстро.
Симпличио. Я чувствую себя совершенно сбитым с толку. Мне кажется, что малый камень, присоединенный к большому, увеличивает вес последнего; но увеличивая вес, он должен если не увеличить скорость, то во всяком случае не уменьшить ее.
Сальвиати. Здесь вы совершаете новую ошибку, синьор Симпличио, так как неправильно, что малый камень увеличивает вес большого.
Симпличио. Ну, это уже превосходит мое понимание.
Сальвиати. Нисколько, все будет понятно, как только я избавлю вас от заблуждения, в которое вы впали. Дело в том, что необходимо {166} делать различие между телами, пребывающими в покое и находящимися в движении. Большой камень, взвешиваемый на весах, приобретает больший вес от наложения на него не только другого камня: положенная на него связка пакли увеличивает его вес на шесть—десять унций, которые весит сама пакля. Но если вы заставляете камень свободно падать с некоторой высоты вместе с наложенной на него паклей, то думаете ли вы, что при движении пакля будет давить на камень и тем увеличивать скорость его движения, или что она его замедлит, поддерживая камень? Мы чувствуем тяжесть на плечах, когда сопротивляемся движению, к которому стремится давящая тяжесть; но если бы мы опускались с такою же скоростью, с какою перемещается свободно падающий груз, то каким образом тяжесть могла бы давить на нас? Не видите ли вы, что это подобно тому, как если бы мы хотели поразить копьем кого-либо, кто бежит впереди нас с равною или большею скоростью? Выведите из этого заключение, что при свободном и естественном падении малый камень не давит на больший и, следовательно, не увеличивает его веса, как то бывает при покое.
Симпличио. Но если положить больший камень на меньший? Сальвиати. Он увеличил бы вес меньшего, если бы движение его было более быстрым; но мы уже нашли, что если бы меньший двигался медленнее, то он замедлил бы отчасти движение большего; таким образом, целое двигалось бы медленнее, будучи больше своей части, что противно нашему положению. Выведем из всего этого, что тела большие и малые, имеющие одинаковый удельный вес, движутся с одинаковой скоростью41.
Симпличио. Ваше рассуждение, действительно, прекрасно; однако мне все же трудно поверить, что крупинка свинца должна падать с такой же быстротою, как пушечное ядро.
Сальвиати. Скажите лучше — песчинка с такой же быстротой, как мельничный жернов. Я не хотел бы, синьор Симпличио, чтобы вы поступали как многие другие, отклоняя беседу от главного вопроса, и придирались к выражению, в котором я допустил отклонение от действительности на один волосок, желая скрыть за этой небольшой погрешностью ошибку другого, грубую, как якорный канат. Аристотель говорит: «железный шар, весом в сто фунтов, падая с высоты ста локтей, упадет на землю, в то время как другой, весом в один фунт, пройдет пространство в один локоть». Я утверждаю, что оба упадут одновременно. Проделав опыт, вы найдете, что больший опередит меньший на два пальца, так что когда больший упадет на землю, то меньший будет от нее на расстоянии толщины двух пальцев. Этими двумя пальцами вы хотите закрыть девяносто девять локтей Аристотеля и, говоря о моей небольшой ошибке, умалчиваете о громадной ошибке другого. Аристотель говорит, что тела {167} различного веса движутся в одной и той же среде (поскольку движение происходит вследствие тяжести) со скоростями, пропорциональными их весу, и приводит в пример тела, на которых можно проследить чистое, абсолютное влияние веса, отбрасывая в сторону все другие соображения как относительно формы, так и относительно других малозначащих моментов, каковые легко подвергаются воздействию среды, изменяющей простое действие одной тяжести; так, мы видим, что золото — вещество, тяжелейшее из всех других,— будучи превращено в тончайшие листки, носится в воздухе; то же делается с ним, когда кусок его обращен в тончайший порошок. Но если вы желаете доказать общее положение, то вам следует показать, что пропорциональность скоростей наблюдается во всех тяжелых телах, так что камень в двадцать фунтов весом падает в десять раз быстрее, чем камень весом в два фунта; а это, как я утверждаю, неверно: падая с высоты пятидесяти — ста локтей, оба они достигнут земли в один и тот же момент.
Симпличио. Быть может, при падении с большей высоты, хотя бы в тысячу локтей, обнаружилось бы то, чего нельзя заметить при меньших высотах?
Сальвиати. Если вы полагаете, что Аристотель так думал, то вы приписываете ему другую ошибку, да еще и ложь. Так как на земле мы не находим таких вертикальных высот, то ясно, что Аристотель не мог производить с ними опытов; а между тем он хочет убедить нас, что делал опыты, говоря, что можно видеть такое явление.
Симпличио. На самом деле Аристотель пользуется не этим принципом, а другим, с которым, я полагаю, не связано таких затруднений.
Сальвиати. Второе утверждение не менее ложно, нежели первое. Меня удивляет, как вы сами не замечаете его неправильности и не видите, что если бы было правильно, что одно и то же тело в средах различной тонкости или плотности, словом, разной сопротивляемости, например, в воде и в воздухе, движется в воздухе со скоростью большей, нежели в воде, во столько же раз, во сколько плотность воздуха меньше плотности воды, то из этого вытекало бы, что все тела, падающие в воздухе, опускаются ко дну также и в воде, что совершенно ложно, так как существуют многие тела, которые не только не тонут в воде, но даже поднимаются в ней на поверхность.
Симпличио. Я не вижу необходимости в вашем заключении и скажу, что Аристотель имел в виду такие тяжелые тела, которые опускаются как в одной, так и другой среде, а не такие, которые в воздухе падают, а в воде поднимаются кверху.
Сальвиати. Вы выдвигаете в защиту этого философа такие аргументы, которыми он, конечно, не воспользовался бы, чтобы не увеличивать {168} своей первоначальной ошибки. Скажите мне, находится ли плотность воды, или, вообще, причина, замедляющая движение в ней, в каком-либо определенном отношении к плотности воздуха, где эта замедляющая причина меньше; если находится, то определите примерно это отношение.
Симпличио. Конечно, находится, и допустим, что это отношение равно десяти; таким образом, скорость твердого тела, опускающегося в том и в другом веществе, будет в воде в десять раз меньше, чем в воздухе.
Сальвиати. Возьмем теперь одно из таких тел, которые падают в воздухе, но не тонут в воде; пусть это будет кусок дерева; предоставляю вам назначить по вашему усмотрению скорость его движения в воздухе.
Симпличио. Предположим, что он падает со скоростью двадцати градусов.
Сальвиати. Прекрасно. Очевидно, что такая скорость будет находиться к другой — меньшей скорости в таком же отношении, какое имеет плотность воды к плотности воздуха, почему меньшая скорость будет равняться двум градусам. Отсюда, рассуждая последовательно, мы должны были бы заключить, согласно правилу Аристотеля, что деревянный шар, который падает в воздухе, в десять раз менее плотном, нежели вода, со скоростью двадцати градусов, должен опускаться в воде со скоростью двух градусов, а не подниматься со дна на поверхность, как то происходит на самом деле. Я не думаю, чтобы вы стали утверждать, будто подниматься в воде и опускаться ко дну со скоростью двух градусов для дерева одно и то же. Но так как кусок дерева в воде не тонет, то вы, надо полагать, допустите вместе со мною, что можно выбрать кусок вещества иного, нежели дерево, который бы опускался в воде со скоростью двух градусов.
Симпличио. Конечно, допускаю, но вещество это должно быть значительно тяжелее дерева.
Сальвиати. Именно такое я и ищу. Но спрашивается, с какой скоростью будет падать в воздухе этот второй кусок, опускающийся в воде со скоростью двух градусов? На этот вопрос вы должны будете ответить (пользуясь правилом Аристотеля), что он будет падать со скоростью двадцати градусов; но ту же скорость в двадцать градусов вы уже приписали куску дерева; следовательно, и этот кусок и другой, значительно более тяжелый, будут двигаться в воздухе с одинаковой скоростью. Каким же образом мог бы согласовать философ этот вывод с другим своим положением, что тела разного веса в одной и той же среде движутся с различными скоростями, пропорциональными их весу? Отвлекаясь теперь от глубоких размышлений, позвольте спросить, каким образом не замечаете вы совершенно очевидных и часто встречающихся явлений, когда из двух тел, движущихся в воде, одно перемещается, например, во сто раз быстрее другого, тогда как при падении в воздухе скорость одного {169} превышает скорость другого едва ли на одну сотую долю? Так, мраморное яйцо опускается в воде во сто раз быстрее куриного яйца; при падении же в воздухе с высоты двадцати локтей оно опережает куриное яйцо едва ли на четыре пальца. Существуют тела, которые в воде опускаются за три часа на глубину десяти локтей, каковое пространство в воздухе они пробегают за один-два удара пульса, тогда как другие (например, свинцовый шарик) падают в воздухе со скоростью приблизительно в два раза большей той, с которой они тонут в воде42. Теперь, синьор Симпличио, вы без сомнения, сознаете, что вам нечего более мне возразить. Согласимся же на том, что приведенный ранее аргумент не заключает в себе ничего опровергающего существование пустоты; а если бы он и был убедительным, то им опровергалось бы лишь допущение таких больших пустот, которые ни я, ни древние не представляли себе естественно существующими и которые, возможно, могут быть созданы насильственно, как то, видимо доказывается опытами, но на этом, однако, было бы слишком долго теперь останавливаться43.
Сагредо. Так как синьор Симпличио хранит молчание, то я воспользуюсь моментом, чтобы сказать несколько слов. Вы совершенно ясно доказали, что тяжелые тела различного веса движутся в одной и той же среде не с различными скоростями, пропорциональными их весу; а с одинаковой скоростью; я полагаю, что это относится к телам из одного и того же вещества или, лучше сказать, одинакового удельного веса, но не к телам разного удельного веса (так как я не думаю, чтобы вы утверждали, будто кусок пробки падает с такою же скоростью, как кусок свинца); далее, вы ясно доказали, что неправильно принимать, будто скорость движения одного и того же тела в различных средах изменяется в той же пропорции, как сопротивляемость среды; мне очень хотелось бы знать, какие же отношения наблюдаются в действительности в том и другом случае?
Сальвиати. Вопросы очень интересные, и я много о них думал; я сообщу вам кое-что из того, к чему я пришел после долгих размышлений. После того, как я убедился, что неправильно, будто одно и то же тело движется в различных средах со скоростями, обратно пропорциональными сопротивляемости среды, и что не менее неправильно и то, будто в одной и той же среде тела различного веса движутся с различными скоростями, пропорциональными их весу (даже если учесть разность в удельном весе), я начал комбинировать эти два явления, наблюдая, что происходит с телами различного веса в средах различной сопротивляемости. При этом я нашел, что разница в скорости всегда значительно больше в средах, более сопротивляющихся, нежели в более податливых; разница эта доходит до того, что из двух тел, падающих в воздухе со скоростями, отличающимися лишь на самую малость, в воде одно движется {170} в десять раз быстрее другого; точно так же есть тела, которые, быстро падая в воздухе, в воде не тонут, но остаются лишенными движения или еще более — поднимаются кверху; можно легко найти дерево такого сорта, что суковатые части или корни его будут оставаться в воде в любом месте без движения, тогда как в воздухе они быстро падают.
Сагредо. Я много раз с большим усердием старался увеличить вес куска воска, который сам по себе не тонет, прибавляя к нему песок так, чтобы он, сравнявшись по весу с водой, мог оставаться в ней без движения; но, несмотря на все старания, это мне не удавалось; не знаю, существует ли другое твердое вещество, настолько близкое к воде по удельному весу, чтобы оно, будучи погружено в воду, могло оставаться в ней без движения.
Сальвиати. В этом отношении, равно как и в тысяче других, многие животные совершеннее нас. В вашем случае хорошим примером могли бы служить рыбы. Они столь искусны в подобных упражнениях, что по желанию могут сохранять равновесие в воде и притом не только чистой, но и значительно измененной по своей природе или благодаря примеси речного ила или соли, создающих существенную разницу; это совершается ими с такой ловкостью, что они могут, не двигаясь, пребывать в воде в покое в любом месте. Этого, как я полагаю, они достигают при помощи данного им природою для этой цели органа— пузыря, находящегося в их теле и соединяющегося довольно узким проходом со ртом. Сообразно цели, они то выталкивают из пузыря часть содержащегося в нем воздуха, то, поднимаясь на поверхность, вновь поглощают последний, делаясь по желанию то тяжелее, то легче воды, то-одинакового с нею веса.
Сагредо. Несколько иной проделкой я обманул, однажды, нескольких своих друзей, похваставшись им, что довел воск до равного с водою веса. Я зачерпнул сначала в сосуд соленой воды, затем налил сверху пресной и показал им, что кусок воска остановился посредине; погруженный на дно или поднятый на поверхность, он опять возвращался в середину.
Сальвиати. Это опыт далеко не бесполезный. Когда медики говорят о различных свойствах воды и, между прочим, о большой легкости или тяжести одной по сравнению с другой, то посредством такого шарика, стоящего по тяжести, так сказать, на границе между опусканием и поднятием в воде, можно обнаружить даже незначительную разницу в весе различных вод: в одной шарик тонет, в другой, более тяжелой,— поднимается. Прибор этот настолько чувствителен, что прибавления двух гран соли к шести фунтам воды достаточно, чтобы поднять со дна на поверхность палочку, которая ранее опустилась. Скажу вам, далее, в доказательство чувствительности этого опыта, а также в подтверждение того, что вода не оказывает никакого сопротивления разделению, что {171} подобное же явление производит не только примесь к воде какого-нибудь более тяжелого вещества, но и нагревание или охлаждение ее; чувствительность столь велика, что прибавления к шести фунтам воды четырех капель горячей или холодной воды достаточно, чтобы заставить шарик двигаться вниз и вверх: он тонет при прибавлении теплой воды и, наоборот, поднимается при прибавлении холодной. Отсюда вы можете видеть, как заблуждались философы, наделявшие воду вязкостью или связностью, заставляющей ее противиться разделению или проникновению.
Сагредо. Я видел много убедительных соображений по этому поводу в одном трактате нашего Академика; и все-таки у меня осталось некоторое сомнение, которое я не могу преодолеть. Если между частицами воды нет никакого сцепления или связности, то каким образом могут удерживаться, например на листьях капусты, довольно большие капли воды без того, чтобы не расплываться и не расходиться44?
Сальвиати. Хотя тот, кто считает свои положения правильными, должен уметь опровергнуть все доводы, приводимые в подтверждение противного, я не осмеливаюсь утверждать, что смогу сделать это в настоящем случае; однако мое бессилие не должно затмевать света истины. Прежде всего, я сознаюсь прямо, что не знаю, каким образом происходит то, что упомянутые довольно большие и выпуклые капли удерживаются, не расплываясь; но я знаю наверное, что это происходит, во всяком случае, не от внутреннего сцепления, существующего между частицами; остается, следовательно, отыскать внешнюю причину такого явления. То, что дело не во внутренней причине, я могу подтвердить, помимо показанных уже опытов, еще одним, чрезвычайно доказательным. Если бы приподнятые части воды, окруженные воздухом, сохраняли свое положение благодаря причине внутренней, то они должны были бы сохранять его в еще сильнейшей степени, будучи окружены такою средою, в которой они имеют меньшую наклонность падать, чем в окружающем воздухе; такою средою могла бы быть любая жидкость более тяжелая, чем воздух, например вино. Но если мы прильем к такой капле воды вина, то мы не сможем окружить ее вином, так как частицы воды, которые должны были удерживаться внутренним сцеплением, растворятся; как только жидкость, приливаемая извне, приблизится, вода, не дожидаясь поднятия уровня этой жидкости, растворится и расплывется, оставаясь внизу, если приливается красное вино; таким образом, явление вызывается причиною внешнею, которую можно приписать окружающему воздуху. И, действительно, между воздухом и водою существует большая несовместимость, которую я наблюдал на следующем опыте. Если наполнить водою стеклянный шар с узким горлышком, толщиной всего в соломинку, и повернуть его горлышком вниз, то вода, хотя и более тяжелая и быстро {172} падающая в воздухе, не выльется, а воздух, способный, как наилегчайшее тело, быстро подниматься через воду, не войдет внутрь, и оба вещества останутся друг против друга в покое. Наоборот, если опустить горлышко в сосуд с красным вином, которое немного легче воды, то тотчас же станут заметны красные струйки, медленно восходящие среди воды, а вода с такою же медленностью будет вытекать в вино, не смешиваясь с ним, так что, в конце концов, шар окажется весь наполненным вином, а вода скопится на дне сосуда, содержавшего вино. Какое иное заключение отсюда должны мы сделать, как не то, что между воздухом и водою существует несовместимость, для меня не ясная; но может быть...
Симпличио. Я почти готов смеяться над той антипатией, которую синьор Сальвиати питает к слову «антипатия», не решаясь произнести его; а между тем, оно так подходит для объяснения такого затруднения.
Сальвиати. Ну, пусть наши сомнения будут разрешены так, как предлагает синьор Симпличио, и после отклонения, возвратимся к первоначальному вопросу45. Мы видели, что разница в скорости падения тел различного веса, в общем, более значительна в средах, представляющих и большее сопротивление. Но что же далее? В ртути золото не только идет ко дну быстрее свинца, но только оно одно и опускается, в то время как все другие металлы и камни поднимаются вверх и плавают на поверхности. А между тем разница в скорости движения в воздухе кусков золота, свинца, меди, порфира и других тяжелых веществ столь незначительна, что при падении с высоты ста локтей шар из золота опередит шар из меди едва ли на четыре пальца. Видя это, думаю, что если бы совершенно устранить сопротивление среды, то все тела падали бы с одинаковой скоростью.
Симпличио. Весьма сомнительное утверждение, синьор Сальвиати. Я никогда не поверю, чтобы в пустом пространстве, если только в нем можно наблюдать падение, клочок шерсти двигался с такою же быстротою, как кусок свинца.
Сальвиати. Будьте осторожнее, синьор Симпличио. Указываемые вами затруднения не столь велики, а я не так неосторожен, чтобы быть застигнутым врасплох и не дать вам ответа. Итак, выслушайте рассуждение, которое я постараюсь сделать для вас понятным и доказательным. Мы задались исследованием вопроса, что произойдет с различными движущимися Телами различного веса в среде, сопротивление которой равняется нулю; при таких условиях всякую разницу в. скорости, которая может обнаружиться, придется приписать единственно разнице в весе. Для того чтобы показать требуемое, необходимо было бы пространство, совершенно лишенное воздуха или какой бы то ни было другой материи, хотя бы самой тонкой и податливой. Так как подобного пространства мы не имеем, то станем наблюдать, что происходит в средах, более податливых, и сравнивать с тем, что наблюдается в средах, менее тонких и более сопротивляющихся. Если {173} мы найдем действительно, что тела различного веса будут все менее и менее отличаться друг от друга по скорости падения, по мере того как последнее будет происходить в средах, представляющих все меньшее сопротивление, пока, наконец, в среде, наиболее легкой, хотя и не вовсе пустой, разница в скорости получится самой малой и почти незаметной, то отсюда с большою вероятностью можно будет заключить, что в пустоте скорость падения всех тел одинакова. Посмотрим, что происходит в воздухе, взяв, чтобы иметь тело определенной формы, но возможно более легкое, надутый пузырь; заключающийся в нем воздух не будет иметь в воздухе никакого веса или же ничтожный, если предположить, что в пузыре воздух будет несколько сжат; поэтому вес пузыря будет почти равен одному весу оболочки и не составит и тысячной доли веса свинцового шара той же величины, что и пузырь. На какое пространство, синьор Симпличио, опередит теперь свинцовый шар, надутый воздухом пузырь при падении с высоты четырех или шести локтей? Поверьте мне, он упадет не втрое и даже не вдвое скорее, хотя, по вашему мнению, он должен был бы обладать скоростью в тысячу раз большею.
Симпличио. Быть может, то, что вы говорите, и происходит в начале движения на первых четырех или шести локтях. Но я думаю, что в дальнейшем, при более продолжительном движении, свинец перегонит пузырь не только на одну двенадцатую часть пути, но и на восемь или десять таких частей.
Сальвиати. Я думаю то же самое и не сомневаюсь, что при громаднейших пространствах свинец может пройти сто миль, в то время как пузырь, не пройдет еще и одной; но, синьор Симпличио, то что вы приводите в опровержение моего положения, наилучшим образом его подтверждает. Повторяю, я хочу показать, что причина различной скорости падения тел различного веса не заключается в самом их весе, а обусловливается внешними причинами, в частности, сопротивлением среды, так что если бы устранить последнее, то все тела падали бы с одинаковою скоростью. Такой вывод я делаю, главным образом, из того, что вы только что сказали и что совершенно справедливо, а именно, что при движении тел различного веса разница в скорости возрастает по мере увеличения пробегаемого ими пространства; это явление не должно было бы иметь места, если бы скорость зависела от различия в весе. Последняя причина, оставаясь постоянной, должна была бы иметь следствием и постоянство отношения пройденных пространств; а мы видим, что это отношение при продолжении движения постоянно увеличивается: в то время как при падении с высоты одного локтя самое тяжелое тело обгонит тело весьма легкое всего на одну десятую долю такого пространства, при падении с высоты двадцати локтей — оно опередит его уже на третью часть, при падении с высоты ста локтей — на 90/100 и т. д.45a {174}
Симпличио. Все это хорошо; но, следуя вашему рассуждению, надо признать, что если разница в весе тел различной тяжести не может являться причиною изменения отношения их скоростей, так как их веса нисколько не изменяются, то заодно и среда, которую мы также предполагаем постоянной, не может внести никакого изменения в отношение скоростей.
Сальвиати. Вы делаете очень меткое возражение против сказанного мною, и на него необходимо ответить обстоятельно. Скажу, что всякое тяжелое тело имеет присущее от природы внутреннее свойство стремиться к общему центру всех тяжелых тел, т. е. центру земного шара, движением, постоянно ускоряющимся и ускоряющимся всегда одинаково, так что в равные промежутки времени получаются равные приращения моментов или степеней скорости. Это должно обнаруживаться всякий раз, когда устранены все случайные и внешние воздействия, из которых одно, однако, неустранимо — это противодействие заполненной среды, которая должна дать проход падающему телу; такому движению, среда, хотя бы самая тонкая, жидкая и находящаяся в покое, оказывает меньшее или большее сопротивление в зависимости от того, насколько быстро она должна раздвинуться, чтобы пропустить падающее тело. Так как последнее, как было уже сказано, падает по природе своей с возрастающей скоростью, то оно встречает и все возрастающее сопротивление среды. Отсюда проистекает замедление и уменьшение в приращении новых степеней скорости, так что, в конце концов, скорость доходит до такого предела, а сопротивление среды до такой величины, что они уравновешивают друг друга, упраздняя всякое приращение скорости и превращая движение тела в однообразное и равномерное, которое оно и сохраняет постоянно в дальнейшем. Таким образом, увеличение сопротивления среды происходит не потому, что меняется ее сущность, но потому, что меняется быстрота, с которой она должна податься и раздвинуться, чтобы открыть путь падающему телу, которое движется с возрастающей скоростью. Отсюда ясно, что сопротивление воздуха ничтожному моменту падающего пузыря очень велико, а тяжелому весу свинца — весьма мало; и я убежден, что если бы мы вовсе устранили воздух и тем облегчили движение пузыря в большой степени, а свинца — в очень малой, то скорости их падения сравнялись бы46. Установив принцип, согласно которому в пустоте или же в среде, по другим каким-либо причинам не оказывающей сопротивления, замедляющего движение тел, скорость падения всех тел одинакова, мы можем довольно точно определить отношения скоростей движения одинаковых и неодинаковых тел в одной и той же или разнородных средах, обладающих разной сопротивляемостью. Этого мы достигнем, приняв в соображение, какой вес отнимает у движущегося тела вес среды, ибо избыток веса тела и является той силой, с которой тело прокладывает себе путь, раздвигая в стороны частицы среды, чего не {175} происходит в пустом пространстве, почему в нем и нельзя ожидать никакой разницы, обусловливаемой разницей в весе тел. Так как ясно, что среда отнимает у находящегося в ней тела такой вес, какой имеет вытесняемый им объем среды, то, уменьшив соответственно скорость падения тела в среде, не представляющей сопротивления, в которой (по нашему предположению) все скорости равны, мы получим искомое. Так, предположим, например, что свинец в десять тысяч раз тяжелее воздуха, черное же дерево только в тысячу раз; от скорости падения этих двух тел, каковые скорости, взятые абсолютно, т. е. при условии устранения всякого сопротивления, были бы равными, воздух отнимает у свинца из десяти тысяч единиц одну единицу и у черного дерева—из тысячи единиц также одну единицу, а следовательно, из десяти тысяч единиц десять единиц. Поэтому, если свинец и черное дерево падают в воздухе с любой высоты, с которой, не будь сопротивления воздуха, они опустились бы одновременно, то воздух отнимает от скорости падения свинца одну десятитысячную, от скорости же падения черного дерева—десять десятитысячных; таким образом, если разделить все пространство, которое тела проходят при падении, на десять тысяч частей, то при конце пути дерево окажется отставшим от свинца на десять частей без одной, т. е. на девять десятитысячных частей пути. Не то же ли самое получается, когда, бросив с башни высотою в двести локтей шары из свинца и дерева, мы находим, что первый опережает второй менее чем на четыре пальца? Черное дерево весит в тысячу раз более воздуха, упомянутый же надутый пузырь—всего в четыре раза более; следовательно, воздух отнимает у естественной скорости падения черного дерева одну тысячную часть, у скорости же падения пузыря, абсолютно равной первой,—одну четвертую часть; поэтому, когда брошенный с башни шар черного дерева достигнет земли, то пузырь не пройдет и трех четвертей пути. Свинец тяжелее воды в двенадцать раз, слоновая же кость только в два раза; поэтому вода отнимает от их естественной одинаковой скорости—у свинца одну двенадцатую, у слоновой же кости—половину; отсюда следует, что когда свинец опустится в воде на одиннадцать локтей, то слоновая кость успеет опуститься всего лишь на шесть. Рассуждая таким образом, мы получим, я полагаю, выводы, более соответствующие результатам опыта, нежели руководствуясь правилами Аристотеля. Подобным же образом можно найти соотношение скоростей движения одного и того же тела в различных жидких средах, беря за исходное не величину сопротивления среды, а избыток веса тела над весом данной среды. Олово, например, в тысячу раз тяжелее воздуха и в десять раз тяжелее воды; поэтому если мы разделим абсолютную скорость падения олова на тысячу частей, то скорость его падения в воздухе будет равна девятистам девяносто девяти частям, так как воздух отнимет одну часть, в воде же скорость падения будет равна всего лишь {176} девятистам частям, так как вода отнимет одну десятую часть его веса. Если возьмем тело немного тяжелее воды, каким является, например, каменный дуб, кусок которого будет весить, скажем, тысячу драхм, в то время как соответственный объем воды имеет вес в девятьсот пятьдесят драхм, а воздух всего лишь в две драхмы, то ясно, что, приняв абсолютную скорость падения за тысячу, мы получим скорость падения в воздухе, в тысячу без двух, т. е. девятьсот девяносто восемь частей, в воде же — только в пятьдесят частей, так как из тысячи частей вода отнимает девятьсот пятьдесят и составляет всего лишь пятьдесят частей. Такое тело будет, следовательно, падать в воздухе в двадцать раз быстрее, нежели в воде, так как излишек тяжести его над тяжестью воды, т. е. удельный вес, составляет одну двадцатую собственного веса. Здесь я хочу заметить, что движение в воде вниз возможно лишь для веществ большего, чем вода, удельного веса и, следовательно, во много сотен раз более тяжелых, нежели воздух; поэтому, отыскивая соотношение скорости движения тела в воздухе и воде, мы можем без заметной ошибки принять, что воздух ничего не отнимает от момента абсолютного веса тела, а следовательно, и от абсолютной скорости такого вещества; поэтому как только мы найдем избыток тяжести тела над тяжестью воды, так можем принять, что скорость падения его в воздухе так относится к скорости падения в воде, как общий вес его относится к избытку его веса над весом равного объема воды. Пусть, например, кусок слоновой кости весит двадцать унций, в то время как равный ему объем воды весит семнадцать; скорость падения слоновой кости в воздухе относится поэтому к скорости падения в воде почти как двадцать к трем.
Сагредо. Я чувствую, что узнал сейчас многое по вопросу, над которым я размышлял много и долго, но все же бесплодно; чтобы быть в состоянии применить на деле рассуждения, мне не хватает одного: способа установить, каково отношение веса воздуха к весу воды, а следовательно, и к весу всяких других тел.
Симпличио. Но если окажется, что воздух обладает не тяжестью, но легкостью, то что придется сказать о всех этих рассуждениях, впрочем, весьма остроумных47?
Сальвиати. Тогда придется сказать, что рассуждения были легки, воздушны и фантастичны. Но неужели вы сомневаетесь в том, что воздух имеет вес, вопреки даже утверждению Аристотеля, говорившего, что все элементы, за исключением огня, а следовательно, и воздух, имеют вес, доказательством чего (по его мнению) служит тот факт, что надутый мех весит больше ненадутого?
Симпличио. То, что надутый мех весит более, думается мне, надо приписать не весу содержащегося в нем воздуха, а примеси различных тяжелых испарений, от которых и возрастает вес меха. {177}
Сальвиати. Мне не хотелось бы слышать от вас такого возражения, особенно сказанного как бы от лица Аристотеля. Если бы, говоря об элементах и желая доказать, что элемент воздуха имеет вес, он показал мне опыт и сказал «возьмем мех, наполним его тяжелыми испарениями, и мы увидим, что вес его увеличится», то я мог бы ответить, что вес меха возрастет еще более, если мы наполним его отрубями, и заметил бы при этом, что подобный опыт доказывает лишь наличие веса у отрубей и испарений, что же касается элементов воздуха, то относительно них вопрос по-прежнему остается открытым. Опыт Аристотеля хорош и предложение его правильно. Не скажу того же об учении другого философа, имени которого не припомню и у которого я вычитал утверждение, что воздух скорее тяжел, нежели легок, так как он легче пропускает книзу тяжелые тела, нежели кверху тела легкие.
Сагредо. Хорошее рассуждение, нечего сказать. Но согласно ему, воздух должен быть много тяжелее воды, так как все тяжелые тела падают в нем много быстрее, нежели в воде, все же легкие тела поднимаются в воде легче, чем в воздухе; к тому же бесчисленное множество тяжелых тел, падающих в воздухе вниз, поднимается в воде вверх, и множество веществ, плавающих на воде, в воздухе не удерживается. Что же касается увеличения веса нашего меха от тяжелых испарений или от самого воздуха, то это, синьор Симпличио, ничего не изменяет в нашем вопросе, так как мы рассматриваем, что происходит с телами при движении в нашей же атмосфере, полной испарениями. Итак, возвращаясь к нашему первому вопросу, я желал бы для полного и окончательного решения его знать, если это, вообще возможно, не только, что воздух имеет вес (в чем я убежден), но и сколько он весит. Поэтому, если вы можете удовлетворить меня и в этом отношении, синьор Сальвиати, то благоволите сообщить, что знаете.
Сальвиати. То, что воздух обладает положительной тяжестью, а вовсе не легкостью, как полагают некоторые, каковой, быть может, нет ни в одном веществе, в достаточной мере доказывается опытом Аристотеля с надутым мехом. Действительно, если бы воздуху была присуща как особое свойство абсолютная и положительная легкость, то при увеличении количества воздуха и сжатии его возрастали бы и легкость его и стремление вверх; между тем опыт показывает обратное. Что касается второго вопроса — каким образом измеряется его вес, то я шел таким путем. Я брал стеклянную бутыль большого размера с довольно узким горлом; последнее было обтянуто плотно прилегающей к нему кожей и имело отверстие, закрываемое со стороны бутыли перепонкой — клапаном, через который я посредством шприца с силою вгонял в бутыль большое количество воздуха; последний был так сжат, что количество его было достаточным для наполнения еще двух-трех бутылей, не считая, конечно, {178} того воздуха, который содержится в них в естественном состоянии. Затем я тщательно взвешивал на чувствительных весах такую бутыль со сжатым воздухом, измеряя вес тонким песком. Открывая затем отверстие и выпуская выходивший с силой сжатый воздух, я снова взвешивал бутыль и находил ее значительно более легкой, так что приходилось снять некоторое количество первоначально насыпанного песка, дабы уравновесить бутыль. Кто же может усомниться, что вес снятого песка и есть вес воздуха, который был сильно сжат в бутыли, а затем выпущен? Такой опыт убеждает меня, однако, лишь в том, что воздух, сильно сжатый в бутыли, весит столько же, сколько снятое количество песка; но я не знаю еще определенно, каков вес воздуха относительно веса воды или какого-либо другого вещества, и не смогу узнать этого, пока не получу возможности измерить количество сжатого воздуха. Для этого необходимо найти способ, и мне думается, что я нашел его, идя двумя путями. Первый способ состоит в том, что берется другая бутыль, подобная первой, с таким же обтянутым кожей горлышком, плотно соединенным с кожаной обшивкой первой бутыли. В дне этой второй бутыли должно быть сделано отверстие таким образом, чтобы через него можно было пропустить острый железный стержень, проколоть по желанию упомянутую выше перепонку и дать тем выход излишку воздуха, заключенного в первой бутыли, взвешенной, как было указано выше; при этом вторая бутыль должна быть наполнена водою. Устроив все аккуратно, как указано выше, и проколов стержнем перепонку, мы увидим, как сжатый воздух, выходя из первой бутыли, устремится во вторую, вытесняя воду через отверстие в дне сосуда; ясно, что объем вытесненной воды будет равен объему вышедшего из бутыли воздуха. Соберем вытесненную таким образом воду и взвесим бутыль, облегченную вследствие выхода сжатого воздуха (предполагается, что она была взвешена и ранее со содержавшимся в ней сжатым воздухом). Отсыпав указанным уже выше образом излишек песка, мы найдем вес воздуха, ибо очевидно, что вес указанного излишка и есть вес воздуха в объеме, равном объему вытесненной воды, собранной нами. Взвесив теперь ту воду и определив, во сколько раз вес ее более веса излишка песка, мы можем без большой ошибки утверждать, что во столько же раз и вода тяжелее воздуха; при этом оказывается, что отношение это равно не десяти, как предполагал Аристотель, а приблизительно четыремстам: такое число дает нам опыт. Второй способ проще и может быть применен при пользовании одним лишь сосудом, снабженным указанным ранее приспособлением. В сосуде будет содержаться лишь такое количество воздуха, которое находится в нем в естественном состоянии; постараемся теперь накачать в сосуд воды так, чтобы одновременно с этим не дать выхода воздуха, который должен уплотниться, будучи сжат водою. Итак, нагнетем в сосуд воды, сколько возможно; без применения {179} особенно большой силы ею можно будет наполнить три четверти объема бутылки; затем положим последнюю на весы и тщательно взвесим. Сделав это и держа бутыль горлышком вверх, прокалываем перепонку и даем тем выход воздуху, которого выходит ровно столько, сколько места заняла в бутыли вода. После того как воздух вышел, ставим бутыль на весы и находим, что вес ее стал меньше от потери части воздуха. Найдя разницу между весами, определяем этим, сколько весит воздух в том объеме, который занимает в бутыли вода.
Симпличио. Нельзя не сказать, что изобретенные вами способы весьма остроумны и тонки, но вместе с тем я думаю, что они дают лишь кажущееся удовлетворение нашему рассудку, создавая в некоторых отношениях большие затруднения. Несомненно, верно то, что элементы, взвешиваемые в среде, состоящей из них же самих, не являются ни тяжелыми, ни легкими; поэтому я не могу признать, что то количество воздуха, которое, по вашему утверждению, уравновешивалось хотя бы четырьмя драхмами песка, действительно имеет такой вес в воздухе, в котором песок поддерживает его в равновесии. Мне кажется, что опыт должен быть произведен не в воздухе, но в какой-либо другой среде, в которой воздух мог бы проявить свой вес, если только он им обладает.
Сальвиати. Возражение синьора Симпличио весьма метко и поэтому оно должно быть либо неопровержимым, либо допускающим лишь весьма тонкое опровержение. То, что воздух, будучи сжат, обнаружил вес, равный некоторому количеству песка, а затем, выпущенный на свободу в свою среду, не может быть взвешен, как взвешивается песок,— вещь ясная; поэтому для опыта следовало бы избрать такое место и такую среду, где не только песок, но и воздух был бы весомым. Как указывалось уже много раз, среда отнимает от веса каждого находящегося в ней тела столько, сколько весит занимаемый им объем среды; поэтому воздух у воздуха отнимает всю тяжесть, и для того, чтобы получить точный результат, следовало бы произвести опыт в пустоте, где каждое тело проявляет свой момент без всякого уменьшения. Итак, синьор Симпличио, если бы мы взвесили часть воздуха в пустоте, то были ли бы вы удовлетворены?
Симпличио. Конечно, да: но это значит выполнить невозможное.
Сальвиати. Тем большим вы будете мне обязаны, если из любви к вам я совершу невозможное. Но я не хочу продавать вам того, что уже отдал, потому что в упомянутом выше опыте мы уже взвешивали воздух в пустоте, а не в воздухе или какой-нибудь иной среде. Тот факт, что масса, погружающаяся в жидкую среду, испытывает потерю веса, происходит, синьор Симпличио, вследствие того, что среда оказывает сопротивление своему разъединению, вытеснению и, в конце концов, поднятию; доказательством этого служит та быстрота, с которой жидкость заполняет пространство, занимаемое погруженным в нее телом, как только {180} последнее удаляют; там, где среда не испытывает никакого погружения, нет места и сопротивлению ему. Скажите мне теперь, когда вы имеете в воздухе бутылку, наполненную уже естественно содержащимся в ней воздухом, какое разделение, вытеснение или вообще передвижение производите вы в окружающем воздухе тем, что с силою вгоняете в бутыль еще новое количество воздуха? Может быть, растет объем бутыли, так что окружающая среда должна раздаться, чтобы дать ему место? Конечно, нет; и мы можем сказать, что новый воздух не погружается в окружающую среду, что он не занимает в ней нового места и находится как бы в пустоте; и действительно, он помещается в последней, так как занимает при нагнетании те мельчайшие пустоты, которые не заполнены обычным несжатым воздухом. Я не нахожу, в самом деле, никакой разницы во взаимоотношениях тела и среды в этих двух случаях: в одном, где нет среды, оказывающей давление на тело, и в другом, где объемлемое тело не оказывает никакого давления на окружающую среду; первый случай имеет место со всяким телом в пустоте, второй — в случае сжатого воздуха в бутыли. Поэтому найденный вес этого сгущенного воздуха совершенно таков же, как если бы последний свободно взвешивался в пустоте. Правда, песок, которым уравновешивался воздух, как находящийся в воздухе свободным, должен весить в пустоте несколько больше; поэтому следует признать, что взвешенный воздух в действительности весит менее, нежели уравновешивающий его песок,—именно настолько, сколько весил бы в пустоте объем воздуха, равный объему снятого песка48.
Симпличио. Мне показалось, что опыты ваши оставляли еще чего-то желать; но теперь я вполне удовлетворен.
Сальвиати. Вопросы, которых я сейчас касался, и в особенности те положения, что разница в тяжести, как бы велика она ни была, не играет никакой роли в различии скорости движения тел, и что если бы дело было только в одном весе, то все тела падали бы с одинаковой быстротой, представляются столь новыми и на первый взгляд столь далекими от истины, что если бы я не нашел способов осветить их и сделать яснее солнца, то я предпочел бы скорее умолчать о них, нежели их излагать. Так как, однако, я уже высказал вам мое положение, то я должен теперь привести и подтверждающие его опыты.
Сагредо. Не только это, но и многое другое в вашем учении столь чуждо и далеко от обычных широко распространенных взглядов, что при опубликовании его вы найдете много противников; в самом деле, большинство обыкновенных людей и при хорошем зрении не видит того, что другие открывают путем изучения и наблюдения, отделяющих истину от лжи, и что остается скрытым для большинства. Награждая ученых мало лестными для большинства эпитетами новаторов, они пытаются разрубать узлы, развязать которые не могут, и подводят мины для разрушения зданий, {181} воздвигнутых трудами и терпением искусных строителей. Так как мы далеки от такого рода попыток, то ваши опыты и доказательства нас вполне удовлетворяют и успокаивают. Однако, если у вас есть еще более наглядные опыты и еще более убедительные доказательства, то мы охотно познакомимся и с ними.
Сальвиати. Опыты с двумя телами, возможно больше отличающимися друг от друга по весу, которые мы заставляем падать с некоторой высоты, наблюдая, перемещаются ли они с одинаковой скоростью, представляют некоторые трудности. Если высота значительна, то среда, которая должна быть раздвинута и перемещена, окажет значительно большее влияние на малый момент весьма легкого предмета, нежели на усилие чрезвычайно тяжелого предмета, почему при большем пространстве первый останется позади; при малой же высоте можно сомневаться, существует ли вообще разница, так как, если она и существует, то почти незаметна. Поэтому я пришел к мысли повторить опыт с падением с малой высоты столько раз, чтобы, отмечая и складывая незначительные разницы, могущие обнаружиться во время достижения конца пути тяжелым и легким телом, получить в итоге разницу не только просто заметную, но и весьма заметную. Затем, чтобы иметь дело с движением по возможности медленным, при котором уменьшается сопротивление среды, изменяющее явление, обусловливаемое простой силой тяжести, я придумал заставлять тело двигаться по наклонной плоскости, поставленной под небольшим углом к горизонту; при таком движении совершенно так же, как и при отвесном падении, должна обнаружиться разница, происходящая от веса. Идя далее, я захотел освободиться от того сопротивления, которое обусловливается соприкосновением движущихся тел с наклонной плоскостью. Для этого я взял, в конце концов, два шара — один из свинца, другой — из пробки, причем первый был в сто раз тяжелее второго, и прикрепил и подвесил их на двух одинаковых тонких нитях длиной в четыре или пять локтей; когда, затем, я выводил тот и другой шарик из отвесного положения и отпускал их одновременно, то они начинали двигаться по дуге круга одного и того же радиуса, переходили через отвес, возвращались тем же путем обратно и т. д.; после того, как шарики производили сто качаний туда и обратно, становилось ясным, что тяжелый движется столь согласованно с легким, что не только после ста, но и после тысячи качаний не обнаруживается ни малейшей разницы во времени, и движение обоих происходит совершенно одинаково. При этом, однако, наблюдается воздействие среды, которая, представляя сопротивление движению, значительно больше уменьшает размах качания пробки, нежели размах качания свинца; но от этого последние но делаются ни более, ни менее частыми, так что, хотя дуги, описываемые пробкою, будут равняться всего пяти-шести градусам, а описываемые {182} свинцом — пятидесяти-шестидесяти градусам, они будут проходиться в одинаковые промежутки времени49.
Симпличио. Если это так, то как же не сказать, что скорость свинца больше скорости пробки: ведь он проходит шестьдесят градусов пути, в то время как пробка не делает и шести?
Сальвиати. Но что скажете вы, синьор Симпличио, если оба шара начнут свой путь в одно и то же время, однако пробковый, будучи отклонен в сторону на тридцать градусов, должен будет проходить дугу в шестьдесят градусов, а свинцовый, отведенный только на два градуса,— дугу в четыре градуса? Не окажется ли в таком случае скорость пробки большею? А опыт показывает, что так и произойдет. Заметьте себе следующее: если мы отведем свинцовый маятник на пятьдесят градусов от отвеса и отпустим его на свободу, то он, перейдя за отвес, пройдет дугу также приблизительно в пятьдесят градусов, и всего опишет дугу почти в сто градусов; возвратившись, он второй раз опишет дугу несколько меньшую, и так далее, пока после большого числа качаний не придет в состояние покоя. Каждое из таких качаний происходит в одинаковый промежуток времени, будь дуга в девяносто градусов или же в пятьдесят, двадцать, десять или четыре. Отсюда как следствие вытекает, что скорость движения постоянно уменьшается, так как тело в одинаковые промежутки времени проходит последовательно дугу все меньшего и меньшего размера. Подобное же и даже совершенно такое же явление происходит и с пробкою, подвешенной к нити одинаковой длины, с тою лишь разницей, что она приходит в состояние покоя после меньшего числа качаний, так как благодаря своей легкости она меньше приспособлена к преодолению сопротивления воздуха; при этом все качания — большие и малые — происходят в одинаковые промежутки времени, и притом в промежутки, равные времени качания свинцового маятника. Совершенно правильно, что если свинец проходит дугу в пятьдесят градусов, а пробка не проходит и в десять, то пробка движется медленнее; но может случиться и наоборот: пробка пройдет дугу в пятьдесят градусов, а свинец — дугу в десять или шесть градусов; таким образом, может оказаться, что в разное время то свинец движется быстрее, то пробка. Но если те же тела проходят в равные промежутки времени дуги одинаковой длины, то можно с уверенностью сказать, что и скорость их движения одинакова.
Симпличио. Ваши рассуждения кажутся мне то правильными, то неправильными; я чувствую себя настолько запутавшимся, что то одно, то другое тело представляется мне движущимся с большей или меньшей скоростью, и я никак не могу уяснить себе, каким образом скорости их оказываются постоянно равными.
Сагредо. Позвольте мне, синьор Сальвиати, сказать два слова. Признаете ли вы, синьор Симпличио, что можно с абсолютной уверенностью {183} утверждать, что скорости движения свинца и пробки одинаковы всякий раз, как выведенные в один и тот же момент из состояния покоя и отклоненные под одним и тем же углом, они проходят одинаковые пространства в одинаковые промежутки времени?
Симпличио. В этом не может быть ни малейшего сомнения, и против этого ничего нельзя возразить.
Сагредо. Мы замечаем в маятниках, что каждый из них может описывать дугу и в шестьдесят градусов, и в пятьдесят, и в тридцать, и в восемь, и в четыре, и в два градуса и т. д.; если оба маятника описывают дугу в шестьдесят градусов, то они проходят ее в одинаковое время, на прохождение дуги в пятьдесят градусов и тому и другому маятнику необходим одинаковый промежуток времени, равно как для прохождения дуг в тридцать градусов, десять градусов и всех других; отсюда заключаем, что скорость свинцового маятника, описывающего дугу в шестьдесят градусов, одинакова со скоростью пробкового, описывающего такую же дугу, что скорости обоих маятников, описывающих дуги в пятьдесят градусов, также равны между собою, и что то же имеет место для всех других дуг. Однако мы не утверждаем, что скорость движения маятника при дуге в шестьдесят градусов равняется скорости его при дуге в пятьдесят или тридцать градусов и т. д.; скорость всегда меньше при меньших дугах; это следует с очевидностью из того факта, что одно и то же тело употребляет столько же времени, чтобы пройти большую дугу в шестьдесят градусов, сколько для того, чтобы пройти дуги меньшие — в пятьдесят или десять градусов; одним словом, оно проходит дуги различной величины в один и тот же промежуток времени. Итак, движение свинца и пробки постепенно замедляется по мере уменьшения описываемых дуг; но это нисколько не меняет того, что тела эти сохраняют одинаковую скорость при прохождении дуг одинакового размера. Я говорю все это для того, чтобы уяснить себе, верно ли я понял изложение синьора Сальвиати, а вовсе не с целью дать синьору Симпличио объяснения более убедительные, нежели те, которые уже даны синьором Сальвиати. Изложение последнего, как всегда, совершенно ясно и позволяет не только разбираться в вопросах, кажущихся темными, но и разрешать действительные загадки природы путем рассуждений, наблюдений и опытов простых и всем доступных. Последнее обстоятельство (как я слышал кое от кого) дало повод одному из ученых профессоров придавать относительно мало цены его новым теориям как слишком низким и построенным на обычных и общеизвестных основаниях, как будто наиболее замечательная и ценная сторона опытных наук не заключается как раз в том, что они проистекают и развиваются именно из общеизвестных, всем понятных и неоспоримых принципов! Но мы будем с радостью продолжать пользоваться и далее этой легкой пищей. Полагая, что сомнения синьора {184} Симпличио рассеялись и что он принимает за доказанное, что тяжесть, присущая движущимся телам, не играет никакой роли в различии скорости их движения, так что все тела, поскольку это зависит от тяжести, движутся с одинаковою скоростью, прошу вас сказать теперь, синьор Сальвиати, чем вы объясняете чувствительную и заметную разницу в скорости движения и что вы ответите на возражение синьора Симпличио, которое и я, со своей стороны, поддерживаю, утверждая не только, что пушечное ядро падает заметно быстрее свинцовой дробинки, но что в некоторых более плотных средах большие предметы проходят за один удар пульса пространство, которое другие предметы, из того же вещества, но меньшие, не проходят ни в час, ни в четыре часа, ни в двадцать часов; таковы, например, камни и мелкий песок; если последний столь тонок, что мутит воду, то в течение нескольких часов он опускается едва на два локтя, тогда как камешек даже небольшой величины проходит это расстояние за один удар пульса.
Сальвиати. То, что среда замедляет движение тел тем сильнее, чем менее их удельный вес, я уже объяснил, показав, что это происходит от уменьшения их веса; для того же, чтобы понять, как одна и та же среда может столь различно воздействовать на скорость движения тел из одного и того же вещества и одинаковой формы, отличающихся друг от друга только величиною, необходимо поискать более тонкого объяснения; здесь недостаточно признания причиною увеличение размеров тела, благодаря которому среда оказывает большее сопротивление и сильнее замедляет движение. Причиною настоящего явления я считаю шероховатость и пористость тел — свойства, которыми неизбежно и одновременно обладает поверхность тел; и такие неровности ударяются при движении о воздух или другую окружающую среду, доказательством служит шум тела, хотя бы оно было возможно гладким, когда оно быстро прорезает воздух; мы слышим не только просто шум, но и свист и шипение, если тело имеет заметную впадину или выступ. При быстром вращении на токарном станке каждое, даже круглое тело поднимает легкий ветер. Но чего же более? Разве мы не слышим сильнейших ударов и раскатов грома, сопровождающих молнию, падающую на землю с огромной быстротой? Звук свиста делается все ниже по мере того, как замедляется скорость движения хлыста, которым мы размахиваем; это доказывает, что шероховатые частицы поверхности, как бы малы они ни были, сталкиваются с воздухом. Поэтому я не могу сомневаться в том, что при опускании в жидкости тела испытывают трение, замедляющее быстроту их движения, и при том в тем большей степени, чем больше их поверхность, что верно для тел малых при сравнении их с большими.
Симпличио. Остановитесь, пожалуйста, потому что я начинаю сбиваться. Я понимаю и признаю, что трение среды о поверхность тела {185} замедляет движение, и замедление это, ceteris paribus50, тем значительнее, чем больше поверхность; но для меня непонятно, на каком основании вы называете поверхность малых тел большею. Кроме того, если, как вы утверждаете, большая поверхность должна испытывать и большее замедление, то большие предметы должны были бы погружаться медленнее, чего на самом деле нет; это затруднение легко разрешить, приняв, что хотя большее тело имеет и большую поверхность, но зато оно имеет и больший вес, который и преодолевает трение поверхности относительно легче, чем это делает меньший вес малого тела, почему скорость большего тела и не становится меньшею. Но я не вижу причины, которая должна была бы изменить равенство скорости движения тела, так как по мере уменьшения веса, вызывающего его движение, уменьшается и поверхность, замедляющая последнее.
Сальвиати. Отвечу сразу на все то, что вы мне возразили. Вы утверждаете и признаете, синьор Симпличио, что когда у одного из двух движущихся тел равных, сделанных из одного вещества и имеющих одинаковую форму (которые, несомненно, должны и двигаться с одинаковою скоростью), уменьшаются в одинаковой степени как вес, так и поверхность (при сохранении подобия формы), то скорость движения уменьшенного тела не должна уменьшаться?
Симпличио. Мне кажется, что таково должно быть следствие, раз мы признаем вашу доктрину, что больший или меньший вес сам по себе не может ускорить или замедлить движения.
Сальвиати. Я подтверждаю последнее, признавая и ваше положение, из которого, мне кажется, вытекает как следствие, что если вес уменьшается в большей степени, нежели поверхность, то движение тела замедляется и притом тем значительнее, чем больше уменьшение веса тела по сравнению с уменьшением его поверхности.
Симпличио. Против этого я не имею возражений.
Сальвиати. В таком случае заметьте, синьор Симпличио, что невозможно в равной мере уменьшить поверхность и вес твердого тела, сохраняя подобие его формы. Так как совершенно ясно, что уменьшение веса происходит пропорционально уменьшению объема, то всякий раз, как объем уменьшится более, нежели поверхность (при сохранении подобия формы), и вес уменьшится в большей степени, нежели поверхность. Но геометрия учит, что отношение объемов подобных тел больше, нежели отношение их поверхностей, что для большей наглядности я поясню на следующем примере. Представим себе куб, ребро которого равно двум дюймам, так что каждая из граней содержит четыре квадратных дюйма, а все шесть граней, т. е. вся его поверхность, содержит, таким образом, двадцать четыре квадратных дюйма. Предположим, теперь, что куб этот разрезан на восемь маленьких кубиков; ребро каждого из последних будет {186} равно одному дюйму, каждая грань — одному квадратному дюйму, вся же поверхность — шести квадратным дюймам, тогда как поверхность большего куба равнялась двадцати четырем квадратным дюймам. Теперь вы видите, что поверхность малого кубика составляет четвертую часть поверхности большего (отношение шести к двадцати четырем), в то время как объем его уменьшился до одной восьмой большего. Объем, а вместе с ним и вес уменьшились, следовательно, в большей степени. Если вы разделите теперь малый кубик еще на восемь частей, то поверхность нового кубика будет содержать полтора квадратных дюйма, что составит всего одну шестнадцатую часть всей поверхности первоначального куба, объем же его будет равен лишь одной шестьдесят четвертой части того же куба. Вы видите, что путем всего лишь двух делений мы уменьшили объем в четыре раза значительнее, нежели поверхность; если же путем последовательных делений мы дойдем до раздробления первоначального тела на частицы, образующие мельчайший порошок, то найдем, что вес этих мельчайших атомов уменьшился в сотни и сотни раз значительнее, нежели поверхность. То, что я показал вам сейчас на примере куба, происходит и со всякими другими подобными друг другу телами, отношение между объемами которых равняется полуторному отношению их поверхностей51. Итак, вы видите, насколько значительнее возрастает сопротивление от соприкосновения поверхности со средой у тел малых по сравнению с большими. Если мы прибавим к этому, что шероховатость поверхности мельчайших порошкообразных частиц едва ли меньше, чем тел больших и хорошо отполированных, то найдем, сколь необходимо, чтобы среда, расступающаяся и дающая проход телу при столь малом давлении, была совершенно жидкою и лишенною сопротивления. Поэтому, синьор Симпличио, я не заблуждался, когда говорил, что поверхность малых тел, больше по сравнению с поверхностью тел больших.
Симпличио. Я совершенно убежден, и поверьте мне, что если бы мне пришлось начать вновь свое обучение, то я последовал бы совету Платона и принялся бы сперва за математику как науку, требующую точности и принимающую за верное только то, что убедительно доказано.
Сагредо. Мне чрезвычайно понравились ваши суждения. Но ранее, чем мы двинемся дальше, я хотел бы как следует уяснить себе термин, для меня совершенно новый. Именно: вы сказали, что подобные тела находятся в полуторном отношении к их поверхностям; хотя я знаю предложение и доказательство того, что поверхности подобных тел относятся между собою, как квадраты сторон, и другое предложение, что объемы тел относятся между собою, как кубы сторон, но предложения, касающегося отношения между телами и их поверхностями, мне, насколько я помню, никогда не приходилось встречать. {187}
Сальвиати. Самый вопрос ваш содержит уже в себе ответ и разъясняет всякое сомнение. Если одно втрое больше чего-то, а другое — вдвое больше того же самого, то не является ли отношение между первым и вторым равным полутора? Конечно, является. А так как поверхности находятся в двойном отношении к линиям, а объемы — в тройном, то не можем ли мы сказать, что объемы тел находятся в полуторном отношении к поверхностям?
Сагредо. Я вполне понял. Если у меня и остались некоторые вопросы в связи с предметом, о котором мы говорили, то я полагаю, что, занявшись ими сейчас, мы еще более уклонились бы в сторону от вашей главной темы, которой я считаю различные случаи сопротивления тел излому. Поэтому не полагаете ли вы, что нам следует вернуться к началу нашей беседы и заняться основным вопросом?
Сальвиати. Вы совершенно правы, синьор, но различного рода вопросы, затронутые нами, отняли у нас столько времени, что мы мало подвинемся вперед, если займемся сегодня основным вопросом, требующим многих геометрических доказательств, к которым необходимо отнестись с особым вниманием. Поэтому я полагаю, что нам лучше будет' отложить наше собеседование до завтра, как по причине, только что упомянутой, так и потому, что я мог бы в этом случае принести листки с изложенными в должном порядке теоремами и проблемами, относящимися к данному предмету; привести их в надлежащем порядке на память мне было бы затруднительно.
Сагредо. Я соглашаюсь с вашим предложением тем охотнее, что это даст возможность закончить нашу сегодняшнюю беседу выяснением некоторых вопросов, возникших у меня в связи с только что обсуждавшимся предметом. Первый из них следующий: может ли сопротивление среды быть достаточным для того, чтобы положить конец ускорению у тел из весьма плотного вещества, тяжелых и обладающих сферической формой? Говорю сферической, так как выбираю форму с наименьшей поверхностью52, следовательно, и наименее подверженную замедлению. Другой вопрос касается маятников и распадается на две части, а именно: во-первых, действительно ли все маятники — большие, средние и совсем маленькие — совершают колебания в совершенно одинаковые промежутки времени, и, во-вторых, какое отношение существует между временем качания тел, подвешенных к нитям различной длины?
Сальвиати. Вы предлагаете прекрасные вопросы, но я сильно опасаюсь, как бы, начав разбирать один из них, мы, как это часто случается, не нашли, что из него можно вывести много интересных и новых следствий, для освещения которых не хватит остатка нынешнего дня.
Сагредо. Если они столь же интересны, как предыдущие, то я охотно посвящу им столько же дней, сколько часов остается сегодня до {188} полуночи. Надеюсь, что и синьор Симпличио будет не прочь их обсудить.
Симпличио. Конечно, нет, особенно если дело будет касаться таких вопросов естествознания, относительно которых мы лишены мнения и учений других философов.
Сальвиати. Приступим в таком случае, к первому вопросу. Я утверждаю без малейшего колебания, что не может быть шара столь большого и столь тяжелого, чтобы сопротивление среды, хотя бы последняя и была весьма тонкой, не противодействовало ускорению, так что при продолжении движения последнее не стало, наконец, равномерным53. Ясные доводы в пользу такого положения дают нам следующие опыты. Какую бы скорость ни было способно приобрести падающее тело при продолжении своего движения и как бы ни было, вообще, велико движение, которое могут сообщить телу внешние силы, не может случиться, чтобы тело не восприняло и не обнаружило сопротивления среды. Пусть, например, пушечное ядро, падающее в воздухе с высоты четырех локтей, приобретает десять градусов скорости и в этот миг погружается в воду; если бы сопротивление воды не могло производить воздействие на ядро, то последнее продолжало бы двигаться ко дну с возрастающей или по крайней мере прежней скоростью. Между тем мы видим, что этого не случается: вода, глубиною хотя бы всего в несколько локтей, задерживает и ослабляет движение так, что дно реки или озера получает от ядра лишь легкий удар. Совершенно ясно, что та скорость, которую вода в состоянии уничтожить на коротком протяжении, не может сохраниться при движении до глубины в тысячу локтей. Как можем мы допустить, что при движении на тысячу локтей приобретается скорость, которая отнимается при движении на четыре локтя? Но пойдем далее: не видим ли мы, что пушечное ядро, обладающее огромным импульсом при выстреле из орудия, настолько ослабляется в своем движении несколькими локтями воды, что судно получает удар, не наносящий ему ровно никакого вреда? Даже столь податливый воздух может уменьшать скорость падающего тела, хотя бы и весьма тяжелого, в чем можно убедиться на следующем опыте. Если с вершины очень высокой башни мы выстрелим вниз из аркебуза, то пуля вонзится в землю на меньшую глубину, чем если мы выстрелим из того же аркебуза с высоты четырех-шести локтей от поверхности: отсюда ясно, что скорость, с которой пуля вылетает из дула ружья на вершине башни, уменьшается при движении вниз к земле. Поэтому и падения с огромной высоты будет недостаточно, чтобы придать телу ту скорость, которой его лишает сопротивление воздуха, каким бы образом она ни была сообщена телу. Точно так же разрушение, производимое в стене пушечным ядром, выпущенным из колубрины54 с расстояния в двадцать локтей, я полагаю, не может быть произведено таким же ядром при {189} отвесном свободном падении его с какой бы то ни было большой высоты. Поэтому я думаю, что есть предел для ускорения естественного движения тела, вышедшего из состояния покоя, и что сопротивление среды, в конце концов, делает движение равномерным, и тело сохраняет это движение.
Сагредо. Подобные опыты кажутся мне действительно весьма доказательными; противник мог бы разве только оспаривать то, что те же явления будут наблюдаться и с телами огромного размера и веса, и утверждать, что пушечное ядро, падающее, например, с Луны или из верхних слоев атмосферы, произведет удар более сильный, нежели ядро, выпущенное из дула орудия.
Сальвиати. Я не сомневаюсь в том, что можно представить много возражений и что не все можно опровергнуть опытным путем. По поводу вашего замечания, можно, однако, заметить следующее: весьма правдоподобно, что тяжелое тело при падении с любой высоты приобретает, достигая земли, такой импульс, какой требуется, чтобы поднять его на ту же высоту; это ясно видно на примере достаточно тяжелого маятника, который, будучи отклонен от отвеса на пятьдесят или шестьдесят градусов, при падении развивает скорость и усилие, достаточные для поднятия его на такую же точно высоту, если не считать той небольшой потери, которая обусловливается сопротивлением воздуха. Чтобы поднять пушечное ядро на такую высоту, при падении с которой на землю оно разовьет такой же импульс, каким оно обладало при выходе из дула орудия, достаточно выстрелить из этого орудия отвесно вверх; при этом можно будет убедиться, что ядро произведет при своем падении такое же действие, как при выстреле с близкого расстояния. Разница в эффекте, думается мне, не будет особенно значительной; замечу, однако, что скорость, которой ядро обладает при выходе из дула орудия, такова, что достигнуть ее при свободном падении, хотя бы и с очень большой высоты, телу будет невозможно вследствие сопротивления воздуха.
Перехожу теперь к другим вопросам, связанным с маятником,— теме довольно сухой по мнению многих, особенно же философов, постоянно занимающихся исследованием самых глубоких проблем природы. Я, однако, не хочу пренебречь этой темой, по примеру Аристотеля, который поражает меня более всего именно тем, что нет, кажется, ни одного достойного внимания явления, мимо которого он прошел бы, не коснувшись его. Поэтому, побуждаемый вашею любознательностью, синьоры, я думаю сообщить вам некоторые свои соображения из области музыки. Эта благородная тема была предметом исследования многих, в том числе и самого Аристотеля, и содержит весьма много интересного. Я надеюсь, что заслужу ваше одобрение, если при помощи простых и убедительных опытов объясню вам чудесные явления из области звуков. {190}
Сагредо. Я не только выражу одобрение, но скажу, что этим вы исполните мое особое желание. Обращаясь со всякими музыкальными инструментами и много размышляя о созвучии, я часто поражался и оставался в полном недоумении, почему одно мне нравится и кажется более приятным, нежели другое, а иное, наоборот, не только не нравится, но представляется крайне неприятным. Общеизвестная проблема о двух натянутых, одинаково звучащих струнах, так что, когда звучит одна струна, другая также приходит в колебание и резонирует, для меня также не совсем ясна, равно как и формы созвучий и многое другое.
Сальвиати. Посмотрим, не сможем ли мы извлечь какой-либо пользы из наших маятников для решения и этих вопросов. Что касается первого пункта, а именно, правильно ли, что один и тот же маятник совершает все свои качания — большие, средние и малые — в совершенно одинаковые промежутки времени, то я сошлюсь на данные нашего Академика, который доказал, что тела, спускающиеся по хорде, соответствующей любой дуге, употребляют для этого одинаковый промежуток времени, будь соответствующая дуга в сто восемьдесят градусов (а хорда — диаметром), сто или шестьдесят градусов, два градуса, полградуса или, наконец, четыре минуты величиною, если предположить, что в конечной низшей точке все эти тела достигают горизонтальной плоскости. Далее, тела, опускающиеся по дугам, соответствующим хордам, наклонным к горизонту и не превышающим четверти круга или девяноста градусов, совершают движение, как показывает опыт, также в равные промежутки времени и притом меньшие, нежели при движении по хордам,— явление тем более удивительное, что можно было бы ожидать как раз противоположного. Если начальная и конечная точки движения одинаковы, и прямая линия есть кратчайшее расстояние между ними, то можно было бы думать, что движение, совершающееся по ней, требует наименьшего времени; на самом деле этого нет: наикратчайшее время, а следовательно, и наибыстрейшее движение мы встречаем при движении по дуге, для которой соответствующая прямая является хордою55. Что касается, далее, отношения времени качания тел, подвешенных к нитям различной длины, то промежутки времени относятся друг к другу, как корни квадратные из длин маятников, и, обратно, длины маятников находятся в двойной пропорции времен, т. е. относятся друг к другу, как квадраты времен качания. Таким образом, если мы пожелаем, чтобы один маятник качался в два раза медленнее, чем другой, то необходимо длину его сделать в четыре раза большею; подобным же образом, в то время как один маятник совершает одно качание, другой, нить которого будет в девять раз короче, совершит три качания. Отсюда вытекает, что длины маятников обратно пропорциональны квадратам чисел их качаний, совершаемых в течение определенного промежутка времени56. {191}
Сагредо. Итак, если я хорошо понял, я могу тотчас же вычислить длину веревки, укрепленной на любой огромной высоте, хотя бы точка подвеса ее и не была видима, раз только я могу наблюдать движение ее нижнего конца. Для этого мне понадобится лишь привязать к нижнему концу достаточный груз, который будет качаться взад и вперед, и в то время, как кто-либо из моих друзей будет считать эти качания, самому наблюдать и считать одновременно качания другого маятника, длина которого равняется точно одному локтю. Из чисел качания этих двух маятников за один и тот же промежуток времени я и вычислю искомую длину нити. Положим, что в то время, как мой друг насчитал двадцать качаний длинного маятника, я нашел, что мой маятник, длиною в один локоть, совершил их двести сорок; возведя числа двадцать и двести сорок в квадрат, получим 400 и 57 600, из чего заключим, что длинный маятник содержит 57 600 таких частей, которых в меньшем, длиною в один локть, содержится 400; а разделив 57 600 на 400, получим число 144; таким образом я узнаю, что веревка имеет длину в 144 локтя.
Сальвиати. Вы не ошибетесь и на толщину одного пальца, особенно, если сосчитаете большое число качаний.
Сагредо. Как часто даете вы мне случай, синьор, удивляться богатству и вместе с тем щедрости природы, делая совершенно новые интересные выводы из простых, известных и, скажу, даже тривиальных вещей, выводы, далекие от того, что может представить воображение. Тысячи раз наблюдал я качание, в особенности церковных паникадил, подвешенных, часто на очень длинных цепях и почему-либо совершающих незначительные движения. Однако самое большее, что я вывел из этих наблюдений, это то, что мнение, будто такие движения поддерживаются окружающей средою — в данном случае воздухом — неосновательно. Мне казалось невозможным, чтобы воздух имел такое правильное движение или чтобы ему нечего было делать, кроме как проводить час за часом в раскачивании с такою размеренностью свешивающихся тяжестей57. Но то обстоятельство, что одно и то же тело, свешивающееся с высоты ста локтей, употребляет на прохождение больших и малых дуг при отклонении на девяносто градусов и на один градус одинаковый промежуток времени, ускользало от моего внимания, и до сих пор кажется мне невозможным. Теперь я нахожусь в ожидании услышать, каким образом эти простейшие соотношения могут объяснить музыкальные проблемы, и хотя отчасти удовлетворить мою любознательность.
Сальвиати. Прежде всего необходимо установить, что каждый маятник имеет время качания столь строго определенное и ограниченное, что невозможно заставить его двигаться в период иной, нежели свойственный ему от природы. Если возьмем в руки веревку с привязанным к ней грузом и попробуем увеличить или уменьшить число качаний, то найдем, {192} что это напрасный труд. С другой стороны, маятник, находящийся в покое, хотя бы и очень тяжелый, мы можем привести в движение и притом очень заметное простым дуновением, если мы будем приостанавливать дыхание при возвращении маятника и вновь дуть в соответствующий его качанию момент. Если при первом дуновении мы откачнем маятник от отвеса на полдюйма, то вторым дуновением по возвращении маятника назад мы сообщим ему новый толчок и так постепенно увеличим размахи; но дуть необходимо вовремя, а не тогда, когда маятник идет навстречу (в таком случае мы мешали бы, а не помогали бы движению). Многими последовательными толчками мы постепенно сообщим маятнику такой импульс, что нужна будет сила, во много раз большая, нежели дуновение, чтобы его остановить58.
Сагредо. Я еще ребенком наблюдал, как один человек подобными многократными вовремя данными толчками заставлял звонить огромный церковный колокол; желая остановить его, четверо и шестеро человек хватались за веревку, но их много раз поднимало кверху, и их совместные усилия были недостаточными, чтобы сразу лишить колокол импульса, сообщенного ему регулярными толчками одного человека.
Сальвиати. Вот пример, который вместе с моей предпосылкой может быть очень подходящим для пояснения удивительных явлений в струнах цитры или струнного кимвала, которые, приходя в движение, заставляют звучать также и другие струны и притом настроенные не только в унисон, но и в октаву и квинту59. Струна после удара по ней издает звук, продолжающийся все время, пока длятся ее колебания; эти колебания заставляют дрожать и колебаться прилегающий к ней воздух, сотрясения и колебания которого распространяются на большое пространство и отзываются на всех струнах того же инструмента и других соседних. Каждая струна, настроенная в унисон с первой, будучи склонна совершать колебания в одинаковые с нею промежутки времени, при первом же толчке начинает слегка колебаться; к первому толчку присоединяется второй, третий, двадцатый и т. д., все в соответственные моменты, так что, в конце концов, получается дрожание, подобное дрожанию первой струны; при этом можно ясно видеть расширение ее колебаний до размеров колебания струны, возбуждающей ее движение. Колебания, распространяющиеся по воздуху, затрагивают и приводят в движение не только струны, но и вообще все иные тела, способные колебаться и вибрировать в промежутки времени, одинаковые со звучащей струной. Если мы прикрепим к краю инструмента различные щетинки или другие тела из весьма гибкого вещества, то, ударяя по струнам инструмента, заметим, что некоторые из них будут приходить в движение, когда мы ударяем по струне, совершающей колебания в одинаковое с ними время, другие будут оставаться при этом в покое, первые же не будут колебаться при звуке {193} иных струн. Если мы будем сильно водить смычком по толстой струне скрипки, приблизив к ней кубок из тонкого гладкого стекла, то, когда звучание струны будет в унисон со звучанием кубка, последний задрожит и явственно зазвучит. Распространение колебаний в среде, окружающей звучащее тело, можно ясно наблюдать, заставив звучать кубок, частью налитый водою, водя концом пальца по его краю: содержащаяся в кубке вода покроется правильными волнами. Это явление наблюдается еще отчетливее, если поставить ножку кубка на дно какого-нибудь достаточно широкого сосуда, наполнив последний водою почти до краев кубка; заставляя трением пальца звучать кубок, мы увидим, как правильные волны побегут с большой быстротой по воде и соберутся на значительном расстоянии от кубка; заставляя звучать указанным способом достаточно большой кубок почти полный воды, я часто видел, как сперва образовывались с совершенной правильностью волны, а когда иной раз звук стекла внезапно повышался на октаву, в тот же момент каждая из волн распадалась на две — явление, ясно указывающее, что форма октавы является двойной.
Сагредо. Подобное же приходилось не раз наблюдать и мне при занятиях музыкой как для удовольствия, так и для пользы. Я долгое время находился в недоумении по поводу формы созвучий, так как мне казались недостаточными те положения и объяснения, которые обычно даются авторами сочинений о музыке. Они говорят, что диапазон или октава стоит в отношении двойном, а диапента или, как мы говорим, квинта — в отношении полуторном к основному тону и т. д.; действительно, если натянутая на монохорде струна дает основной тон, то, заставляя звучать половину струны, разделив ее пополам посредством поставленной в середине дощечки, мы получим октаву; если же мы поставим дощечку на одну треть до конца струны и, придержав меньшую часть, заставим звучать часть из двух третей струны, то получим квинту. Поэтому говорят, что в октаве созвучие состоит в отношении двух к одному, а в квинте—в отношении трех к двум. Скажу, что это рассуждение казалось мне недостаточным для того, чтобы утверждать, будто двойное и полуторное отношения являются естественными формами для диапазона и диапенты, и вот по каким основаниям. Мы можем повысить тон струны тремя способами: укорачиванием, вытягиванием или, скажем, большим натяжением и, наконец, утончением. Сохраняя одну и ту же толщину и степень натяжения, мы должны, если хотим получить октаву, разделить ее подпоркою пополам и сперва заставить звучать всю струну, а затем половину ее. Но если, сохраняя ту же толщину и длину, мы захотим получить октаву посредством большего натяжения струны, то недостаточно будет тянуть ее силою вдвое большей; для этого понадобится сила в четыре раза большая, так что если струна была первоначально натянута грузом, например в один фунт, то, чтобы получить октаву, необходимо будет подвесить груз в {194} четыре фунта. Наконец, чтобы получить октаву, сохраняя ту же длину и степень натяжения, надо взять более тонкую струну, которая составит по толщине четвертую часть первоначальной толстой струны. То, что я говорю здесь об октаве, т. е. о зависимости ее от степени натяжения и от толщины струны и об отношении ее как двух к одному, выводимом из отношения длины струн, одинаково применимо и ко всяким другим музыкальным интервалам. Поэтому, если отношение, найденное на основании сравнения длины, равно полутора, поскольку для получения квинты мы заставляем звучать сначала всю, а затем две трети струны, то для того чтобы получить такое созвучие посредством большего натяжения или утончения струны, отношение трех к двум следует возвести в квадрат, что дает отношение девяти к четырем; таким образом, если в первом случае первоначальный груз, натягивающий струну, равнялся четырем фунтам, то придется взять новый груз не в шесть, а в девять фунтов; во втором же случае придется подобрать струны так, чтобы толщина одной из них относилась к толщине другой, как девять к четырем. После таких точных опытов мне показалось, что нет никаких оснований для утверждения почтенных философов об октаве, будто она имеет форму отношения одного к двум, а не одного к четырем; равным образом и квинта скорее соответствует отношению четырех к девяти, чем двух к трем. Так как сосчитать колебания струны, которая, давая звук, вибрирует с большою быстротою, совершенно невозможно, то я долго оставался в сомнении, действительно ли верно, что струна, звучащая на октаву выше, делает за то же время в два раза больше колебаний, чем струна, дающая основной более низкий тон, пока опыт с дрожащим и звучащим кубком и постоянными водяными волнами не показал мне, что всякий раз, как звук повышается на октаву, тотчас же рождаются новые меньшие волны, которые с величайшей точностью и правильностью разбивают каждую из прежних волн на двое.
Сальвиати. Это прекрасный опыт, дающий возможность различать одну от другой волны, порождаемые дрожанием звучащего тела; это— те же волны, которые распространяясь в воздухе, щекочут барабанную перепонку в нашем ухе и это в нашей душе становится звуком. Так как явление, наблюдаемое с водою, продолжается только до тех пор, пока мы продолжаем водить по кубку пальцем, да и в этот период времени оно непостоянно, ибо волны попеременно и рождаются и расходятся, то, конечно, вы согласитесь, что было бы хорошо, если бы можно было заставить колебания длиться продолжительное время, скажем, месяцы и годы; это дало бы нам возможность их измерять и удобно считать.
Сагредо. Конечно, я бы весьма высоко оценил такое изобретение.
Сальвиати. Изобретение это было делом случая; мне надо было только подметить и оценить должным образом попутное явление, имевшее {195} место в довольно несовершенной обстановке. Я скоблил острым железным долотом пластинку из латуни, чтобы удалить с нее пятна, и при быстром многократном движении долота раз или два услышал ясный и чистый звук; когда я посмотрел на пластинку, то увидел длинные ряды тончайших пылинок, расположенных параллельно и на совершенно одинаковом расстоянии друг от друга. Возобновляя и повторяя соскабливание много и много раз, я заметил, что полосы на пластинке появлялись только в тех случаях, когда повторялся звук; когда же движение долота происходило беззвучно, то не было никакого намека и на рисунок. Я повторял опыт много раз, проводя долотом то с большей, то с меньшей скоростью и получая звук то более высокого, то более низкого тона; я заметил, что при более высоких тонах штрихи получались более сближенными, а при низких — более редкими; в тех случаях, когда в один и тот же раз я проводил долотом сначала с меньшей, а потом, к концу, с большей скоростью и получал звук, постепенно повышающийся в тоне, штрихи получались все более сближенными, но с самой правильной постепенностью и сохраняя постоянную параллельность; кроме того, при соскабливании, порождающем звук, я чувствовал, как дрожало долото, зажатое в моем кулаке, и по руке пробегала как бы дрожь. В общем, в данном случае на примере железа наблюдается то же самое, что происходит, когда мы говорим сначала шепотом, а затем издаем ясный тон, потому что, выпуская дыхание беззвучно, мы не чувствуем в горле и во рту почти никакого движения по сравнению с тем сильным сотрясением, которое испытывает гортань, когда мы говорим полным голосом, особенно при глубоких низких тонах. Я неоднократно пробовал подобрать на струнах кимвала звуки, соответствующие тем, которые получались указанным образом. Два из наиболее разнящихся по тону звука отличались друг от друга ровно на квинту; когда я измерил штрихи и расстояние между ними в том и другом случае, то я нашел, что пространство, содержавшее сорок пять штрихов в одном случае, имело их только тридцать в другом, что действительно соответствует форме, приписываемой диапенте. Прежде чем продолжать далее, я хочу обратить внимание ваше на то, что один из трех способов повысить тон, о котором вы говорили, а именно, утончение струны, правильнее относить к изменению веса последней. При одинаковом материале пропорция сохраняется, конечно, одинаковой, так что из двух струн, сделанных из кишок, одна струна должна быть в четыре раза толще другой, чтобы разница в тоне равнялась октаве; также и в случае латунных струн — одна из них должна быть вчетверо толще другой. Но если я хочу получить октаву из струн — одной латунной, а другой жильной,— то нет надобности, чтобы одна была в четыре раза толще другой; необходимо только, чтобы одна была в четыре раза тяжелее другой. Таким образом, что касается толщины, то металлическая струна будет по сравнению {196} с жильной струной, звучащей на октаву выше, не в четыре раза толще последней, а приблизительно во столько же раз тоньше; но вес первой будет в четыре раза больше веса второй. Отсюда же происходит и то, что если мы возьмем два инструмента со струнами совершенно одинаковой длины, толщины и степени натяжения, но в одном случае сделанными из золота, а в другом из латуни, то тон первого будет ниже, чем второго приблизительно на квинту, так как золото почти в два раза тяжелее латуни. Отсюда можно видеть, что сопротивление скорости движения оказывает по преимуществу вес тела, а не толщина, обратно тому, чего можно было бы ожидать по первому взгляду; казалось бы естественным, что скорость должна быть умеряема сопротивлением среды в большей степени, если последняя должна уступать движению тела толстого и более легкого, чем тела тонкого и тяжелого; в действительности же в данном случае имеет место как раз обратное. Но возвращаясь к первому положению, скажу, что ближайшая и непосредственная причина формы музыкальных интервалов лежит не в длине струны и не в толщине или степени натяжения: она заключается в отношении между числами колебаний и ударов воздушных волн, доходящих до барабанной перепонки нашего уха и заставляющих ее дрожать с соответственной скоростью. Установив это, мы можем с большою уверенностью найти основание тому, почему при многих звуках, различных по тону, некоторые созвучия воспринимаются нами с удовольствием, иные нам менее приятны и третьи, наконец, производят крайне неприятное ощущение, т. е. найти основание для более или менее совершенных консонансов и диссонансов. Неприятное впечатление от последних происходит, думается мне, от несогласованности колебаний, производимых двумя различными тонами и беспорядочно поражающих наш слух; особенно резким является диссонанс в том случае, когда числа колебаний несоизмеримы, например, если при двух в унисон настроенных струнах заставить звучать струну и часть, относящуюся ко всей струне, как сторона квадрата к его диагонали,— диссонанс, подобный тритонусу или полудиапенте. Консонансами, т. е. созвучиями, воспринимаемыми с удовольствием, являются два таких тона, которые производят колебания, ударяющиеся о барабанную перепонку с известною правильностью; здесь, прежде всего, необходимо, чтобы числа колебаний, совершаемых звуками в одинаковый промежуток времени, были соизмеримыми и чтобы, таким образом, хрящ барабанной перепонки не находился в постоянном мучительном состоянии движения двумя различными способами, в зависимости от несогласованных друг с другом ударов. Таким образом, первым и самым совершенным созвучием является октава: на каждый удар, производимый на ухо звуком более низкого тона, в ней приходятся два удара более высокого тона, так что удары обоих тонов то совпадают, то расходятся, и из общего числа ударов половина является {197} совпадающей; при звуках же струн, настроенных в унисон, совпадают все удары, т. е. звучит как бы одна только струна, и созвучия не получается. Приятно звучащая квинта дает на каждые два колебания низкой струны три колебания струны более высокого тона, откуда следует, что из числа всех колебаний, производимых более высоким тоном, одна треть совпадает с колебаниями более низкого тона, так что между каждою парой совпадающих колебаний помещаются два колебания одиночных; в диатоссероне, или кварте, число таких одиночных промежуточных колебаний равно трем. В секунде или тоне полутораоктавном из девяти колебаний высокого тона только одно совпадает с колебаниями низкого тона, все же остальные являются несовпадающими, и от ударов их о барабанную перепонку получается уже впечатление диссонанса.
Симпличио. Мне хотелось бы, чтобы вы дали более подробные объяснения этого вопроса.
Сальвиати. Пусть линия АВ представляет длину и распространение одного колебания струны более толстой, а линия CD — струны более тонкой, дающей с первой созвучие октавы. Разделим теперь линию АВ пополам в точке Е. Ясно, что если движение начинается от точек А и C, то пока колебание более высокого тона дойдет до конца D, колебание низкого тона достигнет только середины пути Е; так как эта последняя не является конечной точкой движения, то в ней не получается того толчка, который имеет место в точке D. Пока второе колебание возвращается из D в C, первое доходит из Е в В, и тогда оба толчка в точках В и С совместно воспринимаются нашим ухом. То же самое повторяется в целом ряде последующих колебаний, так что толчки от
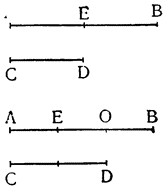 |
Сагредо. Я не могу более молчать и должен выразить восхищение, которое я испытываю, видя, как хорошо и основательно объясняются все те явления, которые столь долгое время держали меня в слепоте и мраке. Теперь я понимаю, почему два тона, звучащих в унисон, ничем не отличаются от одного звука; понимаю, почему октава является лучшим созвучием, но настолько сходным с унисоном, что она как бы подражает последнему; сходство и различие заключаются в том, что все колебания струн, звучащих в унисон, всегда и постоянно совпадают, тогда как в октаве все колебания более низкого тона сопровождаются колебаниями высокого тона, дающими, кроме того, через равные промежутки времени одиночные толчки, ничему не мешающие; вот почему это созвучие {199} представляется таким нежным, но звучащим без особого огня. Квинта же, со свойственными ей контртемпами и промежутками между каждой парой совпадающих толчков, заполненными двумя толчками высокого тона и одним толчком низкого тона, которые все три следуют один за другим через одинаковые интервалы времени, равные половине интервала от двойного совпадающего толчка до первого одиночного толчка высокого тона, производит весьма приятное щекотание слуховой перепонки, при котором нежность и острота умеряют друг друга и кажется, что одновременно получаешь сладостный поцелуй и легкий укол.
Сальвиати. Теперь, синьоры, видя, что вы столь высоко цените мои небольшие сообщения, я считаю необходимым показать вам, каким образом можно видеть и наблюдать глазом ту же игру, которую слышит наше ухо. Подвесьте свинцовые шарики или другие подобные им тяжелые тела на трех нитях разной длины, подобрав последние таким образом, чтобы в то время как самая длинная из них совершала два качания, самая короткая делала бы их четыре, а средняя — три; это будет иметь место, если придать наибольшей нити длину в шестнадцать каких-либо мер, средней — в девять и самой короткой — в четыре. Выведенные из отвесного положения и отпущенные одновременно маятники начнут качаться, причем произойдет как бы беспорядочное пересечение нитей, встречающихся в разных положениях; однако при каждом четвертом качании длинного маятника все три маятника будут совпадать и, начиная одновременно движение, будут начинать и новый период. Это смешение качаний соответствует тому смешению колебаний, которое воспринимается слухом от звуков трех струн, дающих октаву и квинту. Если мы определим подобным же образом длину других нитей сообразно с определенными интервалами, дающими музыкальное созвучие, то получим иное смещение и пересечение нитей, но всегда такое, при котором в известное время через известное число качаний последние совпадают, и маятники (будь их три или четыре) вновь одновременно начинают свое периодическое движение. Если же числа качаний двух или более маятников несоизмеримы, так что последние не кончают одновременно движения через определенное число качаний или же если они и соизмеримы, но совпадают и начинают новый период только через большой промежуток времени и после весьма большого числа колебаний, то глаз окончательно теряется в неправильном беспорядочном движении так же, как и ухо, когда оно мучительно воспринимает сотрясения воздуха, ударяющиеся о барабанную перепонку без всякой правильности и порядка60.
Однако, синьоры, куда же завели нас на столько часов различные проблемы и непредвиденные отступления? Уже вечер, а о том предмете, которым мы первоначально предполагали заняться, мы сказали очень мало или, вернее, не сказали почти ничего. Мы настолько уклонились от {200} нашего пути, что я с трудом вспоминаю его начало и те первоначальные положения, которые были приняты нами как гипотезы и основания для будущих наших рассуждений.
Сагредо. В таком случае покончим на сегодня наши рассуждения и дадим возможность уму воспользоваться отдыхом и ночным покоем, для того чтобы завтра (если только вы, синьор, на это согласны) возвратиться к обсуждению главных вопросов.
Сальвиати. Я не премину быть здесь завтра в том же часу, как и сегодня, чтобы услужить и угодить вам.
Конец первого дня
| {201} |
С |
Сальвиати. Все это я хорошо помню. Возвращаясь к началу нити наших рассуждений, скажу, что чем бы ни вызывалось сопротивление тел мощному растяжению, стремящемуся разломать их, несомненно, что такое сопротивление имеется налицо; сопротивление это очень велико в отношении силы, растягивающей их вдоль, и значительно меньше в отношении силы, действующей поперечно. Таким образом, например, стальной или стеклянный стержень может выдержать груз в тысячу фунтов, {202} если последний подвешен так, что растягивает его в длину, и в то же время, будучи закреплен одним концом в стене, сломается от прикрепления к другому концу груза всего в пять — десять фунтов. О сопротивлении второго рода мы и будем теперь беседовать, стараясь отыскать, в каком отношении оно находится у подобных между собою и несходных друг с другом призм и цилиндров из одного и того же вещества, но имеющих различную длину и толщину. При этих рассуждениях я буду считать известным то положение, которое доказывается в механике относительно так называемого рычага, а именно, что при употреблении рычага сила и сопротивление обратно пропорциональны их расстояниям от точки опоры.
Симпличио. Это предположение было доказано Аристотелем в его «Механике» ранее всех других.
Сальвиати. Предоставим ему право первенства по времени; но что касается убедительности доказательства, то мне кажется, что Архимеда мы должны поставить выше: у него из одного положения, доказанного им в работе «О равновесии плоских фигур...», вытекает не только закон рычага, но и большая часть других предложений, касающихся механических инструментов01.
Сагредо. Но если этот закон является основанием для всего того, что вы собираетесь нам доказать, то было бы нелишним привести полное и точное доказательство его, которое и нам послужит введением, если оно не отнимет у нас много времени.
Сальвиати. Если мне предстоит это сделать, то для того чтобы ввести вас в курс всего последующего, будет лучше идти, как я полагаю, несколько иным путем, чем Архимед, и принять за основное то положение, что равные грузы, действующие на равные плечи весов, остаются в равновесии (принцип, положенный в основание также и Архимедом), а затем показать правильность того, что различные грузы находятся в равновесии в случае плеч разной длины, если только длины эти находятся между собою в отношении, обратном отношению грузов, и что, таким образом, один и тот же закон проявляется как в случае равновесия равных грузов на равноплечих весах, так и в случае равновесия различных грузов, если только плечи весов имеют отношение, обратное отношению грузов.
Для более ясного представления сказанного начертим призму или цилиндр АВ, подвешенный за концы на двух нитях НА и IB к стержню HI. Ясно, что если я подвешу целое в середине С коромысла HI, то призма АВ, согласно принятому нами принципу, останется в равновесии, так как половина ее веса останется по одну сторону, а половина — по другую сторону от точки С. Представим себе теперь, что призма разделена плоскостью по линии D на две неравных части, из которых DA пусть будет большей, a DB — меньшей; чтобы и после этого разделения части призмы {203} оставались в таком же положении по отношению к линии HI, как и раньше, протянем новую нить ЕВ, которая, будучи прикреплена в точке Е, поддержит части призмы АD и DВ. Нельзя сомневаться, что и в этом случае, благодаря отсутствию какого-либо местного перемещения призмы относительно коромысла HI, таковая по-прежнему останется в равновесии. Но то же самое положение будет иметь место и в том случае, если часть призмы, поддерживаемая двумя нитями АН и DE, будет подвешена посредине к одной нити GL, а другая часть призмы — DВ — будет подвешена
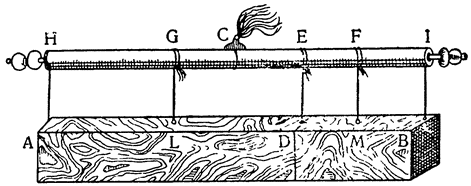 |
Полагаю, что вы не встречаете затруднений в признании того, что обе призмы AD и DВ остаются в равновесии около точки опоры С, поскольку одна половина веса всего тела АВ располагается по одну сторону, а другая половина — по другую сторону от C, и мы можем представить их себе как равные грузы, расположенные на равном расстоянии от точки опоры. Превратим ли мы теперь обе призмы АВ и ВВ в два куба или два шара или в какие-либо иные фигуры (сохраняя неизменно точки подвеса в G и F), равновесие около точки С сохранится; не думаю, чтобы нашелся кто-либо, {204} сомневающийся в том очевидном факте, что форма не изменяет веса тел, если последние содержат одно и то же количество материи. Но отсюда мы можем вывести общее заключение, что два груза, расположенные от точки опоры на расстояниях, обратно пропорциональных их весу, находятся в равновесии2.
Установив этот принцип, мы должны подумать, прежде чем переходить к дальнейшему, как можно представить себе все эти силы, сопротивления, моменты, фигуры и т. д. отвлеченно и отдельно от материи, а с другой стороны — конкретно и в связи с материей; в самом деле, свойства фигур, рассматриваемых в отвлечении от материи, претерпевают некоторые изменения
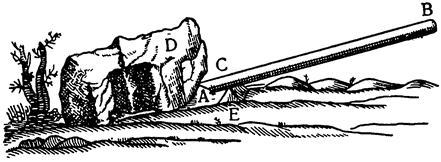 |
Сагредо. Я принужден отступить от первоначального намерения не давать повода к отступлениям; но я не в состоянии следить внимательна за дальнейшим, если у меня остается не рассеянным какое-либо возникшее сомнение. В данном случае последнее таково: мне кажется, что вы сравниваете силу, приложенную в В, с весом всего камня D, в то время как часть последнего, и, вероятно, большая, покоится на горизонтальной плоскости; таким образом . . . {205}
Сальвиати. Прекрасно понял. Вы совершенно правы; в ответ вам замечу только, что я говорил не о всем весе камня, а лишь о моменте, который он имеет и которым он действует на точку А — конец рычага ВА,— который всегда меньше общего веса камня и меняется в зависимости от формы камня и большей или меньшей степени его поднятия.
Сагредо. Хорошо, но теперь у меня рождается желание, чтобы для полноты вопроса мне был указан, если это возможно, способ, которым можно было бы определить, какая часть общего веса поддерживается опорной поверхностью и какая оказывает действие на конец рычага А.
Сальвиати. Я не откажусь дать вам объяснение, которое можно сделать в немногих словах. Представьте себе, что тело, имеющее центр тяжести в А, лежит на горизонтальной плоскости концом В, другой же конец его поддерживается посредством рычага CG, имеющего точку опоры в N, некоторой силой, приложенной в точке G. Из центра А и точки С опустим на плоскость горизонта перпендикуляры АО и CF. Утверждаю, что отношение момента всего веса тела к моменту силы, приложенной в G, равно составному отношению расстояния GN к расстоянию NC и расстояния FB к расстоянию ВО. Пусть отношение линии FB к ВО равно отношению NC к некоторой линии X; так как весь вес А поддерживается двумя силами, приложенными в точках В и C, то силы в точках В и С относятся одна к другой так, как расстояние FO к ОВ. Соединяя силы, действующие в точках В и С в одну, т. е. получая момент всего веса А, находим, что последний относится к силе, приложенной в С, как линия FB к линии ВО, т. е. как NC к X;
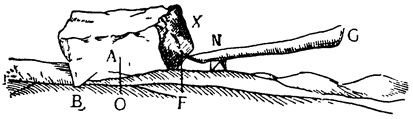 |
Возвращаюсь теперь к нашей первоначальной задаче. После только что доказанного нетрудно будет понять причину того, что твердые цилиндры или призмы из стекла, стали, дерева или иного ломкого материала, будучи подвешены вертикально, выдерживают весьма большой груз, в то время как при горизонтальном положении (как я уже упоминал выше) они могут быть сломаны малым грузом и тем меньшим, чем более длина цилиндра или призмы превосходит их толщину. Представим себе призму ABCD, вделанную в стену своей частью АВ, на другой конец которой действует сила груза Е (предполагаю, что стена возведена отвесно {206} и что призма вделана в стену под прямым углом). Ясно, что если призма должна сломаться, то это произойдет в В, где граница стены служит точкою опоры, а ВС представляет одну часть рычага, на которую действует сила; толщина тела ВА есть другая часть рычага, на которую действует сопротивление, обусловливаемое сцеплением частиц тела BD с теми частицами его, которые находятся в стене. На основании доказанного ранее момент силы, действующей в С, и момент сопротивления, обусловливаемый толщиною призмы, т. е. сцеплением основания призмы ВА со смежною с ним частью, имеют то же отношение, что и длина СВ к половине ВА; поэтому абсолютное сопротивление призмы BD разрыву (под каковым мы подразумеваем сопротивление действию силы в продольном направлении, ибо тогда каково движение движущего, таково движение движимого) так относится к сопротивлению разрыву посредством рычага
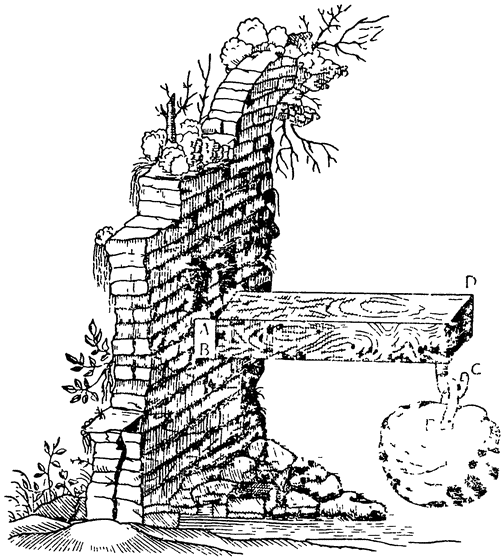
ВС, как длина ВС к половине толщины призмы АВ или к радиусу основания, если взят цилиндр5. Таково наше первое положение. Заметьте себе, что сказанное правильно лишь при условии, что мы не принимаем во внимание собственного веса тела BD, считая последнее невесомым. Если мы пожелаем принять в расчет и его вес, действующий одновременно с грузом Е, то мы должны будем прибавить к весу груза Е половину веса тела BD; таким образом, если, например, тело BD весит два фунта, а груз Е {207} десять фунтов, то необходимо будет принять, что в Е действует сила, равная одиннадцати фунтам.
Симпличио. А почему же не двенадцати фунтам?
Сальвиати. Груз Е, любезный синьор Симпличио, висящий на конце С, действует в отношении рычага ВС всем своим моментом, равным десяти фунтам; если бы в той же точке действовал и вес тела BD, то мы имели бы момент, равный еще двум фунтам; но, как вы видите, частицы тела распределены равномерно на всем протяжении ВС, причем, те из них, которые расположены ближе к концу В, действуют с меньшей силою, чем более отдаленные; уравнивая все эти силы, найдем, что они могут быть заменены одной силой, равной общему весу призмы, приложенному в центре ее тяжести, расположенном в середине рычага ВС; но груз, действующий на конец С, имеет момент вдвое больший, чем тот груз, который действует, будучи подвешен посредине; следовательно, только половина веса призмы должна быть прибавлена к весу Е, если мы рассматриваем моменты обеих сил, относя их действие к точке С.
Симпличио. Теперь понимаю. Кроме того, если я не ошибаюсь, действие обоих грузов BD и Е, приложенных, как указано, будет одинаково с моментом всего веса BD и двойного груза Е, если бы они были приложены в середине рычага ВС.
Сальвиати. Совершенно верно, и это необходимо хорошенько запомнить. Теперь мы можем немедленно определить, в какой степени стержень или еще лучше призма, более широкая нежели толстая,
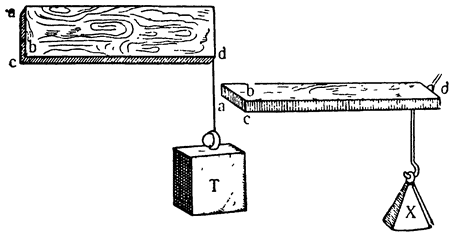 |
Теперь приступим к рассмотрению, в какой мере увеличивается момент собственного веса по сравнению с собственным сопротивлением излому призмы или цилиндра, когда последние, будучи расположены параллельно горизонту, увеличиваются в длину; при этом мы найдем, что момент этот возрастает пропорционально квадрату длины. Для доказательства этого представим себе призму или цилиндр AD прочно вделанным в

стену концом А параллельно горизонту, а затем предположим, что он удлинился до Е, так что к нему прибавилась часть BE. Ясно, что самое удлинение рычага АВ до С, взятое абсолютно, увеличивает момент силы, действующей на сопротивление излому в точке А, в отношении СА к ВА; но прибавление веса тела BE к весу тела АВ увеличивает, кроме того, момент действия веса в том же отношении, в каком призма АЕ находится к {209} призме AD, каковое отношение одинаково с отношением длины АС к длине АВ. Теперь ясно, что сложный момент, получающийся от совокупности обоих приращений — длины и тяжести, будет пропорционален квадрату той или другой. Отсюда заключаем, что моменты сил призм и цилиндров одинаковой толщины, но разной длины, относятся друг к другу, как квадраты длины.
Покажем теперь, во-вторых, в какой пропорции возрастает сопротивление излому призм или цилиндров одинаковой длины при возрастании их толщины. Утверждаю: в призмах или цилиндрах одинаковой длины, но разной толщины, сопротивление излому возрастает как куб отношения толщин или диаметров их оснований.
Пусть имеются два цилиндра А и В, длины которых DG и FH равны, основания же различны и равны кругам с диаметрами CD и EF; утверждаю, что отношение сопротивления излому цилиндра В к такому же сопротивлению цилиндра А будет равно кубу отношения диаметра РЕ к диаметру DC. Рассматривая простое и абсолютное сопротивление оснований EF и CD разрыву под действием растягивающей силы, найдем, без сомнения, что сопротивление цилиндра В во столько раз превосходит сопротивление цилиндра А, во сколько раз круг EF больше круга CD, потому что во столько же раз многочисленнее и волокна, нити или другие элементы, связывающие части твердого тела. Если мы примем теперь во внимание, что силы, действующие поперечно, приложены к двум рычагам, плечи которых или расстояния от действующих сил равны линиям DG и FH, что точки опоры их находятся в D и F, другие же плечи их или расстояния, на которых действуют сопротивления, суть радиусы кругов DC и ЕР, поскольку сопротивление волокон, распространенных по всей площади кругов, может быть отнесено к центрам
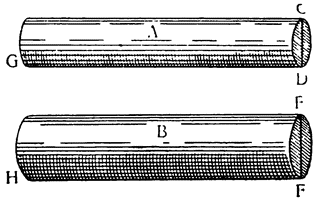 |
Из только что доказанного можно далее вывести, что отношение сопротивлений призм и цилиндров одинаковой длины равняется полуторной степени отношения их объемов. Это следует из того, что призмы и цилиндры одинаковой высоты относятся между собою, как их основания, т. е. как квадраты сторон или диаметров основания; отношение же сопротивлений (как только что было показано) равно отношению кубов тех же сторон или диаметров. Отсюда отношение сопротивлений равняется полуторной степени отношения объемов этих тел или, что то же самое, их весов6.
Симпличио. Прежде чем идти далее, прошу вас разъяснить некоторое мое недоумение. Неясно, почему мы до сих пор не принимаем в соображение сопротивления особого рода, уменьшающегося, по моему мнению, в телах по мере их удлинения и притом не только при поперечном усилии, но и при продольном. Ведь мы находим на деле, что длинный канат менее способен выдержать большой груз, нежели короткий; и я думаю, что деревянный или железный брус может выдержать большую тяжесть, если он короток, нежели если он имеет значительную длину. Говоря это, я подразумеваю продольное растяжение, принимая также во внимание и собственный вес, конечно, больший у длинной веревки и длинного бруса.
Сальвиати. Думаю, синьор Симпличио, что в этом пункте вы, как и многие другие, заблуждаетесь, если только, конечно, я правильно понял ваше положение; вы как будто хотите сказать, что длинная веревка, например в сорок локтей, не может выдержать такого груза, как подобная же веревка в локоть или два длиною?
Симпличио. Это самое я и хотел сказать и думаю, что мое утверждение достаточно правдоподобно.
Сальвиати. Я же считаю его не только не правдоподобным, но и совершенно ложным и полагаю, что легко могу вывести вас из заблуждения. Для этого возьмем веревку АВ, привяжем ее наверху одним концом A, а к другому концу подвесим груз С, от тяжести которого веревка должна разорваться. Наметьте мне теперь, синьор Симпличио, какое-нибудь место, где должен произойти разрыв.
Симпличио. Допустим, что он произойдет в месте В.
Сальвиати. Теперь я спрошу вас, какова причина разрыва веревки в D?
Симпличио. Причиной является то, что в данном месте веревка не в состоянии выдержать, скажем, ста фунтов — веса части веревки DB вместе с привязанным камнем С.
Сальвиати. Следовательно, всякий раз, как на веревку подействует в месте D тот же вес в сто фунтов, она будет разорвана?
Симпличио. Полагаю, что так. {211}
Сальвиати. Но скажите мне теперь, если подвязать тот же груз
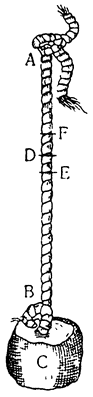 |
Симпличио. Несомненно, если только к весу камня С приложить и вес части веревки ЕВ.
Сальвиати. Таким образом, если веревка вместе В будет испытывать действие груза в сто фунтов, то она, согласно вашему утверждению, разорвется, а между тем часть веревки FE меньше всей веревки АВ. Каким же образом вы утверждаете, что длинная веревка менее прочна, нежели короткая? Признайте теперь, что я освободил вас от заблуждения, в котором пребывают очень многие и притом весьма смышленые люди7. Последуем далее. После того как я показал, что момент, преодолевающий сопротивление излому призм и цилиндров, изменяется пропорционально квадратам их длины (при условии сохранения постоянной одной и той же толщины) и что у тех же тел, равных по длине, но имеющих разную толщину, сопротивление изменяется пропорционально кубам сторон или диаметров их оснований, перейдем к рассмотрению того, что происходит с телами при одновременном изменении длины и толщины. Относительно такого случая говорю: призмы и цилиндры различной длины и толщины оказывают сопротивление
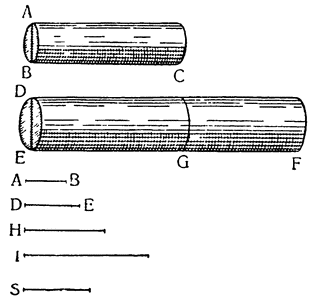 |
Пусть даны два таких цилиндра ABC и BEF. Утверждаю, что отношение сопротивления цилиндра АС к сопротивлению цилиндра BF равно составному отношению куба диаметра АВ к кубу диаметра DE и длины EF к длине ВС. Отложим на более длинном цилиндре часть EG, равную ВС; пусть Н будет третьей пропорциональной линий АВ и BE, а I — четвертой пропорциональной, и пусть отношение EF к ВС будет равно отношению I к S8. Отношение сопротивления цилиндра АС к сопротивлению цилиндра BG равно отношению куба АВ к кубу BE, т. е. линии АВ к I, а отношение сопротивления цилиндра BG к сопротивлению цилиндра BF равно отношению длины FE к длине EG, т. е. линии I к S. На основании этих пропорций заключаем, что сопротивление цилиндра АС относится {212} к сопротивлению цилиндра DF, как линии АВ к S; но отношение линии АВ к S равно составному отношению АВ к I и I к S; следовательно, отношение сопротивления цилиндра АС к сопротивлению цилиндра DF равно составному отношению АВ к I, т. е. отношению куба АВ к кубу DE и отношению линии I к линии S или длины EF к длине ВС, что и требовалось доказать9.
После приведенного доказательства я хочу рассмотреть еще один случай, а именно тот, когда цилиндры или призмы подобны. Относительно таких тел я докажу, что у подобных цилиндров или призм отношение составных моментов, обусловливаемых весом и длиною, равняется полуторной степени отношения сопротивления их оснований.
Чтобы доказать это, начертим два подобных цилиндра АВ и CD. Утверждаю, что отношение момента цилиндра АВ, преодолевающего сопротивление его основания В, к моменту цилиндра CD, преодолевающему сопротивление основания последнего D, равняется полуторной степени отношения сопротивления основания В к сопротивлению основания D. В самом деле, моменты твердых тел АВ и CD и сопротивлений их оснований В и D составляются из веса этих тел и сопротивлений, действующих на плечи рычагов; но плечи рычагов цилиндра АВ относятся между собою, как плечи рычагов цилиндра CD (так как вследствие подобия цилиндров длина АВ относится к радиусу основания В так же, как длина CD
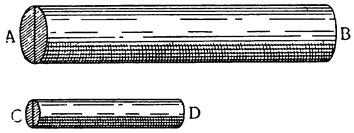 |
Симпличио. Такое положение представляется для меня не только совершенно новым, но и неожиданным, а также весьма далеким от того, что я думал: основываясь на полном подобии фигур, я был уверен, что отношение их моментов к сопротивлениям остается неизменным.
Сагредо. Доказательство касалось того положения, из которого мы исходили в наших рассуждениях и которое сначала представлялось мне темным.
Сальвиати. То, что сказал синьор Симпличио, было некоторое время и моим мнением; я также считал сопротивления подобных фигур пропорциональными, пока некоторые наблюдения не показали мне, {213} что прочность подобных тел не сохраняет того же отношения, которое существует между величиной тел, и что большие тела обладают меньшею способностью противодействия внешним силам; например, при падении взрослые люди претерпевают по сравнению с малыми детьми большие повреждения; при падении с одной и той же большой высоты тяжелая балка или колонна, как мы уже говорили раньше, разбиваются на куски, тогда как небольшой брусок или маленький мраморный цилиндр остаются целыми. Подобные наблюдения побудили меня заняться этим вопросом и привели к заключению, с которым я вас познакомил. Заключение поистине удивительное: оказывается, что из бесчисленного множества подобных тел нельзя найти двух таких, у которых отношение моментов сопротивлениям было бы одним и тем же.
Симпличио. Это заставляет меня припомнить одно место из Аристотеля, который в своих «Проблемах механики» задается вопросом, почему деревянные жерди тем слабее и легче прогибаются, чем они длиннее, хотя бы более короткие были тоньше, а длинные — толще. Если я только верно помню, он сводит причину к действию простого рычага10.
Сальвиати. Это совершенно верно, но так как данное там решение не устранило всех сомнений, то монсиньор ди Гуевара, обогативший и осветивший означенное сочинение своими высокоучеными комментариями, привел другие остроумные соображения для устранения всех затруднений. Однако относительно одного пункта и он остался в заблуждении, полагая, что при увеличении в одинаковой пропорции длины и толщины твердых тел прочность их и сопротивление излому и разрушению остаются без изменения. После долгих размышлений над этим вопросом я пришел к выводам, с которыми вас сейчас и познакомлю. Прежде всего, я докажу, что среди подобных и весомых призм и цилиндров имеется только одно тело, которое находится (под действием собственного веса) на границе между тем, чтобы сломаться или остаться целым, так что всякое тело большего размера не способно выдержать собственного веса и ломается, а всякое меньшее тело еще оказывает сопротивление силе, стремящейся его сломать.
Пусть АВ тяжелая призма, доведенная до предельной длины, так что при увеличении длины ее на самую малость она сломается; утверждаю, что она будет единственной, находящейся в таком избранном нами состоянии среди всех ей подобных (число коих бесконечно), и что всякая большая призма под действием собственного веса сломается, всякая же меньшая будет в состоянии помимо собственного веса выдержать и еще некоторую тяжесть. Пусть СЕ будет призма, подобная АВ, но большая. Утверждаю, что она не сможет держаться, но сломается от действия собственного веса. Отложим на большой призме часть CD, равную по длине АВ. Сопротивление CD относится к сопротивлению АВ, как куб толщины CD к кубу {214} толщины АВ или как призма СЕ к призме АВ (вследствие подобия этих призм); поэтому вес призмы СЕ есть тот предельный вес, который может выдержать призма, равная по длине CD; но так как длина призмы СЕ больше, то призма СЕ сломается. Возьмем теперь меньшую призму FG. Можно доказать подобным же образом (положив FH равным АВ), что сопротивление FG относилось бы к сопротивлению АВ, как призма FG к призме АВ, если бы длина АВ или FH равнялась FG; но на самом деле она больше; следовательно, момент призмы FG, оканчивающейся в G, будет недостаточным для того, чтобы сломать эту призму FG.
Сагредо. Краткое и блестящее доказательство, обнаруживающее правильность и необходимость такого положения, которое на первый взгляд кажется довольно неправдоподобным. Необходимо, следовательно, значительно изменить отношение между длиною и толщиною большей призмы, сократив ее длину или увеличив ее толщину, чтобы привести ее в такой вид, при котором она находилась бы на границе между тем, чтобы сломаться и остаться целой. Думается, что рассмотрение такого случая могло бы показать нам много интересного.
Сальвиати. А вместе с тем очень полезного, хотя и постигаемого не без труда. Я потратил немало времени на решение этого вопроса и хочу теперь поделиться с вами своими соображениями. Даны цилиндры или призма наибольшей длины, при которой они только могут держаться, не ломаясь от собственного веса, и дана некоторая большая длина; требуется найти толщину другого цилиндра или призмы, которые при данной большей длине являлись бы единственными и наибольшими, могущими выдержать собственный вес.
Пусть ВС цилиндр наибольшей длины, выдерживающий свой собственный вес, и пусть дана длина DE, большая, нежели длина цилиндра АС; требуется найти толщину цилиндра, который при длине DE являлся бы наибольшим, выдерживающим свой собственный вес. Положим, что третьей пропорциональной к величинам DE и АС будет I, и что отношение DE к I таково же, как отношение DF, т. е. искомого диаметра цилиндра FE, к диаметру ВА. Утверждаю, что при этих условиях FE и будет искомым цилиндром, единственным из всех ему подобных, наибольшей длины, выдерживающим собственный вес. Пусть третьей пропорциональной к линиям DE и I будет М, а четвертой О, и пусть линия FG, отложенная на большем цилиндре, будет равна АС. Так как диаметр FD относится к диаметру АВ, как линии DE к I, и так как четвертая пропорциональная к линиям DE и I есть О, то куб диаметра FD будет относиться к кубу диаметра ВА, как DE к О. Но сопротивления цилиндров DG и {215} ВС относятся, как кубы их диаметров FD и ВА. Отсюда вытекает, что сопротивление цилиндра DG относится к сопротивлению цилиндра ВС, как линии DE к О. Но так как момент цилиндра ВС равен его сопротивлению,
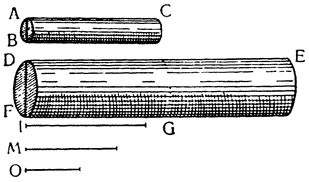 |
Сагредо. Это очень длинное доказательство, синьор Сальвиати, и слишком трудное, чтобы удержать его в памяти, прослушав один только раз; поэтому я очень просил бы вас повторить его.
Сальвиати. Готов исполнить все, что вы пожелаете; однако, думается, лучше привести иное, более краткое доказательство, для которого понадобятся только другие фигуры.
Сагредо. Тем лучше; но я все же буду вам очень признателен, если вы запишите мне и первое доказательство, чтобы я мог лучше вникнуть в него на досуге.
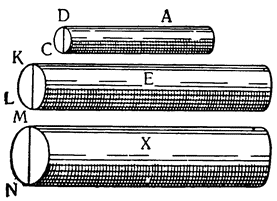 |
Сальвиати. Охотно сделаю. Теперь возьмем цилиндр А, диаметр основания которого равен DC, а пусть этот цилиндр А будет наибольшим, способным выдержать собственный вес. Будем теперь искать другой цилиндр, большей длины, который также был бы единственным наибольшим, выдерживающим свой вес. Представим себе цилиндр, подобный первому А, равный по длине данной линии, скажем, Е; диаметром основания его пусть будет линия KL. Пусть, далее, третьей пропорциональной к линиям DC и KL будет линия MN; приняв эту линию за диаметр основания нового цилиндра X, равного по длине данной линии Е, можно утверждать, что этот новый цилиндр X и есть именно тот, который мы {216} ищем. Действительно, сопротивление DC относится к сопротивлению KL, как квадрат DC к квадрату KL, или как квадрат KL к квадрату MN, или как цилиндр Е к цилиндру X, или как момент Е к моменту X, далее, сопротивление KL относится к сопротивлению MN, как куб KL к кубу MN, или как куб DC к кубу KL, т. е. как цилиндр А к цилиндру Е, или как момент А к моменту Е. Отсюда заключаем обратно, что как сопротивление DC относится к сопротивлению MN, так и момент А относится к моменту X; следовательно, призма X находится по отношению к моменту и сопротивлению в таких же точно условиях, как и призма А12.
Рассмотрим теперь более общую проблему; предложение будет таково: дан цилиндр АС с каким угодно отношением момента к сопротивлению, и дана некоторая длина DE; требуется найти толщину нового цилиндра, равного по длине DE, момент и сопротивление коего сохраняли бы между собою то же отношение, что и у первого цилиндра.
Воспользовавшись приведенными выше фигурами и идя подобным же путем, скажем: так как момент цилиндра FE относится к моменту части DG второго цилиндра, как квадрат ED к квадрату FG, или как линия DE к I, и так как момент цилиндра DG относится к моменту цилиндра АС, как квадрат FD к квадрату АВ, или как квадрат DE к квадрату I, или как квадрат I к квадрату М, или как линия I к линии О, то отношение момента цилиндра FE к моменту цилиндра АС будет ex aequali13 равно отношению линии DE к О, или куба DE к кубу I, или куба FD к кубу АВ, или же отношению сопротивления основания FD к сопротивлению основания АВ, что нам и требовалось получить14.
Из того, что было сейчас доказано, мы ясно видим невозможность не только для искусства, но и для самой природы беспредельно увеличивать размеры своих творений. Так, невозможна постройка судов, дворцов и храмов огромнейшей величины, коих весла, мачты, балки, железные скрепы, словом, все части держались бы прочно. С другой стороны, и природа не может произвести деревьев несоразмерной величины, так как ветви их, отягощенные собственным чрезвычайным весом, в конце концов, сломились бы. Равным образом невозможно представить себе костяка человека, лошади или другого живого существа слишком большой величины, который бы держался и соответствовал своему назначению; достигнуть чрезвычайной величины животные могли бы только в том случае, если бы вещество их костей было значительно прочнее и крепче, нежели обычное, или же если бы кости их изменились, соразмерно увеличившись в толщину, отчего животные по строению и виду производили бы впечатление чрезвычайной толщины. Это, возможно, уже было подмечено тем проницательнейшим поэтом, который, описывая великана, говорит:
|
Нельзя было сказать, насколь он был высок, Так все в нем было непомерно толсто15. {217} |
В качестве краткого примера только что сказанного я покажу вам сейчас рисунок кости, удлиненной только в три раза, но увеличенной в толщину в такой мере, чтобы она могла служить для большого животного с той же надежностью, как меньшая кость служит для животного малого размера. Вы видите, какой несообразно толстой выглядит такая увеличенная кость. Отсюда ясно, что тот, кто желал бы сохранить в огромном великане пропорцию членов обыкновенного человеческого тела, должен был бы найти для построения костей какое-либо иное, более удобное и
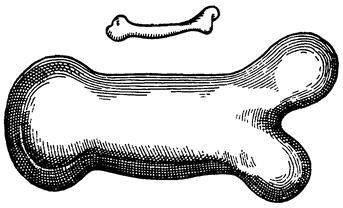 |
Симпличио. У меня есть достаточный повод усомниться, а именно, из-за огромной величины тела, встречаемой у рыб; так, например, кит равен по величине, если я не ошибаюсь, десяти слонам, и, однако, тело его все же держится.
Сальвиати. Ваше сомнение, синьор Симпличио, заставляет меня припомнить еще одно упущенное мною сначала из виду условие, при котором великаны и прочие огромные существа могут жить и двигаться не хуже малых животных. Вместо того, чтобы увеличивать толщину и прочность костей и других частей, предназначенных для поддержания собственного веса и веса прилегающих частей тела, можно, оставив строение и пропорцию костей прежними, уменьшить в значительной мере вес материи как самих костей, так и частей тела, к ним прилегающих и ими поддерживаемых. По этому второму пути и пошла природа в творении рыб, сделав их кости и части тела не только легкими, но и вовсе лишенными веса.
Симпличио. Хорошо вижу, к чему клонится ваша речь, синьор Сальвиати. Вы хотите сказать, что так как местопребыванием рыб является вода, которая в силу своей плотности или, как полагают другие, в силу своей тяжести отнимает вес у погруженных в нее тел, то материя, из коей состоят рыбы, теряя в воде вес, может держаться, не обременяя костей. {218} Однако этого для меня недостаточно, ибо хотя и можно предположить, что кости рыб не отягощаются телом, но материя самих костей, конечно, имеет вес. Кто же может утверждать, что ребро кита, величиною с добрую балку, не имеет достаточного веса и не пойдет ко дну в воде? И в телах такого большого размера, это, не должно было бы встречаться.
Сальвиати. Вы являетесь ярым оппонентом. Чтобы лучше возразить на наши доводы, я сначала предложу вам вопрос: видели ли вы когда-нибудь рыб в спокойной и неподвижной воде, не опускающимися ко дну, не поднимающимися на поверхность и не делающими никаких движений?
Симпличио. Это всем известное явление.
Сальвиати. Но если рыбы могут пребывать в воде без всякого движения, то это является неоспоримым доказательством того, что вся совокупность объема их тела равна по удельному весу воде; а так как в их теле существуют части более тяжелые, нежели вода, то необходимо прийти к заключению, что есть и другие части, которые легче воды и создают равновесие. Так как кости являются более тяжелыми, то мясо или другие какие-либо органы должны быть легче воды, и они-то своею легкостью отнимают вес у костей. Таким образом, в воде имеет место совершенно обратное тому, что мы видим у наземных животных: и то время как у последних кости должны нести свой вес и вес мяса, у водяных животных мясо поддерживает не только собственный вес, но и вес костей. Таким образом, нет ничего чудесного в том, что огромнейшие животные могут существовать в воде, но не на земле, т. е. в воздухе.
Симпличио. Я совершенно удовлетворен. Замечу только, что животные, обычно называемые наземными, с большим правом должны были бы носить название воздушных, так как на самом деле они живут в воздухе, окружены воздухом и дышат им.
Сагредо. Мне очень понравились рассуждения синьора Симпличио, его сомнения и их разрешение. Я заключаю отсюда, что если вытащить на берег одну из таких огромных рыб, то она не сможет долгое время держаться, так как связь между костями ее должна скоро порваться, а тело разрушиться.
Сальвиати. Я думаю то же самое. Подобное же, полагаю, должно случиться с большими кораблями, которые, плавая в море, выдерживают не только собственный вес, но и огромную тяжесть снастей, грузов и вооружения, будучи же выброшенными на берег и находясь в воздухе, разрушаются. Но продолжим наше исследование и докажем следующее: даны призма или цилиндр и указан как вес их, так и тот наибольший груз, который они сверх того могут выдержать; требуется найти наибольшую длину, достигнув которой призма или цилиндр сломаются от собственного веса. {219}
Положим, что дана призма АС и указан ее собственный вес, а также груз D у конца С — наибольший, который может выдержать призма; требуется определить, до какого предела мы можем увеличить длину этой призмы без того, чтобы она сломалась. Составим следующее отношение;
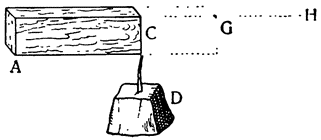 |
До сих пор мы рассматривали моменты и сопротивления твердых призм или цилиндров, один конец которых был закреплен неподвижно, к другому же прилагалась сила, будь то действующий вес стороннего
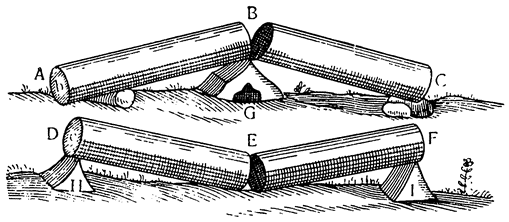
тела, или собственный вес, или и то и другое вместе. Теперь мы рассмотрим, что происходит с призмами и цилиндрами, имеющими точки опоры на концах или же одну точку опоры где-нибудь в середине. Прежде всего я утверждаю, что наибольшая длина цилиндра, при которой он способен выдерживать, не ломаясь, собственный вес, в том случае, если он имеет {220} точку опоры посредине или на обоих концах, превышает в два раза длину такого же цилиндра, вделанного в стену одним концом, следовательно, имеющего точку опоры лишь на одном конце. Это ясно само собою. Если дан цилиндр ABC, и половина его равна наибольшей длине АВ, могущей держаться, имея точку опоры в В, то она точно таким же образом будет держаться, имея опору в точке G, будучи уравновешиваема другой такой же половиной ВС. Равным образом, если дан цилиндр DEF такой длины, что только половина его может держаться, будучи закрепленной на конце D и, следовательно, другая половина EF может держаться, будучи закрепленной на конце F, то, положив концы его D и F на опоры Н и I, мы получим цилиндр, который сломается при приложении в середине его Е малейшей силы или груза.
Более тонкого исследования требует решение следующего вопроса, при котором мы отвлекаемся от собственного веса тела: если имеются груз или сила, достаточные для того, чтобы, будучи приложенными в середине, сломать цилиндр, поддерживаемый на концах, то могут ли они произвести то же действие, будучи приложенными в какой-либо иной точке ближе к тому или другому концу. Так, например, если мы ломаем какую-либо палку, взяв ее руками за концы и упираясь коленом в середину, то достаточно ли будет той же силы, чтобы сломать ее, когда мы будем упираться коленом не в середину, а ближе к одному концу палки.
Сагредо. Мне кажется, что Аристотель затронул эту проблему в своих «Проблемах механики».
Сальвиати. Проблема, затронутая Аристотелем, не совсем та же; он задавался лишь вопросом, по какой причине требуется меньшее усилие для того, чтобы переломить палку, держа ее за концы, т. е. достаточно далеко от колена, нежели взяв ее руками ближе к колену, и указал общую причину, сведя случай к действию более длинного рычага, так как плечи последнего увеличиваются по мере приближения к концам палки17. Наш же вопрос заключает в себе и кое-что новое: мы исследуем, держа постоянно палку за концы, требуется ли одна и та же сила для того, чтобы сломать палку при различных положениях колена — в середине и ближе к концам.
Сагредо. На первый взгляд кажется, что ответить надо утвердительно, так как оба рычага как бы сохраняют тот же момент, ибо на сколько укорачивается один рычаг, на столько же удлиняется другой.
Сальвиати. Вы увидите сейчас, как легко впасть в заблуждение, и сколько нужно осмотрительности и осторожности, чтобы избегнуть ошибок. То, что вы говорите, и что действительно на первый взгляд кажется столь правдоподобным, при пристальном рассмотрении оказывается совершенно ложным. Помещается ли колено, представляющее точку опоры рычага, в середине или другом месте, имеет столь большое значение, {221} что силы, производящей излом в первом случае, будет недостаточно, чтобы сломать палку при другом положении колена, иной раз даже если ее увеличить в десять, сто и тысячу раз. Рассмотрим сперва этот вопрос в общем виде, а затем перейдем к определению того, как изменяется сила, необходимая для излома, в зависимости от места ее положения.
Начертим, во-первых, деревянный брус АВ, который мы хотели бы переломить пополам над точкою опоры С, и, во-вторых, точно такой же брус, обозначенный буквами DE, который требуется переломить над точкою опоры F, удаленной от середины. Прежде всего, ясно, что вследствие равенства расстояний АС и СВ сила распределяется между концами В и А также поровну. Далее ясно, что так как расстояние DF меньше расстояния АС, то момент силы, приложенной в D, будет меньше момента той же силы, приложенной в А и действующей на плечо СА, и тем меньше, чем меньше DF по сравнению с АС; вследствие этого необходимо увеличить силу для того, чтобы преодолеть сопротивление в F. Но расстояние DF может быть бесконечно уменьшено по сравнению с расстоянием АС; отсюда неизбежно вытекает необходимость бесконечного увеличения силы, прилагаемой в D для преодоления
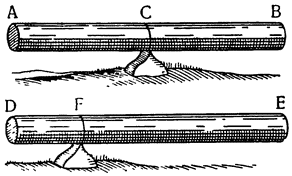 |
Сагредо. Что мы с вами скажем на это, синьор Симпличио? Не должны ли мы признать, что геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать? Не прав ли был Платон, требуя от своих учеников прежде всего основательного знакомства с математикой? Я прекрасно понимал закон рычага и то, что в меру увеличения или уменьшения его длины возрастает и убывает момент силы или сопротивления; при всем том в решении данной проблемы я допустил ошибку и притом не малую, а бесконечно большую. {222}
Симпличио. Действительно, я начинаю сознавать, что логика, представляющая прекрасное средство для правильного построения наших рассуждений, не может направлять мысль с изобретательностью и остротой геометрии.
Сагредо. Мне кажется, что логика учит нас познавать, правильно ли сделаны выводы из готовых уже рассуждений и доказательств; но чтобы она могла научить нас находить и строить такие рассуждения и доказательства — этому я не верю19. Но, пожалуй, теперь лучше всего будет, если синьор Сальвиати покажет нам, в какой мере увеличиваются моменты сил, необходимых для того, чтобы преодолеть сопротивление одного и того же тела, в зависимости от места разлома.
Сальвиати. Искомые отношения могут быть найдены следующим образом: если по длине какого-либо цилиндра наметить две точки, в которых мы желаем сломать этот цилиндр, то сопротивления в этих точках находятся между собой в отношении, обратном отношению и прямоугольников, построенных на расстояниях этих точек от концов цилиндра.
Пусть А и В наименьшие силы, необходимые для того, чтобы сломать цилиндр в точке С, а Е и F также наименьшие силы, ломающие в точке D. Утверждаю, что силы А и В относятся к силам Е и F, как прямоугольник ADB к прямоугольнику АСВ. Так как отношение сил А и В к силам Е и F равно составному отношению сил А и В к силе В, силы В — к силе F и силы F — к F и Е, и так как отношение сил А и В к В равно отношению длины В А к АС, отношение силы В к F равно отношению линий DB и ВС, а отношение силы F к F и Е равно отношению линий DA и АВ, то, следовательно, отношение сил А и В к F и Е является составным из трех, именно: отношений прямых ВА к AC, DB к ВС и DA к АВ. Но
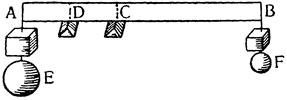 |
На основании этой теоремы мы можем теперь разрешить одну довольно интересную задачу: дан наибольший груз, который могут выдержать призма или цилиндр в середине, т. е. там, где сопротивление излому всего меньше, и дан другой, больший груз; требуется найти такую точку, для которой последний груз был бы как раз наибольшим. {223}
Положим, что мы имеем груз, превышающий тот наибольший груз, который может быть выдержан при помещении его в середине цилиндра АВ, и пусть этот первый груз так относится к последнему, как линия Е к линии F. Требуется найти такую точку цилиндра, для которой данный груз является наибольшим. Пусть средней пропорциональной между линиями Е и F будет G и пусть отношение Е
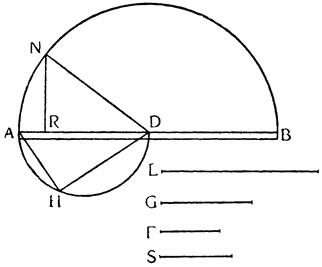 |
как на диаметре полукруг ANB, восставим из точки R перпендикуляр RN и проведем прямую ND. Так как сумма квадратов NR и RD равна квадрату ND, т. е. квадрату AD или сумме квадратов АН и HD, а квадрат HD равен квадрату DR, то, следовательно, квадрат NR, равный прямоугольнику ARB, будет равняться квадрату АН, т. е. квадрату S. Но квадрат S относится к квадрату AD как F к Е или как наибольший груз для средней точки D к данному нам большему грузу; следовательно, этот больший груз является для точки R максимальным, какой она только может выдержать, а это мы и хотели найти21.
Сагредо. Прекрасно понимаю и замечу следующее: так как призма АВ становится все прочнее и выносливее по отношению к нагрузке по мере удаления последней от середины, то у больших и тяжелых балок можно снять немалую часть материала ближе к концам, облегчив значительно их вес, что при перекрытии больших помещений могло бы иметь большое значение и принести немалую пользу. Интересно было бы найти, какую форму должно иметь такое твердое тело, которое во всех своих частях обладало бы одинаковым сопротивлением так, чтобы переломить его грузом, приложенным в середине, было бы не легче, чем приложенным в любом другом месте.
Сальвиати. Я только что собирался сообщить вам по этому вопросу нечто достаточно существенное и довольно изящное. Для большей наглядности я нарисую вам чертеж. Пусть DB будет призма, у которой сопротивление конца AD излому под действием силы, приложенной к концу В, будет во столько раз меньше сопротивления в сечении {224} CI, во сколько раз длина СВ меньше длины ВА, как это уже было доказано. Представим себе теперь эту призму рассеченной диагональной плоскостью вдоль линии FB так, что боковые грани новой призмы будут представлять собою треугольники, одним из коих, обращенным к нам, является треугольник FAB. Мы получим теперь тело, которое в противоположность первой призме легче сломается в месте С, нежели в месте А под действием силы, приложенной на конце В, и притом во столько раз легче, во сколько длина СВ меньше длины ВА. Это очень легко доказать.
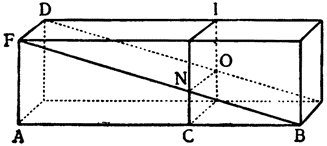 |
Симпличио. Это совершенно ясно, так как при переходе от большего к меньшему мы должны встретить и равное.
Сагредо. Да, но весь вопрос заключается в том, как надо направлять пилу, чтобы получить требуемое сечение.
Симпличио. Мне представляется, что сделать это довольно легко. Если, отнимая половину призмы при диагональном сечении, мы получаем остающееся тело, обладающее свойствами, противоположными свойствам целой призмы, так что во всех тех точках, в которых прочность последней увеличивается, прочность первой уменьшается, то я полагаю, {225} что, следуя средним путем, т. е. отнимая только половину половины, что составит четверть всей призмы, мы получим в остатке тело, прочность которого не будет ни увеличиваться, ни уменьшаться во всех тех точках, в которых увеличение и уменьшение прочности двух первых тел было постоянно одинаковым.
Сальвиати. Вы не угадали, синьор Симпличио. Я покажу вам и вы убедитесь, что та часть, которую мы можем отсечь и отнять от призмы, не уменьшая ее прочности, составляет не четверть, а треть ее. Нам надо (как уже заметил синьор Сагредо) найти линию, по которой должно быть сделано сечение: я докажу, что линией этой является парабола. Но предварительно необходимо будет доказать следующую лемму: если даны два коромысла весов или рычага, разделенные точками опоры таким образом, что длины плеч, на которые действуют силы, относятся между собою, как квадраты плеч, на которые действуют сопротивления, pi если сопротивления относятся друг к другу, как эти плечи, то силы, преодолевающие сопротивления, равны между собою.
Пусть даны два рычага АB и CD, разделенные точками опоры Е и F таким образом, что плечи ЕВ и FD относятся, как квадрат ЕА к квадрату FC, и предположим, что отношение сопротивлений в А и С равно отношению линий ЕА и FC. Утверждаю, что силы, приложенные в В и D и преодолевающие сопротивления в А и С, равны между собою. Отложим EG — среднюю пропорциональную между ЕВ и FD; тогда отношение BE к EG будет равно отношению GE к FD или АЕ к CF; так же относятся

друг к другу по условию и сопротивления в точках А и С, Так как, кроме того, EG относятся к FD, как АЕ к CF, то отношение GE к АЕ равно отношению FD к FC. Далее, оба рычага DC и GA разделены в точках F и Е пропорционально, почему сила, приложенная в D и преодолевающая сопротивление в точке C, будучи перенесена в точку G, сможет преодолеть то же по величине сопротивление C, перенесенное в точку А. Но по условию сопротивления А и С относятся друг к другу, как расстояния АЕ и CF или как BE и EG; следовательно, сила G или, лучше сказать, сила D, приложенная в В, преодолеет сопротивление в точке А, что и требовалось доказать. {226}
Доказав это положение, начертим на боковой грани FB призмы DB параболическую линию FNB с вершиною в точке В и оставим от призмы тело, ограниченное основанием AD, прямоугольником AG, прямой BG и поверхностью, искривленной соответственно параболе FNB. Утверждаю, что такое тело будет обладать во всех частях одинаковым сопротивлением. Рассечем тело плоскостью СО, параллельной AD, и представим себе два рычага с точками опоры в А и С, так что плечами первого из них будут ВА и AF, а второго — ВС и CN. Так как у параболы FBA отношение АВ и ВС равно отношению квадрата FA к квадрату CN, то ясно, что длина плеча ВА одного рычага относится к длине ВС плеча другого рычага как квадрат другого плеча FA к квадрату плеча CN. Поэтому сопротивление, преодолеваемое рычагом ВА, будет относиться к сопротивлению, преодолеваемому рычагом ВС, так же, как относятся друг к другу площади прямоугольников DK и ОС, т. е. как линии AF и NC, являющиеся другими плечами рычагов; отсюда на основании только что доказанной леммы явствует, что та же самая сила, которая, будучи приложена к линии BG, преодолевает сопротивление DA, преодолеет и сопротивление СО. То же самое можно доказать и относительно сечения в любом другом месте, из чего следует, что такое параболическое тело во всех своих частях одинаково прочно. То обстоятельство, что, разрезая призму по параболической линии FNB, мы отнимаем от нее третью часть, видно из следующего: половина параболы FNBA и прямоугольник FB суть основания двух тел, ограниченных двумя параллельными плоскостями, а именно, прямоугольниками FB и DG; объемы их сохраняют то же отношение, какое существует между основаниями; но прямоугольник FB в полтора раза больше полупараболы FNBA; поэтому, разрезая призму по параболической линии, мы отнимаем от нее третью часть. Отсюда ясно, что мы можем уменьшать вес балок более чем на тридцать три процента, нисколько не вредя их прочности; это обстоятельство может привести большую пользу при постройке крупных судов, в особенности при укреплении перекрытий, так как в сооружениях этого рода легкость имеет огромное значение22.
Сагредо. Случаев, где это полезно, столь много, что затруднительно и даже невозможно все их перечислить. Оставляя их, однако, в стороне, я желал бы убедиться, что уменьшение веса действительно происходит в указанном отношении. То, что сечение призмы по диагонали уменьшает вес ее наполовину, я прекрасно себе представляю, но то, что сечение по параболе отнимает третью часть, я могу принять на веру со слов синьора Сальвиати, всегда правдивого; но здесь знание было бы для меня предпочтительнее веры.
Сальвиати: Итак, вы желаете иметь доказательство того, что часть призмы, отсекаемая по параболе, составляет треть призмы. Я {227} однажды уже дал такое доказательство; попробую восстановить в памяти ход рассуждения, для которого, насколько помнится, я воспользовался следующей известной леммой Архимеда, содержащейся в его книге «О спиралях»: если имеется любое число линий, превышающих одна другую по длине на некоторую одинаковую величину, равную наименьшей из них, и такое же число линий, равных наибольшей из них, то сумма квадратов этих последних линий будет составлять менее чем утроенную сумму квадратов первых, отличающихся друг от друга
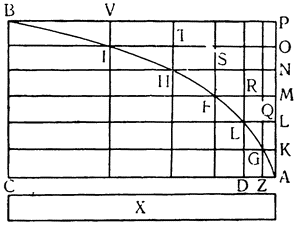 |
Сагредо. Остановитесь прошу вас. Я не вижу, почему избыток площади описанной фигуры над площадью треугольника будет значительно меньше площади прямоугольника ВО.
Сальвиати. Не равен ли прямоугольник ВО сумме всех прямоугольников, через которые проходит наша парабола, т. е. прямоугольников BI, IH, HF, FE, EG и GA, частично выходящих за пределы смешанного треугольника? А прямоугольник ВО не меньше ли, по нашему условию, нежели площадь X? Если, таким образом, треугольник вместе с площадью X будет равен третьей части прямоугольника СР, то описанная фигура, прибавляющая к площади треугольника меньше, нежели {228} площадь X, останется меньшею по сравнению с третьей частью того же прямоугольника СР. Но этого не может быть, так как она составляет более трети прямоугольника; следовательно, наше предположение, что площадь смешанного треугольника меньше трети прямоугольника, неправильно.
Сагредо. Вы разрешили мои сомнения. Но остается доказать, что описанная фигура составляет более трети площади прямоугольника СР, что, думается мне, не так-то легко сделать.
Сальвиати. Но и не так трудно. В параболе отношение квадратов линий DE и ZG равно отношению линий DA и AZ, которое одинаково с отношением прямоугольника КЕ к прямоугольнику AG (так как высоты АК и KL равны); следовательно, квадраты ED и ZG относятся между собою, как квадраты LA и АК или как прямоугольник КЕ и KZ. Совершенно таким же образом доказывается относительно других прямоугольников LF, МН, NI и ОВ, что они относятся друг к другу, как квадраты линий MA, NA, ОА и РА. Обратим теперь внимание на то, что описанная фигура составлена из частей, отношение между которыми равно отношению квадратов линий, последовательно превышающих одна другую на величину, равную меньшей из них, и что прямоугольник СР составлен из такого же числа площадей, из коих каждая равна наибольшей части, т. е. прямоугольнику ОВ. Согласно лемме Архимеда, описанная фигура составит, таким образом, больше трети прямоугольника СР; но в то же время она была и меньше, что, очевидно, невозможно. Поэтому смешанный треугольник не может быть меньше одной трети прямоугольника СР. Утверждаю равным образом, что он и не более трети. Предположим, что он более трети и что площадь X равна излишку площади треугольника над третью площади прямоугольника СР. Производя последовательное деление всего прямоугольника на все меньшие равные между собою прямоугольники, получим, наконец, такие части, которые будут менее площади X. Предположим, что мы это сделали и получили прямоугольник ВО, который меньше X. Проведя такие же линии, как и ранее, мы получим фигуру, вписанную в смешанный треугольник и составленную из прямоугольников VO, TN, SM, RL и QK, которая будет все же не меньше трети большего прямоугольника СР. Смешанный треугольник превосходит вписанную фигуру на меньшую величину, чем он превосходит третью часть прямоугольника СР, потому что излишек площади треугольника над третью прямоугольника СР равен площади X, которая больше прямоугольника ВО, последняя же, в свою очередь, больше излишка площади треугольника над вписанной фигурою; действительно, площадь прямоугольника ВО равняется сумме площадей прямоугольника AG, GE, EF, FH, HI и IB, а у последних лишь часть, меньшая половины, равняется излишку треугольника над вписанной фигурой. Так как треугольник {229} превышает третью часть прямоугольника СР на величину большую (а именно, на величину X), вписанную же фигуру на величину меньшую, то эта фигура должна быть больше трети прямоугольника СР; но, по принятой нами лемме, она меньше последней, ибо прямоугольник СР, как совокупность всех наибольших прямоугольников, относится к прямоугольникам, образующим вписанную фигуру, как сумма квадратов всех наибольших линий к сумме квадратов линий, последовательно превышающих друг друга на определенную величину, за вычетом из последней квадрата наибольшей линии. Далее, вся совокупность наибольших прямоугольников (составляющих в сумме прямоугольник СР) превышает более чем в три раза сумму прямоугольников, последовательно увеличивающихся и составляющих вписанную фигуру, за вычетом из этой суммы наибольшего прямоугольника. Следовательно, смешанный треугольник не может быть ни меньше, ни больше трети прямоугольника СР и должен быть равен ей.
Сагредо. Прекрасное и остроумное доказательство, особенно ценное тем, что оно дает и квадратуру параболы, показывая, что площадь таковой равняется четырем третям вписанного треугольника, как это доказал еще Архимед двумя различными, но равно заслуживающими удивления способами. В последнее время то же было доказано Лукою Валерио — новым Архимедом нашей эпохи; доказательство это можно найти в книге, которую он написал о центре тяжести твердых тел.
Сальвиати. Книга эта действительно замечательна и не уступает сочинениям наиболее известных геометров как современных, так и прошлого времени. Когда наш Академик познакомился с нею, то он оставил свои собственные исследования, начатые по тому же предмету, так как нашел, что все вопросы уже разрешены и доказаны чрезвычайно удачно синьором Валерио.
Сагредо. Обо всем этом я был осведомлен самим Академиком. Я просил его хоть раз ознакомить меня с доказательствами, которые он нашел до знакомства с книгою синьора Валерио, но просьба моя осталась безуспешною.
Сальвиати. У меня имеется копия его работы, и я могу показать ее вам, вы сумеете оценить различие методов, которыми пользуются эти два автора при исследовании и доказательстве одних и тех же положений, причем некоторые положения разъясняются по-разному, хотя и одинаково верно.
Сагредо. Мне очень хотелось бы видеть эту работу, и я был бы очень вам благодарен, если бы вы принесли ее с собою, когда мы снова соберемся для беседы24. Так как, однако, сопротивление твердой призмы, ограниченной сечением, проведенным по параболе, представляется явлением не только весьма интересным, но и полезным для многих механических {230} приспособлений, то было бы интересно дать мастерам какие-либо простые и удобные правила для того, чтобы вычерчивать на грани призмы параболическую линию.
Сальвиати. Существует много способов начертить такую линию, но я познакомлю вас только с двумя наиболее простыми. Один из них действительно изумителен, так как, пользуясь им, в меньшее время, чем то, за которое другие вычерчивают на бумаге циркулем четыре или шесть окружностей разного диаметра, могу начертить тридцать-сорок параболических линий не менее тонких, точных и правильных, чем упомянутые окружности. У меня имеются бронзовый шарик, весьма правильной формы, величиною не более ореха. Брошенный на металлическое зеркало, лежащее не совсем горизонтально, но несколько наклонно, так что при движении он может по нему катиться, производя при этом легкое давление, шарик этот оставляет след в виде тонкой и правильной параболической линии, более длинной или более короткой, смотря по степени наклона металлической плоскости. Здесь мы имеем ясный и наглядный опыт, показывающий, что движение брошенных тел происходит по параболическим линиям,— явление, впервые замеченное нашим другом, который дал ему и доказательство в своей книге о движении, с чем мы познакомимся в нашей следующей беседе. Шарик, вычерчивающий указанным выше образом параболы, необходимо предварительно подержать в руке и тем согреть и увлажнить его для того, чтобы он оставил затем на металлическом зеркале ясные следы. Другой способ начертить искомую параболу на призме состоит в следующем. Вобьем в стену два гвоздя на одинаковой высоте над горизонтом и на таком расстоянии друг от друга, чтобы оно равнялось двойной ширине прямоугольника, на котором желательно построить полупараболу; между одним и другим гвоздем подвесим тонкую цепочку, которая свешивалась бы вниз и была такой длины, чтобы самая низкая точка ее находилась от уровня гвоздя на расстоянии, равном длине призмы. Цепочка эта, свисая, расположится в виде параболы, так что, отметив ее след на стене пунктиром, мы получим полную параболу, рассекаемую пополам перпендикуляром, проведенным через середину линии, соединяющей оба гвоздя. Перевести полученную таким образом линию на боковые грани призмы не представит никаких затруднений; всякий посредственный мастер сумеет это сделать. Можно также и прямо нанести на призме параболическую линию по точкам при помощи геометрических линий, обозначенных на циркуле нашего друга25.
Мы получили уже столько выводов, касающихся вопросов сопротивления твердых тел излому, причем в основание этой науки было положено сопротивление тел разрыву, что можем теперь последовательно подвигаться вперед, открывая все новые и новые соотношения, которых в природе существует бесконечное множество, и давая им доказательства. {231}
В заключение нашей сегодняшней беседы мне хотелось бы только прибавить несколько замечаний относительно сопротивления полых твердых тел, которыми как мастерство, так и природа пользуются на тысячи ладов. В них без возрастания веса достигается возрастание прочности в весьма большой степени, как то легко можно видеть на костях птиц и на тростнике, которые при большой легкости отличаются и большой сопротивляемостью изгибу и излому. Если бы соломинка, несущая колос, превышающий по весу весь стебель, была бы при том же количестве вещества сплошной и массивной, то она была бы значительно менее прочной на изгиб и на излом. Было замечено на деле и подтверждено опытом, что палка, пустая внутри, а также деревянная и металлическая труба, крепче, чем массивное тело той же длины и равного веса, которое неизбежно является более тонким. Мастерство нашло применение этому наблюдению при изготовлении копий для достижения прочности и вместе с тем легкости. Докажем такое положение: сопротивления двух цилиндров одинакового объема и равной длины, один из которых полый, а другой массивный, относятся друг к другу, как их диаметры.
Пусть АЕ будет труба или полый цилиндр и IN массивный цилиндр, равные по весу и по длине. Утверждаю, что сопротивление излому трубы АЕ так относится к сопротивлению сплошного цилиндра IN, как диаметр АВ к диаметру IL. Это в достаточной степени очевидно. Так как труба и цилиндр IN равны по длине и по объему, то круг IL — основание цилиндра — будет равен кольцу АВ — основанию трубы АЕ (называю меньшего
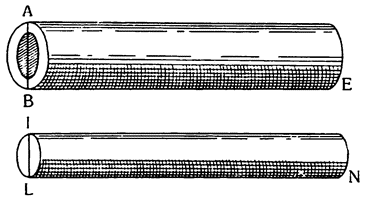 |
Задача эта чрезвычайно проста. Пусть линии АВ — диаметр трубы, a CD — диаметр отверстия. Проведем в большом круге из точки А линию АЕ, равную диаметру CD, и соединим точки Е и В. Так как в полукруге АЕВ угол Е прямой, то круг, диаметром коего является линия АВ, будет равен двум кругам с диаметрами АЕ и ЕВ. Но АЕ есть диаметр отверстия
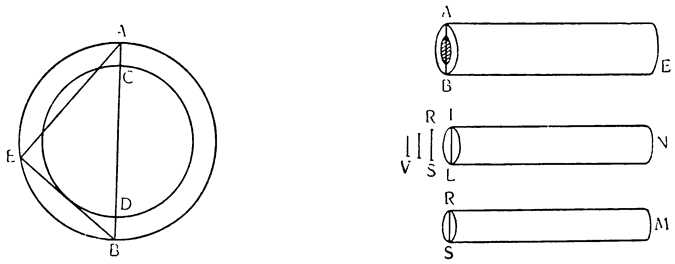
трубы; следовательно, круг диаметра ЕВ будет равен кольцу ACBD; поэтому сплошной цилиндр, основанием которого будет круг диаметра ЕВ, будет по весу равняться трубе равной с ним длины. Доказав это, можно легко найти, какое отношение существует между сопротивлением излому трубы и цилиндра произвольной величины, но одинаковой длины. Даны труба ABE и цилиндр RSM одинаковой длины; требуется найти, какое отношение существует между сопротивлением того и другого. На основании предыдущего предложения находим размеры цилиндра ILN, равного трубе по весу и длине. Пусть теперь четвертой пропорциональной к линиям IL и RS (диаметрам оснований цилиндров IN и RM) будет линия F. Утверждаю, что сопротивление трубы АЕ относится к сопротивлению цилиндра RM, как линия АВ к V. Так как труба АЕ равна по весу и по длине цилиндру IN, то сопротивление трубы относится к сопротивлению этого цилиндра, как линия АВ к IL; но сопротивление цилиндра IN относится к сопротивлению цилиндра RM, как куб IL к кубу RS, т. е. как линия IL к V; следовательно, ex aequali, сопротивление трубы АЕ относится к сопротивлению цилиндра RM, как линия АВ к V, что и требовалось доказать27.
Конец второго дня
| {233} |
М |
Наш трактат распадается на три части. В первой мы рассматриваем единообразное или равномерное движение. Во второй мы описываем естественное ускоренное движение. В третьей речь идет о принужденном движении или о движении брошенных тел.
| {234} |
Прежде всего нам необходимо определить движение равномерное или единообразное.
Определение
Движением равномерным или единообразным я называю такое, при котором расстояния, проходимые движущимся телом в любые равные промежутки времени, равны между собою.
Пояснение
К существовавшему до сего времени определению (которое называло движение равномерным просто при равных расстояниях, проходимых в равные промежутки времени) мы прибавили слово «любые», обозначая тем какие угодно равные промежутки времени, так как возможно, что в некоторые определенные промежутки времени будут пройдены равные расстояния, в то время как в равные же, но меньшие части этих промежутков пройденные расстояния не будут равны2. Данное выше определение связано с четырьмя аксиомами, а именно:
Аксиома I
Расстояние, проходимое при одном и том же равномерном движении в более продолжительное время, больше, нежели проходимое в менее продолжительное время.
Аксиома II
Время, соответствующее при равномерном движении большему расстоянию, больше, нежели соответствующее меньшему расстоянию.
Аксиома III
При большей скорости движения в равные промежутки времени проходятся большие расстояния, нежели при меньшей.
Аксиома IV
Скорость, при которой за определенное время проходится большее расстояние, больше той, при которой за то же время проходится меньшее расстояние.
| {235} |
Теорема I. Предложение I3
Если равномерно движущееся тело проходит с постоянной скоростью два расстояния, то промежутки времени прохождения последних относятся между собой как пройденные расстояния.
Пусть тело, движущееся с постоянной скоростью, проходит два расстояния АВ и ВС и пусть время, потребное для прохождения АВ, представлено линией DE, а для прохождения ВС — линией EF. Утверждаю,

что как АВ относится к ВС, так же относится и время DE к EF. Продолжим в обе стороны как расстояние, так и время до G, Н и I, К и отложим на линии AG произвольное число частей, равных расстоянию АВ, а на линии DI столько же частей, равных времени DE; далее, отложим по другую сторону на линии СИ любое число частей, равных расстоянию ВС, а на FK столько же частей, равных времени EF. Таким образом, расстояние BG и время EI будут произвольными, но равными кратными ВА и ED; подобным же образом расстояние ИВ и время КЕ будут произвольными, но равными кратными СВ и FE. Так как DE есть время, потребное для прохождения расстояния АВ, то весь промежуток времени EI будет соответствовать всему расстоянию BG, и EI будет содержать столько же частей времени, равных DE, сколько частей расстояния, равных ВА, содержится в BG; подобным же образом находим, что КЕ есть время, необходимое для прохождения расстояния ИВ. Если принять теперь, что движение равномерно и что GB равно ВН, то и время IE будет равно ЕК; если GB будет больше ВН, то и IE будет больше ЕК, если же оно будет меньше, то и время будет меньше. Таким образом, имеются четыре величины: первая — АВ, вторая — ВС, третья — DE и четвертая — EF; первая и третья из них, т. е. часть расстояния, равная АВ, и времени, равная DE, содержатся в произвольном, но одинаковом числе в расстоянии GB и времени IE. Мы доказали, однако, что эти последние либо одновременно равны расстоянию ВН и времени ЕК, либо одновременно больше или меньше; поэтому вторая и четвертая величины имеют то же отношение. Отсюда следует, что отношение первой величины ко второй, т. е. расстояния АВ к расстоянию ВС, равно отношению третьей к четвертой, т. е. времени DE ко времени EF, что и требовалось доказать.
| {236} |
Теорема II. Предложение II
Если тело проходит два расстояния в равные промежутки времени, то эти расстояния относятся между собою как скорости движения. Обратно, если расстояния относятся друг к другу как скорости, то промежутки времени равны.
Пусть на том же самом чертеже АВ и ВС будут расстояниями, пройденными в одинаковое время с разными скоростями, а именно: АВ со скоростью DE и ВС со скоростью EF. Утверждаю, что расстояния АВ и ВС относятся между собою как скорости DE и EF. Если взять, как то было показано выше, произвольные, но равные кратные расстояния и скорости, т. е. GB и IE, составленные из отрезков; первое — равных АВ, авторов — DE, а также аналогичные линии НВ и KF, составленные из отрезков ВС и EF, то, следуя путем, подобным изложенному выше, придем к заключению, что составные отрезки GB и IE одновременно либо равны отрезкам ВН и ЕК, либо больше их, либо меньше; этим и доказывается предложение.
Теорема III. Предложение III
При неравных скоростях, но равных пройденных расстояниях, отношение скоростей равно обратному отношению промежутков времени.
Пусть А и В скорости — А б&оacute;льшая и В меньшая, — с которыми было
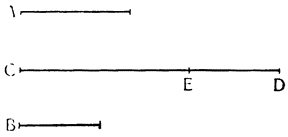 |
Теорема IV. Предложение IV
Если два равномерно движущихся тела имеют различные скорости, то отношение расстояний, пройденных ими в неравные промежутки времени, равно составному отношению скоростей и промежутков времени. {237}
Пусть два тела Е и F движутся равномерно, причем отношение скорости движения тела Е к скорости движения тела F равно отношению
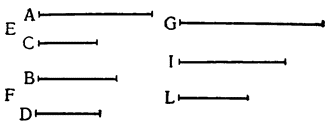 |
Теорема V. Предложение V
Если два тела движутся равномерно с различными скоростями, и пройденные ими расстояния также различны, то отношение промежутков времени, затрачиваемых на прохождение последних, равно отношению расстояний, умноженному на обратное отношение скоростей.
Даны два тела А и В, скорости которых относятся как V к T, а пройденные ими расстояния — как S к R. Утверждаю, что отношение времени
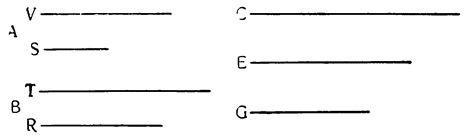 |
Теорема VI. Предложение VI
Если два тела движутся равномерно, то отношение скоростей их равняется отношению пройденных расстояний, умноженному на обратное отношение времен движения.
Пусть тела А и В движутся равномерно, и пройденные расстояния относятся друг к другу как V к Т, времена же движения,— как S к В.
Утверждаю, что отношение скоростей тел А и В равно отношению V к Т, умноженному на отношение В к S. Пусть С есть скорость, с которою тело А проходит расстояние V в течение времени S, и пусть С относится к Е как расстояние V к Т. В таком случае Е будет скорость, с которою тело В проходит расстояние Т в то же самое время S. Если, далее, отношение Е к G равно отношению времени В к S, то G будет тою скоростью, с которою тело В проходит расстояние Т в течение времени В. Таким образом, мы имеем скорость С, с которою тело А проходит расстояние V в течение времени S, скорость G, с которою тело В проходит расстояние Т в течение времени В, и отношение С к G, равное отношению С к Е, умноженному на отношение Е к G; по отношению С к Е равно отношению расстояния V к Т, а отношение Е к G — отношению времени В к S; следовательно, задача решена.
Сальвиати. Вот то, что написал наш Автор о равномерном движении. Теперь мы перейдем к более тонким и новым рассмотрениям, относящимся к естественному ускоренному движению, каковым вообще является движение падающих тяжелых тел. Вот заголовок и введение.
До сих пор мы имели дело с равномерным движением, теперь же переходим к движению ускоренному.
Прежде всего необходимо будет подыскать этому естественному явлению соответствующее точное определение и дать последнему объяснение. Хотя, конечно, совершенно допустимо представлять себе любой вид движения и изучать связанные с ним явления (так, например, можно определять {239} основные свойства винтовых линий или конхоид, представив их себе возникающими в результате некоторых движений, которые в действительности в природе не встречаются, но могут соответствовать предположенным условиям), мы тем не менее решили рассматривать только те явления, которые действительно имеют место в природе при падении тел, и даем определение ускоренного движения, совпадающего со случаем естественно ускоряющегося движения. Такое определение, найденное после долгих размышлений, кажется нам достойным доверия преимущественно на том основании, что результаты опытов, воспринимаемые нашими чувствами, вполне соответствуют выведенным из него свойствам. Наконец, к исследованию естественного ускоренного движения нас непосредственно привело внимательное наблюдение того, что обычно имеет место и совершается в природе, которая стремится применять во всяких своих приспособлениях самые простые и легкие средства: так, я полагаю, например, что никто не станет сомневаться в невозможности осуществить плавание или полет легче или проще, нежели теми способами и средствами, которыми пользуются благодаря своему природному инстинкту рыбы и птицы.
Поэтому когда я замечаю, что камень, выведенный из состояния покоя и падающий со значительной высоты, приобретает все новое и новое приращение скорости, не должен ли я думать, что подобное приращение происходит в самой простой и ясной для всякого форме? Если мы внимательно всмотримся в дело, то найдем, что нет приращения более простого, чем происходящее всегда равномерно. К такому заключению мы легко придем, подумав о сродстве понятий времени и движения. Подобно тому, как равномерность движения мыслилась и определялась нами посредством равенства времени и расстояния (ибо мы называли равномерным такое движение, при котором в равные промежутки времени проходятся и равные расстояния), и приращение скорости мы проще всего можем представить себе, как происходящее в соответствии с такими же равными промежутками времени. Умом своим мы можем признать такое движение единообразным и неизменно равномерно ускоряющимся, так как в любые равные промежутки времени происходят и равные приращения скорости. Таким образом, если взять совершенно равные промежутки времени от начального мгновения движения тела, вышедшего из состояния покоя и падающего вниз, то скорость, приобретенная в течение первого промежутка, испытав приращение в течение второго, возрастет вдвое; за три промежутка времени величина ее станет тройною, а за четыре — в четыре раза большею против первоначальной. Яснее говоря, если бы тело продолжало движение по истечении первого промежутка времени равномерно с приобретенною скоростью, то оно двигалось бы в два раза медленнее, нежели если бы обладало скоростью, приобретенной после двух промежутков {240} времени. Таким образом, мы не ошибемся, если поставим увеличение скорости в соответствии с увеличением промежутка времени. Отсюда и вытекает определение движения, которым мы будем пользоваться: равномерно или единообразно-ускоренным движением называется такое, при котором после выхода из состояния покоя в равные промежутки времени прибавляются и равные моменты скорости4.
Сагредо. Так как мой ум вообще не мирится с различными определениями, даваемыми теми или иными авторами, поскольку они все совершенно произвольны, то я могу, никого не задевая, высказать сомнение, действительно ли приведенное определение, установленное совершенно отвлеченно, правильно и соответствует тому ускоренному движению, которое проявляется при естественном падении тяжелых тел. А так как Автор утверждает, по-видимому, что естественное движение падающих тяжелых тел именно таково, как он его определил, то мне хотелось бы, чтобы были устранены некоторые появившиеся у меня сомнения, после чего я с большим вниманием мог бы отнестись ко всем предложениям и сопровождающим их доказательствам.
Сальвиати. Прекрасно; в таком случае вы и синьор Симпличио потрудитесь высказать ваши затруднения. Я предполагаю, что они совпадают с теми, которые явились и у меня, когда я впервые познакомился с настоящим трактатом, и которые частью были разрешены Автором при моей беседе с ним, частью исчезли в результате собственных размышлений.
Сагредо. Если я представлю себе тяжелое падающее тело выходящим из состояния покоя, при котором оно лишено какой-либо скорости, и приходящим в такое движение, при котором скорость его увеличивается пропорционально времени, истекшему с начала движения, так что за восемь ударов пульса оно приобретает восемь градусов скорости, в то время как за четыре удара пульса оно приобретает таких градусов только четыре, за два удара — два, а за один удар — один, то невольно приходит на мысль, не вытекает ли отсюда, что благодаря возможности делить время без конца мы, непрерывно уменьшая предшествующую скорость, придем к любой малой степени скорости или, скажем, любой большей степени медленности, с которой тело должно двигаться по выходе его из состояния бесконечной медленности, т. е. из состояния покоя. Таким образом, если с той степенью скорости, которую тело приобретает за четыре удара пульса и которая в дальнейшем остается постоянной, оно может проходить две мили в час, а с той степенью скорости, которая приобретается после двух ударов пульса, оно может проходить одну милю в час, то надлежит признать, что для промежутков времени, все более и более близких к моменту выхода тела из состояния покоя, мы придем к столь медленному движению, что при сохранении постоянства скорости {241} тело не пройдет мили ни в час, ни в день, ни в год, ни даже в тысячу лет; даже в большее время оно не продвинется и на толщину пальца,— явление, которое весьма трудно себе представить, особенно, когда наши чувства показывают, что тяжелое падающее тело сразу же приобретает большую скорость5.
Сальвиати. Это одно из тех затруднений, которые первоначально смущали и меня; однако я скоро его устранил, причем в этом мне помог тот же самый опыт, который зародил в вас сомнение. Вы говорите, что опыт показывает, будто падающее тело сразу получает весьма значительную скорость, как только выходит из состояния покоя; я же утверждаю, основываясь на том же самом опыте, что первоначальное движение падающего тела хотя бы весьма тяжелого, совершается с чрезвычайной медленностью. Положите тяжелое тело на какое-нибудь мягкое вещество так, чтобы оно давило на последнее всей своей тяжестью. Ясно, что это тело, поднятое вверх на локоть или на два, а затем брошенное с указанной высоты на то же вещество, произведет при ударе давление большее, чем в первом случае, когда давил один только вес тела. В этом случае действие будет произведено падающим телом, т. е. совместно его весом и скоростью, приобретенной при падении, и будет тем значительнее, чем с большей высоты наносится удар, т. е. чем больше скорость ударяющего тела. При этом скорость падающего тяжелого тела мы можем без ошибки определить по характеру и силе удара. Теперь скажите мне, синьоры, если груз, падающий на сваю с высоты четырех локтей, вгоняет последнюю в землю приблизительно на четыре дюйма, — при падении с высоты двух локтей он вгоняет ее в землю меньше и, конечно, еще меньше при падении с высоты одного локтя или одной пяди, и когда, наконец, груз падает с высоты не более толщины пальца, то производит ли он на сваю больше действия, чем если бы он был положен без всякого удара? Еще меньшим и совершенно незаметным будет действие груза, поднятого на толщину листка. Так как действие удара находится в зависимости от скорости ударяющего тела, то кто может сомневаться в том, что движение чрезвычайно медленно и скорость минимальна, если действие удара совершенно незаметно? Вы видите теперь, какова сила истины; тот самый опыт, который с первого взгляда порождает одно мнение, при лучшем рассмотрении учит нас противному. Но мне кажется, что, и не прибегая к такому опыту (который, без сомнения, является в высшей степени убедительным), нетрудно установить ту же истину путем простого рассуждения. Предположим, что мы имеем тяжелый камень, поддерживаемый в воздухе в состоянии покоя; лишенный опоры и отпущенный на свободу, он, будучи тяжелее воздуха, начнет падать вниз, причем движение его будет не равномерным, но сперва медленным, а затем постепенно ускоряющимся. А так как скорость может увеличиваться и уменьшаться до бесконечности, то что может заставить {242} меня признать, будто такое тело, выйдя из состояния бесконечной медленности (каковым именно является состояние покоя), сразу приобретает скорость в десять градусов скорее, чем в четыре, или в четыре градуса скорее, чем в два градуса, в один, в полградуса, в одну сотую градуса, словом, скорее, чем любую бесконечно малую скорость? Заметьте, пожалуйста, следующее. Я не думаю, чтобы вы стали возражать мне против того положения, что приобретение степеней скорости падающим камнем может происходить в том же порядке, как уменьшение и потеря степеней скорости, когда тот же камень подброшен снизу вверх до той же высоты какой-либо силой. Но если это так, то я не вижу, как можно сомневаться в том, что при уменьшении и, наконец, полном уничтожении скорости подымающегося вверх камня последний может прийти в состояние покоя ранее, нежели пройдя через все степени медленности.
Симпличио. Но если степени все большей и большей медленности бесчисленны, то они никогда не могут быть все исчерпаны. Таким образом, подымающийся камень никогда не пришел бы в состояние покоя, но пребывал бы в бесконечном, постоянно замедляющемся движении, чего, однако, в действительности никогда не бывает.
Сальвиати. Это случилось бы, синьор Симпличио, если бы тело двигалось с каждою степенью скорости некоторое определенное время; но оно только проходит через эти степени, не задерживаясь более чем на мгновение; а так как в каждом, даже самом малом промежутке времени содержится бесконечное множество мгновений, то их число является достаточным для соответствия бесконечному множеству уменьшающихся степеней скорости. То, что такое восходящее тело не сохраняет скорости данной степени в течение конечного промежутка времени, ясно из следующего: предположив возможность этого, мы получим, что в первый и последний момент некоторого промежутка времени тело имеет одинаковую скорость, с которой и должно продолжать движение в течение второго промежутка времени; но таким же образом, каким оно перешло от первого промежутка времени ко второму, оно должно будет перейти и от второго к третьему и т. д., продолжая равномерное движение до бесконечности6.
Сагредо. Мне кажется, что это рассуждение дает достаточные основания для ответа на возбуждаемый философами вопрос о причинах ускорения естественного движения тяжелых тел. Рассматривая тело, брошенное вверх, я нахожу, что мощь, сообщенная ему бросающим, постепенно уменьшается и поднимает тело до тех пор, пока она превосходит противодействующую мощь тяжести; но как только они уравновешиваются, тело перестает подниматься и проходит через состояние покоя, при котором первоначально сообщенный импульс вовсе не уничтожается, а только погашен первоначальный излишек его над весом тела, каковой {243} заставлял тело двигаться вверх. Так как уменьшение этого стороннего импульса продолжается, следствием чего является перевес тяжести, то начинается обратное движение или падение тела, происходящее вначале медленно, вследствие противодействия сообщенной телу мощи, значительная часть которой еще сохраняется в нем; но так как эта последняя постепенно уменьшается и все в большей и большей степени преодолевается тяжестью, то отсюда и возникает постепенное ускорение движения7.
Симпличио. Соображения эти весьма интересны, но более остроумны, нежели убедительны. То, что в них содержится, подходит лишь к таким случаям, когда естественному движению предшествует насильственное движение, и значительная доля внешней мощи сохраняется. Но там, где остатка сторонней мощи нет, и тело выходит из предшествовавшего состояния покоя, все рассуждение теряет основание8.
Сагредо. Полагаю, что вы заблуждаетесь и что проводить различие этих случаев, как вы это делаете, излишне или, лучше сказать, бесполезно. Скажите мне, можно ли сообщить брошенному телу большую или меньшую мощь так, чтобы оно поднялось на сто локтей, а также на двадцать, на четыре или на один?
Симпличио. Не сомневаюсь, что можно.
Сагредо. Так же возможно, что указанная мощь будет превышать сопротивление тяжести столь незначительно, что приподнимает тело вверх всего на один палец. Наконец, мощь бросающего может быть такой, что она сравняется с сопротивлением тяжести, так что тело не поднимется, а будет только поддерживаемо ею. Когда вы держите в руке камень, то что иное делаете вы, как не сообщаете ему столько мощи, заставляющей его двигаться вверх, какова способность его веса тянуть вниз? Не продолжаете ли вы сообщать эту мощь в течение всего того времени, как вы держите камень в руке, и разве она уменьшается за то время, что вы поддерживаете камень? Не все ли равно, в чем заключается эта поддержка, мешающая камню падать,— в вашей ли руке, столе или веревке, к которой привязан камень? Конечно, безразлично. Из этого, синьор Симпличио, сделайте вывод, что предшествует ли падению камня длительный, кратковременный или мгновенный покой, не имеет никакого значения, так как камень не падает до тех пор, пока мощи, противодействующей его тяжести, достаточно только для того, чтобы удержать его в покое.
Сальвиати. Мне думается, что сейчас неподходящее время для занятий вопросом о причинах ускорения в естественном движении, по поводу которого различными философами было высказано столько различных мнений; одни приписывали его приближению к центру, другие — {244} постепенному частичному уменьшению сопротивляющейся среды, третьи — некоторому воздействию окружающей среды, которая смыкается позади падающего тела и оказывает на него давление, как бы постоянно его подталкивая; все эти предположения и еще многие другие следовало бы рассмотреть, что, однако, принесло бы мало пользы. Сейчас для нашего Автора будет достаточно, если мы рассмотрим, как он исследует и излагает свойства ускоренного движения (какова бы ни была причина ускорения), приняв, что моменты скорости, начиная с перехода к движению от состояния покоя, идут, возрастая в том же простейшем отношении, как и время, то есть, что в равные промежутки времени происходят и равные приращения скорости. Если окажется, что свойства, которые будут доказаны ниже, справедливы и для движения естественно и ускоренно падающих тел, то мы сможем сказать, что данное нами определение охватывает и указанное движение тяжелых тел и что наше положение о нарастании ускорения в соответствии с нарастанием времени, т. е. продолжительностью движения, вполне справедливо9.
Сагредо. Насколько я сейчас себе представляю, можно было бы, как мне кажется, дать определению, не изменяя его сущности, следующую более ясную формулировку: равномерно-ускоренное движение есть такое, при котором скорость возрастает пропорционально пройденному пути; так, например, степень скорости, приобретенная телом при падении на четыре локтя, будет вдвое больше приобретенной им при падении на два локтя, а эта последняя будет вдвое больше скорости, приобретенной при падении на один локоть. Нельзя, кажется мне, сомневаться в том, что груз, падающий с высоты шести локтей, производит удар с вдвое большим импульсом, чем тот же груз при падении с высоты трех локтей; в три раза большим, чем при падении с высоты двух локтей, и в шесть раз большим, чем при падении с высоты одного локтя.
Сальвиати. Для меня служит большим утешением, что я имею такого сотоварища по заблуждению; к тому же ваше рассуждение кажется столь простым и правдоподобным, что когда я изложил его нашему Автору, то последний сообщил мне, что и сам он одно время разделял это ложное положение. Но наиболее удивительным оказалась в конце концов достаточность лишь четырех простых слов для доказательства не только ошибочности, но и простой невозможности двух утверждений, столь правдоподобных, что среди многих лиц, которым я излагал их, не нашлось никого, кто бы тотчас же не признал их справедливости.
Симпличио. Вероятно, и я оказался бы среди последних. В самом деле, то, что падающий груз приобретает по пути силу, причем скорость его возрастает пропорционально пройденному пути, и что момент ударяющего тела вдвое больше при падении с двойной высоты,— эти положения могут быть приняты без возражений и сомнений. {245}
Сальвиати. А вместе с тем они так же неправильны и невозможны, как если бы утверждать, что движение происходит мгновенно, и вот вам ясное тому доказательство. Если бы скорости были пропорциональны пройденным или имеющим быть пройденными расстояниям, то такие расстояния проходились бы в равные промежутки времени; таким образом, если бы скорость, с которою падающее тело проходит расстояние в четыре локтя, была вдвое больше скорости, с которою оно проходит расстояние в два первых локтя (на том основании, что одно расстояние вдвое больше другого), то промежутки времени для прохождения того и другого расстояния должны были бы быть одинаковыми. Но прохождение одним и тем же телом четырех локтей и двух локтей в один и тот же промежуток времени могло бы иметь место лишь в том случае, если бы движение происходило мгновенно; мы же видим, что падающее тело совершает свое движение во времени и что два локтя оно проходит в меньший срок, нежели четыре локтя. Следовательно, утверждение, что скорости растут пропорционально пройденным путям, ложно. Неправильность второго положения также легко обнаружить. Так как ударяющее тело предполагается одинаковым, то разница в моменте удара может обусловливаться только разницею в скорости; если, следовательно, ударяющее тело, падая с двойной высоты, ударяет с двойным моментом, то оно должно обладать и двойной скоростью; но при двойной скорости тело проходило бы двойное пространство в то же самое время, мы же видим, что падение с большей высоты требует и большего времени10.
Сагредо. Слишком много ясности и слишком много простоты вносите вы в разъяснение темных вещей; в конце концов, доступность положений имеет следствием то, что знание их кажется нам менее ценным, чем признание достоверности противоположных положений. Я думаю, что познания, общедоступные и приобретаемые с такою малою затратою труда, ценятся меньше по сравнению с теми, которые связаны со сложными и необъяснимыми представлениями.
Сальвиати. Для того, кто кратко и ясно доказывает ложность положений, общераспространенных и принимаемых всеми за правильные, прискорбно вместо одобрения выслушивать упреки. Но еще более неприятное и тяжелое чувство испытывает тот, кто, работая в данной области и считая себя в ней равным всякому другому, видит, что заключения, которые считались им истинными, после краткого и простого рассуждения кого-либо другого оказываются ложными. Я бы не назвал этого чувства завистью, которая обычно выражается в ненависти и злобе к тому, кто разъяснил такие заблуждения; это скорее склонность или желание в большей мере поддержать прежние заблуждения, чем допустить признание вновь открытых истин. Подобное желание не раз побуждало людей выступать против таких открытий, истина коих ими самими в глубине {246} души признавалась, только для того, чтобы унизить других в глазах многочисленной и малообразованной публики. Я не мало слышал от нашего Академика примеров таких общераспространенных ложных и легко опровергаемых учений и даже записал часть их.
Сагредо. Вы не должны скрывать их от нас; вам непременно следует в свое время познакомить нас с ними, хотя бы для этого нам пришлось собраться особо. Теперь же продолжим нить наших рассуждений. Мне кажется, что мы установили следующее определение равномерно ускоренного движения, о коем будем говорить далее: равномерно или единообразно-ускоренное движение есть такое, при котором в равные промежутки времени приобретаются и равные моменты скорости.
Сальвиати. Установив это определение, наш Автор выдвигает и принимает только один принцип: степени скорости, приобретаемые одним и тем же телом при движении по наклонным плоскостям, равны между собой, если высоты этих наклонных плоскостей одинаковы.
Высотою наклонной плоскости здесь называется перпендикуляр, опущенный из наивысшей точки такой плоскости на горизонтальную линию, проходящую через наинизшую точку наклонной плоскости. Для ясности возьмем параллельную горизонту линию АВ, к которой наклонены две плоскости СА и CD; перпендикуляр СВ, опущенный на горизонталь АВ, наш Автор и называет высотою наклонных плоскостей СА и CD, Он полагает, что степени скорости, приобретенные телом, движущимся по наклонным плоскостям СА и CD, при достижении им точек А и D равны между собою, так как плоскости имеют одну и ту же высоту СВ; при этом указанная степень скорости одинакова с той, которую тело приобретает, достигнув точки В при свободном падении из точки С.
Сагредо. Это положение кажется мне действительно столь правдоподобным, что заслуживает быть принятым без возражений, при том условии, конечно, что все внешние препятствия и воздействия устранены, наклонные плоскости тверды и абсолютно гладки, а движущееся тело имеет совершенно правильную круглую форму, так что между плоскостями и телом нет трения. Простой здравый смысл подсказывает мне, что если устранить все препятствия и воздействия, то тяжелый и совершенно круглый шарик, движущийся по линиям СA, CD и СВ, приобретет, достигнув точек A, D и В, одинаковый импульс11.
Сальвиати. Вы считаете это вероятным. Я иду дальше признания вероятности и постараюсь так подкрепить ее опытом, чтобы это мало чем отличалось от непреложного доказательства. Представим себе, что этот лист является стеной, перпендикулярной к горизонту, и что на вбитом в нее гвозде на тонкой нити АВ, длиною в два или три локтя, подвешен свинцовый шарик весом в одну или две унции; начертим на {247} этой стене горизонтальную линию DC, перпендикулярную к нити АВ, отстоящей от стены приблизительно на два пальца. Если мы отведем теперь нить АВ вместе с шариком в положение АС и отпустим шарик, то мы тотчас же увидим, как он, падая, опишет дугу CBD, быстро пройдет за точку В и, следуя по дуге BD, поднимется почти до уровня линии CD, не достигнув
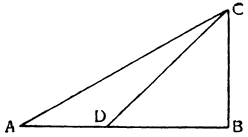 |
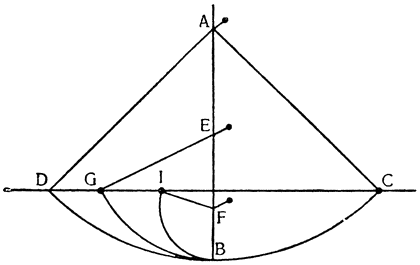 |
Сагредо. Рассуждение это представляется мне столь убедительным, а опыт столь хорошо подтверждающим утверждение, что последнее вполне заслуживает признания — так, как если бы оно было доказано.
Сальвиати. Мне не хотелось бы, синьор Сагредо, чтобы мы задерживались на этом и, особенно, на том, что указанным положением мы будем пользоваться при рассмотрении движения, которое происходит по плоским поверхностям, а не по кривым, при движении по которым ускорение происходит по степеням, значительно отличающимся от тех, которые мы принимаем для движения по плоским поверхностям. Опыт учит нас, что при падении по дуге СВ тело приобретает такой момент, что может подняться на ту же высоту по любой из дуг BD, BG, BI; но мы не в состоянии с такой же очевидностью показать, что то же самое произойдет, если шарик самой совершенной формы будет двигаться по гладким плоским поверхностям, наклоненным, как хорды тех же дуг. Так как эти плоские поверхности образуют в точке В угол, то ясно, что шарик, падающий по хорде СВ, встретит сопротивление плоскостей, наклоненных, как хорды BD, BG, BI, потеряет от удара о них часть своего импульса и не сможет, скользя по ним, подняться на высоту линии CD. Если допустить, однако, что такое препятствие, встречающееся при опыте, устранено, то, как мне кажется, легко представить себе мысленно, что импульс (мощь которого получается за счет высоты падения) будет способен поднять тело на ту же высоту. Итак, примем пока изложенное как постулат, абсолютная правильность которого обнаружится впоследствии, когда мы ознакомимся с выводами из этой гипотезы, точно согласующимися с данными опыта. Предположив этот единственный принцип, Автор переходит к доказательству предложений, являющихся выводами из него. Первое из них таково:
Теорема I. Предложение I
Время, в течение которого тело, вышедшее из состояния покоя и движущееся равномерно-ускоренно, проходит некоторое расстояние, равно времени, в течение которого это же расстояние было бы пройдено тем же телом при равномерном движении, скорость которого равняется половине величины наибольшей конечной скорости, достигаемой при первом равномерно-ускоренном движении. {249}
Пусть линия АВ представляет время, в течение которого тело, выйдя из состояния покоя в точке С, проходит при равномерно-ускоренном движении расстояние CD. Отметим, далее, степени скорости, приобретаемые телом в конце каждой отдельной частицы времени АВ; степени эти, постепенно увеличиваясь, возрастают в конце до величины ЕВ, которую и отложим
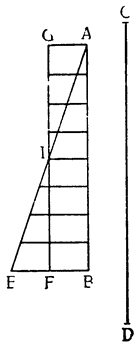 |
Теорема II. Предложение II
Если тело, выйдя из состояния покоя, падает равномерно-ускоренно, то расстояния, проходимые им за определенные промежутки времени, относятся между собою, как квадраты времени. {250}
Изобразим промежуток времени, начинающийся с какого-либо мгновения А, линией АВ и представим себе, что AD и АЕ суть некоторые части этого промежутка времени. Пусть, далее, HI будет линией, вдоль которой падающее тело, вышедшее из состояния покоя, движется равномерно
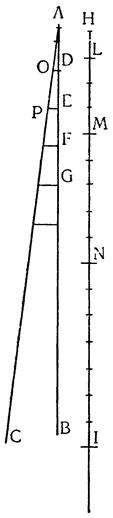 |
Отсюда вытекает, что расстояния относятся и как квадраты максимальных конечных скоростей, т. е. РЕ и OD, ибо отношения РЕ к OD и ЕА к DA равны.
| {251} |
Следствие I
Из вышеизложенного следует, что если от начального мгновения движения взять равные промежутки времени, как AD, DE, EF, FG, в течение которых телом пройдены расстояния HL, LM, MN, NI, то последние будут относиться между собою, как ряд последовательных нечетных чисел, т. е. как 1, 3, 5, 7. Действительно, именно такое отношение существует между разностями квадратов линий произвольной длины, постепенно увеличивающихся на длину наименьшей из этих линий, другими словами, разностями между квадратами всех чисел, начиная с единицы. Таким образом, в то время как скорость возрастает в равные промежутки времени как простой ряд последовательных чисел, расстояния, пройденные за те же промежутки времени, относятся между собой как последовательные нечетные числа13.
Сагредо. Приостановите, пожалуйста, на минуту ваше чтение, так как мне хочется поделиться с вами одной мыслью, пришедшей мне в голову. Для того чтобы лучше изложить ее и сделать более ясной как для самого себя, так и для вас, я сделаю небольшой рисунок. Пусть линия AI изображает промежуток времени, первым мгновением которого
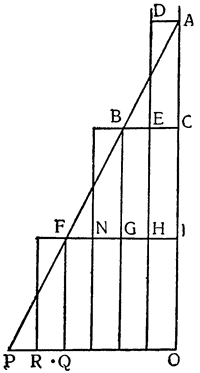 |
Симпличио. Простое и ясное рассуждение синьора Сагредо понравилось мне, право, много более, нежели несколько неясные для меня доказательства нашего Автора. Теперь я в достаточной мере убежден, что явление должно происходить именно так, если только принять указанное определение равномерно-ускоренного движения. Но действительна ли таково ускорение, которым природа пользуется при движении тяжелых падающих тел, остается для меня сомнительным; поэтому для поучения меня и других, мне подобных, не мешало бы теперь привести {253} несколько опытов, из числа многих проделанных, которые показали бы, что различные случаи падения тел совпадают со сделанными заключениями.
Сальвиати. Вы, как подлинный ученый, предъявляете совершенно основательное требование; оно особенно уместно в отношении таких наук, в которых для объяснения законов природы применяются математические доказательства; таковы, например, перспектива, астрономия, механика, музыка и другие аналогичные науки; в них опыт, воспринимаемый чувствами, подтверждает принципы, являющиеся основою для всех дальнейших построений. Однако мне не хотелось бы, чтобы у вас создалось впечатление, будто мы слишком подробно остановились на первом и основном положении, на котором покоится колоссальное здание бесчисленных выводов, лишь в малой доле затронутых нашим Автором в настоящем сочинении; он сделал достаточно уже одним тем, что открыл пытливым умам запертые до сего времени двери. Что касается опытов, то Автор не упустил из виду их произвести, и чтобы убедиться в том, что ускорение естественно падающих тел происходит описанным выше образом, я много раз в обществе нашего Автора производил следующий опыт.
Вдоль узкой стороны линейки или, лучше сказать, деревянной доски, длиною около двенадцати локтей, шириною пол-локтя и толщиною около трех дюймов, был прорезан канал, шириною немного больше одного дюйма. Канал этот был прорезан совершенно прямым и, чтобы сделать его достаточно гладким и скользким, оклеен внутри возможно ровным и полированным пергаментом; по этому каналу мы заставляли падать гладкий шарик из твердейшей бронзы совершенно правильной формы. Установив изготовленную таким образом доску, мы поднимали конец ее над горизонтальной плоскостью когда на один, когда на два локтя и заставляли скользить шарик по каналу (описанному выше), отмечая способом, о котором речь будет идти ниже, время, необходимое для пробега им всего пути; повторяя много раз один и тот же опыт, чтобы точно определить время, мы не находили никакой разницы даже на одну десятую времени биения пульса. Точно установив это обстоятельство, мы заставляли шарик проходить лишь четвертую часть длины того же канала; измерив время его падения, мы всегда находили самым точным образом, что оно равняется всего половине того, которое наблюдалось в первом случае. Производя далее опыты при различной иной длине пути, сравнивая время прохождения всей линейки со временем прохождения половины, двух третей, трех четвертей или любых иных частей ее и повторяя опыты сотни раз, мы постоянно находили, что отношение пройденных путей равно отношению квадратов времени их прохождения при всех наклонах плоскости, т. е. канала, по которому скользил шарик. При этом мы наблюдали также, {254} что промежутки времени пробега пути при различных наклонах относятся между собою именно так, как утверждает и доказывает далее Автор. Что касается способа измерения времени, то мы пользовались большим ведром, наполненным водою и подвешенным наверху; в дне ведра был проделан узкий канал; через этот последний вода изливалась тонкой струйкой и собиралась в маленьком бокале в течение всего того времени, как шарик спускался по всему каналу или части его; собранные таким образом количества воды каждый раз взвешивались на точнейших весах; разность и отношение веса воды для разных случаев давали нам разность и отношение времен падения, и притом с такою точностью, что, как я уже упоминал, повторяя один опыт много и много раз, мы не могли заметить сколько-нибудь значительных отклонений.
Симпличио. Я получил бы большое удовольствие, если бы присутствовал при подобных опытах; но вполне полагаясь на ваше умение произвести такие опыты и правильность передачи их результатов, я успокаиваюсь и принимаю последние за правильные и истинные.
Сальвиати. В таком случае мы можем возобновить наше чтение и продвигаться далее14.
Следствие II
Во-вторых, следует, что если взять от исходной точки движения два любых расстояния, пройденных в какие угодно промежутки времени, то эти
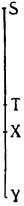 |
В самом деле, так как уже доказано, что пройденные расстояния относятся между собою как квадраты соответствующих промежутков времени, отношение же расстояния VS к ST равно квадрату отношения VS к SX, то ясно, что промежутки времени, затраченные на прохождение расстояний SV и ST, относятся между собой как расстояния VS и SX.
Замечание
То, что доказано в отношении падения тел в вертикальном направлении, справедливо и в отношении падения по любым наклонным плоскостям; и в этом случае скорость увеличивается по тому же закону, т. е. в соответствии с ростом времени, иными словами, как последовательный, ряд целых чисел15. {255}
Сальвиати. На этом, синьор Сагредо, да будет мне позволено, даже с опасностью наскучить синьору Симпличио, прервать на время чтение, чтобы иметь возможность добавить по памяти еще кое-что, основанное на изложенном и доказанном выше, а также на некоторых замечаниях и заключениях нашего Академика, для дальнейшего подтверждения принципов, выведенных нами из рассуждений и опытов; особенно важное значение для геометрических заключений имеет доказательство одной элементарной леммы, относящейся к импульсам.
Сагредо. Если результатом будет приобретение тех сведений, которые вы, синьор, обещаете сообщить, то нет такого времени, какое я не согласился бы потратить на углубление и укрепление познаний в области учения о движении. Что касается меня, то я не только уступаю вашему желанию, но даже усиленно прошу вас поскорее удовлетворить мою любознательность, вами возбужденную. Я надеюсь, что и синьор Симпличио думает так же, как и я.
Симпличио. Вполне присоединяюсь к тому, что вами сказано.
Сальвиати. Поэтому рассмотрим с вашего разрешения прежде всего одно обстоятельство, всем хорошо известное, а именно, что моменты или скорости одного и того же движущегося тела различны при различном наклоне плоскости и что наибольшими из них являются те, при которых движение совершается по линии, перпендикулярной к горизонту; при всяком другом наклоне скорости уменьшаются по мере того, как плоскость удаляется от вертикального положения и становится все менее наклонной. Таким образом, импульс, способность, энергия или, скажем, момент падения уменьшаются в движущихся телах плоскостью, находящейся под ними, на которую они опираются и по которой опускаются.
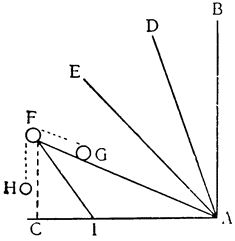 |
Для большей ясности представьте себе линию АВ проведенной перпендикулярно к горизонту АC, а затем проведенной с различным наклоном к горизонту, как AD, AE, AF и т. д. Утверждаю, что тело обладает наибольшим импульсом к падению вдоль вертикали ВА, меньшим — вдоль линии DA, еще меньшим — вдоль ЕА и т. д.; импульс постепенно уменьшается по мере приближения к с наименее наклонной линии AF и совершенно исчезает при достижении горизонтали СА; здесь тело оказывается индиферентным к движению и покою, не имея само по себе никакой склонности к перемещению в какую-либо сторону и не проявляя никакого сопротивления передвижению. В самом деле, если невозможно, чтобы тяжелое тело или соединение таковых поднялось само по себе вверх, удаляясь от общего центра, к которому стремятся все тяжелые тела, то {256} одинаково невозможно, чтобы оно само по себе стало двигаться, если его собственный центр тяжести не приближается при этом к общему центру; поэтому, пребывая на горизонтальной плоскости, представляющей собою поверхность, повсюду равно удаленную от общего центра тяжести и потому совершенно лишенную наклона, тело не будет иметь никакого импульса или момента.
В отношении указанного изменения импульса я считаю нужным при вести то, что было пространно и обстоятельно доказано нашим Академиком в старом трактате по механике, написанном им еще в Падуе исключительно для своих учеников. Исследуя природу и удивительные свойства винтовых механизмов, он показал, в каком отношении изменяется импульс при различных наклонах плоскости16. Возьмем для примера наклонную плоскость AF, один конец которой поднят над горизонтом на высоту FC; импульс тела или момент падения его вдоль этой последней линии является максимальным; спрашивается, в каком отношении находится этот момент к моменту того же тела при падении его по наклонной плоскости FA. Утверждаю, что отношение указанных импульсов равно обратному отношению соответственных длин. Это и есть лемма, которую необходимо предпослать имеющей быть доказанной ниже теореме. Совершенно ясно, что импульс тела к падению столь же велик, как то наименьшее сопротивление или та наименьшая сила, которые достаточны для того, чтобы воспрепятствовать падению и удержать тело; в качестве такой силы или сопротивления, допускающих измерение, я воспользуюсь весом другого тела. Представим себе, что на плоскость FA положено тело G, привязанное к нити, перекинутой через F, к другому концу которой прикреплен груз Н. Заметим себе, что длина пути, проходимого последним при падении или подъеме по вертикали, всегда равна длине пути, проходимого другим телом G при падении или подъеме по наклонной AF, но отнюдь не величине падения или подъема тела G по вертикали, в направлении которой оно (как и все другие тела) производит давление. Это совершенно ясно. Если мы обратимся теперь к треугольнику AFC и будем рассматривать движение тела G хотя бы вверх от А к F, каковое движение составляется из перемещения вдоль горизонтали АС и вертикали CF, то найдем, как уже было упомянуто выше, что горизонталь не оказывает никакого сопротивления движению (ибо при движении по ней ничего не теряется и не приобретается в смысле расстояния от общего центра всех тяжелых тел, каковое при горизонтальной плоскости является неизменным); остается, следовательно, преодолеть лишь сопротивление движению вдоль вертикали CF. Когда, таким образом, тело G, передвигаясь от А до F, преодолевает лишь сопротивление подъему на величину вертикали CF, то другое тело Н неизбежно опускается по вертикали на все расстояние AF, и подобное соотношение их подъема или спуска остается {257} неизменным, как бы ни было мало или велико перемещение этих тел (ибо они связаны вместе). Поэтому мы с уверенностью можем утверждать, что когда наступает равновесие и оба тела приходят в состояние покоя, то моменты, скорости и склонность их к движению, т. е. пространства, которые они прошли бы в одинаковые промежутки времени, должны относиться друг к другу обратно их весам, согласно тому, что доказывается для всяких других случаев механического движения. Таким образом, для предотвращения падения тела G достаточно, чтобы тело Н имело вес, во столько раз меньший веса первого тела, во сколько раз длина CF меньше длины FA. Если сделать отношение FA к FC равным отношению весов G и Н, то наступит равновесие, так как тела Н и G будут иметь равные моменты, и движение их прекратится. Так как мы согласились, что импульс, энергия, момент или склонность тела к движению равны силе или минимальному сопротивлению, достаточному, чтобы прекратить движение, и так как оказалось, что тела Н достаточно, чтобы остановить движение тела G, то, следовательно, меньший вес Н, развивающий весь свой момент в направлении вертикали FC, будет точною мерою частичного момента, развиваемого большим весом G в направлении наклонной плоскости FA. Так как, далее, мерою всего момента тяжелого тела G является оно само (ибо для воспрепятствования падению тела по вертикали необходима противодействующая такого же тяжелого тела, лишь бы оно могло двигаться отвесно), то частичный импульс или момент тела G, развиваемый в направлении наклонной плоскости FA, будет относиться к общему и максимальному моменту того же тела G, развиваемому в направлении вертикали FC, как вес Н к весу G, или, по построению, как вертикаль FC, т. е. высота наклонной плоскости FA, к длине ее. Это и есть то, что требовалось доказать в настоящей лемме и что, как увидим ниже, принято нашим Автором как известное во второй части шестого предложения настоящего трактата.
Сагредо. Из изложенного выше, синьор, можно, кажется, легко заключить, оперируя ex aequali обратными пропорциями, что моменты одного и того же тела, развиваемые в направлении плоскостей, имеющих одну и ту же высоту, но различный наклон, как хотя бы FA и FI, находятся в отношении, обратном отношению длин этих плоскостей.
Сальвиати. Совершенно правильное заключение. Покончив с этим вопросом, перейдем к доказательству следующей теоремы: скорости тела, опускающегося естественным движением с одной и той же высоты по плоскостям, имеющим различный наклон, при достижении горизонта всегда равны между собою, если все препятствия устранены17.
Здесь необходимо прежде всего заметить следующее: если установлено, что тело, выйдя из состояния покоя, движется по плоскости любого {258} наклона с возрастающей скоростью и импульсом, увеличивающимся пропорционально времени (согласно определению, данному Автором естественно-ускоренному движению), то, как это было доказано в предыдущем положении, пройденные пространства относятся как квадраты времен, а вместе с тем и как квадраты степеней скорости; каковы будут импульсы первоначального движения, таковы же пропорционально будут и степени скорости, приобретенные в то же самое время, ибо и те и другие возрастают в одно и то же время в одинаковой пропорции.
Пусть теперь АВ — наклонная плоскость, АС — вертикаль или высота подъема последней над горизонтом и СВ — горизонт. Так как мы только что нашли, что импульс тела, движущегося вдоль вертикали АС,
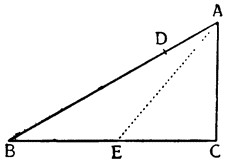 |
Изложенное позволяет нам легко доказать следующее третье предложение Автора, в котором он устанавливает положение, что отношение времени падения по наклонной ко времени падения по вертикали равно отношению между длиною наклонной и ее высотою. Рассуждаем так: если ВА есть время падения по АВ, то время падения по AD на основании второго следствия второго предложения будет средним пропорциональным между двумя последними величинами, т. е. равно АС; но АС, являясь временем падения по AD, будет в то же самое время и временем падения по АС, ибо AD и АС проходятся телом в одинаковое время; таким образом, если ВА является временем падения по АВ, то АС будет временем падения по АС; следовательно, отношение АВ к АС одинаково с отношением времени падения по АВ ко времени падения по АС. {259}
Подобным же образом доказывается, что время падения по АС относится ко времени падения по другой наклонной АЕ как АС к АЕ; следовательно, ex aequali время падения по АВ относится ко времени падения по АЕ как АВ к АЕ и т. д.
Рядом аналогичных заключений, выведенных из той же теоремы, можно было бы, как это сейчас увидит синьор Сагредо, непосредственно доказать шестое предложение Автора. Оставим, однако, в стороне отклонения, показавшиеся нам, быть может, слишком скучными, хотя они и являются весьма полезными при рассмотрении вопроса о движении.
Сагредо. Напротив, я очень доволен и считаю их необходимыми для более глубокого понимания предмета.
Сальвиати. Итак, продолжим чтение текста.
Теорема III. Предложение III
Если одно и то же тело, выйдя из состояния покоя, движется по наклонной плоскости и вертикали, равной высоте наклонной плоскости, то времена падения тела относятся между собою как длина наклонной плоскости к длине вертикали.
Пусть АС будет наклонной плоскостью и АВ — вертикалью, равной заодно высоте подъема наклонной плоскости над горизонтом СВ.
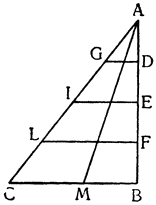 |
Сагредо. Мне кажется, то же самое можно было бы доказать достаточно ясно и кратко на основании положения, что расстояния, проходимые вдоль АС и АВ в случае равномерно ускоренного движения, равны путям, проходимым в случае простого равномерного движения со скоростью, равною половине максимальной, т. е. СВ; так как оба расстояния АС и АВ проходятся за промежутки времени, равные таковым же при равномерном движении, то на основании предложения первого ясно, что времена падения относятся между собою как пройденные пути19.
Следствие
Отсюда следует, что времена падения по плоскостям с различными наклонами, но одинаковою высотою, относятся между собою как длины плоскостей. В самом деле, если имеем любую плоскость AM, поднимающуюся до точки А и оканчивающуюся на том же горизонте СВ, то можно доказать таким же путем, что времена падения по AM и по АВ относятся между собою как линии AM и АВ. Но времена падения по АВ и АС относятся между собою как линии АВ и АС; следовательно, ex aequali времена падения по AM и АС относятся между собою как AM и АС.
Теорема IV. Предложение IV
Времена падения по плоскостям, имеющим одинаковую длину, но различный наклон, относятся между собою обратно корням квадратным из их высот.
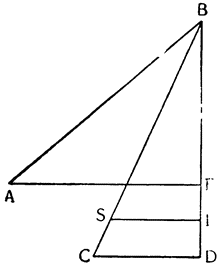 |
Пусть ВА, ВС — две плоскости, имеющие общую начальную точку В и одинаковую длину, но различный наклон, и АЕ, CD — соответствующие им горизонтальные линии, пересекающие вертикаль BD. Высотою плоскости ВА пусть будет линия BE, а плоскости ВС — линия BD; средней пропорциональной между этими высотами DB, BE пусть будет линия BI; таким образом, отношение DB к BI будет, очевидно, равно корню квадратному из отношения DB к BE. Утверждаю, что времена падения по плоскостям ВА и ВС находятся между собою в обратном отношении DB и BI, так что времени падения по ВА соответствует высота BD другой плоскости ВС, времени же падения по ВС — высота BI. Таким образом, надо доказать, что времена падения по ВА и ВС относятся между собою как DB к BI. Проведем IS, параллельную {261} DC; как уже было доказано, времена падения по наклонной плоскости ВА и вертикали BE относятся между собою как расстояния ВА и BE; но времена падения по BE и BD относятся между собою как BE к BI, а времена падения по BD и ВС — как расстояния BD и ВС или как BI и BS; следовательно, ex aequali времена падения по ВА и ВС относятся как ВА к BS или как СВ к BS; но СВ относится к BS, как DB к BI. Таким образом, предложение доказано20.
Теорема V. Предложение V
Отношение времен падения по плоскостям, различающимся по наклону, длине и высоте, составляется из отношения длин и обратного отношения корней квадратных из высот наклонных плоскостей.
Пусть АВ и АС плоскости с различным наклоном, длины и высоты которых не равны. Утверждаю, что отношение времени падения по АС и АВ составляется из отношения расстояний АС и АВ
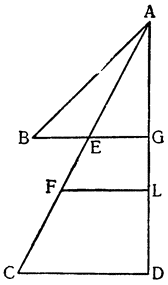 |
Теорема VI. Предложение VI
Если из высшей точки круга, построенного над горизонтом, проведены различные наклонные плоскости, доведенные до окружности, то времена падения по ним одинаковы.
Пусть над горизонталью GH построен круг, через общую точку их, т. е. точку соприкосновения круга с горизонталью, проходит вертикальный {262} диаметр FA, и из высшей точки круга А проведены к любым точкам окружности наклонные плоскости АВ, АС. Утверждаю, что время падения по ним одинаково. Проведем линии BD, СЕ перпендикулярно к диаметру, и пусть средней пропорциональной между высотами ЕА и AD будет AI. Так как прямоугольники FAE и FAD21 равны квадратам АС и АВ и, кроме того, прямоугольник FAE относится к прямоугольнику FAD
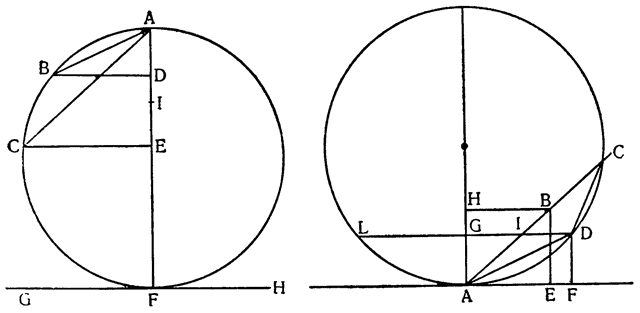
как ЕА к AD, то, следовательно, квадраты СА и АВ относятся между собою, как линии ЕА и AD. Так как, далее, ЕА и DA относятся между собою, как квадрат IA к квадрату AD, то квадраты линий СА и АВ относятся между собою, как квадраты линий IA и AD, а линии СА и АВ — как линии IA и AD. Но выше уже было доказано, что отношение времени падения по АС и АВ составляется из отношений СА к АВ и DA к AI, последнее из которых равно отношению ВА к АС. Следовательно, отношение времени падения по АС ко времени падения по АВ слагается из отношений СА к АВ и ВА к АС, т. е. отношение времен падения переходит в равенство, чем и доказывается теорема.
То же самое доказывается на основании положений механики, что тело проходит в одинаковое время расстояния СА и DA, изображенные на следующем рисунке. Пусть даны: линия ВА, равная DA, и перпендикуляры BE и DF. Из основ механики известно, что момент веса, действующий в случае наклонной плоскости ABC, относится к своему полному моменту, как BE к ВА, а момент того же веса, действующий в случае наклонной плоскости AD, относится к своему полному моменту, как DF к DA или ВА; отсюда следует, что моменты одного и того же веса, действующие в случае наклонных плоскостей DA и ABC, относятся между собою, как линии DF и BE. Расстояния, проходимые в равное время по наклонным плоскостям СА и DA, будут относиться между собой, как линии BE и DF, согласно предложению второму книги первой. Но отношение {263} BE к DF равно отношению АС к AD, что сейчас будет доказано; следовательно, движущееся тело проходит расстояния СА и DA в одинаковые промежутки времени.
То, что BE относится к DF, как СА к DA, доказывается следующим образом.
Проведем линию CD и линии, параллельные AF и проходящие через точки D и В, т. е. линию DGL, пересекающую линию СА в точке I, и линию ВН; при этом угол ADI будет равен углу DCА, так как дуги окружности LA и DA, соответствующие этим углам, будут равны; так как, далее, угол DAC будет общим, то треугольники CAD и DAI будут равноугольными, и стороны их, прилегающие к равным углам, будут пропорциональными, т. е. СА будет относиться к AD, как DA к AI или ВА к AI, или НА к AG, т. е. как BE к DF, что и требовалось доказать. То же самое можно доказать еще короче следующим образом.
Пусть на горизонтали АВ построен круг, диаметр которого CD перпендикулярен к горизонту. Из высшей точки его D проведем к какой-либо точке окружности наклонную плоскость DF. Утверждаю, что время падения тела по DF равно времени падения его по диаметру DC. Проведем линию FG, параллельную горизонту АВ и, следовательно,
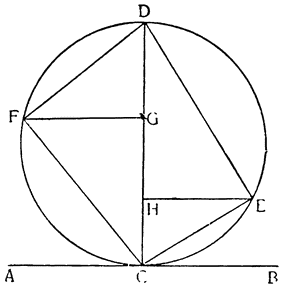 |
Следствие I
Отсюда следует, что времена падения вдоль всех хорд, проведенных из точки С или D, одинаковы.
| {264} |
Следствие II
Далее следует, что если из какой-либо точки проведены вертикаль и наклонная плоскость, времена падения по коим равны, то плоскость эта расположена в полукруге, диаметром которого является указанная вертикаль.
Следствие III
Также следует, что времена падения по наклонным плоскостям равны между собою в том случае, когда высоты равных частей этих плоскостей относятся между собою, как длины плоскостей, ибо было доказано, что времена падения по СА и DA предпоследней фигуры будут равны между собою, если высота части АВ, равной AD, т. е. линия BE, будет относиться к высоте DF как СА к DA.
Сагредо. Приостановите пожалуйста, синьор, на короткое время чтение трактата, чтобы дать мне возможность разобраться в одном соображении, которое только что пришло мне на ум; если оно не заблуждение, то оно подобно одной из тех изящных игр, с которыми мы часто встречаемся в природе и обиходе.
Ясно, что если из какой-либо точки горизонтальной плоскости проведено во всех направлениях бесконечно много прямых линий, и по каждой из последних с одинаковой скоростью движется по одной точке, то, в случае начала движения всех их от указанной выше точки в одно и то же мгновение, все эти движущиеся точки образуют последовательно окружности кругов все большего и большего размера, расположенных концентрически вокруг первоначальной точки, благодаря тому, что скорости движения их одинаковы. То же мы имеем в случае волн, возникающих в стоячей воде, после того как в нее упадет сверху камень, вызывающий своим ударом движение во всех направлениях, причем точка падения камня остается центром всех последовательно увеличивающихся кругов, образуемых волнами. Если же мы представим себе вертикальную плоскость, возьмем на ней какую-либо точку, примем ее за наивысшую и представим себе, что из этой точки исходит бесконечное число линий, наклоненных под всевозможными углами, по которым падают тяжелые тела, каждое, следуя законам естественно-ускоренного движения и со скоростью, соответствующей данному наклону, то, спрашивается, по каким линиям увидим мы располагающимися эти тела, если допустить, что они все время остаются видимыми? В этом-то и заключается чудесное, ибо на основании предшествующих доказательств можно, мне кажется, утверждать с уверенностью, что мы увидим их постоянно располагающимися по окружностям кругов, постоянно {265} увеличивающихся по мере того, как тела эти при своем падении последовательно удаляются от высшей точки, где получило начало их движение. Чтобы лучше пояснить сказанное, возьмем наивысшую точку А, из которой проведем произвольно наклонные линии AF и АН и вертикаль АВ, а затем опишем из точек С и D последней круги, проходящие через точку А и пересекающие наклонные линии и вертикаль в точках F, Н, В и Е, G, I. Из предшествующих доказательств
 |
Сальвиати. Построение, действительно, прекрасное и достойное вашего дарования, синьор Сагредо.
Симпличио. Я вполне представляю себе образование кругов и сфер двумя способами, в соответствии с двумя видами естественного движения, хотя доказательство происхождения этих фигур, в случае ускоренного движения, осталось для меня не совсем понятным. Во всяком случае, возможность приписать начало движения как центральной {266} точке, так и наивысшей точке сферической поверхности, заставляет меня думать, что в этих правильных и удивительных построениях может заключаться некая великая тайна — я подразумеваю тайну сотворения мира (который, как полагают, имеет форму сферы) и первоначальной причины.
Сальвиати. Я не возражаю против такого предположения. Но столь глубокие соображения относятся уже к учениям более высоким, чем наше. Для нас будет достаточно, если мы уподобимся менее искусным рабочим, выламывающим и добывающим из карьеров мрамор, из которого впоследствии опытные скульпторы могут создать удивительные образы, скрывавшиеся ранее под грубой и бесформенной корой. Итак, с вашего позволения, будем продолжать наше чтение.
Теорема VII. Предложение VII
Если высоты двух наклонных плоскостей относятся между собою как квадраты длин, то последние проходятся телом, вышедшим из состояния покоя, в одинаковое время.
Пусть даны две плоскости АЕ и АВ, имеющие различную длину и различный наклон, и высоты их FA и DA; пусть, далее, отношение FA и DA равняется отношению квадратов АЕ и АВ. Утверждаю, что время падения из начальной точки покоя А одинаково для обоих плоскостей АЕ
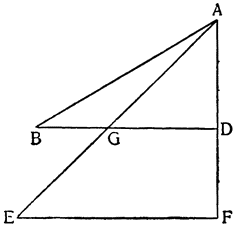 |
Теорема VIII. Предложение VIII
Если плоскости, наклонные к горизонту, располагаются в одном и том же круге, то времена падения по тем из них, кои оканчиваются у верхнего {267} или нижнего конда диаметра, равны между собою и равны времени падения вдоль означенного диаметра; времена же падения по другим
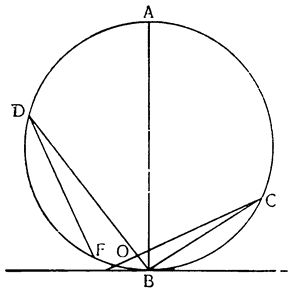 |
Теорема IX. Предложение IX
Если из какой-либо точки горизонтальной линии проведены две произвольные наклонные плоскости, пересеченные линией, образующей с каждой из них угол, равный углу, образуемому другой наклонной плоскостью с горизонтом, то времена падения от начальной точки до точек пересечения наклонных плоскостей с указанной линией равны между собою.
Пусть из точки С горизонтальной линии X проведены две произвольные наклонные плоскости CD и СЕ и в какой-либо точке линии CD построен угол
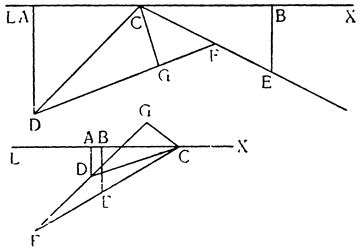 |
Другое доказательство. Проведем FS перпендикулярна к горизонту AS. Так как треугольники CSF и DGC подобны, то SF относится к FC, как GC к CD. Так как, далее, треугольник CFG подобен треугольнику DC А, то FC относится к CG, как CD к DA; следовательно,
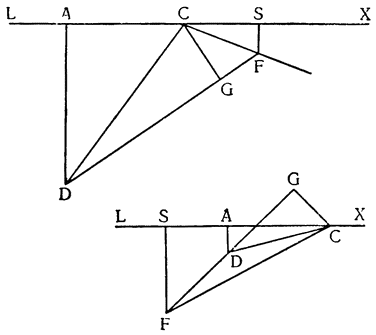 |
Теорема X. Предложение X
Времена падения по плоскостям, имеющим различный наклон, но одинаковую высоту, относятся между собою, как длины этих плоскостей как {269} в том случае, когда движение начинается с выхода из состояния покоя, так и в том, когда ему предшествует падение с одинаковых высот.
Предположим, что движение может происходить по линиям ABC и ABD до горизонта DC, причем движение по АВ предшествует дальнейшему движению по BD и ВС. Утверждаю, что время падения по BD относится ко времени падения по ВС, как длина BD к ВС. Проведем линию AF, параллельную горизонту и пересекающую линию DB в точке F, и пусть FE будет средней пропорциональной между DF и FB; проведя линию ЕО, параллельную ВС, получим АО — среднюю пропорциональную между СА и АВ. Если теперь время падения по АВ будет равно АВ,
 |
как длины BD и ВС. То, что время падения по BD относится ко времени падения по ВС как длина BD к длине ВС в том случае, когда движение тела начинается с выхода из состояния покоя в точке В, доказано выше. Таким образом, времена падения по плоскостям, имеющим различный наклон, но одинаковую высоту, относятся между собою, как длины плоскостей как в том случае, когда движение начинается с выхода из состояния покоя, так и в том, когда ему предшествует падение с равных высот, что и требовалось доказать23.
Теорема XI. Предложение XI
Если плоскость, по которой совершается движение, начинающееся из состояния покоя, разделена каким-либо образом, то время падения но первой части относится ко времени падения по следующей части, как длина первой части к излишку над нею средней пропорциональной между длиною всей плоскости и длиною первой ее части.
Пусть движение совершается от точки покоя А вдоль всей линии АВ, разделенной в точке С на произвольные части; пусть средней пропорциональной между всею ВА и первой ее частью АС будет AF; тогда CF будет излишком средней пропорциональной FА над частью АС. Утверждаю, что время падения по АС относится ко времени последующего падения по СВ как АС к CF. В самом деле, время падения по АС относится {270} ко времени падения по АВ, как АС к средней пропорциональной AF; в случае же деления пути время падения по АС относится ко времени падения по остальной части пути СВ, как АС к CF. Если, таким образом,
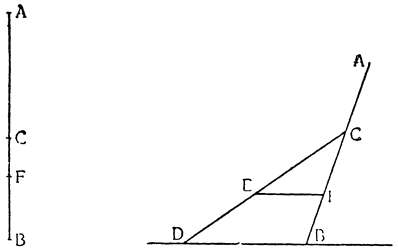 |
Если движение совершается не вдоль одной прямой линии АСВ, но по ломаной линии ACD до горизонта BD, то, проведя через точку F линию FE, параллельную горизонту, можно таким же образом доказать, что время: падения по АС относится ко времени падения по CD, как АС к СЕ. В самом деле, время падения по АС относится ко времени падения по СВ, как АС к CF, а время падения по СВ после прохождения АС относится ко времени падения по CD, также после прохождения АС, как СВ к CD или как CF к СЕ, что было доказано выше; следовательно, ex aequali, время падения по АС будет относиться ко времени падения по CD, как линия АС к линии СЕ.
Теорема XII. Предложение XII
Если две плоскости — одна вертикальная, а другая наклонная к горизонту под каким-либо углом — пересечены горизонтальными линиями: и построены средние пропорциональные между длинами этих плоскостей и отрезками их, заключенными между общей точкой их пересечения и точками пересечения их с верхней горизонталью, то время падения по вертикали относится ко времени падения по ломаной линии, составленной из верхней части вертикали и нижней части наклонной плоскости, как общая длина вертикали к длине линии, составленной из средней пропорциональной между вертикалью и верхней ее частью и излишка всей длины наклонной плоскости над средней пропорциональной между нею и верхней ее частью.
Пусть даны две горизонтали — верхняя AF и нижняя CD, — между которыми заключены две плоскости — вертикальная АС и наклонная DF,— пересекающиеся в точке В, и пусть средней пропорциональной между всей вертикалью СА и верхней частью ее АВ будет AR, а средней пропорциональной между всей длиною DF и верхней частью ее BF будет FS. Утверждаю, что время падения по всей вертикали АС будет относиться ко времени падения по линии, составленной из верхней ее части АВ {271} и нижней части наклонной плоскости, т. е. BD, как АС к средней пропорциональной AR, сложенной с отрезком SD, представляющим излишек общей длины плоскости DF над средней пропорциональной FS. Соединим R и S линией, параллельной горизонту. Так как время падения по всей
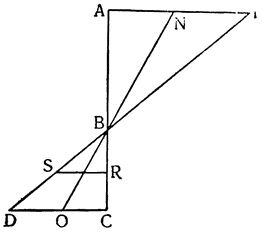 |
То же имеет место, когда вместо вертикальной плоскости дана какая-нибудь другая — наклонная, например NO. Доказательство остается тем же самым.
Задача I. Предложение XIII
Построить наклонную плоскость, высота которой равнялась бы данной вертикали и падение по которой после предшествующего падения по вертикали происходило бы за такой же промежуток времени, как и падение по вертикали, начавшееся с состояния покоя.
Пусть дана вертикаль АВ; продолжив ее до G, отложим отрезок ВС, равный АВ, и проведем горизонтали СЕ и AG; требуется провести через В
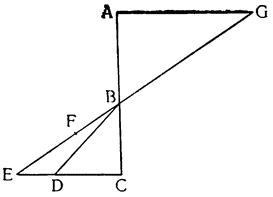 |
Задача II. Предложение XIV
Даны вертикаль и наклонная плоскость; найти на верхней части данной вертикали такой отрезок, время падения по которому, начиная с момента выхода тела из состояния покоя, равнялось бы времени падения по наклонной плоскости после предшествующего падения по искомому отрезку вертикали.
Даны вертикаль DB и наклонная плоскость АС; на части вертикали AD требуется найти такой отрезок, падение по которому по выходе тела из состояния покоя совершалось бы в такой же промежуток времени, как и падение по плоскости АС после предшествующего падения по указанному отрезку. Проведем горизонтальную плоскость СВ, и пусть ВА вместе с удвоенной длиной АС относится к АС, как АС к АЕ, а ВА относится к СА, как ЕА к AR. Опустим из точки R перпендикуляр RX на линию DB. Утверждаю, что X и есть искомая точка. По построению ВА вместе с двумя АС относится к АС, как СА к АЕ; следовательно, BА
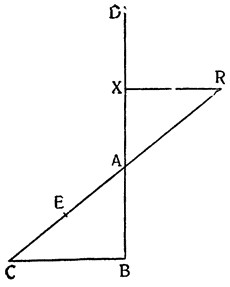 |
Задача III. Предложение XV
Даны вертикаль и пересекающая ее наклонная плоскость; найти на нижней части вертикали такой отрезок, падение по которому совершалось бы в тот же промежуток времени, как и по данной наклонной плоскости после предшествующего падения по данной вертикали.
Пусть даны вертикаль АВ и наклонная плоскость ВС; на нижней части вертикали требуется найти такой отрезок, который проходился бы при падении тела из А в тот же промежуток времени, как и ВС, также при падении тела из А. Проведем горизонталь
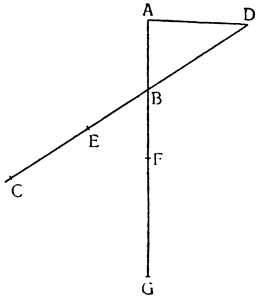 |
Теорема XIII. Предложение XVI
Если части наклонной плоскости и вертикали, выходящих из одной точки, таковы, что падение по ним, начиная с момента выхода тела из состояния покоя, совершается в равные промежутки времени, то тело, падающее с какой-либо большей высоты, скорее проходит часть наклонной плоскости, нежели часть вертикали.
Пусть даны вертикаль ЕВ и наклонная плоскость СЕ, выходящие из одной точки Е, времена падения по которым из точки Е равны, а также какая-либо точка А, лежащая выше на продолжении вертикали, откуда тело может падать. Утверждаю, что после падения тела от А до Е {274} ему потребуется меньше времени для прохождения наклонной плоскости ЕС, нежели для прохождения вертикали ЕВ. Соединим точки С и В и проведем горизонталь AD до пересечения с продолжением СЕ в точке D;
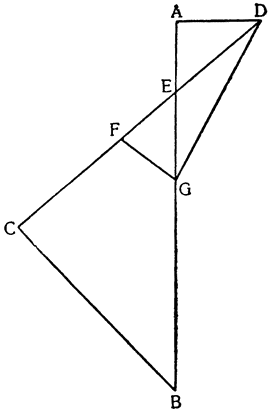 |
Следствие
Из последнего и из ранее доказанных положений вытекает, что тот отрезок вертикали, который тело проходит после падения из высшей точки за тот же промежуток времени, что и наклонную плоскость, меньше того, который проходится по вертикали за промежуток времени, {275} соответствующий прохождению наклонной плоскости без предварительного падения, но больше длины наклонной плоскости. Как уже было доказано выше, время прохождения ЕС, в случае падения тела из высшей
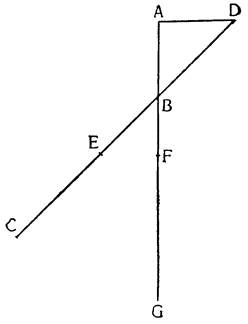 |
Задача IV. Предложение XVII
Даны вертикаль и пересекающая ее наклонная плоскость; найти такую часть этой плоскости, которую тело пройдет после своего падения по вертикали в тот же промежуток времени, в какой им была пройдена по выходе из состояния покоя вертикаль.
Пусть АВ — вертикаль и BE — пересекающая ее наклонная плоскость; требуется найти такую часть BE, которую тело после своего
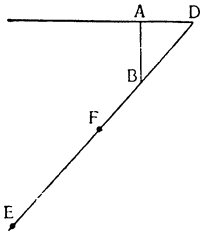 |
Задача V. Предложение XVIII
На данной вертикали отмечен отрезок, проходимый за данное время телом, выходящим из начальной точки. Отметить на той же вертикали отрезок, равный первому и проходимый за некоторый данный меньший промежуток времени.
Пусть AD — вертикаль, АВ — отрезок ее, проходимый телом от начальной точки А за время АВ, и СВЕ — горизонтальная линия; данный промежуток времени, меньший АВ, нанесем на горизонталь как ВС. Требуется отметить на вертикали такой отрезок, равный АВ, который
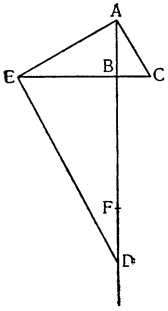 |
Задача VI. Предложение XIX
На данной вертикали отмечен отрезок, проходимый телом при движении из начальной точки за данный промежуток времени; найти время, в течение которого тело пройдет отрезок той же длины, как-либо расположенный на той же вертикали. {277}
Пусть на вертикали АВ отмечен какой-либо отрезок АС, верхняя точка которого совпадает с начальной точкой движения А, и где-нибудь
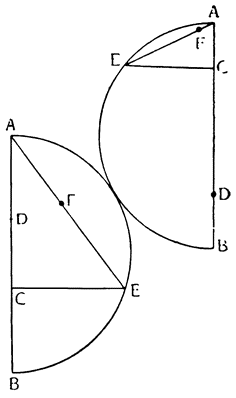 |
Следствие
Отсюда вытекает, что если время падения на какое-либо расстояние, начинающееся от точки покоя, положить равным этому же расстоянию,
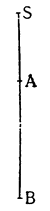 |
Задача VII. Предложение XX
Дана произвольная прямая и на ней отрезок, начинающийся от исходной точки падения; найти другой отрезок, оканчивающийся в той же точке, как и прямая, время падения по которому равнялось бы времени падения по первому отрезку.
Пусть СВ — вертикаль и CD — данный отрезок, начинающийся от исходной точки движения С; требуется отложить от конца В той же {278} вертикали другой отрезок, который проходился бы телом в такой же промежуток времени, как и CD. Найдем среднюю пропорциональную между ВС и CD и отложим на вертикали равный ей отрезок ВА; пусть, далее, третьей
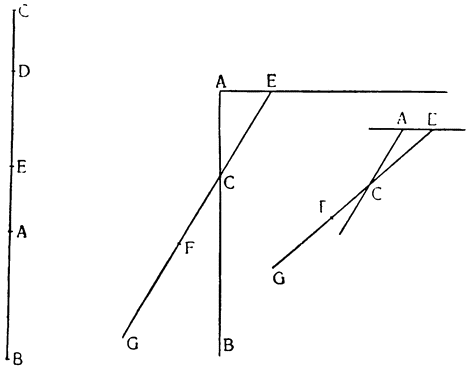 |
Теорема XIV. Предложение XXI
Если падение тела, вышедшего из состояния покоя, совершается сперва по вертикали, а затем, после прохождения в определенное время данной части ее, продолжается по какой-либо наклонной плоскости, то путь, проходимый по этой наклонной плоскости за то же время, что и по указанной части вертикали, более удвоенного, но менее утроенного пути, проходимого по вертикали.
Пусть АЕ — горизонталь и АВ — расположенная под нею вертикаль, по которой из точки А происходит падение на пространство АС; пусть, далее, в точке С к последней линии примыкает какая-либо наклонная плоскость CG, по которой после прохождения телом пути АС и продолжается движение. Утверждаю, что пространство, которое будет пройдено при таком движении по CG за промежуток времени, равный затраченному на прохождение АС, будет более удвоенного, но менее утроенного пути АС. Отложим отрезок CF, равный АС, и продолжим плоскость GC до встречи с горизонталью в точке Е; пусть, далее, СЕ относится к EF, {279} как FE к EG. Если положим теперь, что время прохождения АС есть линия А C, то СЕ будет временем падения по ЕС, a CF или одинаковый с ним отрезок СА — временем падения по CG. Таким образом, требуется доказать, что расстояние CG больше удвоенного, но меньше утроенного отрезка СА. Так как отношение СЕ к EF равно отношению FE к EG, то оно равно и отношению CF к FG. Но ЕС меньше EF, поэтому и CF меньше FG, a GC более удвоенного отрезка FC или АС. Так как, с другой стороны, FE меньше удвоенного отрезка ЕС (ибо ЕС больше СА или CF), то и GF меньше удвоенного отрезка FC, a GC меньше утроенного отрезка CF или СА, что и требовалось доказать.
Этому предложению можно придать и более общую форму, ибо то, что происходит при движении по вертикали и наклонной плоскости, имеет место и в том случае, когда движение по одной наклонной плоскости продолжается по другой, имеющей больший наклон, как показано на прилагаемом чертеже. Доказательство остается тем же самым.
Задача VIII. Предложение XXIII
Даны два неравных промежутка времени и пространство, проходимое в меньший из них телом, вышедшим из состояния покоя и движущимся по вертикали; построить между верхней точкой вертикали и горизонталью наклонную плоскость такой длины, чтобы она проходилась телом за больший из данных промежутков времени.
Пусть из двух неравных промежутков времени А будет большим и В — меньшим, и пусть пространством, проходимым по вертикали из точки покоя за время В, будет CD; требуется построить между точкою С и горизонталью наклонную плоскость такой длины, чтобы она проходилась телом в промежуток времени А. Пусть В относится к А, как CD к некоторой линии СХ, которую и проведем из точки С
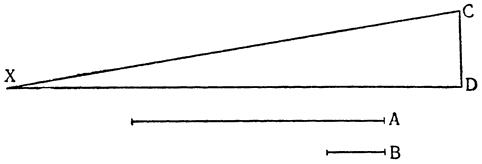 |
| {280} |
Задача IX. Предложение XXIII
Дано пространство, проходимое по вертикали за то или иное время телом, вышедшим из состояния покоя; построить такую наклонную плоскость, примыкающую к нижнему концу означенной вертикали, чтобы время падения по некоторой части ее длины равнялось времени предшествующего падения по вертикали; однако означенная часть должна быть больше удвоенного и меньше утроенного пространства, пройденного по вертикали.
Пусть за время АС телом, вышедшим из состояния покоя в точке А, проходится вдоль вертикали AS пространство АС, и пусть IR больше удвоенного, но меньше утроенного отрезка АС. Требуется построить такую наклонную плоскость, проходящую через точку С, чтобы тело прошло расстояние IR после падения по АС за тот же промежуток времени, в течение которого оно проходит расстояние АС. Пусть отрезки RN и NM равны как между собою, так и отрезку АС, и пусть остаток IM относится к MN, как АС к некоторой линии СЕ, которую и проведем от точки С до горизонтали АЕ; продолжим ее затем в направлении О и отложим на ней части CF, FG и GO, равные RN, NM и Ml. Утверждаю, что время падения по СО после предшествующего падения по АС будет равно времени падения по АС из начальной точки А. В самом деле, так как отношение OG к GF равно отношению FC к СЕ, то, складывая почленно, находим, что отношение OF к FG или FC равно
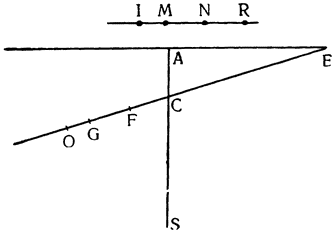 |
Отметим также, что построение не изменяется, если предшествующее движение совершается не по вертикали, а по наклонной плоскости, как на следующем чертеже, где первоначальный путь проходится {281} по наклонной плоскости AS, расположенной ниже горизонтали АЕ; доказательство остается тем же самым.
Замечание
При внимательном рассмотрении становится ясным, что чем менее данная линия IR отличается от утроенной длины АС, тем более наклонная плоскость, по которой совершается последующее движение вдоль СО, приближается к вертикали, по которой в промежуток времени, равный АС, и проходится пространство, составляющее ровно три АС. Чем более IR приближается к утроенной длине АС, тем более длина IM стремится сделаться равной MN. А так как отношение IM к MN равно по построению отношению АС к СЕ, то СЕ лишь немного больше СА, вследствие чего точка Е лежит очень близко от точки А, а линия СО образует с CS весьма острый угол и почти совпадает с последней. Обратно, если данный отрезок IR лишь немного отличается от удвоенного отрезка АС, то IM является линией весьма короткой, а линия АС весьма малой па сравнению с СЕ, которая оказывается весьма длинной и очень близка подходит к горизонтали, проходящей через точку С. Отсюда можно заключить, что если после падения по наклонной плоскости АС произойдет перелом и переход на
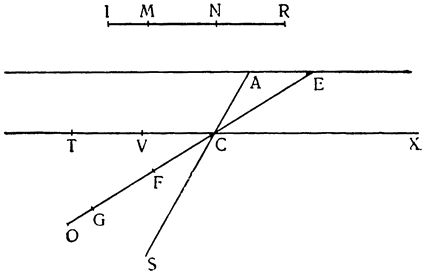 |
К тому же заключению можно было бы прийти и другим путем, следуя соображениям, изложенным в первом предложении. В самом деле, если взять треугольник ABC, в котором линии, параллельные основанию ВС, представляют степени скорости, соответствующие возрастающему времени, то число последних будет бесконечным, как и точек на прямой АС, соответствующих любым мгновениям времени; означенные {282} линии заполнят всю площадь указанного треугольника. Если же мы примем, что движение совершается в течение точно такого же времени, но не ускоренно, а равномерно, со скоростью, соответствующей максимуму,
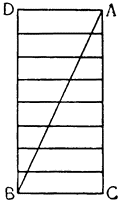 |
Но движение по горизонтальной плоскости является равномерным, так как оно не испытывает ни ускорения, ни замедления; поэтому путь CD, который будет пройден в промежуток времени АС, будет равен удвоенному пространству АС; ускоренному движению соответствуют параллели треугольника, равномерному же движению — параллели параллелограмма, которые, будучи бесконечны числом, вдвое больше параллелей треугольника, чье число тоже бесконечно.
При этом необходимо отметить, что степень скорости, обнаруживаемая телом, ненарушимо лежит в самой его природе, в то время как причины ускорения или замедления являются внешними; это можно заметить лишь на горизонтальной плоскости, ибо при движении по наклонной плоскости вниз наблюдается ускорение, а при движении вверх — замедление. Отсюда следует, что движение по горизонтали является вечным, ибо если оно является равномерным, то оно ничем не ослабляется, не замедляется и не уничтожается. Далее, так как степень скорости, достигнутая телом при свободном падении, неизменно и постоянно присутствует в нем, то ясно, что когда после падения по наклонной плоскости и происходит изменение направления движения и подъем по наклонной плоскости, то в последней коренится причина замедления, ибо падение по той же плоскости сопровождается ускорением. Здесь происходит соединение противоположно направленных стремлений, при котором степень скорости, достигнутая телом при падении и могущая сообщить ему равномерное и вечное движение, а равно и естественное стремление тела двигаться вниз равномерно-ускоренно, встречаются с противодействием движению. Отсюда понятно, почему, исследуя природу новых причин, появляющихся в том случае, когда тело вынуждено подниматься после предшествующего падения по наклонной плоскости, мы можем принять, что и при подъеме своем тело сохраняет максимальную скорость, приобретенную им при падении, но что движение его испытывает естественное замедление в той же мере, в какой оно получало ускорение при падении и выходе из состояния покоя. Для того чтобы легче себе это представить, воспользуемся следующим чертежом. {283}
Пусть падение совершается по наклонной плоскости АВ и движение продолжается по наклонной плоскости ВС; предположим, что обе эти плоскости во всем одинаковы и наклонены к горизонту GH под одним и тем же углом. Как нам уже известно, тело, вышедшее из состояния покоя в точке А и падающее по АВ, приобретает скорости, пропорциональные времени; при этом степень скорости в точке В является максимальной;
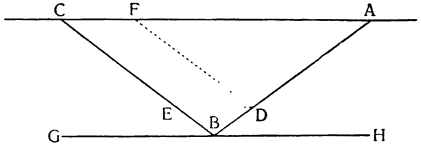 |
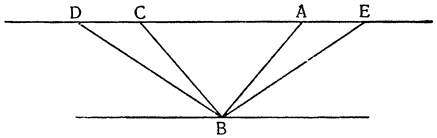 |
Теорема XV. Предложение XXIV
Даны вертикаль и наклонная плоскость, проходящая через нижний конец вертикали, заключенные между двумя параллельными горизонталями; пространство, которое будет пройдено телом вверх по наклонной плоскости после падения его по вертикали и за тот же промежуток времени, будет больше длины вертикали, но меньше удвоенной длины ее.
Пусть между двумя параллельными горизонталями ВС и HG располагаются вертикаль АЕ и
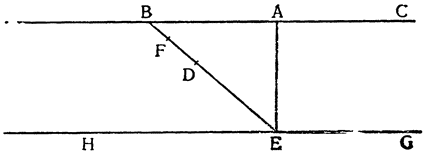 |
То же самое имеет место, если предшествующее движение совершается не по вертикали, а по наклонной плоскости. Доказательство остается тем же самым, пока вторая плоскость, по которой происходит подъем, остается менее крутой и более длинной, нежели плоскость, по которой происходит падение.
Теорема XVI. Предложение XXV
Если после падения по любой наклонной плоскости движение продолжается по горизонтальной плоскости, то время падения по наклонной плоскости относится ко времени движения на любое расстояние по горизонтали, как удвоенная длина наклонной плоскости к указанному отрезку горизонтали.
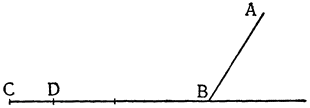 |
Пусть даны горизонталь СВ и наклонная плоскость АВ, и пусть после падения по АВ тело продолжает движение по горизонтали, на которой дан отрезок BD произвольной длины. Утверждаю, что время падения по АВ относится ко времени движения по BD, как удвоенная длина АВ к длине BD. Отложив отрезок ВС, равный двум АВ, заметим, что время падения по АВ, как уже было доказано выше, равно времени движения по ВС; но время движения по ВС относится ко времени движения по DB, как линия СВ к линии BD; следовательно, отношение времени движения по АВ ко времени движения по BD равно отношению удвоенной длины АВ к BD, что и требовалось доказать.
| {286} |
Задача X. Предложение XXVI
Даны вертикаль, заключенная между двумя параллельными горизонталями, и отрезок, длина которого больше длины вертикали, но меньше удвоенной ее длины. Через нижний конец вертикали требуется провести между параллелями такую наклонную плоскость, чтобы при подъеме по ней после предшествующего падения по вертикали и за то же время тело прошло по ней отрезок, равный данному.
Пусть даны горизонтали АО и ВС, заключенная между ними вертикаль АВ и отрезок FE, длина которого больше, чем ВА, но меньше удвоенной ее длинны; через точку В требуется провести между горизонталями такую плоскость, чтобы, поднимаясь по ней после падения из А в В и за то же время, в течение которого оно проходит расстояние АВ, тело прошло по ней расстояние, равное данному отрезку EF. Отложим отрезок ED, равный АВ; остаток DF будет меньше АВ, так как EF меньше двух АВ. Отложим, далее, отрезок DI, равный DF, и пусть EI относится к ID, какDF к FX; проведем, наконец, из точки впрямую ВО, равную EX. Утверждаю, что плоскость ВО есть именно та, по которой тело после падения по АВ и за время, затраченное на падение по АВ, пройдет, поднимаясь, пространство, равное данному EF. Отложим отрезки ВR и RS, равные ED и DF; так как EI относится к ID, как DF к FX, то и ED будет относиться к DI, как DX к XF; далее, ED будет относиться к DF, как DX к XF или ЕХ к XD; следовательно, отношение ВО к OR равно отношению ВО к OS. Если положим теперь, что временем
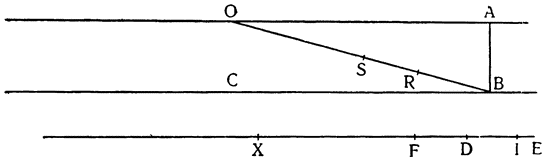 |
Теорема XVII. Предложение XXVII
Если тело падает по плоскостям, имеющим различный наклон, но одинаковую высоту, то пространство, которое оно пройдет по нижней части {287} более длинной плоскости за то же время, в течение которого оно проходит всю более короткую плоскость, равняется сумме длины короткой плоскости с некоторою длиною, к которой длина короткой плоскости относится так же, как длина большей плоскости относится к излишку этой длины над длиною более короткой плоскости.
Даны плоскости АС — большая и АВ — меньшая, имеющие одинаковую высоту AD; отложим на нижней части АС отрезок СЕ, равный
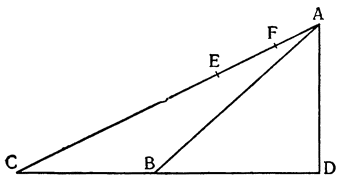 |
Теорема XVIII. Предложение XXVIII
Горизонтальная линия AG касается круга; из точки касания проведен диаметр АВ, а из концов последнего — две хорды АЕ, ЕВ.
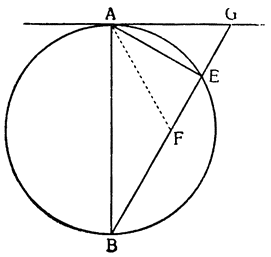 |
Короче следующий способ. Отложим отрезок GF, равный GA; находим, что GF есть средняя пропорциональная между BG и GE, и продолжаем, как выше.
Задача XI. Предложение XXIX
Дан отрезок горизонтали, из одного конца которого восставлен перпендикуляр; от нижней точки последнего отложен вверх отрезок, равный половине данного горизонтального отрезка. Тело, падающее по указанному вертикальному отрезку и продолжающее движение по горизонтали, пройдет оба данных отрезка — горизонтальный и вертикальный — в более короткое время, чем какой-либо другой вертикальный отрезок и тот же горизонтальный.
Дана горизонтальная плоскость и на ней какой-либо отрезок ВС; из конца его В восставлен перпендикуляр, на котором отложен отрезок ВА, равный половине ВС. Утверждаю, что время, в течение которого
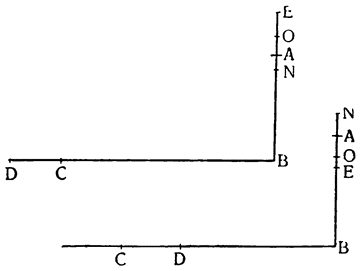 |
Теорема XIX. Предложение XXX
Если из какой-либо точки горизонтали проведена вертикаль, и из некоторой другой точки той же горизонтали должна быть проведена такая наклонная плоскость, по которой тело спускалось бы к той же вертикали в кратчайшее время, то этой плоскостью будет такая, которая отсекает от вертикали часть, равную расстоянию данной на горизонтали точки от конца вертикали.
Пусть дана вертикаль BD, проходящая через точку В горизонтальной линии АС, и какая-либо другая произвольная точка С на этой
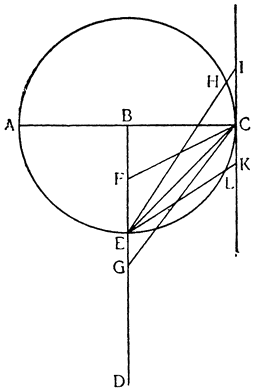 |
Нам уже известно, что время падения по LE равно времени падения по СЕ; время же падения по КЕ больше времени падения по LE; следовательно, время падения по КЕ больше, чем по СЕ, Но время падения по КЕ одинаково с временем падения по CF, так как эти линии равны и {290} имеют одинаковый наклон. Подобным же образом, поскольку CG и IE равны между собою и имеют одинаковый наклон, и время падения по ним одинаково; но время падения по НЕ, более короткой, нежели IЕ, будет короче времени падения по IE; следовательно, время падения по СЕ (равное времени падения по НЕ) будет короче времени падения по IE. Этим и доказывается предложение.
Теорема XX. Предложение XXXI
Если над данной горизонталью провести произвольную наклонную прямую, то наклонной плоскостью, проходящей через данную на горизонтали точку, время падения по которой от наклонной прямой является наименьшим, будет такая наклонная плоскость, которая делит пополам угол, образуемый двумя линиями, проходящими через данную точку горизонтали, из коих одна перпендикулярна к горизонтали, а другая — к наклонной прямой.
Пусть CD — наклонная прямая, расположенная над горизонталью АВ, и А — какая-либо точка горизонтали, из которой проведены линии: АС — перпендикулярно к АВ и АЕ — перпендикулярно к CD. Разделим
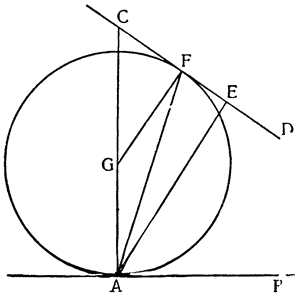 |
Лемма
Если даны два соприкасающихся внутри круга и касательная к внутреннему кругу, пересекающая внешний круг, то три линии, проведенные из точки касания кругов к трем точкам касательной, а именно — точке {291} касания таковой с внутренним кругом и точкам пересечения ее с внешним кругом, образуют при точке касания кругов одинаковые углы.
Пусть точка А является точкою касания двух кругов, причем центр меньшего из них лежит в точке В, а большего — в точке С; пусть, далее,
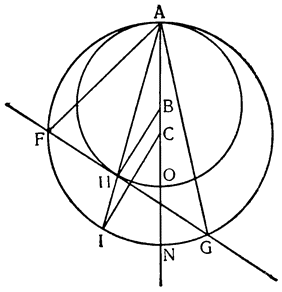 |
Теорема XXI. Предложение XXXII
Если на данной горизонтали взять две точки и провести через одну из них какую-либо наклонную линию, направленную в сторону другой точки, а затем провести через эту последнюю наклонную прямую, отделяющую от начальной точки наклонной часть, равную расстоянию между данными точками горизонтали, то падение по такой линии будет происходить быстрее, нежели по любой другой прямой, проведенной из той же точки к наклонной. По другим линиям, образующим с указанной прямой равные углы, падение будет совершаться в одинаковое время.
Пусть даны две точки А и В, расположенные на горизонтали, и наклонная прямая ВС, проходящая через В, от конца которой В отложен отрезок BD, равный ВА. Соединим точки A, D. Утверждаю, что падение по линии AD происходит быстрее, чем по любой другой линии, проведенной из точки А к наклонной ВС. Проведем из точек А и D линии АЕ и DE, перпендикулярные к ВА к BD и пересекающиеся в точке Е. В равнобедренном треугольнике ABD углы BAD и BDA равны; следовательно, углы DAE и EDA, дополнительные до прямого, также равны: поэтому круг, описанный из центра Е радиусом, равным ЕА, пройдет через точку {292} D и прикоснется к линиям ВА и BD в точках А и D. Так как А является конечной точкой перпендикуляра АЕ, то падение по AD потребует меньше
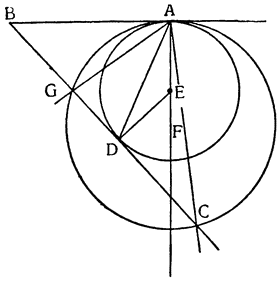 |
Задача XII. Предложение XXXIII
Даны вертикаль и наклонная плоскость, имеющие общую верхнюю точку, причем высота наклонной плоскости равна длине вертикали. Найти на вертикали такую точку, расположенную выше общей конечной точки, чтобы после падения из нее движение продолжалось по наклонной плоскости столько же времени, сколько и падение по вертикали после выхода тела из состояния покоя в указанной общей верхней точке.
Пусть АВ и АС — вертикаль и наклонная плоскость, причем длина
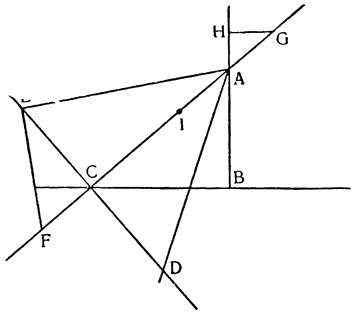 |
Положим, что временем падения по вертикали АВ является АВ; тогда временем падения по АС из начальной точки покоя в А будет АС. Так как в прямоугольном треугольнике AEF линия ЕС является перпендикуляром, опущенным из вершины прямого угла Е на основание AF, то АЕ будет средней пропорциональной между FA и АС, а СЕ — средней пропорциональной между АС и CF или СА и AI. Так как временем падения по АС из точки А является АС, то АЕ будет временем падения по AF, а ЕС — по AI. Так как, далее, в равнобедренном треугольнике AED стороны АЕ и ED равны, то ED будет временем падения по AF, а ЕС — по AI. Следовательно, CD или АВ есть время падения по IF из начальной точки А; иными словами, АВ есть время падения по АС из точки G или Н, что и требовалось доказать.
Задача XIII. Предложение XXXIV
Даны наклонная плоскость и вертикаль, имеющие общую верхнюю точку; найти на продолжении вертикали такую вышележащую точку, чтобы, падая из нее и продолжая затем движение по наклонной плоскости, тело затратило на весь этот путь столько же времени, сколько и на падение по одной наклонной плоскости от верхнего ее конца.
Пусть АВ и АС наклонная плоскость и вертикаль, имеющие общую высшую точку А; на продолжении вертикали требуется найти такую
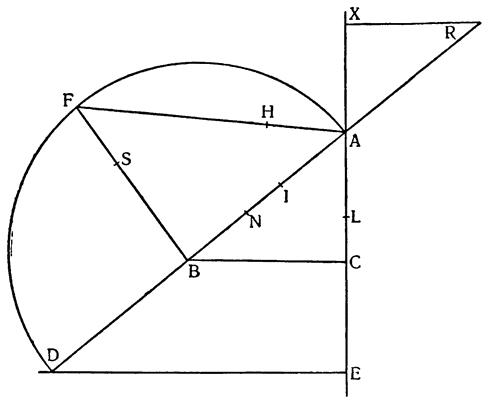 |
Проведем горизонталь ХВ, параллельную ВС и встречающую продолжение линии ВА в точке В; затем, продолжив АВ, проведем линию ED, параллельную СВ и пересекающую продолжение наклонной плоскости в точке D, построим на AD, как на диаметре, полукруг и проведем из точки В линию BF, перпендикулярную к DA и пересекающую окружность. Ясно, что FB будет средней пропорциональной между АВ и BD, а линия, соединяющая точки F и А — средней пропорциональной между DA и АВ, Отложим отрезок BS, равный BI, и FH, равный FB. Отношение АВ к BD равно отношению АС к СЕ, а так как BF есть средняя пропорциональная между АВ и BD и BI — средняя пропорциональная между АС и СЕ, то отношение ВА к АС равно отношению FB к BS. Так как, далее, ВА относится к АС или AN, как FB к BS, то BF будет относиться к FS, как АВ к BN или как AL к LC. Поэтому прямоугольник с размерами FB и CL будет равен прямоугольнику с размерами AL и SF; но последний прямоугольник AL, SF есть излишек прямоугольника из AL, FB или AI, BF над прямоугольником AI, BS или AI, IB, прямоугольник же FB, LC есть излишек прямоугольника AC, BF над прямоугольником AL, BF. Прямоугольник AC, BF со своей стороны равняется прямоугольнику АВ, ВI (ибо отношение ВА к АС равно отношению FB к BI). Поэтому излишек прямоугольника АВ, BI над прямоугольником AI, BF или равным ему AI, FH равняется излишку прямоугольника AI, FH над прямоугольником AI, IB; следовательно, удвоенный прямоугольник AI, FN равняется сумме прямоугольников АВ, BI и AI, IB или же удвоенному прямоугольнику AI, IB, сложенному с квадратом BI. Если прибавить теперь по квадрату AI, то удвоенный прямоугольник AI, IB, сложенный с обоими квадратами AI и IB, т. е. иначе квадрат АВ будет равняться удвоенному прямоугольнику AI, FH, сложенному с квадратом AI. Если снова прибавить по квадрату BF, то сумма квадратов АВ и BF, т. е. один квадрат AF, будет равна удвоенному прямоугольнику AI, FN, сложенному с суммою квадратов AI и FB, т. е. AI и FN. Но квадрат AF равен удвоенному прямоугольнику АН, HF, сложенному с квадратами АН и HF; следовательно, удвоенный прямоугольник AI, FH вместе с квадратами AI и FH равняется удвоенному прямоугольнику АН, HF вместе с квадратами АН и HF; если же мы отнимем по квадрату HF, то получим, что удвоенный прямоугольник AI, FH вместе с квадратом AI будет равен удвоенному прямоугольнику АН, HF, сложенному с квадратом АН. Так как сторона FH является общей для обоих прямоугольников, то линия АН должна быть равна AI; в самом деле, если бы она была больше или меньше, то прямоугольник FH, НА вместе с квадратом {295} НА был бы больше или меньше прямоугольника FH, IA вместе с квадратом IA, что противоречило бы доказанному.
Положим теперь, что временем падения по АВ является АВ; тогда временем падения по АС будет AC; IB — средняя пропорциональная между АС и СЕ — будет временем падения по СЕ, а вместе с тем и по ХА, в случае начала движения из точки X. Так как средней пропорциональной между DA и АВ или RВ и ВА является AF, а средней пропорциональной между АВ и BD или же между ВА и АВ является BF или равная ей линия FH, то, согласно доказанному выше, излишек АН будет временем падения по АВ в случае начала движения из точки В или, что то же самое, из точки X, тогда как время падения по той же линии АВ из точки А было принято равным АВ. Далее, временем падения по ХА является IB, время же движения по АВ, после падения по ВА или, что то же самое, по ХА, равно AI. Следовательно, время движения по пути ХАВ будет равно АВ, т. е. тому времени, которое необходимо для прохождения одной линии АВ в случае начала движения из точки А. Таким образом, предложение доказано35.
Задача XIV. Предложение XXXV
Даны вертикаль и наклонная к ней плоскость; найти часть последней, которая проходится телом, падающим только по ней, за то же время, как и вертикаль вместе с указанной частью наклонной плоскости.
Пусть АВ — данная вертикаль и ВС — наклонная плоскость; требуется найти такую часть ВС, которая проходится телом, падающим только
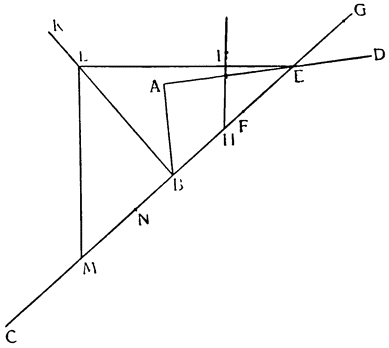 |
Короче следующий способ.
Пусть ВС — наклонная плоскость и АВ — вертикаль. Проведем из точки В линию, перпендикулярную к ЕС, продолжим ее в обе стороны, отложим отрезок ВН, равный излишку отрезка BE над ВА, и построим
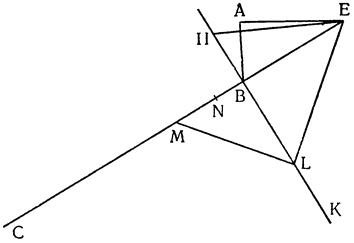 |
Лемма
Пусть линия DC перпендикулярна к диаметру ВА; проведем через точку В какую-либо прямую BED (или BDE) и соединим точки В, F.
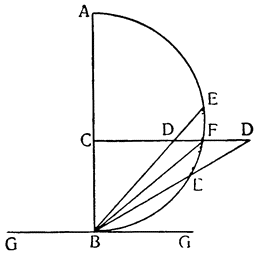 |
Лемма
Пусть линия АС больше линии DF и отношение АВ к ВС больше отношения DE к EF. Утверждаю, что АВ будет больше DE. Так как отношение
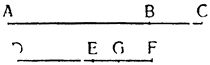 |
EG. Так как АВ относится к ВС, как DE к EG, то, складывая почленно, получаем, что СА относится к АВ, как GD к DE; но СА больше GD, следовательно, и ВА больше DЕ.
Лемма
Пусть дан квадрант ACIB и из точки В проведена линия BE, параллельная АС. Опишем из какой-либо точки этой прямой, как из центра, окружность BOES, касающуюся линии АВ в точке В и пересекающую дугу квадранта в точке I. Проведем, далее, линии СВ и CI и продолжим последнюю до точки S. Утверждаю, что линия CI всегда будет меньше линии СО. Если мы соединим точки А и I прямой, то последняя будет касательной к кругу ВОЕ. В самом деле, если провести линию DI, то она будет равна DB; а так как DB является касательной к квадранту, то и DI будет касательной к нему и перпендикулярной к диаметру AI; следовательно, AI будет касательной к кругу ВОЕ в точке I. Так как угол AIC {298} больше угла ABC, как стягиваемый большей дугой, то и угол SIN будет больше угла ABC; поэтому дуга IES будет больше дуги ВО, а линия CS, как лежащая ближе к центру, будет больше СВ; следовательно, и СО будет больше CI, так как отношение SC к СВ равно отношению OС к CI.
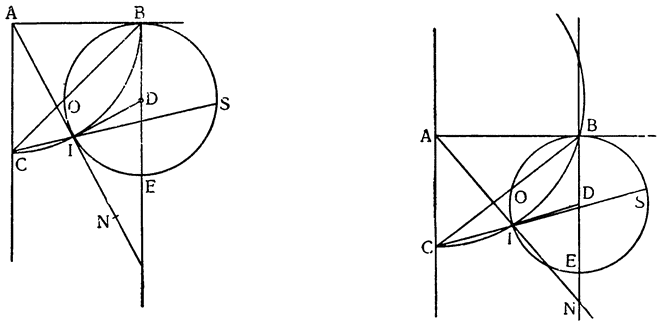
То же имеет место, когда дуга BIC меньше квадранта. В самом деле, в этом случае перпендикуляр DB пересекает круг CIB, линии DI и DB равны между собой, угол DIA является тупым, а линия AIN пересекает круг BIE. Так как угол ABC меньше угла AIC, а последний равняется углу SIN, который, в свою очередь, меньше угла, образуемого линией SI с касательной в точке I, то, следовательно, дуга SEI длиннее дуги ВО и т. д., что и требовалось доказать.
Теорема XXII. Предложение XXXVI
Если из нижней точки круга, возвышающегося над горизонтом, провести плоскость, отсекающую дугу, меньшую квадранта, и из конечных точек этой плоскости провести к какой-либо промежуточной точке дуги две какие угодно плоскости, то время падения по этим двум последним плоскостям будет меньше, чем по одной первоначальной плоскости, и меньше, чем по нижней из двух последних плоскостей.
Дан возвышающийся над горизонтом круг, низшей точкой которого является С, причем дуга его CBD не превышает квадранта. В этом круге проведена плоскость CD, из концов которой D и С проведены к лежащей между ними точке окружности В еще две плоскости. Утверждаю, что время падения по последним двум плоскостям DBC короче времени падения по одной плоскости DC, а также и по одной ВС в случае падения из точки В. Проведем через точку D горизонталь MDA, пересекающую продолжение {299} линии СВ в точке А; проведем далее линии DN и МС, перпендикулярные к MD, и линию BN, перпендикулярную к BD; опишем затем около прямоугольного треугольника DBN полукруг DFBN, пересекающий DC в F, и отложим линию DO — среднюю пропорциональную CD и DF, а также AV — среднюю пропорциональную между СА и АВ. Положим теперь, что PS есть время падения по всей линии DC, a равно и по линии ВС (так как нам уже известно, что время падения по ним одинаково). Пусть, далее, отношение отрезка CD к DO равно отношению времени SP ко времени PR; тогда PR будет временем падения по DF в случае начала движения от D, a RS будет временем прохождения остатка FC. Но PS является также временем падения по ВС в случае начала движения от В; поэтому, если принять, что отношение ВС к CD равно отношению SP к РТ, то РТ будет временем падения от А до С, ибо DC, как уже было доказано, есть средняя пропорциональная между АС и СВ. Положим, далее, что отношение СА к AV равно отношению ТР к PG; тогда PG будет временем падения от А до В, a GT временем падения по остатку ВС, после прохождения телом пространства от А до В. Но так как DN представляет собою перпендикулярный к горизонту диаметр круга DFN, то время падения тела по линиям DF и DB одинаково; если, таким образом, мы сможем доказать, что тело скорее пройдет расстояние ВС после падения по DB, чем расстояние FC после падения по DF, то теорема будет доказана. Но тело движется по линии ВС с одинаковою скоростью как после падения по DB из точки D, так и после падения по АВ из точки А, ибо предшествующее падение по DB и АВ сообщает ему одинаковые
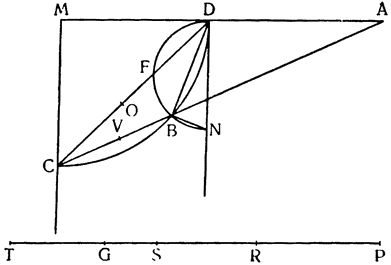 |
Замечание
Из доказанного выше можно заключить, что быстрейшее движение от одной конечной точки до другой происходит не по кратчайшей линии, каковой является прямая, а по дуге окружности. В самом деле, разделим дугу АС квадранта ВАЕС, сторона которого ВС перпендикулярна к горизонту, на произвольное число равных частей AD, DE, EF, FG, GC, проведем из С прямые к точкам A, D, Е, F, G и соединим те же точки линиями AD, DE, EF, FG, GC. Ясно, что падение по ломаной линии ADC совершается скорее, нежели по прямой АС, а также по прямой DC в случае начала движения из точки D. Но в случае начала движения из точки А расстояние DC проходится быстрее, чем ломаная ADC; точно так же ломаная линия DEC проходится быстрее, нежели прямая CD, в случае падения тела из А; следовательно, падение по ломаной линии ADEC, состоящей из трех частей, требует меньше времени, нежели падение по линии АОС, состоящей из двух частей. Подобным же образом падение по EFC после предшествующего падения по ADE происходит быстрее, нежели по одной ЕС, и падение по ломаной линии ADEFC, состоящей из четырех частей, требует меньше времени, чем падение по ломаной линии ADEC, состоящей из трех частей. Наконец, падение по ломаной FGC, состоящей из двух частей, после предшествующего падения по ADEF, требует меньше времени, нежели падение по прямой FC. Следовательно, падение по ломаной линии ADEFGC, состоящей из пяти частей, требует меньшего времени, чем падение по ломаной линии ADEFC, состоящей из четырех частей. Таким образом, чем более вписанный многоугольник приближается к окружности, чем быстрее совершается падение между двумя конечными {301} точками А и С. То, что было доказано относительно квадранта, справедливо и в отношении дуг, меньших четверти окружности; рассуждение остается тем же самым36.
Задача XV. Предложение XXXVII
Даны вертикаль и наклонная плоскость, имеющие одинаковую высоту; найти на наклонной плоскости такую часть, равную по величине вертикали, движение по которой требовало бы столько же времени, сколько и падение по вертикали.
Пусть даны АВ — вертикаль и АС — наклонная плоскость; требуется найти на наклонной плоскости такую часть, равную по длине вертикали АВ, которая проходилась бы телом, начинающим движение из точки А, за то же время, как и вертикаль в случае падения тела из той же точки. Отложим отрезок AD, равный АВ, и разделим DC пополам в точке I. Пусть, далее, отношение АС к CI равно отношению CI к некоторой линии АЕ, равную которой и отложим как DG; таким образом, EG будет равняться AD или АВ. Утверждаю, что EG и будет той частью
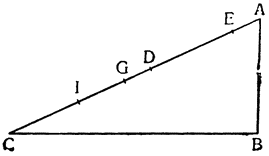 |
Следствие
Из изложенного следует, что искомое расстояние расположено между верхним и нижним отрезками наклонной плоскости, проходимыми движущимся телом в равные промежутки времени37.
| {302} |
Задача XVI. Предложение XXXVIII
Даны две горизонтальные плоскости и пересекающая их вертикаль; найти на последней такую вышележащую точку, при падении из которой тела, продолжающие дальнейшее движение по верхней и нижней горизонтали, проходили бы в равные промежутки времени расстояния, находящиеся между собою в данном отношении.
Даны горизонтальные плоскости CD и BE, пересекаемые вертикалью АСВ, и отношение меньшего пути к большему, равное отношению N к FG; требуется найти на вертикали АВ такую вышележащую точку, при падении из которой тело, продолжающее движение по плоскости CD, прошло бы за время, равное времени его падения по вертикали, расстояние, находящееся в отношении N к FG к расстоянию, проходимому другим телом при движении его по плоскости BЕ после падения из той же точки
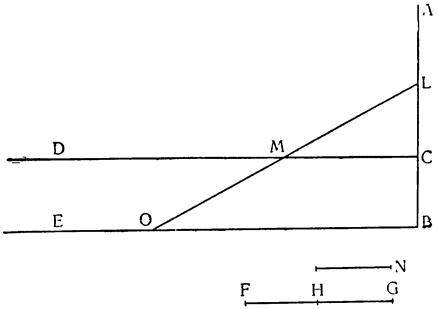 |
Сагредо. Мне кажется, можно, действительно признать, что со стороны нашего Академика не было хвастовством утверждение в начале этого трактата, что он создал новую науку, касающуюся очень старого предмета. Меня приводит в изумление, с какою легкостью и ясностью он выводит из одного простейшего принципа доказательства стольких предложений, а также и то, каким образом этот предмет остался незатронутым Архимедом, Аполлонием, Эвклидом и столькими другими знаменитыми {303} математиками и философами, несмотря на то, что о движении тел написано немало больших томов.
Сальвиати. У Эвклида имеется небольшой отрывок, касающийся движения, но там не видно и намека на то, что он пошел по пути исследования того, как происходит ускорение и как оно изменяется при различных наклонах. Таким образом, можно с полным правом сказать, что только теперь открылись двери для новых исследований, которые могут иметь результатом множество новых удивительных заключений и выводов, если в будущем этим предметом займутся другие ученые.
Сагредо. Я твердо верю, что как немногие свойства круга, установленные в третьей книге «Элементов» Эвклида (говоря для примера), послужили исходным пунктом для обнаружения множества других, более скрытых соотношений, так и то, что изложено и доказано в настоящем кратком трактате, попав в руки других пытливых исследователей, укажет им путь ко многим удивительным открытиям; мне думается, что, так оно и будет, так этот предмет своей значительностью превосходит все другие явления природы.
Беседа нынешнего дня была достаточно продолжительной и трудной, и в течение нее я получал большее удовольствие от простых предложений, нежели от доказательств; из последних многие таковы, что для уяснения их мне необходимо потратить более часа на каждое. Подобной работой я займусь как-нибудь на досуге и просил бы вас, синьоры, оставить мне книгу, после того как мы познакомимся с оставшейся частью ее, касающейся движения тел бросаемых, что можно было бы сделать завтра, если только вы согласны.
Сальвиати. Я всегда готов к вашим услугам.
Конец третьего дня
| {304} |
С |
До сих пор мы рассматривали то, что происходит при равномерном движении и при естественно-ускоренном движении по любым наклонным плоскостям. В дальнейшем я сделаю попытку описать некоторые свойства (а они достойны изучения), сопровождая изложение надежными доказательствами, относящимися к движению тел, которое слагается из двух частей, а именно, движения равномерного и движения естественно-ускоренного, потому что таково движение тел бросаемых и так именно я его образую.
Когда тело движется по горизонтальной плоскости, не встречая никакого сопротивления движению, то, как мы уже знаем из всего того, что было изложено выше, движение его является равномерным и продолжалось бы постоянно, если бы плоскость простиралась в пространстве без конца. Если же плоскость конечна и расположена высоко, то тело, имеющее вес, достигнув конца плоскости, продолжает двигаться далее таким образом, что к его первоначальному равномерному беспрепятственному {305} движению присоединяется другое, вызываемое силою тяжести, благодаря чему возникает сложное движение, слагающееся из равномерного горизонтального и естественно-ускоренного вниз; его я называю движением бросаемых тел. Мы докажем некоторые его свойства, и первым будет следующее.
Теорема I. Предложение I
При сложном движении, слагающемся из равномерного горизонтального и естественно-ускоренного движений, бросаемое тело описывает полупараболу.
Сагредо. Синьор Сальвиати, в интересах моих, а также, думаю, и синьора Симпличио, нам следовало бы сделать небольшую остановку. Я не чувствую себя настолько сведущим в геометрии, чтобы свободно пользоваться трудами Аполлония, писавшего о параболах и других конических сечениях; без знакомства же с этими линиями и их свойствами, я думаю, мы едва ли сможем понять доказательства соответствующих предложений. А так как уже в первом прекрасном предложении нашего Автора требуется доказать, что путь, описываемый брошенным телом, есть парабола, то я полагаю, что мы сперва должны заняться не чем иным, как этими линиями; нам безусловно необходимо основательно ознакомиться, если не со всеми свойствами их, доказанными Аполлонием, то по крайней мере с теми, которые требуются для понимания данного предмета.
Сальвиати. Только излишней скромности с вашей стороны, синьор, могу я приписать ваше желание возвратиться к тому, что немного времени тому назад принималось нами за достаточно хорошо известное; я имею в виду то место трактата о сопротивлении, которое требовало приложения некоторых предложений Аполлония и которое не представило для вас никаких затруднений.
Сагредо. Может быть, я случайно был знаком с ними или же допустил их как известные, в том случае, когда это понадобилось всего один раз в целом трактате; но здесь, где, как кажется, все доказательства будут связаны с подобными линиями, нет надобности экономить время и труд и как бы пить залпом.
Симпличио. Замечу со своей стороны, что, если синьор Сагредо, как кажется, достаточно хорошо вооружен для данного случая, то я встречаю даже первоначальные предпосылки как нечто совершенно новое. Хотя наши философы и занимались вопросом о движении бросаемых тел, но мне не помнится, чтобы они устанавливали, каковы именно линии, описываемые телами; за исключением случаев падения вниз по вертикали, они определяют эти линии вообще только как кривые. Далее, если те немногие {306} познания по геометрии, которые я почерпнул у Эвклида за время наших предшествующих бесед, недостаточны для того, чтобы дать возможность понимать последующие доказательства, то мне придется принимать предложения исключительно на веру, а не усваивать их.
Сальвиати. В таком случае будьте благодарны Автору трактата, который, допустив меня к ознакомлению с настоящим сочинением и узнав, что я в то время не имел под руками книги Аполлония, доказал мне без особых предварительных рассуждений два основных свойства параболических линий, которые и нужны нам в настоящем трактате; эти свойства доказываются также и Аполлонием, но среди многих иных, ознакомление с которыми заняло бы слишком много времени. Я постараюсь возможно сократить путь и вывести первое свойство из самого способа образования параболы, а на основании этого первого свойства тотчас же доказать второе. Итак, приступим к изложению первого вопроса.
Представьте себе прямой конус, основанием которого является круг ibkc, а вершиною — точка l; плоскость, параллельная стороне его lk, пересекает его по линии bас, называемой параболой; основание последней be пересекает диаметр ik круга ibkc под прямым углом, ось же параболы — ad — параллельна стороне lk. Возьмем на кривой bfa любую точку f и проведем через нее прямую линию fe, параллельную bd. Утверждаю, что квадрат bd относится к квадрату fe, как ось da к части ее ае. Представим себе, что через точку е проведена плоскость, параллельная кругу ibkc;
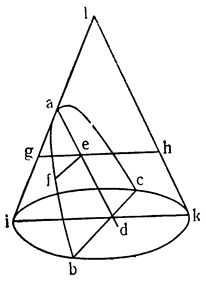 |
Второе предложение, необходимое для настоящего трактата, доказывается следующим образом. Начертим параболу, продолжим ось ее са по направлению к точке d и через какую-либо точку ее b проведем линию bc, {307} параллельную основанию параболы. Если теперь отложим отрезок da, равный части оси еа, то утверждаю, что прямая линия, проведенная через точки d и b, не пересечет параболы, пройдет вне ее и только прикоснется к ней в точке b. Допустим иное, т. е. что прямая линия сверху входит внутрь
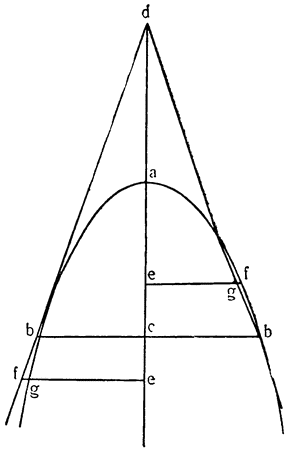 |
Симпличио. Вы слишком быстро подвигаетесь в ваших доказательствах и, кажется, неизменно полагаете, что все теоремы Эвклида мне так же хорошо известны, как и первые его аксиомы, чего на самом деле нет. Вот и сейчас, ваше положение, что четыре прямоугольника ead меньше квадрата de, потому что части еа и ad линии ed неравны, для меня непонятно и оставляет во мне сомнение.
Сальвиати. Действительно, все ученые математики предполагают, что читатель хорошо знаком по крайней мере с «Элементами» Эвклида. Чтобы помочь вам разобраться в возбужденном вами вопросе, мне будет достаточно напомнить одно из предложений последнего, в котором доказывается, что когда линия разделена сперва на две равные, а затем две неравные части, то прямоугольник, построенный из неравных частей, менее прямоугольника, построенного из равных (т. е. квадрата половины данной линии), на величину квадрата отрезка, заключенного между {308} точками деления; отсюда следует, что квадрат целого, содержащий в себе четыре квадрата половины, больше четырех прямоугольников, построенных
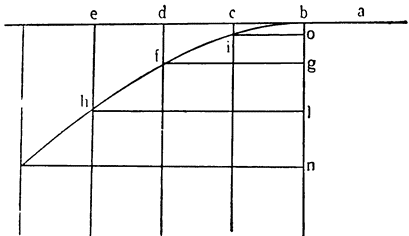 |
Представим себе высоко расположенную горизонтальную линию или плоскость ab, между точками которой a и b равномерно движется тело; за отсутствием дальнейшей поддержки со стороны плоскости тело будет стремиться, вследствие своей тяжести, двигаться от точки b как естественно падающее вдоль вертикали bn. Предположим, что плоскость аb продолжена на расстояние be, которое будет служить для измерения времени, и отложим на этой линии произвольные, но равные промежутки времени be, cd, de. Проведем через точки b, с, d, e линии, параллельные вертикали bn, а затем отложим на первой из этих линий произвольный отрезок ci, на следующей — в четыре раза больший отрезок df, на третьей — в девять раз больший отрезок eh, так что указанные отрезки будут относиться между собою, как квадраты линий cb, db, eb. Если мы представим себе теперь, что к равномерному движению тела от a до с присоединяется падение по вертикали на величину ci, то через промежуток времени be оно будет находиться в точке i. Рассуждая таким же образом, найдем, что через промежуток времени db, равный удвоенному dc, тело упадет на расстояние в четыре раза большее первоначального ci, ибо, как уже было доказано в первом трактате, расстояния, проходимые телами при естественно-ускоренном движении, относятся между собою, как квадраты времен падения. Подобным же образом находим, что пространство eh, пройденное за время be, равняется девяти ci и что вообще пространства eh, df, ci относятся между собою, как квадраты линий eb, db, cb. Проведем через точки i, f, h прямые линии io, fg, hi, параллельные eb. Линии hi, fg, io будут соответственно равны линиям eb, db, cb; равным образом и линии bo, bg, bl будут соответственно равны линиям ci, df, eh. Поэтому отношение квадрата hi к квадрату fg {309} будет равно отношению линии lb к bg, а отношение квадрата fg к квадрату io равно отношению линии gb к bo; следовательно, точки i, f и h расположены на параболе. Взяв любые другие равные отрезки, соответствующие времени движения тела, можно подобным же образом доказать, что все места, занимаемые телом при таком сложном движении, лежат на параболической линии; следовательно, предложение доказано.
Сальвиати. Это заключение вытекает из положения, обратного первой из двух приведенных выше вспомогательных теорем. Предположим, в самом деле, что через точки b и h проведена парабола; если бы какая-либо из двух промежуточных точек f или i не была расположена на параболе, то она лежала бы или внутри или вне последней, и линия fg была бы меньше или больше той линии, которая доходила бы до параболы; поэтому отношение, равное отношению линий lb и bg, имели бы не квадраты hl и fg, а первый из них и какой-либо иной квадрат, большей или меньшей величины. Но мы знаем, что в действительности указанное отношение к первому квадрату имеет именно квадрат fg; следовательно, точка f лежит на параболе, равно как и все остальные точки.
Сагредо. Не могу отрицать, что рассуждение ново, остроумно и доказательно; если исходить из предположения, что движение в поперечном направлении остается всегда равномерным, а естественное падение сохраняет свою особенность ускоряться пропорционально квадрату времени, и что такие движения и скорости слагаются, но не мешают и не препятствуют друг другу, благодаря чему и при продолжительном движении описываемая телом линия не изменяет в конце концов своего вида. Это, однако, представляется мне совершенно невозможным. В самом деле, ось нашей параболы, вдоль которой, как мы полагаем, совершается естественное падение тяжелых тел, должна быть перпендикулярной к горизонту и оканчиваться в центре Земли. Так как параболическая линия идет, постоянно удаляясь от своей оси, то никакое брошенное тело не может окончить движения в центре; если же оно это может, что, кажется, необходимо признать, то линия падения его должна быть какой-либо иной кривой, отличной от параболы3.
Симпличио. К этому затруднению я прибавлю еще и другие. Одно из них заключается в следующем: мы предположили, что горизонтальная плоскость, не имеющая ни наклона, ни подъема, представляет собой как бы прямую линию и что подобная линия во всех своих частях равноудалена от центра; это, однако, неправильно, ибо она идет от середины к концам, постоянно удаляясь от центра, и, следовательно, постоянно повышается. Отсюда как следствие вытекает, что движение не может быть постоянным, что равномерность его не сохраняется даже на коротком расстоянии и что оно постепенно замедляется. Кроме того, я думаю, что невозможно отбросить сопротивление среды, которое препятствует как {310} равномерности движения в поперечном направлении, так и закономерности ускоренного движения падающих тел. В силу всех этих затруднений весьма неправдоподобно, чтобы выводы, основанные на столь неверных предпосылках, могли быть подтверждены практически опытами.
Сальвиати. Все выдвигаемые вами затруднения и возражения настолько основательны, что устранить их невозможно; что касается меня, то я все их принимаю и полагаю, что наш Автор также не стал бы их отрицать. Я допускаю, далее, что выводы, сделанные абстрактным путем, видоизменяются в конкретных случаях и настолько искажаются, что ни поперечное движение не будет равномерным, ни ускоренное движение при падении не будет соответствовать выведенной пропорции, ни траектория брошенного тела не будет параболой и т. д. С другой стороны, я прошу вас разрешить нашему Автору принимать то, что принималось некоторыми величайшими мужами, хотя и неправильно. Авторитет одного Архимеда должен успокоить в этом отношении кого угодно. В своей Механике и в книге о квадратуре параболы он4 принимает, как правильный принцип, что коромысло весов является прямой линией, равноудаленной во всех своих точках от общего центра всех тяжелых тел, и что нити, к которым подвешены тяжелые тела, параллельны между собою. Подобные допущения всеми принимались, ибо на практике инструменты и величины, с которыми мы имеем дело, столь ничтожны по сравнению с огромным расстоянием, отделяющим нас от центра земного шара, что мы смело можем принять шестидесятую часть градуса соответствующей весьма большой окружности за прямую линию, а два перпендикуляра, опущенные из ее концов,— за параллельные линии. Если бы в наших практических делах нам следовало считаться с подобными ничтожными величинами, то нам прежде всего пришлось бы осудить архитекторов, которые берутся воздвигать при помощи отвеса высокие башни с параллельными стенами. В дополнение мы можем сказать, что как Архимед, так и другие ученые исходили в своих рассуждениях из предположения бесконечной удаленности от нас земного центра, а тогда их предпосылки совершенно справедливы и доказательства абсолютно строги. Поэтому, когда мы хотим проверить на практике в конечном пространстве те выводы, которые сделаны в предположении бесконечного удаления, необходимо, кроме точно доказанного, учесть значение не бесконечной удаленности нашей от центра, хотя последнюю можно считать огромной по сравнению с малым размахом действий, которые мы применяем. Наибольших отклонений можно ожидать при бросании тел, особенно при стрельбе из артиллерийских орудий; но и в этом случае выпущенное ядро пролетает в самом лучшем случае четыре мили, тогда как от центра Земли нас отделяет почти столько же тысяч миль; заканчивая свое движение у земной поверхности, снаряд может лишь незначительно изменить параболическую линию, {311} которая, следует признать, в конце концов видоизменялась бы при приближении к центру.
Что касается, далее, неблагоприятного влияния сопротивления среды, то оно более значительно; при этом действие сопротивления настолько разнообразно в отдельных случаях, что подвести его под одно твердое правило и разъяснить его невозможно. Если даже мы будем рассматривать одно только сопротивление изучаемому нами движению со стороны воздуха, то найдем, что оно вносит изменения во все движения, и притом изменения бесконечно разнообразные, в зависимости от бесконечного разнообразия формы, веса и скорости движущихся тел. Так, в отношении, например, скорости надо заметить, что чем она будет большею, тем больше будет и сопротивление движению, оказываемое воздухом. Это сопротивление будет сказываться на телах все сильнее, по мере того как уменьшается их вес. Таким образом, хотя тяжелое падающее тело должно двигаться ускоренно, проходя пути, пропорциональные квадрату продолжительности движения, все же какой бы большой вес ни имело тело, сопротивление воздуха при падении тела с очень большой высоты будет столь значительным, что дальнейшее нарастание скорости станет невозможным, и движение превратится в однообразное и равномерное; подобный результат обнаружится тем скорее и при тем меньшей высоте, чем меньше будет вес тела. Равным образом, то движение по горизонтальной плоскости, которое в случае устранения всех препятствий должно было бы оставаться равномерным и неизменным, будет замедлено и, наконец, совершенно остановлено сопротивлением воздуха; и произойдет это тем скорее, чем легче будет тело. Так как вес, скорость и форма тел могут быть в разных случаях бесконечно разнообразными, то в отношении них невозможно дать какие-либо определенные правила. Поэтому для научного трактования такого предмета необходимо сперва отвлечься от всего этого, а найдя и доказав положения, не приняв во внимание сопротивление, пользоваться ими на практике в тех пределах, которые укажет опыт. Польза от этого будет немалая. Вещество и форму можно при этом выбрать такими, чтобы сопротивление среды сказывалось возможно меньше; поэтому тела должны быть взяты возможно более тяжелыми и круглой формы; что же касается расстояний и скоростей, то они не должны быть столь большими, чтобы мы не могли легко и точно их измерить. У снарядов, которые мы применяем и которые делаются круглой формы из тяжелого вещества, и даже у тел, менее тяжелых и имеющих цилиндрическую форму,— как, например, стрелы, брошенные посредством пращи или лука,—отклонения их движения от точной параболической линии почти незаметно. То, что при обычно применяемых нами приспособлениях малость размеров делает почти незаметными внешние и случайные воздействия, наибольшим из которых является сопротивление среды, я могу показать вам на двух {312} примерах. Я буду рассматривать движения, происходящие в воздухе, потому что о них главным образом идет речь. Воздух проявляет свою силу по отношению к движению в двух направлениях: во-первых, он сильнее препятствует движению тел менее тяжелых, чем более тяжелых; во-вторых, он оказывает более сильное сопротивление при большей скорости, чем при меньшей скорости движения тела. Что касается первого явления, то опыт показывает нам, что два шарика одинаковой величины, из коих один весит в десять или двенадцать раз более другого (а такое отношение веса существует, например, у шариков из свинца и дуба), достигают земли при падении с высоты от 150 до 200 локтей с самой незначительной разницей в скорости; это показывает нам, что сопротивление воздуха и замедление движения обоих тел очень мало. Если бы свинцовый шарик, начавший движение в тот же самый момент, что и деревянный, задерживался в своем движении менее, нежели этот последний, то при довольно значительной высоте свинец, будучи в десять раз тяжелее дерева, должен был бы при падении на землю оставить за собою последнее. В действительности этого не случается: свинцовый шарик не обгоняет деревянного и на одну сотую часть всей высоты; если же взять один шарик из свинца, а другой из камня, причем последний весил бы треть или половину первого, то едва ли можно будет даже заметить разницу в моментах достижения ими земли. Таким образом, принимая во внимание, что импульс, приобретаемый свинцовым шариком при падении с высоты 200 локтей (т. е. такой, что тело могло бы при дальнейшем равномерном движении пройти 400 локтей за то же время, в течение которого оно совершило падение), достаточно велик по сравнению со скоростью, сообщаемой телам, бросаемым луками и другими метательными орудиями (за исключением огнестрельных), мы можем без значительной ошибки устанавливать положения, не считаясь с изменениями, вносимыми сопротивлением среды, и считать их абсолютно правильными. Относительно второго явления можно указать, что сопротивление, испытываемое телом со стороны воздуха при быстром движении, не особенно значительно превышает то, которое тело испытывает при медленном движении; следующий опыт дает этому решительное доказательство. Подвесим на двух нитях одинаковой длины, в четыре или пять локтей, два одинаковых свинцовых шарика и, закрепив верхние концы этих нитей, выведем шарики из отвесного положения, отклонив, однако, один из них на 80 или более градусов, а другой всего на четыре-пять градусов; будучи отпущены на свободу, шарики эти, переходя за вертикаль, станут описывать: первый — большие дуги в 160, 150, 140 градусов и т. д., а второй — малые дуги в десять, восемь, шесть градусов и т. д., причем как те, так и другие будут постепенно уменьшаться. Утверждаю, что первый маятник описывает свои дуги в 180, 160 и т. д. градусов в такой же промежуток времени, как второй свои {313} дуги — в десять, восемь и т. д. градусов. Ясно, что скорость движения первого шарика в шестнадцать или восемнадцать раз больше скорости второго; если бы поэтому большая скорость замедлялась действием воздуха в большей степени, нежели меньшая, то колебания в широких пределах 180—160 градусов должны бы были быть реже, нежели колебания в малых пределах десяти, восьми, четырех градусов, а тем более двух или одного. Но это опровергается опытом: если два наблюдателя начнут считать колебания — один большие, а другой малые, то, сосчитав до десяти и даже до ста, они не разойдутся не только на одно колебание, но даже и на малую часть его. Это наблюдение сразу подтверждает два положения: первое, что большие и малые колебания совершаются все в одни и те же равные промежутки времени, и второе, что сопротивление и замедление движения, обусловливаемые воздухом, сказываются при быстром движении не в большей степени, чем при медленном движении,— обратно тому, что нам ранее казалось и что мы прежде принимали5.
Сагредо. Таким образом, если нельзя отрицать, что воздух оказывает действие в обоих случаях и что поэтому движение замедляется, пока не прекращается вовсе, то не следует ли сказать, что такое замедление происходит в одной и той же мере. Но какой? Если в одном случае сопротивление больше, чем в другом, то от чего иного может это происходить, как не от того, что в одном случае воздух встречает большие импульс и скорость, а в другом — меньшие? Если же это так, то сама величина скорости тела является причиною, а вместе с тем и мерою величины сопротивления. Следовательно, движения всякого рода — медленные и быстрые — испытывают замедление и уменьшение в одном и том же отношении; такое заключение кажется мне не лишенным значения.
Сальвиати. Отсюда мы можем заключить, что и в этом случае отклонения от выводов, которые мы сделали, отвлекаясь от всяких внешних воздействий, окажутся при наших опытах незначительными, поскольку мы будем иметь дело по преимуществу с движениями, совершающимися с большой скоростью, и расстояниями, могущими быть названными ничтожными по сравнению с величиною радиуса или большого круга земного шара.
Симпличио. Я очень желал бы узнать, почему вы, синьор, сделали исключение для огнестрельных орудий, т. е., полагаю, действующих силою пороха, когда вы говорили о других метательных машинах — пращах, луках, арбалетах,— как будто выбрасываемые первыми снаряды не подлежат точно такому же воздействию сопротивления воздуха.
Сальвиати. Сделать это меня побуждает та чрезвычайная и, если можно так выразиться, сверхъестественная сила, с которой в этом случае выбрасываются снаряды; мне думается, что скорость, которой обладает ядро, вылетающее из мушкета или артиллерийского орудия, можно {314} без преувеличения назвать сверхъестественной. Подобное ядро, падающее естественным образом в воздухе с чрезвычайно большой высоты, не будет двигаться с постоянно возрастающей скоростью вследствие сопротивления воздуха; то, что происходит с падающими телами малого веса при небольших пространствах, а именно, превращение в конце концов их движения в равномерное, произойдет и с железным или свинцовым ядром после падения его на несколько тысяч локтей; эта окончательная и крайняя скорость может быть названа максимальной, какую только тело способно развить при падении в воздухе, и я считаю ее значительно меньшею по сравнению с тою скоростью, которую то же самое ядро приобретает после взрыва пороха. Убедиться в этом нам дает возможность следующий опыт. Выстрелим отвесно вниз свинцовой пулей из аркебуза с высоты ста или более локтей в каменную мостовую, а затем выстрелим из того же аркебуза в ту же мостовую с расстояния одного или двух локтей и посмотрим, какая из двух пуль окажется более сплющенной. Если пуля, которая была выпущена сверху, окажется менее сплющенной, нежели другая, то это явится признаком того, что воздух своим сопротивлением уменьшил скорость, сообщенную ей огнем при начале движения, и что, следовательно, воздух не позволит телу приобрести подобной скорости, с какой бы большой высоты тело ни падало. Если бы скорость, сообщаемая огнем, не превосходила той, которую тело может приобрести само по себе при естественном падении, то удар внизу скорее должен был бы оказаться более сильным, нежели более слабым. Я сам не производил такого опыта, но склонен думать, что с какой бы большой высоты ни был произведен выстрел, пуля, выпущенная из аркебуза, и ядро, выпущенное из орудия, никогда не произведут такого удара, какой получается при выстреле в стену с расстояния в небольшое число локтей, т. е. столь близкого, что при прохождении снарядом малого слоя воздуха разделение или, так сказать, разъединение последнего не успевает отнять у снаряда излишка сверхъестественной скорости, сообщенной ему огнем. Чрезвычайно большой импульс подобных огнестрельных снарядов может внести изменения в линию полета, сделав начало параболы менее наклонным и искривленным, чем конец. Но это обстоятельство не имеет ни малейшего значения ни для нашего Автора, ни для практических действий; им составлена таблица для стрельбы, имеющая важное практическое значение, так называемая таблица полета, содержащая данные о дальностях ядер при стрельбе с различными углами возвышения. При метании снарядов небольшого веса посредством мортир, когда такого сверхъестественного импульса не развивается, снаряды описывают достаточно правильные линии полета.
Но теперь можно уже возобновить чтение трактата. Автор приступает сейчас к рассмотрению и изучению импульса тела, движение которого {315} слагается из двух; прежде всего рассматривается случай, когда оно слагается из двух равномерных движений, горизонтального и вертикального.
Теорема II. Предложение II
Если какое-либо тело движется равномерно двойственным образом, а именно горизонтально и вертикально, то импульс или момент его сложного движения равен в потенции совокупности моментов первоначальных движений6.
Пусть какое-либо тело движется равномерно двойственным образом, и пусть движению его в вертикальном направлении соответствует отрезок ab, движению же в горизонтальном направлении
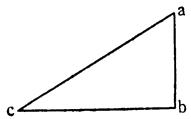 |
Симпличио. Я считал бы необходимым разъяснение одного возникающего у меня вопроса. Мне кажется, что только что доказанное предложение находится в противоречии с другим предложением трактата, в котором утверждалось, что импульс тела, прошедшего от а до b, равняется импульсу тела, прошедшего от а до с; теперь же доказывается, что импульс в с будет больше, чем в b.
Сальвиати. Оба предложения, синьор Симпличио, правильны, но совершенно различны друг от друга. Здесь мы говорим об одном теле, находящемся в состоянии единого движения, которое составляется из двух равномерных движений; там же говорилось о двух телах, двигавшихся равномерно-ускоренно — одно по вертикали ab, а другое — по наклонной ас. К тому же в последнем случае время движения не предполагалось одинаковым; время движения по наклонной ас было больше времени движения по вертикали ab; в том же случае, о котором речь идет сейчас, движения по ab, be и ас предполагаются совершающимися равномерно и в один и тот же промежуток времени.
Симпличио. Извините, и пойдем дальше; я вполне удовлетворен.
Сальвиати. Последуем за Автором в рассмотрении того, что происходит с импульсом движущегося тела, движение которого слагается из двух — одного горизонтального и равномерного и другого вертикального и равномерно-ускоренного; таково, в конце концов, сложное движение бросаемого тела, которое описывает параболическую линию. Для {316} каждой точки этого пути требуется определить величину импульса брошенного тела, и Автор указывает способ или, скажем, метод измерения подобного импульса посредством той самой линии, по которой происходит движение тяжелого тела, падающего по выходе из состояния покоя равномерно-ускоренно.
Теорема III. Предложение III
Пусть движение совершается по линии ab из точки покоя а, и на этой линии дана произвольная точка с; положим, что ас будет временем или мерою времени падения по линии ас и в то же самое время мерилом импульса или момента в точке с, приобретенного телом после падения по ас. Возьмем на той же самой линии аb какую-либо другую произвольную точку, скажем b, для которой и требуется определить импульс, приобретенный телом после падения по ab, в виде отношения его к импульсу, приобретенному в точке с, мерою которого принята линия ас. Отложим линию as — среднюю пропорциональную между bа и ас — и докажем, что импульс в точке b относится к импульсу в точке с, как линия sa к ас. Проведем горизонтальные линии — cd, равную удвоенной ас, и be, равную удвоенной bа. Из ранее доказанного мы знаем, что тело, падающее по ас, а затем продолжающее равномерное движение по горизонтали cd с импульсом, приобретенным в точке с, пройдет расстояние cd в тот же промежуток времени, в какой оно прошло равномерно ускоренным движением расстояние ас; равным образом be будет пройдено в тот же промежуток времени, как аb. Так как временем падения по аb является as,
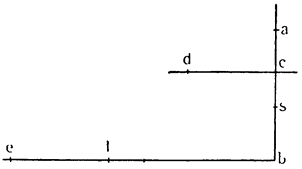 |
Отсюда и выводится способ измерения импульсов, т. е. моментов скорости, на линии, по которой происходит падение, причем принимается, что импульсы возрастают пропорционально времени.
Теперь, прежде чем идти далее, заметим, что нам придется иметь дело с движением, составленным из равномерного горизонтального и равномерно-ускоренного вертикального (так как именно таково сложное движение,
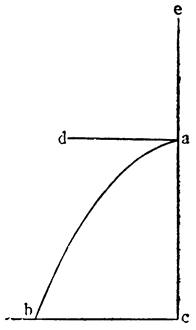 |
Предпослать все вышеуказанное представлялось необходимым.
Заметим при этом, что горизонтальная линия сb носит название амплитуды полупараболы ab; высота ас называется осью параболы; линия еа, падение по которой определяет импульс горизонтального движения, именуется мною сублимитом.
После этих пояснений и определений я приступаю к доказательствам7.
Сагредо. Приостановитесь, пожалуйста; мне кажется, что здесь следует отметить, как прекрасно согласуется мысль Автора с соображениями {318} Платона, касающимися определения скорости равномерного движения обращающихся небесных тел. Последний, напав случайно на мысль, что никакое движущееся тело не может перейти от состояния покоя к состоянию движения с определенной степенью скорости, с которою оно должно равномерно и постоянно перемещаться, иначе как пройдя через все другие последовательные меньшие степени скорости или, скажем, большие степени медленности, находящиеся между данною степенью и максимальною степенью медленности, каковою является состояние покоя, полагал, что бог, сотворив подвижные небесные тела, в целях придания им той скорости, с которою они должны будут затем вечно и равномерно двигаться по круговым линиям, заставил их, по выходе из состояния покоя, двигаться некоторое определенное расстояние естественным движением по прямой линии, подобно тому, как это происходит на наших глазах с падающими телами, которые, выйдя из состояния покоя, движутся с возрастающею скоростью. После того, как небесные тела приобрели ту степень скорости, с какою ему угодно было, чтобы они вечно двигались, он превратил их прямолинейное движение в круговое, которое одно только и может сохраняться всегда равномерным без удаления или приближения к какому-либо определенному концу или цели. Мысль эта вполне достойна Платона и является тем более удивительной, что действительное основание ее было открыто лишь нашим Автором, который снял с него покрывало поэзии и представил его нам в настоящем своем виде. Мне кажется также весьма вероятным, что, имея достаточно точные сведения из области астрономии, касающиеся величины орбит и расстояния планет от центра, вокруг которого последние вращаются, равно как и относительно скорости их движения, наш Автор (которому мысль Платона не осталась неизвестною) может из любознательности попытаться исследовать, нельзя ли определить сублимит, при котором планеты, выйдя из состояния покоя, проходили бы некоторое расстояние прямолинейным естественно-ускоренным движением, а затем, перейдя к равномерному движению с приобретенной скоростью, описывали бы орбиты соответствующей величины с определенными периодами обращения.
Сальвиати. Я хорошо помню, что однажды он сообщил мне о близком совпадении проделанных им вычислений с результатами наблюдений; однако он не хотел говорить об этом подробнее, опасаясь, как бы высказываемые им новые взгляды, многократно возбуждавшие негодование, не зажгли нового пожара; впрочем, если кто-либо пожелает заняться этим вопросом, то он сам сможет удовлетворить свою любознательность, руководствуясь доктриной, изложенной в настоящем трактате. Но вернемся к нашему предмету.
| {319} |
Задача I. Предложение IV
Как на данной параболе, описываемой брошенным телом, определить импульс, соответствующий отдельной точке?
Дана полупарабола bec, с амплитудою cd и высотой db; последняя, будучи продолжена вверх, пересечет касательную к параболе са в точке а; проведем через вершину b горизонтальную линию bi, параллельную cd. Если амплитуда cd равна всей высоте da, то bi равняется bа, а также и bd. Если, далее, за меру времени падения по ab и скорости, приобретенной телом в точке b после падения по ab из точки покоя а, мы примем линию ab, то линия dc (равняющаяся двум bi) будет тем расстоянием, которое проходится по горизонтали после соответствующего отклонения движения под влиянием импульса, приобретенного при падении по ab, за тот же промежуток времени. Но при падении по bd из точки покоя b тело проходит в такой же промежуток времени высоту bd. Итак, тело, падающее из точки покоя а по линии ab с импульсом ab, может пройти после отклонения движения горизонтальное пространство, равное dc. Но здесь присоединяется падение по bd, при котором должно быть пройдено расстояние bd; в результате этого описывается парабола be, и импульс тела в точке с слагается из равномерного поперечного, момент коего равен ab, и другого момента, приобретенного при падении по bd в точке d или с, каковые моменты равны между собою. Если мы предположим, что ab является мерою одного движения, а именно равномерного поперечного, то отрезок bi, равняющийся bd, будет мерою импульса, приобретенного в точке d или с, линия же ia будет представлять величину момента, составленного из обоих; следовательно, она явится мерою величины сложного момента, которым тело обладает в точке с, пройдя по параболе путь bc. Установив это, возьмем на параболе какую-нибудь точку е, для которой требуется установить импульс тела, движущегося по параболе. Проведем горизонтальную линию ef и отложим bg — среднюю пропорциональную между bd и bf. Если положить, что ab или bd будет мерою времени и момента скорости падения по bd из точки покоя b, то bg будет мерою времени и импульса для точки f при падении из точки b. Если теперь отложим отрезок bo, равный bg, и проведем диагональ ао, то последняя будет представлять величину импульса в точке е. В самом деле, линия ab принята нами как мера, определяющая время достижения точки b и соответствующий импульс, каковой и при переходе движения в горизонтальное остается неизменно постоянным; bo определяет импульс в f или е после падения из точки b по {320} вертикали bf; линии же ab и bo в потенции эквивалентны линии ао. Следовательно, то, что требовалось, нами выполнено.
Сагредо. Рассмотрение сложения указанных различных импульсов и величины того импульса, который получается в результате соединения последних, представляется для меня делом столь новым, что я в достаточной степени смущен. Я не говорю здесь о сложении двух равномерных движений, хотя бы не равных между собою и направленных одно по горизонтали, а другое по вертикали; для меня понятно, что в этом случае можно получить движение, равное в потенции сумме обоих компонентов; но относительно возможности соединения равномерного горизонтального и естественно-ускоренного вертикального движения у меня остается сомнение. Поэтому мне хотелось бы, чтобы вы более основательно разобрали этот вопрос.
Симпличио. Я, со своей стороны, нуждаюсь в том же в еще большей степени, так как до сих пор еще не усвоил себе как следует тех основных первоначальных положений, которые являются необходимыми для понимания всего последующего. Прибавлю, что даже при объединении двух равномерных движений — горизонтального и вертикального — я желал бы лучше уяснить себе, какова потенция составного движения. Поэтому, синьор Сальвиати, удовлетворите наше желание.
Сальвиати. Ваше желание представляется совершенно естественным, и поскольку я долго размышлял над затронутым вопросом, я постараюсь сделать его более понятным для вас. Но вы должны быть в данном случае снисходительными и извинить меня, если в своем изложении я опять повторю добрую часть того, что написано нашим Автором.
Говоря о движениях и их скоростях или импульсах, будь то движения равномерные или естественно-ускоренные, мы необходимо должны прежде всего установить меру, при помощи которой мы желаем измерять скорость, а также и время. Что касается времени, то у нас уже имеется всеми признанная мера, выражаемая часами и минутами — первыми и вторыми и т. д.8; подобно мере времени,— для всех понятной и всеми принятой,— необходимо найти и меру скорости — такую, которая была бы для всех понятной, приемлемой и одинаковой в различных случаях. Как уже было упомянуто выше, наиболее подходящей для такой цели представляется, по мнению Автора, скорость естественно падающих тяжелых тел, у коих возрастание скорости во всех частях света происходит в одинаковой степени, так что степень скорости, которая приобретается (для примера) свинцовым шаром, весом в один фунт, вышедшим из состояния покоя и падающим вертикально с определенной высоты, сохраняется для всех мест одинаковою и благодаря этому представляется подходящею для выражения величины импульса, который получается при естественном падении. Таким образом, остается найти способ обозначения величины {321} импульса при равномерном движении, и такой именно, чтобы все, имеющие дело с данным движением, получили одинаковое представление о величине его скорости, и не могло случиться, что один представит его себе более, а другой менее быстрым; необходимо также, чтобы и при сложении равномерного и естественно-ускоренного движения все лица получали одинаковое представление о величине импульса сложного движения. Чтобы определить и обозначить подобного рода импульс и скорость, наш Автор не нашел лучшего способа, как воспользоваться импульсом, приобретаемым телом при естественно-ускоренном движении; такой импульс, приобретенный к любому данному моменту времени, точно сохраняет при переходе к равномерному движению свойственную ему скорость, величина коей такова, что за время, затраченное на падение, тело проходит расстояние, равное удвоенной высоте его падения. Так как это есть главный пункт во всем трактуемом вопросе, то полезно будет дать несколько примеров, чтобы достичь вполне ясного понимания.
Представим себе скорость и импульс, приобретенные телом, упавшим, скажем, с высоты одного локтя, и будем пользоваться этой скоростью как мерою скоростей и импульсов в других случаях; положим, далее, что такое падение потребовало четыре секунды времени. Для того чтобы найти отсюда и выразить величину импульса при падении тела с любой другой высоты, большей или меньшей, мы не можем исходить из отношения, которое новая высота имеет к ранее взятой, рассуждая хотя бы так, что при падении с высоты, вчетверо большей, тело приобретает и скорость в четыре раза большую, ибо это совершенно неправильно. Как уже было
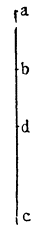 |
Твердо установив это, перейдем к рассмотрению импульса при сложном движении, составленном в первом случае из неизменно равномерного движения по горизонтали и также равномерного движения по перпендикуляру к горизонту, а во втором случае из равномерного движения по горизонтали и равномерно-ускоренного движения по вертикали. Мы уже видели, что в том случае, когда оба движения равномерны, импульс, получающийся в результате их соединения, равен в потенции им обоим, что для большей ясности иллюстрирую следующим примером. Положим, что тело, движущееся по вертикали ab, имеет, например, три градуса
 |
Перейдем теперь к рассмотрению того, что происходит при сложении равномерного горизонтального движения с движением, перпендикулярным к горизонту, причем последнее, начинаясь от точки покоя, протекает естественно-ускоренно. Ясно, что диагональ, т. е. линия, получающаяся в результате сложения обоих движений, будет не прямой линией, а полупараболой, как это уже было доказано; при движении по ней импульс непрерывно увеличивается благодаря постоянному возрастанию скорости вертикального движения. Таким образом, чтобы определить, какова величина импульса в какой-либо определенной точке этой параболической диагонали, необходимо установить, во-первых, величину импульса равномерного движения по горизонтали, во-вторых, величину импульса падающего тела в данной точке, чего, в свею очередь, нельзя сделать без определения промежутка времени, предшествующего сложению обоих движений. При сложении равномерных движений принимать в соображение время не было никакой надобности, так как скорости и импульсы оставались всегда одними и теми же; но здесь, где одним из слагаемых является движение, начинающееся с максимальной медленности и возрастающее в скорости пропорционально времени, количество последнего необходимо обусловливает и величину скорости в данной точке. В конце концов, общий импульс движения, слагающегося из двух указанных выше, как это имело место и при слежении равномерных движений, будет равен в потенции совокупности обоих компонентов. Но лучше поясню сказанное примером. Пусть на перпендикуляре к горизонту ас взята произвольная часть ab, каковая и будет служить мерою пространства, пройденного телом при естественном падении его по этому перпендикуляру, равно как и мерею времени и степени скорости или, скажем, импульса. Совершенно ясно, что импульс тела, падающего из точки покоя а до точки b, после обращения движения в равномерное и направленное по горизонтали bd обусловит такую скорость, при которой за время ab тело пройдет расстояние, в два раза превышающее расстояние ab, {324} а именно линию bd. Отложим теперь отрезок be, равный bа, проведем линию се, параллельную и равную bd, и построим параболическую линию bei, проходящую через точки b и е. Так как за время ab тело проходит, обладая импульсом ab, горизонталь bd или се, в два раза большую, нежели ab, и так как за точно то же время оно проходит вертикаль be и приобретает в точке с импульс, равный той же горизонтали, то ясно, что за промежуток времени, равный ab, оно переместится из b в е по параболе be
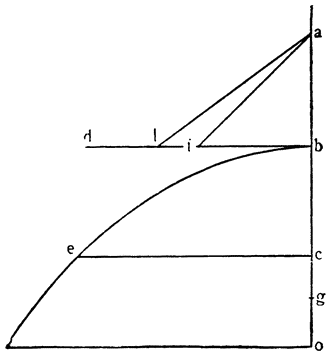 |
К тому, что до сих пор было нами сказано об импульсах, ударах или, скажем, толчках, производимых брошенными телами, необходимо добавить еще одно соображение, имеющее важное значение. Заключается {325} оно в следующем: чтобы определить силу или энергию удара брошенного тела, недостаточно знать только его скорость, необходимо также рассмотреть и учесть положение тела, получающего толчок, и условия, при которых последний происходит; влияние различных условий на результат удара во многих отношениях представляет большой интерес. Каждому понятно, что тело, получающее удар, испытывает действие скорости ударяющего тела только в том случае, когда оно оказывает последнему сопротивление и препятствует полностью или частично движению последнего; если удар получается таким телом, которое не оказывает скорости движения ударяющего тела никакого сопротивления, то и результат такого удара равен нулю. Если кто-либо бежит за своим врагом, чтобы проколоть его копьем, а враг после приближения к нему удаляется с такою же быстротою, то нанести ему удар не удается; результатом является простое прикосновение, не сопровождающееся ранением. Если же удар воспринимается телом, уступающим ударяющему телу не сполна, но лишь частично, то удар имеет место, однако не с полным импульсом, а лишь в меру избытка скорости ударяющего тела над скоростью удаляющегося или уступающего тела, получающего удар. Таким образом, если, например, ударяющее тело приближается со скоростью в десять градусов к другому телу, которое, уступая частично, движется по тому же направлению со скоростью в четыре градуса, то импульс удара равен шести градусам. Наконец, удар со стороны ударяющего тела является максимальным и наиболее действительным, когда тело, принимающее удар, отнюдь не подается, но оказывает сопротивление, отнимая всякое движение у ударяющего тела, если только это возможно. Я прибавил: «со стороны ударяющего тела», ибо если тело, получающее удар, движется само в противоположном направлении, то удар при встрече получается во столько раз более сильным, во сколько раз сумма скоростей двух тел, движущихся навстречу друг другу, больше скорости одного ударяющего тела. К этому необходимо добавить, что большая или меньшая податливость зависит не только от рода вещества, более или менее твердого, т. е. не только от того, например, приходится ли удар по железу, свинцу, или шерсти, но также и от положения тела, получающего удар. Если положение последнего таково, что движение ударяющего тела направлено к нему под прямым углом, то действие импульса является максимальным; если же движение направлено вкось, то удар тем менее действителен, чем значительнее уклон, ибо при подобном положении никакое тело, даже из самого твердого вещества, не может полностью уничтожить импульса ударяющего тела; последнее, скользнув, продолжает хотя бы отчасти двигаться по поверхности тела, которому нанесен удар. Что касается определенной выше величины им-пульса тела в конечной точке параболической линии, то, говоря о ней, следует подразумевать удар, получаемый прямой линией, проходящей под {326} прямым углом к параболе или, точнее, к касательной к параболе в данной точке; так как описанное движение слагается из двух движений — горизонтального и вертикального, то импульс не достигает наибольшей величины ни при горизонтальном, ни при вертикальном положении встречной плоскости, так как и та и другая испытывают косой удар.
Сагредо. Ваши рассуждения, синьор, о толчках и ударах напомнили мне одну проблему или, лучше сказать, один вопрос из области механики, разрешения которого я не встретил ни у одного из авторов; я не нашел даже ничего, что хотя бы отчасти рассеяло мое недоумение и удовлетворило мой ум. Я недоумеваю, откуда проистекает и отчего зависит огромная энергия или сила, проявляющаяся при ударе, когда, например, простыми ударами молота, весящего всего восемь или десять фунтов, мы побеждаем такое сопротивление, которое не поддается весу тяжелого тела, производящего давление без удара, хотя бы этот вес и равнялся многим сотням фунтов. Я хотел бы найти способ измерения силы таких ударов; я думаю, что она не бесконечно велика, что она имеет определенные границы, и что ее можно сравнивать и сопоставлять с другими силами, обусловливаемыми действием тяжести и проявляющимися в рычаге, винте и других механических приспособлениях, относительно которых я хорошо знаю, каким образом увеличивается сила их действия.
Сальвиати. Не только вы один, синьор, находитесь в недоумении, на зная причины этого удивительного явления. Я также долгое время бесплодно раздумывал над этим вопросом, впадая все в большее смущение, пока, наконец, не встретился с нашим Академиком и не был вдвойне им утешен. Во-первых, я узнал, что и он долгое время находился в недоумении по тому же поводу; во-вторых, он сообщил мне, что, потратив много тысяч часов своей жизни на рассуждения и размышления по этому предмету, он открыл многое, далекое от обычных наших представлений, а потому совершенно новое и, благодаря своей новизне, удивительное. Так как я знаю, синьор, что при вашей любознательности вы охотно познакомитесь с этими мыслями, весьма далекими от общепринятых, то я пока не стану отвечать на заданный вами вопрос, но даю вам слово, что когда мы окончим чтение настоящего трактата о движении бросаемых тел, то я постараюсь объяснить вам этот непонятный и изумительный предмет, поскольку рассуждения Академика сохранились в моей памяти. Теперь же последуем за предложениями Автора10.
Задача II. Предложение V
На продолжении оси данной параболы найти лежащую выше точку, при падении из которой тело описывает эту параболу.
Пусть дана парабола аb с амплитудою hb и продолженной осью hе; на {327} последней требуется отыскать сублимит, при падении по которому тело, переменив направление движения на горизонтальное, опишет под действием импульса, приобретенного им в точке а, параболу ab. Проведем горизонтальную линию ag, которая будет параллельна bh, отложим
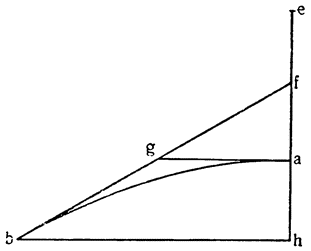 |
Следствие
Отсюда следует, что половина основания или амплитуды полупараболы (что составляет четвертую часть амплитуды целой параболы) является средней пропорциональной между высотою ее и сублимитом, при падении по которому таковая описывается.
Задача III. Предложение VI
Даны сублимит и высота полупараболы; найти ее амплитуду. На перпендикуляре ас к горизонтальной линии dc даны высота cb и сублимит bа; требуется отложить на горизонтали cd амплитуду полупараболы, {328} которая будет описана при падении по сублимиту bа и высоте be. Построим среднюю пропорциональную между cb и bа и отложим отрезок cd, равный удвоенной величине ее. Утверждаю,
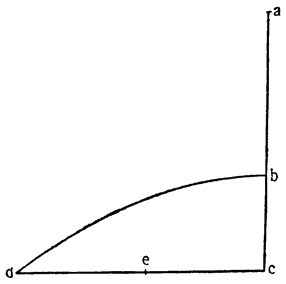 |
Теорема IV. Предложение VII
Из тел, описывающих полупараболы с равными амплитудами, то, которое движется по полупараболе с амплитудою, равной удвоенной высоте, требует меньшего импульса, нежели всякое иное.
Пусть дана полупарабола bd, амплитуда которой cd равна двойной высоте cb; на продолженной вверх оси ее отложим отрезок bа, равный высоте be, и проведем линию ad, которая будет касаться полупараболы в точке d и пересекать горизонталь be в точке е; таким образом, be будет равняться be или же bа. Известно, что парабола описывается телом, равномерный горизонтальный импульс которого равен приобретаемому в b при падении из точки покоя а, а импульс естественного падения равен приобретаемому в с при падении из точки покоя b. Отсюда следует, что составленный из них импульс в точке d выражается диагональю ае, в потенции равной обоим слагаемым. Пусть теперь gd будет какой-либо другой полупараболой с такою же амплитудою cd, но иною высотою eg, большею или меньшею высоты be, hd будет касательной к ней, пересекающей проведенную через g горизонталь в точке k; пусть, далее, отношение hg к gk равняется отношению kg к gl. На основании доказанного выше gl будет тою высотою, при падении с которой тело опишет параболу gd. Построим gm — среднюю пропорциональную между ab и gl; тогда gm будет представлять время и момент или импульс в точке g при падении из I (при том условии, что ab принято за меру времени и импульса в точке b при падении из а). С другой стороны, если gn будет средней пропорциональной между be и eg, то она будет мерою времени и импульса при падении от g до с. Если мы проведем теперь линию mn, то получим выражение импульса тела, движущегося по параболе dg, для конечной точки ее d, каковой импульс, утверждаю я, больше импульса тела, движущегося по парабола bd, выражаемого линией ае. В самом деле, если gn по предположению является средней пропорциональной между be и eg, а, кроме того, отрезок be равен be или kg (ибо оба последние равны половине dc), то отношение eg к gn будет равно отношению ng к gk, а отношение eg или же hg к gk будет равно отношению квадрата ng к квадрату gk. Так как по построению
| {329} |
 |
СТРАНИЦА ИЗ РУКОПИСИ «БЕСЕД» |
| {330} |
отношение hg к gk равно отношению kg к gl, то отношение квадрата ng к квадрату gk будет равно отношению kg к gl. Но отношение kg к gl равно
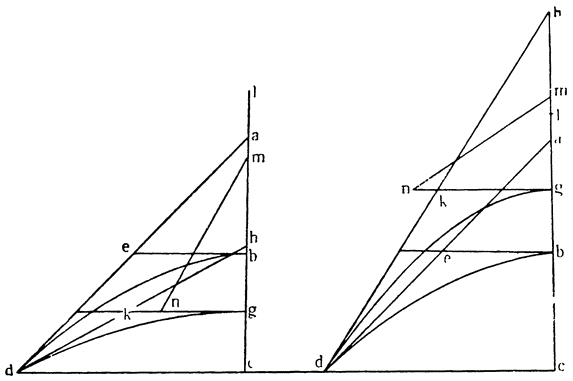
отношению квадрата kg к квадрату gm, ибо gm есть средняя пропорциональная между kg и gl; таким образом, три квадрата ng, kg и gm образуют непрерывную пропорцию, и два крайних ng и gm, взятые вместе и равные квадрату mn, будут больше удвоенного квадрата kg, каковой равен удвоенному квадрату ае; следовательно, квадрат mn больше квадрата ае, и линия mn больше линии еа, что и требовалось доказать.
Следствие
Из сказанного следует, что, обратно, подъем тела по полупараболе db из конечной точки ее d требует меньшего импульса, чем подъем по полу-параболе, имеющей большую или меньшую высоту по сравнению с полу-параболой bd, касательная к которой ad образует с горизонтом угол, равный половине прямого. Далее ясно, что если мы будем бросать тела с одним и тем же импульсом из конечной точки d под разными углами, то наибольшую дальность полета и амплитуду полупараболы или целой параболы мы получим при наклоне, равном половине прямого угла; при больших или меньших углах наклона таковые будут меньше.
Сагредо. Удивительна и вместе с тем восхитительна сила убедительности доказательств, которая присуща одной лишь математике. Я уже был знаком со слов опытных бомбардиров с тем фактом, что из всех выстрелов, при которых снаряды выпускаются из пушек или мортир, наиболее дальнобойным, т. е. переносящим снаряд на наибольшее расстояние, является тот, который производится при угле, равном половине прямого, {331} или, как они говорят, при шестом делении угломера. Но понимание причины, по которой это происходит, дает неизмеримо больше, чем простое сведение, взятое из показаний других лиц или даже из многократно повторенного опыта.
Сальвиати. Ваше замечание, синьор, совершенно справедливо. Познание причины одного только явления дает возможность нашему уму постичь и установить другие явления без необходимости прибегать к помощи опыта, и точно так получилось в настоящем случае. Получив путем доказательного рассуждения, что наиболее далекий полет тела получается при наклоне, равном половине прямого угла, Автор устанавливает, далее, то, что, пожалуй, не было наблюдено опытным путем, а именно, что выстрелы, произведенные под углами возвышения, большими или меньшими половины прямого на одну и ту же величину, дают одинаковые результаты, так что ядра, выпускаемые из орудия при подъеме его в одном случае на пять, а в другом на семь делений угломера, пролетают по горизонтали одно и то же расстояние; подобный же результат дают выстрелы при подъеме на восемь и четыре делений, на девять и три и т. д. Вот как это доказывается12.
Теорема V. Предложение VIII
Амплитуды парабол, описываемых телами, выстреленными с одинаковым импульсом под углами возвышения, отклоняющимися на одинаковую величину в ту или другую сторону от половины прямого, равны между собой.
В треугольнике mcb стороны, образующие прямой угол с — горизонтальная be и вертикальная cm,— равны между собою; угол mbс равен, таким образом, половине прямого. Продолжим cm вверх до точки d и
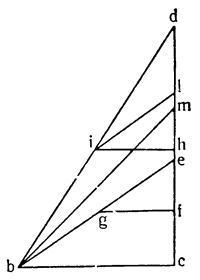 |
Теорема VI. Предложение IX
Амплитуды двух парабол равны между собой, если высоты и сублимиты их обратно пропорциональны.
Высота gf параболы fh относится к высоте cb параболы bd как сублимит bа к сублимиту fe. Утверждаю, что амплитуды hg и dc равны между
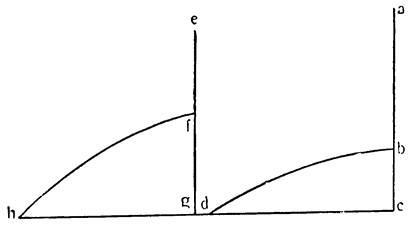 |
Лемма
Если прямая линия любым образом разделена, то сумма квадратов средних пропорциональных между всей линией и каждым из двух ее отрезков равна квадрату всей линии. {333}
Пусть линия аb разделена в какой-либо точке с. Утверждаю, что квадраты линий, являющихся средними пропорциональными между всей
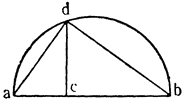 |
Теорема VII. Предложение X
Импульс или момент в конечной точке полупараболы равняется моменту естественного падения по вертикали с высоты, равной сумме сублимита и высоты полупараболы.
Пусть ab полупарабола с сублимитом da и высотою ас, составляющими вместе вертикаль dc. Утверждаю, что импульс в конечной точке полупараболы b будет равен моменту естественного падения из d в с. Положим,
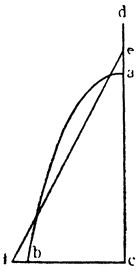 |
Следствие
Отсюда вытекает, что импульсы движения по всем полупараболам, суммы высот и сублимитов которых равны между собой, одинаковы.
| {334} |
Задача IV. Предложение XI
Даны импульс и амплитуда полупараболы; требуется определить ее высоту.
Пусть данный импульс выражается линией ab, отложенной на вертикали, амплитудой же пусть является горизонтальная линия be. Требуется найти сублимит полупараболы, при котором импульс будет равен аb при амплитуде, равной be. Из предыдущего нам известно, что половина амплитуды bс является средней пропорциональной между высотою и сублимитом полупараболы, импульс которой, как было доказано
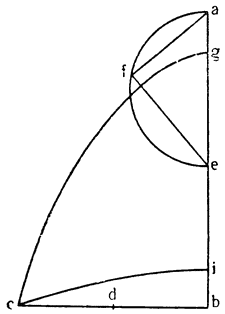 |
Задача V. Предложение XII
Определить посредством вычисления амплитуды всех полупарабол, которые описываются снарядами, выбрасываемыми с одним и тем же импульсом, и составить соответствующую таблицу. {335}
Из доказанного выше нам известно, что параболы описываются бросаемыми телами с одинаковым импульсом в том случае, если сублимиты их, сложенные с их высотами, образуют вертикали одной и той же величины; все такие вертикали должны, следовательно, заключаться между двумя параллельными горизонтальными линиями. Положим, что мы имеем горизонталь сb и равную ей вертикаль bа; проведя диагональ ас, мы получим
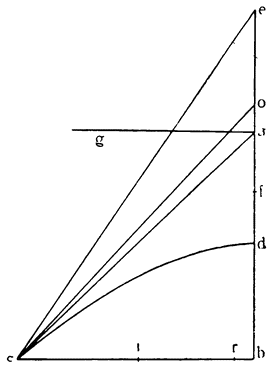 |
по данному углу bce находим тангенс, определяем третью пропорциональную к половине тангенса и половине be, каковою пусть является fо, и вычисляем сr, полагая, что отношение ob к bа равно отношению be к сr; сr и является искомою амплитудою.
Возьмем пример. Пусть угол ecb равен 50 градусам; соответствующий тангенс равен 11918, половина же его или линия bf равна 5959; половина be равна 5000; третьей пропорциональной к этим половинам является 4195; эта величина, будучи сложенной с величиной bf, дает 10154 для bo. Теперь отношение ob к bа или 10154 к 10000 должно равняться отношению bc или 10000 (так как эта линия равна тангенсу угла в 45 градусов) к rс; отсюда находим, что амплитуда rc равна 9848, в то время как bc (максимальная амплитуда) равняется 10000. Амплитуды целых парабол будут вдвое большими и равными 19696 и 20000. Такую же величину будет иметь и амплитуда параболы, наклоненной под углом в 40 градусов, ибо этот угол разнится от угла в 45 градусов на ту же величину14.
Сагредо. Для полного понимания этого доказательства мне необходимо знать, откуда следует, что третья пропорциональная к bf и bi должна необходимо быть (как говорит Автор) больше fa.
Сальвиати. Мне кажется, что это положение может быть выведено следующим путем. Квадрат средней из трех образующих непрерывную пропорцию линий равен прямоугольнику из двух остальных. Таким образом, квадрат bi или равной ей линии bd должен быть равен прямоугольнику из первой величины bf и третьей, которую надо найти; эта третья величина обязательно должна быть больше fa, так как прямоугольник bf, fa меньше квадрата bd, и разница равняется квадрату df, как доказано Эвклидом в одной из теорем. Необходимо также отметить, что точка f, разделяющая тангенс eb пополам, может часто лежать выше точки а и только в одном случае совпадает с нею; понятно, что во всех этих случаях средняя пропорциональная между половиною тангенса и bi (которая определяет сублимит) должна лежать выше а. Но Автор взял такой случай, когда не ясно, что третья пропорциональная, о которой идет речь, обязательно должна быть больше fа, и что поэтому, будучи отложена вверх от точки f, она всегда выйдет за пределы параллели ag. Но пойдем далее15. {337}
При помощи этой таблицы небесполезно будет составить другую, дополнительную, для высот полупарабол, описываемых телами, обладающими одним и тем же импульсом, согласно излагаемому ниже построению.
Задача VI. Предложение XIII
По данным в таблице амплитудам полупарабол определить высоты отдельных полупарабол, сохраняя постоянным импульс, с которым описывается любая из последних.
Пусть дана амплитуда bc; мерою импульса, который предполагается неизменным, пусть будет линия ob, равная сумме высоты и сублимита; требуется найти и вычислить высоту. Приступая к решению, надо разделить
Амплитуды полупарабол, |
Высоты полупарабол при одном |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| {338} |
Амплитуды полупарабол, |
Высоты полупарабол при одном |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
bo таким образом, чтобы прямоугольник, составленный из ее частей, был равен квадрату половины амплитуды be. Положим, что точка деления лежит в f; разделим пополам линии ob и bc в точках d и i. Тогда квадрат ib будет равняться прямоугольнику bfo, квадрат же do будет равен тому же прямоугольнику, сложенному с квадратом fd. Если же отнять от квадрата do квадрат bi, который равновелик прямоугольнику bfo, то останется квадрат fd, сторона которого df, прибавленная к линии bd, и даст требуемую высоту bf. Поэтому поступаем следующим образом:
из найденного квадрата половины bo вычитаем квадрат bi, извлекаем из разности квадратный корень и складываем его с линией db, получая, таким образом, требуемую высоту bf. {339}
Пример. Требуется найти высоту полупараболы, описываемой при угле возвышения в 55 градусов. Согласно предыдущей таблице, амплитуда составляет 9396; половина ее равна 4698; квадрат половины равен 22071204;
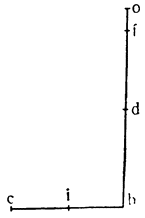 |
Небесполезно составить и третью таблицу, содержащую высоты и сублимиты полупарабол, имеющих равные амплитуды.
Сагредо. Такую таблицу мне очень хотелось бы видеть, так как по ней можно будет судить о различии импульсов и сил, требующихся для того, чтобы выбрасывать снаряд посредством метательного орудия на одинаковое расстояние; думается, что разница должна быть очень большой в зависимости от угла подъема, так что, если мы желаем бросить ядро при угле подъема, например, в три-четыре градуса или 87—88 градусов, на такое же расстояние, на какое оно было брошено под углом в 45 градусов (в каковом случае, как было доказано, требуется наименьший импульс), то нам надо будет затратить несравненно большую силу.
Сальвиати. Вы совершенно правы, синьор, и увидите сейчас, что, отыскивая результат для всех возвышений, мы быстрыми шагами приближаемся к бесконечно большому импульсу.
Итак, познакомимся со способом составления таблицы.
Задача VII. Предложение XIV
Найти высоты и сублимиты полупарабол, имеющих одинаковые амплитуды, при различных углах возвышения.
Выполнить эту задачу очень легко. Если положим, что амплитуда полупарабол всегда равна 10000, что половина тангенса будет представлять высоту при любом угле возвышения. Так, если полупарабола, угол подъема которой равен 30 градусам, имеет амплитуду, равную, как мы приняли, 10000, то высота ее будет равна 2887, потому что такова приблизительно половина тангенса указанного угла. Найдя высоту, определяем сублимит следующим образом. Как уже было доказано выше, половина амплитуды полупараболы является средней пропорциональной между высотою и сублимитом; так как высота уже найдена, а половина амплитуды есть величина постоянная и равная 5000, то, разделив квадрат последней на высоту, мы получим искомый сублимит. В нашем примере высота
| {340} |
Таблица, содержащая высоты и сублимиты
nолупарабол, имеющих одинаковые амплитуды,
равные 10000 единиц, при различных углах возвышения
Градусы |
Высота |
Сублимит |
Градусы |
Высота |
Сублимит |
|
1 |
87 |
286 533 |
35 |
3501 |
7141 |
|
2 |
175 |
142 450 |
36 |
3633 |
6882 |
|
3 |
262 |
95 802 |
37 |
3768 |
6635 |
|
4 |
349 |
71531 |
38 |
3906 |
6395 |
|
5 |
437 |
57 142 |
39 |
4049 |
6174 |
|
6 |
525 |
47 573 |
40 |
4196 |
5959 |
|
7 |
614 |
40 716 |
41 |
4346 |
5752 |
|
8 |
702 |
35 587 |
42 |
4502 |
5553 |
|
9 |
792 |
31565 |
43 |
4662 |
5362 |
|
10 |
881 |
28 367 |
44 |
4828 |
5177 |
|
11 |
972 |
25 720 |
45 |
5000 |
5000 |
|
12 |
1063 |
23 518 |
46 |
5177 |
4828 |
|
13 |
1154 |
21701 |
47 |
5363 |
4662 |
|
14 |
1246 |
20 056 |
48 |
5553 |
4502 |
|
15 |
1339 |
18 663 |
49 |
5752 |
4345 |
|
16 |
1434 |
17 405 |
50 |
5959 |
4196 |
|
17 |
1529 |
16 355 |
51 |
6174 |
4048 |
|
18 |
1624 |
15 389 |
52 |
6399 |
3906 |
|
19 |
1722 |
14 522 |
53 |
6635 |
3765 |
|
20 |
1820 |
13 736 |
54 |
6882 |
3632 |
|
21 |
1919 |
13 024 |
55 |
7141 |
3500 |
|
22 |
2020 |
12 376 |
56 |
7413 |
3372 |
|
23 |
2123 |
11778 |
57 |
7699 |
3247 |
|
24 |
2226 |
11230 |
58 |
8002 |
3123 |
|
25 |
2332 |
10 722 |
59 |
8332 |
3004 |
|
26 |
2439 |
10 253 |
60 |
8600 |
2887 |
|
27 |
2547 |
9 814 |
61 |
9020 |
2771 |
|
28 |
2658 |
9 404 |
62 |
9403 |
2658 |
|
29 |
2772 |
9 020 |
63 |
9813 |
2547 |
|
30 |
2887 |
8 659 |
64 |
10251 |
2438 |
|
31 |
3008 |
8 336 |
65 |
10722 |
2331 |
|
32 |
3124 |
8 001 |
66 |
11230 |
2226 |
|
33 |
3247 |
7 699 |
67 |
11779 |
2122 |
|
34 |
3373 |
7 413 |
68 |
12375 |
2020 |
|
69 |
13 025 |
1919 |
80 |
28 356 |
881 |
|
70 |
13 237 |
1819 |
81 |
31569 |
792 |
|
71 |
14 521 |
1721 |
82 |
35 577 |
702 |
|
72 |
15 388 |
1624 |
83 |
40 222 |
613 |
|
73 |
16 354 |
1528 |
84 |
47 572 |
525 |
|
74 |
17 437 |
1433 |
85 |
57150 |
437 |
|
75 |
18 660 |
1339 |
86 |
71503 |
349 |
|
76 |
20 054 |
1246 |
87 |
95 405 |
262 |
|
77 |
21657 |
1154 |
88 |
143 181 |
174 |
|
78 |
23 523 |
1062 |
89 |
286 499 |
87 |
|
79 |
25 723 |
972 |
90 |
Беско- |
0 |
оказалась равной 2887; квадрат половины амплитуды или 5000 равен 25000000; частное от деления этого числа на 2887 равно 8659 и дает приблизительно величину искомого сублимита.
Вы видите отсюда, во-первых, как справедливо высказанное ранее положение, что при различных углах возвышения требуется тем больший импульс или усилие, чтобы выбросить снаряд на то же самое расстояние, чем более углы отклоняются от среднего в сторону повышения или понижения. В самом деле, общий импульс слагается из двух движений — одного равномерного горизонтального и другого вертикального и естественно-ускоренного, причем импульс этот измеряется суммою высоты и сублимита. Из предложенной таблицы вы можете видеть, что сумма эта имеет наименьшую величину при подъеме под углом в 45 градусов, когда и высота и сублимит равны 5000, а сумма их составляет 10000. Если мы перейдем к большему углу возвышения, например в 50 градусов, то найдем, что высота равняется 5959 и сублимит 4196, что в сумме составляет 10155; ту же величину импульса мы найдем для угла в 40 градусов, отклоняющегося от среднего на такую же величину. Во-вторых, необходимо отметить, что одинаковые импульсы встречаются попарно при углах возвышения, равно отклоняющихся от среднего, с той, однако, удивительною разницею, что высота и сублимит при больших углах соответствуют обратно сублимиту и высоте при меньших углах. Таким образом, если в рассмотренном примере при угле возвышения в 50 градусов высота равнялась 5959 и сублимит — 4196, то при угле возвышения в 40 градусов, {342} наоборот, высота будет равна 4196, а сублимит — 5959. То же самое имеет место и во всех без исключения прочих случаях. Во избежание излишнего труда при вычислениях здесь не приняты во внимание дроби, которые при столь больших числах не имеют никакого значения.
Сагредо. Я замечаю, что чем выше брошен снаряд, тем меньше первый из двух импульсов — горизонтального и вертикального,— именно горизонтальный, и тем больше второй — вертикальный. Наоборот, при подъеме снаряда на малую высоту должна быть велика сила горизонтального импульса. Если я правильно понял все изложенное, то при максимальном подъеме в 90 градусов всех сил мира недостаточно для того, чтобы отклонить брошенное тело на дюйм от вертикали, так как оно неизбежно должно упасть обратно в то же место, откуда оно было брошено. Но у меня не хватит той же решимости утверждать, что при нулевом возвышении, т. е. при горизонтальном направлении, не найдется какой-либо конечной силы, могущей выбросить снаряд на некоторое пространство. Разве не может пушка выпустить чугунное ядро горизонтально или, как говорят, «с белого деления», т. е. при возвышении, равном нулю? Мне кажется, что в этом случае получается какая-то странность; в то же время я не отрицаю категорически этого факта, так как мне приходит на память другой случай, не менее удивительный и вместе с тем подтверждаемый неоспоримыми доказательствами. Случай, который я имею в виду, это невозможность натянуть канат так, чтобы он был совершенно параллелен горизонту; он всегда провисает, и никаких сил не хватает, чтобы его выпрямить.
Сальвиати. Итак, синьор Сагредо, в случае с канатом ваше удивление по поводу столь странного явления рассеялось, так как вы имели ему объяснение. Но если хорошенько рассудить, то, быть может, найдется кое-что общее в случаях с брошенным снарядом и натянутым канатом. Кривизна линии, описываемой горизонтально брошенным телом, обусловливается двумя силами, из коих одна (сила бросившего) двигает его о горизонтальном направлении, а другая (т. е. его собственная тяжесть) тянет его вниз. При натяжении каната также имеются силы, натягивающие канат горизонтально, и его собственный вес, естественно влекущий его вниз. Таким образом, эти два явления имеют между собою много общего. И если вы признаете, что вес каната обладает достаточной мощностью и энергией, чтобы не только противостоять любой огромной силе, стремящейся выпрямить канат, но и преодолеть ее, то почему вы склонны отрицать наличие их у веса снаряда? Скажу вам более: мы должны с удивлением и удовольствием констатировать, что канат, натянутый в большей или меньшей степени, располагается по линии, весьма близкой к параболе. Сходство столь велико, что если вы начертите на вертикальной плоскости параболическую линию и, рассматривая ее в обратном положении, т. е. {343} обратив вершину ее вниз, а основание, параллельное горизонту, вверх, подвесите цепочку, укрепив концы ее в конечных точках основания начерченной параболы, то вы увидите (укорачивая или удлиняя цепочку, смотря по надобности), что она очень близко подходит к параболе; при этом совпадение ее с параболой наблюдается тем большим, чем меньше кривизна параболы, т. е. чем более последняя растянута, так что при параболе, описываемой при угле наклона в 45 градусов, цепочка почти точно совпадает с параболой16.
Сагредо. Таким образом, при помощи подобной тонко сработанной цепочки можно в одну минуту начертить на плоскости большое количество параболических линий?
Сальвиати. Конечно, и притом с немалой пользой, как я вам сейчас покажу.
Симпличио. Но ранее, чем мы пойдем дальше, мне хотелось бы убедиться в справедливости того положения, о котором вы говорите, как об установленном совершенно точно; я имею в виду утверждение, что никакой силой, как бы ни была она велика, невозможно натянуть канат совершенно прямо и параллельно горизонту.
Сагредо. Постараюсь припомнить доказательство. Для понимания последнего, синьор Симпличио, необходимо, чтобы вы наперед признали справедливость следующего положения, доказанного не только опытом, но и теоретическими рассуждениями, в отношении всех механических инструментов: скорость движения тела, хотя бы и обладающего малой силой, может превозмочь сопротивление, хотя бы и очень большое, если предмет, оказывающий сопротивление, движется медленно; это имеет место всегда, когда отношение скорости движущегося тела к медленности сопротивляющегося тела больше, нежели отношение сопротивления тела, приводимого в движение, к силе движущегося тела.
Симпличио. Это мне хорошо известно и доказано Аристотелем в его «Проблемах механики»; подобное явление наблюдается в рычаге или неравноплечих романских весах, где груз, весом не более четырех фунтов, поднимает вес в четыреста фунтов, если расстояние первого от центра весов превышает более чем в сто раз расстояние от того же центра большего груза. Происходит это по той причине, что при качании коромысла весов меньший груз проходит пространство, более чем в сто раз превышающее то, которое проходит больший груз; но это то же самое, что сказать: малый груз движется со скоростью, превышающей более чем в сто раз скорость большого груза.
Сагредо. Вы прекрасно рассуждаете и не подвергаете ни малейшему сомнению, что как бы ни была мала сила движущего тела, она может преодолеть сопротивление любой величины всякий раз, когда скорость его будет с избытком возмещать то, чего недостает силе или весу. {344} Теперь перейдем к случаю с канатом. Сделаем небольшой чертеж и предположим на время, что линия аb проходит поверх двух неподвижных твердых точек а и b, и несет, как вы видите, большие грузы end, подвешенные к ее концам, которые, натягивая ее с большою силою, заставляют ее располагаться совершенно прямо, ибо предполагается, что это простая линия,
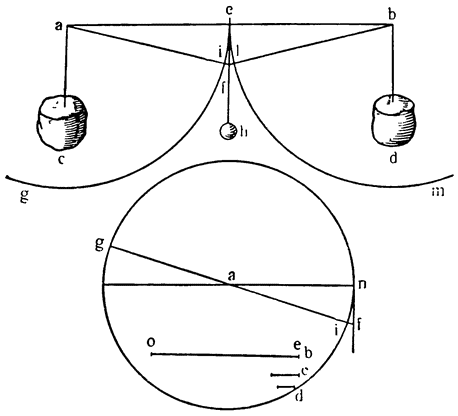 |
Симпличио. Я совершенно удовлетворен. Может быть, синьор Сальвиати теперь пояснит нам, согласно данному обещанию, какую пользу можно извлечь из упомянутой цепочки, а после этого познакомит нас с соображениями нашего Академика относительно силы удара.
Сальвиати. На этот день достаточно уже и того, чем мы до сих пор занимались. Хотя не поздно, но нам времени не хватит для того, чтобы как следует ознакомиться с названным предметом. Поэтому отложим лучше беседу до другого более удобного времени.
Сагредо. Я согласен с вашим мнением, синьор, так как из бесед с ближайшими друзьями нашего Академика я вывел заключение, что вопрос о силе удара представляется весьма темным, и никому из числа ранее занимавшихся им не удалось проникнуть в сущность этого предмета, полную мрака и далекую от обычных человеческих представлений. Одно из удивительнейших заключений, оставшихся в моей памяти, состоит в том, что сила удара неопределенна, чтобы не сказать — бесконечно велика. Итак, подождем, как предлагает синьор Сальвиати, более подходящего времени. Но скажите, о чем говорится далее в трактате после того, что мы слышали о движении брошенных тел?
Сальвиати. Там содержатся некоторые предложения, касающиеся центров тяжести твердых тел и открытые в юности нашим Академиком, которому казалось недостаточным то, что было написано по этому предмету Федериго Командино17. Он полагал, что эти предложения, изложенные далее, могут служить дополнением к тому, что содержится в книге Командино, и включил их в свой труд по совету синьора маркиза Гвидо Убальди-дель-Монте, величайшего математика своего времени, как о том свидетельствуют многочисленные изданные им сочинения18. Последнему он передал копию своего трактата, предполагая продолжить исследование того же предмета на других телах, не затронутых Командино. Однако, познакомившись впоследствии с книгою синьора Луки Валерио, крупнейшего геометра, и найдя, что все вопросы разрешены последним с исчерпывающей полнотой, он отказался от своего намерения, несмотря {346} на то, что он шел путями, совершенно отличными от тех, которыми шел синьор Валерио.
Сагредо. Было бы очень хорошо, если бы на то время, которое пройдет между настоящей и следующей нашей беседою, вы оставили мне рукопись, дабы я мог, синьор, за этот срок ознакомиться с последующими предложениями.
Сальвиати. Охотно исполняю вашу просьбу, синьор, и надеюсь, что вы получите большое удовольствие от ознакомления с этими предложениями19.
Конец четвертого дня
| {347} |
Постулат
Если одинаковые грузы расположены сходным образом на различных рычагах, то в том же отношении, в каком общий центр тяжести грузов делит один какой-либо рычаг, будут разделены соответствующими центрами тяжести и все другие рычаги.
Лемма I
Пусть линия аb разделена пополам в точке с, и одна из половин ее, а именно ас, разделена в точке е таким образом, что отношение be к еа
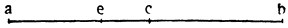 |
Предложение I
Исходя из этого положения, доказать, что если ряд величин, отличающихся друг от друга на некоторую одинаковую долю, равную наименьшей из этих величин, расположен в последовательном порядке на рычаге {348} таким образом, что точки подвеса находятся на равных друг от друга расстояниях, то общий центр тяжести их делит рычаг на части, из коих часть, нагруженная меньшими величинами, в два раза более другой части.
К рычагу аb на равных друг от друга расстояниях подвешено некоторое количество грузов — f, g, h, k, n, из которых наименьший равняется
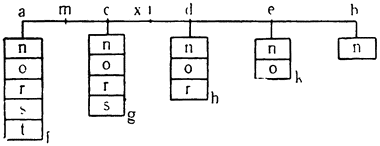 |
Разделим рычаг пополам в точке d, которая необходимо должна либо совпадать с одной из точек подвеса, либо находиться в середине между двумя точками подвеса; остальные отрезки между точками подвеса, расположенные между а и d, разделим пополам точками m и l; затем разделим все подвешенные грузы на части, равные n; при этом число таких частей, заключающихся в теле f, будет равно числу подвешенных к рычагу тел, число таких же частей в g будет на одну меньше и т. д. Обозначим составные части f через n, о, r, s, t, составные части g — через n, о, r, s, такие же части h — через n, о, r и части k — через n, о; общее число всех частей n равняется f; общее число все частей о равняется g, всех r равно h, всех s равно k и, наконец, всех t равно n. Все части n, равные между собой, пребывают в равновесии относительно точки d, которая делит рычаг аb пополам; равным образом части о находятся в равновесии относительно точки r, части r — относительно с, части s — относительно m и, наконец, часть t подвешена в точке а. Таким образом, к рычагу ad окажутся приложенными на равных друг от друга расстояниях в точках d, r, с, m и а грузы, последовательно превосходящие один другой на величину, равную наименьшей из них; наибольший из них, состоящий из наибольшего числа слагаемых n, будет расположен в точке d, и наименьший, которым является t, будет расположен в а; остальные грузы расположатся между ними. Представим себе теперь другой рычаг ad, на котором расположены в том же числе и порядке другие грузы, подобные первым. Рычаги аb и ad разделяются центром тяжести всех грузов в одном и том же отношении. Но центр тяжести первых грузов расположен в х; следовательно, х делит рычаги bа и ad в одном и том же отношении, и bх относится к ха, как ха к xd; поэтому, согласно доказанной выше лемме, bх равняется двум ха, что и требовалось доказать.
| {349} |
Предложение II
Если впишем в параболический коноид2 и опишем около него фигуры, состоящие из цилиндров равной высоты, и разделим ось этого коноида таким образом, чтобы часть, направленная к вершине, была в два раза больше части, направленной к основанию, то центр тяжести вписанной фигуры будет лежать близ точки деления ближе к основанию, а центр тяжести описанной фигуры — близ той же точки, но выше ее, причем расстояния до того и другого центра будут одинаковы и равны одной шестой части высоты одного из цилиндров, из коих составлены фигуры.
Представим себе параболический коноид и фигуры, о коих мы говорили,— одни вписанные, а другие описанные,— и ось коноида ае, разделенную в точке n так, что часть an равна удвоенной части nе. Покажем, что центр тяжести вписанных фигур будет лежать на линии nе, а центр тяжести описанных фигур на линии an. Рассечем фигуру плоскостью, проходящей через ось; линией сечения тела будет при этом парабола bас, линией пересечения плоскости с основанием коноида будет линия be, сечения же цилиндров будут представлять собою прямоугольники, как показано на чертеже. Первый вписанный цилиндр, осью которого является
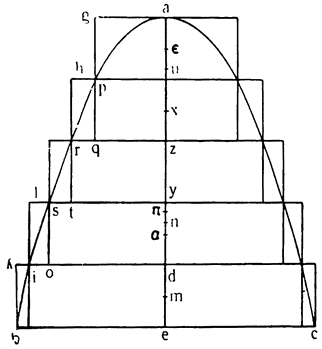 |
Следствие
Из сказанного ясно, что около параболического коноида можно описать и в него можно вписать фигуры так, чтобы центры тяжести их отстояли от точки n на расстояние, меньшее любой данной линии. В самом деле, если мы возьмем данную линию, увеличим ее в шесть раз и сделаем оси цилиндров, из которых составляется фигура, меньшими, чем эта линия, то расстояние центра тяжести этих фигур от точки n будет меньше данной линии.
Другой способ
Разделим ось коноида cd в точке о так, чтобы отрезок со равнялся двум od. Требуется доказать, что центр тяжести вписанных фигур лежит на линии od, а центр тяжести описанных фигур — на линии со. Рассечем фигуру по-прежнему плоскостью, проходящей через точку с и ось. Цилиндры sn, tm, vi, хе относятся между собою как квадраты линий sd, in, vm, xi, т. е. как линии nс, cm, ci и се; последние отличаются друг от друга на одну и ту же величину, равную се; при этом цилиндр tm равняется цилиндру qn, цилиндр vi — цилиндру pn и цилиндр хе — цилиндру ln; следовательно, цилиндры sn, qn, pn и ln превышают друг друга на одну и ту же величину, равную наименьшему из них, т. е. цилиндру ln. Превышение объема цилиндра sn над объемом цилиндра qn представляет собою кольцо, высота которого равна qt или же nd, а ширина основания — sq; превышение {351} объема цилиндра qn над pn есть кольцо, ширина основания которого равна qp, и превышение объема цилиндра pn над ln есть кольцо, ширина основания которого равна pi. Все означенные кольца sq, qp, pi равны между собою и равны цилиндру ln. В то же время кольцо st равняется цилиндру хе; кольцо qv, превышающее st в два раза, равняется цилиндру vi, который превышает цилиндр хе в два раза,
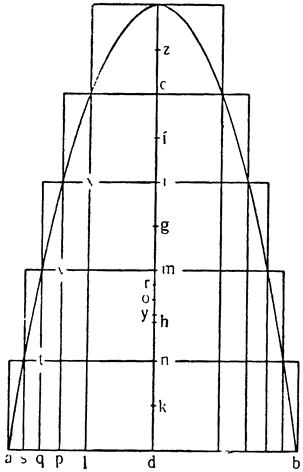 |
Предложение III
На основании изложенного выше докажем, что центр тяжести параболического коноида делит ось таким образом, что часть, обращенная к вершине, в два раза превосходит часть, обращенную к основанию.
Возьмем параболический коноид и разделим ось его аb в точке n так, чтобы часть an равнялась двум nb. Требуется доказать, что центр тяжести коноида лежит в точке n. Если он не лежит в точке n, то он расположен либо ниже либо выше нее. Предположим сначала, что он лежит ниже
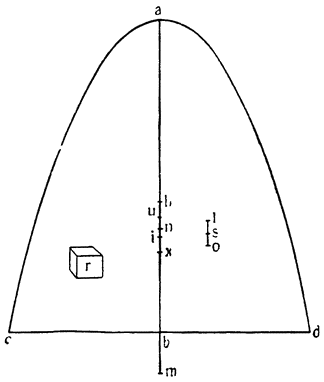 |
Дан коноид, осью которого является аb, причем центр тяжести описанных фигур лежит в точке с, а вписанных — в точке о. Утверждаю, что центр тяжести коноида лежит между точками c и о. Если он не лежит между {354} ними, то он должен лежать либо ниже, либо выше, либо же в одной из этих точек. Предположим, что он лежит ниже, например в точке r, так что эта точка является центром тяжести всего коноида, в то время как центр тяжести вписанных фигур лежит в о; тогда центр тяжести излишка вписанной фигуры над коноидом будет лежать на линии or за точкой r и на таком от нее расстоянии, при котором отношение or к расстоянию от
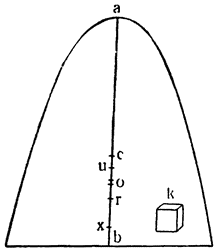 |
| {355} |
Лемма II
Даны три линии в непрерывной пропорции; если отношение наименьшей из них к разнице между наибольшей линией и нею равно отношению некоторой прямой к двум третям излишка наибольшей линии над средней, и отношение составной линии из наибольшей и удвоенной средней к составной линии из утроенных наибольшей и средней равно отношению еще какой-либо линии к излишку, на который наибольшая линия превосходит среднюю, то обе новые линии вместе составляют одну треть наибольшей линии.
Даны три образующие непрерывную пропорцию линии ab, bc и bf, причем отношение bf к af равно отношению ms к двум третям са, а отношение линии, составленной из ab и удвоенной bc, к линии, составленной из утроенных
 |
С другой стороны, отношение ос к са равно отношению утроенной линии cb к утроенной ab вместе с утроенной cb; а так как отношение са к cf равно отношению утроенной линии ab к утроенной bc, то ос относится к cf, как утроенная линия ab к утроенной ab вместе с утроенной bc, а оf относится к fc, как утроенная линия bc к утроенной ab вместе с утроенной bc. Но cf относится к fb, как ас к сb или как утроенная линия ас к утроенной bc; следовательно, отношение of к fb равно отношению утроенной линии ас к утроенной сумме линий ab и bc. Таким образом, вся линия оb относится к bf, как ушестеренная линия ab к утроенной сумме ab и bc. Так как отношения fc к са и cb к bа равны, то fc будет относиться к са, как bc к bа; поэтому fa будет относиться к ас, как bа вместе с bc к bа или как утроенная первая величина к утроенной второй. Таким {356} образом, fa относится к ас как линия, составленная из трех bа и трех bc, к утроенной линии аb. Поэтому отношение fa к двум третям ас будет равно отношению линии, составленной из утроенной bа и утроенной be, к двум третям утроенной линии bа, т. е. к удвоенной линии bа. Но отношение fa к двум третям линии ас равно отношению fb к ms; следовательно, отношение fb к ms равно отношению утроенной линии bа вместе с утроенной bc к удвоенной bа. Но так как отношение ob к fb равно отношению шести аb к утроенной сумме аb и bc, то отношение ob к ms будет равно отношению шести ab к двум bа; следовательно, линия ms составляет третью часть ob; ранее же было доказано, что линия sn составляет третью часть ао; поэтому вся линия mn должна равняться одной трети линии аb, что и требовалось доказать3.
Предложение IV
Усеченный параболический коноид4 имеет центр тяжести на прямой линии, являющейся осью этого отрезка; если разделить эту ось на три равные части, то центр тяжести будет лежать в средней из них и делить ее таким образом, что часть, обращенная к меньшему основанию, будет относиться к части, обращенной к большему основанию, как большее основание к меньшему.
От коноида, осью которого является rb, отсечена плоскостью, параллельной основанию, часть с осью bc; другая плоскость, проходящая через ось, перпендикулярную к основанию, пересекает коноид по параболе urc; эта плоскость пересекается с основаниями усеченного коноида по прямым lm и uc. Тогда lm и uc будут ординатами, а диаметром [параболы] является линия rb5. Разделим eb на три равные части, средней из которых будет qy; пусть точка i делит эту часть таким образом, что отношение основания с диаметром uc к основанию с диаметром lm, или отношение квадрата uc к квадрату lm, равно отношению qi к iy. Докажем, что i центр тяжести усеченного коноида lmc. Проведем линию ns, равную br, отложим отрезок sx, равный еr, возьмем линию sg — третью пропорциональную к ns и sx — и примем, что отношение bq к io равно отношению ng к gs. При этом безразлично, будет ли точка о лежать выше или ниже lm. Так как линии lm и uc являются ординатами сечения urc, то квадрат uc относится к квадрату lm, как линия br к re. Но квадраты uc и lm относятся между собою, как qi и iу, а отношение br к re равно отношению ns к sx; следовательно, отношение qi к iy равно отношению ns к sx. Далее, отношение qy к yi равно отношению ns вместе с sx к sx, вследствие чего отношение eb к yi равно отношению линии, составленной из трех ns и трех sx к sx; поэтому отношение eb к by равно отношению утроенной суммы ns и sx к сумме ns и sx, а отношение eb к bi равно отношению {357} суммы трех ns и трех sx к сумме ns и двух sx. Но три линии ns, sx и gs последовательно пропорциональны, и отношение sg к gn равно отношению линии oi к двум третям eb или к той же части nx. Однако мы уже нашли, что отношение линии, составленной из ns и двух sx к линии, составленной из утроенной ns и утроенной sx, равно отношению некоторой другой линии ib к bc или, что то же самое, к nх. На основании ранее доказанного заключаем,
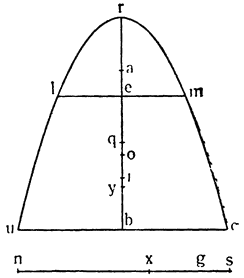 |
Предложение V
Если мы возьмем любое число величин, расположенных по порядку таким образом, что вторая отличается от первой на удвоенную первую, третья от второй — на утроенную первую, четвертая от третьей — на учетверенную первую и т. д., так что каждая последующая величина будет равняться предыдущей, сложенной с первой величиной, повторенной такое число раз, какое место по порядку занимает данная величина,— и подвесим эти величины к рычагу на равных друг от друга расстояниях, то центр тяжести их разделит рычаг таким образом, что часть его, направленная в сторону меньших тел, будет в три раза больше другой его части.
Пусть LT — рычаг и A, F, G, Н, К — подвешенные к нему грузы, о которых было сказано выше, причем первый из них А подвешен в Т. {358} Утверждаю, что центр тяжести делит рычаг TL таким образом, что часть, обращенная к Т, равна утроенной другой части. Пусть, далее, линия TL равна трем LI, SL — трем LP, QL — трем LN и LP — трем LO; отрезки IP, PN, АО и OL будут при этом равны между собою. Представим себе,
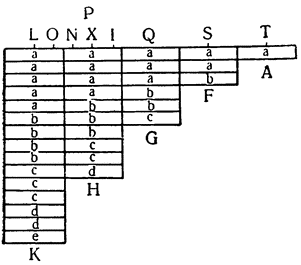 |
Предложение VI
Если мы возьмем какие-либо величины, расположенные таким образом, что вторая превышает первую на три первых, третья вторую — на пять первых, четвертая третью — на семь первых и т. д., так что излишек каждой из величин над предыдущей равняется первой величине, умноженной на соответствующее нечетное число из последовательного ряда их, сами же величины относятся между собою как квадраты линий, {359} постепенно возрастающих на одну и ту же величину, равную наименьшей из них, и подвесим эти величины к рычагу на равных друг от друга расстояниях, то общий центр тяжести всех этих величин разделит рычаг таким образом, что часть, обращенная к меньшим величинам,
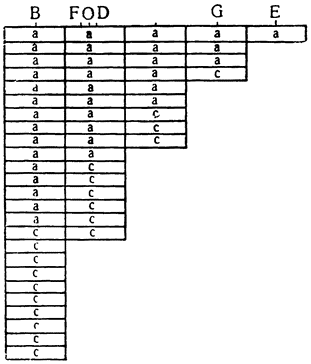 |
Пусть к рычагу BE подвешены грузы, о которых было сказано выше, и выделим из них те грузы, о которых говорилось в предыдущем предложении; тогда мы получим часть, составленную из элементов а, и в остатке аналогичную часть, составленную из элементов с, в которой не будет доставать одного члена. Пусть линия ED будет равна утроенной DB, a GF — утроенной FB; тогда D будет центром тяжести тел, составленных из грузов a, a F — центром тяжести тел, составленных из грузов с; следовательно, центр тяжести всех подвешенных величин а и с будет лежать между точками D и F. Пусть этим центром будет точка О. Ясно, что ЕО превышает ОВ более чем в три раза, тогда как GO меньше, нежели три ОВ, что и требовалось доказать.
Предложение VII
Если в какой-либо конус или часть конуса вписана фигура, состоящая из цилиндров одинаковой высоты, а около того же конуса или части его описана другая фигура из такого же числа цилиндров той же высоты, и ось этого конуса разделена таким образом, что часть ее, обращенная к вершине, равна утроенной части, обращенной к основанию, то центр тяжести вписанных фигур лежит ближе к основанию, чем указанная точка деления оси, а центр тяжести фигур описанных — ближе к вершине.
Пусть дан конус, ось которого nm разделена в точке s таким образом, что линия ns равняется утроенной sm. Утверждаю, что центр тяжести тел, вписанных в конус так, как было сказано выше, лежит на оси nm ближе к основанию, нежели точка s, центр же тяжести описанных тел лежит на той же оси nm выше точки s. Рассмотрим вписанную фигуру, состоящую из цилиндров, оси которых mc, cb, be и еа равны между собой. Первый цилиндр, осью которого является mс, относится ко второму цилиндру, {360} осью которого является cb, как основание первого к основанию второго (ибо высоты их равны) или как квадрат сn к квадрату nb. Точно так же отношение цилиндра, ось которого равна cb, к цилиндру, ось которого равна be, равно отношению квадрата bn к квадрату nе, а отношение цилиндра с осью be к цилиндру с осью еа равно отношению квадрата еn к квадрату nа. Но линии nс, nb, еn и nа превышают друг друга на одинаковую величину, причем эта величина равна наименьшей из этих линий, а именно nа. Следовательно, означенные величины, т. е. вписанные цилиндры, относятся между собою последовательно как квадраты линий, последовательно превышающих одна другую на одинаковую величину, равную наименьшей из них. Если поэтому расположить эти величины на рычаге ti, на котором находится и центр тяжести их, то они расположатся на равных друг от друга расстояниях. Как было доказано выше, общий центр тяжести тел разделит рычаг ti таким образом, что часть, обращенная к t, превысит другую часть более чем в три раза. Положим, что центр лежит в точке о; тогда to будет более трех oi. Так как tn равняется трем im, то mо меньше четверти mn, поскольку ms равняется четверти этой последней линии. Отсюда вытекает, что точка о расположена ближе ix. основанию конуса, чем s. Описанная фигура также состоит из цилиндров, оси которых mс, cb, be, ea, an равны между собой; способом, подобным изложенному выше, доказывается, что они относятся между собою, как квадраты линий mn, nc, nb, nе, an, которые последовательно превышают друг друга на одну и ту же величину, равную наименьшей из них, а именно an. Согласно изложенному выше, центр тяжести всех этих цилиндров расположен в точке u, которая делит рычаг ri таким образом, что часть, обращенная к г, т. е. ru, превышает утроенный остаток ui, в то время как tu меньше, чем тот же утроенный остаток. Так как nt равняется трем im, то линия um больше, чем четверть mn, часть которой ms равна, по предложению, четверти mn. Следовательно, точка u лежит ближе к вершине конуса, чем точка s, что и требовалось доказать.
Предложение VIII
В данный конус можно вписать цилиндры, имеющие равные оси, и около него можно описать подобные же цилиндры таким образом, что расстояние между центрами тяжести вписанных и описанных цилиндров будет меньше любой данной линии. {361}
Даны: конус с осью ab и отрезок k. Возьмем цилиндр l, равный тем, которые вписаны в конус с высотой ab; разделим ab в точке с таким образом, чтобы линия ас была в три раза больше cb, и пусть отношение ас к k будет равно отношению цилиндра l к телу х. Пусть, далее, в конус
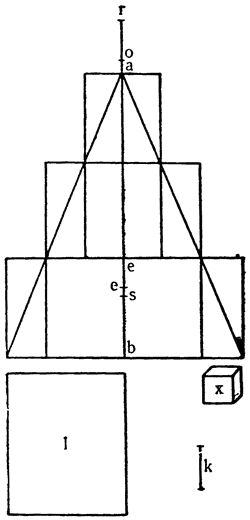 |
Следствие
Из предыдущего видно, что мы можем вписать в данный конус фигуру, состоящую из цилиндров с равными высотами, и описать около него подобную же фигуру таким образом, чтобы расстояние центров тяжести {362} их от точки, разделяющей ось цилиндра на части, верхняя из которых в три раза превышает нижнюю, было менее любой данной линии. Так как по доказанному ранее точка, делящая ось в означенном отношении, лежит всегда между центрами тяжести вписанных и описанных фигур, а расстояние между точками, в которых лежат эти центры, может быть сделано менее любой данной линии, то тем легче то же самое может быть сделано и с расстояниями от центров тяжести до указанной выше точки.
Предложение IX
Центр тяжести любого конуса или пирамиды делит ось таким образом, что часть ее, обращенная к вершине, равняется утроенной части, обращенной к основанию.
Имеется конус, ось коего аb разделена в точке с таким образом, что часть ас равняется утроенной cb; требуется доказать, что с является центром тяжести конуса. Если это не так, то центр тяжести конуса будет лежать либо выше либо ниже точки с. Предположим, что он лежит ниже, например в точке е. Возьмем линию lр, равную се, и разделим ее в точке n таким образом, чтобы отношение be вместе с pn к pnбыло равно отношению конуса к телу х. Впишем, далее, в конус фигуру, состоящую из
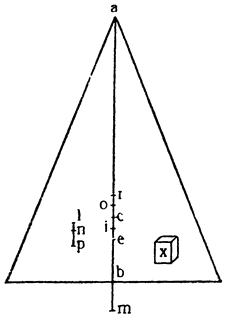 |
Лемма III
Если имеются четыре линии, образующие непрерывную пропорцию, и отношение наименьшей из них к разности между наибольшей и наименьшей равно отношению некоторой линии к трем четвертям разности между наибольшей линией и второй по величине, а линия, равная сумме наибольшей, удвоенной второй и утроенной третьей линий, относится к линии, равной сумме учетверенной наибольшей, учетверенной второй и учетверенной третьей линий, как некоторая другая линия к разности между наибольшей линией и второй, то сумма указанных двух линий составляет четвертую часть наибольшей из данных пропорциональных линий6.
Даны четыре пропорциональных линии ab, bc, bd и be. Пусть отношение be к еа равно отношению линии fg к 3/4ас, а отношение линии, равной сумме аb, удвоенной bc и утроенной bd, к учетверенной сумме линий ab, bc и bd равно отношению линии hg к ас. Требуется доказать, что линия hf равна четвертой части ab. Так как линии ab, bc, bd и be образуют непрерывную пропорцию, то линии ас, cd и de также в непрерывной пропорции, и отношение учетверенной суммы ab, bc и bd к сумме ab, удвоенной bc и утроенной bd будет равно отношению учетверенной {364} суммы ас, cd и de или, что то же самое, учетверенной линии ае к сумме ас, удвоенной cd и утроенной de, каковое отношение равно отношению ас к hg. Следовательно, отношение утроенной линии ае к сумме ас, удвоенной cd и утроенной de равно отношению 3/4ас к hg. Но отношение утроенной ае к утроенной еb равно отношению 3/4ас к gf; следовательно, по предложению двадцать четвертому книги пятой отношение утроенной ае к сумме ас, удвоенной cd и утроенной db равно отношению 3/4ас к hf, a

отношение учетверенной линии ае к сумме ас, удвоенной cd и утроенной db или, что то же самое, к сумме ab, cb и bd равно отношению ас к hf. Отсюда следует, что отношение учетверенной линии ае к ас равно отношению суммы ab, cb и bd к hf. Но отношение ас к ае равно отношению ab к сумме ab, cb и bd; следовательно, отношение учетверенной линии ае к ае равно отношению ab к hf. Отсюда вытекает, что hf составляет четвертую часть ab.
Предложение X
Центр тяжести усеченной пирамиды или усеченного конуса, который заключен между основанием и плоскостью, ему параллельной, лежит на оси его и делит последнюю таким образом, что отношение части ее, направленной в сторону меньшего основания, к остальной части ее равно отношению суммы утроенного большего основания, удвоенного среднего между большим и меньшим основанием и меньшего основания к сумме утроенного меньшего основания, удвоенного среднего и большего основания.
Пусть от конуса или пирамиды с осью ad отсечен плоскостью, параллельной основанию, отрезок, осью которого является ud, и пусть отношение суммы утроенного большего основания, удвоенного среднего и меньшего к сумме утроенного меньшего, удвоенного среднего и большего равно отношению uо к od. Докажем, что точка о является центром тяжести усеченной фигуры. Пусть um равняется четвертой части ud. Проведем линию hx, равную оси ad, и отложим отрезок kx, равный аu. Пусть третьей пропорциональной к линиям hx и kx будет xl, а четвертой xs, и пусть, далее, отношение hs к sx равно отношению md к некоторому отрезку, направленному от о к вершине а, каковым является on. Так как большее основание относится к среднему пропорциональному между большим и меньшим, как da к аu или как hx к хk, а среднее относится к меньшему, {365} как kх к xl, то большее, среднее и меньшее основания относятся между собою, как линии hx, xk и xl. Отсюда вытекает, что отношение утроенного большого основания вместе с удвоенным средним и меньшим к утроенному меньшему основанию вместе с удвоенным средним и большим или, что то же самое, отношение uо к od равно отношению суммы утроенной линии hx, удвоенной хk
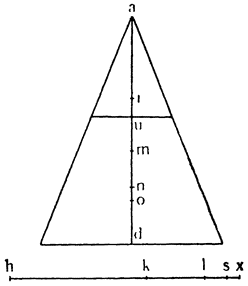 |
Конец приложения
| {366} |
С |
Сагредо. Не стану отрицать, что за эти годы мне приходило в голову много различных соображений по поводу всего того нового, что было внесено нашим почтенным старцем в учение о движении, им обоснованное и построенное на положениях геометрии. Раз вы того желаете, то я попробую припомнить некоторые мои соображения и дам вам случай помочь мне вашими учеными размышлениями.
Итак, начиная по порядку, я возвращаюсь к самому началу трактата о движении и позволяю себе, синьор, выдвинуть старое сомнение, {367} возникающее у меня с новой силой при размышлении над первым предложением нашего Автора относительно равномерного движения. Он основывается (подобно многим другим старым и новым писателям) на предложении о равных кратных. Но мне всегда казалось, что в пятом или, как говорят некоторые, шестом определении пятой книги Эвклида имеется некоторая неясность, и я считаю себя счастливым, что могу, пользуясь настоящим случаем, изложить вам свои сомнения, от которых, надеюсь, вы меня окончательно избавите.
Симпличио. Я также смотрю на эти возобновившиеся беседы с вами, синьоры, как на особый дар судьбы, надеясь, что они прольют некоторый свет на предмет, затронутый синьором Сагредо. В том небольшом курсе геометрии, который я проходил юношей в школе, для меня не было другого более трудного пункта, чем этот; вы можете себе поэтому представить, какую ценность для меня будет представлять возможность получить, наконец, после столь долгого времени удовлетворительное объяснение этого специального вопроса.
Сагредо. Итак, я говорю, что при доказательстве первого предложения о равномерном движении наш Автор пользуется способом равных кратных, согласно пятому или шестому определению книги пятой Эвклида. Так как у меня уже давно существовали некоторые сомнения относительно этого определения, то и в отношении упомянутого выше предложения у меня недостает той ясности, которая была бы желательна. Поэтому мне представляется в высокой степени желательным основательно усвоить себе этот начальный принцип, чтобы получить возможность лучше понять все последующее в учении о движении.
Сальвиати. Я надеюсь удовлетворить высказанное вами желание, синьоры, изложив вам определение Эвклида другим путем, при котором я смогу воспользоваться понятием пропорциональности. Могу сообщить вам, что в ваших сомнениях вы имеете товарищами выдающихся людей, которые долгое время оставались столь же неудовлетворенными, как и вы после нашей беседы на эту тему.
Могу также признаться вам, что в течение нескольких лет после того, как я изучил пятую книгу Эвклида, это место оставалось для меня темным. Я преодолел в конце концов затруднения лишь благодаря тому, что, изучая чудесные «Спирали»2 Архимеда, нашел в прекрасном введении к этой книге доказательство, подобное предложенному нашим Автором. Этот случай дал мне повод к размышлению, не удастся ли найти другой, более легкий путь, которым можно было бы прийти к той же самой цели и установить как для себя, так и для других более точное понятие пропорциональности. Я внимательно занялся этим предложением и изложу вам теперь то, к чему я пришел, размышляя на эту тему, и представлю мои выводы, синьоры, на ваш строгий суд. {368}
Положим прежде всего, как это делает и Эвклид в своих определениях, что имеются пропорциональные величины, т. е. что даны три каких-либо величины, причем пропорция, соотношение или количественное отношение между первой и второй из них таково же, как между третьей и какой-либо четвертой. Для того чтобы дать определение этих пропорциональных величин, и притом такое, которое было бы достаточным для приобретения читателем представления, соответствующего природе этих пропорциональных величин, следует воспользоваться, утверждаю я, одним из их отличительных свойств, и притом таким, которое представляется наиболее простым и благодаря этому наиболее доступным для людей, даже незнакомых с математикой. Так поступал и сам Эквлид во многих других случаях. Как мы помним, он не сказал, что круг есть плоская фигура, обладающая тем свойством, что при пересечении внутри нее двух прямых линий всегда получаются такие отрезки, что прямоугольник, построенный из отрезков одной прямой, равен прямоугольнику, построенному из отрезков другой, или же фигура, обладающая тем свойством, что вписанные в нее четырехугольники, всегда имеют сумму противолежащих углов равной двум прямым. Какое бы из этих определений ни взять, оно правильно и хорошо. Но он знал и другое свойство круга, более очевидное, нежели упомянутые выше, а потому более понятное и дающее надлежащее представление о круге; никто не будет отрицать, думаю я, что он сделал лучше, выбрав для определения круга именно это более простое и очевидное свойство, а затем, выведя из него и доказав, как следствия, прочие свойства.
Сагредо. Конечно, это совершенно правильно, и я полагаю, что редко кто вполне удовлетворится следующим определением, которое я дам, согласно Эвклиду: четыре величины пропорциональны между собою тогда, когда любые равные кратные первой и третьей величины всегда одновременно больше, меньше или же равны любым равным кратным второй и четвертой величины.
Какими необыкновенно счастливыми способностями надо обладать, чтобы сразу же получить уверенность в действительном существовании такого соответствия равных кратных в случае пропорциональности четырех величин! К тому же, кто знает, не имеет ли места такое соответствие даже и тогда, когда величины непропорциональны? В предыдущих определениях Эвклид уже сказал, что пропорция между двумя величинами есть такое соответствие или отношение между ними, которое сводится к количеству. Теперь, после того как читатель составил в уме своем представление о том, что такое отношение между двумя величинами, для него будет неясно, следует ли понимать под отношением первой величины ко второй то же, что и под отношением третьей величины к четвертой в том случае, когда равные кратные первой и третьей величины соответствуют {369} указанным выше образом равным кратным второй и четвертой величины, т. е. всегда в одинаковой мере больше или меньше их или же равняются им.
Сальвиати. Как бы то ни было, мне кажется, что это положение Эвклида более похоже на теорему, требующую доказательства, нежели на предпосылаемое определение. К тому же мне столько раз приходилось видеть, как на этом месте спотыкались даже сведущие люди, что мне захотелось дать общее определение пропорциональности, и притом такое, которое годилось бы и для людей, не знающих геометрии. Это я сделаю следующим образом.
Мы говорим, что четыре величины пропорциональны между собою, т. е. что отношение между первой и второй величиной одинаково с отношением между третьей и четвертой, когда первая величина равна второй, а третья равна четвертой, или же когда первая величина во столько же раз больше второй, во сколько третья больше четвертой. Вы не встречаете, синьор Симпличио, никаких затруднений к признанию этого положения?
Симпличио. Никаких.
Сальвиати. Но так как между четырьмя величинами не часто встречается указанное выше равенство или же точная кратность, то пойду теперь дальше и спрошу синьора Симпличио: признаете ли вы, что четыре величины пропорциональны и тогда, когда первая содержит вторую, скажем, три с половиной раза, а третья содержит четвертую также три с половиною раза?
Симпличио. Прекрасно понимаю и признаю, что четыре величины будут пропорциональными не только в случае, вами указанном, синьор, но также и при всякой другой простой или дробной кратности.
Сальвиати. Итак, суммируя все, до сего времени изложенное, скажем в краткой и общей форме:
мы называем четыре величины пропорциональными между собою тогда, когда избыток первой величины над второй (каков бы он ни был) равен избытку третьей над четвертой3.
Симпличио. До сих пор я не встречал никаких затруднений; но мне кажется, синьор, что таким определением пропорциональности вы охватываете только те случаи, когда предыдущие члены больше последующих, так как вы полагаете, что первая величина превышает вторую в той же мере, как третья четвертую. Но теперь я спрошу вас, чем мне руководствоваться, если предыдущие члены меньше последующих?
Сальвиати. Я отвечу, синьор, что если вы имеете четыре величины, из которых первая меньше второй, а третья меньше четвертой, так что вторая больше первой, а четвертая больше третьей, то вам, синьор, надлежит рассматривать их в обратном порядке и представить себе, что вторая величина занимает место первой, а четвертая третьей. Тогда предыдущие {370} члены снова будут больше последующих, и не придется искать другого определения, отличного от уже установленного нами.
Сагредо. Пусть будет так. Но, пожалуйста, синьор, пойдем далее, исходя из указанного вами предположения, что предыдущие члены всегда больше последующих; это, как мне кажется, значительно облегчит и понимание и ход рассуждения.
Сальвиати. Установив это первоначальное определение, при соединим к нему указание на условие, которому должны удовлетворять четыре пропорциональные между собою величины. Оно заключается в следующем: если первая величина ни на йоту не больше и не меньше той, какой она должна быть, чтобы иметь ко второй величине то же самое отношение, какое имеет третья величина к четвертой, то отношение первой величины ко второй равно отношению третьей величины к четвертой. Пользуясь случаем, дадим также определение большего отношения и установим:
если же первая величина больше той, какой она должна быть, чтобы иметь ко второй величине то же самое отношение, какое имеет третья величина к четвертой, то мы должны сказать, что отношение первой величины ко второй больше отношения третьей величины к четвертой.
Симпличио. Хорошо. Но что будет, если первая величина окажется меньше той, какой она должна быть, чтобы иметь ко второй величине то же самое отношение, какое имеет третья величина к четвертой?
Сальвиати. Если первая величина будет меньше той, какой она должна быть, чтобы иметь ко второй величине то же самое отношение, какое имеет третья величина к четвертой, то ясно, что третья величина больше, чем требуется для сохранения равенства ее отношения к четвертой отношению первой величины ко второй. Таким образом, и в этом случае, синьоры, достаточно будет изменить порядок на обратный и представить себе, что те величины, которые даны как третья pi четвертая, являются первой и второй, и поставить величины, данные как первая и вторая, на место третьей и четвертой.
Сагредо. Пока я прекрасно понимаю вашу мысль, синьор, и тот принцип, который вы хотите положить в основу рассуждения о пропорциональности. Мне кажется, что вы намереваетесь сделать одно из двух: либо доказать на основании ваших принципов все пятое определение Эвклида, либо же вывести из двух данных вами определений два других определения, которые даны Эвклидом как пятое и седьмое и на которых основано все построение его пятой книги. Если вы сможете вывести эти последние как следствия, то мне не останется ничего больше желать по этому вопросу.
Сальвиати. Как раз таково и было мое намерение. В самом деле, если на основании данного определения будет ясно показано, что {371} при наличии четырех пропорциональных величин равные кратные первой и третьей величины всегда и необходимо соответствуют равным кратным второй и четвертой величины, будучи одновременно больше или меньше их или же равными им, то тогда можно будет сразу приступить к пятой книге Эвклида и понять все теоремы, относящиеся к пропорциональным величинам. Равным образом, если, основываясь на данном нами определении большего отношения, мы докажем, что в некоторых случаях, взяв равные кратные первой и третьей величины, а также второй и четвертой, мы получаем кратное первой величины превосходящим кратное второй, в то время как кратное третьей величины не превосходит кратного четвертой, то благодаря этому доказательству нам станут ясными другие теоремы, относящиеся к величинам непропорциональным; ибо это наше заключение будет как раз тем определением, которым как принципом пользуется сам Эвклид.
Симпличио. После того как я удостоверюсь, что свойства равных кратных именно таковы, т. е. что при пропорциональности четырех величин они всегда соответствуют друг другу, будучи равными или же одинаково большими и меньшими, и что в случае четырех непропорциональных величин такого соответствия не существует, мне не потребуется дальнейшей помощи для ясного понимания всей пятой книги «Начал геометрии».
A |
B |
C |
D |
Сальвиати. В таком случае скажите мне, синьор Симпличио: если мы предположим, что четыре величины A, В, С и D пропорциональны, т. е. что отношение первой из них А ко второй В равно отношению третьей величины С к четвертой D, то признаете ли вы, что и отношение удвоенной первой величины ко второй равно отношению удвоенной третьей величины к четвертой?
Симпличио. Я хорошо это понимаю, ибо если некоторая первая величина относится ко второй как некоторая третья величина к четвертой, то я не вижу оснований, почему удвоенная первая величина относилась бы ко второй иначе, чем удвоенная третья величина к четвертой.
Сальвиати. Таким образом, если вы это признаете, синьор, то вы должны признать также, что отношение первой величины, взятой четыре, десять или сто раз, к некоторой второй величине равно отношению третьей величины, взятой четыре, десять или сто раз, к некоторой четвертой.
Симпличио. Конечно, это так. Если мы будем увеличивать величины в одинаковое число раз, то я признаю, что первая величина, взятая два раза или десять, или сто раз, будет относиться ко второй так же, как третья величина, взятая столько же раз, т. е. два, десять или сто, к четвертой. Трудно было бы убедить меня в противном. {372}
Сальвиати. Итак, оказывается нетрудным понять, что кратное первой величины имеет ко второй величине такое же отношение, как аналогичное кратное третьей величины к четвертой, т. е. что первая величина, взятая любое число раз, относится ко второй, как третья величина, взятая такое же число раз, к четвертой. Теперь представьте себе, что все сказанное об увеличении предыдущих величин без изменения последующих
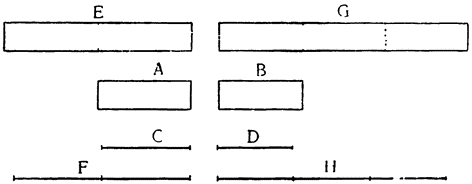
относится к увеличению одних последующих, в то время как предыдущие остаются без изменения, и скажите мне: признаете ли вы, что при четырех данных пропорциональных величинах первая величина будет относиться к удвоенной второй иначе, чем третья к удвоенной четвертой?
Симпличио. Думаю, что это абсолютно невозможно. Если первая величина относится к некоторой второй, как третья к некоторой четвертой, то я полагаю, что та же самая первая величина будет относиться ко второй, взятой два, четыре или десять раз, совершенно так же, как третья величина к четвертой, повторенной два, четыре или десять раз.
Сальвиати. Итак, вы принимаете и признаете совершенно понятным, что если взять четыре пропорциональные величины А, В, С и D и увеличить первую и третью из них в одинаковое число раз, то отношение Е, т. е. кратного А, ко второй величине В будет совершенно одинаково с отношением F, т. е. кратного C, к четвертой величине D. Представьте себе теперь, что Е, В, F и D суть данные нам четыре пропорциональные величины, так что кратное первой величины Е будет первой величиной, вторая величина В останется второй, кратное третьей величины F будет третьей величиной и четвертая величина D останется четвертой. Вы уже признали, синьоры, что, увеличивая в одинаковое число раз последующие члены В и D, т. е. второй и четвертый, и оставляя предыдущие без изменения, мы будем иметь отношение первой величины к кратному второй равным отношению третьей величины к кратному четвертой. Но этими четырьмя величинами будут теперь Е, F — равные кратные первой и третьей величины и G, Н — равные кратные второй и четвертой величины.
Сагредо. Признаю себя совершенно удовлетворенным. Теперь я хорошо понимаю, почему равные кратные четырех пропорциональных {373} величин всегда неизбежно соответствуют одни другим в равенстве или неравенстве в ту или иную сторону. В самом деле, если взять равные кратные первой и третьей величины и разные кратные второй и четвертой величины, то, как вы мне показали, синьор, отношение кратного первой величины к кратному второй будет равно отношению кратного третьей величины к кратному четвертой. Отсюда следует, что если кратное первой величины больше кратного второй, то и кратное третьей величины необходимо должно быть больше (для сохранения пропорции) кратного четвертой, если же оно меньше второго или равно ему, то и кратное третьей величины должно быть меньше кратного четвертой или же равно ему.
Симпличио. У меня также нет по этому поводу никаких возражений. Мне только хотелось бы знать, как доказывается (в том случае, когда четыре величины непропорциональны), что равные кратные не обнаруживают такого постоянного соответствия в равенстве и неравенстве в ту или другую сторону.
Сальвиати. Надеюсь, что и в этом отношении вы будете вполне удовлетворены, синьор.
Положим, что из четырех данных величин АВ, C, D и Е первая АВ несколько больше той, какой она должна была бы быть, чтобы отношение ее ко второй величине С равнялось отношению третьей величины D к четвертой Е. Я докажу, что если взять особым образом равные кратные первой и третьей величины, а также некоторые другие равные кратные второй и четвертой величины, то кратное первой величины станет больше кратного второй, в то время как кратное третьей величины не станет в той же мере больше кратного четвертой, но будет меньше.
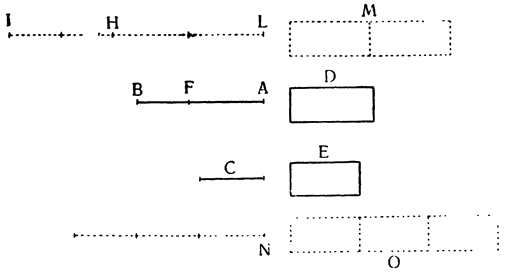
Представим себе, что от величины АВ отнят излишек, который делает ее больше той, какой она должна была бы быть для сохранения пропорциональности, и пусть излишком этим является FB. Тогда мы получим четыре пропорциональные величины, так что остаток AF будет относиться к C, как D к Е. {374}
Увеличим отрезок FB во столько раз, чтобы он стал больше C, и отложим его как HI. Возьмем, далее, отрезок HL, во столько же раз больший AF, и величину М, во столько же раз большую D, во сколько раз HI больше FB. Никто не станет сомневаться в том, что составная величина Ы будет содержать в себе составную величину АВ столько же раз, сколько раз HI содержит FB или М содержит D.
Возьмем теперь величину N, кратную C, с таким расчетом, чтобы эта величина N была возможно близка к LH, но несколько превышала ее; наконец, положим, что во сколько раз N больше С, во столько же раз построенная нами величина О больше Е.
Теперь, так как N несколько больше LH, то если мы отнимем от N одну из составляющих ее величин (которая равняется С), то получим в остатке величину, не превышающую LH; если же мы возвратим величине N часть, равную С (которую мы отняли у нее), а к отрезку LH, превышающему указанный выше остаток, прибавим отрезок HI, который больше прибавляемой к N величины, то весь отрезок LI будет больше N.
Таким образом, мы имеем здесь случай, когда кратное первой величины больше кратного второй. Но так как четыре величины AF, C, D и Е являются пропорциональными, a LH и М представляют собою равные кратные первой и третьей величины, в то время как N и О представляют собою равные кратные второй и четвертой величины, то (по установленному нами выше положению) эти величины всегда будут соответствовать одни другим как в равенстве, так и неравенстве в ту или иную сторону. Так как, далее, величина LH — кратное первой величины — меньше N — кратного второй величины,— то в соответствии с нашим построением и М — кратное третьей величины — будет необходимо меньше О — кратного четвертой.
Итак, мы доказали, что если первая величина несколько больше той, какой она должна была бы быть, чтобы отношение ее ко второй величине равнялось отношению третьей к четвертой, то возможно взять некоторые равные кратные первой и третьей величины и другие равные кратные второй и четвертой величины таким образом, что кратное первой величины будет превышать кратное второй, но кратное третьей величины не будет превосходить кратного четвертой.
Сагредо. Я хорошо понял все, что вы, синьор, нам доказывали. Теперь вам остается только вывести из доказанного, как необходимые следствия, два спорных определения Эвклида; думаю, что сделать это будет очень легко, так как вы уже доказали две обратных теоремы.
Сальвиати. Действительно, сделать это очень легко. Для доказательства пятого определения я рассуждаю так.
Если даны четыре величины А, В, C, D, и любые равные кратные первой и третьей величины всегда одновременно больше или меньше, {375} или равны любым равным кратным второй и четвертой величины, то я утверждаю, что такие четыре величины пропорциональны между собою.
Предположим (если это возможно), что они непропорциональны. Тогда один из предыдущих членов будет больше того, каким он должен был бы быть, чтобы отношение его к своему последующему равнялось отношению другого предыдущего к своему последующему. Пусть такой величиной будет А. Если мы возьмем, как было показано выше, равные кратные А и С, а также равные кратные В и D, то окажется, что кратное А будет больше кратного В, кратное же С не будет во столько же раз больше кратного D, что противно нашей предпосылке.
Для доказательства седьмого определения рассуждаю следующим образом4. Пусть даны четыре величины А, В, C, D; предположим, что имеется такой случай, когда некоторые равные кратные
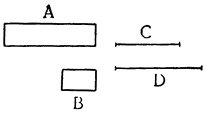 |
Предположим, если это возможно, что А не больше той величины, которая необходима для пропорциональности; в таком случае она может быть либо точно равна этой величине, либо же меньше нее. Что касается первого случая, т. е. точного равенства ее пропорциональной величине, то, как мы уже знаем из доказанного выше, равные кратные первой и третьей величины всегда будут при этом соответствовать равным кратным второй и четвертой величины, сохраняя постоянное равенство или неравенство в ту или иную сторону, а это противоречит нашей предпосылке. Если же первая величина будет меньше той, какой она должна быть для сохранения пропорциональности, то это будет обозначать, что третья величина больше той, какой она должна быть, чтобы отношение ее к четвертой величине равнялось отношению первой величины ко второй. Тогда я скажу, что от третьей величины можно отнять ее излишек, так что остаток явится величиною, точно пропорциональною. Теперь, рассматривая первоначально указанные кратные данных величин, мы убеждаемся с очевидностью, что если кратное первой величины превышает кратное второй, то кратное остатка третьей величины будет превышать кратное четвертой; если же вместо кратного остатка третьей величины мы возьмем одинаковое кратное всей третьей величины в целом, то оно будет больше, чем было кратное остатка, и, следовательно, будет в еще большей степени {376} превышать кратное четвертой величины, что противоречит нашей предпосылке.
Сагредо. Я вполне удовлетворен пояснениями, которые вы, синьор, сообщили нам по этому вопросу, давно уже не дававшему мне покоя. Не могу разобраться теперь, что во мне сильнее — радость ли по поводу приобретения этих новых познаний или же сожаление о том, что я не сообщил вам, синьор, о своих сомнениях ранее при самом начале нашей беседы, тем более, что, как я слышал, вы давали уже такое разъяснение некоторым из своих друзей, имевшим возможность, благодаря близости, посещать вас в вашей вилле. Но теперь, прошу вас, продолжим нашу беседу, если, конечно, синьор Симпличио не имеет каких-либо возражений по поводу вопросов, о которых шла до сего времени речь.
Симпличио. Я могу только присоединиться к вам и заявить, что совершенно удовлетворен рассуждениями и убежден приводившимися доказательствами.
Сальвиати. На заложенных нами основах мы могли бы частично сократить и перестроить заново всю пятую книгу Эвклида; но это завело бы нас слишком далеко и отклонило бы нас от первоначальной цели. К тому же я знаю, что, вы, синьоры, видали подобные сокращенные изложения, напечатанные другими авторами.
Поэтому, после того как мы по вашему предложению рассмотрели пятое и седьмое определения пятой книги Эвклида, я надеюсь, что вы позволите мне изложить вам некоторые старые мои соображения по поводу другого определения того же Эвклида. Предмет этот близок к предыдущему и не чужд цели нашего рассуждения; речь идет о составных отношениях, к которым наш Автор не раз прибегает во многих своих сочинениях.
Среди определений шестой книги Эвклида содержится пятое определение, касающееся составного отношения и гласящее следующее: отношение называется составленным из других отношений, когда величины этих последних отношений, умноженные друг на друга, образуют данное отношение.
Замечу при этом, что ни сам Эвклид, ни другой какой-либо автор древности не пользуется этим определением в том виде, в каком оно изложено в книге. Отсюда проистекают два неудобства: для читателя затруднительно понимание, для писателя излишне определение.
Сагредо. Это совершенно справедливо; но все же мне кажется неправдоподобным, чтобы Эвклид при своей изумительной точности поместил в своих сочинениях это определение по недосмотру и без цели. Поэтому я склонен подозревать, что оно было прибавлено другими или во всяком случае изменено настолько, что мы не узнаем его применения при доказательстве авторами своих теорем. {377}
Симпличио. То, что другие авторы не пользуются этим определением, я принимаю на веру с ваших слов, синьоры, так как я лично не много занимался этим предметом. Было бы очень жаль, если бы сам Эвклид, столь высоко почитаемый всеми вами за точность в своих сочинениях, поместил его зря. Но я должен признаться, что мой ум, имевший довольно мало случаев упражняться в математике, испытывает при встрече с этим определением некоторые затруднения, пожалуй не меньшие, чем те, которые были уже разрешены синьором
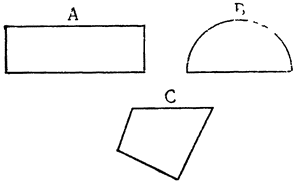 |
Сальвиати. Вы предполагаете, что этот предмет требует глубоких размышлений; на деле оказывается, однако, что здесь достаточно одного весьма простого замечания.
Вообразите, синьор, две однородных величины А и В; величина А будет иметь к В какое-либо отношение; затем представьте себе, что между ними находится какая-либо третья величина С того же рода. Тогда мы в праве сказать, что отношение величин А и В может быть составлено из двух промежуточных отношений, т. е. отношения А к С и отношения С к В. Такой именно смысл имеет упомянутое выше определение Эвклида.
Симпличио. Совершенно верно, что Эвклид именно так и определяет составное отношение; но для меня непонятно, почему отношение величин А и В является составленным из двух отношений, а именно А к С и С к В.
Сальвиати. В таком случае скажите мне, синьор Симпличио, признаете ли вы, что А имеет к В какое-либо определенное отношение, все равно, какое именно?
Симпличио. Если обе величины однородны, то, конечно, признаю, синьор.
Сальвиати. А также и то, что отношение это постоянно и не может отклоняться от той величины, какую оно имеет?
Симпличио. Признаю и это.
Сальвиати. Напомню вам, что точно так же постоянно отношение А к С, а равно и отношение С к В. Отношение между двумя крайними А и В мы называем составным, образованным из двух отношений между средней и крайними величинами, т. е. отношений А к С и С к В. {378}
A |
D |
C |
B |
Прибавлю еще следующее. Если вы представите себе, синьоры, что между указанными величинами А и В находится не одна какая-либо величина, но несколько, которые обозначим буквами, например А, C, D, В, то ясно, что отношение А к В будет составляться из всех промежуточных отношений, т. е. в данном случае из отношений А к C, С к D и D к В. И сколько бы ни было этих промежуточных величин, отношение первой величины к последней всегда может быть составлено из отношений, которые имеют друг к другу все промежуточные величины.
По этому поводу замечу еще, что когда все отдельные отношения равны между собой или, лучше сказать, одинаковы, то отношение первой величины к последней будет, как сказано выше, равно составному отношению из всех промежуточных; но так как эти последние все равны между собой, то можно выразить ту же мысль иначе, сказав, что отношение первой величины к последней равно отношению первой величины ко второй, взятому множителем столько раз, сколько промежуточных отношений находится между крайними величинами. Так, например, если даны три такие величины, что отношение первой ко второй равно отношению второй к третьей, то правильно будет сказать, что отношение первой величины к третьей составное и может быть образовано из отношений, существующих между первой и второй, а также второй и третьей величинами; но так как предполагается, что оба эти отношения равны, т. е. одинаковы, то можно сказать, что отношение первой величины к третьей равно двойному отношению первой величины ко второй. Если бы были даны четыре величины, то можно было бы сказать, что составное отношение первой величины к четвертой может быть образовано из трех промежуточных отношений или что оно равно тройному отношению первой величины ко второй, ибо отношение первой величины к четвертой образуется из отношения первой величины ко второй, взятого трижды, и т. д.5
В конце концов, тут нет надобности ни в рассуждениях, ни в доказательствах, так как дело идет о простом установлении названия. Если вам, синьоры, не нравится слово «составной»,— выберите слово «несоставной», «сложный», «смешанный» или любое другое, которое вам, синьоры, более нравится. Условимся только в том, что когда мы имеем три однородных величины и называем отношение составным, сложным или смешанным, то мы подразумеваем отношение, существующее между крайними величинами, а не какое-либо иное.
Сагредо. Все это я хорошо понимаю. Не раз также удивлялся я искусству, с которым Эвклид доказывает в одном из предложений, что равноугольные параллелограммы имеют составное отношение, образованное из отношений их сторон. В этом случае мы имеем два отношения между четырьмя величинами, каковыми являются четыре стороны параллелограмма. {379} Затем он требует выражения означенных двух отношений при помощи только трех величин, так чтобы в одно отношение входили первая и вторая величина, а во второе отношение — вторая и третья. При доказательстве он довольствуется указанием, что один параллелограмм относится к другому, как первая величина к третьей, т. е. имеет отношение, составленное из двух других, а именно отношения первой величины ко второй и второй к третьей, каковые два отношения были образованы первоначально из четырех величин — сторон параллелограмма.
Сальвиати. Вы прекрасно излагаете вопрос, синьор. Теперь, поскольку мы выяснили и установили определение составного отношения (а под этим следует понимать только то, что под известным наименованием мы условились подразумевать известную вещь), мы можем доказать предложение двадцать третье книги шестой Эвклида так, как он сам это делает, ибо в данном случае он пользуется определением не в той форме, в какой оно получило распространение, а именно в той, в какой мы его только что изложили. После упомянутого выше двадцать третьего предложения я бы и поместил, как добавление к нему, общепринятое пятое определение шестой книги, касающееся составных отношений, придав ему, скорее, вид теоремы.
Пусть даны два отношения: одно — между величинами А и В и другое — между величинами С и D. Обычное определение гласит, что мы можем получить составное отношение из двух данных, перемножив между собою величины этих отношений. Я, однако, согласен с синьором Симпличио, что такое предложение трудно понять, и что оно нуждается в доказательстве. Последнее весьма несложно и заключается в следующем.
Если четыре данных величины, входящих в два отношения, являются какими-либо количествами, отличными от линий, то представим себе,
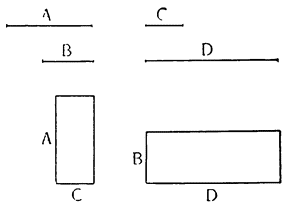 |
Симпличио. Я думаю, что мы не сделали ничего иного, кроме построения двух прямоугольников из четырех первоначально данных линий, а именно из предыдущих А и С и последующих В и D.
Сальвиати. Но геометрическое построение прямоугольников из линий в точности соответствует перемножению чисел в арифметике, как это известно каждому математику, даже начинающему. То, что мы перемножали, суть линии А, С и линии В, D, т. е. соответствующие члены обоих взятых отношений. Вот каким образом, перемножая между собою величины или значения данных простых отношений, мы и получаем величину или значение отношения, которое мы называем составным.
Конец пятого дня
| {381} |
С |
Сальвиати. А я только что хотел спросить вас о синьоре, который вас сопровождает, и о причинах отсутствия нашего синьора Симпличио.
Сагредо. Причиною отсутствия синьора Симпличио, как я полагаю и даже почти с уверенностью могу утверждать, является то, что его слишком затрудняют некоторые доказательства различных проблем, касающихся движения, точно так же как и предложений, касающихся центра тяжести. Я имею в виду такие доказательства, которые состоят из цепи предложений, основанных на геометрических принципах, и которые поэтому непонятны для лиц, незнакомых основательно с последними. Синьор, которого вы видите, по имени Паоло Апроино, дворянин из Тревизо, не только был слушателем нашего Академика во время пребывания {382} последнего в Падуе, но и одним из ближайших его учеников, имевшим со своим учителем постоянные и продолжительные беседы. Вместе с другими учениками (первым из которых следует назвать синьора Даниелло Антонини, дворянина из Удино, человека исключительного ума и доблестей, нашедшего славную смерть при защите своего отечества и светлейшего государя и почтенного признанием своих заслуг со стороны светлейшей Венецианской республики)2 он присутствовал при многочисленных опытах, которые наш Академик производил у себя дома в связи с различными проблемами. Прибыв дней десять тому назад в Венецию, синьор Апроино, по своему обыкновению, посетил меня и, узнав, что у меня находятся трактаты нашего общего друга, пожелал прочесть их вместе со мною. Когда же он услышал, что у нас назначено собеседование, темой которого будет удивительная проблема удара, то сообщил мне, что он не раз говорил по этому поводу с Академиком, но неопределенно, в общих чертах, и вместе с ним, среди опытов, касавшихся разных проблем, ставил также опыты, чтобы определить силу удара и дать ей должное объяснение. Из них он готов описать нам один, по его словам, довольно остроумный и тонкий.
Сальвиати. Я считаю большой удачей для себя, что встретился с синьором Апроино и имею случай познакомиться с ним лично, после того как я слышал о нем столько лестного при разговорах с нашим Академиком. Мне будет также очень приятно иметь возможность ознакомиться хотя бы с частью опытов, касавшихся различных тем и производившихся в доме нашего общего друга при участии столь выдающихся людей, как синьор Апроино и синьор Антонини, о которых с таким восхищением и удивлением говорил мне много раз наш общий друг. Так как мы собрались сегодня для беседы специально об ударе, то синьор Апроино, вероятно, скажет нам, к каким заключениям пришел он относительно этого вопроса на основании опытов, а также не откажется дать обещание сообщить при случае и о других опытах, произведенных по другим поводам. Я знаю, что в них не было недостатка, ибо наш Академик всегда был экспериментатором не менее прилежным, чем любознательным3.
Апроино. Если бы, синьор, я пожелал ответным приветствием уплатить вам долг, налагаемый на меня вашей изысканной любезностью, то мне пришлось бы потратить столько слов, что у нас осталось бы сегодня весьма мало времени для беседы по намеченному вопросу.
Сагредо. Нет, нет, синьор Апроино, оставим комплименты и церемонии придворным и приступим прямо к нашему научному собеседованию. Я готов ручаться, что оба уже вы удовлетворены сказанным каждым из вас; для этого достаточно немногих искренних и прямых слов.
Апроино. Хотя я и не думаю, что могу сообщить синьору Сальвиати что-либо новое, и потому предпочел бы, чтобы вся тяжесть ведения беседы лежала на его плечах, тем не менее, в целях хотя бы некоторого облегчения {383} его задачи, я сообщу о тех первоначальных поводах и том первоначальном опыте, которые побудили нашего друга углубиться в рассмотрение удивительной проблемы удара.
Он отыскивал прием, который позволял бы определить и измерять большую силу удара и вместе с тем, если это возможно, давал бы понятие о принципах и первопричинах действия удара, каковое действие, как кажется, протекает, в смысле приобретения полной своей мощности, совершенно иначе, чем увеличение силы во всех других механических устройствах (говорю — механических, чтобы исключить необычайную мощь огня), в которых скорость небольшого движущегося тела совершенно определенным и понятным образом преодолевает сопротивление большого тела, приводя его в медленное движение4. Так как при определении действия удара приходится сопоставлять движение ударяющего тела, связанное с его скоростью, с движением сопротивляющегося тела и испытываемым им в большей или меньшей степени перемещением при ударе, то наш Академик попытался прежде всего определить, какое влияние на результат удара оказывают, например, вес молота, и какое — большая или меньшая скорость его движения, и найти, если возможно, одинаковый способ измерения и выражения как той, так и другой энергии; чтобы достигнуть поставленной цели, он придумал следующий, как мне кажется, весьма остроумный опыт. Он взял очень прочный брус, длиною в три локтя, и укрепил его так, что брус мог качаться около точки опоры наподобие коромысла весов; к двум концам этого коромысла он прикрепил два равных и достаточно тяжелых груза, один из коих состоял из двух медных сосудов или ведер. Первое из ведер, привязанных к концу коромысла, было наполнено водою, и от ушков его спускались вниз две веревки, длиною около двух локтей каждая, к которым было прикреплено за ушки другое такое же ведро, но пустое и подвешенное таким образом, что оно находилось как раз под первым ведром, наполненным водою. К другому концу коромысла подвешивался противовес из камня или какого-либо другого тяжелого вещества таким образом, что он в точности уравновешивал вес обоих ведер вместе с водою и веревками. Верхнее ведро имело в своем днище отверстие, величиною с яйцо или немного меньше, которое можно было открывать и закрывать. Оба мы первоначально предполагали и представляли себе, что если после приведения устроенных таким образом весов в состояние равновесия открыть отверстие в верхнем ведре и дать выход воде, которая начнет быстро переливаться в нижнее ведро, то сила водяного удара должна будет увеличить момент данной стороны весов, гак что для восстановления равновесия окажется необходимым прибавить еще некоторый груз к противовесу на другом плече; этот добавок, как го совершенно ясно, и соответствовал бы новой силе, обусловливаемой ударом воды. Таким образом, если бы для сохранения равновесия пришлось {384} прибавить десять или двенадцать фунтов, то мы могли бы сказать, что момент удара воды эквивалентен этому весу,
Сагредо. Подобное приспособление кажется мне весьма остроумным, и я с нетерпением ожидаю результатов опыта.
Апроино. Результат, как и во многих других случаях, оказался неожиданным, даже совершенно изумительным. Как только отверстие было открыто, и вода начала вытекать, весы наклонились, но в сторону противовеса; когда же вытекающая вода достигла дна нижнего сосуда — дальнейшее опускание противовеса прекратилось, и последний начал подниматься совершенно равномерно по мере вытекания воды, пока не достиг прежнего положения, и весы не пришли снова в равновесие, не отклонившись и на волос в другую сторону.
Сагредо. Результат этого опыта представляется мне поистине неожиданным. Но хотя он и далек от того, что я предполагал и в чем я думал найти способ определения силы удара, мне кажется тем не менее, что я могу в значительной мере использовать описанное явление, чтобы извлечь из него желаемые данные. Я могу сказать, что сила и момент подобного удара равняются моменту и весу того количества падающей воды, которое находится как бы висящим в воздухе между содержимым обоих сосудов — верхнего и нижнего, каковое количество воды не прибавляет веса ни верхнему, ни нижнему сосуду: верхнему потому, что части воды не связаны между собой и, следовательно, не могут проявить силы, влекущей вниз, как это имело бы место при каком-либо вязком веществе, например смоле или клее; нижнему потому, что движение падающей воды происходит с непрерывным ускорением, вследствие чего вышележащие частицы не могут давить на нижележащие. Таким образом, вся вода, содержащаяся в струе, как бы снята с весов. Это обнаруживается с достаточной ясностью. В самом деле, если бы падающая вода передала свой вес сосуду, то вес этот в соединении с силою удара значительно наклонил бы коромысло, подняв противовес, чего на самом деле не наблюдается. Сказанное подтверждается еще следующим соображением: если мы представим себе, что вся вода между сосудами внезапно замерзла и обратилась в кусок льда, то вес струи прибавится к весу всего прибора, с прекращением же движения пропадет и удар.
Апроино. Ваши соображения, синьор, совершенно совпадают с теми выводами, к которым пришли и мы, после того как произвели опыт. Нам также казалось возможным вывести заключение, что действие скорости, приобретенной данным количеством воды при падении ее с высоты двух локтей, является причиною равенства веса воды, за вычетом веса струи, весу всей воды при отсутствии силы удара. Таким образом, если бы можно было измерить и взвесить количество воды, находящейся в воздухе между сосудами, то мы могли бы с уверенностью утверждать, что удар {385} способен произвести такое же давление, как вес падающей воды в десять или двенадцать фунтов.
Сальвиати. Ваше остроумное приспособление мне очень нравится, и я полагаю, что, не впадая в противоречие с вашими заключениями, в которых все же остается некоторая неопределенность благодаря трудности измерения количества падающей воды, мы могли бы расчистить путь к достижению желаемых познаний посредством другого подобного же опыта. Представьте себе, например, один из тех больших грузов, которые применяют при забивке в землю толстых свай и которые заставляют для этой цели падать с некоторой высоты на сваю (подобные грузы, если я не ошибаюсь, называются «бабами»). Положим, что вес одной из таких баб равен ста фунтам, высота, с которой она падает, равна четырем локтям, а глубина, на которую свая входит в твердую землю от одного удара, составляет четыре дюйма; положим, далее, что для достижения осадки сваи на те же четыре дюйма путем давления без удара нам понадобится приложить груз в тысячу фунтов. Назовем такой груз, действующий одним лишь весом, «мертвым грузом» и спросим себя, можем ли мы без ошибки и с достаточной уверенностью утверждать, что сила и энергия груза в сто фунтов в соединении со скоростью, приобретенной при падении с высоты четырех локтей, будет эквивалентна давлению мертвого груза в тысячу фунтов, так что усилие одной только скорости будет одинаково с давлением девятисот фунтов мертвого груза, ибо такова разница между весом в тысячу фунтов и весом бабы? Вижу, что оба вы колеблетесь дать мне ответ, быть может, потому, что я недостаточно ясно поставил вопрос. Скажу короче: может ли упомянутый выше опыт убедить нас в том, что мертвый груз всегда будет оказывать на сопротивляющееся тело такое же действие, как груз в сто фунтов, падающий с высоты четырех локтей, так что, например (говорю для большей ясности), если та же баба, падающая с той же высоты, но встречающая сваю с большим сопротивлением, вбивает последнюю в землю только на два дюйма, то можем ли мы быть уверенными, что такое же действие произведет мертвый груз в тысячу фунтов, т. е. что он заставит сваю опуститься также на два дюйма?
Апроино. Я думаю, что этого никто не будет оспаривать, по крайней мере с первого взгляда.
Сальвиати. А вы, синьор Сагредо, питаете на этот счет какие-либо сомнения?
Сагредо. В данную минуту нет; но я уже столько раз имел случай убедиться, как легко впасть в заблуждение, что утратил самоуверенность и робко уклоняюсь от ответа.
Сальвиати. Поскольку я вижу, что и вы, синьор, несмотря на остроту вашего ума, которую я имел возможность оценить сотни раз, склоняетесь к принятию ложного положения, я начинаю думать, что из {386} тысячи лиц едва ли можно найти одно или два, которые не совершили бы подобной же ошибки: настолько правдоподобным кажется это положение. Но особенно удивительным оказывается то, что заблуждение, как вы увидите, кроется под весьма легким покрывалом, и одного порыва ветерка достаточно, чтобы его поднять и сдуть, лишив вопрос всякой таинственности и неясности. Возвратимся, однако, к нашему опыту с бабою, падающей с высоты четырех локтей и вбивающей в землю сваю, на которую она падает, с одного удара на глубину четырех дюймов, и положим, что для получения того же результата необходимо применить мертвый груз ровно в тысячу фунтов. Поднимаем теперь бабу вторично на такую же высоту и заставим ее ударить снова нотой же свае и вбить ее в землю, но уже только скажем, на два дюйма, благодаря тому обстоятельству, например, что свая встретила более твердый грунт. Должны ли мы заключить, что такой же результат получился бы и в случае применения того же мертвого груза в тысячу фунтов?
Апроино. Мне кажется, что да.
Сагредо. Ай ай, синьор Паоло, горе нам. Надо было решительно ответить: нет. В самом деле, если в первый раз применение мертвого груза в тысячу фунтов заставило сваю опуститься на четыре дюйма, но не более, то почему же вы хотите, чтобы путем одного лишь снятия и обратного наложения груза мы получили в результате углубление сваи еще на два дюйма? Почему же этого не произошло ранее, чем мы сняли груз, раз он уже был наложен? Полагаете ли вы, что простым удалением и обратным наложением груза мы можем заставить его произвести такое действие, к которому он не был способен первоначально?
Апроино. Мне остается только покраснеть и сознаться, что я рисковал утонуть в стакане воды.
Сальвиати. Не смущайтесь, синьор Апроино; уверяю вас, что вы имеете много сотоварищей, также легко запутывающихся в сетях, развязать которые для других совсем нетрудно. Без сомнения, все заблуждения естественно устранялись бы сами по себе, если бы мы шли, последовательно вскрывая и устанавливая самые основания различных положений, из коих те или иные оказались бы при этом совершенно ложными. В этом отношении наш Академик обладал особым даром сводить посредством краткого рассуждения к абсурду и явной несообразности общераспространенные и принимаемые на веру ложные положения. У меня собран целый ряд положений, обычно принимаемых за истину, ложность которых им, однако, была обнаружена путем кратких и легких доказательств.
Сагредо. Перед нами одна из таких ошибок, конечно, не единственная; и если за нею могут последовать другие, то хорошо было бы, чтобы вы теперь же указали нам на них. Возвратимся, однако, к предмету нашего разговора. Если мы ищем способы определения и установления {387} надлежащей меры силы удара (предполагая, что их возможно найти), то я думаю, что путем ранее описанного опыта мы не достигнем желаемого результата. В самом деле, повторяя удары бабою о сваю, причем, как показывает нам опыт, последняя каждый раз уходит в землю все глубже и глубже, мы убеждаемся, что каждый из последующих ударов работает, чего не происходит при мертвом грузе; последний, произведя первый раз своим давлением определенное действие, неспособен произвести его вторично, т. е. не может вогнать глубже в землю сваю, на которую он наложен; для этого, как оказывается, необходимо во второй раз наложить груз, превышающий тысячу фунтов; если мы захотим получить результаты, соответствующие третьему, четвертому, пятому и т. д. удару бабы, то увидим, что придется Последовательно брать мертвый груз все большего и большего веса. Спрашивается, какую же из этих меняющихся величин веса должны мы принять за точную и определенную меру силы удара, которая сама по себе остается постоянной?
Сальвиати. Это первое из тех удивительных явлений, перед которыми, несомненно, должны остановиться в нерешительности и недоумении пытливые умы. В самом деле, кому не покажется новою мысль, что меру силы удара надо искать не в теле, ударяющем, а скорее в теле, воспринимающем удар? Что же касается упомянутого выше опыта, то, кажется, из него можно вывести заключение, что сила удара бесконечна или, скажем лучше, неопределенна либо неопределима, и что она то больше, то меньше в соответствии с большим или меньшим сопротивлением.
Сагредо. Мне кажется, что я начинаю понимать, каким образом сила удара действительно может быть огромна или бесконечна. Основываясь на приведенном выше опыте и полагая, что первый удар вбивает сваю на четыре дюйма, второй — на три, третий благодаря постоянно происходящему уплотнению земли — на два, четвертый — на полтора, а последующие — на один дюйм, половину, четверть его и т. д., я заключаю, что если сопротивление земли опусканию сваи не станет бесконечно большим, то повторные удары бабы будут постоянно углублять ее, хотя и на все меньшие и меньшие величины. Но как бы ни были малы эти величины, они могут быть последовательно делимы и вновь делимы, пока мы продолжаем удары; а так как при наложении мертвого груза требуется каждый раз больший груз по сравнению с предыдущим разом, то может оказаться, что для достижения результата, одинакового с полученным от силы последнего удара, потребуется груз огромнейшей величины.
Сальвиати. Я думаю то же самое.
Апроино. А разве не может сопротивление быть столь большим, что тело останется в покое и противостоит силе хотя бы легкого удара?
Сальвиати. Думаю, что не может, если только тело, оказывающее {388} сопротивление, не абсолютно неподвижно, т. е. если оно не обладает бесконечно большим сопротивлением.
Сагредо. Замечательными и, можно сказать, изумительными представляются мне эти положения и то, что. только в этом явлении искусство преодолевает и обманывает природу; с первого взгляда кажется, что это имеет место в разных механических приспособлениях, применяемых, например, для подъема огромных тяжестей малой силой при помощи рычагов, воротов, блоков и т. п. Но действие силы удара, когда посредством молота, весом не более десяти или двенадцати фунтов, мы можем разрушить медный пьедестал, остающийся целым и невредимым под давлением не только тяжелой мраморной колонны, но даже целой башни, превосходит, как мне кажется, возможность устранить элемент чудесного путем рассуждения. А потому, синьор Сальвиати, возьмите в свои руки путеводную нить и выведите нас из этого запутанного лабиринта.
Сальвиати. Из всего до сих пор сказанного вытекает, что сущность затруднения состоит в следующем: трудно понять, каким образом действие силы удара, кажущееся бесконечно большим, согласуется с принципами действия всяких других машин, которые при применении малой силы преодолевают огромные сопротивления. Я, однако, не отчаиваюсь в возможности показать вам, что в том и другом случае происходит одно и то же. Я постараюсь проследить этот процесс, кажущийся мне достаточно сложным, и думаю, что смогу, разъясняя ваши сомнения и возражения, осветить вопрос так, что узел можно будет считать, если не совсем развязанным, то хотя бы несколько распутанным.
Ясно, что действие силы движущего тела и сопротивления тела движимого не есть нечто простое: оно слагается из двух элементов, определяющих энергию, которая подлежит измерению. Одним из элементов является вес как движущего, так и сопротивляющегося тела, а другим — скорость, с которой первое движется, а второе должно быть двинуто. Таким образом, если движимое тело должно быть приведено в движение со скоростью, равной скорости движущегося тела, так, чтобы пространства, проходимые обоими в одинаковое время, были одинаковыми, то вес движущего тела не может быть меньше веса движимого тела; первый всегда должен быть несколько больше, ибо из точного равенства рождаются равновесие и покой, как мы это наблюдаем у весов с равноплечим коромыслом. Если же мы хотим поднять больший груз посредством меньшего, то машину необходимо устроить таким образом, чтобы меньший движущий груз передвигался за то же время на большее пространство, чем другой груз, иначе говоря, чтобы он двигался с большею скоростью, чем последний. Это доказывается не только размышлением, но и опытом, например с безменом, где постоянный груз, прикрепленный к одному концу рычага, может уравновесить груз в десять или пятнадцать раз больший, для чего необходимо лишь, {389} чтобы расстояние первого от центра, относительно которого происходит качание, было в десять или пятнадцать раз больше расстояния от того же центра до точки подвеса второго груза; а это равносильно тому, чтобы скорость движущего была в десять или пятнадцать раз больше скорости тела. Так как то же самое явление имеет место и во всех других приборах, то мы можем прочно установить, что вес и скорость соответствуют друг другу, но находятся между собою в обратном отношении. Таким образом, можно сказать вообще, что момент более легкого тела равняется моменту более тяжелого, когда скорость меньшего тела относится к скорости большего, как вес большего тела к весу меньшего; малейший излишек веса тела уже нарушает равновесие и вызывает движение.
Установив это, я говорю, что не только при ударе кажется бесконечно большим его действие, преодолевающее любое сопротивление, так как то же самое наблюдается и во всех прочих механических приспособлениях. Разве же не ясно, что незначительный груз весом, скажем, в один фунт, опускаясь, поднимет другой груз, больший первого в сто, тысячу или любое другое число раз, если только мы подвесим era к коромыслу весов на расстоянии, в сто или тысячу раз большем, нежели то которое отделяет от центра больший груз, и тем заставим его, опускаясь, пройти путь в сто или тысячу раз больший, нежели тот, который проходит, поднимаясь, тяжелый груз, т. е. заставим его двигаться со скоростью, в сто или тысячу раз большей? Но мне все же хочется привести вам один разительный пример, который даст нам возможность убедиться, что опускающийся груз произвольно малой величины может заставить подняться любое тело огромного размера и веса. Представьте себе, синьоры, что такое тело огромного веса висит на веревке, прикрепленной верхним концом к какой-либо неподвижной точке, и что около последней, как центра, описана окружность, проходящая через центр тяжести тела, который, как известно, лежит на вертикали, являющейся продолжением веревки, поддерживающей груз, или, лучше сказать, на той прямой линии, которая соединяет точку подвеса тела с общим центром тяжести всех тел, т. е. центром Земли. Представьте себе затем другую тончайшую нить, к которой подвешен другой малый груз таким образом, что его центр тяжести лежит на упомянутой выше окружности, и предположите, что малый груз касается большого груза, т. е. просто прилегает к нему. Не думаете ли вы теперь, что этот новый малый груз, помещенный сбоку, несколько отодвинет большой груз, удалит центр тяжести его от первоначальной вертикальной линии, на которой он ранее находился, и заставит его переместиться по упомянутой выше окружности, а также отделиться при этом движении от горизонтальной линии, касательной к указанной окружности в нижней ее точке, в которой до того времени находился центр тяжести большого тела? Что касается пространства, то дуга, которую пройдет тяжелое тело, будет такова {390} же, как и дуга, которую пройдет меньшее тело, прикасающееся к первому; однако повышение центра тяжести большого тела не будет равняться понижению центра тяжести малого тела, ибо последнее должно опускаться по пути или пространству, гораздо более наклонному, нежели путь, проходимый при подъеме другим центром тяжести и образующий с касательной к окружности угол, меньший любого острого угла. Если бы я имел дело с людьми, менее вас знакомыми с геометрией, то я показал бы здесь, как легко можно представить себе, что при подъеме тела от низшей точки соприкосновения повышение указанной нижней точки над горизонталью может быть в любое число раз меньше понижения другого равного тела, расположенного где-либо на той же окружности, если только указанная точка соприкосновения должна повышаться. Но я уверен, что в этом отношении у вас нет сомнений. И если простое давление малого груза на тело большого размера может привести последнее в движение и поднять, то что же будет, если мы, отведя малое тело, заставим его затем упасть по окружности и произвести удар?
Апроино. Мне кажется, теперь не может уже быть сомнения в том, что сила удара может быть бесконечно велика, как это следует из приведенного выше опыта. Но такого признания еще недостаточно, чтобы рассеять мрак, окутывающий мой ум, не позволяющий мне видеть, как проявляется действие такого удара, и не дающий мне возможности ответить на те возражения, которые могут быть выдвинуты.
Сальвиати. Прежде чем идти далее, мне хочется устранить одно скрытое и как бы подстерегающее нас недоразумение, заключающееся в следующем. В приведенном выше примере мы считали все удары, которые получает забиваемая свая, равными или, лучше сказать, одинаковыми, ввиду того, что они наносятся одной и той же бабою, падающей на сваю постоянно с одной и той же высоты; это, однако, неправильно. Чтобы лучше понять дело, представьте себе, что вы протянули руку навстречу падающему с высоты шару, и скажите мне: если в тот момент, как шар прикоснется к вашей руке, вы станете опускать ее в направлении падения шара и со скоростью, которой последний обладает, то какой удар вы почувствуете? Конечно, никакого. Если же к моменту приближения шара ваша рука будет отступать только отчасти и опускаться со скоростью, меньшей, чем скорость падения шара, то вы испытаете удар, но не тот, который соответствует полной скорости падения шара, а тот, который соответствует превышению скорости падения шара над скоростью движения вниз вашей руки. Таким образом, если шар движется со скоростью десяти градусов, а рука со скоростью восьми, то удар будет равен произведенному шаром, движущимся со скоростью двух градусов; при движении руки со скоростью в четыре градуса удар будет равен произведенному шаром при скорости в шесть градусов; при скорости опускающейся руки в один градус {391} удар произойдет так, как если бы ударяющее тело двигалось со скоростью в девять градусов, удар же, соответствующий полной скорости в десять градусов, получится в том случае, если рука вовсе не будет опускаться. Применяя теперь сказанное к ударам бабы, при которых свая поддается в первый раз на четыре дюйма, во второй—на два, а в третий — всего на один дюйм, найдем, что сила этих ударов неравна, и что первый удар слабее второго, а второй слабее третьего, ибо движение вниз на четыре дюйма более уменьшает скорость первого удара, чем то имеет место при втором; этот последний, в свою очередь, слабее третьего, ибо уменьшение одной и той же скорости происходит здесь в размере, вдвое большем, чем при третьем ударе. Таким образом, большая податливость сваи при первом ударе, меньшая при втором, еще меньшая при третьем и так последовательно далее и является причиною того, что первый удар слабее второго, а второй слабее третьего. Что же удивительного теперь в том, что для углубления сваи на первые четыре дюйма требуется меньший мертвый груз, для углубления на следующие два дюйма — больший, в следующий раз еще больший и т. д., так что для дальнейшего углубления необходимо постоянное возрастание груза, соответствующее уменьшению осадки сваи вследствие увеличения ее сопротивления5.
Из сказанного, мне кажется, легко заключить, как затруднительно определить силу удара, имея дело с телом, сопротивление которого в разных случаях различно, например со сваей, сопротивление которой возрастает постоянно, но неопределенно. Вот почему я полагаю, что необходимо перейти к рассмотрению таких случаев, когда тело, испытывающее удар, оказывает последнему всегда одно и то же сопротивление. Такое сопротивление можно получить следующим образом. Представим себе тяжелое тело весом, например, в тысячу фунтов, покоящееся на поддерживающей его плоскости; положим, далее, что к этому телу привязана веревка, которая перекинута затем через блок, укрепленный наверху на порядочном расстоянии от указанного тела. Ясно, что, прилагая к другому концу веревки силу, направленную вниз, мы всегда будем встречать со стороны поднимаемого груза одинаковое сопротивление, обусловливаемое весом в тысячу фунтов. Если к свободному концу веревки мы прикрепим груз, весящий столько же, сколько первый, то увидим, что установится равновесие; оба груза, оставаясь на весу без всякой поддержки или опоры, будут пребывать в покое, и второй груз не сможет опуститься и поднять первый иначе, как при некотором излишке веса. Расположив теперь первый груз на плоскости, которая будет его поддерживать, мы можем производить опыты с другими телами различного веса (меньшего, однако, чем тот, который имеет покоящееся тело) и изучать силу различных ударов, привязывая любое из таких тел к другому концу веревки, заставляя его падать с известной высоты и замечая, что происходит при {392} этом с другим тяжелым телом под действием падающего груза, каковое действие является как бы ударом, стремящимся поднять тяжелое тело. По этому поводу я считаю необходимым прежде всего отметить, что как бы ни был мал вес падающего тела, он обязательно должен преодолеть сопротивление большого тела и приподнять его; это положение, мне кажется, вытекает с достаточной убедительностью из хорошо известного нам факта, что меньший вес преодолеет любой больший вес во всех тех случаях, когда отношение скорости меньшего тела к скорости большего тела превышает отношение веса большего тела к весу меньшего тела. В данном случае скорость падающего тела превосходит скорость другого тела в бесконечное число раз, так как у последнего, как пребывающего в покое, она равна нулю; в то же время отношение веса падающего тела к весу другого тела не равно нулю, так как, по предположению, ни вес покоящегося тела не является бесконечно большим, ни вес падающего тела — бесконечно малым; поэтому сила ударяющего тела должна преодолеть сопротивление тела, испытывающего удар. Теперь остается только рассмотреть, каково же будет пространство, на которое тело поднимается благодаря полученному им удару, в соответствии с тем, что наблюдается в других механических приборах. Если мы возьмем, например, безмен, то увидим, что повышение взвешиваемого тела составляет такую же часть пути, описываемого при одновременном понижении постоянного груза на другом конце безмена, какую вес этого постоянного груза составляет по отношению к весу тела. Поэтому и в нашем опыте мы можем рассчитывать увидеть, что если вес тела, пребывающего в покое, превышает вес падающего тела, например, в тысячу раз, то при падении последнего с высоты, скажем, одного локтя большее тело будет приподнято на высоту одной сотой локтя; это соответствовало бы общему правилу, наблюдаемому в других механических приборах. Представьте себе теперь, что мы производим первый опыт, заставляя падать с какой-либо высоты, скажем, с высоты одного локтя, тело, равное по весу другому телу, покоящемуся на плоскости, причем оба они прикреплены к двум концам одной и той же веревки. Как вы думаете, что произойдет с телом, находившимся в покое, после того толчка, стремящегося его поднять, который оно получит от падающего тела? Я охотно узнал бы ваше мнение.
Апроино. Так как вы, синьор, обращаетесь ко мне и как будто от меня ожидаете ответа, то я скажу, что так как оба тела имеют равный вес, а падающее тело обладает при этом импульсом, порождаемым скоростью, то покоящееся тело, мне кажется, будет поднято достаточно высоко по сравнению с тем положением, которое оно занимало при равновесии; раз для установления равновесия достаточно было одного только равного веса, то я полагаю, что поднимающееся тело пройдет пространство, значительно большее одного локтя или пространства, пройденного падающим телом. {393}
Сальвиати. А вы что скажете, синьор Сагредо?
Сагредо. С первого взгляда такое рассуждение кажется мне достаточно веским; но я уже отмечал ранее, что опыт многократно доказывал мне, как легко впасть в заблуждение и с какой осмотрительностью надо исследовать вопрос, прежде чем решительно высказать то или другое утверждение. Поэтому скажу (не без некоторого, однако, сомнения), что вес опускающегося тела, положим, в сто фунтов действительно будет достаточен для того, чтобы поднять другое тело, весом также в сто фунтов, до состояния равновесия, без придания, однако, этому последнему телу какой-либо другой скорости, для чего хватило бы и небольшого излишка в весе, скажем в пол-унции. Но я полагаю, что такое равновесие установится лишь с чрезвычайной медленностью. Когда падающее тело движется с большою скоростью, то оно с такою же скоростью должно увлекать вверх и своего спутника; однако мне кажется несомненным, что для подъема тяжелого тела с большою скоростью нужна большая сила, чем для медленного его подъема; поэтому может случиться, что та степень скорости, которая приобретена телом при свободном падении с высоты одного локтя, окажется растраченной или, лучше сказать, израсходованной на подъем другого тела с соответствующей скоростью на соответствующую высоту. Я склонен думать, что оба эти движения вверх и вниз окончатся и немедленно прекратятся, как только поднимающееся тело пройдет пространство в один локоть, в то время как другое опустится на два локтя, поскольку один локоть оно уже прошло одно при своем свободном падении.
Сальвиати. Я склонен думать то же самое. Действительно, хотя падающий груз и является некоторым сочетанием веса и скорости, все же в деле подъема другого тела действие веса равно нулю, ибо он уравновешивается одинаковым весом другого тела, которое, как то совершенно ясно, не может быть приведено в движение без прибавления ко второму телу хотя бы небольшого дополнительного груза; поэтому необходимо признать, что действие падающего груза, выражающееся в подъеме другого тела, имеет причиною скорость и не что иное, кроме скорости. Так как падающее тело не в состоянии сообщить другому телу скорости, большей той, которая ему присуща, и так как само оно обладает лишь той скоростью, которая развилась по выходе его из состояния покоя и свободном падении с высоты одного локтя, то я полагаю, что падающее тело поднимает другое тело на такую же высоту с той же скоростью, как мы это наблюдаем при многих других опытах, когда тело, выходящее из состояния покоя и падающее с некоторой высоты, обладает в каждой точке своего пути импульсом, достаточным для подъема его на ту же высоту.
Сагредо. Мне помнится, что последнее ясно доказывается опытом с тяжелым телом, подвешенным на закрепленной вверху нити. Такое тело, отведенное от вертикали на дугу любой величины, но не более четверти {394} окружности, а затем отпущенное на свободу, опускается и, перейдя вертикаль, поднимается на дугу, соответствующую описанной им при падении. Отсюда выводят заключение, что подъем обусловливается исключительно скоростью, приобретаемой при падении, ибо вес тела не может принимать никакого участия в подъеме последнего, всегда противодействуя движению вверх и стремясь лишить тело той скорости, которая была приобретена им при падении.
Сальвиати. Если бы опыт с телом, подвешенным к нити, о котором мы, помнится, говорили в одной из прошлых бесед, вполне подходил к тому случаю, который мы обсуждаем в настоящее время, то ваше заключение, синьор, было бы весьма убедительным. Но я нахожу немалую разницу в этих двух явлениях, т. е. движении тяжелого тела, подвешенного к нити, которое, будучи отпущено на некоторой высоте, опускается по дуге окружности и приобретает импульс, достаточный для подъема тела на такую же высоту, с одной стороны, и действии падающего тела, прикрепленного к концу веревки, на подъем другого тела, равного с ним веса, с другой стороны. В первом случае тело, опускаясь по дуге окружности, приобретает, пока не достигнет вертикали, все большую скорость благодаря своему собственному весу, который затем, после перехода за вертикаль, препятствует подъему тела (ибо движение направлено против веса); таким образом, противодействием импульсу, приобретенному при естественном падении, и притом немалым, является противоестественное движение до той же высоты. Во втором же случае падающее тело воздействует на другое тело, равное ему по весу и находящееся в покое, не только приобретенной им скоростью, но также и своим весом, который сам по себе достаточен для того, чтобы преодолеть сопротивление его подъему; таким образом, приобретенная скорость не встречает противодействия со стороны веса поднимаемого тела. Импульс, приобретенный падающим телом, не встречает при дальнейшем движении вниз причины, уничтожающей или уменьшающей его; такой причины нет и в данном случае при движении тела вверх, когда вес его обращен в нуль благодаря противовесу в виде опускающегося тела. Здесь, думается мне, происходит точно то же, что и с положенным на гладкую, слегка наклонную плоскость тяжелым, совершенно круглым движущимся телом, которое, будучи предоставлено самому себе, естественно скатывается вниз, приобретая постоянно все большую скорость; если же, наоборот, мы хотим перекатить его снизу вверх, то нам приходится сообщить ему некоторый импульс, который постепенно уменьшается и, наконец, совсем пропадает. Но если плоскость не наклонна, а строго горизонтальна, то указанное круглое тело, положенное на нее, может пребывать в том состоянии, какое мы захотим ему придать: если мы пожелаем оставить его в покое, то оно будет пребывать в покое; если же мы сообщим ему импульс в каком-либо направлении, то оно будет {395} двигаться в том же направлении, сохраняя постоянно ту скорость, которая была придана ему нашей рукой, и не имея склонности ни к увеличению, ни к уменьшению таковой, ибо плоскость не имеет ни наклона, ни подъема. Точно так же и два равных груза, прикрепленных к двум концам одной и той же веревки, пребывают в покое, уравновешивая друг друга, и если одно из них получает импульс, направленный вниз, то последний сохраняется неизменным. Здесь необходимо сделать оговорку, что все это имело бы место, если бы мы могли полностью устранить возможные случайные и посторонние воздействия, как то: недостаточную гибкость веревки, вес ее и блока, трение при вращении вокруг оси и т. д. Так как мы можем определить скорость, которую приобретает одно тело, падая с определенной высоты это время, как другое тело находится в покое, то мы можем также найти, какова и сколь велика будет скорость, с которою будут двигаться оба тела после предшествовавшего падения одного из них, причем одно тело будет подниматься, а другое опускаться. На основании ранее доказанного мы уже знаем, что тело, вышедшее из состояния покоя и падающее свободно, последовательно приобретает все большую и большую степень скорости; в нашем случае свободно падающее тело будет иметь максимальную скорость в тот момент, когда оно начнет поднимать своего спутника; далее, ясно, что эта степень скорости не будет увеличиваться, так как устранена самая причина такого увеличения — собственный вес падающего тела, который больше уже не действует, ибо склонность его опускаться уничтожается сопротивлением другого тела его подъему. Вследствие этого сохранится максимальная степень скорости, и движение из ускоренного превратится в равномерное; величина же этой ожидаемой скорости, как это ясно из выведенного и доказанного в предыдущие дни, должна быть такой, чтобы за промежуток времени, потребный для падения тела, было пройдено пространство, в два раза большее, чем пройденное падающим телом6.
Сагредо. Выходит, что синьор Апроино рассудил правильнее, чем я. Пока я вполне удовлетворен объяснениями, которые даны вами, синьор, и считаю правильным все, вами сказанное. Однако я не настолько еще усвоил себе предмет, чтобы быть в состоянии освободиться от чрезвычайного удивления при встрече с таким явлением, как, например, возможность преодолеть огромное сопротивление при помощи ударов тела, не обладающего ни особенно большим весом, ни значительной скоростью; в особенности поразило меня ваше утверждение, что не может быть такого сопротивления (за исключением бесконечно большого), которое могло бы противостоять удару, не подаваясь вовсе, а также и то, что для подобного удара мы никоим образом не можем найти определенной меры. Поэтому мне очень бы хотелось, чтобы вы, синьор, взяли на себя труд разъяснить эти темные пункты. {396}
Сальвиати. Так как нельзя дать доказательства такого предложения, в котором условия не были бы точно определены, то при рассуждении о силе удара и сопротивлении тела, получающего удар, необходимо принять, что ударяющее тело имеет постоянно одну и ту же силу, как это имеет, например, место при падении одного и того же тела с неизменной высоты, и что тело, получающее удар, сохраняет всегда одинаковое сопротивление.
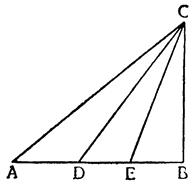 |
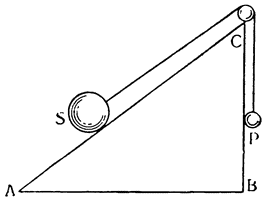 |
После долгих размышлений относительно того, что мне остается еще сказать и чем можно заключить настоящую беседу, я установил следующее положение, которое сейчас изложу и докажу.
Предложение
Если действие, производимое ударом одного и того же груза, падающего всегда с одинаковой высоты, выражается в перемещении на одно и то же расстояние тела, воспринимающего удар и обладающего постоянным сопротивлением, причем для получения того же результата необходим мертвый груз определенной величины, действующий одним давлением без удара, то я утверждаю, что тот же ударяющий груз, встретив при падении другое тело с большим сопротивлением, переместит его на пространство, скажем, вдвое меньшее, чем в первом случае, если для получения подобного же результата недостаточно давления первого мертвого груза и требуется груз, вдвое больший; то же самое будет иметь место и при всяких других соотношениях: перемещение, производимое силою одного и того же {398} удара, будет тем меньше, чем больше будет требуемый мертвый груз по сравнению с первоначальным.
Предположим, что сопротивление какого-либо тела, например сваи, таково, что преодолеть его может мертвый груз, весом не менее ста фунтов, и положим, что вес ударяющего тела составляет всего десять фунтов, причем это тело, падая с высоты, скажем, четырех локтей, вбивает сваю на четыре дюйма. На основании ранее доказанного ясно прежде всего, что груз в десять фунтов, опускающийся вертикально, достаточен для подъема груза весом в сто фунтов по наклонной плоскости, длина которой в десять раз превышает ее высоту, так как для подъема груза в десять фунтов по вертикали и в сто фунтов по наклонной плоскости, длина которой превышает длину перпендикуляра в десять раз, требуется одна и та же сила. Далее, если импульс, приобретенный телом при падении с некоторой высоты по вертикали, применяется для подъема другого тела, равного ему по сопротивлению, то он поднимает последнее на такую же высоту; но сопротивление подъему десяти фунтов по вертикали равно сопротивлению подъему ста фунтов по наклонной плоскости, длина которой в десять раз больше ее высоты; следовательно, импульс, приобретенный телом весом в десять фунтов после падения последнего вертикально с любой высоты и приложенный к телу весом в сто фунтов, переместит последнее вверх по наклонной плоскости на пространство, соответствующее длине перпендикуляра, т. е. на такое пространство, по отношению к которому высота наклонной плоскости составляет одну десятую часть. Из сказанного выше само собою вытекает, что сила, могущая поднять груз по наклонной плоскости, будет достаточна для подъема его и по вертикали, но лишь на соответствующую высоту, каковая в данном случае составляет одну десятую часть пути, пройденного телом по наклонной плоскости; а этот путь равен, в свою очередь, пространству, пройденному при падении первым телом, весящим десять фунтов. Следовательно, груз, весящий десять фунтов и падающий по вертикали, достаточен для подъема груза, весом в сто фунтов, также по вертикали, однако лишь на пространство, составляющее одну десятую часть пути, пройденного при падении грузом в десять фунтов. Но сила, могущая поднять груз в сто фунтов, равняется силе, с которой тот же груз в сто фунтов давит вниз, а это давление было способно углубить сваю в землю. Таким образом, мы разъяснили, как падение груза, весящего десять фунтов, может преодолеть сопротивление, равное тому, которое имеет место при подъеме груза весом в сто фунтов; однако перемещение последнего происходит на пространство, равное лишь одной десятой части пути, проходимого ударяющим телом при его падении. Если мы положим, далее, что сопротивление сваи увеличивается в два или три раза, вследствие чего для преодоления его требуется давление двухсот или трехсот фунтов мертвого груза, то, повторяя приведенное {399} выше рассуждение, мы найдем, что импульс отвесно падающего груза, весом в десять фунтов, достаточен для углубления сваи в землю, однако не на величину, равную одной десятой части пути, проходимого при падении, как в первом случае, а на одну двадцатую часть того же пути во втором случае и на одну тридцатую часть пути в третьем случае. Таким образом, увеличивая сопротивление до бесконечности, мы найдем, что один и тот же удар всегда в состоянии преодолеть последнее, однако перемещая сопротивляющееся тело на все меньшее и меньшее пространство, в соответствии с указанным выше отношением; поэтому, мне кажется, мы можем с достаточной уверенностью утверждать, что сила удара бесконечна. Но тогда нам надлежит признать также, что, с другой стороны, и сила давления без удара бесконечна, ибо, преодолев сопротивление сваи, она углубит ее не только на то пространство, на которое углубил бы ее удар, но будет последовательно углублять ее до бесконечности.
Сагредо. Я вижу, что ваше рассуждение, синьор, действительно ведет прямым путем к установлению истинной причины рассматриваемого явления. Мне кажется, однако, что удар может быть произведен столь различными способами и применен к преодолению столь разнообразных сопротивлений, что необходимо было бы остановиться на разъяснении по крайней мере таких случаев, понимание которых подготовило бы нашу мысль к восприятию вопроса в целом.
Сальвиати. Ваше замечание, синьор, справедливо, и я только что собирался привести вам несколько таких случаев. Одним из них является тот, при котором действие удара сказывается не на теле, воспринимающем удар, а на самом ударяющем; последнее явление имеет место, если мы ударяем, например, по прочной наковальне молотком из свинца: эффект удара сказывается на молотке, который деформируется, но не на наковальне, которая остается на месте. Сходный результат получается также при ударах маленьким молотком, обычно применяемым каменотесами и сделанным из незакаленного, а потому мягкого железа; при продолжительной работе таким молотком на твердой стальной наковальне мы убеждаемся, что он не меняет вида и положения наковальни, сам же сплющивается и изменяет форму. В иных случаях действие удара отражает ударяющее тело, как это можно видеть на примере гвоздя, который мы желаем вбить в весьма твердое дерево: молоток отскакивает назад, нисколько не вбивая гвоздя, и про такой удар мы говорим, что он не «прилип» к предмету. Сходное с этим явление представляют прыжки, совершаемые на твердом и гладком полу надутым пузырем или другим телом, сделанным из такого вещества, что тело легко уступает удару, но затем немедленно же принимает первоначальную форму. Подобные прыжки имеют место не только в том случае, когда само ударяющее тело уступает удару, а затем принимает прежнюю форму, но и тогда, когда последним свойством {400} обладает тело, испытывающее удар; так подскакивает, например, шарик из твердого и неподатливого вещества, падающий на туго натянутую кожу барабана. Иногда наблюдается достойный большого удивления эффект, обусловливаемый соединением удара с давлением без удара. Это явление можно наблюдать у прессов для тканей, для выжимания масла и других. Здесь четыре или шесть человек простым усилием заставляют сперва спуститься винт настолько, насколько это для них посильно; отводя затем винт несколько назад и приводя его опять в быстрое вращение, достигают дальнейшего продвижения винта, причем толчок, развиваемый усилием четырех или шести человек, дает такой же результат, как давление, вызываемое усилием от двенадцати до двадцати человек. Поэтому прессы делаются весьма прочными и из очень твердого дерева, так чтобы прогиб был весьма малым или вовсе отсутствовал; если бы этого не было, то и дерево поддавалось бы, и удар затрачивался бы на его изгиб8.
Во всяком теле, которое должно быть перемещено внешней силой, можно различать, мне кажется, сопротивление двоякого рода. Сопротивление одного рода является внутренним, и мы оцениваем его, говоря, например, что тело, весом в тысячу фунтов, труднее поднять, нежели тело, весом в сто фунтов; сопротивление другого рода связано с расстоянием, которое должно быть пройдено при движении; так, например, чтобы бросить камень на расстояние ста шагов, требуется большая сила, чем на расстояние пятидесяти шагов, и т. д. Этим двум родам сопротивления соответствуют и два различных источника движения, из коих один действует давлением без удара, а другой — посредством удара. При действии без удара движение может иметь место только в том случае, если сопротивление будет хотя бы на самую незначительную величину меньше силы
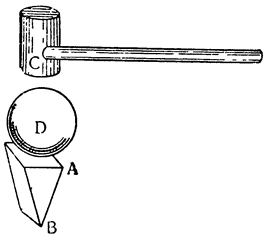 |
Момент тела, производящего удар, представляет собою не что иное, как соединение или совокупность бесконечного числа моментов, из которых каждый равен одному моменту: или внутреннему и естественному (т. е. моменту собственного абсолютного веса, который тело от века проявляет, будучи положено на какую-либо опору), или внешнему принужденному, обусловливаемому движущей силой. Вовремя движения тела такие моменты равномерно нарастают с каждым мгновением; они накапливаются и сохраняются в теле совершенно так же, как и нарастающая скорость падающего тела; подобно тому, как в бесконечное число мгновений хотя бы и весьма короткого промежутка времени тело, проходя через новые и новые равные степени скорости, неизменно сохраняет все те, которые приобретены им в предшествующее время, оно сохраняет и сложные моменты, состоящие из естественных и принужденных моментов, обусловливаемых природою и искусством.
Сила удара имеет бесконечно большой момент в том случае, когда момент передается ударяющим телом веществу, не уступающему удару, что мы сейчас и покажем.
Если вещество уступает удару тела, движущегося с какою-либо скоростью, то это не происходит мгновенно и требует некоторого времени; в самом деле, предполагая обратное, мы допускаем мгновенное перемещение на некоторое определенное пространство, что, как мы уже доказали, невозможно. Но если перемещение вещества в месте удара совершается во времени, то во времени же совершается и передача моментов, приобретенных ударяющим телом при движении; этого времени оказывается достаточным для уничтожения или уменьшения совокупности указанных выше моментов, каковая совокупность при мгновенном действии на ударяемое тело (что имело бы место в том случае, если бы вещество как ударяющего тела, так и тела, воспринимающего удар, было абсолютно твердым и лишенным упругости), конечно, произвела бы гораздо больший эффект, в смысле преодоления сопротивления и приведения тела в движение, чем {402} тот, который получается при действии ее хотя бы в течение весьма краткого промежутка времени. Говорю больший эффект потому, что некоторый эффект тело, воспринимающее удар, всегда получает, как бы ни был незначителен удар и как бы ни было оно упруго; однако такой эффект, хотя и имеющий место, часто остается совершенно незаметным для нас, как это и будет доказано в свое время. В справедливости изложенного можно убедиться из следующего опыта: если равномерно ударять маленьким молотком по концу весьма большой балки, лежащей на земле, то после многих и многих ударов можно будет, наконец, заметить, что балка переместилась на некоторое пространство,— верное доказательство того, что каждый из ударов оказал свое действие на перемещение балки; в самом деле, если бы первый удар не мог оказать никакого действия, то в таком же положении были бы и все последующие удары, которые так же, как и первый, не могли бы произвести никакого действия, что противоречит результату опыта и тому объяснению, которое можно ему дать. И т. д.
Сила удара имеет бесконечно большой момент, ибо не существует такого большого сопротивления, которое не могло бы быть преодолено силою даже самого незначительного удара.
Тот, кто затворяет бронзовые ворота Сан-Джиованни, напрасно пытался бы захлопнуть их одним простым толчком; однако импульсы, сообщаемые последовательным давлением, заставляют эти громадные двери двигаться с такою силою, что когда они закрываются и ударяются о порог, то вся церковь сотрясается. Отсюда видно, как сила передается приводимым в движение телам, даже весьма большим, и как сообщаемая сила накопляется и сохраняется в них в течение некоторого времени. И т. д.
Подобное же явление наблюдается и с очень большим колоколом, который не может быть приведен в необходимое движение, если мы потянем за веревку один только раз, или даже четыре, или шесть раз; для этого необходимо тянуть за веревку последовательно и равномерно много и много раз, причем сила последующих толчков будет прибавляться к силе, уже сообщенной предыдущими. Чем больше и тяжелее колокол, тем больше сила и импульс, приобретаемые им в течение более долгого времени и от большого числа толчков, передаваемых веревкой и излишних для маленького колокола, который очень быстро приходит в движение, но столь же быстро и останавливается, ибо он не поглощает (если можно так выразиться) столько силы, сколько большой колокол.
Подобное же явление наблюдается, наконец, с судами, которые не приходят в быстрое движение сразу, при первом же ударе весел или первом порыве ветра; однако при продолжительной гребле и продолжительном давлении силы ветра на паруса они приобретают огромный импульс, способный повести к разрушений самого судна, если оно при движении ударится о камни. {403}
Гибкий, но большой лук арбалета способен метать стрелы дальше, нежели лук более тугой, но более короткий, потому что первый соприкасается со снарядом более продолжительное время, постепенно передавая ему силу, тогда как второй тотчас же его выпускает.
Конец шестого дня
| {404} |
Стр. | ||||
ДЕНЬ ПЕРВЫЙ | ||||
Механическое подобие................... | 117 | |||
Сравнительная прочность больших и малых тел и животных . . | 118 | |||
Замечательный случай излома колонны.......... | 119 | |||
Сопротивление тел растяжению.............. | 121 | |||
Зависимость трения от давления.............. | 122 | |||
Прибор для безопасного соскальзывания.......... | 123 | |||
Прилипание пластинок и боязнь пустоты.......... | 124 | |||
Боязнь пустоты недостаточна для объяснения связности тел | 126 | |||
Способ измерения связности, обусловливаемой пустотой ... | 126 | |||
Предельная высота всасывания............... | 128 | |||
Сопротивление медной проволоки растяжению........ | 129 | |||
Объяснение связности тел наличием бесконечно малых пустот . | 130 | |||
Качение многоугольников и кругов ............ | 132 | |||
Конус и отрезок чаши, обращающиеся в пределе в точку и ок- | 137 | |||
Конечное и бесконечное.................. | 139 | |||
Различие в свойствах конечного и бесконечного...... | 140 | |||
Числовые ряды...................... | 140 | |||
Невозможность достигнуть бесконечно малой величины путем | 140 | |||
Особые свойства единицы................. | 145 | |||
Система кругов и точек . . . ............... | 146 | |||
Сравнение жидкости и мельчайшего порошка ....... | 147 | |||
Зажигательные зеркала................... | 148 | |||
Скорость света и попытка определить ее.......... | 149 | |||
| ||||
Геометрическое место точек, расстояния которых от двух дан- | 150 | |||
Способ «деления» линии на бесконечно большое число частиц . | 152 | |||
Разрежение и уплотнение................. | 153 | |||
Утончение поверхностного слоя золота при протягивании сереб- | 156 | |||
Отношение боковых поверхностей равновеликих цилиндров | 158 | |||
Отношение объемов цилиндров, боковые поверхности которых | 159 | |||
Практическое применение теоремы............. | 160 | |||
Площади изопериметрических фигур............ | 160 | |||
Сгущение и разрежение.................. | 163 | |||
Учение Аристотеля о падении тел в пустоте......... | 163 | |||
Опровержение этого учения................ | 164 | |||
Влияние среды на падение тел.............. | 167 | |||
Движение тел в воде................... | 168 | |||
Рыбы, плавающие в воде................. | 170 | |||
О каплях воды..................... | 170 | |||
Смешение вина и воды.................. | 171 | |||
Падение тел в пустоте и среде, оказывающей сопротивление . | 172 | |||
Определение абсолютного и удельного веса воздуха .... | 174 | |||
Переход от свободного падения тел к качанию маятника ... | 181 | |||
Влияние размера и шероховатости тел на падение их в сопро- | 184 | |||
Отношение между объемами и поверхностями подобных тел . | 185 | |||
Уменьшение ускорения тела при движении его в среде, ока- | 187 | |||
О линии быстрейшего спуска ............... | 190 | |||
Законы качания маятника................. | 190 | |||
Переход к звуку. Как можно вызвать колебания...... | 192 | |||
Резонанс струн...................... | 192 | |||
Закрепление звуковых волн................ | 193 | |||
Зависимость высоты звука от длины, толщины, веса и натяже- | 193 | |||
Акустические интервалы................. | 195 | |||
Консонансы и диссонансы и аналогия их с качанием маятни- | 196 | |||
ДЕНЬ ВТОРОЙ | ||||
Различие между сопротивлением тел растяжению и сгибанию . | 201 | |||
Закон рычага...................... | 202 | |||
Подъем при помощи рычага тяжелого груза........ | 204 | |||
Общая теорема о сопротивлении тел сгибанию ...... | 205 | |||
Сопротивление сгибанию балок, поставленных плашмя и на | 207 | |||
Сопротивление балки сгибанию при увеличении ее длины . . . | 208 | |||
Сопротивление балки сгибанию при увеличении ее толщины . | 209 | |||
Длина тела не влияет на сопротивление его разрыву .... | 210 | |||
Сопротивление сгибанию тел различной длины и толщины ... | 211 | |||
Сопротивление сгибанию подобных тел.......... | 211 | |||
| ||||
Разрушение балок под действием собственного веса .... | 213 | |||
Возвращение к закону механического подобия. Кости великана | 216 | |||
Предельная длина балок, ломающихся от собственного веса . | 219 | |||
Сопротивление сгибанию балок с опорами по концам и в сере- | 219 | |||
Сопротивление сгибанию балок при изменении расположения | 220 | |||
Точка приложения силы, сгибающей балку, лежащую на двух | 223 | |||
Сопротивление сгибанию балок, имеющих прямоугольное по- | 224 | |||
То же — параболический профиль............. | 225 | |||
Квадратура параболы.................... | 227 | |||
Способы вычерчивания параболы.............. | 230 | |||
Сопротивление сгибанию полых цилиндров......... | 231 | |||
Сопротивление сгибанию полых цилиндров по сравнению со | 231 | |||
ДЕНЬ ТРЕТИЙ | ||||
О местном движении | ||||
О равномерном движении | ||||
Определение и аксиомы.................. | 234 | |||
Теоремы......................... | 235 | |||
Естественно-ускоренное движение | ||||
Определение........................ | 239 | |||
Постепенное нарастание скорости падающего тела..... | 239 | |||
Ошибочное представление этого нарастания ....... | 240 | |||
Падение тела по наклонным плоскостям, имеющим одну и ту | 246 | |||
Колебания маятника................... | 247 | |||
Теорема I. Сравнение времени прохождения телом одного | 248 | |||
Теорема II. Пути, проходимые при падении, относятся, как | 249 | |||
Следствие I. Пути, проходимые при падении за последователь- | 251 | |||
Опытное подтверждение теоремы II............ | 253 | |||
Следствие II. Времена падения по двум отрезкам относятся, | 254 | |||
Падение тел по наклонным плоскостям........... | 254 | |||
Скорость тел, падающих по наклонным плоскостям одинаковой | 258 | |||
Теорема III. Соотношение между временами падения по длине | 259 | |||
| ||||
Теорема IV. Соотношение между временами падения по пло- | 260 | |||
Теорема V. Соотношение между временами падения по плос- | 261 | |||
Теорема VI. Время падения по хордам одного и того же круга . | 261 | |||
Наглядное изображение конечных точек путей, проходимых | ||||
Теорема VII. Время падения по наклонным плоскостям, высоты | 264 | |||
Теорема VIII. Время падения по наклонным плоскостям, дли- | 266 | |||
Теоремы IX—XII. Время падения по наклонным плоскостям, | 267 | |||
Задачи I—III. Определение частей наклонных плоскостей | 271 | |||
Теорема XIII. Сравнение времени падения по вертикали и нак- | 273 | |||
Задачи IV—VII. Определение путей, проходимых по наклон- | 275 | |||
Теорема XIV. Установление пределов пути, проходимого телом | 278 | |||
Задачи VIII и IX. Определение путей, проходимых по наклон- | 279 | |||
Теорема XV. Установление пределов подъема тела по наклон- | 284 | |||
Теорема XVI. Сравнение времени движения по горизонтали со | 285 | |||
Задача X. Построение наклонной плоскости при данном пути | 286 | |||
Теорема XVII. Определение длины нижней части одной нак- | 286 | |||
Теорема XVIII. Сравнение времени падения по вертикальному | 287 | |||
Задача XI. Время движения по вертикальному, а затем гори- | 288 | |||
Теоремы XIX—XXI. Наклонные плоскости, время падения | 289 | |||
Задачи XII—XIV. Определение отрезков вертикалей и наклон- | 292 | |||
Теорема XXII. Сравнение времени падения по хорде, проходя- | 298 | |||
Замечание. Время падения тела по дуге окружности .... | 300 | |||
Задача XV. Определение положения отрезка наклонной плос- | 301 | |||
Задача XVI. Определение высоты, при падении с которой тело | 302 | |||
ДЕНЬ ЧЕТВЕРТЫЙ | ||||
О движении брошенных тел | ||||
Вводные предложения, касающиеся свойств параболы . . . | 304 | |||
Доказательство теоремы I, что брошенное тело описывает пара- | 305 | |||
Теорема II. Сложение скоростей в случае равномерного дви- | 315 | |||
Теорема III. Сложение скоростей в случае равномерного и рав- | 316 | |||
Определение «сублимита».................. | 317 | |||
Задача I. Определение скорости падающего тела для различ- | 319 | |||
Обсуждение вопроса о сложении скоростей ........ | 320 | |||
Задача II. Определение величины сублимита для данной полу- | 326 | |||
Задача III. Определение величины амплитуды гюлупараболы | 327 | |||
Теорема IV. Импульс тела при движении по полупараболе, | 328 | |||
Теорема V. Дальность полета одинакова, если углы наклона | 331 | |||
Теорема VI. Амплитуды полупарабол равны, если высоты | 332 | |||
Теорема VII. Скорость в конечной точке полупараболы равна | 333 | |||
Задача IV. Определение высоты полупараболы по ее амплитуде | 334 | |||
Задачи V и VI. Вычисление амплитуд и высот полупарабол | 334 | |||
Задача VII. Определение высот и сублимитов полупарабол . | 339 | |||
Невозможность строго горизонтального расположения натяну- | 342 | |||
ПРИЛОЖЕНИЕ О ЦЕНТРАХ ТЯЖЕСТИ | ||||
Лемма 1.......................... | 346 | |||
Предложение I. О центре тяжести грузов, подвешенных к ры- | 346 | |||
| ||||
Предложение II. О центрах тяжести совокупностей цилиндров | 349 | |||
Предложение III. О центре тяжести параболического коноида . | 352 | |||
Лемма II......................... | 355 | |||
Предложение IV. О центре тяжести усеченного параболичес- | 356 | |||
Предложения V и VI. О центре тяжести грузов, подвешенных | 357 | |||
Предложения VII и VIII. О центрах тяжести совокупностей | 359 | |||
Предложение IX. О центре тяжести конуса или пирамиды . . | 362 | |||
Лемма III......................... | 363 | |||
Предложение X. О центре тяжести усеченного конуса или усе- | 364 | |||
ДЕНЬ ПЯТЫЙ | ||||
О эвклидовых определениях пропорциональности | ||||
Когда и по какой причине Галилей обратился к соответствую- | 366 | |||
Основная предпосылка.................. | 367 | |||
Определение пропорциональности соизмеримых величин . . . | 368 | |||
Общее определение пропорциональности величин как соизме- | 368 | |||
Другой способ определения пропорциональности величин . . . | 369 | |||
Определение отсутствия пропорциональности как соизмеримых, | 371 | |||
Аксиома.......................... | 371 | |||
Та же аксиома, изложенная в более общем виде...... | 374 | |||
Предложение I, являющееся предложением IV книги V Эв- | 373 | |||
Следствие, обратное пятому определению книги V Эвклида . | 373 | |||
Предложение II, обратное седьмому определению книги V Эв- | 373 | |||
Предложение III, являющееся пятым определением книги | 374 | |||
Предложение IV, являющееся седьмым определением книги | 375 | |||
Пятое определение книги VI Эвклида........... | 376 | |||
Определение, заменяющее пятое определение книги VI Эвкли- | 377 | |||
Предложение V, являющееся пятым определением книги | 377 | |||
Построение и доказательство предложения, касающегося сос- | 379 | |||
| ||||
ДЕНЬ ШЕСТОЙ | ||||
О силе удара | ||||
Нарушение равновесия между грузом и двумя сосудами, под- | 382 | |||
Сила удара и давление мертвого груза.......... | 385 | |||
Безграничность сопротивления, которое можно преодолеть | 387 | |||
Сила удара и закон моментов .............. | 388 | |||
Влияние падения одного груза на другой, равного веса, когда | 391 | |||
Движение тел по наклонным плоскостям.......... | 394 | |||
Предложение, касающееся перемещения тел посредством удара | 396 | |||
Влияние удара на ударяющее тело............ | 397 | |||
Момент ударяющего тела, как совокупность элементарных | 401 | |||
Действие последовательных толчков............ | 402 | |||
| {411} |
|
КОММЕНТАРИИ |
| {412} |
| {413} |
«Механика» относится к числу сравнительно ранних работ Галилея и посвящена в основном статике простых машин.
Точную дату создания трактата установить трудно. Несомненно только, что он был написан во время работы Галилея в Падуанском университете (1592—1610). Галилей в «Беседах» ссылается на «старый трактат по механике, написанный им еще в Падуе исключительно как руководство для своих учеников». Обычно этот трактат датируют 1600 годом или несколько ранее. Окончательному варианту «Механики» предшествовал более короткий1, созданный, вероятно, в 1593 г., т. е. в первый год пребывания Галилея в Падуе.
Одновременно с «Механикой» Галилей написал для своих студентов и частных учеников трактаты по военной архитектуре, фортификации и космографии. Однако «Механика» среди этих трактатов оказалась наиболее ценным произведением. И это заметили уже современники Галилея. Трактат «Механика» получил широкую известность в ученых кругах не только в Италии, но и за границей. Еще при жизни Галилея он был переведен на французский и английский языки. Французский перевод Марена Мерсенна был издан в 1634 г.2, английский же перевод Роберта Пайена, {414} выполненный в 1636 г., остался неопубликованным и хранится в Британском музее1. Итальянский текст трактат «Механика» был издан вскоре после смерти Галилея2. Он включался во все собрания его сочинений.
Настоящий перевод сделан с последнего национального издания сочинений Галилея3, в котором текст «Механики» был установлен на основании сличения многих рукописей и первых печатных изданий, так как авторской рукописи этого труда Галилея не сохранилось.
От своего учителя Риччи, принадлежавшего к эмпирической школе Тартальи, Галилей воспринял идеи кинематической статики и интерес к практическим задачам. По трудам своего друга и покровителя Гвидо Убальди он познакомился с геометрической статикой. Но лучшей школой для Галилея было изучение трудов Архимеда, Аристотеля и ученых XVI в., которое он сочетал с конструированием механических приборов и ознакомлением с инженерной практикой своего времени.
В «Механике» Галилея элементы кинематической и геометрической статики тесно переплетаются.
Прежде чем рассматривать действия различных механических орудий, так называемых простых машин, Галилей дает определения основных понятий механики: тяжести, момента и центра тяжести. Уже здесь соседствуют элементы геометрической статики (центр тяжести) с элементами кинематической статики (момент). Для дальнейшего изложения фундаментальным является определение понятия момента.
«Момент — это стремление двигаться вниз, вызванное не столько тяжестью движущегося тела, сколько тем, как различные тяжелые тела размещаются относительно друг друга; при этом часто наблюдается, что благодаря моменту более тяжелые тела перевешиваются более легкими; например, в безмене, где крошечный противовес поднимает огромный груз не из-за избытка тяжести, а из-за удаленности от точки, где безмен поддерживается, из-за удаленности, которая, в сочетании с тяжестью меньшего груза, увеличивает ему момент и импето опускаться вниз, которым он может превысить момент другого, более тяжелого тела. Итак, момент — это импето опускаться вниз, состоящее из тяжести, положения и всего остального, что может вызвать такое стремление»4.
Это определение момента еще несовершенно. Из него неясно, что же такое «положение» тела и «все остальное», что вызывает стремление тяжелого тела двигаться {415} вниз. Если «положение» тела определяется его удаленностью от точки опоры рычага, которая, как указывает далее Галилей, равна длине перпендикуляра, опущенного из точки опоры рычага на прямую линию, проведенную из точки подвеса груза к центру Земли, то, не учитывая «всего остального», «момент» Галилея будет моментом силы тяжести относительно точки опоры рычага в нашем современном понимании этого слова. Однако в дальнейшем Галилей отошел от такого геометрического понимания момента. Далее это определение приспособлено только для сил тяжести. Однако при рассмотрении задач о действии лебедки и ворота Галилей использует также силы тяги, действующие по различным направлениям.
После определений следуют три допущения, из которых последнее аналогично первому постулату Архимеда.
Далее дается чисто геометрическое доказательство закона равновесия рычага («самого общего, главнейшего принципа большей части механических орудий»), состоящего в том, что «неравные грузы, подвешенные на неравных расстояниях, уравновешиваются каждый раз, когда эти расстояния обратно пропорциональны грузам».
В следующем параграфе Галилей подтверждает эту истину исходя из кинематических соображений.
При этом Галилей отвлекается от различия между движением и равновесием системы. Ола, движущая груз, лишь незначительно отличается от силы, уравновешивающей его. Галилей смог отвлечься и от трения и сопротивления в системе и как бы перебросил мост между статикой и динамикой, чего не удавалось сделать его предшественникам (Гвидо Убальди, Стевину и др.).
Далее Галилей в элементарной форме высказывает принцип виртуальных перемещений, выведенный из закона равновесия рычага, и принцип виртуальных скоростей.
«Из этого рассуждения узнаем,— заключает он,— что скорость движения оказывается в состоянии увеличить момент в движущемся теле в том же отношении, в котором возрастает сама скорость движения»1.
Отсюда можно сделать вывод, что в качестве «всего остального», входящего в понятие «момента», он прежде всего имел в виду скорость тела. Если теперь считать, что положение тела не входит в понятие «момента» какой-либо количественной характеристикой, то «момент» тогда представится произведением силы тяжести (или вообще силы) на скорость тела. Направление скорости считается вертикальным, поскольку рассматривается отклонение от положения равновесия рычага с горизонтальными плечами. Принцип равновесия заключается в равенстве «моментов» двух грузов, связанных в простой машине.
В более поздних работах по механике Галилей углубляет и уточняет понятие «момента» и свой принцип виртуальных скоростей. Так, в «Рассуждении о телах, пребывающих в воде» (1612) он дает следующее определение «момента»:
«Под моментом в механике разумеется та сила, то качество, то действие, с которым двигатель двигает и движимое сопротивляется; эта сила зависит не только от {416} простой тяжести, но и от скорости движения и от различного наклонения путей, по которым совершается движение, потому что тяжесть производит большее действие при опускании по более наклонному пути, чем по менее наклонному...»1.
Из этого определения «момента» понятие «положения тела» явно исключено, но зато фигурирует скорость и сделана попытка учесть угол между направлением силы и направлением скорости. Галилей не уточняет, как этот угол входит в определение «момента». Он ограничивается в дальнейшем рассмотрением случая, когда «оба движения предполагаются происходящими при одинаковом наклоне».
Именно для этого случая он дает четкую формулировку принципа виртуальных скоростей:
«Такое соотношение между тяжестью и скоростью существует у всех механических орудий и принимается Аристотелем как принцип в его «Проблемах механики», почему мы можем принять за достоверное то положение, что неравные по абсолютной величине грузы могут взаимно уравновешиваться и приобретать равные моменты всякий раз, когда их вес будет обратно пропорционален скорости их движения, т. е. когда один груз будет во столько же раз легче другого, во сколько раз скорость его движения будет больше скорости другого»2.
Оценивая достижения Галилея в «Механике», академик В. А. Стеклов очень высоко ставил именно их обобщающую роль. Он писал:
«Галилей обобщает все эти частные случаи, распространяя начало возможных перемещений на все простые машины, связанные с рычагом и наклонной плоскостью
В этом обобщении и состоит заслуга Галилея. Интуитивная способность, заметив известное свойство явлений на некоторых частных случаях, угадать в них общий закон, провидеть его и распространить на более обширный класс случаев, играет первостепенную роль в развитии любой науки о природе, а мыслитель, совершающий такое обобщение единичных наблюдений, постигающий всеобщность замечательных частных фактов, должен быть признан занимающим почетное место в ряду двигателей науки»3.
На всеобщность принципа виртуальных скоростей Галилей указывает и в «Беседах» (1638), где он применяет его при рассмотрении задачи о равновесии грузов на наклонной плоскости и дает одну из наиболее совершенных своих формулировок этого принципа.
Здесь Галилей впервые говорит о возможных перемещениях, т. е. о тех «пространствах, которые они (т. е. тела.— Е. Р.) прошли бы в одинаковые промежутки времени», если их вывести из положения равновесия. У всех предшествующих авторов речь шла о конкретных движениях тел (поднятии и передвижении грузов) и о действительно реализующихся скоростях и перемещениях.
Вернемся к основному содержанию трактата «Механика». После установления основных законов Галилей приступает к обсуждению действия механических орудий: {417} безмена, рычага, лебедки, ворота, блока, полиспастов, наклонной плоскости, винта и водяной улитки Архимеда. Ко всем этим орудиям он применяет принцип рычага и принцип виртуальных перемещений в форме закона сохранения работы.
Очень важным и интересным для истории механики является способ решения Галилеем задачи о равновесии грузов на наклонной плоскости. Этот способ заключается в следующем. Вместо того чтобы рассматривать стремление груза опускаться вниз по наклонной прямой (плоскости), Галилей рассматривает стремление груза опускаться вниз по окружности, расположенной в вертикальной плоскости и касающейся названной прямой в той точке, где расположен точечный груз. Возможность замены первой задачи второй задачей преподносится Галилеем как само собой разумеющаяся. Фактически же это означает утверждение Галилеем справедливости принципа эквивалентности связей. При этом Галилей вынужден рассматривать бесконечно малые перемещения груза (перемещения в «начальный или первый момент движения»). В свою очередь, перемещения груза вдоль окружности Галилей заменяет перемещениями груза, находящегося на конце опускающегося плеча рычага, другой конец которого остается горизонтальным. Таким образом, он свел задачу к ломаному рычагу, теория которого была уже достаточно разработана еще со времени анонимного ученого XIII в. «Момент» груза, находящегося на конце наклоненного плеча рычага, т. е. на наклонной плоскости, пропорционален проекции радиуса вспомогательного круга на горизонтальный диаметр. Далее рассмотрение подобных треугольников приводит к заключению, что «общий и абсолютный момент, который движущееся тело имеет на перпендикуляре к горизонту, и тот, который оно имеет на наклонной плоскости так... относятся друг к другу..., как длина наклонной плоскости относится к перпендикуляру, который из нее же был опущен на линию горизонта»1.
Применяет Галилей к системе грузов, находящейся на наклонной плоскости, и принцип виртуальных перемещений.
По сути дела Галилей применяет здесь принцип сравнения работ. Эти рассуждения Галилей полностью повторяет в «Беседах».
1 (К стр. 7). Галилей здесь безусловно имеет в виду изобретателей perpetuum mobile, которых много было тогда в Италии, как и в других странах Европы. Галилей относился к этим изобретателям резко отрицательно, он называет их ниже росо intendenti ingegneri, volgari mecanici и т. п. В этой главе Галилей доказывает, что механические орудия не способны создавать работу. Эта же мысль красной нитью проходит через весь трактат.
2 (К стр. S). В трактате «Механические проблемы» псевдо-Аристотеля в § 1 имеется сходное место: в связи с рычагом подлежат рассмотрению три вещи: точка опоры, представляющая собою подвес и центр вращения, и два груза — движущий и движимый.
3 «Сила или мощь» (forza о potenza — этот термин теперь в физике обозначает {418} мощность) здесь — равнозначны. Ниже Галилей употребляет слова virtu, potere и др. для обозначения понятия силы.
4 (К стр. 9). Говоря о скорости движения, Галилей называет ее prestezza e velocity, эти термины здесь синонимы.
5 (К стр. 10). Галилей, как истинный сын нового времени, подчеркивает экономический эффект от применения механических орудий.
6 (К стр. 11). Хотя Галилей говорит здесь о движении вниз и о силах тяжести, но он понимает «момент» более обще. Ниже при разборе задачи о лебедке и о вороте он распространяет это понятие и на силы тяги, действующие в различных направлениях. Под «всем остальным», входящим в определение «момента», Галилей, вероятно, имеет в виду скорость тела.
7 Сравните с первым постулатом Архимеда в трактате «О равновесии плоских фигур»: «Равные тяжести на равных длинах уравновешиваются, на неравных же длинах не уравновешиваются, но перевешивают тяжести на большей длине» (Архимед. Сочинения. Перевод, вступ. ст. и коммент. И. Н. Веселовского. М., 1962, стр. 272). Принцип достаточного основания, который здесь применил Галилей, играет роль постулата Архимеда о наклоне весов в направлении стороны, несущей более тяжелый груз.
8 (К стр. 12). То есть в этих случаях проявляется один и тот же закон. Ниже следует доказательство закона равновесия неравноплечего рычага. Оно в некотором смысле обратно тому доказательству, которое дал для этого закона Архимед (см. его Сочинения, стр. 274—276). Архимед исходил из системы, равновесие которой надо доказать, и сводил ее путем введения замещающих грузиков, не нарушающих положение равновесия, к системе, равновесие которой очевидно. Галилей, наоборот, исходил из системы, равновесие которой очевидно (однородное тело «колоннарной», т. е. цилиндрической формы, подвешенное за середину), и посредством операций, не нарушающих равновесия (подвески и разрезания на две произвольные части), сводил ее к системе, равновесие которой следовало доказать. Это доказательство повторено Галилеем в «Беседах и математических доказательствах» (см. настоящий том, стр. 202—204). Там же Симпличио указывает, что «это предложение было доказано Аристотелем в его «Механике» ранее всех других», на что Сальвиати, выражающий точку зрения Галилея, отвечает: «Предоставим ему право первенства по времени; но что касается твердого доказательства этого положения, то мне кажется, что мы должны приписать таковое Архимеду...»
Аналогичное галилеевскому доказательство закона равновесия рычага имеется у Стевина в трактате «Начала статики», изданном впервые в 1586 г. на фламандском языке. Галилей не ссылается на Стевина, и нет оснований считать, что он был знаком с его трудом.
9 (К стр. 14). Галилей приводит далее кинематическое доказательство закона рычага как возможное и вероятное.
10 Здесь выражен в элементарной форме принцип виртуальных перемещений для рычага. {419}
11 (К стр. 15). Элементарная форма принципа виртуальных скоростей. Оба принципа выводятся из закона равновесия рычага и одновременно как бы подтверждают его.
12 (К стр. 17). Здесь для рычага и далее для других орудий Галилей излагает закон сохранения работы.
13 (К стр. 21). Слово fatica (труд, работа) имеет здесь значение усилия, напряжения, но никак не произведения силы на пройденный путь.
14 (К стр. 22). «Механические проблемы» § 9 («псевдо-Аристотеля»).
15 (К стр. 29). Эта аксиома и предшествующие ей рассуждения, связаны с законом инерции. Они содержались уже в более раннем, не напечатанном прижизненно труде Галилея» «О движении» («De motu», Le Opere di Galileo Galilei, v. I. Firenze, 1929, p. 296—307).
16 (К стр. 30). См. примеч. 15.
17 (К стр. 31). Этими словами Галилей, вероятно, хочет сказать, что движение по окружности и движение вдоль наклонной прямой, касательной к ней, совпадают только локально, в точке касания.
18 (К стр. 32). Это условие равновесия груза на наклонной плоскости имелось уже в трактате «О движении» (см. примеч. 15), где оно было получено аналогичным образом. Гвидо Убальди, между прочим, не сумел справиться с этой задачей. Условие равновесия на наклонной плоскости было получено Галилеем и Стевиным независимо друг от друга.
19 (К стр. 36). Это очень важное замечание. Из него вытекает, что, применяя принцип виртуальных перемещений для сил тяжести, следует рассматривать только вертикальные составляющие перемещений. А это является основой для принципа виртуальных работ. Одна из формулировок этого принципа приводится в конце комментируемой фразы.
20 (К стр. 38). Обещанные здесь Галилеем «механические проблемы» не обнаружены. Проблему удара Галилей намеревался осветить во втором издании своего трактата о двух новых науках. Оставшиеся после его смерти рукописи по этому вопросу были оформлены в виде шестого дня «Бесед».
Е. Н. Ракчеев
| {420} |
Когда в 1611 г. Галилей вернулся во Флоренцию из Рима, у него не было оснований жаловаться на судьбу. «Звездный вестник», подтверждение его астрономических открытий римскими астрономами во главе с Клавием, почетный прием в Риме сделали его знаменитым и прославляемым. Это укрепило его положение при дворе великого герцога Тосканского Козимо II, чьим философом и главным математиком он стал в 1610 г. Он был свободен от утомлявших его в Падуе педагогических обязанностей и вместе с тем, в качестве главного математика при университете в Пизе, мог существенно влиять на ход академических дел в Тоскане. Теперь он отдавал все свои силы науке. Планы его были обширны: продолжение и уточнение астрономических наблюдений, имея в виду решение проблемы определения долгот, создание трактата о системе мира по Копернику, обоснование и развитие уже открытых им законов падения тел. Но силою обстоятельств все это было отодвинуто на второй план той дискуссией с перипатетиками, которой мы обязаны «Рассуждением о телах, пребывающих в воде».
Вероятно, в доме ученика и друга Галилея, Сальвати, чье имя дано одному из собеседников в «Диалоге» и «Беседах», летом 1611 г. Галилей вступил в научную дискуссию с двумя профессорами Пизанского университета, Винченцо ди Грациа и Джорджо Корезио. Предметом спора были природа холода и поведение тел при охлаждении, а уже в связи с этим — причины плавания и погружения тел. К оппонентам {421} Галилея присоединился еще один перипатетик, Лодовико делле Коломбе1. Возможно, что дело не исчерпывалось научными и методологическими разногласиями: пизанская профессура могла быть недовольна привилегированным положением Галилея при университете и над университетом, а при Тосканском дворе у Галилея тоже были враги, которые рады были бы подорвать расположение к нему герцога2. Предполагалось организовать публичный диспут с демонстрацией опытов, но герцогу это показалось нежелательным: поражение первого математика Тосканского двора бросило бы тень и на его сиятельную особу, а на полный успех в таких условиях трудно было рассчитывать. Галилей ссылается на соответствующее указание герцога в начале своего рассуждения (см. стр. 42). Поэтому он начал готовить письменное изложение своих взглядов и опровержение доводов оппонентов в форме письма к герцогу (рукопись этой первой редакции сохранилась). Но в сентябре 1611 г. в гостях у Козимо II были два кардинала — любители научных и литературных споров, и в это же время приехал представиться герцогу новоназначенный (по рекомендации Галилея) профессор философии Пизанского университета, Фламинио Папацони, видный представитель аристотелизма. Это дало возможность Галилею завязать полемику с ним в присутствии двора Медичи. Один из кардиналов был на стороне Папацони, второй, а это был Маффео Барберини, будущий папа Урбан VIII, принял сторону Галилея. В ходе спора демонстрировались опыты. Галилей был признан победителем. И окончательный текст его «Рассуждения», заново написанный, после тяжелой болезни, зимой 1611 г., действительно звучит победно. Это произведение не только «первого математика», но и «философа», это не только провозглашение и доказательство определенных физических истин, но и обоснование новой методологии и методики исследования. Поэтому оно стало не завершением дискуссии, а началом борьбы, и ее упорство и тяжесть оценить Галилей тогда, конечно, не мог.
«Рассуждение о телах, пребывающих в воде» было напечатано весной 1612 г. Оно написано по-итальянски — это было обращением к самому широкому кругу читателей. В течение ближайших месяцев из печати вышли четыре книжки противников Галилея: Корезио, Коломбе, Грациа и анонимный автор, вероятно, куратор Пизанского университета Артуро д'Эльчи, или Папацони, выступили со своими возражениями. Галилей ограничился вторым изданием своей работы, в котором добавил некоторые пояснения. Продолжение дискуссии взял па себя выдающийся ученик и сторонник Галилея Бенедетто Кастелли (его книга появилась в 1615 г.; в ней были использованы и материалы Галилея, а значительная ее часть написана им самим). Перипатетики {422} не сдавались, но все сколько-нибудь серьезные их аргументы несомненно были опровергнуты. И отныне список врагов Галилея становится заметно обширнее.
Таково место «Рассуждения» в биографии Галилея и в летописи его эпохи. А в историю гидростатики и физики оно вписалось навечно — между Стевиным и Паскалем. Работы Стевина по гидростатике появились на голландском языке в 1586 г., в латинском переводе — в 1608 г. и, вероятно, были известны Галилею, но не повлияли на его «Рассуждение». Изложение у Стевина — строго геометрическое, «в духе древних». Принципиально новым было использование Стевиным в гидростатике принципа невозможности вечного движения, главные его результаты состоят в установлении законов давления жидкости на дно и боковые стенки сосудов. Большое значение их для техники очевидно, и были вызваны эти исследования техническими запросами. Галилей тоже отвергал возможность вечного движения и был весьма близок к техническим проблемам своего времени. Но, как видно из сказанного выше, его «Рассуждение» возникло в связи с чисто научной дискуссией, метод изложения у Галилея, обращавшегося не только к специалистам, естественно, не математичен, и исходит он из других положений.
Галилей в основу своих выводов и доказательств кладет принцип возможных перемещений, использованный им раньше в «Механике» для теории простых машин. Лагранж называл Галилея автором самого принципа, но это не точно (в числе итальянских предшественников Галилея имеем Леонардо да Винчи и Иеронима Кардано). И сам Галилей явно не притязает на авторство в этом пункте. Но Галилей первый применил принцип возможных перемещений к гидростатике, и притом весьма плодотворно. Впоследствии Лагранж писал, что только на этой основе можно связать вместе статику твердых тел и гидростатику, и указывал, что Галилей «выводит непосредственно из этого принципа равновесие воды в сифоне... и доказывает подобным же образом равновесие жидкостей и погруженных тел...». Итак, первая заслуга Галилея — введение в гидростатику принципа возможных перемещений и получение с его помощью новых результатов о плавающих телах1.
Вторая заслуга Галилея — опровержение различных возражений, которые выдвигались сторонниками Аристотеля против закона Архимеда и вытекающего из него условия плавания. У Аристотеля нет систематизированного изложения теории плавания. Зато его поздние последователи, современники Галилея, старались дать такую теорию, опираясь на отдельные высказывания Аристотеля и отвергая Архимеда. Победа Галилея изгнала аристотелизм из гидростатики. Заодно она была торжеством экспериментального метода в науке и била по догматизму, взывающему к авторитетам.
Галилей не знал поверхностного натяжения жидкостей, поэтому его объяснение плавания пластинок из вещества с большим удельным весом, чем у воды, не является вполне удовлетворительным. Однако и тут, в наиболее слабой, с современной точки {423} зрения, части «Рассуждения», он проявил свою тонкую наблюдательность и мастерство экспериментатора. И, наконец, нельзя не упомянуть о литературных достоинствах этого произведения Галилея, которые можно оценить и в переводе.
Трактат Галилея впервые был издан на русском языке в переводе А. Н. Долговой и С. Н. Долгова в сборнике «Начала гидростатики. Архимед, Стевин, Галилей, Паскаль», под редакцией и с примечаниями А. Н. Долгова (Гостехтеоретиздат, М.—Л., 1932, 2-е изд.— 1933 г.). Перевод был сделан с итальянского текста XII тома полного собрания сочинения Галилея издания 1854 г.— текста, который в точности был воспроизведен и в IV томе Собрания сочинений Галилея издания 1894 г. Этот же перевод был для настоящего издания проверен и отредактирован нами, на основе итальянского текста в IV томе Собрания сочинений Галилея издания 1932 г. (перепечатка Ed. Naz.). Чертежи воспроизведены по русскому изданию 1932 г. (под редакцией А. Н. Долгова). Из этого же издания взяты примечания (см. ниже) 11—18 и 20—23.
И. Б. Погребысский
ПРИМЕЧАНИЯ1
1 (К стр. 41). «Астрономический вестник» (Avviso astronomico) — так Галилей перевел на итальянский язык название написанного им по латыни «Звездного вестника» (см. I т. наст, изд.), где есть и заголовок «Nuncius astronomicus».
2 Относительно астрономических открытий Галилея см. «Звездный вестник» (I т. наст, изд.) и примечания к нему. Галилей не мог в свой тридцатикратного увеличения телескоп правильно определить причину впервые замеченного им изменения формы Сатурна и пришел к выводу, что эта планета состоит из трех смежных тел. Только примерно полвека спустя Гюйгенс с помощью более совершенного телескопа установил, что Сатурн окружен «кольцом».
3 (К стр. 42). Здесь Галилей вкратце говорит о своих астрономических открытиях и наблюдениях, сделанных после издания «Звездного вестника». Галилей придавал большое значение уточнению данных о движении открытых им спутников Юпитера («Медицейских звезд»), так как рассчитывал дать на этой основе достаточно точный метод определения долготы, т. е. решить проблему, имевшую тогда особое значение для мореплавания. Результаты наблюдений и вычисления, о которых здесь идет речь, сохранились, они приведены в IV т. Ed. Naz. Вопрос о природе солнечных пятен (и возможность доказать, наблюдая их, что Солнце вращается вокруг некоторой своей оси) был для Галилея не чисто астрономическим вопросом, а связывался с общими космологическими и философскими проблемами (см. «Диалог» в I т. наст, изд.). В первом издании «Рассуждения» Галилей не высказался определенно по этому вопросу: там отсутствовала последняя фраза (начинающаяся словами: «Продолжительные {424} наблюдения...»). Дело в том, что к этому времени астроном Шейнер, принадлежавший к ордену иезуитов, уже выпустил книгу о солнечных пятнах, в которой доказывал, что они наблюдаются с Земли при прохождении каких-то небольших планет, вращающихся вокруг Солнца. Галилей, оправившись после тяжелой для него зимы 1611—1612 гг., снова взялся за наблюдения и убедился в ошибочности гипотезы Шейнера уже тогда, когда первое издание «Рассуждения» было в печати. Поэтому вполне определенный вывод о природе пятен с ссылкой на «продолжительные наблюдения...» Галилей смог поместить только во втором издании «Рассуждения», а его работа, посвященная специально этому вопросу, появилась в 1613 г. (Delle Macchie Solari — см. V t. Ed. Naz.).
4 (К стр. 43). Алкиной (AlcinooV) — платоник, известный нам только по имени. Ему приписывался трактат, излагающий учение Платона и впервые напечатанный в Венеции в 1521 г. Теперь считается установленным, что этот трактат принадлежит Альбинусу (Albinus, последователь Платона, II в. н. э.).
5 (К стр. 44). Этим заканчивается вводная часть «Рассуждения». По поводу нее см. Введение к примечаниям.
6 «Весьма серьезным автором» — имеется в виду Франческо Буонамичи (Буонамико), автор обширного трактата «О движении». Буонамичи с 1560 г. в течение 43 лет читал лекции в Пизанском университете (сначала по логике, потом по философии). Его считали одним из наиболее видных и эрудированных представителей аристотелизма, современники высоко ставили его как ученого. Галилей слушал его лекции, будучи студентом.
7 Это заявление Галилея характерно для его методологии. Он стремится свести причины явлений «к внутренним и непосредственным принципам» — лишь после этого он переходит к последовательному выводу следствий, применяя и математические средства. Галилей имел основания считать свое исходное положение, соответствующее принципу возможных перемещений, более «внутренним и непосредственным», чем у Архимеда (последний исходит из постулируемых свойств жидкостей), в силу его общности (он сам плодотворно применял то же положение в своей «Механике») и, может быть, учитывая его связь с принципом невозможности perpetuum mobile (см. «Механику»).
8 (К стр. 46) Равные по удельному весу — у Галилея «egualmente gravi in specie» (примерно: «одинаково тяжелой породы»).
9 Последний абзац (от слов «Под моментом...») показывает, что Галилей учитывает здесь и направление. Итальянское momento происходит от латинского momentum, а одно из значений последнего: важность, значительность. Взятые в кавычки русские фразы являются переводом следующих обиходных выражений, в которых слово momento применяется в последнем смысле: «Questo ё ben negozio grave, ma l'altro e di poco momento»; «Noi consideriamo le cose leggiere, e trapassiamo quelle che son di momento». В том, что эти метафоры взяты из механики, Галилей, может быть и умышленно, ошибался. {425}
10 (К стр. 47). В «Проблемах механики» псевдо-Аристотеля (во времена Галилея это произведение считалось несомненно принадлежащим самому Аристотелю) действительно можно усмотреть зачаточную форму принципа виртуальных перемещений, но только в применении к выводу условий равновесия рычага. Стевин, в отличие от Галилея, полностью отвергал применимость такого положения в статике и считал соответствующие рассуждения в «Механических проблемах» ошибочными.
11 (К стр. 49). Пусть площадь основания призмы f', поверхность воды, окружающей призму f и площадь основания призматического сосуда F; очевидно, что F = f' + f.
Пусть далее объем части призмы, погруженной до нового уровня воды, υ', и объем воды, поднявшейся с первоначального до нового уровня, υ; изложенная теорема выражается, следовательно, так:
υ : υ' = f : (f + f'). |
(А. Д.) |
12 (К стр. 50). Если призма поднята на высоту h', а уровень воды опустился на высоту h, то при тех же обозначениях f и f', что и в примеч. 11, имеем, очевидно:
h : h' = f' : f. |
(А. Д.) |
13 (К стр. 51). Обозначим через G' и G абсолютный вес призмы и, соответственно, окружающей воды, через γ' и γ — удельный вес вещества призмы и, соответственно, воды. Изложенное рассуждение представится тогда в следующем виде.
По предположению γ > γ', следовательно, G : G' > υ : υ'; но υ : υ' = f : f' и мы знаем, что f : f' = h' : h.
Поэтому
G : G' > h : h'.
Отсюда вывод Галилея, что «момент» веса воды G и скорости (velocità) ее опускания больше «момента» веса призмы G' и медленности (tardività) ее поднятия. (А. Д.)
14 (К стр. 52). Пусть D, E, F — длины отрезков, удовлетворяющих пропорциям:
D : Е = γ' : γ; Е : F = υ' : υ''.
Ясно, что
D : F = γ' · υ' : γ'' · υ''.
Пусть, далее, для третьего тела С:
υ''' = υ' и γ''' = γ''.
Тогда
G' : G''' = γ' : γ''' = γ' : γ'' = D : Е;
G''' : G'' = υ''' : υ''' = υ' : υ'' = Е : F.
Отсюда G' : G'' = D : F и, следовательно, G' : G'' = γ'υ' : γ''υ''. {426}
Необходимо отметить, что Галилей, следуя как в данном случае, так и в последующих теории пропорций Евклида, вынужден был прибегать к довольно сложным доказательствам, излишним при современной трактовке пропорций. (А. Д.)
15 (К стр. 53). В дополнение к обозначениям предыдущих примечаний введем одно новое, именно обозначим объем GD заглавной буквой V.
По условию γ' : γ = FB : DF; но FB : DF = υ' : V; следовательно, γ' : γ = υ' : V; далее, υ' : υ = (υ' : V) · (V : υ), или на основании предыдущего равенства υ' : υ = (γ' : γ)(V : υ) = γ'V : γ · υ = G' : G (на основании леммы, см. примеч. 14).
Далее, очевидно, что
υ' : υ = f' : f = h : h' (на основании предыдущего, см. примеч. 13), откуда
h : h' = G' : G,
что указывает, по выражению Галилея, на равенство «моментов».
Заметим, что примененное в начале доказательства этой теоремы выражение «отношение объема BG к объему GD вместе с отношением объема GD к объему AF» и т. д., представляющее точный перевод соответствующего текста, имеет в виду «сложное отношение». То же относится к некоторым последующим доказательствам. (А. Д.)
16 Пусть g' — абсолютный вес воды, взятой в объеме призмы BG. Тогда
g' : G' = (υ' : V)(γ : γ'),
но
γ : γ' = V : υ',
поэтому
g' : G' = (υ' : V)(V : υ') = 1. |
(А. Д.) |
17 (К стр. 56). Этим замечанием оканчивается часть трактата Галилея, содержащая обоснование закона Архимеда методом возможных перемещений. Далее начинается полемическая по преимуществу часть трактата, которой полезно предпослать несколько кратких общих замечаний.
Полемика Галилея с аристотелианцем Буонамичи (Буонамико), которой открывается эта часть трактата, весьма интересна для характеристики взглядов современных Галилею перипатетиков и не требует комментариев. После этого Галилей переходит к «главному пункту» своего спора с аристотелианцами, к вопросу — какое значение имеет различие в форме тел по отношению к покою или движению их в жидкости, и доказывает, что последнее может обусловливать только быстроту или медленность движения тел, но не пребывание их в состоянии покоя или движения; в своих рассуждениях и примерах Галилей стоит на совершенно правильной точке зрения, что частицы жидкости обязательно будут перемещаться под влиянием малейшего усилия и что вязкость жидкости может только замедлить это перемещение, но не уничтожить его. Количественные соотношения быстроты и медленности опускания или подъема тел в жидкости, кое-где приводимые Галилеем (дерево, которое легче воды по удельному весу едва на два процента, будет стремиться подняться в ней «раз в тысячу слабее», чем стремится опуститься в ней золото), надо рассматривать только как {427} иллюстративные. Теоретическое и экспериментальное изучение сопротивления жидкостей перемещению в них тел разной формы и с различными скоростями представляет собой вообще весьма трудную задачу, которая во времена Галилея еще не могла быть серьезно поставлена по общему состоянию математических и механических познаний.
Обращаясь затем к факту плавания тонкой пластинки, более тяжелой по удельному весу, чем вода, Галилей подмечает, что она располагается ниже поверхности воды, что последняя образует по краям пластинки валики и что погруженной в воду оказывается не только пластинка, но и некоторый объем воздуха, как бы присоединившегося, или прилипшего, к пластинке. По этому поводу необходимо заметить, что Галилей правильно описывает как данное явление, так и влияние смачивания плавающей пластинки, а равно и «прилипание» воды к телу, извлекаемому из нее, но не дает ему простого объяснения, исходящего из наличия в жидкости поверхностного натяжения, вследствие которого, как известно из физики, поверхность жидкости является как бы растянутой упругой пленкой, стремящейся сократить свою площадь до возможного минимума, и которое обусловливает ряд таких явлений, как кривизна поверхности жидкости в сосудах и проч. Некоторое представление о поверхностном натяжении ко времени Галилея уже сложилось, и еще Леонардо да Винчи исследовал его силу; однако Галилей нигде здесь о нем не упоминает. Что же касается теории поверхностного натяжения, то она была установлена лишь много позже в работах Лапласа, а затем Гаусса.
По поводу самого выражения Галилея, что в случае плавания тяжелой пластинки мы имеем дело с присоединенным к ней воздухом или агрегатом из пластинки и воздуха (которое повторяется многократно в различных местах трактата), то его надо понимать скорее как способ описания явления, чем как объяснение физической сущности явления; во всяком случае в этом вопросе Галилей проявляет большую осторожность.
Следующий раздел трактата — о плавании в воде тел различной формы, более тяжелых но удельному весу, чем вода,— нуждается только в одном общем замечании: в целях упрощения геометрических исчислений Галилей пренебрегает наличием выпуклых бортиков воды, расположенных по периметру верхнего основания опущенного в воду тела, и представляет себе объем, заполненный воздухом, в виде призмы или цилиндра с тем же основанием; некоторые исчисления Галилея, могущие затруднить читателя, снабжены отдельными примечаниями.
Заключительная часть трактата посвящена полемике Галилея с аристотелианцами по тому же «главному пункту» и разбору спора между Аристотелем и Демокритом, в котором Галилей берет под свою защиту некоторые положения последнего. Она весьма интересна для характеристики как некоторых учений древних греческих философов, так и отдельных физических теорий, существовавших еще во времена Галилея; мы видим, как Галилей, защищая свою точку зрения, что только разница в удельном весе обусловливает движение тела в данной среде, вынужден оперировать четырьмя элементами древних, понятиями пустого и полного и т. д. (А. Д.).
18 «...la pulsione degli elementi». (А. Д.) {428}
19 (К стр. 74). Слова Галилея: «выходит, точно я хочу приписать воздуху как бы свойство магнита...» (come che io voglio, in un certo modo, dare una quasi virtu di calamita all'aria...) дали повод к неправильным толкованиям как при его жизни, так и позже: дело изображалось так, будто Галилей допускал подобное свойство воздуха. Опровергать это довелось уже самому Галилею и вот по какому поводу. Осенью 1612 г. Ноццолини (Nozzolini, Tolomeo, 1569—1643), в свое время преподававший в Пизе логику, физику и математику, а затем ставший, с 1606 г., священником, обратился к флорентийскому архиепископу с обширным письмом по поводу «Рассуждения» Галилея1.
Ноццолини - на стороне Галилея и достаточно энергично нападает на его противников, но его смущает, что Галилей приписывает воздуху «притягательную и магнитную силу», и это представляется ему весьма уязвимым положением. Письмо Ноццолини в копии дошло и до Галилея, который ответил на него достаточно пространно2. Галилей писал, что письмо Ноццолини ему «немало понравилось, так как написано человеком, который столько понимает и которого я с давних времен весьма уважаю; и оно тем больше доставило мне удовольствие, что в нем, с той свободой, которая всегда должна была бы сопутствовать истинному философствованию, одобряется то, с чем согласиться автор считает нужным, и порицается то, что автор отвергает». И дальше мы читаем: «Вы говорите, что я ввожу некую магнитную силу, благодаря чему воздух, прилегающий к эбеновой дощечке, поддерживает ее, не давая ей уйти под воду. По этому поводу следует вам сказать, что выражение «магнитная сила» принадлежит не мне, а одному важному дворянину, противнику моих взглядов и приверженцу моих оппонентов... И почему надо мне приписывать то, чего я не говорю? И почему надо подменять то, что я высказываю в ясных выражениях и достаточно пространно, каким-то словом, примененным только как метафора? Примененным, чтобы напомнить его тем, кто его ввел, дабы они знали, что я не считаю его верным, и дабы они могли в том убедиться путем сравнения со сказанным мною непосредственно перед этим»3.
20 (К стр. 82). Пусть h — высота валика воды AI и h' — высота тела OI; пусть далее υ' и g' — объем и соответственно вес тела IS, g — вес воды в объеме этого тела, V и G — объем и соответственнно вес тела ABSO.
Тогда имеем
h : h' = (g' – g) : g.
Отсюда:
(h + h') : h' = g' : g
и, обратно,
g : g' = h' : (h + h').
| {429} |
Но
h' : (h + h') = υ' : V = g : G
(если заменить объемы весом воды, взятой в тех же объемах). Из второй и последней пропорции имеем, следовательно, что
g' = G,
т. е. что вес тела IS равен весу воды, взятой в объеме тела AS. (А. Д.)
21 (К стр. 84). Обозначим соответственно объем, абсолютный и удельный вес тел А, В, С буквами υ', υ'', υ'''; g', g'', g'''; γ', γ'', γ'''; объем тела АС будет, очевидно, равен υ' + υ''', а вес g' + g'''; заметим далее, что υ'' = υ'''; и γ' = γ'''.
По условию
(υ' + υ''') : υ'' = γ'' : γ'
и по построению
g'' : g''' = γ'' : γ''' = γ'' : γ';
следовательно,
g'' : g''' = (υ' + υ''') : υ'' = (υ' + υ''') : υ'''.
Но
(υ' + υ''') : υ''' = (g' : g''') : g''',
откуда
g' : g''' = (g' : g''') : g'''
и, следовательно,
g' : g''' = g''. |
(А. Д.) |
22 (К стр. 85). Пусть h — высота велика DB, Н — высота конуса ABC или цилиндра ЕС, V — объем того же цилиндра, υ — объем цилиндра DC и υ' — объем конуса ABC, имеющего удельный вес γ'.
По условию
γ' : γ = h : |
1 3 |
H. |
Из чертежа видно, что υ : V = h : H,
V : υ' = H : |
1 3 |
H. |
Следовательно,
υ : υ' = h : |
1 3 |
H, |
откуда
υ : υ' = γ' : γ
и, согласно лемме, g' = g.
(А. Д.)
23 (К стр. 94). «Secundum quid».
| {430} |
Те, кто видели Галилея сразу после процесса 1633 г., могли считать его конченым человеком. И неудивительно: тяжек был удар, обрушившийся на семидесятилетнего, с подорванным здоровьем, старика. Из прославленного ученого, занимавшего почетное место при дворе своего бывшего ученика, великого герцога Тосканского, Галилей превратился в поднадзорного инквизиции, оставленного «под сильным подозрением в ереси». Он мог уже не бояться сожжения на костре, его не посадили в тюрьму, но его могли отправить туда в любую минуту, он должен был жить в указанном ему городе, доме, под наблюдением были все его связи с окружающим миром. И в начале тех месяцев, которые Галилей провел в Сиене, в доме архиепископа (после того как ему было разрешено оставить Рим и перед тем как он смог поселиться в Арчетри под Флоренцией), он не выходит из глубокого уныния. Но проходит несколько недель, и Галилей снова становится Галилеем. Такая упругость мысли и воли на восьмом десятке лет — явление поразительное. Вероятно, сказалась не только мощь гения: Галилей мог убедиться за эти несколько недель, что он не остался одинок, а запрет, наложенный на гелиоцентрическое учение, не мог отстранить Галилея от науки, от осуществления давних планов, задуманных еще до создания «Диалога». Действительно, начало работы над произведением, которое позже Галилей назвал «Беседами и математическими доказательствами, относящимся к двум новым наукам...» и которое он оценивал как свой главный труд, приходится на тот же 1633 г.
В письме к одному из своих друзей, Э. Диодати, от 7 марта 1634 г. Галилей сообщает, что, находясь в Сиене, он составил трактат из области механики, на новую {431} тему, и в нем немало любопытных и полезных соображений. Этот трактат, очевидно, был первой редакцией «Бесед» или стал их основой.
Конечно, в «Беседы» вошли многие результаты достаточно давнего происхождения. Законы падения тел в пустоте были открыты Галилеем еще в Падуанский период, т. е. до 1610 г. В «Беседы» вошла в качестве приложения и юношеская работа Галилея о центрах тяжести. Трудно указать годы, когда Галилей получил первые теоремы и формулы сопротивления материалов — в переписке Галилей почти не касался этих тем,— но и эти результаты вряд ли целиком получены тогда, когда писались «Беседы». Однако создание «Бесед» не было чисто литературным трудом. Галилей всегда стремился в познании природы дойти до «простых и непосредственных принципов». Он не удовлетворялся установлением и описанием фактов, что хотел ему поставить «в заслугу» Э. Мах, а искал их внутреннюю связь и сводил их в определенную систему.
Верно то, что в отличие, скажем, от Декарта, Галилей старался не увеличивать чрезмерно «объем» принципов — он ограничивал свои общие положения, сводя к минимуму гипотетическое.
В «Беседах», вникая в причины прочности материала, Галилей не может обойти проблему строения материи. И в этой связи, и в поисках математических средств для описания движения, Галилей должен говорить о неделимых, о континууме, об актуальной и потенциальной бесконечности. Здесь перед нами итоги давних и долгих размышлений. И везде, где гипотеза слишком обща для подлежащих объяснению фактов и выходит за пределы осязаемого и проверяемого, Галилей переходит к условным утверждениям. Он никогда не догматичен, он всегда проводит разграничительную линию между тем, что доказано и установлено, и тем, что проблемно и гипотетично. Но он ставит и нерешенные вопросы, он дает и неполные ответы: в последнем и главном своем труде великий ученый хочет рассказать обо всем, что ему удалось и не удалось сделать, и не касается только того, на чем лежит запрет церкви. То, что Галилею удалось привести в систему и изложить, пользуясь доступными ему математическими средствами, стало главным содержанием и определило название «Бесед». Все остальное вошло в форме отступлений, в разной мере связанных с основным текстом. Систематика Декарта раздражали эти отступления, он упрекал Галилея за то, что тот переходит к новому предмету, не исчерпав предыдущей темы. Можно понять, почему Декарт столь критичен: он-то был уверен, что им создана система, в которой все наблюдаемое в природе находит свое объяснение. Но система Декарта давно стала достоянием истории, а в «Беседах» Галилея и в наши дни слышен голос живой науки, и в этом их поучительность и привлекательность.
Сказанное, быть может, помогает оценить меру вдохновенного труда, положенного Галилеем на то, чтобы в 1634—1635 гг. создать «Беседы». Уже в первые месяцы 1635 г., продолжая литературную отделку и расширяя изложение (в пределах первых четырех «дней»), Галилей озабочен тем, как напечатать свою новую книгу. Тяготеющее над ним осуждение оказывается и в этом деле серьезной помехой. И в Венеции, и во Франции, и в Германии, и в Австрии возникают затруднения, и Галилей {432} не хочет рисковать рукописью. Но в мае 1636 г. через своего венецианского друга Миканцио он вступает в соглашение с приехавшим в Венецию представителем известной голландской издательской фирмы Эльзевиров — Людвигом Эльзевиром. Миканцио получил от Галилея «два первых Диалога» в июле 1636 г., в августе — продолжение, «две книги о движении», и в сентябре Л. Эльзевир увез все это в Лейден. В течение следующего года шло печатание, Галилей досылал дополнения к третьему и четвертому дню, тогда же он включил и свой трактат о центре тяжести тел с доказательствами и выводами, «найденными мною в возрасте 22 лет после двух лет изучения геометрии, и лучше, чтобы они не затерялись», как писал Галилей Диодати в декабре 1636 г. В январе 1638 г. уже был напечатан полный текст (т. е. первые четыре дня) «Бесед» и оставалось добавить титульный лист, посвящение и перечень главных тем. В июле 1638 г. книга вышла из печати, но в Риме первые экземпляры были получены лишь в конце года, а в Арчетри ослепший к тому времени автор смог взять ее в руки только в июне 1639 г.
История создания «Бесед» этим не заканчивается. Ее продолжение читатель найдет в примечаниях к «Посвящению», к пятому и шестому дню. Общая оценка этого произведения дана в «Предисловии» к нашему изданию академика А. Ю. Ишлинского и в статье профессора Б. Г. Кузнецова. В помещенных ниже «Введениях» к отдельным дням рассматривается их содержание.
Первый перевод «Бесед» на русский язык был сделан А. Сомовым. Он напечатан в «Журнале Главного управления путей сообщения и публичных зданий» за 1860—1861 гг. (тт. 31—34, отдел II): «Г. Галилей. Разговоры и математические доказательства о двух новых учениях в механике и движении» (первые два дня). Отдельной книгой на русском языке «Беседы» были изданы в серии «Классики естествознания» как первый том Собрания сочинений Галилея1 в переводе С. Н. Долгова, под редакцией, с предисловием и примечаниями А. Н. Долгова. Для настоящего издания перевод С. Н. Долгова был нами проверен и заново отредактирован на основе текста итальянского и латинского оригинала в Edizione Nazionale (перепечатка), т. VIII, Флоренция, 1933 г. Оттуда же взяты чертежи. В примечаниях нами использованы примечания А. Эттингена (A. Oettingen) к немецкому переводу «Бесед» в серии Ostwalds Klassiker и некоторые примечания А. Н. Долгова. Подробное оглавление, воспроизводимое в настоящем издании, составлено А. Н. Долговым.
День первый
1 (К стр. 111). Франциск де Ноайль (Noailles, 1584—1645) учился у Галилея частным образом в Падуе, слушал у него лекции по фортификации. В 1634 г., в звании советника французского короля Людовика XIII Ноайль был назначен послом в Рим, где от своего бывшего соученика Кастелли узнал о положении Галилея и неоднократно пытался хлопотать в его пользу. Единственное, чего ему удалось добиться {433} от Урбана VIII, было разрешение Галилею встретиться с Ноайлем, когда тот возвращался во Францию. Это произошло в октябре 1636 г., и тогда Галилей действительно преподнес Ноайлю рукопись «Бесед», по крайней мере — два первых дня. Но, как мы знаем, в Лейдене в это время «Беседы» уже печатались. Только в следующем году Галилей через Диодати договорился с Ноайлем относительно посвящения. Сохранилось письмо Ноайля, где он заявляет, что видеть свое имя на книге Галилея для него большая радость и честь и что в знак благодарности он готов выполнить любое пожелание ученого. Описанная в посвящении история с печатанием «Бесед» не соответствует фактам (см. «Введение»). Очевидно, она должна была отвести от Галилея обвинение в том, что он без разрешения выпустил «Беседы» в свет, сделав виновником их появления посла Франции — весьма влиятельной державы, которая тогда была главным союзником папы. Вообще Галилей всячески подчеркивает в «Посвящении» свою «благонадежность» — и тогда, когда он говорит, что смущен и напуган несчастной судьбой других своих сочинений («Диалог»!), и тогда, когда заявляет о том, что будет знакомить со своими трудами лиц, достаточно знающих трактуемые предметы. Все это было защитным маневром, как и выбор влиятельного французского сановника в качестве лица, которому посвящена книга.
2 (К стр. 113). Сохранившаяся переписка Галилея времени печатания «Бесед» позволяет с несомненностью заключить, что для предисловия «Читателям от издателей» Галилей сам указал все основные положения. Впрочем, достаточно вероятно и то, что весь текст предисловия принадлежит автору книги. Во всяком случае стремление подчеркнуть свою преданность религии достаточно явно. Галилей еще надеялся в то время на отмену тяготевшего над ним приговора.
3 (К стр. 114). Когда мы читаем о телескопе, что он «появился в наших краях», это означает, что телескоп появился в Голландии, так как предисловие написано от имени лейденских издателей. Теперь можно считать установленным, что первый телескоп был изготовлен в Италии (имя изобретателя неизвестно) около 1590 г., потом около 1605 г. он появляется в Голландии, и там налаживают производство телескопов. Эти первые телескопы изготовлялись с обыкновенными очковыми линзами и были низкого качества: они давали незначительное увеличение при весьма неясном изображении. Галилей действительно довел телескоп до большого совершенства по сравнению с первоначальной конструкцией и сделал из него инструмент, имеющий научное значение. См. по этому вопросу работы В. Ронки, в частности статью «Galileo, maestro di tecnica» (Luce e Immagini, Anno XVIII, N 2, Marzo — Aprile 1964).
В перечислении астрономических открытий Галилея снова упоминается «тройственное строение Сатурна» — это та ошибка в истолковании наблюдений, которая была обусловлена недостаточной разрешающей способностью телескопа Галилея и которую через четверть века после появления «Бесед» исправил Гюйгенс.
4 (К стр. 115). «Перечень (в оригинале — «таблица») главных тем» в Лейденском первоиздании 1638 г. заканчивается в этом месте. Вероятно, он был напечатан с каким-то отклонением от авторского текста, потому что в теме второго дня говорится о связности тел так, как будто о ней уже упоминалось и, кроме того, эта тема больше {434} соответствует первому дню, а тема первого дня — второму. О пятом и шестом днях см. соответствующие вводные примечания.
5 (К стр. 116). В первом дне «Бесед», как и в последующих днях, кроме шестого, три участника, имена которых нам знакомы по «Диалогу» (см. I том, примечания). Роли их несколько изменились. Сальвиати по-прежнему высказывает и доказывает мысли автора, но в соответствии с характером предмета он только изредка полемизирует, а чаще всего последовательно излагает доводы и математические доказательства. Сагредо не только внимательный и сочувственный слушатель, помогающий своими продуманными вопросами развитию темы,— его задача иной раз заключается в том, чтобы оговоркой или критическим замечанием указать на неполноту проведенного исследования или на неполную достоверность результата. В таких случаях надо считать и Сагредо полноправным выразителем взглядов Галилея. А Симпличио «Бесед» — это вовсе не ограниченный, узколобый, догматичный и не раз смешной перипатетик «Диалога». Симпличио и в «Беседах» знаток аристотелизма и слаб в математике, но он уже не сражается за авторитеты и искренне заинтересован в установлении истины. Поэтому он с сочувствием следит в меру сил за аргументацией Сальвиати и Сагредо и противопоставляет новым взглядам старые, проверяя обоснованность излагаемых в его присутствии построений.
Главной темой первого дня является не сопротивление материалов (выражаясь по-современному). В связи с проблемой подобия и сравнительной прочности больших и малых тел такая тема только ставится здесь. Собеседники быстро переходят к анализу общих причин связности тел, можно сказать — к первопричинам того, что тела сопротивляются разрушению при растяжении и изгибе (Галилей рассматривает два этих вида деформации). Излагая законы падения тел, Галилей считал неуместным, входить в обсуждение той первопричины, вследствие которой тела падают на Землю, здесь он занимает другую позицию. Ясно, что дело не в том, будто он вообще стремился снять вопрос «почему» и отвечать только на вопрос «как» — такой вывод делает Э. Мах. Видимо, о природе тяготения Галилей мог говорить только гипотетически, а причины связности он мог анализировать, в известной мере опираясь на данные опыта о строении тел и о размере той силы, которую он еще вынужден был приписывать «боязни пустоты».
Итак, анализ причин связности приводит собеседников к проблеме строения материи. Атомистические представления, развиваемые Сальвиати, заставляют снова задуматься над соотношением дискретного и сплошного, неделимых и континуума, а затем — конечного и бесконечного. Надо обойти или разрешить давние парадоксы, дошедшие от античности и бывшие предметом размышления схоластов. Не все здесь удалось Галилею, но встречаются поразительные догадки (о неприменимости «логики» конечных величин к бесконечным) и нигде нет абсолютизированных истин. Говоря о пустоте, Сальвиати попутно опровергает учение Аристотеля о падении тел в пустоте, отсюда — переход к сопротивлению среды, и опыты с маятником, о которых заходит речь, дают повод перейти к акустическим вопросам, к анализу музыкальных консонансов и диссонансов. Наконец, Сальвиати спохватывается: «Уже вечер, а о том {435} предмете, которым мы первоначально предполагали заняться, мы сказали очень мало, или, вернее, не сказали почти ничего». Только второй день дает последовательное изложение результатов, полученных Галилеем в «первой новой науке», касающейся сопротивления твердых тел разрушению. Первый день остается блестящим образом диалогизированного изложения как законченных (акустические исследования), так и незаконченных глав из того свода трудов, который был итогом жизни великого ученого и дошел до нас в его напечатанных произведениях не полностью.
6 (К стр. 117). Вступительные замечания Сальвиати и Сагредо (реальный Сагредо действительно был венецианцем) как бы дают тот основной тон, по которому настраивается звучание всего произведения: создается «в области механики» новая наука и бесполезно обращаться при решении ее задач за помощью к древним, которые не знали ее, а надо использовать тот опыт, который есть у людей практики. Не случайно, что при этом речь заходит о венецианском арсенале. Первоначально слово «арсенал» означало мастерские (верфь) для постройки и ремонта военных судов, затем и для изготовления вооружения для судов, а еще позже — вооружения всякого рода. Во времена Галилея арсенал в Венеции, основанный еще в начале XII в., был крупнейшим в Италии и, вероятно, в мире. Сооруженное на его территории в 1579—1585 гг. здание новых мастерских имело длину свыше 300 м, а ширину — около 20 м.
7 (К стр. 118). Здесь впервые высказано (и ниже обосновано) положение о различии условий геометрического и механического подобия, т. е. впервые поставлена (и в определенном смысле решается) проблема механического подобия. Предварительно Галилей считает нужным отвести ссылки на «несовершенство материи», как причину снижения прочности машин при увеличении их размеров. По Аристотелю, земная материя, состоящая из четырех стихий (элементов), несовершенна: преходяща, тленна и т. п. в отличие от идеальной «пятой сущности», из которой состоят небесные тела.
8 (К стр. 120). Приводим комментарии А. Н. Долгова к этому месту: Если мы обратимся к последующему тексту, то найдем положение: «Утверждаю, что наибольшая длина цилиндра, при которой он способен выдерживать, не ломаясь, собственный вес в том случае, если он имеет точку опоры посредине или на обоих концах, превышает в два раза длину такого же цилиндра, вделанного в стену одним концом и, следовательно, имеющего точку опоры лишь на одном конце». Отсюда, ясно, что Галилей признает момент, сгибающий рассматриваемую им мраморную колонну в наиболее опасном среднем сечении ее, равным в обоих описанных им случаях, т. е. при наличии как двух крайних опор, так и одной средней. Кажущееся противоречие с приводимым Галилеем объяснением, что колонна сломалась после постановки средней опоры благодаря осадке одной из крайних, легко объяснить, представив себе, как это и должно было иметь место в действительности, что крайние опоры располагались не у самых концов ее, а несколько ближе к середине. В этом случае момент для среднего сечения балки был меньше, когда балка покоилась на двух крайних опорах, чем когда она оказалась лежащей на крайней и средней опорах.
8а (К стр. 120). Галилей имеет в виду доказанный им ниже («день Второй») {436} результат: момент сопротивления стержня круглого сечения пропорционален третьей степени его диаметра.
9 (К стр. 120). «Наш Академик» — для собеседников это Галилей. Сальвиати здесь формулирует научный идеал Галилея: доказывать истинность положений, исходя «из их первоначальных и бесспорных основ» (da i loro primarii e indubitati fondamenti). Об этом Галилей не раз говорит в своей переписке, та же формулировка встречается и в его сочинении «Рассуждение о телах, пребывающих в воде».
10 (К стр. 121). Отсюда начинается тот анализ причин «связности» тел, который потребует затем изложения взглядов Галилея на строение материи. Объяснение прочности тел волокнистого строения, излагаемое далее Сальвиати, вполне основательно.
11 (К стр. 123). И теперь одно из значений итальянского слова susta — толстый канат (Suste — форма множественного числа).
12 (К стр. 124). Сразу после этого Галилей сам поставит под сомнение данное здесь объяснение. Всякий раз, когда он вводит «пресловутую (decantata) боязнь пустоты», он делает оговорки и не скрывает от читателя, что не считает вопрос исчерпанным.
13 (К стр. 125). Опровержение учения Аристотеля, что в пустоте движение совершается мгновенно, было одной из необходимых предпосылок новой механики Галилея. Анализ опыта, данный Сагредо, важен для третьего и четвертого дня «Бесед».
14 (К стр. 126). Вряд ли Галилей был удовлетворен этим объяснением, раз его излагает Симпличио, с которым, за неимением лучшего, не без иронии соглашается Сагредо.
15 (К стр. 126). Шутливое пожелание Сальвиати напоминает о языческом поверье, что у каждого человека есть свой добрый демон (отсюда ангел-хранитель христианской религии).
16 Имеются в виду соображения, изложенные в «Рассуждении о телах, пребывающих в воде».
17 (К стр. 127). Так как ниже мы находим, что атмосферное давление («сопротивление пустоте») Галилей определяет довольно точно, около 1 кг/см2, то, следовательно, здесь он определяет разрывающее усилие для мрамора как равное примерно 5 кг/см2. Это отличается от истинной величины (около 20 кг/см2) настолько, что не может быть объяснено неточностью измерительных средств того времени. Поэтому высказывалось предположение, что в данном случае Галилей не ставил соответствующих опытов: «Основу его исследований, вероятно, составляли не эксперименты, а наблюдения» (С. А. Бернштейн, Очерки по истории строительной техники, М., 1957, стр. 18).
18 (К стр. 130). Высота подъема воды во всасывающих насосах (конечно, не с трубами «толщиною не более соломинки» — см. стр. 130,— таких насосных труб не делали, а то Галилей заметил бы добавочный эффект капиллярности), по Галилею, равна «восемнадцати локтям», а так как она реально близка к 10 м, то отсюда следует, что в «локте» Галилея несколько меньше 50 см. Приходится на это ссылаться, так как итальянское слово braccio обозначало в разные времена и в разных итальянских {437} государствах разную длину. Нельзя согласиться с С. А. Бернштейном (см. примеч. 17), который принимает braccio » 119 см. А. Н. Долгов, считающий «локоть» = 45 см у прав, указывая на этом основании, что оценка Галилеем временного сопротивления меди разрыву близка к истине.
19 См. стр. 126, где речь идет о золоте, получаемом из Испании «для оплаты военных расходов». Под властью или контролем Испании в то время была значительная часть Италии.
20 (К стр. 131). Галилей сам оговаривает, что он не может дать ясную схему действия этих малых пустот. Безусловно, он строго отличал это действие от силы сопротивления пустоте («в большом»), которую он смог измерить. Заметим также, что термин «момент» применяется Галилеем часто, но не всегда в одном и том же строго определенном значении. Не раз он обозначает произведение силы (в современном смысле; обычно силой является вес) на путь, проходимый точкою ее приложения, или па скорость перемещения этой точки (по направлению силы). См. определения момента в «Механике» (этот том, стр. 10—11) и в «Рассуждении о телах, пребывающих в воде» (этот том, стр. 46). Ср. с употреблением этого термина ниже, на стр. 175 и 180. Иной раз «момент» у Галилея является синонимом импульса (impeto), а последний термин у Галилея не определяется и соответствует (без определенной количественной характеристики!) то количеству движения, то живой силе, то силе, то просто побуждению к движению, действию.
21 (К стр. 132). Гуеварa (Giovanni di Guevara, 1561—1641) — видный прелат католической церкви, с 1627 г. епископ. К Галилею относился доброжелательно. В свое время, когда ему было поручено прорецензировать книгу Галилея «Пробирщик», он дал похвальный отзыв и тем помог ее напечатать. Гуевара встречался с Галилеем и был с ним в переписке, в частности, просил Галилея разъяснить ему некоторые трудные места в «Механических проблемах» псевдо-Аристотеля, к которым составлял комментарий. Издав этот комментарий (там содержатся те соображения, о которых упоминает Сальвиати), Гуевара послал его Галилею.
Проблема, о которой идет речь здесь, в средневековой литературе называлась «колесом Аристотеля» и формулировалась так: почему при совместном качении двух концентрических кругов больший проходит ту же линию, что и меньший, тогда как при независимом качении проходимые ими за один оборот линии относятся как их радиусы? Получить ответ с помощью (выработанных много позже) кинематических представлений не представляет труда: мгновенный центр вращения рассматриваемой плоской фигуры находится в точке ее соприкосновения с нижней горизонталью, и, следовательно, низшая точка малого круга обладает в каждый момент отличной от нуля скоростью, иными словами — малый круг не просто катится по соответствующей горизонтали, но одновременно скользит вдоль нее. Галилей опровергал аргументами Сальвиати предположение Сагредо, что малый круг не только катится (по линии СЕ), но и скользит по ней, так как не учитывал разницы в порядках малости бесконечно малых путей, проходимых низшими точками большого и малого круга.
22 (К стр. 135). См. примеч. 21. {438}
23 (К стр. 136), Еще одно заявление, рассчитанное на то, что оно дойдет до папского престола.
24 (К стр. 138). Ненадежность этих парадоксальных выводов понимал и сам Галилей — это видно из следующей затем реплики Сагредо.— Для разъяснения сути дела надо, как указал, например, переводчик «Бесед» на немецкий язык Эттинген (см. Galilei, Unterredungen, Ostwalds Klassiker, N 11, L., 1890, стр. 130, примеч. 3), учесть порядок бесконечно малых, входящих в расчет: кольцевая полоса имеет площадь, равную 2πRh, где R — конечно, h — бесконечно мало, а площадь круга, стягивающегося в точку, равна πr2, где r — бесконечно мало, и равенство этих двух бесконечно малых величин доказывает, что h — малая величина второго порядка относительно г. Аналогичные соображения применимы к соотношению между «кольцеобразной полосой» и «кольцевой бритвой».
25 (К стр. 139). Валерио, Лука (Valerio Luca, 1552—1618), выдающийся математик, с 1600 г. профессор математики и греческого языка в Риме. В свое время после знакомства с рукописью его работы о центрах тяжести тел, упоминаемой в тексте (она вышла из печати только в 1604 г. в Риме, 2-е изд.— Болонья, 1661), молодой Галилей отказался о г опубликования своей работы на ту же тему и только в «Беседах» дал ее в виде приложения. Галилей был очень высокого мнения о математическом даровании Л. Валерио и сохранил с ним добрые отношения, хотя Валерио был противником системы Коперника и в 1616 г. вышел из состава Accademia dei Lincei (принят туда в 1612 г.), так как большинство ее членов высказывалось в пользу гелиоцентризма.
Валерио опубликовал еще книгу Quadratura parabolae per simplex falsum (Рим., 1606). Он один из предтеч анализа бесконечно малых.
26 Галилей снова «воздает должное» учению церкви. Провозглашаемый им здесь примат «откровения» над догадками науки стоит в резком противоречии с его мировоззрением, как оно выражено в «Пробирщике», в «Диалоге», в основном тексте «Бесед». Конечно, и здесь перед нами только тактический ход — одна из деклараций, которые должны были, на худой конец, избавить «Беседы» и их автора от новых преследований, а при благоприятных обстоятельствах (Галилей высказывал такие надежды) дать основание для пересмотра приговора.
27 (К стр. 141). Эти рассуждения и пример, показывающий, говоря современным языком, что множество квадратов равно мощно с множеством всех натуральных чисел, замечательны. Дальше Галилея по этому пути пошел, спустя два с половиной века, только основатель теории множество Георг Кантор.
28 (К стр. 142). Конечно, Сагредо исходит в своем замечании из смешения разных понятий: плотности множества квадратных чисел в натуральном ряде и величины чисел. Трудно объяснить, почему с ним соглашается Сальвиати — Галилей. Может быть, Галилей хотел привести возможно больше «парадоксов бесконечного», даже таких, несостоятельность которых он видел пли подозревал.
29 (К стр. 145). Два средних пропорциональных (с, d) между двумя данными числами {439} (а, b) удовлетворяют условию:
|
a c |
= |
c d |
= |
d b |
между двумя кубами целых чисел р13, р23 всегда можно вставить два (целых) средних пропорциональных:
|
р13 р12 р2 |
= |
р12 р2 р1 р22 |
= |
р1 р22 р23 |
Вывод, что «нет другого бесконечного числа, кроме единицы», оказывается совершенно неожиданным, но вряд ли можно усмотреть в нем какой-либо мистицизм: он служит только обоснованием заключительного положения, разграничивающего бесконечное и конечное.
30 (К стр. 147). Эттинген в своих примечаниях (см., изд. цит. в примеч. 24, стр. 131), видимо, первый отметил, что Галилей здесь описывает гиперболическую систему окружностей. На бесконечной прямой соотносятся друг другу пара фиксированных точек А, В и пара переменных точек C, Е так, что они образуют гармоническую четверку. Когда две точки совпадают с В, другие две совпадают с А. Средняя точка О соответствует единственной бесконечно удаленной точке прямой АВ (рассматривается проективная плоскость). В таком истолковании, конечно, не приходится говорить о сопротивлении, оказываемом природой превращению конечной величины в бесконечную.
31 (К стр. 148). Кавальери, Бонавентура (Cavalieri Bonaventura, 1598—1647) — выдающийся математик, ученик Бенедетто Кастелли, который познакомил его с Галилеем. В течение многих лет переписывался с Галилеем, высоко ценившим его способности. В свою книгу о зеркалах и линзах «Specchio Ustorio»1 (1632) Кавальери включил доказательство того, что траектория брошенного тела (в пустоте) — парабола, это могло лишить Галилея приоритета на открытие и вызвало его негодование. Принесенные Кавальери извинения и старания загладить этот поступок смягчили Галилея и восстановили добрые отношения между ними. Идеи главного произведения Кавальери «Геометрия неделимых» (Geometria indivisibilibus continuorum nova quaedam ratione promota, 1635; имеется русский перевод) тоже были предметом обсуждения в его переписке с Галилеем. Вивиани имел достаточно оснований в своей биографии Галилея назвать Кавальери в числе тех «пяти знаменитых публичных лекторов в Риме, Пизе и Болонье», которые были учениками Галилея и стали профессорами математики.
32 (К стр. 150). Впервые скорость света была определена астрономическими методами (по затмениям спутников Юпитера, открытых Галилеем, Ремером, в 1675—1676 гг.; по явлению аберрации света — Брадлеем, в 1728 г.). Измерительные средства, доступные Галилею, не могли привести к цели. Но заключительное замечание показывает, что Галилей, вопреки не раз высказывавшемуся мнению, считал скорость света конечной. Его ссылка на характер свечения молнии, разумеется, не была убедительна и в то время. {440}
33 (К стр. 156). Эти слова Сальвиати напоминают читателю, что все изложенные выше соображения о бесконечном и о неделимых не являются бесспорной истиной для автора. «Антидогматичность» Галилея была столь же важна для становления новой науки, как и его открытия.
34 (К стр. 158). Еще раз приходится оговорить, что многие доказательства Галилея представляются нам громоздкими, так как он «для строгости» оперирует отношениями только однородных величин, алгебраическую выкладку заменяет геометрическим построением и все результаты, промежуточные и окончательный, записывает в виде пропорций. Иной раз его геометрические доказательства, как правило изящные, ведут к результату кратчайшим путем, но гораздо чаще они растянуты по сравнению с изложением на языке современной алгебры. Знаменитые математики Buem (старший современник Галилея) и Ферма (младший современник Галилея) соблюдали жесткое требование однородности, переход к современному алгебраическому языку осуществлен Декартом (1596—1650), новая символика становится общеупотребительной уже после смерти Галилея, в течение второй половины XVII в.
Читателю, вероятно, легче следить за мыслью Галилея, записывая и проверяя его утверждения привычным для нас способом. Например, последнее утверждение и его доказательство можно записать так:
Дано: V1 = π r12 h1 = π r22 h2 = V2. Поэтому
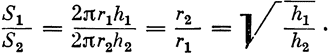
Для положения, которое Сальвиати формулирует и доказывает ниже (см. стр. 160), соответствующая запись такова:
Дано: S1 = 2π r1 h1 = 2π r2 h2 = S2. Поэтому
|
V1 V2 |
= |
π r12 h1 π r22 h2 |
= |
r1 r2 |
= |
h2 h1 |
. |
35 (К стр. 159). Галилей всякий раз дает понять читателю, что он считает гипотезой, пусть весьма правдоподобной, и четко разграничивает гипотетичное и точно установленное.
36 (К стр. 161). Иоганн Сакробоско (латинизированное имя Джона Голивуда, или Голибуша, ум. в 1256 г.) — математик и астроном, профессор Парижского университета. В тексте упоминается наиболее популярное его произведение «De sphaera mundi»1 — изложение сферической астрономии, следовавшее главным образом «Альмагесту» Птолемея. В течение столетий оно было обязательным предметом изучения в средневековых университетах и к нему составлялись комментарии. Известно около 60 печатных изданий «Сферы», с 1472 г. до конца XVII ст. Галилей, занимая кафедру в Падуанском университете, тоже читал курс лекций по «Сфере» Сакробоско. {441}
37 (К стр. 162). «Сочетая и переставляя» (componendo e permutando) — математические термины того времени.
Переход от пропорции
|
a b |
= |
c d |
к пропорции |
a + b b |
= |
c + d d |
назывался сочетанием (композицией), переход от
|
a b |
= |
c d |
к |
a c |
= |
b d |
назывался перестановкой.
38 После слов: «весьма тонкое» Галилей добавил в экземпляре Лейденского издания (и указал на это добавление посещавшему его в Арчетри священнику Клементе Сеттини) следующее: «и на первый взгляд содержащее как бы противоречие; ибо то, что многоугольник с большим числом сторон больше изопериметричного с ним многоугольника с меньшим числом сторон, связано с тем, что описанный многоугольник с большим числом сторон меньше описанного с меньшим числом сторон». Есть еще три добавления или поправки к первому дню, дошедшие до нас через Сеттини (род. 1612 г.; преподавал частным образом математику во Флоренции, и его учеником был Вивиани; его привлекали в 1640—1641 гг. к церковному суду как сторонника и последователя Галилея и переместили в Сицилию, после чего его след теряется). Они будут приведены в соответствующих местах.
39 (К стр. 164). В ходу были выражения: аргумент ad hominem, т. е. «к человеку», субъективный, с учетом чувств и взглядов оппонента, и аргумент ad rem, т. е «к предмету», объективный, по сути предмета спора.
40 (К стр. 165). В этом месте Галилей (см. примеч. 38) вместо: «следовательно, выходит, что более тяжелое тело движется с меньшей скоростью, чем более легкое» вписал: «следовательно, выходит, что составное тело (которое тяжелее одного первого) будет двигаться медленнее, нежели одно первое, которое, однако, легче».
Слово «градус» в выражении «скорость в восемь градусов» и во многих других сходных случаях обозначает какую-то условную единицу той величины, о которой в данном месте идет речь.
По сути остроумного рассуждения Галилея, которое совершенно обескураживает Симпличио (см. следующую реплику), надо сказать, что в наши дни оно выглядит не безупречным. Симпличио мог бы возразить, опираясь на аддитивность весовых масс, что всякая связь между двумя телами, заставляющая их двигаться совместно, делает из них одно тело, вес которого равен сумме весов слагаемых, и противоречия (логического) здесь нельзя получить.
41 (К стр. 166). Обращаем внимание на то, что пока, в соответствии с постановкой вопроса у Аристотеля, считается доказанным «одинаковость» падения только тел одинакового удельного веса. Общее положение будет доказано ниже.
42 (К стр. 169). Вместо слов: «тогда как другие (например, свинцовый шарик) падают в воздухе со скоростью приблизительно в два раза большей той, с которой они тонут в воде», Галилей (см. примеч. 38) вписал: «Из этого опыта вытекает, что плотность воды превышает плотность воздуха более чем в тысячу раз. Однако другие тела (например, свинцовый шарик) проходят в воде те же десять локтей в течение такого, примерно, времени, которое лишь в два с небольшим раза превышает время, необходимое {442} им для того, чтобы пройти такое же пространство в воздухе. Из этого второго опыта мы должны заключить, что плотность воды лишь немногим превышает удвоенную плотность воздуха».
43 Это упоминание об опытах, которые, видимо, доказывают возможность насильственного создания пустоты, показывает, что Галилей уже был близок к тому, чтобы отвергнуть «пресловутую боязнь пустоты», о которой шла речь выше.
44 (К стр. 171). «Трактат нашего Академика» — это «Рассуждение о телах, пребывающих в воде...» Галилей еще раз возвращается к явлениям, истолковать которые он не мог, отстаивая, с одной стороны то, что вода не оказывает сопротивления разделению, и не располагая, с другой стороны, представлением о поверхностном натяжении жидкостей.
45 (К стр. 172). Сальвиати, рупор Галилея, действительно избегает слова «антипатия», так как учение о «симпатиях» и «антипатиях» различных элементов в средневековой физике, физике качеств, широко применялось для объяснения различных явлений, с точки зрения Галилея ничего не объясняя по сути. Отсюда антипатия Сальвиати к «антипатии», и когда он говорит, что «пусть наши сомнения будут разрешены так, как предлагает синьор Симпличио», это надо понимать, как отказ от поисков настоящего объяснения.
45а (К стр. 173). Галилей допускает ошибку в последнем рассуждении: только из того, что постоянно отношение весов, нет никаких оснований сделать вывод, что постоянным должно быть отношение проходимых при падении путей.
46 (К стр. 174). Этот «качественный» анализ действия сопротивления среды превосходен. Попытка Галилея, излагаемая ниже, ввести количественную оценку силы сопротивления среды неудачна. Галилей, правда, здесь, в отличие от предыдущей части рассуждения, прибегает к несколько условным формулировкам. См. также ниже стр. 185 и сл. Проблему количественного расчета сопротивления среды нельзя считать решенной и в наше время.
47 (К стр. 176). Симпличио опять выступает как представитель средневековой физики качеств. Легкость рассматривается как особое свойство, противоположное тяжести; легкие элементы поднимаются вверх (огонь, воздух), тяжелые опускаются вниз (земля, вода); тела, состоящие из смеси этих элементов, легки или тяжелы в зависимости от того, что преобладает в их составе.
48 (К стр. 180). Здесь Галилей добавил (см. примеч. 38): «Сагр. Действительно остроумное рассуждение, кажущееся даже чудесным, так как оно заключает в себе разрешение одной проблемы, сводящейся, коротко говоря, к установлению способа находить вес тела, который оно имеет в пустоте, взвешивая его не в пустоте, а в воздушной среде. Объяснение таково. Воздух отнимает от абсолютного веса всякого тяжелого тела, помещающегося в нем, такой вес, какой имеет объем воздуха, равный объему этого тела. Поэтому, если мы сможем прибавить к этому телу столько воздуха, сколько его содержится в объеме этого тела, и притом не увеличивая объема последнего, то при взвешивании этого тела мы получим его абсолютный вес, т. е. такой, какой оно имеет в пустоте; действительно, мы прибавляем тот вес, который был отнят у тела {443} окружающей воздушной средой, не увеличивая его объема. Возьмем пустую бутылку, содержащую в себе естественный воздух; если мы, не выпуская этого воздуха, впрыснем в бутылку некоторое количество воды, то воздух, естественно, должен будет сжаться и занять меньший объем, дабы дать место впрыснутой воде; ясно также, что уменьшение объема сжатого воздуха будет равно объему введенной в бутылку воды. Если теперь мы взвесим в воздухе устроенный таким образом сосуд с его содержимым, то понятно, что вес воды будет сопровождаться и весом заключенного воздуха; частью общего веса будет вес воды вместе с весом соответствующего объема воздуха, т. е. тот самый вес, который вода имела бы в пустоте. Взвесим сначала весь сосуд и заметим общий его вес, затем дадим выход сжатому воздуху и взвесим остаток, который будет иметь меньший вес вследствие выхода наружу части воздуха; найдя разницу между результатами первого и второго взвешивания, мы получим вес сжатого воздуха, который занимал объем, равный объему воды; взяв затем вес одной воды и прибавив к нему найденный нами вес сжатого воздуха, мы получим тот самый вес, какой эта вода имела бы в пустоте. Для того чтобы узнать, как велик вес воды, надо, очевидно, вылить воду из сосуда и, взвесив его пустым, вычесть найденный вес из определенного ранее веса сосуда вместе с водой; ясно, что разница и будет весом одной воды в воздухе».
49 (К стр. 182). И здесь, и ниже Галилей утверждает, что колебания маятника изохронны (это приближенно верно для достаточно малых углов отклонения) при любой амплитуде. Высказывалось мнение, что нарушение изохронизма можно заметить при сравнении качаний с амплитудой 50—60° с качаниями амплитуды 5—10°, даже измеряя время ударами пульса. Отсюда делали вывод, что в данном случае Галилей, который не мог прибегнуть к теоретическому анализу, не предпринял тщательного экспериментального исследования. Однако этому противоречит рассказ Вивиани, ученика и первого биографа Галилея. В 1659 г. по поручению принца Леопольдо Медичи Вивиани в форме письма к принцу изложил историю работ Галилея над созданием маятниковых часов. Целью Вивиани и Леопольда Медичи было отстоять в этом вопросе приоритет Галилея: к тому времени над маятниковыми часами работали вне Италии, и в 1658 г. была напечатана работа Гюйгенса о них. Мы приведем ту часть письма Вивиани, которая касается колебаний маятника (письмо целиком опубликовано в XIX томе Edizione Nazionale, 1938, стр. 648—659; приводимый нами отрывок см. на стр. 648—649). «В 1583 г., имея около двадцати лет от роду, Галилей находился в Пизе, где, следуя совету отца, изучал философию и медицину. Однажды, находясь в соборе этого города, он, со свойственной ему любознательностью и смекалкой, решил наблюдать за движением люстры, подвешенной к самому верху, — не окажется ли продолжительность ее размахов, как вдоль больших дуг, так и вдоль средних н малых, одинаковой; ибо ему казалось, что продолжительность прохождения большой дуги может сократиться за счет большей скорости, с которой, как он видел, движется люстра на более высоких и наклонных участках. И пока люстра размеренно двигалась, он сделал грубую прикидку — его обычное выражение — того, как происходит ее движение взад и вперед, с помощью биений собственного пульса, а {444} также темпа музыки, в которой он тогда уже был искушен с немалою от того для себя пользой. И ему на основании таких подсчетов показалось, что он не заблуждался, подсчитав, что времена колебаний одинаковы, но не удовлетворенный этим, вернувшись домой, он, чтобы надежнее в этом удостовериться, решил сделать следующее.
Он привязал два свинцовых шара на нитях совершенно одинаковой длины так, чтобы они могли свободно раскачиваться... и, отклоняя их от вертикали на разное число градусов, например один шар на 30, другой на 10, он отпускал их в одно и то же мгновение; с помощью товарища он наблюдал, что пока один маятник делал такое-то число колебаний по большим дугам, другой делал в точности столько же по малым дугам.
Сверх того, он сделал два сходных маятника, только достаточно разной длины. Он наблюдал, что пока малый маятник делал какое-то число колебаний, например 300 по большим дугам, большой за то же время делал всегда одно и то же число колебаний, скажем 40, как по своим большим дугам, так и по совсем маленьким, и повторив это несколько раз..., он заключил отсюда, что вполне одинакова продолжительность размахов одного и того же маятника, будут ли они весьма велики или весьма малы, и что почти нет при этом заметных различий, каковые надо приписать помехе со стороны воздуха, который больше противится быстрее движущемуся тяжелому телу, чем медленнее движущемуся.
Он видел также, что ни различие в абсолютном весе, ни разный удельный вес шаров не вызывали заметного изменения — все шары, лишь бы они были на нитях равной длины от их центров до точек подвеса, сохраняли достаточно постоянно равенство (времени) прохождения по всяким дугам; лишь бы не был взят легчайший материал, вроде пробки, движению которого в воздухе... легче препятствовать, так что оно быстрее сводится к покою». Нет оснований не доверят рассказу Вивиани. Из него, кстати, следует, что на качаниях люстры Пизанского собора Галилей не подметил изохронизма, а проверял, верна ли его, так сказать, теоретическая догадка об изохронности колебаний маятника. Мы должны признать также, что Галилей подверг этот вопрос тщательному экспериментальному исследованию. Возможно, он не заметил чувствительных нарушений изохронизма при больших отклонениях, потому что проводил наблюдения над большими сериями затухающих колебаний,— сериями, в которых должно было сказаться преобладание средних и малых отклонений.
50 (К стр. 185). Ceteris paribus (лат.) — при прочих равных условиях.
51 (К стр. 186). Полуторное отношение — отношение величин в степени 3/2.
Аналогично этому в математике того времени говорили о двойном отношении (= отношение вторых степеней) и т. п. Галилей пользуется этими терминами наряду с привычными нам: отношение квадратов, отношение кубов и т. п.
52 (К стр. 187). Подразумевается: при заданном объеме.
53 (К стр. 188). Обращаем внимание читателя на то, что слово «ускорение» здесь и везде в тексте «Бесед» обозначает процесс, а не величину, не «производную от скорости по времени». Во избежание двусмысленности можно было бы переводить {445} ассеlerazione Галилея словом «убыстрение», если бы последнее было общеупотребительным.
54 Колубрина (colubrina) — «змейка» — название пушки того времени с удлиненным стволом.
55 (К стр. 190). Последняя формулировка, как известно, не точна. Галилей еще вернется к этому вопросу (см. стр. 391 и примеч. 36 к Дню третьему).
56 Указанный здесь закон (при отсутствии сопротивления среды) равносилен такому: Т (время колебания маятника) пропорционально √l (l — длина маятника).
Формулу Т = 2π √l/g (g — ускорение силы тяжести) вывел (теоретически) Гюйгенс.
Как получил Галилей свой результат, из текста «Бесед» не видно. В письме Вивиани (см. примеч. 49) мы читаем, правда: «Руководствуясь геометрией и своей новой наукой о движении, он нашел, что длины маятников находятся в двойном отношении по сравнению с отношением времен одинакового числа их колебаний» (стр. 650). Стало быть, к этому результату Галилей пришел теоретически. Но путь, которым он шел, не указан и здесь.
57 (К стр. 190). Галилей попутно опровергает одну из теорий средневековой физики, согласно которой движение поддерживается средой, в которой движется тело.
58 (К стр. 192). Здесь совершенно отчетливо высказано положение, что данному телу (маятнику) свойственна определенная частота колебаний. Относительно того, в какой мере ново то, что сказано тут и ниже о колебаниях и о звучании тел, см. ниже примеч. 60.
59 Кимвал — древний восточный ударный инструмент (две прикрепляемые к рукам металлические тарелки, которыми ударяли друг о друга); в тексте идет речь о струнном кимвале (его сейчас принято называть цимбалом) — музыкальном инструменте в форме ящика с натянутыми струнами, по которым ударяют молоточками. Цитра — инструмент типа цимбала, отличается от последнего тем, что число струн в ней меньше и играют на цитре пальцами или смычком (смычковая цитра).
Из употребляемых Галилеем музыкальных терминов требуют пояснения еще два: диапазон у Галилея, как и в древнегреческой литературе, обозначает то же, что октава; диапента (или диапенте) обозначает то же, что квинта.
60 (К стр. 199). То, что сказано о колебаниях, музыкальных тонах и звучании струн в конце Первого дня, было, ко времени опубликования «Бесед», наиболее ярким и полным изложением фактов и закономерностей в области акустики и теории колебаний. Нас естественно, интересует, что было известно до Галилея и что было открыто им самим — не ради решения приоритетных вопросов, а для того чтобы иметь более точное и полное представление об эпохе становления современной физики. В связи с этим придется дать обширную и все же не исчерпывающую справку: Сальвиати и Сагредо ни на кого по имени не ссылаются, но обсуждают проблемы, которыми много занималась и античная наука (от нее мало что дошло), и средневековая {446} наука (о ней наши сведения явно не полны), и старшие и младшие современники Галилея1.
У нескольких дошедших до нас древних авторов (среди них — Аристотель, Евклид, Птолемей) звук связывался с колебательным движением тел. Заодно указывалось, что более высокому тону отвечает большая частота колебаний, сила звука («громкость») связывалась с величиной или интенсивностью движений звучащего тела, все это — без формулировки каких-либо количественных зависимостей. Так обстоит дело у Боэция (ум. в 524 г.), который и в математике, и в акустике (музыке, согласно терминологии того времени) был передаточным звеном между древностью и ранним средневековьем. Более четкие утверждения высказывались о звучании струн. Пифагору приписывали открытие того, что высоты тонов (очевидно, основных) двух струн находятся в отношении, обратном отношению их длин (при прочих равных условиях) и что высота тона звучащей струны зависит не только от ее длины, но и от ее толщины, и от ее натяжения, но без уточнения характера такой зависимости. С древности известно было также явление резонанса, подмеченное на музыкальных инструментах. Несомненно, запас наблюдений в этой области пополнялся и в средние века, но расставить здесь вехи пока нет возможности. Леонардо да Винчи описывает явление резонанса, не ссылаясь на предшественников, и применяет «метод всадника», чтобы выявить наличие слабых колебаний. В книге Фракасторо «О симпатии и антипатии предметов» (Fracastoro, De sympathia et antipathia rerum liber unus), изданной в Венеции в 1546 г. (Леонардо умер в 1519 г.), явление резонанса описывается и объясняется вполне корректно, примерно так, как это делает Галилей. Фракасторо не ограничивается струнами: он пишет, что видел, как в церкви, где вокруг часовни стояло несколько восковых фигур, только одна из фигур сдвинулась, когда раздался звон. «И причиной было не что иное, как то, что только одна статуя была в унисоне». Трусделл на основе анализа книги Фракасторо приходит к выводу, что вряд ли она — произведение оригинального ученого, скорее это хорошее изложение сведений, собранных из разных источников. Но для Фракасторо звук безусловно является колебательным движением определенной частоты, Фракасторо различает колебательное движение струны и движение воздуха, он правильно толкует явление резонанса, он считает, видимо, что любое тело имеет свойственную ему частоту колебательного движения. Поэтому надо сделать вывод, что все эти понятия и представления более раннего происхождения.
Книга Бенедетти «О различных математических и физических рассуждениях» (Giovanni Baptista Benedetti, Diversarum speculationum mathematicanim et physicarum libei) была издана в 1585 г., а в 1599 г. вышла третьим (и последним) изданием. С нею мы уже вступаем в эпоху Галилея. В ней есть глава «О музыкальных интервалах». Там описывается опыт с монохордом, разделенном зажимом на две равные части: одна часть будет издавать тот же звук, что и другая, потому что она столько {447} же раз бьет по воздуху, как и другая, и воздушные волны будут одинаково распространяться и полностью будут согласовываться, не пересекаясь и не разрушая друг друга. Согласно Бенедетти, является хорошо известным фактом, что высота тона определяется его частотой; согласно Бенедетти, всем также известно, что скорость струны, при прочих равных условиях, обратно пропорциональна ее длине, и он приходит к выводу, что отношение высот тонов равно отношению частот, с которыми колеблются издающие их струны. Но из текста Бенедетти не следует, чтобы он формулировал в качестве особого положения изохронизм звуковых колебаний (одного и того же тела).
Таков запас сведений и представлений, которыми располагала формирующаяся акустика к концу XVI столетия, и достаточно вероятно, что все это было известно Галилею. Давность и здесь, как в учении о падении тел, была порядка двух тысячелетий, но в учении о звуке надо было не начинать все заново, а продолжать медленный, но достаточно последовательно развертывавшийся процесс накопления и анализа фактов. Выделить то, что сделано отдельными учеными, вследствие длительности и обезличенности традиции было трудно, а то и невозможно. Это объясняет отсутствие всяких ссылок у Галилея.
Но у Галилея были два выдающихся современника, занимавшихся колебаниями тел и звуковыми явлениями: голландец Бекман и француз Мерсенн. Бекман ничего не напечатал, и лишь после его смерти (и смерти Галилея) в 1644 г. были опубликованы небольшие извлечения из его научного дневника. Сейчас дневники Бекмана изданы полностью (Journal tenu par J. Beeckman de 1604 a 1634, ed. C. de Waard, в 4-х томах, 1939—1953), и можно резюмировать его достижения в акустике следующим образом. На основании наблюдений и опыта он в 1614—1618 гг. пришел 1) к выводу об изохронизме звуковых колебаний и 2) к утверждению, что частота колебаний струны обратно пропорциональна длине струны l:
|
(1) |
Соотношение (1) Бекман пытался обосновать и математически. Наиболее убедительное доказательство изохронизма у Бекмана таково: струна в конце концов прекращает движение, поэтому «пространство, проходимое ею при первом ударе, меньше, чем при втором, и т. д., а так как для уха эти звуки остаются одинаковыми до конца, то все удары должны быть разделены равными промежутками времени...» И Бекман сравнивает колебание струны с движениями подвешенной на веревке люстры, движениями, которые, по Бекману, изохронны в пустоте. Все это очень близко к Галилею. И, может быть, та же аналогия, только в обратном направлении — от звука к колебаниям подвешенного тела — укрепила в Галилее уверенность в изохронизме колебаний маятника любой амплитуды?
Акустические исследования Бекмана относятся к 1614—1618 гг. В 1618 г. с Бекманом знакомится Декарт, лет через десять с ним встречается и, затем, переписывается Мерсенн. Таким образом, опыты и рассуждения Бекмана становятся известными {448} во Франции, но вряд ли они могли дойти до Галилея. Да и открытия Бекмана были, в основном, переоткрытиями и Бенедетти не увидел бы в них ничего нового. Мерсенн в 1623 г., когда он еще не был знаком с результатами Бекмана, уже располагал аналогичными выводами, а в 1625 г. он опубликовал несколько экспериментально полученных законов колебания струн, которые сводятся к формуле
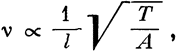 |
(2) |
где Т — натяжение (натягивающий струну вес), А — площадь поперечного сечения («толщина») струны.
В 1635 и 1636 гг. Мерсенн издал две книги, посвященные акустике и теории музыки. В них собран большой экспериментальный материал, частично новый (Мерсенну принадлежит, например, открытие биений), но в установлении закономерностей формула (2) остается высшим достижением Мерсенна.
При сравнении результатов Мерсенна с тем, что изложено у Галилея, выделяются два пункта. Во-первых, Галилей исправил формулу (2), заменив «толщину» А — «весом» (точнее — весом единицы длины струны) и указав на независимость частоты от материала. Во-вторых, Галилей вкладывает в уста Сагредо неуточненную формулировку,— это наводит на мысль, что Галилей считал эту формулировку хорошо известной. Но нет никаких указаний на то, что Галилей был знаком с трудами Мерсенна (хотя Мерсенн живо интересовался всем, что относилось к Галилею, так как был о нем самого высокого мнения). Не являются ли законы Мерсенна математическими сформулированными и экспериментально им проверенными правилами, которые были уже известны мастерам музыкальных инструментов, а Галилей должен был знать людей такой профессии?
Объяснение консонансов и диссонансов, изложенное в первом дне «Бесед», кажется весьма естественным выводом из тех данных, которыми располагали и Бекман, и Мерсенн, но дано оно впервые Галилеем, притом, вероятно, задолго до опубликования его книги. Можно сослаться на следующее. В ноябре 1627 г.1 Мерсенн запрашивал одного из своих римских корреспондентов, верно ли, что книга Галилея «О движении Земли» печатается с разрешения папы, который видел ее и одобрил доказательство2. И. Мерсенн продолжал: «Если упомянутый Галилей находится в Риме или если вы знаете какого-нибудь другого отменного математика — музыканта, я прошу вас узнать у него, почему из всех созвучий приятны только те, что составляют октаву, квинту, кварту, терцию и сиксту, и им соответствующие, и какой из всех диссонансов наиболее неприятен, и почему; мне говорили, что упомянутому Галилею известны причины этого...».
| {449} |
(К стр. 202). День второй написан Галилеем иначе, чем День первый: меняется тон, меняется характер изложения. Там обсуждалось, со всей общностью и с многочисленными отступлениями, строение материи, чтобы найти объяснение прочности тел. Здесь Сальвиати удовлетворяется тем, что наличие у тел способности к сопротивлению силе, стремящейся их сломать, не подлежит сомнению. Там математические построения привлекаются только попутно. Здесь последовательно математическими средствами исследуется четко поставленная проблема о сопротивлении тел изгибу. Там отступления от основной проблемы вызваны философскими или общефизическими интересами и далеко уводят читателя от основной темы. Здесь отступления гораздо плотнее примыкают к основному сюжету и все выдержано в инженерном духе. Первый день написан философом-физиком, второй — механиком-инженером.
Историки науки сходятся на том, что с этой части «Бесед» начинается развитие новой дисциплины — учения о сопротивлении материалов и об упругости тел. Конечно, известное представление об упругости было в античной науке — во всяком случае, это верно относительно Филона (из Византии) и Герона, ученого александрийской школы. Иордан Неморарий (XIII в.) и Леонардо да Винчи ставят вопрос о поведении тел при изгибе, в частности об изгибе консоли, чем займется Галилей, и о продольном изгибе колонны, чем займется Эйлер. Леонардо набрасывает схемы экспериментов для измерения прочности тел и даже указывает правила количественного характера для определения несущей способности колонны. Но все это — разрозненные мысли и догадки, вряд ли имевшие какое-либо влияние на интересы и ход мыслей более поздних исследователей, включая Галилея. Можно считать, что, в отличие от акустических проблем, здесь практически не было никакой традиции в науке, и Галилей начинал исследование, имея в своем распоряжении только тот запас фактов и представлений, которым могли с ними поделиться знакомые ему практики — строители зданий, кораблестроители и др. «Галилей первый в истории человечества поставил вопрос о прочности тел и первый попытался его решить»1. Первым был Галилей и в научном анализе вопроса о механическом подобии, хотя, несомненно, вопрос этот интересовал инженеров много раньше. Некоторые правила для изменения масштабов при строительстве баллистических орудий дают упомянутый выше Филон и Герон, но эти правила либо эмпирического происхождения, либо исходят из требования геометрического подобия. Идейных предшественников Галилей не имел и здесь.
Теорию прочности на изгиб, развитую Галилеем, не раз критиковали не вполне справедливо, а потому ее часто недооценивали. В науке о сопротивлении материалов и в теории упругости, начиная с XIX в., стало общепринятым рассчитывать рабочее состояние: предполагается, что деформации достаточно малы и что поэтому применим (обобщенный) закон Гука. К тому же в расчетные формулы входят постоянные, характеризующие материал, тот или иной «модуль». Галилей не мог располагать данными {450} о таких постоянных, он систематически сравнивает между собой геометрически подобные фигуры. Поэтому его результаты не могут, например, служить для расчета отдельно взятой балки; но они ориентируют, как изменяется сопротивление балки при изменении ее размеров, и дают инженеру средства уйти от опасного рубежа. Самым же существенным в теории Галилея (что часто не учитывалось его критиками) является то, что это теория прочности, исходящая не из рабочего, а из предельного состояния конструкции. В предельном состоянии материал заведомо не подчиняется закону Гука. Критиковать результаты Галилея, исходя из совершенно иной теории прочности, нет оснований. Теоретически безупречными расчетами в пластической зоне для задачи Галилея об изгибе мы еще не располагаем.
Безусловно неверна модель изгиба, из которой исходит Галилей: он считает, что и опасном сечении все усилия растягивающие, и что они распределены равномерно по сечению. По этой схеме он получает, что прочность стержня прямоугольного сечения (призма у Галилея) пропорциональна ширине и квадрату высоты, а у стержня круглого сечения прочность пропорциональна кубу диаметра. Этот результат в сочетании с тем, что изгибающий момент собственного веса растет вместе с длиной стержня как ее квадрат, является основой для выводов и оценок Галилея, и этот результат верен. Он получен Галилеем потому, что он не зависит от закона распределения усилий по сечению балки. Пусть σ = f(g) выражает усилие σ в функции координаты y, указывающей положение слоя материла. Впервые Паран (начало XVIII в.) указал на то, что в сечении действуют и растягивающие, и сжимающие усилия, и сделал вывод о наличии нейтрального слоя. Это выявило ошибочность гипотезы Галилея и гипотезы Лейбница и Мариотта (около 1680 г.): f(y) = Сy, где С — постоянный коэффициент, y отсчитывается от нижнего края сечения. И тот же Паран доказал, что для прямоугольного профиля момент сопротивления равен kbh2, где b — ширина, h — высота профиля и где только коэффициент k зависит от выбора функции f(y). Аналогичный результат верен и для кругового профиля.
Все эти соображения вполне оправдывают ту оценку результатов Галилея, которую дает С. А. Бершнтейн в книге «Очерки по истории строительной механики»1. «Таким образом, своеобразие постановки задачи позволило Галилею избежать как определения прочностных свойств материалов, так и изыскания истинного закона распределения напряжений. Задача о сравнительной прочности геометрически подобных тел не требовала ни того, ни другого, а потому была решена Галилеем совершенно правильно».
1 (К стр. 202). Название работы Архимеда приведено Галилеем на латинском языке, его можно перевести также как «О равновесомых». В указанном выше русском издании сочинений Архимеда эта работа озаглавлена «О равновесии плоских фигур, или о центрах тяжести плоских фигур»2. {451}
2 (К стр. 204). Это доказательство закона рычага совпадает, по сути, с тем, которое Галилей дал в «Механике» — см. в наст, том, стр. 12—13.
3 У Галилея термин «момент» употребляется в разных смыслах, и здесь он вводится еще в одном значении. Впрочем, в дальнейшем изложении указанные здесь термины почти не применяются, и поэтому некоторые формулировки приходится истолковывать с учетом их контекста.
4 (К стр. 205). Составным, или сложным, отношением называлось во времена Галилея произведение двух исходных («простых») отношений.
5 (К стр. 206). Не следует буквально понимать слова, которыми начинается эта фраза: «На основании доказанного...» — ведь выше доказано только правило рычага. Абсолютным названо здесь сопротивление разрыву при растяжении, «ибо тогда каково движение движущего, таково движение движимого»: это значит, что (в предельном состоянии) когда начинается разрыв из-за продольно действующей силы, последняя равна сопротивлению, так как равны соответствующие (виртуальные) перемещения, чего нет при поперечно действующей изгибающей силе. Все же при всех оговорках эта фраза содержит формально противоречивые утверждения, так как и отношение сил, и отношение моментов этих же сил оказываются, если понимать все буквально, одинаковыми. Способ выражения, примененный здесь, неудачен, смысл же таков: говоря об отношении моментов сил, Галилей имеет в виду отношение плеч того (воображаемого) коленчатого рычага, к концам которого приложены силы, согласно его схеме изгиба; стало быть, уже здесь Галилей, не оговаривая этого явно, представляет себе силу сопротивления приложенной в центре симметрии опасного сечения; эту силу сопротивления он считает одинаковой в случае растяжения («абсолютное сопротивление») и в случае изгиба. В первом случае приложенное ломающее усилие равно силе сопротивления (все время имеется в виду предельное состояние), во втором случае в предельном состоянии равны моменты, поэтому отношение сил равно отношению длины ВС к половине толщины призмы АВ.
Если обозначим через Rt и Pt сопротивление и ломающую силу при растяжении, через Rb и Рb — соответственно силы при изгибе, через l — длину консоли, через d — ее диаметр или толщину, то утверждения Галилея (сформулированные им неточно) запишутся так:
Rt = Pt (1); Rb = Rt (2); Rb |
d 2 |
= Pbl (3); |
следовательно:
|
Pt Pb |
= |
l d/2 |
. |
6 (К стр. 210). В предыдущем рассуждении Галилей ввел гипотезу, что Rt = Rb (см. примеч. 5) пропорционально площади сечения балки(призматической или цилиндрической): Rt = Rb = kS. Сопротивлением (изгибу) Галилей теперь называет не Rb, а момент этой силы, приложенной в центре тяжести сечения, относительно точки В {452} (см. рисунок на стр. 206). Отсюда непосредственно следуют сформулированные в тексте утверждения.
7 (К стр. 211). Рассуждение Сальвиати эффектно и, на первый взгляд, вполне убедительно. Но оно основано на молчаливо принятом допущении, что отрезок веревки BE имеет единственную функцию: передать действие груза С неизмененным, а такое допущение равносильно тому, что доказывается в тексте (указано Трусделом).
8 Третьей пропорциональной к двум отрезкам а и b во времена Галилея называли отрезок α3 = b2/a (определяемый из пропорции a/b = b/α3); четвертой пропорциональной к отрезкам а и b называли отрезок α4 = b3/a2 (определяемый из пропорции a/b = α3/α4) и т. д.
9 (К стр. 212). Эти результаты Галилея непосредственно следуют из его исходных допущений:
Pb = Pt |
1/2d l |
, |
пропорционально d 2, следовательно, Pb пропорционально d 3/l (обозначения см. выше в примеч. 6 и 7).
Однако то, что Сальвиати доказывает ниже, а именно, что у подобных цилиндров или призм отношение составных моментов, обусловливаемых весом и длиною, равно полуторной степени отношения сопротивления их оснований, не верно. Сопротивление основания у Галилея иной раз сила, иной раз момент силы, и в зависимости от этого оно пропорционально либо площади основания, т. е. квадрату диаметра, либо кубу диаметра. Поэтому, если коэффициент подобия для длин обозначим через k, отношение этих сопротивлений для подобных фигур равно k2 или k3, тогда как отношение моментов сил веса тех же фигур будет k4. Итак, то, что Галилей называет отношением моментов подобных цилиндров, равно, при его исходных допущениях, либо второй (а не полуторной) степени отношения «сопротивлений их оснований», либо степени 4/3.
10 (К стр. 213). Симпличио имеет в виду XVII главу «Механических проблем» псевдо-Аристотеля. Там объясняется, почему толстая деревянная жердь, даже если она толще короткой, прогибается при подъеме (за один конец, например с земли) больше, чем короткая: у короткой жерди опора и точка приложения силы близки друг к другу, а у длинной они разделены большим расстоянием, такая жердь сразу прогибается и при дальнейшем подъеме ее прогиб возрастает.
11 (К стр. 215). Доказательство Галилея, если пользоваться современной записью, можно заменить следующим. Пусть l и d — длина и диаметр (данного) цилиндра «наибольшей длины, который выдерживает свой собственный вес», L и D— длина и диаметр второго цилиндра. Заданы l, d и L. Дано также, что изгибающий момент веса первого цилиндра
ρ |
π d 2 4 |
l |
l 2 |
, (где ρ — плотность материала) |
равен моменту сопротивления
αd 2 |
a 2 |
, (где α — константа, характерная для материала) |
откуда
|
ρπl2 = 4αd. |
(1) |
| {453} |
Требуется определить D, причем, по условию, и для нового цилиндра должно быть
|
ρπL2 = 4αD. |
(2) |
Из (1) и (2) получаем, что
D = |
L2 l 2 |
d, |
что составляет результат Галилея.
12 (К стр. 216). Воспользуемся обозначениями предыдущего примечания. Имеем DC = d, Е = L. Галилей вводит в рассмотрение цилиндр, подобный цилиндру (d, l) и имеющий длину L. Его диаметр KL обозначим через D'. Линия MN, как третья пропорциональная к d и D', равна D' 2/d и она, по утверждению Галилея, равна искомому D. Это верно, так как D'/L = d/l, поэтому
MN = |
D' 2 d |
= |
d 2L2 l 2d |
= d |
L2 l 2 |
, |
что совпадает с доказанным выше.
13 Ex aequali (лат.) — «по равенству»; в данном случае — приравнивая произведение левых частей двух равенств произведению правых частей тех же равенств.
14 В последнем доказательстве Галилей пользуется обозначениями и рисунком первого решения задачи, сформулированной на стр. 215. Обозначим моменты (собственных весов) цилиндров FE1, DG и АС через М1 М2, М3, соответственно и напомним, что I есть третья пропорциональная к DE и АС, т. е. I = АС2/DE; кроме того, по построению, DE/I = DF/AB, a M есть третья, О есть четвертая пропорциональная к DE и I, т. е.
M = |
I2 DE |
= |
AC4 DE2 |
, O = |
M2 I |
= |
I3 DE2 |
= |
AC6 DE5 |
. |
Кроме того, очевидно,
|
M1 M2 |
= |
DE2 FG2 |
= |
DE I |
(FC = AC); |
M2 M3 |
= |
FD2 AB2 |
. |
Отсюда
|
M2 M3 |
= |
DE2 I 2 |
= |
I 2 M 2 |
= I : |
M 2 I |
= |
I O |
. |
Перемножая, получим
|
M1 M3 |
= |
DE O |
= |
DE6 AC6 |
= |
DE3 I3 |
= |
FD3 AB3 |
. |
Этим заканчивается доказательство. Здесь Галилей называет сопротивлением не силу сопротивления, пропорциональную площади сечения балки, т. е. квадрату диаметра или радиуса в случае круглого сечения, а момент этой силы.
15 Эти строки взяты из Ариосто, любимого поэта Галилея:
|
Non si può compartir quanto sia lungo, Si smisuratamente è tutto grosso. Ariosto. Orlando furioso, XVII, 30. |
| {454} |
16 (К стр. 219). В алгебраической записи решение представляется в следующем виде. Пусть АС = l, вес призмы АС = р. По условию, момент сопротивления, развиваемого призмой, составляет
p |
l 2 |
+ Dl = |
l (p + 2D) 2 |
. |
При удлинении призмы, пусть l заменяется на l'. Тогда ломающий момент ее веса равен
p |
l' l |
· |
l' 2 |
= |
pl' 2 2l |
. |
Приравнивая, получаем
|
pl' 2 2l |
= l (p + 2D), |
откуда
l' 2 = l2 |
p + 2D p |
. |
Галилей рассматривает правую часть последнего равенства, как произведение двух длин:
l и l |
p + 2D p |
(= L); |
тогда l' есть средняя пропорциональная для l и L. С этого Галилей и начинает.
17 (К стр. 220). Здесь идет речь о задаче, рассматриваемой в XV главе «Механических проблем» псевдо-Аристотеля. Сальвиати вполне точно резюмирует формулировку древнегреческого автора и его разъяснения.
18 (К стр. 221). В этом рассуждении, как и при доказательстве того, что короткая веревка не прочнее, чем длинная (см. стр. 211—212), неявно применяется важное для теории сплошных тел положение: с какой силой действует одна часть тела на другую, скажем, левая на правую, с такой же силой правая часть действует на левую. Действительно, при разломе стержня над опорой в F изгибающий момент силы, приложенной в D, приравнивается изгибающему моменту силы, приложенной в Е.
19 (К стр. 222). Изучение формальной логики (логики Аристотеля) во времена Галилея занимало значительную часть учебного времени в университетах и коллежах. Напротив, математика была, можно сказать, в загоне: ей отводилось самое скромное место в учебных планах, а профессору математики обычно платили в два-три раза меньше, чем профессорам богословия, философии, логики. Галилей, в соответствии со своими философскими и методологическими установками, подчеркивает примат математики над логикой.
20 «Прямоугольник ADB», «прямоугольник АСВ» — это произведения AD · DB, АС · СВ. Такой способ выражения неоднократно встречается и в дальнейшем тексте. Само доказательство таково:
|
A + B E + F |
= |
A + B B |
· |
B F |
· |
F F + E |
. |
Нам известно, что
|
A + B B |
= |
BA AC |
; |
B F |
= |
DB BC |
; |
F F + E |
= |
DA AB |
. |
Отсюда получаем, что
|
A + B E + F |
= |
AD · DB АС · СВ |
. |
| {455} |
21 (К стр. 223). Согласно предыдущей теореме, дело сводится к отысканию на отрезке АВ такой точки Я, чтобы было
|
AR · RB AD2 |
= |
F E |
, |
где F и Е — заданные линии (собственно, задано отношение этих линий). Построение, данное Галилеем, изящно и ведет кратчайшим путем к цели.
22 (К стр. 226). Мы имеем здесь первую постановку задачи о «теле равного сопротивления», и первое ее решение — для невесомой балки, нагруженной в одном конце. Отыскание тел равного сопротивления (при различных постановках задачи) стало предметом ряда работ еще в XVII в., но на строительную практику того времени эти исследования не повлияли.
23 (К стр. 227). Книга «О спиралях» вошла в указанное выше издание сочинений Архимеда (стр. 227—265). Галилей ссылается на следствие из Предложения X этой книги (цит. изд., стр. 235 и ел.). Это предложение в геометрическом виде дает формулу для суммы квадратов целых чисел от 1 до любого целого n, а следствие, на которое как на лемму ссылается Галилей, может быть записано так:
3(а12 + а22 + . . . + an–12) < nan2 < 3(а12 + а22 + . . . + an2),
где
аk = kа1 (k = 1, 2, . . ., n).
24 (К стр. 229). Речь идет о юношеской работе Галилея, которую он поместил в «Беседах», как Приложение, после Дня четвертого. См. ниже, стр. 348—366 и примечания к ним.
25 (К стр. 230). Второй способ вычерчивания параболы дает основание сделать вывод, что Галилей считал формулу тяжелой цепи, подвешенной в двух точках, параболической, т. е. отождествлял цепную линию и параболу. Однако в одной из рукописей Галилея есть чертеж, на котором изображена подвешенная в двух точках цепь и тут же нанесены точки, лежащие на параболе, соприкасающейся с этой (реальной) цепной линией в нижней точке. Из чертежа видно хорошее совпадение параболы с цепной линией в нижней части и отличие этих линий при удалении от нижней части. Безоговорочное отождествление цепной линии с параболой трудно согласовать с этим чертежом1. В Дне четвертом Галилей, действительно, вполне четко указывает на различие этих линий (см. стр. 343). История же вопроса о цепной линии такова. Уже упоминавшийся нами Бекман скорее догадался, чем доказал, что по параболе располагается невесомая нить под равномерно распределенной по горизонтали вертикальной нагрузкой (схема висячего моста). Отсюда следует, что цепная линия не может быть параболой. Выводы Бекмана не были опубликованы, но вероятнее всего стали известны Декарту, который отозвался о способах вычерчивания параболы, предложенных Галилеем, {456} как «строго геометрически» ошибочных (1638 г.). Решение проблемы висячего моста, т. е. обоснование результата Бекмана, дал Гюйгенс в одной из своих ранних работ (1646 г.). Эта работа осталась неопубликованной. В 1690 г., в порядке состязания, открытого вызовом Якова Бернулли, задача о цепной линии была разными способами решена Лейбницем, Гюйгенсом, Яковом Бернулли и его братом Иоганном.
26 (К стр. 231). Сделанный Галилеем общий вывод о возрастании прочности при переходе от сплошного цилиндра к полому (той же длины и того же веса) верен. Его утверждение, что отношение «сопротивлений» этих цилиндров равно отношению их диаметров, является строгим следствием в теории Галилея, но расходится с более сложным результатом, который дает современная теория упругости.
27 (К стр. 232). По поводу терминов «четвертая пропорциональная» и ex aequali см. выше, примеч. 9 и 14. Приведенный результат верен условно, т. е. в теории, развитой Галилеем, и расходится с формулами теории упругости.
1 (К стр. 233). Днем третьим начинается часть «Бесед», содержащая вторую новую науку — науку о местных движениях. Этот термин, использованный Галилеем в заголовке книги, обозначал движение падающих тел. Тема третьего дня — свободное падение, тема четвертого дня — движение тел, брошенных под углом к горизонту (снарядов).
То, как начинается День третий, может удивить читателя: не указано, от чьего имени идет речь, вместо реплик собеседников мы читаем введение к трактату о движении. Читателю оригинала легче сориентироваться: перед ним латинский текст, и когда он перелистает несколько страниц и найдет снова итальянский (у нас — на стр. 241), ему все становится ясным после первого же обмена репликами между Сагредо и Сальвиати. Оказывается, что собеседники знакомятся с латинским трактатом Академика, т. е. Галилея. Сальвиати читает трактат, он же отвечает на недоуменные вопросы остальных и комментирует текст. В переводе текст трактата не выделяется своим языком, но стиль и вводные замечания собеседников позволят и нашему читателю без труда отличить латинский текст трактата с его последовательным, аксиоматически построенным изложением от непринужденных комментариев и замечаний, написанных по-итальянски и вложенных в уста Сальвиати, Сагредо и Симпличио.
День третий содержит великое открытие Галилея: то, что тела падают на Землю, если отвлечься от сопротивления воздуха, одинаково, равномерно-ускоренным движением, и кинематику этого движения. Рассматриваются различные случаи падения тел — сочетания падения по вертикали и по наклонной плоскости. В первую очередь определяются и сравниваются между собой времена падения в различных условиях. Изобретательность, проявленная здесь Галилеем, изумительна. Его геометрические доказательства часто сложнее, чем почти автоматически работающий аппарат нашей алгебры, но не раз изящные построения Галилея ведут к цели быстрее и проще. Тот, кто внимательно прочтет День третий, согласится с самооценкой, высказанной от имени Сагредо {457} (см. стр. 303). И все это действительно было вполне новой наукой об очень старом предмете, который «своею значительностью превосходит все другие явления природы» (стр. 304).
2 (К стр. 234). Разъясняемое Галилеем значение вставки слова «любые» в определение равномерного движения состоит и в том, что оно открывает путь к введению понятия мгновенной скорости. Следующие далее четыре аксиомы не все заслуживают этого названия: Аксиома II вытекает из аксиомы I, аксиома IV — из аксиомы III; кроме того, в последних двух аксиомах речь идет о скорости, определение же скорости» не дано.
3 (К стр. 235). Теоремы, относящиеся к равномерному движению, весьма просты, и растянутость их доказательств вызвана только тем, что Галилей все величины представляет отрезками, а не обозначает буквами, и оперирует отношениями однородных величин. Скорость у Галилея — величина особая, даже в равномерном движении, она не сводится к отношению пути ко времени. Двойная запись: Теорема I. Предложение I и т. п. становится понятной во второй части латинского трактата. Там имеются не только «теоремы», но и «проблемы», которые получают свои номера и одновременно, вместе с теоремами, составляют «Предложения», нумерация которых ведется особо.
4 (К стр. 240). Здесь кончается первая часть латинского трактата. Следующая реплика Сальвиати (на итальянском языке) образует переход ко второй части (стр. 240). Там уже первое определение — равномерно-ускоренного движения — вызовет дискуссию, которую собеседники ведут по-итальянски. Она начинается замечанием Сагредо (стр. 241).
5 (К стр. 241). Сомнения и затруднения Сагредо во времена Галилея былп вполне естественны. Средневековой науке были хорошо известны трудности («парадоксы»), связанные с понятием непрерывного изменения и, в частности, непрерывного движения. Поэтому очень сильна была тенденция избегать введения непрерывности. Галилей, вводя в механику континуальные представления, действовал со смелостью, которую теперь уже трудно оценить. Помочь может знакомство с реакцией современников Галилея. Оказывается, что континуальные представления Галилея вызвали сомнения у Кавальери (Галилей в письме к нему от 21 марта 1626 г. делится с ним теми соображениями, которые в своем ответе Сагредо излагает ниже Сальвиати); с ними не мог вполне примириться Мерсенн; Декарт в 1638 г. заявлял, что он считает утверждение Галилея о переходе падающего тела через все степени скорости не всегда верными, а в 1639 г. он высказывается более определенно, решительнее отвергает представление Галилея: «Ибо следует знать, что бы не говорили против этого Галилей и некоторые другие, что тела, начинающие падать или двигаться... вовсе не проходят через все степени-медленности, а имеют с первого момента определенную скорость, которая затем значительно возрастает»1. {458}
На сторону Галилея в этом вопросе становятся постепенно его ученики и последователи в Италии, молодой Гюйгенс отстаивает перед Мерсенном концепции Галилея, последовавшие успехи новой механики постепенно заставляют забыть о «парадоксах непрерывного», которые так затрудняли усвоение идей Галилея современниками. Смелость Галилея тем более замечательна, что «лабиринт континуума», как выражались схоласты, был ему хорошо известен (см. День первый «Бесед»). Но Галилея вела вперед практика — подтверждение выводов из его теорем опытом и наблюдением. В конце XVII в. Лейбниц будет упрекать Галилея за то, что тот не развязал узел парадоксов континуума (Лейбниц имел в виду логическое разрешение этих парадоксов), а разрубил его. Но именно в этой смелости движения вперед и в безбоязненном формировании новых понятий — одна из великих и революционных заслуг Галилея.
6 (К стр. 242). Ответ Сальвиати разъясняет понятие мгновенной скорости, к которому Галилей был приведен логикой исследования. Заодно мы видим, что в ходе анализа физического процесса Галилей начинает смелее обращаться с бесконечностями, чем в первом дне: он пользуется «равномощностью» бесконечного множества мгновений и бесконечного множества уменьшающихся степеней скорости.
7 (К стр. 243). Взгляды, изложенные Сагредо, нельзя безоговорочно приписывать Галилею: его постоянный alter ego, Сальвиати, на следующей странице отведет дискуссию от вопроса «о причинах ускорения в естественном движении». Сагредо же излагает один из вариантов теории «импето» (импульса). Сила Галилея сказалась и в том, что ему была ясна неудовлетворительность всех имевшихся в его распоряжении гипотез о причине ускоренного падения тел.
8 Симпличио, как и полагается перипатетику, проводит строгое различие между «естественным» движением падающих и «насильственным» движением брошенных тел. Одна из заслуг Галилея заключается в том, что он показал необоснованность такого разграничения.
9 (К стр. 244). Отказ Галилея от того, чтобы выяснить первопричину падения тел, и самоограничение кинематикой, т. е. описанием этого движения, отнюдь не имеет принципиального характера: это — трезвая оценка возможностей науки своего времени. В других случаях Галилей настаивал на том, что задачей науки является отыскание первопричин явлений. Все же, основываясь на комментируемом заявлении Сальвиати, Галилею ставили в заслугу то, что он якобы вообще искал ответа на вопрос «как», а не на вопрос «почему» (Э. Мах).
10 (К стр. 245). Галилей в предпоследней реплике с полной откровенностью признал, что он в свое время ошибался, принимая для скорости при падении тел закон: υ = ks (1), где s — путь, пройденный падающим телом от исходного положения покоя, k — постоянный коэффициент (Галилей, собственно, записал бы это так: υ1/υ2 = s1/s2) вместо правильного υ = kt (2) (t — время падения). Рукописи и переписка Галилея показывают, что он, уже зная зависимость пути от времени при падении тел (s = аt2), еще принимал формулу (1) и пытался из нее получить зависимость между s и t (письмо к Паоло Сарпи от 16 октября 1604 г.). Переход к формуле (2) — результат, полученный {459} Галилеем не ранее 1609—1610 гг.1 То, что Галилей начинал свои поиски принципа, из которого вытекали бы все остальные свойства движения падающих тел, с формулы (1), а не (2), вполне объяснимо. По тому же пути шли и его предшественники — Леонардо да Винчи, Бенедетти. Поучительно, что Декарт повторяет (а не исправляет) ошибку Галилея. Движение происходит в пространстве зримо, отнесение ко времени — более высокая ступень абстракции, и выбор в качестве независимого переменного s должен был быть первым шагом. Отказ от s в пользу t произошел под давлением фактов, а первоначально непосредственно регистрируемые наблюдения указывали на то, что чем ниже падающее тело, т. е. чем больший путь оно прошло, тем быстрее оно движется. Галилей отверг (1), так как заметил ошибочность вывода закона s = at2 из (1), и обосновал выбор (2) в качестве исходного положения выводом из (2) этого закона, подтверждаемого опытом. Однако «теоретическое» опровержение формулы (1), изложенное только что Сальвиати, неубедительно: Галилей рассуждает так, как будто весь путь sf пройденный за время t, проходится со скоростью, достигаемой лишь в конце пути! Прямым путем физическую несообразность формулы (1) можно показать так: если
υ |
( |
= |
ds dt |
) |
= ks, то kdt = |
ds s |
, |
откуда
|
ds s |
= ln |
s s0 |
= k (t – t0) |
и нельзя применить этот закон, если значению t0 соответствует s0 = 0, как это должно быть по постановке задачи. Да и зависимость s = s0ek(t–t0) не соответствует законам падения тел. Подобного рода вывод мы находим у Эйлера, в его «Механике» (1736).
11 (К стр. 246). Этот второй принцип Галилея — энергетический: поле силы тяжести потенциально. Сальвиати подтверждает этот принцип опытами, которые стали классическими (см. ниже). В связи с этим же принципом см. стр. 256—260 и примечание к ним.
12 (К стр. 249). Теорема I (с нее возобновляется чтение латинского текста), выражающая общее свойство равномерно-ускоренного движения, впервые была сформулирована в трудах ученых XIV в., преподавателей Merton College'a в Оксфорде. Мы находим ее у Вильяма Гейтсбери, Ричарда Свайнхеда, Джона Дамблтона, начиная с 30-х годов XIV в. Им же принадлежат первые доказательства этой теоремы, правда, не вполне законченные. Позже эту же теорему доказывают Джованни Казали (1346 г.) и Николай Орем (ок. 1350 г.),— см. его «Трактат о конфигурации качеств»; перевод и примечания В. П. Зубова в «Историко-математических исследованиях», вып. 11, 1958 г. Доказательства Казали и Орема, особенно Казали, очень близки к доказательству Галилея. И после Орема эта теорема не раз встречается в средневековых трактатах, {460} в частности у Блазиуса из Пармы (Biagio Pelacani di Parma; конец XIV в.), чья работа (Questiones super tractatum de latitudine formarum) была напечатана в 1505 г. в Венеции. По подсчету историка средневековой науки, Маршалла Клагетта, эта теорема не менее семнадцати раз встречается в печатных изданиях XVI в. Вероятнее всего, что Галилею были известны некоторые его предшественники и что он никого не указывает именно потому, что их было немало. См. M.Glagett. The Science of Mechanics in the Middle Ages, 1959, особенно — гл. V, The Merton Theorem of Uniform Accelaration. У Галилея в его выводе проходит представление о площади, как о «сумме линий», это соответствует геометрическому истолкованию интеграла у Лейбница.
13 (К стр. 251). Это доказательство равносильно применению формулы: [(n + 1)а]2 – (nа)2 = 2na + 1 при а = 1 (n = 1, 2,...). Излагаемое ниже (Сагредо) второе доказательство является по форме геометрическим и кажется Симпличио более простым и ясным, несмотря на свою растянутость: еще один пример того, насколько отличались математические навыки того времени от современных.
14 (К стр. 254). Опыты, о которых говорил выше Сальвиати, описаны с подробностями, не позволяющими сомневаться в том, что они были действительно произведены. Правда, теперь нас смущают ссылки на то, что все подтверждалось на опыте вполне точно, что нельзя было уловить разницу во времени «даже на одну десятую времени биения пульса» и т. п., но такое безоговорочное изложение результатов эксперимента встречается у Галилея не раз.
15 Доказанным выше следствием Галилей будет широко пользоваться в дальнейшем изложении, и оно действительно удобно при решении различных задач на равномерноускоренное движение: если пути s1 соответствует время t1, пути s2 соответствует время t2, то
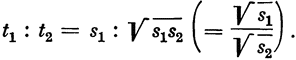
Доказательство же «замечания» Галилея в первом издании «Бесед» отсутствует.
В первом издании «Бесед» за последним «Замечанием» шло продолжение латинского текста (Теорема III. Предложение II, см. стр. 260). Все, что излагается ниже на стр. 256—260 (до Теоремы III), представляет собой дополнение, впервые появившееся в болонском издании собрания сочинений Галилея (1656 г., т. II, стр. 132—134). Организатор и редактор этого издания Вивиани поместил дополнение с пометкой «Добавление автора (посмертное)». В форме диалога это дополнение было изложено самим Вивиани, как то следует из письма Галилея, адресованного Кастелли и помеченного «Арчетри, 3 декабря 1639 г.». Ниже приводим это интересное письмо, опустив только обращение и концовку:
«Более чем ясно, что в науке сомнение —. отец открытия, так как оно пролагает дорогу к истине. Возражения против принципа, принятого мною в трактате об ускоренном движении, которые вот уже несколько месяцев выдвигал этот юноша (Вивиани.— И. П.), ныне мой гость и ученик, с большим усердием изучавший мой трактат, заставили меня настолько все продумать (чтобы убедить в приемлемости и верности этого принципа), что в конце концов, к немалому моему и его удовольствию, я натолкнулся {461} на, если не ошибаюсь, исчерпывающее доказательство, и это доказательство я сообщил здесь нескольким лицам. И он записал это доказательство для меня, так как я, совсем лишенный зрения, напутал бы, быть может, в необходимых рисунках и обозначениях. Это изложено в виде диалога, как пришедшее Сальвиати на ум, так чтобы его можно было, при новом издании моих «Бесед и доказательств», вставить непосредственно после схолии второго предложения упомянутого трактата, на стр. 177 печатного издания, в качестве теоремы, весьма существенной для обоснования развиваемого мною учения о движении. Письменно я сообщаю вам это прежде, чем кому бы то ни было, чтобы узнать ваше мнение об этом, а затем мнение наших здешних друзей, имея в виду послать затем другие копии другим друзьям в Италии и Франции, если вы мне это посоветуете»1.
16 (К стр. 256). См. в этом томе «Механику» — это и есть трактат, написанный еще в Падуе исключительно для учеников. Излагаемые далее соображения (стр. 257–258) можно охарактеризовать, как (единственную в «Беседах») попытку динамического подхода к падению тел.
17 (К стр. 257). Ниже излагается доказательство принципа, который на стр. 247 был выдвинут в качестве заранее принимаемого основного положения. Эта непоследовательность объясняется тем, что дополнение на стр. 256–260 (см. примеч. 15) было изложено Вивиани для Галилея как нечто самостоятельное (см. письмо Галилея к Кастелли в примеч. 15), а вставляя дополнение в посмертное издание, Вивиани, очевидно, не счел возможным изменять предыдущий текст.
18 (К стр. 258). Напомним, что третья пропорциональная к АВ и АС — это АС2/АВ. Центральный пункт в доказательстве Галилея — то, что «тело за тот же промежуток времени, за который оно прошло бы вертикаль АС, пройдет по наклонной АВ расстояние AD (ибо моменты относятся как пройденные пути)». Этот пункт не обоснован, если не принять, что приращение скорости (при падении) пропорционально силе (веса), действующей по направлению движения. Лишь на этом основании мы можем сделать вывод, что за время падения из A в C по АВ точка скатится на такое расстояние AD, что будет
|
AD АС |
= |
AC АB |
, |
т. е. что AD будет «третьей пропорциональной» к АВ и АС.
19 (К стр. 260). Вариант доказательства, предложенный Сагредо, действительно простейший: средняя скорость в обоих движениях одинакова, и остается сослаться на Предложение I первой части латинского трактата.
20 (К стр. 261). Доказать эту и следующую теорему весьма просто, если исходить из формулы для движения по наклонной плоскости с постоянным ускорением, равным
g sin α = g |
h l |
(h — высота, l — длина наклонной плоскости; этот результат содержится в предыдущих выводах Галилея). Для двух наклонных плоскостей имеем
l1 = |
1 2 |
g |
h1 l1 |
t12; |
l2 = |
1 2 |
g |
h2 l2 |
t22. |
| {462} |
и отсюда при l1 = l2 (Предложение IV)
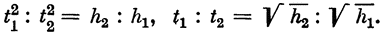
В общем случае (Предложение V)
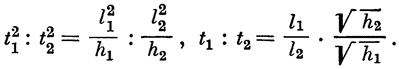
21 (К стр. 262). Напоминаем, что «прямоугольник FAE» обозначает FA · AE, «прямоугольник FAD» обозначает FA · AD.
22 (К стр. 268). В обозначениях примеч. 20 получаем связь между высотами и длинами двух рассматриваемых наклонных плоскостей из пропорций
|
h1 l1 |
= |
H l2 |
, |
h2 l2 |
= |
H l1 |
, |
где Н — высота CG треугольника DCF. Отсюда
|
l2 h1 l1 |
= |
l1 h2 l2 |
и l12 : h1 = l22 : h2, |
следовательно (Предложение V или примеч. 20),
t12 = t22, t1 = t2.
23 (К стр. 269). Так как предшествующее падение в обоих случаях (движение по вертикали и движение по наклонной плоскости) происходит с одной и той же высоты, оно дает одну и ту же начальную скорость. Средняя скорость последующих ускоренных движений остается одинаковой, поэтому применимо более простое доказательство Предложения III (доказательство Сагредо; см. примеч. 19).
24 (К стр. 271). Геометрический вывод Галилея в данном случае и нагляднее и проще, чем сравнительно громоздкая алгебраическая выкладка, как в этом нетрудна убедиться.
25 (К стр. 273). Обозначим через h и l высоту и длину наклонной плоскости, через х — искомый отрезок вертикали. По известным формулам, или на основе уже доказанных Галилеем соотношений получаем, что
x = |
l2 h + 2l |
; |
это можно записать в виде пропорции
(h : 2l) : l = l : x.
Согласно построению Галилея, имеем
(h : 2l) : l = l : АЕ,
| {463} |
так что построением отрезка АЕ решение заканчивается. Галилей (необычный у него случай!) усложняет решение, строя АХ (= АЕ) не сразу, а продлевая наклонную плоскость до R, опуская перпендикуляр RX на вертикаль и доказывая равенство АЕ = АХ. Это, казалось бы, излишнее построение дает ему попутно ту наклонную плоскость RАС, скатываясь по которой из состояния покоя, тело пройдет отрезок АС за то же время, что и после падения из X до А по вертикали.
26 Это значит, что AG = AF2/BA.
27 (К стр. 274). Это положение можно доказать проще, ограничиваясь средствами Галилея. Если равномерно-ускоренное движение по наклонной ЕС и по вертикали АВ из состояния покоя совершается за одно время, то из предыдущих результатов сразу следует, что ЕС < АВ. Дополнительная скорость за счет падения по АЕ одинаково увеличивает среднюю скорость движения по ЕС и АВ, следовательно, за счет этого более короткий путь будет пройден за меньшее время. Напоминаем, что «прямоугольник BEА» — это ВЕ · ЕА и т. д.
28 (К стр. 276). Задача IV отличается от задачи II переменой ролей отрезка вертикали х и длины наклонной плоскости l (наклон последней задан, и высота наклонной плоскости h = kl, где k — известный коэффициент, синус угла наклона α). Поэтому (см. примеч. 25) имеем
(h + 2l) х = l (k + 2) х = l2,
откуда
l = x (k + 2) = х sin α + 2х.
Решение Галилея дает построение l по заданным α и х.
29 Если времена падения по АВ, AF и AD обозначим через t0, t1, t1 + t2, соответственно (t0, t2 известны, ищем t1; АВ = FD), то будем иметь
|
АВ FD |
= |
t02 (t1 + t2)2 – t12 |
= 1, |
откуда
t1 = |
t02 – t22 2t2 |
. |
Построение Галилея дает отрезок t1 (при задании отрезков t0 и t2), вероятно, самым простым и изящным образом.
30 (К стр. 278). То есть CF = CA2/BC.
31 (К стр. 284). Весьма распространено мнение, что Галилей не дал законченной формулировки принципа инерции и что это было сделано только Декартом. В «Диалоге о двух главных системах мира» (см. I том настоящего издания), действительно, инерциальными признаются движения небесных тел по круговым орбитам.
Но комментируемое нами «Замечание» написано Галилеем в период подведения итогов и в нем принцип инерции сформулирован достаточно точно: «Степень скорости, {464} обнаруживаемая телом, ненарушимо лежит в самой его природе, в то время, как причины ускорения или замедления (т. е. любого изменения скорости.— И. П.) являются внешними» — к этому можно добавить только указание на то, что изменение скорости происходит и тогда, когда сохраняется ее величина («степень») и меняется только направление. Но векторная природа скорости учитывалась Галилеем (см. День четвертый «Бесед») и неполнота его формулировки, думается, вызвана только неполнотой того набора терминов, который был в распоряжении Галилея, «...движение по горизонтали является вечным, ибо если оно является равномерным, то оно ничем не ослабляется, не замедляется и не уничтожается» — это разъяснение несомненно указывает на прямолинейность равномерного движения, вечного при отсутствии причин «ускорения или замедления».
32 (К стр. 287). Перевод в точности воспроизводит текст оригинала. Следовало бы сказать: «...непрерывно пропорциональны», так как GF — средняя пропорциональная для BG и GE (BG : GF = GF : GE).
33 (К стр. 289). Этой теоремой начинается серия предложений, представляющих собой решение ряда задач на минимум — на минимум времени падения по траекториям различного типа. Геометрические решения этих задач остроумны и поучительны. Наиболее сильным является результат, изложенный в теореме XXII и Замечании к ней (см. стр. 299—301): падение по дуге окружности происходит быстрее, чем по стягивающей эту дугу хорде.
34 (К стр. 293). Это значит, что АС : BI = BI : СЕ. Пусть АВ = l, АС = h, СЕ = х. Согласно построению Галилея,
x = |
BI2 АС |
= |
(AB – AL)2 АС |
. |
Но
|
AL LC |
= |
AB BN |
, |
откуда
|
AL AC |
= |
AB AB + BN |
= |
AB 2AB – AC |
, |
т. е.
AL = |
lh 2l – h |
, |
Следовательно,
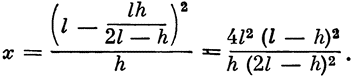
Ниже доказывается, что отрезок АХ такой длины дает решение задачи.
35 (К стр. 295). Алгебраическая выкладка, доказывающая утверждение Галилея, сейчас кажется проще, чем его геометрическое доказательство. Обозначим время падения по вертикали ХА через t, по наклонной плоскости после падения по вертикали — {465} через t1, а длину наклонной плоскости RA через lx/h (х — длина ХА). В нашем распоряжении три зависимости между t, t1, x (зависимости между путями и временами при движении по АХ, по АВ и по ХАВ). Исключение t и t1 дает выражение для х, совпадающее с найденным выше (см. примеч. 34).
36 (К стр. 301). Доказательство Теоремы XVII, данное Галилеем, изящно и проще, чем соответствующая элементарная, но громоздкая алгебраическая выкладка. Утверждение, которым начинается Замечание на стр. 301, неверно: «быстрейшее движение от одной конечной точки происходит не по кратчайшей линии, каковой является прямая» — это Галилеем доказано путем сравнения движения по прямой с движением по дуге окружности, но кривой наибыстрейшего падения — брахистохроной — является не дуга окружности, а дуга циклоиды. Однако, как справедливо указал А. Н. Долгов, в конце «Замечания» Галилей вполне точно формулирует свой результат, не придавая ему неоправданной общности. Правда, в тексте Дня первого (стр. 190, примеч. 55) Галилей дает столь же общую (и потому неверную) формулировку, как и в начале Замечания на стр. 301.
Решение задачи о брахистохроне дано было (средствами анализа бесконечно малых) в конце XVII в. Лейбницем, братьями Я. и И. Бернулли, Ньютоном.
37 Алгебраическая выкладка, которая дает решение задачи XV, проще, чем геометрические построения Галилея, но из нее нельзя было бы усмотреть замечательного Следствия, да и доказательство этого следствия требует дополнительных вычислений.
1 (К стр. 304). День четвертый построен, как и День третий: продолжается чтение латинского трактата, его третьей части «О движении бросаемых тел» и это чтение прерывается замечаниями собеседников. В День четвертый вошло изложение открытия Галилея, от которого ведет свое начало (внешняя) баллистика: траектория тела, брошенного под углом к горизонту, есть парабола (если отвлечься от сопротивления воздуха). Первые применения этого открытия: определение угла возвышения, дающего наибольшую дальность, и построение первых баллистических таблиц тоже принадлежат Галилею и излагаются тут же. Сложение скоростей двух движений, применяемое здесь Галилеем, имело принципиальное значение для механики. Во-первых, так как складывались скорости «естественного» движения падающего тела и «насильственного» движения брошенного тела, это снимало различие таких движений, отстаиваемое последователями Аристотеля. Во-вторых, это было сложение не арифметически-алгебраическое, а геометрическое, подводило к понятию о скорости, как о величине направленной. В-третьих, это сложение основывалось на независимости действия силы (тяжести) от состояния движущегося тела, так что обобщением такого подхода явился закон независимости действия сил. {466}
2 (К стр. 308). Так как рассматриваемая траектория представляет собой дугу параболы, начинающуюся в вершине, Галилей ее называет полупараболой. Этим заканчивается замечание Сальвиати, дальше — латинский текст.
3 (К стр. 309). Сагредо вполне ясно указывает, что доказательство параболичности траектории основано и на законе инерции, и на законе независимости движений (законе независимости действия сил).
Но Сагредо выдвигает возражение, которое основано на таком положении: траектория тела, притягиваемого к некоторому центру, должна приближаться к этому центру. Надо признать, что Сальвиати в своем ответе не опровергает явным образом это общее положение. В этом пункте традиция, видимо, была еще слишком сильна и для Галилея.
4 (К стр. 310). У Архимеда нет сочинения под названием «Механика» — Галилей, очевидно, имеет в виду работу «О равновесии плоских фигур».
5 (К стр. 313). По поводу этих неверных утверждений см. примеч. 49 к Дню первому.
6 (К стр. 315). С этого места Галилей начинает употреблять выражение «равен в потенции» в смысле нашего «равен геометрической сумме».
7 (К стр. 317). Галилей точно определяет, что он называет латинским словом сублимит. Этот термин, по-видимому, не встречается до Галилея, он не вошел в обиход и после издания «Бесед».
8 (К стр. 320). Вторые минуты (secundae minutae) позже стали называться короче — вторые (secundae), отсюда наши «секунды».
9 (К стр. 334). В итальянском оригинале читаем: l'impeto composto di essi sara in potenza eguale ad ambedue, cioe doppio di uno (Ed. Naz., VIII, стр. 290, строки 18—20). Нельзя понимать doppio di uno буквально, как «удвоенному одному» (таков перевод в русском издании «Бесед» 1934 г.). Это явно противоречит тому векторному правилу сложения скоростей, которое разъясняется в тексте.
10 (К стр. 326). Галилей действительно занимался явлением удара и в первые годы своей деятельности (см. его «Механику»), и в последние годы жизни. Обещание, сделанное от имени Сальвиати, было выполнено только частично, и из оставшихся после смерти Галилея фрагментарных рукописей на тему об ударе составлен День шестой «Бесед» (см. ниже).
11 (К стр. 327). То есть fa : ag = ag : ае.
12 (К стр. 331). Галилей пользуется каждым случаем, чтобы воздать должное силе математического метода, но не забывает указать на взаимоотношение этого метода и опыта: надо познать с помощью опыта причину одного явления, тогда применение математики дает возможность «постичь и установить другие явления без необходимости прибегать к опыту».
13 (К стр. 334). Доказательства последних предложений упрощаются, если воспользоваться алгебраической символикой. Галилей систематически рассматривает параболу, уравнение которой можно взять в виде y2 = рх, причем ось х направлена горизонтально влево, ось y — вертикально вниз. Амплитуда параболы a, высота ее h, {467} сублимит s и параметр р связаны соотношениями:
a2 = ph, s = |
р 4 |
, s = |
a2 4h |
. |
Горизонтальная скорость при движении по параболе выражается через s — так же, как вертикальная через высоту падения, т. е. первая скорость равна √2gs , вторая равна √2gh , поэтому их геометрическая сумма (импульс) получается в виде
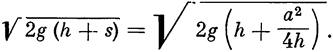
Сумма h + a2/4h состоит из слагаемых, произведение которых постоянно при постоянном a, поэтому эта сумма при постоянном а принимает минимальное значение, когда слагаемые равны, т. е. когда h = а/2 (т. е. когда а = 2h). Это доказывает теорему IV, Предложение VII.
Формула: импульс = √2g (h + s) доказывает теорему VII, Предложение X. И т. д. Например, для решения последней задачи IV надо исходить из того, что заданием импульса задана, согласно приведенным формулам, сумма h + s (пусть она равна с), а при задании амплитуды сублимит s зависит только от h,
s = |
a2 4h |
. |
Итак, h + a2/4h = с, что дает квадратное уравнение для h, имеющее два решения:
h = |
с ± √с² – a² 2 |
. |
Галилей указывает оба эти решения.
14 (К стр. 336). Вплоть до Эйлера в тригонометрических расчетах пользовались не синусами, тангенсами и т. д., а линиями синуса, линиями тангенса, ... При этом радиус «тригонометрического круга» принимали равным 10n и выбор n определялся желательной точностью вычислений. Галилей принимает n = 4, поэтому у него тангенс угла в 45° (и «полный синус», как тогда выражались) равен 10 000.
15 С этого места снова начинается латинский текст.
16 (К стр. 343). Здесь Галилей с полной ясностью проводит различение между цепной линией (которую он теоретически рассчитать не может) и параболой. Ср. примеч. 25 к Дню второму.
17 (К стр. 345). Командино (Commandino, Federigo, 1509—1575) — врач и математик, известен как усердный переводчик на латинский язык древнегреческих математиков и астрономов: Евклида (комментированный перевод «Начал»), Архимеда, Аристарха Самосского, Аполлония, Герона Александрийского, Птолемея. Из двух изданных им самостоятельных произведений одно — «Книга о центре тяжести твердых тел» (Liber de centro gravitatis solidorum, Bologna, 1562). {468}
18 Гвидо Убальди дель-Монте (правильнее: Гвидобальдо дель Монте; del Monte, Guidobaldo, 1545—1607) — выдающийся математик и механик, ученик Командино. Пользовался влиянием в Риме и при дворе Медичи. Автор ряда научных произведений, дающих основание считать его непосредственным предшественником Галилея. Одним из первых оценил дарования Галилея; по его рекомендации Галилей был приглашен на кафедру математики Пизанского университета. О Валерио см. примеч. 25 к Дню первому.
19 (К стр. 346). Заключительные реплики собеседников образуют переход от второй части «Бесед», как естественно рассматривать День третий и День четвертый, к «Приложению», содержащему теоремы о центрах тяжести, и к Дню шестому «О силе удара».
1 (К стр. 347). То, что Галилей говорит от имени Сальвиати (см. стр. 346—347) относительно Приложения, появившегося уже в первом издании «Бесед» 1638 г., полностью ориентирует читателя и подтверждается документами. В рукописном экземпляре этой работы Галилея, сохранившемся в одной из итальянских библиотек, засвидетельствовано четырьмя лицами, что «настоящие заключения и доказательства найдены Галилео Галилеем». Это свидетельство датировано 12 декабря 1587 г. Ниже добавлено следующее: «Дня 29 декабря 1587. Я, Джузеппе Молето, лектор по математике Падунской Школы, заявляю, что читал эти Леммы и Теоремы, одобряю их и считаю, что их автор хороший и опытный геометр. И написал это указанный Джузеппе собственной рукой»1. Сохранился в бумагах Галилея и неподписанный отзыв о той же его работе, данный кем-то из Болонского университета. Кроме того, в одном из писем Галилея периода подготовки и издания «Бесед» он сообщает, что нашел теоремы, вошедшие в «Приложение», когда ему шел 22-й год, после двух лет занятий геометрией»2. Итак, работа была выполнена в 1585—1586 гг., и не позже 1587 г. была окончательно отредактирована.
«Приложение» написано на латинском языке и показывает, что Галилей уже в первые годы своих занятий математикой и механикой основательно изучил Архимеда и творчески усвоил его инфинитезимальный метод.
2 (К стр. 349). Коноид — термин древнегреческой математики, обозначавший фигуру, образованную вращением параболы или гиперболы. У Архимеда в сочинении «О коноидах и сфероидах»3 параболоид вращения, т. е. параболический коноид Галилея, назван прямоугольным коноидом, гиперболоид вращения — тупоугольным коноидом, эллипсоиды вращения называются сфероидами или сфероидальными {469} фигурами, удлиненными или сплющенными в зависимости от того, является ли осью вращения большая или малая ось Эллипса.
3 (К стр. 356). Доказательство этой леммы значительно упрощается для современного читателя, если перевести его на язык алгебры.
Обозначим длины отрезков: al — через В, ас — через C, bf — через F, mn — через М, ms — через S.
Дано:
|
|
|
Надо выразить М через В. Из (2) следует:
|
F B |
= |
S 2/3C + S |
. |
Исключая отсюда и из (1) F, получим:
|
B – C B |
= |
BS (B – C) · 2/3C + S(B – C) |
, |
откуда находим S:
так как [B2 – (B – C)2]S = 2/3C(B – C)2,
то
S = |
2(B – C)2 3(2B – C) |
. |
Подставляя в (3), получаем:
|
M C |
= |
2(B – C)2 3(2B – C)C |
+ |
B + 2(B – C) 3(2B – C) |
= |
2B2 – BC 3(2B – C)C |
= |
B 3C |
, |
т. е. M = B/3, что требовалось доказать.
4 Усеченный параболический коноид (см. рис. на стр. 358) в оригинале назван «отрезком» (frustrum) параболического коноида.
5 В оригинале: erit rb diameter proportions, vel diametro aequidistans; lm, uc erunt ordinatim applicatae. Галилей пользуется здесь необычной у него терминологией, идущей от Аполлония.
6 (К стр. 363). О четырех величинах (А, В, C, D) говорили, что они образуют непрерывную пропорцию (у Галилея: continue proportionate), если
|
A B |
= |
B C |
= |
C D |
(1). |
Если обозначить через А, В, C, D, X и Y длины отрезков, соответственно АВ, ВС, BD, BE, FG и GK, то лемма III запишется так:
|
Дано: (1); |
|
|
| {470} |
Тогда X + Y = 1/4А. Все дальнейшее доказательство Галилея соответствует, в геометрической форме, компактно проведенному исключению из этих соотношений величин В, C, D.
1 (К стр. 366). День пятый впервые был напечатан в книге Вивиани, озаглавленной: «Пятая книга начал Евклида, или же Общее учение о пропорциях, рассматриваемое согласно Галилею и изложенное новым образом и впервые опубликованное Винченцио Вивиани, последним учеником Галилея, с различными приложениями, принадлежащими Галилею и Торричелли» (Флоренция, 1674 г., на стр. 61—77). После этого Пятый день всегда включался в текст «Бесед» при их переиздании в собраниях сочинений Галилея и отдельно. В Edizione Nazionale он помещен после Дня шестого. Что День пятый в том виде, в каком он появился в книге Вивиани, принадлежит самому Галилею, вряд ли можно усомниться. Из воспоминаний о Галилее и сохранившихся писем известно, что когда в апреле 1641 г. Бенедетто Кастелли посетил Галилея в Арчетри, он предложил своему ослепшему и слабеющему наставнику и другу в помощь Торричелли. Торричелли смог приехать в Арчетри только в октябре 1641 г., всего за три месяца до смерти Галилея, но он еще успел записать со слов Галилея начало нового Дня для «Бесед», предметом которого были пятое и седьмое определения 5-й книги Евклида. Эта запись Торричелли была передана потом Вивиани и опубликована последним в 1674 г., как указано выше, под заглавием «Об евклидовых определениях пропорциональности. Начало пятого дня Галилея. Добавление к четырем дням «Бесед» и математических доказательств».
День пятый по содержанию представляет собой вполне самостоятельное произведение, связанное с остальными днями «Бесед» только именами (и характерами) собеседников. Эта работа Галилея имеет лишь исторический интерес, но двоякий. Галилей отвергает, как слишком сложное, определение пропорциональности из Пятой книги Евклида, у него все получается гораздо проще: четыре величины пропорциональны, если отношение первой ко второй равно отношению третьей к четвертой. Такое определение приемлемо, если всякие две величины (у Галилея однородные, хотя он этого прямо не оговаривает) имеют отношение, и если всякие два отношения сравнимы. Это для Галилея нечто само собою разумеющееся, ибо его отношения — числа, и он уверен в выразимости числом всякого отношения (однородных величин). Итак, Галилей исходит из «наивного» убеждения, что «все — число». Но у Галилея, и это — итог длительного развития и результат работы математиков, астрономов, вычислителей столетий, отделяющих Галилея от эпохи античной науки,— число означает любое действительное число (а не только целое, как у древних греков). С этой точки зрения определения V книги Евклида совершенно излишне усложнены. Но пройдут еще три столетия, прежде чем во второй половине XIX в. математики создадут теорию действительного числа, сопоставимую по логической строгости с тем, что имеется у Евклида. Это будет оправданием того определения отношения, которое дает Галилей, которое {471} давали многие другие после Галилея. Заодно это будет доказательством того, что Галилей в своей критике Евклида несправедлив и не мог быть справедливым: полное понимание логической структуры теорий, изложенных в «Началах», достигнуто благодаря труду математиков и историков науки ряда поколений после Галилея и сравнительно недавно
Любопытно, что в VII книге «Начал» Евклида содержится определение, по сути совпадающее с определением Галилея: «Числа пропорциональны, если первое от второго будет таким же кратным, или такой же частью, или такими же частями, как третье от четвертого». Оно было приемлемо для греков, так как относилось к (целым!) числам, оно было неприложимо к любым величинам, хотя бы к отрезкам, так как если два отрезка несоизмеримы, то один из них по отношению к другому никак не может рассматриваться как результат умножения или деления на (целое!) число, или как результат применения этих обеих операций. Именно потому, что греки знали несоизмеримые величины и не имели аппарата иррациональных чисел (логически строго его не имел и Галилей), определение V книги было необходимо для построения теории пропорциональных величия. И это тонкое определение, которое ван дер Варден справедливо называет удивительным (он приписывает его Евдоксу), давало решение одной из основных проблем древнегреческой математики1.
В итальянском оригинале День пятый напечатан с пометками на полях (маргиналиями), представляющими собою, собственно, подзаголовки. А. Н. Долгов перенес эти маргиналии в составленное им оглавление всех Дней «Бесед». То же сделано в нашем издании.
2 (К стр. 367). См. примеч. 23 к Дню второму. В «Спиралях» в качестве вводных формулируются и доказываются две теоремы (Галилей одну из них приводит в начале латинского текста Третьего дня «Бесед») о равномерном движении вдоль некоторой линии. Обозначим s1 и s2 пути, проходимые в таком движении одной и той же точкой за времена, соответственно, t1 и t2; через d1 и d2 — пути, проходимые за те же времена другой точкой (в другом равномерном движении). Теоремы Архимеда выражаются пропорциями:
|
s1 s2 |
= |
t1 t2 |
(1); |
s1 s2 |
= |
d1 d2 |
(2) |
Галилей пользовался достаточно общим понятием скорости и для него любое отношение было число. Неудивительно, что эти теоремы Архимеда могли навести его на мысль об упрощенном определении пропорциональности. Но что значит «угол зрения»! — доказательство Архимеда, о котором с благодарностью говорит Сальвиати,— соответствует определению пропорциональности по Евдоксу, данному в V книге Евклида (см. указанное выше издание сочинений Архимеда, стр. 230). {472}
3 (К стр. 369). Перевод точен: в итальянском оригинале читаем: Teccesso (избыток, превышение) della prima sopra la seconda (первой над второй)... Очевидно, подразумевается «избыток» в смысле кратности — «во сколько», а не в смысле разности — «на сколько».
4 (К стр. 375). Согласно седьмому определению V книги «Начал», если кратное первой величины больше (такого же) кратного второй величины, а кратное третьей величины больше (такого же) кратного четвертой, то отношение первой величины ко второй больше отношения третьей величины к четвертой.
5 (К стр. 378). В итальянском тексте употреблены термины duplicata della proporzione — двойное (или удвоенное) отношение, triplicata della proporzione — тройное (или утроенное) отношение, что в данном случае означает вторую, соответственно, третью степень отношения — результат перемножения двух, трех равных отношений.
1 (К стр. 381). Впервые три отрывка, из которых состоит День шестой, появились при переиздании «Бесед» во втором томе собрания сочинений Галилея, изданного в начале XVIII в. во Флоренции (Opere di Galileo Galilei, In Firenze, MDCCXVIII, tomo II, 693—710). Заголовок был дан такой: «День шестой Галилея. О силе удара. В качестве дополнения к „Беседам и математическим доказательствам»
Явления удара были предметом размышлений и экспериментальных исследований Галилея почти с самого начала его научной деятельности. Не располагая сколько-нибудь законченной теорией, Галилей ничего не опубликовал по этому вопросу, кроме отрывка, включенного в «Механику» (см. стр. 37—38 в настоящем томе). Датировать отрывки, из которых составлен День шестой, трудно. Но многое здесь относится к последнему периоду деятельности Галилея. Это видно из переписки Галилея с Балиани1; в 1639 г. В ответ на хвалебный отзыв Балиани о рассуждении по поводу силы удара, вошедшем в «Механику»2, Галилей пишет, что на исследование этого вопроса он затратил многие сотни и тысячи часов и наконец нашел настолько простое объяснение, что понять его можно за полчаса; но это найдено всего несколько лет тому назад, так что написанное им раньше не может быть чем-то совершенным3. Когда же Балиани переслал ему переписанный им отрывок из «Механики», Галилей сообщил: «Это безусловно написано мною, но тому уже свыше 40 лет; с тех пор я значительно расширил изложение и дал значительно более пространные объяснения»4. Таковы последние упоминания о силе удара в переписке Галилея. {473}
Вивиани, описывая последние месяцы жизни Галилея, сообщает, что уже после опубликования «Бесед» Галилей собирался подготовить еще два Дня, и во втором из них изложить новое учение, «трактуя геометрически удивительную силу удара». Галилей говорил, что он открыл и может доказать весьма тонкие и скрытые положения, и они значительно превосходят то, что им уже опубликовано. Осуществлению этих планов помешала смерть1.
Собеседников в шестом дне по-прежнему трое, но вместо Симпличио появляется Апроино. Это имя одного из учеников Галилея по Падуанскому университету — Паоло Апроино (1586—1638). Реальный Апроино успешно закончил университет, в 1612 г. принял духовный сан и с тех пор до смерти оставался служителем церкви. Вряд ли Галилей назвал бы так третьего собеседника при жизни Апроино, и, вероятно, выбор имени был сделан Галилеем под впечатлением известия о смерти еще одного из его учеников. Если принять эти соображения, то первый отрывок Шестого дня написан или отредактирован не ранее 1638 г.
2 (К стр. 382). Антонини Даниелло (Antonini Daniello, 1588—1616) — изучал математику в Болонском университете у Катальди, потом в Падуанском у Галилея. Избрал военную карьеру, отличился на службе у венецианской республики. Пал на поле боя и с большими почестями был похоронен в его родном городе Удине.
3 ...essere l'Accademico nostro stato sempre non meno curioso che diligente sperimentatore.— Это заявление служит еще одним доказательством того, насколько ошибочна тенденция некоторых историков науки преуменьшать или даже отрицать роль эксперимента в работах Галилея. Галилей писал эти слова тогда, когда годы и слепота лишили его возможности ставить опыты, речь шла о прошлом, и его оценку надо считать достаточно объективной.
4 (К стр. 383). Галилей и здесь указывает, как основную цель исследования, выявление принципов и первопричин, определяющих сущность явления. Говоря о необычайной мощи огня (rimmenso vigore del fnoco), он имеет в виду взрывчатые вещества.
5 (К стр. 392). Как видно из текста, Галилей вполне ясно сформулировал вывод, что «сила удара» зависит от скорости, притом от относительной скорости соударяющихся тел. Второй его вывод, что сила удара может быть бесконечно велика, звучит несколько шокирующе, но в сущности, он не более парадоксален, чем распространенная трактовка конечного импульса, сообщаемого при ударе, как произведение из бесконечно большой силы на бесконечно малый промежуток времени, в течение которого сила действует. Галилею не удалось дойти в анализе явлений удара до каких-либо более определенных количественных формулировок, так как не удалось выделить необходимые для этого динамические понятия. Одной из причин является то, что Галилей анализирует слишком сложные практические задачи: забивание молотом сваи и т. п. Первые успехи в теории удара были достигнуты в середине XVII в. при анализе проще схематизируемого явления — соударения шаров (Декарт, допустивший, как известно, ряд ошибок, Марци, Гюйгенс, Врен, Валлис). {474}
6 (К стр. 396). Явление, анализируемое здесь Галилеем, сложнее, чем это следует из его схемы, даже при условии, что можно «полностью устранить возможные случайные и посторонние воздействия». При падении одного из тел в тот момент, когда оно натянет веревку, связывающую его со вторым телом (второе тело надо представлять себе поддерживаемым до этого момента, а поддержку — мгновенно снятой в тот же момент), произойдет удар, характер которого определяется степенью упругости веревки. Этот удар, вообще говоря, должен вызвать потерю кинетической энергии. Кроме того, благодаря наложению связи (внезапному натяжению веревки) произойдет перераспределение кинетической энергии между двумя рассматриваемыми телами. В схеме Галилея кинетическая энергия не может возрастать за счет уменьшения потенциальной энергии, так как центр тяжести системы после удара остается на одном и том же уровне (массой веревки пренебрегаем). Поэтому вывод, что «сохранится максимальная степень скорости», неприемлем, а «движение из ускоренного превратится в равномерное» не сразу с момента удара.
7 (К стр. 398). В первом издании «Бесед», включающем Шестой день, к этому месту дано следующее примечание: «Предупреждаем читателя, что последующее рассуждение не совсем связано с предыдущим текстом, так как Автор решил изложить его иначе, чем имел в виду, когда записывал приведенные выше соображения». Итак, здесь начинается второй из отрывков, составляющих День шестой.
8 (К стр. 401). В первом издании «Бесед», включающем Шестой день, перед следующим ниже текстом, представляющим третий и последний отрывок из числа составивших День шестой, дано такое примечание: «Среди рукописей Галилея об ударе на отдельном листе находится приведенный далее текст: он должен быть включен в Шестой день».
То, что сказано ниже, можно рассматривать как последний итог размышлений Галилея о силе удара. К каким-либо определенным результатам он и здесь не пришел и не мог прийти, не располагая еще понятиями количества движения и живой силы. Однако сказанное в этом отрывке идейно достаточно близко к тому, что дала в теории удара классическая механика после Галилея.
И. В. Погребысский
| {475} |
(К стр. 130). Приводимые Галилеем латинские термины были в его время столь обычными, что он не счел нужным переводить их на итальянский язык: deorsum значит вниз, sursum — верх, ad medium — к середине, a medio — от середины, eadem est ratio totius et partium — отношение целого таково же, как и его частей.
(К стр. 131). «С отрицающим аксиомы научные споры невозможны».
(К стр. 158). «Природа ничего не делает напрасно».
(К стр. 180). «Мрак есть отсутствие света».
(К стр. 206). «Так он сказал» — выражение, подчеркивающее безусловное признание авторитета.
(К стр. 235). «Кроме того, все, что движется круговым движением, кажется отстающим и движется больше, чем одним движением, за исключением первой сферы, почему и Земле, находящейся около центра или в центре, необходимо было двигаться двумя движениями. А если бы это случилось, необходимы были бы перемещения и сдвиги неподвижных звезд; этого, однако, не наблюдается и они всегда восходят и заходят в одних и тех же своих местах».
(К стр. 245). «Приобретают силы в пути».
(К стр. 290). «Наше знание есть некоторое припоминание».
(К стр. 295). Ad destruendum sufficit unum — буквально: «для разрушения достаточно одного», в переносном смысле: «для опровержения утверждения достаточно всего одного обстоятельства, ему противоречащего». {476}
(К стр. 302). «Сфера касается плоскости в одной точке».
(К стр. 304). Доказательство «неизвестного путем еще менее известного».
(К стр. 331). «А что вращение Земли невозможно, доказываем так».
(К стр. 336). «Если от внешнего, то не бог ли его вызывает посредством непрерывного чуда? Или ангел? Или воздух? Ведь и последнему многие приписывают (причину). Но, напротив...»
(К стр. 337). «Встают труднейшие, даже неразрешимые вопросы другого рода. Есть ли этот внутренний принцип акциденция или субстанция: если первая, то какая именно? Ибо до сих пор, кажется, не было известно круговращающегося качества».
(К стр. 338). «И даже если бы оно было, как могло бы оно обретаться в вещах столь противоположных? В огне, как и в воде? В воздухе, как и в земле? В живом, как и в лишенном жизни»?
(К стр. 339). «Si secundum... etc.» «Если же второе (а именно, если скажешь, что такой принцип есть субстанция), то это либо материя, либо форма, либо сочетание их; но и этого не позволяет столь различная природа вещей, каковы суть птицы, улитки, камни, стрелы, снег, дым, град, рыбы и т. д., которые, будучи различны по виду и роду, все, однако, двигались бы по природе своей кругообразно, при полном различии их природы и т. д.».
«Si Terra... non posset». «Если бы Земля по воле божией остановилась, то не прекратилось ли бы и остальное вращение? Если да, то неверно, будто она вращается от природы; если нет, то возвращаются первые вопросы, и, конечно, было бы удивительно, что даже при желании не могли бы устремляться чайка на рыбу, жаворонок к своему гнезду, ворон на улитку или на скалу».
(К стр. 340). «Insuper ... quiescant?» Кроме того, как происходит, что эти вещи, столь разнообразные, вращаются только с запада на восток, параллельно экватору? И что всегда они движутся и никогда не покоятся?»
«Quare... tardius?» «Почему, чем они выше, тем (движутся) быстрее, чем ниже, тем медленнее?»
«Quare... feruntur?» «Почему лежащие ближе к экватору движутся по большему кругу, дальше лежащие — по меньшему кругу?»
«Quare... volveretur» «Почему тот же шар на экваторе вращался бы весь вокруг центра по наибольшей земной окружности с быстротой невероятной, а у полюса вокруг собственного центра, без кругового пути с величайшей медленностью?»
(К стр. 341). «Почему та же вещь, например свинцовый шар, обойдя однажды Землю по наибольшему кругу, не всюду обходит ее по большому кругу, но, переместившись с экватора, он пойдет по меньшим кругам»?
(К стр. 345). «Не видит, что делает либо годовой круг меньшим, либо земной шар, поистине, гораздо большим».
(К стр. 346). «И, во-первых, если принять мнение Коперника, то критерий натуральной философии хотя и не упраздняется совершенно, но все же, как видно, сильно расшатывается».
(К стр. 352). «...cum terra... deceptio?» «...с Землею движется окружающий воздух, {477} движение же его, хотя и более скорое и быстрое, нежели любой самый быстрый ветер, не ощущается нами, но почитается за полнейший покой, если не привходит другое движение. Что же такое действительный обман чувств, если это не является обманом?».
«Praeterea... etc.» «Кроме того, мы также вращаемся от кругообращения Земли и т. д.».
(К стр. 354). «Из этого мнения вытекает, что необходимо не доверять нашим чувствам, как совершенно обманчивым или тупым при распознавании чувственного, даже ближайшего и различимого; на какую, значит, можем мы рассчитывать истину, которая берет начало от способности, столь обманчивой?».
(К стр. 369),. «Представим только, вслед за Коперником, что Земля некоей своей силой и внутренним принципом гонима с запада на восток в плоскости эклиптики, а также обращается, далее, вследствие внутреннего же принципа, вокруг собственного центра с востока на запад, в-третьих, отклоняется собственной склонностью к югу и обратно».
(К стр. 375). «В точке поворота назад наступает покой».
(К стр. 424). «Недавно видел я себя (свое изображение) у берега, когда в безветрии покоилось море».
(К стр. 450). «Таким образом, Землю вместе с Луной и всей нашей сферой стихий Коперник...»
| {480} |
|
ПРИЛОЖЕНИЯ |
| {481} |
(Очерк жизни и научного творчества)
Основные идеи Галилея — его представления о равномерном и равноускоренном движении, об относительности равномерного движения и однородности пространства, его схема круговых движении планет — были звеньями последовательного приближения картины мира к объективной действительности. Более того, именно с Галилея началось развитие классической науки, которое могло уточнить, ограничить, обобщить уже приобретенные знания, но уже не могло их отбросить. Декарт ввел представление о прямолинейном движении по инерции, Ньютон дополнил схему инерционных движений схемой силовых полей, искривляющих прямолинейные движения тел, галилеева мысль об однородности пространства (ей соответствует сохранение импульса) была обобщена в учении об однородности времени (сохранение энергии); далее, в XX столетии,— в учении об однородности псевдоэвклидова пространственно-временного континуума (сохранение энергии-импульса в специальной теории относительности) и, несколько позже,— неэвклидового четырехмерного континуума (общая теория относительности). Идеи Галилея кажутся логическим этапом подобной эволюции. Но труды Галилея в этом отношении резко отличаются от трудов следующего поколения основателей классической науки, от трудов Декарта и еще более, разумеется, от ньютоновых «Начал». Дело, в конечном счете, объясняется тем, что труды Галилея служат началом классической науки. Основы последней еще не приобрели строго логического и строго математического, характера, не отлились в канонические формы, не потеряли {482} бьющей в глаза связи с эмпирическими истоками, с социальной борьбой, с полемикой, с событиями окружающей жизни, с интеллектуальным и эмоциональным развитием и перипетиями жизни самого мыслителя. Полемика, личные реминисценции, автобиографические отступления перемежаются в трудах Галилея с теоремами динамики. Вернее, они неотделимы от позитивного содержания трактатов, а самые трактаты под час трудно отличить по жанру от памфлетов и даже от личных писем Галилея. Сказанное относится не только к таким, написанным в пылу полемики, памфлетам, как «Пробирные весы», но и к основным произведениям Галилея — к «Диалогу» и даже к «Беседам». Скрытый, логически неощутимый, по психологически необходимый подтекст, литературная форма и стиль произведений,— все это можно понять в связи с биографией Галилея и с ходом общественной борьбы конца XVI и первой половины XVII в. Поэтому, окажется, быть может, не лишним сопроводить собранные в этом издании труды Галилея не только их анализом с позиций современной науки, но и кратким очерком жизни Галилея.
Остановимся сначала на тосканских истоках мировоззрения и творчества Галилея. Он родился в Пизе 15 февраля 1564 г., в один год с Шекспиром, через пять лет после подчинения значительной част Италии испанскому владычеству, через год после Тридентского собора — важнейшего события контрреформации. Это был заключительный период итальянского Возрождения — XVI век, Чинквеченто, время, когда центр тяжести борьбы за новое мировоззрение начал перемещаться из области гуманистической литературы и искусства в область науки. Резкое перемещение произошло в результате деятельности самого Галилея. Но уже во второй половине XVI в. флорентийская толпа стала интересоваться научными вопросами и связывать споры о структуре вселенной с этическими, религиозными и политическими проблемами не в меньшей степени, чем это делало предыдущее поколение по отношению к эстетическим и литературным спорам.
Галилей вырос в гуманистической среде. Его отец Винченцо Галилей — известный флорентийский музыкант, автор трактатов по теории и истории музыки, происходил из рода, давшего Флоренции, начиная с XIV в., нескольких крупных государственных деятелен. Прах маэстро Микеля Галилея — врача, ученого, «знаменосца правосудия» (т. е. главы флорентийской республики) поныне покоится в церкви Санта Кроче под мраморным надгробием. Винченцо был его правнуком. Он женился на Джулии Амманати — дочери пизанского патриция, и здесь в Пизе родился Галилео Галилей. В 1574 г. десятилетний Галилей с матерью и годовалой сестрой Вирджинией переехали во Флоренцию, вслед за еще раньше уехавшим туда Винченцо. Младшая сестра Галилея, Ливия, родилась уже во Флоренции.
В конце XVI в., в годы отрочества и юности Галилея, во Флоренции явственней, чем в других итальянских городах, чувствовался переход к новой, по сравнению с Возрождением, культурной полосе. В течение трех столетий Возрождения — Треченто, Кватроченто и Чинквеченто — основной фарватер новой культуры проходил в области искусства, художественной литературы, историко-филологической эрудиции — того, что получило название гуманизма. Все это переплеталось с естественно-научными {483} интересами, но последние были на втором плане. К концу Чинквеченто положение начало меняться. Широкие круги населения итальянских городов, как уже говорилось, интересовались не столько пересказами и анализом античной поэзии, сколько прикладной механикой и созревавшими в этой области новыми научными понятиями. Во Флоренции эти интересы были тесно связаны с развитием ремесленной и мануфактурной техники, в Венеции, сверх того, с морской торговлей, морскими путешествиями, а следовательно, и с астрономическими наблюдениями, и в обоих городах — с артиллерией и фортификацией. Галилей последовательно воспринял и воплотил те направления культурного развития, которые могут быть условно ассоциированы с Флоренцией и Венецией.
Когда Крестовые походы вызвали быстрое экономическое развитие итальянских городов, Тоскана оказалась в особых условиях. Средиземноморская торговля сосредоточилась в Пизе, а в непосредственной близости от нее, на пересечении внутренних путей Аппенинского полуострова, в центре богатейшей области, уже давно расцветала Флоренция. Здесь торговля привела к стремительному промышленному развитию. Быстрота промышленного подъема и высокий пространственный градиент (Тоскана была окружена гораздо менее экономически развитыми, феодальными государствами) были причиной невиданного накала общественной борьбы, тесно связанной с перипетиями внешней политики. После того, как в XII в. горожане разрушили замки синьоров, во Флоренции не затихали заговоры и восстания. Они были связаны с религиозными спорами, подчас с мыслями о мироздании и об отношении человека к миру, с ранними рационалистическими представлениями о суверенности разума. Мысль об универсальном характере понятий механики, о простой, постижимой, рациональной схеме бытия могла рассчитывать в этой среде на широкую и активную поддержку.
Вернемся к судьбе Галилея. Винченцо хотел видеть сына врачом и в 1581 г. отправил его учиться в Пизу. Здесь, в Пизанском университете, интерес к прикладной механике и математике не мог реализоваться. Студенты изучали средневековых комментаторов Аристотеля. Схоластическая премудрость вызывала у Галилея непреодолимое отвращение. Ему хотелось бросить университет и вернуться во Флоренцию. Но это значило сделать бесплодными жертвы, на которые шла семья бедного музыканта, чтобы дать Галилею медицинское образование. В конце концов Галилей не выдержал и незадолго до окончания университета покинул его и вновь оказался во Флоренции.
Он тянулся к механико-математическим знаниям. У Винченцо был друг — Остиллио Риччи. Он обучал математике молодых придворных великого герцога Тосканы и преподавал математику во Флорентийской художественной академии. Втайне от Винченцо он начал давать уроки Галилею. Под руководством Риччи Галилей изучал Эвклида и позднейших математиков. Он познакомился с произведениями Архимеда. В 1586 г. Галилей пишет несколько работ (о гидростатических весах, о центре тяжести и др.). Они не публикуются, но становятся известными группе флорентийских ученых. Двадцатидвухлетний юноша приобретает первых последователей и ценителей. {484}
Среди них — маркиз Гвидобальдо дель Монте, автор механико-математических трактатов. Он представляет Галилея великому герцогу. Последний обещает юноше кафедру в Пизе. В 1589 г. она и достается Галилею. Он проводит в Пизе два года и затем покидает Тоскану. Галилей переезжает во владения Венецианской республики в качестве профессора Падуанского университета. Начинается новый, венецианский период его жизни.
В Пизе Галилей написал по-латыни трактат «О движении» (De molu). Он долго работал над текстом. Сначала трактат был полон полемических выпадов против механиков, поддерживающих аристотелевскую традицию. Потом появляется вторая редакция — в духе позднего гуманизма, с частыми риторическими отступлениями. Третья редакция придаст трактату форму диалога. Риторика исчезает вслед за полемическими выпадами. Уже в Пизе Галилей вырабатывает новый стиль научной литературы — прозрачный, точный, рассчитанный на читателя, не связанного схоластической традицией.
В Тоскане Галилей формулирует и свою эстетическую программу, свои взгляды на соотношение науки и поэзии. В 1587 г. он готовит для Флорентийской академии «Лекции о форме, положении и величине дантова ада», а позже составляет заметки о Тассо и об Ариосто. Галилей выступает против вычурности в поэзии и, одновременно, против нанизывания произвольных декоративных орнаментов в научной литературе. Трактаты, памфлеты и письма Галилея, написанные по-итальянски, были одним из основных истоков новой итальянской прозы.
Эти произведения в основном относятся к венецианско-падуанскому периоду жизни Галилея. В Падуе и в Венеции Галилей встретил новую среду. Здесь в центре прикладных проблем науки стояло море. Адриатика, суда, уходившие в отдаленные порты Средиземноморья, венецианский арсенал, где строились и оснащались корабли, приливы и отливы, которые казались Галилею доказательством новой астрономической схемы,— все это заставляло переходить от проблем земной механики к проблемам астрономии. Об этих проблемах говорили во дворцах венецианских патрициев, и развернувшаяся на страницах «Диалога» беседа во дворце Сальвиати на Большом канале имела реальные прообразы. В Венеции Галилей столкнулся и с другим. Здесь меньше чувствовались веяния контрреформации и авторитет римской курии. В годы, когда Галилей жил в пределах Венецианской республики, развернулась борьба республики против папы. Во главе группы, наиболее резко выступавшей против Рима, стоял друг Галилея Паоло Сарпи. Когда борьба привела к изгнанию иезуитов из Венеции, Галилей приветствовал этот удар, нанесенный сторонникам вмешательства папы в дела республики.
Приехав в Венецию, Галилей первое время жил у своего друга Пинелли, затем снял квартиру; приехавшая старшая сестра Вирджиния вела хозяйство. У Галилея собирались друзья: упомянутые уже Пинелли, Сарпи и Сальвиати, а также Сагредо, чье имя, как и имя Сальвиати, стало бессмертным благодаря «Диалогу», и другие венецианские патриции. Вскоре Галилей обзавелся собственной семьей. Он встретил в Венеции одинокую девушку Марину Гамба, поселил ее в Падуе, а после рождения в {485} 1600 и в 1601 г. двух дочерей (их назвали в честь сестер Галилея Вирджинией и Ливней) Гамба переехала в дом Галилея. В 1606 г. родился сын Галилея Винченцо.
У Галилея существовала мастерская, сначала механическая, а к концу пребывания в Падуе и оптическая. У него была школа: к нему ходили, а иногда у него жили молодые аристократы, в том числе отпрыски правящих домов Европы и, в их числе, сын тосканского герцога принц Козимо. Галилей обучал их математике, механике, основам артиллерии и фортификации. В этой среде царили механико-математические интересы и они определили основные направления падуанских трудов Галилея. Здесь были написаны два трактата по фортификации, был изобретен пропорциональный циркуль и подготовлена небольшая «Механика», посвященная теории простых машин.
Если рассматривать ретроспективно падуанско-венецианский период, то наиболее важным содержанием творческого пути Галилея в этот период его жизни представляется переход от задач, навеянных прикладной механикой, к применению выработанных здесь понятий к кинематике солнечной системы. Галилей стал сторонником коперниканской схемы давно, еще в юности. В Падуе в 1597 г. Галилей писал Кеплеру: «Много лет назад я обратился к идеям Коперника и с помощью его теории мне удалось полностью объяснить многие явления, которые не могли быть в общем объяснены посредством противоположных теорий. У меня появилось множество аргументов, опровергающих противоположные представления, но я их до сих пор не решился опубликовать из боязни столкнуться с топ же судьбой, которая постигла нашего Коперника, хотя и заслужившего бессмертную славу среди немногих, но представлявшегося большинству заслуживающим освистания и осмеяния, до того велико количество глупцов. Я бы все же решился выступить с моими размышлениями, если бы было побольше таких люден, как Вы, поскольку же это не так, я избегаю касаться указанной темы»1.
Обстановка в Падуе, как казалось Галилею, не давала возможности разрабатывать астрономические проблемы н находить новые аргументы в пользу коперниканской системы мира. Вообще эта обстановка не позволяла целиком отдаться научному творчеству. Галилея тяготила необходимость тратить много времени на преподавание в университете — излагать по-латыни традиционные перипатетические представления. Ближайшее окружение — друзья, ученики, корреспонденты за пределами Падуи и Венеции — образовали некоторую аудиторию, которой Галилей рассказывал по-итальянски о новых концепциях. Но ему хотелось отдавать все свое время разработке и пропаганде этих новых концепций. Венецианская республика не могла иметь ученого, освобожденного от университетских традиций в содержании излагаемых представлений и в стиле и языке изложения. Галилей надеялся получить свободу от традиционных университетских требований при дворе просвещенного монарха и — чем дальше, тем больше — стремился назад во Флоренцию. В 1608 г. тосканский герцог Фердинанд поддержал мысль о возвращении Галилея, а в следующем году, когда {486} престол перешел к ученику Галилея принцу Козимо, вопрос о переезде был сравнительно быстро решен.
В это время произошло одно из самых«важных событий биографии Галилея и вместе с тем одно из самых важных событий истории науки нового времени. Галилей впервые в истории науки обратил на небо незадолго до того созданную зрительную трубу и открыл ряд закономерностей, весьма существенных не только для астрономии, но и для характера мышления людей о мироздании.
В начале XVII в. голландские мастера изготовляли зрительные трубы, которые давали некоторое увеличение при наблюдении — сравнительно отдаленных предметов на поверхности Земли и, в частности, на море. Галилей узнал о существовании таких труб. Он решил поместить в трубе две линзы — двояковыпуклую и двояковогнутую. Изготовленная труба была направлена на звездное небо. В ночь на 7 января 1610 г. Галилей увидел холмистый ландшафт Луны. Он сразу же обратил внимание на значение этого открытия для принципиальных проблем космологии.
В космологии Аристотеля совершенное небо противостояло несовершенной Земле. Эта мысль была канонизирована богословской схоластикой средневековья. Сходство лунного пейзажа с земным казалось Галилею решающим аргументом против перипатетической схемы. Далее, Галилей обнаружил дискретную природу Млечного пути: сплошное свечение распалось на множество отдельных звезд. Затем Галилей увидел возле Юпитера небольшие звезды, причем на следующую ночь они сместились по отношению к Юпитеру. На третью ночь одна из новых звезд исчезла. У Галилея появилась мысль о спутниках Юпитера, обращающихся вокруг планеты. Такая схема казалась ему моделью солнечной системы: круговые обращения планет объясняют всю сумму астрономических наблюдений. В течение дня Галилей был обуреваем сомнениями, а затем в ночь на 12 января он убедился, что догадка его справедлива. Через два дня был открыт четвертый спутник Юпитера. Четырем спутникам Юпитера Галилей дал имя Медицейских звезд в честь герцогского дома Тосканы и четырех принцев — герцога Козимо Медичи и трех его братьев.
Галилей писал об этом открытии флорентийскому министру Велизарио Винта:
«Но наибольшим из всех чудес представляется то, что я открыл четыре новые планеты, и наблюдал свойственные им их собственные движения и различия в их движениях относительно друг друга и относительно движений других звезд. Эти новые планеты движутся вокруг другой очень большой звезды таким же образом, как Венера и Меркурий и, возможно, другие известные планеты движутся вокруг Солнца. Как только будет напечатан мой трактат, который, в форме сообщения, я разошлю всем философам и математикам, я направлю копию великому герцогу вместе с замечательным телескопом, который дает возможность убедиться в истинности сообщения»1»
Трактат, о котором идет речь, был кратким отчетом об открытиях, предназначенным для ученых Италии и других стран и написанным по-латыни,— знаменитым «Звездным вестником». {487}
Наблюдения ночного неба продолжаются. В конце 1610 г. Галилей открывает фазы Венеры и пишет тосканскому послу в Праге Джулиано Медичи: «Я посылаю Вам шифрованное сообщение о еще одном моем новом необычном наблюдении, которое приводит к разрешению важнейших споров в астрономии и которое содержит решающий аргумент в пользу пифагорейской и коперниканской системы»1.
Еще раньше он сообщил тому же Джулиано Медичи об открытых им небольших звездочках возле диска Сатурна. Они оказались видимыми краями кольца Сатурна, но об этом узнали много позже.
В 1610 г. Галилей открыл и существование пятен на Солнце.
Все эти астрономические открытия быстро приобрели широкую известность — первые благодаря «Звездному вестнику», а последующие — через письма, адресованные из Флоренции друзьям Галилея в других городах: аугсбургскому бургомистру Марку Вельзеру, Паоло Сарпп — в Венецию, Джулиано Медичи — в Прагу. В Праге «Звездный вестник» был прочитан Иоганном Кеплером, который был тогда астрономом императора. Кеплер высоко оценил присланный ему трактат и написал очень интересное «Рассуждение о «Звездном вестнике».
Немало было и враждебных откликов. Направленные против «Звездного вестника» перипатетические памфлеты послужили поводом для ответных полемических выступлений Галилея, и сейчас еще поражающих удивительной ясностью, убедительностью и глубиной аргументов, блестящим стилем и огненным темпераментом мыслителя.
Но полемика не могла устранить новые и новые нападки на гелиоцентрические идеи Галилея. Эти нападки выражали растущую реакцию и были началом серии доносов, интриг, расследований, переплетавшихся с научными спорами и приведших в конце концов к инквизиционному процессу.
Внешне судьба Галилея, ставшего в 1610 г. «первым философом и математиком великого герцога Тосканы», была блестящей. Во Флоренции он был приближенным Козимо II, получил право поселиться в любой из загородных вилл герцога, носил золотую цепь — знак придворного достоинства. Но все увеличивалось число враждебных выступлений и, еще больше, число тайных интриг.
Галилей чувствовал, что над гелиоцентризмом нависли тучи, и хотел предотвратить грозу. Он решил поехать в Рим. Эта поездка и вообще вся деятельность Галилея, направленная на защиту коперниканства в церковных кругах, стали непонятны уже следующему поколению. Во второй половине XVII в. ученые были убеждены в том, что объективная достоверность научной теории достаточна для ее признания. Впоследствии эта мысль еще более укрепилась. Эйнштейн писал о Галилее:
«Что касается Галилея, я представлял себе его иным. Нельзя сомневаться в том, что он страстно добивался истины — больше, чем кто-либо иной. Но трудно поверить, что зрелый человек видит смысл в воссоединении найденной истины с мыслями поверхностной толпы, запутавшейся в мелочных интересах. Неужели такая задача была для него важной настолько, чтобы отдать ей последние годы жизни?.. Он без особой {488} нужды отправляется в Рим, чтобы драться там с духовенством и политиканами. Такая картина не отвечает моему представлению о внутренней независимости старого Галилея. Не могу себе представить, чтобы я, например, предпринял бы нечто подобное, чтобы отстаивать теорию относительности. Я бы подумал: истина куда сильнее меня, и мне бы показалось смешным донкихотством защищать ее мечом, оседлав Росинанта...»1
Но то, что могло показаться смешным в XX в., было весьма серьезным в XVII в., в его первой трети, в момент подготовки «Диалога». На заре классической науки нужно было не только преобразовать представления людей о мире, но и преобразовать самый стиль их мышления, с тем, чтобы новая наука могла войти в человеческие головы.
Поэтому пропагандистский темперамент Галилея был исторически оправданным. Неоправданными оказались его надежды на поддержку в среде прелатов и светских властителей Италии.
В марте 1611 г. Галилей прибыл в Рим, поселился во дворце тосканского посольства, начал обход кардиналов, появился в иезуитской коллегии и, наконец, получил аудиенцию у папы. Все встречают его весьма благосклонно. Астрономы римской иезуитской коллегии проверяют наблюдения Галилея и склонны признать их. Кардинал Маттео Барберини — будущий папа Урбан VIII — давнишний сторонник Галилея и ценитель его механико-математических работ пишет самые лестные для Галилея ответные письма флорентийским аристократам, снабдившим ученого своими рекомендательными посланиями. Наиболее видный римский теолог, фактический глава иезуитов и инквизиции кардинал Роберто Беллармино запрашивает иезуитскую коллегию об открытиях Галилея и получает положительный отзыв. Галилея торжественно принимают в состав Академии деи Линчей — общества естествоиспытателей. Папа встречает Галилея благосклонно. Но вся благосклонность не выражала, а скрывала действительную позицию церкви. Иезуиты, доминиканцы, инквизиция, римская курия в целом рассчитывали на то, что Галилей ограничится чисто условной трактовкой гелиоцентризма и не станет приписывать схеме Коперника объективную реальность. Такая надежда позволяла курии не торопиться с официальным осуждением коперниканства и, тем более, не торопиться с репрессиями по отношению к Галилею. Но церковь не отвергала, а резервировала и осуждение, и репрессии. Галилеи не почувствовал в Риме веяний реакции, но другие их чувствовали и понимали, что тридентский дух контрреформации становится все более враждебным научным концепциям.
Новый тосканский посол Гвиччардини приехал в Рим, когда там находился Галилей, и впоследствии писал:
«Когда я сюда впервые прибыл, я его застал здесь, и он провел несколько дней в этом доме. Его учение и кое-что другое не доставило никакого удовольствия советникам и кардиналам святого судилища, в числе других Беллармино сказал мне, что хотя почтение, питаемое ко всему, что касается его светлости, и велико, но что если Галилей зашел бы слишком далеко, то как бы не пришлось прибегнуть к какой-нибудь {489} квалификации его деяний. Мне кажется, что некоторые указания и предупреждения, которые он тогда получил от меня, находясь в этом доме, пришлись ему не по вкусу. Не знаю, изменилось ли его учение или его настроение, но знаю только, что некоторые братья доминиканского ордена, которые имеют большое влияние в святой инквизиции, весьма к нему не расположены, а здесь не такая страна, чтобы являться сюда для диспута о Луне и чтобы желать в наш век защищать или предлагать новые учения»1.
Дальнейшие события жизни Галилея были предопределены нараставшим стремлением римской курии воспрепятствовать объективной трактовке гелиоцентризма и, с другой стороны, постоянным стремлением Галилея обосновать подобную трактовку, вывести ее из наиболее общих представлений о движении (относительность равномерного движения). Такая тенденция нарастала. Галилей по самым различным поводам возвращался к мысли о независимости объективной действительности от познания, о достоверных научных представлениях, соответствующих объективной действительности. В 1611 г. Галилей высказывает эту мысль в весьма характерной для того времени форме. Он хотел ответить на письмо некоего Сассетти, отрицавшего значение астрономических открытий Галилея, так как найденные им факты не упоминались в канонизированных старых книгах. Отсюда следует, возражает Галилей в ответном памфлете, что для Сассетти объективное бытие процессов природы зависит от того, известны ли они ученым. «Разумеется, я не поверю,— пишет Галилей,— что в древние, более невежественные столетия природа отказалась от создания огромного разнообразия растений, животных, драгоценных камней, металлов и минералов, не наделила животных частями тела, мышцами и органами, не привела в движение небесные сферы, в целом не создала и не управляла всеми явлениями только потому, что непросвещенные люди того времени не знали свойств растений, камней и ископаемых, не разбирались в функциях живого организма и ими не были открыты звездные пути. И в самом деле смешно верить, что начало бытия предметов природы следует за возникновением наших представлений о них. Но коль скоро чистый разум должен быть причиной существования вещей, необходимо признать, что эти же вещи одновременно существуют и не существуют (существуют для тех, кто их представляет, и не существуют для тех, кто о них не знает), или согласиться, что представления нескольких или даже одного человека уже обеспечивают их существование; но в этом последнем, не требующем всеобщности случае достаточно, если кто-либо один составит представление о свойствах Медицейских планет, чтобы они появились на небе и чтобы остальные удовлетворились их созерцанием»2.
С такой гносеологической установкой было связано отношение Галилея к традиционным представлениям. Оно проявилось в очень яркой форме при подготовке основной работы Галилея по гидростатике «Рассуждения о телах, пребывающих {490} в воде». Для истории науки наибольшее значение имеют позитивные идеи, высказанные в этом трактате: определение удельного веса, применение понятия momento к проблеме гидростатического равновесия и т. д. Для биографии Галилея в более узком смысле такое же значение имеет полемика против перепатетических представлении о плавающих телах.
Трактат вызвал ряд враждебных откликов, были напечатаны работы, оспаривающие выводы Галилея об удельном весе и плавании тел, и защищающие перипатетическое учение о зависимости плавания тела от его формы. Но линия обороны перипатетизма переместилась теперь в новую область. Противники Галилея отвечали ему уже не столько трактатами, сколько доносами в инквизицию. Впрочем, граница тут не была четкой: ссылки на «очевидность» и на авторитеты перемежались ссылками на тексты святого писания, из которых видно противоречие между взглядами Галилея и догматами религии. Этот перенос линии обороны соответствовал переходу Галилея от проблем земной механики к проблемам кинематики неба. Во всяком случае, подходя к этому периоду жизни Галилея, историк должен пользоваться не столько литературными источниками, сколько архивными материалами. Подготовка инквизиционных процессов, резко изменивших жизнь Галилея, происходила по большей части втайне и ее раскрыли (далеко неполностью) документы римской курии, опубликованные в течение последнего столетия, а также переписка Галилея (кое-что становилось известным Галилею и его друзьям).
Клерикальная реакция все чаще отказывалась от научных, хотя бы по форме, аргументов в пользу геоцентрической схемы и заменяла их чисто догматическим аргументом: движение Солнца — истинное движение, потому что оно соответствует буквальному смыслу библейских текстов, а свободное толкование этих текстов веде! к ереси. Один из приближенных папы монсиньор Агукки в 1613 г. писал об аргументах против Коперника: «Первое — это авторитет святого писания, которое во многих местах с большой ясностью утверждает противное. Я не игнорирую ответов, которые можно предложить для защиты, но я думаю, что они не удовлетворят тех, кто к подобному истолкованию текстов, имеющих очень ясный смысл, не считает возможным прибегать, особенно потому, что еретики, охотно пользуясь такими толкованиями, тем самым делают их очень подозрительными»1.
Об относительности движения было известно; о ней писали многие. Задача, если ее сформулировать современным языком, заключалась в поисках привилегированной системы отсчета. Официальная точка зрения состояла в следующем: из различных возможных систем отсчета привилегированной будет система, в которой тела движутся в соответствии с текстами святого писания, т. е. система, в которой Земля неподвижна. Движение Солнца вокруг Земли — истинное движение, движение Земли может быть в лучшем случае лишь условной схемой, не претендующей на объективный смысл.
Галилей принял бой. На выступления своих противников он ответил в известном смысле обратной концепцией: истолкование церковных книг неоднозначно и мы должны {491} выбирать из них такое, которое соответствует научным, в данном случае астрономическим наблюдениям. В письме к своему другу, пизанскому профессору Кастелли (это письмо распространялось в большом числе экземпляров и было предназначено для широкого круга) Галилеи говорил: «Поскольку речь идет о явлениях природы, которые непосредственно воспринимаются нашими чувствами или о которых мы умозаключаем при помощи неопровержимых доказательств, нас нисколько не должны повергать в сомнение тексты писания, слова которых имеют видимость иного смысла, ибо ни одно изречение писания не имеет такой принудительной силы, какую имеет любое явление природы»1.
В декабре 1614 г. доминиканец Томмазо Каччини выступил против Галилея с проповедью, которая была, по-видимому, частью детально разработанной интриги. В феврале следующего года, одновременно с выходом в Неаполе коперниканскон книги Фоскарини «Письмо отца настоятеля Паоло Антонио Фоскарини, члена ордена кармелитов, к Себастьяну Фантони, генералу ордена, о мнении пифагорейцев и Коперника о движении Земли и неподвижности Солнца и о новой пифагорейской системе мира», патер Лорини написал донос на Галилея в римскую инквизицию и Каччини отвез этот донос в Рим.
В Риме друзья Галилея пытались выяснить реакцию инквизиции. Беллярмино сказал им, что ничего не знает о доносе. В действительности донос Лорини уже обсуждался в присутствии Беллярмино и было решено затребовать из Флоренции оригинал письма Галилея к Кастелли. Сам Беллярмино, участвуя в подготовке инквизиционного преследования коперниканцев, толкал их в непосредственных беседах и письмах к конвенционалистической трактовке гелиоцентризма. Он писал Фоскарини: «Во-первых, мне кажется, что Ваше священство и господин Галилео мудро поступают, довольствуясь тем, что говорят предположительно, а не абсолютно, я всегда полагал, что так говорили Коперник. Потому что, если сказать, что предположение о движении Земли и неподвижности Солнца позволяет представить все явления лучше, чем принятие эксцентров и эпициклов, то это будет сказано прекрасно и не влечет за собой никакой опасности. Для математика этого вполне достаточно. Но желать утверждать, что Солнце и действительно является центром мира и вращается только вокруг себя, не передвигаясь с востока на запад, что Земля стоит на третьем небе и с огромной быстротой вращается вокруг Солнца,— утверждать это очень опасно, не только потому, что это значит возбудить всех философов и теологов-схоластов, это значило бы нанести вред святой вере, представляя положения святого писания ложными»2.
Между тем инквизиционное судопроизводство шло своим порядком. Галилей узнал о нем и решил поехать в Рим. Он снова посетил прелатов и влиятельных светских аристократов, и снова был принят папой, и снова получил ряд устных и письменных заверений об отсутствии серьезных обвинений. Галилея согласились пока не {492} трогать. Но гелиоцентризм решили осудить. 5 марта 1616 г. конгрегация индекса внесла книгу Коперника в число запрещенных книг.
Декрет 1616 г. разорвал связи Галилея с его учениками, единомышленниками, корреспондентами. Галилей замолчал. Но неполностью и не навсегда. Через 7—8 лет после запрещения гелиоцентризма появились две работы Галилея — «Пробирные весы» и «Послание к Инголи», где изложены исходные, наиболее общие идеи Галилея, из которых он выводил гелиоцентрическую концепцию. В первом из этих произведении, в «Пробирных весах», в связи с галилеевой, вообще говоря, ошибочной теорией комет формулируется основа нового мировоззрения — сведение объективных свойств тел к их пространственным свойствам.
«Никогда,— говорит Галилей, — я не стану от внешних тел требовать чего-либо иного, чем величина, фигура, количество и более или менее быстрые движения для того, чтобы объяснить возникновение ощущений вкуса, запаха и звука, я думаю, что если бы мы устранили уши, языки, носы, то остались бы только фигуры, числа, движения, но не запахи, вкусы и звуки, которые, по моему мнению, вне живого существа являются не чем иным, как только пустыми именами»1.
«Пробирные весы» были направлены против теории комет, выдвинутой Орацио Грасси в римской иезуитской коллегии. Орден иезуитов хотел ответить Галилею, но этому помешал новый папа. Незадолго до выхода «Пробирных весов» Маттео Барберини занял папский престол под именем Урбана VIII. Галилей рассчитывал на некоторое смягчение антикоперниканской реакции и позволил себе опубликовать работу, содержавшую прямую защиту и обоснование гелиоцентризма. Это был ответ на принадлежащее Франческо Инголи и появившееся в 1616 г. «Рассуждение о месте Земли и о ее неподвижности, против системы Коперника». Теперь Галилей решил, что новый понтификат делает возможной защиту коперниканства, и в 1624 г. подготовил «Послание к Инголи», которое распространилось в списках во всех культурных центрах Италии
«Послание к Инголи» содержит идею относительности равномерного движения, идею, которая здесь противостоит перипатетическим аргументам: если бы Земля двигалась, это можно было бы обнаружить по отклонению падающего с башни груза от вертикальной линии, существованием ветра, образованного воздухом, отстающим от движения земной поверхности, и. т. д. Галилей рисует мысленный эксперимент: в каюте корабля струйка дыма поднимается строго вверх, бабочки летают с одинаковой скоростью во всех направлениях, капли воды попадают точно в подставленное узкое горлышко сосуда.
Эти первоначальные наброски понятия инерции и относительности, впоследствии вошедшие в «Диалог», имеют первостепенное значение для характеристики метода Галилея. Галилей стремился к тому, что позже, в нашем столетии, Эйнштейн назвал «внутренним совершенством» научной теории, к максимальной общности ее исходных принципов, к ее естественности, к максимальному исключению допущений, сделанных {493} ad hoc. Галилеи вывел гелиоцентрическую схему из весьма общих кинематических соображений, из принципа относительности равномерного движения.
О жизни Галилея в период между «Пробирными весами» и «Диалогом» мы имеем довольно много сведений, благодаря сохранившимся письмам его старшей дочери. Напомним, что эта дочь, ее назвали Вирджинией, родилась в Падуе в 1600 г., а ее младшая сестра Ливия — в следующем году. Когда Галилей переехал во Флоренцию, он оставил Марину Гамба в Падуе, а детей взял с собой. Перед Вирджинией и Ливией — незаконорожденными бесприданницами лежала лишь одна, не слишком веселая, дорога — в монастырь. Осенью 1613 г. их взяли послушницами во францисканский монастырь в Арчетри — предместье Флоренции, а позже они стали монахинями. Вирджиния приняла в монашестве имя Марии Челесты, а Ливия — Арканджелы. Сохранилось 124 письма Марин Челесты, отправленных Галилею с 1623 г. до конца 1633 г., до безвременной смерти девушки. Переписка была прервана в 1631 г., когда Галилей оставил свой дом в Белласгардо — другом предместьи Флоренции — и поселился в Арчетри. Потом, в 1632—1633 гг., во время поездки Галилея в Рим и инквизиционного процесса переписка возобновилась — ненадолго. Галилей писал дочери очень часто, но его письма не найдены. Вероятно, после процесса Галилея и смерти Марии Челесты монастырское начальство уничтожило эти опасные по тому времени рукописи узника инквизиции.
Письма Марии Челесты рисуют трогательный образ чистой и преданной души, живущей интересами Галилея. Бедная затворница сообщает о деталях безрадостной монастырской жизни и пересылает Галилею переписанные ее рукой документы — копии посланий, полученных Галилеем от его многочисленных корреспондентов, а также копии его ответов. Мы можем восстановить ту атмосферу, в которой Галилей жил в период подготовки «Диалога». В письмах Марии Челесты содержатся сведения о быте в Белласгардо, о родственниках, живших в Белласгардо, о судьбе сына Галилея Винченцо (он был признан в Риме законным сыном Галилея, получил стипендию, но, не пожелав надеть необходимую для этого сутану, вернулся во Флоренцию, женился на сестре монастырской подруги Марии Челесты; в переписке много внимания уделено этим событиям, как и жизни семьи Галилея в целом). И, наряду с этим потоком повседневности,— отражение борьбы за гелиоцентризм, попыток Галилея повлиять на Урбана VIII и прелатов Рима, и, прежде всего,— работа над подготовкой «Диалога».
В марте 1630 г. рукопись «Диалога» была, наконец, готова. Кастелли уже говорил в Риме об опубликовании книги. Приближенные папы: Риккарди (он носил титул магистра святого дворца и был цензором Рима, ставившим «Imprimatur», т. е. официальное разрешение для печатания рукописи) и секретарь Урбана VIII Чиамполи обнадежили его. В начале мая Галилей отправился с рукописью в Рим. Там сразу же начались задержки. Первоначальное название книги (она была названа: «Приливы и отливы») было отвергнуто. Дело в том, что Галилей считал явления приливов и отливов результатом сложения суточного и годового движения Земли и решающим доказательством объективной истинности гелиоцентризма, а именно такая трактовка была {494} наиболее одиозной в глазах церкви. Далее, от Галилея потребовали приложить к книге заключение о неисповедимости путей провидения и возможности создания мира совсем иным, непостижимым для разума способом. Речь опять-таки шла об отказе от однозначной истинности результатов науки. Далее, нужно было сказать, что защита коперниканства в «Диалоге» — чисто условная защита. Галилей написал в предисловии, что аргументы в пользу гелиоцентризма должны лишь показать компетентность католицизма по отношению к учению, отвергнутому «спасительным декретом» 1616 г.
Почему Галилеи шел на компромиссы? В этом, прежде всего, выражалась глубокая уверенность в абсолютной убедительности астрономических аргументов, которые разрушат Карфаген перипатетизма, несмотря на любые оговорки и благочестивые ссылки на условность осужденной церковью схемы. Галилей видел в «Диалоге» завершение многолетнего труда, которое должно появиться любой ценой и он ни на мгновение не сомневался в том, что снаряд попадет в цель. Компромисс не коснулся того, что в творчестве Галилея принадлежало векам. Забегая вперед, нужно сказать, что компромиссные оговорки (так же как неправильная по существу теория приливов, так же как все места «Диалога», где Галилей не мог оперировать позднейшими, более точными и общими понятиями и констатациями) не могли помешать решению исторической задачи книги.
В июне Галилей вернулся во Флоренцию и вскоре получил от Кастелли сообщение о новых затруднениях. Кастелли советовал печатать книгу во Флоренции и как можно скорее. Но в Риме отказывались поставить «Imprimatur» на книге, выходящей во Флоренции. По-видимому, в Риме вели какую-то неясную для Галилея игру. Это было тяжелое лето. Больной, усталый, измученный жарой флорентийского лета, бесконечными заботами, постоянной тревогой за «Диалог», Галилей подготовлял книгу к печати. В июле Риккарди послал флорентийскому инквизитору текст предисловия. Книгу начали печатать. В начале 1632 г. она вышла в свет под названием: «Диалог Галилео Галилея академии Линчей Экстраординарного Математика Пизанского Университета и Главного Философа и Математика Светлейшего Великого Герцога Тосканского, где в четырехдневных беседах ведется обсуждение двух Основных систем Мира Птолемеевой и Коперниковой. Предлагаются неокончательные философские и физические аргументы как с одной, так и с другой стороны». На оборотной стороне титульного листа редко встречавшееся количество «Imprimatur»: Риккарди, генерального викария Флоренции, генерального флорентийского инквизитора и цензора тосканского двора.
«Диалог» — беседа трех венецианских патрициев во дворце Сагредо на Большом канале. Сагредо и Сальвиати высказывают взгляды Галилея и аргументируют систему Коперника. Это имена уже знакомых нам умерших друзей Галилея (Сальвиати — в 1614 г., Сагредо — в 1620 г.).
Традиционную систему мира защищает перипатетик Симпличио, чье имя принадлежало одному из ранних комментаторов Аристотеля. Беседа первого дня посвящена проблеме мировой гармонии, Аристотель видел ее в статической схеме естественных {495} мест, Галилей — в кинетической схеме равномерных движений. Далее речь идет о суточном вращении Земли. Галилей хочет показать, что «все опыты, могущие быть произведенными на Земле, не дают достаточных доказательств ее подвижности, что все явления могут происходить совершенно одинаково как при подвижности Земли, так и в случае пребывания ее в покое». Это доказательство основано на идее равномерного движения предоставленного себе тела и относительности такого движения. Указанные идеи излагаются в течение второго дня беседы. На третий день беседа касается годового обращения Земли и других планет вокруг Солнца. Сальвиати и Сагредо заставляют Симпличио, не способного противостоять их аргументам, нарисовать на бумаге схему концентрических круговых орбит планет. Четвертый день — изложение галилеевой теории приливов и отливов.
В августе 1632 г. во Флоренции было получено распоряжение римской курии о конфискации «Диалога». Урбан VIII назначил комиссию для подготовки инквизиционного процесса. Получив доклад этой комиссии с обвинениями по адресу Галилея, папа созывает конгрегацию инквизиции и вызывает Галилея в Рим. Начинается процесс, и Урбан подвергает Галилея лицемерной и грубой процедуре инквизиционных допросов (в том числе допросов с угрозой пытки). Гнев папы обрушивается на его приближенных, виновных в выпуске книги Галилея. Жестокость расправы с Галилеем объясняется характером Урбана и особенностями исторического момента.
Урбан VIII был представителем второго поколения прелатов контрреформации. Высшее католическое духовенство до Реформации соединяло политические интриги с религиозным индеферентизмом и в общем соответствовало по своему облику известной характеристике, которую мы находим у Маколея: «Когда началось в Европе великое умственное движение, когда был опровергаем догмат за догматом, когда народ за народом расторгал свою связь с преемником св. Петра,— тогда стала очевидной опасность вверять церковь главам, которых высшая слава состояла в том, что они были хорошими ценителями латинских сочинений, картин и статуй, ученые занятия которых имели языческий характер и которых подозревали в том, что они тишком смеялись над совершаемыми ими таинствами...»1.
На смену изысканному скептицизму пришла догматическая непоколебимость и фанатическая жестокость прелатов контрреформации. Но в XVII в., особенно с началом Тридцатилетней войны, господствующий тип деятелей римской курии стал иным. Он соединил пороки двух предыдущих поколений, и Римом правили беспринципные участники и организаторы заговоров, коалиций, дипломатической игры и военных столкновении. Их фанатическая энергия была направлена на накопление фамильных сокровищ и укрепление личной власти. Типичным представителем высшего духовенства этой эпохи был Урбан VIII, происходивший из флорентийской семьи, накопившей торговыми операциями колоссальное состояние, удачливый карьерист, нунций во Франции, выдвинутый французской партией на престол св. Петра. Это был человек, у которого догмат непогрешимости стал постоянной и личной самооценкой, подозрительный, {496} грубый, не терпевший какой бы то ни было самостоятельной мысли. Как пишет Ольшки, «слепая самоуверенность, питавшаяся придворной угодливостью выбранного им самим окружения, заставляла считать его сангвинический темперамент силой духа, его упрямство — энергией, его капризы — гениальностью, его любовь к театральной пышности — эстетическим вкусом и его отношение к поэтам и ученым — подлинным меценатством»1.
В начале 30-х годов Урбан VIII находился в весьма сложном положении. В борьбе против императора Испании и австро-испанской партии в Италии он опирался на поддержку Ришелье, Густава-Адольфа и протестантских князей Германии. Падение Ля-Рошели, развязавшее руки Ришелье, отстранение Валленштейна, интриги «серого кардинала» отца Жозефа в Германии и победы Густава-Адольфа улучшили положение Урбана VIII как светского главы папской области, но союз с протестантами стал поводом для нападок австро-испанской партии на главу католической церкви. В 1632 г. после гибели Густава-Адольфа союз со шведами стал явным и, вместе с тем, бесполезным. Нападки на папу усиливались. В этот тяжелый для него момент разъяренный Урбан VIII выслушал доклад инквизиции о «Диалоге». Раздражение соединилось с расчетом: инквизиционный процесс должен был восстановить вселенский духовный авторитет Рима, пошатнувшийся после перипетий Тридцатилетней войны.
Урбан вызывает Галилея в Рим. В случае задержки, ученого должны были привезти в Рим в кандалах. В январе 1633 г. Галилей отправляется в Рим и 12 апреля предстает перед генеральным комиссаром инквизиции Винченцо Макулано. Галилею вменяют в вину сознательное нарушение прямого, объявленного ему в 1616 г. предписания инквизиции. Для этого, как можно думать, акты процесса 1616 г. были подделаны: фигурирующее там «увещевание» — неофициальная беседа с Беллармино, было заменено официальным предписанием. Кроме того, в актах, там, где речь идет о запрещении защиты коперниканства, появились слова: «каким бы то ни было образом». Это отнимало возможность ссылаться на условный характер коперниканских аргументов. Но Галилей предъявил письмо Беллярмино, где удостоверялось, что Галилей не подвергался процедуре официального запрещения, а также письмо Беллярмино к Фоскарини с одобрением позиции Галилея — приписанной ему здесь условной трактовки гелиоцентризма. После этого первоначальный план процесса был по существу оставлен. От Галилея потребовали признания того, что он вышел в «Диалоге» за пределы условной трактовки. Галилей признал свою вину, объяснив ее жаждой славы, заставившей его с максимальной убедительностью излагать условные аргументы. Далее, в июне 1633 г., заседание конгрегации под председательством Урбана VIII постановило подвергнуть Галилея допросу с угрозой пытки (поправки в акте заставили Вольвиля заподозрить и здесь последующий подлог: было выброшено, как думал Вольвиль, упоминание о действительной пытке). В акте говорится: «Ознакомившись {497} со всем ходом дела и выслушав показания, святейший определил допросить Галилея под угрозой пытки и, если устоит, то после предварительного отречения, как сильно подозрительного в ереси, в пленарном собрании конгрегации святой инквизиции, приговорить к заключению по усмотрению святой конгрегации. Ему предписано не рассуждать более письменно пли устно каким-либо образом о движении Земли и о неподвижности Солнца и о противном, под страхом наказания как неисправимого. Книгу же, сочиненную им под заглавием «Диалог Галилея Линчео» запретить»1.
Галилей на допросе настаивал на своих предшествующих объяснениях и поэтому был признан «сильно подозрительным в ереси», а не «неисправимым еретиком». Ему грозил не костер, а заключение. 22 июня в доминиканском монастыре Santa Maria Sopra Minerva Галилей выслушал приговор — отречение и заключение — и произнес формулу отречения.
Компромисс начался раньше — с благонамеренных оговорок в предисловии и в тексте «Диалога». Теперь он сохранил Галилею жизнь, не сохранив личной свободы. Но он сохранил возможность развить идеи «Диалога» дальше, в таком направлении, где они стали началом классической картины мира, в которой не оставалось места не только богословским догмам, но и какому бы то ни было креационизму. Когда, на значительно более высоком уровне развития классической картины мира, Лаплас на вопрос, почему в его работах не упоминается бог, ответил Наполеону, что он при изложении системы мира «не встретил необходимости в подобной гипотезе», это было историческим оправданием компромисса 1633 г.
Легенда приписала Галилею фразу: «И все-таки вертится» (Eppur si muove), якобы произнесенную после отречения. Такая фраза не была произнесена. Тем не менее, легенда обладает в известном смысле исторической достоверностью или, лучше сказать, она в какой-то мере отвечает действительному историческому смыслу деятельности Галилея после приговора и отречения. «Eppur si muove» — это символ той напряженной работы мысли, которая устранила из картины природы статическую гармонию и заменила ее кинетической гармонией мироздания. В «Диалоге» эта гармония складывалась из равномерных движений предоставленных себе тел. В следующем, написанном после процесса 1633 г., в условиях бдительного надзора инквизиции, фундаментальном труде Галилея сделан шаг к более сложной механической картине мира, складывающейся из ускоренных движений в силовых полях.
Этот труд — «Беседы и математические доказательства» — был начат в самое ближайшее время после трагической сцены в Santa Maria Sopra Minerva. Прожив недолгое время в палаццо тосканского посольства в Риме, Галилей поселился у пригласившего его к себе архиепископа Сиены Асканио Пикколомини — ученика Кавальери, живо интересовавшегося новыми механико-математическими теориями. Научные интересы и начатая работа над новой книгой преобразили Галилея. Еще недавно разбитый следствием и приговором, он обрел силы для нового наступления на твердыни традиционной концепции. Прожив пять месяцев в Сиене, Галилей вернулся в Арчетри. {498} Здесь его ждал новый удар: Мария Челеста, ослабевшая от горя, не вынесла болезни и умерла. Галилей тяжело переживал эту утрату. Он поселился в своем доме в Арчетри, где агенты инквизиции наблюдали за ним, чтобы воспрепятствовать связям с друзьями и единомышленниками.
Инквизиции удалось затруднить эти связи, в некоторых случаях оборвать их целиком, но не удалось помешать публикации «Бесед».
В 1634 г. французский посол граф Ноайль приехал в Рим с радостной для Урбана VIII вестью. Ришелье решил начать войну с Испанией. Ноайль мог требовать от папы многого. Уезжая, он попросил разрешить Галилею выехать из Арчетри. Встреча Ноайля с Галилеем состоялась между Флоренцией и Сиеной и ученый вручил французскому вельможе рукопись «Бесед». Но и во Франции книгу не удалось опубликовать. Она была издана в 1638 г. в протестантском Лейдене. К этому времени зарубежные друзья Галилея выпустили латинский и английский переводы «Диалога». В Лейдене новая книга была напечатана по-итальянски. Она имеет название: «Беседы и математические доказательства о двух новых науках, относящихся к механике и местному движению, синьора Галилео Галилея первого философа и математика великого герцога Тосканы».
В «Беседах» участвуют снова Сальвиати, Сагредо и Симпличио. Последний уже не спорит с новыми идеями, и его вопросы лишь помогают позитивному изложению новых идей. Затем он уступает место новому собеседнику Апроино — так звали умершего в 1638 г. венецианского единомышленника Галилея.
Две новые науки, о которых идет речь в названии книги,— это сопротивление материалов и учение о равномерно-ускоренном движении. Галилей рассматривает вопрос о механическом подобии: конструкция небольших размеров устойчива, а подобная ей большая конструкция разрушается вследствие собственного веса. Анализ указанной проблемы приводит к учению о внутренних порах в веществе, объясняющих сцепление его частиц.
Внутри этих частиц также, существуют поры, гарантирующие компактность частиц, и иерархия все меньших пор и, соответственно, все меньших дискретных частиц твердого вещества бесконечна. Из бесконечно малых элементов состоит жидкость. Переход твердого вещества в жидкое — это переход к бесконечному числу бесконечно малых элементов. В этой связи Галилей излагает свое учение о бесконечности.
Учение о равномерно-ускоренном движении также связано с понятием бесконечности. Основной закон равномерно-ускоренного движения падающих тел — пропорциональность пройденного пути квадрату прошедшего времени — исключает аристотелевскую мысль о зависимости скорости падения тела от его массы. Вместе с тем этот закон вводит представление о скорости, меняющейся от мгновения к мгновению и от точки к точке. Тем самым на каждом конечном отрезке проходимого пути движение рассматривается как бесконечное множество состояний тела. Равномерное движение также рассматривается с подобной точки зрения. Если существует понятие непрерывного изменения скорости, то и ее сохранение рассматривается от мгновения к мгновению и от точки к точке. Именно таков смысл требования Галилея: рассматривать {499} скорость в случае равномерного движения в любые равные промежутки времени. Если равномерное движение служит физическим эквивалентом негативного определения бесконечного множества состояний тела (его скорость одна и та же в следующие один за другим бесконечно малые промежутки времени), то равномерно-ускоренное движение — эквивалент позитивного определения такого множества, невырожденного различия между состояниями в последовательно следующие одно за другим бесконечно малые промежутки. Такое позитивное определение непрерывного движения — исходный пункт новой полосы в развитии классической науки.
Эта новая полоса характеризовалась новыми центрами научного прогресса. Теперь уже не первые форпосты новой культуры и новой науки — города Средиземноморья, а города стран, связавших свою судьбу с океанской торговлей и, главное, с промышленностью, выросшей на основе такой торговли, стали наиболее крупными центрами мировой науки. Судьба Галилея отражала этот исторический сдвиг. В условиях переноса мировых торговых путей, террор инквизиции мог затормозить развитие науки в итальянских городах. К северу от Альп зарождались новые школы и новые направления. Поэтому в последние годы жизни Галилея связи со странами северной Европы приобрели для него такое большое значение. Галилей надеялся, что Голландия воспользуется его астрономическими открытиями. Велась тайная переписка с Гуго Гроцием, Константином Гюйгенсом (отцом Христиана Гюйгенса) и другими друзьями Галилея. Но переговоры оборвались, так как инквизиция узнала о криминальных письмах и намерении Генеральных штатов получить от Галилея указания о применении наблюдений движения спутников Юпитера для определения долгот.
Итальянские связи Галилея также не были полностью оборваны. В 1639 г. в Арчетри приехал семнадцатилетний Вивиани, а два года спустя — Торричелли и Кавальери. Галилею удавалось пересылать письма научного содержания. Он следил за работами Кавальери, Торричелли, Вивиани, Борелли. Галилей диктовал собственные письма-трактаты, из которых некоторые внесли существенный вклад в астрономию. К ним относится письмо к венецианскому военному теоретику Альфонсо Антонини, написанное в феврале 1638 г. В нем дается сравнительно систематическое изложение галилеевой теории либрации Луны. Далее, Галилей написал памфлет, направленный против Фортунио Личети, который предположил, что пепельное свечение Луны связано с наличием на ее поверхности фосфоресцирующего минерала, только что найденного возле Болоньи и получившего название болонского камня. Галилей возвращается к своей теории пепельного свечения (Луна освещена светом, отраженным Землей) и критикует метод Личети — беспорядочное нанизывание чисто словесных сближений и схоластической эрудиции. Полемика с Личети заканчивается адресованными противнику строками: «Если философия это то, что содержится в книгах Аристотеля, то Ваша милость была бы, мне кажется, величайшим философом в мире, потому что тогда она вся в Ваших руках и Вы готовы всему дать свое место. Я же верю, что книгу философии составляет то, что постоянно открыто нашим глазам, но так как она написана буквами, отличными от нашего алфавита, ее не могут прочесть все: буквами такой книги {500} служат треугольники, четырехугольники, круги, шары, конусы, пирамиды и другие математические фигуры»1.
Последнее из писем Галилея посвящено гелиоцентризму. Это — живое и реальное воплощение легендарного «eppur si muove». Весной 1641 г. флорентийский посол в Венеции Франческо Ринуччини написал Галилею о выходе очередного антикоперниканского памфлета. Кроме того, Ринуччини упоминает об одном аргументе противников гелиоцентризма, для которого он не находит контраргумента: мы видим половину неба над горизонтом, значит, Земля — в середине звездной сферы. Галилей отвечает указанием на однородность пространства, отсутствие, как мы сказали бы сейчас, привилегированных точек и априорный характер мнимой «очевидности».
«Тот, кто сказал, что мы видим половину неба и, следовательно, Земля помещается в центре, сначала мысленно утвердил Землю в центре и поэтому стал утверждать, что мы видим половину неба, ибо так должно было бы получиться, если бы Земля была в центре. Таким образом, не из того, что мы видим половину неба, сделан вывод, что Земля в центре, а наоборот, из предположения, что Земля в центре, заключили, что видна половина неба. Нужно, чтобы Птолемей и другие такие авторы научили нас распознавать на небе начальные точки (a princi punti) Овна и Весов, ибо, что касается меня, я никак не мог бы их отличить»2.
Субъективный характер геоцентрической очевидности и объективный характер гелиоцентризма остаются в течение всей жизни Галилея основным мотивом в его творчестве. В год выхода «Бесед» Галилей, ослепший, потерявший возможность видеть звездное небо, города, где он провел лучшие годы, друзей и книги — в их числе появившуюся свою книгу, пишет Миканцио о том, какие картины непрерывно возникают в его сознании. И, прежде всего, это картина адриатического прилива, который, как думал Галилей, доказывает объективный характер движения Земли.
«Когда море входит в канал Маламокко или Дуе Кастелли и разливается, вздувая лагуну за Венецией, за Мурано и за Маргера, вплоть до последних отмелей по направлению к Тревизо, то вслед за тем, при отливе, вода около Дуе Кастелли или около Маламокко начинает понижаться раньше, чем начнет понижаться в Венеции, Мурано и в других более отдаленных местах. Из этого явления, если оно происходит именно так, я делаю вывод, что можно дать этому явлению природы название, довольно обычное для других движений воды, а именно, что прилив — одна большая волна, которая движется таким образом, что бесчисленные меньшие воды, называемые у нас барашками, движутся к побережью моря и поверх него, разбегаясь и разливаясь на далекое расстояние, а затем непосредственно, без промежутка покоя, возвращаются назад. Я много раз наблюдал это явление в Венеции и видел, как вода, поднимаясь, движется какими-то ручейками, точно расстилающимися на поверхности, мало-помалу убегая и удаляясь от большой воды в смежном канале, и когда кончит убегать, она непосредственно без единого момента покоя обращается, как я видел, {501} назад. Вот как в моих потемках,— заключает слепой Галилей,— я брожу, фантазируя то об одном, то о другом явлении природы, и не могу, как мне хотелось бы, дать хоть некоторый покой моему беспокойному мозгу,— волнение это мне очень вредит, так как заставляет меня почти непрерывно бодрствовать»1.
Компромиссы 1633 г. принадлежат этому году, а бескомпромиссное внутреннее убеждение в объективной истинности новой картины мира принадлежит всем годам и всем векам. Такое убеждение — сквозная линия творчества и жизни мыслителя.
Эта жизнь закончилась в начале 1642 г. 8 января Галилей скончался на руках Вивиани и Торричелли.
Когда весть об этом дошла до Рима вместе со слухами о готовящемся погребении, Урбан VIII запретил хоронить Галилея в флорентийской церкви Сайта Кроче и воздвигнуть там надгробие. Преследование церкви пережило Галилея на долгие годы. Слава Галилея пережила его на века.
Б. Г. Кузнецов
| {502} |
В «Диалоге» (День третий) значительное место занимают возражения Галилея против Киарамонти, который в своей книге «De tribus novis stellis quae annuis 1572, 1600, 1604 comparuera» (1628) отстаивал мнение, что расстояние до новой звезды 1572 г. меньше, чем расстояние до Луны. Рассуждения Галилея сводятся к следующему. Если бы новая звезда находилась среди неподвижных звезд, то разность ее высот, измеренных на разных широтах, равнялась бы разности высот полюса на этих широтах. Но если новая звезда находилась бы на близком расстоянии от Земли, то ее высота при переходе к большим широтам росла бы быстрее, чем высота полюса. Из разности прироста этих высот легко вычислить расстояние от звезды до центра Земли.
Киарамонти из 13 наблюдений звезды астрономами на разных широтах составляет 12 пар наблюдений, которые дают расстояние до звезды меньше, чем расстояние до Луны. Галилей показывает, что другие пары наблюдений дают значительно большие расстояния, и, кроме того, если отбросить все нелепые результаты, а в другие наблюдения внести минимальные исправления, то большинство наблюдений отнесут новую звезду на сферу неподвижных звезд.
Основная ценность этих рассуждений Галилея не в том, что он пришел к правильному выводу, что значительно вероятнее «представляется, что звезда находилась на расстоянии самых далеких неподвижных звезд», а в том, что он в процессе рассуждений сделал выводы, имеющие большое значение как для теории ошибок, так и для теории вероятностей в целом. {503}
Для того чтобы выяснить значение рассматриваемого отрывка (см. т. I, стр. 387—391), мы должны в нескольких строках сказать о зарождении теории вероятностей, как науки.
Теория вероятностей возникла в новое время, она приобрела черты самостоятельной науки во второй половине XVII столетия. Стимулами для ее развития послужили вопросы вероятностного характера, выраставшие в то время в актуальные проблемы в различных областях человеческой деятельности.
Такие вопросы требовали своего разрешения, например, при организации разнообразных страховых обществ, которые к XVII в. получили довольно широкое распространение. Развитие статистики и, в частности, демографии требовало также решения вопросов вероятностного характера. Азартные игры, имевшие широкое распространение, выдвигали свои задачи, которые привлекали многих простотой формулировок и трудностью решения. Математиков азартные игры привлекали в первую очередь, как удобная схема для вероятностных задач из других областей.
Одной из распространенных задач была задача о числе различных исходов при бросании нескольких игральных костей, ею занимались многие математики в течение длительного времени. Основная трудность в этой задаче, для того времени, было определение всех равновозможных случаев. Галилей в работе «Considerazione sopra il Giuoco dei Dadi» дал полное решение этой задачи, использовав комбинаторные рассуждения и внеся четкость в подсчет равновозможных случаев.
В этой работе Галилей подошел к определению такого основного понятия теории вероятностей, как вероятность через отношение равновозможных событий.
В процессе подготовки, зарождения и начального развития теории вероятностей существенную роль сыграли и такие науки, как астрономия и физика. Все шире и шире в практику этих наук стали входить наблюдения и измерения; в особенности роль наблюдений усилилась в астрономии после изобретения телескопа. В связи с этим все актуальней становился вопрос об оценке ошибок наблюдений.
Одним из первых эту проблему поставил Галилей в рассматриваемом отрывке. И хотя он не дал количественного или аналитического решения вопроса, многие высказанные им положения необычайно глубоки.
Галилей приходит к выводу, что случайные ошибки при наблюдениях неизбежны, и далее рассматривает, как их следует учитывать. Он считает, что вероятность малых отклонений больше, чем вероятность больших отклонений, что следует отбрасывать грубо ошибочные результаты, далеко отстающие от основного количества результатов. Он высказывает мысль о том, что закон распределения ошибок симметричен. Галилей говорит, что закон распределения ошибок наблюдений должен обладать одним максимумом. Он предупреждает, что ошибки наблюдения на определенном инструменте нельзя смешивать с ошибками окончательных выводов, основанных на этих наблюдениях, и закон распределения ошибок относится только к первым ошибкам.
В этих соображениях и высказываниях Галилея видны черты нормального закона распределения ошибок наблюдения, который был окончательно установлен в самом начале XIX в. и оставался одним из центральных в теории вероятностей на протяжении всего прошлого столетия.
Л. Е. Мaйстров
| {504} |
Рене Декарт (1596—1650) был младшим современником Галилея. Он, безусловно,— один из самых выдающихся представителей физико-математических наук в первой половине XVII в. Многое в его творчестве связано с Галилеем — и там, где Декарт следует за ним, и там, где Декарт противопоставляет себя ему. Для современников Декарт был, вероятно, наиболее компетентным судьей главных произведений Галилея. Оценки Декарта в значительной мере определяли отношение к научному наследию Галилея ближайших поколений ученых.
Галилей, его процесс и его главные произведения («Диалог» и «Беседы») занимают видное место в переписке и размышлениях Декарта с начала 30-х годов XVII в.1 Впервые Декарт упоминает Галилея в письме к Мерсенну по вопросу о скорости падающих тел. В 1633 г., в конце ноября, Декарт писал Мерсенну: «Когда я на этих днях осведомлялся в Лейдене и Амстердаме, нет ли там «Системы мира»2 Галилея, мне подтвердили, что ее напечатали, но сказали, что все экземпляры были тогда же сожжены в Риме, а сам Галилей как-то наказан. Это меня поразило настолько, что я почти что решился сжечь все мои бумаги или по крайней мере никому их не показывать. Потому что не могу представить себе, чтобы его, итальянца, который, как я {505} слышал, пользовался благоволением папы, осудили за что-либо иное, чем за желание доказать движение Земли. Такое учение, как я твердо знаю, было осуждено некоторыми кардиналами, и я слыхал, что его нельзя излагать публично даже в Риме, но я признаю, что если оно ложно, то ложны все основы моей философии, ибо из них оно явно следует». И Декарт заканчивает письмо просьбой сообщить ему все, что известно о «деле Галилея».
В письме из Амстердама в феврале 1634 г. Декарт пишет об отношении церкви к вопросу о вращении Земли, о Галилее и об отношении к нему X. Шейнера (1575—1650) — астронома, известного своими исследованиями в области наблюдательной астрономии, сторонника геоцентрической системы1.
Учение о движении Земли, как видим, занимало почетное место в системе мира Декарта. Участь «Диалога» и его автора живо интересовала Декарта и повлияла на его линию поведения. Декарт правильно и высоко оценил стремление Галилея применить средства математики для описания и анализа физических явлений. Однако гениальное сочетание у Галилея методов мысленного и фактического эксперимента, предварительный анализ явлений, применявшийся Галилеем, чтобы выделить «в чистом виде» основное в том или ином процессе — все это не было оценено Декартом. Из-за этого он часто не понимал Галилея. Например, в письме к Мерсенну от апреля 1634 г. читаем: «Что касается указанных Вами опытов Галилея, я их все отрицаю. И пушечное ядро, выстреленное с вершины башни, должно опускаться гораздо медленнее, чем при падении по отвесу («сверху вниз»), потому что оно на своем пути встречает больше воздуха и это мешает ему не только двигаться параллельно горизонту, но и опускаться»2. Гениальная абстракция, примененная Галилеем при исследовании падения тел,— отвлечение от сопротивления среды, осталась невоспринятой Декартом. Поэтому Декарт не мог согласиться с тем, что траектории тел, брошенных под разными углами к горизонту, однотипны (sont de meme genre, mais non pas pour cela toutes semblables ni de memo espece.— см. Correspondance, т. I, стр. 260), т. е. что все они — параболы. Декарт, правда, делал при этом оговорку, что он еще не исследовал, каковы могут быть эти линии.
В силу подобных же причин Декарт приходил к выводу, что «он (Галилей) достаточно хорошо философствует относительно движения, хотя я нахожу вполне правильными только весьма немногое из того, что он говорит о движении»3. Это не означает, что Декарт не бывал прав иной раз в своей критике Галилея. В только что цитированном письме он говорит о Галилее следующее: «Насколько я мог заметить, он грешит еще более тогда, когда следует за уже принятыми мнениями, чем тогда, когда от них отходит, за исключением того, что он говорит о приливах и отливах — последнее, по-моему, отчасти притянуто за волосы». В этом пункте Декарт прав, теория приливных явлений Галилея ошибочна, как ошибочна, впрочем, и теория приливов, предложенная Декартом. {506}
Наиболее поучительные и характерные высказывания Декарта о Галилее содержатся в его письме Мерсенну от 11 апреля 1638 г.1, где он разбирает «Беседы». Письмо начинается с признания, что Галилей «рассуждает гораздо лучше, чем это обычно делают (que le vulgaire), всячески опровергая ошибки Школы (т. е. последователей Аристотеля — И. П., У. Ф.), и старается рассматривать вопросы физики, привлекая математические соображения. В этом я с ним вполне согласен, и я того мнения, что нет другого способа обнаружить истину. Но мне кажется недостатком его постоянные отступления и то, что он не дает исчерпывающих объяснений. Это показывает, что он вел исследования не планомерно и, не рассматривая первопричин природы, искал объяснения только некоторых частных явлений, следовательно, он строил без фундамента». Итак, то, в чем мы усматриваем силу Галилея: глубокий и не предвзятый анализ физических явлений и весьма осторожный, совершенно не догматичный подход к формулировкам гипотетических первопричин,— было недостатком для систематизатора и классификатора Декарта, стремившегося все вместить в единую схему. В своих возражениях Галилею по отдельным вопросам, рассматриваемым в первых двух Днях «Бесед» (относящимся к сопротивлению), Декарт большей частью неправ. Относительно следующих двух Дней, в которых заложены основы динамики, он сделал только беглые замечания. Поль Таннери, комментируя это письмо Декарта, вполне справедливо оценивает его следующим образом: «Он (Декарт) ограничивается отрицанием постулатов, положенных Галилеем в основу динамики, потому что, по его мнению, движение можно рассматривать только в какой-то среде, и Декарт не допускает, что физически нереализуемые абстракции могут служить прогрессу науки. Декарту не хватает чувства условий приложимости математики к вопросам, отличным от вопросов о числах и о геометрических формах и величинах, в противоположность Галилею, у которого такое чувство было в высшей степени развито»2.
Действительно, Декарт писал: «Он (Галилей) предполагает, что скорость падающих тяжелых тел все время увеличивается одинаковым образом, как и я считал в свое время; но сейчас я считаю, на основании доказательства (par démonstration), что это неверно. Он предполагает также, что степени скорости одного и того же тела на различных (наклонных плоскостях) равны, если равны высоты плоскостей, что не является в точности верным; а так как все последующее зависит только от этих двух предположений, можно сказать, что все его построения воздвигнуты на песке (qu'il a entièrement bâti en l'air)»3
Поучительно такое сопоставление: Галилей, рассматривая падение тел, оговаривает, что он не считает уместным или возможным вдаваться в исследование вопроса о причине, вызывающей падение4. Декарт же говорит о Галилее: «Все, сказанное им {507} о скорости тел, падающих в пустоте и т. д., лишено основания, так как ему следовало сперва определить, что такое тяжесть; и если бы он знал ее сущность, он знал бы, что она равна нулю в пустоте»1.
Декарт основательнее в своей критике, когда касается математических вопросов, но и здесь он иной раз отделывается поверхностными замечаниями, например: «Неудовлетворительно все, что он говорит о бесконечности, поскольку признавая, что человеческий ум, будучи конечным, не способен понять бесконечность, он тем не менее рассуждает о бесконечном так, как если бы это было ему понятно»2.
Итак, многое у Галилея и в Галилее Декарту было чуждо и непонятно. В методе Галилея Декарт смог в полной мере оценить лишь математическую, а не физическую составляющую. Науку о местных движениях Галилея Декарт пытался опровергнуть, науку о прочности критиковал. Но Декарт был единомышленником Галилея во взглядах на систему мира, в борьбе со Школой, в отстаивании бесконечности мира и единства его материальной сущности. Реальным союзником Галилея Декарт был и благодаря своим математическим открытиям, столь важным для дальнейшего развития математических методов естествознания.
В опубликованных им произведениях Декарт избегает упоминаний о Галилее. Нет сомнения, что причина этого — осуждение Галилея католической церковью, столкновения с которой Декарт хотел избежать. Он писал в «Началах философии»: «Я хотел бы также, чтобы отметили (подчеркнуто нами.— И. П., У. Ф.), что хотя я и пытался осветить всю материальную природу, я не воспользовался ни одним началом, которое не было бы принято и одобрено Аристотелем и всеми остальными философами всех времен; поэтому моя философия вовсе не нова, она наиболее древняя и общераспространенная».
Характерен и маргиналий этого параграфа:
«Настоящий трактат не содержит также никаких начал, какие не были бы всеми и всегда признаваемы, вследствие чего изложенная в нем философия не нова, а является древнейшей и наиболее общераспространенной из всех возможных»3.
Признавая, вслед за Галилеем, относительный характер движения, Декарт во второй части «Начал философии» не ссылается на Галилея и не упоминает его имени4. Декарт полагал, что учение о движении Земли так тесно связано со всеми частями его «Трактата», что если его исключить, то все остальное делается негодным. Это генетически связано с тем, о чем Декарт писал Мерсенну: «Но так как я ни за что в мире {508} не пожелаю, чтобы мною было написано сочинение, в котором оказалось хотя бы одно слово, не одобренное церковью, то я лучше уничтожу его, чем выпущу с пропусками».
«Диоптрика» была начата Декартом за несколько лет до осуждения Галилея. Именно этим можно объяснить слова, сказанные им в отношении споров коперникианцев. «Но поскольку мне придется говорить о свете лишь для того, чтобы объяснить, как его лучи входят в глаз и как они отклоняются различными телами, встречающимися на пути, то мне нет надобности вскрывать его истинную природу... В этом я подражаю астрономам, которые, хотя их гипотезы почти всегда ошибочны или недостоверны, делают весьма правильные заключения, опирающиеся на различные выполненные ими наблюдения1.
Молчанием обходит Декарт и вопрос о вращении Земли в «Метеорах». «Рассмотрим теперь, в частности, свойства и происхождения главнейших ветров. Прежде всего, наблюдения показывают, что весь воздух движется вокруг Земли с востока на запад; это нам сейчас придется принять на веру, ибо причину этого можно выяснить должным образом, лишь объяснив всю механику вселенной, что я не намерен здесь делать2.
И. Б. Погребысский, У. И. Франкфурт
| {509} |
О Христиане Гюйгенсе (1629—1695) Лагранж писал, что ему суждено было усовершенствовать и развить важнейшие открытия Галилея. Действительно, Гюйгенс, вступивший в науку рано, шестнадцати-семнадцати лет от роду, вскоре после смерти Галилея, в течение нескольких десятилетий плодотворно работал в тех же областях, что и великий итальянец. Гюйгенс очень близок к Галилею характером своих дарований и направлением своих интересов. В молодости он испытал сильное влияние Декарта, он хорошо знал других выдающихся мыслителей XVI—XVII вв., но среди них Галилей занимал у Гюйгенса особое место. Уже в конце своего пути, без пристрастий и увлечений молодости, оценивая достижения людей, чьими трудами была создана новая эпоха в науке, Гюйгенс писал1: «Такие ученые нового времени, как Телезий, Кампанелло, Гильберт, как и аристотелианцы, допускали ряд скрытых качеств и не обладали в достаточной мере ни изобретательностью, ни математическими средствами, чтобы создать цельную систему. То же относится и к Гассенди, хотя он понимал и видел беспомощность аристотелианцев. Веруламий тоже видел недостаточность этой философии перипатетиков и, кроме того, он дал хорошие методы для построения лучшей философии — как проводить опыты и как следует их использовать. Один удачный пример ему принадлежит — это относится к теплоте, тут он пришел к выводу, что она — только движение частиц, из которых состоят тела. Но он совсем не разбирался в математике {510} и ему нехватало физической проницательности. Так, он не мог постичь того, что Земля может двигаться, и он насмехается над этим, как над чем-то вздорным. Галилей в отношении ума и знания математики обладал всем, что нужно для того, чтобы в физике пойти вперед, и следует признать, что он был первым, кто сделал замечательные открытия относительно природы движения, хотя и после него оставалось сделать весьма важные открытия. Он не обладал такой дерзостью и самоуверенностью, чтобы взяться за объяснение всех явлений природы, у него не было тщеславия, чтобы стать главой секты. Он был скромен и слишком любил истину, кроме того, он считал, что добился достаточной известности, которая навсегда сохранится благодаря его открытиям. А Декарт, у которого, мне кажется, слава Галилея вызывала сильную ревность, очень хотел, чтобы его считали автором новой системы». И Гюйгенс дальше отмечает, что в физике заслуги Декарта невелики, что Декарт, стремясь все объяснить на основе своих общих принципов, во многом ошибался, а силу его ума доказывает то, что он сделал в алгебре и геометрии.
Если не считаться с рьяными адептами картезианства, для которых в системе их учителя содержалось все, что нужно для познания мира, то надо признать оценку Галилея, данную Гюйгенсом, итоговой для XVII в. И больше всего доводов для обоснования этой оценки дают работы самого Гюйгенса.
В самом начале своей научной деятельности Гюйгенс в переписке с Мерсенном (1646 г.) отстаивает результаты и принципиальные основы учения Галилея о падении тел. Он по-своему выводит квадратичный закон зависимости пройденного при падении пути от времени, он принимает, как единственно возможное, представление Галилея о том, что скорость тела меняется непрерывно при выходе тела из состояния покоя. В том же году Гюйгенсу удается доказать, что по параболе располагается нить, нагрузка которой распределена равномерно по горизонтали («висячий мост»), и Гюйгенс выделяет то следствие, что «никакая цепь не провисает по параболической линии»1, исправляя ошибку Галилея, правда, ошибку, на наш взгляд, редакционного характера, как показывает сопоставление всех сюда относящихся мест из «Бесед»2. В позднейших работах и в своей переписке Гюйгенс не раз говорит о «галилеевых принципах» в связи с рассмотрением проблем механики. Гюйгенс точно формулирует принцип инерции, указывая на Галилея и на Декарта, как на его авторов, он пользуется принципом относительности, ссылаясь на его обоснование Галилеем в «Диалоге». Учением о центробежной силе Гюйгенс, по оценке Лагранжа, завершает установление основных принципов механики, так как в сочетании с принципом инерции оно позволяет установить связь между силой и изменением скорости в любом криволинейном движении.
В работе «О центробежной силе», опубликованной только после смерти Гюйгенса в самом начале XVIII в., Гюйгенс ссылается на опыты Галилея, Риччиоли и свои по падению тел. Отмечая необходимость учета при падении тел малых отклонений, зависящих от сопротивления воздуха, Гюйгенс пишет: «Все-таки рассуждения Галилея {511} об этом движении остаются превосходными и полезными; они во всяком случае не уступают всей механике весомых тел, в которой ведь принимается, что весомые тела падают по параллельным линиям, в то время как эти линии сходятся к центру Земли. Впрочем, нам для доказательства тех теорем, с которыми мы будем иметь дело, достаточно, что на произвольно малом участке ускорение растет, считая от точки покоя, как ряд нечетных чисел, как установил Галилей»1.
В астрономии Гюйгенс тоже является продолжателем дела Галилея: он много работал над усовершенствованием телескопа и, благодаря инструментам более высокого качества, он смог установить наличие кольца у Сатурна, исправив вывод Галилея о «тройственном строении» этой планеты. Гюйгенс, как и Галилей, много занимался техническими средствами наблюдения и измерения. Больше всего труда Гюйгенс положил на изобретение маятниковых часов, что навлекло на него несправедливые обвинения в заимствовании у Галилея конструкции. На самом же деле Гюйгенс был здесь конгениальным продолжателем дела Галилея и в теории (он сумел дать и более полную, чем у Галилея, теорию математического маятника, и теорию физического маятника — первую главу динамики твердого тела), и на практике.
16 июня 1657 г. Гюйгенс получил голландский патент на изобретение маятниковых часов, в 1658 г. напечатал брошюру «Horologium», а через пятнадцать лет, в 1673 г., был напечатан мемуар «Horologium Oscillatorium» («Маятниковые часы»). Разрешаемые Гюйгенсом в этом мемуаре проблемы тесно связаны с творчеством Галилея.
5 июня 1636 г. в письме к Лаврентию Реалю Галилей писал о соединении маятника со счетчиком, отсчитывающим число колебаний. В 1657 г. Гюйгенс, не придумав для маятника нового счетчика, принял старую конструкцию часов, связав ее с маятником. Дальнейшие исследования Гюйгенса показали, однако, что простой маятник нельзя считать равномерным измерителем времени. В поисках решения вопроса
Об изохронности колебаний Гюйгенс обратился к циклоиде и к анализу законов падения тел.
«Для проведения этих доказательств потребовалось,— пишет Гюйгенс,— укрепить и, где нужно, дополнить учение великого Галилея о падении тел. Наиболее желательным плодом, как бы величайшей вершиной этого учения, и является открытое мною свойство циклоиды»2.
В работах Гюйгенса мы можем найти и критические замечания по поводу некоторых доказательств и выводов Галилея; не всегда при этом Гюйгенс был прав. Но Гюйгенс должным образом оценил творчество Галилея и его методологию и сделал очень много для того, чтобы развитие механики и всей физики не сошло с пути, которым шел Галилей.
И. Б. Погребысский, У. И. Франкфурт
| {512} |
Первые упоминания о телескопических наблюдениях Галилея мы находим уже в рукописных сочинениях Московской Руси. В астрологической компиляции «Сказание царя Соломона, что есть печать большая, откуду, как ему приде» (известной под названием «Премудрости Соломона»), при описании планеты Зевса (Юпитера) говорилось, что он (Зевс) «ходит в четырех звездах, сама пятая». Здесь, видимо, речь шла о четырех спутниках Юпитера, открытых Галилеем в 1610 г. В этой же рукописи приводилось описание планеты Крона (Сатурна) с рисунками: «а дано ей хождение таково: две звезды по сторонам, а она среди них третия, сим образом, якоже зриши зде...» Скорее всего здесь имелось в виду открытое Галилеем кольцо Сатурна, которое он наблюдал в виде придатков по сторонам планеты. (Ясно рассмотрел кольцо только X. Гюйгенс в 1659 г.) Все это позволяет предполагать, что составитель компиляции был знаком с классическим трудом Галилея «Sidereus nuncius» (1610), содержавшим результаты первых астрономических наблюдений ученого1.
Развитие астрономии началось в России фактически лишь в петровское время. Тогда же появилась и первая переводная научная литература, где Галилей иногда {513} упоминался как последователь Коперника1. Решающую роль в распространении научных знаний в стране сыграло учреждение в Петербурге Академии наук. Г.-Б. Бильфингер, говоря об этапах развития науки, среди великих ученых прошлого назвал имя Галилея, «мужа великого по своему таланту и заслугам», подчеркнув, что Галилей придал новую форму физическим исследованиям, что он «проложил и укрепил дорогу, по которой, и только по ней,— можно уверенно идти вперед и дойти до истины»2.
Обзор научной литературы XVIII в. (представленной в основном изданиями Академии наук) показывает, что имя знаменитого итальянца и его работы были хорошо известны в России. Во многих статьях по астрономии говорилось об изобретении Галилеем зрительной трубы3, об открытии и наблюдении спутников Юпитера. Именно благодаря этому открытию удалось разработать способ определения долготы по затмениям спутников Юпитера, сыгравший значительную роль в развитии астрономических и географических исследований4. В статье «О планете Венере» (1739) сообщалось об открытии Галилеем фаз Венеры5, а в статье «О Луне» (1740—1743 гг.) — о наблюдениях на Луне атмосферы6. В «Месяцеслове на 1781 год» было помещено «Собрание разных астрономических знаний», где особо отмечалось открытие Галилеем солнечных пятен. Освещались попытки Галилея и Гевелия объяснить природу солнечных {514} пятен: «Галилей и Гевелий почитали их за некоторый вид дыма, облаков или пены, делающейся на поверхности Солнца и плавающей в океане тонкого и жидкого вещества»1. Упоминалось также и открытие Галилеем кольца Сатурна2.
Внимание петербургских академиков привлекали не только астрономические наблюдения Галилея, но и его теоретические работы. Так, Г.-В. Крафт в статье «О Земле» разобрал вопрос о суточном и годичном движении Земли3; А. Н. Гришов в «Речи о величине Земли, видимой с планет, и о величине ея пути около Солнца, видимой со звезд неподвижных, или о употребительном у астрономов способе как находить подлинные величины и расстояния тел небесных от Земли нашей» проанализировал предложенный Галилеем способ определения годичного параллакса неподвижных звезд4.
Во второй половине XVIII в. были широко распространены переводы на русский язык иностранных книг естественнонаучного содержания, где часто описывались открытия Галилея в области астрономии, механики и физики. В 1770 г была переведена с немецкого языка небольшая работа Ф.-У.-Т. Эпинуса «Рассуждение о строении мира»; автор, рассказывая о борьбе за утверждение коперниканской системы, мира, упоминал и о судебном процессе над Галилеем, и о его покаянии «в беззаконии своем, которое в одном том состояло, что он был умнее всея Римской синедрии»5. П. Богданович перевел на русский язык «Историю математики» французского ученого Ж. Монтюкла. В этом обширном обзоре развития математических наук с древнейших времен до XVIII в. несколько страниц было отведено работам Галилея по астрономии и механике6. В переводе «Сокращения астрономии» Ж. Лаланда сообщалось о наблюдении Галилеем четырех спутников Юпитера. Там же впервые была дана ссылка на его работу о приливах и отливах7. Подробное обозрение астрономических работ Галилея содержалось в «Истории о звездословии, преложенной с французского на российский морского флота капитан-лейтенантом Николаем Ивановым»8.
На современников Галилея особое впечатление произвели его астрономические открытия, которым придавали первостепенное значение. Теоретические его исследования {515} были оценены значительно позже — в XVIII в. Известный французский математик Ж. Лагранж писал в предисловии к своей «Динамике»: «Открытие спутников Юпитера, фаз Венеры, солнечных пятен и т. д. потребовало лишь наличия телескопа и известного трудолюбия, но нужен был необыкновенный гений, чтобы открыть законы природы в таких явлениях, которые всегда пребывали перед глазами, но объяснение которых, тем не менее, всегда ускользало от изысканий философов»1.
Теоретические работы Галилея, по сравнению с результатами его астрономических наблюдений, были доступны лишь узкому кругу специалистов-теоретиков Однако и эти его труды нашли отражение в русской научной литературе.
Первые краткие сведения о законах падения тел, открытых Галилеем, мы находим в «Рассуждении о метании бомбов и стрелянии из пушек» (1708). Чертеж, изображающий траекторию падения ядра, сопровождается примечанием: «Галилеас в книге своей о локалическом движении2 оказывает, что тяжелое тело, на воздухе поверженное, окружает кривою линею в движении своем»3.
Русские ученые высоко ценили вклад Галилея в развитии механики, что нашло отражение, например, в речи академика Я. Германа «О месте и развитии геометрии», произнесенной в публичном собрании Академии наук 1 августа 172G г.4 Открытия Галилея в области механики и астрономии использовал в своих работах Леонард Эйлер5. Отдельные ссылки на экспериментальные и теоретические работы Галилея встречаются в различных учебниках физики XVIII в.6
М. В. Ломоносов в предисловии к переводу «Волфианской экспериментальной физики» писал: «Едва понято, коль великое приращение в астрономии неусыпными наблюдениями и глубокомысленными рассуждениями Кеплер, Галилей, Гугений, де ла Гир и великий Невтон в краткое время учинили...»7. Ломоносовский перевод «Волфианской физики» служил учебником для нескольких поколений русских ученых.
Л. Н. Жигалова
| {570} |
Издание настоящего собрания сочинений Галилео Галилея, осуществленное па решению Президиума Академии наук СССР, начато и закончено в текущем году, в год четырехсотлетия со дня рождения великого ученого. Редакционная коллегия считает своим долгом выразить признательность и благодарность издательству «Наука», сделавшему все, чтобы галилеевский двухтомник был должным образом оформлен и своевременно издан.
В нашем издании использованы переводы главных произведений Галилея, «Диалога» и «Бесед», а также «Рассуждения о телах, пребывающих в воде», выполненные при участии и под редакцией А. Н. Долгова. Их литературные достоинства несомненны, но в них допущен ряд неточностей и отклонений от оригинала, не всегда последовательно выдержана терминология, она отчасти модернизована в ущерб точности. Это относится особенно к первым трем дням «Бесед». При подготовке настоящего собрания сочинений Галилео Галилея все переводы были сверены с оригиналом и отредактированы И. Б. Погребысским. Новым является почти весь аппарат комментариев и примечаний. Некоторые комментарии оказалось целесообразным дать в виде отдельных статей, и они включены в отдел Приложений, дополнительно к биографической статье, написанной Б. Г. Кузнецовым, и библиографией изданий трудов Галилея и работ о нем.
Мы надеемся, что это первое собрание трудов Галилея на русском языке даст возможность читателям познакомиться с творчеством великого итальянца, которое многими нитями связано с современной наукой и запечатлено в образцово написанных произведениях.
* По природе вещей (лат.)
* Вопреки ожиданию (лат.)
1 Опубликован Фаваро в Метопе del. R. Jstituto Veneto di scienze, lettere ed arte, XXVI, 5, Venezia, 1899.
2 Les Mecaniques de Galilee, mathemacien ingenieur du due de Florence, avec plysieurs additions, traduites de l'ltalien par Mercenne. Paris, 1624.
1 Указание Стиллмана Дрейка. Впервые на английском языке «Механика» Галилея была опубликована Солсбери (Salusbury) в Mathematical Collections and Translations. Недавно издан новый перевод этого трактата: G. Galilei. On motion and on mechanics comprising De motu (ca. 1590) translated with introduction and notes by J. E. Drabkin and Le Mecchaniche (ca. 1600) translated with introduction and notes by Stillman Drake, Madison, 1963.
2 Delia Scienza Meccanica, e della Utilita che ci traggono di quella, ed. Luca Danesi. Ravenna, 1649.
3 Opere di Galileo Galilei. Edizioue Nationale. 2d. ed., v. II, Firence, 1932.
4 См. стр. 10—И в настоящем томе.
1 См. стр. 15 в настоящем томе.
1 См. стр. 46 в настоящем томе.
2 См. стр. 47 в настоящем томе.
3 В. А. Стеклов. Галилео Галилей. Берлин, 1923, стр. 30.
1 См. стр. 32 в настоящем томе.
1 Последний был непримиримым врагом Галилея. О нем мало что известно. Он был членом Флорентийской академии, в протоколах которой его именуют «знаменитым математиком» и до нас дошла такая его характеристика: «...философ, астроном, математик и поэт, вообще человек эрудированный и начитанный в литературе всякого рода, но вместе с тем крайне критичный, сатирический и язвительный... Высокого роста, сухощав и не очень приятного вида».
2 Это довольно убедительное предложение высказал С. Дрэйк (Drake),— см. его «Введение» в книге G. Gаlilеi. Discoure on Boodies in Water, Urbana, 1960, стр. XIII.
1 Формулировка принципа возможных перемещений в «Рассуждении» уточнена (по сравнению с «Механикой»); см. комментарий Е. Н. Ракчеева к «Механике», стр. 413, наст. тома.
1 Примечания А. Н. Долгова [отмечено (А. Д.)] и И. Б. Погребысского.
1 Напечатано в Собр. соч. Галилея (Ed. Naz.), IV, 287—293.
2 Там же, стр. 295—310.
3 Там же, стр. 298 и 299.
1 Гостехтеоретиздат, М.— Л., 1934.
1 «Зажигательное стекло».
1 «О сфере мира».
1 Мы следуем в дальнейшем, в основном, изложению Трусдела (С. Truesdell) во 2-й части XI тома 2-й серии Полного собрания сочинений Эйлера, изд. 1960 г.
1 Дата, правда, не установлена вполне точно. Мы цитируем отрывок, приведенный в Ed. Naz., XX, изд. 1939 г., стр. 603.
2 Этот запрос либо был вызван ложными слухами, либо мог относиться к «Посланию к Инголи».
1 С. А. Бернштейн. Очерки по истории строительной механики. М., 1957, стр. 13.
1 А. С. Бернштейн, стр. 17.
2 Архимед. Сочинения. М., 1962, стр. 272—297; комментарий, стр. 554.
1 См. в Ed. Naz., VIII (1933), стр. 650 и, в приложении, лист, помеченный 107 г.
1 Письмо к Мерсенну от 25 декабря 1639 г.; цит. по Galilei, Opere. Ed. Naz.„ XX (1939), стр. 611.
1 Такова хорошо аргументированная датировка, которую принимают известные исследователи творчества Галилея Вольвил и Койре.
1 G. Galilei. Ореrе, Ed. Naz., XVIII, p. 125—126.
1 См. Ed. Naz., I, 1929, стр. 182—183.
2 Письмо к Диодати от 6 декабря 1633 г. См. там же, стр. 182.
3 См.: Архимед. Сочинения, перевод, вступ. статья и комментарии И. Н. Веселовского. М., 1962, стр. 168.
1 См. ван дер Варден. Пробуждающаяся наука. Перевод с голл. И. Н. Веселовского. М., 1959; гл. VI, особ. стр. 238—261.
1 Балиани (Baliani Giovanni Battista, 1582 — ок. 1666) был видным должностным лицом генуэзской республики, а также занимался механикой, издал в 1638 и 1646 гг. в Генуе две книги о естественном движении тяжелых твердых и жидких тел, был большим почитателем Галилея.
2 См.: Ed. Naz., XVIII, 68—69; письмо от 1 авг. 1639 г.
3 Там же, стр. 78—79.
4 Там же, стр. 95; письмо от 1 сент. 1639 г.
1 См. Ed. Naz., XIX, 623.
1 Ed. Naz., X, 67.
1 Ed. Naz., X, 280—281.
1 Ed. Naz. X, 483.
1 См : С. Sееlig Albert Einstein, Zurich, 1960, S. 210—211
1 Ed. Naz. XII, 206—207. (Русск. пер. в книге: М. Я. Выгодский. Галилей и инквизиция, М.—Л., 1934, стр. 52—53.)
2 Ed. Naz., XI, 108.
1 Ed. Naz., XI, 533. (Выгодский, 86—87.)
1 Ed. Naz., V, 282—283. (Выгодский, 96—97.)
2 Ed. Naz., XII, 171. (Выгодский, 130.)
1 Ed. Naz., VI, 350.
1 Б. Маколей. Полное собр. соч., т. IV, СПб., 1862, стр. 112—113.
1 Л. Ольшки. История научной литературы на новых языках, т. III, M.— Л., 1933, стр. 200.
1 Ed. Naz., XIX, 283.
1 Ed. Naz. XVIII, 295.
2 Ed. Naz. XVIII, 316.
1 Ed. Naz. XVII, 271
1 Descartes a Mersenne. Nov. ou Dec. 1632. Цитируем по изданию Descartes, Correspondancee, t. I, Paris, 1936.
2 Имеется в виду «Диалог о двух главных системах мира».
1 Descartes. Corr., t. I, p. 250.
2 Там же, стр. 254.
3 Там же, стр. 265.
1 Descartes, Corr., t. Ill, p. 77 etc.
2 Там же, примеч. на стр. 83.
3 Там же, стр. 83.
4 Мах истолковывал это в пользу своих концепций, как сознательное желание поставить не вопрос «почему», а вопрос «как». Такое истолкование идет вразрез со всем направлением творчества Галилея и со многими его высказываниями. Но понятно, что, не имея убедительных гипотез о природе силы тяготения и законе ее действия, Галилей не хотел связывать твердо установленные им законы падения с неясными и спорными предположениями.
1 Там же, стр. 81—82.
2 Там же, стр. 80.
3 Рене Декарт. Избранные произведения. Гос. Изд-во политической литературы. 1950, стр. 536.
Точно дата написания «Principia Philosophica» неизвестна, они были изданы в Амстердаме, в 1644 г. В 1647 г. появился французский перевод, просмотренный Декартом.
4 Там же, стр. 471.
1 Рене Декарт. Диоптрика в книге: Р. Декарт. Рассуждение о методе с приложениями. Диоптрика, Метеоры, Геометрия. Изд-во АН СССР, 1953, стр. 70.
2 Там же, стр. 221.
1 В замечаниях по поводу книги Baillet о Декарте.— См. Chr. Huуgens, Oeuvres complètes, X, стр. 398—399.
1 Oeuvres completes, I, p. 37: Propositio 9. ...Nulla ergo catena pendet secundum lineam papabolicam.
2 См. примеч. к Дню первому и к Дню четвертому в этом томе.
1 X. Гюйгенс. Три мемуара по механика. Изд-во АН СССР, 1951, стр. 250.
2 Там же, стр. 10.
1 О времени составления этой компиляции существуют различные мнения. А. И, Соболевский утверждал, что компиляция составлена «не позднее конца XVI века на основании источников греческого происхождения и литературы «жидовствующих» (XV—XVI вв.)». (А. И. Соболевский. Переводная литература Московской Руси XIV—XVII веков. СПб., 1903, стр. 428). Но прав, конечно, Д. О. Святский, который относил составление компиляции к 1633 г., уже хотя бы потому, что к рукописи была приложена пасхальная таблица на 100 лет (1633—1733 г.). (Д. О. Святский. Сказание о Чигирь-звезде и телескопические наблюдения Галилея. Мироведение, 1928, № 1 (60), стр. 6).
1 География генеральная, небесный и земноводный круги купно с их свойствы и действы в трех книгах описующа, преведена с латинска языка на российский и напечатана в Москве повелением царского пресветлого величества лета господня 1718 в июне. (О Галилее см. стр. 40.) Этот перевод сделан Федоровым Поликарповым с книги Бернхарда Варениуса: Bernh. Varenio. Geographia generalis in qua affectiones generalis- Telluris explicantur. Med. D. Amstelodami (одно из амстердамских изданий 1650, 1664 или 1661 гг.).
2 Sermones in primo solenni Academiae Sciontiarum imperialis conventu die XVI decembris anni MDCCXXV publice rectiati. Petropoli, 1726, p. 10.
3 О зрительных трубах. Собрание географических, астрономических и физических примечаний, ч. I. СПб., 1787, стр. 180, 197—199; О Земле вообще. Там же, ч. II, СПб., 1791, стр. 35; см. также: С. Я. Румовский. Речь о начале и приращении оптики до нынешних времен. . ., говоренная в публичном собрании ими. Академии наук июля 2 дня 1763 года. СПб., 1763, стр. 11—12; П. И. Гиларовский. Руководство к физике, сочиненное Петром Гиларовским. СПб., 1793, стр. 294 и 480 (здесь дает описание и чертеж телескопа Галилея).
4 О планете Юпитере и его спутниках. Собр. соч., выбранных из Месяцесловов на разные годы, ч. I. СПб., 1785, стр. 66; Известие о изобретениях, до долготы места касающихся. Там же, ч. II. СПб., 1787, стр. 105.
5 Там же, ч. I, стр. 106.
6 Там же, стр. 138—139.
1 Там же. ч. II, стр. 415.
2 Там же, стр. 419; см также: Ф. И. Соймонов. Краткое изъяснение о астрономии, в котором показаны величины и расстояния небесных тем, крупно с порядком в их расположении и движении по разным системам и величине и о движении земного глобуса. Выписано из разных астрономических и физических авторов. М., 1765, стр. 15 и 57.
3 Собр. географических, астрономических и физических примечаний, ч. II, стр. 37.
4 Речи, говоренные в публичном собрании Академии наук сентября 6 дня 1755 года. СПб., стр. 54—55.
5 Ф.-У.-Т. Эпинус. Рассуждение о строении мира. Пер. с нем. СПб., 1770, стр. 12.
6 Акад. изв., ч. VII. СПб., 1781, стр. 125—128, 281, 284 и 297.
7 Сокращение астрономии или звездозакония г. Де-Ла-Ланда. СПб., 1789, стр. 469 и 619.
8 Новые ежемесячные сочинения, 1796, ч. 115, стр. 6—14.
1 Ж. Лагранж. Аналитическая механика, т. I, пер. с фр. В. С. Гохмана, изд. 2. М.—Л., Гостехиздат, 1950, стр. 292.
2 Речь идет о знаменитом труде Галилея «Discorsi с diinustrazioni malematiclie, intorno a duenuove scienzeattenenti alia Mecanicaetc. i Mmmenti localb. Laida, 1633.
3 Подробнее об этой книге см.: Описание издания гражданской печати. 1708—январь 1725 г. Сост. М. М. Гуревич и Т. А. Быкова. М.—Л., Изд-во АН СССР, 195.1 , стр. 80—82.
4 Sermones in secundo solenni Academiac scieutnauni iniperialis conventu die I augusti anni 1726, Petropoli, 1726, p. 88.
5 (Leonardi Euleri). Mechanica she motus scientia analyti ce exposita auctore Leo-nhardo Eulero..., I. 1—2. Petropoli, 1736.
6 В качестве примера (см. сноску 1) можно назвать «Руководство к физике) II. Гиларовского (стр. 49—50).
7 М. В. Ломоносов. Полное собр. соч., т. I. M.—Л., Изд-во АН СССР, 1950, стр. 424.
| {571} |
5 | ||
39 | ||
109 | ||
111 | ||
113 | ||
Перечень главнейших тем, излагаемых в настоящем сочинении..... | 115 | |
116 | ||
201 | ||
233 | ||
304 | ||
347 | ||
366 | ||
381 | ||
404 | ||
413 | ||
420 | ||
430 | ||
475 | ||
Б. Г. Кузнецов. Галилео Галилей (Очерк жизни и научного творчества) . . | 481 | |
Л. Е. Майстров. Галилей и теория вероятностей........... | 502 | |
И. Б. Погребысский, У. И. Франкфурт. Галилей и Декарт....... | 504 | |
И. Б. Погребысский, У. И. Франкфурт. Галилей и Гюйгенс....... | 509 | |
Л. В. Жигалова. Первые упоминания о Галилее в русской научной литера- | 512 | |
517 | ||
Le opere di Galileo Galilei (Собрания сочинений Галилея)........ | 519 | |
Bibliografia Galileana (Издания Галилея на иностранных языках. 1606—1963) | 523 | |
562 | ||
570 | ||
| {572} |
Галилео Галилей
Избранные произведения в двух томах
т. II
Утверждено к печати
Редколлегией научно-популярной литературы
Академии наук СССР
Редактор Издательства В. А. Никифоровский.
Художник К. Н. Никохристо
Технический редактор Л. В. Каскова
Сдано в набор 19/VI 1964 г. Подписано к печати 17/IX 64 г.
Формат 70×901/16. Печ. л. 35,75+2 вкл.=41,83 усл. печ. л.
Уч.-изд. л. 36(35,9+0,1 вкл.) Тираж 2200 экз. Изд. № 5012.
Тип. зак. № 826. Темплан 1964 г. № 1215а
Цена 2 р. 70 к.
Издательство «Наука». Москва, К-62, Подсосенский пер., 21
2-я типография изд-ва «Наука». Москва, Г-99, Шубинский пер., 10

