

 |
 |
| {i} |
|
Michael C. Mackey Time's Arrow: With 24 Figures 
Springer-Verlag New York Berlin Heidelberg London Paris |
| {ii} |
Michael C. Mackey
Center for Nonlinear Dynamics
in Physiology and Medicine
McGill University
Montreal PQ, Canada H3G 1Y6
Library of Congress Cataloging-in-Publication Data
Mackey, Michael C, 1942-
Time's arrow : The origins of thermodynamic behavior/ Michael C. Mackey. - 1st ed.
p. cm.
Includes bibliographical references and index.
ISBN 0-387-94093-6 (New York : alk. paper : pbk.). - ISBN 3-540-94093-6 (Berlin : alk. paper : pbk.)
I. Thermodynamnics. 2. Entropy. I. Title.
QC311.M176 1993
536'.7--dc20 93-30004
Printed on acid-free paper.
© 1992,by Springer-Verlag New York, Inc.
All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer-Verlag New York, Inc., 175 Fifth Avenue, New York, NY 10010, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use of general descriptive names, trade names, trademarks, etc., in this publication, even if the former are not especially identified, is not to be taken as a sign that such names, as understood by the Trade Marks and Merchandise Marks Act, may accordingly be used freely by anyone.
Production managed by Jim Harbison; manufacturing supervised by Vincent Scelta.
Photocomposed copy prepared using AMS-TEX files.
Printed and bound by Braun-Brumfield, Inc., Ann Arbor, Michigan.
Printed in the United States of America.
9 8 7 6 5 4 3 2 1
ISBN 0-387-94093-6 Springer-Verlag New York Berlin Heidelberg (softcover)
ISBN 3-540-94093-6 Springer-Verlag Berlin Heidelberg New York
ISBN 0-387-97702-3 Springer-Verlag New York Berlin Heidelberg (hardcover)
ISBN 3-540-97702-3 Springer-Verlag Berlin Heidelberg New York
| {iii} |
To Fraser
who loves to discuss all these questions
| {iv} |
"It is not very difficult to show that the combination of the reversible laws of mechanics with Gibbsian statistics does not lead to irreversibility but that the notion of irreversibility must be added as a special ingredient...
...the explanation of irreversibility in nature is to my mind still open.”
Bergmann (1967)
| {v} |
In 1935, Eddington wrote “The law that entropy always increases—the second law of thermodynamics — holds, I think, the supreme position among the laws of Nature.” Much has changed in science in the intervening half century, but I believe that Eddington's pronouncement still carries a great deal of truth.
The central question this book addresses is the dynamic origin of the Second Law of thermodynamics. Specifically, the goal is to define the dynamical foundation of the evolution of entropy to maximal states. This is accomplished through an application of recent results in ergodic theory to so-called “chaotic” dynamical systems (Lasota and Mackey, 1985; M.C. Mackey, 1989).
The Second Law of thermodynamics comes in so many forms that it is often confusing to understand precisely what a given author understands by the use of this term. This is unfortunate since the first statement of the Second Law was so clear. It was first enunciated by Clausius (1879), in his remarkable work building on the considerations of Carnot, when he wrote “Die Energie der Welt ist Konstant. Die Entropie der Welt strebt einem Maximum zu” (The energy of the world is constant. The entropy of the world tends to a maximum.). Though this simple declaration has been rephrased so many times that it is often unrecognizable, I find that Clausius' formulation is the most transparent. However, I will distinguish two variations on the original theme. Let STD(t) denote the thermodynamic entropy at time t.
–∞ < STD(t0) < STD(t) ≤ 0 for all times t0 < t and there exists a set (finite or not) of equilibrium entropies 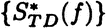 dependent on the initial preparation f of the system such that
dependent on the initial preparation f of the system such that
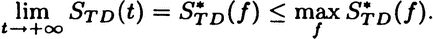
Thus the entropy difference 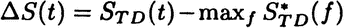 satisfies ΔS(t) ≤ 0 and
satisfies ΔS(t) ≤ 0 and
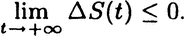
In this case system entropy converges to a steady state value 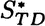 which may not be unique. If it is not unique it characterizes a metastable state. The second form of the Second Law of thermodynamics is more interesting.
which may not be unique. If it is not unique it characterizes a metastable state. The second form of the Second Law of thermodynamics is more interesting.
–∞ < STD(t0) < STD(t) ≤ 0 for all times t0 < t and there is a unique limit 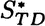 (i.e. independent of the initial system preparation f) such that
(i.e. independent of the initial system preparation f) such that
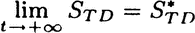
| {x} |
for all initial system preparations f. Under these circumstances,
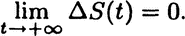
In this case the system entropy evolves to a unique maximum irrespective of the way in which the system was prepared.
In my investigations of the connection between dynamics and entropy evolution, I have been heavily influenced by the work of Khinchin (1949), Dugas (1959), Kurth (I960), Truesdell (1960), Farquhar (1964), O. Penrose (1970, 1979), Lebowitz (1973), Lebowitz and Penrose (1973), G.W. Mackey (1974), Wehrl (1978), and Prigogine (1980). Because of the approach taken here and the nature of the material presented, a brief outline of the main points may be helpful.
Chapter 1 defines a thermodynamic system in terms of measure spaces, draws a one to one correspondence between a density and a thermodynamic state, and introduces the Boltzmann-Gibbs entropy of a density.
In Chapter 2, using a Maximal Entropy Postulate, it is a simple demonstration that the entropy of a density will assume a maximal value if and only if this density is (in the terminology of Gibbs) either the density of the microcanonical or a generalized canonical ensemble. Then it is shown that the Boltzmann-Gibbs entropy of a density can be plausibly argued to coincide with the thermodynamic entropy STD of a system characterized by that density.
Chapter 3 introduces Markov operators. These are linear integral operators that describe the evolution of densities by dynamical or semi-dynamical systems. Fixed points of Markov operators, known as stationary densities, define states of relative or absolute thermodynamic equilibrium depending on whether there are multiple or unique stationary densities. Thus, a central question that must be answered in any treatment of thermodynamics is under what circumstance will the entropy change from its original value (determined by the way in which the system was prepared) to a final state corresponding to one of these states of relative or absolute equilibrium. Following this the conditional entropy, a generalization of the Boltzmann-Gibbs entropy, is introduced and identified with ΔS. Under particular conditions, the conditional entropy is shown to have its maximal value of zero if the stationary density of the state of thermodynamic equilibrium is that of the canonical ensemble. Then the distinction between invertible and noninvertible systems is made. This is used to provide the not too surprising proof that entropy is constant for invertible systems. It is only in noninvertible systems that the entropy may increase. Thus, irreversibility is necessary but not sufficient for the entropy to increase. Following this, a variety of sufficient conditions are derived for the existence of at least one state of thermodynamic equilibrium based on convergence properties of the system state density average.
Chapter 4 introduces a special type of Markov operator, the Frobenius-Perron operator. Following illustrative material demonstrating its utility {xi} in studying the evolution of densities by a variety of dynamical and semi-dynamical systems, we turn to a consideration of the conditions that guarantee the existence of a unique state of thermodynamic equilibrium. The necessary and sufficient condition for this existence is the property of ergodicity, which may be shared by both invertible and noninvertible systems.
Chapter 5 presents the concept of mixing, introduced in a qualitative sense by Gibbs, which is a stronger property than ergodicity though it still may be shared by noninvertible and invertible systems. However, it is not sufficient to permit the entropy of a system to change from its initial value.
Chapter 6 introduces a particular form of dynamical behavior, called asymptotic periodicity, that is sufficient for the evolution of the entropy to a metastable state of relative equilibrium (weak form of the Second Law).
Chapter 7 is, in a sense, the core of this work. There it is shown that for there to be a global evolution of the entropy to its maximal value of zero (strong form of the Second Law) it is necessary and sufficient that the system have a property known as exactness.
In a very real way, the results of Chapter 7 raise as many questions as they answer. Though providing totally clear criteria for the global evolution of system entropy, at the same time these criteria suggest that all currently formulated physical laws may not be at the foundation of the thermodynamic behavior we observe every day of our lives. This is simply because these laws are formulated as (invertible) dynamical systems, and exactness is a property that only noninvertible systems may display.
One possibility is that the current invertible, dynamical system statements of physical laws are incorrect and that more appropriate formulations in terms of noninvertible semidynamical systems await discovery. Alternately, other phenomena may mask the operation of these invertible systems so they appear to be noninvertible to the observer. Chapters 8 through 11 explore this latter possibility.
In Chapter 8, we examine the effects of coarse graining of phase space, due either to measurement error or to an inherent graininess of phase space that is imposed by Nature. It is easy to show that if we observe a system with mixing dynamics, but operating in a coarse grained phase space, then the entropy of the coarse grained density will evolve to a maximum as time goes either forward (t → +∞) or backward (t → –∞). Thus, though coarse graining induces entropy increase to a maximum of zero it fails to single out any unique direction of time for this to occur. This illustrates that the origin of noninvertible behavior is not a consequence of invertible dynamics operating in a coarse grained phase space.
Chapter 9 explores the consequence of taking a trace in which we observe only some of the important dynamical variables of a dynamics operating in a higher dimensional space (hidden variables). In this case the complete dynamics may be invertible and, consequently, have a constant entropy while the entropy of the trace system may smoothly evolve to a maximum (weak or strong form of the Second Law). {xii}
Chapters 10 and 11, respectively, examine the effects of external perturbations on discrete and continuous time dynamics. This situation is usually called interaction with a heat bath. Interactions with a heat bath, depending on how they occur, can be shown to lead to either local (metastable) or global states of thermodynamic equilibrium.
In Chapter 10 we show that under very mild assumptions concerning the nature of the perturbation, discrete time systems with the most uninteresting dynamics in the unperturbed situation will become either asymptotically periodic or exact in the presence of perturbations. Thus they will display evolution of entropy toward states of thermodynamic equilibrium (either form of the Second Law).
Chapter 11 continues this theme by examining the effects of white noise perturbations of continuous time systems whose dynamics are described by systems of ordinary differential equations. Again these perturbations induce exactness and the consequent increase of the conditional entropy to its maximum value of zero (strong form of the Second Law).
As should be evident from this survey of the contents, it is not my intent to develop statistical mechanics as a subject. This is done rather nicely from several points of view in a variety of texts. Kestin and Dorfman (1971), Reichl (1980), Ma (1985), Pathria (1985), and Grandy (1988) are representative of some of the more thought provoking of these.
Throughout, I have tried to include as much material as necessary so this book can be read as a unit. Proofs of almost all of the theorems are given, though they need not be read to grasp the thread of the argument. Examples are offered to try to illustrate the physical significance of the results discussed. To more clearly delineate material, the end of proofs are marked with a “□” and the end of examples by a “•”.
This work was started at the Universities of Oxford and Bremen, 1986-1987, and I thank Profs. J.D. Murray (Oxford) and H. Schwegler (Bremen) for their hospitality during this period. Several colleagues have helped me clarify various points, and I hope that they will not be offended by my lack of explicit acknowledgment of their interest. They know who they are. I am especially indebted to Helmut Schwegler for his continued interest and support in reading and commenting on almost every aspect of this work. He has given of his time and energy as only a true friend can.
My wife, Nancy, and my children — Fraser, David, Alastair, Linda, and Christopher — have all contributed a great deal through their love, interest, and encouragement.
And Fraser, to whom I dedicate this book, has always asked “Hi Mike, how's it going?”
Montreal |
Michael C. Mackey |
| {xiii} |
PREFACE .......................................................... | ix | ||||
CHAPTER 1. STARTERS ........................................... | 1 | ||||
A. Thermodynamic Systems ....................................... | 1 | ||||
B. Dynamics ...................................................... | 2 | ||||
C. Thermodynamic States ......................................... | 4 | ||||
D. Boltzmann-Gibbs Entropy ...................................... | 5 | ||||
E. Summary....................................................... | 8 | ||||
CHAPTER 2. MAXIMAL ENTROPY PRINCIPLES................. | 9 | ||||
A. Microcanonical Ensembles ...................................... | 9 | ||||
B. Canonical Ensembles .......................................... | 11 | ||||
C. The Thermodynamic Connection .............................. | 12 | ||||
D. Boltzmann and Other Statistics ............................... | 16 | ||||
E. Blackbody Radiation .......................................... | 18 | ||||
F. General Entropy Maxima...................................... | 19 | ||||
G. Maximal Entropy Principles ................................... | 20 | ||||
H. Summary ..................................................... | 20 | ||||
CHAPTER 3. INVERTIBLE AND NONINVERTIBLE SYSTEMS .. | 21 | ||||
A. Markov Operators ............................................. | 21 | ||||
B. Conditional Entropy ........................................... | 27 | ||||
C. Existence of Equilibria......................................... | 34 | ||||
D. Summary ..................................................... | 37 | ||||
CHAPTER 4. ERGODICITY AND UNIQUE EQUILIBRIA......... | 39 | ||||
A. Frobenius-Perron Operator .................................... | 39 | ||||
B. The Koopman Operator ....................................... | 43 | ||||
C. Recurrence .................................................... | 45 | ||||
D. Densities and Flows ............................................ | 46 | ||||
E. Ergodicity..................................................... | 48 | ||||
F. Summary...................................................... | 57 | ||||
CHAPTER 5. MIXING............................................. | 58 | ||||
A. Mixing ........................................................ | 58 | ||||
B. Kolmogorov Systems .......................................... | 66 | ||||
C. The Decay of Correlations ..................................... | 67 | ||||
D. Summary ..................................................... | 68 | ||||
| |||||
CHAPTER 6. ASYMPTOTIC PERIODICITY AND ENTROPY | |||||
EVOLUTION .................................................... | 70 | ||||
A. Asymptotic Periodicity ........................................ | 70 | ||||
B. Asymptotic Periodicity Illustrated ............................. | 75 | ||||
C. The Weak Form of the Second Law ............................ | 80 | ||||
D. Asymptotic Periodicity and Correlations ....................... | 86 | ||||
E. Summary...................................................... | 88 | ||||
CHAPTER 7. GLOBAL EVOLUTION OF ENTROPY ............. | 89 | ||||
A. Exactness ..................................................... | 89 | ||||
B. The Strong Form of the Second Law ........................... | 98 | ||||
C. Summary .................................................... | 101 | ||||
CHAPTER 8. COARSE GRAINING............................... | 103 | ||||
A. Coarse Grained Entropy...................................... | 103 | ||||
B. Coarse Graining of Mixing Systems ........................... | 106 | ||||
C. Sampling..................................................... | 107 | ||||
D. Summary .................................................... | 109 | ||||
CHAPTER 9. TRACES AND FACTORS .......................... | 110 | ||||
A. Traces ....................................................... | 110 | ||||
B. Factors....................................................... | 112 | ||||
C. Coarse Graining and Traces .................................. | 113 | ||||
D. Summary.................................................... | 114 | ||||
CHAPTER 10. OPEN DISCRETE TIME SYSTEMS .............. | 115 | ||||
A. An Operator Equation ....................................... | 116 | ||||
B. Loosely Coupled Systems ..................................... | 117 | ||||
C. Strongly Coupled Systems .................................... | 120 | ||||
D. Asymptotic Periodicity and Additive Perturbations ........... | 123 | ||||
E. Exactness and Additive Perturbations ........................ | 129 | ||||
F. Parametric Perturbations ..................................... | 131 | ||||
G. Markov Operators and Deterministic Processes ............... | 136 | ||||
H. Summary .................................................... | 138 | ||||
CHAPTER 11. OPEN CONTINUOUS TIME SYSTEMS........... | 140 | ||||
A. Wiener Processes and Stochastic Differential Equations ....... | 140 | ||||
B. The Fokker-Planck Equation.................................. | 142 | ||||
C. Solutions of the Fokker-Planck Equation ...................... | 145 | ||||
D. The Behavior of Entropy ..................................... | 148 | ||||
E. Phase Transitions and Additive Perturbations................. | 151 | ||||
| |||||
F. Parametric Perturbations and Phase Transitions .............. | 156 | ||||
G. Summary .................................................... | 158 | ||||
REFERENCES .................................................... | 159 | ||||
INDEX............................. | 167 | ||||
| {167} |
Abraham, R., and Marsden, J.E. 1978. Foundations of Mechanics. Benjamin Cummings, Reading, Massachusetts.
Anosov, D.V. 1963. Ergodic properties of geodesic flows on closed Riemannian manifolds of negative curvature. Sov. Math. Dokl. 4 1153–6.
Anosov, D.V. 1967. Geodesic flows on compact Riemannian manifolds of negative curvature. Proc. Steklov Inst. Math. 90 1–209.
Arnold, V.I. and Avez, A. 1968. Ergodic Problems of Classical Mechanics. Benjamin, New York.
Bergmann, P.G. 1967. Foundations research in physics, in Delaware Seminar in the Foundations of Physics, (ed. M. Bunge), pp 1–14, Springer–Verlag, New York.
Birkhoff, G.D. 1931. Proof of the ergodic theorem. Proc. Natl. Acad. Sci. U.S.A. 17 656–660.
Boltzmann, L. 1909. Wissenschaftliche Abhandlungen. (ed. Fr. Hasenohri), Barth, Leipzig.
Brown, J.R. 1966. Approximation theorems for Markov operators. Pac. J. Math. 16 13–23
Brunovsky, P. 1983. Notes on chaos in the cell population partial differential equation. Nonlin. Anal. 7 167–176.
Brunovsky, P. and Komomik, J. 1984. Ergodicity and exactness of the shift on C[0, ∞] and the semiflow of a first order partial differential equation. J. Math. Anal. Applic. 104 235–245.
Clausius, R. 1879. The Mechanical Theory of Heat. Macmiilan, London.
Cornfeld, L.P., Fomin, S.V., and Sinai, Ya. G. 1982. Ergodic Theory. Springer Verlag, New York.
Crutchfield, D., Farmer, D., Packard, N., and Shaw, R. 1980. Power spectral analysis of a dynamical system. Phys. Lett. 76A 1–4.
Davies, P.C.W. 1974. The Physics of Time Asymmetry. University of California Press, Berkeley and Los Angeles.
Denbigh, K.G. and Denbigh, J.S. 1985. Entropy in Relation to Incomplete Knowledge. Cambridge University Press, Cambridge.
Devaney, R. 1986. An Introduction to Chaotic Dynamical Systems. Benjamin Cummings, Menlo Park. {160}
Dugas, R. 1959. La Theorie Physique au sens de Boltzmann. Griffon, Neuchatel (Suisse).
Dunford, N. and Schwartz, J.T. 1957. Linear Operators. Part I. General Theory. Wiley, New York.
Eddington, A. 1935. The Nature of the Physical World. E.P. Dutton, New York.
Ehrenfest, P. and Ehrenfest, T. 1959. The Conceptual Foundations of the Statistical Approach in Mechanics, (translation by M.J. Moravcsik of their 1912 article in Encyklopadie der mathematischen Wissenschaften, IV.2.II.6, B.G. Teubner, Leipzig), Cornell University Press, Ithaca.
Farquhar, I.E. 1964. Ergodic Theory in Statistical Mechanics. John Wiley and Sons, London.
Fer, F. 1977. L'irréversibilité fondement de la stabilite du monde physique. Gauthier–Villars, Paris.
Gal-Or, B. 1974. Statistical mechanics, fallacy and a new school of thermodynamics, in Modern Developments in Thermodynamics, (ed. B. Gal-Or), pp 3–51, John Wiley and Sons, New York.
Gal-Or, B. 1981. Cosmology, Physics, and Philosophy. Springer–Verlag, New York.
Gibbs, J.W. 1902. Elementary Principles in Statistical Mechanics. Yale University Press, New Haven.
Gikhman, I.I. and Skorokhod, A.V. 1969. Introduction to the Theory of Random Processes. Saunders, Philadelphia.
Goldstein, S. and Penrose, O. 1981. A nonequilibrium entropy for dynamical systems. J. Stat. Phys. 24 325–343.
Goldstein, S., Misra, B., and Courbage, M. 1981. On intrinsic randomness of dynamical systems. J. Stat. Phys. 25 111–126.
Grad, H. 1952. Statistical mechanics of dynamical systems with integrals other than energy. J. Phys. Chem. 56 1039–1048.
Grandy, W.T. 1988. Foundations of Statistical Mechanics, volumes I and II, Reidel, Dordrecht.
Grossmann, S., and Thomae, S. 1977. Invariant distributions and stationary correlation functions of one-dimensional discrete processes. Z. Naturforsch. 32a 1353–1362.
Grossmann, S., and Thomae, S. 1981. Correlations and spectra of periodic chaos generated by the logistic parabola. J. Stat. Phys. 26 485–504. {161}
an der Heiden, U. 1985. Stochastic properties of simple differential delay equations, in Delay Equations, Approximation and Application. (eds. G. Meinardus, G. Nurnberger), pp 147–164, Birkhauser Verlag, Basel.
an der Heiden, U., and Mackey, M.C. 1982. The dynamics of production and destruction: Analytic insight into complex behavior. J. Math. Biol. 16 75–101.
Hopf, E. 1932. Complete transitivity and the ergodic principle. Proc. Nat. Acad. Sci. U.S.A. 18 204–209.
Hopf, E. 1932. Proof of Gibbs' hypothesis on the tendency toward statistical equilibrium. Proc. Nat. Acad. Sci. U.S.A. 18 333–340.
Horbacz, K. 1989a. Dynamical systems with multiplicative perturbations. Ann. Pol. Math. 50 11–26.
Horbacz, K. 1989b. Asymptotic stability of dynamical systems with multiplicative perturbations. Ann. Pol. Math. 50 209–218.
Horsthemke, W., and Lefever, R. 1984. Noise Induced Transitions: Theory and Applications in Physics, Chemistry, and Biology. Springer Verlag, Berlip.
Ito, S., Tanaka, S., and Nakada, H. 1979. On unimodal linear transformations and chaos. I. Tokyo J. Math. 2 221–258.
Jabloriski, M., Kowalski, Z.S., and Malczak, J. 1985. The rate of convergence of iterates of the Frobenius–Perron operator for Lasota Yorke transformations. Universitatis Jagellonicae Acta Math. 25 189–193.
Jabloriski, M. and Malczak, J. 1983. The rate of convergence of iterates of the Frobenius–Perron operator for piecewise convex transformations. Bull. Polish Acad. Sci. Math. 31 249–254.
Jabloiiski, M. and Malczak, J. 1985. The rate of convergence of iterates of the Frobenius–Perron operator for transformations on the real line. Universitatis Jagellonicae Acta Math. 25 203–208.
Jaynes, E.T. 1957. Information theory and statistical mechanics. Phys. Rev. 106 620–630.
van Kampen, N.G. 1981. ltd versus Stratonovich. J. Stat. Phys. 24 175–187.
Katz, A. 1967. Principles of Statistical Mechanics. Freeman, San Francisco.
Keener, J. P. 1980. Chaotic behavior in piecewise continuous difference equations. Trans. Am. Math. Soc. 261 589–604. {162}
Kestin, J. and Dorfman, J.R. 1971. A Course in Statistical Thermodynamics. Academic Press, New York.
Khinchin, A.I. 1949. Mathematical Foundations of Statistical Mechanics. Dover, New York.
Kim, C.-W. 1968. Uniform approximation of doubly stochastic operators. Pac. J. Math. 26 515–527.
Kim, C.-W. 1972a. Approximation theorems for Markov operators. Z. Wahrscheinlichkeitstheorie verw. Geb. 21 207–214.
Kim, C.-W. 1972b. Approximations of positive contractions on L∞[0,1]. Z. Wahrscheinlichkeitstheorie verw. Geb. 21 335–337.
Kormonik, J. 1991. Asymptotic periodicity of Markov and related operators. Dynamics Reported, in press.
Komornik, J. and Lasota, A. 1987. Asymptotic decomposition of Markov operators. Bull. Polish. Acad. Sci. (Math.) 35 321–327.
Koopman, B.O. 1931. Hamiltonian systems and transformations in Hilbert space. Proc. Natl. Acad. Sci. U.S.A. 17 315–318.
Krylov, N.S. 1979. Works on the Foundations of Statistical Physics. Princeton University Press, Princeton.
Kuczma, M. 1985. An Introduction to the Theory of Functional Equations and Inequalities. Silesian University Press, Katowice (Poland).
Kurth, R. 1960. Axiomatics of Classical Statistical Mechanics. Pergamon Press, Oxford.
Lasota, A. 1979. Invariant measures and a linear model of turbulence. Rend. Sem. Mat. Univ. Padova 61 42–51.
Lasota, A. 1981. Stable and chaotic solutions of a first order partial differential equation. Nonlin. Anal. 5 1181–1193.
Lasota, A. and Mackey, M.C. 1985. Probabilistic Properties of Deterministic Systems. Cambridge University Press, Cambridge.
Lasota, A. and Mackey, M.C. 1987. Noise and statistical periodicity. Physica 22D 143–154.
Lasota, A. and Mackey, M.C. 1989. Stochastic perturbation of dynamical systems: The weak convergence of measures. J. Math. Anal. Apple. 138 232–248.
Lasota, A. and Mackey, M.C. 1991. Statistical and Chaotic Behaviour of Dynamical Systems. Springer–Verlag, New York. {163}
Lasota, A. and Yorke, J. A. 1982. Exact dynamical systems and the Frobenius–Perron operator. Trans. Am. Math. Soc. 273 375–384.
Lasota, A., Li, T.Y., and Yorke, J.A. 1984. Asymptotic periodicity of the iterates of Markov operators. Trans. Am. Math. Soc. 286 751–764.
Lebowitz, J.L. 1973. Ergodic theory and statistical mechanics of nonequilibrium processes, in Nonlinear Problems in the Physical Sciences and Biology, (eds. I. Stakgold, D.D. Joseph, D.H. Sattinger), pp 193–209, Lecture Notes in Mathematics 322, Springer Verlag, Berlin.
Lebowitz, J.L. and Penrose, O. 1973. Modern ergodic theory. Physics Today, February, 1073, 23–29.
Lewis, R.M. 1967. A unifying principle in statistical mechanics. J. Math. Phys. 8 1448–1459.
Lorenz, E.N. 1980. Noisy periodicity and reverse bifurcation. Ann. N.Y. Acad. Sci. 357 282–291.
Loschmidt, J. 1876. Uber den Zustand des Wdrmegleichgewichtes eines Systeme von Korpern mit Rucksicht auf die Schwerkraft. Wien. Ber. 73 128–142.
Loskot, K. 1985. Thrbulent solutions of a first order partial differential equation. J. Diff. Eqn. 58 1–14.
Losson, J. 1991. Multistability and the statistical properties of differential delay equations. M.Sc. dissertation, McGill University.
Ma, S.-K. 1985. Statistical Mechanics. World Scientific, Philadelphia and Singapore.
Mackey, G.W. 1974. Ergodic theory and its significance for statistical mechanics and probability theory. Adv. Math. 12 178–268.
Mackey, M.C. 1989. The dynamic origin of increasing entropy. Rev. Mod. Phys. 61 981–1016.
Mackey, M.C. and Glass, L. 1977. Oscillation and chaos in physiological control systems. Science 197 287–289.
Mackey, M.C, Longtin, A., and Lasota, A. 1990. Noise induced global asymptotic stability. J. Stat. Phys. 60 735–751.
Misra, B. and Prigogine, I. 1981. Time, probability, and dynamics, in Long Time Prediction in Dynamics, (eds. C.W. Horton, L.E. Reichl, and V.G. Szebehely), 21–43. John Wiley and Sons, New York.
Misra, B., Prigogine, I., and Courbage, M. 1979. From deterministic dynamics to probabilistic descriptions. Physica 98A 1–26. {164}
von Neumann, J. 1932. Proof of the quasi-ergodic hypothesis, Proc. Natl. Acad. Sci. U.S.A. 18 70–82.
Pathria, R.K. 1985. Statistical Mechanics. Pergamon Press, Oxford.
Penrose, O. 1970. Foundations of Statistical Mechanics. Pergamon Press, Oxford.
Penrose, O. 1979. Foundations of statistical mechanics. Rep. Prog. Phys. 42 1937–2006.
Penrose, R. 1979. Singularities and time-asymmetry, in General Relativity, (eds. S.W. Hawking and W. Israel), pp. 581–638, Cambridge University Press, Cambridge.
Penrose, R. 1989. The Emperor's New Mind. Oxford University Press, New York, Oxford.
Peters, H. 1980a. Globales Losungsverhalten Zeitverzgerter Differential–gleichungen am Beispeil vol Modellfunktionen. Doctorate dissertation, Universitat Bremen.
Peters, H. 1980b. Comportment chaotique d'une equation differentielle retardee. C.R. Acad. Sci. Paris 290A 1119–1122.
Peters, H. 1983. Chaotic behaviour of nonlinear differential delay equations. Nonlin. Anal. 7 1315–1334.
Petersen, K. 1983. Ergodic Theory. Cambridge University Press, Cambridge.
Prigogine, I. 1980. From Being to Becoming: Time and Complexity in the Physical Sciences. W.H. Freeman and Company, San Francisco.
Provatas, N. and Mackey, M.C. 1991a. Asymptotic periodicity and banded chaos. Physica D, in press.
Provatas, N. and Mackey, M.C. 1991b. Noise induced asymptotic periodicity. J. Stat. Phys. 63 661–688.
Reichl, L.E. 1980. A Modern Course in Statistical Physics. University of Texas Press, Austin.
Reichenbach, H. 1957. The Direction of Time. University of California Press, Berkeley.
Rochlin, V.A. 1964. Exact endomorphisms of Lebesgue spaces. Am. Math. Soc. Transl. (2) 39 1–36.
Rudnicki, R. 1985a. Invariant measures for the flow of a first order partial differential equation. Ergod. Th. Dynam. Sys. 5 437–443. {165}
Rudnicki, R. 1985b. Ergodic properties of hyperbolic systems of partial differential equations. Bull. Polish Acad. Sci. Math. 33 595–599.
Rudnicki, R. 1988. Strong ergodic properties of a first order partial differential equation. J. Math. Anal. Applic. 132 14–26.
Rudnicki, R. 1991. Asymptotic stability in L1 of parabolic equations. Preprint, Silesian University.
Ruelle, D. 1969. Statistical Mechanics. W.A. Benjamin, Reading, Mass.
Sachs, R.G. 1987. The Physics of Time Reversal. University of Chicago Press, Chicago.
Scalapino, D.J. 1961. Irreversible statistical mechanics and the principle of maocimum entropy. Ph.D. dissertation, Stanford University.
Sharkovski, A.N. 1965. On cycles and structure of contiuous maps. Ukrainian Math J. 17 104–111.
Sinai, Y. 1963. On the foundations of ergodic hypothesis for a dynamical system of statistical mechanics. Sov. Math. Dokl. 4 1818–1822.
Sinai, Y. 1970. Dynamical systems with elastic reflections. Russian Math. Surveys 25 137–189.
Skagerstam, B.S. 1974. On the mathematical definition of entropy. Z. Naturforsch. 29a 1239–1243.
Spohn, H. 1978. Entropy production for quantum dynamical semigroups, J. Math. Phys. 19 1227–1230.
Tolman, R.C. 1938. The Principles of Statistical Mechanics. Oxford University Press, Oxford.
Traple, J. 1988. Discrete processes with dynamical and semidynamical perturbations. J. Math. Anal. Applic. 129 118–130.
Truesdell, C. 1960. Ergodic theory in classical statistical mechanics, in Ergodic Theories, (ed. P. Caldirola), pp 21–56, Academic Press, New York.
Voigt, J. 1981. Stochastic operators, information, and entropy, Commun. Math. Phys. 81 31–38.
Walters, P. 1982. Ergodic Theory – Introductory Lectures. Lecture Notes in Mathematics 458, Springer–Verlag, New York.
Wehrl, A. 1978. General properties of entropy. Rev. Mod. Phys. 50 221–260. {166}
Yoshida, T., Mori, H., and Shigematsu, H. 1983. Analytic study of chaos of the tent map: Band structures, power spectra, and critical behaviors. J. Stat. Phys. 31 279–308.
Zeh, H.D. 1989. The Physical Basis of the Direction of Time. Springer–Verlag, Heidelberg.
Zermelo, E. 1896. Über einen Satz der Dynamik und der Mechanischen Wärmetheorie. Ann. Phys. 57 485–494.
| {167} |
A
Abstract ergodic theorem, 35
Additivity, 6, 14
Adjoint operators, 43, 145
Anosov
diffeomorphism, 59
flow, 60
Asymptotic periodicity, 72
conditions for, 73, 75, 84
and correlations, 86
and entropy, 80
and ergodicity, 74
and exactness, 96
and Keener map, 126
in loosely coupled systems, 118
period of, 72, 125
and perturbations, 118, 122, 126
and quadratic map, 78
and smoothing, 71
and stationary densities, 72
in strongly coupled systems, 122, 123
and tent map, 75, 82
and Weak Form of Second Law, 80
Average, 67
B
Baker transformation, 60
and additive perturbations, 123
and dyadic transformation, 112
and entropy, 64, 66, 106
Frobenius-Perron operator for, 64, 113
and invertibility, 60, 113
and K-systems, 67, 112
and Lebesgue measure, 60
and Liouville equation, 114
and microcanonical ensemble, 65
and mixing, 60, 63
quadratic, 112
stationary density for, 65
and trace, 112, 123
Birkhoff ergodic theorem, 44
extended to ergodic dynamics, 53
Blackbody radiation, 18
Boltzmann, 6, 31-33
constant, 16
equation, 114
μ-space, 5
and Loschmidt, 32, 45
statistics, 16
and Zermelo, 45
Boltzmann-Gibbs entropy, 5
additivity, 6, 14
and baker transformation, 64, 106
and canonical ensemble, 11
coarse grained, 104
and conditional entropy, 28
and correlations, 86
and exactness, 100
and grand canonical ensemble, 19
maximal, 9, 19
and microcanonical ensemble, 9
and mixing, 64
and quadratic map, 28
sampled, 107
and tent map, 100
and thermodynamic entropy, 13
uniqueness of, 6
C
Canonical ensemble, 14
and entropy, 11, 101
and exactness, 92, 94, 98, 101
and mixing, 63
and stationary density, 64
Cauchy-Holder inequality, 93
Cesaro convergence, 56 {168}
Chebyshev inequality, 118
Clausius, 33
Coarse graining, 103
and baker transformation, 106
of densities, 104
and dynamics, 106
of entropy, 104, 105, 112
and errors, 105
and Gibbs, 103, 106, 109
and invertibility, 107
of mixing systems, 106
of phase space, 103
and Strong Form of Second Law, 107
temporal, 107
and trace, 113
Conditional entropy, 27
and asymptotic periodicity, 80
and baker transformation, 66
and Boltzmann-Gibbs entropy, 28, 29
coarse grained, 105
and correlations, 87
dependence on initial density, 80, 126
and exactness, 98
and invertible dynamics, 31, 66
and Keener map, 126
and Liouville equation, 32
and mixing, 64, 66
and ordinary differential equations, 32
and perturbations, 119, 126, 131, 149, 150
properties of, 29
and quadratic map, 78, 100
sampled, 107
and tent map, 82, 95
and thermodynamic entropy difference, 29
Convergence
Cesaro, 56
strong, 35, 92
weak, 35, 63
Correlation, 67
and asymptotic periodicity, 86
and entropy, 86
and Frobenius-Perron operator, 68
and Koopman operator, 68
and mixing, 68
Covariance, 67
and mixing, 68
normalized, 67
D
Delay differential equation
and exactness, 91
and laws of physics, 101
Density, 4
and thermodynamic states, 4
coarse grained, 104
evolution, 43
Gaussian, 141, 151
illustrated, 4
of measure, 4
stationary, 23, 38
Diffusion term, 145, 148
Drift term, 145
Dyadic transformation, 94
and baker transformation, 112
and exactness, 94
as a factor, 112, 114, 123
Frobenius-Perron operator for, 94
and Liouville equation, 114
and microcanonical ensemble, 94
and noninvertibility, 114
and perturbations, 123
stationary density for, 95
and trace, 112
Dynamical system, 3
Dynamics
asymptotically periodic, 72
and coarse grained entropy, 106
constructing exact, 95
ergodic, 48
exact, 89
and Frobenius-Perron operator, 39
Hamiltonian, 33, 45, 48, 101
invertible, 2
irreversible, 3
and Koopman operator, 43
loosely coupled to perturbations, 117
measurable, 39 {169}
measure preserving, 41
mixing, 58
noninvertible, 3
nonsingular, 39
reversible, 2
and strong perturbations, 120
time reversal invariant, 2
trajectory of, 2, 110
versus perturbations, 120
E
Energy, 10, 12
continuous spectrum, 17
discrete spectrum, 18
Helmholtz, 16
and Maxwell-Boltzmann distribution, 17
Ensemble, 5
Entropy
for baker transformation, 64
Boltzmann-Gibbs, 5
coarse grained, 104, 105, 107, 114
conditional, 28
and correlations, 86
dependence on preparation, 80, 125
and dynamics, 30
and invertibility, 31
for K-systems, 67
and mixing, 66
for quadratic map, 28, 78, 83, 100
for tent map, 82, 95
and trace, 111
Ergodic theorem
abstract, 35
Birkhoff, 44
for space and trajectory averages, 53
Ergodicity, 48
and asymptotic periodicity, 74
and Birkhoff theorem, 53
and canonical ensemble, 54
and Cesaro convergence, 56
and Hamiltonian dynamics, 51
and harmonic oscillator, 49
and Frobenius-Perron operator, 52, 56
illustrated, 49
and Koopman operator, 51
and Markov operator, 57
and microcanonical ensemble, 54
and mixing, 63
and perturbations, 121
and sampled systems, 109
and space and time averages, 54
and stationary density, 52
and tent map, 75
and thermodynamic equilibrium, 52, 54
Errors, see Coarse graining; Sampling
Euler-Bernstein equations, 142
Exactness, 89
and asymptotic periodicity, 96
and canonical ensemble, 92, 94, 98, 101
constructing, 95
convergence rate, 96
and delay differential equations, 91
and dyadic transformation, 94
and entropy, 98, 100
and factors, 113
illustrated, 90
and invertibility, 90
and Keener map, 131
and K-systems, 113
and lower bound function, 97
and Markov operator, 93
and microcanonical ensemble, 94, 100
and partial differential equations, 91
and perturbations, 119,122, 131, 135, 149, 152, 158
and quadratic map, 95, 100
and sampled sequence, 108
and strong convergence, 92
and Strong Form of Second Law, 98, 100, 150, 152, 158
and tent map, 91, 95, 96, 100
Extension in phase, 10
F
Factor, 112 {170}
and dyadic transformation, 112, 114, 123
and exactness, 113
and K-system, 113
and projection operators, 113
and quadratic baker transformation, 112
and Strong Form of Second Law, 113
and trace, 112
Fixed point, 23
Fokker-Planck equation, 22, 144
derivation, 142
generalized solution, 146
and Liouville equation, 22, 148
and Markov operator, 22, 145, 147
and noninvertibility, 24
and stationary density, 23, 150
and thermodynamic equilibrium, 150
Frobenius-Perron operator, 24, 39
approximating Markov operators, 136
for baker transformation, 64, 113
and correlations, 68
for dyadic map, 94
and ergodicity, 52, 56
and evolution of densities, 44
for Hamiltonian systems, 48
for invertible dynamics, 41
and Koopman operator, 44
and Liouville equation, 47, 114, 148
and mixing, 63
and ordinary differential equations, 23, 47, 114, 148
properties of, 40
for quadratic baker transformation, 113
for quadratic map, 28, 78
stationary density of, 23, 25
for tent map, 25, 75
G
γ-space, 5
Gas dynamics, 61
Gaussian density, 141, 151
Generalized solution, 146
Geodesic flows, 62
Gibbs
and coarse graining, 103, 106, 109
and mixing, 64
extension in phase, 10
γ-space, 5
index of probability, 5
microcanonical ensemble, 10
Gibbs function, 16
Gibbs inequality, 7
integrated, 8
God theorem, 111
Grand canonical ensemble, 19
H
Hamiltonian dynamics, 33, 45, 48, 101
and ergodicity, 51
and Frobenius-Perron operator, 48
and Lebesgue measure, 48, 101
and maximal entropy, 101
Harmonic oscillator, 49
Hat map, see Tent map
Helmholtz free energy, 16
I
Index of probability, 5
Initial density
dependence of entropy on, 80, 126
Irreversible, see Noninvertible
Invariant measure, 41
illustrated, 42
and stationary density, 42
and thermodynamic equilibrium, 43
Invariant set, 48
Invertibility, 2
and baker transformation, 60, 113
and coarse graining, 107
and entropy, 31, 66
and exactness, 90 {171}
and laws of physics, 101
and Liouville equation, 24, 114
and Markov operator, 23
and mixing, 60
Ito calculus, 141
J
Jensen inequality, 30
K
Keener map, 126
asymptotic periodicity in, 126
and entropy, 126
exactness in, 131
and perturbations, 126
Kolmogorov equation, 144, 145
Koopman operator, 43
and correlations, 68
and ergodicity, 51
and evolution of densities, 44
and Probenius-Perron operator, 44
and ordinary differential equations, 46
and time averages, 43
Krylov, 64
K-systems, 66
and baker transformation, 67, 112
and entropy, 67
and exactness, 113
and factors, 113
and mixing, 67
and traces, 112
L
Landau equation, 153
Laws of physics, 101
Lebesgue measure, 4, 42
and baker transformation, 60
and Hamiltonian systems, 48, 101
and microcanonical ensemble, 9, 42, 54, 63, 94, 100
and mixing, 60
and quadratic map, 42
and Radon-Nikodym theorem, 26
and tent map, 91
Liapunov function, 122, 148
Liouville equation, 22, 47
and baker transformation, 114
and dyadic transformation, 114
and entropy, 32
and Fokker-Planck equation, 22, 148
and Probenius-Perron operator, 47, 114, 148
and invertibility, 24, 114
and perturbations, 148
Liouville theorem, 47
Loschmidt, 32, 45
Lower bound function, 97
M
Markov operator, 22
approximated by Probenius-Perron operators, 136
asymptotically periodic, 72
ergodic, 57
exact, 93
fixed point of, 23
from perturbations, 117, 119, 120, 124, 131
and Fokker-Planck equation, 22, 145, 147
invertible, 23
mixing, 64
noninvertible, 24
properties, 23
smoothing, 70
stationary density of, 23, 38
and stochastic differential equations, 22, 147
Maximal entropy
and blackbody radiation, 18
and canonical ensemble, 11, 101
and grand canonical ensemble, 19
and Hamiltonian dynamics, 101
and Maxwell-Boltzmann distribution, 17
and microcanonical ensemble, 9
and thermodynamic equilibrium, 12 {172}
Maxwell-Boltzmann distribution
continuous, 17
discrete, 18
Measurable transformation, 39
Measure, 4
and density, 4
illustrated, 4, 42
invariant, 41
Lebesgue, 4, 42
Measure preserving transformation, 41
Measure space, 1
σ-finite, 2
and thermodynamic systems, 2
Metric indecomposability, see Ergodic
Metric transitivity, see Ergodic
Microcanonical ensemble, 9
and baker transformation, 65
and Boltzmann-Gibbs entropy, 9
density of, 10
and dyadic transformation, 94
and ergodicity, 54
and exactness, 94, 100
and Gibbs, 10
and Lebesgue measure, 9, 42, 54, 63, 94, 100
and maximal entropy, 9
and stationary density, 54, 64
Mixing, 59
and baker transformation, 60, 63
and canonical ensemble, 63
and coarse graining, 106
and correlations, 68
and covariance, 67
and entropy, 64, 66
and ergodicity, 63
and Frobenius-Perron operator, 63
gas model, 61
and geodesic flows, 62
and Gibbs, 64
illustrated, 59
and invertibility, 60
and K-systerns, 67
and Lebesgue measure, 60
Markov operator, 64
and perturbations, 121
and sampling, 108
and weak convergence, 63
μ-space, 5
N
Noise, see Perturbations
Noninvertibility, 3
and Boltzmann equation, 114
and conditional entropy, 33
and dyadic transformation, 114
and exactness, 90
and Fokker-Planck equation, 24
and laws of physics, 101
and Markov operators, 24
Nonsingular transformation, 39
Normalized covariance, 67
O
Observable, 5
and canonical ensemble, 11
and grand canonical ensemble, 19
and maximal entropy, 12
and Maxwell-Boltzmann distribution, 16
Ordinary differential equations
and conditional entropy, 32, 45
and density evolution, 22
and Probenius-Perron operator, 23, 47, 114, 148
Hamiltonian system, 33, 45, 48, 101
and Koopman operator, 46
and Liouville equation, 22, 48
and perturbations, 140
P
Partial differential equations and exactness, 91
Partition, 103
Partition function, 12
Perturbations
additive, 121, 123, 153, 155
and asymptotic periodicity, 118, 122, 126
and baker transformation, 123
and dyadic transformation, 123 {173}
and dynamics, 115
and entropy, 119, 126, 131, 149, 150
and ergodicity, 121
and exactness, 119, 122, 131, 149, 152, 158
of Keener map, 126
and Liouville equation, 148
and mixing, 121
of ordinary differential equations, 139
by other systems 119, 121
parametric, 131, 156
and phase transitions, 151
and stationary density, 119, 125, 150, 152, 153
and strong form of Second law, 119, 122, 131, 135, 149, 150
and thermodynamic equilibrium, 119, 125
and traces, 119, 121
and weak form of Second law, 118, 122, 123, 124, 126, 133
versus dynamics, 120, 121
Phase space, 1
coarse grained, 103
Phase transitions
first order, 155, 157
second order, 154, 158
Planck blackbody radiatiori, 18
Poincare recurrence theorem, 45
extension, 55
Probability current, 152
Projection operator, 113
Q
Quadratic baker transformation, 112
and factors, 112
Frobenius-Perron operator for, 113
stationary density for, 113
and trace, 112
Quadratic map, 27
and asymptotic periodicity, 78, 83
and entropy, 28, 78, 83, 100
exactness of, 95, 100
as factor, 113
Frobenius-Perron operator for, 28, 78
invariant measure for, 42
stationary density for, 28, 42
and tent map, 27
Quantized behavior, 72
R
Radon-Nikodym theorem, 26
Rayliegh-Jeans radiation law, 19
Recurrence, 45
theorem, 45, 54
recurrent point, 45
Reversibility, see Invertibility
S
Sampling, 107
and entropy, 109
and ergodicity, 109
and exactness, 108
illustrated, 108
and mixing, 108
Scalar product, 35
Second Law of Thermodynamics, see Strong Form of Second Law of Thermodynamics; Weak Form of Second Law of Thermodynamics
Semidynamical system, 3
σ-algebra, 1
σ-finite measure space, 2
Smoothing operator, 70
Spatial averages
convergence, 96
in ergodic systems, 54
Spectral decomposition theorem, 71
Stationary density, 23, 38
and asymptotic periodicity, 72
for baker transformation, 65
and canonical ensemble, 64
for dyadic map, 95
and ergodicity, 52
for Fokker-Planck equation, 23, 150
for Frobenius-Perron operator, 23, 25
and invariant measures, 42 {174}
and microcanonical ensemble, 54, 64
and perturbations, 119, 125, 150, 152, 153
for quadratic baker transformation, 113
for quadratic map, 28, 42
for tent map, 25, 76
and thermodynamic equilibrium, 4, 23, 34, 42, 52
Stochastic differential equations, 22, 141
Fokker-Planck equation for, 22, 144
and Markov operators, 22, 147
and phase transitions, 151
Stochastic kernel, 117
Stratonovich calculus, 141
Strong convergence, 35
and exactness, 92
and thermodynamic equilibrium, 36
Strong Form of Second Law of Thermodynamics, ix
and coarse graining, 107
and exactness, 98, 100, 150, 152, 158
and factors, 113
and global stability, 13
and laws of physics, 101
and perturbations, 119, 121,131, 135, 149, 150
System state density averages, 34
T
Temperature, 13
Temporal coarse graining, see Sampling
Tent map, 24
and asymptotic periodicity, 75, 82
and entropy, 82, 95, 100
ergodicity of, 75
and exactness, 91, 95, 96, 100
Frobenius-Perron operator for, 25, 75
and Lebesgue measure, 91
and quadratic map, 27
and stationary density, 25, 76
and Weak Form of Second Law
of Thermodynamics, 83
stationary density for, 25, 76
Thermodynamic entropy difference, ix
and conditional entropy, 29
Thermodynamic entropy, ix, 12, 13
and Boltzmann-Gibbs entropy, 13
Thermodynamic equilibria, ix, 13
and ergodicity, 52
and Fokker-Planck equation, 150
and invariant measures, 43
and maximal entropy, 12
and perturbations, 119, 125
and stationary density, 4, 23, 34, 42, 52
and strong convergence, 36
and upper bound function, 36
and weak convergence, 35
and weak precompactness, 36
conditions for existence, 34
global, 13
metastable, 13
Thermodynamic limit, 5
Thermodynamic state, 4
Thermodynamic system, 4
and density, 4
and measure space, 2
state of, 4
Time reversal invariance, see Invertibility
Trace, 110
and baker transformation, 112, 123
and coarse grained entropy, 113
and dyadic transformation, 112
and entropy, 111
and factor, 112
and God theorem, 111
and K-systems, 112
and perturbations, 119, 121
and quadratic baker transformation, 112
and trajectories, 110
Trajectories, 2, 110
average along, 43, 54 {175}
convergence of, 96
and trace, 110
Transient operator, 71
Trivial invariant set, 48
U
Uniform parabolicity condition, 143
V
Voigts theorem, 30
W
Weak convergence, 35
and existence of equilibria, 35
and mixing, 63
Weak Form of Second Law of Thermodynamics, ix
and asymptotic periodicity, 80
dependence on initial preparation, 80, 83
and metastable states, 13
and perturbations, 118, 122, 123, 124, 126, 133
and quadratic map, 83
and tent map, 83
Weak precompactness, 36
White noise, 141
Wien radiation law, 19
Wiener process, 141
Z
Zermelo, 45