

 |
 |
| {i} |
 |
Technical International Network of Engineers Report |
Andre Gsponer Jean-Pierre Hurni
Independent Scientific Research Institute (ISRI)
P.O. Box 30,1211 Geneva 12, Switzerland
Technical Report No. 1 |
Seventh edition: September 2000 |
| {ii} |
Third printing (October 2002) with a few corrections and updates of the seventh corrected and expanded edition of a report first distributed at the 1997 INESAP Conference, Shanghai, China, September 8-10, 1997.
The second edition of this report was translated in Russian in 1998 by the Russian Foreign ministry in Moscow.
The authors welcome any suggestion or comment on this report. These should be mailed to ISRI, at the address on the front cover, or sent by electronic mail to gsponer@vtx.ch.
Orders should be sent to IANUS, at the address on the back cover, by fax to No. (+49) 6151-16-6309, or by e-mail to ianus@hrzpub.tu-darmstadt.de.
ISBN 3-933071-02-X
© Copyright, 1997, 1998, 1999, 2000, 2001, 2002. INESAP, c/o IANUS, Darmstadt University of Technology, Germany. All rights reserved.
An eighth edition, which will be a major revision and update with at least two more chapters, will be published in 2003 either in the form of a report or a book.
| {v} |
This report is an assessment of the prospect of developing new (i.e., fourth generation) nuclear weapons in the context of the Comprehensive Nuclear Test-Ban Treaty (CTBT) that was adopted by the UN General Assembly in 1996 and of the current moratorium on nuclear testing in effect in all nuclear-weapon States.
The first chapter is a primer on thermonuclear weapons based on a scientific understanding of the physical principles of existing nuclear weapons and on the results of ISRINEX, a simple thermonuclear explosion simulation program specially developed for independent disarmament experts. Using this insight, it is shown that the construction of hydrogen bombs is in fact much less difficult than is generally assumed. Using present-day nuclear and computer technology, almost any modern industrial country could, in principle, build such a weapon. Similarly, it is shown that “boosting,” i.e., the technique of using a small amount of tritium to enhance the performance of a fission bomb, is also much easier than generally assumed. In particular, using this technique, building highly efficient and reliable atomic weapons using reactor-grade plutonium is straightforward. Moreover, independently of the type of fissile material used, the construction of “simple” and “deliverable” tritium-boosted nuclear weapons can be easier than the construction of primitive Hiroshima or Nagasaki type atomic bombs. In May 1998, both India and Pakistan showed that they had successfully developed boosted fission weapons. Moreover, India claimed to have tested an advanced hydrogen bomb concept, and it is believed that two of their other four devices have used plutonium that was not classified as weapons grade.
The second chapter is a technical and legal analysis of the nuclear tests which are allowed by the CTBT: microexplosions and subcritical experiments. It is found that this treaty explicitly forbids only nuclear explosions in which a divergent fission chain reaction takes place. Therefore, it is possible to develop new types of fission explosives in which subcritical fission-bum is the yield generation mechanism. Similarly, new kinds of fusion explosives, in which the trigger is no longer a fission explosive, are legal under the CTBT.
The third chapter is devoted to the military applications of inertial confinement fusion (ICF) and other pulsed-power technologies. The capabilities of modern {vi} laboratory simulation techniques for weapons physics research are shown to significantly overlap with those of underground nuclear testing. Moreover, these technologies are found to enable the study of a number of physical processes — especially electromagnetic energy cumulation techniques and advanced nuclear processes that are not restricted by existing arms control treaties — which are useful in refining existing nuclear weapons and essential in developing fourth generation nuclear weapons.
The fourth chapter is devoted to fourth generation nuclear weapons. These new fission or fusion explosives could have yields in the range of 1 to 100 ton equivalents of TNT, i.e., in the gap which today separates conventional weapons from nuclear weapons. These relatively low-yield nuclear explosives would not qualify as weapons of mass destruction. Seven physical processes which could be used to make such low-yield nuclear weapons, or to make compact non-fission triggers for large scale thermonuclear explosions, are investigated in detail: subcritical fission-burn, magnetic compression, superheavy elements, antimatter, nuclear isomers, metallic hydrogen and superlasers (i.e., ultrapowerful lasers with intensities higher than 1019 W/cm2).
The conclusion stresses that considerable research is underway in all five nuclear-weapon States (as well as in several other major industrialized States such as Germany and Japan) on ICF and on many physical processes that provide the scientific basis necessary to develop fourth generation nuclear weapons. Substantial progress has been made in the past few years on all these processes, and the construction of large ICF microexplosion facilities in both nuclear-weapon and non-nuclear-weapon States is giving the arms race a fresh boost. The world runs the risk that certain countries will equip themselves directly with fourth generation nuclear weapons, bypassing the acquisition of previous generations of nuclear weapons.
In this context, the invention of the superlaser, which enabled a factor of one million increase in the instantaneous power of tabletop lasers, is possibly the most significant advance in military technology of the past ten years. This increase is of the same magnitude as the factor of one million difference in energy density between chemical and nuclear energy.
A major arms control problem of fourth generation nuclear weapons is that their development is very closely related to pure scientific research. The chief purpose of the CTBT is to freeze the technology of nuclear weapons as a first step toward general and complete nuclear disarmament. In order to achieve that, it is necessary to implement effective measures of preventive arms control, such as international legally binding restrictions in all relevant areas of research and development, whether they are claimed to be for military or civilian purposes.
| {vii} |
Executive summary | v | ||||
| xiii | ||||
| xv | ||||
| xvii | ||||
1 | The Physical Principles of Thermonuclear Explosives | 1 | |||
1.1 Introduction............................. | 1 | ||||
1.2 ISRINEX 2.6 physics........................ | 2 | ||||
1.3 Fission explosives and boosting................... | 7 | ||||
1.4 Modern boosted fission explosives................. | 11 | ||||
1.5 The principle of the hydrogen bomb................ | 18 | ||||
1.6 The Teller-Ulam method...................... | 22 | ||||
1.7 “Mike,“ the first hydrogen bomb.................. | 27 | ||||
1.8 B-28: The first “miniature” | 32 | ||||
1.9 1970-1980 thermonuclear designs................. | 36 | ||||
1.10 Thermonuclear detonation waves and | 39 | ||||
2 | Nuclear Weapons Development under the CTBT | 47 | |||
2.1 The Comprehensive Test Ban Treaty................ | 47 | ||||
2.2 Subcritical tests and treaty limitations............... | 48 | ||||
2.3 Microexplosions and treaty limitations............... | 50 | ||||
| |||||
2.4 Nuclear explosions and the “zero-yield” CTBT.......... | 53 | ||||
2.5 Nuclear activities not prohibited by the CTBT and advanced | 55 | ||||
3 | Nuclear Weapons Applications of Inertial Confinement Fusion | 59 | |||
3.1 Introduction............................. | 59 | ||||
3.2 Inertial Confinement Fusion (ICF)................. | 60 | ||||
3.3 Total energy versus energy density | 66 | ||||
3.4 Equation of state (Fig. 15) ..................... | 68 | ||||
3.5 Opacity (Fig. 16).......................... | 69 | ||||
3.6 Compressible turbulence (Fig. 17)................. | 71 | ||||
3.7 Radiation-driven hydrodynamics (Fig. 18)............. | 72 | ||||
3.8 Pure hydrodynamics (Fig. 19) ................... | 73 | ||||
3.9 Radiative transport (Fig. 20).................... | 73 | ||||
3.10 ICF and nuclear weapons proliferation............... | 74 | ||||
4 | Fourth Generation Nuclear Weapons | 81 | |||
4.1 Introduction............................. | 81 | ||||
4.2 Subcritical and microfission explosives............... | 84 | ||||
4.3 Transplutonic and superheavy elements.............. | 88 | ||||
4.4 Antimatter.............................. | 93 | ||||
4.5 Nuclear isomers........................... | 103 | ||||
4.6 Super-explosives and metallic hydrogen.............. | 108 | ||||
4.7 Pure-fusion explosives....................... | 114 | ||||
4.8 Superlasers............................. | 124 | ||||
4.9 Technology of fourth generation | 130 | ||||
5 | Conclusion | 137 | |||
6 | Bibliography | 145 | |||
6.1 Nuclear armament and disarmament................ | 147 | ||||
6.2 Fission weapons........................... | 152 | ||||
6.3 Fusion weapons........................... | 153 | ||||
6.4 Third and fourth generation nuclear weapons ........... | 156 | ||||
6.5 Inertial confinement fusion..................... | 157 | ||||
6.6 Subcritical fission and microfission................. | 161 | ||||
6.7 Shockwaves............................. | 162 | ||||
6.8 Equations of state.......................... | 163 | ||||
6.9 Opacities .............................. | 164 | ||||
| |||||
6.10 Instabilities............................. | 164 | ||||
6.11 Superheavy elements........................ | 165 | ||||
6.12 Antimatter.............................. | 168 | ||||
6.13 Nuclear isomers........................... | 174 | ||||
6.14 Super-explosives and metallic hydrogen.............. | 177 | ||||
6.15 Pure-fusion explosives....................... | 180 | ||||
6.16 Cumulation of energy........................ | 184 | ||||
6.17 High-energy-density and pulsed-power facilities.......... | 186 | ||||
6.18 Superlasers............................. | 188 | ||||
6.19 Technology............................. | 192 | ||||
Figures | 195 | ||||
| {x} |
1 Metric prefixes........................... | xviii |
1.1 Normalized maximum energy contents of nuclear fuels...... | 45 |
1.2 Sequence of events and timing of a thermonuclear explosion ... | 46 |
2.1 Major atomic and nuclear processes of importance to present and | 58 |
3.1 Major operating or planned particle-beam driven ICF facilities. In | 80 |
3.2 Major operating or planned laser driven ICF facilities. In the last | 81 |
4.1 Major operating or planned superlaser facilities.......... | 137 |
| {xiii} |
The work presented here would not have been possible without the financial and moral support of the Fondation Charles Leopold Mayer pour le progres de l'Homme (FPH). In particular, we wish to thank Pierre Calame and Maurice Cosandey, as well as the other members of the Council and the executive staff of FPH, for their continuous support and encouragement.
In the three years during which the material on which this report is based was assembled and studied, we have benefited from conversations and correspondence with numerous people. We would like to thank in particular the following persons for their contribution — which in each case was significant to us:
Masud Ahmad, Frank Barnaby, Thomas Cochran, Tom Zamora Collina, Freeman Dyson, Suren Erkman, Richard Garwin, Valery Gov-orukhin, Chuck Hansen, Frank von Hippel, P.K. Iyengar, Suzanne Jones, Martin Kalinowski, Ronald C. Kirkpatrick, Stefan Klement, J.G. Linhart, Milo Nordyke, Christopher Pain, L. John Perkins, Vadim Simonenko, Carey Sublette, I.V. Sokolov, Naeem Tahir, Ted Taylor, Wang Xianpeng, William Westermeyer and Friedwardt Winterberg.
| {xv} |
There are many good reasons for having independent expertise on nuclear weapons. The main reason, however, is simply that there are no scientific secrets on their physical principles: a State or organization wanting to make nuclear weapons can easily find the necessary basic information in the open literature. Access to modern computers of moderate capacity is therefore sufficient to design a nuclear weapon. Similarly, the same information is available to those who oppose nuclear weapons and wish to improve the quality of their arguments.
On the other hand, the manufacture of a thermonuclear weapon, together with the special nuclear materials it is made of, has always been (and remains) a formidable engineering challenge, especially for technologically less advanced countries. For this reason, as long as independent expertise concentrates on scientific principles and not on engineering details, there is little risk it will contribute to horizontal proliferation.1 With this in mind, chapter one gives an introduction to the physics of thermonuclear weapons. We believe there is no compelling reason why such knowledge should remain the privilege of government experts working behind the curtain of secrecy.
The main anti-proliferation impact of independent expertise on nuclear weapons is potentially on vertical proliferation. A good understanding of nuclear weapons physics is important to evaluate the future evolution of nuclear weapons technology, especially in the context of international agreements, such as the Comprehensive Nuclear Test-Ban Treaty (CTBT) and the Nuclear Non-Proliferation Treaty (NPT), which are supposed to put a halt to the development of new nuclear weapons. {xvi}
In particular, such an understanding is essential for the assessment of the links between modern simulation techniques2 and nuclear weapons, and for the analysis of fourth generation nuclear weapon concepts. These topics are the subject of chapters two, three and four.
The concluding chapter of this report is followed by a bibliography containing more than 500 items. This bibliography is not exhaustive. It contains only those references that we have studied and which are cited in this report. These references (which comprise a number of review articles) have been selected in view of their scientific, technical, strategic, or historical importance, as well as for their pedagogical utility for acquiring a deeper understanding of the subject matter. To help those who are interested in one particular subject, the references have been assembled by subjects, and are listed in chronological order.
Finally, the question, “Why fourth generation nuclear weapons?” is not directly addressed in this report. In effect, trying to answer this most important question would require taking into account many strategic, economic, social and political aspects that go beyond the scope of this technical report. Nevertheless, we hope that the report will positively contribute to a thorough discussion of fourth generation nuclear weapons, and that it will provide a sound technical basis to this continuing debate.3
| {xvii} |
The international system of units (M KSA) is used throughout. However, in the case of plasmas, practical units are used for the temperatures (electron-Volts instead of degrees Kelvin) and pressures (Megabars instead of Pascals).
In the case of energies, electron-Volts are often used instead of Joules. And, in the case of explosions, the yields are expressed in kilogram or kiloton equivalents of TNT (to avoid confusion, while weights are written kg or kt, explosive yields are written kg or kt). Sometimes we use calories, e.g., in the definition of the kt.
The following definitions and conversion factors apply:
1 eV=11604°K
1 eV = 1.602 x KT19 J
1 bar=105Pa
1 Mbar=100GPa
1 kg = 106 cal
1 kg = 4.184 MJ
1 kg = 2.61 x 1019 MeV
1 kt =1012 cal = 4.184 x 106 MJ
1 kt = 2.61 x 1025 MeV
| {xviii} |
International system of units (SI) prefixes
prefix |
symbol |
factor |
prefix |
symbol |
factor |
milli |
m |
10–3 |
kilo |
k |
103 |
micro |
μ |
10–6 |
mega |
M |
106 |
nano |
n |
10–9 |
giga |
G |
109 |
pico |
P |
10–12 |
tera |
T |
1012 |
femto |
f |
10–15 |
peta |
P |
1015 |
atto |
a |
10–18 |
exa |
E |
1018 |
zepto |
z |
10–21 |
zetta |
Z |
1021 |
yocto |
y |
10–24 |
yotta |
Y |
1024 |
Table 1: Metric prefixes
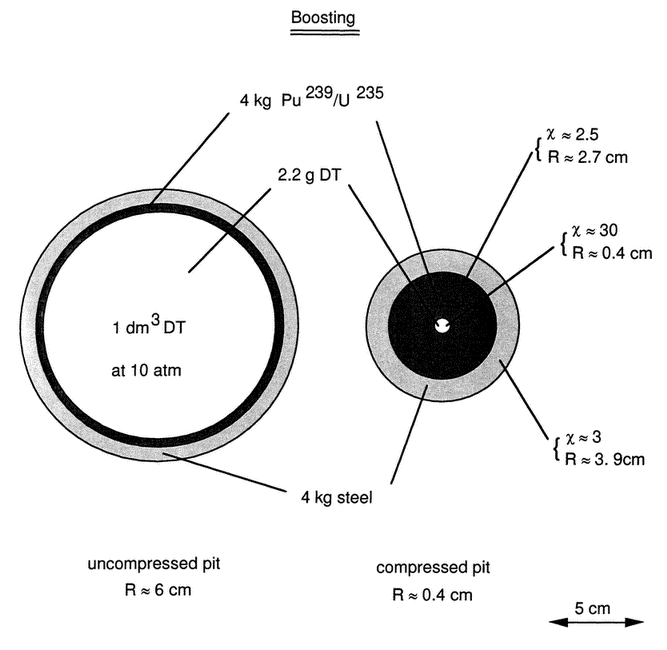
Figure 1 Fissile material pit containing 2.2 g of deuterium tritium fusion fuel shown before and after compression by the shock waves generated by about 10 kg of high explosives.
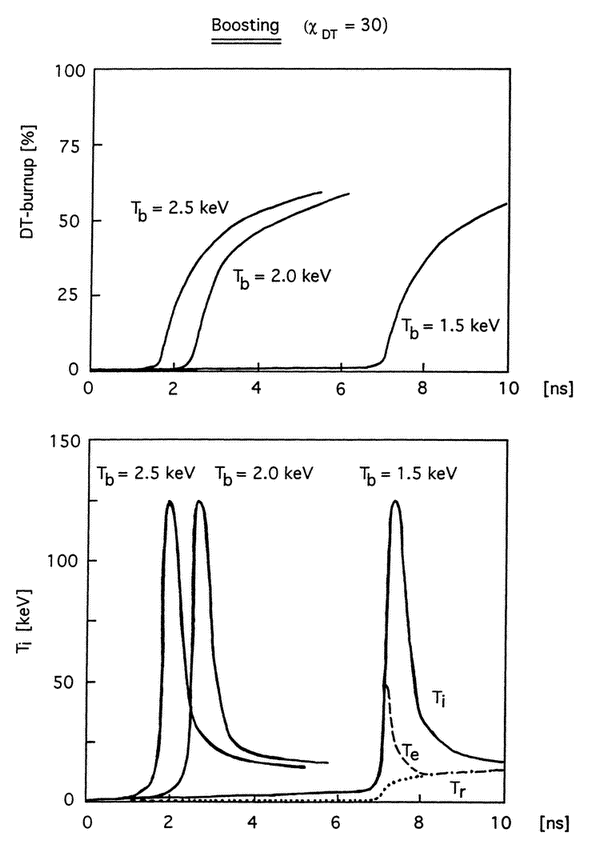
Figure 2. Time evolution of DT burn efficiency and plasma ion temperature as a function of the fissile material temperature Tb. For Tb = 1.5 keV, all three plasma temperatures are indicated, showing significant runaway of Ti relative to Te and Tr. The compression of DT is χ = 30 in all cases.
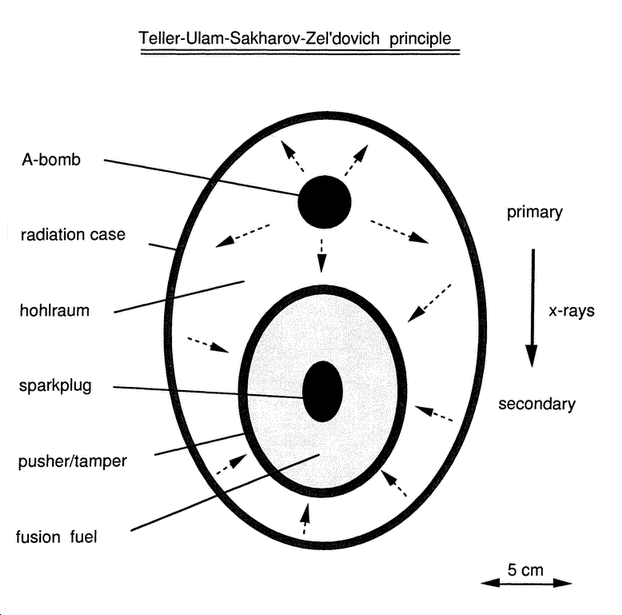
Figure 3 “In thermonuclear weapons, radiation from a fission explosive can be contained and used to transfer energy to compress and ignite a physically separate component containing thermonuclear fuel. (February 1979)“.
Reference: U.S. Department of Energy, Office of Declassification, “Drawing back the curtain of secrecy - Restricted data declassification policy, 1946 to present”, RDD-1, (June 1,1994) page 94.
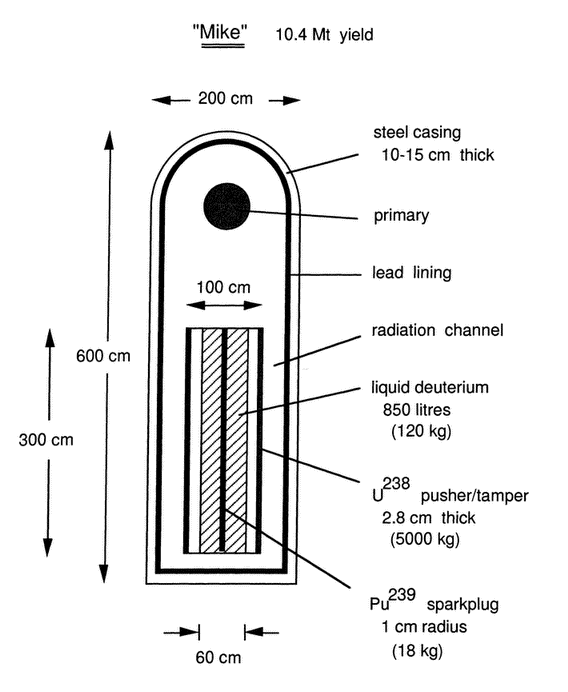
Figure 4 Main components of “Mike”, the first hydrogen bomb, schematically drawn using plausible estimates for their dimensions and weights.
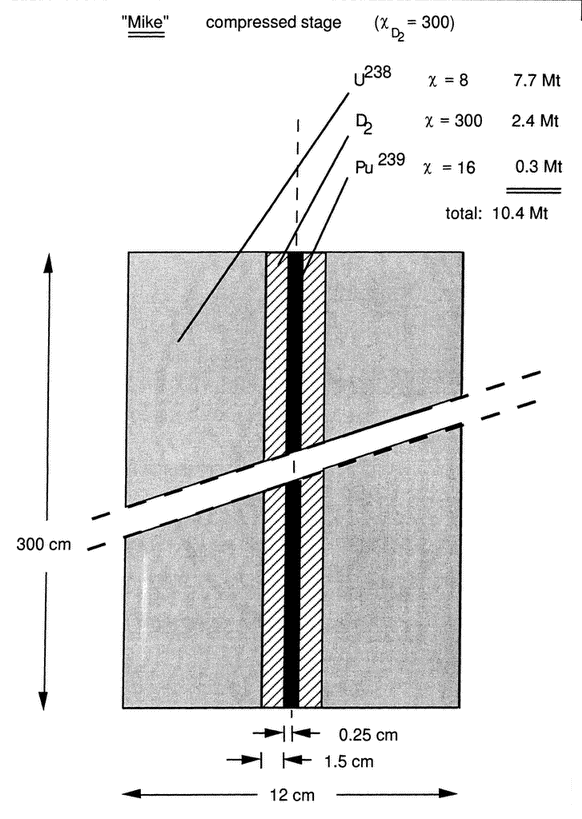
Figure 5 At maximum compression the 100 cm diameter, 2.8 cm thick, uranium blancket is squeezed down to a 12 cm diameter hollow uranium bar, compressing the liquid deuterium to 300 times its solid density.
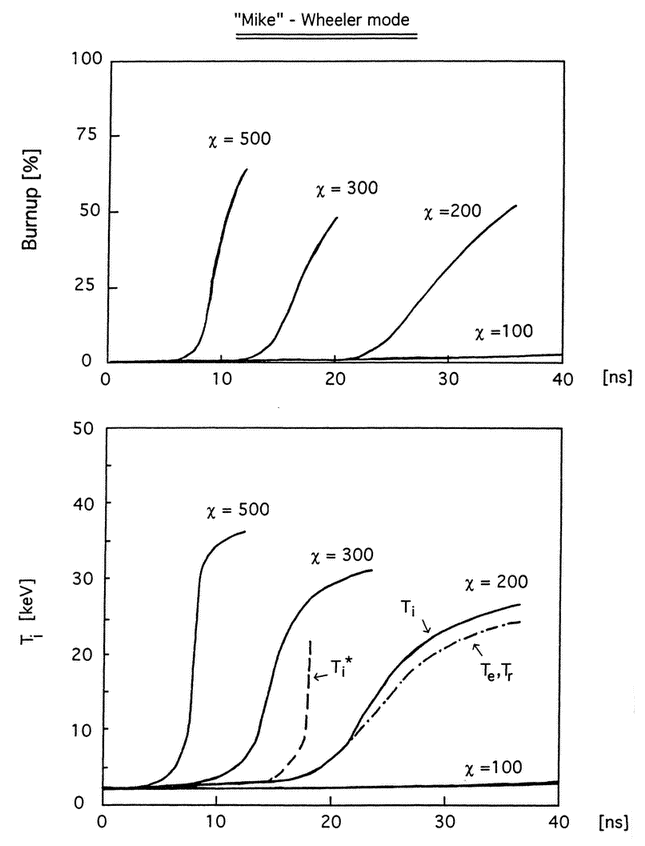
Figure 6. Time evolution of D2 burn efficiency and plasma ion temperature in Wheeler mode (ignition by self-heating) as a function of the compression factor χ. For χ = 200, all three plasma temperatures are depicted, showing little runaway of Ti relative to Te and Tr. Ti* is the temperature the ions would have in the absence of inverse Compton scattering effects.
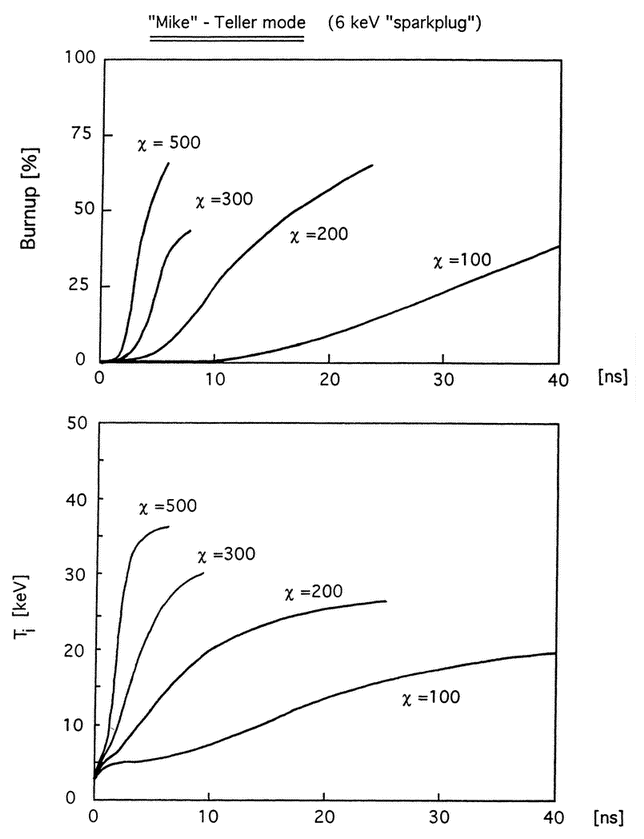
Figure 7. Time evolution of D2 burn efficiency and plasma ion temperature in Teller mode (sparkplug assisted ignition) as a function of the compression factor χ. The maximum sparkplug temperature is assumed to be 6 keV.
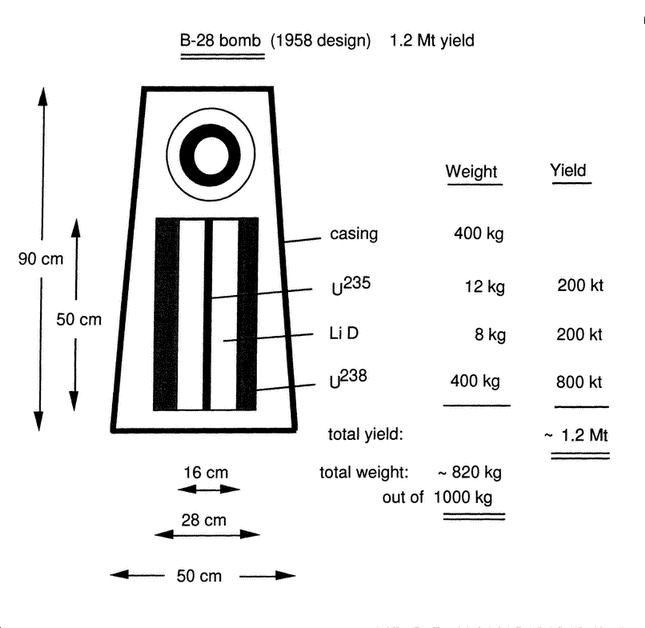
Figure 8 Using realistic estimates for the amount of thermonuclear fuel, the weight of the uranium tamper, and the size of the primary, there is sufficient space to fit everything within the volume of the B-28.
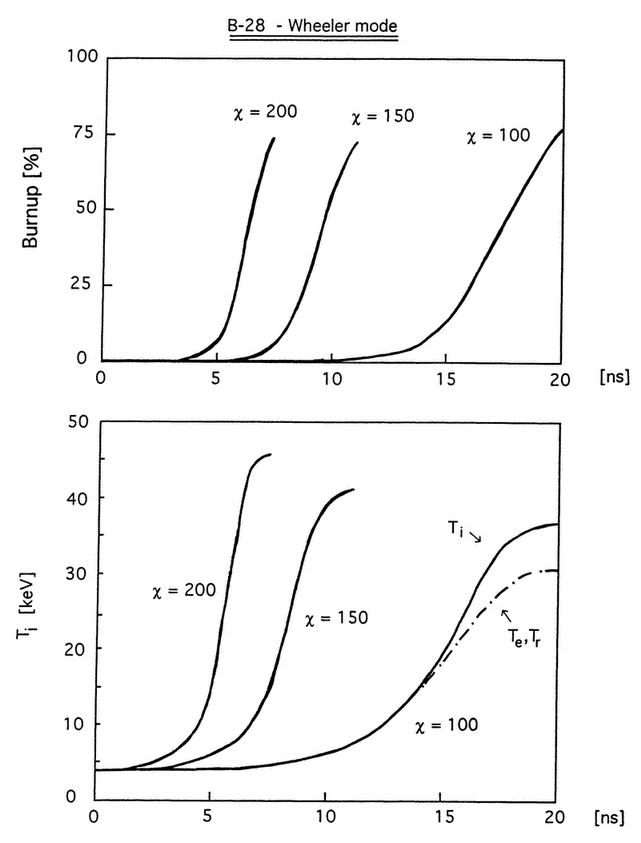
Figure 9. Time evolution of LiD burn efficiency and plasma ion temperature in Wheeler mode (ignition by self-heating) as a function of the compression factor χ. For χ = 100, all three plasma temperatures are depicted, showing slight runaway of Ti relative to Te and Tr for Ti > 25 keV.
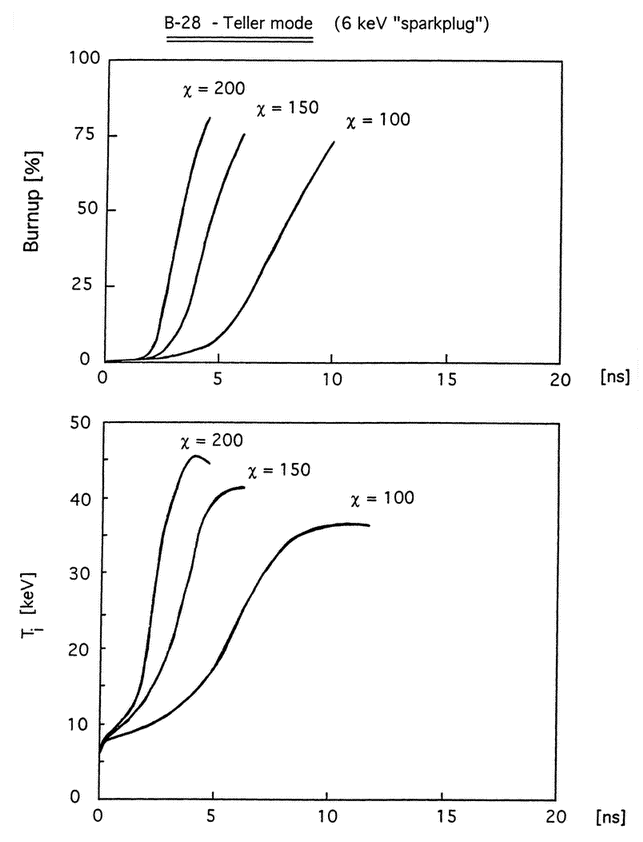
Figure 10. Time evolution of LiD burn efficiency and plasma ion temperature in Teller mode (sparkplug assisted ignition) as a function of the compression factor χ. The maximum sparkplug temperature is assumed to be 6 keV.
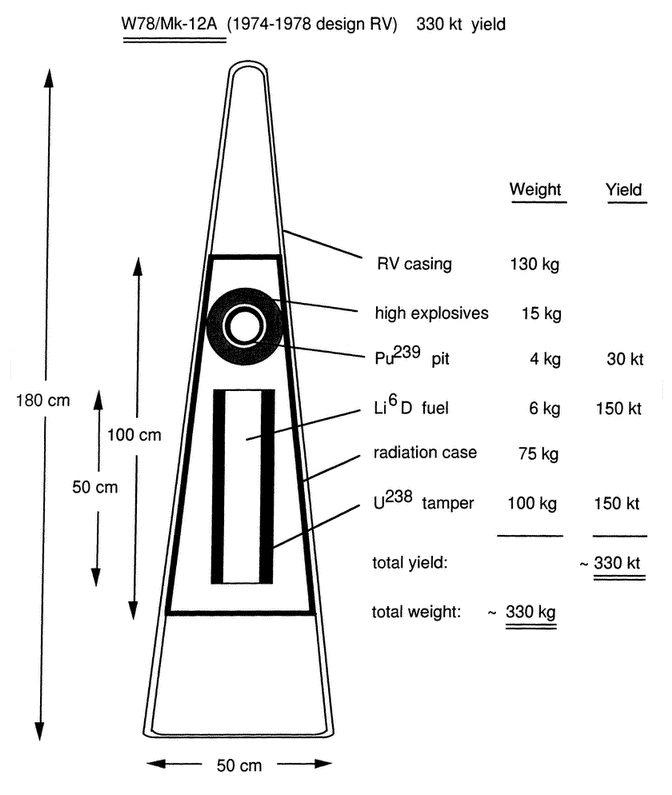
Figure 11 The weight of the W78 warhead is about 200 kg for a total MK-12A reentry vehicle weight of 330 kg. This corresponds to a yield-to-weight ratio of 1.65 kt/kg. To increase yield, the U-238 tamper may be enriched in U-235.
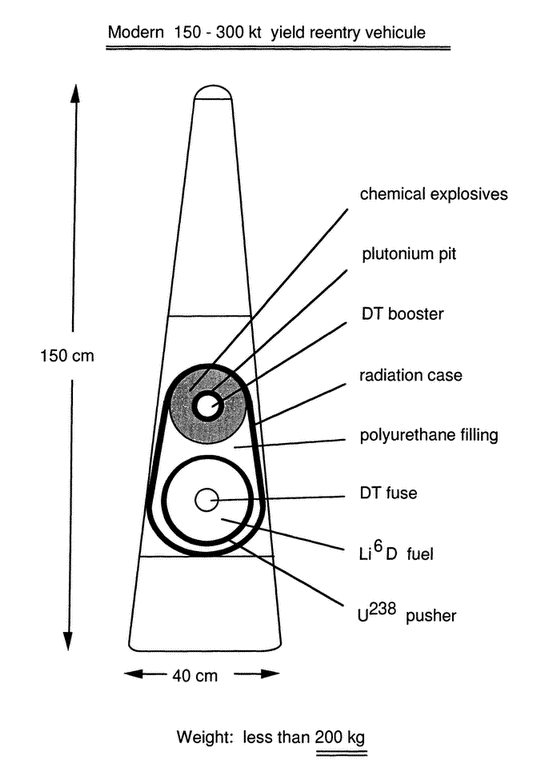
Figure 12 Spherical symmetry of the secondary enables to reach the highest thermonuclear burn efficiency. A reentry vehicle weight of 200 kg for a yield of 200 kt is almost the engineering limit. The warhead itself may weigh as little as 100 kg, implying a yield-to-weight ratio of about 2 kt/kg.
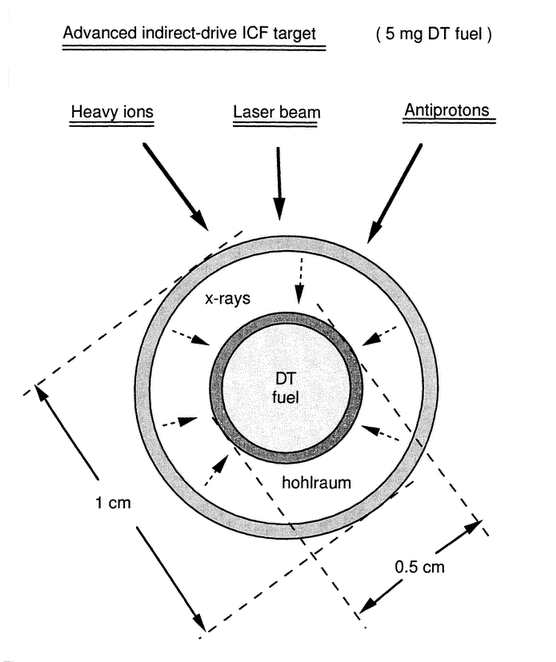
Figure 13 “In some ICF targets, radiation from the conversion of the focussed energy (e.g laser or particle beam) can be contained and used to transfer energy to compress and ignite a physically separate component containing thermonuclear fuel. (February 1979)”.
Reference: U.S. Department of Energy, Office of Declassification, “Drawing back the curtain of secrecy - Restricted data declassification policy, 1946 to present”, RDD-1, (June 1, 1994) page 103.
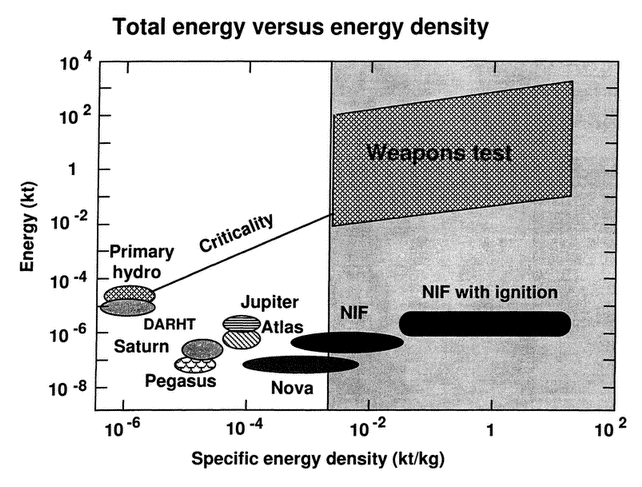
Figure 14 Total energy versus energy density for primary hydrodynamic tests (DARHT), pulsed power facilities (Saturn, Pegasus, Atlas and Jupiter), inertial confinement fusion facilities (NOVA and NIF, and weapons tests.
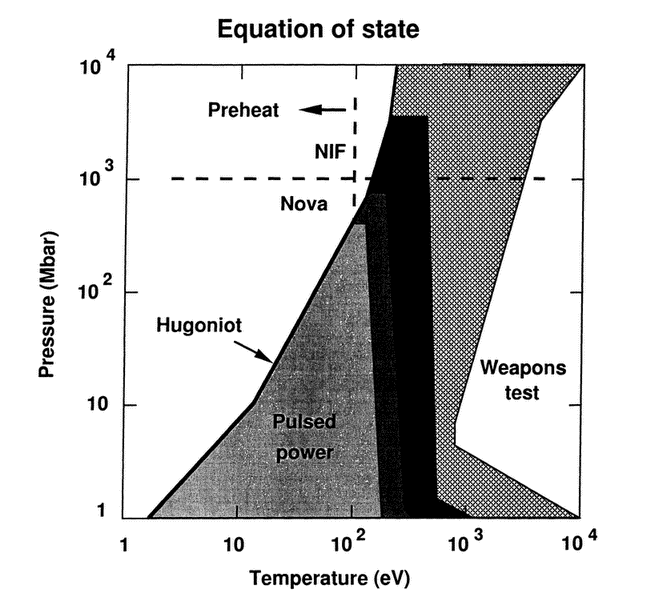
Figure 15 Equation of state measurements achievable on megajoule-scale facilities like NIF or LMJ overlap significantly the weapons-test regime.
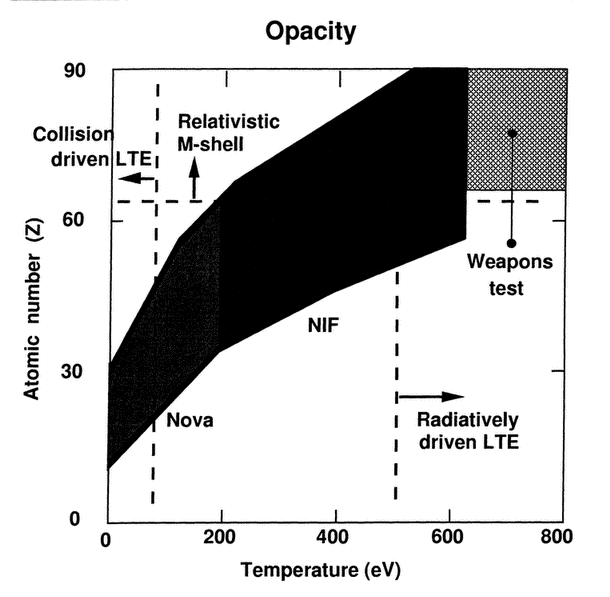
Figure 16a M-shell dominated opacity measurements on NIF are possible in the radiatively driven local thermal equilibrium typical of the weapons-test regime.
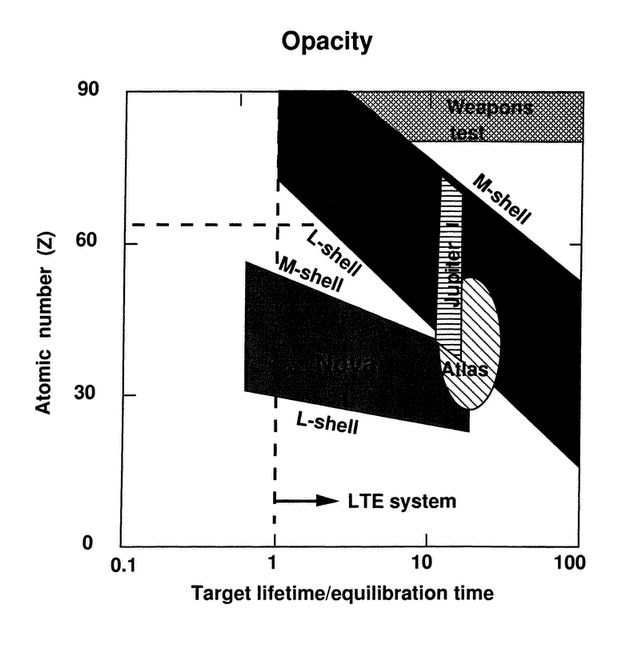
Figure 16b Local thermal equilibrium opacity measurements are possible on NIF, Atlas and Jupiter because the target size is sufficient for its inertial lifetime to be larger than the thermal equilibration time.
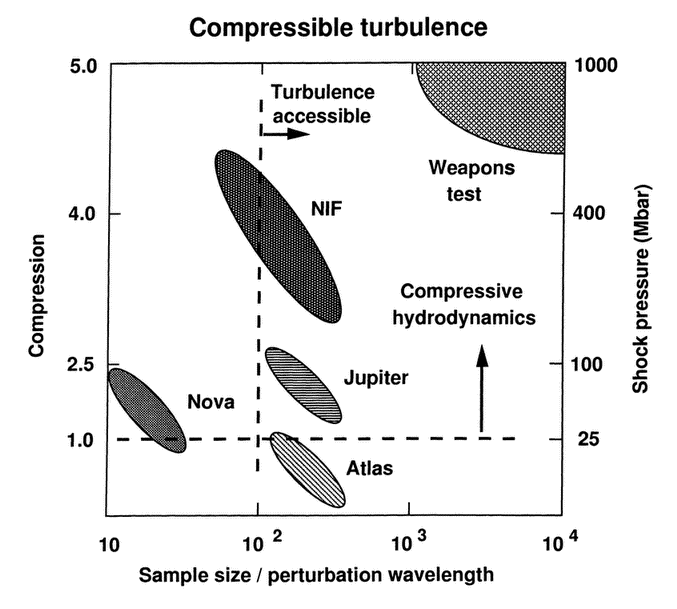
Figure 17a Whereas the moderate compression on NOVA allows to follow the transition from linear instability to weak turbulence, the high compression and larger scale volumes on NIF allows to follow this all the way to turbulent mix.
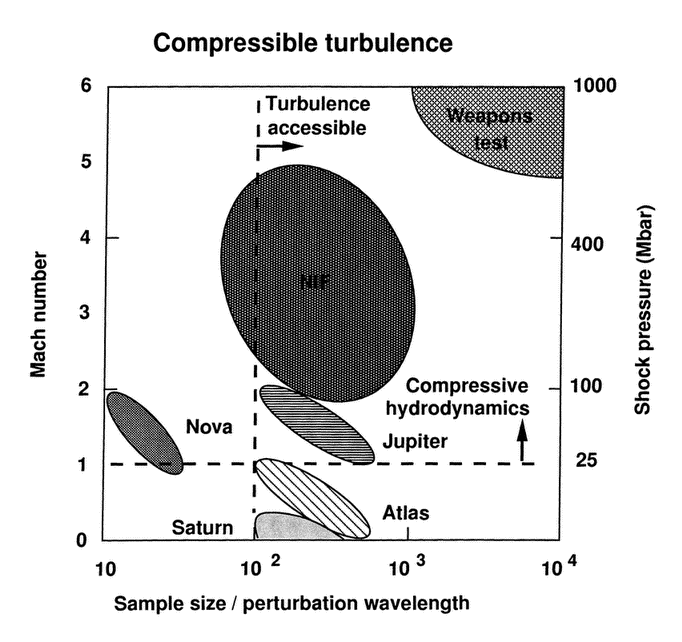
Figure 17b The secondary of a nuclear weapon operates under conditions of strong turbulent mix. Whereas the moderate compression on Nova corresponds to only slightly supersonic shock waves (Mach number 1 to 2), the strong compression of NIF (and the large sample size of Saturn, Atlas and Jupiter) allows to reach the weapons-test regime.
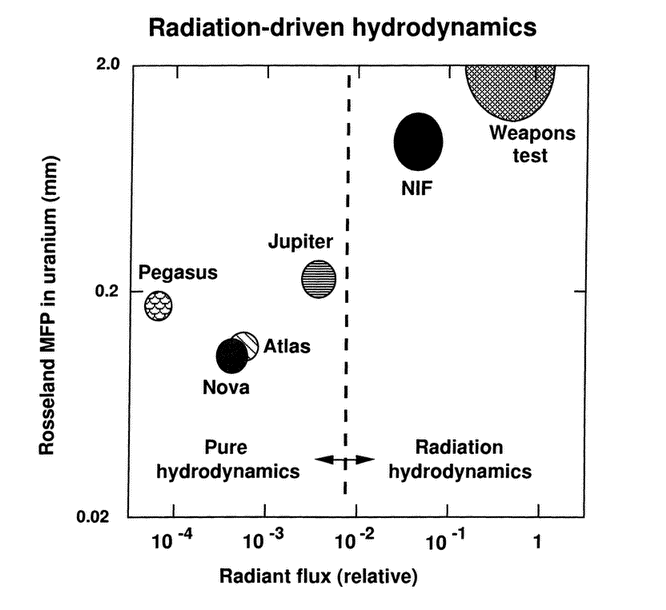
Figure 18 Radiation-driven hydrodynamics is a unique feature of nuclear weapons operation. NIF allows to study radiation hydrodynamics close to weapons-test conditions.
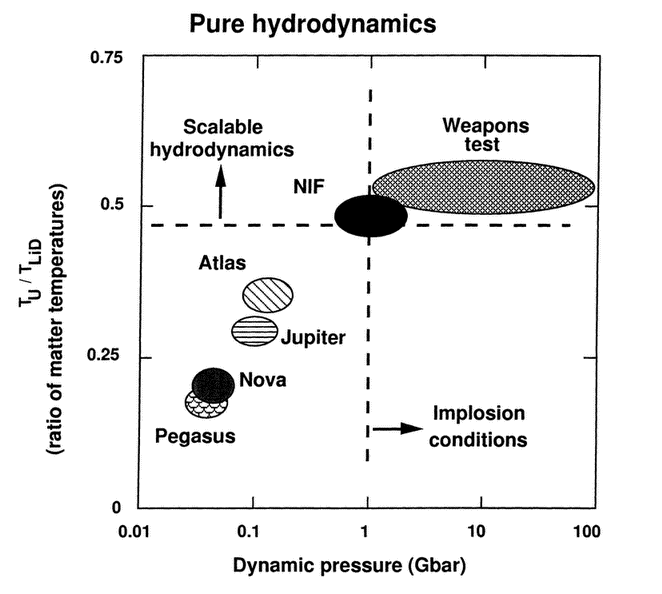
Figure 19 The implosion of a secondary prior to ignition of the thermonuclear fuel (LiD) is a problem of pure hydrodynamics which can be studied on NIF.
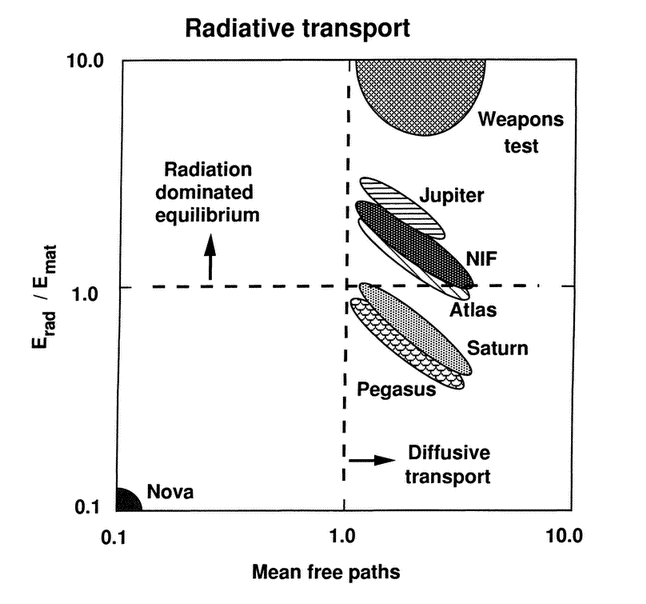
Figure 20 Radiative energy transport is typical of the operation of nuclear weapons. The diffusive approximation applies because of the large size of the NIF targets and because the radiation temperature on NIF is sufficient for the samples to operate in the radiation dominated thermal equilibrium regime.
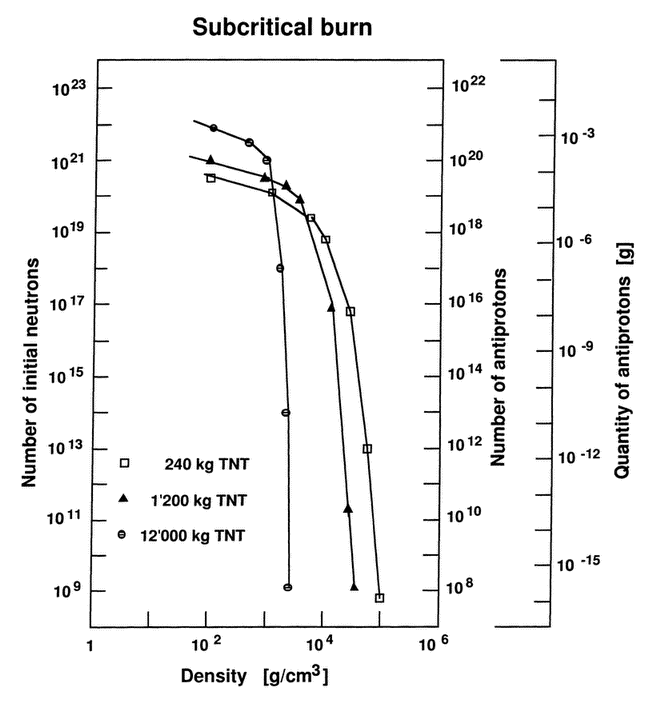
Figure 21 Dependence of the number of initial neutrons (or antiprotons) required for a 100% burn versus the final pellet density for three pellet sizes. Adapted from R.A. Lewis et al, Nucl. Sci. Eng., Vol. 109 (1991) p. 413.
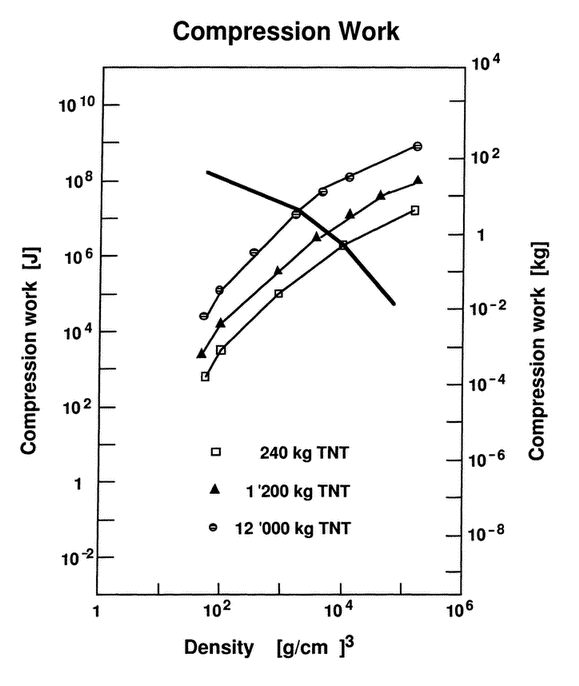
Figure 22 Compression work (in Joule or kilogram equivalent of high-explosives) related to the final pellet density for three pellet sizes (14, 70 and 700 milligrams of plutonium). The curve indicates the boundary between the critical and the subcritical regimes.
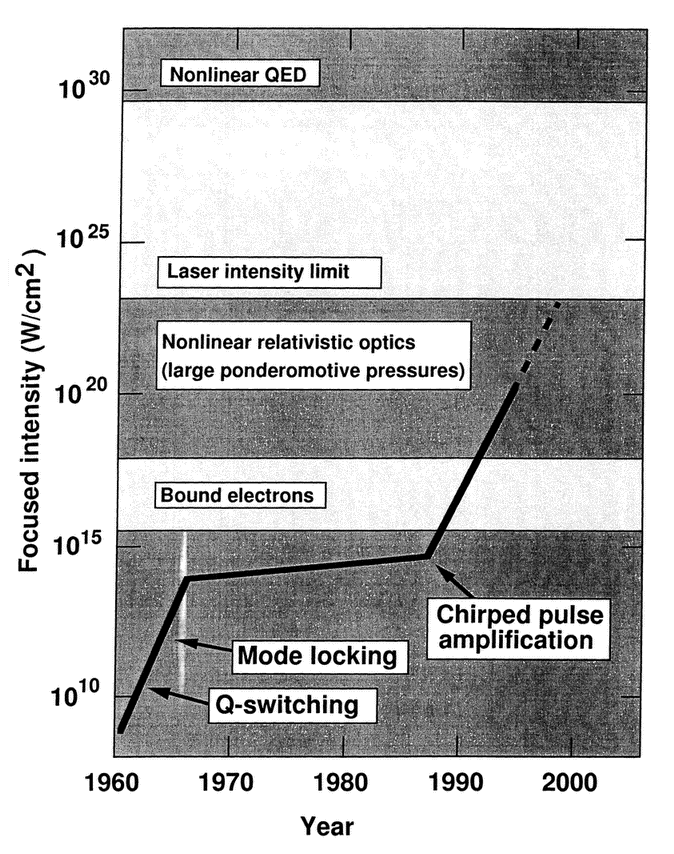
Figure 23 Laser intensity versus year for tabletop systems. Over the past decade the intensity has increased by a factor of one million. Adapted from G. Mourou et al, Physics Today (January 1998) p. 25.
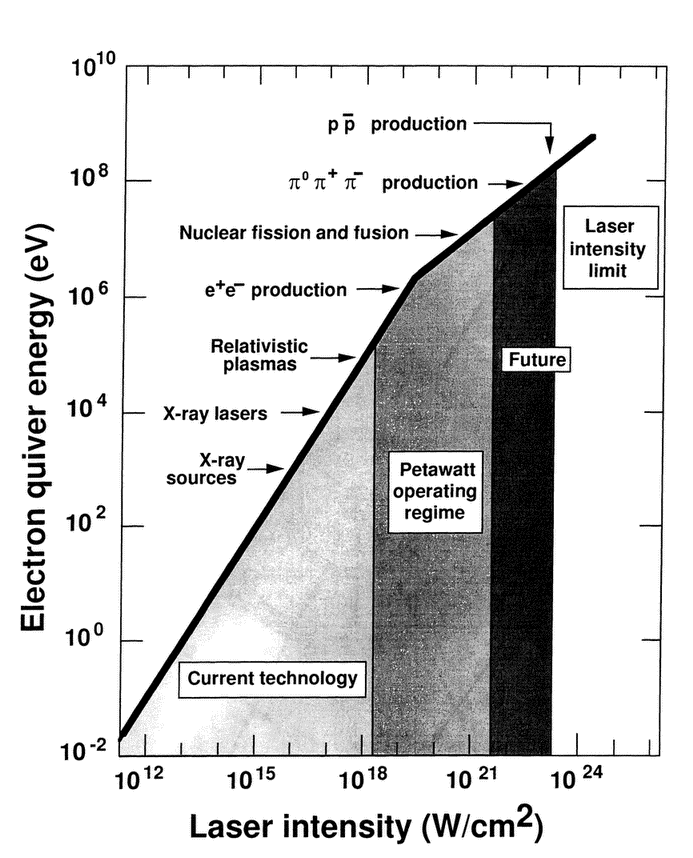
Figure 24 Electron quiver energy and accessible phenomena as a function of Nd:glasss laser intensity. The quiver energy is the cycle-averaged oscillatory energy of free electrons in the laser field. The break at 1019 W/cm2 corresponds to quiver energies on the order of the electron mass, i.e., to the beginning of the relativistic regime characteristic of superlasers. The 1023 w/cm2 threshold intensity for proton-antiproton pair production assumes a CO2 laser. Adapted from M.D. Perry and G. Mourou, Science (14 May 1994) p. 918.
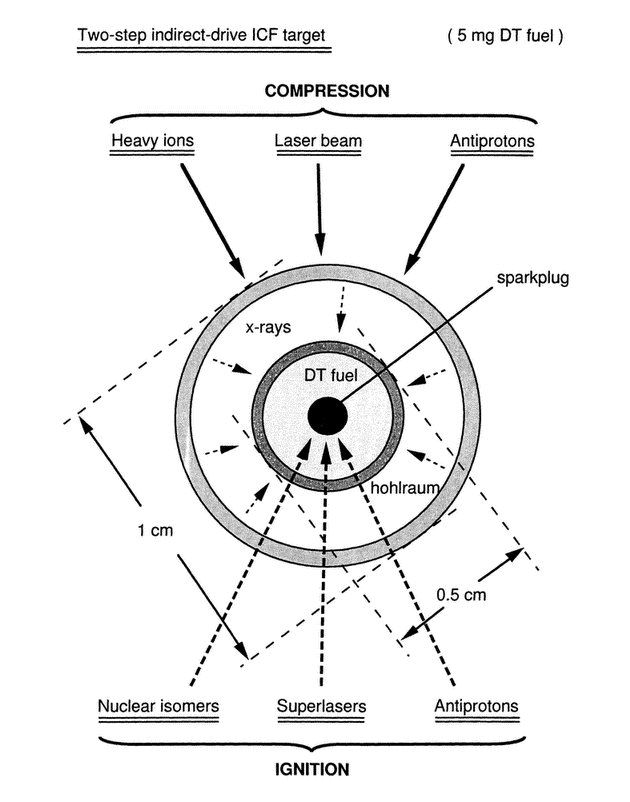
Figure 25 The most promising indirect-drive ICF targets achieve high compression and fast ignition by a two-steps process similar to the “sparkplug” ignition concept used in early hydrogen-bombs.
Footnotes
1 The term “proliferation of nuclear weapons” covers (i) the increase in the number and the quality of such weapons within the five nuclear-weapon States (namely China, France, Russia the U.K. and the U.S.A.); and (ii) the spread of nuclear weapons to other countries. While the former is known as vertical proliferation, the latter is called horizontal proliferation.
2 Such as megajoule-scale inertial confinement fusion, ultrahigh-intensity lasers (i.e., “super-lasers”), pulsed-power technology, subcritical testing, supercomputing, etc.
3 The second edition of this report was translated in Russian in 1998 by the Russian Foreign ministry and approved for public release in March 1999. This translation is not just a recognition of the value of the efforts made at ISRI and INESAP in order to raise the technical understanding on the very serious concern represented by the development of new types of nuclear weapons, but also a signal that the Russian Foreign ministry wants its own concern on the subject to be known.