

| << | {2} | >> |

| << | {3} | >> |
Почти четыреста лет тому назад, 24 марта 1543 г., лежа на смертном одре, мало кому известный до той поры каноник Николай Коперник из Торна коснулся рукой свежеотпечатанного экземпляра своей гениальной работы в шести книгах De Revolutionibus Orbiumo celestium (т. е. «Об обращении небесных миров»), подводившей итоги его наблюдениям и размышлениям над этим вопросом в течение более тридцати лет и содержавшей основы гелиоцентрической системы мира.
Идеи Коперника, изложенные им в строго математической форме и выработанные на основе богатейшего фактического материала, лишь медленно и постепенно стали распространяться в кругу ученых различных стран, встречая с их стороны различную оценку. Так, наиболее известный астроном-наблюдатель рассматриваемой эпохи Тихо Браге (1546–1601) не признавал системы Коперника и в противовес ей выдвинул в 1588 г. свою собственную, согласно которой вокруг Солнца вращались все планеты, за исключением Земли; последняя же оставалась неподвижной и вокруг нее обращались Солнце с планетами и Луна. Это было некоторым шагом вперед по сравнению с системой Птоломея, но решительным шагом назад по сравнению с системой Коперника (De Mundi Aetherei recentioribus phenomenis liber secundus, 1602). В то же время Кеплер (1571–1630) являлся не только убежденным сторонником гелиоцентрической системы, но и гениальным ученым, которому удалось развить учение Коперника, установив три закона планетных движений, носящие его имя (первые два были опубликованы им в Astronomia nova, 1609; третий был установлен им в мае 1618 г.). Мнение других, менее заметных ученых средне-европейских стран не представляет для нас существенного интереса; можно только констатировать, что учение Коперника, правда, с опозданием на 50–60 лет, стало им знакомо и трактовалось ими как серьезная научная теория.
Как было первоначально воспринято учение Коперника в Италии, Галилей повествует весьма красочно в начале второго дня «Диалога», вкладывая в уста Сагредо описание его беседы с посетителями лекций Христиана Вурстейзена (1544–1588), в которых последний пропагандировал это учение. Однако, и в этой стране были, хотя и малочисленные, приверженцы «пифагорейского» учения. Среди них особого внимания заслуживает глубокий мыслитель Джордано Бруно (1548–1600), сожженный в Риме на костре по приговору инквизиции. Тех же воззрений придерживался Джакобо Маццони, учитель Галилея, единственный из профессоров Падуанского университета, не принадлежавший к стану перипатетиков. Интересно также, что под влиянием новых фактов и доказательств, т. е. значительно позже, поколебался в непогрешимости системы Птоломея и такой заслуженный ученый, как Клавий (1537–1612), автор многократно переиздававшихся комментариев к «Сфере» Сакробоско, который в течение всей своей долгой жизни занимался изложением и защитой ее. {4}
Что касается Галилея, то он, повидимому, очень рано склонился к идеям Коперника. Об этом свидетельствуют его письма Маццони и Кеплеру, причем в письме к последнему (от 4 августа 1597 г.) Галилей указывает, что он продолжает работать над учением Коперника, которого придерживается «уже много лет». То обстоятельство, что, будучи с 1592 г. профессором математики в Падуанском университете и вследствие этого лектором сферической астрономии и теории планет, Галилей в первоначальный, по крайней мере, период излагал эти предметы в установившейся форме (как об этом свидетельствуют частично опубликованные после его смерти лекции Trattato della Sfera о Cosmografia, 1656), не следует рассматривать как факт, находящийся в противоречии с собственным заявлением Галилея. Едва ли какое-либо иное изложение было в то время вообще возможно в стенах университета; к тому же Галилей пока не обладал ни окончательно сложившимися механическими воззрениями (см., например, его еще более раннюю работу Sermones de motu gravium, опубликованную только в 1854 г. и относящуюся к пизанскому периоду его деятельности, т. е. 1589–1592 гг.), ни такими наглядными доводами в пользу системы Коперника, как наличие спутников Юпитера, фаз Венеры, солнечных пятен и т. д.
Так, медленно и постепенно идеи Коперника находили признание немногих крупных и независимых ученых. Иначе отнеслась к ним церковь. Одними из первых испугавшихся действительно глубокой «революционности» книг Коперника, потрясавшей основы геоцентрической системы мира, а вместе с тем не только узко астрономические, но и значительно дальше идущие общие положения философии Аристотеля, оказались известные деятели реформации: Лютер (1483–1546) и Меланхтон (1497–1560). Первый назвал Коперника дураком, который намерен перевернуть вверх дном всю вселенную, а второй, являвшийся ученым идеологом реформации, считал необходимым, чтобы гражданские власти укротили астронома, который заставил Землю двигаться, а Солнце — стоять неподвижно. Существенной разницы между этими суждениями и позднейшими актами католической церкви нет. Последняя оказалась только более последовательной в своих выводах, как это явствует из «декрета святой конгрегации» от 5 марта 1616 г. и приговора, объявленного Галилею 22 июня 1633 г. Но на это были свои, особые, причины.
Характер официальной науки конца XVI и начала XVII веков, культивировавшейся в университетах, в частности итальянских, достаточно хорошо известен. Авторитет Аристотеля стоял еще весьма высоко; изучение действительных явлений природы давно уже отошло на задний план и было заменено сопоставлением мнений, высказанных по поводу них Аристотелем или другими авторитетами из числа его комментаторов и последователей; научные работы носили поэтому характер только схоластических филологических упражнений; новые открытия и научные данные, на которые нельзя было закрыть глаза, объяснялись путем подведения их под уже готовые формулы, заимствуемые из того же богатого книжного арсенала без новой опытной проверки. К этому надо добавить, что философия Аристотеля и его последователей официально разделялась католической церковью, а весьма влиятельный иезуитский орден, основанный в 1534 г., уделял очень большое внимание тому, чтобы все новые научные данные не стояли в видимом противоречии с учением перипатетиков и в целях обеспечения единства направления мысли не дозволяли никому из членов ордена опубликовывать свои работы без санкции его высшей духовной администрации. Таким образом, критика философии Аристотеля граничила с выступлением против церковных канонов, а полемика {8} с отдельными патерами-иезуитами затрагивала интересы и достоинство этого ордена, как целого. Отсюда ясно, как трудна и опасна была научная деятельность тех новаторов, которые, под влиянием глубоких сдвигов во всей структуре современных им экономических отношений и развития техники, неизбежно вовлекались в конфликт со схоластическими доктринами.
Знакомясь с жизнью и научной деятельностью Галилея, мы ясно видим, как первоначальная борьба его против отдельных заблуждений Аристотеля, касавшихся законов падения тел, их плавания и т. д., разгоралась все ожесточеннее и захватывала все бо́льшие области знания, пока не вылилась в столкновение двух мировоззрений. В конечном счете Галилея судили и осудили за пропаганду учения Коперника не те десять монахов, которые были для этого назначены, и не те семь, которые подписали приговор, а католическая церковь, как таковая, увидевшая в Диалоге крайне опасное сочинение, сильнейшим образом подрывающее ее авторитет.
В этом она не ошиблась: несмотря на оговорки, сделанные Галилеем (о чем мы скажем несколько ниже), Диалог является исключительно ярким документом, направленным против тех положений, с которыми солидаризовалась католическая церковь. Действительно, последняя взяла под свою защиту геоцентрическую систему Аристотеля-Птоломея, объявив, что признание Солнца неподвижным центром мира глупо и абсурдно с точки зрения философии и еретично по существу, как явно противоречащее многим текстам священного писания; придание же Земле суточного движения является по меньшей мере заблуждением в вопросах веры. Между тем весь основной текст Диалога свидетельствует о том, что единственной реальной системой мира Галилей считал гелиоцентрическую систему Коперника, в защиту которой собрал большое количество разнообразных убедительных аргументов. В этом сила Диалога как сочинения, носящего объективно антирелигиозный характер, не утраченный им до наших дней.
Полное название рассматриваемой работы Галилея, помещенное на титульном листе, может ввести недостаточно подготовленного читателя в заблуждение. Возможно, что он отнесется к ней как к большому, выдержанному в классическом стиле математическому труду и будет искать в ней подробное изложение учений Птоломея и Коперника, объяснение преимуществ, которые дает последнее по сравнению с теорией эпициклов, указание на слабые места этого учения, может быть, частичное улучшение его, трактование законов Кеплера и т. д. Но почти ничего этого в Диалоге не содержится. Галилей в своем изложении до крайности упрощает систему Коперника, рассматривая движение планет, как совершающееся точно по концентрическим кругам, и только в одном случае у него проскальзывает выражение — среднее расстояние от Земли до Солнца; о Кеплере он упоминает только мимоходом и совсем не в связи с его законами; теорию эпициклов оставляет почти не затронутой. Вместо этого он суммирует все имеющиеся в его распоряжении данные из области механики, физики и астрономии, чтобы доказать как непреложную детину, что Земля обладает суточным и годовым движением, а Солнце стоит неподвижно, мастерски разбивая противоположные доводы и сознательно допуская рассуждения, которые могут на первый взгляд показаться отступлениями от основного хода мысли, но которые на самом деле подчинены одной целостной идее. Правда, и в обращении к читателю, и в заключительной части четвертого дня Диалога и во многих местах текста Галилей говорит о системе Коперника только как о гипотезе; однако, эти {6} формальные и вынужденные изъяснения ни в какой мере не колеблют убедительнейших доводов в пользу ее реальности и не позволяют читателю ни на минуту усомниться в истинных намерениях творца Диалога. Содержание своего сочинения Галилей разбивает на четыре дня. Первый отводится им критике учения перипатетиков о совершенно различной природе небесных тел и Земли и доказательствам их большого сходства; второй день посвящается доказательству совместимости движений тел, находящихся на Земле, с суточным обращением последней вокруг своей оси; в течение третьего дня в основном разбирается вопрос об обращении Земли вокруг Солнца, причем к этому же дню отнесено доказательство большого удаления от Земли новой звезды, появившейся в 1572 г. в созвездии Кассиопеи, хотя этот вопрос, как затрагивающий изменяемость неба, скорее касается темы первого дня; наконец, четвертый день уделяется рассмотрению того, как явления приливов и отливов легко объясняются наличием в первую очередь суточного вращения Земли.
В этой работе Галилей, хотя и не с той силой, как впоследствии в Discorsi, выявил глубину своего гения, позволяющую ему с кажущейся легкостью находить теоретическое обоснование различных физических явлений, иногда давным-давно известных, и давать им обобщение, изумительное по своей ясности и простоте. Дух формализма, современный ему, был Галилею абсолютно чужд. Недаром он так тяготился педагогической деятельностью и уделял так много внимания практической механике и технике, дававшим ему богатый материал для наблюдения опытов и выводов. Это красной нитью проходит через его Discorsi. Может быть, здесь же уместно будет отметить, что и рассуждения об отсутствии заметной разницы между наблюдениями отдельных предметов в подзорную трубу с вершины мачты и у ее подножия, о котором трактуется во втором дне Диалога, имеет прикладную цель: Галилей хотел этим разбить возражения, которые ему делались в связи с его предложением определять долготу места по наблюдениям спутников Юпитера.
Свой Диалог Галилей писал не для узкого круга ученых, а для тех, кто, обладая хотя бы незначительными познаниями в области математических наук, мог понять и оценить его доводы. Этому стремлению сполна подчинен характер изложения трактуемых вопросов; им же вызвано и указанное выше упрощение схемы движения небесных тел; поэтому понимание предмета облегчено до чрезвычайности. Данное сочинение, так же как и большинство своих работ, Галилей написал на итальянском языке; применение последнего чрезвычайно расширяло круг его читателей в данной стране и одновременно суживало круг его читателей из среды цеховых ученых за границей, владевших латинским, но не итальянским языком; однако, первое обстоятельство Галилей считал более важным и соответствующим интересам науки, чем второе.
Диалог в том виде, как он публикуется нами сейчас, был закончен Галилеем в 1630 г. и вышел в свет в 1632 г. При этом совершенно несомненно, что некоторые отдельные части, вошедшие в текст Диалога с той или иной степенью переработки, были написаны им в разное время, иногда задолго до окончания всего труда. Самая же мысль написать сочинение, посвященное системе Коперника, зародилась у Галилея уже в относительно ранний период его жизни. В упомянутом выше письме к Кеплеру (4 августа 1597 г.) Галилей упоминает, что при помощи новой гипотезы ему удалось найти объяснение некоторых явлений природы, непонятных с точки зрения старых гипотез, и что он только что написал обоснование нового учения и опровержение противоположных взглядов. Никаких {7} прямых следов того, что именно Галилей написал в указанное время, мы не имеем; можно только предположить, что в рассуждениях его о трехмерном пространстве и некоторых других соображениях начала первого дня содержатся следы первоначальных идей Галилея, относящихся к указанному времени, а под явлениями, никак не объяснимыми с точки зрения старых гипотез, подразумеваются приливы и отливы, поскольку Галилей впоследствии считал, что этот довод является основным при доказательстве движения Земли. В марте 1610 г. вышло его знаменитое сочинение Sidereus nuncius, содержащее описание первых его астрономических наблюдений и открытий, произведенных с помощью телескопа. Сделав из них выводы, вполне соответствующие идеям Коперника, он указывает, что этот вопрос будет изложен им более обстоятельно в особой работе De systemate mundi. To же он подтверждает в письме от 7 мая 1610 г., адресованном министру Тосканского дворца Винта, в котором он называет среди работ, выполнением которых он занят, сочинение в двух книгах De systemate sou constitutions universi. Что было сделано Галилеем в этом направлении, нам также остается неизвестным. Во всяком случае, поскольку сочинение было задумано Галилеем на латинском языке, форма его должна была бы быть весьма отличной от принятой в Диалоге. Шесть лет спустя, приехав снова в Рим, Галилей ознакомил со своим объяснением приливов и отливов кардинала Орсини и 8 января 1616 г. препроводил ему свою работу, которая после небольших изменений полностью вошла в текст Диалога в качестве первой половины четвертого дня. В том же году Галилей получил в Риме от Инголи из Равенны рукопись-письмо, в котором тот излагал некоторые общепринятые, иногда чрезвычайно наивные доводы против системы Коперника. Письмо это оставалось без ответа со стороны Галилея в течение восьми лет, и только весной 1624 г., опять находясь в Риме, Галилей послал ответ Инголи, занявшему к этому времени весьма видную должность секретаря конгрегации de propaganda fide (пропаганды веры). Этот ответ представляет для нас значительный интерес, так как, во-первых, очень многие части его вошли в Диалог, а во-вторых, Галилей, будучи удручен крушением своих надежд на пересмотр декрета конгрегации от 5 марта 1616 г., повидимому, попробовал найти в этом документе такой способ изложения, который позволил бы ему продолжать защиту учения Коперника. Письмо это было опубликовано впервые лишь в 1812 г., однако, текст его получил в свое время некоторое распространение, в частности, был доведен до сведения папы Урбана VIII и переслан Корсини, архиепископу Болонскому.
Вскоре после возвращения из Рима, в том же 1624 г., Галилей обратился к оформлению своего сочинения о системах мира и приданию ему той формы, которая позволяла бы рассчитывать на возможность его опубликования. Работа эта отняла у Галилея шесть лет. Установить более или менее точно, когда была написана та или иная часть Диалога, возможно только в отношении некоторых из них. Так, конец третьего дня, трактующий о магнетизме, написан, вероятно, в 1626 г., когда Галилей снова занялся этим вопросом. Первый день был написан, очевидно, до 1628 г., так как в нем не только не содержится нигде упоминания о книге Киарамонти De tribus novis stellis, вышедшей в указанном году, но бросается упрек тому же автору, что в своем Antitycho (1621 г.) он не уделил достаточного внимания вопросу о новых звездах; поскольку критика взглядов Киарамонти, изложенных в его новой книге, дается лишь, во втором и третьем днях, надо считать, что эти части писались уже после ее выхода в свет. Весьма вероятно, далее, что части Диалога, отведенные резкой полемике с Лохером, автором весьма неудачной книжки Disquisitiones mathematicae, относятся к 1629 г. Сама по себе эта книжечка настолько убога по содержанию, что Галилей не уделил бы ей такого внимания, если {8} бы за Лохером не стоял иезуит Шейнер, с которым у Галилея происходили длительные споры о приоритете в наблюдении солнечных пятен и истолковании их природы. Услышав о намерении Шейнера опубликовать большую работу, посвященную солнечным пятнам, Галилей, повидимому, поспешил изложить свою точку зрения на этот вопрос, попутно приведя данные, которые доказывали бы его приоритет, и использовал книжку Лохера только как повод для дискуссии. Кстати сказать, в вопросе о приоритете Галилей не был прав: Шейнер обнаружил солнечные пятна несколько раньше, чем Галилей, но обоих их опередил фрисляндский астроном Фабриций. Работа Шейнера Rosa Ursina вышла в 1630 г.; к этому времени «Диалог» был Галилеем уже полностью подготовлен к печати, и какого-либо упоминания об этой работе Шейнера в нем не содержится. В письме к Чези, написанном 24 декабря 1629 г., Галилей сообщает, что Диалог его почти готов и что ему остается только вставить связующие звенья между отдельными частями и написать введение; 12 января 1630 г. Галилей извещает Марсили, что он занят просмотром рукописи, В начале мая того же года с вполне готовой рукописью Диалога Галилей отправился в Рим.
Таков был длительный период работы Галилея над давно задуманным им сочинением о системах мира. В публикуемом тексте осталась все же некоторая неоднородность в изложении материала, вызванная, главным образом, отмеченной выше разновременностью составления отдельных частей Диалога. Однако, останавливаться на этом вопросе едва ли есть надобность, поскольку он не отражается ни на общей цельности работы, ни на убедительности доводов, ни на художественности изложения. Чтобы понять, чем обусловливается форма Диалога и стремление Галилея убедить читателя в гипотетичности учения Коперника, нужно кратко ознакомиться с обстоятельствами, связанными с декретом конгрегации от 5 марта 1616 г.
Первые астрономические открытия Галилея, опубликованные им в Sidereus nuncius в 1610 г. и касавшиеся неровности поверхности Луны, четырех спутников Юпитера и неисчислимости звезд Млечного Пути, принесли ему громкую славу и возбудили величайший интерес среди ученых различных стран. Во второй половине того же года Галилей обнаружил «тройственность» Сатурна, фазы Венеры и, по его уверению, солнечные пятна. Все эти наблюдения с неопровержимой ясностью доказывали правильность учения Коперника. Так, конечно, расценивал их и Галилей, указавший в отношении первых своих открытий, что Землю не следует исключать из числа светил из-за отсутствия у нее движения и света. Однако, выступать в защиту системы Коперника более обстоятельно он пока воздержался, правильно полагая, что надо сперва заручиться признанием сделанных им открытий со стороны не только ученых, но и высших духовных авторитетов. К этому его побуждало и то обстоятельство, что уже первые его открытия вызвали беспомощные, правда, но достаточно неприятные устные и письменные выступления философа Либри, астролога Горки и других.
Во второй половине марта 1611 г. Галилей, занявший в сентябре 1610 г. должность «первого философа и математика великого герцога Тосканского», отправился в Рим, снабженный рекомендательными письмами к влиятельным особам этого города. Здесь Галилеи встретил весьма радушный прием: он многократно имел случай производить наблюдения в обществе ученых, в частности астрономов Римской коллегии, являвшейся авторитетным научным центром иезуитского ордена, а также различных именитых лиц, и вести с ними оживленные диспуты, в которых, {9} несомненно, затрагивался и вопрос об учении Коперника; в конце апреля он был принят в число членов «Академии рысьеглазых», в переносном смысле — зорких (Accademia dei Lincei), основанной за восемь лет до этого князем Чези; к нему весьма доброжелательно отнесся кардинал Барберини (будущий папа Урбан VIII); наконец, он имел аудиенцию у главы инквизиции кардинала Беллармина и удостоился официального приема у папы Павла V. В результате энергичной и блестящей своей деятельности Галилей добился значительных успехов: на специальный запрос Беллармина, правильны ли наблюдения Галилея, касающиеся скоплений неподвижных звезд, Сатурна, Венеры, Луны и Юпитера, Римская коллегия за подписью своих четырех авторитетных членов — астрономов Клавия, Гринбергера, Малькотио и Лембо — ответила утвердительно, хотя и с некоторыми несущественными оговорками. Таким образом, несомненность открытий Галилея была подтверждена высшими духовными авторитетами; однако, вопрос о связи этих новых фактов с учением Коперника был ими оставлен открытым, поскольку он не затрагивался запросом Беллармина.
Последующие четыре года ознаменовались развитием борьбы между сторонниками Галилея, число которых быстро росло, и их противниками, начинавшими проявлять все большую активность. Об этом приходится судить частью по опубликованным работам, как например, четырем возражениям на трактат Галилея «I Cralleggianti» («О плавающих телах», 1612 г.), главным же образом по переписке, которая в то время весьма оживленно велась между различными заинтересованными лицами и в виде копий писем часто распространялась в большем или меньшем количестве экземпляров. Не останавливаясь на подробностях, отметим основное. Галилею и его сторонникам не представляло никакого труда разбивать доводы противников, основанные на отрицании или ложном истолковании фактов; конечно, этим они наживали себе врагов, иногда влиятельных, как Шейнер и другие. Но это им не было особенно опасно, поскольку в этих вопросах они пользовались поддержкой еще более высоких авторитетов католической церкви. Это прекрасно понимали и их противники, которые стали все настойчивее выдвигать против воззрений Галилея доводы богословского характера, доказывая, что учение Коперника противоречит священному писанию. Долго оставлять такие обвинения без ответа не представлялось возможным, и постепенно как Галилей, так и его ученики вопреки своему желанию оказались вынужденными вступить на путь толкования текстов богословских сочинений, не суливший им ничего доброго: допустить свободное толкование священного писания руководители католической церкви, занятые напряженной борьбой с протестантизмом, кальвинизмом и другими ересями, конечно, не могли, в первую очередь, по политическим соображениям. Однако, Галилей придерживался других взглядов.
Он высказывался в том смысле, что священное писание не может быть главным доводом в естественно-научных вопросах, в которых решают опыт и рассуждения, имеющие силу необходимости и доказательности. Тексты же священного писания приспособлены к мышлению необразованного простонародья, не могущего подняться до понимания сложных вопросов построения мира. Эти тексты требуют истолкования, которое может быть дано в самых противоположных смыслах — как за систему Птоломея, так и против нее. В качестве примера такого толкования он берет библейский рассказ о том, как бог по мольбе Иисуса Навина остановил Солнце. Согласно геоцентрическому учению Солнце участвует в двух противоположных движениях: суточном — с востока на запад и годовом — с запада на восток. Только второе из них принадлежит Солнцу. Суточное же движение, от которого зависит деятельность дня и ночи, принадлежит {10} небесной сфере, на которой находится Солнце. Поэтому, остановив Солнце, т. е. годичное движение, бог не продолжил бы день, а наоборот, уменьшил бы его, ибо он остановил бы движение, противоположное тому, от которого зависит смена дня и ночи. Но можно дать этому тексту толкование, не противоречащее учению Коперника: если считать, что суточное вращение Земли, от которого зависит смена дня и ночи, имеет своим источником Солнце, как и всякое движение в солнечной системе, то остановка Солнца будет означать по существу остановку суточного движения Земли, а стало быть, увеличение дня. Критерием истины является сама природа, которая, как говорит Галилей, «непреклонна и неизменна и совершенно не заботится о том, будут или не будут ее скрытые основы и образ действия доступны пониманию людей, так что она никогда не преступает пределы законов, на нее наложенных. Поэтому, мне кажется, что, поскольку речь идет о явлениях природы, которые непосредственно воспринимаются нашими чувствами или о которых мы умозаключаем при помощи неопровержимых доказательств, нас нисколько не должны повергать в сомнение тексты писания, слова которых имеют видимость иного смысла, ибо ни одно изречение писания не имеет такой принудительной силы, какую имеет любое явление природы». Эти соображения Галилей изложил 21 декабря 1613 г. в письме к своему ближайшему ученику Бенедетто Кастелли в ответ на сообщение о том, какие споры последнему приходится вести в присутствии членов семьи великого герцога Тосканского, находившегося в то время в Пизе. Письмо это получило в копиях широкое распространение, о чем, между прочим, позаботился и сам Галилей. Примерно те же мысли он развивает в более позднем очень обширном письме к вдовствующей герцогине Тосканской — Христине (матери Козимо II), приводя подходящие цитаты из сочинений блаженного Августина.
В декабре 1614 г. произошло событие, весьма взволновавшее Галилея и его друзей, именно, выступление доминиканца Каччини с проповедью, в которой он обрушился на учение Коперника и доказывал совершенную недопустимость даваемого приверженцами Галилея толкования священного писания. Для того же, чтобы было понятно, против кого направлена его речь, Каччини начал ее цитатой из «Деяний апостолов»: «Галлилеяне, что вы стоите и смотрите на небо». Как видно, он допустил помимо того ряд резких выпадов против математиков и математики вообще, что дало повод Галилею немедленно сообщить об этом Чези в Рим. Последний ответил Галилею советом, какие меры можно предпринять против таких недопустимых выпадов, попутно указав, что и Беллармин придерживается мнения о еретичности учения Коперника и несовместимости движения Земли со священным писанием. Спустя очень короткий срок, доминиканец Лорини ознакомил Каччини с копией письма Галилея к Кастелли, о котором мы только что говорили. Почтенные патеры нашли, что этот документ достаточно компрометирует Галилея: 7 февраля 1615 г. Лорини составил на него официальный донос инквизиции, который Каччини и отвез в Рим. По рассмотрении доноса, копии письма Галилея, допроса Каччини и производства дополнительного следствия во Флоренции инквизиция не обнаружила ничего особо предосудительного во взглядах и деятельности Галилея и его сторонников. Очевидно, личная преданность Галилея католической церкви и искренность его религиозных убеждений никаких сомнений у инквизиции не вызвали.
Пока в Риме шло секретное разбирательство этого дела, Галилей получил книгу, изданную в Неаполе в феврале 1615 г. и выпущенную кармелитом Паоло Антонио Фоскарини, под заглавием Lettere del... Foscarini sopra Vopinione dei Pittagorici e del Copernico, della mobiliia della Terra, e Stabibita del Sole и т. д. В этом сочинении автор-богослов поднимал те же самые вопросы о согласовании учения Коперника со священным {11} писанием, что и Галилей, и излагал мысли, весьма близкие к тем, которых придерживался последний. Совершенно ясно, что появление нового единомышленника, до той поры ему неизвестного, обрадовало Галилея. И хотя ему стал известен ответ, который Беллармин дал Фоскарини, он продолжал верить в приемлемость для католической церкви своих воззрений. В этом ответе, убогом по содержанию, Беллармин прямо указал, что принятие гипотезы о неподвижности Солнца и движении Земли вполне допустимо, если явления объясняются этим лучше, чем эксцентриками и эпициклами, и что для математиков этого должно быть достаточно; но утверждать, что это имеет место в действительности, не только опасно, но и вредно для веры. Указанное ответное письмо Беллармина датировано 12 апреля 1615 г.
Имея достаточно оснований предполагать, что в скором времени наступит решительный момент в суждении об учении Коперника, а также желая отвести возможные обвинения, направленные лично против него, Галилей снова отправился в Рим, куда и прибыл 11 декабря 1615 г. Личное дело окончилось для него вполне благополучно: ему, видимо, удалось рассеять всякие подозрения и доказать полную свою лойяльность в отношении католической церкви. Оставалось второе, общее дело, в благополучный исход которого Галилей продолжал верить до последнего дня. В действительности же для этого никаких оснований не было: 19 февраля 1616 г. теологи-цензоры инквизиции получили на рассмотрение следующие два своеобразно сформулированные предложения: 1) Солнце есть центр мира и совершенно неподвижно в отношении перемещения (motu locali — местного движения); 2) Земля не есть центр мира и не неподвижна, но движется, как таковая, целиком, а также суточным движением. Рассмотрев эти положения, цензоры пришли 24 февраля к единогласному заключению, что первое из них глупо и абсурдно с точки зрения философии и, сверх того, формально еретично, как явно противоречащее многим текстам священного писания; что касается второго, то в философском отношении оно таково же, а с теологической точки зрения является по меньшей мере заблуждением в вопросах веры.
Судя по дошедшим до нас фактам, на следующий же день, т. е. 25 февраля, на основе этого заключения цензоров конгрегация инквизиции дала поручение Беллармину вызвать к себе Галилея и предложить ему отказаться от мнения, что Солнце неподвижно, Земля же вращается вокруг Солнца и, кроме того, имеет и суточное движение; если он не откажется, то в присутствии нотариуса и свидетелей сообщить ему предписание, чтобы он совершенно воздержался от преподавания, защиты или трактования этого мнения; если же он и тут не согласится, то подвергнуть его заключению. В акте, датированном 26 февраля 1616 г., сообщается, что Беллармин вызвал Галилея и предложил ему совершенно оставить и в дальнейшем каким бы то ни было образом указанного мнения не придерживаться, не преподавать и не защищать ни устно, ни письменно. В протоколе конгрегации от 3 марта кратко отмечено сообщение Беллармина, что он увещевал Галилея отказаться от указанного мнения, с чем тот и согласился. Несколько забегая вперед, отметим и еще один существенный документ. До Галилея дошли сведения, что его враги распространяют ложные слухи о том, будто в Риме он был признан виновным в ереси, на него наложено церковное взыскание и т. д. Поэтому перед отъездом из Рима он попросил Беллармина выдать ему документ, который свидетельствовал бы об истинном ходе событий. Такое удостоверение, датированное 26 мая, Беллармин ему передал. В нем значится, что слухи об отречении и церковном покаянии Галилея являются клеветническими, что это места не имело и что Галилею было лишь объявлено постановление, признавшее учение Коперника противным священному писанию, почему этого учения нельзя ни защищать, {12} ни придерживаться. Рассматривая эти четыре документа, легко убедиться, что второй из них (акт от 26 февраля) стоит в противоречии с двумя последующими, поскольку в нем говорится о предписании (т. е. второй стадии воздействия, предусмотренной актом от 25 февраля), тогда как в двух прочих говорится только о первой стадии, т. е. увещевании или объявлении постановления конгрегации; кроме того, в нем содержатся дополнительные слова, которых мы не находим ни в одном из прочих документов, а именно — каким бы то ни было образом придерживаться и т. д. Откуда же они взялись? — Уже довольно давно возникло предположение, что мы имеем здесь дело с фальсификацией указанного документа. Этот вопрос мы кратко затронем в связи с последующим процессом Галилея; пока же отметим, что во всей дальнейшей своей деятельности Галилей поступал формально так, как ему указывали только увещевание Беллармина и декрет от 5 марта 1616 г.
Первый раздел этого знаменитого декрета трактует о запрещении книг, не имеющих отношения к астрономии, — Кальвинистическая теология, Возрождающийся шотландец и т. д. Второй раздел относится к трем сочинениям, касающимся учения Коперника, причем два из них, а именно, самого Николая Коперника Об обращении миров и Дидака Астуника Комментарии к Иову, временно задерживаются, как подлежащие исправлению, третье же — упомянутое выше Письмо Фоскарини — осуждается и запрещается. Мотивируется это решение тем, что принятие и распространение учения Коперника, как истинного и не противоречащего священному писанию, пагубно для католической истины. Таким образом, с точки зрения декрета, трактование учения Коперника, как гипотезы, не подлежит безусловному запрещению, о чем Беллармин и писал в свое время Фоскарини; это же подтверждается теми несущественными изменениями, которые были внесены в сочинение Коперника, переизданное в 1620 г. Однако, защита учения Коперника, как истинного и не противоречащего священному писанию, является проявлением еретических воззрений. Таков был смысл декрета «священной» конгрегации.
Как мы видим, совершенно защитить систему Коперника Галилею не удалось; он убедился только в том, что лично против него инквизиция не выдвигает никаких обвинений. С этими данными и письмом Беллармина, которое полностью его реабилитировало, Галилей вернулся во Флоренцию из второй своей поездки в Рим.
Последующие годы ознаменовались оживленной полемикой Галилея и его учеников с противниками по вопросу о природе комет. Поводом для этого послужил доклад профессора Римской коллегии Грасси о трех кометах 1618 г. Галилей через своего ученика Марио Гвидуччи опубликовал в июне 1619 г. Discorso delle Comete di Mario Guiducci, на что Грасси также через своего ученика Лотарио Сарси ответил памфлетом, носящим длинный титул Libra astronomica ae philosophica qua Galilaei Galilaei opiniones de cometis a Mario Guiducci in Florentina Academia expositae и т. д., 1619 г. Поскольку упреки Грасси и Сарси затрагивали непосредственно Галилея, последний решился на них ответить и в октябре 1622 г. закончил свою работу Il Saggiatore, одну из наиболее блестящих по форме, содержащую много интересных и глубоких мыслей, но не совсем удачную по существу, поскольку он отстаивал в ней земное происхождение комет. Во многих местах этой работы Галилей касается и вопроса о системе мира. Рукопись свою Галилей переслал в Рим, где она, пройдя через римскую цензуру в лице весьма ученого доминиканца Риккарди, и была издана в октябре 1623 г. на средства Академии dei Lincei. Во время печатания этой книги {13} известный уже нам кардинал Барберини, высоко ценивший Галилея, был избран папой под именем Урбана VIII; ему-то и посвятил Галилей свою работу, конечно, с его разрешения.
Беспрепятственное прохождение этого сочинения через цензуру, принятие папой посвящения и прошлое отношение его к Галилею внушили друзьям последнего, да и ему самому, мысль поднять вопрос о пересмотре декрета от 5 марта 1616 г. в отношении учения Коперника. В этих целях Галилей в апреле 1624 г. предпринял третье свое путешествие в Рим. Здесь он был радушно принят папой, но цели своей не достиг; повидимому, и сношения его с Урбаном VIII по этому вопросу велись им не непосредственно, а через кардинала Гогенцоллерна.
После ознакомления с событиями 1616 и 1624 гг., описанными здесь вкратце, нам станет совершенно понятной та форма, которую Галилей вынужден был придать своему Диалогу и которая сближала его по стилю изложения с известными диалогами Платона. Сходство это распространяется, однако, только на форму; содержание Диалога, конечно, совершенно иное: в нем нет идеализма Платона, и его можно рассматривать до некоторой степени как возвращение к обновленному древнегреческому материализму.
Итак, защищать реальность системы Коперника декретом было категорически воспрещено; однако, трактовать ее как гипотезу, удобную для математиков и астрономов, не возбранялось; появление в печати Il Saggiatore и распространение письма — ответа Инголи — не вызвали никаких осложнений. Поэтому сочинение, излагающее учение Коперника в гипотетической форме, могло рассчитывать на опубликование. Но для такого изложения наиболее удобной являлась форма свободной беседы, участники которой имеют право, как на диспуте, выдвигать и опровергать любые доводы и соображения; лицо автора является до некоторой степени завуалированным; мысли свои он может вкладывать в уста не единственного из собеседников, истинные же свои намерения высказать особо во вступлении или посвящении. Именно эту форму Галилей и избрал, выведя собеседниками двух своих уже умерших друзей — Сальвиати (1583–1614) и Сагредо (1571–1620) — и перипатетика Симпличио; под последним нельзя подразумевать кого-либо из современников Галилея — это художественно обрисованный тип исследователя и глубокого знатока сочинений Аристотеля и его комментаторов. Следует также иметь в виду, что и два первых собеседника иногда судят о вещах, которые не могли быть известны им при жизни; поэтому и их приходится считать до некоторой степени художественными образами, созданными Галилеем.
Как мы уже указывали, в начале мая 1630 г. Галилей выехал в Рим, чтобы хлопотать о разрешении опубликования Диалога. Вскоре же (18 мая) он удостоился милостивого приема у папы, рукопись же его была передана на просмотр доминиканцу Рафаэлю Висконти, от которого, так же как и от папского цензора Риккарди, Галилей получил через некоторое время успокоительные заверения. Ему было указано со ссылкой на папу, что прежде всего надо изменить заглавный лист, в первоначальном варианте которого значились «приливы» и «отливы», так как папа придерживается иных взглядов на эти явления; кроме того, необходимо было во введении и заключении ясно подчеркнуть гипотетичность учения Коперника и указать на всемогущество божие, как на решающий аргумент; в остальном речь шла лишь о мелких исправлениях, которыми и должен был заняться Висконти. После этого было набросано предисловие, которое должно было удовлетворять поставленным требованиям. В середине июня {14} Галилей вернулся во Флоренцию, имея на руках Imprimatur, т. е. разрешение на печатание Диалога, выданное Риккарди. Здесь он должен был написать посвящение, составить оглавление и т. д., после чего осенью вернуться в Рим, где и должен был печататься Диалог. Однако, в конце августа 1630 г. Галилей получил неожиданное извещение от Кастелли, находившегося в то время в Риме, что по многим серьезным причинам печатание книги желательно выполнить во Флоренции и притом возможно скорее. Шаги, предпринятые Галилеем в этом направлении, увенчались успехом: он быстро нашел издателя, а 11 сентября получил разрешение на печатание от духовной и светской цензуры Флоренции. Однако, дальше возникло формальное затруднение: Imprimatur Риккарди не имел юридической силы в этом городе, и нужно было особое разрешение, исходящее от папы. Кастелли сообщает Галилею в письме от 21 сентября 1630 г., что Риккарди просит Галилея выслать копию Диалога, дабы он и Чиамполи (секретарь Урбана VIII) могли внести необходимые изменения, а потом выдать разрешение на опубликование его во Флоренции. Значительно позже в письме к Тосканскому послу в Риме Никколини, датированном 28 апреля 1631 г., тот же Риккарди сообщает, что по получении предисловия и заключения и установлении их соответствия ранее предъявленным требованиям он сможет дать удостоверение, что книга им одобрена; далее он пишет, что если копия всего сочинения им не будет получена, то он письменно уведомит флорентийского инквизитора о том, что ему, Риккарди, приказано, дабы тот следил и дал разрешение. Через месяц (24 мая 1631 г.) Риккарди действительно пишет флорентийскому инквизитору Клементу Эджидио письмо, в котором довольно кратко излагает уже известные нам требования относительно титульного листа и характера изложения учения Коперника как гипотезы, так, чтобы никто не мог принять его за абсолютную истину; далее он указывает, что начало и конец книги он вышлет позже, после их исправления. Эджидио, который уже в сентябре 1630 г. дал свое согласие на опубликование Диалога, очень быстро (31 мая) ответил на это, что Галилей с полной готовностью идет на все исправления. Наконец, 19 июля Риккарди выслал Эджидио из Рима введение, указав в сопроводительном письме, что делает он это «по повелению нашего господина» (т. е. папы) в дополнение к ранее данным им, Риккарди, указаниям и с тем, чтобы автор ограничился в отношении как введения, так и заключения только стилистическими поправками, буде он пожелает их внести, но ни в чем не менял их сущности.
Такова история печатаемого текста, обращения к читателю и заключительной части четвертого дня. Мы не будем излагать их здесь: полное несоответствие их основному тексту Диалога и по вложенным в них мыслям, и по стилю поистине разительно. Но Галилей шел на это, лишь бы получить право на опубликование своего труда. И не случайно он писал, пересылая в Рим свой текст введения и заключения, что он предоставляет высшим духовным властям называть его мысли химерами, фантазиями, паралогизмами и вносить в текст те изменения, кои они сочтут за благо. В феврале 1632 г. печатание Диалога было закончено; 22 февраля Галилей преподнес первый экземпляр великому герцогу Тосканскому Фердинанду II, которому он посвятил этот труд; на следующий же день он отправил 52 экземпляра Диалога Чезаре Марсили в Болонью. На этом можно было бы и закончить наш очерк, поскольку он касается только Диалога и ни в какой мере не претендует даже на краткую общую характеристику жизни и деятельности Галилея. Однако, перед читателем может встать теперь законный вопрос: каковы же были поводы для возбуждения против Галилея столь громкого процесса и тем более его осуждения? Ответ на этот вопрос мы и попытаемся дать. {15}
Дальнейшие события развивались следующим образом. Уже в августе 1632 г. продажа Диалога, возбудившего восторг последователей и учеников Галилея и ярость его врагов, была запрещена по специальному приказанию папы; 23 сентября инквизицией было вынесено постановление о вызове Галилея в Рим в октябре. Последний под разными предлогами затянул, однако, свой выезд и прибыл в Рим только 13 февраля 1633 г. Два месяца Галилей прожил у тосканского посланника Никколини, ничего не зная официально о характере выдвинутых против него обвинений, и только 12 апреля был подвергнут первому допросу. Второй допрос последовал 30 апреля, причем все эти дни Галилей провел в здании инквизиционного трибунала, однако, не в тюрьме, а на квартире фискала-прокурора инквизиции Синчеро, где он, по собственному его заверению, чувствовал себя хорошо. Третий допрос был произведен 10 мая и четвертый, последний, 21 июня. Время с 30 апреля по 21 июня Галилей снова провел во дворце Никколини. Наконец, 22 июня на торжественном заседании инквизиции в монастыре «Святой Марии над Минервой» («Sopra Minerva») Галилею был объявлен приговор, после чего он, стоя на коленях и касаясь рукой евангелия, должен был прочесть заранее заготовленную и подписанную им формулу отречения. По истечении двух дней, т. е. 24 июня, Галилей снова вернулся к Никколини; 30 июня ему было разрешено поселиться в Сиене под надзором местного архиепископа Пикколомини, бывшего его ученика; здесь он прожил до декабря, после чего ему было разрешено поселиться на собственной вилле в Арчетри, близ Флоренции.
Текст приговора точно и ясно формулирует «преступления» Галилея. Прежде всего в нем указывается, что в письмах «О солнечных пятнах» Галилей излагал учение о неподвижности Солнца и движении Земли как истинное, опровержение же воззрений, основанных на священном писании, делал собственным толкованием текстов последнего и, кроме того, написал письмо бывшему своему ученику, в котором также ложно толковал смысл писания. Далее отмечается, что в целях противодействия все ширящемуся распространению этого пагубного для веры воззрения богословами-квалификаторами была дана известная уже нам оценка последнего. На основе такового Беллармином было объявлено Галилею в присутствии нотариуса и свидетелей, что он должен совершенно оставить и в дальнейшем каким бы то ни было образом указанного мнения не придерживаться, не защищать и не преподавать ни устно, ни письменно. Как видно, в приговор вошла текстуальная формула, содержащаяся в известном нам акте от 26 февраля 1616 г. Указав далее на декрет конгрегации от 5 марта 1616 г., приговор отмечает, что в Диалоге обнаруживается явное нарушение того повеления, которое Галилею было объявлено, и что последний ввел в заблуждение цензуру, умолчав об этом обстоятельстве. При этом Галилей признал, что многие места его сочинения действительно могут быть истолкованы читателем как доводы, предназначенные скорее для убеждения в вероятности ложного учения, чем соображения, предназначенные для легкого их опровержения, но объяснил это не пристрастием к ложным воззрениям, а стремлением показать себя искусным сочинителем. Переходя к удостоверению кардинала Беллармина, которое было выдано им Галилею, приговор отмечает, что последний, по собственным его словам, мог за 14–16 лет забыть об объявленном повелении и, испрашивая разрешение цензуры, руководствоваться только упомянутым документом, умолчав о повелении, причем такое свое поведение Галилей объяснил не пристрастием к заблуждению и злой волей, а только тщеславием. Такое трактование удостоверения Беллармина приговор считает, однако, не извиняющим, а усугубляющим вину Галилея, поскольку и в нем вышеупомянутое учение трактуется, как противоречащее священному писанию, Галилей {16} же пытался его защищать и представлять как вероятное. Усомнившись в правдивости показания Галилея, говорит далее приговор, признано было необходимым подвергнуть его строгому испытанию, причем он отвечал «по-католически». На языке инквизиции это означает, что и под угрозой пытки Галилей, подтверждая прежние свои показания, продолжал отрицать наличие в его поведении злого умысла, иначе говоря, «общения с дьяволом». После разбора всех этих обстоятельств в приговоре излагается заключительная часть: Галилей оказывался под сильным подозрением в ереси, что он верил и придерживался ложного учения о неподвижности Солнца и движении Земли; чтобы освободить себя от наказания, полагающегося за подобные воззрения, он должен от них отречься, следуя указанной ему формуле; Диалог запрещается публичным приказом, а сам Галилей присуждается к формальному тюремному заключению и церковному покаянию, состоящему в чтении псалмов; в заключение указывается на возможность полного или частичного уменьшения и отмены указанных санкций.
В соответствии с текстом этого приговора была написана и формула отречения. В ней Галилей во всеуслышание заявлял, что он всегда верил, верит и в будущем при помощи божией будет верить в истинность того, чему учит святая католическая церковь; что в целях отведения от себя всяких законных подозрений он с чистым сердцем и верою неложною отрекается от упомянутых заблуждений и ересей, проклинает и ненавидит их; что в случае обнаружения кого-либо подозрительного в ереси он не преминет донести об этом по начальству и что в случае нарушения этой клятвы он готов подвергнуться всем наказаниям, кои на сей предмет установлены.
Из этого краткого изложения хода процесса Галилея видно, что перед его судьями стояла весьма нелегкая задача: с одной стороны, перед ними лежал текст акта от 26 февраля 1616 г., а с другой — удостоверение Беллармина, которое Галилей предъявил при допросе, о существовании которого они ранее не подозревали и которым Галилей, по его словам, руководствовался, как составляя Диалог, так и домогаясь в цензуре разрешения на его опубликование. Это заставило их войти в рассмотрение сочинения Галилея по существу и притти к заключениям, изложенным в приговоре. В результате получилось компромиссное решение: наличие «злого умысла» со стороны Галилея было отвергнуто, и он был признан виновным лишь в составлении сочинения, дающего основания считать его под сильным подозрением в ереси. Двойственность отношения к Галилею выразилась и в самом обращении с ним: сперва ему пригрозили арестом и препровождением в Рим в кандалах, а затем предоставили возможность пребывать почти все время во дворце Никколини; «узником инквизиции» он пробыл всего лишь три недели, находясь и здесь в условиях, далеко не обычных. Невольно создается впечатление, что Диалог надо было осудить во что бы то ни стало, к автору же его отнестись возможно снисходительнее.
Такое предположение является совершенно обоснованным. Истинный смысл Диалога, конечно, нельзя было скрыть уловками в виде предисловия, заключения и некоторых осторожных выступлений Сальвиати; опубликование же этого сочинения явилось событием, крайне неприятным для Урбана VIII и в высокой степени затрагивающим его престиж. Политическая обстановка требовала от него величайшей осторожности. Принадлежа к более умеренному крылу католической церкви и придерживаясь французской ориентации, он вел упорную борьбу с испано-немецкой партией, более ортодоксальной и более непримиримой в отношении {17} инаковерующих. В этих условиях появление в печати книги, почти открыто пропагандирующей официально запрещенное еретическое учение, было актом, который легко мог быть использован партией, боровшейся против политики Урбана VIII, тем более, что опубликование данного сочинения не могло формально произойти без санкции папы. Поэтому надо было, во-первых, выяснить все обстоятельства, связанные с составлением Диалога Галилеем, и, во-вторых, установить, каким образом было допущено или, вернее, организовано получение разрешения на его печатание. Виновные должны были быть найдены и понести заслуженную кару. Однако, если бы акта от 26 февраля 1616 г. в дошедшей до нас редакции не существовало, то не было бы и юридических оснований для привлечения к ответственности Галилея. В самом деле, если последний не давал столь ограничивающих его обязательств и получил законное разрешение на печатание Диалога, то в чем же можно было усмотреть его вину? Конечно, если бы речь шла не о Галилее, судьбой которого живо интересовались далеко за пределами Италии, и если бы процесс проходил в менее напряженной политической обстановке, то инквизиция едва ли проявила бы такое внимание к юридической стороне дела. Но в данном случае она вынуждена заняться и ею. Акт, содержащий расширительное толкование запрета, был необходим; и в нужный момент он появился в виде документа, вторая половина которого явно подложна. В фальсификации этого документа сейчас почти не приходится уже сомневаться. Однако, Галилей предъявил удостоверение Беллармина, до той поры инквизиторам совершенно неизвестное, безусловно подлинное и совершенно недвусмысленное по содержанию. Этим он на некоторое время спутал карты обвинения и направил его на иной путь, уже известный нам из приговора.
Документы процесса освещают обстоятельства, связанные с составлением Диалога, но совершенно не касаются обстоятельств, связанных с разрешением на его печатание. Пользуясь, однако, другими источниками, удалось установить, что здесь имела место закулисная игра, организованная сторонниками испано-немецкой партии; в ней главную роль играл Чиамполи, секретарь Урбана VIII, который без ведома и согласия последнего действовал от его имени и давал соответствующие указания Риккарди, явно желая дискредитировать папу. В этих целях издание Диалога было перенесено из Рима, где оно встретило бы непреодолимые препятствия, во Флоренцию, в этих же целях писались письма флорентийскому инквизитору со ссылкой на несуществующие «повеления нашего господина» и т. д. За свою лицемерную политику Чиамполи был смещен и выслан из Рима. Непричастность Галилея к этим махинациям, отсутствие у него пристрастия к испано-немецкой партии и огромные личные его заслуги были отлично известны папе; если верить донесению Никколини от 27 февраля 1633 г., то Урбан VIII сам чрезвычайно метко охарактеризовал положение Галилея, выразившись, что для последнего была устроена «ciampolata» (как бы «западня», одновременно намек на Чиамполи).
Только в свете этих обстоятельств, теснейшим образом связанных с общей политической обстановкой того времени, и роли в них папы становятся понятными и ход процесса, и дальнейшая участь Галилея. Сейчас нам кажутся крайне наивными уверения прежних исследователей эпохи Галилея, что последний пал жертвой происков иезуитов, в частности Шейнера, что папа разгневался на него то ли за непризнание объяснения приливов и отливов божьим всемогуществом, то ли за осмеяние в лице Симпличио лично его, Урбана VIII, и т. д. Если среди католического духовенства данной эпохи и было очень много фанатиков и полных невежд в научных вопросах, то этого отнюдь нельзя сказать ни о приближенных Урбана VIII, ни о нем самом. Этот достаточно образованный человек, тайный союзник Ришелье и Густава Адольфа, руководствовался {18} в своих действиях в первую очередь политическими соображениями, и ему надо было провести процесс Галилея именно как политический, показав прежде всего, что он, папа Урбан VIII, готов энергично бороться с распространением еретического «пифагорейского» учения.
Несколько слов о последних годах жизни Галилея. Формально он находился под бдительным надзором инквизиции, и ему было запрещено как переиздавать прежние свои сочинения, так и публиковать новые. Однако, это не помешало ему сделать дополнительные пометки на экземпляре первого издания Диалога, хранящегося сейчас в библиотеке Падуанской семинарии, и дать свое согласие на предпринятое в 1635 г. в Голландии издание Диалога на латинском языке. Равным образом это не помешало ему переправить для опубликования в той же стране рукопись своих Discorsi, вышедших в 1638 г., в которых он снова опровергает учение Аристотеля и выводит знакомых нам по Диалогу собеседников — Сальвиати, Сагредо и Симпличио. Совершенно ясно, что дух Галилея не был сломлен процессом и что до конца дней своих он не отказался от своих подлинных взглядов, считая отречение только вынужденным и формальным актом.
А. Долгов
5 ноября 1937 г.
1 Ссылки, отмеченные цифрами, относятся к примечаниям, помещенным мною в конце книги.
| << | {19} | >> |

| << | {20} | >> |

| << | {21} | >> |
Как ни велика разница, существующая между человеком и другими животными, все же нельзя было бы назвать неразумным утверждение, что едва ли в меньшей степени отличаются друг от друга и люди. Что значит один по сравнению с тысячью? И, однако, пословица гласит, что один человек стоит тысячи там, где тысяча не стоит одного. Такая разница обусловливается неодинаковостью развития умственных способностей человека или, — что по-моему одно и то же, — тем, является человек философом или же нет, ибо философия, как настоящая духовная пища, возвышает над общим уровнем массы тех, кто может ее вкушать, возвышает в большей или меньшей степени в зависимости от качества этой пищи. Кто устремляется к высшей цели, тот занимает более высокое место; вернейшее же средство направить свой взгляд вверх — это изучать великую книгу природы, которая и является настоящим предметом философии. Хотя все, что можно прочесть в этой книге, является творением всемогущего художника и расположено самым совершенным образом, наиболее достойно изучения в первую очередь то, что показывает нам творения и творца с более возвышенной стороны. Из достойных изучения естественных вещей на первое место, по моему мнению, должно быть поставлено изучение устройства вселенной. Поскольку вселенная все содержит в себе и превосходит все по величине, она определяет и направляет все остальное и главенствует над всем. Если кому-либо из людей удалось подняться в умственном отношении высоко над общим уровнем человечества, то это были, конечно, Птоломей и Коперник, которые сумели прочесть, усмотреть и объяснить столь много высокого в строении вселенной. Вокруг творений этих двух мужей вращаются преимущественно настоящие мои беседы, почему мне казалось, что я не могу посвятить их никому иному, кроме вашей светлости. Поскольку содержание бесед покоится на трудах этих ученых, являющихся, по моему мнению, величайшими умами из всех тех, кто оставил нам сочинения по этому предмету, их подобает поставить, дабы не умалить значение предмета, под покровительство лица высокого, через которое они могли бы получить славу и защиту. И если эти два мужа так просветили мой разум, что предлагаемое сочинение может в значительной части считаться принадлежащим и им, то то же самое можно сказать и по отношению к вашей светлости, ибо в избытке великодушия вы не только дали мне свободу и покой, необходимые для сочинения моей книги, но и оказали мне честь действительной поддержкой, которая сделала возможной ее опубликование. Примите это сочинение, ваше высочество, с обычной своей благосклонностью; и если в нем найдется что-либо, что доставит любителям истины пользу или удовольствие, то это должно считаться делом вашего высочества, которое своим постоянным попечением достигло {22} того, что в его счастливом государстве никто не чувствует обычных мирских тревог. Молю небо о ниспослании Вам благополучия на долгие годы для продолжения благочестивой и великодушной деятельности, и остаюсь с глубочайшим почтением
Вашего светлейшего высочества
почтительнейший и преданнейший слуга и вассал
Галилео Галилей
В последние годы в Риме был издан спасительный эдикт, который для прекращения опасных споров нашего времени своевременно наложил запрет на пифагорейское мнение о подвижности Земли. Не было недостатка в тех, кто открыто заявлял, что этот декрет был издан не на основании надлежащего рассмотрения вопроса, а под влиянием страстей и людьми мало осведомленными; раздавались голоса, что судьи, совершенно несведущие в астрономических наблюдениях, не должны были своим неожиданным запрещением связывать крылья пытливого духа. Слыша такие безрассудные жалобы, я не мог остаться безучастным и хранить молчание. Будучи хорошо осведомлен об этом мудром решении, я решил выступить перед лицом света как свидетель непреложной истины. В то время я находился в Риме и не только имел слушателями высших духовных лиц тамошнего двора, но и заслужил их одобрение. Опубликование декрета последовало не без предварительного моего об этом осведомления. Поэтому моим намерением является показать в настоящем труде чужеземным народам, что в Италии вообще и в Риме в особенности знают по этому предмету не менее того, что могут знать исследователи за границей, и, собрав воедино все собственные наблюдения, относящиеся к системе Коперника, заявить, что знакомство с ними предшествовало постановлению римской цензуры и что от последней исходят не только догмы для спасения души, но также и остроумные открытия, удовлетворяющие разум.
Ради этой цели я взял на себя в беседах роль сторонника системы Коперника и излагаю ее сначала как чисто математическую гипотезу, стараясь далее при помощи разных искусственных приемов доказать ее превосходство не над учением о неподвижности Земли вообще, а над тем, которое защищается людьми, являющимися перипатетиками по профессии, ложно носящими это имя, ибо они довольствуются безоговорочным почитанием тени и, не пытаясь размышлять самостоятельно, держатся лишь за заученные напамять, но плохо понятые четыре принципа3. Здесь обсуждаются три главных предмета. Во-первых, я стараюсь показать, что все опыты, могущие быть произведенными на Земле, не дают достаточных доказательств ее подвижности, что все явления могут происходить совершенно одинаково как при подвижности Земли, так и в случае пребывания ее в покое. Надеюсь, что в этой части мною приведены многие наблюдения, не известные древним. Во-вторых, здесь рассматриваются небесные явления, подкрепляющие гипотезу Коперника настолько, что она как будто должна восторжествовать. При этом излагаются результаты новых наблюдений, которые, однако, являются скорее вспомогательными средствами астрономии, нежели законами природы. В-третьих, я излагаю оригинальные мои домыслы. Несколько лет тому назад я высказал мысль, что загадочная проблема морских приливов и отливов {23} могла бы получить некоторое освещение при допущении движения Земли. Это мое заявление, передаваясь из уст в уста, нашло сострадательных приемных отцов, которые не прочь выдать ее за собственное детище. Дабы никто чужой не мог выступить, вооруженный нашим оружием, упрекая нас в том, что мы уделили слишком мало внимания такому важному обстоятельству, я счел необходимым изложить основания, по которым это явление должно иметь место при предположении, что Земля движется. Надеюсь, что изложенные здесь соображения докажут всему миру, что если другие нации и занимаются мореплаванием в большей мере, то мы не уступаем им в научных исследованиях, и что если мы принимаем неподвижность Земли и признаем противоположное мнение математическим парадоксом, то основой нашего убеждения является не неведение того, что думают другие, а иные соображения и мотивы — благочестие, религия, сознание всемогущества божия и признание несовершенства человеческого разума.
Я думал далее, что наиболее удобным будет изложить эти мысли в форме диалога, который, не требуя строгой последовательности математического доказательства, дает возможность делать отступления и касаться попутно предметов, не менее интересных, чем основная тема.
В течение нескольких лет я много раз посещал удивительный город Венецию, где встречался и вел беседы с синьором Джиован-Франческо Сагредо, человеком высокого происхождения и весьма острого ума. Одновременно находился там и приехавший из Флоренции синьор Филиппо Сальвиати, наименьшим украшением которого являлись чистота крови и блестящее состояние — благородный ум, не знавший наслаждения более высокого, чем исследование и размышление. С этими двумя лицами я часто имел случай обсуждать упомянутые выше вопросы в присутствии одного философа перипатетика, которому, как кажется, ничто так не препятствовало в познании истины, как слава, приобретенная им в истолковании Аристотеля.
Теперь, когда жестокая смерть лишила Венецию и Флоренцию этих знаменитых граждан в полном цвете лет, я решил для прославления их имени попытаться, насколько хватит моих слабых сил, заставить их жить на этих страницах, сделав их участниками настоящих бесед. Не будет позабыт также и добрый перипатетик; по причине крайней его приверженности к комментариям Симплиция мне показалось уместным, не называя собственного его имени, заставить его выступать под именем любимого им автора4. Пусть души этих двух замечательных людей, столь глубоко мною почитаемых, примут этот публичный памятник моей неумирающей любви и пусть воспоминание об их речах поможет мне яснее изложить для потомства обещанные им рассуждения.
Между указанными синьорами, как это обыкновенно бывает, часто происходили отдельные разговоры по данному поводу, но они скорее разжигали, нежели удовлетворяли их жажду познания. Поэтому они приняли мудрое решение собраться как-нибудь вместе и, отрешившись от всяких других дел, заняться более последовательно рассмотрением чудес творца на небе и на земле. После того, как они собрались во дворце знатного синьора Сагредо, синьор Сальвиати после обычных кратких приветствий начинает беседу следующими ниже словами:
| << | {24} | >> |

Собеседники: Сальвиати, Сагредо и Симпличио.
Сальвиати. — В заключение вчерашней нашей беседы мы решили, что нам следует сегодня рассмотреть, насколько возможно тщательнее и подробнее, существо и действительность тех естественных оснований, которые до сего времени приводились, с одной стороны, защитниками позиции Аристотеля и Птоломея, а с другой, — последователями коперниковой системы1.
|
Коперник считает, что Земля такой же шар, как и планеты. |
|
По мнению Аристотеля, в природе необходимо признать существование субстанций небесных (неизменных) и стихийных (изменчивых). |
Исходной точкой рассуждения перипатетиков служит Аристотелево доказательство законченности и совершенства мира, причем он ссылается на то, что мир — не простая линия и не только поверхность, а тело, обладающее длиной, шириной и глубиной.
|
Аристотель считает мир совершенным, так как он трехмерен. |
Симпличио. — А разве нет превосходных доказательств, приведенных в пунктах 2-м, 3-м и 4-м вслед за определением непрерывности?
|
Доказательство Аристотеля в пользу того, что измерений существует только три. |
|
Тройственное число восхваляется пифагорейцами |
Сальвиати. — По правде сказать, во всех этих рассуждениях я готов признать только то, что все, обладающее началом, серединой и концом, можно и следует называть совершенным; однако, я не вижу необходимости признавать, будто из того, что начало, середина и конец составляют 3, следует, что число 3 есть число совершенное и что оно наделено способностью сообщать совершенство всему, что обладает троичностью; точно так же я не могу понять и признать, чтобы, например, применительно к ногам, число 3 было совершеннее, чем 4 или 2, или что число 4 свидетельствует о несовершенстве элементов и что было бы более совершенно, если бы их было 3. Было бы лучше поэтому предоставить такие измышления риторам и доказать свое утверждение более убедительно, как то подобает доказательным наукам.
Симпличио. — Вы, повидимому, принимаете эти доводы в шутку; между тем таково все учение пифагорейцев, которые придавали столь большое значение числам; и вот вы, математик, и, насколько я знаю, разделяющий во многом пифагорейские взгляды, теперь как будто обесцениваете тайны их учения.
|
Ум человеческий причастен божеству, потому что разумеет числа, по мнению Платона. |
|
Тайны пифагорейских чисел — басня. |
Симпличио. — Я не отношу себя к числу тех, кто особенно интересуется тайнами пифагорейцев. Но, возвращаясь к нашему вопросу, повторю, что доводы, приводимые Аристотелем в доказательство того, что не существует и не может существовать более трех измерений, кажутся мне убедительными; и что если бы нужно было привести доказательство более строгое, то Аристотель не преминул бы привести его.
Сагредо. — Добавьте, однако, если бы он его знал или если бы он вспомнил о нем. Но вы, синьор Сальвиати, доставите мне большое удовольствие, если приведете какое-нибудь очевидное доказательство, настолько ясное, чтобы оно было доступно моему пониманию.
Сальвиати. — И вашему, и синьора Симпличио; оно не только доступно пониманию; оно, кроме того, уже известно вам, хотя, может быть, вы не отдавали себе в этом отчета.
|
Геометрическое доказательство трехмерности. |
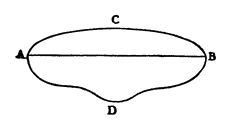 затем проведем от одной точки к другой кривые АСВ и ADB и прямую АВ; теперь я спрашиваю вас, какая из этих линий, по вашему понятию, определяет расстояние между конечными точками А и В и почему?
затем проведем от одной точки к другой кривые АСВ и ADB и прямую АВ; теперь я спрашиваю вас, какая из этих линий, по вашему понятию, определяет расстояние между конечными точками А и В и почему?
Сагредо. — Я бы сказал — прямая, а не кривые, потому, что прямая — кратчайшая; а также потому, что прямая — одна, единственная и определенная линия, тогда как других бесконечно много, они не равны и более длинны, а для определения, кажется мне, следует пользоваться тем, что едино и известно.
Сальвиати. — Итак, длина между двумя точками определяется прямой. Проведем теперь другую прямую, параллельную AB, которую назовем CD, так чтобы между ними заключалась некоторая плоская поверхность; я хотел бы, чтобы вы определили мне ее ширину. Поэтому, скажите мне, где и как, отправляясь от точки A, вы достигнете линии CD,
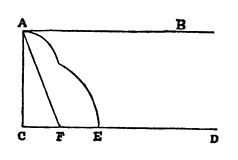 чтобы определить ширину, заключенную между этими линиями, т. е. определите вы ее по длине кривой АЕ, или по прямой AF, или...
чтобы определить ширину, заключенную между этими линиями, т. е. определите вы ее по длине кривой АЕ, или по прямой AF, или...
Симпличио. — По прямой AF, а не по кривой, ибо мы уже признали, что кривые не годятся для этой цели.
Сагредо. — А я не воспользовался бы ни той, ни другой, так как вижу, что прямая AF идет наискось; я провел бы линию, составляющую с линией CD прямой угол, потому что она, как мне кажется, будет кратчайшей и единственной наряду с бесконечным числом более длинных и неравных друг другу линий, которые можно провести из точки А к разным точкам противолежащей линии CD.
Сальвиати. — По-моему, ваш выбор и основание, которое вы приводите, превосходны; таким образом, мы пришли к тому результату, что первое измерение определяется прямой линией; второе, т. е. ширина, определяется другой линией, также прямой, но не всякой, а такой, которая образует прямой угол с линией, определяющей длину; таким образом, мы установили оба измерения плоской поверхности, т. е. длину и ширину, Но допустим, вам нужно определить высоту, например, как высоко {27} находится этот потолок от пола, находящегося у нас под ногами. Так как от любой точки потолка можно провести бесконечное число линий, кривых и прямых, все разной длины, к бесконечному числу точек находящегося под нами пола, то какой из этих линий вы воспользовались бы?
Сагредо. — Я прикрепил бы к потолку нить с грузом на ней и свободно спустил бы ее, пока она не достигла бы самого пола; длина этой нити, как прямая и кратчайшая из линий, которые можно провести из той же точки к полу, покажет действительную высоту этой комнаты.
Сальвиати. — Прекрасно. А когда из точки пола, отмеченной этой подвешенной нитью (предполагая, что пол — горизонтален, а не наклонен), вы проведете две другие прямые, одну — для определения длины, а другую — для определения ширины поверхности пола, то какие углы они образуют с этой нитью?
Сагредо. — Несомненно, они образуют прямые углы, если эта нить снабжена грузом и если пол действительно плоский и горизонтальный.
Сальвиати. — Итак, если вы примете какую-нибудь точку за начальный и исходный пункт измерения и от нее проведете прямую, определяющую первое измерение, т. е. длину, то совершенно необходимо, чтобы та линия, которая должна определить ширину, шла под прямым углом к первой и чтобы та линия, которая должна отмечать высоту, т. е. третье измерение, будучи проведена от той же точки, точно так же образовала с двумя другими не косые углы, а прямые; таким образом, тремя
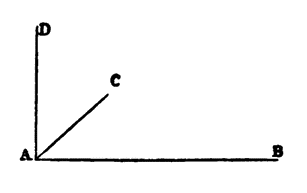 перпендикулярами, как тремя линиями единственными, определенными и кратчайшими, определяются три измерения: АВ — длина, АС — ширина, AD — высота. Так как ясно, что через ту же точку не может проходить еще какая-нибудь линия, которая образовала бы с данными прямые углы, а измерения должны определяться только прямыми линиями, образующими между собой прямые углы, то существуют только три измерения; но то, что обладает тремя, обладает всеми измерениями, то, что обладает всеми, делимо во всех направлениях, а то, что таким образом делимо, совершенно и так далее.
перпендикулярами, как тремя линиями единственными, определенными и кратчайшими, определяются три измерения: АВ — длина, АС — ширина, AD — высота. Так как ясно, что через ту же точку не может проходить еще какая-нибудь линия, которая образовала бы с данными прямые углы, а измерения должны определяться только прямыми линиями, образующими между собой прямые углы, то существуют только три измерения; но то, что обладает тремя, обладает всеми измерениями, то, что обладает всеми, делимо во всех направлениях, а то, что таким образом делимо, совершенно и так далее.
Симпличио. — А кто сказал, что нельзя провести других линий? Почему я не могу провести снизу какую-нибудь линию до точки А, которая образует с другими прямой угол?
Сальвиати. — Вы не можете, без сомнения, от одной и той же точки провести больше трех прямых, образующих между собой прямые углы.
Сагредо. — Конечно, потому что та линия, которую имеет в виду синьор Симпличио, будет, мне кажется, той же DA, но продолженной книзу; таким же способом можно было бы провести и еще две линии, но все они были бы прежними тремя с той лишь разницей, что теперь они только соприкасаются, а тогда пересекались бы, не прибавляя, однако, новых измерений.
Симпличио. — Я не скажу, что этот ваш довод нельзя признать убедительным, но все же скажу вместе с Аристотелем, что
|
В доказательствах естественных не следует искать точности геометрической. |
Сагредо. — Пожалуй, в тех случаях, когда ее нельзя достигнуть; но если она имеется, почему вы не хотите ею воспользоваться? Но не будем больше расточать слова по поводу этой частности, ибо я уверен, что синьор Сальвиати и без дальнейших доказательств согласится с Аристотелем и с вами, что мир есть тело совершенное и в высшей степени совершенное, как величайшее творение божье.
Сальвиати. — Это верно. Поэтому оставим общие рассуждения обо «всем» и перейдем к рассмотрению его частей, каковых
|
Частей вселенной по Аристотелю две: небесная и стихийная — друг другу противоположные. |
Исходя, так сказать, из мира чувственного и переходя в мир идеальный, он начинает свое построение с того соображения, что так как природа — начало движения, то, значит, естественным телам присуще местное движение. Вслед за тем он утверждает, что
|
Движения местные — трех родов: прямолинейное, круговое и смешанное. |
|
Движения прямолинейное и круговое — простые, потому что совершаются по простым линиям. |
Сагредо. — Позвольте остановиться на этом, синьор Сальвиати, потому что это рассуждение вызывает во мне такую вереницу самых разнообразных сомнений, что нужно или обсудить их, дабы я мог внимательно слушать дальше, или учесть, что мое внимание будет отвлечено от ваших слов старанием удержать в памяти свои сомнения.
Сальвиати. — Охотно остановлюсь, потому что я сам нахожусь в таком же состоянии и в любой момент могу сбиться. Мне приходится плыть среди скал и волн с риском, как говорится, потерять направление; а потому изложите ваши сомнения, пока их не набралось слишком много.
Сагредо. — Вы, вместе с Аристотелем, с самого начала отвлекаете меня от чувственного мира, чтобы показать мне план, по которому он должен быть построен, и к моему удовлетворению вы начинаете с утверждения, что естественное тело по природе обладает движением, ибо, согласно другому определению, природа есть начало движения. Здесь у меня рождается маленькое недоумение, а именно: почему Аристотель не говорит, что из естественных тел некоторые по природе обладают движением, а другие неподвижны, хотя в определении говорится, что
|
Определение природы, данное Аристотелем, или неправильно, или несовершенно. |
Когда он дальше разъясняет свое понимание простых движений и как они определяются по их путям, называя простыми движениями те, которые совершаются по простым линиям, каковыми являются только круг и прямая, то я это спокойно принимаю и не буду затруднять его тонкостями, указывая хотя бы на
|
Спираль, обвивающая цилиндр, может быть названа простой линией. |
|
Аристотель прилаживает план к мирозданию, а не строит здание по плану. |
|
Движение прямолинейное — иногда простое, иногда смешанное, по Аристотелю. |
Симпличио. — Не признаете ли вы это различие достаточным, если примете во внимание, что простое и абсолютное движение совершается гораздо быстрее движения, происходящего от преобладающей части? — Насколько быстрее движется вниз кусок чистой земли, чем кусочек дерева?
Сагредо. — Прекрасно, синьор Симпличио, но если простота движения может изменяться, то прежде всего получится сто тысяч смешанных движений, и вы не в состоянии будете определить простое; больше того, если бо́льшая или меньшая скорость могут менять простоту движения, то ни одно простое тело никогда не будет двигаться простым движением, потому что во всех естественных прямолинейных движениях скорость непрерывно возрастает и, следовательно, непрерывно изменяет простоту, каковая, чтобы называться простотою, должна оставаться неизменной; и, что еще важнее, вы делаете Аристотелю новый тяжкий упрек, состоящий в том, что он при определении сложного движения не упомянул ни о медленности, ни о скорости, каковые вы теперь считаете признаком необходимым и существенным. Присоедините к этому еще и то, что из такого признака вы не сумеете извлечь никакого плодотворного результата, ибо бывают такие смешанные тела, и их немало, из коих одни движутся медленнее, а другие скорее, чем тела простые, как, например, свинец и дерево по сравнению с землей; и какое же из этих движений вы назовете простым и какое сложным? {30}
Симпличио. — Я назвал бы простым движением то, которое совершается простым телом, а смешанным — то, которое совершается сложным телом.
Сагредо. — Поистине прекрасно. Как же вы рассуждаете, синьор Симпличио? Только что вам хотелось, чтобы простое или сложное движение научили меня различать, какие тела простые и какие смешанные, а теперь вы хотите, чтобы я, исходя от простых и смешанных тел, научился распознавать, какое движение простое и какое сложное, — превосходный прием, чтобы никогда не суметь разобраться ни в движениях, ни в телах. К тому же вы готовы признать, что вам уже недостаточно одной большей скорости, и вы ищите третье условие для определения простого движения, тогда как Аристотель довольствовался только одним, а именно — простотою проходимого пути; по-вашему же, теперь выходит, что простым движением будет то, которое совершается по простой линии, с некоторой определенной скоростью, простым движущимся телом. Ну, что же, пусть будет по-вашему; вернемся, однако, к Аристотелю; он определял смешанное движение как такое, которое слагается из движения прямолинейного и кругового; однако, он не указал бы мне ни одного тела, естественно движущегося таким движением.
Сальвиати. — Итак, я возвращаюсь к Аристотелю. Он начал свое рассуждение превосходно и методически, но, имея в виду скорее достигнуть некоторой конечной цели, заранее установившейся у него в уме, чем притти туда, куда прямо вел весь ход рассуждения, прервал нить его, утверждая, как вещь известную и очевидную, что, поскольку речь идет о прямолинейных движениях вверх и вниз, последние, естественно, присущи огню и земле. Поэтому необходимо, чтобы, кроме тел, находящихся рядом с нами, в природе существовало какое-то другое тело, которому присуще круговое движение и которое к тому же должно быть настолько превосходнее этих тел, насколько круговое движение совершеннее движения прямолинейного; а насколько первое совершеннее второго, он выводит, исходя из совершенства окружности по сравнению с прямой линией и называя окружность совершенною, а прямую линию — несовершенною.
|
Окружность, по Аристотелю, совершенна, а прямая — несовершенна, и почему. |
|
В мире, по допущению автора, господствует совершенный порядок. |
Сальвиати. — Установив такое начало, мы можем непосредственно из него сделать тот вывод, что если тела, составляющие вселенную, должны по природе своей обладать движением, то невозможно, чтобы движения их были прямолинейными и вообще какими бы то ни было, кроме как круговыми; основание этого просто и ясно9. Ведь то, что движется прямолинейным движением, меняет место, и если движение продолжается, то
|
Прямолинейное движение не может существовать в хорошо упорядоченном мире. |
|
Прямолинейное движение по природе бесконечно. Движение прямолинейное невозможно по природе. |
|
Природа не предпринимает ничего, что не может быть выполнено. |
|
Прямолинейное движение в первичном хаосе. |
|
Прямолинейное движение пригодно для того, чтобы внести порядок в тела плохо упорядоченные. |
|
Тела во вселенной движутся сперва прямолинейно, а затем по кругу — по мнению Платона. |
|
Подвижное тело, находящееся в состоянии покоя, не придет в движение, если у него нет влечения к какому-нибудь особому месту. |
|
Движущееся тело ускоряет движение, когда оно двигается к тому месту, к которому имеет влечение. |
|
Движущееся тело, отправляясь от покоя, проходит все степени медленности. |
|
Покой есть степень бесконечной медленности. |
|
Движущееся тело приобретает ускорение только тогда, когда движется к назначенному пункту. |
|
Природа, чтобы довести движущееся тело до некоторой степени скорости, заставляет его двигаться прямолинейно. |
|
Равномерная скорость присуща круговому движению. |
Сагредо. — Я слушаю это рассуждение с большим удовольствием и уверен, что оно еще возрастет после того, как вы разрешите одно затруднение, а именно: я не совсем понимаю, почему необходимо, чтобы движущееся тело, отправляясь от состояния покоя и переходя к движению,
|
Между покоем и какой бы то ни было степенью скорости посредствует бесконечное количество степеней меньших скоростей. |
Сальвиати. — Я не сказал и не смею сказать, что для природы и для бога было бы невозможно сообщить ту скорость, о которой вы говорите,
|
Природа не сообщает непосредственно определенной степени скорости, хотя могла бы. |
Сагредо. — Таким образом, вы думаете, что камень, выйдя из состояния покоя, в своем естественном движении к центру Земли проходит через все степени медленности, лежащие ниже любой степени скорости?
Сальвиати. — Не только думаю, но даже уверен в этом и уверен с такой непоколебимостью, что могу и вас привести к этой уверенности. {33}
Сагредо. — Если бы из всей нашей сегодняшней беседы я вынес одно только это знание, то я считал бы это для себя крупным приобретением.
Сальвиати. — Насколько я понимаю ваше соображение, главная трудность состоит для вас в том, что тело должно пройти в течение некоторого и притом кратчайшего времени через те бесконечные степени медленности, которые предшествуют любой скорости, приобретаемой движущимся телом в данное время. Поэтому, прежде чем переходить к дальнейшему, я попытаюсь устранить это недоумение. Это нетрудно сделать, раз я вам отвечу, что
|
Движущееся тело, отправляясь от состояния покоя, проходит все степени скорости, не задерживаясь ни на одной из них. |
Сагредо. — Это я понимаю; однако, мне кажется удивительным, что пушечное ядро, падающее с такой стремительностью, что менее чем за десять биений пульса оно пройдет более двухсот локтей, — так я представляю себе движение падающего тела, — оказывается обладающим в своем движении столь ничтожной степенью скорости, что, если бы оно непрерывно двигалось с этой скоростью, не испытывая никакого ускорения, то не прошло бы своего пути за целый день.
Сальвиати. — Скажите даже за целый год, даже за десять и за тысячу лет, как я постараюсь вам доказать, в особенности, если вы не возражаете против некоторых простых вопросов, которые я вам задам. Итак, скажите мне, представляется ли вам затруднительным допустить, что ото ядро при своем падении приобретает все большие импульс и скорость?
Сагредо. — В этом я совершенно уверен.
Сальвиати. — А если я вам скажу, что импульс, приобретенный в любом месте движения, таков, что его достаточно, чтобы вернуть ядро на ту высоту, с которой оно начало свое движение, то согласитесь ли вы со мной?
|
Движущееся тяжелое тело, падая, приобретает импульс, достаточный для того, чтобы вернуть тело на прежнюю высоту. |
Сальвиати. — Вы рассуждаете безукоризненно. И вы, без сомнения, допустите, как я в том уверен, что приобретение импульса идет по мере удаления от отправного пункта движущегося тела и по мере приближения к центру, к которому устремляется его движение. Встречаете ли вы затруднения к тому, чтобы допустить, что два разных движущихся тела, даже если они падают вниз без всякого препятствия по различным линиям, приобретут и равные импульсы, лишь бы приближение их к центру было равным?
Сагредо. — Я не совсем понимаю вопрос. {34}
Сальвиати. — Я поясню свою мысль на маленьком чертеже. Итак, я проведу эту линию АВ горизонтально и из точки В восставлю перпендикуляр ВС, затем проведу эту наклонную СА. Под линией СА мы будем разуметь наклонную плоскость, тщательно отполированную и твердую.
 Если по этой плоскости движется вниз ядро, совершенно круглое и из самого твердого материала, и такое же ядро будет свободно двигаться вниз по перпендикуляру СВ, то я спрошу, согласитесь ли вы, что импульс ядра, спускающегося по плоскости СА, при достижении пункта А может быть равен импульсу, приобретенному другим ядром в точке В, после того как оно опустится по перпендикуляру СВ?
Если по этой плоскости движется вниз ядро, совершенно круглое и из самого твердого материала, и такое же ядро будет свободно двигаться вниз по перпендикуляру СВ, то я спрошу, согласитесь ли вы, что импульс ядра, спускающегося по плоскости СА, при достижении пункта А может быть равен импульсу, приобретенному другим ядром в точке В, после того как оно опустится по перпендикуляру СВ?
Сагредо. — Я, безусловно, думаю, что равен: ведь в итоге оба ядра одинаково приблизились к центру, и в силу того, что я уже признал,
|
Импульсы движущихся тел, приблизившихся к центру, равны. |
Сальвиати. — Скажите мне еще, как вы думаете, что произойдет с тем же ядром, если мы поместим его на горизонтальную плоскость АВ?
|
На горизонтальной плоскости тело остается без движения. |
Сальвиати. — Но по наклонной плоскости СА оно будет спускаться, хотя и медленнее, чем по вертикали СВ?
Сагредо. — На это я только что ответил решительным «да», причем, по-моему, движение по перпендикуляру СВ необходимо должно совершаться скорее, чем по наклонной СА. Однако, если это так, то как может тело, падающее по наклонной, достигнув точки А, обладать таким же импульсом, т. е. тою же степенью скорости, какую получит тело, падающее по вертикали, в точке В? Эти два положения кажутся мне противоречивыми.
Сальвиати. — Тем более ложным покажется вам то, что я еще скажу, а именно, что скорости тел, падающих по вертикали и по наклонной, абсолютно равны. И все-таки это положение совершенно истинно;
|
Скорость по наклонной плоскости равна скорости по перпендикуляру, но движение по перпендикуляру быстрее движения по наклонной. |
Сагредо. — Для меня эти положения звучат противоречиво; а для Симпличио?
Симпличио. — И на мой взгляд точно так же.
Сальвиати. — Пожалуй, вы посмеиваетесь надо мной, притворяясь, будто не улавливаете того, что понимаете лучше меня. Ну, тогда скажите мне, синьор Симпличио, когда вы представляете себе, что одно движущееся тело обладает большей скоростью, чем другое, что вы под этим подразумеваете?
Симпличио. — Я представляю себе, что одно тело проходит в то же время большее пространство, чем другое, или же что оно проходит то же пространство, но в меньшее время.
Сальвиати. — Превосходно. А под одинаковой скоростью движущихся тел что вы подразумеваете?
Симпличио. — Я представляю себе, что они проходят равные пространства в равное время.
Сальвиати. — И вы ограничиваетесь только таким определением?
Симпличио. — Мне кажется, что это надлежащее определение равных движений.
|
Скорости называются равными тогда, когда пройденные пространства пропорциональны времени. |
Сальвиати. — Это верно, потому что оно обнимает равные пространства, проходимые в равные времена, а также неравные пространства, проходимые в неравные времена, но пропорциональные этим пространствам. Теперь обратитесь к тому же чертежу и к понятию, какое вы составили о более скором движении, и скажите, почему вам кажется, что скорость тела, падающего по СВ, больше скорости тела, спускающегося по СА?
Симпличио. — Мне кажется потому, что в течение того времени, в которое падающее тело пройдет всю СВ, спускающееся тело пройдет на СА часть, которая будет меньше СВ.
Сальвиати. — Так и есть, а раз это так, то тело движется с большей скоростью по перпендикуляру, чем по наклонной. Посмотрите, нельзя ли теперь при помощи того же чертежа как-нибудь оправдать и другое понятие и найти, что тела будут двигаться с равными скоростями по обеим линиям СА и СВ.
Симпличио. — Я не могу этого усмотреть; напротив, мне кажется, это противоречит только что сказанному.
Сальвиати. — А что скажете вы, синьор Сагредо? Мне не хотелось бы учить вас тому, что вы сами знаете и определение чего вы мне только что предложили.
Сагредо. — Определение, которое я привел, гласило, что скорости движущихся тел можно назвать равными, когда проходимые ими пространства относятся так же, как времена, в течение которых они пройдены. Поэтому, если мы хотим, чтобы определение имело силу и в данном случае, необходимо, чтобы время спуска по СА так же относилось ко времени падения по СВ, как сама линия СА к СВ; но я не понимаю, как это может быть, раз движение по СВ совершается скорее, чем по СА.
Сальвиати. — А все-таки нужно, чтобы вы поняли. Скажите-ка: не совершаются ли эти движения с непрерывным ускорением?
Сагредо. — Безусловно, с ускорением, но это ускорение больше при движении по перпендикуляру, чем по наклонной.
Сальвиати. — Но таково ли это ускорение при движении по перпендикуляру в сравнении с ускорением по наклонной, что если мы возьмем два равных отрезка в любом месте этих линий, перпендикулярной и наклонной, то движение на отрезке перпендикуляра всегда совершается скорее, чем на отрезке наклонной?
Сагредо. — Нет, синьор, напротив, я могу взять какой-нибудь отрезок на наклонной, где скорость значительно больше, чем на отрезке такой же величины, взятом на перпендикуляре; в особенности это будет заметно, если отрезок на перпендикуляре — близ точки С, а на наклонной — значительно дальше.
Сальвиати. — Таким образом, вы видите, что положение, которое гласит: «движение по перпендикуляру совершается скорее, чем по наклонной», оказывается не общим положением, а приложимо только там, где движения идут от начального пункта, т. е. от состояния покоя; без этой оговорки положение было бы столь недостаточно, что даже противоречащее ему могло быть истинным, т. е. что движение по наклонной совершается скорее, чем по вертикали. Ибо, в самом деле, на наклонной мы можем взять отрезок, проходимый движущимся телом в меньшее время, чем отрезок, проходимый по перпендикуляру. Далее, так как движение по наклонной в некоторых местах совершается скорее, а в других медленнее, чем по перпендикуляру, то, значит, в некоторых местах наклонной время движения тела будет находиться в большем отношении ко времени движения тела в некоторых местах перпендикуляра, чем отрезок, проходимый телом на одной линии, к отрезку, проходимому телом на другой линии; в других местах, наоборот, отношение времен будет меньше, {36} чем отношение отрезков. Так, например, если два тела движутся от состояния покоя, т. е. от точки С, одно по перпендикуляру СВ, а другое по наклонной СА, то за время, когда вертикально движущееся тело пройдет всю линию СВ, другое тело пройдет меньшее пространство СТ; таким
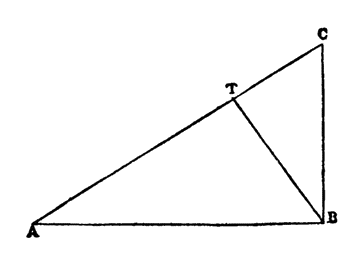 образом, отношение времени движения по СТ ко времени движения по СВ (а эти времена равны) больше, чем отношение линии ТС к линии СВ, так как одна и та же величина находится в большем отношении к меньшей величине, чем к большей. А также, и обратно, если бы на СА, продолжив насколько нужно, мы взяли отрезок, равный СВ, но проходимый в более короткое время, то время движения по наклонной находилось бы ко времени движения по перпендикуляру в меньшем отношении, чем одно пространство к другому. Если поэтому на наклонной и на перпендикуляре мы можем находить отрезки и скорости такого рода, что отношения между отрезками будут то меньшими, то большими, чем отношения времен, то мы можем с достаточным основанием допустить, что существуют также и такие отрезки, на которых времена движения сохраняют то же самое отношение, как и сами отрезки.
образом, отношение времени движения по СТ ко времени движения по СВ (а эти времена равны) больше, чем отношение линии ТС к линии СВ, так как одна и та же величина находится в большем отношении к меньшей величине, чем к большей. А также, и обратно, если бы на СА, продолжив насколько нужно, мы взяли отрезок, равный СВ, но проходимый в более короткое время, то время движения по наклонной находилось бы ко времени движения по перпендикуляру в меньшем отношении, чем одно пространство к другому. Если поэтому на наклонной и на перпендикуляре мы можем находить отрезки и скорости такого рода, что отношения между отрезками будут то меньшими, то большими, чем отношения времен, то мы можем с достаточным основанием допустить, что существуют также и такие отрезки, на которых времена движения сохраняют то же самое отношение, как и сами отрезки.
Сагредо. — Этим мое важнейшее сомнение устранено, и я понимаю не только возможность, но, скажу прямо, — необходимость того, что мне казалось противоречием. Но я еще не улавливаю из этого, чтобы один из этих возможных или необходимых случаев был тем, который нас занимает в настоящее время: действительно ли время спуска по СА находится в таком же отношении ко времени падения по СВ, в каком линия СА находится к линии СВ, на основании чего можно было бы бесспорно утверждать, что скорости движений по наклонной СА и по вертикальной СВ равны.
Сальвиати. — Довольствуйтесь пока тем, что я устранил вашу недоверчивость; что касается полного знания, то подождите до другого раза, когда вы познакомитесь с рассуждениями нашего Академика по вопросу о местных движениях. Там вы найдете доказательство того, что за время, в течение которого движущееся тело пройдет в своем падении всю линию СВ, другое тело опустится по СА до точки Т. В эту точку попадет перпендикуляр, опущенный из точки В; а чтобы найти, где окажется то же падающее по перпендикуляру тело, когда другое достигло точки А, надо восставить из точки А перпендикуляр к СА, продолжив его, а также и СВ до их пересечения: там и будет искомая точка. Тем временем заметьте, как справедливо, что движение по СВ совершается скорее, чем по наклонной СА (принимая точку С за начало движений, которые мы сравниваем);
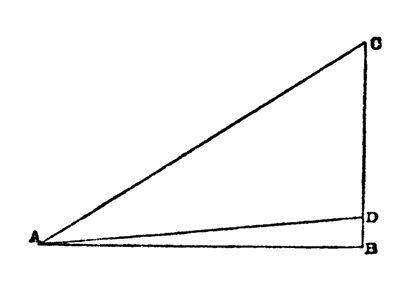 линия СВ длиннее СТ, а линия, идущая из С до пересечения с перпендикуляром, восставленным из точки А к линии СА, длиннее линии СА, и следовательно, движение по ней совершается скорее, чем по СА. Но если мы сравниваем движение по всей СА не со всем движением за то же время по продолженному перпендикуляру, но с движением за часть этого времени только по отрезку СВ, то нельзя отрицать, что тело, движущееся по СА, продолжая опускаться дальше Т, может достигнуть А в течение определенного времени и что такое же отношение, какое существует между линиями СА и СВ, существует и между соответствующими временами. Теперь вернемся к нашей первоначальной задаче. Она состояла в том, чтобы показать, как тяжелое тело, отправляясь от состояния покоя, приобретает {37} опускаясь, все степени медленности, предшествующие любой степени приобретенной им скорости. Обратимся к тому же чертежу и припомним, как мы согласились в том, что тело, падающее по перпендикуляру СВУ и тело, опускающееся по наклонной СА, в точках В и А приобретают, оказывается, одинаковые степени скорости. Если мы пойдем теперь дальше, то, думаю, для вас не составит затруднения согласиться, что на некоторой другой плоскости с меньшим наклоном, чем АС, например на плоскости DA, движение опускающегося тела будет еще медленнее, чем на плоскости СА. Поэтому, несомненно, можно наметить плоскости с таким малым наклоном по отношению к горизонтальной АВ, что движущееся тело, т. е. то же ядро, достигнет точки А в сколь угодно продолжительное время, тогда как для того, чтобы достигнуть его на плоскости ВА, недостаточно и бесконечного времени; движение всегда происходит тем медленнее, чем меньше наклон. Таким образом, необходимо признать, что над точкой В можно взять точку, столь близкую к В, что если мы проведем от нее плоскость до точки А, то ядро не пройдет этой плоскости и за год. Далее, вы должны знать, что импульс, т. е. степень скорости, которую ядро приобретает, достигнув точки А, таков, что, если бы ядро продолжало двигаться с той же степенью скорости равномерно, т. е. без ускорения и замедления, то в такое же количество времени, в какое оно прошло наклонную плоскость, оно прошло бы отрезок, по длине вдвое больший наклонной плоскости; иными словами, например, если бы ядро прошло плоскость DA в один час и продолжало двигаться равномерно с той степенью скорости, какой оно обладало при достижении точки А, то оно прошло бы в следующий час пространство, равное двойной длине DA, а так как (о чем уже было сказано) степени скорости, приобретаемые в точках В и А движущимися телами, которые отправляются от любой точки, взятой на вертикали СВ, причем одно спускается по наклонной плоскости, а другое по перпендикуляру, всегда равны, то тело, падающее по перпендикуляру, может выйти из точки, столь близкой к В, что степени скорости, приобретаемой телом в В, было бы недостаточно (если бы она оставалась всегда тою же), чтобы заставить движущееся тело пройти пространство, вдвое более длинное, чем наклонная плоскость, в год, в десять лет и в сто лет. Итак, мы можем сделать вывод: если верно, что, согласно обычному ходу вещей в природе, тело по устранении внешних и привходящих препятствий движется по наклонной плоскости с тем большей медленностью, чем меньше будет наклон, так что в конце концов медленность становится бесконечной, когда наклон кончается и получается горизонтальная плоскость, и если верно также, что степень скорости, приобретенная телом в какой-нибудь точке наклонной плоскости, равна той степени скорости, которой обладает тело, упавшее по перпендикуляру до точки пересечения перпендикуляром линии, параллельной горизонтали и проходящей через названную точку наклонной плоскости, то необходимо признать, что падающее тело, выходящее из состояния покоя, проходит все бесконечные степени медленности и что, следовательно, для приобретения определенной степени скорости оно должно двигаться сперва по прямой линии14, проходя меньший или больший отрезок, смотря по тому, должна ли быть им приобретена меньшая или большая скорость, и смотря по тому, насколько наклонна прямая, по которой оно опускается; таким образом, может найтись плоскость с таким малым наклоном, что для приобретения заданной степени скорости тело должно было бы пройти чрезвычайно длинное пространство в течение чрезвычайно долгого времени; на горизонтальной же плоскости естественным порядком никогда не приобретается никакая скорость, так как тело на ней никогда не придет в движение. Но движение по горизонтальной линии, у которой нет ни наклона, ни подъема, есть круговое движение вокруг центра. Следовательно, {38} круговое движение не приобретается естественным путем без
линия СВ длиннее СТ, а линия, идущая из С до пересечения с перпендикуляром, восставленным из точки А к линии СА, длиннее линии СА, и следовательно, движение по ней совершается скорее, чем по СА. Но если мы сравниваем движение по всей СА не со всем движением за то же время по продолженному перпендикуляру, но с движением за часть этого времени только по отрезку СВ, то нельзя отрицать, что тело, движущееся по СА, продолжая опускаться дальше Т, может достигнуть А в течение определенного времени и что такое же отношение, какое существует между линиями СА и СВ, существует и между соответствующими временами. Теперь вернемся к нашей первоначальной задаче. Она состояла в том, чтобы показать, как тяжелое тело, отправляясь от состояния покоя, приобретает {37} опускаясь, все степени медленности, предшествующие любой степени приобретенной им скорости. Обратимся к тому же чертежу и припомним, как мы согласились в том, что тело, падающее по перпендикуляру СВУ и тело, опускающееся по наклонной СА, в точках В и А приобретают, оказывается, одинаковые степени скорости. Если мы пойдем теперь дальше, то, думаю, для вас не составит затруднения согласиться, что на некоторой другой плоскости с меньшим наклоном, чем АС, например на плоскости DA, движение опускающегося тела будет еще медленнее, чем на плоскости СА. Поэтому, несомненно, можно наметить плоскости с таким малым наклоном по отношению к горизонтальной АВ, что движущееся тело, т. е. то же ядро, достигнет точки А в сколь угодно продолжительное время, тогда как для того, чтобы достигнуть его на плоскости ВА, недостаточно и бесконечного времени; движение всегда происходит тем медленнее, чем меньше наклон. Таким образом, необходимо признать, что над точкой В можно взять точку, столь близкую к В, что если мы проведем от нее плоскость до точки А, то ядро не пройдет этой плоскости и за год. Далее, вы должны знать, что импульс, т. е. степень скорости, которую ядро приобретает, достигнув точки А, таков, что, если бы ядро продолжало двигаться с той же степенью скорости равномерно, т. е. без ускорения и замедления, то в такое же количество времени, в какое оно прошло наклонную плоскость, оно прошло бы отрезок, по длине вдвое больший наклонной плоскости; иными словами, например, если бы ядро прошло плоскость DA в один час и продолжало двигаться равномерно с той степенью скорости, какой оно обладало при достижении точки А, то оно прошло бы в следующий час пространство, равное двойной длине DA, а так как (о чем уже было сказано) степени скорости, приобретаемые в точках В и А движущимися телами, которые отправляются от любой точки, взятой на вертикали СВ, причем одно спускается по наклонной плоскости, а другое по перпендикуляру, всегда равны, то тело, падающее по перпендикуляру, может выйти из точки, столь близкой к В, что степени скорости, приобретаемой телом в В, было бы недостаточно (если бы она оставалась всегда тою же), чтобы заставить движущееся тело пройти пространство, вдвое более длинное, чем наклонная плоскость, в год, в десять лет и в сто лет. Итак, мы можем сделать вывод: если верно, что, согласно обычному ходу вещей в природе, тело по устранении внешних и привходящих препятствий движется по наклонной плоскости с тем большей медленностью, чем меньше будет наклон, так что в конце концов медленность становится бесконечной, когда наклон кончается и получается горизонтальная плоскость, и если верно также, что степень скорости, приобретенная телом в какой-нибудь точке наклонной плоскости, равна той степени скорости, которой обладает тело, упавшее по перпендикуляру до точки пересечения перпендикуляром линии, параллельной горизонтали и проходящей через названную точку наклонной плоскости, то необходимо признать, что падающее тело, выходящее из состояния покоя, проходит все бесконечные степени медленности и что, следовательно, для приобретения определенной степени скорости оно должно двигаться сперва по прямой линии14, проходя меньший или больший отрезок, смотря по тому, должна ли быть им приобретена меньшая или большая скорость, и смотря по тому, насколько наклонна прямая, по которой оно опускается; таким образом, может найтись плоскость с таким малым наклоном, что для приобретения заданной степени скорости тело должно было бы пройти чрезвычайно длинное пространство в течение чрезвычайно долгого времени; на горизонтальной же плоскости естественным порядком никогда не приобретается никакая скорость, так как тело на ней никогда не придет в движение. Но движение по горизонтальной линии, у которой нет ни наклона, ни подъема, есть круговое движение вокруг центра. Следовательно, {38} круговое движение не приобретается естественным путем без
|
Круговое движение не может быть приобретено естественным путем без предшествовавшего прямолинейного движения. |
|
Круговое движение непрерывно и равномерно. |
|
Величина орбит в скорости движения планет соответствуют их исхождению из одного места. |
Сальвиати. — Вычисление это, действительно, длинное и трудное; и кроме того, я не уверен, что мог бы выполнить его сразу; поэтому отложим его до другого раза15.
Симпличио. — Позвольте мне просить вас о снисхождении к моему навыку в математических науках; откровенно признаться, ваши рассуждения, основанные на больших и меньших отношениях и на других терминах, — которые не настолько мне понятны, насколько следовало бы, — не устранили моего сомнения или, лучше сказать, моего неверия, будто свинцовое ядро огромной тяжести, в сто фунтов весом, будучи пущено с известной высоты и исходя из состояния покоя, пройдет через всякую, даже самую высокую степень медленности, тогда как видно, что {39} за четыре биения пульса оно прошло расстояние больше, чем в сто локтей. Это явление возбуждает во мне полное недоверие к утверждению, будто ядро может находиться в какой-либо момент в состоянии такой медленности, что если бы оно продолжало двигаться, сохраняя ее, то оно и в тысячу лет не прошло бы расстояния в полдюйма. Если это тем не менее верно, то я хотел бы, чтобы меня убедили в этом.
Сагредо. — Синьор Сальвиати как человек высокой учености часто думает, что термины, самому ему хорошо известные и близкие, должны быть точно так же знакомы и другим, а потому он иной раз забывает, беседуя с нами, что он должен был бы притти на помощь нашему слабому разумению, пользуясь рассуждениями, более доступными. И потому я, не претендуя на столь высокую ученость, попытаюсь с его позволения, хотя бы частично, устранить недоверие синьора Симпличио наглядным способом. Имея в виду попрежнему пушечное ядро, прошу вас сказать мне, синьор Симпличио, не согласитесь ли вы с тем, что при переходе от одного состояния к другому более естественным и легким является переход к состоянию, более близкому, чем к более отдаленному?
Симпличио. — Это я понимаю и с этим я согласен. Я не сомневаюсь, например, что кусок раскаленного железа при охлаждении скорее перейдет с 10 степеней тепла на 9, чем с 10 на 6.
Сагредо. — Превосходно. Скажите мне дальше: это пушечное ядро, пущенное кверху силою выстрела, не будет ли двигаться, все время замедляя свое движение, пока, наконец, не достигнет наивысшего пункта покоя? И не будет ли разумно предположить, что при уменьшении скорости или, если хотите, при увеличении медленности оно перейдет с 10 степеней на 11 ранее, чем с 10 на 12? И с 1000 на 1001 ранее, чем на 1002? И вообще с любой степени — на ближайшую к ней, а не на более отдаленную?
Симпличио. — Это вполне разумно.
Сагредо. — Но какая же степень медленности так отдалена от какого бы то ни было движения, чтобы состояние покоя, т. е. бесконечной медленности, не было еще более отдаленным? Поэтому не подлежит сомнению, что наше ядро, прежде чем оно достигнет точки покоя, пройдет через все степени медленности, все большие и большие, а следовательно, и через ту, при которой оно и в тысячу лет не прошло бы пространства в один дюйм. Но если так, а это действительно так, то вам, синьор Симпличио, не должно казаться невероятным, что, возвращаясь вниз, то же ядро, выйдя из состояния покоя, будет восстанавливать скорость движения по мере того, как будет проходить те же степени медленности, через которые оно прошло, поднимаясь кверху; иначе оно должно было бы, минуя степени медленности, ближайшие к состоянию покоя, совершить прыжок к степени более удаленной.
Симпличио. — Из этого рассуждения я уразумел больше, чем из прежних математических тонкостей; и потому синьор Сальвиати может вернуться к своему рассуждению и продолжать его.]
Сальвиати. — Итак, вернемся к нашему первому положению и начнем вновь с того места, где мы уклонились в сторону, когда, если я не ошибаюсь, мы установили, что прямолинейное движение не может иметь места в упорядоченной вселенной; затем мы говорили, что не так дело обстоит с движениями круговыми, из коих то, которое совершается движущимся телом самим по себе, всегда удерживает его в одном и том же месте, а то, которое состоит в движении тела по окружности круга около своего постоянного и неподвижного центра,
|
Круговые движения, законченные и определенные, не вносят беспорядка в части вселенной. |
|
В круговом движении каждая точка окружности — начальная и конечная точка. |
|
Движение круговое — единственное равномерное. |
|
Круговое движение продолжается непрерывно. |
|
Прямолинейное движение при естественных условиях не может быть постоянным. |
|
Прямолинейное движение предназначено естественным телам для того, чтобы приводить их в совершенный порядок, когда они из него выведены. |
|
Только покой и круговое движение пригодны для сохранения порядка. |
|
Чувственный опыт должен быть предпочтен человеческим рассуждениям. |
|
Кто отрицает чувство, заслуживает, чтобы у него отняли чувство. |
|
Чувство показывает, что тяжелое движется к середине, а легкое — к своду. |
Сальвиати. — В силу этого вашего рассуждения самое большое, чего вы можете требовать, — это признания, что части Земли, оторванные от целого, т. е. от того места, где они естественно находятся, т. е. в конце концов приведенные в неправильное и беспорядочное расположение, возвращаются на свое место сами собой, а потому, естественно, прямолинейным движением; совершенно так же (допуская, что eadem est ratio totius et partium) следовало бы заключить, что и земной шар, силою удаленный с места, предназначенного ему самой природой, вернулся бы туда прямолинейным движением. Это — самое большее, говорю я, с чем мы могли бы согласиться, всячески идя вам навстречу. Но тот, кто захотел бы строже отнестись к вашим утверждениям, отказался бы признать, что части Земли при возвращении к своему целому будут двигаться прямолинейно, а не круговым или каким-либо смешанным движением; и вам, без сомнения, нелегко было бы доказать противное, как вы ясно
|
Сомнительно, движутся ли тяжелые падающие тела прямолинейно. |
|
Земля сферична вследствие стремления частей к своему целому. |
|
Более вероятно, что в центре вселенной находится Солнце, а не Земля. |
Раз из согласованного стремления всех частей Земли образовать свое целое следует, что они стекаются туда со всех сторон в силу одинакового влечения, и для того, чтобы объединиться сколь возможно теснее, располагаются сферически, — то почему бы нам не признать, что Луна, Солнце и другие тела вселенной также принимают округлую форму только вследствие того же влечения и естественного скопления всех составных частей их? И если иногда одна из этих частей будет как-нибудь насильственно отделена от целого, то разве неразумно предположить, что она сама собой вследствие естественного влечения вернется к целому, и разве не естественно, таким образом, притти к заключению, что прямолинейное движение присуще всем мировым телам?
Симпличио. — Так как вы хотите отрицать не только начала наук, но очевидные опыты и даже чувства, то нет никакого сомнения, что вас уже нельзя убедить или освободить от каких бы то ни было предвзятых мнений; и я скорее успокоюсь на том, что contra negantes principia non est disputandum, чем убежденный силою ваших доводов17. Остановимся хотя бы на том, что вы только что сказали, а именно — на вашем сомнении, прямолинейно или непрямолинейно движение тяжелых тел? Какие могут быть у вас основания отрицать, что части Земли, т. е. наиболее тяжелой материи, опускаются к центру Земли прямолинейным движением? Если, например, они будут сброшены с очень высокой башни со стенами, совершенно ровными и построенными по отвесу, то они пойдут, так сказать, скользя, и ударятся о Землю как раз в той самой точке, куда попал бы и отвес, висящий на веревке, укрепленной у вершины башни в точности там, откуда был сброшен камень. Разве это не очевидное доказательство того,
|
Прямолинейное движение тяжелых тел, воспринимаемое чувствами. |
|
Доказательство Аристотеля, что тяжелые тела движутся по направлению к центру вселенной. Тяжелые тела движутся к центру Земли per ассidens. Спрашивать о том, что воспоследовало бы за невозможным, тщетное занятие. Тела небесные, по Аристотелю, ни легки, ни тяжелы. |
Сальвиати. — Насколько основательно мое сомнение в том, действительно ли тяжелые тела движутся по прямой и вертикальной линии, вы увидите, как я только что сказал, когда мы рассмотрим этот вопрос особо. Что касается второго пункта, то меня удивляет, что нужно еще раскрывать вам паралогизм Аристотеля, тогда как он столь очевиден сам по себе. Неужели вы не замечаете, как Аристотель допускает то, что заключается в вопросе? А потому заметьте...
Симпличио. — Прошу вас, синьор Сальвиати, говорите об Аристотеле более почтительно. И кого удастся вам когда-либо убедить, что он, который был первым, единственным и изумительным изъяснителем силлогистики, доказательства, эленхий, способов распознавания софизмов,
|
Аристотель не может ошибаться, потому что он — основоположник логики. |
Сальвиати. — Синьор Симпличио, мы сошлись здесь, чтобы в дружеской беседе исследовать некоторые истины; я нисколько не обижусь, если вы откроете мне мои ошибки; если я не понял мысли Аристотеля, откровенно укажите мне, и я буду благодарен. Позвольте же мне изложить свои затруднения, а также и ответить еще на один пункт в вашем последнем слове. Заметьте, что логика, как вы прекрасно знаете, есть инструмент, которым пользуются в философии; и как можно быть превосходным мастером в построении инструмента, не умея извлечь из него ни одного звука, так же можно быть великим логиком, не умея как следует пользоваться логикой; многие знают на память все правила поэтики и все же неспособны сочинить даже четырех стихов, а иные, обладая всеми наставлениями Винчи, не в состоянии нарисовать хотя бы скамейку. Играть на органе научишься не у того, кто умеет делать орган, но только у того, кто заставляет его звучать. Поэзии мы научаемся путем постоянного чтения поэтов; живописи — путем постоянного рисования и письма; доказательствам — путем чтения книг, содержащих доказательства, а таковы только книги по математике, а не по логике. Но вернемся к нашей теме. Я говорю, что то движение легких тел, которое видит Аристотель, есть только движение огня, который отделяется от любого места поверхности земного шара и прямолинейно удаляется от нее, поднимаясь вверх; это на самом деле значит двигаться по направлению к окружности, превосходящей окружность Земли, почему сам
|
Паралогизм Аристотеля при доказательстве того, что Земля находится в центре мира. |
Сагредо. — Этот аргумент Аристотеля показался мне и в другом отношении недостаточным и малоубедительным, даже если допустить вместе с ним, что та самая окружность, к которой прямолинейно движется огонь, замыкает собою мир. Ведь если взять внутри круга не только центр, но какую угодно другую точку, то каждое движущееся тело, отправляющееся от нее и идущее по прямой линии в любом направлении, идет, несомненно, к окружности и, продолжая движение, достигнет ее; значит, вполне правильно можно сказать, что тело движется по направлению к окружности, но уже совсем неправильно будет утверждение, что тело, двигаясь по тем же самым линиям в обратном направлении, движется к центру, разве только взятая исходная точка сама является центром, или движение происходит по той единственной линии, которая проходит от исходной точки через центр. Таким образом, сказать — «Огонь, двигаясь прямолинейно, направляется к окружности мира; следовательно, части Земли, которые
|
Паралогизм Аристотеля вскрывается и с другой стороны. |
Сальвиати. — Вы, синьор Сагредо, весьма остроумно приводите Аристотеля к той же самой несообразности, показывая очевидную его двусмысленность; но вы, кроме того, обращаете внимание и еще на одно обстоятельство. Мы знаем, что Земля сферична, и потому уверены, что она
|
Доказывается, что с бо́льшим правом можно говорить, что тяжелые тела тяготеют к центру Земли, чем к центру мира. |
|
Условия, согласно которым небесные тела отличаются от элементарных, зависят от движений, приписанных им Аристотелем. |
Симпличио. — Подобный способ философствования ведет к ниспровержению всей философии природы и потрясению неба, Земли и всей вселенной. Но, по-моему, основы перипатетической философии таковы, что нельзя думать, будто путем ее разрушения мы можем построить новые науки.
Сальвиати. — Не заботьтесь о небе и Земле и не бойтесь их потрясения, равно как и ниспровержения философии, так как в отношении неба напрасно вам опасаться за то, что вы сами считаете неизменным и непреходящим, а в отношении Земли — мы стараемся облагородить ее и сделать более совершенной, стремясь уподобить ее небесным телам и в известном смысле поместить ее на небо, откуда ваши философы ее изгнали.
|
Философия может только выиграть от споров и разногласий философов. |
Симпличио. — Пока я еще не вижу, чтобы Аристотель нуждался в помощи, так как он остался на ногах крепким и сильным и пока еще не был даже атакован вами, не то что повержен. А чем будете защищаться вы от этой атаки? — Аристотель пишет: все возникающее образуется из противоположности в каком-нибудь объекте и равным образом уничтожается
|
Рассуждение Аристотеля в доказательство нетленности неба. |
|
По Аристотелю, возникновение и разрушение существуют только при наличии противоположностей. Круговому движению никакое другое движение не противоположно. Небо — обитель бессмертных богов. Неизменность неба воспринимается чувством. Доказательство того, что круговое движение не имеет противоположного. |
Сальвиати. — Но ведь это — всего только уже отмеченная мною цепь заключений Аристотеля, и если я буду здесь отрицать, что движение, которое вы приписываете небесным телам, не подходит к Земле, то вывод его отпадет. Я же утверждаю, что то круговое движение, которое вы отводите одним небесным телам, подобает также и Земле. Если признать остальное ваше рассуждение убедительным, то из этого следует одна из {45} трех следующих вещей, как это было сказано немногим раньше и как я вам теперь повторяю, а именно: или что Земля так же невозникающа и неуничтожаема, как и небесные тела, или что небесные тела, как и элементарные, возникающи, изменчивы и т. д., или что различие движений не имеет никакого отношения к возникновению и уничтожению. Рассуждение Аристотеля и ваше содержат много предпосылок, которые не так-то легко принять, и для того, чтобы иметь возможность лучше их исследовать, полезно придать им более четкую и определенную формулировку. Прошу прощения у синьора Сагредо, если, может быть, я немного наскучу ему, повторяя много раз одно и то же; пусть он представит себе, что слушает доводы на публичном диспуте. Вы говорите: «возникновение и уничтожение существуют только там, где есть противоположности; противоположности существуют только среди простых природных тел, которые движутся противоположными движениями; противоположные движения — это только те, которые совершаются по прямым линиям между противоположными точками, и их только два, т. е. от середины и к середине, и эти движения совершаются из других природных тел только Землею, огнем и другими двумя элементами. Следовательно, возникновение и уничтожение существуют только среди стихий. И так как третье простое движение, т. е. круговое вокруг середины, не имеет противоположного (ибо противоположны два других, и каждое из них имеет другое в качестве противного), то поэтому у того природного тела, которому свойственно такое движение, отсутствует противоположность; а раз нет противоположности, то оно оказывается невозникающим, неуничтожаемым и т. д., так как где нет противоположности, нет ни возникновения, ни уничтожения и т. д., но такое движение присуще одним
|
Гораздо легче удостовериться в том, движется ли Земля, чем в том, обусловлено ли уничтожение противоположностями. |
|
Простое перемещение частей может представить тела в различных видах |
Сагредо. — Синьор Сальвиати, простите мне, если я прерву ваше рассуждение, хотя оно мне и очень нравится, так как я чувствую, что у меня возникают затруднения, и я начинаю сомневаться, сможем ли мы вообще договориться до конца, если только не отложим совершенно нашу основную тему. Поэтому, если можно продолжать первоначальное рассуждение, я считал бы более правильным отложить до другой отдельной и специальной беседы этот вопрос о возникновении и уничтожении. Таким же образом, если это не встретит возражений с вашей стороны и со стороны синьора Симпличио, можно было бы поступать и с другими частными вопросами, которые предстанут перед нами в течение беседы; я замечу их в отдельности, чтобы предложить в другой раз и тогда тщательно их исследовать. Что касается настоящего случая, то, поскольку вы отрицаете положение Аристотеля, что Земле в отличие от других небесных тел не свойственно круговое движение, из этого следует, что все происходящее с Землей в смысле возникновения, изменчивости и т. д. относится также и к небу. Но оставим открытым вопрос, существуют или не существуют в природе возникновение и уничтожение, и вернемся к исследованию того, что происходит с земным шаром.
Симпличио. — Я совершенно не могу заставить себя слушать, как
|
Отрицая начала науки, можно поддерживать какой угодно парадокс. |
Сагредо. — Напротив, мы видим все это и потому признаем рассуждение Аристотеля, поскольку дело касается того, что возникновение и уничтожение обусловлены противоположностями; но если я вам докажу на основе тех же самых предпосылок, допускаемых Аристотелем, что небесные тела также не меньше элементарных, возникающи и уничтожаемы, то что вы на это скажете?
Симпличио. — Скажу, что вы сделали то, что невозможно сделать.
Сагредо. — Скажите мне все же, синьор Симпличио: разве эти свойства не противоположны друг другу?
Симпличио. — Какие?
Сагредо. — А вот какие: изменчивость, неизменность, преходящесть, непреходящесть, возникаемость, невозникаемость, уничтожаемость, неуничтожаемость?
Симпличио. — Они совершенно противоположны.
Сагредо. — Если это так, и если правда также, что небесные тела невозникающи и неуничтожаемы, то я вам докажу, что небесные тела неизбежно должны быть возникающими и уничтожаемыми.
|
Небесные тела возникающи и уничтожаемы, так как они невозникающи и неуничтожаемые |
Сагредо. — Выслушайте аргумент, а потом называйте его и распутывайте. Небесные тела, раз они невозникающи и неуничтожаемы, имеют в природе противоположности, т. е. тела возникающие и уничтожаемые; {47} но где существует противоположность, там существует возникновение и уничтожение; значит, небесные тела возникающи и уничтожаемы.
Симпличио. — Не говорил ли я вам, что это может быть только софизмом. Это одно из тех своеобразных рассуждений, которые называются
|
Своеобразное рассуждение, называемое соритом. |
Сагредо. — До сих пор вы его только назвали, теперь вам остается его распутать, показав ошибку.
|
Среди небесных тел нет противоположностей. |
Сагредо. — Позвольте, синьор Симпличио. Пребывает ли та противоположность, в силу которой, по вашему убеждению, некоторые простые тела уничтожаемы, в самом таком теле, или же связана с другим телом? Пребывает ли, например, спрашиваю я, влажность, в силу которой разрушается некоторая часть Земли, в самой Земле, или же в другом теле, например, в воздухе или воде? Вы скажете, я думаю, что как движение вверх и вниз, так и тяжесть и легкость, которые вы считаете основными противоположностями, не могут находиться в одном и том же объекте, и этого не может быть также с влажностью и сухостью, с теплом и холодом; приходится, следовательно, вам сказать, что когда тело разрушается, то разрушение происходит в силу того свойства, которое находится в
|
Противоположности, которые являются причиной разрушения, не пребывают в том самом теле, которое разрушается. |
Симпличио. — Нет, этого недостаточно, дорогой синьор. Элементы изменяются и разрушаются потому, что соприкасаются и перемешиваются друг с другом и, таким образом, могут воздействовать друг на друга своими противоположностями; но небесные тела отделены от элементов; элементы не оказывают действия на них, хотя небесные тела и воздействуют
|
Небесные тела воздействуют на элементы, но не подвергаются воздействию со стороны элементов. |
Сагредо. — Тогда я вам найду их и среди небесных тел. Первым источником, из которого вы черпаете противоположности стихий, это противоположность их движений вверх и вниз; необходимо, значит, чтобы равным образом были противны друг другу те начала, от которых зависят эти движения; и так как одно движется вверх в силу легкости, а второе вниз в силу тяжести, то легкость и тяжесть необходимо должны быть противоположны друг другу; не меньше, как нужно думать,
|
Тяжесть и легкость, редкость и плотность — противоположные свойства. |
|
Звезды бесконечно превосходят по плотности субстанции остального неба. |
Симпличио. — Нет необходимости ни в том, ни в другом, так как
|
Редкость и плотность небесных тел отличны от редкости и плотности элементов (Кремонино). |
Сагредо. — Таким образом, вы хотите, чтобы плотность и редкость, которые у элементов должны являться причиной тяжести и легкости, в свою очередь могущих быть причинами противоположных движений sursum et deorsum, обусловливающих противоположности возникновения и разрушения, определялись не только, как плотность и редкость в зависимости от того, много или мало материи содержится в том же размере или, лучше сказать, объеме, но необходимо, чтобы тела были плотны и редки благодаря первоначальным свойствам холода и тепла; иначе ничего
|
Аристотель, видно, преуменьшил перечисление причин того, что элементы возникаемы и уничтожаемы. |
Симпличио. — Только потому, что таких свойств нет у небесных тел, ибо они не теплы и не холодны.
Сальвиати. — Мы снова, я вижу, начинаем удаляться в бесконечное море, откуда никогда не выйдем, так как это плавание без компаса, без звезд, без весел и без руля, почему нам по необходимости придется пробираться от одного подводного камня к другому, или сесть на мель, или плыть все время наугад. Поэтому, если мы хотим, согласно вашему совету, продвинуть вперед нашу главную тему, нам нужно отложить теперь в сторону это общее рассуждение о том, необходимо ли в природе прямолинейное движение и свойственно ли оно некоторым телам, и перейти к отдельным доказательствам, наблюдениям и опытам, рассмотрев сначала все те, которые до сих пор приводились Аристотелем, Птоломеем {49} и другими для доказательства неподвижности Земли; затем попробовать их распутать и, наконец, перейти к таким, на основе которых можно убедиться в том, что Земля не меньше, чем Луна или другая планета, может быть причислена к природным телам, движущимся кругообразно.
Сагредо. — Я тем охотнее пристану к этому берегу, что меня больше удовлетворяет ваше общее построение, чем рассуждение Аристотеля, так как ваше даст мне спокойное удовлетворение, тогда как аристотелево на каждом шагу ставит мне какую-нибудь помеху; я не понимаю, как синьор Симпличио не оказался сразу же убежденным приведенными вами доводами в доказательство того, что прямолинейное движение не может иметь места в природе, раз предполагается, что части вселенной расположены в наилучшей системе и в наиболее совершенном порядке.
Сальвиати. — Подождите, пожалуйста, синьор Сагредо, так как сейчас мне припомнился способ удовлетворить также и синьора Симпличио, если только он не захочет оставаться настолько связанным каждым словом Аристотеля, чтобы считать за святотатство отклонение от него в чем бы то ни было. Нет никакого сомнения, что для поддержания наилучшего расположения и совершенного порядка частей вселенной, поскольку речь идет о месторасположении, нет ничего другого, кроме кругового движения и покоя; поскольку же речь идет о прямолинейном движении, я не вижу, чтобы оно могло служить для чего-нибудь, кроме как для приведения к своему естественному положению какой-нибудь частицы одного из целых тел, которая в силу какого-нибудь обстоятельства была отделена от своего целого, как мы говорили об этом выше. Рассмотрим теперь земной шар в целом и поглядим, что именно может происходить с ним, если и он и другие мировые тела должны сохранять наилучшее и естественное расположение. О нем необходимо сказать, что или он остается и постоянно пребывает неподвижным на своем месте, или, оставаясь всегда в одном и том же месте, обращается вокруг самого себя, или, наконец, обращается вокруг некоторого центра, двигаясь по окружности круга; из этих возможностей Аристотель, Птоломей и все их
|
Аристотель и Птоломей считают земной шар неподвижным. |
|
Более естественно говорить о земном шаре, что он сохраняет покой, чем то, что он прямолинейно движется вниз. |
|
Больше оснований приписывать прямолинейные движения частям, чем стихиям в целом. |
То, что говорится о Земле, может быть сказано с таким же основанием об огне и о большей части воздуха; этим стихиям перипатетики приписывают в качестве их внутреннего и естественного движения, одно из таких движений, которым они никогда не двигались и не будут двигаться, и противоестественным называют то их движение, которым они двигались и которым они будут двигаться вечно. Я говорю это потому, что они
|
Перипатетики без всякого основания приписывают стихиям в качестве естественных те движения, которыми они никогда не двигались, и называют противоестественными те, которыми они движутся всегда. Чувственный опыт нужно предпочесть человеческим рассуждениям. |
Симпличио. — На все это у нас есть чрезвычайно подходящие ответы, но я пока оставляю их в стороне, чтобы перейти к более специальным доводам и к чувственным опытам: их в конце концов следует предпочесть, как правильно говорит Аристотель, тому, к чему может привести человеческое рассуждение.
Сагредо. — Итак, пусть послужит нам все сказанное до сих пор для того, чтобы лучше обсудить, какое из двух главных рассуждений обладает большей вероятностью, т. е. рассуждение ли Аристотеля, которое стремится нас убедить в том, что природа подлунных тел возникающа, уничтожаема и т. д. и потому совершенно отлична от сущности небесных тел, так как они непреходящи, невозникающи, неуничтожаемы и т. д., как это получается из различия простых движений, или же рассуждение синьора Сальвиати, где предполагается, что отдельные части мира расположены по самой лучшей системе, и потому в качестве необходимого следствия у простых природных тел отрицаются прямолинейные движения, как не находящие применения в природе, и где Земля признается также одним из небесных тел со всеми подобающими им привилегиями; это рассуждение до сих пор больше нравилось мне, чем первое. Итак, пусть синьор Симпличио будет настолько добр, чтобы привести по отдельности все основания, опыты и наблюдения, как естественные, так и астрономические, согласно которым можно убедиться в том, что Земля отлична от небесных тел, неподвижна и помещается в центре мира, а также всякие иные факты, если они у него есть, исключающие возможность подвижности Земли наподобие Юпитера, Луны и других планет; и синьор Сальвиати будет так любезен, что ответит вам пункт за пунктом.
Симпличио. — Вот вам на первый раз два могущественнейших доказательства того, что Земля совершенно отлична от небесных тел. Во-первых, тела возникающие, уничтожаемые, изменчивые и т. д. совершенно отличны от невозникающих, неуничтожаемых, неизменных и т. д.; Земля возникающа, уничтожаема, изменчива и т. д., а небесные тела невозникающи, неуничтожаемы, неизменны и т. д.; следовательно, Земля совершенно отлична от небесных тел.
Сагредо. — В качестве первого доказательства вы выкладываете на стол то, что у нас уже было сегодня сказано и что было только что опровергнуто.
Симпличио. — Потише, синьор, выслушайте остальное и посмотрите, насколько это доказательство отлично от прежнего. В первом меньшая {51} посылка доказывалась a priori, а теперь, я вам хочу доказать ее a posteriori; смотрите — то же ли это самое? Итак, я доказываю меньшую посылку, так как бо́льшая совершенно очевидна. Чувственный опыт показывает нам, что на Земле происходят непрерывные рождения, разрушения, изменения и т. д., но ни одно из этих явлений ни по свидетельству наших чувств, ни по преданиям или воспоминаниям наших предков не наблюдалось на небе; следовательно, небо неизменно и т. д., а Земля
|
Небо неизменно, так как никогда на нем не было видно изменений. Светоносные тела по природе отличаются от темных. |
Сальвиати. — Что касается первого довода, силу которого вы черпаете из опыта, то я просил бы вас указать мне более точно, какие изменения видите вы происходящими на Земле, но не на небе, на основании которых вы называете Землю изменчивой, а небо нет.
Симпличио. — Я вижу, как на Земле непрерывно рождаются и разрушаются травы, деревья, животные, как поднимаются ветры, дожди, грады, бури; словом, как весь этот облик Земли находится в непрерывных превращениях; ни одно из этих превращений не наблюдается в небесных телах, расположение и образ которых совершенно точно согласуются со всеми воспоминаниями, причем издревле на небе не наблюдалось зарождения чего-либо нового, а также ничего, что разрушалось бы.
Сальвиати. — Но раз вы основываетесь на данных, доступных глазу или, лучше сказать, очевидных, то вы должны считать Китай и Америку небесными телами, так как, конечно, вы в них никогда не видели тех изменений, которые вы видите здесь в Италии, и поэтому, согласно вашему пониманию, эти страны должны быть неизменными.
Симпличио. — Хотя я не наблюдаю посредством чувства этих изменений в указанных местах, все же существуют об этом достоверные сведения; кроме того, что cum eadem sit ratio totius et partium: раз эти страны, как и наши, являются частями Земли, то они должны быть так же изменчивы, как и она.
Сальвиати. — А почему вы не наблюдали и не видели их собственными глазами, чтобы не полагаться на сведения других?
Симпличио. — Потому что эти страны не стоят перед нашими глазами, и, кроме того, настолько удалены, что наше зрение не может воспринять подобных изменений.
Сальвиати. — Теперь вы видите, как вы сами случайно вскрыли ошибку вашего рассуждения. Ведь если вы говорите, что тех изменений, которые наблюдаются на Земле рядом с нами, вы не можете из-за слишком большого расстояния наблюдать в Америке, то еще меньше можете видеть их на Луне, во много сотен раз более далекой; и если вы верите в существование изменений в Мексике на основе известий, пришедших оттуда, то какие сведения дошли до вас с Луны в подтверждение того, что на ней не происходит изменений? Следовательно, раз вы не видите изменений на небе, где, если бы они и были, вы не могли бы их видеть из-за большого расстояния, раз вы не имеете сообщений, так как и иметь их нельзя, то вы не можете делать вывода, что их там нет, как из наблюдения а понимания их на Земле вы правильно заключаете, что здесь они имеются.
Симпличио. — Я найду вам столь большие изменения, происходившие на Земле, что если бы такие же случались на Луне, то их отлично можно было бы наблюдать отсюда снизу. Мы знаем на основании чрезвычайно древних преданий, что раньше у Гибралтарского пролива скалы {52}
|
Средиземное море образовалось в результате разделения Абилеи Кальпе. |
Сальвиати. — Что столь обширные изменения происходили на Луне, этого я не осмелюсь утверждать; но я не уверен, что они там и не могли происходить. Подобное изменение могло бы представиться нам только в виде какого-нибудь различия более светлых и более темных частей той же Луны; я не знаю, существовали ли на Земле достаточно любопытные селенографы, которые представили бы нам за длинный ряд лет точные селенографические данные, на основании которых мы могли бы быть вполне уверены, что никакого подобного изменения никогда не происходило с обликом Луны. Я вообще не нахожу никакого точного описания лика Луны, так как по словам одних она представляет собой человеческое лицо, по словам других она похожа на львиную морду, третьи видят на ней Каина со связкой хвороста на плече. Следовательно, утверждение «небо неизменно, так как на Луне или на другом небесном теле не видно тех изменений, которые наблюдаются на Земле», не имеет решительно никакой силы.
Сагредо. — Но, по-моему, остается еще некая деталь в этом первом доказательстве синьора Симпличио, которую мне очень хотелось бы разрешить. Поэтому я спрашиваю его, была ли Земля до Средиземноморского потопа возникаема и уничтожаема или же только после этого она стала таковою?
Симпличио. — Несомненно, она и раньше была возникаемой и уничтожаемой, но это было настолько обширное изменение, что даже и с Луны его можно было бы наблюдать.
Сагредо. — О, если Земля была и до такого наводнения возникаемой и уничтожаемой, то почему и Луна не может быть равным образом таковою даже без подобного изменения? Почему для Луны необходимо то, что не имеет решающего значения для Земли?
Сальвиати. — Чрезвычайно остроумное возражение. Но меня берет сомнение, не вкладывает ли синьор Симпличио несколько иной смысл в тексты Аристотеля и других перипатетиков. Они считают небо неизменным потому, что на нем никогда не наблюдалось ни возникновения, ни разрушения ни одной звезды, которая составляет, вероятно, меньшую часть по отношению к небу, чем город по отношению к Земле, а ведь бесчисленное множество городов было разрушено так, что от них не осталось даже никакого следа.
Сагредо. — Конечно, я предполагал иное и думаю, что синьор Симпличио дает такое истолкование текста, чтобы не отягощать Учителя и своих соучеников замечаниями еще более неудачными. Ведь нелепо было бы утверждать: «сфера небес неизменна и т. д., так как на ней не зарождаются и не разрушаются звезды». Разве кто-нибудь видел разрушение земного шара и возрождение из него нового? И разве не признается всеми философами, что лишь немногие звезды на небе меньше Земли, но очень многие из них гораздо больше? Значит, разрушение звезды на небе — не меньшее событие, чем разрушение всего земного шара; поэтому, если для введения во вселенную возникновения и уничтожения необходимо, {53}
|
Разрушение звезды столь же невозможно, как и разрушение всего земного шара. |
Сальвиати. — Но чтобы с избытком удовлетворить синьора Симпличио и избавить его по мере возможности от ошибки, я скажу, что у нас в наш век есть такие новые обстоятельства и наблюдения, которые, в этом я нисколько не сомневаюсь, заставили бы Аристотеля, если бы он жил
|
Аристотель переменил бы мнение, если бы видел новости нашего века. |
Симпличио. — Аристотель, делая главным своим основанием рассуждение a priori, доказывал необходимость неизменяемости неба своими естественными принципами, очевидными и ясными; и то же самое он устанавливал после этого a posteriori путем свидетельства чувств и древних преданий.
Сальвиати. — То, что вы говорите, является методом, которым он изложил свое учение, но я не думаю, чтобы это был метод его исследования. Я считаю твердо установленным, что он сначала старался путем чувственных опытов и наблюдений удостовериться, насколько только можно, в своих заключениях, а после этого изыскивал средства доказать их, ибо обычно именно так и поступают в доказательных науках; это делается потому, что если заключение правильно, то, пользуясь аналитическим методом, легко попадешь на какое-нибудь уже доказанное положение или приходишь к какому-нибудь началу, известному самому по себе; в случае же
|
Достоверность заключения помогает найти доказательство посредством аналитического метода. Пифагор совершил гекатомбу за найденное геометрическое доказательство. |
|
Новые звезды, появившиеся на небе. Пятна, которые появляются и распадаются на лике Солнца. Солнечные пятна больше всей Азии и Африки. |
Симпличио. — Я не знаю, что сделал бы и что сказал бы Аристотель, который был властителем наук, но я знаю немного, что делают и говорят и что должны делать и говорить его последователи, чтобы не остаться без руководителя, без проводника, без главы в философии. Что касается комет, то разве не были опровергнуты Антитихо те современные астрономы, которые хотели сделать их небесными телами, и опровергнуты их собственным оружием; ибо, говорю я, параллаксы и прочие выполненные на сто ладов вычисления привели в конце концов к заключению в пользу
|
Астрономы, опровергнутые Антитихо. |
Сальвиати. — Спокойнее, синьор Симпличио. Что говорит ваш современный автор о звездах 1572 и 1604-го годов и о солнечных пятнах? Поскольку речь идет о кометах, то я по крайней мере не очень задумывался над тем, возникли ли они выше или ниже Луны, никогда не считая солидным основанием разглагольствования Тихо, и не собираюсь возражать против предположения, что материя их — стихийная и что они могут подниматься куда им будет угодно, не встречая никаких препятствий со стороны непроницаемости перипатетического неба, которое, по-моему, значительно реже, податливее и тоньше нашего воздуха; поскольку же речь идет о вычислениях параллаксов, то прежде всего сомнительно, есть ли они вообще у комет, а затем недостаточность наблюдений, на основании которых произведены подсчеты, делают для меня равно подозрительными и те и другие мнения, в особенности раз мне кажется, что Антитихо истолковывает наблюдения на свой лад или объявляет
|
Антитихо приспосабливает астрономические наблюдения к своим целям. |
Симпличио. — Что касается новых звезд, то Антитихо отлично разделывается с ними в двух словах; эти современные новые звезды, говорит он, не являются частями небесных тел, и противникам его, если они хотят доказать существование наверху изменения и возникновения, необходимо описать перемены, происшедшие в звездах, которые описаны уже давно и относительно которых никто не сомневается, что это тела небесные, а этого возражающие никогда и никаким образом не смогут сделать. О тех образованиях, которые, по словам некоторых, возникают и распадаются на лике Солнца, он вообще не упоминает; из этого я заключаю, что он считает их сказкой, или иллюзиями зрительной трубы, или самое большее — помрачениями, вызванными воздухом, словом, чем угодно, только не изменениями небесной материи.
Сальвиати. — Но вы то, синьор Симпличио, что предполагаете вы сами ответить на свидетельство этих докучливых пятен, которые появились для помрачения неба, а еще больше — перипатетической философии? Наверное вы, как ее бесстрашный защитник, нашли выход и решение, и этого вам не следует скрывать от нас.
Симпличио. — Я слышал разные мнения по этому частному вопросу. «Одни говорят, что это — звезды, которые по своим собственным
|
Различные мнения о солнечных пятнах. |
Сальвиати. — Если бы предметом нашего спора было какое-нибудь положение юриспруденции или одной из других гуманитарных наук, где нет ни истинного, ни ложного, то можно было бы вполне положиться
|
В науках о природе ораторское искусство недействительно. |
|
Аргумент, который необходимо доказывает, что солнечные пятна возникают и распадаются. |
|
Движение пятен у окружности Солнца кажется медленным. |
|
Очертания пятен узки около окружности солнечного диска и почему это так кажется. Солнечные пятна не обладают сферической формой; они растянуты, как тонкие слои |
Симпличио. — Я, по правде говоря, не производил ни столь прилежных наблюдений, чтобы стать хозяином quod est данной темы, но мне всячески хотелось бы произвести их и потом попробовать самому, удастся ли мне согласовать данные опыта с положениями Аристотеля, так как ясно, что две истины не могут противоречить друг другу.
Сальвиати. — Во всяком случае, если вы захотите согласовать то, что вам показывают чувства, с наиболее прочными положениями Аристотеля, то это не будет для вас самой трудной работой на свете.
|
По Аристотелю, нельзя с определенностью говорить о небе из-за его громадного удаления. |
Симпличио. — Он открыто говорит это.
Сальвиати. — Не утверждает ли он также, что показываемое нам
|
По Аристотелю, чувство нужно предпочесть рассуждениям. |
Симпличио. — Говорит.
Сальвиати. — Значит, из двух данных положений, — а оба они входят в учение Аристотеля, — второе, которое гласит, что нужно предпочесть чувство рассуждению, является гораздо более прочным и решительным, чем первое, которое считает небо неизменным; и потому вы будете философствовать более по-аристотелевски, если скажете: «Небо изменчиво, потому что таковым мне показывает его чувство», чем если
|
В согласии с учением Аристотеля небо скорее можно назвать изменяющимся, чем неизменяющимся. |
|
Благодаря телескопу мы можем лучше Аристотеля рассуждать о предметах неба. |
Сагредо. — Я весьма сочувствую синьору Симпличио и вижу, что он чувствует себя весьма затронутым силой этих очень убедительных доводов; но, с другой стороны, он видит тот огромный авторитет, который стяжал себе Аристотель во всем мире; он учитывает число знаменитых интерпретаторов, трудившихся над разъяснением мыслей Аристотеля; он видит другие науки, столь полезные и необходимые для общества и обосновывающие в значительной мере свою ценность и репутацию на доверии к Аристотелю; и это его смущает и очень страшит. Мне кажется, я слышу, как он говорит: «К кому будем мы прибегать для разрешения
|
Речи Симпличио. |
Сальвиати. — Нет, синьор Симпличио, пока еще не нужно бояться подобной катастрофы: я с гораздо меньшими для него затратами возьмусь избавить его от убытков. Опасность не в том, что огромное число проницательных и тонких философов даст себя осилить одному или двум людям, поднявшим немного шума; наоборот, не только не обращая
|
Перипатетическая философия неизменна. |
Симпличио. — Я помню это очень хорошо. Мы рассматривали ответы Антитихо на возражения против неизменности неба, и вы включили в число их возражение на основании наблюдения солнечных пятен, им не затронутое; вы собирались, полагаю я, обсудить его ответы на,соображение о новых звездах.
Сальвиати. — Теперь я вспоминаю и остальное; последуем же за темой. Мне кажется, что в ответе Антитихо кое-что заслуживает возражения. Во-первых, если две новые звезды, которые он не может поместить ниже самых высоких частей неба, которые длительно существовали и в конце концов исчезли, не помешали ему поддерживать неизменность неба, ибо они не являются определенными его частями или изменениями, {58} происшедшими в старых звездах, зачем нападать с такой тревогой и таким беспокойством на кометы, чтобы изъять их любым способом из небесных областей? Разве не достаточно ему сказать о них то же самое, что и о новых звездах, т. е. что раз они не являются ни определенными частями неба, ни изменениями, произошедшими с какими-нибудь из небесных звезд, то они не наносят никакого вреда ни небу, ни учению Аристотеля? Во-вторых, я не понимаю, как следует, сущности его убеждений, когда он признает, с одной стороны, что те изменения, которые могли бы происходить в звездах, окажутся разрушительными для прерогатив неба, т. е. для его неизменности и т. д., и это потому, что звезды являются телами небесными, как это очевидно из единодушного согласия всех; с другой стороны, его ничуть не беспокоит, если те же самые изменения будут происходить за звездами, в остальном небесном пространстве. Может быть, он полагает, что само небо не является вещью небесной? Я-то считал, что звезды называются небесными потому, что они находятся на небе, или потому, что они сделаны из небесной материи и что поэтому небо должно быть более небесным, чем они, как нельзя, например, назвать какую-нибудь вещь более земной или более огненной, чем сама земля или сам огонь. И раз он не упомянул о солнечных пятнах, о которых было убедительно доказано, что они возникают и распадаются, что они очень близки к солнечному телу и вращаются вместе с ним или вокруг него, то это внушает мне сильное подозрение, что наш автор пишет больше в угоду другим, чем для собственного удовлетворения; и говорю я так потому, что раз он показывает себя понимающим в математических науках, то невозможно, чтобы он не был убежден доказательствами того, что подобного рода материи необходимо связаны с солнечным телом и являются порождениями и нарушениями большими, чем те, какие когда-либо происходили на Земле; и если столь большие и столь частые изменения происходят в самом теле Солнца, которое с полным основанием может считаться одной из самых благородных частей неба, то какое соображение окажется в силах разубедить нас, что другие изменения не смогут случиться и с другими телами?
Сагредо. — Я не могу без большого удивления и даже большого сопротивления разума слушать, как в качестве атрибутов особого благородства и совершенства природным и целостным телам вселенной приписывают невозмутимость, неизменность, неразрушаемость и т. д., и, наоборот, считают великим несовершенством возникаемость, разрушаемость,
|
Возникаемость и изменчивость — большее совершенство в мировых телах, чем противоположные свойства. Земля особенно благородна из-за многих происходящих в ней изменений. |
|
Земля, лишенная изменений, бесполезна и преисполнена праздности. |
|
Земля более благородна, чем золото и драгоценности. |
|
Недостаток и избыток придают цену и унижают вещи. Неуничтожаемость превозносится только из-за страха смерти. Хулящие уничтожаемость заслуживают быть превращенными в статую. |
Сальвиати. — Может быть, такая метаморфоза пойдет им на пользу, так как, по-моему, лучше совсем не рассуждать, чем рассуждать превратно.
Симпличио. — Нет никакого сомнения, что Земля много более совершенна такой, какой она есть, т. е. будучи изменчивой и меняющейся, чем если бы она была каменной массой, даже состоящей из целого алмаза, чрезвычайно твердого и непроницаемого. Но если бы эти условия и сообщали благородство Земле, то, с другой стороны, они сделали бы небесные тела менее совершенными, являясь для них излишними: раз небесные тела, т. е. Солнце, Луна и другие звезды, устроены только для служения Земле, то для достижения своей цели им не нужно ничего иного,
|
Небесные тела, устроенные для служения Земле, нуждаются только в движении и в свете. |
Сагредо. — Значит, природа создала и привела в движение также громаднейшие, совершеннейшие и благороднейшие небесные тела, непреходящие, бессмертные, божественные, только для служения Земле, преходящей, бренной и смертной? На служение тому, что вы называете подонками мира, помойной ямой всяческих нечистот? И зачем делать небесные тела бессмертными и т. д., чтобы они служили бренному и т. д.? Если отнять эту единственную пользу — служение Земле, то бесчисленное скопище всех небесных тел оказывается совершенно бесполезным и излишним, раз у последних нет и не может быть никакого обоюдного взаимодействия друг с другом, раз все они неизменны, непереходящи, недоступны воздействиям и т. д.; если, например, Луна недоступна воздействиям, то как может повлиять на нее Солнце или другая звезда? Это будет без всякого сомнения не больший эффект, чем тот, который
|
У небесных тел нет обоюдного взаимодействия друг с другом. |
Симпличио. — Разрушение, изменение, перемена и т. д. не относятся к земному шару в целом; он в своей совокупности так же вечен, как Солнце или Луна, а возникновение и разрушение свойственны только
|
Изменчивость не пребывает в земном шаре в целом, а только в некоторых частях. |
Сагредо. — Все это очень хорошо; но если вековечности земного шара ничуть не вредит разрушимость его поверхностных частей и, наоборот, от порождаемости, разрушаемости, изменчивости и т. д. он только выигрывает в красоте и совершенстве, то почему вы не можете и не смеете допустить также изменения, возникновения и т. д. и во внешних частях небесных тел? Эти изменения, зарождения и т. д. прибавляют им красоту,
|
Небесные тела изменчивы во внешних частях. |
Симпличио. — Этого не может быть, так как если бы возникновения, изменения и т. д. происходили, например, на Луне, то они были бы бесполезными и напрасными, et natura nihil frustra facix24.
Сагредо. — А почему они были бы бесполезными и напрасными? Симпличио. — Потому, что мы ясно видим и можем ощутительно
|
Движения и изменения, происходящие на Земле, — все для блага человека. |
Сагредо. — Что на Луне или на другой планете родятся травы или
|
На Луне отсутствуют рождения, похожие на наши, и она не населена людьми. |
|
На Луне могут рождаться вещи, отличные от наших. |
|
Кто не знает стихии воды, тот никогда не сможет представить себе кораблей и рыб. |
Сальвиати. — Я много раз фантазировал на эту тему и в конце концов, мне кажется, можно указать кое-что, чего нет и не может быть на Луне, но ничего такого, что там находится или могло бы находиться,
|
На Луне могут быть субстанции, отличные от наших. |
Сагредо. — Это — такие вещи, которые там могут быть, говоря совершенно о́бще, но я охотно послушал бы, каких вещей, по вашему мнению, там нет и не может быть и которые желательно было бы несколько более обстоятельно перечислить.
Сальвиати. — Я предупреждаю вас, синьор Сагредо, что это уже третий раз, как мы, сами того не замечая, шаг за шагом отклоняемся от нашей главной темы и что мы долго еще не придем к концу наших рассуждений, если будем делать отступления; поэтому если бы мы согласились выделить этот вопрос наравне с другими, которые мы решили отложить для особого рассмотрения в другой раз, то поступили бы, вероятно, лучше.
Сагредо. — Пожалуйста, раз мы уже оказались на Луне, рассмотрим то, что к ней относится, чтобы нам не пришлось еще раз проделывать столь долгий путь.
Сальвиати. — Пусть будет по-вашему. Начну с более общего. Лунный шар, я думаю, очень отличен от земного, хотя кое в чем наблюдается и сходство. Сначала я скажу о сходстве, а потом о различии.
Луна и Земля сходны, конечно, по форме, которая, несомненно, шарообразна, как это неизбежно следует из того, что диск Луны виден совершенно круглым, и из того, как она воспринимает свет Солнца. Если бы поверхность ее была плоской, то вся она одновременно одевалась бы светом,
|
Первое сходство между Луной и Землей — это форма, что доказывается тем, как Луна освещается Солнцем. |
|
Второе сходство в том, что Луна темна, как и Земля. |
|
Третье — вещество Луны плотно и гористо, как в у Земли. |
|
Четвертое — Луна делится на две части, отличающиеся по светлоте и темноте, как и земной шар — на моря и на земную поверхность. Поверхность моря покажется издалека темнее, чем поверхность земли. Пятое — изменение фаз Земли подобно изменению фаз Луны и происходит в тот же самый период. |
В-шестых,...
Сагредо. — Подождите немного, синьор Сальвиати. Что касается освещения Земли, то, поскольку речь идет о различных фазах, представляющихся взору наблюдателя, находящегося на Луне, и совершенно подобных тем, какие мы наблюдаем на Луне, — это я понимаю очень хорошо; но я не постигаю, как это изменение фаз может происходить за тот же самый период, раз то, что производит освещение Солнца на лунной поверхности, происходит в один месяц, а на земной в двадцать четыре часа?
Сальвиати. — Действительно, чтобы осветить эти два тела и покрыть своим сиянием их поверхность, Солнцу нужен для Земли один обычный день, а для Луны — один месяц; но смена фаз, в которых будут видны с Луны освещенные части земной поверхности, зависит не только от этого, но и от различных взаиморасположений Луны и Солнца; таким образом, если бы, например, Луна всегда в точности следовала за движением Солнца и всегда стояла на прямой линии между ним и Землей (в таком положении, которое мы называем соединением), то она всегда видела бы одну и ту же полусферу Земли, которая обращена к Солнцу, и неизменно видела бы ее целиком блестящей; и, обратно, если бы она всегда оставалась в противостоянии с Солнцем, то она никогда не видела бы Земли, которая была бы постоянно обращена к Луне темной частью и потому была бы невидима; когда же Луна находится в квадратурах с Солнцем, то из той земной полусферы, которая видима с Луны, одна половина, обращенная к Солнцу, освещена, а другая, противоположная Солнцу, темна, и потому освещенная часть Земли представляется с Луны в виде полукруга.
Сагредо. — Теперь я понимаю все это очень хорошо; так, я отлично представляю себе, что когда Луна отходит от противостояния с Солнцем, откуда она совершенно не видела освещенной земной поверхности, и с каждым днем передвигается по направлению к Солнцу, то постепенно она начинает замечать некоторые части освещенного лика Земли, который представится Луне сначала в виде тонкого серпа, так как Земля шарообразна; по мере же того, как Луна в своем движении день ото дня будет становиться все ближе к Солнцу, все больше и больше будет раскрываться освещенная земная полусфера, так что в квадратурах раскроется ровно ее половина, как мы это часто видим и на Луне; затем, когда она продолжает двигаться к соединению, последовательно раскрывается еще большая часть освещенной поверхности, и, наконец, в положении соединения вся полусфера видна освещенной. Словом, я прекрасно понимаю как то, что происходит для обитателей Земли с изменениями Луны, случится также и с Землей для находящихся на Луне, но в обратном порядке, а именно: когда Луна для нас является полной и находится в противостоянии с Солнцем, для нее Земля будет находиться в соединении с Солнцем и будет совершенно темна и невидима; наоборот, то положение, которое для нас является соединением Луны с Солнцем и когда, поэтому, Луна скрыта и не видна, тогда для Луны будет противостояние Земли с Солнцем, и Земля, так сказать, будет полной, т, е. будет вся освещена; {63} и, наконец, какая часть лунной поверхности в определенный момент видна нам освещенной, такая же часть Земли в то же время будет видна с Луны темной, и насколько Луна оказывается для нас лишенной света, настолько же кажется освещенной с Луны Земля, так что только в квадратурах одни видят освещенной полукруг Луны, а другие — полукруг Земли. Эти взаимоотношения, мне кажется, должны различаться лишь в одном: если принижается, как данное, что на Луне находится некто, кто может оттуда смотреть на Землю, то он будет видеть ежедневно всю земную поверхность вследствие движения Луны вокруг Земли в двадцать четыре или двадцать пять часов, мы же видим только половину Луны, так как она не обращается сама около себя, как это было бы необходимо, чтобы она могла показать нам себя целиком25.
Сальвиати. — Если только это не происходит от обратного, т. е. обращения Луны, которое является причиной того, что мы никогда не увидим другой ее половины; а это необходимо должно быть так, если она имеет эпицикл. Но почему забываете вы другое различие, которое как бы заменяет подмеченное вами?26.
Сагредо. — Какое же? Ничто другое мне сейчас не приходит в голову.
Сальвиати. — А вот что. Если Земля (как вы правильно отметили) видит только половину Луны, тогда как с Луны видна вся Земля, то, обратно, вся Земля видит Луну, Земля же видна только с половины Луны;
|
Вся Земля видит только половину Луны, и только половина Луны видит всю Землю. |
|
С Земли видно больше половины лунного шара. |
|
Два пятна на Луне, из наблюдения которых следует, что она обращена в своем движении к центру Земли. |
Сагредо. — Когда же наступит конец новым наблюдениям и открытиям при помощи этого удивительного инструмента?
Сальвиати. — Если успехи в этом будут итти так же, как и в других великих изобретениях, то нужно надеяться, что с течением времени мы увидим такие вещи, каких сейчас мы не можем вообразить. Но вернемся к нашему первоначальному рассуждению. Я утверждаю в качестве шестого пункта сходства между Луной и Землей, что как Луна в течение значительной части времени восполняет отсутствие солнечного света и делает для нас ночи довольно светлыми посредством своего отражения, так и Земля в благодарность Луне, когда это последней особенно нужно,
|
Шестое — Земля и Луна обоюдно освещаются. |
Сагредо. — Довольно, довольно, синьор Сальвиати. Дайте мне насладиться, рассказав вам, как при этом первом указании я проник в причину одного явления, о котором я думал тысячу раз, но в которое я никогда не мог проникнуть. Вы хотите сказать, что своеобразный тусклый свет, наблюдаемый на Луне, в особенности когда она серпообразна, вызван
|
Свет, отраженный Землей на Луну. |
Сальвиати. — Как раз именно это я и хотел сказать. Вообще большое удовольствие разговаривать с людьми умными и понятливыми, в особенности когда другие проходят мимо, не воспринимая истины. Мне многократно приходилось встречать настолько тупые умы, что хотя я тысячу раз повторял им то, что вы тотчас же самостоятельно уловили, они все же никак не могли этого понять.
Симпличио. — Если вы хотите сказать, что не могли убедить их так, чтобы они это поняли, то я чрезвычайно этому удивляюсь; я вполне уверен, что если они не поняли этого из вашего объяснения, то они, вероятно, не поймут этого и из объяснений других, так как ваш способ изложения кажется мне весьма ясным; если же вы имеете в виду, что не могли убедить их так, чтобы они в это поверили, то этому я ничуть не удивляюсь, так как и сам я, признаюсь, являюсь одним из тех, которые понимают ваши рассуждения, но не успокаиваются на них; наоборот, для меня остается и в этом, и отчасти в других шести пунктах сходства, {65} много трудностей, которые я выскажу, когда вы кончите рассказывать обо всех их.
Сальвиати. — Мое желание найти некоторую истину, — в чем мне могут сильно помочь возражения таких понимающих людей, как вы, — заставляет меня быть особенно кратким в разъяснении остающегося. Итак, пусть седьмой пункт сходства заключается в соответствии взаимных обид и удовлетворений, ибо Луна, которая довольно часто в расцвете своего освещения вследствие вторжения Земли между нею и Солнцем оказывается лишенной света и затемненной, также сама в отместку становится между Землей и Солнцем и своей тенью затемняет Землю; и если даже месть ее не равна оскорблению, так как Луна очень часто и притом на довольно продолжительное время остается целиком погруженной в тень Земли, Земля же никогда целиком и никогда на долгое время не затемняется Луной, то все же, принимая во внимание малые размеры тела Луны по сравнению с размерами тела Земли, нельзя не признать до известной степени отваги ее души. Вот и все, что касается сходства. Теперь следовало бы поговорить о различиях, но так как синьор Симпличио хочет дать нам удовлетворение, подвергая сходства сомнению, то хорошо было бы выслушать и взвесить их прежде, чем двигаться дальше.
Сагредо. — Да, тем более, что синьор Симпличио, вероятно, не будет возражать против отличий и расхождений между Землей и Луной, раз он считает их субстанции совершенно разными.
Симпличио. — Из сходств, перечисленных вами при сравнении Земли с Луной, я могу принять без возражений только первое и следующие два. Я допускаю первое сходство, т. е. сферическую форму, хотя и здесь не все благополучно, так как, по-моему, лунный шар совершенно гладок и чист, как зеркало, тогда как земной шар, если мы его потрогаем рукой, весьма шероховат и неровен; но это относится к неодинаковости поверхности и должно быть рассмотрено при другом пункте сходства, названном вами; поэтому я оставляю за собой право высказать об этом свои соображения при обсуждении соответствующего сходства. Из того, что вы говорите во втором сходстве, т. е. что Луна сама по себе не прозрачна и темна, как и Земля, я допускаю лишь первое свойство — непрозрачность; это мне удостоверяют солнечные затмения; если бы Луна была прозрачной, то воздух при полном солнечном затмении не становился бы таким темным, каким он на самом деле становится, и вследствие прозрачности лунного тела проходил бы преломленный свет, как мы видим это у особенно плотных облаков. Что же касается темноты, то я не думаю, чтобы Луна была совершенно лишена света, как Земля; наоборот, тот свет, который наблюдается на остальной части ее диска, сверх тонкого рога, освещенного Солнцем, я считаю ее собственным и естественным светом, а не отраженным от Земли; по-моему, Земля бессильна из-за своей крайней неровности и темноты отражать лучи Солнца. В третьей параллели
|
Вторичный свет признается собственным светом Луны. Земля бессильна отражать лучи Солнца. |
|
По Аристотелю, небесные субстанции непроницаемы. |
Сагредо. — Какой прекрасный материал доставляло бы небо для постройки дворцов, если бы можно было его получить, — такой твердый и такой прозрачный.
Сальвиати. — Наоборот, очень плохой, так как в силу совершенной прозрачности он абсолютно невидим, и нельзя было бы ходить по комнатам без большой опасности наткнуться на притолки и расшибить себе голову. {66}
Сагредо. — Этой опасности не существовало бы, если правда, что небесная материя, как утверждают некоторые перипатетики, неосязаема;
|
Небесная материя — неосязаема. |
Сальвиати. — Даже это не принесет никакого облегчения, так как, хотя к небесной материи нельзя прикоснуться, раз она лишена свойства осязаемости, все же она может прикасаться к элементарным телам; и, к нашему огорчению, это значит то же самое, как если бы она наталкивалась на нас, а последнее еще хуже, чем если бы мы наталкивались на нее. Но оставим эти дворцы или, лучше сказать, воздушные замки, и не будем мешать синьору Симпличио.
Симпличио. — Вопрос, который вы так случайно затронули, является одним из самых трудных, какие только разбираются в философии, и я в курсе прекраснейших мыслей по этому поводу одного великого профессора из Падуи30; но сейчас не время заниматься этим и потому вернемся к нашей теме. Я повторяю, что считаю Луну чрезвычайно прочной, прочнее Земли, но доказываю это не так, как делаете вы, неровностью и шероховатостью ее поверхности, а совершенно противоположным, т. е. ее способностью воспринимать (как мы это видим у особо твердых драгоценных камней) полировку и высший блеск, подобно какому угодно наиболее
|
Поверхность Луны глаже поверхности зеркала. |
|
Возвышенности и углубления на Луне — иллюзии, вызванные прозрачностью и непрозрачностью. |
Сальвиати. — Если я правильно понял ваш ответ, то, мне кажется, у нас с вами остаются еще спорными некоторые свойства, которые я сделал общими для Луны и для Земли; они таковы. Вы считаете Луну гладкой и вылощенной, как зеркало, и, как таковое, способной отражать к нам свет Солнца; обратно тому, Земля, по-вашему, из-за своей шероховатости не в силах дать подобное отражение. Вы допускаете, что Луна прочна и тверда, и доказываете это тем, что она ровна и гладка, а не тем, что она гориста; причину же того, что она представляется гористой, вы видите в существовании более или менее прозрачных и непрозрачных частей. И, наконец, вы считаете вторичный свет собственным светом Луны, а не отражением Земли, хотя в отношении моря, так как поверхность его гладкая, вы не отрицаете некоторого отражения. Я питаю мало надежды избавить вас от ошибочного мнения, что отражение от Луны происходит не так, как от зеркала, раз я вижу, что написанное по этому поводу в Весовщике золота и в Солнечных письмах нашим общим другом вовсе не пошло на пользу вашему представлению, если только вы внимательно прочли то, что там написано по этому предмету.
Симпличио. — Я пробежал их очень поверхностно, так как у меня оставалось мало свободного времени от более серьезных занятий; поэтому, если вы думаете повторением некоторых из таких доводов или приведением других разрешить мои затруднения, я выслушаю их более внимательно.
Сальвиати. — Я выскажу то, что мне приходит на память сейчас; это будет, вероятно, смесью моих собственных представлений и того, что я раньше прочел в названных книгах; последние, я отлично припоминаю это, совершенно убедили меня, хотя выводы на первый взгляд показались весьма парадоксальными. Мы собираемся исследовать, синьор Симпличио, необходимо ли для отражения света, подобного свету, идущему к нам от Луны, чтобы та поверхность, от которой исходит отражение, была так же ровна и отполирована, как поверхность зеркала, или же для этого более приспособлена не ровная и не отполированная поверхность, а шероховатая и плохо выровненная. Итак, если до нас доходят два отражения, одно более, а другое менее блестящее от двух стоящих против нас поверхностей, то, спрашиваю вас, какая из этих двух поверхностей, по вашему мнению, представится нашим глазам более светлой и какая более темной?
Симпличио. — Несомненно, по-моему, что та поверхность, которая более живо отразит ко мне свет, покажется мне по виду более светлой, а другая более темной.
Сальвиати. — Будьте любезны, возьмите это зеркало, висящее здесь на стене, и выйдем во двор. Идемте, синьор Сагредо. Повесьте зеркало
|
Подробно доказывается, что у Луны шероховатая поверхность. |
Сагредо. — Я предоставляю отвечать синьору Симпличио, ведь у него были затруднения; сам-то я с самого начала опыта был убежден, что поверхность Луны неизбежно должна быть чрезвычайно плохо выровненной.
Сальвиати. — Скажите, синьор Симпличио, если бы вам нужно было срисовать эту стену с этим повешенным на ней зеркалом, то где воспользовались бы вы более темными красками — рисуя стену или рисуя зеркало?
Симпличио. — Гораздо более темными, изображая зеркало.
Сальвиати. — Значит, если от той поверхности, которая представляется более светлой, идет более сильное отражение света, то стена живее отразит нам лучи Солнца, чем зеркало. {68}
Симпличио. — Прекрасно, мой дорогой синьор; нет ли у вас опытов получше этого? Вы нас поставили в такое место, куда не падает отражение зеркала; но отойдите со мной немного дальше, сюда; ну, идите же.
Сагредо. — Вы, вероятно, ищите место того отражения, которое дает зеркало?
Симпличио. — Да, синьор.
Сагредо. — О, вы увидите его там, на противоположной стене, совершенно такой же величины, как и зеркало, и лишь немного менее светлым, чем если бы туда прямо светило Солнце.
Симпличио. — Так пойдемте же туда и посмотрите оттуда на поверхность зеркала и осмельтесь сказать мне, что поверхность его темнее поверхности стены.
Сагредо. — Смотрите на него сами, я еще не хочу ослепнуть; я прекрасно знаю, и не глядя на зеркало, что оно так же ярко, как и само Солнце, или немногим меньше.
Симпличио. — Так как же говорите вы, что отражение зеркала слабее отражения стены? Я вижу, что на этой противоположной стене, куда доходит отражение освещенной части ограды вместе с отражением зеркала, отражение зеркала много ярче; я вижу равным образом, что оттуда и само зеркало мне представляется много более ярким, чем стена.
Сальвиати. — Вы с вашей обычной проницательностью предупредили меня, так как мне было нужно это же самое наблюдение для разъяснения остающегося. Итак, вы видите разницу между двумя отражениями, вызванными двумя поверхностями, — поверхностью стены и поверхностью зеркала; на них совершенно одинаково падают солнечные лучи, и вы видите, как отражение от стены распространяется во все противоположные ей направления, а отражение зеркала идет лишь в одну сторону, причем оно ничуть не больше самого зеркала; вы видите равным образом, как поверхность стены, с какого бы места ее ни рассматривать, всегда кажется по яркости равномерной и в общем гораздо более яркой, чем поверхность зеркала, за исключением только того маленького места, куда падает отражение зеркала, так что оттуда оно представляется значительно более ярким, чем стена. Из этих столь ощутимых и наглядных опытов, мне кажется, можно очень легко притти к познанию того, идет ли отражение, которое доходит к нам от Луны, как от зеркала или же как от стены, т. е. от гладкой поверхности или же от шероховатой.
Сагредо. — Если бы я оказался на самой Луне, то, думаю, не мог бы более ощутимо убедиться в неровности ее поверхности, чем сейчас, наблюдая ее под углом зрения нашего разговора. Луна, видимая в любом положении по отношению к Солнцу и к нам, показывает свою освещенную Солнцем поверхность всегда равномерно яркой; это явление в точности соответствует явлению со стеной: при рассматривании с любого места она представляется одинаково яркой и отличается от зеркала, которое только с одного места кажется светоносным, а со всех других — темным. Кроме того, свет, доходящий до меня от отражения стены, умерен и слаб по сравнению со светом от зеркала, чрезвычайно сильным и лишь немного менее опасным для зрения, чем первичный и прямой свет Солнца; нам теперь приятно смотреть на лик Луны, но если бы она была подобна зеркалу и казалась нам из-за своей близости такой же величины, как и само Солнце, то блеск ее был бы совершенно нестерпим, и нам казалось бы, что мы видим почти второе Солнце.
Сальвиати. — Не приписывайте, пожалуйста, синьор Сагредо, моему доказательству больше того, что оно само допускает. Я собираюсь выдвинуть против вас одно возражение, не так-то легко разрешимое. Вы считаете главным различием между Луной и зеркалом то, что она равномерно посылает свое отражение во все стороны, как и стена, тогда как {69} зеркало шлет его только в одно определенное место; отсюда вы заключаете, что Луна подобна стене, а не зеркалу. Я же вам говорю, что это зеркало шлет отражение в одно единственное место только потому, что его поверхность плоская, и так как отраженные лучи должны исходить под
|
Плоские зеркала посылают отражение в одно место, а сферические повсюду. |
Симпличио. — Как раз таково одно из тех возражений, которое я хотел выдвинуть.
Сагредо. — Если это является одним, то у вас необходимо должны быть и другие; поэтому выскажите их, так как, мне кажется, это первое скорее против вас, чем вам на пользу.
Симпличио. — Вы провозгласили в качестве вещи очевидной, что отражение от этой стены должно быть таким же ярким и сияющим, как и то, которое доходит до нас от Луны, а я считаю его ничтожным по сравнению с ней, так как «в этом вопросе освещения необходимо принимать во внимание и различать сферу активности; а кто сомневается в том, что
|
Сфера активности у небесных тел больше, чем у элементарных. |
Сагредо. — Я думаю, что и здесь вы ошибаетесь очень сильно. Но перехожу к первому соображению, выдвинутому синьором Сальвиати; я принимаю во внимание, что если какой-нибудь предмет должен казаться нам светоносным, то недостаточно, чтобы на него падали лучи освещающего тела, а нужно также, чтобы отраженные лучи шли к нашему глазу; это ясно видно на примере данного зеркала; к нему, несомненно, идут светоносные лучи Солнца, но при всем том оно кажется нам ярким и освещенным только тогда, когда мы поместим глаз в то особое место, куда идет отражение. Рассмотрим теперь, что случится с зеркалом со сферической поверхностью: мы очень просто найдем, что из того отражения, которое образуется всей освещенной поверхностью, лишь самая маленькая часть доходит до глаза отдельного наблюдателя, так как существует лишь малейшая частичка всей сферической поверхности, наклон которой отражает луч в определенное место, т. е. в глаз; следовательно, очень маленькой должна быть та часть сферической поверхности, которая глазу кажется блестящей, тогда как все остальное представляется темным. Значит, если бы Луна была гладкой, как зеркало, то только самая маленькая часть Луны казалась бы глазам отдельного наблюдателя освещенной Солнцем, даже если бы вся полусфера была открыта
|
Если бы Луна была подобна сферическому зеркалу, то она была бы невидима. |
Сальвиати. — Подождите, пожалуйста, синьор Сагредо, по выражению лица и жестам синьора Симпличио я замечаю, что он или не хорошо понимает, или не удовлетворен тем, что вы высказали с такой {70} очевидностью и абсолютной правильностью. Сейчас мне припомнилось, что можно другим опытом устранить всяческое его сомнение. Я видел в одной из верхних комнат большое сферическое зеркало; велим доставить его сюда, а пока его несут, пусть синьор Симпличио вернется к рассмотрению того, как велика та яркость отражения от плоского зеркала, которая ложится на стену здесь под лоджией.
Симпличио. — Я вижу, что оно лишь немногим менее ярко, чем если бы сюда прямо светило Солнце.
Сальвиати. — Это действительно так. Теперь скажите мне: если мы уберем это маленькое плоское зеркало и поставим на то же место большое сферическое зеркало, то какое действие, по вашему мнению, должно произвести его отражение на той же стене?
Симпличио. — По-моему, оно будет давать свет гораздо более сильный и шире распространенный.
Сальвиати. — А если освещенность будет равна нулю или будет такой маленькой, что вы едва ее заметите, то что вы тогда скажете?
Симпличио. — Когда я увижу такое явление, тогда и подумаю об этом.
Сальвиати. — Вот зеркало; пусть его поставят рядом с прежним. Но сначала подойдем поближе к отражению этого плоского зеркала и внимательно посмотрим на его яркость: вы видите, как светло там, куда падает его отражение, и как отчетливо видны все эти детали стены.
Симпличио. — Я видел и заметил очень хорошо; велите поставить другое зеркало рядом с первым.
Сальвиати. — Вот оно. Его поставили, как только вы начали рассматривать детали, а вы ничего и не заметили, — так сильно возросло освещение остальной стены. Теперь долой плоское зеркало. Исчезло всякое отражение, хотя и осталось большое выпуклое зеркало. Отодвигайте его, а потом придвигайте, как вам будет угодно; вы не увидите никакого изменения в освещении на всей стене. Итак, этим вам наглядно показано, как отражение Солнца от выпуклого сферического зеркала не освещает ощутительно окружающие места. Что же вы ответите теперь на этот опыт?
Симпличио. — Я боюсь, нет ли здесь какого-нибудь фокуса. Ведь рассматривая это зеркало, я вижу, что от него исходит огромный блеск, который почти слепит меня, и, — а это особенно важно, — я вижу его постоянно, с какого бы места я на него ни смотрел; я вижу также, что он меняет свое место на поверхности зеркала в зависимости от того, как я становлюсь в то или иное место, чтобы смотреть на него: необходимое доказательство того, что свет отражается очень живо во все стороны и, следовательно, так же сильно на всю эту стену, как и на мой глаз.
Сальвиати. — Теперь вы видите, с какой осторожностью и осмотрительностью надо принимать то, что нам представляет только одно рассуждение. То, что вы сказали, кажется вполне правильным, и все же вы можете видеть, что чувственный опыт показывает обратное.
Симпличио. — Так как же обстоит дело?
Сальвиати. — Я скажу вам, что думаю, и не знаю, насколько вы этим удовольствуетесь. Во-первых, столь яркое сияние, которое вы видите в зеркале и которое, как вам кажется, занимает в нем значительную часть, не так велико и не так значительно; наоборот, оно очень и очень мало; яркость же его порождается в вашем глазу благодаря отражению во влаге, распространяющейся поверх зрачка у краев век, — некое побочное сияние, подобное тому венцу, который, как нам кажется, мы видим вокруг пламени свечи с некоторого удаления; если хотите, его можно уподобить побочному блеску звезды; если вы сравните маленькое тельце, например Сириус, таким, каким он виден днем посредством телескопа, {71} т. е. без указанного излучения, с тем же самым Сириусом, видимым ночью невооруженным глазом, то вы без всякого сомнения поймете, что вместе с таким излучением оно представляется в тысячу раз бо́льшим, чем голое и реальное тельце; подобное или еще большее увеличение
|
Излучающее свет тельце звезд кажется в тысячу раз бо́льшим, чем голое. |
Симпличио. — Я чувствую себя запутавшимся больше, чем когда-либо; к этому у меня присоединяется еще и другое затруднение: как это может быть, чтобы стена, которая состоит из столь темной материи, со столь плохо выровненной поверхностью, могла отражать свет более сильно и более живо, чем зеркало, весьма гладкое и отполированное.
Сальвиати. — Нет, не более живо, но гораздо более всесторонне; ведь, поскольку речь идет о живости, вы видите, что отражение от этого маленького плоского зеркальца освещает место там под лоджией очень сильно, а остальная часть стены, получающая отражение той стены, где повешено зеркало, освещена далеко не так сильно, как та маленькая часть, куда доходит отражение от зеркала. Стремясь понять это явление в целом, примите во внимание, что если поверхность этой стены шероховата, то это означает, что она образована из бесчисленного количества
|
Свет, отраженный от шероховатых тел, более всесторонен, чем от гладких, и почему. |
|
Если бы Луна была гладкой и чистой, то она была бы невидимой. |
Симпличио. — Я очень хорошо понимаю ваше рассуждение; все же, мне кажется, его можно без большого труда опровергнуть и прекрасно оставить Луну круглой, гладкой и посылающей свет Солнца к нам наподобие зеркала; изображение Солнца не должно быть видно в середине, так как «не из-за образов самого Солнца можно видеть на столь большом расстоянии маленькую фигуру Солнца, но оно воспринимается нами через свет, исходящий от Солнца и производящий освещение всего лунного тела. Нечто подобное можем мы видеть на вызолоченной и хорошо отшлифованной пластинке: освещенная светоносным телом, она кажется смотрящему на нее издали целиком блестящей; и только вблизи наблюдается по середине ее маленькое изображение светоносного тела» {72}
Сальвиати. — Откровенно признаюсь в своем непонимании; я постиг из вашего рассуждения только то, что относится к вызолоченной пластинке; и, если вы мне позволите высказаться совершенно откровенно, я сильно подозреваю, что вы также его не понимаете, а заучили на-память эти слова, написанные кем-нибудь из желания противоречить и показаться умнее противника, показаться умнее в глазах тех слушателей, которые, желая в свою очередь иметь вид таких же умников, рукоплещут тому, чего сами не понимают, и составляют об авторе тем более
|
Некоторые писатели пишут то, чего не понимают, а потому непонятно то, что они пишут. |
|
Брильянты выделываются со многими гранями, и почему. |
|
Шлифованное серебро представляется более темным, чем нешлифованное, и почему. |
Сагредо. — Значит, если бы эти синьоры философы удовольствовались тем допущением, что Луна, Венера и другие планеты обладают не столь блестящей и гладкой поверхностью, как зеркало, но чуть только меньшей, т. е. такой, какая бывает только у отбеленной серебряной пластинки, но не у отшлифованной, то этого было бы достаточно, чтобы сделать Луну видимой и приспособленной для отражения к нам света Солнца?
Сальвиати. — Отчасти было бы достаточно, но Луна не посылала бы столь сильного света, какой она посылает, будучи гористой, словом, полной больших возвышенностей и углублений. Но наши синьоры философы никогда не согласятся допустить для Луны шлифовку, менее совершенную, чем у зеркала; в их представлении она гораздо больше, если только можно себе это вообразить, ибо, если они считают, что наиболее совершенным телам свойственны и наиболее совершенные формы, то необходимо, чтобы сферичность этих небесных тел была абсолютнейшей; кроме того, как только они мне уступят, допустив какую-нибудь, хотя бы даже самую маленькую неровность, я сейчас же подвергну величайшему подозрению, нет ли там и гораздо большей, так как если совершенство заключается в форме, то один волос нарушает его столь же, как и гора.
Сагредо. — Здесь у меня возникают два сомнения: во-первых, я не понимаю, почему большая неровность поверхности должна давать более сильное отражение света; во-вторых, почему господа перипатетики так жаждут этой точной формы?
Сальвиати. — На первое я отвечу, предоставив синьору Симпличио озаботиться ответом на второе. Итак, предварительно нужно установить, что одни и те же поверхности освещаются одним и тем же светом
|
Более шероховатая поверхность отражает свет сильнее, чем менее шероховатая. Перпендикулярные лучи освещают больше, чем косые, и почему. |
Сагредо. — Я вижу, но не понимаю причины.
Сальвиати. — Если вы подумаете об этом хотя бы сотую долю часа, то найдете ее; но, чтобы не тратить времени, вот вам маленькое доказательство на этом чертеже.
Сагредо. — Один лишь взгляд на чертеж разъяснил мне все, поэтому продолжайте.
Симпличио. — Расскажите, пожалуйста, остальное мне, так как я неспособен воспринимать так быстро.
Сальвиати. — Представьте себе, что все параллельные линии, исходящие из точек А и B, являются лучами, которые до линии CD доходят {74}
|
Косые лучи освещают меньше, и почему. |
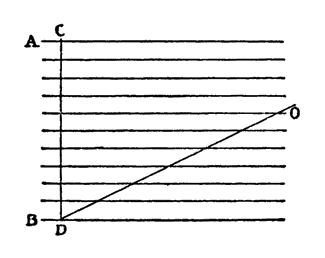 нам более блестящими, чем другие, находящиеся около окружности, а этого не наблюдается. Вообразите себе теперь лик Луны усеянным очень высокими горами; разве вы не видите, как их склоны и скаты, возвышаясь на выпуклости совершенной сферической поверхности, оказываются обращенными к Солнцу и способными воспринимать лучи гораздо менее косо, а потому казаться освещенными так же, как и остальное?
нам более блестящими, чем другие, находящиеся около окружности, а этого не наблюдается. Вообразите себе теперь лик Луны усеянным очень высокими горами; разве вы не видите, как их склоны и скаты, возвышаясь на выпуклости совершенной сферической поверхности, оказываются обращенными к Солнцу и способными воспринимать лучи гораздо менее косо, а потому казаться освещенными так же, как и остальное?
Сагредо. — Все это хорошо. Действительно, если там существуют такие горы, то Солнце будет освещать их гораздо более прямо, чем наклонные ровные поверхности, но правда и то, что между этими горами останутся темными все долины вследствие громаднейших теней, которые исходят в это время от гор; средние же части, хотя они и полны гор и долин, останутся без теней, раз Солнце над ними высоко, и потому будут гораздо более светлыми, чем крайние части, где тени не меньше, чем света: все же мы не наблюдаем такого различия.
Симпличио. — Подобная трудность возникла и в моем воображении.
Сальвиати. — Насколько более скор синьор Симпличио в понимании тех трудностей, которые благоприятствуют мнениям Аристотеля, чем тех, которые его опровергают! Но я подозреваю, что, даже имея доказательство, он хочет иногда умолчать о нем; и в данном частном случае, раз он сам мог найти возражение, все же очень остроумное, я не могу поверить, чтобы он не предусмотрел также и ответа, а потому я попытаюсь, как говорится, вырвать его у него изо рта. Поэтому скажите мне, синьор Симпличио, полагаете ли вы, что может быть тень там, куда падают лучи Солнца?
Симпличио. — Я полагаю, и даже вполне уверен, что нет, так как раз Солнце является величайшим источником света, прогоняющим своими лучами тьму, то невозможно, чтобы там, куда оно достигает, было темно; к тому же мы имеем определение: tenebrae sunt privatio luminis33.
Сальвиати. — Значит, Солнце, глядя на Землю, или на Луну, или на другое непрозрачное тело, никогда не видит ни одной из их частей затемненной, раз у Солнца нет других глаз, чтобы смотреть, кроме своих лучей, носителей света; и следовательно, находящийся на Солнце никогда не видел бы ничего затененного, так как его зрительные лучи всегда шли бы в обществе освещающих солнечных лучей.
Симпличио. — Это совершенно правильно, без всякого сомнения.
Сальвиати. — А когда Луна находится в противостоянии с Солнцем, какое различие существует между путем лучей вашего зрения и путем лучей Солнца?
Симпличио. — Теперь я понял; вы хотите сказать, что если лучи зрения и лучи Солнца идут по одним и тем же линиям, то мы не сможем открыть ни одной затемненной долины на Луне. Пожалуйста, не думайте, чтобы я был притворщиком или обманщиком; даю вам слово дворянина, {75} что я не предвидел такого ответа и, может быть, не нашел бы его без вашей помощи или без долгих размышлений.
Сагредо. — Решение, которое вы нам обоим привели относительно этой последней трудности, действительно, удовлетворило также и меня; но в то же время то обстоятельство, что зрительные лучи идут вместе с лучами Солнца, пробудило во мне сомнение другого рода; не знаю только, смогу ли я его объяснить, так как оно возникло у меня только сейчас, и я сам для себя не привел его еще в порядок; попробуем же вместе выяснить его. Нет никакого сомнения, что части близ окружности гладкой, но неотшлифованной полусферы, освещаемой Солнцем, воспринимают лучи косо и потому получают их значительно меньше, чем средние части, получающие их прямо; и может случиться, что полоса шириной, например, в двадцать градусов близ края полусферы получит не больше лучей, чем другая полоса около середины, шириной всего около четырех градусов; значит, первая на самом деле будет много темнее второй; таковыми они покажутся всякому, кто наблюдает их обе прямо перед собой и видит их, так сказать, в лицо. Но если глаз зрителя будет находиться в таком месте, что темная полоса шириной в двадцать градусов будет представляться ему не шире полосы в четыре градуса, находящейся по середине полусферы, то я не считаю невероятным, что она может ему показаться такой же светлой и освещенной, как и другая; ведь в конце концов под двумя равными углами, т. е. в четыре градуса каждый, идут к глазу отражения двух равных количеств лучей, именно тех, которые отражаются от средней полосы шириной в четыре градуса, и тех, которые отражаются от второй полосы в двадцать градусов, но видимой в перспективном освещении величиной в четыре градуса; а такое место займет глаз, если будет находиться между названной полусферой и освещающим ее телом, так как тогда зрение и лучи идут по одним и тем же линиям. Таким образом, не является невероятным допущение, что Луна может обладать очень ровной поверхностью и тем не менее в полнолуние казаться нам не менее светоносной по краям, чем в средних частях.
Сальвиати. — Сомнение остроумное и заслуживает рассмотрения; и как оно только что внезапно возникло у вас, так и я отвечу то, что внезапно пришло мне на ум; может быть, если бы я подумал больше, то нашел бы и лучший ответ. Но прежде чем я выскажу что-нибудь по этому поводу, хорошо было бы нам удостовериться опытом, соответствует ли ваше возражение фактам в такой мере, в какой оно кажется убедительным по видимости. Поэтому возьмем снова ту же самую бумагу, придадим ей наклон, согнув маленькую часть над остальным листом, и посмотрим: если выставить ее на свет так, чтобы на меньшую часть лучи света падали прямо, а на другую — косо, то покажется ли та, которая получает прямые лучи, более светлой. Так вот, опыт показывает, что она освещена заметно больше. Значит, если бы ваше возражение было правильно, то должно было бы получиться следующее: при понижении нашего глаза до такого положения, когда при взгляде на большую, менее освещенную часть она казалась бы нам в перспективном сокращении не шире другой более освещенной части и, следовательно, была бы видна не под большим углом, чем первая, освещенность ее должна была бы возрасти настолько, что она показалась бы нам такой же светлой, как и другая часть. Вот я смотрю на нее и вижу ее так косо, что она мне кажется уже другой; но при всем том ее темнота для меня ничуть не становится светлее. Теперь посмотрите, не получится ли то же самое у вас?
Сагредо. — Я видел; и хотя я опускаю глаз, я не замечаю, чтобы данная поверхность от этого больше освещалась или просветлялась; наоборот, мне кажется скорее, что она становится темнее. {76}
Сальвиати. — Значит, пока мы удостоверились в несостоятельности возражения. Что же касается объяснения, то я думаю следующее: так как поверхность этой бумаги не совершенно ровна, то лишь очень немного лучей отражается в направлении падающих лучей по сравнению с тем множеством, которое отражается в противоположные стороны, а из этих немногих всегда теряется тем больше, чем больше приближаются зрительные лучи к этим светоносным отраженным лучам; и так как не падающие лучи, а отражающиеся в глазу заставляют казаться предмет освещенным, то при понижении глаза больше теряется, чем приобретается, как это показалось и вам самим, когда вы видели лист более темным.
Сагредо. — Я удовлетворен опытом и объяснением. Теперь синьору Симпличио остается ответить мне на мой второй вопрос, разъяснив, что именно побуждает перипатетиков жаждать столь точной шарообразности в небесных телах.
Симпличио. — Раз небесные тела не рождены, неуничтожаемы,
|
Почему перипатетиками признается совершенная сферичность небесных тел. |
Сальвиати. — А откуда берете вы эту неуничтожаемость?
Симпличио. — Непосредственно — из отсутствия обратного, и посредственно — из простого кругового движения.
Сальвиати. — Таким образом, насколько я заключаю из вашего рассуждения, при установлении сущности небесных тел, как то: неуничтожаемости, неизменности и т. д., вы не вводите сферическую форму в качестве причины или необходимого реквизита; ведь если бы она являлась причиной неуничтожаемости, то мы могли бы сделать по своему усмотрению неуничтожаемыми воск, дерево и другие элементарные материи, придав им сферическую форму.
Симпличио. — А разве не очевидно, что деревянный шар лучше и дольше сохраняется, чем пирамида или другая фигура с углами, сделанная из такого же количества того же самого дерева?
Сальвиати. — Это совершенно правильно, но от этого она из уничтожаемой
|
Форма не является причиной неуничтожаемости, а только большей продолжительности существования. Разрушаемость может быть большей и меньшей, но не неуничтожаемость. |
|
Совершенство формы оказывает влияние в разрушаемых телах, но не в вечных. |
Сагредо. — Я иду еще дальше и говорю: если допустить, что сферическая форма обладает свойством сообщать неуничтожаемость, то все
|
Если бы сферическая форма сообщала вечность, то все тела были бы вечными. |
Сальвиати. — Ход мыслей прекрасен; таким образом, если, например, сферический хрусталь должен быть неуничтожаемым, т. е. обладать способностью противостоять всем внутренним и внешним изменениям в силу своей формы, то непонятно, почему от прибавления к нему другого хрусталя и приведения его, например, к форме куба он должен меняться и внутри, а не только снаружи, и должен стать менее устойчивым по отношению к новому окружению, состоящему из той же самой материи, чем к прежнему из отличной от него материи, в особенности, если разрушение действительно образуется противоположностями, как говорит Аристотель; а чем еще менее противоположным, как не самим хрусталем, можно окружить этот хрустальный шар? Но мы не замечаем, как бегут часы; поздно придем мы к концу наших рассуждений, если по поводу каждой частности будут происходить у нас столь длинные разговоры. Кроме того, память так запутывается во множестве вопросов, что я с трудом могу припомнить те положения, которые по порядку предлагал для рассмотрения синьор Симпличио.
Симпличио. — Я отлично помню их; в частности, по вопросу о гористости Луны остается еще в полной силе мое объяснение; его прекрасно можно спасти, сказав, что это — иллюзия, происходящая от того, что части Луны неодинаково прозрачны.
Сагредо. — Немного раньше, когда синьор Симпличио приписывал видимую неодинаковость Луны, в согласии с мнением своего друга, известного перипатетика, различно прозрачным и непрозрачным частям этой Луны, подобно тому, как такие же иллюзии наблюдаются в хрустале и драгоценных камнях многих сортов35, я вспомнил об одной материи, гораздо более удобной для иллюстрации таких явлений, о такой материи, за которую, как я уверен, этот философ заплатил бы какую угодно цену: это — перламутр; при обработке ему придают разные формы,
|
Перламутр способен подражать видимым неодинаковостям поверхности Луны. |
Сальвиати. — Поистине прекрасная мысль; и что не было сделано до сих пор, должно быть сделано в другой раз; и если приводились как пример другие драгоценные камни и хрусталь, не имеющие ничего общего с иллюзиями перламутра, то хорошо будет привести и его. Однако, не желая никого лишать возможности найти подходящий ответ, я пока умолчу о нем и попытаюсь только устранить сейчас возражения, выдвинутые синьором Симпличио. Я говорю, что ваше объяснение имеет слишком общий характер, и так как вы не применяете его последовательно ко всем явлениям, наблюдаемым на Луне и принуждающим меня и других считать ее гористой, то я не думаю, чтобы вы могли найти много людей, готовых удовлетвориться таким учением; я думаю также, что ни вы, ни сам автор не найдут в нем большего успокоения, чем в любом другом, далеком от вашего мнения. Из многих и многих различных явлений, которые
|
Видимым неровностям Луны нельзя подражать при помощи более или менее прозрачной и непрозрачной материи. Различные виды Луны доступны подражанию любой непрозрачной материей. |
|
Различные явления, которыми доказывается гористость Луны. |
Сагредо. — За исключением одного, чему все же можно подражать, — полнолуния, так как тогда все освещено и не видно ни теней, ни прочих изменений, происходящих от возвышенностей и впадин. Но, пожалуйста, синьор Сальвиати, не теряйте больше времени на эту частность, так как всякого, кто имел терпение производить наблюдения в течение одного или двух лунных месяцев и не убедился в этой очевиднейшей истине, нужно считать совершенно лишенным разума; а к чему с подобными людьми напрасно тратить время и слова?
Симпличио. — Действительно, я не производил этих наблюдений, так как у меня не было ни любознательности, ни такого инструмента, при помощи которого их можно произвести, но в будущем я хочу заняться ими; пока же мы можем оставить этот вопрос нерешенным и перейти к следующему пункту, занявшись доводами, в силу которых вы считаете, что Земля может отражать свет Солнца не менее сильно, чем Луна, тогда как мне Земля кажется настолько темной и непрозрачной, что подобное явление представляется совершенно невозможным.
Сальвиати. — Причина, в силу которой вы считаете Землю неспособной освещать, совершенно не та, синьор Симпличио. Но хорошо ли будет, если я проникну в суть ваших рассуждений лучше, чем вы сами?
Симпличио. — Хорошо или плохо я рассуждаю, это, может быть, вы знаете лучше меня; но, хорошо ли, плохо ли я рассуждаю, я никогда не поверю, чтобы вы могли лучше меня проникнуть в суть моих рассуждений.
Сальвиати. — И все же я вас заставлю этому поверить. Скажите мне: если Луна почти что полная, так что ее можно видеть и днем, и среди ночи, то когда она кажется вам более яркой — днем или ночью?
Симпличио. — Ночью, без всякого сомнения; и мне кажется, что
|
Ночью Луна кажется более сияющей, чем днем. |
|
Луна, видимая днем, подобна облачку. |
Сальвиати. — Так что, если бы вам никогда не случалось видеть Луну иначе, как только днем, вы считали бы ее не ярче того облачка?
Симпличио. — В этом я совершенно уверен. {79}
Сальвиати. — Скажите мне теперь: думаете ли вы, что Луна действительно более блестяща ночью, чем днем, или же что она кажется более блестящей в силу какого-нибудь обстоятельства?
Симпличио. — Я думаю, что в действительности Луна сама по себе сияет днем так же, как и ночью; но ночью свет ее кажется бо́льшим, так как тогда мы видим ее на темном фоне неба; а днем, когда все окружающее очень светло, она лишь немного превосходит фон по свету и представляется нам менее блестящей.
Сальвиати. — Теперь скажите мне: видели ли вы когда-нибудь среди ночи земной шар освещенным Солнцем?
Симпличио. — Такой вопрос, мне кажется, можно задать только в шутку или же тому, кого принимают за совершенного глупца.
Сальвиати. — Совсем нет, я считаю вас человеком очень разумным и задаю вопрос всерьез; поэтому отвечайте же, а если потом вам покажется, что я говорю не относящееся к делу, то я готов буду признать глупцом себя; ведь гораздо глупее тот, кто глупо спрашивает, чем тот, кого спрашивают.
Симпличио. — Если, значит, вы не считаете меня совершенным простаком, то учтите, что я вам должен ответить, а именно: невозможно для находящегося на Земле, — а таковы именно мы, — видеть ночью ту часть Земли, где день, т. е. куда падает свет Солнца.
Сальвиати. — Значит, вам никогда не приходилось видеть Землю освещенной иначе, как только днем, а Луну вы видите сияющей на небе даже самой глубокой ночью; это, синьор Симпличио, и является причиной, заставляющей вас думать, что Земля не сияет, как Луна; ведь если бы вы могли видеть Землю освещенной, сами находясь в это время в темном, как у нас ночью, месте, то вы увидели бы ее сияющей больше Луны. Итак, если вы хотите чтобы сравнение протекало правильно, то нужно проводить параллель между светом Земли и светом Луны, видимой днем, а не ночью, так как нам не приходится видеть Землю освещенной иначе, как только днем. Разве не так?
Симпличио. — Конечно, так.
Сальвиати. — А раз вы сами уже признались, что видели Луну днем среди белесоватых облачков и чрезвычайно похожей по виду на одно из них,
|
Облака способны освещаться Солнцем не меньше Луны. |
Сагредо. — Но к чему еще другие рассуждения? Вон там наверху Луна, а вот здесь — высокая стена, освещенная Солнцем; отступите
|
Освещенная Солнцем стена по сравнению с Луной блестит не меньше ее. Больше освещает третье отражение солнечного света от стены, чем первое от Луны. |
Симпличио. — О, этого я не думаю, так как свет Луны, в особенности, когда она полная, освещает очень сильно.
Сагредо. — Он кажется сильным из-за мрака окружающих темных мест, но абсолютно он невелик и меньше света сумерек через полчаса
|
Свет Луны слабее света сумерек. |
Сальвиати. — Теперь, синьор Симпличио, вы можете понять (если только вы удовлетворены), что вы действительно сами уже знали то, что Земля блестит не меньше Луны; одно лишь напоминание о некоторых вещах, уже известных вам, а не преподанных мною, убедило вас в этом; ведь не я учил вас, что Луна кажется более блестящей ночью, чем днем,— это вы знали сами; вы знали также, что облачко кажется таким же светлым, как и Луна; вы знали равным образом, что освещенность Земли не видна ночью, словом, вы знали все, не сознавая, что знаете это. Отсюда, разумно рассуждая, вам не должно представиться затруднительным допустить, что отражение Земли может освещать темную часть Луны не меньшим светом, чем тот, которым Луна озаряет ночной мрак, а наоборот, гораздо большим, поскольку Земля в сорок раз больше Луны.
Симпличио. — Действительно, я думал, что вторичный свет — это собственный свет Луны.
Сальвиати. — Также и это вы знаете сами, но не замечаете, что знаете. Скажите мне: разве вы сами не знали, что Луна кажется ночью
|
Освещенные тела кажутся более светлыми при темном окружении. |
Симпличио. — Это я знаю прекрасно.
Сальвиати. — Когда Луна имеет вид серпа и вам кажется очень светлым этот вторичный свет, то разве она в это время не близка всегда к Солнцу и, следовательно, видна во время сумерек?
Симпличио. — Именно, и много раз я жаждал, чтобы стало темнее, дабы можно было видеть этот свет более ярким, но Луна заходила до наступления темной ночи.
Сальвиати. — Значит, вы прекрасно знаете, что глубокой ночью этот свет представлялся бы гораздо более сильным?
Симпличио. — Да, синьор, и еще более сильным, если бы можно было убрать большой свет рогов, тронутых Солнцем: присутствие их весьма помрачает другой, меньший свет.
Сальвиати. — А не случается ли иногда так, что можно видеть среди самой темной ночи весь диск Луны, совершенно не освещенный Солнцем?
Симпличио. — Я не знаю, случается ли это когда-нибудь, разве только при полном затмении Луны.
Сальвиати. — Тогда, значит, этот ее свет должен был бы казаться особенно живым, так как тогда он является на совершенно темном фоне и не омрачен яркостью светоносных рогов; но сколь сильно блестящей видели вы ее в этом положении?
Симпличио. — Я видел ее иногда цвета меди и слегка беловатой, а иногда она становилась такой темной, что я совершенно терял ее из вида36.
Сальвиати. — Так как же может быть ее собственным светом тот, который вы видите столь ярким в белизне сумерек, несмотря на большой {81} и смежный блеск рогов, и который потом, в самую темную ночь, когда отсутствует всякий другой свет, совершенно не появляется?
Симпличио. — Я слышал мнение, что этот свет Луна заимствует от других звезд, в частности от Венеры, своей соседки.
Сальвиати. — И это равным образом вздорно, так как во время своего полного затмения она все же должна была бы казаться более блестящей, чем когда-либо; ведь нельзя же утверждать, что тень Земли заслоняет от нее Венеру или другие звезды, а света она в это время лишается потому, что на обращенной в это время к Луне земной полусфере как раз царит ночь, т. е. полное отсутствие света Солнца. При тщательных наблюдениях вы отчетливо увидите, что Луна, когда она имеет форму тонкого серпа, совсем мало освещает Землю, и что по мере того, как на ней растет освещенная Солнцем часть, растет для нас и блеск, который от нее доходит к нам отраженным; так же и Луна представляется нам очень светлой, когда она имеет форму тонкого серпа и из-за своего положения между Солнцем и Землей видит очень значительную часть земной полусферы освещенной; при удалении же от Солнца и приближении к квадратуре этот свет все уменьшается и за квадратурой виден очень слабым, так как тогда все больше теряется из вида светоносная часть Земли; обратное должно было бы происходить, если бы этот свет был ее собственным или если бы он был сообщен ей звездами, так как тогда мы могли бы видеть его глубокой ночью и при очень темном окружении.
Симпличио. — Остановитесь, пожалуйста, так как я только что вспомнил, как читал в одной современной книжке заключений37, полной многих новостей, «что этот вторичный свет не порожден звездами,
|
По мнению некоторых, вторичный свет Луны порожден Солнцем. |
Сальвиати. — Если бы этот философ был первоначальным автором данного мнения, то я не удивился бы его влюбленности в собственное мнение, заставляющей считать его истинным. Но, поскольку он получил это мнение от других, я не могу найти достаточных оснований для его извинения, ибо он не понял ошибочности этого объяснения даже после того, как слышал об истинной причине такого явления и мог тысячью опытов и очевидных совпадений удостовериться в том, что вторичный свет происходит от отражения Земли и ни от чего другого. Знание всего этого заставляет предъявлять большие требования к проницательности нашего автора и всех других, не признающих открыто такого объяснения, тогда как отсутствие подобного знания является в моих глазах достаточным извинением для более старых авторов; я совершенно уверен, что, познакомившись с нашим объяснением, они без всякого колебания приняли бы его. Если мне будет позволено высказаться вполне откровенно, я не могу поверить, чтобы наш современный автор не верил этому объяснению; я подозреваю, что, не имея возможности приписать его открытия себе, он пытается унизить или опозорить его по крайней мере в главах простаков, число которых, как мы знаем, огромно; очень многие гораздо больше радуются одобрению толпы, чем признанию со стороны немногих незаурядных людей.
Сагредо. — Подождите немного, синьор Сальвиати; по-моему, ваша речь не прямо бьет в цель: ведь тот, кто раскидывает сети для уловления большинства, сумеет также выдать себя и за автора чужих открытий, разве только эти открытия настолько стары и так разглашены с кафедр и площадей, что более чем хорошо всем известны.
Сальвиати. — О, я еще худшего мнения, чем вы. Что говорите вы
|
Одно и то же: мнения ли новы для людей или люди новы для мнений. |
|
Вторичный свет Луны проявляется в форме кольца, т. е. он ярок у края окружности, а не по середине, и почему. |
|
Способ наблюдения вторичного света Луны. |
Симпличио. — Однако, мне помнится, будто он писал, что пользовался подобным ухищрением, чтобы скрыть от себя сияющий серп.
Сальвиати. — О, если это так, то то, что я считал невнимательностью с его стороны, становится ложью, граничащей даже с наглостью, так как каждый может повторять этот опыт сколь угодно часто. А что {83}
|
Диск Луны при затмениях Солнца можно видеть только из-за отсутствия света. |
|
Автор книжки заключений приспосабливает вещи к своим положениям, а не положения к вещам. |
Сагредо. — Вы приводите мне на память случай с одним изобретателем, который предлагал продать секрет изобретения, дающего возможность
|
Шутка, сыгранная с человеком, желавшим продать секрет того, как можно разговаривать с кем-нибудь на расстоянии тысячи миль. |
Сальвиати. — Именно находящиеся на Луне горы свидетельствуют об этом, ибо, озаренные с одной стороны Солнцем, они бросают в противоположную сторону густые тени, более определенные и резкие, чем наши тени. Если бы они были прозрачными, то мы не могли бы заметить никаких неровностей на поверхности Луны и не могли бы видеть освещенных вершин, отделенных от той грани, которая разделяет освещенные части от неосвещенных; равным образом мы не видели бы так отчетливо эту грань, если бы в самом деле солнечные лучи проникали в глубь Луны. В силу сказанного автором переход и границу между освещенными и неосвещенными частями следовало бы также видеть неопределенными и состоящими из смеси света и мрака, ибо необходимо признать, что такое вещество, которое пропускает солнечные лучи на глубину двух тысяч миль, уничтожает всякое различие, происходящее от разницы в одну сотую или еще меньшую часть такой глубины; а между тем граница, разделяющая освещенную и неосвещенную части, явственна и настолько резка, насколько резко отличие белого от черного, в особенности там, где эта граница проходит по той части Луны, которая является по природе более яркой и более неровной; там же, где находятся издавна известные пятна, которые суть равнины, идущие со сферическим наклоном и получающие таким образом солнечные лучи более косвенно, граница теряет свою резкость благодаря более слабому освещению. Наконец, то, что вторичный свет Луны, по вашим словам, не уменьшается и не ослабевает по мере роста Луны, но постоянно сохраняет ту же силу, ложно; свет мало заметен в квадратурах, когда, наоборот, он должен был бы казаться более ярким, ибо тогда мы могли бы видеть его не только в сумерках, но и среди темной ночи. Итак, мы можем притти к заключению, что отражение Земли чрезвычайно значительно на Луне; особенно заслуживает вашего внимания то, что отсюда можно почерпнуть другое прекраснейшее совпадение, а именно: если правда то,
|
Земля может воздействовать светом на небесные тела. |
Симпличио. — Вам не найти ни одного философа, который говорил бы, что низшие тела действуют на тела небесные. Аристотель же утверждает прямо противоположное.
Сальвиати. — Аристотель и другие, которые не знали, что Земля и Луна взаимно освещают друг друга, достойны извинения, но заслуживают порицания те, которые, требуя, чтобы, мы признали и поверили им, что Луна действует на Землю своим светом, и допуская вместе с нами, что Земля освещает Луну, отрицают возможность воздействия Земли на Луну.
Симпличио. — В результате я все же крайне нерасположен к признанию возможности тех взаимоотношений Луны и Земли, в существовании которых вы хотите меня убедить, ставя последнюю, так сказать, на одну доску со звездами. Как бы то ни было, но обособленность и большое расстояние, отделяющее ее от небесных тел, как мне кажется, должны привести к огромной между ними разнице.
Сальвиати. — Видите ли, синьор Симпличио, это — старая привязанность к установившемуся мнению; оно настолько прочно укоренилось, что те факты, которые вы сами приводите против себя, кажутся вам подтверждающими его. Если обособленность и удаление являются {85} факторами, достаточными для того, чтобы вызвать большие различия в природе, то, наоборот, смежность и близость должны вызывать подобие; а разве Луна не ближе к Земле, чем любое из других небесных тел? Признайте
|
Сродство между Землей и Луной в зависимости от близости. |
Симпличио. — Вряд ли остается еще что-либо по вопросу о твердости Луны, о которой я утверждал, что она гладка и полирована, а вы,— что она гориста. Другое, возникшее у меня затруднение, вытекало из убеждения, что отражение моря должно быть вследствие своей ровной поверхности более светлым, чем отражение от земли, поверхность которой неровна и непрозрачна.
Сальвиати. — Относительно первого сомнения я скажу, что из частиц Земли, которые в силу своей тяжести все стремятся приблизиться насколько возможно к центру, некоторые все же остаются более удаленными от него, чем другие; например, горы более удалены, чем равнины, что происходит от их прочности и твердости (ибо если бы они состояли из материи жидкой, то они выровнялись бы); точно так же то, что некоторые части Луны остаются приподнятыми над сферической поверхностью
|
Твердость лунного тела доказывается тем, что оно гористо. |
|
Отражение света от моря гораздо слабее, чем от земли. |
|
Опыт, показывающий, что отражение воды менее светло, чем отражение земли. |
Симпличио. — Отсюда я вижу мокрую часть более светлой, чем остальной пол, и вижу также, что это происходит оттого, что свет, падающий из окна, отражается по направлению ко мне.
Сальвиати. — Налитая вода не делает ничего другого, кроме того, что заполняет мельчайшие углубления, которые имеются на плитах, и превращает их поверхность в совершенную плоскость, от которой отражающиеся лучи идут вместе к одному и тому же месту; остальной пол, оставшийся сухим, сохраняет свою неровность, т. е. бесконечное разнообразие наклонов мельчайших частиц, откуда отражающиеся световые лучи идут в разные стороны более слабыми, чем если бы они шли вместе, а потому он мало или вовсе не изменяется по внешнему виду при наблюдении с разных точек; изо всех мест он кажется одинаковым и притом менее светлым, чем то прямое отражение от мокрого места. Отсюда заключаем, что поверхность моря, видимая с Луны, представлялась, за исключением островов и скал, совершенно ровной и в то же время менее светлой, чем поверхность гористой и неровной Земли. Если бы я не боялся показаться желающим слишком многого, то сказал бы вам, что по моим
|
Вторичный свет Луны ярче перед соединением, чем после него. |
Симпличио40. — «Итак, по вашему мнению, Земля должна по виду казаться такой же, как обе основные части поверхности, которые мы различаем на Луне». Но полагаете ли вы, что те большие пятна, которые замечаются на лунном лике, действительно моря, а остальная более светлая часть — суша или ее подобие?
Сальвиати. — То, о чем вы спрашиваете, является главным различием, которое я нахожу между Луной и Землей, на которую нам пора спуститься, ибо, пожалуй, мы слишком долго оставались на Луне. Итак, я говорю, что если бы в природе не существовало иных причин, по которым две поверхности, освещенные Солнцем, казались бы одна светлее другой, кроме той, что одна есть поверхность земли, другая — поверхность воды, то необходимо пришлось бы признать, что поверхность Луны состоит частью из земли, частью из воды, но так как нам известно много причин, могущих давать такие же эффекты, и, вероятно, еще большее число их остается нам неизвестными, я не возьму на себя смелость утверждать, что то и другое должно существовать на Луне. Мы уже видели ранее, как пластинка отбеленного серебра после полировки и шлифовки превращается из светлой в темную, мокрая часть земли представляется более темной, чем сухая; горы в части, покрытой лесами, кажутся более темными, чем голые и бесплодные; последнее происходит от того, что на лесистые склоны падает множество теней, тогда как голые места залиты Солнцем; эта примесь тени действует таким же образом, какой вы можете видеть на узорчатом бархате: подстриженный шелк кажется гораздо более темным, чем неподстриженный, вследствие теней, рассеянных между отдельными ворсинками; равным образом, простой бархат много темнее эрмизина, сотканного из того же шелка41, так что если бы на Луне существовало нечто, подобное огромнейшим лесам, то по виду они могли бы представляться нам теми пятнами, которые мы наблюдаем; такое же различие было бы и в том случае, если бы они были морями; и, наконец, не исключается возможность, что эти пятна в действительности более темного цвета, чем остальное, вроде того, как снег делает горы более светлыми. Во всяком случае, ясно видно, что на Луне части, более темные, — это равнины с немногими, но все же встречающимися
|
Более темные части Луны — ровные, а более светлые — гористые. Вокруг лунных пятен тянутся длинные цепи гор. |
|
На Луне зарождаются вещи, не подобные нашим, а чрезвычайно отличные, если только там существует зарождение. |
|
Луна не состоит из земли и воды. |
|
Положения Солнца, необходимые для наших зарождений, не таковы на Луне. |
|
Естественный день на Луне длится один месяц. |
|
На Луне Солнце понижается и повышается с paзницей в 10 градусов, а на Земле — в 47 градусов. |
|
На Луне не бывает дождей. |
Сагредо. — На это можно было бы возразить, что или там бывают сильнейшие росы, или что дожди идут там во время ночей, т. е. когда Солнце не освещает Луну.
Сальвиати. — Если бы в силу других совпадений у нас были указания, что на Луне происходят рождения, подобные нашим, и отсутствовало бы только содействие дождей, то мы могли бы найти то или другое средство для замены их, как это происходит в Египте с разливами Нила. Но раз из многих условий, необходимых для произведения подобных явлений, мы не встречаем ни одного, которое совпадало бы с нашими, то не приходится стараться ввести одно единственное, могущее быть допущенным, и то не в силу достоверного наблюдений, а просто в силу отсутствия возражений. Кроме того, если бы меня спросили, что именно диктуют мне первое впечатление и чистое естественное рассуждение о возникающих там вещах, похожи ли они на наши или же отличны от них, то я всегда отвечу, что они совершенно отличны и для нас совершенно невообразимы, и это, как мне кажется, соответствует богатству природы и всемогуществу создателя и правителя.
Сагредо. — Крайней дерзостью всегда казалось мне стремление сделать человеческую способность разумения мерой того, что природа может и умеет сотворить, тогда как, наоборот, нет ни одного явления в природе, как бы мало оно ни было, к полному познанию которого могли бы притти самые глубокомысленные умы, Эта столь вздорная претензия
|
Никогда ничего не поняв в совершенстве, некоторые думают, что понимают все. |
Сальвиати. — Рассуждение ваше чрезвычайно убедительно; в подтверждение его у нас есть опыт тех, которые понимают или не понимали чего-нибудь: чем более они мудры, тем скорее они сознают и тем искреннее признают, что знают мало; и самый мудрый человек Греции, признанный оракулами, открыто говорил, что он знает только то, что ничего не знает.
Симпличио. — Приходится, значит, сказать, что или оракул, или сам Сократ был лжецом, так как первый считает его самым мудрым, а второй говорит, что признается в своем полном незнании.
Сальвиати. — Отсюда не вытекает ни то, ни другое, так как оба изречения могут быть истинными. Оракул признает Сократа мудрейшим
|
Вещание оракула правильно, когда он признает Сократа мудрейшим |
Сагредо. — Мне кажется, я прекрасно понимаю это положение. У людей, синьор Симпличио, есть власть действовать, но она не в одинаковой степени причастна всем; и, несомненно, могущество императора гораздо больше могущества частного лица; но и то, и другое — ничто по сравнению с всемогуществом божиим. Среди людей одни понимают земледелие лучше, чем многие другие; но что общего между умением посадить виноградный черенок в яму и умением заставить его пустить корни, извлекать питание, из последнего выделить части — одну, пригодную для образования листьев, другую — для формирования побегов, третью — для гроздьев и еще другие для сока или кожицы, — т. е. со всем тем, что творит мудрейшая природа? А это лишь один пример из
|
Божественное знание бесконечное число раз бесконечно. |
Сальвиати. — А вот и другой пример. Не говорим ли мы, что умение открыть в куске мрамора прекраснейшую статую вознесло гений
|
Возвышенный гений Буонаротти. |
Сагредо. — И чем, по-вашему, отличается голубь Архита от природного голубя?43.
Симпличио. — Или я не принадлежу к числу понимающих людей, или в этом вашем рассуждении имеется явное противоречие. Из всех способностей, приписываемых человеку, созданному природой, вы ставите выше всего присущий ему дар познания, а немного раньше вы {89} говорили вместе с Сократом, что его познание было ничтожно; следовательно, нужно сказать, что даже природа не уразумела способа создать разум, способный к познанию.
Сальвиати. — Вы очень остроумно возражаете; для ответа на ваше замечание приходится прибегнуть к философскому различению и сказать, что вопрос о познании можно поставить двояко: со стороны интенсивной
|
Человек многое разумеет интенсивно, но мало разумеет экстенсивно. |
Симпличио. — По-моему, это сказано очень решительно и смело.
Сальвиати. — Это — общие положения, далекие от всякой тени дерзости или смелости; они не наносят никакого ущерба величию божественной мудрости, как совершенно не умаляет его всемогущества утверждение, что бог не может сделать созданное несозданным. Но я подозреваю, синьор Симпличио, что вы боитесь моих слов потому, что поняли их не совсем правильно. Поэтому для лучшего разъяснения моей мысли я скажу следующее. Истина, познание которой нам дают математические доказательства, та же самая, какую знает и божественная мудрость; но я охотно соглашаюсь с вами, что способ божественного познания
|
Способ познания бога отличен от способа познания у людей. |
|
Человек идет к познанию путем рассуждения. |
|
Определения охватывают потенциально все свойства определяемых вещей. Бесконечное число свойств, может быть, составляет одно единственное свойство. |
|
Переходы, которые человеческое рассуждение осуществляет во времени, божественный разум осуществляет мгновенно. |
Сагредо. — Я много раз наедине с собой размышлял по поводу только
|
Удивительная острота гения человеческого. |
|
Изобретение письма изумительнее всех других изобретений. |
| << | {91} | >> |

Сальвиати. — Во время вчерашней беседы у нас было так много разнообразных отклонений от прямого пути наших основных рассуждений, что без вашей помощи я, пожалуй, не сумею вернуться на их след для того, чтобы итти далее.
Сагредо. — Я не удивляюсь, что вы, стараясь запомнить и удержать в голове как все то, что уже было сказано, так и то, что остается еще сказать, находитесь теперь в затруднении. Но я, будучи простым слушателем, удержал в памяти лишь услышанное и потому, вероятно, смогу, припомнив все это в самой общей форме, восстановить основную нить рассуждения.
Итак, если память мне не изменяет, главная тема вчерашних рассуждений заключалась в исследовании двух мнений и того, какое из них более вероятно и обосновано: то ли, которое считает субстанцию небесных тел невозникающей, неуничтожаемой, неизменной, непреходящей, словом, свободной от всякой перемены, за исключением перемены места, а потому признает существование пятой стихии, весьма отличной от наших стихий, образующих земные тела, возникающие, уничтожаемые, изменчивые и т. д., или другое, которое отрицает такое различие частей вселенной и считает, что Земля наделена тем же самым совершенством, как и другие тела, входящие в состав вселенной, т. е. является подвижным и блуждающим шаром, подобным Луне, Юпитеру, Венере и другим планетам. Напоследок приводилось много частных параллелей между Землей и Луной, именно Луной, а не другой планетой, может быть, потому, что по причине меньшей удаленности мы имеем о ней больше сведений, почерпнутых из чувственного опыта. Так как в конце концов мы пришли к заключению, что это второе мнение вероятнее первого, то, мне кажется, дальнейший наш путь должен заключаться в исследовании того, должно ли считать Землю неподвижной, как до сих пор думает большинство, или же подвижной, как думали некоторые античные философы и как полагают некоторые современные; и если Земля подвижна, то каким может быть ее движение.
Сальвиати. — Теперь я понимаю и узнаю направление нашего пути. Но прежде, чем итти дальше, я должен вам кое-что заметить по поводу ваших последних слов, будто мы пришли к тому выводу, что мнение, считающее Землю одаренной теми же самыми свойствами, что и небесные тела, более вероятно, чем противоположное. Я не делал такого вывода, как не собирался поддерживать ни то, ни другое из этих противоположных мнений; моим намерением было привести те доводы и возражения, доказательства и опровержения, которые до сих пор {92} выставлялись с обеих сторон другими, а также и еще некоторые, которые по длительном размышлении на эту тему пришли мне в голову; решение же я предоставляю другим.
Сагредо. — Меня увлекло мое собственное чувство. Думая, что с другими должно происходить то же самое, что и со мной, я сделал общий вывод, тогда как должен был сделать частный. Действительно, я допустил ошибку, тем бо́льшую, что не знаю взглядов присутствующего здесь синьора Симпличио.
Симпличио. — Признаюсь вам, что всю эту ночь я передумывал вчерашние рассуждения и, действительно, нахожу в них много прекрасного, нового и смелого. При всем том я чувствую себя гораздо больше связанным авторитетом многих великих писателей, в частности... Вы качаете головой, синьор Сагредо, и улыбаетесь, как если бы я сказал нечто ужасное.
Сагредо. — Я только улыбаюсь, но поверьте мне, я почти лопаюсь, стараясь удержаться от хохота, так как вы заставили меня вспомнить один замечательный случай, происшедший при мне несколько лет тому назад. Там же были и некоторые из моих благородных друзей, которых я мог бы даже назвать вам.
Сальвиати. — Хорошо бы вам рассказать этот случай, а то, может быть, синьор Симпличио не перестанет думать, что вы смеетесь над ним.
Сагредо. — Пусть будет так. Как-то был я в доме одного весьма уважаемого в Венеции врача, куда иногда собирались — одни, чтобы поучиться, а другие из любопытства — посмотреть на рассечение трупа, производимое рукою этого не только ученого, но искусного и опытного анатома. Как раз в тот день ему случилось заняться изысканием происхождения и зарождения нервов, по каковому вопросу существует
|
Комический ответ одного философа в связи с изысканием начала нервов. |
|
Начало нервов, по Аристотелю и по мнению врачей. |
Симпличио. — Прошу вас заметить, синьоры, что спор о происхождении нервов далеко еще не закончен и не решен, как, может быть, кое-кто себе представляет.
Сагредо. — Он никогда и не придет к концу, поскольку будут существовать подобного рода оппоненты; но то, что вы говорите, ничуть не уменьшает необычайности ответа перипатетика: против столь убедительного чувственного опыта он приводит не другие опыты или соображения Аристотеля, а только лишь авторитет и чистое Ipse dixit2.
Симпличио. — Аристотель приобрел такой огромный авторитет только благодаря силе доказательств и глубине своих рассуждений; однако, необходимо понимать его, и не только понимать, но и обладать
|
Что требуется для того, чтобы быть хорошим философом наподобие Аристотеля. |
Сагредо. — Однако, дорогой синьор Симпличио, если отрывки, разбросанные то тут, то там, не наскучивают вам и если вы думаете выжать сок путем соединений и сопоставлений разных частиц, то уверяю вас, что то же самое, что вы и другие храбрые философы делаете с текстами Аристотеля, я сделаю со стихами Виргилия и Овидия и, составляя из них центоны, объясню ими все поступки людей и тайны природы3.
|
Остроумное средство научиться философии из любой книги. |
Сальвиати. — Еще живут и здравствуют некоторые дворяне, которые присутствовали при том, как один доктор, лектор знаменитого учебного заведения, сказал, прослушав описание невиденного им еще телескопа, что изобретение это заимствовано у Аристотеля: доктор велел
|
Изобретение подзорной трубы заимствовано у Аристотеля. |
Сагредо. — Это положение об охвате всего знания весьма похоже на другое, согласно которому мраморная глыба содержит в себе прекраснейшую статую и даже тысячи прекраснейших статуй; задача заключается только в том, чтобы суметь ее обнаружить. Однако, это подобно пророчествам Иоахима4 или же ответам языческих оракулов, которые становятся понятными только после того, как случится предсказанное.
Сальвиати. — А почему не упоминаете вы о предсказаниях астрологов, которые так хорошо читают по гороскопу и даже по расположению небесных светил то, что уже произошло?
Сагредо. — Таким путем алхимики под влиянием меланхолических соков5 находят, что все самые возвышенные умы писали только
|
Алхимики видят в вымыслах поэтов указания на секрет делать золото. |
Симпличио. — Я думаю и отчасти знаю, что на свете нет недостатка в весьма причудливых умах; однако, вздорность их не должна была бы итти во вред Аристотелю, о котором, мне кажется, вы иногда говорите недостаточно уважительно. Казалось бы, одна древность его и тот авторитет, который Аристотель приобрел в глазах многих выдающихся людей, должны быть достаточными, чтобы сделать его достойным уважения всех ученых.
Сальвиати. — Дело обстоит не так, синьор Симпличио; это только некоторые из его малодушных последователей дают повод или, лучше
|
Многие приверженцы Аристотеля унижают его достоинство, всячески стараясь преувеличить его значение. |
Сагредо. — Подобные люди напоминают мне того скульптора, который придал большой глыбе мрамора образ, не помню — то ли Геркулеса, то ли Громовержца Юпитера, и сообщил ему с удивительным искусством такую живость и свирепость, что каждого смотревшего на него охватывал ужас и даже сам скульптор начал испытывать страх, хотя все движение и выражение фигуры были делом его рук. Страх его
|
Комическая история одного ваятеля. |
Сальвиати. — Я много раз удивлялся, как могло получиться, что эти люди, стремящиеся поддерживать буквально каждое слово Аристотеля, не замечают того вреда, который они наносят репутации Аристотеля, и как они, вместо того, чтобы увеличивать его авторитет, подрывают к нему доверие. Ибо, когда я вижу, как они упорно стараются поддержать те положения, ложность которых на мой взгляд совершенно очевидна, как они стремятся убедить меня в том, что именно так и надлежит поступать истинному философу и что именно так поступил бы и сам Аристотель, то у меня сильно уменьшается уверенность в том, что он правильно рассуждал и в других областях, для меня более далеких. В то же время, если бы я видел, что они готовы уступить и изменить свое мнение перед очевидной истиной, я, может быть, подумал бы, что в тех случаях, когда они стоят на своем, можно представить другие, более основательные доказательства, мне непонятные или неизвестные.
Сагредо. — А может быть, чувствуя, что рискуешь репутацией и своей, и Аристотеля, если сознаешься в незнании того или иного заключения, найденного другими, можно все же заняться поисками такового в его сочинениях путем соединения отдельных мест по способу, преподанному синьором Симпличио? Ведь раз в трудах Аристотеля заключается всяческое знание, то значит, его там можно найти. {95}
Сальвиати. — Синьор Сагредо, не относитесь легко к подобной предусмотрительности; ибо мне кажется, что вы провозгласили этот тезис шутя. Ведь не так давно один философ с большим именем написал книгу «О душе», где, излагая мнение Аристотеля по вопросу о бессмертии души, привел много текстов, но не из текстов Александра6, так как в последних
|
Бессовестный образ действий одного философа-перипатетика. |
Сагредо. — О, этот доктор! У него стоит поучиться: он не хочет, чтобы Аристотель его подвел, он сам собирается провести его за нос и заставить говорить на свой лад! Вы видите, как важно суметь выбрать подходящее время. Иметь дело с Геркулесом следует не тогда, когда он свирепствует, обуреваемый гневом, а тогда, когда он болтает с Меонийскими девами7. О, неслыханная низость раболепных умов! Добровольно
|
Узость многих приверженцев Аристотеля. |
Симпличио. — Но если мы оставим Аристотеля, то кто же будет служить нам проводником в философии? Назовите какого-нибудь автора.
Сальвиати. — Проводник нужен в странах неизвестных и диких, а на открытом и гладком месте поводырь необходим лишь слепому. А слепой хорошо сделает, если останется дома. Тот же, у кого есть глаза во лбу и разум, должен ими пользоваться в качестве проводников. Однако, я не говорю, что не следует слушать Аристотеля, наоборот, я хвалю тех, кто всматривается в него и прилежно его изучает. Я порицаю только склонность настолько отдаваться во власть Аристотеля, чтобы вслепую
|
Чрезмерная приверженность к Аристотелю достойна порицания. |
|
Тот, кто никогда не философствует, не должен присваивать себе титула философа. |
Сагредо. — С большим удовольствием, однако при условии, что за мной останется право приводить иногда то, что диктует простой здравый смысл.
Сальвиати. — Как раз именно об этом я вас особенно прошу. Ведь из доказательств более легких и, так сказать, материальных лишь очень немногие, я думаю, не приняты во внимание писателями; поэтому желательно выдвинуть какие-нибудь более тонкие и скрытые, их-то как раз и недостает. Но для их понимания и постижения, требующего утонченности мысли, чей ум может быть более пригоден, чем ум синьора Сагредо, такой острый и проницательный?
Сагредо. — Я готов быть чем вам угодно, синьор Сальвиати, но, пожалуйста, не будем уклоняться в сторону церемоний, ведь сейчас я — философ и нахожусь в школе, а не на площади при собирании голосов.
Сальвиати. — Итак, начнем наше рассуждение с того, что, какое
|
Движения Земли незаметны для ее обитателей. |
|
Земле могут принадлежать лишь такие движения, которые кажутся нам присущими всем частям вселенной вообще, кроме Земли. |
|
Суточное движение, повидимому, есть движение, общее всему миру, за исключением Земли. |
|
Аристотель и Птоломей оспаривают приписываемое Земле суточное движение. |
Сагредо. — Я очень хорошо понимаю необходимость, вытекающую из ваших рассуждений. Но у меня возникает сомнение, от которого я не {97} могу избавиться. Оно заключается в следующем. Коперник приписывает Земле еще одно движение, кроме суточного, и проявление его, согласно разъясненному до сих пор, должно оставаться для нас на Земле незаметным, но видимым во всем остальном мире. Отсюда, мне кажется, можно неизбежно заключить или что он явно ошибался, приписывая Земле такое движение, которое не имеет общего видимого соответствия на небе, или, если такое соответствие есть, что Птоломея можно обвинить в недосмотре, поскольку он не разобрал этого движения так, как он разобрал первое8.
Сальвиати. — Ваши сомнения вполне основательны, и когда мы подойдем к разбору второго движения, то вы увидите, насколько Коперник превзошел прозорливостью и проницательностью Птоломея, ибо он увидел то, что Птоломей не видел, — удивительное соответствие, которым такое движение отражается на всех остальных небесных телах. Но отложим сейчас эту тему в сторону и вернемся к первоначальному рассуждению. Начиная с вопросов более общих, я буду приводить те доводы, которые, по-моему, благоприятствуют подвижности Земли, чтобы затем выслушать возражения синьора Симпличио. Во-первых, если мы примем во внимание огромный объем звездной сферы по сравнению с ничтожностью земного шара, содержащегося в ней много и много миллионов
|
Почему суточное движение скорее должно принадлежать одной Земле, чем всему остальному миру. |
Сагредо. — Если решительно все явления природы, могущие стоять в зависимости от таких движений, порождают как в одном, так и в другом случае без всякого различия одни и те же следствия, то я сразу признал бы того, кто считает более правильным заставить двигаться всю вселенную, лишь бы сохранить неподвижность Земли, еще более неразумным, чем того человека, который, взобравшись на вершину купола вашей виллы, чтобы посмотреть на город и его окрестности, потребовал бы, чтобы вокруг него вращалась вся местность и ему не пришлось трудиться, поворачивая голову. Многочисленны и велики должны быть преимущества первой системы над другой, чтобы заставить меня, не взирая на этот абсурд, признать первую теорию более вероятной, чем вторую. Но, может быть, Аристотель, Птоломей и синьор Симпличио смогут найти такие преимущества, и хорошо было бы их привести нам сейчас, если только они существуют, или же прямо заявить, что их нет и не может быть.
Сальвиати. — Как много я ни думал об этом, я не мог найти никакой разницы, и поэтому мне кажется, что никакой разницы и быть не может. Поэтому я считаю, что и искать ее дальше — бесплодно. Поэтому заметьте следующее. Движение является движением и воздействует как таковое, поскольку оно имеет отношение к вещам, его лишенным, но на вещи, которые равным образом участвуют в этом движении, оно не воздействует
|
Для предметов, захваченных равномерным движением, это последнее как бы не существует и проявляет свое действие только на вещах, не принимающих в нем участия. |
Симпличио. — Такое учение правильно, основательно и является именно учением перипатетиков.
Сальвиати. — По-моему, оно значительно старше, и я предполагаю, что Аристотель, заимствовав его от какой-нибудь хорошей школы, не проник в нее всецело и поэтому, записав его в измененном виде, оказался причиной путаницы среди тех, кто стремится поддержать каждое
|
Положение Аристотеля взято им от предшественников, но изменено. |
Сагредо. — Пожалуйста, не будем терять нити, продолжайте начатое рассуждение.
Сальвиати. — Итак, поскольку очевидно, что движение, общее для
|
Первое доказательство того, что суточное движение принадлежит Земле. |
|
Природа не употребляет многих средств там, где она может обойтись немногими. |
Симпличио. — Я не совсем понимаю, как это грандиозное движение оказывается как бы несуществующим для Солнца, Луны, других планет и для бесчисленного скопища неподвижных звезд. Скажете ли вы, что Солнце не переходит от одного меридиана к другому, не поднимается над этим горизонтом и не садится затем, вызывая то день, то ночь? Что такие же изменения не проделывают Луна, прочие планеты и даже неподвижные звезды?
Сальвиати. — Все перечисленные вами изменения существуют только по отношению к Земле. Чтобы убедиться в справедливости этого, вообразите
|
Из суточного движения не возникает никаких изменений в расположении небесных тел относительно друг друга; все изменения имеют отношение только к Земле. |
|
Второе доказательство суточного движения Земли. |
Симпличио. — Что касается противоположности движений, то это — пустяки, так как Аристотель доказывает, что круговые движения не противоположны друг другу и что кажущаяся противоположность их не
|
По Аристотелю не существует противоположностей в круговых движениях. |
Сальвиати. — Доказывает ли это Аристотель или же только утверждает, поскольку это завершает его определенный план? Если, как он сам утверждает, противоположны те движения, которые взаимно уничтожаются, то я не вижу, почему два движущихся тела, встречающихся на круговой линии, должны пострадать меньше, чем при встрече на прямой линии?
Сагредо. — Пожалуйста, подождите немного. Скажите мне, синьор Симпличио, когда встречаются два всадника, сражаясь в открытом поле, или же когда в море сталкиваются, сокрушают друг друга и топят два отряда или две морские эскадры, то назовете ли вы такие встречи взаимно противоположными?
Симпличио. — Мы называем их противоположными.
Сагредо. — Так как же нет противоположностей в круговых движениях? Ведь все эти движения происходят на поверхности земли или воды, имеющих, как вы знаете, сферическую форму, и потому должны быть круговыми. Знаете ли вы, синьор Симпличио, каковы те круговые движения, которые не противоположны друг другу? Это — движения двух кругов, соприкасающихся внешней частью, так что вращение одного естественным порядком заставляет другой вращаться в другую сторону. Но если один круг будет внутри другого, то невозможно, чтобы движения их, происходящие в разные стороны, не были противоположны друг другу.
Сальвиати. — Противоположны или не противоположны — это спор о словах, и я знаю, что на деле гораздо проще и естественнее объяснить все одним единственным движением, чем вводить два движения. Если вы не хотите называть их противоположными, то называйте обратными. Я не считаю невозможным их введение и не претендую на извлечение из этого доказательства необходимости вращения Земли; я только указываю на большую его вероятность.
Неправдоподобность утраивается от полного нарушения того порядка, который, как мы видим, существует среди небесных тел, круговращение
|
Третье подтверждение того же мнения. |
|
Чем больше орбиты, тем продолжительнее движение по ним. |
|
Сроки обращения Медицейских звезд. |
Такая полная согласованность ничуть не изменится, если приписать двадцатичетырехчасовое движение земному шару самому по себе. Если {100} же мы пожелаем удержать Землю в неподвижности, то необходимо придется переходить от наиболее короткого периода Луны к другим, последовательно все большим, до двухлетнего периода Марса, от него — к еще большей двенадцатилетней сфере Юпитера, а от нее — к еще большей сфере Сатурна, период которого составляет тридцать лет, и необходимо, говорю я, переходить от одной сферы к другой, непосредственно большей, заставляя и ее заканчивать полное обращение в двадцать четыре часа. А это еще наименьший из могущих возникнуть беспорядков. Ведь если мы перейдем от сферы Сатурна к звездной сфере, настолько превосходящей сферу Сатурна, насколько этого требует отношение ее движения, чрезвычайно медленного и длящегося много тысяч лет, то нам придется
|
24-часовое движение высшей сферы нарушает порядок сфер низших. |
|
Четвертое подтверждение. |
|
Движения постоянных звезд становятся в разное время то быстрее, то медленнее, если движется звездная сфера. |
|
Шестое подтверждение. |
|
Седьмое подтверждение. |
|
Свободно плавающая, взвешенная в жидкой сфере Земли, повидимому, неспособна к сопротивлению силе суточного движения. |
Сагредо. — В моем уме вертятся некоторые неясные мысли, пробужденные заслушанным рассуждением; для внимательного участия в предстоящих разговорах мне необходимо попробовать привести их в больший порядок и извлечь из них выводы, если только их действительно можно сделать. Может быть, метод вопросов поможет легче объясниться. Поэтому я спрошу синьора Симпличио. Во-первых, думает ли он, что одному и тому же простому движущемуся телу могут быть естественно свойственны различные движения или же что ему подобает одно единственное, его собственное и естественное?
Симпличио. — У одного простого движущегося тела может быть лишь одно движение, свойственное ему естественным порядком, а все
|
Одно простое подвижное тело имеет только одно естественное движение; все остальные движения ему сообщены извне. |
Сагредо. — Во-вторых, скажите мне: то движение, которое через соучастие сообщается какому-нибудь движущемуся телу, когда тело само по себе движется другим движением, отличным от первого, необходимо ли пребывает в каком-либо предмете или оно может существовать в природе само по себе, без носителя?
Симпличио. — Аристотель дает вам ответы на все эти вопросы. Он говорит: как у одного движущегося тела существует одно движение, так и у одного движения — одно движущееся тело; следовательно, без причастности к своему предмету не может быть и даже нельзя себе
|
Нет движения без движущегося предмета. |
Сагредо. — Мне хотелось бы от вас услышать, в-третьих, обладают ли, по вашему мнению, Луна и другие планеты и небесные тела своими собственными движениями и какими именно?
Симпличио. — Обладают. И именно такими, согласно которым они проходят Зодиак: Луна — за месяц, Солнце — за год, Марс — за два года, звездная сфера — во столько-то тысяч лет. И такие движения суть их собственные и естественные.
Сагредо. — Но каким считаете вы то, движение, посредством которого, как я вижу, неподвижные звезды, а вместе с ними и все планеты одинаково движутся с востока на запад и возвращаются на восток за двадцать четыре часа?
Симпличио. — Они обладают этим движением через соучастие.
Сагредо. — Значит, оно не пребывает в них. А раз оно в них не пребывает и не может существовать без какого-либо предмета, в котором оно пребывает, то необходимо сделать его собственным и естественным для какой-нибудь другой сферы?
Симпличио. — Именно ради этого астрономы и философы нашли еще одну самую высокую сферу без звезд, которым естественно свойственно {102} суточное обращение. Они назвали ее «первым движителем». Она увлекает за собой все нижние сферы, сообщая им свое движение и заставляя их участвовать в нем.
Сагредо. — Но если можно обойтись без введения новых неизвестных и обширнейших сфер и без соучастия в других движениях, оставить каждой сфере только ее собственное и простое движение, не смешивая его с противоположными движениями, и достигнуть всего этого лишь одним вращением (как это и необходимо, если все зависит от одного единственного начала) и если при этом все будет соответствовать совершеннейшей гармонии, то к чему отвергать такое предположение и одобрять столь странные и искусственные допущения?
Симпличио. — Трудность в том, чтобы найти такой способ, столь простой и окончательный.
Сагредо. — Способ, мне кажется, неплохо найден. Пусть Земля будет «первым движителем», т. е. заставьте ее обращаться вокруг самой себя в двадцать четыре часа и в том же самом направлении, как и все другие сферы; тогда все планеты и звезды, и не участвуя в таком движении, займут свои места, будут восходить и, словом, являть обычный вид.
Симпличио. — Важно заставить ее вращаться без тысячи несообразностей.
Сальвиати. — Все несообразности будут устраняться по мере того, как вы будете их приводить. Сказанное до сих пор — только первые и наиболее общие соображения, и в соответствии с ними нам представляется не совсем невероятным, что суточное обращение принадлежит скорее Земле, чем всей остальной вселенной; я предлагаю их вам не как непреложные законы, но как соображения, которые имеют видимую основательность. И так как я отлично понимаю, что одного единственного опыта
|
Один единственный опыт или строгое доказательство обращают в ничто соображения, основанные на вероятности. |
Симпличио. — Сначала я скажу кое-что вообще обо всех этих рассуждениях, а потом перейду к некоторым частностям. Вы, как мне кажется, основываетесь, главным образом, на большей простоте и легкости вызывать одни и те же явления, когда считаете, что, поскольку речь идет о причине этих явлений, безразлично, движется ли одна Земля или весь остальной мир, за исключением Земли, но с точки зрения воздействия гораздо более легко достижимо первое, чем второе. На это я вам отвечу, что и мне кажется то же самое, когда я думаю о своей силе, не только конечной, но даже очень незначительной; но для мощи Движителя,
|
Бесконечное могущество, вероятно, проявит себя скорее в большом, нежели в малом. |
Сальвиати. — Если бы я хоть раз сказал, что вселенная недвижима из-за недостатка могущества у Движителя, то я заблуждался бы, и ваша поправка была бы уместна. Я признаю вместе с вами, что для бесконечного могущества так же легко двигать сто тысяч, как и единицу. Но то, что я сказал, относится не к Движителю, а только к движущимся телам, а в них — не только к сопротивлению, которое, несомненно, у Земли меньше, чем у вселенной, но и ко многим другим частностям, только что рассмотренным. На другое ваше замечание, что бесконечное могущество скорее проявит себя на большой части, чем на малой, я вам отвечу, что {103} в бесконечности одна часть не больше другой, если обе они конечны. Нельзя сказать, что в бесконечном числе сто тысяч составляет бо́льшую
|
В бесконечности нет ни больших, ни меньших частей, хотя бы таковые были неодинаковы. |
Симпличио. — Приводя аксиому, вы выпустили часть ее, которая важнее всего, особенно в данном случае; пропущенная часть гласит: aeque bene*. Значит, нужно исследовать, может ли одинаково хорошо удовлетворить всему как первое, так и второе допущение.
Сальвиати. — Одинаково ли хорошо удовлетворяет то и другое допущение, можно усмотреть из рассмотрения отдельных явлений, которые подлежат объяснению. Ибо до сих пор мы рассуждали и будем пока рассуждать ex hypothesi**, предполагая, что для удовлетворительного объяснения явлений оба движения одинаково пригодны. Что же касается части, которая, по вашим словам, была мною выпущена, то я склонен думать, что вы ее излишне добавили: ведь сказать «одинаково хорошо»,
|
При аксиоме Frustra fit per plura etc. — прибавка aeque bene излишня. |
Сагредо. — Если мы не хотим, чтобы с нами случилось то же, что вчера, то вернемся, пожалуйста, к теме, и пусть синьор Симпличио начнет приводить те факты, которые ему кажутся противоречащими новому миропорядку.
Симпличио. — Этот миропорядок совсем не нов, наоборот, он очень древен. В справедливости этого вы можете удостовериться из того, что Аристотель его опровергает. Опровержения же его таковы: «Во-первых,
|
Соображения Аристотеля в пользу неподвижности Земли. |
Сальвиати. — Доводы, которые приводятся по этому вопросу, бывают двух родов: одни имеют основанием происходящее на Земле, без всякого отношения к звездам, другие черпаются из явлений и наблюдений
|
Соображения двоякого рода по вопросу о том, движется ли Земля или нет. Основания Птоломея, Тихо и других, помимо Аристотеля |
Симпличио. — Лучше, если вы их приведете, так как вы занимались этим вопросом больше, и они у вас всегда наготове и притом в большем числе.
Сальвиати. — В качестве самого сильного довода все приводят опыт
|
Первый аргумент, почерпнутый из движения твердого тела, падающего сверху вниз. |
|
Подтверждение его примером тела, падающего с вершины корабельной мачты. |
|
Второй аргумент, почерпнутый из движения тела, подброшенного высоко вверх. |
|
Третий аргумент, почерпнутый из стрельбы из пушки к востоку и к западу. |
|
Подтверждение аргумента практикой выстрелов, направленных к югу и северу. То же подтверждается практикой выстрелов к востоку и западу. |
Симпличио. — О, это — действительно такие основания, против которых невозможно представить сколько-нибудь стоящих возражений.
Сальвиати. — Для вас они являются как будто новыми?
Симпличио. — Именно. И теперь я вижу, какими прекрасными опытами природа великодушно пожелала притти нам на помощь в познании истины. Как прекрасно одна истина согласуется с другой и как все они объединяются, чтобы сделаться неопровержимыми! {106}
Сагредо. — Как жаль, что во времена Аристотеля артиллерия еще не существовала; с ее помощью он сразил бы невежество и говорил бы о мировых явлениях без колебаний.
Сальвиати. — Мне очень приятно, что эти соображения представляются для вас новыми и что вы, таким образом, не останетесь при мнении большинства перипатетиков, будто, если кто отклоняется от учения Аристотеля, это происходит только оттого, что он не понял и не проникся как следует его доказательствами. Вы, наверно, услышите и другие новые вещи и услышите их от последователей новой системы, которые приводят против самих себя наблюдения, опыты и рассуждения
|
Коперниканцы пришли к своему взгляду не вследствие незнания доводов противоположной стороны. |
Сагредо. — По этому случаю мне хочется рассказать вам некоторые происшествия, случившиеся со мной вскоре после того, как я впервые услышал разговоры об этом учении. Когда я был еще совсем юным и только что окончил курс философии, которую затем оставил для других занятий, случилось, что некий северянин из Ростока (кажется, имя его было Христиан Вурстейзен), последователь Коперника, приехал в наши
|
Христиан Вурстейзен прочел несколько лекций, посвященных учению Коперника; каков был результат их? |
|
Коперниканцы ранее придерживались противоположных воззрений; приверженцы Аристотеля и Птоломея никогда ранее не разделяли противного мнения. |
Симпличио. — Если только ожидания и надежды не окажутся обманчивыми и вы не окажетесь в конечном счете еще более сбитым с толку, чем ранее.
Сагредо. — Я уверен, что этого никоим образом не может случиться.
Симпличио. — А почему нет? Я сам — хорошее тому подтверждение: чем более мы подвигаемся, тем более я запутываюсь.
Сагредо. — Это признак того, что те доводы, которые до сих пор казались вам убедительными и поддерживали в вас уверенность в истинности вашего мнения, начинают в вашем уме изменять свой вид, постепенно побуждая вас если не переходить, то по меньшей мере склоняться к противоположному. Но я, остававшийся в этом вопросе индифферентным, весьма надеюсь на то, что обрету уверенность и покой; и вы сами не станете этого отрицать, если захотите выслушать, что вселяет в меня такую надежду.
Симпличио. — Охотно выслушаю, и мне было бы не менее желательно, чтобы это оказало такое же действие и на меня.
Сагредо. — Благоволите же ответить на мои вопросы. Прежде всего, скажите мне, синьор Симпличио, не заключается ли вопрос, разрешения которого мы ищем, в том, должны ли мы вместе с Аристотелем и Птоломеем считать, что одна Земля остается в центре вселенной, а все небесные тела движутся, или же при неподвижной звездной сфере с Солнцем в центре Земля находится вне этого центра, и ей принадлежит то движение, которое кажется нам движением Солнца и неподвижных звезд.
Симпличио. — По этому вопросу и идет спор.
Сагредо. — Не таковы ли эти два решения, что по необходимости одно из них должно быть истинным, а другое ложным?
Симпличио. — Да, таковы; мы имеем дело с дилеммой, одна часть коей по необходимости должна быть истинной, а другая ложной, ибо между движением и покоем, которые противоположны, не может находиться ничего третьего, так что нельзя сказать: «Земля не движется и не стоит недвижимо; Солнце и звезды не движутся и не стоят недвижимо».
Сагредо. — Что за вещи в природе — Земля, Солнце и звезды? Ничтожные или, наоборот, значительные?
Симпличио. — Это — тела наисущественнейшие, благороднейшие, отдельные части вселенной, обширнейшие, значительнейшие.
|
Движение и покой — главнейшие свойства природы. |
Симпличио. — Столь великие и существенные, что сама природа свойства получает через них свое определение.
Сагредо. — Таким образом, вечное движение и полная неподвижность суть два весьма значительных состояния в природе, являющиеся признаками огромнейшего различия, в особенности, когда они приписываются наисущественнейшим телам вселенной и от них могут произойти лишь совершенно различные явления?
Симпличио. — Бесспорно, это так.
Сагредо. — Ответьте теперь на другой вопрос. Полагаете ли вы, что в диалектике, риторике, физике, метафизике, словом, во всех отраслях знания существуют способы рассуждения, могущие доказать ложные выводы не менее убедительно, чем истинные?
Симпличио. — Нет, синьор, наоборот, я считаю бесспорным и вполне убежден, что для доказательства истинного и необходимого вывода в {108}
|
Ложное не может быть так хорошо доказуемо, как истинное. |
|
Для правильных положений всегда находятся многие убедительные аргументы; но не то по отношению к доказательству положений ложных. |
Сагредо. — Итак, если вечное движение и вечный покой суть свойства, столь важные и столь различные в природе, что они могут являться причиной лишь совершенно различных следствий, в особенности применительно к Солнцу и Земле — этим столь пространным и замечательным телам вселенной, и если, кроме того, невозможно, чтобы из двух противоречивых предложений одно не было истинным, а другое ложным, и если для доказательства ложного предложения нельзя привести ничего, кроме ложных аргументов, тогда как в истинном можно убедиться доводами и доказательствами разного рода, то как вы хотите, чтобы тот из вас, кто будет защищать истинное положение, не смог убедить меня? Мне нужно быть слабым умом, шатким в суждениях, тупым в понимании, слепым в рассуждении, чтобы не отличить света от тьмы, алмаза от угля, истины от лжи.
Симпличио. — Я говорю вам и говорил уже в других случаях, что величайшим мастером, научившим распознавать софизмы, паралогизмы и другие ложные аргументы, был Аристотель, который в этом отношении не может ошибаться.
Сагредо. — Однако, вы ошибаетесь вместе с Аристотелем, который не может говорить; а я уверяю вас, что будь Аристотель здесь, он
|
Аристотель опроверг бы доводы противников или изменил бы свое мнение. |
Сальвиати. — Прежде чем итти дальше, я должен сказать синьору Сагредо, что в этих наших беседах я выступаю как коперниканец и разыгрываю его роль как актер, но не хочу, чтобы вы судили по моим речам о том, какое внутреннее действие произвели на меня те доводы, которые я как будто привожу в его пользу, пока мы находимся в разгаре представления пьесы; сделайте это потом, после того как я сниму свой наряд и вы найдете меня, быть может, отличным от того, каким видите меня на сцене. Но двинемся дальше. Птоломей и его последователи приводят другой опыт, подобный опыту с брошенными телами; они указывают
|
Аргумент, взятый из движения облаков и птиц. |
|
Аргумент, взятый из опыта с воздухом, который кажется нам при езде дующим нам навстречу. Аргумент, почерпнутый из силы отбрасывания и рассеивания, присущего вращательному движению. |
Сагредо. — Что скажете, синьор Симпличио? Не кажется ли вам, что синьор Сальвиати может и умеет разъяснять доводы Птоломея и Аристотеля? Думаете ли вы, что кто-нибудь из перипатетиков в такой же мере владеет доказательствами Коперника?
Симпличио. — Если бы на основании бесед, которые мы вели до сих пор, я не составил столь высокого мнения о солидности образования синьора Сальвиати и об остроте ума синьора Сагредо, я предпочел бы с их благосклонного согласия уйти, не слушая ничего далее, поскольку мне кажется невозможным противостоять столь осязательным опытам; я хотел бы, не слушая ничего другого, остаться при прежнем своем мнении, так как, по-моему, будь оно даже ложным, представляется извинительным и придерживаться его, раз оно опирается на столь правдоподобные основания; если даже последние ошибочны, то какие даже истинные доказательства были когда-либо так прекрасны?
Сагредо. — Однако, послушаем ответы синьора Сальвиати; если они соответствуют истине, то должны быть еще более прекрасными и даже бесконечно более прекрасными, а прежние должны оказаться безобразными {110} и даже безобразнейшими, если возможно положение метафизики,
|
Правда и красота идентичны, так же как ложь и безобразие. |
Сальвиати. — Если память не изменяет мне, первый аргумент, приведенный синьором Симпличио, таков. Земля не может двигаться кругообразно, так как подобное движение было бы для нее насильственным, а потому не могло бы продолжаться вечно; далее, объяснение, почему оно было бы насильственным, заключалось в том, что, будь оно естественным, части Земли также естественно вращались бы, что невозможно, так как этим частям по природе присуще прямолинейное движение вниз. На это отвечу так: мне было бы желательно, чтобы Аристотель выразился
|
Возражение на первый довод Аристотеля. |
Симпличио. — Это доказано Аристотелем в том же месте, где он говорит, что для частей естественным является прямое движение к центру вселенной, почему круговое движение по природе уже не может быть им присуще.
Сальвиати. — Но не видите ли вы, что в этих же словах заключается и опровержение такого утверждения?
Симпличио. — Каким образом и где?
Сальвиати. — Не говорит ли он, что круговое движение было бы для Земли насильственным и потому невечным? И что это было бы нелепостью, так как миропорядок вечен?
Симпличио. — Говорит.
|
Насильственное не может быть вечным, а что не может быть вечным, не может быть естественным. |
Симпличио. — Прямолинейное движение для частей Земли наиболее естественно, оно вечно, и никогда не случится, чтобы они не двигались прямолинейным движением, предполагая, конечно, что препятствия к тому неизменно устраняются.
Сальвиати. — Вы играете словами, синьор Симпличио, во я постараюсь избавить вас от двусмысленностей. А потому скажите мне, полагаете ли вы, что корабль, идущий из Гибралтарского пролива к берегам Палестины, может плыть вечно к этому берегу, двигаясь постоянно равномерно?
Симпличио. — Никоим образом.
Сальвиати. — А почему так? {111}
Симпличио. — Потому что это плавание замкнуто и ограничено Геркулесовыми столбами и побережьем Палестины, а поскольку расстояние ограничено, оно проходится в конечное время, если только, возвращаясь назад встречным движением, не хотят повторить тот же самый путь; но это было бы движением прерванным, а не непрерывным.
Сальвиати. — Ответ совершенно верный. Но плавание от Магелланова пролива по Тихому океану через Молуккские острова, мыс Доброй Надежды, а оттуда через тот же пролив вновь по тому же пути и т. д. могло бы длиться постоянно? Как вы полагаете?
Симпличио. — Могло бы, так как оно, будучи круговращением, возвращающимся к самому себе, путем повторения бесконечного множества раз могло бы продолжаться постоянно, без всякого перерыва.
Сальвиати. — Итак, корабль на этом пути мог бы плыть вечно?
Симпличио. — Мог бы, если бы корабль был вечным; при разрушении корабль по необходимости кончил бы плавание.
Сальвиати. — А в Средиземном море, будь даже корабль вечным, он не мог бы двигаться к Палестине без конца, так как путь этот ограничен.
|
Два необходимых условия для вечного движения — неограниченность пространства и неразрушаемость тела. |
Симпличио. — Все это необходимо.
Сальвиати. — Следовательно, вы сами себя вынуждаете признать, что движущемуся телу невозможно двигаться вечно прямолинейным
|
Прямолинейное движение не может продолжаться вечно и потому не может быть от природы присуще Земле. |
Симпличио. — Что касается неподвижности, то аргументы Аристотеля, а еще более те другие, которые были выдвинуты вами, пока что, как мне кажется, необходимо убеждают нас в этом, и опровергнуть их, полагаю я, будет стоить большого труда.
|
Возражение на второй аргумент. |
Симпличио. — Не видел и до сих пор не вижу.
Сальвиати. — Невозможно, ибо он вам слишком ясен.
Симпличио. — Мне хотелось бы, с вашего разрешения, взглянуть на текст.
Сальвиати. — Прикажем принести сейчас текст. , Симпличио. — Я всегда ношу его в кармане; вот он, и я в точности знаю место: О небе, книга вторая, глава XIV. Вот этот текст:
«Praeterea, omnia quae feruntur latione circulari, subdeficere videntur, ac moveri pluribus una latione, praeter primam spheram; quare et Terram necessarium est, sive circa medium sive in medio posita feratur, duabus moveri lationibus. Si aittem hoc accident, necessarium est fieri mutationes ac conversiones fixorum astrorum. Hoc autem non videtur fieri, sed semper eadem apud eadem loca ipsius et oriuntur et occidunt»16.
Здесь я не вижу никакой ошибки, и рассуждение кажется мне вполне убедительным.
Сальвиати. — А мне новое чтение подтвердило неправильность аргументации и, кроме того, открыло другую ошибку. Итак, заметьте. Аристотель хочет опровергнуть два положения или, я сказал бы, два заключения: одно принадлежит тем, кто помещает Землю в средоточие мира и заставляет ее двигаться вокруг собственного центра; другое принадлежит тем, кто, полагая ее вдали от средоточия, заставляет ее двигаться круговыми движениями вокруг этого средоточия. Оба эти положения вместе он опровергает одним и тем же способом. Так вот, я говорю, что как в том, так и в другом опровержении он заблуждается и что ошибка в отношении первого положения заключается во внутреннем противоречии
|
Рассуждение Аристотеля против движения Земли несостоятельно с двух сторон. |
|
Возражение на третий аргумент. |
|
Возражение на четвертый аргумент. |
Симпличио. — Чувственным восприятием; оно убеждает нас, что данная башня — прямая и отвесная, и показывает, что камень при падении скользит вдоль нее, ни на волос не отклоняясь в ту или другую сторону, и ударяется у подножья как раз над тем местом, откуда он был выпущен. {114}
Сальвиати. — Но если бы случайно земной шар вращался и, следовательно, переносил бы с собой и башню, и при всяких условиях наблюдалось бы, что камень при падении скользит вдоль прямой линии башни, то каким должно бы было быть его движение?
Симпличио. — В этом случае скорее следовало бы сказать «его движения», так как одно было бы то, которым он двигался бы сверху вниз, а другое то, которое ему надлежало бы иметь, чтобы следовать за движением башни.
Сальвиати. — Следовательно, движение его слагалось бы из двух, а именно из того, которым он отмеривает башню, и из другого, которым он за ней следует. Из такого сложения вытекало бы, что камень описывает не простую прямую и отвесную линию, а наклонную и, может быть, не прямую.
Симпличио. — Не прямую ли — не знаю, но вполне понимаю, что она по необходимости была бы наклонной и отличной от той отвесной прямой, которую камень описывает, если Земля неподвижна.
Сальвиати. — Следовательно, на основании одного только наблюдения, что падающий камень скользит вдоль башни, вы не можете с достоверностью утверждать, будто он описывает прямую и отвесную линию, если не предположить заранее, что Земля стоит неподвижно.
Симпличио. — Это так и есть, ибо, если бы Земля двигалась, движение камня было бы наклонным, а не отвесным.
Сальвиати. — Итак, вот паралогизм Аристотеля и Птоломея — очевидный и ясный и открытый вами самим, в котором предполагается
|
Ошибка Аристотеля и Птоломея, которые принимают за известное то, что требуется доказать. |
Симпличио. — Как так? Мне он кажется силлогизмом в надлежащей форме, а не petitio principii17.
Сальвиати. — А вот как: скажите мне, не предполагается ли вывод при доказательстве неизвестным?
Симпличио. — Конечно, ибо иначе доказательство его было бы излишним.
Сальвиати. — Но ведь среднее положение в умозаключениях должно быть известным?
Симпличио. — Это необходимо, ибо в противном случае мы стремились бы доказать ignotum per aeque ignotum.
Сальвиати. — Наш вывод, требующий доказательства и пока еще неизвестный, не есть ли вывод о неподвижности Земли?
Симпличио. — Да.
Сальвиати. — А среднее положение, которое должно быть известно, не есть ли положение о прямой и отвесном падении камня?
Симпличио. — Да, среднее положение таково.
Сальвиати. — Но не было ли недавно сделано заключение, что мы не можем знать, действительно ли это падение прямое и отвесное, не зная ранее, неподвижна ли Земля? Следовательно, в вашем силлогизме достоверность среднего термина черпается из недостоверности заключения. Итак, вы сами видите, что это настоящий паралогизм.
Сагредо. — Я хотел бы в угоду синьору Симпличио защитить, если возможно, Аристотеля или по меньшей мере лучше постигнуть силу вашего вывода. Вы говорите: того наблюдения, что камень скользит вдоль башни, недостаточно для доказательства отвесности его движения (а это есть среднее положение силлогизма), если только не предположить, что Земля неподвижна (что является выводом, требующим доказательства), ибо если бы башня двигалась вместе с Землей и камень скользил бы вдоль нее, то движение камня было бы наклонным, а не отвесным. Но я отвечу, что если бы башня двигалась, невозможно было бы камню падать вдоль нее, а потому из такого падения вытекает неподвижность Земли. {115}
Симпличио. — Это так, ибо, если бы мы предположили, что камень скользит вдоль башни, в то время как она уносится Землей, следовало бы допустить, что камень имеет два естественных движения, а именно, прямое к центру и круговое вокруг центра, что невозможно.
Сальвиати. — Защита Аристотеля заключается, следовательно, в невозможности или по крайней мере в предположении невозможности для камня двигаться движением, смешанным из прямолинейного и кругового; ибо, если бы он не считал невозможным для камня двигаться одновременно и к центру, и вокруг центра, он понял бы, что камень может падать, скользя вдоль башни как при ее движении, так и при ее неподвижности, и следовательно, заметил бы, что из такого скольжения нельзя извлечь ничего относительно движения или покоя Земли. Но это ничуть не извиняет Аристотеля как потому, что если он имел такую предпосылку, являющуюся столь важным пунктом всего рассуждения, то он должен был бы высказать ее, так еще более и потому, что нельзя сказать, будто такое явление вообще невозможно. Первого нельзя сказать, ибо, как я покажу немного далее, оно не только возможно, но и необходимо; тем
|
Аристотель принимает, что огонь движется прямо вверх по своей природе и по кругу — в силу соучастия. |
Симпличио. — Я этого не думаю, так как когда стихия огня движется по кругу вместе с воздухом, то крайне легко и даже необходимо допустить, что частица огня, поднимающаяся ввысь от Земли, при прохождении через движущийся воздух получает его движение, поскольку огонь есть тело тонкое и легкое и в высшей степени поддающееся движению; но что очень тяжелый камень или артиллерийское ядро, падающее сверху вниз и предоставленное самому себе, позволяет перемещать себя воздухом или чем-либо другим, то это совершенно невероятно. Кроме того, существует очень подходящий опыт с камнем, сброшенным с вершины корабельной мачты: пока корабль стоит неподвижно, камень падает к подножью мачты, когда же корабль плывет, он падает настолько дальше от прежнего места, насколько корабль продвинулся вперед за время падения камня, что составит немало локтей, когда корабль идет быстро.
Сальвиати. — Большая разница между случаем с кораблем и случаем с Землей, если только земной шар обладает суточным движением19.
|
Различие между падением камня с мачты корабля и падением с высоты башни. |
|
Часть атмосферы ниже высоких гор следует за движением Земли. |
Симпличио. — Я все же не понимаю, как воздух может передать
|
Движение воздуха может увлекать очень легкие вещи, но не тяжелые. |
Сальвиати. — Разница между вашим опытом и нашим случаем весьма велика. Вы заставляете ветер воздействовать на камень, находящийся в покое; мы же вводим в воздух, который уже движется, камень, обладающий движением с той же скоростью; таким образом, воздуху не приходится сообщать камню нового движения, а только поддерживать движение или, лучше сказать, не мешать движению, уже начавшемуся; вы хотите воздействовать на камень движением, чуждым и не свойственным его природе, мы же хотим сохранить его в его естественном состоянии. Если вы хотите привести более подходящий опыт, то вам следовало бы сказать, что наблюдалось бы, если не глазами во лбу, то очами умственными, когда орел, несомый силой ветра, выпустит из своих когтей камень; так как последний, находясь в когтях, летел наравне с ветром и при падении вступает в среду, двигающуюся с той же скоростью, то я весьма склонен думать, что мы увидали бы камень падающим вниз не отвесно, но наклонно, следуя течению ветра и прибавляя к этому движение в силу собственной тяжести.
Симпличио. — Следовало бы произвести такой опыт, а затем судить по результату; пока что наблюдения на корабле свидетельствуют в пользу нашего мнения.
Сальвиати. — Вы правильно сказали «пока что», потому что вскоре видимость может измениться. Чтобы, как говорится, не томить вас более, спрошу у вас, синьор Симпличио, кажется ли вам самому опыт с кораблем настолько подходящим к нашему положению, чтобы с разумным основанием можно было полагать, что то, что наблюдается нами в случае о кораблем, должно так же совершаться и с земным шаром? {117}
Симпличио. — До сих пор мне это так казалось, и хотя вы привели некоторые различия, мне они кажутся недостаточно значительными для того, чтобы заставить меня отступить от своего мнения.
Сальвиати. — Я также хочу, чтобы вы продолжали твердо держаться того, что явления на Земле должны соответствовать явлениям на корабле; ведь если бы это оказалось несоответствующим вашей цели, вам не жаль было бы изменить мнение. Вы говорите: так как, когда корабль стоит неподвижно, камень падает к подножью мачты, а когда движется, падает далеко от подножья, то, следовательно, и наоборот, из падения камня к подножью вытекает, что корабль стоит неподвижно, а падение камня на некотором расстоянии доказывает, что корабль находится в движении; а так как то, что происходит на корабле, равным образом происходит и на Земле, то из падения камня к подножью башни вытекает с необходимостью неподвижность земного шара. Не таково ли ваше рассуждение?
Симпличио. — Совершенно верно, таково оно, изложенное в простой форме, которая делает его в высшей степени удобным для усвоения.
Сальвиати. — Скажите же мне, если бы камень, выпущенный с вершины мачты плывущего с большой скоростью корабля, упал в точности в то же самое место, куда он падает, когда корабль стоит неподвижно, то какую службу сослужил бы вам этот опыт с падением для решения вопроса, стоит ли судно неподвижно или же плывет?
Симпличио. — Решительно никакой; точно так же, например, по биению пульса нельзя узнать, спит ли кто или бодрствует, поскольку пульс бьется одинаково как у спящих, так и у бодрствующих.
Сальвиати. — Отлично. Производили ли вы когда-нибудь опыт на корабле?
Симпличио. — Я его не производил, но вполне уверен, что те авторы, которые его производили, Тщательно его рассмотрели; кроме того, причины различия столь ясны, что не оставляют места для сомнения.
Сальвиати. — Возможно, что эти авторы ссылались на опыт, не производя его; вы сами являетесь тому хорошим примером, когда, не производя опыта, объявляете его достоверным и предлагаете нам на слово поверить им; совершенно так же не только возможно, но и достоверно, что авторы поступали таким же образом, отсылая к своим предшественникам и никогда не доходя до того, кто этот опыт проделал сам, ибо всякий, кто его проделает, найдет, что опыт показывает совершенно обратное написанному, а именно, что камень всегда упадет в одно и то же место корабля, неподвижен ли он или движется с какой угодно скоростью.
|
Камень, падающий с корабельной мачты, всегда попадет в одно и то же место, движется ли корабль или стоит на месте. |
Симпличио. — Если бы вы отослали меня к иным доводам, а не к опыту, то споры наши, я думаю, окончились бы не так скоро, ибо предмет этот кажется мне столь недоступным для человеческого разума, что исключается возможность что-либо утверждать или предполагать.
Сальвиати. — И, однако, я считаю возможным это сделать.
Симпличио. — Как же это, не проделав ни ста испытаний, ни даже одного, вы выступаете столь решительным образом? Я возвращаюсь к своему неверию и к убеждению, что опыт был произведен первоначальными авторами, которые на него ссылаются, и что он показывает то, что они утверждают.
Сальвиати. — Я и без опыта уверен, что результат будет такой, как я вам говорю, так как необходимо, чтобы он последовал; более того, я скажу, что вы и сами так же знаете, что не может быть иначе, хотя притворяетесь или делаете вид, будто не знаете этого. Но я достаточно {118} хороший ловец умов и насильно вырву у вас признание. Однако, синьор Сагредо совсем умолк, хотя, мне кажется, я заметил какое-то движение, точно он хотел что-то сказать.
Сагредо. — Я в самом деле хотел кое-что сказать, но любопытство, вызванное вашим заявлением, что вы вынудите синьора Симпличио открыть намеренно скрываемое от нас знание, заставило меня отложить всякое иное попечение; прошу вас осуществить обещанное.
Сальвиати. — Лишь бы синьор Симпличио соблаговолил отвечать на мои вопросы, а за мной дело не станет.
Симпличио. — Я буду отвечать то, что знаю, и уверен, что затруднений у меня будет мало, так как о вещах, которые я считаю ложными, думается, нельзя знать ничего, поскольку наука есть наука об истинном, а не о ложном.
Сальвиати. — Я не хочу ничего, кроме того, чтобы вы говорили или отвечали только то, что сами достаточно знаете. Поэтому скажите мне: если у вас имеется плоская поверхность, совершенно гладкая, как Зеркало, а из вещества твердого, как сталь, не параллельная горизонту, но несколько наклонная, и если вы положите на нее совершенно круглый шар из вещества тяжелого и весьма твердого, например из бронзы, то что, думаете вы, он станет делать, будучи предоставлен самому себе? Не думаете ли вы (как я думаю), что он будет неподвижным?
Симпличио. — Если эта поверхность наклонна?
Сальвиати. — Да, таково задание.
Симпличио. — Никоим образом не думаю, чтобы он остался неподвижным; наоборот, я уверен, что он сам собою двигался бы по наклону.
Сальвиати. — Вдумайтесь хорошенько в свои слова, синьор Симпличио, ибо я уверен, что он будет пребывать в неподвижности в любом месте, куда бы вы его ни поместили.
Симпличио. — Если вы, синьор Сальвиати, станете пользоваться подобного рода предположениями, я перестану удивляться тому, что вы сделаете совершенно ложные выводы.
Сальвиати. — Значит, вы считаете совершенно достоверным, что шар будет двигаться по наклону сам собой?
Симпличио. — Разве в этом можно сомневаться?
Сальвиати. — И вы считаете это неоспоримым не потому, что я вам это внушил (ведь я старался убедить вас в противном), но на основании собственного суждения?
Симпличио. — Теперь я понимаю вашу хитрость; вы говорили так, чтобы испытать меня или подловить, как говорится в просторечии, а вовсе не потому, что думали так на самом деле?
Сальвиати. — Именно. И как долго продолжал бы двигаться шар и с какой скоростью? Заметьте, что я говорил о шаре совершенно круглом и о плоскости совершенно гладкой, чтобы устранить все внешние и случайные препятствия. Я хочу также, чтобы вы отвлеклись от сопротивления, оказываемого воздухом своему разделению, и от всех случайных помех, какие могут встретиться.
Симпличио. — Я все прекрасно понял и на ваш вопрос отвечу так: шар продолжал бы двигаться до бесконечности, лишь бы продолжалась такая плоскость, и притом движением непрерывно ускоряющимся, ибо такова природа тяжелых движущихся тел, которые vires acquirant eundo20; и чем больше будет наклон, тем больше будет и скорость.
Сальвиати. — Но если бы кому-нибудь захотелось, чтобы этот же шар двигался по той же плоскости вверх, думаете ли вы, что он пошел бы таким образом?
Симпличио. — Самостоятельно нет, но втащить его или с силой бросить вверх можно. {119}
Сальвиати. — А если бы он был приведен в такое движение насильственно переданным ему импульсом, каково и сколь продолжительно было бы его движение?
Симпличио. — Движение шло бы, постепенно ослабевая и замедляясь, поскольку оно противоестественно, и было бы более продолжительным или более кратким в зависимости от большей или меньшей крутизны подъема.
Сальвиати. — Как будто вы объяснили мне сейчас случаи движения по двум разного рода плоскостям: на плоскости наклонной движущееся тело самопроизвольно опускается, двигаясь с непрерывным ускорением, так что требуется применить силу для того, чтобы удержать его в покое; на плоскости, поднимающейся вверх, требуется сила для того, чтобы двигать тело вверх, и даже для того, чтобы удержать его в покое, причем сообщенное телу движение непрерывно убывает, так что в конце концов вовсе уничтожается. Добавим еще, что, кроме того, в том и другом случае возникает различие в зависимости от того, больше или меньше наклон или подъем плоскости, причем при большем наклоне имеет место большая скорость, и наоборот, при поднимающейся плоскости то же тело, движимое той же самой силой, продвигается на тем большее расстояние, чем меньше высота подъема. А теперь скажите мне, что произошло бы с тем же движущимся телом на поверхности, которая не поднимается и не опускается?
Симпличио. — Здесь мне нужно немного подумать над ответом. Раз там нет наклона, то не может быть естественной склонности к движению, и раз там нет подъема, не может быть противодействия движению, так что тело оказалось бы безразличным по отношению как к склонности к движению, так и противодействию ему; мне кажется, следовательно, что оно естественно должно оставаться неподвижным. Однако, я совсем забыл, что синьор Сагредо еще совсем недавно растолковал мне, что это так и должно быть.
Сальвиати. — Так, думаю я, было бы, если бы шар положить неподвижно; но если придать ему импульс движения в каком-нибудь направлении, то что воспоследовало бы?
Симпличио. — Воспоследовало бы его движение в этом направлении.
Сальвиати. — Но какого рода было бы это движение: непрерывно ускоряющееся, как на плоскости наклонной, или постепенно замедляющееся, как на плоскости поднимающейся?
Симпличио. — Я не могу открыть здесь причины для ускорения или для замедления, поскольку тут нет ни наклона, ни подъема.
Сальвиати. — Так, но если здесь нет причины для замедления, то тем менее может находиться здесь причина для покоя. Поэтому сколь долго, полагаете вы, продолжалось бы движение этого тела?
Симпличио. — Столь долго, сколь велика длина такой поверхности без спуска и подъема.
Сальвиати. — Следовательно, если бы такое пространство было беспредельно, движение по нему равным образом не имело бы предела, т. е. было бы постоянным?
Симпличио. — Мне кажется, что так, если бы тело было из прочного материала.
Сальвиати. — Это уже предполагается, поскольку было сказано, что устраняются все привходящие и внешние препятствия, а разрушаемость движущегося тела есть одно из привходящих препятствий. Скажите мне, что именно считаете, вы причиной того, что этот шар движется по наклонной плоскости самостоятельно, а по плоскости поднимающейся не иначе, как насильственно? {120}
Симпличио. — То, что тяжелые тела имеют свойство естественно двигаться к центру Земли и лишь насильственно вверх к периферии, наклонная же поверхность такова, что приближает к центру, а поднимающаяся удаляет.
Сальвиати. — Следовательно, поверхность, которая не имела бы ни наклона, ни подъема, должна была бы во всех своих частях одинаково отстоять от центра. Но из подобных плоскостей есть ли где такие в мире?
Симпличио. — Такие есть, — хотя бы поверхность нашего земного шара, будь только она вполне гладкой, а не такой, какова она на самом деле, т. е. неровной и гористой; такова, например, поверхность воды, когда она тиха и спокойна.
Сальвиати. — Следовательно, корабль, движущийся по морской глади, есть одно из тех движущихся тел, которые скользят по одной из таких поверхностей без наклона и подъема и которые поэтому имеют склонность в случае устранения всех случайных и внешних препятствий двигаться с раз полученным импульсом постоянно и равномерно?
Симпличио. — Кажется, что так должно быть.
Сальвиати. — И тот камень, который находится на вершине мачты, не движется ли он, переносимый кораблем по окружности круга, вокруг центра, следовательно, движением, в нем не уничтожаемым при отсутствии внешних препятствий? И это движение не столь же ли быстро, как движение корабля?
Симпличио. — До сих пор все идет хорошо. Но дальше?
Сальвиати. — Не выведете ли вы, наконец, сами и последнее заключение, если сами знаете вперед все предпосылки?
Симпличио. — Вы хотите назвать последним заключением то, что этот камень, благодаря движению, в него вложенному, не способен ни отставать от хода корабля, ни опережать его и должен в конце концов упасть в то самое место, куда упал бы, когда корабль стоит неподвижно; это, я думаю, и случилось бы, не будь здесь внешних препятствий, нарушающих движение камня после того, как он выпущен, а таких препятствий два: одно — это неспособность тела рассекать воздух одним своим импульсом, поскольку оно лишается импульса силы весел, которым оно обладало, будучи частью корабля, пока находилось на вершине мачты; второе — новое движение, т. е. падение вниз, которому надлежит быть препятствием для другого, поступательного движения.
Сальвиати. — Что касается препятствия со стороны воздуха, то я его не оспариваю, и, будь падающее тело из очень легкого вещества, как например, пух или клочок шерсти, замедление было бы очень значительным, но для тяжелого камня оно ничтожно. Вы сами недавно сказали, что сила самого стремительного ветра недостаточна, чтобы сдвинуть с места большой камень; подумайте теперь, что может сделать спокойный воздух при встрече с камнем, двигающимся не быстрее корабля; тем не менее я, как уже сказал, допускаю тот незначительный эффект, который может зависеть от такого препятствия. Я знаю, вы, со своей стороны, согласитесь со мной в том, что если воздух будет двигаться со скоростью корабля и камня, то сопротивление сведется к нулю. Что же касается другого движения, происходящего по направлению вниз, то прежде всего очевидно, что эти два движения, а именно, круговое вокруг центра и прямолинейное к центру, не противоположны друг другу, друг друга не разрушают и вполне одно с другим совместимы, ибо у движущегося тела нет никакого противодействия подобному движению, поскольку вы сами уже признали, что сопротивление направлено против движения, удаляющего от центра, склонность же относится к движению, приближающему к центру. Отсюда с необходимостью вытекает, что к движению, не удаляющему от центра и не приближающему к нему, тело не имеет ни склонности, {121} ни сопротивления, а следовательно, нет и причины для уменьшения вложенной в него силы; а так как причина движения, которая должна была бы ослабевать под влиянием нового воздействия, не единственная, но их имеется две, друг от друга отличные, из коих тяжесть стремится только влечь тело к центру, а вложенная в него сила — водить вокруг центра, то не остается никаких оснований для уменьшения сообщенного его телу импульса.
Симпличио. — По правде сказать, рассуждение с виду довольно правдоподобно, но по существу оно немного испорчено одним трудно преодолеваемым затруднением. Вы, несомненно, исходите из предположения, с которым нелегко согласится вся перипатетическая школа, поскольку оно решительно противоречит Аристотелю, а именно: вы допускаете в качестве чего-то известного и очевидного, что брошенное тело,
|
Брошенное тело движется, по Аристотелю, не вложенной в него силой, но средой. |
Сальвиати. — Мне кажется, из вашей речи можно заключить, что если камень не будет брошен чьей-либо рукой, то его собственное движение не может оказаться бросанием?
Симпличио. — В собственном смысле его нельзя назвать движением брошенного тела.
Сальвиати. — Следовательно, то, что Аристотель говорит о движении, движущемся теле и силе бросания, не имеет никакого отношения к нашей теме; а если нам нечего с этим делать, то к чему вы это приводите?
Симпличио. — Привожу из любви к этой вложенной силе, упомянутой и введенной вами, каковая, не существуя на свете, ничего не может производить, ибо non entium nullae sunt operationes21, а потому причину движения не только брошенных тел, но и всяких других движений, не являющихся естественными, следует приписывать среде, что не было надлежащим образом принято во внимание, почему все сказанное до сих пор остается бездоказательным.
Сальвиати. — Подождите, все в свое время. Но скажите мне, раз ваша позиция целиком основывается на отсутствии существования вложенной силы, то, если бы я вам доказал, что среда не имеет никакого отношения к продолжению движения брошенных тел, после того как они отделились от бросившего их, признаете ли вы существование вложенной силы или же ринетесь в новую атаку для ее разрушения?
Симпличио. — Если устранено действие среды, то я не вижу, чтобы можно было прибегнуть к чему-либо другому, кроме силы, сообщенной двигателем.
Сальвиати. — Для того чтобы по возможности устранить поводы к бесконечным спорам, было бы хорошо, если бы вы как можно отчетливее объяснили, каково действие среды при продолжении движения у брошенного тела? {122}
|
Действие среды при продолжающемся движении брошенного тела. |
Сальвиати. — И вы были столь легковерны, что дали убедить себя таким вздором, тогда как имеете чувства для его опровержения и для уразумения истины? Скажите, если большой камень или артиллерийский снаряд, только положенные на стол, остаются неподвижными даже при
|
Разные опыты и доводы против принимаемой Аристотелем причины движения брошенного тела. |
Симпличио. — Знаю наверное, что ветер унес бы их прочь и тем быстрее, чем легче было бы вещество; вот почему мы видим, как облака несутся со скоростью, равной скорости самого ветра, который их гонит.
Сальвиати. — А что такое ветер?
Симпличио. — Ветер, согласно определению, есть не что иное, как движущийся воздух.
Сальвиати. — Следовательно, движущийся воздух переносит вещества легчайшие гораздо быстрее и на большее расстояние, чем тяжелые?
Симпличио. — Конечно.
Сальвиати. — Но если вам надо бросить рукой камень, а затем клочок хлопка, то что будет двигаться с большей скоростью и на большее пространство?
Симпличио. — Конечно, камень; наоборот, хлопок упадет к моим ногам.
Сальвиати. — Но, если то, что движет брошенное тело после того, как его выпустила рука, есть не что иное, как воздух, движимый рукой, а движущийся воздух легче переносит легкие вещества, нежели тяжелые, то почему же брошенное тело, состоящее из хлопка, не уносится дальше и быстрее, чем тело из камня? Необходимо, значит, чтобы в камне оставалось кое-что, помимо движения воздуха? Кроме того, если с какой-нибудь балки спустить два шнура равной длины, на конце одного прикрепить шарик из свинца, а на конце другого шарик из хлопка, одинаково отклонить оба от перпендикуляра, а затем предоставить их самим себе, то и тот и другой, несомненно, двинутся к перпендикуляру, гонимые собственным импульсом, перейдут за него на некоторое пространство и затем вернутся назад. Который же из этих двух маятников, думаете вы, продолжал бы двигаться дольше, прежде чем остановиться отвесно?
Симпличио. — Свинцовый шар будет качаться туда и сюда тысячу раз, а шар из хлопка раза два или три, самое большее.
Сальвиати. — Таким образом, импульс и подвижность, какова бы ни была их причина, сохраняются дольше в телах тяжелых, чем в легких. Перехожу теперь к другому пункту и спрашиваю вас: почему воздух не уносит померанца, который лежит на том столе?
Симпличио. — Потому что сам воздух не движется.
Сальвиати. — Надобно, следовательно, чтобы бросающий сообщил воздуху то движение, которым последний будет затем двигать брошенное тело. Но если такая способность не может передаваться, поскольку нельзя заставить перейти свойство одного предмета к другому, то как может она перейти от руки к воздуху? Разве рука не является иным предметом, чем воздух?
Симпличио. — Ответ гласит, что воздух, не будучи ни тяжелым, ни легким в своей области, способен воспринимать совершенно свободно всякий импульс, а также и сохранять его. {123}
Сальвиати. — Но если маятники нам только что показали, что чем менее движущееся тело причастно тяжести, тем менее способно оно сохранять движение, то как же может случиться, что воздух, который совсем не имеет тяжести, один сохраняет начатое движение? Я полагаю и знаю, что и вы теперь также думаете, что как только останавливается рука, так останавливается и воздух. Войдем в комнату и будем сколь возможно больше возмущать воздух, размахивая полотенцем; затем, оставив полотенце, внесем в комнату небольшую зажженную свечку или пустим лететь тончайший листик золота; по спокойному поведению их вы увидите, что воздух не замедлил успокоиться. Я мог бы привести вам тысячу таких опытов, но в отношении того, кто не довольствуется одним из них, всякое старание безнадежно.
Сагредо. — Когда стрела пускается против ветра, то сколь невероятно, чтобы струйка воздуха, гонимая тетивой, шла наперекор его течению, сопровождая стрелу! Но я хотел бы узнать у Аристотеля еще одну частность, почему прошу синьора Симпличио почтить меня ответом. Если из одного и того же лука вы пустите две стрелы, одну острием вперед, как обычно, а другую боком, т. е. положив ее вдоль тетивы и выпустив плашмя, то мне хотелось бы знать, которая из них полетит дальше? Благоволите мне ответить, хотя, быть может, мой вопрос и кажется вам скорее смешным, чем серьезным? И извините меня, что я, будучи, как видите, в бедственном положении, не могу подняться выше при помощи собственной умозрительной способности.
Симпличио. — Я никогда не видел, чтобы пускали стрелы поперек: все же думаю, что стрела, поставленная поперек, не совершит и двадцатой части того пути, который совершает, летя острием вперед.
Сагредо. — Так как я думал то же самое, то и нашел здесь повод усомниться в согласии слов Аристотеля с опытом. Ибо, что касается опыта, то если я положу на этот стол две стрелы, в то время как дует сильный ветер, поместив одну из них вдоль струи ветра, а другую — поперек, то ветер скорее унесет последнюю и оставит на месте первую; то же самое, кажется мне, должно было бы случиться, если бы учение Аристотеля было истинным, и с двумя стрелами, выпущенными из лука. В самом деле, стрела, расположенная поперек, уносится большим количеством воздуха, приведенного в движение тетивой, соответствующим длине стрелы, тогда как другая получает импульс только от воздуха, расположенного маленьким кружочком, соответствующим толщине стрелы. Я не в силах найти причины такого различия и желал бы ее узнать.
Симпличио. — Причина мне кажется в достаточной мере ясной; заключается же она в том, что стрела, выпущенная острием, должна рассекать малое количество воздуха, тогда как другая должна рассекать столько воздуха, сколько его находится по всей ее длине.
Сагредо. — Значит, пущенные стрелы должны рассекать воздух? Но если воздух движется с ними и даже является тем, что их перемещает, то какое же тут может быть рассекание? Не видите ли вы, что в таком случае стреле нужно было бы двигаться с большей скоростью, чем воздуху? А что же сообщает стреле эту большую скорость? Скажете ли вы, что воздух дает ей скорость бо́льшую, чем его собственная? Поймите же, синьор Симпличио: дело происходит как раз обратно тому, что говорит Аристотель, и что в той же мере ложно мнение, будто среда сообщает движение брошенному телу, в какой справедливо то мнение, что она
|
Среда не вызывает движения, но препятствует ему. |
Сальвиати. — Как много положений я заметил у Аристотеля (я всегда имею в виду натуральную философию), которые не просто ошибочны, но ошибочны так, что истинным оказывается диаметрально им противоположное, как мы видим в этом случае! Но возвратимся к нашей теме. Я думаю, синьор Симпличио убедился, что из наблюдений над падением камня всегда в одно и то же место нельзя вывести заключение о движении или неподвижности корабля, а если сказанного до сих пор недостаточно, то есть еще опыт со средой, который может ему все доказать: в этом опыте самое большое, что можно наблюдать, это отставание падающего тела, если оно сделано из вещества весьма легкого и если воздух не следует за движением корабля; но если бы воздух двигался с равной скоростью, никакого воображаемого различия не оказалось бы ни в этом, ни в любом другом опыте, как я вскоре вам покажу. И если в этом случае не обнаруживается никакого различия, то как можно претендовать на то, чтобы видеть его при падении камня с вершины башни, где круговое движение для камня не случайное и привходящее, но естественное и вечное, и где воздух в точности следует за движением башни, а башня за движением земного шара? Имеете ли вы, синьор Симпличио, еще что-нибудь возразить по этому поводу?
Симпличио. — Ничего, кроме того, что я еще до сих пор не вижу, чтобы и подвижность Земли была доказана.
Сальвиати. — Я совсем и не претендовал доказать ее; я хотел только показать, что из опыта, приводимого противниками в качестве аргумента в пользу ее неподвижности, ничего нельзя извлечь; то же я попытаюсь показать и по отношению к другим аргументам.
Сагредо. — Пожалуйста, синьор Сальвиати, прежде чем перейти к другому, позвольте мне изложить одно затруднение, которое пришло мне в голову, пока вы с таким терпением подробно разбирали для синьора Симпличио опыт с кораблем.
Сальвиати. — Мы собирались здесь для беседы, и потому каждому следует выдвигать те затруднения, с которыми он встречается, ибо таков путь, ведущий к познанию истины. Итак, говорите.
Сагредо. — Если верно, что импульс, с которым движется корабль, остается ненарушимо сохраняющимся в камне после того, как он отделился от мачты, и если верно, кроме того, что это движение не создает препятствия или замедления для прямого естественного движения вниз, то из этого необходимо вытекает удивительное явление в природе. Пусть
|
Замечательное свойство движения брошенных тел. |
Сальвиати. — Ваше рассуждение прекрасно по своей новизне, и если явление действительно таково, то оно достойно удивления, а в истинности его я не сомневаюсь; если бы не имелось привходящего сопротивления воздуха, я считал бы бесспорным, что если одним ядром выстрелить из пушки, а другому дать упасть с той же высоты отвесно вниз, то оба они достигнут Земли в одно и то же мгновение, хотя первое пройдет расстояние, быть может, в десять тысяч локтей, а второе — только в сто; при этом предполагается, что поверхность Земли совершенно ровная, почему для верности следовало бы стрелять на каком-нибудь озере. Препятствие, которое представлял бы собой воздух, сказалось бы в замедлении чрезвычайно быстрого движения ядра после выстрела. Теперь, если вам угодно, перейдем к разрешению других возражений, если только синьор Симпличио, как я полагаю, уже вполне убежден в несостоятельности первого, почерпнутого из опыта с телами, падающими сверху вниз.
Симпличио. — Я еще не чувствую себя совершенно свободным от всех сомнений; может быть, это присущий мне недостаток, но я усваиваю не столь легко и быстро, как синьор Сагредо. Мне кажется, что если то движение, которому причастен камень, пока он находится на мачте корабля, должно сохраняться в нем нерушимо, как вы говорите, даже после того, как он оказывается разобщенным с кораблем, то подобное этому должно было бы происходить и со всадником, быстро скачущим на коне, если он выпустит из рук шар, каковой после падения на землю должен будет продолжать следовать в своем движении за бегом коня, не отставая от него. Я не думаю, что такое явление наблюдалось, исключая, может быть, только тот случай, когда всадник бросит шар с силой в сторону движения; без этого же я думаю, шар останется на земле там, куда он упадет.
Сальвиати. — Я думаю, вы весьма заблуждаетесь, и уверен, что опыт покажет вам противное: шар, достигнув земли, будет двигаться вместе с конем и не отстанет от него, если только его не остановят негладкость и неровность пути, И основание для того кажется мне достаточно ясным: ведь, когда вы, стоя неподвижно, покатите шар по земле, не продолжает ли он движение даже вне вашей руки? И на расстояние, тем более далекое, чем ровнее поверхность, так что по льду, например, он укатится очень далеко.
Симпличио. — Это несомненно, если я дам ему импульс рукой, но в нашем случае предполагается, что всадник просто дает шару возможность упасть.
Сальвиати. — Так. я это и предполагаю. Но когда вы катите шар рукой, что иное остается у него, вышедшего уже из вашей руки, кроме движения, порожденного рукой, которое сохраняется в нем и продолжает вести его вперед? А какая разница, будет ли этот импульс сообщен шару {126} вашей рукой или конем? Разве, когда вы на коне, ваша рука, а следовательно, и шар, не движутся столь же быстро, как сам конь? Конечно, так; следовательно, и при одном разжатии руки шар выходит уже с движением, но порожденным не вашей рукой, не особым ее движением, но движением, зависящим от самого коня, которое сообщается вам, руке, пальцам и, наконец, шару. Но я хочу сказать вам и более того: если всадник на-скаку бросит шар рукой в сторону, противоположную движению, то, достигнув земли, шар, хотя и брошенный в противоположную сторону, иногда все же будет следовать за бегом коня, а иногда останется неподвижным на земле и только в том случае будет двигаться в сторону, противоположную движению коня, когда движение, полученное от руки, будет по скорости превосходить бег коня. И вздор говорит тот, кто утверждает, будто всадник может метнуть дротик в воздух в сторону движения, на коне последовать за ним, догнать и, наконец, опять схватить его; это, говорю я, — вздор, ибо для того, чтобы брошенное тело вернулось вам в руку, надобно подбросить его вверх совершенно так, как находясь в неподвижности; ибо как бы быстро ни было движение, если только оно равномерно, а брошенное тело не является вещью очень легкой, то тело это всегда упадет обратно в руку бросившего, на какую бы высоту оно ни было брошено.
Сагредо. — Исходя из этого учения, я прихожу к познанию некоторых довольно любопытных проблем, касающихся таких брошенных
|
Различные любопытные проблемы, связанные с движением брошенных тел. |
Симпличио. — Я скажу, во-первых, что подобного наблюдения не производил; во-вторых, что я этому не верю, и, наконец, в-третьих, что если вы меня в этом убедите и мне это покажется, то вы будете великим демоном.
Сагредо. — Но демоном Сократа, а не демоном ада. Однако, вы все еще требуете поучения. Я же говорю вам, что, если кто-либо не знает истины сам от себя, невозможно, чтобы другие заставили его это узнать; я могу прекрасно учить вас вещам, которые ни истинны, ни ложны, но то, что истинно, т. е. необходимо, чему невозможно быть иным, — это каждый заурядный ум знает сам по себе или же невозможно, чтобы он это вообще узнал. Я знаю, что и синьор Сальвиати думает так же. Поэтому, говорю вам, что основания настоящих проблем вам известны, хотя, быть может, вы и не отдаете себе в них отчета.
Симпличио. — Оставим этот спор: согласитесь с моим заявлением, что я ничего не понимаю и не знаю о тех вещах, о которых идет речь, и постарайтесь сделать так, чтобы я одолел эту проблему. {127}
Сагредо. — Эта первая зависит от другой, а именно: почему происходит то, что при метании диска с помощью веревки он идет гораздо дальше и, следовательно, с большей силой, чем брошенный просто рукой?
Симпличио. — Аристотель также ставит некоторые проблемы касательно этих брошенных тел.
Сальвиати. — Да, и весьма остроумные, в частности, почему круглые диски движутся лучше четырехугольных.
Сагредо. — И у вас нехватило духу дать этому объяснение, синьор Симпличио, не прибегая к помощи поучения со стороны?
Симпличио. — Будет, будет, оставим насмешки.
Сагредо. — Тогда вы знаете объяснение также и другой проблемы. Скажите мне, знаете ли вы, что движущееся тело при встрече с препятствием останавливается?
Симпличио. — Знаю, однако, лишь когда препятствие достаточно для этого.
Сагредо. — Знаете ли вы, что большее препятствие создает для движения тела земля, нежели воздух, поскольку земля неровна и тверда, а воздух мягок и податлив?
Симпличио. — И так как я это знаю, то знаю и то, что диск пойдет по воздуху быстрее, чем по земле. Так что мое заключение совершенно противоположно тому, которое вы предполагаете.
Сагредо. — Не спешите, синьор Симпличио. Знаете ли вы. что у частей движущегося тела, обращающихся вокруг своего центра, имеются движения во все стороны? Так что одни части поднимаются, другие опускаются, эти идут вперед, а те назад.
Симпличио. — Знаю, и этому научил меня Аристотель.
Сагредо. — Путем какого доказательства? Пожалуйста, скажите.
Симпличио. — Путем свидетельства чувств.
Сагредо. — Следовательно, Аристотель заставил вас увидеть то, что без него вы не увидали бы? Одолжил ли он вам когда-либо свои глаза? Вы хотите сказать, что Аристотель вам это сказал, отметил, напомнил, но не научил. Итак, когда диск, не меняя места, вращается вокруг себя, будучи расположен не параллельно, а перпендикулярно к горизонту, тогда некоторые его части поднимаются, противоположные опускаются, верхние идут в одну сторону, нижние в противоположную. Представьте себе теперь диск, который, не меняя места, быстро вращается вокруг себя, находясь в воздухе; если ему дана возможность, попрежнему вращаясь, упасть отвесно на землю, думаете ли вы, что, достигнув земли, он будет продолжать вращаться вокруг самого себя, не меняя места, как и раньше?
Симпличио. — Нет, синьор.
Сагредо. — А что же он будет делать?
Симпличио. — Он быстро побежит по земле.
Сагредо. — Ив каком направлении?
Симпличио. — В том, куда его понесет его вращение.
Сагредо. — Его части при вращении движутся разно, а именно — верхние движутся противоположно нижним; потому надо сказать, каким он будет подчиняться. Что же касается частей поднимающихся и опускающихся, то они не уступают друг другу, а целое не будет двигаться ни вниз, поскольку этому препятствует земля, ни вверх из-за своей тяжести.
Симпличио. — Диск пойдет, вращаясь, по земле, в том направлении, куда его увлекают верхние его части.
Сагредо. — А почему не туда, куда влекут противоположные, т. е. те, которые касаются земли?
Симпличио. — Потому что находящимся у земли будут препятствовать неровности в месте соприкосновения, т. е. шероховатость земли, {128} верхние же, находясь в воздухе, податливом и тонком, почти совсем не испытывают препятствий или испытывают их в самой малой степени: потому диск и пойдет в их сторону.
Сагредо. — Так что это, если можно так сказать, прикрепление к земле нижних частей и вызывает то, что они остаются на месте и только верхние подаются вперед?
Сальвиати. — А потому, если бы диск упал на лед или другую совершенно гладкую поверхность, то он побежал бы вперед не так хорошо и мог бы, пожалуй, продолжать вращаться вокруг себя, не приобретая нового поступательного движения?
Сагредо. — Это очень легко могло бы случиться; и во всяком случае, он шел бы не столь быстро, как падая на поверхность, несколько шероховатую. Но пусть скажет мне синьор Симпличио, если диск, приведенный в быстрое вращение вокруг себя, пущен свободно, почему в воздухе он не идет вперед, как делает это потом, упав на землю?
Симпличио. — Поэтому что, поскольку воздух окружает его сверху и снизу, ни те, ни другие части не имеют, на что опереться, и диск, не имея причины итти вперед более, чем назад, падает отвесно.
Сагредо. — Так что одно вращение вокруг себя без иного импульса может гнать диск, достигший земли, достаточно быстро. Перейдем теперь к остальному. Какое действие производит в диске бечевка, которую привязывают к руке и при помощи которой, обмотав ее вокруг диска, бросают диск.
Симпличио. — Разматывание веревки понуждает диск вращаться вокруг себя.
Сагредо. — Так что, когда диск достигает земли, он благодаря веревке обладает вращением вокруг себя. Не было ли, следовательно, в нем самом причины двигаться на земле быстрее, чем во время пребывания в воздухе?
Симпличио. — Конечно, да, ибо в воздухе он не имел другого импульса, кроме импульса руки бросающего, и хотя бы он обладал еще и вращением, последнее, как было сказано, вовсе не гонит его в воздухе; только по достижении земли к движению руки присоединяется поступательное движение от вращения, отчего скорость усиливается; и я прекрасно уже понимаю, что при подбрасывании диска вверх скорость его уменьшается, потому что помощь круговращения у него отсутствует, а при падении обратно на землю ему удается ее вернуть и потому опять притти в более быстрое движение, чем в воздухе. Мне остается только понять, почему при этом втором движении по земле диск идет быстрее, чем при первом, ибо тогда, при продолжении движения до бесконечности, оно должно было бы все ускоряться.
Сагредо. — Я совсем не говорил, что это второе движение непременно будет быстрее первого; я только утверждал, что иногда может случиться, что оно будет быстрее.
Симпличио. — Именно этого я и не понимаю и хотел бы это себе уяснить.
Сагредо. — И это также вы знаете сами по себе. В самом деле, скажите, если вы даете шару падать из руки без того, чтобы он вращался вокруг себя самого, что сделает он, упав на землю?
Симпличио. — Ничего, он там и останется.
Сагредо. — Не может ли случиться так, что при ударе о землю он получит движение? Подумайте-ка получше.
Симпличио. — Разве только, если бы мы дали ему упасть на какой-нибудь камень, имеющий наклон, как делают дети, играя в орлянку, и он, ударившись косо о выступающий камень, приобрел бы круговращение {129} вокруг себя, с которым и продолжал бы затем двигаться поступательно по земле. Я не знаю иного случая, где он мог бы сделать что-нибудь другое, кроме как остановиться там, где упал.
Сагредо. — Так вот, значит, каким образом он может приобрести новое вращение. Итак, когда диск, подброшенный вверх, падает обратно вниз, почему он не может удариться о какой-нибудь находящийся на земле камень, имеющий наклон в сторону движения, и, приобретая от такого удара новое вращение сверх первого, сообщенного веревкой, ускорить свое движение и сделать его более быстрым, чем оно было при первом ударе о землю?
Симпличио. — Теперь я понимаю, что это может случиться. И я полагаю, что если диск получит вращение в обратную сторону, то по достижении земли это даст обратный эффект, а именно — движение вращения замедлит движение от бросания.
Сагредо. — Замедлит, а иногда и совсем уничтожит его, лишь бы вращение было достаточно быстрым. Отсюда вытекает объяснение того приема, который применяют себе на пользу более опытные игроки в мяч, чтобы обмануть противника и срезать (таков их термин) мяч; прием этот заключается в том, чтобы при помощи наклонной ракетки отбить мяч так, чтобы он приобрел вращение, противоположное движению бросания; вследствие этого, достигнув земли, мячик не делает того скачка, который сделал бы, если бы не вращался, по направлению к противнику, давая ему обычно требующееся время, чтобы успеть его отбить, но останется как бы мертвым и приставшим к земле или же отскочит гораздо меньше, чем обычно, и не даст времени его отбить22. По этой же причине при игре деревянными шарами, заключающейся в том, чтобы подойти возможно ближе к определенному знаку, если играют на каменистой дороге, полной препятствий, способных тысячью способов отклонить шар от движения по направлению к знаку, поступают так: во избежание всех отклоняющих препятствий шар не катят по земле, а бросают его по воздуху, как если бы бросили плоскую дощечку; при этом учитывают, что при бросании шар выходит из руки с некоторым вращением, сообщаемым ему пальцами руки; если, как обычно в таких случаях, рука при бросании находится под шаром, то шар, ударившись о землю около знака, благодаря движению от бросания и движению от вращения может уйти далеко от цели; для того чтобы он остановился, охватывают шар, держа руку искусственным приемом сверху, а шар снизу, почему последнему при выскальзывании из пальцев придается противоположное вращение, благодаря которому при ударе о землю возле знака шар там и останавливается или только немного уходит вперед. Однако, возвращаясь к главной проблеме, которая породила все остальные, я говорю, что быстро движущийся человек может выпустить из руки шар, который, достигнув земли, не только будет следовать за движением человека, но еще и опередит его. двигаясь с большей скоростью. Чтобы убедиться в этом, представим себе, что в движении находится повозка, у которой сбоку снаружи приделана наклонная доска, нижняя часть которой обращена к лошадям, а верхняя к задним колесам. Если при быстром движении повозки кто-нибудь, в ней находящийся, даст упасть шару вниз по скату этой доски, то шар, скатываясь вниз, приобретет вращение вокруг себя, каковое в соединении с движением, сообщенным повозкой, понесет шар по земле еще быстрее повозки; а если бы была прилажена другая доска, наклоненная в противоположном направлении, можно было бы соразмерить движение повозки так, чтобы шар, скатившись вниз по доске, остался по достижении земли без движения, а иногда даже двигался в направлении, противоположном повозке. Но я слишком долго распространялся об этом предмете; если синьор Симпличио удовлетворен разрешением первого, {130} довода против подвижности Земли, почерпнутым из отвесного падения тел, то можно будет перейти к другим.
Сальвиати. — Отступления, сделанные до сих пор, не столь чужды разбираемому предмету, чтобы можно было назвать их совершенно с ними не связанными. Кроме того, рассуждения зависят от того, что приходит в голову не одному, а троим, и, беседуя по своему вкусу, мы не связаны той строгостью, которая обязательна для рассуждающего ex professo* методически об одном предмете, к тому же, быть может, с намерением обнародовать свое рассуждение. Я не хочу, чтобы наша поэма была настолько связана требованием единства, чтобы у нас не оставалось свободного поля для эпизодов; для их введения нам должно быть достаточно каждого малейшего повода, как будто мы здесь собрались, чтобы рассказывать сказки. И пусть мне будет позволено говорить так, вспоминая слышанное от вас.
Сагредо. — Это мне очень нравится; и раз мы так свободны, то да позволено мне будет, прежде чем перейти к дальнейшему, узнать от вас, синьор Сальвиати, приходила ли вам когда-либо мысль о том, какой следует представлять себе линию, описываемую движущимся телом, естественно падающим с вершины башни вниз; если вы над этим размышляли, то скажите, пожалуйста, что вы думаете?
Сальвиати. — Мне не случалось об этом думать, и я ничуть не сомневаюсь, что если бы мы были вполне уверены в природе движения, с которым тяжелое тело опускается, направляясь к центру земного шара, сочетая его с общим круговым движением суточного обращения, то в точности было бы найдено, какого рода линию описывает центр тяжести движущегося тела при сочетании этих двух движений.
Сагредо. — Простое движение к центру, зависящее от тяжести, думается мне, можно без всякой ошибки считать происходящим по прямой линии, что именно имело бы место, если бы Земля была неподвижной.
Сальвиати. — Что касается этого, то мы не только можем так думать, но это удостоверяет нам и опыт.
Сагредо. — Но как же удостовериться в этом на опыте, если мы никогда не видим иного движения, кроме составленного из двух — кругового и движения вниз.
Сальвиати. — Совсем нет, синьор Сагредо, мы видим только простое движение вниз, ибо другое, т. е. круговое движение, общее Земле, башне и нам, остается неуловимым и как бы несуществующим, и единственно доступным нам остается то движение камня, в котором мы не участвуем; а относительно последнего чувство показывает нам, что оно происходит по прямой линии, оставаясь всегда параллельным той башне, которая воздвигнута на земной поверхности прямо и отвесно.
Сагредо. — Вы правы; с моей стороны было большой недогадливостью, что я сам не сообразил столь простой вещи. Но раз это совершенно понятно, чего еще вам нужно, чтобы понять природу такого движения вниз?
Сальвиати. — Недостаточно понять, что оно прямое, но требуется узнать, равномерное ли оно или же неравномерное, т. е. сохраняет ли оно всегда одну и ту же скорость или же идет замедляясь или ускоряясь?
Сагредо. — Ясно, что оно идет, непрерывно ускоряясь.
Сальвиати. — Этого недостаточно; следовало бы узнать, в какой пропорции совершается это ускорение; задача эта, я думаю, до сих пор не была разрешена ни одним из философов или математиков, хотя философами, в частности перипатетиками, были написаны о движении целые огромные томы. {131}
Симпличио. — Философы занимаются, главным образом, вопросами универсальными: они находят определения и наиболее общие признаки, оставляя затем те или иные тонкости, те или иные подробности, являющиеся скорее курьезами, математикам. Аристотель удовольствовался прекрасным определением движения вообще и указанием главных атрибутов местного движения, т. е. что одно естественно, а другое неестественно, одно — простое, другое — сложное, одно — равномерное, другое ускоренное; в отношении ускоренного он удовольствовался указанием причины ускорения, оставляя изучение вопроса о мере ускорения и других привходящих свойствах механику или другому ниже стоящему ремесленнику.
Сагредо. — Согласен, дорогой синьор Симпличио. Но вам, синьор Сальвиати, не случалось ли иногда нисходить с трона перипатетического величия и забавляться изучением пропорциональности ускорения движения у падающих тяжелых тел?
Сальвиати. — У меня не было необходимости думать об этом, так как наш общий друг Академик уже показал мне свой трактат о движении, где все это доказано вместе со многими другими частностями23. Но было бы слишком большим отклонением в сторону, если бы из-за этого мы прервали настоящее рассуждение, которое само по себе уже является отклонением, и устроили бы, как говорится, комедию в комедии.
Сагредо. — Я согласен с тем, чтобы вы воздержались от этого сообщения теперь, но с условием, что этот вопрос будет одним из тех, которые оставляются для рассмотрения на другом особом собрании, потому что ознакомление с ним является для меня весьма желательным. Пока обратимся к линии, описываемой тяжелым телом, падающим с высоты башни к ее основанию.
Сальвиати. — Если бы прямое движение к центру Земли шло равномерно, то, поскольку и круговое движение к востоку также равномерно, оказалось бы, что из обоих складывается одно движение по одной из спиральных линий, определение которым дано Архимедом в его книге «О спиралях». Спирали образуются тогда, когда точка равномерно движется по прямой линии, которая также равномерно движется около одной из своих конечных точек, неподвижно установленной в качестве центра ее обращения. Но так как прямое движение падающего тела непрерывно ускоряется, то необходимо, чтобы линия движения, составленного из двух движений, шла, все в большей степени удаляясь от окружности того круга, который описал бы центр тяжести камня, если бы он оставался все время наверху башни, и надобно, чтобы это удаление вначале было маленьким, минимальным, минимальнейшим, ибо падающее тело, выходящее из состояния покоя, т. е. лишенное движения книзу и начинающее это движение вниз, должно пройти все степени медленности, находящиеся между покоем и какой бы то ни было скоростью; степеней же этих бесконечное множество, как это уже было подробно объяснено и установлено.
Итак, раз таково возрастание ускорения и раз, кроме того, верно, что падающее тело движется, чтобы притти к центру Земли, то линия его
|
Линия, описываемая свободно падающим телом при предположении вращения Земли около своего центра, вероятно, была бы окружностью круга. |
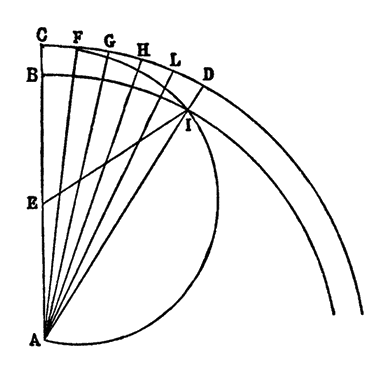 и BI, представят нам ту же башню СВ, переносимую земным шаром к DI; точки пересечения этих линий дугою полукруга CI суть места, где с течением времени оказывается падающий камень; эти точки все в большей мере удаляются от вершины башни, а это как раз соответствует тому, что прямое движение, совершающееся вдоль башни, все более ускоряется. Видно также, как благодаря бесконечной остроте угла, образующегося от соприкосновения обоих кругов DC и CI, отклонение падающего тела от окружности CFD, т. е. от вершины башни, вначале крайне мало; это значит, что движение вниз будет крайне медленным и все более и более медленным до бесконечности в зависимости от большей близости к точке С, т. е. к состоянию покоя; и наконец, становится понятным, как в конце концов такое движение кончилось бы в центре Земли А.
и BI, представят нам ту же башню СВ, переносимую земным шаром к DI; точки пересечения этих линий дугою полукруга CI суть места, где с течением времени оказывается падающий камень; эти точки все в большей мере удаляются от вершины башни, а это как раз соответствует тому, что прямое движение, совершающееся вдоль башни, все более ускоряется. Видно также, как благодаря бесконечной остроте угла, образующегося от соприкосновения обоих кругов DC и CI, отклонение падающего тела от окружности CFD, т. е. от вершины башни, вначале крайне мало; это значит, что движение вниз будет крайне медленным и все более и более медленным до бесконечности в зависимости от большей близости к точке С, т. е. к состоянию покоя; и наконец, становится понятным, как в конце концов такое движение кончилось бы в центре Земли А.
Сагредо. — Я прекрасно все понимаю и не могу представить себе, чтобы падающее тело описывало своим центром тяжести какую-либо иную линию, кроме подобной.
Сальвиати. — Не спешите, синьор Сагредо, я собираюсь привести
|
Тело, падающее с вершины башни, движется по окружности круга. |
|
Оно движется не больше и не меньше, чем если бы оставалось наверху. Оно движется не ускоренным, а равномерным движением. |
Сагредо. — Признаюсь вам, я не в силах в достаточной мере выразить словами, сколь чудесными они мне кажутся; поскольку сейчас представляется моему уму, не думаю, чтобы дело происходило иначе; дай бог, чтобы все доказательства философов имели хотя половину такой вероятности. Для полного внутреннего удовлетворения я желал бы только услышать доказательство, каким образом эти дуги оказываются равными. Сальвиати. — Доказательство очень легкое. Допустим, что проведена линия IE; так как полудиаметр круга CD, т. е. линия СА, вдвое больше полудиаметра СЕ круга CI, то одна окружность будет вдвое {133} больше другой окружности, а любая дуга большего круга вдвое больше любой подобной дуги меньшего; следовательно, половина дуги большего круга равна дуге меньшего. И так как угол СЕI образован при центре Е меньшего круга и опирается на дугу CI, то он вдвое больше угла CAD, образованного при центре А большего круга и стягиваемого дугой CD; следовательно, дуга CD является половиной дуги большего круга, подобной дуге CI, а потому обе дуги CD и CI равны между собой; таким же образом это может быть доказано в отношении всех частей. Но что дело происходит в точности так при движении тяжелых падающих тел, этого я здесь утверждать не хочу; скажу только, что если линия, описываемая падающим телом, не совсем в точности такова, то в общем она будет к ней
|
Прямолинейного движения, кажется, вовсе не существует в природе. |
Сагредо. — А я, синьор Сальвиати, раздумываю сейчас о другой чудесной вещи, а именно: ведь на основании этих рассуждений выходит, что прямолинейное движение вообще упраздняется и что природа им никогда не пользуется, поскольку даже то назначение, которое ему сначала приписывалось, а именно, водворять им на свое место части целостных тел, в случае, если они разобщены со своим целым и потому находятся в несвойственном им положении, оказывается у него отнятым и приписывается движению круговому.
Сальвиати. — Это с необходимостью следовало бы, если бы было установлено, что земной шар движется кругообразно, чего я не берусь утверждать; пока что мы собираемся только рассмотреть силу доводов, приводившихся философами в доказательство неподвижности Земли, из коих первый, почерпнутый из наблюдения над отвесным падением тел, встречается с затруднениями, которые вы заметили. Не знаю, сколь существенными показались они синьору Симпличио, поэтому, прежде чем перейти к исследованию других аргументов, следовало бы услышать то, что он имеет возразить.
Симпличио. — Что касается этого первого аргумента, то, признаюсь откровенно, я услышал столько разных тонкостей, о которых ранее не думал, что, поскольку они мне встречаются впервые, я не могу дать столь быстрого ответа; но доказательство, почерпнутое из опыта с падающими отвесно телами, я не причисляю к наиболее сильным доводам в пользу неподвижности Земли и не знаю, что случится с артиллерийской стрельбой, в особенности со стрельбой, направленной против суточного движения.
Сагредо. — Больше хлопот и затруднений, чем артиллерийские орудия и все другие упоминавшиеся раньше опыты, доставляет мне полет птиц. Эти птицы, которые по своему произволу летают вперед и назад, кружатся на тысячу ладов и, что еще важнее, целыми часами кажутся висящими в воздухе, говорю я, сбивают меня с толку, и я не могу понять, как среди стольких кружений они не утрачивают движения Земли или как могут они держаться против такой скорости, которая в конце концов в огромное число раз превосходит быстроту их полета?
Сальвиати. — Ваше сомнение в самом деле не лишено основания; и, пожалуй, сам Коперник не нашел бы для него вполне удовлетворительного решения, почему, быть может, он о нем и умалчивает; впрочем и при рассмотрении других доводов в пользу противного он весьма лаконичен, думаю, из-за возвышенного склада ума и потому, что он опирался на созерцание вещей более величественных и высоких, уподобляясь, таким образом, льву, мало обращающему внимания на заносчивый лай собачонок. Отложим, однако, вопрос о птицах напоследок, а пока постараемся удовлетворить синьора Симпличио в другом отношении, показав ему, как обычно, что решение находится у него самого в руках, хотя он сам этого и не замечает. Начнем со стрельбы на расстояние, производимой {134} из одной и той же пушки (заряженной одинаковым порохом и ядром), один раз к востоку, другой — к западу; пусть синьор Симпличио скажет мне, что заставляет его думать, будто ядро, пущенное к западу (если земному шару присуще суточное обращение), должно будет уйти гораздо дальше, чем при выстреле к востоку?
Симпличио. — Меня побуждает так думать то, что при стрельбе
|
Соображения, в силу которых кажется, что дальность выстрела из орудия к западу должна быть больше, чем при выстреле к востоку. |
Сальвиати. — Мне хотелось бы найти какой-нибудь способ произвести опыт, соответствующий движению этих снарядов, наподобие опыта с кораблем, соответствующего движению тел, падающих сверху вниз, и я обдумываю, как бы это сделать.
Сагредо. — Думаю, что примером, достаточно пригодным для доказательства,
|
Опыт с двигающейся повозкой для обнаружения разницы в дальности выстрелов. |
Симпличио. — Мне кажется, что такой опыт вполне пригоден, и я не сомневаюсь, что дальность выстрела, т. е. расстояние между стрелой и местом, где находится повозка в тот момент, когда стрела вонзается в землю, будет гораздо меньше в том случае, когда стреляют по направлению движения повозки, чем когда стреляют в сторону противоположную. Пусть, например, дальность выстрела сама по себе составит триста локтей, а путь повозки за то время, пока стрела находится в воздухе, будет сто локтей. Тогда при выстреле по направлению движения повозки последняя пройдет сто локтей, пока стрела пролетает триста, почему при падении стрелы на землю расстояние между нею и повозкой составит только двести локтей; и обратно этому, при другом выстреле, когда повозка движется в сторону, противоположную стреле, пока последняя пройдет свои триста локтей, повозка пройдет свои сто в направлении противоположном, и расстояние между ними окажется в четыреста локтей.
Сальвиати. — Имеется ли у нас какой-нибудь способ сделать дальность выстрелов одинаковой?
Симпличио. — Не знаю другого способа, как остановить повозку.
Сальвиати. — Это понятно, но я спрашиваю, как это сделать, если повозка движется во весь опор?
Симпличио. — Натягивать лук туже при выстреле в направлении движения и слабее при выстреле, противоположном движению.
Сальвиати. — Итак, значит, для этого существует и другое средство. Но насколько сильнее нужно было бы натягивать лук и насколько затем его ослаблять?
Симпличио. — В нашем примере, где мы предположили, что лук стреляет на триста локтей, его нужно было бы при выстреле в {135} направлении движения натягивать так, чтобы он стрелял на четыреста локтей, а в другой раз настолько слабее, чтобы он стрелял не дальше, чем на двести, потому что в этом случае как тот, так и другой выстрел дадут в итоге триста локтей в отношении повозки, которая своим движением на сто локтей отнимает их у выстрела на четыреста и прибавляет к выстрелу на двести локтей, сведя в конечном счете тот и другой к тремстам.
Сальвиати. — Но какое действие производит на дальность выстрела большее или меньшее натяжение лука?
Симпличио. — Сильно натянутый лук гонит стрелу с большей скоростью, а более слабо натянутый — с меньшей; одна и та же стрела летит в одном случае настолько дальше, чем в другом, насколько бо́льшую скорость она имеет, слетая с тетивы, в одном случае, по сравнению с другим.
Сальвиати. — Итак, для того чтобы стрела, пущенная в том и другом направлении, одинаково удалилась от движущейся повозки, надобно поступить так, чтобы при первом выстреле в нашем примере она вылетела, скажем, с четырьмя степенями скорости, а при другом — только с двумя. Но если пользоваться одним и тем же луком, то он всегда даст три степени.
Симпличио. — Да, и потому, если стрелять из одного и того же лука, то при движении повозки дальность выстрела не может получиться равной.
Сальвиати. — Я забыл спросить, какая скорость предполагается в этом частном случае у движущейся повозки?
Симпличио. — Скорость повозки следует предположить равной одной степени по сравнению со скоростью, сообщаемой луком, которая равна трем.
Сальвиати. — Так, так: счет, таким образом, сходится. Но скажите мне, когда повозка движется, не движутся ли также с той же скоростью и все вещи, находящиеся в повозке?
Симпличио. — Без сомнения.
Сальвиати. — Следовательно, и стрела также, и лук и тетива, на которую стрела наложена?
Симпличио. — Конечно, так.
Сальвиати. — Следовательно, когда стрела выпущена в направлении повозки, лук сообщает свои три степени скорости стреле, которая уже имеет одну степень благодаря повозке, перемещающей ее с такой скоростью в ту сторону; поэтому, слетая с тетивы, стрела обладает, оказывается, четырьмя степенями скорости; наоборот, когда стреляют в обратную сторону, тот же лук сообщает те же свои три степени скорости стреле, которая движется в противоположную сторону с одной степенью, так что по отделении ее от тетивы у нее останется всего две степени скорости. Но вы уже сами заметили, что, если мы хотим сделать выстрелы равными, стрелу нужно выпускать один раз с четырьмя степенями скорости, а другой раз — с двумя; итак, даже при одном и том же луке само движение повозки выравнивает начальные степени скорости, что опыт подтверждает затем для тех, кто не хочет или не может уразуметь основание этому. Примените теперь это рассуждение к пушечному ядру
|
Опровержение аргументов, почерпнутых из рассмотрения стрельбы из пушки на восток и на запад. |
Симпличио. — Но, боже мой! Если бы он двигался наклонно, каким образом увидел бы я его движущимся прямо и отвесно? Это равносильно отрицанию очевидности; а если не верить свидетельству чувств, то через какие другие врата можно проникнуть в философию?
Сальвиати. — По отношению к Земле, башне и нам, которые все совокупно движутся суточным движением вместе с камнем, суточного движения как бы не существует; оно оказывается невоспринимаемым, неощутимым, ничем себя не проявляющим, и единственно поддающимся наблюдению оказывается то движение, которого мы лишены, а именно, движение вниз, скользящее вдоль башни. Вы не первый, кто с такой неохотой признает, что движение ничего не производит среди тех вещей, для которых оно является общим.
Сагредо. — Мне припоминается одна фантазия, зародившаяся в моем
|
Замечательный пример Сагредо для доказательства того, что общее движение не производит никакого действия. |
Симпличио. — Новизна того, что я слышу, не только заставляет меня согласиться вас выслушать, но крайне возбуждает мое любопытство; поэтому говорите.
Сагредо. — Если бы конец пишущего пера, находившегося на корабле в продолжение всего моего плавания от Венеции до Александретты, был способен оставлять видимый след всего своего пути, то какой именно след, какую отметку, какую линию он оставил бы?
Симпличио. — Оставил бы линию протяжением от Венеции до конечного места, не совершенно прямую, а вернее сказать, протянутую в виде дуги круга, однако более или менее волнистого, в зависимости от того, в какой степени качался в пути корабль; но это отклонение местами на локоть или на два вправо или влево, вверх или вниз при расстоянии многих сотен миль внесло бы лишь незначительные изменения в общее протяжение линии, так что едва было бы ощутимо; и без особой ошибки ее можно было бы назвать частью совершенной дуги.
Сагредо. — Так что настоящее истинное движение конца пера было бы дугой совершенного круга, если бы движение корабля по устранении колебаний волн было спокойным и ровным. А если бы я непрерывно держал это самое перо в руке и только иногда передвигал его на один-два пальца в ту или другую сторону, какое изменение внес бы я в его главный и длиннейший путь?
Симпличио. — Меньше, чем то, которое произвело бы у прямой линии длиной в тысячу локтей отклонение от абсолютной прямизны в равные стороны на величину блошиного глаза.
Сагредо. — Если бы, следовательно, художник по выходе из гавани начал рисовать этим пером на листе бумаги и продолжал бы рисование до Александретты, то он мог бы получить от его движения целую картину из фигур, начерченных в тысячах направлений, изображения стран, {137} зданий, животных и других вещей, хотя бы след, оставленный истинным, действительным и существенным движением, отмеченным концом пера, был бы не чем иным, как весьма длинной и простой линией. Что же касается действий самого художника, то они были бы совершенно те же самые, как если бы он рисовал в то время, как корабль стоит неподвижно. Таким образом, от длиннейшего движения пера не остается иного следа, кроме черт, нанесенных на лист бумаги, причиной чего является участие в этом общем продолжительном движении от Венеции до Александретты и бумаги, и пера, и всего того, что находится на корабле. Но небольшие движения вперед и назад, вправо и влево, сообщаемые пальцами художника перу, а не листу, будучи присущи только первому, могут оставить по себе след на листе, который по отношению к таким движениям оставался неподвижным. Совершенно так же справедливо и то, что при движении Земли движение камня при падении вниз есть на самом деле длинный путь во много сотен или даже тысяч локтей, и если бы можно было в недвижимом воздухе или на другой поверхности обозначить путь его движения, то оно оставило бы длиннейшую наклонную линию; но та часть всего этого движения, которая обща башне, камню и нам, оказывается для нас неощутимой и как бы несуществующей, и единственно доступной наблюдению остается та часть, в которой ни башня, ни мы не участвуем и которая в конце концов есть то движение, которым камень, падая, отмеривает башню.
Сальвиати. — Чрезвычайно тонкая мысль, способствующая разъяснению этого пункта, весьма трудного для понимания многих. Итак, если синьор Симпличио не имеет ничего возразить, мы можем перейти к другим опытам, при объяснении которых окажет нам немалую поддержку то, что было изложено до сих пор.
Симпличио. — Мне нечего сказать, и я весьма поражен примером этого рисунка и той мыслью, что эти линии, проведенные по стольким направлениям, туда, сюда, вверх, вниз, вперед, назад и переплетающиеся сотней тысяч петель, по существу и на самом деле являются только частицами одной единственной линии, проведенной от начала до конца в одном и том же направлении, без какого-либо иного изменения, кроме отклонения немного вправо, немного влево от совершенно прямого пути и движения конца пера, то более, то менее быстрого, но с различием весьма незначительным. И я соображаю, что таким же образом могло быть написано и письмо и что, если бы изощреннейшие писцы, которые, желая показать ловкость руки, не отнимают пера от листа, а пишут одним росчерком тысячи завитушек, находились в быстро движущейся лодке, то это движение изменило бы все движение пера и свело бы его к простой черте — единственной линии, идущей от начала до конца в одном направлении с весьма незначительными уклонениями от совершенной прямизны. Я очень рад, что синьор Сагредо навел меня на такую мысль; потому пойдем вперед; надежда услышать; что будет дальше, приковывает мое внимание.
Сагредо. — Если вам любопытно послушать о подобных вещах,
|
Достаточно безвкусные тонкости, заимствованные из некоей энциклопедии и приведенные иронически. |
Симпличио. — Таким образом, когда человек идет, он совершает больший путь головой, чем ногами?
Сагредо. — Вы сами собственным умом прекрасно это сообразили. Но не будем прерывать синьора Сальвиати. {138}
Сальвиати. — Мне приятно видеть, что синьор Симпличио делает успехи, если только это мысль его собственная, а не позаимствована из некоей книжечки заключений, где есть и другие, не менее забавные и приятные вещи25. Теперь нам надлежит поговорить о пушке, направленной
|
Возражения против суточного движения, основанные на отвесном пушечном выстреле. |
|
Опровержение возражения с указанием логической ошибки. |
Сагредо. — Это прекрасно все объясняет. Но так как я заметил, что синьор Симпличио любит, что называется, подловить собеседника,
|
Другое опровержение того же возражения. |
Симпличио. — Я полагаю, что явление должно произойти в точности так.
Сагредо. — Но если бы орудие было поставлено не отвесно, а наклонно в какую-нибудь сторону, то каковым было бы движение ядра. Пошло ли бы оно, как при первом выстреле, по отвесной линии и возвратилось ли бы затем по ней же?
Симпличио. — Этого ядро не сделает, но, выйдя из пушки, оно продолжит свое движение по прямой линии, продолжающей прямую линию ствола, поскольку его собственный вес не заставит его отклониться от этой прямой линии к земле.
Сагредо. — Значит, прямизна ствола дает направление движению
|
Брошенные тела продолжают движение по тем же самым прямым линиям, которые они описывали, когда еще находились в соединении с бросающим. |
Симпличио. — Мне кажется, что так.
Сагредо. — Теперь представьте себе, что ствол поставлен отвесно и что Земля обращается вокруг самой себя суточным движением, {139} уносящим с собой и орудие; скажите, каково будет движение ядра внутри ствола, после того как будет сделан выстрел?
Симпличио. — Движение будет прямое и отвесное, если ствол поставлен прямо по отвесу.
|
Поскольку Земля вращается, ядро, проходящее прямой канал пушки, движется не по прямой, а по кривой линии. |
 что движение центра тяжести ядра происходит по линии наклонной. Для более ясного уразумения положим, что АС есть орудие, поставленное прямо, и В — ядро в нем; ясно, что когда пушка стоит неподвижно, ядро после выстрела выйдет из отверстия А, пройдя по пушке своим центром перпендикулярную линию ВА, и будет следовать ее прямизне и далее, вне пушки, двигаясь к зениту. Но если Земля вращается и, следовательно, уносит с собой орудие, то в то время как ядро, гонимое огнем, движется по стволу, орудие, переносимое Землей, перейдет в положение DE, и ядро В при выходе из дула окажется в точке D, движение же центра ядра произойдет по линии BD уже не отвесной, а наклонной, и так как ядро, раз уже мы пришли к такому заключению, должно продолжать свое движение в воздухе соответственно направлению движения в пушке, то движение будет итти соответственно наклону линии BD и, таким образом, вовсе не будет отвесным, но наклонным к востоку, куда движется и орудие, почему ядро и может следовать за движением Земли и орудия. Так вот, синьор Симпличио, вам показано, что выстрел, который, казалось, должен был бы быть отвесным, на самом деле вовсе не таков.
что движение центра тяжести ядра происходит по линии наклонной. Для более ясного уразумения положим, что АС есть орудие, поставленное прямо, и В — ядро в нем; ясно, что когда пушка стоит неподвижно, ядро после выстрела выйдет из отверстия А, пройдя по пушке своим центром перпендикулярную линию ВА, и будет следовать ее прямизне и далее, вне пушки, двигаясь к зениту. Но если Земля вращается и, следовательно, уносит с собой орудие, то в то время как ядро, гонимое огнем, движется по стволу, орудие, переносимое Землей, перейдет в положение DE, и ядро В при выходе из дула окажется в точке D, движение же центра ядра произойдет по линии BD уже не отвесной, а наклонной, и так как ядро, раз уже мы пришли к такому заключению, должно продолжать свое движение в воздухе соответственно направлению движения в пушке, то движение будет итти соответственно наклону линии BD и, таким образом, вовсе не будет отвесным, но наклонным к востоку, куда движется и орудие, почему ядро и может следовать за движением Земли и орудия. Так вот, синьор Симпличио, вам показано, что выстрел, который, казалось, должен был бы быть отвесным, на самом деле вовсе не таков.
Симпличио. — Я это что-то не совсем понимаю, а вы, синьор Сальвиати?
Сальвиати. — Понимаю лишь отчасти; у меня есть здесь некое сомнение, и дай бог, чтобы я сумел его разрешить. Мне кажется, в соответствии со сказанным, что если пушка поставлена отвесно, а Земля движется, то ядро не только не должно упасть обратно далеко к западу от пушки, как хочется Аристотелю и Тихо, или даже на пушку, как хочется вам, а на значительном расстоянии к востоку. Ведь, согласно вашему разъяснению, ядро обладает двумя движениями, которые совместно выбрасывают его в этом направлении, а именно — общим движением Земли, которое перемещает орудие и ядро из СА в ED, и импульсом огня, который гонит ядро по наклонной линии BD; оба эти движения направлены к востоку и потому превосходят движение Земли.
Сагредо. — Нет, синьор. Движение, перемещающее ядро к востоку, целиком происходит от Земли; огонь в нем никак не участвует; движение, толкающее ядро вверх, целиком принадлежит огню, и Земля не имеет к нему никакого отношения; это действительно так, ибо если вы не приложите огня, то ядро никогда не выйдет из пушки и не поднимется ни на волос; и совершенно так же, если вы остановите Землю и дадите огонь, то ядро, ничуть не отклоняясь, пойдет по отвесу. Следовательно, ядро имеет два движения — одно вверх, а другое по кругу, из коих составляется одно наклонное движение AD, причем импульс вверх сполна принадлежит огню, а круговое движение сполна происходит от Земли {140} и равно движению Земли, а раз оно ему равно, то ядро постоянно держится над дулом орудия и в конечном итоге падает в него обратно; всегда держась на прямой линии пушки, ядро постоянно видно над головой стоящего рядом с пушкой и кажется ему поднимающимся по отвесу к нашему зениту.
Симпличио. — У меня остается другое затруднение, а именно: так как движение ядра в пушке крайне быстро, то кажется невозможным, чтобы за этот момент времени перемещение орудия из СА в ЕВ сообщало такой наклон линии СВ; чтобы благодаря ему ядро могло следовать за движением Земли.
Сагредо. — Вы заблуждаетесь во многих отношениях: во-первых, наклон косой линии СВ, думаю, будет гораздо большим, чем вы себе представляете, так как я считаю несомненным, что скорость земного обращения не только у экватора, но даже и в наших широтах, будет значительно большей, чем скорость ядра, пока оно движется внутри пушки; поэтому расстояние СЕ будет безусловно большим, чем вся длина пушки, а наклон косой линии, следовательно, большим половины прямого угла; но велика ли, мала ли скорость Земли по сравнению со скоростью огня, это не играет никакой роли, ибо если скорость Земли незначительна и, следовательно, наклон косой линии невелик, то малый наклон нужно сделать и для того, чтобы ядро продолжало держаться при своем полете над пушкой; в итоге, если вы внимательно вдумаетесь, вы поймете, что движение Земли вместе с перемещением орудия из СА в ЕВ сообщает наклонной линии СВ больший или меньший наклон, потребный для того, чтобы приноровить выстрел к его цели. Но вы заблуждаетесь еще и в другом, желая приписать импульсу огня способность ядра следовать за движением Земли, и впадаете в ту же ошибку, в какую, повидимому, впал недавно синьор Сальвиати, ибо движение вместе с Землей есть движение древнейшее и постоянное, присущее этому ядру в качестве земной вещи и не отделимое от него, которым оно обладает и будет постоянно обладать по своей природе.
Сальвиати. — Успокоимся же на этом, синьор Симпличио, ибо дело обстоит именно так. И теперь благодаря этому рассуждению я прихожу к пониманию разрешения задачи, стоящей перед охотниками, бьющими из аркебуза птицу в лёт26. Я представлял себе, что, для того
|
Как стрелки попадают в птиц, летящих по воздуху? |
|
Опровержение возражения, основанного на выстрелах из пушки, направленных на юг или на север. |
Сагредо. — Прошу вас, остановитесь немного, синьор Сальвиати, пока я изложу одну мысль, пришедшую мне в голову по поводу этих стрелков по летающим птицам. Способ их действия, думаю я, таков, как вы говорите, и, следуя ему, они должны попадать в птицу; однако, мне кажется, что такое действие не во всем соответствует выстрелам из орудия, которые должны попадать в цель как при движении пушки и цели, так и при общем им обоим покое. Различия, кажется мне, таковы. При выстрелах из орудия и оно само, и цель движутся с одинаковыми скоростями, оба перемещаемые движением земного шара, и если бы, скажем, пушка иногда находилась несколько ближе к полюсу, чем цель, и следовательно, движение ее, совершаемое по меньшему кругу, было бы несколько более медленным, то такая разница неощутима из-за незначительности расстояния от пушки до цели. Но при выстреле охотника движение аркебуза, следующего за птицами, крайне медленно по сравнению с полетом последних, из чего, как мне кажется, следует, что то небольшое движение, которое сообщается поворачиванием ствола находящейся внутри пуле, не может по выходе на воздух возрасти до скорости полета птицы, так, чтобы пуля всегда была направлена к птице; мне кажется, что последняя должна опережать ее и оставлять за собой. Следует добавить, что в этом случае не предполагается, что тот воздух, по которому проходит пуля, должен обладать движением птицы, тогда как в случае с орудием и оно, и цель, и лежащий между ними воздух равно участвуют во всеобщем суточном движении. Таким образом, если охотники попадают в цель, тому, надо полагать, есть иные причины; следуя движением ствола за полетом птиц, они держат прицел несколько впереди, опережая цель, и, кроме того, стреляют, как я думаю, не одной пулей, но изрядным количеством дроби, которая, разбрасываясь в воздухе, занимает довольно большое пространство; помимо этого, имеет значение большая скорость, с которой дробь по выходе из ствола перемещается к птице.
Сальвиати. — Вот видите, насколько полет мысли синьора Сагредо опережает медлительность моей; я, быть может, и заметил бы эти различия, но лишь после долгого размышления. Теперь вернемся к нашей теме. Нам остается рассмотреть случай с горизонтальными выстрелами, направленными на восток и на запад, из которых первые в случае движения Земли должны были бы проходить выше цели, а вторые — ниже ее; ведь восточные части Земли движутся суточным движением, постоянно опускаясь по отношению к касательной, параллельной горизонту, почему звезды на востоке кажутся нам восходящими, и, наоборот, западные части поднимаются, отчего звезды на западе кажутся заходящими; поэтому {142} направленные по названной касательной к цели на востоке (каковая, пока ядро идет по касательной, опускается) должны были бы попадать выше цели, а направленные на запад — ниже вследствие подъема цели, пока ядро движется по касательной. Ответ подобен предыдущим: как восточная цель из-за движения Земли оказывается постоянно опускающейся по отношению к касательной, которая принята неподвижной,
|
Разрешение проблемы, возникающей в связи с выстрелами по направлению к востоку и к западу. Коперниканцы, идя навстречу противникам, принимают за правильные многие сомнительные утверждения. |
Симпличио. — Я не беру на себя смелости ответить столь основательно, как мог бы ответить кто-либо другой, более меня сведущий, но скажу то, что думаю, экспромтом: они, вероятно, ответили бы, что дело обстоит так, как уже было сказано, т. е. что если бы Земля двигалась, то выстрелы в направлении на восток попадали бы всегда выше и т. д., поскольку кажется правдоподобным, что ядро должно двигаться по касательной.
Сальвиати. — Но если бы я стал утверждать, что так на самом деле и бывает, то как бы вы поступили для опровержения моих слов?
Симпличио. — Следовало бы прибегнуть к опыту, чтобы уяснить, как обстоит дело.
Сальвиати. — Но думаете ли вы, что найдется такой опытный бомбардир, который возьмется попадать в цель каждым выстрелом с расстояния, скажем, пятисот локтей?
Симпличио. — Нет, и думаю, что нет никого, кто мог бы, как бы искусен он ни был, обещать не уклоняться от цели хотя бы в пределах локтя.
Сальвиати. — Как же, следовательно, можем мы столь неверными выстрелами удостовериться в том, в чем сомневаемся?
Симпличио. — Мы могли бы удостовериться двояким образом: во-первых, произведя много выстрелов, а во-вторых, учтя, что вследствие большой скорости движения Земли отклонение от цели, кажется мне, должно было бы быть весьма значительным.
Сальвиати. — Весьма значительным, т. е. гораздо больше одного локтя, так как предполагается, что такое и даже большее отклонение обычно происходит и при покое земного шара.
Симпличио. — Я твердо верю, что отклонение было бы гораздо большим.
Сальвиати. — Так вот я хотел бы, с вашего позволения и к общему нашему удовольствию, сделать небольшой расчет в общих цифрах. Это
|
Вычисление величины, на которую при предположении движения Земли должны отклоняться от цели пушечные выстрелы. |
|
Весьма остроумно доказывается, что при предполагаемом движении Земли пушечные выстрелы давали бы не большее отклонение, чем при покое. |
Сальвиати. — Тонкое замечание, достойное синьора Сагредо. Но, рассмотрев разницу между тем, что происходит при движении, и тем, что происходит при покое Земли, мы видим, что она совершенно ничтожна и не может не быть поглощена другими весьма значительными отклонениями, постоянно случающимися из-за многих обстоятельств. И все это пусть будет сказано и допущено как некий дар для синьора Симпличио и только в виде предупреждения, с какой {144}
|
Можно только с большой осторожностью признавать правильными опыты, на которые ссылаются люди, никогда их не производившие. |
|
Опыт и доводы против движения Земли кажутся нам доказательными, пока мы не уяснили себе дела вполне. |
Сагредо. — Я со своей стороны до сих пор полностью удовлетворен и прекрасно понимаю, что всякий, кто запечатлел в своем воображении эту причастность суточному движению всех земных вещей, которым оно по природе присуще, точно так же, как в старом представлении предполагалось, что им присущ покой в отношении центра, тот без всякого затруднения распознает ошибочность и двусмысленность доводов, казавшихся ранее убедительными. У меня остается еще только одно сомнение, о котором я упоминал выше, а именно — полет птиц. Раз они в качестве одушевленных существ обладают способностью двигаться по своему усмотрению тысячью движений и держаться, оторвавшись от Земли, долгое время в воздухе, кружась в нем без всякого порядка, я не совсем понимаю, как при таком смешении движений не теряется первоначальное общее движение и каким образом птицы, оказавшись лишенными его, могут компенсировать и возмещать его полетом, не отставая от башен и деревьев, уносящихся столь стремительным общим движением к востоку, столь стремительным, говорю я, что у наибольшего круга земного шара оно немного меньше тысячи миль в час, тогда как полет ласточек, думается, не достигает и пятидесяти.
Сальвиати. — Если бы птицы должны были следовать за движением деревьев при помощи своих крыльев, то они были бы беспомощны. Если бы они были непричастны всеобщему круговращению, то настолько отставали бы, что стремительность их движения к западу представлялась бы наблюдателю значительно превосходящей быстроту движения стрелы; думаю даже, что мы вообще не могли бы их наблюдать, как не видим пушечного ядра, когда оно, выброшенное огнем, несется по воздуху. Но истина заключается в том, что собственное движение птиц, т. е. их полет, не имеет ничего общего со всеобщим движением, которое им ничем не помогает и не мешает. То, что поддерживает неизменным такое движение в птицах, — это сам воздух, по которому они носятся, увлекающий за собой и облака, и птиц, и все другие вещи, какие бы ни оказались в нем висящими; поэтому птицам не приходится думать о том, чтобы следовать за Землей, и они могут спать без всяких забот в этом отношении.
Сагредо. — Я без труда понимаю, что воздух может перемещать вместе с собой облака, как вещество, благодаря своей легкости в высшей степени подвижное и лишенное всякой склонности к противопоставлению движению, хотя бы как вещество они и были причастны земным условиям и свойствам. Но что у птиц, существ одушевленных, могущих двигаться движением, даже противоположным суточному, последнее, будучи прервано, может быть восстановлено воздухом, — это кажется мне не совсем правдоподобным, в особенности потому, что птицы — тела твердые и тяжелые, а мы видим, как о том говорилось выше, что камни и другие тяжелые тела сопротивляются импульсу воздуха и если когда и дают себя увлечь, то никогда не приобретают такой скорости, как скорость несущего их ветра. {145}
Сальвиати. — Мы не сказали бы, синьор Сагредо, что сила движущегося воздуха столь мала, раз при быстром движении он способен двигать и перемещать тяжело груженные корабли, вырывать с корнем деревья и разрушать башни, несмотря на то, что движение воздуха при столь могучих действиях все же нельзя не признать далеко не столь быстрым, как движение суточного обращения.
Симпличио. — Так, значит, движущийся воздух все же может поддерживать движение брошенных тел в согласии с учением Аристотеля; мне и казалось весьма странным, будто он заблуждался в этом отношении.
Сальвиати. — Без сомнения, может, однако лишь поскольку он сам продолжает двигаться; но как только ветер стихнет, ни корабли не движутся, ни деревья не ломаются; и раз движение воздуха не продолжается после того, как рука выпустила камень и остановилась, необходимо имеется что-то другое, отличное от воздуха, что заставляет двигаться брошенное тело.
Симпличио. — Разве как только прекратился ветер, так прекращается и движение корабля? Наоборот, мы видим, что и после того, как прекратился ветер и даже паруса опали, судно продолжает плыть целые мили.
Сальвиати. — Но это говорит против вас, синьор Симпличио, ведь после того, как ветер, перемещавший корабль, надувая его паруса, прекратился, корабль продолжает свой путь во всяком случае без помощи среды.
Симпличио. — Можно было бы сказать, что вода является той средой, которая перемещает корабль и поддерживает в нем движение.
Сальвиати. — Это можно было бы сказать лишь для того, чтобы сказать совершенно противоположное истине, ибо истина заключается в том, что вода оказывает большое сопротивление своему разделению телом корабля, с большим шумом ему противодействует и далеко не дает ему развить ту скорость, которую сообщил бы ему ветер, если бы не существовало препятствия со стороны воды. Вы, синьор Симпличио, должно быть, никогда не обращали внимания на то, с какой яростью вода ударяет в борта лодки, когда последняя, быстро гонимая веслами или ветром, бежит по неподвижной воде; если бы вы когда-нибудь подумали о таком действии, вам не пришло бы в голову говорить подобную бессмыслицу. Я начинаю думать, что вы до сих пор принадлежите к числу тех, кто, желая узнать, как происходит какое-либо явление, и приобрести познание о силах природы, обращается не к лодкам, самострелам или артиллерийским орудиям, а уединяется в кабинет для перелистывания оглавлений и указателей в поисках, не сказал ли чего-либо об этом Аристотель; удостоверившись в правильном понимании текста, они ничего более не желают и полагают, будто ничего иного и знать нельзя.
Сагредо. — Великое счастье, которому можно позавидовать, ибо
|
Великое, завидное счастье тех, кто мнит, что он все знает. |
Сальвиати. — Рассуждение ваше имеет по видимости много правдоподобного, и сомнение принадлежит незаурядному уму; однако, отрешившись от видимости, думаю, что по существу у него нет ни на волос больше основательности, чем у других, уже рассмотренных и опровергнутых.
Сагредо. — Нет никакого сомнения, что если возражение не будет иметь необходимых доказательств, то ценность его сведется к нулю, ибо только когда заключение с необходимостью ведет к одному единственному выводу, то в пользу противоположного нельзя привести сколько-нибудь стоящего основания.
Сальвиати. — Если в этом случае вы испытываете бо́льшие затруднения, чем в других, то это, кажется мне, зависит от того, что птицы — существа одушевленные и потому могут пользоваться по усмотрению своей силой даже против первичного движения, заложенного во всех земных вещах; так, мы видим, что, пока они живы, они летают даже кверху, движением для них, как для тяжелых тел, невозможным; но после того, как они умрут, они могут падать только вниз; и потому вы полагаете, что рассуждения, имеющие место в отношении всех видов брошенных тел, упомянутые выше, не могут иметь применения к птицам. Это вполне правильно и правильно потому, синьор Сагредо, что брошенные тела ведут себя не так, как птицы: если с вершины башни вы бросите птицу мертвую и птицу живую, то первая будет делать то же, что и камень, т. е. во-первых, будет следовать общему суточному движению, а во-вторых, как тяжелое тело двигаться вниз; если же брошенная птица будет живой, то что воспрепятствует ей, неизменно участвуя в суточном движении, броситься взмахами крыльев в ту сторону горизонта, какая ей более нравится? И это новое движение, как ее частное и нами не разделяемое, должно быть для нас заметным. И если птица в своем полете двигалась к западу, что воспрепятствует ей столькими же взмахами крыльев вернуться на вершину башни? Ибо в конце концов направить
|
Опровержение возражения против движения Земли, основанного на полете птиц. |
|
Опыт, показывающий несостоятельность всех опытов, приводимых против движения Земли. |
Сагредо. — Хотя во время плавания мне не приходило на ум намеренно производить такие наблюдения, я во всяком случае более чем уверен, что они происходят именно так, как рассказано; в подтверждение этого припоминаю, что сотни раз, сидя в своей каюте, я спрашивал себя, движется корабль или стоит неподвижно; иногда, в задумчивости, я полагал, что корабль движется в одном направлении, тогда как движение его шло в сторону противоположную. Поэтому я теперь чувствую себя удовлетворенным и совершенно убежден в отсутствии всякой ценности всех опытов, проводимых для доказательства большей вероятности отсутствия, чем существования обращения Земли. Теперь остается возражение, основанное на наблюдении, как быстрое вращение способно разрушить {148} и рассеять вещества, прикрепленные к вращающейся машине. На этом основании многим, в том числе и Птоломею, казалось, что если бы Земля обращалась вокруг себя самой с такой скоростью, то камни и животные должны были бы быть отброшены к звездам, а здания не могли бы быть прикреплены к фундаментам известкой, достаточно прочной, чтобы не допустить такого разрушения.
Сальвиати. — Прежде чем перейти к разбору этого возражения, не могу умолчать о том, что, как я не без смеха тысячи раз наблюдал, приходит на ум почти всем людям, впервые услышавшим о движении Земли, которую они полагали столь неподвижной и прочно установленной, что не только никогда не сомневались в ее покое, но твердо верили, будто и все другие люди вместе с ними считали Землю созданной неподвижной и пребывавшей такой в течение всех прошедших веков; утвердившись в этом представлении, они удивляются потом, слыша, что
|
Глупость людей, полагающих, что Земля начала вращаться с того времени, как пифагорейцы начали утверждать, что она движется. |
Сагредо. — Значит, синьор Сальвиати, вы полагаете, что Птоломей считал нужным поддерживать в споре неподвижность Земли против таких людей, которые допускали, будто она была неподвижной до времени Пифагора, и что она только тогда стала подвижной, когда Пифагор приписал ей движение?
Сальвиати. — Нельзя думать иначе, если мы хорошенько всмотримся в способ, каким он стремится опровергнуть их утверждение.
|
Аристотель и Птоломей, кажется, оспаривают движение Земли перед людьми, думающими, что она сначала находилась в покое и пришла в движение во времена Пифагора. |
Симпличио. — Я все же не вполне понимаю несообразность со стороны Аристотеля и Птоломея.
Сальвиати. — Птоломей возражает или против тех, кто считал Землю всегда движущейся, или против тех, кто считал, что она некоторое время была неподвижной, потом пришла в движение. Если бы он возражал против первых, то должен был бы сказать: «Земля никогда не двигалась, потому что иначе не было бы на Земле ни людей, ни животных, ни зданий, поскольку земное обращение не допускало бы их пребывания». Но раз он аргументирует так: «Земля не движется, потому что люди и звери, и здания, уже находящиеся на Земле, были бы иначе отторгнуты», то он предполагает, что Земля когда-то находилась в таком {149} состоянии, которое позволяло зверям и людям находиться на ней и строиться, откуда вытекает, что некоторое время она была неподвижной, т. е. пригодной для обитания животных и сооружения зданий. Понимаете ли вы теперь то, что я хотел сказать?
Симпличио. — Понимаю и не понимаю, но это имеет мало значения для существа дела, и ошибка Птоломея, совершенная по недосмотру, недостаточна для того, чтобы привести в движение Землю, если она неподвижна. Но оставим шутки и перейдем к существу аргумента, который кажется мне неопровержимым.
|
Быстрое вращение производит отбрасывание и рассеивание. |
Симпличио. — Возражение кажется мне прекрасно обоснованным и увязанным, и много старания потребуется, по моему мнению, чтобы его опровергнуть или развязать.
Сальвиати. — Опровержение его зависит от некоторых вещей, известных вам не менее, чем мне, и разделяемых нами обоими, но так как вы их забыли, то не находите и опровержения. Я не буду учить вас им (так как вы их уже знаете) и путем простого напоминания добьюсь того, что вы сами опровергнете возражение.
Симпличио. — Я много раз присматривался к вашему способу рассуждать, который внушил мне мысль, что вы склоняетесь к мнению Платона, будто nostrum scieri sit quoddam reminisci28; прошу вас поэтому,
|
Наше знание, согласно Платону, есть род припоминания. |
Сальвиати. — То, что я думаю о мнении Платона, я могу подтвердить и словами, и фактами. При рассуждениях, имевших место до сих пор, я не раз прибегал к объяснению при помощи фактов; буду придерживаться того же способа и в данном частном случае, который затем может служить вам примером для лучшего уяснения моего понимания приобретения знания, о чем мы поговорим в другой день, если у нас останется время и если мы не наскучим таким отступлением синьору Сагредо.
Сагредо. — Наоборот, мне это будет только очень приятно, ибо я помню, что, изучая в свое время логику, я никак не мог постигнуть этого столь прославленного сильнейшего доказательства Аристотеля. {150}
Сальвиати. — Итак, продолжаем. Пусть скажет мне синьор Симпличио, какое движение совершает камешек в расщепе трости, когда мальчик взмахивает ею, чтобы метнуть камень?
Симпличио. — Движение камня, пока он в расщепе, круговое, т. е. идет по дуге круга, у которого неподвижным центром является сочленение плеча, а полудиаметром трость с рукой.
Сальвиати. — А когда камень вылетает из расщепа, каково его движение? Продолжает ли он свое предшествующее круговое движение или идет по другой линии?
Симпличио. — Он уже более не двигается по кругу, так как тогда он не удалялся бы от плеча бросающего, а мы видим, что он улетает очень далеко.
Сальвиати. — Так каким же движением он движется?
Симпличио. — Дайте мне немного подумать, так как я никогда не размышлял об этом.
Сальвиати. — Между нами, синьор Сагредо, вот оно quoddam reminisci, правильно понимаемое, перед нами налицо. Вы что-то долго думаете, синьор Симпличио.
Симпличио. — По-моему, движение камня, начавшееся при выходе
|
Движение брошенного тела может быть только прямолинейным. |
Сальвиати. — Но по какой прямой линии? Ибо бесконечное множество прямых можно провести во все стороны от конца трости и точки отрыва камня от пращи.
Симпличио. — По той прямой, которая является продолжением движения, проделанного камнем в праще.
Сальвиати. — Движение камня, пока он в расщепе, вы уже определили как круговое, но ведь движение по кругу и движение по прямой несовместимы, поскольку в круговой линии нет никакой части прямой.
Симпличио. — Я имею в виду то, что движение брошенного тела будет продолжением не всего движения по кругу, а лишь движения в последней точке, где кончится круговое движение. Внутренно я понимаю это, но не умею как следует объяснить.
Сальвиати. — Я также замечаю, что вы понимаете предмет, но не имеете подходящих терминов для выражения; этому я вас вполне могу научить, т. е. научить вас словам, но не истинам самим по себе. Чтобы заставить вас убедиться, что вы знаете предмет и что вам недостает только слов для выражения мысли, спрошу вас: когда вы стреляете пулей из аркебуза, в каком направлении к движению приобретает она импульс?
Симпличио. — Она приобретает импульс к движению по той прямой линии, которая продолжает прямую линию ствола, т. е. которая не уклоняется ни вправо, ни влево, ни вверх, ни вниз.
Сальвиати. — В итоге это равносильно тому, что она не образует никакого угла с линией прямого движения, совершаемого в стволе.
Симпличио. — Это я и хотел сказать.
Сальвиати. — Значит, если линия движения брошенного тела должна продолжаться, не образуя угла с круговой линией, описанной ранее, пока тело было связано с бросающим, и если от этого кругового движения оно должно перейти к прямому движению, то какой же должна быть эта прямая линия? {151}
Симпличио. — Она не может быть иной, кроме той, которая касается круга в точке отрыва, ибо все другие, думается мне, при продолжении пересекут окружность и потому образуют с ней какой-нибудь угол.
Сальвиати. — Вы отлично рассуждаете и доказали, что вы — наполовину геометр. Итак, запомните, что ваше правильное представление выражается такими словами: брошенное тело приобретает импульс к движению по касательной к дуге, описанной движением бросающего, в точке отрыва брошенного тела от бросающего.
Симпличио. — Прекрасно понимаю; именно это я и хотел сказать.
Сальвиати. — У прямой линии, касающейся круга, какая из точек ближе всего к центру круга?
Симпличио. — Без сомнения, точка касания, потому что она находится на окружности круга, а все другие — вне его, а точки окружности все одинаково удалены от центра.
Сальвиати. — Следовательно, движущееся тело, уходя от точки касания и двигаясь по касательной прямой, непрерывно удаляется от точки касания и вместе с тем от центра круга.
Симпличио. — Бесспорно, это так.
Сальвиати. — Теперь, если вы удержали в памяти положения, которые вы мне высказали, соедините их вместе и скажите, что из этого получится?
Симпличио. — Не думаю, чтобы я был настолько забывчив и не мог их вспомнить. Из сказанного вытекает, что брошенное тело, быстро вращаемое бросающим, при отрыве от него сохраняет импульс к продолжению своего движения по прямой линии, которая является касательной
|
Брошенное тело движется по касательной круга прежнего движения в точке отрыва. |
Сальвиати. — Значит, теперь вы понимаете, почему тяжелые тела, прикрепленные к поверхности быстро движущегося колеса, оказываются отторгнутыми и отброшенными за пределы окружности прочь от центра.
Симпличио. — Мне кажется, что я это достаточно усвоил, но такое познание скорее увеличивает, чем уменьшает во мне недоверие к тому, что Земля может вращаться с такой быстротой, не отбрасывая к небу камней, животных и т. д.
Сальвиати. — Тем же путем, каким вы это себе усвоили, вы узнаете и остальное; вернее, вы знаете это уже теперь; поразмыслив, вы сами самостоятельно все припомните, но для сокращения времени я помогу вам припомнить. До сих пор вы сами самостоятельно постигли, что круговое движение бросающего оставляет в бросаемом теле (в момент, когда они разлучаются) импульс движения по прямой, касательной к кругу движения в точке отрыва, и стремление продолжать по ней движение, постоянно удаляясь от бросившего; и вы сказали, что по такой прямой линии брошенное тело продолжало бы двигаться, если бы его собственная тяжесть не прибавляла склонения вниз, вследствие чего получается изгиб линии движения. Как мне кажется, еще вы сами заметили, что этот изгиб всегда направлен к центру Земли, ибо туда направляются все тяжелые тела. Теперь я иду немного далее и спрашиваю вас: идет ли движущееся тело, продолжающее свое движение после отрыва, все время равномерно удаляясь от центра или, если угодно, от окружности круга, частью которого было предшествующее движение, или, что то же самое, удаляется ли движущееся тело, выходя из точки касания и двигаясь по этой касательной, равномерно от точки касания и от окружности круга?
Симпличио. — Нет, синьор, потому что касательная вблизи точки касания отходит совсем ничтожно от окружности, с которой она образует {152} незначительнейший угол; но при удалении все большем и большем расстояние от окружности возрастает все в большей пропорции, так что в круге, имеющем, например, десять локтей в диаметре, точка касательной, удаленная от точки касания на две пяди, окажется удаленной от окружности круга в три или четыре раза более, чем точка, отстоящая от точки соприкосновения на одну пядь, и точка, удаленная на полпяди, равным образом, думаю, едва ли удалится на четверть расстояния второй; вблизи же точки касания на расстоянии одного или двух дюймов от нее едва заметно, что касательная отделяется от окружности.
Сальвиати. — Так что удаление брошенного тела от окружности предшествующего кругового движения вначале совсем ничтожно?
Симпличио. — Почти неощутимо.
Сальвиати. — Скажите мне теперь, пожалуйста, брошенное тело, которое от движения бросающего получает импульс движения по касательной прямой и которое пошло бы так и дальше, если бы собственный вес не тянул его вниз, с какого момента после отрыва начнет склоняться вниз?
Симпличио. — Думаю, что начнет склоняться сразу, потому что за отсутствием поддержки собственная тяжесть не может не оказывать
|
Тяжелое брошенное тело с самого момента его отрыва от бросающего начинает склоняться вниз. |
Сальвиати. — Таким образом, если бы камень, отброшенный вращающимся с огромной скоростью колесом, имел такую же естественную склонность двигаться к центру этого колеса, с какой он движется к центру Земли, то ему нетрудно было бы вернуться к колесу, или, скорее, вовсе не удаляться от него, ибо, раз вначале отрыва удаление столь ничтожно из-за бесконечной остроты угла при точке касания, малейшего уклонения по направлению к центру колеса было бы достаточно, чтобы удержать его на окружности29.
Симпличио. — Я ничуть не сомневаюсь, что если принять существование того, чего нет и быть не может, а именно, если принять склонность тяжелых тел стремиться к центру колеса, то они не оказались бы отторгнутыми и отброшенными.
Сальвиати. — Я не принимаю этого и не имею необходимости принимать то, чего нет, ибо я не собираюсь отрицать, что камни будут отброшены. Но я говорю предположительно для того, чтобы вы досказали мне остальное. Вообразите себе теперь, что Земля — это большое колесо, которое движется с огромной скоростью и должно отбрасывать камни. Вы уже отлично сумели мне сказать, что движение брошенного тела должно будет происходить по той прямой линии, которая касается земли в точке отрыва; как идет эта касательная? Заметно ли удаляется она от поверхности земного шара?
Симпличио. — Думаю, что за тысячу локтей она не удалится и на один дюйм.
Сальвиати. — А не говорили ли вы, что брошенное тело, увлекаемое собственной тяжестью, отклоняется от касательной к центру Земли?
Симпличио. — Говорил и теперь доскажу остальное. Я прекрасно понимаю, что камень не отделится от земли, так как его удаление вначале было бы столь ничтожно, что во много тысяч раз большим оказалось бы стремление камня двигаться к центру Земли, а этот центр в данном случае тот же, что центр у колеса. И действительно, необходимо приходится допустить, что камни, животные и другие тяжелые тела не могут быть отброшены, но новое затруднение создают теперь для меня самые легкие тела, у которых стремление опускаться к центру крайне слабо; так как у них отсутствует способность удерживаться на поверхности, то я не вижу, почему бы им не оказаться отброшенными, а вы ведь знаете, что «ad destruendum sufficit unum»30. {153}
Сальвиати. — Дадим и этому удовлетворительное объяснение. Скажите мне сначала, что понимаете вы под легкими вещами, т. е. подразумеваете ли вы вещества, действительно столь легкие, что они идут вверх, или же легкие не абсолютно, но столь мало тяжелые, что они идут вниз, хотя и медленно, ибо если вы имеете в виду тела абсолютно легкие, то я вам уступлю, и пусть они будут отброшены еще дальше, чем вам бы хотелось.
Симпличио. — Я имею в виду второе, например пух, шерсть, вату и тому подобное; достаточно малейшей силы, чтобы их поднять, и, однако, мы видим, что они совершенно спокойно лежат на Земле.
Сальвиати. — Как бы мала ни была естественная склонность пуха опускаться на поверхность земли, я утверждаю, что ее достаточно, чтобы не дать ему подняться, а это и вам не безызвестно; потому скажите мне, если бы пух был отброшен вращением Земли, то по какой линии он двигался бы?
Симпличио. — По касательной в точке отрыва.
Сальвиати. — И если бы он должен был повернуть для того, чтобы воссоединиться, то по какой линии он двигался бы?
Симпличио. — По той, которая идет от него к центру Земли.
Сальвиати. — Таким образом, здесь принимаются в расчет два движения: одно от бросания, начинающееся в точке касания и продолжающееся по касательной, и другое, обусловленное стремлением вниз, начинающееся в брошенном теле и идущее по секущей к центру; и для того, чтобы движение от бросания продолжалось, необходимо, чтобы импульс по касательной преобладал над стремлением по секущей, не так ли?
Симпличио. — Мне кажется, что так.
Сальвиати. — Но что, по-вашему, необходимо должно содержаться в движении от бросания, дабы последнее преобладало над движением склонения и вызвало отрыв и удаление от земли?
Симпличио. — Этого я не знаю.
Сальвиати. — Как не знаете? Движущееся тело здесь одно и то же, а именно — тот же пух; так вот, как может то же самое движущееся тело одолевать в движении и превосходить самого себя?31
Симпличио. — Я не понимаю, как оно может превосходить или уступать самому себе в движении, иначе как двигаясь или быстрее или медленнее.
Сальвиати. — Значит, вы это и ранее знали. Итак, если должно иметь место движение пуха от бросания и его движение по касательной должно преобладать над движением по секущей, то какими должны быть их скорости?
Симпличио. — Необходимо, чтобы движение по касательной было быстрее движения по секущей. О, я несчастный! Не превышает ли оно в сто тысяч раз движение вниз не только пуха, но и движения камня? А я, поистине, как простак, дал убедить себя, будто камни не могут быть отброшены вращением Земли! Отрекаюсь от этого и заявляю, что если бы Земля двигалась, то камни, слоны, башни и города неизбежно полетели бы к небу, а раз это не так, я утверждаю, что Земля не движется.
Сальвиати. — О, синьор Симпличио, вы так легко возбуждаетесь, что я начинаю больше бояться за вас, чем за пух32. Успокойтесь немного и выслушайте. Если для удержания камня или пуха на поверхности земли необходимо, чтобы падение их вниз превышало или хотя бы равнялось движению по касательной, то вы имели бы основание говорить, что движение по секущей вниз должно быть столь же или еще более быстрым, чем движение по касательной к востоку; но не сказали ли вы мне недавно, что тысяча локтей расстояния по касательной от точки касания {154} отдаляют едва ли на один дюйм от окружности? Недостаточно, значит чтобы движение по касательной, т. е. движение от суточного обращения было просто более быстрым, нежели движение по секущей, т. е. движение пуха вниз; ему необходимо быть настолько более быстрым, чтобы времени достаточного для удаления пуха, скажем, на тысячу локтей по касательной, было недостаточно для продвижения на один лишь дюйм вниз по секущей, а этого, уверяю вас, никогда не будет, каким бы быстрым ни делали вы первое движение и медленным второе.
Симпличио. — А почему движение по касательной не могло бы быть настолько быстрым, чтобы не давать пуху времени достигнуть поверхности земли?
Сальвиати. — Попробуйте дать этому вопросу точную формулировку, и я вам отвечу. Скажите, насколько более быстрым достаточно, по-вашему, сделать первое движение по сравнению со вторым?
Симпличио. — Скажу для примера, что если бы оно было в миллион раз быстрее, то пух и даже камень оказались бы отброшенными.
Сальвиати. — Вы так говорите и говорите ложь единственно но незнанию не логики, или физики, или метафизики, но лишь геометрии, потому что, если бы вы были знакомы даже только с основными ее элементами, то вы знали бы, что от центра круга можно провести прямую линию до касательной, которая пересечет ее так, что часть касательной между точкой касания и секущей будет в миллион, в два и три миллиона раз больше той части секущей, которая находится между касательной и окружностью; и по мере того, как секущая будет приближаться к точке касания, это отношение будет увеличиваться до бесконечности; поэтому, как бы быстро ни было вращение и как бы медленно ни было движение вниз, нечего опасаться, что пух или другое легкое тело может начать подниматься, ибо всегда склонение книзу превысит быстроту бросания.
Сагредо. — Я не совсем понимаю такое рассуждение.
Сальвиати. — Я приведу вам доказательство, совершенно общее
|
Геометрическое доказательство невозможности отбрасывания тел вследствие вращения Земли. |
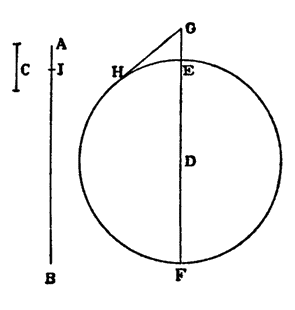 ВА будет во сколько угодно раз больше С. Пусть дан круг, центром которого является D, откуда надо провести секущую так, чтобы касательная относилась к этой секущей, как ВА к С. Найдем третью пропорциональную AI двух линий АВ и С, и пусть, как BI и IA, так же относятся друг к другу и диаметр FE и отрезок EG; из точки G проведем далее касательную GH. Утверждаю, что сделано все, что требовалось и что как ВА относится к С, так будет относиться и HG к GE33. В самом деле, так как FE относится к EG, как BI к IA, то и FG относится к GE как ВА к AI. Но С есть средняя пропорциональная между ВА и AI, a GH — средняя пропорциональная между FG и GE; поэтому как ВА относится к С, так будет относиться и FG к GH или EG к GE, что и требовалось доказать.
ВА будет во сколько угодно раз больше С. Пусть дан круг, центром которого является D, откуда надо провести секущую так, чтобы касательная относилась к этой секущей, как ВА к С. Найдем третью пропорциональную AI двух линий АВ и С, и пусть, как BI и IA, так же относятся друг к другу и диаметр FE и отрезок EG; из точки G проведем далее касательную GH. Утверждаю, что сделано все, что требовалось и что как ВА относится к С, так будет относиться и HG к GE33. В самом деле, так как FE относится к EG, как BI к IA, то и FG относится к GE как ВА к AI. Но С есть средняя пропорциональная между ВА и AI, a GH — средняя пропорциональная между FG и GE; поэтому как ВА относится к С, так будет относиться и FG к GH или EG к GE, что и требовалось доказать.
Сагредо. — Я понимаю это доказательство; тем не менее не все сомнения для меня окончательно устранены; наоборот, я чувствую, как у меня в голове поднимается некое смущение, которое, подобно густой и темной туче, не дает мне видеть необходимость вывода с той ясностью, которая обычно свойственна математическим рассуждениям. То, что меня смущает, заключается в следующем. Действительно, промежутки между касательной и окружностью убывают до бесконечности по направлению к точке касания, но, с другой стороны, верно и то, что склонность движущегося тела опускаться делается все меньше, чем ближе оно оказывается к исходной точке своего падения, т. е. к состоянию покоя, {155} как то ясно из того, что вы нам ранее сказали, показав, что опускающееся тело, выходя из состояния покоя, должно пройти все степени медленности, промежуточные между покоем и любой взятой степенью скорости, которые становятся все меньше и меньше до бесконечности. К этому присоединяется то, что скорость эта и склонность к движению убывают также до бесконечности по другой причине; последнее происходит от возможности уменьшать до бесконечности тяжесть движущегося тела; таким образом, причин, уменьшающих склонность тела опускаться и, следовательно, благоприятствующих движению отбрасывания, две, а именно: легкость движущегося тела и близость к точке покоя, и обе они способны возрастать до бесконечности; с другой стороны, в качестве противоположности они имеют одну единственную причину, препятствующую движению отбрасывания; хотя она и способна равным образом увеличиваться до бесконечности, но мне непонятно, как она одна может оказаться не побежденной соединенным действием двух других, которые равным образом способны возрастать до бесконечности.
Сальвиати. — Сомнение, достойное синьора Сагредо; чтобы разъяснить его и сделать более легким для нашего понимания, раз вы говорите, что оно представляется вам смутно, мы рассмотрим его подробно, прибегнув к помощи чертежа, который должен облегчить нам решение задачи34. Итак, начертим отвесную линию, направленную к центру; пусть это будет линия АС. Под прямым углом к ней проведем горизонтальную линию АВ, по которой должно происходить движение бросания и по которой брошенное тело продолжало бы двигаться равномерным движением, если бы тяжесть не отклоняла его книзу.
Проведем, далее, из точки А прямую линию, образующую с АВ произвольный угол; пусть это будет линия АЕ. Отметим на АВ несколько
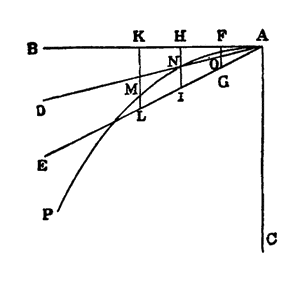 равных отрезков AF, FH и HK и проведем отвесные линии FG, HI и KL до пересечения с АЕ. Как было сказано в другом месте, падающее тяжелое тело, выходя из состояния покоя, приобретает по мере течения времени все большую степень скорости, и мы можем вообразить себе, что промежутки AF, FH и НК представляют нам равные промежутки времени, а отвесные линии FG, HI и KL — степени скорости, приобретенные за эти промежутки, так что степень скорости, приобретенная за все время АК, будет линия KL, соответствующая степени HI, приобретенной за время АН, и степени FG — за время AF. Эти степени KL, HI и FG находятся (как это очевидно) в том же отношении, что и времена КА, HА и FA35, и если будут проведены другие отвесные линии из точек, произвольно взятых на линии FA, то по мере продвижения к точке А, представляющей первое мгновение времени и первоначальное состояние покоя, будут находиться все меньшие и до бесконечности меньшие степени. И это продвижение к А представляет нам первоначальную склонность движения вниз, уменьшающуюся до бесконечности по мере приближения движущегося тела к первоначальному состоянию покоя — приближения, способного возрастать до бесконечности. Найдем теперь другое уменьшение скорости, которое равным образом может продолжаться до бесконечности от уменьшения тяжести движущегося тела36; оно представится путем проведения других линий от точки А, образующих углы, меньшие, чем угол ВАЕ, например линии AD, которая, пересекая параллели KL, HI и FG в точках М, N и О, изображает степени FO, HN и КМ, приобретенные за времена AF, АН и АК и меньшие других степеней FG, HI и KL, приобретенных за те же времена, но те — от более тяжелого движущегося тела, а эти — от более легкого. И очевидно, {156} что при приближении линии ЕА к АВ путем уменьшения угла ЕАВ (что может продолжаться до бесконечности, как до бесконечности может быть уменьшаема и тяжесть) и скорость падающего тела окажется равным образом уменьшающейся до бесконечности, а следовательно, и причина, мешавшая движению бросания; таким образом окажется, что соединение этих двух одновременно уменьшающихся до бесконечности причин, противодействующих движению отбрасывания, не может задержать последнего. Сводя все доказательства к немногим словам, скажем: с уменьшением угла ЕАВ уменьшаются степени скорости LK, IH и GF; и, сверх того, при приближении параллелей KL, IH и FG к вершине угла А те же степени также уменьшаются, причем то и другое уменьшение простирается до бесконечности, следовательно, скорость движения вниз вполне может уменьшиться настолько (будучи способна убывать до бесконечности двояким образом), что ее будет недостаточно для того, чтобы возвратить движущееся тело на окружность колеса и, следовательно, сделать так, чтобы движение бросания оказалось задержанным и устраненным. Обратно, для того чтобы движения отбрасывания не воспоследовало, необходимо, чтобы отрезки пространства, по которым брошенное тело должно опускаться для соединения с колесом, сделались столь короткими и ничтожными, что, сколь бы медленно, даже замедленно до бесконечности, ни было опускание движущегося тела, оно все же было бы достаточно для того, чтобы возвратить тело. Поэтому нужно, чтобы нашлось такое уменьшение этих отрезков, которое не только совершалось бы до бесконечности, но до такой бесконечности, которая превосходила бы двойную бесконечность уменьшения скорости падающего вниз тела37. Но как может одна величина уменьшаться более другой, которая уменьшается до бесконечности вдвойне? Итак, пусть заметит синьор Симпличио, как хорошо можно философствовать о природе без геометрии. Степени скорости, уменьшающиеся до бесконечности как от уменьшения тяжести движущегося тела, так и от приближения к исходной точке движения, т. е. к состоянию покоя, всегда определяются отношением параллелей, заключенных между двумя прямыми линиями, образующими угол, соответствующий углу ВАЕ или BAD или иному все более острому до бесконечности, но всегда прямолинейному. А уменьшение отрезков пространства, по которому движущееся тело должно вернуться на окружность колеса, пропорционально сокращению другого рода, ограниченному линиями, образующими бесконечно более узкий и острый угол, чем любой угол прямолинейный, каким является первый. Возьмем на отвесной линии АС произвольную точку С и, сделав ее центром, опишем расстоянием СА дугу AMP, которая пересечет параллели, определяющие степени скорости, как бы малы они ни были и в каком бы самом остром образуемом прямыми линиями угле они ни заключались; у этих параллелей части, находящиеся между дугой и касательной АВ, выразят величину отрезков пространства, которое надо пройти для возвращения на колесо, все меньших и меньших во все большей пропорции, по мере приближения к точке касания, — меньших, говорю я, чем те параллели, частями которых они являются. Параллели, заключенные между прямыми линиями, по мере приближения к углу уменьшаются все в той же пропорции; так например, если АН разделена пополам в точке F, то параллель HI будет вдвое больше FG; при делении FA вновь пополам параллель, проведенная из точки деления, будет половиной FG, и при продолжении деления до бесконечности последующие параллели всегда будут половиной непосредственно предшествующих. Но не то будет с линиями, заключенными между касательной и окружностью круга, ибо если сделать то же деление FA и предположить, например, что параллель, идущая из точки Н до окружности, вдвое больше той, которая {157} идет из точки F, то эта последняя будет длиннее следующей больше, чем вдвое, и по мере того, как мы будем итти к точке касания А, мы будем находить, что предшествующие линии будут содержать непосредственно следующие линии, три раза, четыре, десять, сто, тысячу, сто тысяч, сто миллионов и т. д. до бесконечности. Следовательно, эти линии сокращаются в такой степени, которая более чем достаточна для того, чтобы брошенное тело, как бы легко оно ни было, вернулось или держалось на окружности.
равных отрезков AF, FH и HK и проведем отвесные линии FG, HI и KL до пересечения с АЕ. Как было сказано в другом месте, падающее тяжелое тело, выходя из состояния покоя, приобретает по мере течения времени все большую степень скорости, и мы можем вообразить себе, что промежутки AF, FH и НК представляют нам равные промежутки времени, а отвесные линии FG, HI и KL — степени скорости, приобретенные за эти промежутки, так что степень скорости, приобретенная за все время АК, будет линия KL, соответствующая степени HI, приобретенной за время АН, и степени FG — за время AF. Эти степени KL, HI и FG находятся (как это очевидно) в том же отношении, что и времена КА, HА и FA35, и если будут проведены другие отвесные линии из точек, произвольно взятых на линии FA, то по мере продвижения к точке А, представляющей первое мгновение времени и первоначальное состояние покоя, будут находиться все меньшие и до бесконечности меньшие степени. И это продвижение к А представляет нам первоначальную склонность движения вниз, уменьшающуюся до бесконечности по мере приближения движущегося тела к первоначальному состоянию покоя — приближения, способного возрастать до бесконечности. Найдем теперь другое уменьшение скорости, которое равным образом может продолжаться до бесконечности от уменьшения тяжести движущегося тела36; оно представится путем проведения других линий от точки А, образующих углы, меньшие, чем угол ВАЕ, например линии AD, которая, пересекая параллели KL, HI и FG в точках М, N и О, изображает степени FO, HN и КМ, приобретенные за времена AF, АН и АК и меньшие других степеней FG, HI и KL, приобретенных за те же времена, но те — от более тяжелого движущегося тела, а эти — от более легкого. И очевидно, {156} что при приближении линии ЕА к АВ путем уменьшения угла ЕАВ (что может продолжаться до бесконечности, как до бесконечности может быть уменьшаема и тяжесть) и скорость падающего тела окажется равным образом уменьшающейся до бесконечности, а следовательно, и причина, мешавшая движению бросания; таким образом окажется, что соединение этих двух одновременно уменьшающихся до бесконечности причин, противодействующих движению отбрасывания, не может задержать последнего. Сводя все доказательства к немногим словам, скажем: с уменьшением угла ЕАВ уменьшаются степени скорости LK, IH и GF; и, сверх того, при приближении параллелей KL, IH и FG к вершине угла А те же степени также уменьшаются, причем то и другое уменьшение простирается до бесконечности, следовательно, скорость движения вниз вполне может уменьшиться настолько (будучи способна убывать до бесконечности двояким образом), что ее будет недостаточно для того, чтобы возвратить движущееся тело на окружность колеса и, следовательно, сделать так, чтобы движение бросания оказалось задержанным и устраненным. Обратно, для того чтобы движения отбрасывания не воспоследовало, необходимо, чтобы отрезки пространства, по которым брошенное тело должно опускаться для соединения с колесом, сделались столь короткими и ничтожными, что, сколь бы медленно, даже замедленно до бесконечности, ни было опускание движущегося тела, оно все же было бы достаточно для того, чтобы возвратить тело. Поэтому нужно, чтобы нашлось такое уменьшение этих отрезков, которое не только совершалось бы до бесконечности, но до такой бесконечности, которая превосходила бы двойную бесконечность уменьшения скорости падающего вниз тела37. Но как может одна величина уменьшаться более другой, которая уменьшается до бесконечности вдвойне? Итак, пусть заметит синьор Симпличио, как хорошо можно философствовать о природе без геометрии. Степени скорости, уменьшающиеся до бесконечности как от уменьшения тяжести движущегося тела, так и от приближения к исходной точке движения, т. е. к состоянию покоя, всегда определяются отношением параллелей, заключенных между двумя прямыми линиями, образующими угол, соответствующий углу ВАЕ или BAD или иному все более острому до бесконечности, но всегда прямолинейному. А уменьшение отрезков пространства, по которому движущееся тело должно вернуться на окружность колеса, пропорционально сокращению другого рода, ограниченному линиями, образующими бесконечно более узкий и острый угол, чем любой угол прямолинейный, каким является первый. Возьмем на отвесной линии АС произвольную точку С и, сделав ее центром, опишем расстоянием СА дугу AMP, которая пересечет параллели, определяющие степени скорости, как бы малы они ни были и в каком бы самом остром образуемом прямыми линиями угле они ни заключались; у этих параллелей части, находящиеся между дугой и касательной АВ, выразят величину отрезков пространства, которое надо пройти для возвращения на колесо, все меньших и меньших во все большей пропорции, по мере приближения к точке касания, — меньших, говорю я, чем те параллели, частями которых они являются. Параллели, заключенные между прямыми линиями, по мере приближения к углу уменьшаются все в той же пропорции; так например, если АН разделена пополам в точке F, то параллель HI будет вдвое больше FG; при делении FA вновь пополам параллель, проведенная из точки деления, будет половиной FG, и при продолжении деления до бесконечности последующие параллели всегда будут половиной непосредственно предшествующих. Но не то будет с линиями, заключенными между касательной и окружностью круга, ибо если сделать то же деление FA и предположить, например, что параллель, идущая из точки Н до окружности, вдвое больше той, которая {157} идет из точки F, то эта последняя будет длиннее следующей больше, чем вдвое, и по мере того, как мы будем итти к точке касания А, мы будем находить, что предшествующие линии будут содержать непосредственно следующие линии, три раза, четыре, десять, сто, тысячу, сто тысяч, сто миллионов и т. д. до бесконечности. Следовательно, эти линии сокращаются в такой степени, которая более чем достаточна для того, чтобы брошенное тело, как бы легко оно ни было, вернулось или держалось на окружности.
Сагредо. — Я прекрасно понимаю все рассуждение и силу его убедительности, но тем не менее мне кажется, что если бы кто-нибудь захотел поколебать его, он мог бы выдвинуть кое-какие возражения, говоря, что из двух причин, делающих движение тела вниз все более и более медленным до бесконечности, только та, которая зависит от близости к исходной точке падения, постоянно возрастает все в той же пропорции соответственно тому, как и параллели сохраняют между собой то же соотношение и так далее, но то, что уменьшение той же скорости, зависящее от уменьшения тяжести движущегося тела (а это является второй причиной), происходит в той же пропорции, не представляется столь очевидным. Кто нас убедит, что оно не совершается пропорционально длине линий, заключенных между касательной и окружностью, или в отношении еще большем?
Сальвиати. — Я принял за достоверное, что скорости тел, естественно движущихся книзу, пропорциональны отношению их веса, в угоду синьору Симпличио и Аристотелю, который во многих местах утверждает это как положение очевидное; вы к выгоде противника ставите это под сомнение и предполагаете, что скорость, быть может, возрастает в пропорции, большей и даже до бесконечности большей, по сравнению с тяжестью, от чего все предыдущее рассуждение рассыпается прахом; чтобы его подкрепить, мне остается утверждать, что отношение между скоростями гораздо меньше отношения между весами, и тем не только восстановить, но и укрепить то, что было сказано. В доказательство я приведу опыт, который покажет нам, что одно тело, в тридцать или сорок раз более тяжелое, чем другое, например пуля из свинца, не будет двигаться даже при помощи мощного орудия быстрее, чем вдвое, по сравнению с пулей из пробки. Итак, если движения от бросания не происходит даже тогда, когда скорость падения уменьшается пропорционально весу, то тем менее оно будет иметь место в том случае, если скорость уменьшается значительно менее уменьшения веса. Но даже если предположить, что скорость уменьшается в пропорции, значительно превосходящей ту, с которой убывает тяжесть, пусть даже она убывает пропорционально упомянутым параллельным линиям между касательной и окружностью, я все же не вижу никакой необходимости в том, чтобы притти к заключению, будто от этого должно будет произойти отбрасывание тел, хотя бы из самой легкой материи; напротив, я утверждаю, что такого отбрасывания не произойдет, всегда имея в виду, что речь идет не о материях легчайших, т. е. лишенных всякой тяжести и по природе своей идущих вверх, но о таких, которые опускаются, хотя и очень медленно, и имеют хотя бы и самую незначительную тяжесть. Думать так побуждает меня то обстоятельство, что уменьшение тяжести, совершающееся пропорционально параллелям между касательной и окружностью, имеет последним и крайним пределом нуль тяжести, как и параллели последним пределом своего уменьшения имеют самое касание, т. е. неделимую точку.
Но тяжесть никогда не уменьшается до самого последнего предела, потому что в таком случае движущееся тело не было бы тяжелым; в то же время путь возвращения брошенного тела к окружности сокращается {158} до самых малых размеров; это бывает тогда, когда движущееся тело находится на окружности в точке касания, так что, для того чтобы вернуться, ему нет надобности проходить какое бы то ни было расстояние; поэтому, как бы мала ни была склонность к движению вниз, все же она всегда будет более чем достаточна для того, чтобы вернуть движущееся тело на окружность, от которой оно отстоит на предельно малое расстояние, т. е. никакое.
Сагредо. — Поистине, рассуждение весьма тонкое и в такой же мере убедительное; надо признаться, что попытка трактовать естественные проблемы без геометрии есть попытка сделать невозможное.
Сальвиати. — Синьор Симпличио, однако, этого не скажет, хотя я не думаю, чтобы он был из числа тех перипатетиков, которые отговаривают своих учеников изучать математику, как нечто такое, что вредит рассудку и делает его менее способным к созерцанию.
Симпличио. — Я не сделал бы такого упрека Платону, хотя и сказал бы вместе с Аристотелем, что он слишком погружается в свою любимую геометрию и слишком увлекается ею. Ведь в конце концов эти математические тонкости, синьор Сальвиати, истинно абстрактны, в приложении же к чувственной и физической материи они не оправдываются. Так например, пусть математики доказывают на основании своих принципов, что sphaera tangit planum in puncto38 — положение, подобное нашему, но, как только дело дойдет до материи, все происходит иначе; то же самое хочется мне сказать об этих углах касания и пропорциях; они все ни к чему, когда дело доходит до вещей материальных и чувственных.
Сальвиати. — Так, значит, вы вовсе не думаете, что касательная соприкасается с поверхностью земного шара в одной точке?
Симпличио. — Не только в одной, но думаю, что на много и много десятков, а может быть, и сотен локтей идет прямая линия, касаясь поверхности воды, а не то что земли, прежде чем от нее отделиться.
Сальвиати. — А если я в этом с вами соглашусь, то не замечаете ли вы, что это тем хуже для вас? Ведь есть в предположении, что касательная отделяется от земной поверхности за пределами одной только точки, было все же доказано, что из-за большой остроты угла касания (если только он может назваться углом) брошенное тело не отделится, то сколь менее будет оно иметь причину отделиться, если угол совершенно сомкнётся, а поверхность и касательная пойдут вместе? Не видите ли вы, что, таким образом, движение бросания пошло бы по самой земной поверхности, а это равносильно тому, что его вообще не было бы?
Итак, вы видите, какова сила истины: в то время как вы пытаетесь
|
Сила правды иногда укрепляется нападками на нее. |
Симпличио. — Я счел бы его за совершенно лишенного рассудка.
Сальвиати. — В таком же точно положении находится и тот, кто
|
И материальная сфера касается материальной плоскости только в одной точке. |
|
Определение сферы. |
Сальвиати. — Так что, если бы такие линии не были равными, то такое твердое тело вовсе не было бы сферой?
Симпличио. — Нет, синьор.
Сальвиати. — Скажите мне далее, думаете ли вы, что из многих линий, которые могут быть проведены между двумя точками, только одна может быть прямой?
Симпличио. — Конечно, синьор.
Сальвиати. — Но вы понимаете, что эта единственная прямая будет, кроме того, по необходимости кратчайшей из них?
Симпличио. — Понимаю и, кроме того, имею ясное доказательство этого, данное одним великим философом-перипатетиком; и кажется, если память мне не изменяет, он приводит его в упрек Архимеду, который полагает эту истину очевидной, имея возможность ее доказать.
Сальвиати. — Великим математиком будет тот, кто докажет то, чего не сумел и не смог доказать Архимед; и если вы помните доказательство, я охотно прослушал бы его, ибо отлично помню, что Архимед в книге «О сфере и цилиндре» относит это положение к постулатам и твердо считает, что оно недоказуемо.
Симпличио. — Думаю, что вспомню, потому что оно довольно ясное и короткое.
Сальвиати. — Тем больше будет посрамление Архимеда и слава вашего философа.
Симпличио. — Я приведу его чертеж. Между точками А и В проведены прямая АВ и кривая АСВ, относительно коих требуется доказать, что прямая короче; доказательство таково: на кривой берется точка,
|
Доказательство одним перипатетиком того, что прямая линия есть кратчайшая. |
 скажем, С и от нее проводятся две другие прямые АС и СВ, каковые вместе будут длиннее одной АВ, как это доказал Евклид; но кривая АСВ больше двух прямых АС и СВ, следовательно, a fortiori кривая АСВ будет и подавно большей, чем прямая АВ, что и требовалось доказать.
скажем, С и от нее проводятся две другие прямые АС и СВ, каковые вместе будут длиннее одной АВ, как это доказал Евклид; но кривая АСВ больше двух прямых АС и СВ, следовательно, a fortiori кривая АСВ будет и подавно большей, чем прямая АВ, что и требовалось доказать.
|
Ошибка этого перипатетика, доказывающего ignotum per ignotius. |
Симпличио. — Каким образом?
Сальвиати. — Как каким образом? Разве неизвестное положение, которое вы хотите доказать, не состоит в том, что кривая АСВ длиннее прямой АВ? А средний член, принимаемый в качестве известного, не тот ли, что кривая АСВ будет больше, чем АС и СВ вместе, которые, как известно, больше АВ? Но, если вам неизвестно, что кривая больше одной прямой АВ, разве не будет еще гораздо менее известным, что она больше двух прямых АС и СВ, которые больше одной АВ? А вы принимаете это за известное.
Симпличио. — Я еще не совсем понимаю, в чем заключается ошибка.
Сальвиати. — Если две прямые будут больше АВ (что известно из Евклида), то всякий раз, как кривая будет больше обеих прямых АС и СВ, не будет ли она и подавно длиннее одной прямой АВ?
Симпличио. — Да, синьор.
Сальвиати. — Что кривая АСВ больше прямой АВ, — положение, более известное, нежели средний член, а именно, что та же кривая больше {160} двух прямых АС и СВ, а когда средний член менее известен, чем заключение, это и называется доказательством ignotum per ignotius. Но вернемся к нашему положению: с меня достаточно вашего понимания, что прямая есть кратчайшая из всех линий, могущих быть проведенными между двумя точками. Что касается главного положения, то вы утверждаете, что материальная сфера касается плоскости не в одной единственной точке. Каково же будет ее касание?
Симпличио. — Оно будет частью ее поверхности.
Сальвиати. — Таким же образом место касания и другой сферы, равной первой, будет подобной же частицей ее поверхности?
Симпличио. — Нет оснований, чтобы было иначе.
Сальвиати. — Значит, и обе сферы при соприкосновении будут соприкасаться двумя одинаковыми частицами поверхности, потому что,
|
Доказательство того, что сфера касается плоскости только в одной точке. |
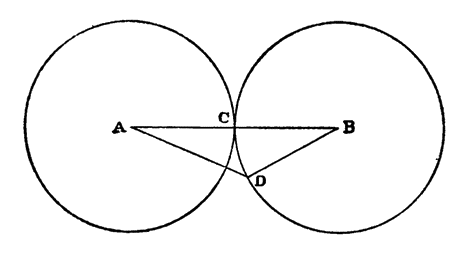 если каждая из них порознь прилегает так к одной и той же плоскости, то необходимо, чтобы они прилегали и друг к другу. Итак, представьте себе две соприкасающиеся сферы с центрами А и В; соединим их центры прямой линией АВ, которая пройдет через место соприкосновения. Пусть она проходит через точку С; взяв в месте соприкосновения другую точку D, проведем от нее две прямые линии AD и BD так, чтобы образовался треугольник ADB, у которого стороны AD и DB вместе будут равны третьей ACB, содержащей два полудиаметра, которые по определению сферы все между собой равны. Итак, прямая АВ, проведенная между двумя центрами А и В, не будет кратчайшей из всех, поскольку AD и АВ вместе равны ей, а это, по вашему же признанию, абсурдно.
если каждая из них порознь прилегает так к одной и той же плоскости, то необходимо, чтобы они прилегали и друг к другу. Итак, представьте себе две соприкасающиеся сферы с центрами А и В; соединим их центры прямой линией АВ, которая пройдет через место соприкосновения. Пусть она проходит через точку С; взяв в месте соприкосновения другую точку D, проведем от нее две прямые линии AD и BD так, чтобы образовался треугольник ADB, у которого стороны AD и DB вместе будут равны третьей ACB, содержащей два полудиаметра, которые по определению сферы все между собой равны. Итак, прямая АВ, проведенная между двумя центрами А и В, не будет кратчайшей из всех, поскольку AD и АВ вместе равны ей, а это, по вашему же признанию, абсурдно.
Симпличио. — Это доказательство относится к сферам абстрактным, а не материальным.
Сальвиати. — Так скажите же мне, в чем заключается неправильность моей аргументации, почему заключение не может быть распространено на сферы материальные, а относится лишь к нематериальным и абстрактным?
|
Почему абстрактная сфера касается абстрактной плоскости в одной точке, а материальная, конкретная — не в одной. |
Сальвиати. — О, все это я охотно допускаю, но это весьма далеко от нашей темы. Желая показать мне, что материальная сфера соприкасается с материальной плоскостью не в одной точке, вы пользуетесь сферой, которая не есть сфера, и плоскостью, которая не есть плоскость, поскольку, по вашим словам, или этих вещей в мире нет, или если они и есть, то они портятся при применении их к делу. Было бы, значит, правильнее принять заключение, хотя бы условно, а именно, что если бы в природе существовали и сохранялись без изменения совершенные сферы и плоскости, то они соприкасались бы в одной единственной точке, а затем уже отрицать возможность этого в действительности.
Симпличио — Думаю, что положение философов нужно понимать именно в этом смысле, потому что, несомненно, несовершенство материи {161} является причиной того, что вещи, взятые конкретно, не соответствуют вещам, рассматриваемым в абстракции.
Сальвиати. — Как не соответствуют? Наоборот, то, что вы сами сейчас говорите, доказывает, что они в точности соответствуют.
Симпличио. — Каким образом?
Сальвиати. — Не говорите ли вы, что из-за несовершенства материи то тело, которое должно бы быть совершенно сферичным, и та плоскость, которая должна бы быть совершенно плоской, конкретно не оказываются такими, какими вы их представляете себе в абстракции?
Симпличио. — Говорю.
Сальвиати. — Значит, всякий раз, как вы конкретно прикладываете материальную сферу к материальной плоскости, вы прикладываете несовершенную сферу к несовершенной плоскости и говорите, что они соприкасаются не в одной единственной точке. А я вам говорю, что и в абстракции нематериальная сфера, которая является несовершенной сферой, может касаться нематериальной, также несовершенной плоскости, не одной точкой, а частью поверхности. Так что то, что происходит конкретно, имеет место и в абстракции. Было бы большой неожиданностью, если бы вычисления и действия, производимые абстрактно над числами, не соответствовали затем конкретно серебряным и золотым монетам и товарам. Но знаете ли, синьор Симпличио, что происходит на деле и как для выполнения подсчетов сахара, шелка и полотна необходимо скинуть
|
Абстрактные положения вполне согласуются с конкретными. |
Симпличио. — В таких, я думаю, у нас недостатка не будет.
Сальвиати. — Каковы бы они ни были, они также могут соприкасаться в одной точке, ибо соприкасаемость в одной точке вовсе не является исключительной привилегией совершенного сферического тела и
|
Касание в одной точке не является исключительно особенностью совершенных сфер, а свойственно всем криволинейным фигурам. Труднее найти фигуры, которые соприкасались бы частью своих поверхностей, чем соприкасающиеся в одной точке. |
Симпличио. — Значит, вы считаете, что два камня или два куска железа, взятые наудачу и приложенные друг к другу, в большинстве случаев соприкасаются в одной точке?
Сальвиати. — При случайных сближениях, думаю, что нет, поскольку поверх них обычно имеется хотя бы немного податливой грязи {162} и поскольку при прикладывании их друг к другу не стараются избежать всякого толчка; этого немногого достаточно для того, чтобы одна поверхность несколько уступила другой и поверхности взаимно формировали друг друга, по крайней мере на маленьком пространстве, вдавливаясь одна в другую; но если поверхности их будут хорошо отполированы, если оба они будут положены на стол так, чтобы один не давил на другой, а затем осторожно придвинуты один к другому, то я не сомневаюсь, что они могли бы притти в соприкосновение в одной единственной, точке.
Сагредо. — С вашего разрешения мне необходимо изложить здесь один вопрос, возникший у меня, когда я слышал заявление синьора Симпличио о невозможности найти твердое материальное тело, имеющее совершенно сферическую форму, и видел, что синьор Сальвиати, не противореча, некоторым образом с этим соглашался. Я хотел бы знать, не возникает ли та же трудность при придании твердому телу другой какой-либо формы, или, вернее говоря, представляется ли более трудным придать куску мрамора форму совершенной сферы, чем форму совершенной пирамиды, или совершенного коня, или совершенной саранчи.
Сальвиати. — Давая вам ответ, я прежде всего хочу снять с себя упрек в согласии, которое, как вам кажется, я дал синьору Симпличио; это было только временно, потому что я также намеревался, прежде чем перейти к другим вопросам, сказать то, что, пожалуй, будет тождественно или весьма сходно с вашей мыслью. Отвечая на ваш первый вопрос,
|
Сферическая фигура легче воспроизводится, чем всякая другая. Построение круга, принятое как постулат. |
|
Круглые тела различной величины могут быть воспроизведены при помощи одного и того же инструмента. |
Симпличио. — Не знаю, расхожусь ли я с вами в чем-нибудь. Мое мнение таково: ни одна из названных фигур не может получиться совершенной, но если говорить о возможном приближении к совершенной степени, то, конечно, несравненно легче придать твердому телу форму сферическую, нежели форму коня или саранчи.
Сагредо. — А от чего, думаете вы, эта большая трудность зависит?
Симпличио. — Подобно тому, как абсолютная простота и единообразие
|
Неправильные формы трудно воспроизводимы. |
Сагредо. — Стало быть, раз неправильность есть причина трудности, то и форма камня, разбитого наудачу молотком, вероятно, будет принадлежать к числу наиболее трудных для воспроизведения, поскольку она, пожалуй, еще более неправильна, чем фигура коня?
Симпличио. — Так должно быть.
Сагредо. — Но скажите мне, та форма, которую имеет камень, какова бы она ни была, является ли для него совершенной или нет? {163}
Симпличио. — Та форма, которую он имеет, является столь совершенной, что никакая другая не подойдет к нему столь же точно.
Сагредо. — Значит, если среди неправильных и потому трудных для воспроизведения форм у нас все же оказывается бесконечное множество весьма совершенных, то на каком основании можно утверждать, что форму простейшую и потому легчайшую из всех невозможно встретить?
Сальвиати. — Синьоры, с вашего разрешения, мне кажется, что мы вступили в спор, весьма недалекий от пустословия; в то время как наши рассуждения должны были бы касаться вещей серьезных и значительных, мы тратим время в пустых и бессодержательных словопрениях. Не будем забывать, что изыскание о строении мира — одна из самых
|
Вопрос о системе мироздания — одна из самых высоких проблем. |
Поэтому, если у нас нет более ничего, что можно было бы привести для окончательного опровержения возражения, основанного на вращении Земли и являющегося последним из аргументов для доказательства ее неподвижности по отношению к собственному центру, то мы можем перейти к исследованию аргументов за и против годового движения.
Сагредо. — Мне не хотелось бы, синьор Сальвиати, чтобы вы измеряли наши умы мерою вашего; вы, всегда занятый высочайшими созерцаниями, считаете пустыми и низкими некоторые вопросы, такие, которые нам кажутся достойной пищей для наших умов; поэтому ради нашего удовлетворения соблаговолите иногда снизойти до некоторых уступок нашему любопытству. Что касается опровержения последнего возражения, основанного на суточном вращении, то, чтобы удовлетворить меня, достаточно было бы значительно меньшего, чем было здесь сказано; но, во всяком случае, то, что говорилось с таким избытком, показалось мне столь любопытным, что не только не утомило меня, но своей новизной доставило мне удовольствие, больше которого трудно и желать; потому, если вам остается добавить еще какое-нибудь соображение, приведите его — я, со своей стороны, выслушаю его весьма охотно.
Сальвиати. — Я всегда находил величайшее наслаждение, делая свои открытия; после этого наслаждения, являющегося максимальным, я испытываю наибольшую радость, делясь ими с некоторыми из друзей, которые их понимают и обнаруживают к ним вкус; и вот, поскольку вы один из них, я, ослабив несколько узду моего тщеславия, которое заставляет меня радоваться, когда я кажусь себе более проницательным, чем некоторые другие, почитающиеся зоркими, приведу в завершение прошлого спора другую ошибку последователей Птоломея и Аристотеля, допущенную в приведенном доказательстве41.
Сагредо. — Я с жадностью готов это выслушать.
Сальвиати. — Мы до сих пор обходили молчанием и уступили Птоломею в качестве явления бесспорного, что при отбрасывании камня скоростью вращающегося около своего центра колеса причина отбрасывания возрастает настолько, насколько увеличивается скорость вращения. Отсюда вытекало, что раз скорость земного вращения несравненно больше скорости любой машины, которую мы можем искусственно вращать, то соответственно и отбрасывание камней, животных и т. д. должно было бы быть чрезвычайно сильным. Теперь я замечаю, что в этом рассуждении имеется большая ошибка, ибо мы сравниваем между собой эти скорости абсолютно и без различения их. Действительно, если я сравниваю скорости одного и того же колеса или же двух равных колес, то колесо, {164} которое вращается быстрее, отбросит камень с большим импульсом, и при возрастании скорости в той же пропорции будет возрастать и причина отбрасывания, но если скорость будет возрастать не путем увеличения скорости движения колеса, т. е. не путем сообщения ему большего числа оборотов в равные промежутки времени, а вследствие удлинения диаметра и увеличения самого колеса, так что при сохранении того же самого времени на один оборот как у малого, так и у большого колеса скорость у большого будет больше лишь от того, что его окружность
|
Причина отбрасывания не возрастает пропорционально возрастанию скорости, обусловленной увеличением колеса. |
Сагредо. — То, что вы, синьор Сальвиати, мне говорите, должно происходить, как я понимаю, именно так, но я не могу столь быстро найти причину, почему одинаковые скорости не оказывают одинакового действия при отбрасывании тел, так что действие скорости меньшего колеса гораздо больше действия скорости колеса большего; прошу вас объяснить мне, как обстоит дело?
Симпличио. — Вы, синьор Сагредо, на этот раз оказались непохожим на самого себя: обычно вы сразу все схватываете, а теперь вы прошли мимо ошибки в опыте с тростью, которую я смог подметить; заключается она в различии способа движения при бросании тростью длинной и тростью короткой. Действительно, если мы хотим, чтобы камень выскочил из расщепа, то нужно не продолжать равномерное движение, а наоборот, в тот момент, когда оно весьма быстро, удержать руку и умерить скорость трости; благодаря этому камень, уже находящийся в быстром движении, выскакивает и движется с импульсом; но нельзя таким образом задержать большую трость, которая благодаря своей длине и гибкости не вполне повинуется сдерживающей руке и, продолжая сопровождать камень на некоторое расстояние и слегка его сдерживая, сохраняет соединение с ним, не испытывая остановки как бы от твердой преграды, которая дала бы ему выскочить; если бы обе трости наталкивались на останавливающее их препятствие, я полагаю, что камень одинаково выскочил бы из той и другой трости, поскольку их движения будут одинаково быстры.
Сагредо. — С разрешения синьора Сальвиати я кое-что отвечу синьору Симпличио, поскольку он обратился ко мне; скажу, что в его рассуждении есть и хорошее и плохое: хорошее, потому что почти все верно, плохое, потому что в общем это не относится к нашей теме. Совершенно верно, что когда нечто, быстро перемещающее камни, наталкивается на неподвижную преграду, последние с импульсом выбрасываются вперед; подобное ежедневно совершается на наших глазах с лодками, которые на быстром ходу наскакивают на мель или наталкиваются
|
Если существует суточное вращение Земли, то постройки, горы и даже, быть может, весь земной шар разрушились бы, если бы Земля была каким-либо препятствием остановлена. |
Сальвиати. — Я готов дать вам такое удовлетворение, какое только будет в моих силах, и хотя из первых моих слов вам может показаться, будто я исследую вещи, не относящиеся к нашей цели, тем не менее в процессе рассуждения мы найдем, что они не таковы. Поэтому пусть скажет мне синьор Сагредо, в чем, по его мнению, заключается противодействие движению какого-либо движущегося тела?
Сагредо. — Я сейчас не вижу в движущемся теле внутреннего противодействия движению, за исключением разве его естественной склонности и влечения к противоположному движению, как например, у тяжелых тел, имеющих влечение двигаться вниз, у которых есть противодействие движению вверх; я сказал — внутреннего противодействия, ибо полагаю, что вы имеете в виду именно его, а не внешние случайные и многочисленные препятствия.
Сальвиати. — Это именно я и хотел сказать, и ваша проницательность предвосхитила мое суждение. Но если я был скуп на вопросы, то ответ синьора Сагредо полностью соответствует тому, что нам нужно. Я полагаю, что в движущемся теле, помимо естественной склонности к противоположному концу, есть другое, чисто внутреннее и природное свойство, делающее его противящимся движению. Поэтому, скажите мне
|
Склонность тяжелых тел к движению вниз равняется их сопротивлению к движению вверх. |
Сагредо. — Думаю, что она будет в точности равна; поэтому-то и видно, как на весах два равных груза остаются неподвижными в равновесии, поскольку тяжесть одного противится подъему благодаря действию той тяжести, с которой другой груз давит вниз и стремится поднять первый.
Сальвиати. — Отлично; таким образом, для того чтобы один груз Поднял другой, нужно или увеличить давящий вес одного или уменьшить вес другого. Но если противодействие движению вверх заключается в одной только тяжести, отчего происходит то, что на весах с неравными плечами, как например, безмене, иногда груза в сто фунтов, тянущего вниз, бывает недостаточно для поднятия груза в четыре фунта, ему противостоящего, и этот груз в четыре фунта сможет, опускаясь, поднять груз в сто фунтов? Ибо таково действие безмена по отношению к тяжелому грузу, который мы хотим взвесить. Если противодействие перемещаемого заключается в одной тяжести, то как может гиря весом только в четыре фунта противодействовать грузу из тюка шерсти или шелка в восемьсот или тысячу фунтов и, тем более, как может она преодолеть своим моментом вес этого тюка и поднять его? Приходится, значит, сказать, синьор Сагредо, что здесь работа производится иным противодействием и иной силой, нежели сила простой тяжести.
Сагредо. — Необходимо, чтобы это было так; поэтому скажите, какова эта вторая сила? {166}
Сальвиати. — Это то, чего не было у весов с равными плечами. Посмотрите, что новое есть у безмена; в этом по необходимости и будет заключаться причина нового действия.
Сагредо. — Ваш допрос заставил меня, кажется, вспомнить кое о чем. В обоих приборах пользуются грузом и движением; у весов движения равны, и потому один груз обязательно должен превосходить тяжестью другой, чтобы привести последний в движение; у безмена меньший груз будет двигать больший, если только этот последний движется очень мало, будучи подвешен на меньшем расстоянии, а первый движется много, будучи подвешен на большем расстоянии; необходимо, значит, сказать, что меньший вес преодолевает противодействие большего посредством большего движения, так как больший движется мало.
Сальвиати. — А это равносильно утверждению, что большая скорость менее тяжелого движущегося тела возмещает тяжесть более тяжелого, но менее быстро движущегося тела.
Сагредо. — Но думаете ли вы, что скорость в точности возмещает
|
Большая скорость возмещает в точности большую тяжесть. |
Сальвиати. — Конечно, да; и я мог бы показать вам это посредством многих опытов, но пока что вам достаточно для подтверждения — одного безмена; на нем вы увидите, что легкая гиря сможет поддерживать и уравновешивать тяжелый тюк тогда, когда ее удаленность от центра, на котором держится и поворачивается безмен, будет во столько раз больше другого, меньшего расстояния, на котором висит тюк, во сколько раз абсолютный вес тюка больше веса гири. То, что больший тюк не может своим весом поднять гораздо менее тяжелую гирю, повидимому, не может иметь другого основания, кроме разницы в движениях, которые оба они должны совершить, когда тюк, опускаясь на один дюйм, заставляет гирю подниматься на сто дюймов (предполагая, что тюк весит в сто раз больше, чем гиря, а расстояние гири от центра безмена в сто раз больше расстояния между тем же центром и точкой подвеса тюка); но сказать, что гиря передвигается на расстояние в сто дюймов за то время, за которое тюк передвигается только на один дюйм, все равно, что сказать, что скорость движения гири в сто раз более скорости движения тюка. Теперь запомните хорошенько в качестве истинного и достоверного принципа, что противодействие, происходящее от скорости движения, возмещает то, которое зависит от тяжести другого движущегося тела; благодаря этому тело весом в фунт, движущееся со скоростью в сто степеней, настолько же противодействует задержке, насколько и другое тело, весом в сто фунтов, у которого скорость равна всего одной степени; и два одинаковых тела будут в одинаковой степени противодействовать перемещению, если их нужно заставить двигаться с одинаковой скоростью; но если одно нужно заставить двигаться быстрее другого, то оно будет оказывать большее противодействие, соответственно большей скорости, которую ему нужно сообщить. Разобрав это, перейдем к объяснению нашей проблемы и для более ясного понимания сделаем маленький чертеж.
Пусть около одного и того же центра А вращаются два неравные колеса и пусть у меньшего окружность будет BG, а у большего СЕН; полудиаметр ABC пусть будет перпендикулярен к горизонту, а через точки В и С проведены прямые касательные линии BF и CD; возьмем на дугах BG и СЕ равные части BG и СЕ и предположим, что оба колеса вращаются вокруг своего центра с одинаковой скоростью, так что два движущихся тела, например два камня, расположенные в точках В и С, окажутся перемещаемыми по окружности BG и СЕ с равными скоростями; {167} таким образом, в то время, в какое камень В пройдет дугу BG, камень С пройдет дугу СЕ. Теперь я утверждаю, что вращение меньшего колеса гораздо более способно отбросить камень В, нежели вращение большего колеса — камень С. Ведь если, как уже было разъяснено, движение отброшенного тела должно совершаться по касательной, то когда камни В
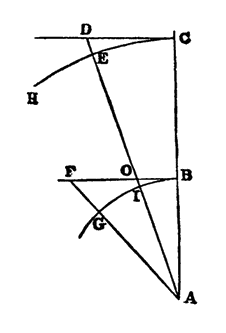 и С должны были бы отделиться от своих колес и начать движение из точек В и С, они были бы отброшены импульсом, возникшим от вращения, по касательной BF и CD. Значит, оба камня имели бы одинаковые импульсы к движению по касательной BF и CD и двигались бы по ним, если бы никакая иная сила их не отклоняла. Не так ли, синьор Сагредо?
и С должны были бы отделиться от своих колес и начать движение из точек В и С, они были бы отброшены импульсом, возникшим от вращения, по касательной BF и CD. Значит, оба камня имели бы одинаковые импульсы к движению по касательной BF и CD и двигались бы по ним, если бы никакая иная сила их не отклоняла. Не так ли, синьор Сагредо?
Сагредо. — Мне кажется, дело обстоит так.
Сальвиати. — Но какая же сила, по-вашему, может отклонять камни от движения по касательной, по которой их действительно гонит импульс от вращения?
Сагредо. — Либо их собственная тяжесть, либо какой-нибудь клей, задерживающий их на колесе или в связи с последним.
Сальвиати. — Но для отклонения движения тела, перемещающегося под влиянием импульса, не требуется ли бо́льшая или меньшая сила в зависимости от того, больше или меньше отклонение? Иначе говоря, сообразно этому должно ли тело при отклонении проходить за одно и то же время большее или меньшее пространство?
Сагредо. — Да, потому что уже ранее мы пришли к выводу, что для приведения тела в движение движущая сила должна быть тем большей, чем с большей скоростью требуется заставить тело двигаться.
Сальвиати. — Теперь посмотрите: для отклонения камня, отбрасываемого малым колесом от движения, которое он совершал бы по касательной BF, и удержания его в связи с колесом требуется, чтобы собственная его тяжесть отвлекала его на длину секущей FG или, правильнее, перпендикуляра, опущенного из точки G на линию BF, тогда как для большего колеса отклонение не должно превышать длины секущей BE или, вернее, перпендикуляра, опущенного из точки Е на касательную DC, значительно меньшей, чем FG, и становящейся все меньшей и меньшей по мере увеличения колеса; и так как эти отклонения должны совершаться в равные промежутки времени, т. е. пока проходятся две равные дуги BG и СЕ, то отклонение камня B, т. е. отклонение FG, должно быть более быстрым, чем другое отклонение DE, и потому значительно большая сила потребуется для удержания камня В в связи с его малым колесом, нежели для удержания С в связи с его большим, а это равносильно утверждению, что незначительная причина, которая воспрепятствует отбрасыванию от большого колеса, не помешает ему у малого. Ясно, следовательно, что чем больше растет колесо, тем меньше становится причина отбрасывания.
Сагредо. — То, что я понимаю благодаря вашему пространному анализу, я, кажется, могу выразить в форме следующего довольно короткого рассуждения, удовлетворяющего моему разумению, а именно: благодаря одинаковой скорости обоих колес в обоих камнях возникает одинаковый импульс к движению по касательной, но мы видим что большая окружность идет, незначительно удаляясь от касательной и как бы следуя за ней, так сказать, до некоторой степени распускает узду и, лишь слегка натягивая ее, нежно сдерживает в камне стремление отделиться от окружности, так что любое незначительное сопротивление, будь то от собственной ли склонности или от какого-нибудь клея, достаточно здесь для удержания камня в связи с колесом; но это сопротивление окажется недостаточным для того, чтобы произвести то же действие {168} в малом колесе, которое мало следует за направлением касательной и с чрезмерной жадностью стремится удержать при себе камень; и так как узда и клей здесь не сильнее тех, которые удерживают камень на большом колесе, то здесь он разорвет узду и устремится по касательной. Поэтому я не только понимаю теперь, что заблуждались все те, кто полагал, будто причина движения бросания возрастает до мере возрастания скорости вращения, но, более того, принимая во внимание ослабление движения бросания от возрастания колеса, если только в обоих колесах сохраняется та же скорость, я считаю вытекающим отсюда, что если мы хотим заставить большое колесо отбрасывать так же, как и малое, то необходимо увеличить для этого скорость в такой же мере, в какой возрастает диаметр, что случится, когда полные обороты будут совершаться в равные промежутки времени. Таким образом, можно считать, что вращение Земли способно отбрасывать камни не в большей мере, чем любое иное малое колесо, вращающееся столь медленно, что в двадцать четыре часа оно совершит всего лишь один оборот.
Сальвиати. — Мне не хотелось бы сейчас дальше заниматься этим вопросом; довольно с нас того, что мы, если не ошибаюсь, с достаточной подробностью показали несостоятельность возражения, которое на первый взгляд казалось наиболее убедительным и считалось таковым величайшими людьми. Я готов считать слова и время затраченными не даром, если они убедили синьора Симпличио, не скажу в подвижности Земли, но в том, что мнение тех, кто так думает, вовсе не столь смешно и нелепо, как это утверждает полчище заурядных философов.
Симпличио. — Приведенные вами до сих пор ответы на возражения, выдвигавшиеся против такого суточного обращения Земли и почерпнутые из фактов движения тел, падающих с вершины башни или брошенных вверх отвесно или с каким-либо наклоном на восток, запад, юг или север и т. д., до некоторой степени ослабили во мне давнее недоверие, питаемое против такого мнения; но другие, еще большие трудности приходят мне на память; из них, безусловно, я не сумею выпутаться и не думаю, чтобы вы сами могли их разрешить; быть может, о них вам не приходилось еще и слышать, так как они совсем новые. Это возражения двух авторов, которые ex professo пишут против Коперника: одни изложены в книжке заключений о природе, другие, принадлежащие большому философу и вместе с тем математику, включены в его трактат, составленный в защиту Аристотеля и его мнения о неизменности небес, где он доказывает, что не только кометы, но и новые звезды, подобные звезде в Кассиопее семьдесят второго года и в Стрельце тысяча шестьсот четвертого года, никоим образом не находятся выше планетных сфер, но, безусловно, ниже лунного свода, в сфере элементов; и это он доказывает против Тихо, Кеплера и многих других астрономов-наблюдателей,
|
Другие возражения двух новейших писателей против Коперника. |
Сальвиати. — Поскольку наша главная цель заключается в изложении и рассмотрении всего того, что приводилось за и против обеих систем — птоломеевской и коперниканской, нехорошо было бы пройти мимо чего-нибудь из написанного на эту тему.
Симпличио. — Итак, я начну с возражений, содержащихся в книжке
|
Первое возражение современного автора книжки заключений. |
|
Пушечное ядро, по мнению современного автора книжки Заключений, затратило бы более шести дней, чтобы упасть с лунной сферы до центра Земли. |
Так вот, если бы абсолютной божественной мощью или силою некоего ангела было чудесным образом перенесено туда вверх огромное затратило бы более артиллерийское ядро, помещено в нашем зените и свободно пущено оттуда, то как ему, так и мне представляется совершенно невероятным, чтобы сферы до центра при падении оно могло итти вниз, постоянно держась на нашей вертикальной линии; следовательно, оно продолжает в течение этих дней обращаться с Землей вокруг ее центра, описывая над экватором спиральную линию в плоскости большого круга, над другими широтами — спиральные линии вокруг конусов, и только на полюсах оно просто падает по прямой линии. Далее, он подкрепляет и подтверждает невероятность такой вещи, выдвигая путем вопросов множество трудностей, которые последователям Коперника невозможно устранить. Заключаются же они, если память мне не изменяет...
Сальвиати. — Погодите, пожалуйста, синьор Симпличио. У меня слабая память, и мне нужно итти шаг за шагом. Я припоминаю, что когда-то сам пытался вычислить, в какое время подобное тяжелое тело, падая с лунного свода, достигло бы центра Земли, и, насколько помню, я не получал столь долгого времени падения; было бы хорошо, если бы вы сказали нам, каким путем автор производил свои вычисления.
Симпличио. — Он производил его, чтобы доказать свое положение a fortiori, способом, достаточно выгодным для противной стороны, исходя из предположения, что скорость тела, падающего по вертикальной линии к центру Земли, будет равна скорости его кругового движения, совершаемого по большому кругу лунного свода; при таком предположении оно должно было бы совершать в час двенадцать тысяч шестьсот немецких миль, что, конечно, представляется совершенно невозможным; тем не менее для пущей верности и предоставляя все преимущества противной стороне, он принимает такую скорость за истинную и приходит к заключению, что время падения во всяком случае должно быть более шести дней43.
Сальвиати. — И в этом все его достижение? И таким путем он доказывает, что время падения должно быть более шести дней?
Сагредо. — Мне кажется, что он ведет себя очень скромно, ибо, имея возможность по своему желанию дать любую произвольную скорость такому падающему телу, а следовательно, заставить его достигнуть Земли в шесть месяцев и даже в шесть лет, он удовлетворился всего шестью днями. Но, пожалуйста, доставьте мне удовольствие, синьор Сальвиати, и расскажите, каким образом производилось вычисление вами, раз вы говорите, что когда-то проделывали его? Я уверен, что если бы решение этой задачи не требовало применения какого-нибудь остроумного приема, то вы не обратили бы на нее внимания.
Сальвиати. — Недостаточно, синьор Сагредо, чтобы заключение было значительным и благородным, нужно суметь благородно его вывести. Кто не знает, что при рассечении членов животных могут открываться бесконечные чудеса предусмотрительной и мудрейшей природы? Однако, на одно животное, вскрываемое анатомом, приходится тысяча разрубаемых мясниками; и я, пытаясь удовлетворить вашу просьбу, {170} не знаю, в каком из этих двух обличий мне придется выступить теперь на сцену; все же, собравшись с духом перед лицом автора синьора Симпличио, я не премину рассказать вам (насколько припомню), каким способом я пользовался. Но, прежде чем приступить к дальнейшему, не могу не сказать, что весьма сомневаюсь, верно ли передал синьор Симпличио способ, посредством которого этот его автор находит, будто артиллерийское ядро потратило бы на путь от лунного свода до центра Земли более шести дней, потому что если он предположил, что скорость ядра при падении была равна скорости свода (а именно это он, по словам синьора Симпличио, и предполагает), то тем самым он обнаружил незнание самых основных и элементарных положений геометрии; меня удивляет, что сам синьор Симпличио, допуская высказанное им предположение, не видит заключающейся в нем несообразности.
Симпличио. — Что я при изложении допустил ошибку, это может быть, но чтобы в заключении находилась неправильность, этого я не думаю.
Сальвиати. — Может быть, я нехорошо понял то, что вы передавали. Не сказали ли вы, что этот автор делает скорость движения ядра при падении равной той скорости, которую оно имело, обращаясь вместе с лунным сводом, на котором оно находилось, и что, падая с такой скоростью, оно достигло бы центра в шесть дней?
Симпличио. — Так, кажется мне, он пишет.
Сальвиати. — И вы не видите чудовищной несообразности этого утверждения? Конечно, вы ее скрываете: ведь не может быть, чтобы вы
|
Нелепость возражения, основанного на падении тела с лунной сферы. |
Симпличио. — Теперь я прекрасно понимаю ошибку, но мне не хотелось бы приписывать ее автору незаслуженно; надо думать, что я ошибся, передавая его рассуждения; чтобы не приписывать ему чужих грехов, мне хотелось бы посмотреть его книгу; если бы можно было кого-нибудь послать за ней, я был бы весьма признателен.
Сагредо. — Я пошлю слугу и он мгновенно вернется, а пока что пусть синьор Сальвиати, не теряя времени, порадует нас своим вычислением.
Симпличио. — Пусть он пойдет и принесет книгу, которую найдет открытой на моем рабочем столе вместе с другой, в которой также приводятся аргументы против Коперника.
Сагредо. — Велим ему для большей верности принести также и эту, а тем временем синьор Сальвиати проделает свое вычисление. Я послал слугу.
Сальвиати. — Прежде всего следует принять во внимание, что движение падающих тел не является равномерным, но что тела, выйдя из состояния покоя, движутся с постоянным ускорением, — явление,
|
Точное вычисление времени падения пушечного ядра с лунной сферы до центра Земли. |
|
Естественное ускорение движения падающего тела происходит соответственно последовательному ряду нечетных чисел, начиная с единицы. |
|
Пройденные падающим телом пространства относятся как квадраты времени. |
Сагредо. — Удивительную вещь я слышу; и этому, говорите вы, имеется математическое доказательство?
Сальвиати. — Чисто математическое; и не-только это явление, но и многие другие, относящиеся к естественным движениям, включая и случаи бросания, найдены и доказаны нашим другом. И я разбирал
|
Вся область знания, касающаяся местного движения, открыта Академиком. |
Сагредо. — Вы заставляете меня терять желание продолжать начатые нами рассуждения; теперь мне хочется слушать только упомянутые вами доказательства, поэтому или сообщите мне их сейчас же, или по крайней мере твердо обещайте мне устроить отдельное собеседование со мной, в присутствии синьора Симпличио, если и он пожелает послушать о явлениях, вытекающих из действия первичных сил природы.
Симпличио. — Без сомнения, желаю; хотя, по-моему, натурфилософу нет надобности вдаваться в рассмотрение таких частностей, а достаточно знать общее определение движения, различие движения естественного и насильственного, равномерного и ускоренного и так далее; если бы этого было недостаточно, то, думаю, Аристотель не преминул бы научить нас всему недостающему.
Сальвиати. — Может быть. Но не будем сейчас терять на это времени, так как я обещаю вам особо посвятить полдня для удовлетворения вашей любознательности; впрочем я припоминаю, что уже дал вам раньше такое же обещание. Вернемся к начатому нами вычислению времени, в течение которого тяжелое падающее тело дойдет от лунного свода до центра Земли44. Чтобы действовать не произвольно и случайно, а при помощи убедительного метода, постараемся сначала удостовериться опытом, многократно повторявшимся, в какое время достигнет земли, скажем, чугунное ядро, падающее с высоты ста локтей.
Сагредо. — Взяв при этом ядро определенного веса, именно того, для которого мы хотим вычислить время падения с Луны.
Сальвиати. — Это не имеет никакого значения, поскольку ядро в фунт, десять, сто и тысячу фунтов проходит те же сто локтей в одно и то же время.
Симпличио. — О, этому я не верю, как не верил и Аристотель, который пишет, что скорости падающих тяжелых тел находятся между
|
Ошибка Аристотеля, утверждавшего, что тяжелые тела при падении движутся со скоростью, пропорциональной их весу |
Сальвиати. — Если вы, синьор Симпличио, хотите принять это за истину, то вам придется поверить, что если дать падать в один и тот же момент с высоты ста локтей двум ядрам из одного и того же материала, одному — в сто фунтов, а другому — в один, то большее дойдет до земли, в то время как меньшее опустится едва ли на один локоть; теперь {172} постарайтесь, если только сможете, представить себе в воображении большое ядро уже лежащим на земле, а меньшее — находящимся на локоть от вершины башни.
Сагредо. — Что это положение совершенно ложно, в этом я ничуть не сомневаюсь, но что ваше совершенно истинно, этого я не постигаю; я верю ему, так как вы это решительно утверждаете, и я знаю, что вы не стали бы этого делать, если бы не располагали достаточными опытами и твердыми доказательствами.
Сальвиати. — У меня есть и то и другое, и когда мы будем особо разбирать вопрос о материи и движениях, я сообщу вам их; теперь же, чтобы не было больше поводов прерывать нить рассуждений, положим, что мы собираемся произвести вычисление относительно чугунного ядра в сто фунтов, которое, как показывают повторные опыты, падает с высоты ста локтей в пять секунд45. Поскольку, как я уже вам сказал, пространства, отмериваемые падающим телом, возрастают в двойном отношении, т. е. соответственно квадратам времени, и поскольку минута в двенадцать раз больше промежутка времени в пять секунд, то если мы умножим сто локтей на квадрат двенадцати, т. е. на сто сорок четыре, мы получим 14400; это будет число локтей, которое данное движущееся тело пройдет в одну минуту. Будем дальше придерживаться того же правила. Поскольку в часе 60 минут, умножая 14400, т. е. число локтей, проходимых в одну минуту, на квадрат 60, т. е. на 3600, мы получим 51840000 — число локтей, проходимых в один час, что составит 17280 миль. Если мы пожелаем узнать, какое пространство будет пройдено за четыре часа, то умножим 17280 на 16 (т. е. квадрат четырех) и получим 276480 миль, каковое число значительно больше расстояния от лунного свода до центра Земли, равного 196000 миль, принимая расстояние от свода в 56 земных полудиаметров, как это и делает современный автор, а полудиаметр Земли в 3500 миль по 3000 локтей каждая, каковы наши итальянские мили. Значит, синьор Симпличио, то пространство от лунного свода до центра Земли, которое, по словам вашего вычислителя, может быть пройдено немного более, чем в шесть дней, на самом деле, если производить вычисления на основе опыта, а не брать их с потолка, потребует для прохождения значительно менее четырех часов, а именно, по более точным подсчетам — три часа двадцать две минуты и четыре секунды.
Сагредо. — Прошу вас, дорогой синьор, не скрывайте от меня этого точного вычисления; оно должно быть прекрасно.
Сальвиати. — Оно, действительно, таково.
100 5 588000000 |
||
1 |
14700000000 |
|
22 |
||
241 |
60 |
12124 |
2422 |
||
24240 |
||
Сагредо. — Я видел производившееся действие, но совсем не понимаю основания, по которому так поступают; но, может быть, теперь не время об этом спрашивать?
Сальвиати. — Я сам хотел сообщить вам его, чтобы вам не пришлось его искать: оно очень простое. Обозначим эти три числа буквами: первое А, {173} второе В и третье С; А и С — числа пространства, В — число времени; ищется четвертое число — времени же. Мы знаем, что то отношение, в каком находится пространство А к пространству С, должен иметь и квадрат времени В к квадрату искомого времени; поэтому, по золотому правилу, число С нужно умножить на квадрат числа В и произведение разделить на число А и частное будет квадратом искомого числа; корень квадратный из него будет самим искомым числом. Видите, как легко это понять?46
Сагредо. — Таковы все истинные положения, после того как они найдены, но суть в том, чтобы их найти. Теперь я вполне понял и благодарю вас. И если у вас есть еще что-нибудь интересное по этой части, прошу вас рассказать, потому что, с разрешения синьора Симпличио, говоря откровенно, из ваших рассуждений я всегда извлекаю что-нибудь новое, а из рассуждений его философа — не знаю, научился ли я до сих пор чему-либо ценному.
Сальвиати. — В довершение всего нам осталось бы поговорить о местном движении, но, поскольку мы согласились отложить эту тему до особого собеседования, скажу кое-что, относящееся к автору, упоминаемому синьором Симпличио, которому кажется, что он сделал большую уступку другой стороне, приняв, что пушечное ядро при падении с лунного свода может итти со скоростью, равной скорости его движения по кругу, которым оно, будучи наверху, перемещалось суточным вращением. Я скажу ему, что такое ядро, падая с лунного свода до центра, приобретает скорость, более чем в два раза превышающую скорость суточного движения лунного свода, и я покажу это при помощи предпосылок, совершенно правильных, а не произвольных. Вы должны уже знать, что тяжелое тело, падая и приобретая все новую скорость в указанной выше
|
Если бы падающее тяжелое тело продолжало в течение равного времени двигаться равномерно со скоростью, им достигнутой, то оно прошло бы пространство, двойное против того, которое прошло, двигаясь ускоряющимся движением. |
Сагредо. — Рассуждение было бы вполне хорошо и удовлетворило бы меня, если бы было доказано это положение о прохождении движущимся телом двойного пространства за время, равное времени, затраченному на падение, при условии равномерного движения с наибольшей степенью скорости, приобретенной при падении; предложение это вы ранее приняли за истинное, но не доказали его. {174}
Сальвиати. — Это одно из положений, доказанных нашим другом, и вы в свое время увидите доказательство. Пока мне хочется при помощи некоторых допущений не научить вас чему-нибудь новому, а освободить вас от некоторого противоположного мнения, показав, что может, пожалуй, быть и иначе. Когда, подвесив на длинной и тонкой нитке, прикрепленной к потолку, свинцовый шар и отклонив его от перпендикуляра, мы отпускаем его затем на свободу, не заметили ли вы, что он, опускаясь, сам собой переходит за линию перпендикуляра почти на такое же пространство?
Сагредо. — Я прекрасно это наблюдал и видел (в особенности, если шар тяжел), что он поднимается на пространство, столь незначительно меньшее по сравнению со спуском, что порой я думал, будто дуга подъема
|
Движение качающихся тяжелых тел при устранении препятствий продолжалось бы вечно. |
Сальвиати. — Движение не продолжалось бы постоянно, синьор Сагредо, даже если бы было совершенно устранено препятствие со стороны воздуха, потому что здесь есть другое, гораздо более глубокое препятствие47.
Сагредо. — Какое же? Ничего другого не припомню.
Сальвиати. — Вам будет интересно услышать это, но я скажу вам об этом позже, а пока продолжаем. Я вам предложил наблюдение над маятником, чтобы вы поняли, что импульс, приобретенный на ниспадающей дуге, где движение естественно, сам по себе способен гнать насильственным движением тот же шар на такое же пространство по сходной восходящей дуге; таков он, говорю я, сам по себе по устранении всех внешних препятствий. Никаких сомнений, думаю, не вызывает также то, что по дуге падения скорость все возрастает до самой низкой точки перпендикуляра, а от нее по другой восходящей дуге все уменьшается до крайней высшей точки, причем уменьшается в том же отношении, в каком ранее возрастала, так что степени скорости в точках, одинаково удаленных от нижней точки, будут между собой равны. Отсюда, кажется мне, можно заключить (до некоторой степени условно), что если бы земной шар был просверлен через
|
Если бы земной шар был просверлен насквозь, то тяжелое тело, падающее по такому колодцу, поднялось бы по другую сторону центра на такую же высоту, с которой оно спустилось. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
0 |
1 |
2 |
3 |
4 |
5 |
Сагредо. — Думается, что я вас вполне понял, и могу доказать это, вкратце изложив, что понял. Вы хотели сказать, что если движение начинается от покоя и идет с последовательным возрастанием скорости равными приращениями, подобными приращениям последовательного ряда чисел, начиная от единицы или, пожалуй, даже от нуля, представляющего состояние покоя, то, расположив их в ряд, где наименьшая степень была бы нулем, а наибольшая каким-нибудь числом, скажем, пятью, мы получим, что все степени скорости, с которыми тело двигалось, составят в сумме пятнадцать; но если бы движущееся тело двигалось со столькими же степенями по числу, сколько их есть, но каждая была бы равна наибольшей, т. е. пяти, то совокупность всех этих скоростей была бы вдвое больше первой, т. е. равнялась бы тридцати; и потому при движении тела в течение такого же времени, но со скоростью, постоянной и равной скорости наибольшей степени, т. е. пяти, оно должно будет пройти пространство двойное по сравнению с тем, которое оно прошло с ускорением, начинающимся от состояния покоя.
Сальвиати. — С подобающей вам быстротой и тонкостью понимания вы разъяснили все гораздо понятнее, чем я, и к тому же навели меня на мысль добавить к сказанному еще кое-что. В самом деле, если приращение
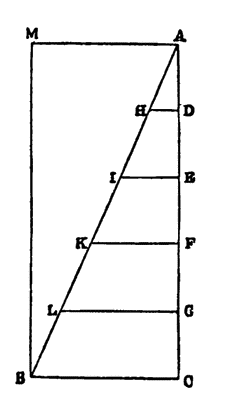 скорости в ускоренном движении идет непрерывно, то нельзя разбить его на какое-то определенное число постоянно возрастающих степеней скорости, потому что, изменяясь каждое мгновение, они бесчисленны; поэтому мы лучше можем пояснить нашу мысль примером, изобразив треугольник, например ABC, отложив на стороне АС произвольные равные части AD, DE, EF, FG и проведя через точки D, Е, F и G
скорости в ускоренном движении идет непрерывно, то нельзя разбить его на какое-то определенное число постоянно возрастающих степеней скорости, потому что, изменяясь каждое мгновение, они бесчисленны; поэтому мы лучше можем пояснить нашу мысль примером, изобразив треугольник, например ABC, отложив на стороне АС произвольные равные части AD, DE, EF, FG и проведя через точки D, Е, F и G
|
Ускорение движения свободно падающего тела растет постоянно с мгновения на мгновение. |
Сагредо. — Я вполне удовлетворен. И если вы считаете, что это рассуждение доказывает только вероятность, то какое же рассуждение нужно для доказательства необходимости? Дай бог, чтобы во всей философии нашлось одно, столь же убедительное.
Симпличио. — В естественных науках незачем искать совершенной
|
В естественных науках математическая строгость не нужна. |
Сагредо. — Но разве вопрос о движении не относится к наукам естественным? И все же я не нахожу, чтобы Аристотель доказал мне хотя бы малейшее его свойство. Не станем, однако, отклоняться от нашего рассуждения; и вы, синьор Сальвиати, не откажите в любезности сказать мне о том, что, как вы мимоходом упомянули, является причиной остановки маятника, помимо сопротивления среды разделению51.
Сальвиати. — Скажите мне: из двух тел, подвешенных на различных
|
Тело, подвешенное на длинной нити, колеблется медленнее, чем подвешенное на короткой. |
Сагредо. — Да, если они совершают движение на одинаковых расстояниях от перпендикуляра.
Сальвиати. — Большее или меньшее удаление от перпендикуляра не имеет значения, так как один и тот же маятник совершает свои колебания всегда в одинаковые промежутки времени, будут ли эти колебания очень длинными или очень короткими, т. е. отклоняется ли маятник много или мало от перпендикуляра; и если промежутки времени все же не совсем
|
Колебания одного и того же маятника происходят одинаково часто, велики ли эти колебания или малы. |
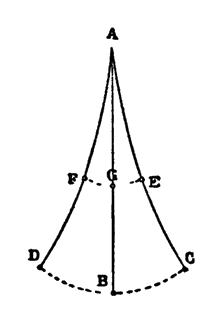 является таким маятником, прикрепленным все ближе и ближе к точке A, а потому предрасположенным совершать свои колебания все более и более часто и вследствие этого способным оказывать непрерывное противодействие грузу С. Это подтверждается тем, что, наблюдая за нитью АС,
является таким маятником, прикрепленным все ближе и ближе к точке A, а потому предрасположенным совершать свои колебания все более и более часто и вследствие этого способным оказывать непрерывное противодействие грузу С. Это подтверждается тем, что, наблюдая за нитью АС,
|
Причины, задерживающие маятник и приводящие его к состоянию покоя. Нить или цепочка, на которой подвешен маятник, при колебаниях сгибается дугой, а не остается прямой. |
Сагредо. — Вот прибыли книги; возьмите, синьор Симпличио, и найдите место, вызывающее сомнение.
Симпличио. — Вот оно; там, где он начинает аргументацию против суточного движения Земли, опровергнув сначала годовое: «Motus Terrae annuus asserere Copernicanos cogit conversionem eiusdem quotidianam; alias idem Terrae hemispherium continenter ad Solem esset conversum, obumbrato semper averso»52. Таким образом, половина Земли никогда бы не видела Солнца.
Сальвиати. — По этому первому выступлению мне кажется, что этот человек неверно представляет себе позицию Коперника, так как, если бы он обратил внимание на то, что последний считает ось земного шара постоянно параллельной самой себе, он не сказал бы, что половина Земли никогда не видела бы Солнца, а сказал бы, что год был бы естественным днем, т. е. что все части Земли имели бы шестимесячный день и шестимесячную ночь, как это и бывает для жителей у полюса. Но простим ему это и перейдем к дальнейшему.
Симпличио. — Далее следует: «Hanc autem gyraiionem Terrae impossibilem esse, sic demonstramus»53. После этого идет объяснение рисунка, на котором изображено множество падающих тяжелых тел, поднимающихся легких, несущихся по воздуху птиц и т. д.
Сагредо. — Покажите, пожалуйста. О, какие прекрасные рисунки: что за птицы, что за ядра! А это что такое?
Симпличио. — Это ядра, идущие с лунного свода, Сагредо. — А это что?
Симпличио. — Это улитка, которую у нас в Венеции называют buovoli; она также идет с лунного свода.
Сагредо. — Так, так; так вот почему луна имеет столь великое влияние на этих покрытых твердой кожей рыб, которых мы называем armai54.
Симпличио. — Далее идет вычисление, о котором я говорил, а именно, вычисление того пути за естественный день, час, минуту и секунду, который совершала бы точка Земли, находящаяся над экватором и над сорок восьмой параллелью. А затем следует то, в чем я сомневаюсь, не ошибся ли, пересказывая; поэтому прочтем это место: «His positis, necesse est, Terra circulariter mota, omnia ex aere eidem etc. Quod si hasce pilas aequales {178} ponemus pondere, magnitudine, gravitate, et in concavo spherae lunaris positas liber о descensui permittamus, si motum deorsum aequemus celeritate motui circum (quod tamen secus est, cum pila A etc.), elabentur minimum (ut multum cedamus adversariis) dies sex: quo tempore sexies circa Terram etc.»55.
Сальвиати. — Вы, наоборот, слишком верно пересказали возражение этого человека. Из этого вы можете заключить, синьор Симпличио, с какой осторожностью надо давать веру тому, кто хочет уверить других в таких вещах, которым он и сам, пожалуй, не верит. Ибо мне кажется невозможным, чтобы этот автор не заметил, что он представляет себе круг, коего диаметр, составляющий, согласно измерению математиков, менее одной трети окружности, должен быть в 12 раз больше этой последней. Это такая же ошибка, как если бы кто выдавал за 36 величину менее единицы.
Сагредо. — Быть может, эти математические положения, которые истинны в абстракции, не подойдут в точности при конкретном приложении их к физическим материальным кругам. Однако, мне кажется, что бондари, для того чтобы найти полудиаметр днища, которое должно быть сделано для бочки, пользуются абстрактным правилом математиков, хотя днища и являются вещами, достаточно конкретными и материальными. Поэтому послушаем, что скажет теперь синьор Симпличио в извинение своего автора, а также, кажется ли ему, что физика может настолько разниться от математики.
Симпличио. — Достаточного извинения, по-моему, не может быть, потому что разница слишком велика; и в этом случае я не мог бы сказать ничего иного, кроме как quandoque bonus etc. Но, предполагая, что вычисление синьора Сальвиати более правильно и что время спуска ядра не превышает трех часов, я считал бы во всяком случае удивительным, если бы, идя от лунного свода, удаленного на столь большое расстояние, ядро имело от природы побуждение держаться всегда над той же точкой Земли, над которой оно находилось в своем наивысшем положении, а не отстало бы на огромнейшее расстояние.
Сальвиати. — Явление может быть удивительным и неудивительным, но естественным и обычным в соответствии с тем, что ему предшествовало; в самом деле, если ядро (согласно предпосылкам, сделанным автором), находясь на лунном своде, имело двадцатичетырехчасовое круговое обращение вместе с Землей и всем тем, что находится внутри этого свода, то та же самая сила, которая заставляла его двигаться по кругу до падения, будет попрежнему заставлять его итти так же и при падении, и tantum abest, что оно не будет следовать за движением Земли и должно будет отставать; оно, скорее, должно его опережать, ибо при приближении к Земле круговое движение должно совершаться по кругам все меньшим; таким образом, при сохранении в ядре той же скорости, какую оно имело на своде, оно должно было бы опережать, как сказано, круговращение Земли. Но если у ядра на своде не было круговращения, то оно не обязано при падении держаться отвесно над той точкой Земли, которая находилась под ним при начале падения. Ни Коперник, ни кто-либо из его приверженцев этого и не скажет.
Симпличио. — Но автор, как вы видите, возражает, спрашивая, от какого принципа зависит это круговое движение тяжелых и легких тел — от принципа внутреннего или внешнего?
Сальвиати. — Оставаясь в пределах той проблемы, о которой идет речь, я скажу, что тот принцип, который заставлял двигаться ядро по кругу, пока оно было на лунном своде, поддерживает в нем круговращение и при падении; затем предоставляю автору делать его внутренним или внешним по своему усмотрению. {179}
Симпличио. — Автор докажет, что он не может быть ни внутренним, ни внешним.
Сальвиати. — А я отвечу, что ядро на своде не двигалось, и буду избавлен от обязанности объяснить, как при падении оно остается всегда на вертикали над одной и той же точкой, предположив, что оно на ней не останется.
Симпличио. — Хорошо; но так как тяжелые и легкие тела не могут иметь ни внутреннего, ни внешнего принципа своего кругового движения, то и земной шар не будет двигаться круговым движением, т. е. будет доказано то, что требовалось.
Сальвиати. — Я не сказал, что у Земли нет ни внутреннего, ни внешнего принципа кругового движения, а говорю, что не знаю, какой из двух она имеет, а мое незнание не в силах упразднить его. Но если автор знает, какой принцип движет по кругу другие мировые тела, которые движутся наверное, я скажу, что принцип, движущий Землю, подобен тому, благодаря которому движется в мире Юпитер и даже самая звездная сфера, которую автор считает движущейся. И если он определит мне природу движителя одного из этих движущихся тел, то я обязуясь сказать ему, что заставляет двигаться Землю. Но более того, я сделаю то же самое, если он сумеет объяснить мне, что именно движет частицы Земли вниз.
Симпличио. — Причина этого явления общеизвестна, и всякий знает, что это тяжесть.
Сальвиати. — Вы ошибаетесь, синьор Симпличио, вы должны были бы сказать — всякий знает, что это называется тяжестью, но я вас спрашиваю
|
Мы не лучше знаем то, что движет тяжелые тела вниз, чем то, что заставляет звезды двигаться по кругу; мы знаем только обычное для этого явления название. |
Симпличио. — Мне кажется, что этот автор просит о гораздо меньшем,чем то, на что вы не находите ответа; ведь он спрашивает вас не о том, каков на самом деле в данном случае принцип движения тяжелых и легких тел по кругу, а только, считаете ли вы его, каков бы он ни был, внутренним или внешним; так например, если бы я и не знал, что такое тяжесть, благодаря которой Земля падает, я все же знаю, что она — принцип внутренний, поскольку при отсутствии препятствий она движет самопроизвольно; и обратно, я знаю, что принцип, который движет ее вверх, внешний, хотя и не знаю, что такое сила, приложенная бросающим.
Сальвиати. — Во сколько вопросов нужно было бы нам вникнуть, если бы мы пожелали разрешить все трудности, вытекающие одна из другой! Вы называете принципом внешним и даже противоестественным и насильственным тот, который движет брошенное тяжелое тело вверх, но, быть может, он не менее внутренний и естественный, чем тот, который движет вниз. Он может называться внешним и насильственным по случайному признаку, пока движущееся тело соединено с бросающим, но что́ внешнее остается в качестве движителя, например стрелы или ядра, когда движущееся тело отделилось от бросающего? Приходится, значит, с необходимостью сказать, что та сила, которая перемещает тело вверх, является {180}
|
Сила, которая заставляет брошенные тела подниматься вверх, для них не менее естественна, чем тяжесть, двигающая их вниз. |
Симпличио. — C этим я никогда не соглашусь, потому что у последнего — внутренний, естественный и постоянный принцип, а у первого — внешний, насильственный и конечный.
Сальвиати. — Если вы не соглашаетесь уступить мне, что принципы движения тяжелых тел вниз и вверх в одинаковой мере являются внутренними и естественными, что будете вы делать, если я вам скажу, что они могут быть и численно одинаковыми?
Симпличио. — Предоставляю судить вам самому.
Сальвиати. — А я хочу, чтобы вы сами рассудили. Поэтому скажите мне,
|
Противоположные принципы не могут естественно находиться в одном и том же субъекте. |
Симпличио. — Думаю, что никоим образом.
Сальвиати. — Какое, думаете вы, естественное внутреннее предрасположение имеется у земли, свинца, золота и вообще у подобных тяжелых тел; иными словами, к какому движению, думаете вы, влечет их внутренний их принцип?
Симпличио. — К движению к центру тяжелых тел, т. е. к центру вселенной и Земли, куда они при отсутствии препятствий и направились бы.
Сальвиати. — Так что, если бы земной шар был просверлен колодцем, проходящим через его центр, то пушечное ядро, брошенное в него и движимое принципом естественным и внутренним, перемещалось бы к центру; и все это движение оно совершало бы самопроизвольно и благодаря внутреннему принципу, не так ли?
Симпличио. — Считаю бесспорным, что так.
Сальвиати. — Но, достигнув центра, перейдет ли оно, по-вашему, за него или же немедленно прекратит движение?
Симпличио. — Думаю, что оно продолжало бы двигаться на далекое расстояние.
Сальвиати. — Но не было ли бы это движение за центр движением вверх, т. е., по вашим словам, противоестественным и насильственным?
|
Естественное движение превращается само собой в такое, которое именуется противоестественным и насильственным. |
Симпличио. — Думается мне, что на все эти возражения есть ответы, хотя сейчас я и не припомню их; но как бы то ни было, автор продолжает спрашивать, от какого принципа зависит это круговое движение тяжелых и легких тел, а именно — от внутреннего или от внешнего, и далее доказывает, что оно не может происходить ни от того, ни от другого, говоря: «Si ab externo, Deusne ilium excitat per continuum miraculum? an vero angelus? an аёr? Et hunc quidem multi assignant. Sed contra...»57.
Сальвиати. — Не трудитесь читать возражения, потому что я не из числа тех, кто приписывает этот принцип окружающему воздуху. Что же касается чуда или ангела, то к этому я скорее склонился бы, потому что если начало, т. е. перемещение пушечного ядра на лунный свод, объясняется божественным чудом или действием ангела, то весьма вероятно, что в силу того же принципа будет происходить и все остальное. Что же касается воздуха, для меня достаточно того, что он не мешает круговому движению тел, которые, как говорят, движутся благодаря ему, а для этого достаточно (и больше искать нечего), чтобы он двигался тем же самым движением и заканчивал свое обращение с той же скоростью, как и земной шар.
Симпличио. — А он найдет ответ и на это и спросит: что перемещает воздух по кругу — природа или насилие? И исключит природу, говоря, что это противно истине, опыту, противно самому Копернику.
Сальвиати. — Противно Копернику? Ни в коем случае, ибо Коперник ничего такого не пишет, и ваш автор приписывает это ему с излишней предупредительностью. Наоборот, Коперник говорит, и, как мне кажется, правильно, что часть воздуха по соседству с землей, являющаяся скорее земным испарением, будет иметь ту же природу и естественную склонность продолжать ее движение или, вернее, примыкая к ней, будет следовать за ней таким же образом, каким, по словам перипатетиков, верхние слои воздуха и стихия огня следуют за движением лунного свода, так что это их дело выяснить, будет ли такое движение естественным или насильственным.
Симпличио. — Автор возражает, что если Коперник заставляет двигаться одну только нижнюю часть воздуха, лишая такого движения верхнюю, то он не сможет объяснить, как этот покоящийся воздух будет иметь способность перемещать вместе с собой самые тяжелые тела и заставлять их следовать за движением Земли.
Сальвиати. — Коперник скажет, что эта естественная склонность элементарных тел следовать за земным движением имеет ограниченную
|
Склонность элементарных тел следовать за Землей имеет ограниченную сферу. |
Симпличио. — Раз это не так, то нужно сказать, что такие явления зависят от принципа внутреннего; против этого положения — «oboriuntur difficillissimae, immo inextricabiles, questiones secundae», а именно следующие: «Principium illud iftternum vel est accidens, vel substantia: si primum, quale nam illud? nam qualitas loco motiva circum, hactenus nulla videtur esse agnita»58.
Сальвиати. — Как не было известно? Не являются ли круговращающимися все эти элементарные вещества вместе с Землей? Вы видите, как этот автор принимает за истину то, что находится под вопросом?
Симпличио. — Он говорит, что этого не видно, и мне кажется, что в этом он прав.
Сальвиати. — Не видно нам, потому что мы вращаемся вместе с ними. {182}
Симпличио. — Выслушайте другое возражение: «Quae etiam si esset, quomodo tamen inveniretur in rebus tam contrariis? in igne ut in aqua? in аёrе ut in terra? in viventibus ut in anima carentibns?»59.
Сальвиати. — Предположим на время, что вода и огонь противоположны, так же как воздух и земля (хотя об этом еще многое можно было бы сказать); самое большое, что из этого может следовать, это то, что у них не могут быть обеими те движения, которые друг другу противоположны; так что, например, движение вверх, по природе присущее огню, не может быть присуще воде, которая, будучи по природе противоположна огню, должна обладать и движением, противоположным движению огня, каковым будет движение deorsum. Но почему же движение круговое, которое не является противоположным движениям sursum и deorsum и, напротив, может смешиваться с обоими, как утверждает и сам Аристотель, не может в одинаковой мере быть присущим и тяжелым, и легким телам? Далее, движения, которые не могут быть общими живому и неживому, суть те, которые зависят от души; но почему же те из них, которые присущи телу, поскольку оно состоит из элементов и потому причастно свойствам элементов, не могут быть общими трупу и живому существу? А потому, если круговое движение присуще элементам, то оно должно быть общим и для сложных тел.
Сагредо. — Выходит, по мнению автора, что если мертвая кошка падает из окна, то невозможно, чтобы могла падать и живая, так как не подобает мертвому иметь свойства, присущие живому.
Сальвиати. — Значит рассуждение этого автора не имеет силы против того, кто сказал бы, что принцип кругового движения тяжелых и легких тел есть внутреннее свойство: не знаю, в какой мере он сможет доказать, что этот принцип не может быть субстанцией.
Симпличио. — Он восстает против этого, приводя многие возражения. Первое из них таково: «Si secundum (nempe si dicas, tale princi-pium esse subs tan tiam), illud est aut materia, aut forma, aut compositum; sed repugnant iterum tot diversae rerum naturae, quales sunt aves, limaces, saxa, sagittae, nives fumi, grandines, pisces etc., quae tamen omnia, specie et genere differentia, moverentur a natura suo circulariter, ipsa naturis diversissima, etc.»60.
Сальвиати. — Если эти поименованные вещи имеют различную природу, а вещи, имеющие различную природу, не могут иметь общего движения, то, поскольку оно должно годиться для всех, нужно подумать о движении другом, нежели движение вверх и вниз; и если должно найтись одно для стрел, другое для улиток, третье для камней, четвертое для рыб, нужно будет подумать также о дождевых червях, топазах и грибах, которые не менее отличаются по своей природе друг от друга, нежели град и снег.
Симпличио. — Вы как будто издеваетесь над этими аргументами?
Сальвиати. — Совсем нет, синьор Симпличио, но на это уже раньше был дан ответ, а именно, если движение вниз или вверх может быть присуще названным вещам, то не менее может оказаться присущим им и круговое; оставаясь на почве перипатетического учения, не устанавливаете вы большего различия между стихийной кометой и небесной звездой, нежели между рыбой и птицей? И тем не менее и та и другая движутся кругообразно. Теперь переходите ко второму аргументу.
Симпличио. — «Si Terra staret per voluntatem Dei, rotarentne caetera annon? si hoc, f alsum est, a natura gyrari; si illud, redeunt priores quaestiones; et sane mirum esset, quod gavia pisciculo, alauda nidulo suo, et corvus limaci petraeque, etiam volens, imminere non posset»61.
Сальвиати. — Я, с своей стороны, дал бы общий ответ: если предположить, что по воле божией Земля прекратит суточное вращение, то эти {183} птицы будут делать то, что угодно той же воле божией. Но если тем не менее этому автору захочется получить более определенный ответ, то я скажу, что они будут делать совершенно противоположное тому, что они делали бы, оказавшись разобщенными с Землей и держась в воздухе, когда земной шар по воле божественной неожиданно пустился бы в стремительнейшее движение; теперь дело вашего автора рассказать нам о том, что произошло бы в таком случае.
Сагредо. — Прошу вас, синьор Сальвиати, уступите, по моей просьбе, этому автору в том, что при остановке Земли по воле божией другие вещи, разобщенные с Землею, будут продолжать итти по кругу естественным своим движением, и посмотрим, какие невозможные или несообразные последствия отсюда проистекут, так как я, с своей стороны, не знаю большего беспорядка, чем тот, который устраивает тот же автор, а именно: жаворонки, если бы даже и хотели, не смогут держаться над своими гнездами, а вороны — над улитками или скалами, из чего вытекает, что воронам следовало бы отказаться от удовольствия есть улиток, а жаворонкам пришлось бы умереть от голода и холода, не имея возможности ни быть накормленными, ни высиженными своими матерями. Вот то разрушение, которое, насколько я могу описать, последовало бы, если бы случилось так, как говорит автор. Смотрите сами, синьор Симпличио, не должны ли последовать беспорядки еще большие.
Симпличио. — Я не умею указать больших, но весьма вероятно, что автор видит, кроме этих, еще и другие беспорядки в природе, которые он по уважительным соображениям не захотел изложить. Итак, я перейду к третьему возражению: «Insuper, qui fit ut istae res tarn variae tantum moveantur ab occasu in ortum, parallelae ad aequatorem? ut semper mo-veantur, numquam quiescant?»62.
Сальвиати. — Движутся с запада на восток параллельно экватору без остановки таким же точно образом, каким, по вашему мнению, движутся с востока на запад параллельно экватору без остановки неподвижные звезды.
Симпличио. — «Quare quo sunt altiores celerius, quo. humiiiores tardius?»63.
Сальвиати. — Потому что в сфере или круге, который обращается вокруг своего центра, части более удаленные описывают бо́льшие круги, а более близкие описывают за то же время меньшие круги.
Симпличио. — «Quare quae aequinoctiali propiores in maiori, quae remotiores in minori, circulo feruntur?»64
Сальвиати. — В подражание звездной сфере, в которой ближе лежащие к экватору движутся по бо́льшим кругам, нежели более удаленные.
Симпличио. — «Quare pila eadem sub aequinoctiali, tota circa centrum Terrae ambitu maximo, celeritate incredibili; sub polo vero circa centrum proprium gyro nullo, tarditate suprema, volveretur»65.
Сальвиати. — В подражание звездам на небесном своде, которые делали бы то же, если бы суточное движение принадлежало им.
Симпличио. — «Quare eadem res, pila, v. g. plumbea, si semel Terrain circuivit, descripto circulo maximo, eamdem ubique non circummigret secundum circulum maximum, sed translate extra aequinoctialem in circulis minoribus agetur?»66.
Сальвиати. — Потому что так делали бы и даже делали, по учению Птоломея, некоторые неподвижные звезды, которые были раньше в непосредственном соседстве с экватором и описывали наибольшие круги, а теперь, удалившись, описывают меньшие67.
Сагредо. — О, если бы я мог запомнить все эти прекрасные вещи, я показался бы самому себе сделавшим великое приобретение; вам {184} следовало бы, синьор Симпличио, одолжить мне эту книжечку, потому что в ней заключается, должно быть, целое море самых редкостных и исключительных вещей.
Симпличио. — Я подарю вам ее.
Сагредо. — О нет, я никогда не лишу вас ее. Но вопросы уже кончились?
Симпличио. — Нет, синьор. Слушайте дальше: «Si latio circularis gravibus et levibus est naturalis, qualis est ea quae fit secundum lineam rectam? nam si naturalis, quomodo et is motus qui circum est, naturalis est, cum specie differat a recto? si violentus, qul fit ut missile ignitum, sursum evolans, scintillosum caput sursum a Terra, non autem circum, volvatur, etc.?»68.
Сальвиати. — Уже тысячу раз говорилось, что круговое движение
|
В смешанных движениях мы не замечаем круговой его части, так как сами движемся кругообразно. |
Симпличио. — «Quare centrum spherae delapsae sub aequatore spiram describit in eius piano, sub aliis parallelis spiram describit in cono? sub polo discendit in axe, lineam giralem decurrens in superficie cylindrica consignatum?»69.
Сальвиати. — Потому что из линий, проведенных от центра к окружности сферы, по которым падают тяжелые тела, та, которая кончается на экваторе, описывает круг, а те, которые кончаются на других параллелях, описывают конические поверхности, а ось ничего не описывает, но остается сама собой. И если бы я мог высказать вам свой взгляд откровенно, то сказал бы, что не могу извлечь из всех этих вопросов ничего, что было бы полезно для опровержения движения Земли; ведь если бы я спросил у этого автора (согласившись с ним, что Земля не движется), что со всеми этими частностями случилось бы, предположив ее движение, как хотелось того Копернику, то, я уверен, он сказал бы, что проистекут все те явления, которые он теперь выставляет как несообразные, дабы опровергнуть возможность движения; таким образом, в голове этого человека необходимые следствия считаются абсурдными. Однако, скажите, пожалуйста, что там есть еще, и покончим с этим скучным занятием.
Симпличио. — То, что здесь следует, направлено против Коперника и его последователей, которым хочется, чтобы движение частей, отделенных от своего целого, происходило только ради воссоединения со своим целым, но что абсолютно естественным является только движение суточное, круговое; против них-то он и восстает, говоря, что согласно их мнению: «Si tota Terra una cum aqua in nihilum redigeretur, nulla grando aut pluvia e nube decideret, sed naturaliter tantum circumferretur; neque ignis ullus aut igneum ascenderet, cum, illorum non improbabili sententia, ignis nullus sit supra»70.
Сальвиати. — Проницательность этого философа удивительна и достойна всякой похвалы, ведь он не довольствуется размышлениями о вещах, {185} которые могут случиться при настоящем ходе вещей в природе, а хочет рассмотреть, что случилось бы в таком случае, который, как он достоверно знает, никогда не может произойти. Поэтому, чтобы услышать какую-нибудь изящную тонкость, я хочу согласиться с ним, что когда земля и вода превратятся в ничто, больше не будет падать ни град, ни дождь и огненные вещества больше не будут подниматься вверх, а только перемещаться кругообразно. Что будет затем? И что мне возразит философ?
Симпличио. — Возражение заключается непосредственно в следующих словах, вот они: «Quibus tamen experientia et ratio adversatur»71.
Сальвиати. — Теперь мне придется сдаться, так как у него есть столь великое преимущество передо мною, как опыт, а его-то у меня и нет; ведь до сих пор мне никогда не доводилось видеть, чтобы земной шар со стихией воды обратился в ничто и чтобы я мог наблюдать, что делают при таком маленьком светопреставлении град и вода. Но, может быть, он по крайней мере расскажет нам в назидание, что они делали?
Симпличио. — Он ничего не говорит.
Сальвиати. — Я дал бы что угодно, лишь бы побеседовать с этим лицом и спросить его: если земной шар исчезнет, то уничтожится ли вместе с ним и общий центр тяжести? Я полагаю, что в таком случае град и вода остались бы бесчувственными и глупыми среди туч, не зная, что им делать с собой; могло бы случиться также, что под влиянием того большого пустого пространства, которое получится в результате исчезновения земного шара, все окружающее разрядится, и, в частности, воздух, особенно способный рассеиваться, с величайшей быстротой устремился бы для заполнения его; и, может быть, более твердые вещественные тела, как птицы, которых надо думать, должно оказаться много в воздухе, направятся ближе к центру большой пустой сферы (так как кажется вполне правомерным, чтобы субстанциям, которые в меньшем объеме содержат много материи, были предназначены места более тесные, тогда как для более редких оставались бы места более пространные) и здесь, умерев в конце концов от голода и обратившись в землю, образуют новый малый шар с тем небольшим количеством воды, которое тогда находилось среди туч. Могло бы также случиться, что те же самые материи, как те, что не видят света, не заметили бы исчезновения Земли и вслепую опускались бы, как обычно, думая ее встретить, и мало-помалу достигли бы центра, куда и теперь доходили бы, если бы самый земной шар не мешал им. И наконец, чтобы дать этому философу менее нерешительный ответ, я скажу, что столько же знаю о том, что произошло бы после уничтожения земного шара, сколько он знает о том, что было с ним и вокруг него до того, как он был создан. И так как он сказал бы, что он не знает и даже не может представить себе ничего из происходившего, чему один опыт может его научить, то он должен будет простить и извинить меня, если я не знаю того, что знает он о том, что произошло бы после уничтожения этого шара, считаясь с отсутствием у меня того опыта, который имеет он. Скажите теперь, есть ли там еще что-нибудь.
Симпличио. — Вот рисунок, изображающий земной шар с большой пустотой вокруг его центра, наполненной воздухом; и для доказательства того, что тяжелые тела движутся вниз не затем, чтобы соединиться с земным шаром, как говорит Коперник, автор помещает этот камень в центре и спрашивает, что тот будет делать, предоставленный самому себе; другой камень он помещает в пустоту этой большой пещеры и предлагает тот же вопрос, говоря относительно первого: «Lapis in centro constitutes aut ascendet ad Terrain in punctum aliquod, aut non: si secundum, falsum est, partes ab solam seiunctionem a toto ad illud moveri; si primum, omnis ratio et experientia renititur, neque gravia in suae gra vitatis centro conquiescent. {186} Item si suspensus lapis liberatus decidat in centrum, separabit se a toto contra Copernicum; si pendeat, refragatur omnis experientia cum videamus integros fornices corruere»72.
Сальвиати. — Я отвечу, хотя мое положение и очень невыгодное, поскольку мне приходится иметь дело с тем, кто видел на опыте, как ведут себя камни в этой большой пещере, — то, чего я не видел; скажу,
|
Сначала должны быть налицо тяжелые субстанции, а потом уже центр тяжести. |
|
Если переместить большую часть тяжелых субстанций в другое место, то оторвавшиеся от них частички пойдут вместе с ними. |
Симпличио. — Остается еще некое заблуждение, которое автор отмечает у одного последователя Коперника, заставляющего Землю двигаться годовым и суточным движением, подобно тому, как колесо повозки движется и по кругу Земли, и вокруг самого себя73; он делает либо земной шар слишком большим, либо большую орбиту слишком малой, поскольку 365 обращений экватора гораздо меньше, чем окружность большой орбиты.
Сальвиати. — Заметьте, что вы ошибаетесь и говорите противоположное тому, что должно было быть написано в книжке, так как следует сказать, что этот автор сделал или земной шар слишком малым, или большую орбиту слишком большой, а не земной шар слишком большим и годовую орбиту слишком малой.
Симпличио. — Ошибка во всяком случае не у меня» Вот слова книжки: «Non videt, quod vel circulum annuum aequo minorem, vel orbem terreum jus to multo fabricet majorem»74.
Сальвиати. — Заблуждался ли первый автор, я не могу узнать, потому что автор книжки его не называет, но вполне явна и непростительна ошибка книжки, безразлично, заблуждался или нет тот первый последователь Коперника, ибо автор книжки проходит, не замечая, мимо столь осязательной ошибки, не отмечает ее и не исправляет. Но простим ему это, как ошибку более по недосмотру, чем по чему-либо другому. Кроме того, если бы я не был уже утомлен и пресыщен столь долгими занятиями и довольно непроизводительной тратой времени на эти весьма мало значительные споры, то я мог бы показать, каким образом
|
Не исключена возможность, что окружностью маленького, не много раз вращающегося круга можно пройти или описать линию, которая больше какого угодно большого круга. |
Сагредо. — По правде говоря, это нужно и мне, хотя трудились только мои уши, и если бы я не надеялся услышать вещи еще более остроумные у этого другого автора, то я предпочел бы освежиться прогулкой в гондоле.
Симпличио. — Думаю, что вы услышите вещи большей силы, потому что это философ в высшей степени искусный и, кроме того, он — большой математик: он опроверг Тихо в вопросе о кометах и новых звездах.
Сальвиати. — Быть может, он тот же, что и автор Антитихо?
Симпличио. — Он самый, но опровержение, направленное против новых звезд, находится не в Антитихо, если не считать доказательства, что они не противоречат неизменяемости и невозникаемости неба, о чем я уже вам говорил. Но после Антитихо, найдя при помощи параллаксов способ доказать, что новые звезды — тела стихийные, находящиеся внутри лунного свода, он написал эту другую книгу De tribus novis stellis etc. и включил в нее также аргументы против Коперника. Я уже рассказал вам, что он написал об этих новых звездах в Антитихо, не отрицая, что они находятся в небе, он доказывал, что их возникновение ничем не мешает неизменяемости неба, и делал это посредством чисто философского рассуждения, которое я вам и передал. Не помню сейчас, говорил ли я вам, как он нашел затем путь к устранению их с неба, но так как при этом опровержении он идет путем вычислений и параллаксов предметов, для меня мало или совсем непонятных, я не читал этой части и изучил только чисто естественные доводы против движения Земли.
Сальвиати. — Я прекрасно понимаю и полагаю, что после того, как мы выслушаем возражения Копернику, нам нужно будет выслушать или по крайней мере взглянуть, каким способом доказывается при помощи параллаксов, что те новые звезды, которые многими астрономами с большим именем принимались за высочайшие и находящиеся среди звезд небесного свода, являются телами стихийными; и если автор доводит до конца такое предприятие, как совлечение новых звезд с неба в пределы сферы стихий, то он вполне заслуживает великих почестей и вознесения к звездам или по крайней мере того, чтобы слава увековечила среди них его имя. Потому поспешим сначала к той части, которую он противопоставляет мнению Коперника. Начинайте приводить его возражения.
Симпличио. — Их не придется приводить ad verbum, потому что они слишком пространны, но я, как видите, много раз внимательно читая, выписал на полях слова, заключающие в себе весь нерв доказательства, и достаточно будет прочесть их. Первый аргумент здесь начинается так: «Et primo, si opinio Copernici recipiatur, criterium naturalis philosophiae, ni prosrus tollatur vehementer saltern labefactari videtur»75.
Под таким критерием он понимает, в согласии с мнением философов
|
Коперниково учение обращает в ничто критерий философии. |
Сальвиати. — Это первый аргумент, выдвигаемый Аристотелем и Птоломеем и всеми их последователями; на него было отвечено пространно, был показан паралогизм и достаточно четко разъяснено, как движение, общее нам и всем другим движущимся телам, как бы не существует. Но
|
Общее движение — как бы движение несуществующее. |
|
Аргумент, заимствованный из отвесного падения тел, опровергается иным способом. |
Симпличио. — Я воспринимаю его падение по отношению к башне, потому что вижу его сначала наравне с каким-нибудь знаком этой башни, затем пониже и так далее, пока не замечаю, что он достиг земли.
Сальвиати. — Значит, если бы этот камень падал из когтей летящего орла и опускался бы в чистом невидимом воздухе, а у вас не было бы другого видимого и устойчивого предмета, с которым можно было бы его сравнить, то вы не могли бы воспринимать его движения?
Симпличио. — Напротив, все-таки я его замечал бы, так как, чтобы
|
Каким образом замечается движение падающего тела? |
Сальвиати. — Вот вы и дали верный ответ. Стало быть, вы убеждаетесь в покое камня, когда, совсем не двигая глазами, вы всегда видите
|
Движение глаза доказывает нам движение наблюдаемого объекта. |
Симпличио. — Думаю, что это необходимо будет так.
Сальвиати. — Представьте себе теперь, что вы находитесь на корабле и устремили глаз на вершину мачты: думаете ли вы, что если даже корабль движется с огромной быстротой, вам надо двигать глазом для того, чтобы все время удерживать зрение на конце мачты и следить за движением?
Симпличио. — Я уверен, что не потребовалось бы вносить никакого изменения, и не только в зрение; если бы даже я нацелился туда самострелом, то никогда и ни при каком движении корабля мне не нужно было бы сдвинуть прицел ни на волос, чтобы сохранить его наведенным на цель.
Сальвиати. — И это происходит потому, что движение, которое корабль сообщает мачте, он сообщает также и вам и вашему глазу; таким образом, вам совсем не нужно двигать последний, чтобы смотреть на вершину мачты, и вследствие этого она кажется вам неподвижной76. [Луч зрения идет от глаза к мачте так же, как веревка, протянутая между двумя точками корабля; но сотни веревок, укрепленных в разных точках, останутся на том же месте, движется ли корабль, или стоит неподвижно.] Теперь примените это рассуждение к вращению Земли и находящемуся на вершине башни камню. Здесь вы его движения различить не можете, так как то движение, за которым вы должны следить, есть и у вас наравне с ним и о Землей, и вам незачем двигать глазом. Когда же затем к этому присоединяется движение вниз, принадлежащее исключительно ему, а не вам, смешивающееся с круговым, то часть круговая, которая является общей камню и глазу, продолжает быть неощутимой, и единственно ощутимым остается прямое, так как для следования за ним вам нужно двигать
|
Опыт, доказывающий, что движение общее не замечается. |
Сагредо. — Эти рассуждения до некоторой степени успокоили мой желудок, который рыбы и улитки несколько растревожили; первый же пункт заставил меня вспомнить об исправлении одной ошибки, в такой мере обладающей видимостью истины, что не знаю, поставит ли ее под сомнение даже один из тысячи. Дело заключается в следующем. Когда
|
Тонкий вопрос — может ли подзорная труба так же хорошо применяться на вершине мачты, как у ее подножия. |
Сальвиати. — А я оказался бы единомышленником моряков и разделил бы ваше первоначальное мнение.
Симпличио. — И я оказался бы таковым же, да и сейчас являюсь им; полагаю, что если бы я размышлял даже сотню лет, то не стал бы думать иначе.
Сагредо. — Я смогу, значит, на этот раз выступить против вас обоих, имея (как говорится) за спиной учителя. И так как способ вопросов, как мне кажется, весьма способствует разъяснению вещей, — не говоря уже об удовольствии одолеть собеседника, вызывая из его уст признание того, чего он не сумел сам постигнуть, — я воспользуюсь этим приемом. Прежде всего я предполагаю, что корабли, галеры или другие суда, которые надобно открыть и распознать, весьма удалены, а именно, на 4, 6, 10 или 20 миль, так как для распознавания близких предметов зрительной трубы не нужно; телескоп на таком расстоянии, как 4 или 6 миль, дает возможность без труда заметить всякое судно, а также всякое иное сооружение, достаточно большое. Теперь я спрашиваю, какого рода и сколь часты будут движения, происходящие на марсе вследствие качки парохода?
Сальвиати. — Представим себе, что корабль направляется к востоку; при совершенно спокойном море не будет никакого другого движения, кроме этого поступательного, но когда присоединится колебание волн, то одни волны, поднимая и опуская поочередно корму и нос, явятся {190}
|
Различные происходящие от качки корабля движения. |
|
Два рода изменений положения трубы вызываются качкой корабля. |
Сагредо. — Скажите мне далее: если мы, направив телескоп сначала вон туда, на башню Бурано, отстоящую отсюда на шесть миль, затем отклоним его на угол вправо или влево, вверх или вниз только на величину черного слоя под ногтем, то какое действие это произведет у нас в смысле видимости башни?
Сальвиати. — Это заставило бы ее немедленно исчезнуть из поля зрения, потому что такое отклонение, хотя бы и весьма незначительное здесь, может достигнуть там сотен и тысяч локтей.
Сагредо. — Но если, не меняя угла и все время сохраняя трубу параллельной себе самой, мы переместим ее на 10 или 12 локтей дальше, вправо или влево, вверх или вниз, то какое действие это произведет в отношении башни?
Сальвиати. — Совершенно неощутимое; ведь, поскольку пространства здесь и там заключены между параллельными лучами, постольку изменения, происшедшие здесь и там, должны быть равны, и так как пространство, открываемое там инструментом, способно охватить много таких башен, то мы никоим образом не потеряем ее из виду.
Сагредо. — Возвращаясь теперь к кораблю, мы можем без колебаний утверждать, что движение телескопа вправо или влево, вверх или вниз, а также вперед или назад на 20 или 25 локтей при сохранении его параллельности самому себе не может отклонить зрительного луча от наблюдаемой в предмете точки более, чем на те же 25 локтей, и так как при удалении на 8 или 10 миль поле зрения инструмента охватывает пространство, гораздо более широкое, нежели галера или другое увиденное судно, то поэтому столь малое изменение не заставляет меня терять его из виду. Следовательно, препятствие и причина исчезновения предмета могут проистекать только от изменения в угле, раз от качки корабля перемещение телескопа вверх и вниз, вправо или влево не может достигать большого количества локтей. Теперь предположите, что у вас имеются два неподвижно укрепленных телескопа, один у основания корабельной мачты, другой даже не просто на вершине мачты, а на самой верхней рее, причем оба они направлены на судно, отстоящее на 10 миль; скажите, думаете ли вы, что, какова бы ни была качка корабля и наклон мачты, большее изменение угла произойдет у верхней трубы, нежели у нижней? Подъем волны заставит конец реи податься назад на 30 или 40 локтей более, нежели основание мачты; на такое же пространство он будет отклонять назад верхнюю трубу, тогда как нижнюю он отклонит только на пядь; однако, угол изменяется у одного инструмента так же, как и у другого. Равным образом, волна, набегающая сбоку, перемещает верхнюю трубу вправо или влево во сто раз больше, чем нижнюю; однако, углы или не меняются, или меняются одинаково. Но перемещение вправо или влево, вперед или назад, вверх или вниз не создает ощутительной помехи для наблюдения отдаленных предметов, которая возникает только от изменения угла; следовательно, надобно по необходимости признать, что пользование телескопом на вершине мачты не более трудно, чем у ее подножия, поскольку угловые изменения равны в обоих местах. {191}
Сальвиати. — Сколь осмотрительным надо быть, прежде чем утверждать или отрицать какое-нибудь положение! Всякий, я повторяю, слыша, как решительно заявляют, что большее движение совершается у вершины мачты, нежели у ее подножия, будет убежден, что пользование телескопом гораздо труднее вверху, чем внизу. Поэтому я хотел бы извинить и тех философов, которые безнадежно, но все же жестоко нападают на всех, кто не хочет допустить, что пушечное ядро, явно идущее на их глазах вниз по прямой и отвесной линии, не безусловно движется таким образом, а наоборот, утверждают, что его движение совершается по дуге, к тому же все более и более наклонной и горизонтальной. Но оставим их в этом заблуждении и выслушаем другие возражения автора находящейся у нас в руках книги против Коперника.
Симпличио. — Автор продолжает далее доказывать, как, принимая учение Коперника, необходимо отрицать чувственное восприятие и сильнейшие ощущения, которые имели бы место, если бы мы, ощущающие дуновение легчайшего ветерка, не могли чувствовать импульса постоянного ветра, разящего нас со скоростью более 2529 миль в час, ибо таково
|
Годовое движение Земли должно было бы вызывать постоянный и весьма сильный ветер. |
Сальвиати. — Повидимому, этот философ думал, будто та Земля, которую Коперник заставляет двигаться вместе с окружающим воздухом по окружности большой орбиты, не та, на которой мы живем, а другая, особая; ведь эта наша Земля перемещает с собой и с тою же скоростью нас и окружающий воздух. И какие удары можем мы ощущать, раз мы мчимся со скоростью, равной скорости того, кто хочет нас поразить?
|
Если мы остаемся в соприкосновении с одной и той же частью атмосферы, мы не чувствуем никакого толчка. |
Симпличио. — Вовсе нет; вот слова, непосредственно следующие: «Praeterea nos quoque rotamur ex circonductione Terrae etc.»78.
Сальвиати. — Тут я не могу ни помочь ему, ни оправдать его, и помогите ему вы, синьор Симпличио.
Симпличио. — В данную минуту, так сказать экспромтом, мне не приходит в голову удовлетворительный способ защиты.
Сальвиати. — Ну, что же, вы подумайте, этой ночью и защитите его завтра, а пока выслушаем другие возражения.
Симпличио. — Далее идет то же самое возражение и утверждение, что, идя по пути Коперника, нужно отрицать собственные ощущения. Ибо тот принцип, в силу которого мы вращаемся вместе с Землей, является или нашим внутренним, или же внешним для нас, иными словами, возникающим
|
С точки зрения Коперника необходимо отказаться от показания чувственного опыта. |
Сальвиати. — Таким образом, смысл возражения этого философа заключается в том, что, будет ли тот принцип, в силу которого мы движемся вместе с Землей, внешним или внутренним, во всяком случае мы {192} должны были бы его ощущать; а так как мы его не ощущаем, то он ни тот, ни другой, а потому мы не движемся, а следовательно, не движется и Земля. Я же говорю, что он может быть и тем и другим, а мы ничего не будем ощущать. То, что он может быть внешним, доказывается более чем достаточно опытом с лодкой; говорю, более чем достаточно, ибо,
|
Наше движение может происходить от внутренних или внешних причин без того, чтобы мы его замечали или чувствовали. |
|
Движение судна неощутимо для находящихся на нем. |
|
Движение лодки может быть заметно благодаря чувству зрения и при помощи разумных соображений. |
|
Движение Земли познается по звездам. |
Симпличио. — Еще это восклицание: «Ex hac itaque opinione necesse est diffidere nostris sensibus, ut penitus fallacibus vel stupidis in sensibilibus, etiam conjunctissimis, dijudicandis; quam ergo veritatem sperare possumus a facilitate adeo fullaci ortum trahentem?»79.
Сальвиати. — О, я хотел бы выводить правила, более полезные и надежные, наученный большей осмотрительности и меньшей доверчивости к тому, что на первый взгляд представляют нам чувства, способные нас легко обмануть. Мне жаль, что этот автор так беспокоится, желая дать нам понять посредством чувств, что движение падающих тяжелых тел является простым прямым, а не каким-нибудь иным, и сердится, удивляясь тому, что вещь столь ясная, очевидная и явная подвергается сомнению; ведь этим он дает повод думать, будто тому, кто говорит, что такое движение не совершенно прямое, а скорее круговое, падающий камень ощутимо представляется идущим по дуге, раз он для разъяснения подобного явления обращается скорее к их чувствам, нежели к рассудку. Это неверно, синьор Симпличио, так как и я, относящийся безразлично к этим мнениям и только на манер актера в этих наших представлениях замаскировавшийся под Коперника, никогда не видел и никогда не предполагал увидеть камни, падающие иначе, чем по отвесу; и я думаю, что и глазам всех прочих представляется то же самое. Лучше, стало быть, оставить видимость, в отношении которой мы все согласны, и постараться посредством рассуждения или подтвердить реальность предположения, или разоблачить его обманчивость. {193}
Сагредо. — Если бы я мог когда-нибудь встретиться с этим философом, который, как мне кажется, стоит гораздо выше многих других последователей того же учения, то в знак приязни я напомнил бы ему о явлении, которое он, безусловно, тысячу раз видел и из которого в полном согласии с тем, что мы изложили, можно понять, сколь легко можно оказаться обманутым простой видимостью или, скажем, чувственным представлением. Явление это заключается в следующем: людям, идущим ночью по улице, кажется, будто луна идет тем же шагом, что и они, пока они видят ее скользящей вдоль водосточных желобов на крыше, над которыми она показывается совершенно так же, как кошка, которая действительно, идя по крыше, следовала бы за ними. Видимость эта слишком очевидно вводила бы зрение в заблуждение, если бы не вмешивался рассудок.
Симпличио. — Действительно, нет недостатка в опытах, которые удостоверяют нам обманчивость голых чувств, потому выключим на время эти чувства и выслушаем дальнейшие аргументы, почерпнутые, как говорится, ex rerum natura80. Первый из аргументов заключается в том, что Земля не может двигаться по природе своей тремя движениями в высокой степени различными, иначе потребовалось бы отвергнуть многие очевидные аксиомы; Первая из аксиом заключается в том, что всякое
|
Аргументы против движения Земли ex rerum natura. Три аксиомы, которые принимаются как явно правильные. |
|
Простое тело, каким является Земля, не может двигаться тремя различными движениями. |
|
Земля не может выполнять ни одного из приписанных ей Коперником движений. |
|
Возражения против аргументов, опровергающих движение Земли ex rerum natura. |
Симпличио. — На этом ответе автор возражения отнюдь не успокоится; наоборот, этот ответ оказывается совершенно опровергнутым тем, что он добавляет для большего подкрепления своего возражения, как вы сейчас услышите. Он подтверждает, говорю, аргумент еще одной аксиомой, а именно: у природы нет ни недостатка, ни избытка в необходимых вещах. Это очевидно для наблюдателей природы в особенности в отношении животных, у которых, поскольку они должны двигаться многими движениями, природа сделала много членов и связала части удобно для движения, как например, в коленях и бедрах животных для
|
Четвертая аксиома против движения Земли. Члены животных необходимы для выполнения различных движений. Другой аргумент против троякого движения Земли. |
Сальвиати. — Вы говорите серьезно или иронически?
Симпличио. — Я говорю со всей серьезностью, на какую способен.
Сальвиати. — Значит, вы должны чувствовать себя достаточно сильным, чтобы защитить этого философа еще и от другого возражения, которое можно было бы выдвинуть против него; поэтому ответьте мне, прошу вас, в его пользу, раз уж он не может присутствовать сам. Прежде всего вы принимаете за истину, что природа создала члены, сочленения и суставы у животных, дабы они могли двигаться многими и различными движениями, а я отрицаю это ваше положение и говорю, что сочленения
|
Члены животных не предназначены для того, чтобы производить ими различные движения. |
|
Движения животных все одного рода. |
|
Концы всех подвижных костей круглы. |
|
Указания на то, что по необходимости концы костей должны быть круглы, а движения всех животных кругообразны. |
Симпличио. — Я это понимаю не в таком смысле; наоборот, я вижу, что животное движется сотнями движений не круговых, совершенно между собой различных: и бегом, и прыжками, и подъемом, и спуском, и плаванием, и многими другими.
Сальвиати. — Хорошо, но эти движения — вторичные, зависящие от первых, каковыми являются движения членов и сочленений; {195}
|
Вторичные движения животных обусловлены первичными. Для движения Земли не требуется членов. |
Симпличио. — Это (скажет противная сторона) могло бы быть, если бы движение было одно, но так как их три и притом совершенно различных друг от друга, то они не могут одновременно пребывать в нерасчлененном теле.
Сальвиати. — Таков, думаю, и на самом деле был бы ответ философа. На это я нападаю с другой стороны и спрашиваю вас, думаете ли вы, что посредством членов и сочленений земной шар мог бы приноровиться к участию в трех различных круговых движениях? Вы не отвечаете? Раз вы молчите, я отвечу за философа, который, безусловно, сказал бы «да», так как иначе было бы совершенно излишним и совершенно не относящимся к делу указывать, что природа создает сочленения, дабы движущееся тело могло двигаться различными движениями, и что раз у земного шара нет сочленений, то он не может иметь трех приписываемых ему движений; ведь если бы он считал, что даже посредством сочленений земной шар не мог бы стать способным к таким движениям, то он открыто заявил бы, что земной шар не может двигаться тремя движениями. Теперь, раз это так, прошу вас, а через вас, если возможно, и философа — автора аргумента, быть столь любезными научить меня, каким образом следовало бы расположить сочленения, чтобы такие три движения могли без
|
Хотят знать, посредством каких членов земной шар может выполнять три разных движения. Один единственный принцип может вызывать многие движения. |
Симпличио. — Самое большее, в чем с вами следовало бы согласиться, — это что подобное могло бы случиться с одним единственным движением, а с тремя, на взгляд мой и автора, невозможно, как он и пишет далее, продолжали подкрепляя возражение. Представим себе вместе с Коперником, что Земля движется собственной силой и вследствие внутреннего принципа с запада на восток в плоскости эклиптики; и что, кроме того, она обращается вследствие внутреннего же принципа вокруг
|
Другое возражение против троякого движения. |
Сальвиати. — Остановитесь на минуту и отыщите мне это место в книге; покажите-ка: Fingamus modo cum Gopernico, Terrain aliqua sua vi et ab indito principio impelli ab occasu ad ortum in eclipticae piano, turn rursus revolvi ab indito etiam principio circa suimet centrum ab ortu in occasum,
|
Грубая ошибка противников Коперника. |
Я сомневался, синьор Симпличио, не ошиблись ли вы, передавая слова автора, но вижу, что он сам, и весьма глубоко, заблуждается; к своему {196} огорчению, я убеждаюсь, что он решился оспаривать положение, которого хорошенько не понял, потому что это не те движения, которые Коперник приписывает Земле. Откуда берет он, что Коперник делает годовое движение по эклиптике противоположным движению вокруг собственного центра? Повидимому, он не читал его книги, где в сотне мест и даже в первых главах написано, что оба эти движения происходят в одном и том же направлении, а именно, с запада на восток. Но разве, и не слыша от других, он сам не должен был понять, что если приписываются Земле движения, из коих одно отнимается у Солнца, а другое — у первого движителя, оба они по необходимости должны совершаться в одном и том же направлении?
Симпличио. — Смотрите, как бы не ошиблись вы вместе с Коперником. Разве суточное движение первого движителя не происходит с востока на запад? А годовое движение Солнца по эклиптике не обратно, о запада на восток? Так как же хотите вы, чтобы они же, будучи перенесены на Землю, из противоположных стали согласными?
|
Хитроумное и вместе с тем глупое возражение против Коперника. |
Сальвиати. — Теперь, если возможно, выведем из заблуждения хотя бы синьора Симпличио. Видя, как звезды при восходе поднимаются над восточным горизонтом, он без труда поймет, что если бы это движение было присуще не звездам, то необходимо следовало бы сказать, что горизонт опускается противоположным движением и что, следовательно,
|
Ошибка противника обнаруживается и объясняется тем, что годовое и суточное движения, если они присущи Земле, направлены в одну сторону, а не противоположны друг другу. |
Симпличио. — Я понял вполне и не знаю, что сделать в извинение такой ошибки.
Сальвиати. — Не спешите, синьор Симпличио, потому что тут есть еще и другая, превосходящая первую, и заключается она в том, что автор заставляет Землю двигаться суточным движением вокруг собственного центра с востока на запад и не отдает себе отчета, что будь это так,
|
Из другой грубой ошибки вытекает, что противник Коперника мало учился. |
Симпличио. — О, даже и я, который едва видел первые основы астрономии, уверен, что не ошибся бы столь глубоко.
Сальвиати. — Судите же сами, насколько внимательно изучал этот противник книги Коперника, если он извращает эту главную и важнейшую гипотезу, на которой основываются все расхождения Коперника
|
Представляется сомнительным, понял ли противник третье, приписываемое Коперником Земле движение. |
Что же касается третьего движения, которое автор, опять якобы в духе Коперника, приписывает земному шару, то не знаю, какое движение он имеет в виду, во всяком случае не то, которое Коперник {197} приписывает Земле совместно с двумя другими — годовым и суточным — и которое не имеет ничего общего с отклонением к югу и северу, но служит единственно для того, чтобы постоянно сохранять ось суточного движения параллельной самой себе. Таким образом, следует сказать, что противник или этого не понял, или об этом умолчал. Однако, хотя одного этого важного пробела было бы достаточно, чтобы избавить нас от обязанности заниматься далее рассмотрением его возражений, тем не менее я хочу отнестись к ним с большим уважением, поскольку они действительно заслуживают более высокой оценки, нежели тысячи других, принадлежащих невежественным противникам. Итак, возвращаясь к возражению, скажу, что оба движения — годовое и суточное — совсем не противоположны, но совершаются в одном и том же направлении и потому могут зависеть от одного и того же принципа: третье естественно вытекает из годового само собой, так что незачем (как я докажу в своем месте) привлекать особый внутренний или внешний принцип, от которого оно могло бы зависеть, как от своей причины.
Сагредо. — Мне хочется по внушению естественного разумения также сказать кое-что этому противнику. Он хочет осудить Коперника на том основании, что я не могу в точности разрешить возникающие у него сомнения и ответить на все возражения, которые он представляет, как будто из моего неведения с необходимостью вытекает ошибочность учения Коперника. Но если этот повод осуждать писателей кажется ему законным, то ему не должно казаться лишенным основания, что я не одобрю Аристотеля и Птоломея, если он не лучше меня разрешит подобные же затруднения, которые я указываю ему в их учении. Он спрашивает меня, каковы те принципы, в силу которых земной шар движется годовым движением по зодиаку и суточным — по экватору вокруг себя самого.
|
Опровержение того же возражения подобными примерами других небесных тел. |
Симпличио. — Автор будет отвергать все это, как обман зрения, причиняемый стеклами телескопа.
Сагредо. — О, это было бы чересчур; утверждая, что невооруженный глаз не может ошибаться в суждении о прямом движении падающих тяжелых тел, он хочет, чтобы теперь произошли ошибки в восприятии других движений, после того как его зрительная способность оказывается усовершенствованной и возрастает в тридцать раз. Так скажем же ему, что Земля причастна множественности движений, подобно тому или, пожалуй, совершенно так же, как магнит, который движется вниз в качестве тяжелого тела и в то же время обладает круговыми движениями, горизонтальными и вертикальными по меридиану83. Но чего же больше? Скажите мне, синьор Симпличио, между чем, думаете вы, полагает этот автор больше различия, между прямым и круговым движением или между движением и покоем?
Симпличио. — Между движением и покоем, бесспорно. И это очевидно, потому что круговое движение не противоположно прямому, по Аристотелю; наоборот, он допускает, что они могут смешиваться, что невозможно
|
Движение более отлично от покоя, чем прямолинейное движение от кругового. Скорее можно допустить наличие у Земли двух принципов для прямолинейного и кругового движения, нежели одного принципа для движения, а другого для покоя. |
Сагредо. — Значит, более вероятным положением является допущение в натуральном теле двух внутренних принципов — одного для движения {198} прямого, а другого — для кругового, нежели двух других внутренних принципов, одного — для движения, а другого — для покоя. Но благодаря естественно присущей частям Земли склонности возвращаться к своему целому в случае насильственного разъединения, оба положения приходят в согласие и разнятся только в отношении действия целого, ибо первое требует, чтобы посредством внутреннего принципа она стояла неподвижно, а второе приписывает ей круговое движение; но, согласно допущению вашему и этого философа, два принципа — один для движения, другой для покоя — друг с другом несовместимы, как несовместимы и их действия, но это не касается двух движений, прямого и кругового, которые ничуть не исключают друг друга.
Сальвиати. — Прибавьте к этому, что движение, совершенное
|
Движения частиц Земли при возвращении к своему целому, возможно, кругообразны. |
Симпличио. — Автор подкрепляет возражение указанием на нелепость,
|
Различие движений дает возможность познания разнообразия вещей. |
Сагредо. — Я уже два или три раза замечал в рассуждениях этого автора, что для доказательства, будто дело обстоит так-то и так-то, он прибегает к утверждению, что так оно согласуется с нашим разумением, или
|
Природа создала сначала вещи по-своему, а только потом человеческий разум со способностью их понимать. |
Сальвиати. — Я держусь того же мнения. Но скажите, синьор Симпличио, каковы эти различные по природе вещи, которым вопреки наблюдению и рассудку Коперник приписывает одни и те же движения и действия?
|
Коперник ошибочно приписывает разным вещам одинаковое действие. |
Сальвиати. — Я непременно прочту его, однако, считаю излишним его излагать, потому что уверен, что никто из сторонников движения Земли этого отрицать не будет. Поэтому, опустив доказательство, поговорим о самом возражении; оно, как мне кажется, не имеет большой доказательной силы против положения Коперника, поскольку ничто не нарушается у тех движений и тех действий, посредством которых мы приходим к познанию природы и т. д. Ответьте мне, пожалуйста, синьор Симпличио. Те свойства, в которых некоторые вещи совершенно {199}
|
Общие свойства не могут дать познания разнородности предметов. |
Симпличио. — Нет, синьор, совсем наоборот, так как тождественность действий и свойств может быть доказательством только тождественности их природы.
Сальвиати. — Так что различие природы воды, земли, воздуха и других вещей, находящихся в этих стихиях, вы почерпаете не из тех действий, в которых все эти элементы и то, что с ними связано, совпадают, а из других действий, не так ли?
Симпличио. — Именно так.
Сальвиати. — Значит, если оставить в стихиях все эти движения, действия и другие свойства, посредством коих различают их природу, то это не помешает нам познать последние, даже если и устранить то действие, в котором все они без исключения совпадают и которое потому не имеет никакого значения для различия этих вещей?
Симпличио. — Думаю, что рассуждение ведется вполне правильно.
Сальвиати. — Но что земля, вода и воздух по природе в одинаковой мере расположены неподвижно вокруг центра, не есть ли мнение ваше, автора, Аристотеля, Птоломея и всех их последователей?
Симпличио. — Оно принято, как неоспоримая истина.
Сальвиати. — Значит, не из этого общего естественного условия — покоя вокруг центра — черпается аргумент в пользу различия природы этих стихий и вещей, из них состоящих; следует знать другие качества, не общие; и потому тот, кто отнимет у стихий только этот общий всем им покой и оставит все другие действия, нисколько не преградит пути, ведущего нас к познанию их сущностей. Но Коперник не отнимает у них
|
Согласованность элементов в одном и том же движении значит не больше и не меньше, чем согласованность в одном и том же состоянии покоя. |
Симпличио. — Следует четвертое возражение, заимствованное из одного
|
Тела одного и того же рода имеют движения одинакового рода. Другой аргумент, также направленный против Коперника. |
Сальвиати. — Форма аргумента кажется мне убедительной, но полагаю, что приложение его или содержание имеют изъяны; если автор пожелал бы упорствовать в своем утверждении, следствие будет говорить прямо против него. Ход рассуждения таков: среди мировых тел имеется шесть, постоянно движущихся, и это — планеты; относительно других, а именно относительно Земли, Солнца и неподвижных звезд, неизвестно, какие из них движутся и какие недвижимы, так как если Земля стоит недвижимо, необходимо, чтобы двигались Солнце и неподвижные звезды, и так как возможно также, что Солнце и неподвижные звезды стоят недвижимо, то должна двигаться Земля; спрашивается, раз находится под сомнением самый факт, чему с большим правом может быть приписано {200} движение, и чему — покой? Естественное рассуждение подсказывает, что движение должно считаться принадлежащим тому, что в большей степени по роду и сущности совпадает с теми телами, которые, бесспорно, движутся,
|
Из темноты Земли или световой силы Солнца и неподвижных звезд может быть сделано заключение о движении первой и о неподвижности последних. |
Симпличио. — Но автор не согласится, что шесть планет темны, и этого отрицания будет держаться твердо, т. е. будет доказывать великое по природе сходство между шестью планетами, Солнцем и неподвижными звездами и несходство между ними и Землею, основываясь на других признаках, чем тьма и свет; как я теперь замечаю, в пятом возражении, которое следует, выдвигая высшее несходство между Землею и небесными телами, автор пишет: великое смятение и путаница возникнут, согласно гипотезе Коперника, в системе вселенной и между частями ее, следовательно, между небесными телами, неизменными и неуничтожаемыми, согласно Аристотелю, Тихо и другим; между телами, говорю я, столь
|
Другое различие между Землей и небесными телами, касающееся чистоты и нечистоты. |
Сальвиати. — Действительно, система Коперника вносит беспорядок
|
Коперник вносит беспорядок во вселенную Аристотеля. |
|
Ошибочный вывод автора Антитихо. |
|
Глупость утверждения, что Земля находится вне неба. |
Симпличио. — Вот шестой и последний аргумент. В нем он считает
|
Аргумент, заимствованный от животных, которые нуждаются в отдыхе, хотя их движения естественны. |
|
Аргумент Кеплера в пользу Коперника. |
|
Автор Антитихо представляет возражение против Кеплера. |
|
Быстрота кругового движения возрастает вместе с возрастанием диаметра круга. |
Сальвиати. — Я не думаю, чтобы этот автор составил себе о Кеплере столь незначительное и низкое представление, чтобы думать, будто тот не понимал, что высочайший предел линии, проведенной из центра до звездной орбиты, движется скорее, нежели точка той же линии, отстоящая
|
Объяснение истинного смысла слов Кеплера и защита его. |
|
Большая и малая величины тела обусловливают различие при движении, но не при покое. |
|
Порядок природы таков, что меньшие пути проходятся в меньшие сроки, большие — в более продолжительные. |
Сагредо. — Мне кажется, я слышу ответ Кеплера, говорящего ему,
|
Воображаемый ответ Кеплера со скрытой иронией. |
Сальвиати. — Вы, синьор Сагредо, слишком остроумны и насмешливы, но оставим шутки в стороне, разбирая серьезные вопросы.
Сагредо. — Извините, синьор Сальвиати; то, что я говорю, совсем не так уж не относится к делу, как, может быть, вы это полагаете; ведь движение, служащее для отдыха и устранения усталости в утомленном странствием теле, гораздо легче может предотвратить ее, подобно тому как предохранительные лекарства действительнее врачующих. И я считаю
|
Животные не уставали бы, если бы их движение происходило так, как происходит движение, приписываемое Земле. Причины утомления у животных. Движение животных можно назвать скорее насильственным, чем естественным. |
|
Сила не уменьшается там, где она не встречает противодействия. |
Симпличио. — Таковы противоположные движения, которыми земной шар, как представляют себе, движется, и на них автор основывает свое возражение.
Сагредо. — Уже сказано, что они ничуть не противоположны и что в этом автор глубоко заблуждался, так что сила всего возражения обращается против самого нападающего, раз он хочет, чтобы первый движитель
|
Возражение Киарамонти обращается против него самого. |
|
Для правильных положений находятся убедительные доказательства, но не для ложных. |
Сальвиати. — Вы, синьор Сагредо, увлекаемый быстротой вашего ума, предвосхитили одно мое рассуждение, в котором я собирался сказать кое-что в ответ на этот последний аргумент автора; и хотя вы ему ответили более чем в достаточной мере, все же я хочу добавить то, что мне пришло тогда в голову. Автор почитает весьма неправдоподобным, чтобы тело, подверженное разрушению и тлену, каковым является Земля, могло постоянно двигаться равномерным движением, в особенности потому, что мы видим, как животные в конце концов устают и требуют отдыха; и неправдоподобность усиливается тем, что такое движение должно было бы иметь скорость, несравнимую и неизмеримо большую по сравнению со скоростью животных. Так вот, я не могу понять, почему скорость Земли его смущает, тогда как скорость звездной сферы, во столько раз ее превосходящая, заставляет его задуматься не больше, чем скорость машины, совершающей в 24 часа только один оборот. Если из сравнения скорости движения Земли со скоростью модели машины никаких выводов в отношении большей эффективности не делается, то пусть автор перестанет бояться утомления Земли, ибо, по моему мнению, всякое, даже самое слабое и ленивое животное, даже и хамелеон, не утомилось бы, передвигаясь движением, не превышающим пять-шесть локтей в 24 часа; но если он {204}
|
Скорее можно опасаться усталости небесных сфер, нежели усталости земного шара. |
Симпличио. — Я могу только сказать, что сегодняшние рассуждения показались мне полными остроумнейших и оригинальнейших мыслей, приведенных в пользу Коперника для подтверждения движения Земли, но все же я не чувствую себя убежденным в необходимости поверить ему, потому что сказанное в конечном счете не позволяет сделать иного заключения, кроме как того, что основания в пользу неподвижности Земли не являются безусловными, но это не значит еще, что приведено какое-нибудь доказательство в пользу противной стороны, с необходимостью убеждающее и позволяющее сделать заключение о движении Земли.
Сальвиати. — Я совсем не намеревался, синьор Симпличио, заставить вас отказаться от своего мнения и еще того менее желал бы выносить окончательное решение по столь большому спорному вопросу; моим намерением было и будет в последующих прениях лишь сделать для вас очевидным, что те, кто полагали это быстрейшее движение в 24 часа принадлежащим только Земле, а не вселенной, за исключением одной Земли, пришли к убеждению, что так может и должно быть, как говорится не вслепую, и что они отлично видели, слышали и исследовали доводы противоположного мнения и не легкомысленно отвечали на них. Руководясь тем же самым намерением, если это будет угодно вам и синьору Сагредо, мы сможем перейти к рассмотрению другого движения, впервые приписанного тому же земному шару Аристархом Самосским, а затем Николаем Коперником, совершающегося, как вы уже слышали, я думаю, по зодиаку в течение года вокруг Солнца, неподвижно расположенного в центре зодиака85.
Симпличио. — Вопрос столь велик и столь благороден, что я с великим любопытством выслушаю споры о нем, предполагая, что услышу все, что на этот счет может быть сказано. Пока пораздумаю один на досуге о том, что слышал и услышу, и если даже я ничего другого не приобрету, то достаточно будет и если я смогу рассуждать с большей основательностью.
Сагредо. — Итак, чтобы не задерживать больше синьора Сальвиати, кончим наши сегодняшние рассуждения, а завтра возобновим, по обыкновению, беседу с надеждой услышать великие новости.
Симпличио. — Я оставляю книгу о новых звездах и беру с собой книгу заключений, чтобы пересмотреть все, написанное там против годового движения, которое должно быть предметом завтрашних рассуждений.
| << | {205} | >> |
Сагредо. — Благодаря великому нетерпению, с которым я ожидал вашего прихода, синьор, желая услышать новые мысли относительно годового обращения нашего земного шара, мне показались чрезвычайно долгими часы прошедшей ночи и даже сегодняшнего утра, хотя я провел их не праздно, а наоборот, бодрствуя добрую их часть, перебирая в памяти вчерашние рассуждения и взвешивая доводы, приводимые сторонами в пользу двух противоположных позиций — Аристотеля и Птоломея, с одной стороны, и Аристарха и Коперника — с другой. И поистине мне кажется, что если кто-либо из них и ошибается, то он вполне заслуживает извинения: видимая убедительность доводов такова, что им трудно противостоять, во всяком случае, если мы будет придерживаться тех из них, которые приводились этими главнейшими и важнейшими авторами. Но хотя воззрение перипатетиков, в силу своей древности, имеет многочисленных последователей и почитателей, а другое — лишь очень немногих прежде всего в силу трудности понимания, а затем вследствие новизны, все же, мне кажется, нельзя не отметить, что среди названных многочисленных представителей первого воззрения, в особенности из числа современников, есть такие, которые для поддержания мнения, признаваемого ими истинным, приводят иной раз доводы совершенно детские, чтобы не сказать смешные.
Сальвиати. — То же самое впечатление получил и я, и даже в еще большей степени, чем вы, синьор, поскольку я слышал, как приводятся иногда такие доводы, которые я постыдился бы повторить не из боязни обесславить их авторов, — имена их можно и не упоминать, — но чтобы не запятнать этим чести рода человеческого. В конце концов, размышляя над тем, что я наблюдал, я убедился, что встречаются люди, которые идут
|
Некоторые исходят в своих рассуждениях из готового сложившегося в их уме положения, в которое они верят и к которому затем подгоняют свои выводы. |
Сагредо. — Эти люди, следовательно, не выводят заключение из предпосылок и не обосновывают его доводами, но прилаживают или, лучше сказать, разлаживают и переворачивают предпосылки и доводы {206} таким образом, чтобы они согласовывались с наперед установленными и вбитыми в голову заключениями. Не стоит поэтому меряться силами с подобными людьми, тем более что их образ действий не только неприятен, но и угрожает опасностью. Поэтому будем продолжать беседу с нашим синьором Симпличио, которого я давно знаю как человека, обладающего прямодушием, лишенного и тени недоброжелательства и, кроме того, осведомленного в учении перипатетиков настолько, что если он не найдет довода для поддержки мнения Аристотеля, то такой довод едва ли может быть приведен кем-либо другим. Но вот и он сам, совсем запыхавшийся; сегодня он заставил нас довольно долго ждать себя. А мы как раз злословили относительно вас, синьор Симпличио.
Симпличио. — За столь большое опоздание вам следует винить не меня, а Нептуна, ибо во время сегодняшнего утреннего отлива он так увел воду, что гондола, которая меня везла, войдя не очень далеко отсюда в незамещенный канал, оказалась на мели, и мне пришлось задержаться там больше, чем на целый час, в ожидании возвращения моря; и там, стоя на месте и не будучи в состоянии выйти из лодки, которая почти внезапно врезалась в песок, я заметил явление, показавшееся мне чрезвычайно удивительным, а именно: при спаде воды видно было, как
|
Движение воды между отливом и приливом не прерывается покоем. |
Сагредо. — Вам, значит, не часто приходилось пребывать так на мели среди мельчайших ручейков, имеющих столь незначительный уклон, что понижения или повышения поверхности открытого моря на высоту, равную толщине листа бумаги, достаточно, чтобы заставить воду приливать или отливать такими ручейками на очень большие пространства; так, на некоторых морских побережьях повышение моря только на 4 или 6 локтей заставляет воду разливаться по таким равнинам на много сотен и тысяч пертик1.
Симпличио. — Это я понимаю очень хорошо, но я думал, что между концом понижения и самым началом повышения должен находиться некоторый заметный промежуток покоя.
Сагредо. — Так и представляется дело, если вы будете судить по стенам или сваям, где эти изменения совершаются по вертикальной линии, но в действительности и здесь не бывает состояния покоя.
Симпличио. — Мне казалось, что так как эти два движения противоположны, то между ними по середине должно было бы быть некоторое состояние покоя, что согласно также с доктриной Аристотеля, который доказывает, что in puncto regressus mediat quies2.
Сагредо. — Я очень хорошо помню это место, но я помню также, что когда я изучал философию, то не был убежден доказательством Аристотеля; наоборот, у меня было много опытов, этому противоречащих, которые я мог бы привести также и вам, но мне не хотелось бы отклоняться в сторону, так как мы собрались здесь, чтобы говорить о нашей теме, не допуская перерывов, подобных тем, какие мы делали в предшествующие дни.
Симпличио. — А все-таки придется если не прерывать нашу беседу, то во всяком случае очень затянуть ее, потому что, вернувшись вчера вечером домой, я принялся перечитывать книжку заключений, где нашел много убедительных доказательств против годового движения, приписываемого Земле; и так как я не был уверен, что смогу точно изложить их, то я предпочел принести с собой книгу. {207}
Сагредо. — Вы прекрасно сделали, но если мы хотим придерживаться порядка рассуждений, принятого нами вчера, то нам придется сначала выслушать то, что имеет доложить синьор Сальвиати относительно книги о новых звездах, а потом, не делая больше перерывов, перейти к годовому движению. Итак, что скажет синьор Сальвиати по поводу новых звезд? Действительно ли они перенесены с неба в более низкие области силою вычислений автора, приводимых синьором Симпличио?
Сальвиати. — Вчера вечером я принялся за чтение его рассуждений, а сегодня утром еще раз пробежал их, чтобы посмотреть, действительно ли там написано то, что, как мне казалось, я прочитал вечером, или же это были ночные призраки и плоды моей фантазии. К большому сожалению, я нашел, что там действительно написано и напечатано то, чего я не желал бы видеть в интересах доброго имени этого философа. Мне кажется невозможным, чтобы он не сознавал безнадежности своего предприятия, так как, с одной стороны, это очевидно, а с другой, — я припоминаю, как о нем с похвалою отзывался наш друг Академик3; мне кажется также весьма неправдоподобным, чтобы он, в угоду другим, поставил на карту свое доброе имя, решившись опубликовать произведение, которое со стороны понимающих людей не может встретить ничего, кроме порицания.
Сагредо. — Добавьте, что таких понимающих будет не более одного на сотню по сравнению с теми, кто станет его восхвалять и превозносить выше всех великих умов прошлого и настоящего. Ведь это он сумел поддержать перипатетическую неизменяемость неба против рати астрономов и к вящему их позору побил их их же собственным оружием! А что могут сделать четыре или шесть человек на провинцию, замечающие его легковесность, против бесчисленного множества тех, которые не в состоянии разобраться в вопросе и понять его и, увлеченные общим криком, аплодируют ему тем больше, чем меньше сами понимают? Добавьте, что даже немногие понимающие воздержатся от возражения против столь ничтожного и бездоказательного писания и, конечно, с полным основанием, ибо для понимающих в этом нет надобности, а в отношении тех, кто не понимает, это будет бесполезно затраченным трудом.
Сальвиати. — Самым подходящим наказанием для них действительно было бы молчание, если бы не существовало причин, в силу которых почти необходимо на них отозваться; одна из этих причин заключается в том, что все мы, прочие итальянцы, прослывем за людей невежественных и дадим повод смеяться живущим по ту сторону гор, в особенности же тем, кто исповедует религию, отличную от нашей. Я мог бы назвать вам некоторых очень известных людей, которые насмехаются над нашим Академиком и всеми итальянскими математиками за то, что они без возражений позволили выйти в свет и обращаться глупостям некоего Лоренцини, направленным против астрономов4. Но даже это можно было бы оставить без внимания перед лицом другого, еще большего повода для насмешек, который дают ученые, поощряющие, повидимому, легкомыслие людей, опровергающих учение, которого они не понимают.
Сагредо. — Нельзя найти более разительного примера, чем наглость этих людей и несчастное положение такого человека, как Коперник, который принужден бороться с теми, кто не понимает даже того основного положения его учения, из-за которого они объявили ему войну.
Сальвиати. — Вы немало будете изумлены тем способом, которым опровергаются воззрения астрономов, утверждающих, что новые звезды находятся выше планетных орбит и, может быть, на самом небесном своде6.
Сагредо. — Но как могли вы в столь краткий срок изучить всю эту книгу? Ведь все же это большой том и доказательств там должно быть очень много? {208}
Сальвиати. — Я остановился на тех первых его опровержениях, где он двенадцатью примерами, основанными на наблюдениях двенадцати астрономов, которые все полагали, что новая звезда 1572 года, появившаяся в Кассиопее, должна находиться на небесном своде, доказывает, вопреки им, что она находилась ниже лунной орбиты. Для этого он сопоставляет попарно меридианные высоты, определенные различными наблюдениями в местах разной широты, продвигаясь вперед способом, о котором вы получите понятие несколько позже. И так как мне кажется, что при рассмотрении хода этого первого его рассуждения я сразу открыл в авторе полную неспособность сделать выводы, которые говорили бы против астрономов в пользу философов-перипатетиков, и увидел, что гораздо больше можно привести в подкрепление мнения первых, то мне не хотелось тратить труд на исследование с тем же вниманием других его доказательств и я лишь поверхностно пробежал их, будучи вполне уверен, что несостоятельность его первых опровержений обнаружится в равной степени и в других. И, как вы увидите на самом деле, достаточно очень немногих слов, для того чтобы опровергнуть все это произведение, несмотря на то, что оно, как вы видите, опирается на множество трудолюбивых
|
Метод Киарамонти для опровержения астрономов и метод Сальвиати, его опровергающий. |
Симпличио. — Несомненно, нужно сказать, что она должна находиться в одном единственном месте и на одном единственном и определенном расстоянии от Земли.
Сальвиати. — Следовательно, если бы наблюдения, произведенные астрономами, были правильны и если бы вычисления, произведенные этим автором, не заключали ошибки, то в результате тех и других получалось бы всегда в точности одно и то же удаление? Не правда ли?
Симпличио. — Насколько я понимаю, это по необходимости должно быть так. Я не думаю, чтобы автор стал этому противоречить.
Сальвиати. — Но если среди многих и многих произведенных подсчетов нет даже двух, которые бы сходились, то каково будет ваше суждение об этом?
Симпличио. — Я скажу, что все они были неправильны или по вине вычислителя, или в силу неточности, допущенной наблюдателями; и самое большее, что можно было бы сказать и что я сказал бы, — это что, может быть, один какой-нибудь результат и верен, но я не знаю, какой выбрать.
Сальвиати. — Захотите ли вы, однако, исходя из ложных оснований, вывести и установить в качестве истинного заключения сомнительное? Конечно, нет. А вычисления этого автора таковы, что ни одно не согласуется с другим; вы видите, следовательно, насколько он заслуживает доверия.
Симпличио. — Действительно, если дело обстоит так, то это явный промах.
Сагредо. — Я все же хочу помочь синьору Симпличио и автору, сказав синьору Сальвиати, что его соображение было бы совершенно доказательно, {209} если бы автор стремился точно определить, какова была удаленность звезды от Земли; но я не думаю, чтобы таково было его намерение, ибо он хотел только доказать, что из этих наблюдений следует, что звезда находилась ниже Луны. Так что, если из названных наблюдений и из всех подсчетов, сделанных на их основании, высота звезды всегда получается меньшей, чем высота Луны, то этого автору достаточно, для того чтобы уличить в грубом невежестве всех тех астрономов, которые из-за недостаточности познаний в геометрии или арифметике не сумели вывести правильных заключений из своих же собственных наблюдений.
Сальвиати. — Повидимому, мне придется обращаться к вам, синьор Сагредо, раз вы так искусно поддерживаете этого автора. Желая, чтобы и синьор Симпличио, хотя он и неопытен в вычислениях и доказательствах, смог по меньшей мере увидеть неубедительность доказательств этого автора, я прежде всего обращаю внимание на то, что и он, и все астрономы, с которыми он расходится во мнениях, согласны, что новая звезда была лишена собственного движения и следовала лишь за круговым суточным движением первого движителя; расходятся же они лишь относительно ее места, так как одни помещают ее в небесной области, т. е. над Луною и, может быть, среди неподвижных звезд, другие считают, что она находится по соседству с Землею, т. е. под вогнутостью лунной орбиты. И так как место новой звезды, о которой идет речь, находилось в направлении севера и не очень далеко от полюса, так что для нас, северян, она никогда не заходила, то легко было определить с помощью астрономических инструментов ее меридианные высоты, как наименьшие — под полюсом, так и наибольшие — над полюсом; из сравнения этих высот, полученных в разных местах Земли, находящихся на неодинаковых расстояниях от севера, т. е. местах, отличающихся друг от друга высотой полюса, можно было сделать выводы относительно удаленности звезды. Ибо, если бы она находилась на небесном своде среди других неподвижных звезд, то ее различные меридианные высоты, определенные в местах с разными высотами полюса,
|
Минимальные и максимальные высоты новой звезды отличаются друг от друга не более, чем высоты полюса, как скоро новая звезда стоит на небесном своде. |
1. Мавролика и Хайнцеля; на основании этих наблюдений получается, что звезда должна быть удалена от центра меньше, чем на 3 земных полудиаметра, при разнице параллакса в 4 градуса 42 минуты и 30 секунд |
3 полудиаметра. |
|
2. Делается вычисление на основании наблюдений Хайнцеля и Шулера при параллаксе 8 минут и 30 секунд и получается удаленность от центра больше, чем на..................... |
25 полудиаметров. |
|
3. По наблюдении Тихо и Хайнцеля при параллаксе в 10 минут получается расстояние от центра немногим меньше................. |
19 полудиаметров. |
|
4. По наблюдениям Тихо и Ландграфа при параллаксе в 14 минут расстояние от центра оказывается равным приблизительно.............. |
10 полудиаметрам. |
|
5. По наблюдениям Хайнцеля и Гемма при параллаксе в 42 минуты и 30 секунд получается расстояние около................. |
4 полудиаметров. |
|
6. По наблюдениям Ландграфа и Камерария при параллаксе в 8 минут расстояние снижается приблизительно до................... |
4 полудиаметров. |
|
7. По наблюдениям Тихо и Хачека при параллаксе в 6 минут получается расстояние....... |
32 полудиаметра. |
|
8. Из наблюдений Хачека и Урсино при параллаксе в 43 минуты расстояние звезды от поверхности Земли оказывается равным............ |
1/2 полудиаметра. |
|
9. По наблюдениям Ландграфа и Буша при параллаксе в 15 минут расстояние от поверхности Земли оказывается равным............... |
1/48 полудиаметра: |
|
10. По наблюдениям Мавролика и Муньоса при параллаксе в 4 градуса 30 минут расстояние от поверхности Земли оказывается равным....... |
1/5 полудиаметра. |
|
11. Из наблюдений Муньоса и Гемма при параллаксе в 55 минут расстояние от центра оказывается равным приблизительно.......... |
13 полудиаметрам. |
|
12. Из наблюдений Муньоса и Урсино при параллаксе в 1 градус 36 минут расстояние от центра получается меньше................ |
7 полудиаметров. |
Таковы 12 вычислений, произведенных автором по своему выбору из тех очень многих, которые, как он говорит, можно было сделать, комбинируя наблюдения этих 13 наблюдателей; эти 12, как можно думать, наиболее благоприятны для доказательства его предположения.
Сагредо. — Но мне хотелось бы знать, нет ли среди других многочисленных и опущенных автором исследований таких, которые были бы не в его пользу, иными словами, таких, из которых путем вычислений получалось бы, что новая звезда была выше Луны, ибо именно это, как мне кажется, на первый взгляд можно предположить по вполне разумным основаниям; пока же, как я вижу, результаты подсчетов настолько отличаются друг от друга, что одни дают мне удаленность новой звезды от Земли в 4, 6, 10, 100, тысячу и полторы тысячи раз бо́льшую, чем другие; таким образом, я имею основание подозревать, что среди вычислений непроизведенных могут оказаться такие, которые благоприятны противной стороне; думать так я могу с тем большим правом, что не предполагаю у этих астрономов отсутствия понятливости и опыта в таких подсчетах, не принадлежащих, на мой взгляд, к числу особо мудреных вещей. И мне показалось бы более чем удивительным, если бы помимо этих 12 исследований, из которых одни помещают звезду в немногих милях от Земли, а {211} другие чуть-чуть пониже Луны, не нашлось какого-нибудь одного, которое в пользу противной стороны поместило бы звезду хотя бы лишь на двадцать локтей выше лунной орбиты. И уж совсем было бы странно, если бы все эти астрономы оказались столь слепы, что не заметили своей столь явной ошибки.
Сальвиати. — Готовьте теперь свой слух к тому, чтобы с бесконечным изумлением выслушать, до каких крайностей в доверии к собственному авторитету и убеждении в глупости других людей доводит, желание противоречить и показывать себя умнее других. Среди пропущенных автором исследований есть и такие, которые помещают новую звезду не только выше Луны, но даже выше неподвижных звезд, и таких исследований не мало; наоборот, их большинство, как вы увидите это на другом листе, где я их отметил.
Сагредо. — Но что говорит о них автор? Может быть, он с ними незнаком?
Сальвиати. — Прекрасно знаком, но, по его словам, наблюдения, на которых основаны подсчеты, помещающие звезду бесконечно далеко, ошибочны и не могут быть сопоставлены друг с другом.
Симпличио. — О, это кажется мне очень слабой отговоркой, так как противная сторона могла бы с таким же основанием утверждать, что ошибочны те наблюдения, согласно которым он низводит звезду в область стихий.
Сальвиати. — О, синьор Симпличио, если бы мне удалось дать вам представление об этом искусстве нашего автора, хотя оно и не высокого полета, то я, наверное, вызвал бы у вас удивление и даже негодование; вы увидели бы, как он, пряча свою проницательность и свой ум под покровом вашего простодушия и простодушия других философов, хочет добиться вашего расположения путем лести, раздувая ваше тщеславие, делая вид, будто он победил и заставил замолчать тех астрономишек, которые собирались атаковать несокрушимую неизменяемость перипатетического неба, и, что еще важнее, привел их к молчанию и победил их собственным их оружием. Я приложу все старания сделать это, а пока пусть простит синьор Сагредо меня и синьора Симпличио за то, что мы, быть может, заставим его немного поскучать, слушая, как я с излишним многословием (излишним, говорю, для его чрезвычайно быстрой сообразительности) постараюсь сделать явным то, что не хорошо было бы оставлять скрытым и неизвестным.
Сагредо. — Я не только не буду скучать, но с удовольствием послушаю ваши рассуждения, и то же самое должны были бы сделать все философы-перипатетики, чтобы понять, насколько они обязаны такому своему покровителю.
Сальвиати. — Скажите мне, синьор Симпличио, хорошо ли вы понимаете, что если новая звезда помещается на круге меридиана на севере, а кто-нибудь идет с полудня в полуночную сторону, то по мере его продвижения эта новая звезда должна подниматься над горизонтом, так же как и полюс, в том случае, однако, если она действительно помещается среди неподвижных звезд; но если она находится значительно ниже, т. е. ближе к Земле, то будет казаться поднимающейся больше, чем полюс, и притом тем больше, чем она ближе?
Симпличио. — Мне кажется, что я вполне это понимаю; для доказательства я начерчу математическую фигуру; на этом большом круге я отмечу полюс P, а на этих двух нижних кругах я отмечу две звезды, видимые из одной точки на Земле. Пусть эта точка будет A, а две звезды пусть будут В и C, видимые на одной и той же линии ABC, направленной к неподвижной звезде D; если мы потом пройдем по Земле до точки Е, то две звезды покажутся нам отделившимися {212} от неподвижной звезды В и приблизившимися к полюсу P, причем больше приблизится более низкая звезда В, которая мне покажется в G, и меньше — звезда C, которая мне покажется в F; но неподвижная звезда В сохранит ту же самую удаленность от полюса.
Сальвиати. — Я вижу, что вы понимаете очень хорошо. Думаю, что вам понятно также, что раз звезда В ниже звезды C, то угол, который образуется зрительными лучами, исходящими из двух мест А и Е и соединяющимися в С, т. е. угол АСЕ, уже или, лучше сказать, острее угла, образованного в В лучами АВ и ЕВ.
Симпличио. — Это видно очень хорошо.
Сальвиати. — Далее, так как Земля чрезвычайно мала и почти неощутима по сравнению с небесным сводом, и следовательно, пространство АЕ, которое можно пройти по Земле, чрезвычайно коротко по сравнению с огромной протяженностью линий EG и EF от Земли до небесного свода, то вы понимаете, что звезда С должна находиться так высоко и далеко от Земли, что угол, образованный в ней лучами, исходящими из тех же точек А и E, должен стать чрезвычайно острым, как бы абсолютно неощутимым нулем.
Симпличио. — И это я понимаю превосходно.
Сальвиати. — Так знайте, синьор Симпличио, что астрономы и математики нашли путем геометрии и арифметики безошибочные правила, чтобы, исходя из величины этих углов В и С и сопоставления их с известным расстоянием между двумя местами А и E, в точности находить удаленность возвышенных предметов, однако, если только это расстояние и эти углы определены точно.
Симпличио. — Таким образом, если правила, зависящие от геометрии и арифметики, верны, то все заблуждения и ошибки, встречающиеся при исследовании высоты новых звезд, или комет, или иных тел, должны зависеть от неточности измерения расстояний АЕ и углов В и С. Следовательно, все те различия, которые наблюдаются в этих 12 исследованиях, зависят не от недостатков правил вычислений, но от ошибок, сделанных при определении углов и расстояний посредством употребляемых для наблюдений инструментов.
Сальвиати. — Это так, но не отсюда возникает трудность. Вы должны обратить свое внимание на то, как при удалении звезды он В к С, отчего угол становится все более острым, луч EBQ непрерывно удаляется от луча ABD в нижней части угла, как это показывает линия ECF, нижняя часть которой ЕС дальше от части АС, чем ЕВ; но никогда не может случиться так, что в результате сколь угодно огромного удаления линии АВ и EF совершенно разъединятся, так как в конце концов они должны соединиться в звезде; можно только сказать, что они разошлись бы и стали параллельными тогда, когда удаление будет бесконечным, а такого случая на самом деле не может быть. Но так как (заметьте хорошенько) удаленность небесного свода по уравнению с ничтожностью Земли, как уже сказано, принимается за бесконечную, то и угол, образованный лучами, которые исходят из точек А и Е и заканчиваются в неподвижной звезде, расценивается как нуль, а сами лучи — как две параллельные линии; и отсюда делается такой вывод: только тогда можно утверждать, что новая звезда находится на небесном своде, когда из сравнения наблюдений, произведенных в разных местах, путем вычислений будет показано, что названный угол окажется неощутимым, а линии как бы параллельными. Но если угол будет заметных размеров, то, следовательно, новая звезда необходимо должна быть ниже неподвижных звезд и даже ниже Луны в том случае, если угол ABE больше того, который образуется в центре Луны.
Симпличио. — Значит, удаленность Луны не столь уже велика, чтобы такой угол оказался для нее неощутимым. {213}
Сальвиати. — Нет, синьор, он ощутим в отношении не только Луны, но даже и Солнца.
Симпличио. — Но если это так, то этот угол может оказаться доступным наблюдению и в отношении новой звезды, даже если она не ниже не только Луны, но и Солнца?
Сальвиати. — Может оказаться; и так оно и есть в настоящем случае, как вы увидите в своем месте. Я постараюсь так выравнять путь, что даже вы, неискушенный в астрономических вычислениях, сможете наглядно убедиться в том, что этот автор старался писать скорее для удовольствия перипатетиков, маскируя и скрывая разные вещи, чем для установления истины и изложения ее с полной искренностью. Итак, двинемся дальше. Из того, что было разъяснено до сих пор, я думаю, вы очень хорошо усвоили, что удаленность новой звезды никогда не может оказаться настолько огромной, чтобы многократно упоминавшийся угол совершенно исчез и чтобы два луча наблюдателей из мест А и Е стали совершенно параллельными линиями, и следовательно, вы превосходно понимаете, что когда по вычислении на основе наблюдений такой угол оказывается равным нулю и линии действительно параллельными, мы можем быть уверены, что наблюдения, по крайней мере в какой-то хотя бы минимальной части, были ошибочными; но когда по вычислению те же самые линии должны разойтись не только до равного расстояния, т. е. стать параллельными, но и перейти границу и расшириться больше вверху, чем внизу, тогда, безусловно, нужно признать, что наблюдения были произведены еще менее тщательно, словом, что они ошибочны, так как приводят нас к очевидной невозможности. Затем вы должны мне поверить и принять за совершенную истину, что две прямые линии, которые исходят из двух точек, намеченных на третьей прямой, вверху шире, чем внизу в том случае, когда углы, заключенные внутри них над этой прямой, больше двух прямых углов; если углы равны двум прямым, тогда линии параллельны, если же углы меньше двух прямых, то линии становятся сходящимися и при продолжении, несомненно, образуют треугольник.
Симпличио. — Я знаю это даже не по доверию к нам; я не настолько профан в геометрии, чтобы не знать положения, которое тысячу раз имел случай читать у Аристотеля, а именно, что три угла каждого треугольника равны двум прямым; таким образом, если я беру на моем чертеже треугольник ABE, приняв линию ЕА за прямую, то я прекрасно понимаю, что три его угла А, Е и В равны двум прямым и что, следовательно, оба угла Е, А меньше двух прямых на величину угла В; поэтому, если разводить линии АВ, ЕВ (удерживая их, однако, неподвижными в точках А, Е) до того, что угол, образуемый ими у В, исчезнет, то два нижних угла окажутся равными двум прямым и эти линии окажутся сведенными к параллельным; если же их разводить еще больше, то углы у точек Е, А станут больше двух прямых.
Сальвиати. — Вы прямо Архимед; вы освободили меня от траты многих слов на разъяснение того, каким образом всякий раз, когда из подсчетов вытекает, что два угла А и Е больше двух прямых, сразу становится очевидным, что наблюдения ошибочны. Как раз я и хотел, чтобы именно это вы усвоили в совершенстве, и сомневался, смогу ли я разъяснить так, чтобы чистый философ-перипатетик твердо это уразумел. Перейдем теперь к тому, что еще остается. Возвратимся к вашему недавнему утверждению, что раз новая звезда не может быть во многих местах, а должна находиться в одном единственном месте, то всякий раз, когда вычисления, сделанные по наблюдениям этих астрономов, не помещают ее в то же место, необходимо признать, что произошла ошибка в наблюдениях, или при определении высоты полюса, или при определении высоты звезды, или при каком-либо другом действии. Но так как из множества исследований, {214} сделанных посредством попарной комбинации наблюдений, лишь очень немногие помещают звезду в одно и то же место, то, значит, лишь эти немногие могут быть признаны правильными, все же другие обязательно содержат ошибки.
Сагредо. — Значит, нужно верить этим немногим больше, чем всем другим вместе; и раз вы говорите, что единодушны лишь очень немногие, и я среди этих 12 вижу только 2 определяющие расстояния звезды от центра Земли в 4 полудиаметра, именно пятое и шестое, то, следовательно, более вероятно, что новая звезда была скорее стихийной, чем небесной.
Сальвиати. — Это не так; посмотрите хорошенько; там написано не то, что расстояние составляет в точности 4 полудиаметра, а лишь около 4 полудиаметров; как вы можете видеть, эти два расстояния отличаются друг от друга на многие сотни миль. Вот они: вы видите, что пятое, равное 13 389 милям, превосходит шестое, дающее 13 000 миль, почти на 300 миль.
Сагредо. — Так где же те немногие, которые согласно помещают звезду в одно и то же место?
Сальвиати. — Существуют, к несчастию, для этого автора пять исследований, которые все относят ее на небесный свод, как вы увидите это на другой записке, где я отметил много других комбинаций. Но я собираюсь уступить автору больше того, что он, может быть, запросил бы у меня: словом, пусть в каждой комбинации наблюдений будет какая-нибудь ошибка; я думаю, что это совершенно неизбежно, так как если в основу одного вычисления необходимо положить 4 наблюдения, т. е. два для разных высот полюса и два для разных высот звезды, произведенных разными наблюдателями в разных местах и посредством разных инструментов, то всякий, кто имеет хоть какое-нибудь представление о таких действиях, скажет, что в этих 4 наблюдениях не может не оказаться какой-нибудь ошибки; в самом деле, мы видим, что даже при определении одной только высоты полюса посредством одного и того же инструмента в одном и том же месте и одними тем же наблюдателем, которое может быть повторено тысячу раз, всегда получается отклонение в пределах минуты, а часто даже и нескольких минут, как вы можете это увидеть в той же
|
Астрономические инструменты могут легко давать ошибочные показания. |
Симпличио. — Не может быть, чтобы он не считал их за людей весьма осторожных и понимающих, так как если бы в его глазах они были людьми неумелыми в таких операциях, то он должен был бы поставить крест на своей книге, как ничего не доказывающей, ибо она основана на предпосылках, преисполненных ошибок; и за слишком больших простаков принимал бы он и нас, рассчитывая на нашу неопытность, чтобы выдать нам за истину свое ложное предположение.
Сальвиати. — Итак, раз эти наблюдатели хороши и, однако, при всем том ошибались и нужно исправить их ошибки, чтобы можно было извлечь из их наблюдений как можно больше сведений, то самым подходящим будет внести поправки и исправления, наименьшие и наиболее близкие, какие только возможно, для того, чтобы свести наблюдения из области невозможного в область возможного; так, например, если можно смягчить явную ошибку и бьющую в глаза невозможность какого-либо наблюдения прибавлением или вычитанием 2 или 3 минут и посредством такого исправления сделать результат наблюдений возможным, то не следует стремиться исправлять их добавлением или отнятием 15, 20 или 50 минут.
Симпличио. — Я не думаю, чтобы автор стал возражать против этого; ведь если допущено, что они люди рассудительные и сведущие, то, надо думать, они скорее сделали ошибки меньшие, нежели большие. {215}
Сальвиати. — Теперь замечайте дальше. Из тех мест, которые отводятся для новой звезды, одни явно невозможны, другие же возможны. Совершенно невозможно, чтобы она была бесконечно выше неподвижных звезд, ибо такого места нет в мире, а если бы даже и было, то находящаяся там звезда была бы для нас невидима; невозможно, также, чтобы она скользила по поверхности Земли, и еще более невозможно, чтобы она находилась внутри земного шара. Возможные места — это такие, относительно которых идет спор, так как наш разум не противится тому, что видимый предмет, звезда по внешности, может быть как выше Луны, так и ниже ее. Итак, когда пытаются найти путем наблюдений и вычислений, произведенных с такой точностью, какой только может достигнуть человеческое прилежание, каково же было ее действительное место, оказывается, что большая часть этих вычислений относит ее больше чем на бесконечное пространство выше небесного свода, другие помещают ее совсем близко к поверхности Земли, а некоторые даже под ее поверхностью; из тех же, которые помещают ее не в невозможных местах, ни одно не согласуется с другим; таким образом, приходится по необходимости сказать, что все наблюдения были ошибочны и что если мы все же хотим из столь великих трудов извлечь какой-либо плод, то необходимо внести коррективы, исправляя все наблюдения.
Симпличио. — Но автор скажет, что на наблюдения, относящие звезду в невозможные места, вовсе нельзя полагаться, так как они бесконечно ошибочны и ложны, и что следует брать только те, которые помещают ее не в невозможные места, и что только пользуясь последними, путем более вероятных и более многочисленных совпадений нужно стараться если не найти точное местонахождение, т. е. истинное расстояние, звезды от центра Земли, то по меньшей мере узнать, находилась ли она среди стихий или же среди небесных тел.
Сальвиати. — Именно это высказанное вами соображение и есть то самое, которое автор выдвигает в свою пользу, но пользуется им в ущерб противникам слишком неразумно. Это и есть тот главный пункт, который заставил меня свыше меры удивляться излишней уверенности его не столько в своем собственном авторитете, сколько в слепоте и невнимательности астрономов. За них буду говорить я, а вы отвечайте за автора. Прежде всего я вас спрошу, могут ли астрономы при наблюдении посредством своих инструментов и определении, например, высоты звезды над горизонтом отклоняться от истины как в большую, так и в меньшую сторону, т. е. ошибочно считать ее то выше, чем в действительности, то ниже? Или же ошибка непременно должна быть только одного рода, иными словами, может ли погрешность при ошибке выражаться только в избытке и никогда в недостатке или же всегда в недостатке и никогда в избытке?
Симпличио. — Я не сомневаюсь, что можно одинаково легко ошибаться как тем, так и другим образом.
Сальвиати. — И автор, я думаю, ответил бы то же самое. Итак, из этих двоякого рода ошибок, являющихся противоположными, в которые в равной мере могли бы впасть наблюдатели новой звезды, ошибки одного рода, в приложении к вычислению, будут помещать звезду выше, чем она находится в действительности, а другого — ниже. И так как мы уже согласились, что все наблюдения ошибочны, то на каком же основании автор хочет заставить нас признать более согласующимися с истиной те наблюдения, которые показывают, что звезда была близко, чем другие, которые показывают ее крайнюю удаленность?
Симпличио. — Насколько я мог до сих пор понять, из сказанного я не вижу, чтобы автор отводил те наблюдения и исследования, которые могут поместить звезду дальше Луны и даже дальше Солнца; он отбрасывает только те, которые удаляют ее (как вы сами сказали) больше, чем на {216} бесконечное пространство; такое расстояние вы сами считаете невозможным, и он отбрасывает подобные наблюдения, как изобличенные в ложности и приводящие к невозможности. Поэтому мне кажется, что если вы хотите победить автора, то вам следует произвести исследования более точные, на основании наблюдений более многочисленных или проделанных более тщательными наблюдателями, которые помещали бы звезду на таком-то и таком-то удалении от Луны или Солнца, словом, в месте, возможном для ее нахождения, как это и делают те 12; все они помещают новую звезду ниже. Луны в местах, на свете существующих, где и она могла бы быть.
Сальвиати. — Но, синьор Симпличио, здесь-то и заключается уловка и ваша, и автора: ваша в одном отношении, автора — в другом. Я заключаю из ваших слов, что вы составили себе такое представление, будто нелепости, обнаруживающиеся при установлении удаленности звезды, возрастают пропорционально ошибкам инструмента, производящего наблюдения, и обратно, по размерам нелепостей можно судить о размерах ошибок; поэтому если мы слышим, что на основании таких-то наблюдений удаленность звезды оказывается бесконечной, необходимо признать, что ошибка при наблюдениях была бесконечной и потому непоправимой, и такое наблюдение подлежит отводу. Но, мой дорогой синьор Симпличио, дело обстоит не так, и если я извиняю вам то, что вы не поняли, как это происходит на самом деле, вследствие вашей неопытности в таких вопросах, то я не могу под таким же покровом скрывать ошибку автора; он, притворяясь понимающим то, чего мы, по его мнению, не можем понять, надеялся воспользоваться нашим невежеством, чтобы приобрести еще большее доверие к своему учению у множества мало понимающих людей. Поэтому для предупреждения тех, кто скорее принимает на веру, чем понимает, и чтобы предостеречь вас от ошибки, я скажу: знайте, может оказаться (и это частенько случается), что наблюдение, которое даст вам звезду, например, на удалении Сатурна, прибавлением или отнятием одной только минуты высоты, определенной инструментом, относит ее на бесконечное расстояние и потому из возможного делает его невозможным; и обратно, вычисления, проделанные на основе таких наблюдений, которые помещают звезду бесконечно далеко, часто добавлением или вычитанием одной только минуты могут вернуть ее в возможное место, и то, что я говорю об одной минуте, может случиться также при исправлении на половину, на шестую минуты и даже еще меньше. Теперь усвойте как следует, что при чрезвычайно больших расстояниях, как, например, расстояние до Сатурна или до неподвижных звезд, малейшие ошибки наблюдающего посредством инструмента делают место определенное и возможное — бесконечным и невозможным. Совсем не то бывает с расстояниями подлунными и близкими к Земле, где может случиться, что наблюдение, согласно которому звезда оказывается на удалении, например, 4 земных полудиаметров, можно увеличивать или уменьшать не только на одну, но на десять, на сто и еще большее число минут, и при всем том вычисление все же будет относить ее не только не бесконечно далеко, но даже не выше Луны. Отсюда вы поймете, что величину ошибок, так сказать, инструментальных следует оценивать не по результату вычисления, но по количеству тех градусов и минут, которые отсчитываются на инструменте; и те наблюдения должны называться более точными и менее ошибочными, которые путем прибавления или отнятия немногих минут возвращают звезду в возможное место, а среди возможных мест истинное местонахождение, надо думать, будет то, вокруг которого группируется наибольшее число расстояний, вычисленных на основе наиболее точных наблюдений.
Симпличио. — Я не совсем хорошо понимаю, что вы говорите, и сам по себе не могу постигнуть, как это может быть, чтобы при максимальных расстояниях бо́льшая неправильность могла быть порождена ошибкой {217} всего в одну минуту, скорее чем при малых расстояниях ошибкой в 10 или 100 минут, а мне очень хотелось бы разобраться в этом.
Сальвиати. — Если не теоретически, то по крайней мере практически вы увидите это из моей краткой выборки, которую я сделал из всех комбинаций и части изысканий, пропущенных автором; я произвел вычисления и выписал их на одном листе.
Сагредо. — Выходит, значит, что вы со вчерашнего дня и до сих пор, т. е. больше чем 18 часов, только и делали, что вычисляли, не вкушая ни сна, ни пищи.
Сальвиати. — Совсем нет, я подкреплялся и тем и другим, но я делаю такие вычисления очень кратко; по правде говоря, я немало удивлялся, как затягивает дело этот автор, производя подсчеты, совершенно не являющиеся необходимыми для решения поставленного вопроса. Чтобы лучше понять и чтобы сразу можно было увидеть, что на основании наблюдений астрономов, которыми пользуется автор, наиболее вероятным представляется местоположение новой звезды выше Луны и даже выше всех планет, т. е. среди неподвижных звезд, а может быть, даже еще выше, я выписал на этом листе бумаги все наблюдения, приведенные автором, которые были произведены 13 астрономами; здесь отмечены высоты полюса и высоты звезды на меридиане как минимальные под полюсом, так и максимальные над ним; и они таковы8.
ТИХО |
||||||
Высота полюса....... |
55 гр. 58 мин. |
|||||
Высота звезды........ |
84 гр. 0 мин. максимальная |
|||||
27 гр. 57 мин. минимальная |
||||||
Так в первой записи: |
||||||
а во второй......... |
27 гр. 45 мин. минимальная |
|||||
ХАЙНЦЕЛЬ |
||||||
Высота полюса....... |
48 гр. 22 мин. |
|||||
Высота звезды........ |
76 гр. 34 мин. |
|||||
76 гр. 33 мин. 45 сек. |
||||||
76 гр. 35 мин. |
||||||
20 гр. 9 мин. 40 сек. |
||||||
20 гр. 9 мин. 30 сек. |
||||||
20 гр. 9 мин. 20 сек. | ||||||
|
ПЕУКЕР И ШУЛЕР |
ЛАНДГРАФ | |||||
|
Высота полюса....... |
51 гр. 54 мин. |
Высота полюса....... |
51 гр. 18 мин. |
|||
Высота звезды........ |
79 гр. 56 мин. |
Высота звезды........ |
79 гр. 30 мин. |
|||
|
23 гр. 33 мин. |
23 гр. 3 мин. |
|||||
|
КАМЕРАРИЙ |
||||||
Высота полюса....... |
52 гр. 24 мин. |
|||||
Высота звезды........ |
80 гр. 30 мин. |
|||||
80 гр. 27 мин. |
||||||
80 гр. 26 мин. |
||||||
24 гр. 28 мин. |
||||||
24 гр. 20 мин. |
||||||
24 гр. 17 мин. | ||||||
|
ХАЧЕК |
МУНЬОС | |||||
|
Высота полюса....... |
48 гр. 22 мин. |
Высота полюса....... |
39 гр. 30 мин. |
|||
Высота звезды........ |
20 гр. 15 мин. |
Высота звезды........ |
67 гр. 30 мин. |
|||
11 гр. 30 мин. |
||||||
|
||||||
|
ГЕММА |
УРСИН | |||||
|
Высота полюса....... |
50 гр. 50 мин. |
Высота полюса....... |
49 гр. 24 мин. |
|||
Высота звезды........ |
79 гр. 45 мин. |
Высота звезды........ |
79 гр. 0 мин. |
|||
22 гр. 0 мин. |
||||||
|
МАВРОЛИК |
БУШ | |||||
|
Высота полюса....... |
38 гр. 30 мин. |
Высота полюса....... |
51 гр. 10 мин. |
|||
Высота звезды........ |
62 гр. 0 мин. |
Высота звезды........ |
79 гр. 20 мин. |
|||
22 гр. 40 мин. |
||||||
|
РЕЙНГОЛЬД |
||||||
Высота полюса....... |
51 гр. 18 мин. |
|||||
Высота звезды........ |
79 гр. 30 мин. максимальная |
|||||
23 гр. 2 мин. минимальная |
||||||
Теперь, чтобы увидеть весь ход моих мыслей, мы можем начать о тех 5 подсчетов, которые пропущены автором, вероятно, потому, что они против него, так как они помещают звезду на много земных полудиаметров выше Луны. Первый из них выполнен по наблюдениям Ландграфа Гессенского и Тихо, являющихся превосходными наблюдателями даже по признанию автора; на этом первом вычислении я разъясню порядок, какого я придерживаюсь при исследовании; эти сведения пригодятся вам и при всех других вычислениях, поскольку таковые следуют тому же самому правилу, отличаясь только величиной данных, т. е. числом градусов высот полюса и высот звезды над горизонтом; отсюда находится отношение расстояния ее от центра Земли к полудиаметру земного шара; при этом в данном случае совершенно не важно знать, сколько миль в этом расстоянии; поэтому определять его в милях и измерять расстояние между теми местами, где были произведены наблюдения, как делает это автор, значит напрасно терять труд и время; я не знаю, зачем он это делал, тем более что под конец найденные мили он превращает обратно в полудиаметры земного шара.
Симпличио. — Может быть, он это делает для того, чтобы определить такими более мелкими мерами и их частями расстояние звезды с точностью до 4 дюймов; ведь мы, простые смертные, не понимающие ваших арифметических правил, остаемся пораженными выводами, когда читаем, например, следующее: «Итак, комета или новая звезда была удалена от центра Земли на триста семьдесят три тысячи восемьсот семь целых и двести одиннадцать четыре тысячи девяносто седьмых мили (373807211/4097)», и благодаря такой исключительной точности, при которой учитываются даже подобные мелочи, у нас складывается представление, что раз вы учитываете в своих вычислениях даже один дюйм, то вы не можете в конечном счете ошибаться на 100 миль.
Сальвиати. — Это ваше соображение можно было бы принять, если бы при расстоянии в тысячу миль разница на локоть больше или меньше могла иметь какое-либо значение, предпосылки же, принятые нами за истинные, были настолько надежны, что давали бы нам уверенность в том, что мы найдем в конце концов истину; но здесь вы видите из 12 вычислений автора, что получающиеся при этом величины удаленности звезды отличаются друг от друга (и потому уклоняются от истины) на многие сотни и тысячи миль. А раз я более чем уверен, что искомое мною по необходимости должно отличаться от правильного на сотни миль, то зачем мучиться над вычислением с точностью до одного дюйма? Но перейдем, наконец, к действию, которое я произвожу таким образом. {219}
Тихо, как это видно из заметки, наблюдал звезду при высоте полюса в 55 гр. 58 мин. Высота полюса Ландграфа была 51 гр. 18 мин., высота звезды на меридиане, определенная Тихо, была 27 гр. 45 мин. Ландграф нашел ее высоту равной 23 гр. 3 мин. Эти высоты я помещаю здесь рядом, как вы видите:
Тихо: полюс . . . . . . |
55 гр. 58 мин. |
звезда . . . |
27 гр. 45 мин. |
||
Ландграф: полюс . . |
51 гр 18 мин. |
звезда . . . |
23 гр. 3 мин. |
||
Сделав это, я вычитаю меньшее из большего; остается разность |
|||||
4 гр. 40 мин. |
4 гр. 42 мин. |
||||
Параллакс 2 мин. |
|||||
Разность высот полюса, 4 гр. 40 мин., меньше разности высот звезды, 4 гр. 42 мин., и потому разность параллакса равна 2 мин. Найдя это, я беру тот же чертеж автора, на котором точка В — место Ландграфа, D — место Тихо, С — место звезды, А — центр Земли, ABE — вертикальная линия Ландграфа, ADF — Тихо и угол BCD — разность параллакса. И так как угол BAD, заключенный между вертикалями, равен разности высот полюса и составляет 4 гр. 40 мин., то я и отмечаю здесь:

|
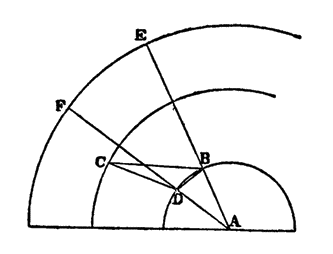 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В таблице дуг и хорд я подыскиваю соответствующую хорду и отмечаю ее рядом; она состоит из 8142 таких частей, 1000000 которых составляют полудиаметр АВ9. Затем я легко нахожу угол BDC, так как половина угла BAD, т. е. 2 гр. 20 мин., прибавленная к прямому углу, даст угол BDF, т. е. 92 гр. 20 мин.; прибавляя к нему угол CDF, т. е. расстояние звезды от вертикали при наибольшей ее высоте, т. е. в данном случае 62 гр. 15 мин., получаем величину угла BDC в 154 гр. 45 мин.; его я отмечаю вместе с его синусом, определенным по таблице; последний равен 42657; под ним я отмечаю угол параллакса BCD, т. е. 2 мин., с его синусом 58; и так как в треугольнике BCD сторона DB относится к стороне ВС так же, как синус противолежащего угла BCD к синусу противолежащего угла BDC, то, следовательно, когда линия BD будет равна 58, ВС окажется равной 42657. И раз хорда DB содержит 8142 таких части, которых в полудиаметре ВА 100000, а мы хотим узнать, сколько таких частей будет в ВС, то скажем по золотому правилу: если хорда BD равна 58, а хорда ВС равна 42657, то какова будет хорда ВС, если хорда BD равна 8142? Для этого я множу вторую величину на третью: у меня получается 347313294; эту величину нужно разделить на первую, т. е. на 58, и частное окажется числом таких частей линий ВС, 100000 которых составляют {220} полудиаметр АВ, а чтобы узнать, сколько полудиаметров ВА содержит та же самая линия ВС, нужно снова разделить то же самое найденное частное на 100000, и мы получим число полудиаметров, заключенных в ВС. Итак, число 347313294, деленное на 58, даст 59881601/4, как это видно здесь:
| 5 | 9 | 8 | 8 | 1 | 6 | 0 | 1/4 | ||||||
| 5 | 8 | 3 | 4 | 7 | 3 | 1 | 3 | 2 | 9 | 4 | |||
| 5 | 7 | 1 | 7 | 9 | 4 | 1 | |||||||
| 5 | 4 | 3 | |||||||||||
Деленное на 100000 оно даст нам 5988160/100000
| 5 | 0 | 0 | 0 | 0 | 0 | 5 | 9 | 8 | 8 | 1 | 6 | 0 | ||||||
Мы можем, однако, значительно сократить действие, деля первое произведение, т. е. 347313294, на произведение от умножения двух чисел 58 и 100000, т. е.
| 5 | 9 | ||||||||||||||||||||
| 5 | 8 | 0 | 0 | 0 | 0 | 0 | 3 | 4 | 7 | 3 | 1 | 3 | 2 | 9 | 4, | ||||||
| 5 | 7 | 1 | |||||||||||||||||||
| 5 | |||||||||||||||||||||
откуда также получается 595113294/5800000.
Столько полудиаметров содержится в линии ВС; прибавляя к ней один для линии АВ, мы получаем немного меньше 61 полудиаметра для двух линий ABC, и потому прямое расстояние от центра А до звезды С будет больше 60 полудиаметров; следовательно, она оказывается выше Луны — по Птоломею больше чем на 27 полудиаметров, а по Копернику — больше чем на 8, если принять вслед за Коперником, что удаленность Луны от центра Земли, как говорит этот автор, равна 52 полудиаметрам.
Таким же путем я нахожу из наблюдений Камерария и Муньоса, что звезда находилась на подобном же удалении, т. е. даже больше 60 полудиаметров10. Вот наблюдение и рядом вычисление:
Высота полюса |
{ | Камерарий: |
52 гр. |
24 мин. |
Высота звезды . . |
{ | 24 гр. |
28 мин. |
|||||
Муньос: |
39 гр. |
30 мин. |
11 гр. |
30 мин. |
|||||||||
Разность высот полюса |
12 гр. |
54 мин. |
Разность высот |
12 гр. |
58 мин. |
||||||||
Разность параллакса 0 гр. 4 мин. и угол BCD |
|||||||||||||
Углы |
{ | BAD |
12 гр. |
54 мин. |
и его хорда |
22466 |
||||||
BDC |
161 гр. |
59 мин. |
} | Синусы |
{ | 30930 |
||||||
BCD |
0 гр. |
4 мин. |
116 |
|||||||||
Золотое правило |
|||||||||||||||||||||||
| 2 | 2 | 4 | 6 | 6 | |||||||||||||||||||
| 1 | 1 | 6 | 3 | 0 | 9 | 3 | 0 | 22466 | |||||||||||||||
| 6 | 7 | 3 | 9 | 8 | 0 | ||||||||||||||||||
| 2 | 0 | 2 | 1 | 9 | 4 | ||||||||||||||||||
| 6 | 7 | 3 | 9 | 8 | |||||||||||||||||||
| 5 | 9 | Расстояние |
BC полудиаметров 59 |
||||||||||||||||||||
почти 60 |
|||||||||||||||||||||||
| 1 | 1 | 6 | 6 | 9 | 4 | 8 | 7 | 3 | 3 | 8 | 0 | ||||||||||||
| 1 | 1 | 4 | 4 | ||||||||||||||||||||
| 1 | 0 | ||||||||||||||||||||||
Следующее вычисление произведено по двум наблюдениям — Тихо и Муньоса; из них получается, что звезда была удалена от центра Земли на 478 полудиаметров и больше.
| {221} |
Высота полюса |
{ | Тихо: |
55 гр. |
58 мин. |
Высота звезды . . |
{ | 84 гр. |
0 мин. |
|||||
Муньос: |
39 гр. |
30 мин. |
67 гр. |
30 мин. |
|||||||||
Разность высот полюса |
16 гр. |
28 мин. |
Разность высот |
16 гр. |
30 мин. |
||||||||
Разность параллакса |
0 гр. |
2 мин. |
|||||||||||
Углы |
{ | BAD |
16 гр. |
28 мин. |
и его хорда |
28640 |
||||||
BDC |
104 гр. |
14 мин. |
} | Синусы |
{ | 96930 |
||||||
BCD |
0 гр. |
2 мин. |
58 |
|||||||||
Золотое правило |
|||||||||||||||||
| 5 | 8 | 9 | 6 | 9 | 3 | 0 | 28640 | ||||||||||
| 2 | 8 | 6 | 4 | 0 | |||||||||||||
| 3 | 8 | 7 | 7 | 2 | 0 | 0 | |||||||||||
| 5 | 8 | 1 | 5 | 8 | |||||||||||||
| 7 | 7 | 5 | 4 | 4 | |||||||||||||
| 1 | 9 | 3 | 8 | 6 | |||||||||||||
| 4 | 7 | 8 | |||||||||||||||
| 5 | 8 | 2 | 7 | 7 | 6 | 0 | 7 | 5 | 2 | 0 | 0 | ||||||
| 4 | 5 | 0 | 6 | ||||||||||||||
| 5 | 3 | ||||||||||||||||
Следующее за этим вычисление дает звезду удаленной от центра больше чем на 358 полудиаметров.
Высота полюса |
{ | Пеукер: |
51 гр. |
54 мин. |
Высота звезды . . |
{ | 79 гр. |
56 мин. |
|||||
Муньос: |
39 гр. |
30 мин. |
67 гр. |
30 мин. |
|||||||||
Разность высот полюса |
12 гр. |
24 мин. |
Разность высот |
12 гр. |
26 мин. |
||||||||
Разность параллакса |
0 гр. |
2 мин. |
|||||||||||
Углы |
{ | BAD |
12 гр. |
24 мин. |
и его хорда |
21600 |
||||||
BDC |
106 гр. |
16 мин. |
} | Синусы |
{ | 95996 |
||||||
BCD |
0 гр. |
2 мин. |
58 |
|||||||||
Золотое правило |
|||||||||||||||||
| 5 | 8 | 9 | 6 | 9 | 3 | 0 | 21600 | ||||||||||
| 2 | 1 | 6 | 0 | 0 | |||||||||||||
| 5 | 7 | 5 | 9 | 7 | 6 | 0 | 0 | ||||||||||
| 9 | 5 | 9 | 9 | 6 | |||||||||||||
| 1 | 9 | 1 | 9 | 9 | 2 | ||||||||||||
| 3 | 5 | 7 | |||||||||||||||
| 5 | 8 | 2 | 0 | 7 | 3 | 5 | 1 | 3 | 6 | 0 | 0 | ||||||
| 3 | 3 | 3 | 9 | ||||||||||||||
| 4 | 2 | ||||||||||||||||
Еще по одному вычислению звезда оказывается удаленной от центра больше чем на 715 полудиаметров11.
Высота полюса |
{ | Ландграф: |
51 гр. |
18 мин. |
Высота звезды . . |
{ | 79 гр. |
30 мин. |
|||||
Хайнцель: |
48 гр. |
22 мин. |
76 гр. |
33 мин. |
45 сек. |
||||||||
Разность высот полюса |
2 гр. |
56 мин. |
Разность высот |
2 гр. |
56 мин. |
15 сек. |
|||||||
Разность параллакса |
0 гр. |
0 мин. |
15 сек. |
||||||||||
Углы |
{ | BAD |
2 гр. |
56 мин. |
и его хорда |
5120 |
||||||||
BDC |
101 гр. |
58 мин. |
} | Синусы |
{ | 97845 |
||||||||
BCD |
0 гр. |
2 мин. |
15 сек. |
7 |
||||||||||
| {222} |
Золотое правило |
|||||||||||||||||||
| 7 | 9 | 7 | 8 | 4 | 5 | 5 | 1 | 2 | 0 | ||||||||||
| 5 | 1 | 2 | 0 | ||||||||||||||||
| 1 | 9 | 5 | 6 | 9 | 0 | 0 | |||||||||||||
| 9 | 7 | 8 | 4 | 5 | |||||||||||||||
| 4 | 8 | 9 | 2 | 2 | 5 | ||||||||||||||
| 7 | 1 | 5 | |||||||||||||||||
| 7 | 5 | 0 | 0 | 9 | 6 | 6 | 4 | 0 | 0 | ||||||||||
| 1 | 3 | 4 | |||||||||||||||||
Таковы, как видите, пять исследований, помещающих звезду значительно выше Луны. Мне хотелось бы, чтобы вы здесь обратили внимание на одну частность, о которой я вам говорил немного раньше, а именно: при больших расстояниях изменение, или, скажем, исправление очень немногих минут отодвигает звезду на громаднейшее пространство; так например, в первом из этих исследований, где вычисление помещает звезду в расстоянии 60 полудиаметров от центра при параллаксе в 2 минуты, желающий утверждать, что она была на небесном своде, должен исправить в наблюдениях только 2 минуты и даже еще меньше, ибо тогда параллакс исчезает или же становится столь малым, что отодвигает звезду на огромное расстояние, которое всеми принимается за удаленность небесного свода. Во втором вычислении поправка меньше чем на 4 минуты приводит к тому же. В третьем и четвертом, так же как и в первом, поправка только в две минуты отодвигает звезду даже выше неподвижных звезд. В последнем четверть минуты, т. е. 15 секунд, дает то же самое. Но не то произойдет с подлунными высотами, потому что, если вы представите себе любое удаление и попробуете исправить изыскания, произведенные автором, и уточнить их так, чтобы все они соответствовали одному и тому же определенному удалению, то вы увидите, насколько большие поправки вам нужно будет для этого сделать.
Сагредо. — Было бы неплохо для нашего полного понимания разобрать какой-нибудь пример того, о чем вы говорите.
Сальвиати. — Установите по своему усмотрению для звезды какое-нибудь определенное удаление, не превышающее, однако, расстояния до Луны, и мы без больших хлопот сможем удостовериться, приведут ли ее в установленное вами место исправления, аналогичные тем, каких, как мы видели, было достаточно, чтобы поместить ее среди неподвижных звезд.
Сагредо. — Чтобы взять наиболее благоприятное для автора расстояние, примем наибольшее из всех разобранных им в его 12 изысканиях; ведь если существует разногласие между астрономами и им и если первые говорят, что звезда была выше Луны, а он, что она ниже, то каждый маленький промежуток, на который, как докажет он, звезда была ниже, принесет ему победу.
Сальвиати. — Итак, возьмем седьмое вычисление, произведенное на основании наблюдений Тихо и Таддеуса Хачек; из них автор находит, что звезда была удалена от центра на 32 полудиаметра; это место для него наиболее благоприятно. Предоставляя ему все преимущества, я хочу, кроме того, чтобы мы приняли самое неблагоприятное для астрономов удаление для звезды, поместив ее даже выше небесного свода. Итак, приняв это, посмотрим, какие направления оказалось бы необходимо сделать в других его 11 изысканиях, чтобы поднять звезду до расстояния 32 полудиаметров12. Начнем с первого исследования, вычисленного по наблюдениям Хайнцеля и Мавролика. Здесь автор находит расстояние от центра примерно в 3 полудиаметра при параллаксе в 4 гр. 42 мин. 30 сек. Посмотрим теперь, поднимется ли звезда до 32 полудиаметров при сведении его только к 20 минутам. Вот подсчет краткий и точный. Я множу синус угла ВВС на хорду BD и делю результат, отняв последние пять знаков, на синус параллакса. {223} Получается 28 с половиной полудиаметров. Таким образом, даже при исправлении на 4 гр. 22 мин. 30 сек., вычтенных из 4 гр. 42 мин. 30 сек., звезда не поднимается до высоты 32 полудиаметров; такое исправление, чтобы было понятно синьору Симпличио, равно 262 с половиной минутам.
Хайнцель: полюс |
48 гр. |
22 |
мин. |
звезда |
76 гр. |
34 мин. |
30 сек. |
|||||||
Мавролик: полюс |
38 гр. |
30 |
мин. |
звезда |
62 гр. |
|||||||||
9 гр. |
52 |
мин. |
14 гр. |
34 мин. |
30 сек. |
|||||||||
9 гр. |
52 мин. |
|||||||||||||
Параллакс . . |
4 гр. |
42 мин. |
30 сек. |
|||||||||||
Углы |
{ | BAD |
9 гр. |
52 мин. |
Хорда |
17200 |
||||||||
BDC |
108 гр. |
21 мин. |
30 сек. |
} | Синусы |
{ | 94910 |
|||||||
BCD |
0 гр. |
20 мин. |
582 |
|||||||||||
Золотое правило |
|||||||||||||||||||
| 9 | 4 | 9 | 1 | 0 | |||||||||||||||
| 1 | 7 | 2 | 0 | 0 | |||||||||||||||
| 1 | 8 | 9 | 8 | 2 | 0 | 0 | 0 | ||||||||||||
| 6 | 6 | 4 | 3 | 7 | |||||||||||||||
| 9 | 4 | 9 | 1 | ||||||||||||||||
| 2 | 8 | ||||||||||||||||||
| 5 | 8 | 2 | 1 | 6 | 3 | 2 | 4 | 5 | 2 | 0 | 0 | 0 | |||||||
| 4 | 6 | 8 | 8 | ||||||||||||||||
| 2 | |||||||||||||||||||
Во втором вычислении, произведенном по наблюдениям Хайнцеля и Шулера, при параллаксе 0 гр. 8 мин. 30 сек. звезда находится на высоте около 25 полудиаметров, как это видно из следующего подсчета13.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если же свести параллакс с 0 гр. 8 мин. 30 сек. к 7 мин., синус чего равен 204, то звезда поднимается приблизительно до 30 полудиаметров; недостаточно, следовательно, исправления на 1 мин. и 30 сек.
| 2 | 9 | ||||||||||||||
| 2 | 0 | 4 | 6 | 0 | 4 | 1 | 8 | 7 | 8 | 4 | 2 | ||||
| 1 | 9 | 6 | 5 | ||||||||||||
| 1 | 2 | ||||||||||||||
Теперь посмотрим, каково должно быть исправление в третьем исследовании, произведенном по наблюдениям Хайнцеля и Тихо, которые помещают звезду на высоте около 19 полудиаметров при параллаксе в 10 мин. Обычные углы, их синусы и хорда, найденные автором, указаны ниже, и они помещают звезду, как и по вычислениям автора, на удалении около 19 полудиаметров.
Значит, чтобы поднять ее, необходимо уменьшить параллакс, согласно правилу, которое и автор применяет в девятом вычислении; для этого положим, что параллакс составляет 6 мин.; синус его 175; произведя деление, находим все же меньше 31 полудиаметра для удаления звезды. Значит, исправления в 4 мин. недостаточно для автора.
| {224} |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Перейдем к четвертому и прочим оставшимся вычислениям, оперируя тем же самым правилом и хордами и синусами, найденными самим автором. В четвертом вычислении параллакс равен 14 мин., а найденная высота составляет меньше 10 полудиаметров; уменьшая параллакс с 14 мин. до 4 мин., вы все же увидите, что звезда не поднимается даже до 31 полудиаметра; значит, недостаточно исправления в 10 мин. при 14 мин.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В пятом примере автора синусы и хорда, как вы видите, таковы14:
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Параллакс равен 0 гр. 42 мин. 30 сек., он определяет высоту звезды примерно в 4 полудиаметра. Если исправить параллакс, сведя его с 42 мин. 30 сек. только к 5 мин., то и этого нехватит, чтобы поднять звезду даже до 28 полудиаметров. Значит, поправка на 37 мин. 30 сек. мала.
В шестом примере хорда, синусы и параллакс таковы:
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Звезда оказывается на высоте около 4 полудиаметров. Посмотрим, где она будет, если уменьшить параллакс с 8 до одной только минуты. По этому подсчету и звезда поднялась только приблизительно до 27 полудиаметров! Значит, недостаточно исправления на 7 мин. при 8 мин.
В восьмом примере хорда, синусы и параллакс, как вы видите, таковы15:
| {225} |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
отсюда автор вычисляет высоту звезды в 11/2 полудиаметра при параллаксе в 43 мин.; если свести его к 1 мин. то все же он даст нам удаленность звезды меньше, чем на 24 полудиаметра; значит, исправления на 42 мин. недостаточно.
Рассмотрим теперь девятый пример. Вот хорда, синусы и параллакс, равный 15 мин. Отсюда автор вычисляет, что удаленность звезды от поверхности Земли была меньше одной сорок седьмой полудиаметра. Но это — ошибка в вычислении, так как на самом деле она, как мы видим здесь рядом, больше одной пятой; получается около 90/436, что больше одной пятой:
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
То, что добавляет потом автор во исправление наблюдений, т. е. что недостаточно уменьшить разность параллакса не только до 1 мин., но даже восьмой части 1 мин., — правильно. Но я говорю, что даже и десятая часть 1 мин. не сведет высоту звезды к 32 полудиаметрам; действительно, синус десятой части 1 мин., т. е. 6 сек., равен 3; если на него по нашему правилу мы разделим 90, или, лучше сказать, если мы разделим 9058672 на 300000, то получим 3058672/100000; или немногим больше 30 с половиной полудиаметров16.
Десятое вычисление даст высоту звезды в одну пятую полудиаметра при таких углах, синусах и параллаксе, равном 4 гр. 30 мин. Я вижу, что сведенный с 4 гр. 30 мин. к 2 мин., он не отодвинет звезду даже до 29 полудиаметров.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Одиннадцатое вычисление дает автору звезду на удалении около 13 полудиаметров при параллаксе в 55 мин. Сведя его к 20 мин., посмотрим, куда поднимется звезда. Вот вычисление: оно повышает ее немного меньше, чем до 33 полудиаметров; итак, исправление составляет немного меньше 35 мин. при параллаксе в 55 мин.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| {226} |
Двенадцатое вычисление при параллаксе в 1 гр. 36 мин. относит звезду на высоту меньше чем 6 полудиаметров; если уменьшить параллакс до 20 мин., то звезда оказывается удаленной меньше, чем на 30 полудиаметров; итак, поправки на 1 гр. 16 мин. недостаточно.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вот поправки параллаксов 10 вычислений автора, которые необходимы, чтобы поместить звезду на высоте 32 полудиаметров. |
|||||||||||||
|
|
4 |
гр. |
22 |
мин. |
30 |
сек. |
при |
4 |
гр. |
42 |
мин. |
30 |
сек. |
|
|
|
|
4 |
» |
— |
|
» |
|
|
10 |
|
— |
|
|
|
|
|
10 |
» |
— |
|
» |
|
|
14 |
|
— |
|
|
|
|
|
37 |
» |
— |
|
» |
|
|
42 |
|
30 |
сек. |
|
|
|
|
7 |
» |
— |
|
» |
|
|
8 |
|
— |
|
|
|
|
|
42 |
» |
— |
|
» |
|
|
43 |
|
— |
|
|
|
|
|
14 |
» |
30 |
сек. |
» |
|
|
15 |
|
— |
|
|
|
4 |
» |
28 |
» |
— |
|
» |
4 |
» |
30 |
|
— |
|
|
|
|
|
35 |
» |
— |
|
» |
|
|
55 |
|
— |
|
|
|
1 |
» |
16 |
» |
— |
|
» |
1 |
» |
36 |
|
— |
|
|
|
|
|
216 |
|
|
|
|
|
|
296 |
|
60 |
|
|
|
|
|
540 |
|
|
|
|
|
|
540 |
|
9 |
|
|
|
|
|
756 |
|
|
|
|
|
|
836 |
|
540 |
|
Отсюда видно, что для того чтобы поднять звезду на высоту 32 полудиаметров, нужно из суммы параллаксов 836 вычесть 756 и свести ее к 80; но даже и этой поправки недостаточно.
Отсюда явствует (как я только что отметил), что если бы автор пожелал установить истинное местоположение новой звезды на расстоянии 32 полудиаметров, то поправка в остальных его 10 исследованиях (я говорю 10, так как второе, помещая звезду чрезвычайно высоко, сводит ее к удалению на 32 полудиаметра при поправке в 2 мин.) для того, чтобы все они поместили звезду на этом расстоянии, потребовала бы такого уменьшения параллаксов, что все вычеты составили бы больше 756 мин.; в то же время в 5 случаях, вычисленных мною, помещающих звезду выше Луны, для исправления их так, чтобы все они помещали ее на небесном своде, достаточно поправки всего на 10 с четвертью минут. Теперь прибавьте к этим исследованиям еще и другие 5, помещающие звезду как раз на небесном своде без необходимости прибегать к каким-либо поправкам. Тогда мы получим 10 исследований, согласно помещающих звезду на небесном своде с исправлением только 5 из них (как вы видели) на 10 с четвертью минут. В то же время для исправления других 10 исследований автора, чтобы отнести звезду на высоту 32 полудиаметров, нужно сделать поправку на 756 мин. при 836 мин., т. е. нужно из суммы 836 вычесть 756, если мы хотим поднять звезду на высоту 32 полудиаметров, но даже и такой поправки недостаточно.
Те 5 исследований, которые непосредственно, без всяких поправок, дают звезду без параллакса и тем самым относят ее на небесный свод и даже в наиболее удаленные его части, словом, помещают ее на высоте самого полюса, суть следующие: {227}
Камерарий |
} |
Высота полюса |
52 гр. 24 мин. |
} |
Высота звезды |
{ |
80 гр. 26 мин. |
0 гр. 30 мин. |
0 гр. 30 мин. |
Ландграф |
} |
Высота полюса |
51 гр. 18 мин. 2 гр. 56 мин. |
} |
Высота звезды |
{ |
79 гр. 30 мин. 2 гр. 56 мин. |
Тихо |
} |
Высота полюса |
55 гр. 58 мин. 4 гр. 4 мин. |
} |
Высота звезды |
{ |
84 гр. 4 гр. 4 мин. |
Рейнгольд |
} |
Высота полюса |
51 гр. 18 мин. 2 гр. 56 мин. |
} |
Высота звезды |
{ |
79 гр. 30 мин. 2 гр. 56 мин. |
Камерарий |
} |
Высота полюса |
52 гр. 24 мин. 4 гр. 2 мин. |
} |
Высота звезды |
{ |
24 гр. 17 мин. 4 гр. 2 мин. |
Вообще среди попарных сочетаний, которые могут быть сделаны из наблюдений всех этих астрономов, те, которые помещают звезду чрезвычайно высоко, гораздо более многочисленны; их примерно на 30 более, чем других, помещающих звезду согласно вычислениям ниже Луны. Как мы уже согласились, можно ожидать со стороны исследователей скорее меньших, чем бо́льших ошибок, и совершенно очевидно, что значительно меньшие поправки требуется внести в наблюдения, дающие для звезды бесконечную высоту, для помещения звезды на небесном своде, чем в подлунной области. Таким образом, все эти изыскания говорят в пользу мнения тех, кто помещает звезду среди неподвижных звезд. Добавьте, что поправки, которые вносятся для подобных исправлений, значительно меньше тех, посредством которых звезда из неправдоподобной близости может быть отнесена на высоту, наиболее благоприятную для этого автора, как мы видели на предыдущих примерах; из них невозможную близость дают 3, так как они отодвигают звезду от центра Земли на расстояние, меньшее одного полудиаметра, заставляя ее вращаться некоторым образом под Землею; это такие комбинации, в которых высота полюса одного из наблюдателей больше высоты полюса другого наблюдателя, высота же звезды определена первым меньшей, чем высота звезды, установленная вторым. Такие комбинации отмечены здесь рядом.
Первая из них — это Ландграф и Гемма; здесь высота полюса у Ландграфа — 51 гр. 18 мин. — больше высоты полюса у Геммы — 50 гр. 50 мин.; но высота звезды у Ландграфа — 79 гр. 30 мин. — меньше высоты звезды у Геммы — 79 гр. 45 мин.
Ландграф |
} |
Высота полюса |
51 гр. 18 мин. |
} |
Высота звезды |
{ |
79 гр. 30 мин. |
Две другие таковы:
Буш |
} |
Высота полюса |
51 гр. 10 мин. |
} |
Высота звезды |
{ |
79 гр. 20 мин. |
Рейнгольд |
} |
Высота полюса |
51 гр. 18 мин. |
} |
Высота звезды |
{ |
79 гр. 30 мин. |
Из того, что я до сих пор вам показал, вы можете понять, насколько этот первый способ определения удаленности звезды и доказательства ее нахождения ниже Луны, применяемый автором, не благоприятствует его цели и насколько более вероятным представляется, что звезда находилась на расстоянии самых далеких неподвижных звезд. {228}
Симпличио. — Пока что, мне кажется, с совершенной очевидностью раскрыта несостоятельность доводов автора; но я вижу, что все это изложено на немногих страницах книги; другие его соображения, может быть, более доказательны, чем первые.
Сальвиати. — Напротив, они могут быть только еще менее убедительными, если считать, что первые являются примером для остающихся; совершенно ясно, что недостоверность и слабая убедительность их (как мы хорошо это понимаем) происходят от ошибок, вкравшихся в наблюдения при посредстве инструментов; считалось, что высоты полюса и звезды были определены точно, тогда как на самом деле все эти определения легко могли быть ошибочными, хотя для определения высоты полюса астрономы располагали столетиями, чтобы заниматься этим на свободе; высоты же звезды при прохождении через меридиан наиболее удобны для наблюдения, так как они вполне отчетливы и допускают некоторую свободу для наблюдателя, в смысле продолжительности наблюдения, благодаря менее ощутимым изменениям за очень короткий промежуток времени, чем то бывает со звездами, удаленными от меридиана. Но если это так, — а это самая подлинная истина, — то как можем мы верить вычислениям, основанным на более многочисленных и более трудных для выполнения наблюдениях над предметами, более быстро изменяющимися, вдобавок при применении инструментов, более неудобных и менее точных? Из беглого просмотра я увидел, что последующие доказательства построены на определении высот звезды, взятых в разных вертикальных кругах, называемых арабским словом азимуты; при этих наблюдениях применяются инструменты, способные перемещаться не только в вертикальной плоскости, но в то же самое время и в горизонтальной; нужно в тот же самый момент, когда определяется высота над горизонтом, наблюдать и расстояние от меридиана того вертикального круга, на котором находится звезда. Кроме того, через определенный промежуток времени нужно повторить это наблюдение и тщательно учесть протекшее время, полагаясь на часы или другие наблюдения над звездами. Такая группа наблюдений сопоставляется потом с другой такой же группой, полученной другим наблюдателем, в другой стране, другими инструментами и в другое время, и из этого автор пытается извлечь познание того, каковы были высоты и горизонтальные широты звезды во время и час других — первых — наблюдений; на созданном таким образом основании он проделывает напоследок свои вычисления. Теперь я предоставляю судить вам самим, насколько можно доверять тому, что получается из подобных сопоставлений. Кроме того, я ничуть не сомневаюсь, что если бы кто-нибудь захотел потрудиться над такими длиннейшими вычислениями, то нашлось бы, как и раньше, больше таких, которые благоприятствуют противной стороне, а не автору; но мне кажется, не стоило браться за подобный труд ради того, что не составляет самого главного в интересующем нас вопросе.
Сагредо. — В этом я с вами согласен, однако, если подобное предприятие окружено такой путаницей, недостоверностью и ошибками, то на основании чего столь многие астрономы решительно провозгласили, что новая звезда находилась чрезвычайно высоко?
Сальвиати. — На основании двоякого рода наблюдений, чрезвычайно простых, чрезвычайно легких и совершенно истинных; одного из них вполне достаточно, чтобы убедить нас в том, что звезда помещалась на небесном своде или по крайней мере гораздо выше Луны. Одно заключается в равенстве или весьма малой разнице ее удаленности от полюса как тогда, когда она находилась в нижней части меридиана, так и тогда, когда она была в верхней его части. Другое — это то, что она постоянно сохраняла одинаковые расстояния от некоторых неподвижных {229} звезд, к ней близких, в частности от одиннадцатой звезды Кассиопеи, удаленной от нее не больше, чем на полтора градуса17; из этих двух главных положений с несомненностью вытекает или абсолютное отсутствие параллакса, или такая его незначительность, которая убеждает нас после чрезвычайно быстро выполняемых вычислений в ее огромной удаленности от Земли.
Сагредо. — Но разве это не было принято во внимание автором? А если он это видел, то как он от этого оборонялся?
Сальвиати. — Когда кто-нибудь, не находя лучших отговорок, способных покрыть его промахи, приносит легкомысленные извинения,
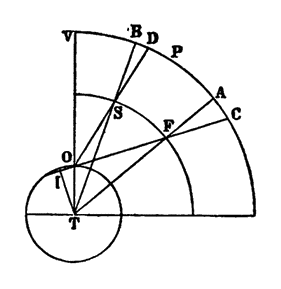 мы обычно говорим, что он пытается ухватиться за веревку с неба; но этот автор прибегает даже не к веревкам, а к паутинкам с неба. Вы ясно увидите это, если рассмотрите два обстоятельства, которые я сейчас вам укажу. Прежде всего, то, что нам показывают полярные расстояния каждого из наблюдателей, я отметил здесь в этих кратких вычислениях; для полного понимания их я прежде всего должен заметить вам, что каждый раз, как новая звезда или иное небесное явление будет близко к Земле, вращаясь суточным движением вокруг полюса, оно покажется более отдаленным от него тогда, когда оно находится в нижней части меридиана, чем когда оно находится в верхней его части, как это видно на следующем чертеже: здесь точка Т обозначает центр Земли, О — место наблюдателя, дуга VPC — небесный свод, Р — полюс. Явление, двигаясь по кругу FS, видно то под полюсом по лучу OFC, то над ним по лучу OSD, так что места, видимые на небесном своде, будут D и С. Но истинные места, по отношению к центру T, — это А и B, равноудаленные от полюса; отсюда уже ясно, что видимое место небесного явления S, т. е. точка D, ближе к полюсу, чем другое видимое место С, наблюдаемое по лучу OFC; это нужно заметить прежде всего. Во-вторых, вам следует заметить, что превышение нижнего видимого расстояния от полюса над верхним видимым расстоянием также от полюса больше, чем нижний параллакс явления; другими словами, превышение дуги СР (нижнего видимого расстояния) над дугой PD (верхним видимым расстоянием) больше, чем дуга СА (нижний параллакс). Это легко доказывается: ведь дуга СР превышает PD на большую величину, чем РВ, так как РВ больше PD; но РВ равно РА, и превышение СР над РА составляет дугу СА следовательно, превышение дуги СР над дугой PD больше дуги СА, т. е. больше параллакса небесного явления, находящегося в F; это и требовалось доказать.
мы обычно говорим, что он пытается ухватиться за веревку с неба; но этот автор прибегает даже не к веревкам, а к паутинкам с неба. Вы ясно увидите это, если рассмотрите два обстоятельства, которые я сейчас вам укажу. Прежде всего, то, что нам показывают полярные расстояния каждого из наблюдателей, я отметил здесь в этих кратких вычислениях; для полного понимания их я прежде всего должен заметить вам, что каждый раз, как новая звезда или иное небесное явление будет близко к Земле, вращаясь суточным движением вокруг полюса, оно покажется более отдаленным от него тогда, когда оно находится в нижней части меридиана, чем когда оно находится в верхней его части, как это видно на следующем чертеже: здесь точка Т обозначает центр Земли, О — место наблюдателя, дуга VPC — небесный свод, Р — полюс. Явление, двигаясь по кругу FS, видно то под полюсом по лучу OFC, то над ним по лучу OSD, так что места, видимые на небесном своде, будут D и С. Но истинные места, по отношению к центру T, — это А и B, равноудаленные от полюса; отсюда уже ясно, что видимое место небесного явления S, т. е. точка D, ближе к полюсу, чем другое видимое место С, наблюдаемое по лучу OFC; это нужно заметить прежде всего. Во-вторых, вам следует заметить, что превышение нижнего видимого расстояния от полюса над верхним видимым расстоянием также от полюса больше, чем нижний параллакс явления; другими словами, превышение дуги СР (нижнего видимого расстояния) над дугой PD (верхним видимым расстоянием) больше, чем дуга СА (нижний параллакс). Это легко доказывается: ведь дуга СР превышает PD на большую величину, чем РВ, так как РВ больше PD; но РВ равно РА, и превышение СР над РА составляет дугу СА следовательно, превышение дуги СР над дугой PD больше дуги СА, т. е. больше параллакса небесного явления, находящегося в F; это и требовалось доказать.
Чтобы предоставить теперь все преимущества автору, предположим, что параллакс звезды в F составляет все превышение дуги СР (т. е. нижнего расстояния от полюса) над дугой PD (верхним расстоянием). Отсюда я перехожу к изучению того, что нам дают наблюдения всех астрономов, приведенных автором; среди них нет ни одного, которое было бы в его пользу и которое не противоречило бы его намерению18. Начнем с наблюдений Буша; он нашел, что верхнее расстояние звезды от полюса равно 28 гр. 10 мин., а нижнее — 28 гр. 30 мин., так что превышение составляет 0 гр. 20 мин.; примем (в пользу автора), что все оно составляет параллакс звезды в F, т. е. угол TFO; расстояние от вертикали, т. е. дуга CV, составляет 67 гр. 20 мин. Найдя две эти величины, продолжим линию СО, опустим на нее перпендикуляр TI и рассмотрим треугольник TOI: в нем угол I — прямой, угол IOТ известен, так как он равен углу VOC, т. е. расстоянию звезды от вертикали; кроме того, в треугольнике TIF, также прямоугольном, известен угол F, принятый за параллакс. Итак, пометим в стороне величины углов IOТ и IFT и по ним определим синусы, {230} которые, как вы видите, здесь и отмечены19. И так как в треугольнике IOТ весь синус ТО состоит из 100000 таких частей, каких синус TI содержит 92276, а в треугольнике IFT синус TF состоит из 100000 таких частей, каких в синусе TI содержится 582, то чтобы найти, сколько в TF будет таких частей, каких в ТО содержится 100000, скажем, по золотому правилу: если TI равно 582, то TF равно 100000; но если TI равно 92276, то каково будет TF? Множим 92276 на 100000 и получаем 9227600000; это число нужно разделить на 582; получим, как это видно, 15854982; в TF будет, следовательно, именно столько таких частей, каких в ТО содержится 100000. Теперь, чтобы узнать, сколько отрезков ТО содержится в TF, разделим 15854982 на 100000; получим приблизительно 158 с половиной; столько именно полудиаметров составляет расстояние звезды F от центра Т. А чтобы сократить действие, поскольку произведение от умножения 92276 на 100000 нам нужно было делить сначала на 582, а потом частное на 100000, мы можем, не умножая 92276 на 100000, одним лишь делением синуса 92276 на синус 582 быстро получить то же самое, как это видно здесь ниже, где 92276, деленное на 582, даст нам то же самое — приблизительно 158 с половиной. Запомним, следовательно, что одно только деление синуса ТI, как синуса угла TOI, на синус ТI, как синус угла IFT, дает нам искомое расстояние TF в полудиаметрах ТО.
Углы |
{ | IOT |
67 гр. |
20 мин. |
} | Синусы |
{ | 92276 |
15854982 |
||
IFT |
0 гр. |
20 мин. |
582 |
582 |
9227600000 |
||||||
3407002246 |
|||||||||||
TI |
TF |
TI |
TF |
49297867 |
|||||||
582 |
100000 |
92276 |
0 |
325414 |
|||||||
|
100000 |
158 |
54982 |
|||||||||
158 |
|||||||||||
|
582 |
92276 |
||||||||||
34070 |
|||||||||||
492 |
|||||||||||
3 |
|||||||||||
Посмотрим теперь, что нам дают наблюдения Пеукера. У него нижнее расстояние от полюса равно 28 гр. 21 мин., верхнее — 28 гр. 2 мин. разность — 0 гр. 19 мин., расстояние от вертикали — 66 гр. 27 мин.; из этих данных легко получается, что расстояние звезды от центра равно почти 166 полудиаметрам.
Углы |
{ | IAC 66 гр. 27 мин. |
} | Синусы |
{ | 91672 |
165 |
427/553 |
|
IEC 0 гр. 19 мин. |
553 |
91672 |
|||||||
|
553 |
36397 |
||||||||
312 |
|||||||||
4 |
Вот, что нам показывают наблюдения Тихо, если мы даже примем данные, наиболее благоприятные для противников; нижнее расстояние от полюса 28 гр. 13 мин., верхнее 28 гр. 2 мин., и разность в 0 гр. 11 мин. целиком принимается за параллакс; расстояние от вертикали 62 гр. 15 мин. Здесь ниже приведено вычисление, и найденное расстояние звезды от центра составляет 2769/16 полудиаметра:
Углы |
{ | IAC 62 гр. 15 мин. |
} | Синусы |
{ | 88500 |
276 |
9/16 |
|
IEC 0 гр. 11 мин. |
320 |
320 |
88500 |
||||||
2418 |
|||||||||
21 |
|||||||||
Следующее за этим наблюдение Рейнгольда даст нам расстояние звезды от центра в 793 полудиаметра.
Углы |
{ | IAC 66 гр. 58 мин. |
} | Синусы |
{ | 92012 |
793 |
38/116 |
|
IEC 0 гр. 4 мин. |
116 |
92026 |
|||||||
|
116 |
10888 |
||||||||
33 |
|||||||||
| {231} |
Из следующих наблюдений Ландграфа расстояние звезды от центра исчисляется в 1057 полудиаметров.
Углы |
{ | IAC 66 гр. 57 мин. |
} | Синусы |
{ | 92012 |
1057 |
53/87 |
|
IEC 0 гр. 3 мин. |
87 |
87 |
92012 |
||||||
5663 |
|||||||||
5 |
|||||||||
Взяв у Камерария два из его наблюдений, наиболее благоприятных для автора, находим удаленность звезды от центра в 3143 полудиаметра.
Углы |
{ | IAC 65 гр. 43 мин. |
} | Синусы |
{ | 91152 |
3143 |
||
IEC 0 гр. 1 мин. |
29 |
29 |
91152 |
||||||
4295 |
|||||||||
1 |
|||||||||
Наблюдение Муньоса не дает параллакса и потому относит новую звезду к самым высоким неподвижным звездам. Наблюдение Хайнцеля указывает на ее бесконечную удаленность, но при исправлении на полминуты помещает ее среди неподвижных звезд; то же самое получается у Урсина при поправке в 12 мин. У других астрономов нет верхнего и нижнего расстояний от полюса, и потому из их наблюдений ничего нельзя извлечь.
Теперь вы видите, как все наблюдения всех астрономов, вопреки автору, согласно помещают звезду в областях небесных и чрезвычайно высоких.
Сагредо. — Но чем защищается он против столь противоречащих ему показаний?
Сальвиати. — Как я уже говорил, он хватается за нить паутины, утверждая, что параллаксы уменьшаются благодаря рефракции: она, действуя в противоположном направлении, поднимает наблюдаемое тело там, где параллаксы его понижают20. Теперь судите, какова ценность этого жалкого прибежища: действие рефракции, если считать эффект ее таким, как принимали его в последнее время некоторые астрономы, вызывает видимое повышение небесного явления над горизонтом, если оно находится уже на высоте 23 или 24 градусов, самое большее настолько, что уменьшает параллакс примерно на 3 минуты; такое изменение слишком недостаточно, чтобы помещать звезду ниже Луны, и в некоторых случаях меньше излишка, вытекающего из допущения нами того, что превышение нижнего расстояния от полюса над верхним составляет весь параллакс; такой излишек — вещь много более ясная и ощутимая, чем эффект рефракции, в величине которого я не без основания сомневаюсь. Кроме того, я спрашиваю этого автора, думает ли он, что те астрономы, наблюдениями которых он пользуется, имели представление об этом эффекте рефракции и учитывали его или же нет; если они его знали и учитывали, то, нужно думать, они приняли его во внимание при определении истинной высоты звезды, внося в те градусы высоты, которые отмечаются при пользовании инструментами, соответствующие поправки на рефракцию, так что определенные ими расстояния оказываются правильными и точными, а не видимыми и ложными. Если же он думает, что такие авторы не задумывались над рефракцией, то, нужно признать, все они одинаково ошибались в определении всех тех вещей, которые не могут быть в совершенстве установлены, без учета изменений в силу рефракции; одна из таких вещей — это точное установление высот полюса, которые обычно определяются из двух меридианных высот какой-нибудь незаходящей неподвижной звезды; эти высоты изменяются рефракцией совершенно так же, как высоты новой звезды; таким образом высота полюса, которая из них выводится, оказывается ошибочной и причастной {232} тому же самому недостатку, который этот автор приписывает высотам, установленным для новой звезды, т. е. и высота полюса, и высота новой звезды, благодаря одинаковым ошибкам, оказываются выше, чем в действительности. Но такая ошибка, поскольку она относится к разбираемому нами теперь вопросу, вовсе не вредит, ибо раз нам нужно знать только разность между двумя расстояниями новой звезды от полюса, — когда она ниже и когда выше его, — то ясно, что такие расстояния будут теми же самыми, оставим ли мы искажение, вносимое рефракцией, общее для звезды и для полюса, или же внесем поправки, одинаковые в обоих случаях. Некоторую силу, хотя и чрезвычайно слабую, имел бы аргумент автора, если бы он доказал нам, что высота полюса была установлена точно и освобождена от ошибок, связанных с рефракцией, но этого не было сделано теми же самыми астрономами при установлении высоты новой звезды; однако, он не ручается нам за это, может быть, потому, что не может этого сделать, а может быть, потому (и это более вероятно), что такая предосторожность не была принята наблюдателями.
Сагредо. — Мне кажется, что это положение целиком уничтожено; поэтому скажите мне, как же он справляется с тем, что новая звезда всегда сохраняла одно и то же расстояние от окружающих ее неподвижных звезд?
Сальвиати. — Попросту хватаясь за две нити, еще более слабые. Одна из них также связана с рефракцией, но еще менее прочна, поскольку он говорит, что рефракция, воздействуя на видимость новой звезды и поднимая ее выше ее настоящего места, делает недостоверным расстояние, принимаемое за истинное, по отношению к соседним с нею неподвижным звездам. Я не могу в достаточной мере надивиться, как он притворяется невидящим, что та же самая рефракция будет воздействовать одинаково как на новую звезду, так и на соседнюю старую, одинаково поднимая их обе, так что от этого обстоятельства расстояние между ними не изменится. Другое прибежище еще менее удачно и просто смехотворно; оно заключается в ссылке на ошибку, которая может возникнуть при пользовании инструментами21, так как наблюдатель не может установить центр зрачка в центре секстанта (инструмента, употребляемого при наблюдении расстояний между двумя звездами) и вынужден держать его выше этого центра на расстоянии зрачка от скулы, к которой прикладывается головка инструмента, то угол с вершиной в зрачке оказывается более острым, чем тот, который образован сторонами секстанта. Но ведь этот угол зрительных лучей меняется и сам по себе, если рассматривать сперва звезды, мало возвышающиеся над горизонтом, а затем их же, когда они поднялись на значительную высоту. Этот угол меняется, говорит он, если поднимать инструмент и держать голову неподвижной; если же при поднимании секстанта сгибать шею назад и откидывать голову вместе с инструментом, то угол сохранится тем же самым. Итак, возражение автора основано на предположении, что при употреблении инструмента наблюдатели поднимали голову не так, как это было нужно, что является вещью невероятной. Но предположив даже, что это было так, я предоставляю вам судить, какова может быть разность между двумя острыми углами двух равнобедренных треугольников, если стороны одного из них будут длиною в четыре локтя каждая, а стороны другого меньше четырех локтей на диаметр хрусталика; больше во всяком случае не может быть разница между длиной двух зрительных лучей, если в одном случае линия опускается перпендикулярно из центра зрачка на плоскость оси секстанта (длина этой линии не превышает толщины большого пальца), и длиною тех же лучей, если в другом случае при поднимании секстанта не поднимать одновременно с ним головы, так что такая линия больше не будет перпендикулярна к этой плоскости, но отклонится в сторону {233} образуя с ней острый угол. Чтобы совершенно покончить с этими злосчастными и жалкими попытками автора, скажу следующее: пусть он знает (ибо, как видно, он не очень опытен в употреблении астрономических инструментов), что по сторонам секстанта или квадранта устраиваются два визира — один в центре, другой — на противоположном конце; они отстоят на дюйм или больше от плоскости, и через верхние края таких визиров должен проходить луч зрения. Глаз также держится на расстоянии пяди или двух или еще дальше от инструмента, так что ни зрачок, ни скула, ни вся особа астронома не касается инструмента и не опирается на него; тем менее этот инструмент поддерживается или поднимается руками, в особенности, если это один из тех обычных больших инструментов, которые весят десятки, сотни или даже тысячи фунтов и устанавливаются на чрезвычайно солидных фундаментах. Таким образом, все построение рассыпается. Таковы доводы этого автора. И если бы даже они были столь же несокрушимы, как сталь, они не могли бы принести ему подъема и на одну сотую часть минуты, а он думает, будто убедил нас в том, что ими он скомпенсировал ту разность, которая составляет сто и больше минут. Я говорю, что не наблюдалось заметного различия в расстояниях между какой-либо неподвижной звездой и новой звездой за все время их суточного обращения, а если бы звезда находилась примерно на расстоянии Луны, то различие должно было бы быть очень заметным даже для простого глава, без какого бы то ни было инструмента, в особенности при сопоставлении ее с одиннадцатой звездой Кассиопеи, удаленной всего на полтора градуса; различие в расстоянии должно было бы меняться больше, чем на два лунных диаметра, как это было отмечено наиболее знающими астрономами того времени.
Сагредо. — Мне кажется, что я вижу несчастного земледельца, который после того как буря повалила и уничтожила весь его долгожданный урожай, идет с понурым лицом, собирая по зернышку ничтожные остатки, которых ему нехватит даже на прокормление цыпленка в течение одного единственного дня.
Сальвиати. — Действительно, слишком плохо вооруженным поднялся этот автор против тех, кто оспаривает неизменность неба, и слишком слабыми цепями пытался он совлечь новую звезду в созвездии Кассиопеи с самых высоких областей в низкие области стихий. Теперь, после того как, мне кажется, очень ясно была показана огромная разница между аргументами астрономов и этого их противника, хорошо было бы вернуться к нашей основной теме. Здесь нам следует обсудить годовое движение, которое обычно приписывается Солнцу, но которое сначала Аристарх Самосский, а затем Коперник отнимают у Солнца и переносят на Землю. Против такого положения, я чувствую, будет доблестно выступать синьор Симпличио, вооруженный мечом и щитом из книжки заключений или математических исследований; хорошо было бы начать с этих возражений.
Симпличио. — Я предпочел бы с вашего позволения сохранить их напоследок, так как и открыты они были последними.
Сальвиати. — Итак, соответственно применявшемуся до сих пор методу вам следует по порядку изложить соображения в пользу противоположного мнения как Аристотеля, так и других древних; то же самое сделаю и я, чтобы ничто не было оставлено без внимания и без обсуждения. Равным образом и синьор Сагредо со всей живостью своего ума будет делиться с нами теми мыслями, которые в течение нашей беседы могут притти ему в голову.
Сагредо. — Я сделаю это со своей обычной откровенностью, и вы обязаны будете извинить ее, раз я следую вашему предложению.
Сальвиати. — Не извинение требуется с нашей стороны, а благодарность. Пусть же синьор Симпличио начнет теперь излагать те трудности, {234} которые препятствуют ему признать, что Земля, подобно другим планетам, может обращаться вокруг неподвижного центра.
Симпличио. — Первая и самая большая трудность — это противоречие и несовместимость между нахождением в центре и нахождением в отдалении от него; ведь если земной шар должен двигаться в течение одного года по окружности круга, именно под зодиаком, то невозможно, чтобы в то же самое время он находился в центре зодиака, а что Земля находится в этом центре, было доказано многими способами Аристотелем, Птоломеем и другими.
Сальвиати. — Вы рассуждаете очень хорошо, и нет никакого сомнения, что тому, кто хочет заставить Землю двигаться по окружности некоего круга, нужно сначала доказать, что она не находится в центре этого круга. Следовательно, теперь нам нужно посмотреть, находится или не находится Земля в том центре, вокруг которого, говорю я, она вращается и в котором, говорите вы, она находится; но прежде мы должны еще уяснить себе, одно ли и то же представление имеется об этом центре у вас и у меня или же нет. Поэтому скажите мне, каков этот разумеемый вами центр и где он находится?
Симпличио. — Под центром я разумею центр вселенной, центр мира, центр звездной сферы, центр неба.
Сальвиати. — Хотя я и мог бы на вполне разумных основаниях
|
До сих пор никем не доказано, конечен ли мир или бесконечен. |
Симпличио. — Аристотель приводит сотню доказательств того, что мир конечен, ограничен и сферичен.
Сальвиати. — Но все его доказательства сводятся к одному единственному, а это одно единственное обращается в ничто; ведь если я буду
|
Доказательства Аристотеля, приводимые в пользу конечности вселенной, все отпадают, если отрицать ее подвижность. |
|
Аристотель делает центром вселенной ту точку, вокруг которой вращаются все небесные сферы. Спрашивается, какую из двух предпосылок, противоречащих учению Аристотеля, он предпочел бы, если бы был вынужден выбрать одну. |
Симпличио. — Думаю, что если бы произошел такой случай, то перипатетики...
Сальвиати. — Я спрашиваю не о перипатетиках, я спрашиваю о самом Аристотеле; о них-то я прекрасно знаю, что они ответили бы. Они, как почтительнейшие и смиреннейшие слуги Аристотеля, стали бы отрицать все опыты и наблюдения в мире, отказывались бы даже посмотреть их, чтобы не оказаться вынужденными их признать, и сказали бы, что мир устроен так, как пишет Аристотель, а не так, как хочет природа; ведь, если отнять у них поддержку такого авторитета, то с чем появятся {235} они на поле сражения? А потому скажите мне, что, по вашему мнению, сделал бы сам Аристотель?
Симпличио. — Право, я не знаю, какую из двух несообразностей он счел бы меньшей.
Сальвиати. — Не пользуйтесь, пожалуйста, этим термином и не называйте несообразностью то, что должно быть по необходимости. Несообразностью было бы стремление помещать Землю в центре небесных обращений. Но раз вы не знаете, в какую сторону склонился бы Аристотель, то, считая его за человека великого ума, посмотрим, какой выбор из двух предпосылок является наиболее разумным, и будем считать его за сделанный Аристотелем. Итак, начнем опять наше рассуждение сначала и примем ради Аристотеля, что мир (о величине которого, кроме неподвижных звезд, у нас нет никаких доступных чувству показаний) есть нечто такое, что имеет сферическую форму и движется кругообразно и по необходимости имеет, — принимая во внимание форму и движение, — центр; а так как, кроме того, мы достоверно знаем, что внутри звездной сферы существует много орбит, одна внутри другой, с соответствующими звездами, которые также движутся кругообразно, то спрашивается, чему более разумно верить и что более разумно утверждать: то ли, что эти внутренние орбиты движутся вокруг одного и того же мирового центра, или же что они движутся вокруг другого, очень далекого от первого? Скажите теперь, синьор Симпличио, каково ваше мнение на этот счет?
Симпличио. — Если бы мы могли остановиться на этом одном
|
Объемлющему и объемлемому более подходит вращаться вокруг одного и того же центра, нежели вокруг разных. |
Сальвиати. — Значит, если правильно, что центром мира является точка, вокруг которой движутся орбиты небесных тел, т. е. планет, то гораздо более правдоподобно, что не Земля, а Солнце находится в центре
|
Если центр вселенной совпадает с точкой, вокруг которой движутся планеты, то в нем находится Солнце, а не Земля. |
Симпличио. — Но из чего вы заключаете, что не Земля, а Солнце находится в центре обращения планет?
Сальвиати. — Это следует из очевиднейших и потому неизбежно доказательных наблюдений. Наиболее убедительным для удаления Земли
|
Наблюдения, из которых можно заключить, что Солнце, а не Земля расположено в центре небесных обращений. |
Симпличио. — Но каковы признаки того, что движения их совершаются вокруг Солнца?
Сальвиати. — Относительно трех верхних планет — Марса, Юпитера и Сатурна — это доказывается тем, что они особенно близки к Земле, когда находятся в противостоянии с Солнцем, и особенно далеки, когда находятся в соединении; это приближение и удаление настолько значительны, что Марс вблизи виден в 60 раз большим, чем когда он очень далек. Что Венера и Меркурий обращаются вокруг Солнца, убеждает нас то,
|
Смена фаз Венеры доказывает движение ее вокруг Солнца. Луна не может отделиться от Земли. |
Сагредо. — Как видно, в связи с годовым движением Земли мне придется выслушать вещи, гораздо более удивительные, чем в связи с суточным движением.
Сальвиати. — Вы нисколько не ошибаетесь; ведь в отношении суточного движения небесных тел не существует и не может быть наблюдаемо ничего другого, кроме того, что заставляет весь мир казаться движущимся
|
Годичное движение Земли в соединении с движением других планет вызывает удивительные явления. |
Симпличио. — Я еще не очень хорошо уразумел эту структуру; может быть, при помощи маленького чертежа она станет понятнее и о ней можно будет легче говорить.
Сальвиати. — Пусть будет так; для большего вашего удовлетворения
|
Схема устройства мира на основании явлений. |
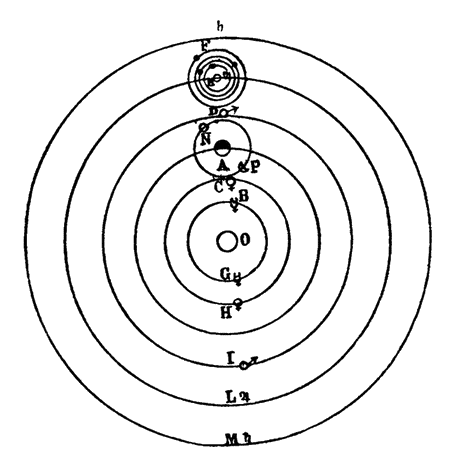 что вы прекрасно понимаете эту структуру, хотя и думаете, что не поняли; только чертите аккуратно в соответствии с ответами на мои вопросы.
что вы прекрасно понимаете эту структуру, хотя и думаете, что не поняли; только чертите аккуратно в соответствии с ответами на мои вопросы.
Итак, возьмите бумагу и циркуль; пусть этот белый лист будет огромным пространством вселенной, на котором вы должны расположить и привести в порядок части вселенной так, как это вам продиктует разум. Прежде всего, раз вы и без моего поучения считаете, что Земля находится в этой вселенной, то отметьте по своему усмотрению точку, в которой, как вы полагаете, она помещается, и обозначьте ее какой-нибудь буквой.
Симпличио. — Пусть А обозначает место земного шара.
Сальвиати. — Хорошо. Во-вторых, как мне известно, вы прекрасно знаете, что Земля находится не внутри солнечного тела и даже не соприкасается с ним, но отстоит от него на некотором расстоянии; поэтому отметьте Солнце в каком-либо другом месте, какое вам больше понравится, удаленном от Земли по вашему усмотрению, и обозначьте также и его.
Симпличио. — Сделано. Пусть место солнечного тела будет обозначено через О.
Сальвиати. — Установив эти два места, нам нужно подумать, как бы поместить тело Венеры таким образом, чтобы положение и движение ее могли удовлетворить тому, что нам показывают воспринимаемые чувствами явления. Поэтому, основываясь на прежних беседах или же на ваших собственных наблюдениях, припомните, что происходит о данной звездой, а потом обозначьте то положение, какое вам покажется подобающим ей.
Симпличио. — Если признать истинными описанные вами явления, о которых я читал также в книжке заключений, а именно, что эта звезда {237} никогда не удаляется от Солнца больше, чем на некоторый определенный промежуток, примерно в 40 градусов, так что она никогда не оказывается не только в противостоянии с Солнцем, но и в квадратурах и даже под углом в 60 градусов; далее, если правильно, что она представляется в определенное
|
Венера кажется наибольшей во время вечернего и наименьшей во время утреннего соединения с Солнцем. Убедительное доказательство того, что Венера обращается вокруг Солнца. |
Сальвиати. — Поместив Венеру, хорошо было бы вам подумать о Меркурии, который, как вы знаете, всегда держится близко к Солнцу, удаляясь от него еще меньше Венеры; поэтому размыслите, какое место назначить ему.
Симпличио. — Несомненно, что раз он подражает Венере, то самым
|
Доказательство того, что обращение Меркурия вокруг Солнца происходит внутри орбиты Венеры. |
Сальвиати. — А куда мы поместим Марс?
Симпличио. — Поскольку Марс бывает в противостоянии с Солнцем,
|
Марс необходимо включает в свою орбиту и Землю, и Солнце. |
|
Марс в противостоянии с Солнцем кажется в 60 раз большим, чем в соединении. |
|
Юпитер и Сатурн также охватывают Землю и Солнце. Приближение и удаление трех верхних планет на двойное расстояние до Солнца. Различие в видимой величине у Сатурна меньше, чем у Юпитера, а у Юпитера меньше, чем у Марса, и причины этому. Орбита Луны обнимает Землю, но не Солнце. |
Сальвиати. — До сих пор вы поступали отлично. И раз (как вы видите) приближение и удаление трех верхних планет различаются на двойное расстояние от Земли до Солнца, то это вызывает бо́льшие отклонения {238} у Марса, чем у Юпитера, поскольку круг DI Марса меньше круга EL Юпитера; равным образом, поскольку круг EL Юпитера меньше круга FM Сатурна, то же самое отклонение еще меньше у Сатурна, чем у Юпитера, и это в точности согласуется с явлениями. Остается теперь подумать где отметить место Луны?
Симпличио. — Следую тому же методу, который мне кажется чрезвычайно убедительным; раз Луна бывает в соединении и в противостоянии с Солнцем, то необходимо сказать, что круг ее обнимает Землю; но нет необходимости, чтобы он обнимал также и Солнце, так как тогда при соединении она представлялась бы не серпообразной, а всегда круглой и полностью освещенной: кроме того, иначе она не могла бы, как это часто случается, вызывать солнечных затмений, становясь между Солнцем и нами. Значит, необходимо отвести ей круг около Земли; пусть это будет круг NP, так что, находясь в Р Луна кажется Земле А соединенной с Солнцем и потому иногда может затмевать его, а находясь в N, видна в противостоянии с Солнцем и в этом положении может попасть в тень Земли и сама затмиться.
Сальвиати. — Что же мы теперь сделаем, синьор Симпличио, с неподвижными звездами? Рассеем ли мы их по огромным безднам вселенной на разных удалениях от какой-нибудь определенной точки или же соберем их на одной поверхности, сферически расположенной вокруг своего центра так, что каждая из них будет равно отстоять от одного и того же центра?
Симпличио. — Скорее я выбрал бы средний путь и отвел бы им сферу
|
Вероятное положение постоянных звезд. Как можно представить себе сферу вселенной? |
Сальвиати. — Итак, синьор Симпличио, к настоящему моменту мы уже расположили мировые тела в точном соответствии с системой Коперника; сделано это было вашей собственной рукой и даже больше: всем им, за исключением Солнца, 3емли и звездной сферы, вы приписали собственные их движения: Меркурию с Венерой вы придали круговое движение вокруг Солнца, не охватывая этим движением Землю; вокруг Солнца же вы заставили двигаться три верхние планеты — Марс, Юпитер и Сатурн, — причем они заключают Землю внутри своих кругов; затем Луна не может двигаться иначе, как вокруг Земли, не охватывая Солнца, и относительно этих движений вы также вполне согласны с тем же Коперником. Что касается
|
Покой, годичное и суточное движение должны быть поделены между Солнцем, Землей и небесной сферой. |
|
При движущейся сфере больше оснований считать неподвижным центр ее, нежели какую-либо другую ее часть. |
|
Если допустить годичное движение Земли, то ей же нужно приписать и суточное. |
Сагредо. — Я вижу это очень хорошо. Однако, если вы эту простоту принимаете за основание большей вероятности истинности такой системы, то другие, может быть, наоборот, могли бы вывести отсюда обратные заключения, сомневаясь не без оснований, почему же такое древнее воззрение пифагорейцев, столь хорошо согласующееся с явлениями, имело в течение тысячи лет лишь немногих последователей, было отвергнуто самим Аристотелем, да и после Коперника влачит прежнюю свою судьбу?
Сальвиати. — Если бы вам, синьор Сагредо, хоть раз пришлось послушать, как это зачастую случалось со мной, каких глупостей достаточно, чтобы сделать народ глухим и упрямо не желающим не только одобрять, но даже просто выслушивать новые мысли, то, я думаю, вы перестали бы так сильно удивляться тому, что вы находите лишь немногих последователей этого мнения Но не стоит, как мне кажется, слишком долго останавливаться на тех, которые, стремясь подтвердить и упрямо сохранить
|
Достаточно самых детских доводов, чтобы заставить глупцов держаться за свое мнение о неподвижности Земли. |
|
Доказывается, сколь неправдоподобным кажется учение Коперника. |
|
Разум и логика у Аристарха и Коперника господствуют над показаниями чувственного опыта. |
Сагредо. — Значит, у нас будут еще и другие солидные возражения против годового движения?
Сальвиати. — Будут, и они столь очевидны и доступны чувствам, что если чувство, более возвышенное и более совершенное, чем обычное и природное, не объединится с разумом, то я сильно сомневаюсь, не отрекусь, ли даже я от системы Коперника, которая до сих пор была для меня только факелом, светящим мне несколько ярче обычного. {240}
Сагредо. — Итак, синьор Сальвиати, теперь, как говорится, в бой,— каждое слово, которое тратится на что-либо другое, кажется мне сказанным напрасно.
Сальвиати. — Я к вашим услугам22.
Симпличио. — Пожалуйста, синьоры, разрешите мне успокоить мою душу, так как сейчас я очень взволнован одним замечанием, только что брошенным синьором Сальвиати. Только тогда, когда уляжется мое волнение, я смогу более отчетливо воспринимать ваши рассуждения: ведь плохо запечатлеваются образы на волнующейся зеркальной поверхности, как это изящно сказал латинский поэт:
. . nuper me in littore vidi |
Сальвиати. — Вы совершенно правы, а потому выскажите свои сомнения.
Симпличио. — Вы в конечном итоге считаете одинаково тупоумными как тех, кто отрицает у Земли суточное движение, поскольку они не видят, чтобы оно переносило их в Персию или в Японию, так и тех, кто возражает против годового движения, считая невозможным признать, что чрезвычайно обширная и тяжелая масса земного шара может подниматься вверх и оттуда падать вниз, как она и должна была бы делать, если бы кружилась таким движением около Солнца. Не краснея от того, что меня причислят к этим глупцам, я ощущаю то же самое противодействие в своем мозгу, поскольку дело касается второго пункта возражений против годового движения, особенно когда я вижу, какое сопротивление движению даже в горизонтальном направлении оказывает, не говорю уже — гора, а всего лишь камень или маленькая часть горного утеса. Поэтому я прошу вас не пренебрегать подобными соображениями и дать разъяснения не столько для меня, сколько для других, кому они могут казаться чрезвычайно доказательными; ведь я считаю, что очень трудно кому-либо, как бы прост он ни был, признаться в своей простоте только на том основании, что его считают за простака.
Сагредо. — Конечно, и чем более прост кто-либо, тем более будет он упорствовать в своем заблуждении. По этому случаю, я думаю, хорошо было бы не только ради удовлетворения синьора Симпличио, но и по другим не менее важным причинам разобрать как это, так и другие соображения подобного рода; ведь мы видим, что нет недостатка в людях, которые чрезвычайно сведущи в обычной философии и других науках, но из-за недостаточного знания астрономии, или математики, или других дисциплин, оттачивающих ум для проникновения в истину, оказываются убеждены одними пустыми разговорами. Поэтому мне кажется достойной сожаления участь бедного Коперника: он не может быть уверен, что критика его учения не попадет случайно в руки лиц, неспособных воспринять его доводы, чрезвычайно тонкие и потому трудные для понимания, но уже наперед убежденных подобной пустой видимостью в их ложности и провозглашающих их ложными и ошибочными. А так как подобные люди не могут постигнуть этих наиболее сложных доводов, то хорошо было бы позаботиться хотя бы о том, чтобы они распознали несостоятельность других доводов; такое знание должно смягчить их приговор и умерить осуждение доктрины, которую они теперь считают ошибочной. Итак, я приведу теперь два других возражения против суточного движения, которые я не так давно слышал от лиц чрезвычайно образованных; потом мы перейдем к годовому движению. Первое из них состояло в том, что если на самом деле не Солнце и другие звезды поднимаются над горизонтом с востока, а восточная часть Земли опускается ниже их, сами же они остаются неподвижными, то горы, расположенные на несколько часов к востоку, наклоняясь {241} вниз, при вращении земного шара неизбежно должны были бы оказаться в таком положении, что там, где раньше приходилось для достижения вершины взбираться по крутизне вверх, теперь пришлось бы спускаться по склону вниз. Другое возражение состояло в том, что если бы суточное движение принадлежало Земле, то оно должно было бы быть настолько быстрым, что человек, находящийся на дне колодца, мог бы только в течение одного мгновения видеть звезду, находящуюся отвесно над ним; он мог бы видеть ее только то очень короткое время, за которое окружность Земли проходит 2 или 3 локтя, т. е. столько, сколько локтей составляет ширина колодца; однако на опыте оказывается, что видимое прохождение такой звезды над колодцем продолжается довольно долго; из этого доказательства с необходимостью следует, что отверстие колодца не движется с той стремительностью, которая соответствовала бы суточному обращению Земли; следовательно, Земля неподвижна.
Симпличио. — Второе из этих двух доказательств представляется мне весьма убедительным, что же касается первого, то я думаю, что и сам мог бы его опровергнуть. Я рассуждаю так: все равно, переносит ли земной шар гору на восток, вращаясь вокруг собственного центра, или земной шар стоит на месте, а гора, вырванная у подножья, движется по Земле; я не вижу разницы между движением горы по поверхности Земли и движением корабля по поверхности моря; ведь, если бы пример горы имел силу, то в равной мере оказывалось бы, что и на корабле, продолжающем свой путь и удаленном от наших гаваней на много градусов, нам нужно было бы не подниматься, чтобы взобраться на его мачту, но двигаться сперва горизонтально, а потом даже опускаться. Но ведь так не бывает, и я никогда не слыхал ни от одного моряка, даже из тех, которые объехали весь земной шар, чтобы существовало какое-либо различие в такого рода действии или в какой-либо другой службе, какую им приходится нести на корабле, находится ли судно в нашей или какой угодно другой части света.
Сальвиати. — Вы рассуждаете очень хорошо, и если бы автору такого возражения когда-либо пришло в голову, что соседняя гора, находящаяся от него к востоку, при вращении земного шара в результате такого движения оказалась бы через два часа перенесенной туда, где сейчас находится, например, гора Олимп или Кармель, то он должен был бы понять, что его собственный способ доказательства вынуждает признать, что для достижения вершины названных гор de facto приходится спускаться. Этого сорта головы склонны отрицать антиподов на том основании, что нельзя ходить вниз головой, прилепляясь ногами к потолку. Из правильных представлений, даже превосходно ими понятых, они не умеют извлечь самого простого разрешения своих сомнений; я хочу сказать, что они великолепно понимают, что тяготение и движение вниз есть стремление к центру земного шара, а поднятие — удаление от него; но затем они уже перестают понимать, что нашим антиподам не доставляет никакого труда стоять прямо и ходить, ибо поступают они совершенно так же, как и мы, т. е. держат ступни ног направленными к центру Земли, а голову — направленной к небу.
Сагредо. — И все же мы знаем, что люди даже возвышенного ума, сведущие в других науках, заблуждаются в такого рода знании. Поэтому я еще больше настаиваю на том, что я недавно говорил, т. е. что хорошо было бы рассмотреть все возражения, даже самые слабые, а потому ответим также на возражение, вытекающее из примера с колодцем.
Сальвиати. — Это второе соображение все же имеет некоторую видимость убедительности. Однако, я твердо уверен, что если бы можно было попросить у самого автора этого возражения лучше раскрыть и разъяснить, в чем состоит то явление, которое должно было бы произойти, если {242} бы существовало суточное обращение Земли, и которого на самом деле не происходит, то я думаю и утверждаю, что он запутался бы в изложении своих возражений и выводов, может быть, не меньше того, кто попытается распутать его мысли.
Симпличио. — По правде говоря, я думаю, что именно так и случится. Ведь и я сейчас нахожусь в таком же смущении, ибо соображение это на первый взгляд кажется мне убедительным, но, с другой стороны, правильно продолжая рассуждение, я вижу, как бы сквозь туман, что та огромная скорость, которая замечалась бы у звезды, если бы движение принадлежало Земле, должна в еще большей степени замечаться у той же звезды, если движение принадлежит ей: движение должно быть во много тысяч раз более быстрым у звезды, чему Земли. С другой стороны, если видимость звезды должна теряться после прохождения отверстия колодца диаметром в два или три локтя, то раз колодец вместе с Землей проходит много больше 2000000 локтей в час, то казалось бы, что такое прохождение должно быть чем-то столь мгновенным, что оно даже не может быть воспринято; однако же со дна колодца звезда видима в течение очень долгого промежутка времени. Поэтому мне очень хочется уяснить себе. в чем тут дело.
Сальвиати. — Теперь я еще больше укрепляюсь во мнении о путанице у автора этого возражения, поскольку я вижу, что даже вы, синьор Симпличио, не только не вполне понимаете, но и затемняете то, что хотите сказать. Это я заключаю, главным образом, из того, что вы пропускаете одно различие, составляющее самый главный пункт в этом деле. А потому скажите мне: при проведении такого опыта — я говорю о прохождении звезды над отверстием колодца — вызывает ли какое-нибудь различие большая или меньшая глубина колодца, т. е. нахождение наблюдателя более или менее далеко от отверстия? Ведь я не слышал, чтобы вы обращали на это внимание.
Симпличио. — Правда, я не подумал об этом. Но ваш вопрос пробуждает мой ум и указывает мне, что такое различие необходимо должно быть сделано, и я уже начинаю понимать, что при определении времени прохождения звезды глубина колодца как будто может иметь не меньшее значение, чем его ширина.
Сальвиати. — Я, наоборот, думаю, что ширина не оказывает никакого влияния или лишь чрезвычайно небольшое24.
Симпличио. — Однако, мне кажется, что если нужно пробежать десять локтей, то для этого нужно в десять раз больше времени, чем для пробега одного локтя, и я уверен, что лодочка в десять локтей скорее пройдет перед моими глазами, чем галера длиною в сто локтей.
Сальвиати. — Однако, мы все еще упорствуем в том застарелом представлении, будто мы двигаемся лишь постольку, поскольку нас переносят наши ноги. То, что вы говорите, дорогой синьор Симпличио, правильно, если видимый объект движется, а вы стоите неподвижно и наблюдаете его, но если вы окажетесь в колодце, когда колодец и вы вместе с ним переноситесь земным обращением, то разве вы не видите, что ни за час, ни за тысячу часов, ни за целую вечность отверстие колодца не пройдет перед вами? То, что в данном случае происходит с вами вследствие движения или неподвижности Земли, можно распознать не по отверстию колодца, а только по другому предмету, отделенному и не причастному к тем же самым условиям, т. е. к движению или покою.
Симпличио. — Все это хорошо. Но если принять, что, я находясь в колодце, буду переноситься вместе с ним суточным движением и что звезда, видимая мною, будет неподвижна, отверстие же колодца, через которое только и видно мне прохождение звезды, будет в три локтя из тех многих миллионов локтей остальной земной поверхности, которые {243} мешают мне видеть, то как может быть время видимости звезды ощутительной частью того времени, когда она скрыта?
Сальвиати. — И опять вы становитесь жертвой того же самого недоразумения; действительно, мне нужно помочь вам освободиться от него. Ширина колодца, синьор Симпличио, не есть мера времени видимости звезды, ибо в таком случае вы видели бы ее постоянно, если бы отверстие колодца постоянно открывало путь вашему зрению; за такую меру нужно принимать величину той части неподвижного неба, которая видна вам через отверстие колодца.
Симпличио. — Но разве то, что открывается мне на небе, не составляет такой же части всей небесной сферы, какую составляет отверстие колодца по отношению ко всему земному шару?
Сальвиати. — Мне хотелось бы, чтобы вы ответили сами; поэтому скажите мне, составляет ли отверстие одного и того же колодца всегда одну и ту же часть земной поверхности?
Симпличио. — Без сомнения, всегда одну и ту же.
Сальвиати. — А часть неба, видимая тому, кто находится в колодце, всегда ли составляет ту же самую часть всей небесной сферы?
Симпличио. — Теперь сознание мое начинает проясняться, и я начинаю понимать то, на что вы мне недавно указали, именно, что глубина колодца имеет большое значение в этом вопросе; ведь, несомненно, чем больше удаляется глаз от отверстия колодца, тем меньше часть неба остается открытой и, следовательно, тем скорее проходит и пропадает для глаз того, кто рассматривает ее из глубины колодца?
Сальвиати. — Но есть ли хоть одно такое место в колодце, для которого оставалась бы открытой совершенно такая же часть небесной сферы, какую составляет отверстие колодца по отношению к земной поверхности.
Симпличио. — Мне кажется, что если бы углубить колодец до центра Земли, то, может быть, оттуда откроется такая часть неба, которая составит по отношению к его отверстию столько же, сколько это последнее по отношению к Земле. Но по мере удаления от центра и приближения к поверхности будут раскрываться все большие и большие части неба.
Сальвиати. — Так что в конце концов, когда глаз окажется на уровне отверстия колодца, то раскроется половина небесного свода или немногим меньше, для прохождения которой (предположим, что мы находимся под экватором) нужно 12 часов.
Я уже нарисовал вам схему системы Коперника. Против истинности
|
Марс яростно выступает против системы Коперника. |
|
Явления, замеченные на Венере, стоят в противоречии с системой Коперника. |
|
Другое затруднение, создаваемое Венерой для Коперника. |
|
Венера, по Копернику, или обладает собственным светом, или состоит из прозрачной субстанции. Коперник умалчивает о малом изменении видимой величины Венеры и Марса. Луна нарушает порядок других планет. |
|
Ответы на три первые возражения против системы Коперника. |
Сагредо. — Но каким образом это оказалось скрытым от Коперника и стало известным вам?
Сальвиати. — Эти вещи могут быть уловлены только посредством чувства зрения, а оно дано людям от природы не настолько совершенным, чтобы можно было достигать и распознавать такого рода различия; орган зрения даже сам по себе чинит помехи. Но после того как в наш век богу угодно было даровать человеческому разуму столь удивительное изобретение, которое может совершенствовать наше зрение, увеличивая его в 4, 6, 10, 20, 30 и 40 раз, посредством телескопа оказалось чрезвычайно хорошо видимым бесконечное множество предметов, которые из-за своего удаления или из-за своих весьма малых размеров были для нас ранее невидимы.
Сагредо. — Но ведь Венера и Марс не являются предметами, невидимыми из-за своего удаления или малых размеров; наоборот, мы воспринимаем их простым естественным зрением, так почему же мы не замечали различий в их размерах и фазах?
Сальвиати. — В этом значительную помеху чинит нам самый наш глаз, как я вам только что указал, а именно: предметы блестящие и далекие
|
Причины того, что Венера и Марс изменяют свою видимую величину не в той мере, в какой следовало бы. |
Сагредо. — Теперь я припоминаю, что читал что-то по этому вопросу, не знаю то ли в Солнечных письмах, то ли в Весовщике золота нашего общего друга. Но было бы неплохо для освежения в памяти прочитанного мною, а также и для сведения синьора Симпличио, который, может быть, не видел этих сочинений, разъяснить нам более точно, как обстоит дело; знание этого, думается мне, совершенно необходимо для полного понимания того, о чем сейчас идет речь.
Симпличио. — Действительно, для меня является новым все то, что было сейчас изложено синьором Сальвиати; по правде говоря, я не поинтересовался прочесть эти книги и до сих пор не слишком верил во вновь открытые очки; напротив, идя по стопам других философов-перипатетиков,
|
Показания телескопа считаются перипатетиками обманчивыми. |
Сальвиати. — Доверие, которые люди такого рода питают к своей собственной проницательности, не менее безрассудно, чем недооценка суждения других, и очень знаменательно, что они считают себя способными лучше судить об этом инструменте, никогда его не испытав, чем те, которые произвели и производят с ним ежедневно тысячи и тысячи опытов. Но оставим лучше такого рода упрямцев: с ними не стоит даже считаться, так как тем самым окажешь им честь, большую, чем та, какую они заслуживают. Возвращаясь к нашей теме, я говорю, что блестящие предметы —
|
Причины, по которым светящиеся тела кажутся тем более увеличенными, чем они меньше. |
Симпличио. — Вы хотели, я думаю, сказать «в три раза», так как прибавка четырех дюймов с той и другой стороны к диаметру круга в четыре дюйма утраивает его размеры, а не увеличивает их в девять раз.
Сальвиати. — Немного геометрии, синьор Симпличио, диаметр действительно увеличивается в три раза, но площадь, о чем мы сейчас и говорим, возрастет в девять раз, потому что, синьор Симпличио, площади
|
Площади фигур возрастают в отношении квадратов по сравнению с линейными размерами. |
Сагредо. — Затруднения, которые причинили беспокойство синьору Симпличио, у меня не возникали. Однако, есть другие вещи, в которых {246} я хотел бы разобраться более ясно В частности, я хотел бы знать, на каком основании вы утверждаете, что такое увеличение всегда будет одинаковым у всех видимых предметов?
Сальвиати. — Отчасти я уже разъяснил это, сказав, что так увеличиваются только светящиеся, а не темные предметы. Теперь я добавлю остальное; те из блестящих предметов, которые более ярки, дают особенно яркие и сильные отражения на нашем зрачке и потому представляются
|
Чем ярче предметы, тем более увеличенными они кажутся. Легко производимый опыт, показывающий увеличение размера звезд вследствие привходящих лучей. |
|
Юпитер испытывает меньшее увеличение, чем Сатурн. Солнце и Луна испытывают только ничтожное увеличение. Очевидным опытом доказывается, что у тел более блестящих происходит более сильное излучение, чем у менее блестящих. |
|
Подзорная труба является лучшим средством лишить звезды венца из лучей. |
|
Вторая причина незначительного видимого прироста величины Венеры. |
Сагредо. — О, Николай Коперник, как приятно было бы тебе видеть подтверждение твоей системы столь ясным опытом!
Сальвиати. — Да, но насколько меньше была бы слава его возвышенного ума среди людей понимающих? Мы видим, как я уже говорил раньше, что он, направляемый единственно доводами разума, все время
|
Коперник был убежден доводами рассудка вопреки противоречащим показаниям чувственного опыта. |
Сагредо. — Различия видимых величин у Юпитера, Сатурна и Меркурия, я думаю, также должны наблюдаться в точном соответствии с их меняющимися удалениями?
Сальвиати. — У двух верхних планет я это наблюдал со всей тщательностью почти ежегодно в течение двадцати двух лет. Над Меркурием
|
Меркурий не поддается точным наблюдениям. |
|
Устранение затруднения, порожденного тем, что Земля обращается вокруг Солнца не одна, но в сопровождении Луны. |
Сагредо. — На каком основании называете вы лунами четыре юпитеровых планеты?
Сальвиати. — Именно лунами покажутся они тому, кто будет рассматривать
|
Медицейские звезды являются четырьмя лунами у Юпитера. |
Симпличио. — Эти явления так важный так значительны, что невозможно, чтобы Птоломей и его последователи не имели о них понятия, а если они это знали, то необходимо должны были найти также способ дать достаточное объяснение этим столь очевидным явлениям и притом достаточно уместное и правдоподобное, так как оно принималось многими и многими в течение столь долгого времени.
Сальвиати. — Вы рассуждаете очень хорошо. Но вы должны знать, что главная цель чистых астрономов состоит только в том, чтобы дать
|
Главная цель астрономии — это давать объяснения явлениям. |
|
Коперник реформировал астрономию на основании предпосылок Птоломея. |
|
Что побудило Коперника построить свою систему? |
Симпличио. — Но каковы те нелепости птоломеевой системы, которые не были бы превзойдены в коперниковой?
Сальвиати. — У Птоломея мы находим болезни, а у Коперника —
|
Несообразности, присущие системе Птоломея. |
Сагредо. — Я хотел бы лучше понять, как эти остановки, возвращения и продвижения, которые всегда казались мне совершенно невероятными, объясняются в системе Коперника.
Сальвиати. — Вы увидите такое их объяснение, синьор Сагредо, что его одного должно быть достаточно для всякого не слишком дерзкого упрямца, чтобы заставить его выразить одобрение и всему остальному в этом
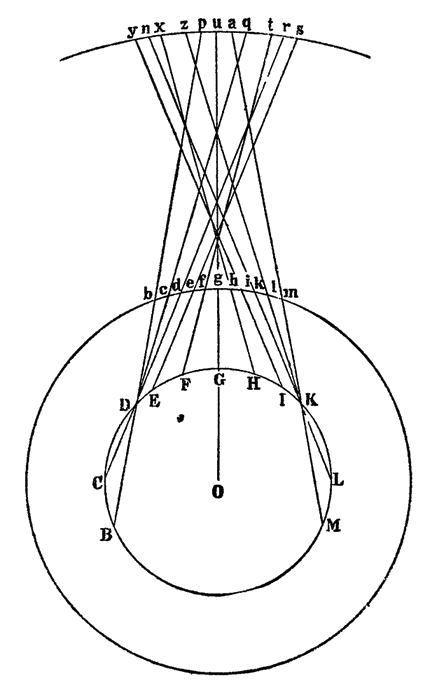
|
В высокой степени важный аргумент в пользу Коперника — это устранение стояния и попятного движения планет. Одно только годичное движение Земли вносит большую неравномерность в видимое движение пяти планет. Доказательство неравномерности движения трех верхних планет, обусловливаемое годичным движением Земли. |
|
Возвратные движения чаще у Сатурна, реже у Юпитера и еще реже у Марса; объяснения этого. Доказательства возвратного движения Венеры и Меркурия Аполлонием и Коперником. |
Вы видите, синьоры, с какой легкостью и простотой годичное движение,
|
Годичное движение Земли лучше всего объясняет неправильность движения пяти планет. |
|
Само Солнце свидетельствует о том, что годичное движение присуще Земле. |
Человеком, впервые открывшим и наблюдавшим солнечные пятна, равно как и все другие новые небесные явления, был наш друг, член Академии
|
Академик Линчео является первым открывшим солнечные пятна, а также все остальные новые небесные явления. История продолжительных систематических наблюдений, произведенных Академиком над солнечными пятнами. |
|
Внезапная мысль, пришедшая в голову Академику Линчео, относительно важности следствий, вытекающих из движения солнечных пятен. |
|
Удивительные изменения, наблюдаемые в движении пятен, предусмотренные Академиком для случая, если годичное движение свойственно Земле. |
Сагредо. — Я знаю, мой дорогой синьор Сальвиати, что невежливо прерывать ваши рассуждения, но не менее плохо, я думаю, продолжать рассуждения, если слова рискуют оказаться, как говорится, брошенными на ветер. Признаюсь откровенно, что не могу составить себе определенного представления ни об одном из провозглашенных вами выводов; но так как, даже воспринятые смутно и в столь общей форме, они представляются мне ведущими к удивительным следствиям, то я хотел бы каким-нибудь путем усвоить их получше.
Сальвиати. — То же самое, что испытываете вы, случилось и со мной, когда выводы были сообщены мне моим гостем в голых словах; впоследствии он облегчил мне понимание, изобразив для меня этот процесс на приборе, который был всего-навсего простой сферой; он пользовался при этом некоторыми из нанесенных на ней кругов, но с целью, отличной от той, для которой они обычно назначаются. Теперь же, раз у нас нет сферы, я заменю ее тем, что буду по мере надобности делать рисунки на бумаге27. Для изображения первого из изложенных мною соображений,
|
Первая особенность, которую следует отметить в движении солнечных пятен; в дальнейшем будут объяснены и остальные. |
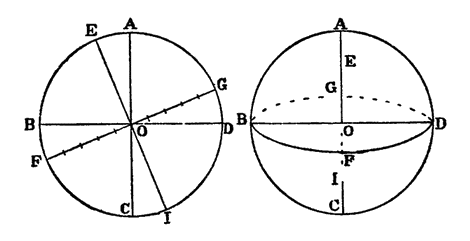 этой линией будет BOD; если восставить на ней перпендикуляр АОС, то он будет осью эклиптики и годового движения земного шара. Предположим теперь, что солнечное тело (не изменяя центра) вращается само по себе, но уже не вокруг оси АОС (которая перпендикулярна к плоскости эклиптики), а вокруг несколько наклонной, — пусть этой наклонной будет EOI; эта ось всегда твердо и неизменно сохраняет один и тот же наклон и направление к одним и тем же точкам небесного свода и вселенной. И так как при вращении солнечного тела каждая точка его поверхности (за исключением полюсов) описывает окружность какого-нибудь круга, большего или меньшего, в зависимости от того, находится ли он более или менее далеко от этих полюсов, то, взяв точку F, равно от них удаленную, проведем диаметр FOG, который будет перпендикулярен к оси EI и будет диаметром наибольшего круга, описанного при полюсах Е и I. Если предположить теперь, что Земля и мы вместе с нею находимся в таком месте эклиптики, откуда обращенная к нам полусфера Солнца ограничивается кругом ABCD, который, проходя (как это всегда бывает) через полюсы A и C, пройдет также через Е и I, то ясно, что наибольший круг с диаметром FG будет перпендикулярен к кругу ABCD; к последнему перпендикулярен также луч, который из нашего глаза падает на центр О; следовательно, тот же самый луч попадет в плоскость круга с диаметром FG, и поэтому окружность его покажется нам прямой линией, совпадающей с FG; значит, если бы в точке F было пятно, переносимое потом солнечным обращением, то оно описало бы на поверхности Солнца окружность такого круга, который покажется нам прямой линией. Итак, прямым покажется его путь и прямым покажутся также движения других пятен, которые при этом обращении описывают меньшие круги, так как все они параллельны наибольшему кругу и глаз наш расположен на огромном расстоянии от них. Теперь, если вы рассудите, что после того, как Земля пройдет за шесть месяцев половину своей орбиты и окажется против той полусферы Солнца, которая сейчас скрыта от нас, так что границей видимой тогда части будет тот же самый круг ABCD, также проходящий через полюсы Е и I, то вы поймете, что с путями пятен будет то же самое, т. е. все они будут казаться совершающимися по прямым линиям. Но так как это обстоятельство имеет место только тогда, когда граница круга проходит через полюсы Е и I, и так как эта граница с каждым мгновением изменяется вследствие годового движения Земли, то поэтому мгновенно и ее прохождение через неподвижные полюсы Е и I, а следовательно, мгновенно то время, когда движения этих пятен будут казаться прямыми. Из того, что до сих пор было сказано, становится понятным также, что если пятна появляются и начинают движения со стороны F, направляясь к G, то пути их идут слева, восходя направо; но если предположить, что Земля находится в диаметрально противоположном положении, то появление пятен будет происходить также слева от зрителя около G, путь же их будет нисходить направо к F. Предположим теперь, что Земля находится {254} на одну четверть своей орбиты дальше от того места, где она находится сейчас; отметим на этом другом чертеже, как и раньше, границу ABCD и ось АС, через которую проходит плоскость нашего меридиана28. В этой плоскости будет лежать также и ось обращения Солнца с его полюсами, одним — обращенным к нам, т. е. находящимся на видимой полусфере, который мы обозначим точкой ЕI и другим — попадающим в скрытую от нас полусферу; я обозначу его через I. Итак, если ось EI наклонена верхней частью Е к нам, то наибольший круг, описанный при вращении Солнца, будет BFDG; половина его, видимая нами, т. е. BFD, покажется нам уже не прямой линией, так как полюсы ее Е и I не находятся на окружности ABCD, а будет иметь вид искривленной линии, обращенной своею выпуклостью к нижней части С, и очевидно, что то же самое будет и
этой линией будет BOD; если восставить на ней перпендикуляр АОС, то он будет осью эклиптики и годового движения земного шара. Предположим теперь, что солнечное тело (не изменяя центра) вращается само по себе, но уже не вокруг оси АОС (которая перпендикулярна к плоскости эклиптики), а вокруг несколько наклонной, — пусть этой наклонной будет EOI; эта ось всегда твердо и неизменно сохраняет один и тот же наклон и направление к одним и тем же точкам небесного свода и вселенной. И так как при вращении солнечного тела каждая точка его поверхности (за исключением полюсов) описывает окружность какого-нибудь круга, большего или меньшего, в зависимости от того, находится ли он более или менее далеко от этих полюсов, то, взяв точку F, равно от них удаленную, проведем диаметр FOG, который будет перпендикулярен к оси EI и будет диаметром наибольшего круга, описанного при полюсах Е и I. Если предположить теперь, что Земля и мы вместе с нею находимся в таком месте эклиптики, откуда обращенная к нам полусфера Солнца ограничивается кругом ABCD, который, проходя (как это всегда бывает) через полюсы A и C, пройдет также через Е и I, то ясно, что наибольший круг с диаметром FG будет перпендикулярен к кругу ABCD; к последнему перпендикулярен также луч, который из нашего глаза падает на центр О; следовательно, тот же самый луч попадет в плоскость круга с диаметром FG, и поэтому окружность его покажется нам прямой линией, совпадающей с FG; значит, если бы в точке F было пятно, переносимое потом солнечным обращением, то оно описало бы на поверхности Солнца окружность такого круга, который покажется нам прямой линией. Итак, прямым покажется его путь и прямым покажутся также движения других пятен, которые при этом обращении описывают меньшие круги, так как все они параллельны наибольшему кругу и глаз наш расположен на огромном расстоянии от них. Теперь, если вы рассудите, что после того, как Земля пройдет за шесть месяцев половину своей орбиты и окажется против той полусферы Солнца, которая сейчас скрыта от нас, так что границей видимой тогда части будет тот же самый круг ABCD, также проходящий через полюсы Е и I, то вы поймете, что с путями пятен будет то же самое, т. е. все они будут казаться совершающимися по прямым линиям. Но так как это обстоятельство имеет место только тогда, когда граница круга проходит через полюсы Е и I, и так как эта граница с каждым мгновением изменяется вследствие годового движения Земли, то поэтому мгновенно и ее прохождение через неподвижные полюсы Е и I, а следовательно, мгновенно то время, когда движения этих пятен будут казаться прямыми. Из того, что до сих пор было сказано, становится понятным также, что если пятна появляются и начинают движения со стороны F, направляясь к G, то пути их идут слева, восходя направо; но если предположить, что Земля находится в диаметрально противоположном положении, то появление пятен будет происходить также слева от зрителя около G, путь же их будет нисходить направо к F. Предположим теперь, что Земля находится {254} на одну четверть своей орбиты дальше от того места, где она находится сейчас; отметим на этом другом чертеже, как и раньше, границу ABCD и ось АС, через которую проходит плоскость нашего меридиана28. В этой плоскости будет лежать также и ось обращения Солнца с его полюсами, одним — обращенным к нам, т. е. находящимся на видимой полусфере, который мы обозначим точкой ЕI и другим — попадающим в скрытую от нас полусферу; я обозначу его через I. Итак, если ось EI наклонена верхней частью Е к нам, то наибольший круг, описанный при вращении Солнца, будет BFDG; половина его, видимая нами, т. е. BFD, покажется нам уже не прямой линией, так как полюсы ее Е и I не находятся на окружности ABCD, а будет иметь вид искривленной линии, обращенной своею выпуклостью к нижней части С, и очевидно, что то же самое будет и
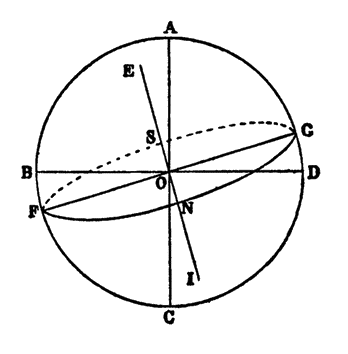 со всеми меньшими кругами, параллельными наибольшему кругу BFD. Понятно также, что когда Земля займет диаметрально противоположное этому положение, так что видна будет другая полусфера Солнца, ранее скрытая, то часть DGB того же наибольшего круга будет видна изогнутой своей выпуклостью к верхней стороне А, и пути пятен при этом положении будут проходить в первом случае по дуге BFD, а во втором случае — по другой дуге DGB; места первого их появления и последнего исчезновения около точек В и D будут в равновесии, т. е. одни не будут ни выше, ни ниже других. Если же мы поместим Землю в такое место эклиптики, что ни граница ABCD, ни меридиан АС не будут проходить через полюсы оси EI, как я вам сейчас покажу, нарисовав этот третий чертеж, где видимый полюс Е лежит между дугой границы АВ и сечением меридиана АС, то диаметр наибольшего круга будет FOG, видимая половина круга — FNG и скрытая — GSF; первая изогнута своей выпуклостью N по направлению к нижней части, вторая обращена своим горбом S по направлению к верхней части Солнца; места восхода и захода пятен, т. е. концы F и G, не будут уравновешены, как прежние В и D, но F будет ниже, a G — выше, хотя разность между ними будет меньше, чем на первом чертеже; также и дуга FNG будет изогнута, но не так, как предыдущая BFG; значит, в таком положении пути пятен будут восходить с левой стороны F к правой G и итти по кривым линиям. Если же предположить, что Земля находится в диаметрально противоположном месте, так что будет видна ныне скрытая полусфера Солнца, ограниченная притом той же самой границей ABCD, то, очевидно, мы увидим, как пятна будут двигаться по дуге GSF, появляясь у самой верхней точки G, которая будет, однако, слева от зрителя, и исчезать они будут, опустившись вправо, в точке F. Если понятно все, что я до сих пор изложил, то, я думаю, не останется никаких трудностей для понимания того, как от изменения положения границы солнечных полусфер, которая то проходит через полюсы вращения Солнца, то более или менее отходит от них, проистекают все различия в видимых путях пятен, так что чем полюсы дальше от границы, тем больше будут изогнуты и менее наклонны указанные пути. При наибольшем удалении — что происходит тогда, когда эти полюсы лежат в плоскости меридиана, кривизна доходит до максимума, а наклон — до минимума, т. е. до равновесия, как это показывает второй чертеж; наоборот, когда полюсы лежат на границе, как это показывает первый чертеж, наклон максимален, а кривизна минимальна и сводится к прямолинейности; по мере того как граница отходит от полюсов, кривизна начинает становиться ощутимой, все время возрастая, наклон же становится все меньшим. {255}
со всеми меньшими кругами, параллельными наибольшему кругу BFD. Понятно также, что когда Земля займет диаметрально противоположное этому положение, так что видна будет другая полусфера Солнца, ранее скрытая, то часть DGB того же наибольшего круга будет видна изогнутой своей выпуклостью к верхней стороне А, и пути пятен при этом положении будут проходить в первом случае по дуге BFD, а во втором случае — по другой дуге DGB; места первого их появления и последнего исчезновения около точек В и D будут в равновесии, т. е. одни не будут ни выше, ни ниже других. Если же мы поместим Землю в такое место эклиптики, что ни граница ABCD, ни меридиан АС не будут проходить через полюсы оси EI, как я вам сейчас покажу, нарисовав этот третий чертеж, где видимый полюс Е лежит между дугой границы АВ и сечением меридиана АС, то диаметр наибольшего круга будет FOG, видимая половина круга — FNG и скрытая — GSF; первая изогнута своей выпуклостью N по направлению к нижней части, вторая обращена своим горбом S по направлению к верхней части Солнца; места восхода и захода пятен, т. е. концы F и G, не будут уравновешены, как прежние В и D, но F будет ниже, a G — выше, хотя разность между ними будет меньше, чем на первом чертеже; также и дуга FNG будет изогнута, но не так, как предыдущая BFG; значит, в таком положении пути пятен будут восходить с левой стороны F к правой G и итти по кривым линиям. Если же предположить, что Земля находится в диаметрально противоположном месте, так что будет видна ныне скрытая полусфера Солнца, ограниченная притом той же самой границей ABCD, то, очевидно, мы увидим, как пятна будут двигаться по дуге GSF, появляясь у самой верхней точки G, которая будет, однако, слева от зрителя, и исчезать они будут, опустившись вправо, в точке F. Если понятно все, что я до сих пор изложил, то, я думаю, не останется никаких трудностей для понимания того, как от изменения положения границы солнечных полусфер, которая то проходит через полюсы вращения Солнца, то более или менее отходит от них, проистекают все различия в видимых путях пятен, так что чем полюсы дальше от границы, тем больше будут изогнуты и менее наклонны указанные пути. При наибольшем удалении — что происходит тогда, когда эти полюсы лежат в плоскости меридиана, кривизна доходит до максимума, а наклон — до минимума, т. е. до равновесия, как это показывает второй чертеж; наоборот, когда полюсы лежат на границе, как это показывает первый чертеж, наклон максимален, а кривизна минимальна и сводится к прямолинейности; по мере того как граница отходит от полюсов, кривизна начинает становиться ощутимой, все время возрастая, наклон же становится все меньшим. {255}
Таковы те удивительные изменения, о которых говорил мне мой гость и которые должны были бы проявляться время от времени в перемещениях солнечных пятен, если только, действительно, годовое движение принадлежит Земле и если Солнце, находящееся в центре эклиптики, вращается само по себе около оси, не перпендикулярной, а наклонной к плоскости этой эклиптики.
Сагредо. — Я очень хорошо усвоил эти выводы и думаю, что еще лучше смогу запечатлеть их в воображении, если приспособлю глобус с соответствующим наклоном и буду смотреть на него с разных сторон. Теперь вам остается сказать, как оправдались на деле эти воображаемые выводы.
Сальвиати. — Случилось вот что: мы продолжали в течение многих и многих
|
Наблюдаемое в действительности соответствует предсказаниям. |
Сагредо. — Синьор Симпличио, если то, что говорит синьор Сальвиати, правда (а нам не приходится сомневаться в его словах), то последователи Птоломея и Аристотеля должны обладать солидными аргументами, твердо обоснованными положениями и надежнейшими опытами, чтобы противопоставить их таким доводам и спасти свое мнение от полного крушения.
Симпличио. — Потише, мой дорогой синьор, мы, может быть, еще и не зашли так далеко, как вас в этом уверили. Ведь если по существу я не вполне усвоил рассуждения синьора Сальвиати, то, рассматривая их со стороны формы, я не нахожу, чтобы логика заставляла меня признать, будто из такого умозаключения с какой-либо необходимостью вытекают выводы в пользу гипотезы Коперника, т. е. в пользу неподвижности Солнца в центре круга зодиака и движения Земли в пределах его окружности. Ибо если верно, что при предположении такого вращения Солнца
|
Хотя годичное движение, приписываемое Земле, вполне соответствует явлениям солнечных пятен, отсюда еще не следует, что из явления солнечных пятен можно сделать обратный вывод о том, что Земле присуще годичное движение. |
Сагредо. — Мужественно ведет себя синьор Симпличио и очень остроумно возражает и поддерживает сторону Аристотеля и Птоломея; и, правду говоря, мне кажется, что разговор с синьором Сальвиати, хотя он и продолжался очень недолго, хорошо научил его рассуждать убедительно; то же имел я случай наблюдать и на других собеседниках. Что же касается вопроса о том, можно ли для видимых неправильностей в движениях солнечных пятен получить достаточное объяснение, если оставить Землю неподвижной и сохранить движущимся Солнце, то я жду, что синьор Сальвиати поделится с нами своими мыслями, ибо ведь он весьма вероятно раздумывал об этом и извлек все, что только можно привести в пользу такого положения.
Сальвиати. — Я много думал об этом и даже разговаривал на эту
|
Истинные перипатетики будут высмеивать солнечные пятна и касающиеся их явления как иллюзии, относимые к стеклам телескопа. |
Если предположить, что видимые движения солнечных пятен таковы,
|
Если бы Земля была неподвижна в середине круга зодиака, то Солнцу пришлось бы приписать четыре движения, как будет объяснено далее. |
Вот, синьор Симпличио, то, что наш друг и я смогли привести в объяснение этого явления о точки зрения последователей Коперника и последователей Птоломея для поддержания их мнений. Вы же оцените это так, как вам подсказывает ваше убеждение.
Симпличио. — Я не чувствую себя достаточно компетентным, чтобы принимать столь важное решение, и предпочту остаться нейтральным. Но я надеюсь, что придет время, когда откровение, более высокое, чем наше человеческое рассуждение, снимет покров с нашего разума и рассеет окутывающий его туман.
Сагредо. — Прекрасное и благочестивое решение принял синьор Симпличио, достойное того, чтобы все его разделили и все ему следовали, так как только то, что исходит от высшей мудрости и верховного авторитета, может почитаться вполне достоверным. Но, поскольку исследование дозволено и человеческому разуму, постольку, оставаясь в пределах предложений и вероятных обоснований, я скажу немного более решительно, чем синьор Симпличио: среди множества тонкостей, которые я когда-либо слышал, я никогда не встречал ничего, что показалось бы моему разуму более удивительным и что произвело бы на меня большее впечатление (за исключением чисто геометрических и арифметических доказательств), чем эти два доказательства — одно, опирающееся на стояние и попятное движение пяти планет, и другое — на эти странности в движениях солнечных пятен. И мне кажется, что эти положения легко и блестяще дают правильное объяснение столь странным явлениям посредством одного лишь простого движения в сочетании со многими, также простыми, но отличными друг от друга движениями, не порождая при этом никаких трудностей и, наоборот, избавляя от всех затруднений, которые сопровождают другую систему; поэтому сам для себя я решаю, что глухи к этому учению могут быть лишь те, кто или не слышал или не понял этих столь очевидных и убедительных доводов.
Сальвиати. — Я не буду приписывать им эпитета «убедительные» или «неубедительные», ибо, как я говорил уже много раз, внимание мое было направлено не на то, чтобы принять то или иное решение в этом столь {258} высоком вопросе, а всего лишь на изложение тех естественных и астрономических оснований, которые могут быть приведены мною в пользу той и другой позиции, решение же я предоставляю другим. Такое недвусмысленное решение должно быть в конце концов принято, так как только одна из двух систем необходимо должна быть истинной, другая же необходимо ложной, и невозможно, чтобы основания, приводимые истинной стороной (оставаясь в пределах лишь человеческой науки), не являлись в такой же степени убедительными, в какой противоположные доводы — пустыми и бездоказательными.
Сагредо. — Итак, теперь настало время выслушать возражения из книжки заключений или исследований, которую снова принес с собой синьор Симпличио.
Симпличио. — Вот эта книга и вот то место, где автор прежде всего вкратце описывает систему мира, согласно учению Коперника в таких словах: Terram igitur una cum Luna totoque hoc elementari mundo Copernicus etc.31.
Сальвиати. — Остановитесь на минутку, синьор Симпличио; мне кажется, что этот автор в самом начале вступления обнаруживает чрезвычайно мало понимания той системы, которую он собирается опровергнуть, поскольку он утверждает, что Коперник заставляет Землю совместно с Луной описывать в течение года орбиту вокруг Солнца, двигаясь с востока на запад. Насколько это неправильно и невозможно, настолько же это никогда и не было предложено Коперником; он заставляет Землю двигаться как раз наоборот, именно с запада на восток, т. е. согласно порядку знаков зодиака, вследствие чего таким же представляется нам годичное движение Солнца, неподвижно помещенного в центре зодиака. Посмотрите, какова смелость и самонадеянность автора! Приняться за опровержение чужого учения и не знать самых первых основ, на которых покоятся самая главная и наиболее важная часть всего построения! Плохое начало для того, чтобы завоевать доверие читателя! Но продолжаем дальше.
Симпличио. — Разъяснив систему вселенной, автор принимается высказывать
|
Иронические возражения против Коперника в одной известной книжке. |
Сальвиати. — Я могу примириться со всем, но только не с таким смешением мест из священного писания, к которому надо всегда относиться с почтением и благоговением, с шутками и ребяческими замечаниями. Автор собирается поражать противника священным оружием, а приводит шутливые и смехотворные аргументы; он не защищает и не оспаривает никакого определенного положения, а только свободно рассуждает по поводу некоторых предположений или гипотез.
Симпличио. — Действительно, это и мне также не понравилось и даже очень, в особенности поскольку он позднее добавляет, что если даже коперниканцы и ответят, хотя бы очень изворотливо, на эти и другие {259} подобные доводы, то все же они не смогут удовлетворительно ответить на то, что следует дальше.
Сальвиати. — Вот это уже хуже всего, так как показывает, что у него имеется нечто более действительное и убедительное, чем авторитет священного писания. Но, пожалуйста, отдав должное почтение последнему, перейдем теперь к естественным и человеческим рассуждениям. Или же, если ваш автор среди естественных оснований не приводит ничего более осмысленного, чем высказанное им до сих пор, то оставим его аргументацию в стороне, так как мне совершенно не хочется тратить слов для ответа на столь наивные глупости; если он говорит, что коперниканцы отвечают на эти соображения, то это, безусловно, ложь. Нельзя поверить, чтобы кто-нибудь стал убивать время так бесполезно.
Симпличио. — И я склоняюсь к такому же суждению. Поэтому выслушаем другие соображения, которые он считает много более сильными. И вот здесь, как вы видите, чрезвычайно точными вычислениями он доказывает, что если большая орбита, по которой Коперник заставляет Землю обегать Солнце в течение года, оказывается как бы неощутимо
|
Если принять, что годичное движение свойственно Земле, то неподвижные звезды должны быть больше, чем вся земная орбита. |
Сальвиати. — Я уже видел, что нечто подобное приводил против Коперника Тихо, и не сегодня я раскрыл ошибку или, лучше сказать, ошибки этого рассуждения, основанного на совершенно ложных предположениях
|
Аргумент Тихо основан на ложных предпосылках. Те, кто не правы в споре, придираются к каждому случайному слову противника. |
|
Видимое изменение движения планет не заметно на неподвижных звездах. |
|
Если предположить, что неподвижная звезда шестой величины не больше, чем Солнце, то изменение, значительное для планет, почти не заметно для неподвижных звезд. Расстояние до Солнца составляет 1208 полудиаметров Земли. Поперечник Солнца равен половине градуса. Поперечник неподвижных звезд первой и шестой величины. Во сколько раз видимый поперечник Солнца больше видимого поперечника неподвижной звезды? Как велико должно быть расстояние до неподвижной звезды шестой величины в предположении, что такая звезда по величине равна Солнцу. |
Прежде всего я предполагаю, вместе с самим Коперником и в согласии с его противниками, что полудиаметр земной орбиты, т. е. расстояние {260} от Земли до Солнца, составляет 1208 земных полудиаметров32; во-вторых, я полагаю, в согласии и с ними, и с истиной; что видимый диаметр Солнца при среднем его расстоянии составляет около половины градуса, т. е. 30 минут, что составляет 1800 секунд или 108000 терций. И так как видимый диаметр неподвижной звезды первой величины не превышает 5 секунд, т. е. 300 терций, а диаметр неподвижной звезды шестой величины — 50 терций (здесь — самая большая ошибка противников Коперника), то, следовательно, диаметр Солнца содержит диаметр неподвижной звезды шестой величины 2160 раз; поэтому, если предположить, что неподвижная звезда шестой величины в действительности равна Солнцу и не больше его, то это все равно, что сказать: если бы Солнце удалилось настолько, что диаметр его показался бы одной 2160-ой частью того, каким оно нам кажется сейчас, то расстояние его было бы в 2160 раз больше действительно существующего ныне, но это все равно, что сказать: расстояние неподвижной звезды шестой величины составляет 2160 полудиаметров земной орбиты. А так как расстояние Солнца от Земли составляет по общему признанию 1208 земных полудиаметров, расстояние же до неподвижных звезд (как сказано) равно 2160 полудиаметрам земной орбиты, то, следовательно, по сравнению с земной орбитой полудиаметр Земли значительно, а именно почти вдвое, больше, чем диаметр земной
|
Для неподвижных звезд изменение видимого положения, вызываемое перемещением Земли, меньше, чем вызываемое величиной Земли изменение видимого положения Солнца. |
Сагредо. — Это называется оступиться с первого же шага.
Сальвиати. — Ошибка действительно не малая. Ибо по подсчетам этого автора для поддержания справедливости слов Коперника неподвижная звезда шестой величины должна была бы иметь величину всей земной
|
Звезды шестой величины приняты Тихо и автором книжки в десять миллионов раз большими, чем нужно. |
Сагредо. — Сделайте для меня, пожалуйста, этот подсчет.
Сальвиати. — Подсчет легок и очень краток. Диаметр Солнца равен
|
Вычисление размеров неподвижной звезды по отношению к большой орбите. |
Сагредо. — Значит, ошибка их заключается в том, что они сильно заблуждались в определении видимого диаметра неподвижных звезд?
Сальвиати. — Ошибка в этом, но не только в этом одном. Поистине, я чрезвычайно удивляюсь, как столько астрономов, даже с большими
|
Общая ошибка всех астрономов относительно величины звезд. |
|
Венера уличает астрономов в непростительной ошибке при определении величины звезд. |
Сагредо. — Но если у них не было телескопа, а вы уже сказали, что вы с вашим другом пришли к познанию истины посредством такого инструмента, то других астрономов следует извинить, а не обвинять в небрежности.
Сальвиати. — Это было бы правильно, если бы без телескопа нельзя было осуществить задуманного. Правда, этот инструмент, показывая диск звезды голым и увеличенным в сто и тысячу раз, делает наблюдение много
|
Способ измерения видимого диаметра звезды. |
Сагредо. — Я понимаю эту предосторожность, хотя здесь есть что-то — не знаю, что именно, — сомнительное; но вот что меня больше всего беспокоит: если это наблюдение проделывается во мраке ночи, то, мне кажется, измеряется диаметр излучающего диска, а не настоящий и голый диск звезды.
Сальвиати. — Нет, синьор, так как шнур, закрывая голое тельце звезды, снимает ее лучистое окружение, ибо оно принадлежит не ей, а нашему глазу, она лишается его сейчас же, как только закрывается ее настоящий диск, и когда вы будете производить такое наблюдение, то увидите, как у вас совершенно неожиданно закроется тоненьким шнуром {262} довольно большой огонь, заслонить который, казалось, может только значительно большее заграждение. Затем, чтобы измерить совершенно точно и найти, сколько раз толщина этого шнура укладывается в расстоянии до глаза, я беру не один единственный диаметр шнура, а раскладываю на столе много отрезков этого же шнура так, чтобы они соприкасались друг с другом, определяю циркулем ширину пространства, занятого 15 или 20 такими отрезками, и этой мерой измеряю, но уже посредством другой, более тонкой нити, расстояние от шнура до точки схождения зрительных лучей. И посредством такой довольно точной операции я нахожу, что видимый диаметр неподвижной звезды первой величины, оцениваемый обычно в 2 минуты, а у Тихо в его Астрономических письмах (стр. 167)
|
Диаметр неподвижной звезды первой величины не может быть больше пяти секунд. |
Сагредо. — Вижу и понимаю очень хорошо. Но прежде чем двинуться дальше, я хотел бы разрешить сомнение, которое зародилось у меня относительно места схождения зрительных лучей за пределом глаза, когда пристально всматриваешься в предметы, охваченные очень острым углом. Затруднение заключается в следующем: мне кажется, что это место схождения может быть иногда дальше, иногда ближе, и притом не столько из-за большей или меньшей величины рассматриваемого предмета, сколько от того, что при рассматривании предмета одной и той же величины, как мне кажется, место схождения лучей в силу некоторых других обстоятельств должно становиться то более, то менее удаленным от глаза.
Сальвиати. — Я уже вижу, куда клонит проницательность синьора Сагредо, прилежнейшего наблюдателя явлений природы. Я готов держать какое угодно пари, что из тысячи людей, наблюдавших, как у кошек
|
Зрачок в глазу расширяется и суживается. |
Сагредо. — Именно это, и мне приятно, что мои мысли оказались не безосновательными, в чем убеждает меня совпадение их с вашими. По этому поводу я хотел бы выслушать, каким путем можно определить расстояние до точки схождения зрительных лучей.
|
Как находится расстояние от зрачка до места схождения лучей. |
Сагредо. — Я понял это очень хорошо; теперь послушаем, что скажет синьор Симпличио в защиту противников Коперника.
Симпличио. — Хотя это важнейшее и существеннейшее затруднение, выдвинутое противниками Коперника, и было рассуждением синьора Сальвиати сильно видоизменено, однако, мне кажется, что оно все же еще не убрано с пути и что в нем остается еще достаточно силы, чтобы опровергнуть изложенное мнение, ибо, если я правильно понял это общее в последнее заключение, то, хотя бы мы и допустили, будто звезды шестой величины равны по размерам Солнцу (чему, однако, мне кажется, трудно поверить), все же остается правильным то, что земная орбита должна порождать на звездной сфере такие же изменения и различия, какие полудиаметр Земли производит с Солнцем, а последние все же доступны наблюдению; значит, если мы не может заметить такого или даже еще меньшего изменения на неподвижных звездах, то, мне кажется, этим самым годовое движение Земли оказывается безнадежно опровергнутым.
Сальвиати. — Ваши выводы были бы правильны, если бы нам не оставалось ничего другого, что можно было бы привести в пользу партии Коперника, но у нас остается еще много другого. Что же касается сделанного вами возражения, то ничто не препятствует нам принять удаленность неподвижных звезд еще значительно большей, чем та, которую мы предположили. И вам самому, и всякому другому, кто не желает отступить от предпосылок, допускаемых последователями Птоломея, нужно считать наиболее подходящим положение, что звездная сфера по своим размерам {264} значительно превосходит те, которые мы только что должны были, как сказано, ей приписать. Ведь все астрономы согласны в том, что бо́льшая
|
Астрономы согласны в том, что большая величина орбит является причиной большей медленности обращения. |
|
При других принятых астрономами предпосылках вычисления показывают, что удаленность неподвижных звезд составляет 10800 полудиаметров земной орбиты. Из соотношений с Юпитером и Марсом мы находим, что звездная сфера удалена еще гораздо более. |
Симпличио. — На это можно было бы ответить, мне кажется, что движение звездной сферы по наблюдениям, производившимся после Птоломея, не столь медленно, как он предполагал. Мне кажется даже, что я слышал, будто сам Коперник это наблюдал37.
Сальвиати. — Вы говорите совершенно правильно, но не приводите ничего такого, что хоть в чем-нибудь шло бы на пользу последователям Птоломея: они никогда не отказывались от движения звездной сферы в 36000 лет, потому что от такой медленности проистекала ее огромность и обширность; если же такую огромность нельзя допустить в природе, то они должны были раньше, а не теперь только, отрицать столь медленное обращение, которое в должной пропорции может согласоваться только со сферой недопустимых размеров.
Сагредо. — Пожалуйста, синьор Сальвиати, не будем больше терять времени на рассуждения о таких пропорциях с людьми, которые способны допускать вещи самые непропорциональные; таким путем от них ничего нельзя добиться. Можно ли себе представить какую-либо более непропорциональную пропорцию, чем та, которую они принимают и допускают, когда, с одной стороны, пишут, что не может быть более подходящего способа расположения небесных сфер, чем в порядке периодов времени их обращения, и помещают постепенно более медленные над более быстрыми; а с другой стороны, установив звездную сферу в качестве самой высшей, как самую медленную из всех, затем помещают над нею еще более высокую, а потом еще большую и заставляют ее двигаться в 24 часа, тогда как находящаяся под нею движется в 36000 лет. Но об этой непропорциональности говорилось достаточно в прошлый раз.
Сальвиати. — Мне хотелось бы, синьор Симпличио, чтобы вы, отказавшись на минутку от пристрастия к своим единомышленникам, сказали мне откровенно: думаете ли вы, что они в своем уме представляют себе ту величину, о которой потом выносят суждение, будто из-за своей огромности она не может быть приписана вселенной. Я по крайней мере этого не думаю. Мне кажется, что в понимании чисел, когда начинают появляться эти тысячи миллионов, воображение теряется, и мы не в состоянии {265}
|
Огромные величины и числа не охватываются нашим умом. |
Симпличио. — Эти рассуждения совершенно правильны, и никто не отрицает, что величина неба может превосходить наше воображение, а также что бог мог создать его еще в тысячу раз бо́льшим, но мы не смеем допускать, чтобы хоть что-нибудь было создано впустую и существует во вселенной напрасно. И раз мы видим ныне этот прекрасный порядок планет, расположенных вокруг Земли на пропорциональных расстояниях, чтобы оказывать на нее влияние для нашего блага, то для чего еще помещать между верхней орбитой Сатурна и звездной сферой какое-то обширнейшее пространство, без единой вве8ды, лишнее и напрасное? Для чего? Для чьей радости и пользы?
Сальвиати. — Мне кажется, мы слишком зазнаемся, синьор Симпличио, когда думаем, что забота о нас исчерпывает всю творческую силу и ставит предел, за которым божественная мудрость и могущество ничего не создают и не устраивают; мне не хотелось бы, чтобы мы так ограничивали силу божественной руки. Удовольствуемся же уверенностью, что бог и природа так заняты попечениями о вещах человеческих, что большего
|
Природа и бог заботятся о людях так, как если бы у них не было других забот. Забота бога о роде человеческом на примере Солнца. |
|
Великая дерзость называть излишним во вселенной то, пользу чего для нас мы не постигаем. |
Сагредо. — Скажите лучше: мы не знаем того, чем это служит для нас, и я думаю, что это будет всего правильнее. И я считаю одной из величайших наглостей и глупостей, когда говорят: «Раз я не знаю, для чего мне служит Юпитер или Сатурн, то, значит, они излишни и даже не существуют в природе». Ведь я не знаю также, о безрассуднейший человек, для чего мне служат артерии, хрящи, селезенка или желчь, я даже не знал бы, что имею желчь, селезенку или почки, если бы они не были мне показаны на многих рассеченных трупах; и только тогда я могу понять, что именно делает во мне селезенка, когда я ее лишусь. Чтобы понять, как воздействует на меня то или другое небесное тело (если уж ты хочешь, только удалив с чтобы каждое их действие было направлено на нас), нужно было бы на некоторое
|
Только удалив с неба какую-нибудь звезду, можно было бы узнать, как она воздействует на нас. |
|
Многое на небе может быть невидимо для нас. |
Сальвиати. — Не стоит, синьор Сагредо, предаваться такому бесплодному пафосу; последуем лучше нашему обычному правилу — исследовать основательность доводов, приводимых каждой из сторон, ничего не предопределяя и предоставив суждение тому, кто знает об этом больше нас. Возвращаясь к нашим естественным и человеческим рассуждениям, я говорю, что эти понятия: большое, малое, огромное, незначительное и т. д.
|
Большое, малое, огромное и т. д. — суть понятия относительные. Несостоятельность мнения тех, которые считают звездную сферу слишком обширной по учению Коперника. |
|
Пространство, отведенное для одной неподвижной звезды, много меньше пространства, отведенного для одной планеты. Звезда называется малой по отношению к величине окружающего ее пространства. Вся звездная сфера с большого расстояния может показаться столь же малой, как одна единственная звезда. |
Сагредо. — Великой кажется мне глупость тех, которые хотят, единственная чтобы бог сотворил вселенную скорее соответственно малой способности их разумения, чем соответственно огромному, даже бесконечному своему могуществу.
Симпличио. — Все, что вы говорите, очень хорошо, но то, против чего противная сторона возражает, — это признание, что неподвижная звезда должна быть не только равна Солнцу, но даже больше его, хотя оба они являются обособленными телами, расположенными внутри звездной сферы. И мне кажется, что весьма кстати спрашивает этот автор:
|
Возражения в форме вопросов автора книжки. |
Сальвиати. — Из вопросов, предлагаемых этим человеком, мне кажется,
|
Ответы на возражения автора книжки. |
|
Автор книжки в своих вопросах путается и противоречит сам себе. |
|
Вопросы автору книжки, которые показывают несостоятельность его вопросов. |
Симпличио. — Действительно, и я, читая это место, сейчас же заметил очевидное противоречие; он говорит, что звезды, так сказать Коперника, являющиеся такими маленькими, не могут действовать на Землю, и не замечает, что допустил действие на Землю звезд Птоломея и своих, которые не только являются крохотными, но по большей части невидимы.
Сальвиати. — Перехожу к другому пункту. На каком основании
|
То, что удаленные предметы кажутся маленькими, является следствием несовершенства глаза, как это и доказывается. |
Сагредо. — Я ответил бы за них отрицательно, тем более что в этом
|
Ни Тихо, ни его приверженцы не пытались посмотреть, существует ли какое-либо явление на небе, говорящее против или в пользу годичного движения. |
Сальвиати. — Я того же мнения и даже думаю, что они аргументируют против одного человека больше для защиты другого человека, чем из желания притти к познанию истины. И я думаю, что ни один из них не занимался такого рода наблюдениями; и я даже не уверен, знает ли кто-нибудь из них, какое различие должно было бы вызвать в неподвижных
|
Астрономы едва ли отдавали себе отчет о тех небесных явлениях, которые должны были вытекать из годичного движения Земли. Кое-чего Коперник не знал из-за отсутствия необходимых инструментов. |
|
Тихо и другие возражают против годового движения, основываясь на неизменной высоте полюса. |
Симпличио. — По правде сказать, синьор Сальвиати, и мне также кажется, что так должно было бы быть. Ведь вы, я думаю, не будете отрицать, что если мы пройдем всего только 60 миль к северу, то полюс поднимется на один градус, а если мы передвинемся еще на 60 миль к полуночи, то полюс поднимется еще на градус, и так далее; значит, если приближение и удаление только на 60 миль делает столь заметным изменение высоты полюса, то каким же оно должно оказаться, если Земля перенесется и мы вместе с нею, скажем, не на 60 миль, а на 60 тысяч миль?
Сальвиати. — Придется допустить (сохраняя ту же пропорцию), что полюс должен подняться на тысячу градусов. Видите, синьор Симпличио, к чему может привести застарелый предрассудок. Запечатлев в своем воображении за много лет, что небо, а не Земля, обращается в двадцать четыре часа и что, следовательно, полюсы этого обращения находятся на небе, а не на земном шаре, вы не можете даже на час отрешиться от этого привычного взгляда и проникнуться противоположным, представив себе, что Земля и есть само движущееся тело, хотя бы представив это только на такое время, какого окажется достаточным для понимания того, что воспоследует, если эта ложь станет истинной. Если Земля, синьор Симпличио, и есть то, что вращается вокруг самой себя в двадцать четыре часа, то на ней находятся полюсы, в ней находится ось, на ней находится экватор, т. е. наибольший круг; описываемый точкой, равноудаленной от полюсов, на ней находятся бесконечные параллели, бо́льшие и меньшие, описываемые точками ее поверхности, более или менее удаленными от {270} полюсов; на ней находится все это, а не на звездной сфере, у которой, раз она неподвижна, нет ничего; и только воображением все это можно туда перенести, представив себе земную ось продолженной настолько, чтобы она своими концами обозначила две точки, стоящие против наших полюсов, а плоскость растянутого экватора изображающей на себе соответствующий ему круг. Значит, раз настоящая земная ось, настоящие земные полюсы, настоящий земной экватор не изменяются на Земле, то, поскольку вы остаетесь в том же самом месте Земли, пусть Земля переносит вас куда вам угодно — вы ни в чем не измените своего обычного положения ни по отношению к полюсам, ни по отношению к параллелям, ни по отношению к другой любой земной вещи; и это потому, что такое перенесение является общим для вас и для всех земных вещей, а движение,
|
Движение, поскольку оно общее, как будто не существует. |
Сагредо. — Разрешите мне, пожалуйста, синьор Сальвиати, объяснить
|
Пример, удобный для того, чтобы разъяснить, что высота полюса не должна изменяться в результате годового движения Земли. |
Симпличио. — Думаю и понимаю, что она не прибавится ни на волос в результате пути в тысячу и в сто тысяч миль, а не то что в 30 шагов; но я твердо убежден, что если при наведении на верхушку фок-мачты инструмента на прямой линии встретится неподвижная звезда, то, говорю я, установив твердо квадрант и проплыв в направлении звезды 60 миль, мы найдем, что хотя мушка и совпадает попрежнему с верхним концом мачты, она уже не совпадает со звездой, которая, по-моему, должна подняться на один градус.
Сагредо. — Но ведь вы не думаете, что визир не попадет в ту же точку звездной сферы, которая соответствует направлению верхушки фок-мачты?
Симпличио. — Нет, но точка будет другой, лежащей ниже звезды, наблюдавшейся первоначально.
Сагредо. — Именно так. Но как в данном примере то, что соответствует высоте верхушки мачты, является не звездой, а той точкой небосвода, которая находится на прямой линии, проходящей от глаза через {271} вершину мачты, так же и в этом случае, для которого мы подыскивали пример, то, что на небосводе соответствует полюсу Земли, является не звездой или другой неподвижной вещью небосвода, а той точкой, в которой заканчивается продолженная до него земная ось; эта точка не неподвижна, но следует за движениями земного полюса; поэтому Тихо или другие выставлявшие это возражение обязаны были сказать, что при годовом движении Земли, если бы оно действительно существовало, должны были бы распознаваться и наблюдаться некоторые различия
|
Годичное движение Земли могло бы иметь следствием изменение положения каких-нибудь неподвижных звезд, но не полюса. |
Симпличио. — Теперь я очень хорошо понимаю совершаемую ими ошибку, но от этого, по моему мнению, не убывает сила — а, мне кажется, она очень велика — обратного аргумента, поскольку он направляется теперь на изменения звезд, а не полюса; принимая во внимание, что перемещение галеры всего на 60 миль поднимает для меня звезду на один градус, как может не произойти подобного и даже гораздо большего изменения, когда галера перенесется по направлению к той же самой звезде на пространство, равное диаметру большой орбиты, который вы считаете вдвое превышающим расстояние от Земли до Солнца.
Сагредо. — Здесь, синьор Симпличио, имеется другое недоразумение;
|
Опровергается неправильное мнение, будто при годовом движении Земли должны происходить большие изменения в высоте неподвижных звезд. |
Симпличио. — Конечно нет, так как изменение произошло в положении инструмента, а не наблюдателя, который должен был бы изменить место, двигаясь по направлению к звезде.
Сагредо. — А если вы плывете или идете по поверхности Земли, то скажете ли вы, что с тем же самым квадрантом не происходит никакого изменения и что всегда сохраняется одна и та же высота относительно неба, если только вы сами не наклоняете квадрант, а оставляете его в первоначальном положении?
Симпличио. — Дайте мне немного подумать. Я скажу, конечно, что не сохраняет, так как путь, который я совершаю, проходит не по плоскости, а по окружности земного шара, который с каждым шагом меняет наклон относительно неба и, следовательно, заставляет меняться наклон инструмента, постоянный по отношению к Земле.
Сагредо. — Вы превосходно сказали и вы понимаете также, что чем больше будет тот круг, по которому вы двигаетесь, тем больше миль нужно пройти, чтобы звезда поднялась над вами еще на один градус, и что в конце концов когда движение по направлению к звезде будет происходить по прямой линии, то придется двигаться еще дальше, чем по окружности сколь угодно большего круга.
Сальвиати. — Да, так как в конце концов окружность бесконечно
|
Прямая линия и окружность бесконечно большого круга — одно и то же. |
Сагредо. — О, этого я не понимаю и не думаю, чтобы понимал и синьор Симпличио; здесь должна скрываться какая-то тайна, так как круга мы знаем, что синьор Сальвиати никогда не говорит зря и не сказал бы парадокса, если бы он не привел к какому-нибудь совершенно необычному представлению; поэтому в свое время и в своем месте я попрошу вас разъяснить, почему прямая линия и окружность бесконечно большого круга одно и то же; сейчас же я не хочу прерывать занимающего нас разговора. {272} Возвращаясь к нашему случаю, я обращаю внимание синьора Симпличио на то, что приближение и удаление Земли относительно неподвижной звезды, которая близка к полюсу, происходит как бы по прямой линии, составляющей диаметр земной орбиты; таким образом, желание определять повышение или понижение Полярной звезды посредством движения по этому диаметру так же, как посредством движения по совсем маленькому кругу Земли, является признаком большого непонимания.
Симпличио. — Но мы все-таки остаемся в том же самом затруднительном положении, так как даже то небольшое различие, которое должно было бы существовать, обнаружилось бы наблюдением; если же это различие равно нулю, то нам нужно признать, что и годовое движение по большой орбите, приписываемое Земле, равно нулю.
Сагредо. — Здесь я предоставлю продолжение синьору Сальвиати. Он, мне кажется, не считал равным нулю повышение или понижение Полярной звезды или какой-либо другой из неподвижных звезд, хотя оно никем не наблюдалось, и сам Коперник принимает его — не скажу, чтобы за нуль, но за нечто, недоступное наблюдению из-за своих малых размеров.
Сальвиати. — Как я уже сказал раньше, я не думаю, чтобы хоть кто-нибудь
|
Спрашивается, в каких звездах и какие изменения должны были бы наблюдаться в результате годового движения Земли. Раз астрономы не определили точно, какие изменения могли бы проистекать из годового движения Земли, то это является признаком того, что они как следует этого не понимали. |
|
Изменения у неподвижных звезд должны быть у одних бо́льшими, у других меньшими, а у третьих сводиться к нулю. |
Сагредо. — У меня, кажется, голова пойдет кругом от такого клубка хитросплетений, которые, бог весть, смогу ли я когда-нибудь распутать; признаваясь в своем бессилии синьору Сальвиати, скажу, что я многократно над этим думал, но никогда не мог найти конца; я говорю не столько о том, что относится к неподвижным звездам, сколько о другом, роковом вопросе; о котором вы мне напомнили этими меридианными высотами, азимутами восхождения, расстояниями от зенита и т. д.41. Я вам сейчас скажу, отчего мутится мой ум. Коперник полагает, что звездная сфера неподвижна
|
Главный аргумент против Коперника — это то, что проявляется на Солнце и на неподвижных звездах. |
Сальвиати. — Эти трудности достойны ума синьора Сагредо; и сомнения здесь так велики, что даже сам Коперник почти потерял надежду разъяснить их удовлетворительным образом; это видно как из того, что он сам признавал здесь неясность, так и из того, что он дважды двумя разными способами принимался ее разъяснять; и я откровенно признаюсь, что понял его объяснения только после того, как сделал его понятным посредством другого приема, очень простого и ясного, и то не без долгой и трудной работы мысли.
Симпличио. — Аристотель видел ту же самую трудность и пользовался
|
Возражения Аристотеля против античных философов, желавших сделать Землю планетой. |
Сальвиати. — Чем больше и крепче узел, тем прекраснее и достойнее удивления распутывание его. Но я вам не обещаю этого на сегодня и прошу освободить меня до завтра. А сейчас обсудим и разъясним те изменения и различия, какие должны были бы наблюдаться в неподвижных звездах в результате годового движения, как мы только что говорили. При рассмотрении этого нужно установить предварительно некоторые положения для разрешения самой главной трудности. Итак, мы возвращаемся к двум движениям, приписываемым Земле (говорю двум, так как третье не является собственным движением, как в своем месте я разъясню), т. е. годовому и суточному; под первым нужно понимать движение, совершаемое центром Земли по окружности большой орбиты, т. е. наибольшего круга, описанного в плоскости эклиптики, неподвижной и неизменной; второе, т. е. суточное движение, совершается земным шаром самим по себе вокруг
|
Годичное движение центра Земли по эклиптике и суточное движение Земли вокруг собственного центра. |
|
Ось Земли всегда параллельна самой себе, описывает цилиндрическую поверхность и наклонна по отношению к большой орбите. |
|
Земной шар никогда не изменяет наклона и сохраняет его неизменным. |
|
Неподвижные звезды, находящиеся в плоскости эклиптики, никогда не повышаются и не понижаются вследствие годового движения Земли, а только приближаются или удаляются. Соображения против годового движения Земли, вызванные находящимися на эклиптике неподвижными звездами. |
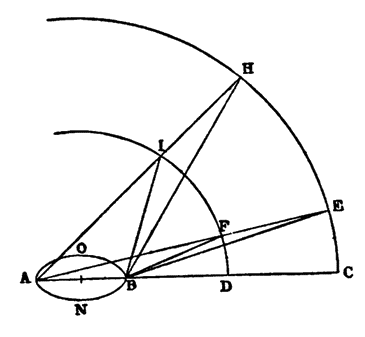 в направлении одной и той же линии ABC, хотя удаленность ВС меньше СА на весь диаметр ВА; значит, самое большее, что можно заметить в отношении звезды С и какой угодно другой, находящейся на эклиптике, это — увеличение или уменьшение видимой величины ее в результате приближения или удаления Земли.
в направлении одной и той же линии ABC, хотя удаленность ВС меньше СА на весь диаметр ВА; значит, самое большее, что можно заметить в отношении звезды С и какой угодно другой, находящейся на эклиптике, это — увеличение или уменьшение видимой величины ее в результате приближения или удаления Земли.
Сагредо. — Будьте любезны, подождите немного, так как я испытываю некоторое сомнение, смущающее меня. Дело в следующем. Что звезда С будет видна вдоль одной и той же линии ABC, находится ли Земля в А или же в В, я понимаю очень хорошо; так же хорошо я понимаю, что то же самое происходило бы со всеми точками на линии АВ, если бы Земля переходила из А в В по этой линии; но так как она переходит, как это предполагается, по дуге ANB, то совершенно очевидно, что когда она будет в точке N или в какой-нибудь другой точке, кроме А и В, то звезда будет наблюдаться уже не вдоль линии АВ, а вдоль многих других линий. Таким образом, если видимость звезды вдоль разных линий должна являться причиной видимых изменений, то некоторые отличия должны наблюдаться. Я скажу даже больше, пользуясь той философской свободой, которую нужно считать допустимой среди философов-друзей: мне кажется, что вы, противореча самому себе, отрицаете сейчас то, что недавно, к нашему удивлению, установили как нечто, совершенно истинное и великое; я говорю о том, что происходит с планетами и, в частности, с тремя верхними планетами, которые, находясь непрерывно на эклиптике или чрезвычайно близко к ней, не только кажутся то близкими к нам, то чрезвычайно отдаленными, но настолько нарушают правильность своих движений, что иногда представляются нам неподвижными, иногда же отступающими на много градусов; и все это не по какой-либо другой причине, а только из-за годового движения Земли.
Сальвиати. — Хотя у меня и были тысячи поводов убедиться в проницательности синьора Сагредо, все же я хочу посредством нового испытания еще больше удостовериться, чего я могу еще ожидать от его остроумия себе на пользу, так как если мои положения смогут выйти целыми из-под молота или из пробирного тигля его суждений, то я могу быть уверен, что они состоят из настоящего хорошего материала. Скажу, однако, что я нарочно скрывал это возражение, но совсем не для того, чтобы серьезно вас обманывать и убеждать в чем-нибудь ложном, как это могло бы случиться, если бы возражение, скрываемое мною и упущенное вами, на самом деле было таким, каким оно кажется на первый взгляд, т. е. действительно сильным и убедительным; но оно не таково, и сейчас я даже сомневаюсь, не притворились ли вы не понимающим его ничтожность, чтобы испытать меня. Но в этом вопросе я хочу вас перехитрить, вырвав у вас {275} насильно признание того, что вы так искусно хотели скрыть. Поэтому скажите мне: откуда именно вы знаете, что стояние и попятное движение планет зависят от годового движения Земли и оно настолько велико, что по крайней мере хоть какой-нибудь след подобного явления должен был бы наблюдаться на звездах эклиптики?
Сагредо. — Ваше обращение содержит два вопроса, на каждый из которых мне приходится ответить: первый касается обвинения вами меня в притворстве; второй — того, что может проявляться в звездах и т. д. Что касается первого, то я скажу для вашего удовлетворения, что неправда, будто я притворялся непонимающим несостоятельность такого соображения, а чтобы уверить вас в этом, я утверждаю, что теперь прекрасно понимаю его несостоятельность.
Сальвиати. — Но теперь уже я не понимаю, как это может быть, чтобы вы не притворялись, говоря, что не сознавали ошибки, которую теперь, по вашему признанию, вы понимаете очень хорошо.
Сагредо. — Самое признание в понимании ошибки может вас уверить, что я не притворялся непонимающим, так как, если бы я сейчас, как и раньше, притворялся, то что могло бы меня удержать и помешать продолжать это притворство, отказываясь все время понимать ошибку? Итак, я говорю, что не понимал ее раньше, но хорошо понимаю теперь, благодаря тому, что вы пробудили мой разум, сперва решительно указав мне ничтожность возражения, а затем предложив мне общие вопросы,
|
Стояние, поступательное и попятное движение у планет узнаются по их отношению к неподвижным звездам. |
Сальвиати. — Именно это, а вы еще прибавили к нему тонкое остроумие. И если я маленьким словцом подтолкнул ваш ум, то вы другим словом напомнили мне, что не исключена возможность того, что с течением
|
Показания неподвижных звезд, подобные наблюдаемым у планет, как доказательство годового движения Земли. |
|
Неподвижные звезды вне эклиптики повышаются и понижаются больше или меньше в зависимости от их расстояния от эклиптики. |
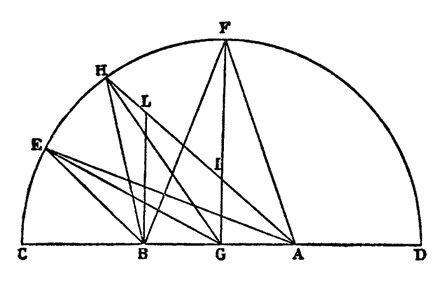 ее с двух мест А и В разница будет еще больше, поскольку угол АЕВ делается больше угла при Е; этот угол все время растет в зависимости от все большего удаления наблюдаемой звезды от эклиптики, так что в конце концов наибольшее изменение проявится в той звезде, которая будет помещаться на самом полюсе эклиптики. Для полного понимания мы можем доказать это так. Пусть АВ будет диаметр земной орбиты, a G ее центр; представим себе диаметр продолженным до звездной сферы в точках D и С и пусть из центра G проведена перпендикулярно плоскости эклиптики ось GF, продолженная до той же сферы; предположим, что на ней же расположен меридиан DFC, перпендикулярный к плоскости эклиптики; взяв на дуге FC любые точки Е и Е, как места неподвижных звезд, проводим линии FA, FB, АН, HG, HВ, АЕ, GE и BE. Таким образом, углом различия высот или, скажем, параллаксом звезды, находящейся на полюсе F, будет AFB, параллаксом звезды, находящейся в H, будет угол АHВ и параллаксом звезды в Е будет угол АЕВ. Я утверждаю, что угол различия высот полярной звезды F будет самым большим и что другие углы, наиболее близкие к самому большому, будут больше, чем более удаленные, т. е. что угол F будет больше угла H, а угол H больше угла Е. Предположим, что вокруг треугольника FAB описан круг; так как угол F острый (ибо его основание АВ меньше диаметра ВС полукруга DFC), то он будет лежать в большем отрезке описанного круга, отсеченном основанием АВ, и так как это основание АВ разделено в середине под прямыми углами линией FG, то центр описанного круга будет лежать на линии FG; пусть это будет точка I. Далее, так как из всех линий, проведенных из точки G, не являющейся центром окружности описанного круга, до этой последней, самая большая — та, которая проходит через центр, то FG будет больше всякой другой линии, которая из точки G проводится до окружности этого круга; поэтому такая окружность пересечет линию GE (равную линии GF) и, пересекая GE, пересечет также АЕ, допустим, в L; проведя линию LB, получим два угла AFB и ALB, равных между собой, так как они опираются на одну и ту же часть описанного круга, но ALB — внешний угол, он больше внутреннего угла H и, следовательно, угол F больше угла H. Таким же способом мы докажем, что угол H больше угла Е, так как центр круга, описанного около треугольника АЕВ, лежит на перпендикуляре GF, к которому линия GH ближе, чем линия GE, и потому окружность его пересекает GE, а также АЕ; значит, положение доказано. Итак, мы приходим к заключению, что различие видимого положения (которое, применяя техническую терминологию, мы можем назвать параллаксом неподвижных звезд) бывает больше или меньше в зависимости от того, находятся ли наблюдаемые звезды более или менее близко к полюсу {277} эклиптики, так что в конце концов у звезд, находящихся на самой эклиптике, это различие сводится к нулю. Далее, что касается приближения Земли к звездам или удаления от них в результате ее движения, то по
ее с двух мест А и В разница будет еще больше, поскольку угол АЕВ делается больше угла при Е; этот угол все время растет в зависимости от все большего удаления наблюдаемой звезды от эклиптики, так что в конце концов наибольшее изменение проявится в той звезде, которая будет помещаться на самом полюсе эклиптики. Для полного понимания мы можем доказать это так. Пусть АВ будет диаметр земной орбиты, a G ее центр; представим себе диаметр продолженным до звездной сферы в точках D и С и пусть из центра G проведена перпендикулярно плоскости эклиптики ось GF, продолженная до той же сферы; предположим, что на ней же расположен меридиан DFC, перпендикулярный к плоскости эклиптики; взяв на дуге FC любые точки Е и Е, как места неподвижных звезд, проводим линии FA, FB, АН, HG, HВ, АЕ, GE и BE. Таким образом, углом различия высот или, скажем, параллаксом звезды, находящейся на полюсе F, будет AFB, параллаксом звезды, находящейся в H, будет угол АHВ и параллаксом звезды в Е будет угол АЕВ. Я утверждаю, что угол различия высот полярной звезды F будет самым большим и что другие углы, наиболее близкие к самому большому, будут больше, чем более удаленные, т. е. что угол F будет больше угла H, а угол H больше угла Е. Предположим, что вокруг треугольника FAB описан круг; так как угол F острый (ибо его основание АВ меньше диаметра ВС полукруга DFC), то он будет лежать в большем отрезке описанного круга, отсеченном основанием АВ, и так как это основание АВ разделено в середине под прямыми углами линией FG, то центр описанного круга будет лежать на линии FG; пусть это будет точка I. Далее, так как из всех линий, проведенных из точки G, не являющейся центром окружности описанного круга, до этой последней, самая большая — та, которая проходит через центр, то FG будет больше всякой другой линии, которая из точки G проводится до окружности этого круга; поэтому такая окружность пересечет линию GE (равную линии GF) и, пересекая GE, пересечет также АЕ, допустим, в L; проведя линию LB, получим два угла AFB и ALB, равных между собой, так как они опираются на одну и ту же часть описанного круга, но ALB — внешний угол, он больше внутреннего угла H и, следовательно, угол F больше угла H. Таким же способом мы докажем, что угол H больше угла Е, так как центр круга, описанного около треугольника АЕВ, лежит на перпендикуляре GF, к которому линия GH ближе, чем линия GE, и потому окружность его пересекает GE, а также АЕ; значит, положение доказано. Итак, мы приходим к заключению, что различие видимого положения (которое, применяя техническую терминологию, мы можем назвать параллаксом неподвижных звезд) бывает больше или меньше в зависимости от того, находятся ли наблюдаемые звезды более или менее близко к полюсу {277} эклиптики, так что в конце концов у звезд, находящихся на самой эклиптике, это различие сводится к нулю. Далее, что касается приближения Земли к звездам или удаления от них в результате ее движения, то по
|
Земля приближается к неподвижным звездам эклиптики и удаляется от них на расстояние диаметра большой орбиты. |
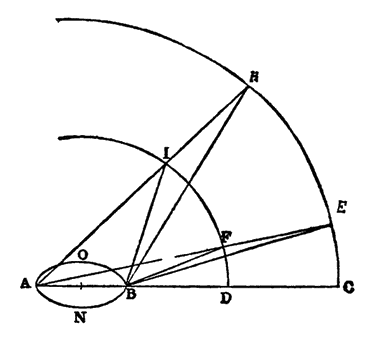 от нас наблюдаемой звезды; если мы нанесем еще один меридиан в меньшем расстоянии от Земли, каковым пусть будет DFI, то звезда, находящаяся в F, будет видна в том же направлении AFE, если Земля находится в А;
от нас наблюдаемой звезды; если мы нанесем еще один меридиан в меньшем расстоянии от Земли, каковым пусть будет DFI, то звезда, находящаяся в F, будет видна в том же направлении AFE, если Земля находится в А;
|
Большие изменения происходят с более близкими звездами, чем с более далекими. |
Сагредо. — С большим удовольствием, а также и пользой слушал я ваши рассуждения и,
|
Обзор явлений, наблюдаемых у неподвижных звезд, порождаемых годовым движением Земли. |
Симпличио. — Действительно, я, откровенно говоря, очень затрудняюсь признать расстояния до неподвижных звезд столь огромными, чтобы такие разобранные вами различия стали совершенно неуловимыми.
Сальвиати. — Не отчаивайтесь, синьор Симпличио, может быть, найдется еще какое-нибудь средство разрешить ваши затруднения. Во-первых, вам вовсе не должно казаться невероятным, что видимая величина звезд ощутимо не изменяется, ибо вы можете видеть, что при оценке {278}
|
Приближение и удаление очень далеких светящихся предметов неуловимо. |
Симпличио. — Не затрудняйте себя больше этой частностью, синьор; я уже вполне хорошо понял все то, что было сказано о неизменности видимых величин неподвижных звезд. Но что скажем мы о другой трудности, проистекающей от того, что мы не замечаем никакого изменения в их взаимном расположении?
Сальвиати. — Скажем кое-что, что, быть может, сможет вас успокоить также и с этой стороны. Короче говоря, не будете ли вы удовлетворены, если на самом деле на звездах будут подмечены те изменения, которые, по вашему мнению, должны были бы наблюдаться, если бы годовое движение принадлежало Земле?
Симпличио. — Несомненно, буду, поскольку это относится к данной частности.
Сальвиати. — Я предпочел бы, чтобы вы сказали так: если это различие
|
Если бы в неподвижных звездах было заметно какое-нибудь годичное изменение, то против движения Земли нельзя было бы возражать. |
|
Доказательство того, как мало можно полагаться на астрономические инструменты при точных наблюдениях. |
|
Недоверие Птоломея к инструменту, изготовленному Архимедом. |
Симпличио. — Но если инструменты и самые наблюдения так сомнительны, то как можем мы в конце концов получить достоверные знания {279}
|
Инструменты Тихо сделаны с большими затратами. |
Сальвиати. — Все это я допускаю, но ни первого, ни второго недостаточно, чтобы мы могли быть уверены в столь важном вопросе. Я хочу,
|
Какие инструменты требуются для чрезвычайно точных наблюдений? |
|
Точное наблюдение вхождения и выхождения Солнца при летнем солнцестоянии. |
|
Место, подходящее для наблюдения неподвижных звезд, поскольку это касается годового движения Земли. |
Сагредо. — Я очень хорошо понимаю весь этот замысел, и вся эта операция кажется мне столь легкой и приспособленной для надлежащей цели, что с большим основанием можно предположить, что сам Коперник или другие астрономы применяли этот способ.
Сальвиати. — А я думаю совершенно обратное, так как мало вероятно, чтобы кто-нибудь его испытал и не упомянул о результатах, безразлично, говорят ли они в пользу того или другого мнения; кроме того, ни для этой, ни для какой другой цели никто не прибегал к такому способу наблюдения, потому что без точного телескопа оно даже не может быть как следует осуществлено.
Сагредо. — Я совершенно успокоен вашими словами. Но так как нам остается еще много времени до ночи, то, если вы хотите, чтобы я провел ее спокойно, возьмите на себя труд объяснить нам те проблемы, разъяснение которых вы раньше просили отсрочить до завтра; верните добровольно данное нами согласие и, оставив в стороне все другие соображения, объясните нам, как из признания тех движений, которые Коперник приписывает Земле, и предположения о неподвижности Солнца и о неподвижных звездах могут вытекать те же самые явления в отношении повышения и понижения Солнца, изменения времен года, неравенства дней и ночей и т. д., которые так просто и легко объясняются системой Птоломея.
Сальвиати. — Не следует и даже невозможно пренебрегать тем, что интересует синьора Сагредо. И отсрочка, о которой я просил, нужна была только для того, чтобы выиграть время и привести в порядок в памяти те предпосылки, которые служат для широкого и ясного объяснения того, как названные явления вытекают и из системы Коперника так же, как и из системы Птоломея, причем из первой даже с гораздо большей легкостью и простотой, чем из второй, откуда с очевидностью следует,
|
Система Коперника представляет трудности для понимания, но не для существования. Предпосылки, необходимые для того, чтобы правильно понять следствия, вытекающие из движения Земли. |
Первая. Если принять, что Земля — сферическое тело — вращается вокруг собственной оси и полюсов, то каждая точка, отмеченная на ее поверхности, описывает окружность круга, большего или меньшего, в зависимости от того, находится ли она более или менее далеко от полюсов; наибольший из этих кругов — тот, который очерчивается точкой, равно удаленной от полюсов; все такие круги параллельны друг другу; мы их будем называть параллелями.
Вторая. Если Земля имеет сферическую форму и состоит из непрозрачного вещества, то одна половина ее поверхности непрерывно освещается Солнцем, в то время как другая половина остается темной; и так как граница, разделяющая освещенную часть от темной, является большим кругом, то мы будем называть его пограничным кругом света.
Третья. Когда пограничный круг света пройдет через полюсы Земли, то он рассечет (раз он большой круг) все параллели на равные части; если же он проходит не через полюсы, то он рассекает параллели на неравные части, за исключением одного только среднего круга, который, являясь большим, снова будет рассечен на равные части.
Четвертая. Если Земля вращается вокруг собственных полюсов, то величина дней и ночей определяется дугами параллелей, пересеченных пограничным кругом света; дуга, которая приходится на освещенную полусферу, определяет длину дня, а остающаяся — величину ночи.
Предположив все это, для более ясного понимания того, что будет сказано далее, сделаем такой чертеж: во-первых, наметим окружность {281}
|
Чрезвычайно простой чертеж, представляющий систему Коперника и ее следствия. |
|
Как происходит в системе Коперника годичное движение Солнца. |
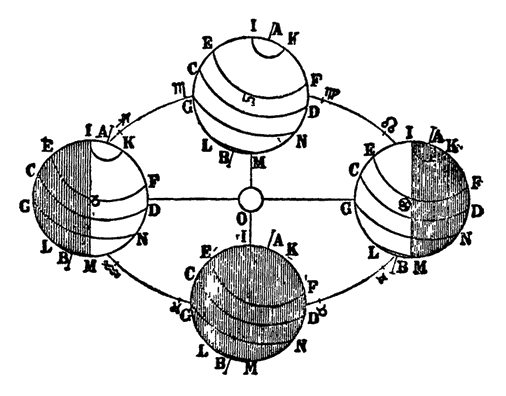 Очевидно, что когда Земля находится в Козероге, то Солнце видно в Раке, а когда Земля передвигается по дуге Козерог — Овен, то Солнце видно движущимся по дуге Рак — Весы, словом, пробегающим зодиак согласно порядку знаков на протяжении одного года; этим первым допущением без противоречий удовлетворяется видимое годовое движение Солнца по эклиптике.
Очевидно, что когда Земля находится в Козероге, то Солнце видно в Раке, а когда Земля передвигается по дуге Козерог — Овен, то Солнце видно движущимся по дуге Рак — Весы, словом, пробегающим зодиак согласно порядку знаков на протяжении одного года; этим первым допущением без противоречий удовлетворяется видимое годовое движение Солнца по эклиптике.
Переходя теперь к другому движению, т. е. к суточному движению Земли самой по себе, нужно установить ее полюсы и ее ось; последнюю нужно принимать не перпендикулярной к плоскости эклиптики, т. е. не параллельной оси земной орбиты, но отклоняющейся от прямого угла приблизительно на 23 с половиной градуса, причем ее северный полюс обращен к оси земной орбиты, если центр Земли находится в точке солнцестояния Козерога. Итак, предполагая, что центр земного шара находится в точке Козерога, обозначим полюсы Земли и ее ось через АВ, с наклоном от перпендикуляра к диаметру Козерог — Рак на 23 с половиной градуса, так что угол А Козерог — Рак является дополнительным до четверти, т. е. составляет 60 с половиной градусов; этот наклон нужно понимать неизменным; верхний полюс А будем считать северным, другой — В — южным. Если мы представим себе теперь, что Земля обращается сама по себе вокруг оси АВ в двадцать четыре часа также с запада на восток, то всеми точками, отмеченными на ее поверхности, будут описаны параллельные друг другу круги; обозначим в этом первом положении Земли наибольший круг через CD, два удаленных от него на 23 с половиной градуса — EF сверху и GN снизу — и два других — IK и LM — крайних, удаленных на такой же промежуток от полюсов А и В; и как мы наметили эти пять кругов, так же мы можем представить себе бесчисленное множество других кругов, параллельных этим, описанных бесчисленными точками земной поверхности. Предположим теперь, что Земля при годовом движении своего центра переносится в другие уже намеченные места, но следует при этом такому закону: ее собственная ось АВ не только не меняет наклона к плоскости эклиптики, но никогда не изменяет и направления, так что, оставаясь всегда параллельной самой себе, она всегда обращена к одним и тем же местам вселенной или, можем сказать, небосвода; если мы представим себе ее таким образом продолженной, то она самым верхним своим концом очертит круг, параллельный и равный земной орбите,— Весы, Козерог, Овен, Рак,— как верхнее основание цилиндра, описанного ею самой при годовом движении на нижнем основании Весы, Козерог, Овен, Рак. Поэтому, установив такую неизменность наклона, начертим три другие фигуры вокруг центров Овна, Рака и Весов, решительно во всем сходные с первой, описанной вокруг центра Козерога. {282}
Рассмотрим теперь первую фигуру Земли: таккак ось АВ отклонена от перпендикуляра к диаметру Козерог — Рак на 23 с половиной градуса в направлении Солнца О и так как дуга AI тоже составляет 23 с половиной градуса, то свет Солнца озарит обращенную к нему полусферу земного шара (от которой здесь видна только ее половина), отделенную от темной части границей света IM, его параллель CD как наибольший круг будет разделена на равные части, все же другие будут разделены на части неравные, так как граница света IM не проходит через их полюсы А и В47; и параллель IК вместе со всеми другими параллелями, описанными внутри ее и более близкими к полюсу А, останется в пределах освещенной части, тогда как, наоборот, противоположные параллели у полюса В, заключенные внутри параллели IM, останутся во мраке. Кроме того, так как дуга AI равна дуге FD, а дуга AF — общая, то две дуги IKF и AFD будут равны, и каждая будет составлять четверть круга; и так как вся дуга IFM есть полукруг, то дуга MF будет четвертью круга и будет равна другой дуге FKI, поэтому Солнце О будет при этом положении Земли для находящегося в точке F стоять в зените. Но вследствие суточного обращения вокруг постоянной оси АВ все точки параллели EF проходят через ту же точку F, поэтому в такой день Солнце в полдень будет стоять в зените для всех обитателей параллели EF, и им будет казаться, что оно описывает в своем видимом движении круг, который мы называем тропиком Рака. Для обитателей всех параллелей, которые находятся выше параллели EF по направлению к северному полюсу А, Солнце отклоняется от зенита к югу; и наоборот, для всех обитателей тех параллелей, которые находятся ниже EF по направлению к экватору CD и южному полюсу B, полуденное Солнце перешло за их отвесную линию по направлению к северному полюсу А. Отсюда же видно, как из всех параллелей только наибольшая CD рассечена на равные части границей света IM, а все другие, находящиеся ниже и выше названной наибольшей параллели, рассечены на неравные части; все верхние, т. е. полуденные, дуги, являющиеся дугами той части земной поверхности, которая освещена Солнцем, больше полуночных, остающихся в темноте; противоположное этому происходит у остальных, которые находятся ниже наибольшей параллели CD в направлении к полюсу В: у них полуденные дуги меньше полуночных. Отсюда также ясно видно, что разности этих дуг увеличиваются в зависимости от того, насколько параллели ближе к полюсам, так что в конце концов параллель IK окажется целиком в освещенной части и у жителей ее будет день в двадцать четыре часа без ночи; обратно этому, параллель LM, полностью оставаясь в темноте, обладает ночью в двадцать четыре часа без дня.
Перейдем теперь к третьей фигуре Земли, когда центр ее находится в точке Рака, откуда Солнце видно в первой точке Козерога; уже совершенно ясно, что раз ось АВ не изменила наклона и осталась параллельной самой себе, то вид и положение Земли в точности те же самые, как и на первой фигуре, за исключением того, что та полусфера, которая на первой фигуре была освещена Солнцем, на этой остается в темноте, освещается же та, которая в первом положении была затемнена; поэтому все то, что происходило на первой фигуре в смысле разности дней и ночей, в смысле того, что первые были больше или меньше вторых, теперь происходит в обратном порядке. Прежде всего, видно, что круг IK, который на первой фигуре был полностью на свету, оказался теперь полностью, в темноте; противоположный круг LM теперь полностью на свету, тогда как раньше он был полностью затемнен; у параллелей между наибольшим кругом CD и полюсом А все полуденные дуги теперь меньше полуночных, тогда как раньше это было наоборот; равным образом у дуг около полюса {283} В теперь полуденные дуги больше полуночных, обратно тому, что происходило в первом положении Земли; видно, что теперь Солнце стало в зените для жителей тропика GN и что оно понизилось к югу для жителей параллели EF на всю дугу ECG, т. е. на 47 градусов, и что, словом, оно прошло от одного тропика до другого, перейдя экватор, повышаясь и понижаясь на меридиане на указанную величину — 47 градусов. И все это изменение происходит не оттого, что Земля наклоняется или поднимается, а напротив, оттого, что она никогда не поднимается и не наклоняется, словом, оттого, что она всегда сохраняет одно и то же положение относительно вселенной, только лишь обходя кругом Солнца, находящегося в середине той самой плоскости, по которой она движется вокруг него в годовом движении. Здесь следует отметить следующее удивительное
|
Удивительное явление, происходящее оттого, что ось Земли не наклоняется. |
Перейдем теперь к объяснению остающегося и рассмотрим Землю на четвертой фигуре, т. е. когда центр ее находится в первой точке Весов, откуда Солнце видно в начале Овна; земная ось, которая на первой фигуре разумелась наклонной к диаметру Козерог — Рак и потому лежащей в той же самой плоскости, которая, пересекая плоскость земной орбиты по линии Козерог — Рак, была к последней перпендикулярна, остается, как мы это утверждаем, параллельной самой себе и потому окажется в плоскости, также перпендикулярной к плоскости земной орбиты и параллельной той плоскости, которая под прямыми углами пересекает ту же плоскость по диаметру Козерог — Рак. Поэтому линия, которая идет от центра Солнца к центру Земли, т. е. линия О — Весы, будет перпендикулярна к оси В А; но та же самая линия, идущая от центра Солнца к центру Земли, всегда перпендикулярна также к пограничному кругу света; поэтому данный круг пройдет через полюсы А и В на четвертой фигуре, ось АВ будет лежать в его плоскости. Но наибольший круг, проходящий через полюсы параллелей, делит их все на равные части; следовательно, все дуги IK, EF, CD, GN и LM будут полукругами; освещенная полусфера будет та, которая обращена к нам и Солнцу; границей света будет тот же круг ACBD, и когда Земля находится в этом месте, для всех ее обитателей будет наблюдаться равноденствие. То же самое происходит {284} и на второй фигуре, где Земля, имея освещенную полусферу со стороны Солнца, показывает нам другую, темную, с ее ночными дугами, также являющимися полукругами; следовательно, и здесь также наблюдается равноденствие. И наконец, если линия, проведенная из центра Солнца к центру Земли, перпендикулярна к оси АВ, к которой равным образом перпендикулярен наибольший круг параллелей CD, то та же самая линия O — Весы неизбежно должна лежать в плоскости параллели CD, пересекая ее окружность в середине дневной дуги CD; поэтому для находящегося в этом пересечении Солнце будет стоять в зените, но через это пересечение проходят, переносимые суточным обращением Земли, все обитатели данной параллели; значит, для всех них в этот день полуденное Солнце будет отвесно, и всем обитателям Земли Солнце покажется описывающим наибольшую параллель, называемую экватором. Далее, когда Земля находится в обеих точках солнцестояния, один из полярных кругов IK и LM остается целиком на свету, а другой — в темноте; когда же Земля находится в точках равноденствия, то одни половины этих полярных кругов находятся на свету, тогда как другие пребывают в темноте; нетрудно понять, что когда Земля переходит, например, от Рака (где вся параллель IK находится в темноте) ко Льву, то часть параллели IK со стороны точки I начинает вступать в свет, и что граница света IM начинает отступать к полюсам А и В, пересекая круг ACBD уже не в I и M, но в двух других точках, находящихся между концами I и А, М и В дуг IА и MB, где тогда обитатели круга IK начинают наслаждаться светом, обитатели же круга LM, наоборот, начинают чувствовать наступление ночи. Вот каким образом, приписывая земному шару два совсем простых движения, происходящих в отрезки времени, пропорциональные их величинам, не противоречащих друг другу, происходящих так же, как и у всех других движущихся мировых тел, с запада на восток, мы выводим все те явления, ради объяснения которых при неподвижности Земли необходимо (отказываясь от той симметрии, которая наблюдается между скоростями и величинами движущихся тел) приписывать сфере, более обширной, чем все другие, непостижимую быстроту, а другим, меньшим сферам — движение чрезвычайно медленное. Больше того, нужно делать это первое движение противоположным движению последних и, что еще увеличивает невероятность, допускать, что этой высшей сферой увлекаются все более низкие, вопреки их собственной склонности. И здесь я предоставляю вам самому судить, что именно является более правдоподобным.
Сагредо. — На мой взгляд и по моему разумению разница между простотой и легкостью объяснения явлений при помощи средств, намеченных в этой новой системе, и сложностью, запутанностью и трудностью,
|
Аксиомы, обычно принимаемые всеми философами. |
Симпличио. — Эти умозрения (если я смею откровенно высказать свое мнение) кажутся мне теми геометрическими тонкостями, за которые
|
Аристотель упрекает Платона в слишком большом пристрастии к геометрии. |
Сальвиати. — Я одобряю совет этих перипатетиков, удерживающих
|
Перипатетические философы осуждают изучение геометрии. |
Симпличио. — По правде говоря, я в этом не вполне разобрался, может быть, потому, что не располагаю сейчас теми основаниями, которые для тех же явлений приводятся Птоломеем; я говорю об этих стояниях, отступлениях, приближениях и удалениях планет, увеличении и уменьшении дней, изменениях времен года и т. д. Но, оставляя в стороне следствия, которые зависят от первоначальных предпосылок, я чувствую в самих предпосылках немалые трудности; если эти предпосылки опрокинуть, то они влекут за собою разрушение всего построения. А так как все здание Коперника, как мне кажется, построено на неустойчивом фундаменте, поскольку оно опирается на подвижность Земли, как если бы таковая могла менять место, то если подвижность устранить, нам не придется пускаться и в дальнейшие споры, а чтобы устранить ее, мне кажется, вполне достаточно аксиомы Аристотеля, что одному простому телу может, быть присуще только одно движение; здесь же Земле, простому телу,
|
Четыре различных движения, приписываемых Земле. |
Сальвиати. — В отношении движения вниз мы уже пришли к заключению,
|
Движение вниз свойственно не земному шару, а его частям. Годичное и суточное движения Земли совместимы. |
|
Каждое взвешенное и парящее тело, переносимое по окружности какого-либо круга, приобретает движение вокруг самого себя, противоположное первому. |
|
Опыт, наглядно показывающий, что два противоположные от природы движения могут быть присущи одному и тому же движущемуся телу. |
|
Третье движение, приписываемое Земле, есть, скорее, сохранение неизменяемости положения. |
|
Удивительная внутренняя сила земного шара — всегда смотреть на одни и те же части неба. |
|
Земной шар является магнитом. |
Симпличио. — Значит, вы принадлежите к тем, которые сочувствуют
|
Магнетическая философия Вильяма Гильберта. |
Сальвиати. — Принадлежу, конечно, и думаю, что моими товарищами будут все те, кто внимательно прочтет его книгу и ознакомится с его опытами; я не теряю надежды, что и с вами может случиться то же, что произошло в данном случае со мной, если только любознательность, подобная моей, и признание существования бесчисленного множества вещей в природе, еще непонятных для человеческого разума, освободят вас от рабской покорности тому или другому отдельному писателю по вопросам природы, ослабят путы, наложенные на ваш разум, и смягчат непримиримость и сопротивление вашего чувства, так что вы перестанете впредь отказываться прислушиваться к речам, еще не слыханным. Но ограниченность (да будет мне позволено воспользоваться этим термином) заурядных умов зашла столь далеко, что они не только слепо несут в виде дара
|
Ограниченность заурядных умов. |
Симпличио. — Я откровенно признаюсь, что был одним из этих заурядных умов, и только лишь несколько дней тому назад, когда мне пришлось столкнуться с вашими рассуждениями, я почувствовал себя несколько в стороне от избитых и обычных путей, но все же я еще не чувствую себя настолько поднявшимся над ними, чтобы шероховатости этого нового фантастического мнения не казались мне слишком большими и трудными для преодоления.
Сальвиати. — Если то, что описывает Гильберт, правильно, то это не мнение, а предмет познания, совсем не новый, а столь же старый, как и сама Земля. Если это учение соответствует правде, оно не может представляться шероховатым или трудным; путь его является гладким и чрезвычайно приятным. Если вам угодно, я дам вам наглядно убедиться, что вы сами себе создаете тени и боитесь чего-то такого, что не содержит в себе ничего страшного, точно малый ребенок, который испытывает страх перед букой, зная ее только по имени, так как кроме имени ничего и нет.
Симпличио. — Я буду рад, если вы меня просветите и избавите от ошибки.
Сальвиати. — Так отвечайте на поставленные мною вопросы. Во-первых, скажите мне, думаете ли вы, что наш земной шар, на котором мы живем и который мы называем Землей, состоит из одной единственной и простой материи или же что он является совокупностью материй, отличающихся друг от друга?
Симпличио. — Я вижу, что он состоит из весьма различных субстанций
|
Земной шар состоит из разнородной материи. |
Сальвиати. — Оставим пока в стороне моря и другие воды и поговорим о твердых частях; скажите мне, кажутся ли они вам одной и той же вещью или же различными вещами?
Симпличио. — Я вижу, что по внешности они различны, так как существуют громаднейшие пространства неплодородного песка и другие — с плодородными и плодоносными землями; множество бесплодных и диких гор, преисполненных твердыми скалами и камнями самых разнообразных сортов, как порфирами, алебастрами, яшмами и тысячами различных сортов мрамора; там существуют обширнейшие рудники металлов чрезвычайно разнообразных видов и, словом, такое различие материй, что целого дня нехватит, чтобы только их перечислить.
Сальвиати. — А считаете ли вы, что все эти разные материи, составляя общую массу, входят в нее равными количествами или же что существует одна из них, которая во много раз превосходит другие, являясь как бы главной материей и субстанцией огромной массы? {288}
Симпличио. — Я думаю, что камни, мраморы, металлы и другие весьма различные материи являются как бы внешними и поверхностными драгоценностями и украшениями первичного тела, которое по массе, я думаю, неизмеримо превосходит все остальное.
Сальвиати. — А из какой материи, думаете вы, состоит эта главная и обширная масса, для которой названные вещи являются как бы наростами и украшениями?
Симпличио. — Я думаю, что она простой или более чистый элемент земли.
Сальвиати. — Но что же вы понимаете под Землею? Может быть, она и есть то, что рассеяно до полям, что возделывают лопатами и плугами, куда высевают зерно и сажают фруктовые деревья, где естественно зарождаются громаднейшие леса и что, словом, является обиталищем и матерью всего растущего?
Симпличио. — Именно она, сказал бы я, является первичной субстанцией земного шара.
Сальвиати. — Ну, я не думаю, чтобы вы сказали это очень удачно; ведь та земля, которая возделывается, засеивается, которая приносит плоды, является лишь частью, и притом очень тонкой, земной поверхности; она уходит вглубь лишь на небольшое пространство по сравнению с расстоянием до ее центра; и опыт нам показывает, что стоит лишь прокопать немного вниз, как обнаруживаются материи, чрезвычайно отличные от этой внешней коры, более плотные и не способствующие произрастанию растительности; кроме того, вполне вероятно, что части, лежащие ближе к центру, придавленные огромными лежащими на них тяжестями, уплотнены и тверды, как любая самая твердая скала. Прибавьте к этому, что напрасно была бы дана способность к плодородию тем материям, которым никогда не суждено производить плоды, оставаясь вечно похороненными в глубоких и темных недрах Земли.
Симпличио. — А кто удостоверит нам, что части, близкие к центру, бесплодны? Может быть, и они производят что-нибудь, нам неизвестное.
Сальвиати. — Это лучше других должны знать вы и те, кто уверен, что тела, составляющие вселенную, созданы лишь для блага рода человеческого; если это так, то внутреннее тело Земли скорее всякого другого должно быть предназначено только для блага нас — его обитателей. Но какое благо сможем мы извлечь из материй, настолько от нас скрытых и удаленных, что мы никогда не будем в состоянии сделать их доступными обработке? Следовательно, внутренняя субстанция земного шара не может быть материей хрупкой, рассыпчатой и ничего не связующей, как та материя на поверхности, которую мы называем землей; но ей подобает быть телом чрезвычайно плотным и чрезвычайно прочным, словом, крепчайшим
|
Внутренние части земного шара должны быть чрезвычайно прочными. |
Симпличио. — Что внутренние части земного шара более сжаты, а потому более плотны и крепки и тем больше, чем дальше вглубь они идут, — это я допускаю, и это допускает также Аристотель, но я не чувствую ничего такого, что принуждало бы меня признать, что они вырождаются и представляют собой нечто, отличное от той же самой земли поверхностных частей.
Сальвиати. — Я предпринял это рассуждение не с целью убедить вас строгим доказательством, что первичной и реальной субстанцией земного шара является магнит, но только для того, чтобы показать вам, что нельзя найти основания, почему труднее признать Землю состоящей {289} из магнита, чем из какой-либо другой материи. И если вы как следует порассудите, то признаете вполне вероятным, что только простое произвольное название побудило людей считать ее состоящей из земли, так как обычно они пользуются с самого начала общим названием земля как для обозначения той материи, которую пашут и засевают, так и для наименования нашего земного шара; и если бы название последнего было произведено от камня, — а оно могло быть заимствовано от него так же,
|
Обитаемый нами шар назывался бы «Камнем», а не «Землей», если бы это название было ему дано сначала. |
Из тех оснований, которые убедительно доказывают de facto, что наш земной шар состоит из магнита, я вам не приводил пока ни одного, да теперь и не время приводить их, тем более что вы при желании сможете
|
Ход мыслей Гильберта в его философствовании. |
|
Многообразные свойства магнита. |
|
Убедительный аргумент в пользу того, что земной шар является магнитом. |
Симпличио. — Я скажу без всяких колебаний, что это кусок магнита.
Сальвиати. — Если это так, то скажите решительно, что под покровом и корой из земли, камней, металлов, воды и т. д. скрывается громадный магнит, ибо в нем распознаются всяким, кто потрудится его понаблюдать, все те свойства, которые соответственно замечаются на настоящем открытом шаре из магнита; если бы не наблюдалось ничего другого, кроме склонения иглы, которая, если ее переносить вокруг Земли, склоняется все больше и больше при приближении к северному полюсу и все меньше и меньше при приближении к экватору, под которым она становится в равновесии, то этого одного должно было бы быть достаточно для убеждения всякого самого упрямого судьи. Добавлю еще одно удивительное явление, которое наглядно видно на всех кусках магнита: для нас, жителей северного полушария, южный полюс такого магнита много сильнее другого, и разность эта заметна тем больше, чем мы дальше от экватора; под экватором обе стороны обладают равной силой, но заметно более слабой; в южных же областях, далеких от экватора, природа его меняется, и та сторона, которая у нас была слабее, приобретает там перевес над другой. Все это согласуется с тем, что мы видим на маленьком кусочке магнита в присутствии большего, сила которого, превосходя силу меньшего, заставляет его себе повиноваться, и, в зависимости от перемещения последнего по ту или другую сторону от экватора большого магнита, в нем происходят те же самые изменения, которые, как я сказал, происходят во всяком магните, переносимом по ту или другую сторону экватора Земли.
Сагредо. — Я был убежден Гильбертом при первом же чтении его книги и, найдя кусок превосходнейшего магнита, долгое время производил многочисленные наблюдения. Все они достойны крайнего удивления, но поразительнее всего мне кажется то, что у магнита значительно
|
Магнит в оправе удерживает несравненно больше, чем без оправы. |
Сальвиати. — Я видел его много раз и много ему удивлялся, но еще поразительнее маленький кусочек магнита, которым обладает наш Академик; этот кусочек весит не больше шести унций, и без оправы он поддерживает едва две унции, в оправе же сто шестьдесят унций, так что он удерживает в оправе в 80 раз больше, чем без оправы, причем он удерживает груз, в 26 раз превосходящий его собственный вес; это много удивительнее того, с чем встречался Гильберт, который пишет, что ему не приходилось видеть магнита, могущего поддерживать четырехкратный собственный вес.
Сагредо. — Мне кажется, что этот камень представляет человеческим умам обширное поле для философских размышлений. Тысячу раз я размышлял наедине, как это может быть, чтобы он придавал оправе из железа силу, настолько превосходящую свою собственную; и в конце концов я не нашел ничего, что удовлетворило бы меня; немного почерпнул я и из того, что пишет по этому поводу Гильберт, Не знаю, так ли это было с вами?
Сальвиати. — Я воздаю величайшую хвалу и завидую этому автору, так как ему пришло на ум столь поразительное представление о вещи, бывшей в руках у бесконечного числа других людей возвышенного ума, но никем не подмеченной; он кажется мне достойным величайшей {291} похвалы также и за много сделанных им новых и достоверных наблюдений, к стыду многочисленных лживых и пустых авторов, которые пишут не только о том, что знают, но и обо всем том, что черпают из разговоров глупой черни, не пытаясь удостовериться в справедливости услышанного с помощью опыта, может быть, для того, чтобы не уменьшить числа своих книг. По отношению к Гильберту я хотел бы только, чтобы он был немного больше математиком и, в частности, был лучше осведомлен в геометрии: практика в геометрии сделала бы его менее решительным в признании убедительными доказательствами тех доводов, которые он выставляет как истинные причины правильности наблюдаемых им явлений. Эти доводы (откровенно говоря) не доказывают и не убеждают с той силой, с какой должны делать это доводы, которые могут быть извлечены из естественных, необходимых и вечных следствий. И я не сомневаюсь, что с течением времени эта новая наука будет совершенствоваться путем новых наблюдений и в особенности путем правильных и необходимых доказательств. Но от
|
Первые наблюдатели и изобретатели достойны особого удивления. |
|
Истинная причина значительного увеличения силы магнита благодаря оправе. |
|
Для нового явления должна быть новая причина. |
|
Доказывается, что железо состоит из частиц более тонких, чистых и теснее расположенных, чем магнит. |
|
Наглядно показывается нечистота магнита. |
Сагредо. — Все это рассуждение показалось мне очень убедительным, и опыт с иглой мне представляется лишь немногим ниже математического доказательства; я искренно признаю, что во всей философии по магнетизму не слышал и не читал ничего такого, что приводило бы такие убедительные основания для объяснения какого-либо из других столь многих удивительных свойств магнита. Если бы у нас было такое же удовлетворительное объяснение их причин, я не знаю, какой еще более сладкой пищи мог бы пожелать наш разум.
Сальвиати. — При изучении неизвестных нам причин явлений нужно иметь счастье направить с самого начала рассуждения по истинному пути; если пойдешь по нему, то легко может случиться, что повстречаешься со многими другими положениями, признаваемыми за истинные, или в силу рассуждений, или в силу опытов, и от достоверности их истинность нашего пути приобретает силу и очевидность, как это в точности случилось и со мною в настоящей проблеме. Желая убедиться посредством какого-нибудь другого совпадения в истинности предполагаемой мною причины, т. е. в том, что субстанция магнита действительно менее целостна, чем субстанция железа или стали, я велел мастерам, работающим в галлерее моего государя, великого герцога, выровнять одну сторону того самого куска магнита, который раньше принадлежал вам, и потом как можно лучше отполировать и отшлифовать его; тогда, к моей радости, у меня в руках оказалось то, чего я искал. Ведь тогда открылось много пятен, по цвету отличных от остального и блестящих, как любой самый плотный и твердый камень; остальной же фон был полирован, но только {293} наощупь, так как он совершенно не блестел, а был как бы завуалирован; такова была субстанция магнита; блестящая же субстанция принадлежала другим камням, замешанным в магнит, как это наглядно распознавалось при поднесении выровненной стороны к железным опилкам; они в большом количестве подпрыгивали к магниту, но ни один кусочек не приставал к этим пятнам, которые были очень многочисленными: одни величиною в четверть ногтя, другие несколько меньше, совсем маленьких было чрезвычайно много, а едва видимых почти неисчислимое множество.
Тут я убедился, что мое представление было совершенно правильным, когда я с самого начала предполагал, что субстанция магнита должна быть не однородной и плотной, а пористой или, лучше сказать, губчатой, с тою лишь разницей, что углубления и ячейки у губки содержат воздух или воду, а у магнита они заполнены чрезвычайно плотным и тяжелым камнем, как это показывает исключительный блеск, который они приобретают. Поэтому, как я и говорил с самого начала, при соприкосновении поверхности железа с поверхностью магнита из мельчайших частиц железа, хотя и сжатых, может быть, больше, чем у любого другого тела (как это видно по тому, что они шлифуются лучше любой другой материи), не все, а лишь немногие встречают чистый магнит, а так как точек соприкосновения немного, то и связь получается слабая. Но так как оправа не только касается магнита значительной частью своей поверхности, но приобретает также свойство соседних частей, даже и не касаясь их, то, если точно выровнена та ее сторона, к которой пристает другая, так же хорошо выровненная сторона того куска железа, который должен быть поддержан, то соприкосновение происходит в огромном числе мельчайших частиц, если не в бесконечном числе точек обеих поверхностей, почему и связь получается очень крепкой. Такое явление, зависящее от выравнивания приводимых в соприкосновение поверхностей железа, не было подмечено Гильбертом. Он брал куски железа, закругленные так, что соприкосновение их было мало, отчего получалась значительно меньше и та прочность, с которой эти куски железа соединялись.
Сагредо. — Приведенные выше основания, как я это и говорил раньше, оставляют меня удовлетворенным разве немногим менее, чем если бы они были чистыми геометрическими доказательствами; а так как речь идет о физической проблеме, то,я думаю, будет удовлетворен и синьор Симпличио, поскольку от естественной науки, как он знает, нельзя требовать геометрической очевидности.
Симпличио. — Действительно, мне кажется, что синьор Сальвиати изящными и красивыми словами так ясно растолковал причину этого явления, что самый посредственный ум, даже не искушенный в науках, не мог бы этого не понять. Но мы, могущие пользоваться терминами нашего искусства, сводим причину этих и других подобных явлений природы к симпатии, т. е. некоторому соответствию и обоюдной склонности,
|
Симпатии и антипатии — термины, употребляемые философами для облегчения понимания причин многих явлений природы. Шутливый пример для доказательства несостоятельности некоторых философских рассуждений. |
Сагредо. — Таким образом этими двумя словами объясняется великое множество свойств и явлений, которые, как мы не без удивления видим, происходят в природе. Но такой способ философствования, мне кажется, обладает большим сходством с манерой живописи одного моего друга, несостоятельности который писал на полотне мелом: «Я хочу, чтобы здесь был родник с Дианой и ее нимфами; там — несколько охотничьих собак; с этого края я хочу, чтобы был охотник с головой оленя; остальное — поле, роща и холмы»; далее он предоставлял живописцу писать красками изображение; так он убеждал себя, что сам нарисовал эпизод с Актеоном, поместив туда {294} от себя только слова. Но куда завели нас эти столь длинные отступления от наших уже установленных положений? У меня почти выскочило из головы, на какую тему мы говорили до тех пор, пока не сбились на путь этого рассуждения о магнетизме; а я хотел что-то — не помню, что именно,— сказать по этому поводу.
Сальвиати. — Мы доказывали, что третье движение, приписываемое Коперником Земле, вовсе не движение, а покой и сохранение неизменного положения ее определенных частей по отношению к определенным частям вселенной, т. е. постоянное сохранение осью ее суточного вращения параллельности по отношению к самой себе и направленности к таким-то неподвижным звездам; это совершенно неизменное положение, говорили мы, свойственно всякому телу, взвешенному и парящему в текучей и податливой среде; хотя тело и переносится по Кругу, но оно не изменяет направления относительно внешних предметов и кажется вращающимся само по себе только в отношении того, кто его переносит, и к сосуду, в котором оно переносится. Потом мы добавили к этому простому и естественному свойству магнетическую силу, вследствие которой земной шар тем более устойчиво может сохранять неподвижность и т. д.
Сагредо. — Теперь я все припомнил; тогда мне пришло в голову и я хотел высказать некоторое соображение относительно затруднения и возражения синьора Симпличио, заставляющего его выступать против движения Земли, поскольку множественность движений нельзя приписать одному простому телу, у которого, по учению Аристотеля, естественно
|
Три различных естественных движения магнита. |
Симпличио. — Это не только не поражает его положения, но даже не направлено в его сторону, так как он говорит о простом теле и о том, что может ему естественно подходить, а вы возражаете тем, что подходит
|
Аристотель допускает для смешанных тел сложные движения. |
Сагредо. — Подождите немного, синьор Симпличио, и ответьте мне на вопросы, которые я вам задам. Вы говорите, что магнит не простое тело, а смесь; так я вас спрашиваю, каковы те простые тела, которые, смешиваясь, образуют магнит?
Симпличио. — Я не сумею вам назвать точно ни составных частей, ни доз, но достаточно того, что это — элементарные тела.
Сагредо. — Этого достаточно и для меня. А какие движения естественны для этих простых элементарных тел?
Симпличио. — Два простых прямых движения — sursum et deorsum.
Сагредо. — Скажите мне теперь, думаете ли вы, что движение, остающееся естественным у такого смешанного тела, должно быть таким, которое может получиться в результате сложения двух простых {295} естественных движений простых составляющих его тел, или же оно может быть таким, которое не может складываться из них?
Симпличио. — Я думаю, что смешанное тело будет двигаться
|
Движение смешанных тел должно быть таким, чтобы оно могло получиться в результате движений простых тел, их составляющих. Из двух прямолинейных движений не составляется кругового движения. |
Сагредо. — Но, синьор Симпличио, из двух прямых движений вы никогда не составите кругового движения, а магнит обладает двумя или тремя различными круговыми движениями. Итак, вы видите, в какие теснины заводят плохо обоснованные начала или, лучше сказать, плохо обоснованные следствия из хороших начал; сейчас вы принуждены будете сказать, что магнит является смесью из элементарных и небесных субстанций, если вы хотите сохранить за элементарными телами только
|
Философы должны признать, что магнит состоит из небесных и элементарных субстанций. |
|
Ошибка тех, кто называет магнит сложным телом, а земной шар простым. |
Это, мне кажется, то же самое, как если бы кто-нибудь назвал сложным телом хлеб, а простым телом ольяпотриду — похлебку, в которую помимо сотни разных других составных частей входит не малое количество хлеба54. Поистине удивительным представляется мне у перипатетиков следующее: они допускают (и отрицать этого они не могут), что наш земной шар de facto состоит из бесконечного числа различных материй; допускают тут же, что у сложных тел и движение должно быть сложным;
|
Перипатетические рассуждения полны ошибок и противоречий. |
Сальвиати. — Пожалуйста, синьор Сагредо, не будем утруждать себя больше этими деталями, в особенности, раз вы знаете, что нашей целью было не окончательное установление или признание истинности того или другого мнения, а только лишь изложение с целью испытания в нашей беседе тех доводов и возражений, которые могут быть выставлены в пользу как одной, так и другой стороны, причем синьор Симпличио выступает как защитник своих перипатетиков. Поэтому оставим вопрос открытым и предоставим внести решение тому, кто знает об этом больше нас. И так как мне кажется, что за эти три дня мы достаточно долго рассуждали о системе вселенной, то теперь наступило время перейти к главному вопросу, с которого начались наши рассуждения: я говорю о морских приливах и отливах, причину которых, как кажется, можно с большой вероятностью отнести к движениям Земли. Но это, если вам угодно, мы оставим до следующего дня. Пока же, чтобы не забыть, я хотел вам упомянуть об одном особом обстоятельстве, на которое, по моему мнению, Гильберту не следовало указывать. Я говорю о том его допущении, что если бы {296}
|
Невероятное свойство, ошибочно допускаемое Гильбертом в магните. |
Сагредо. — Я прекрасно понимаю, и это приводит мне на память одно
|
Вздорное рассуждение некоторых писателей в доказательство того, что элемент воды обладает сферической поверхностью. |
Сальвиати. — Ошибка действительно детская, и если бы ее допустил только один Сакробоско, то легко можно было бы ее и не касаться; однако, поскольку она не чужда также и его комментаторам и другим великим людям, вплоть до самого Птоломея, то я не могу этого сделать, хотя и краснею слегка за их репутацию. Но уже поздно; настало время нам проститься с тем, чтобы завтра, как обычно, встретиться здесь для того, чтобы сделать окончательные выводы из всех прошлых рассуждений.
| << | {297} | >> |

Сагредо. — Не знаю, действительно ли вы прибыли позже, чем всегда, для нашей обычной беседы или же желание услышать мысли синьора Сальвиати по такому интересному поводу обмануло меня и заставило время казаться столь долгим, но я добрый час простоял у окна, ожидая с минуты на минуту прибытия гондолы, которую я за вами послал.
Сальвиати. — По правде говоря, я думаю, что это, скорее, ваше воображение, чем наше запоздание, заставило время так тянуться. Чтобы не заставлять вас более ждать, хорошо будет, не тратя лишних слов, сразу приступить к делу и показать, как природа допустила (то ли iu rei veritate, то ли в шутку я как бы для того, чтобы потешиться
|
Природа как бы в шутку заставляет приливы и отливы свидетельствовать о подвижности Земли. |
|
Периодичность движения моря и движения Земли подтверждают друг друга. |
|
Наблюдаемые на Земле явления, за исключением периодичности движения морей, недостаточны для доказательства движения или покоя Земли. |
|
Первое основное положение о невозможности приливов и отливов при неподвижности Земли. |
Сагредо. — Положения весьма важные как сами по себе, так и по своим следствиям; с тем большим вниманием я ожидаю объяснений и доказательств.
Сальвиати. — В вопросах естествознания, к которым принадлежит и тот, которым мы сейчас занимаемся, познание явлений есть то, что ведет {298} нас к изысканию и нахождению причины. Без этого мы будем блуждать
|
Изучение явлений приводит к исследованию их причин. |
|
Троякие периоды изменения — суточные, месячные и годичные. |
Сначала побеседуем о суточном периоде как самом главном, который от вторичного воздействия со стороны Луны и Солнца испытывает
|
Различные обстоятельства, привходящие при суточном движении. |
Таковы эти немногие истинные и достоверные явления, которые, как мне кажется, даже если бы ничего другого не наблюдалось, с достаточной вероятностью побудят всякого, кто желает держаться в границах естественных объяснений, допустить подвижность Земли. В самом деле, желать сохранить неподвижным бассейн Средиземного моря и заставлять содержащуюся в нем воду производить движения, какие она производит, — это превосходит мое воображение, как, пожалуй, и воображение всякого другого, кто не скользит по поверхности предмета, а пытается проникнуть глубже.
Симпличио. — Эти явления, синьор Сальвиати, начались не со вчерашнего дня, они стары и наблюдались бесконечное число раз, и многие пытались дать им то или другое объяснение. Так, недалеко отсюда живет
|
Объяснение приливов и отливов, даваемое одним современным философом. |
|
Причина приливов и отливов некиим прелатом приписывается Луне. |
|
Джироламо Борро и другие перипатетики объясняют прилив и отлив умеренной теплотой Луны. |
Сагредо. — Пожалуйста, не распространяйтесь далее, синьор Симпличио. Мне кажется, не стоит тратить время и труд на изложение таких мнений, а тем более на их опровержение. Если бы вы согласились с одним из таких легкомысленных объяснений, это не сделало бы чести вашему рассудку, а мы знаем, что вы рассуждаете достаточно трезво.
Сальвиати. — Я немного более флегматичен, чем вы, синьор Сагредо, и все же потрачу с полсотни слов ради синьора Симпличио, если только он думает, что в изложенных им взглядах есть хоть капля вероятности. Я возражаю на это: воды, синьор Симпличио, у которых наружная
|
Указания на несостоятельность всех приводимых объяснений происхождения приливов и отливов. |
|
Острова являются признаками неровностей морского дна. |
Тем же, кто говорит об умеренной теплоте, способной поднять воду, предложите поставить на огонь наполненный водой котел и держать в нем правую руку до тех пор, пока вода не поднимется от теплоты хотя бы на один палец; тогда пусть они ее вынут и пишут о вздымании морей. Или попросите их, по крайней мере, объяснить, каким образом Луна разрежает
|
Два рода поэтически настроенных натур. |
|
Истина источает такой свет, что он не может остаться незамеченным среди темноты ошибок. |
Сальвиати. — Вы рассуждаете весьма осторожно и в согласии с учением Аристотеля, который, как вы знаете, в начале своих механических
|
Аристотель называет чудесными такие явления, причины которых неизвестны. |
Симпличио. — Я собираюсь прибегнуть к чуду, если вы не отклоните меня от этого указанием каких-либо естественных причин, кроме движения морских водоемов, так как я знаю, что водоемы эти не движутся, поскольку весь шар земной по природе неподвижен.
Сальвиати. — Но не думаете ли вы, что земной шар сверхестественным образом, т. е. благодаря всемогуществу божию, мог бы быть приведен в движение?
Симпличио. — Кто может в этом сомневаться? {301}
Сальвиати. — В таком случае, синьор Симпличио, если для объяснения приливов и отливов нам необходимо ввести чудо, заставим чудесным образом двигаться Землю, от движения которой естественным образом произойдет движение морей; и это явление будет настолько более простым и, скажем, естественным по отношению к чудесам, насколько сообщить шару вращение (чему мы видим столько примеров) легче, нежели заставить огромную массу воды передвигаться вперед и назад, то быстрее, то медленнее, подниматься и опускаться, где больше, где меньше, а где и оставаться на. одном уровне, причем все эти различия происходят в одном и том же содержащем ее водоеме; не говорю уже о том, что у вас множество различных чудес, а здесь — одно единственное. Прибавьте к этому, что чудесное движение воды делает необходимым другое чудо — сохранение Земли неподвижной под ударами воды, стремящейся заставить ее податься то в ту, то в другую сторону, если она не будет удерживаться чудесным образом.
Сагредо. — Прошу вас, синьор Симпличио, повременим немного выносить решение, осуждающее новое мнение, которое хочет нам изложить синьор Сальвиати, и не будем бросать его в одну кучу со старым хламом. Что касается чуда, то не будем равным образом прибегать к нему, пока не выслушаем рассуждений, остающихся в пределах естественного; хотя, пожалуй, выскажу свое мнение: мне представляются чудесными все творения природы и бога.
Сальвиати. — И я думаю то же самое; и признание того, что естественной причиной прилива и отлива является движение Земли, не устраняет того, что такое действие представляется чудесным. Итак, возвращаясь к нашему рассуждению, я повторяю и утверждаю, что до сих пор не представляется возможным объяснить, как могут воды, заполняющие наше Средиземное море, совершать те движения, которые, как мы видим, они совершают, если это море или водоем остается неподвижным. То, что представляет затруднения и безнадежно осложняет вопрос, это следующие факты, которые наблюдаются ежедневно. Итак, слушайте. Пусть мы находимся здесь в Венеции, где сейчас воды низки, море спокойно и воздух тих. Потом вода начинает подниматься и в течение 5—6 часов поднимется на десять пядей и более2; такой подъем происходит не от разрежения первоначальной, но от притока новой воды, имеющей совершенно те же свойства, что и первоначальная, такой же соленой, той же плотности;
|
Доказательство невозможности естественного объяснения прилива и отлива при признании неподвижности Земли. |
Сагредо. — Это я прекрасно понимаю и с жадностью ожидаю услышать, каким образом эти удивительные явления могут беспрепятственно происходить от движений, приписанных ранее Земле.
Сальвиати. — Поскольку эти явления должны происходить в результате движений, естественно присущих Земле, необходимо, чтобы они не только не встречали препятствий или помех, но чтобы они протекали с легкостью, и не только с легкостью, но и с необходимостью, так, чтобы невозможно было им протекать иначе, ибо таково характерное
|
Действительно естественные явления всегда происходят без затруднений. |
Два рода движений могут быть сообщены сосуду, в силу которых содержащаяся в нем вода может приобрести способность переливаться в нем то к одному, то к другому концу и там то подниматься, то опускаться.
|
Два рода движения сосуда, заставляющие содержащуюся в нем воду подниматься и опускаться. |
|
Земные водоемы не могут приблизиться к своему центру или удалиться от него. |
|
Неравномерное поступательное движение сосуда может вызвать перемещение содержащейся в нем воды. |
|
Части земного шара испытывают при своем движении ускорения и замедления. |
Симпличио. — Мне, не математику и не астроному, на первый взгляд это кажется большим парадоксом, и если бы было верно, что при совершенно равномерном движении целого движение частей, пребывающих в постоянной связи с целым, может быть неравномерным, то этот парадокс разрушает аксиому, утверждающую eamdem esse rationem totius et partium.
Сальвиати. — Я докажу свой парадокс, а вам, синьор Симпличио, оставлю задачу защищать против него аксиомы или привести их в соответствие. Доказательство будет кратко и легко для понимания, так как оно покоится на вещах, подробно разобранных нами в прошлых беседах, без введения малейшего допущения в пользу прилива и отлива. Как мы сказали, существуют два движения, приписываемые земному шару: первое — годовое, совершаемое его центром по большой орбите, расположенной
|
Доказательство того, что части земного шара испытывают ускорения и замедления. |
|
Части равномерно вращающегося вокруг своего центра круга в разное время производят противоположные движения. |
|
Сочетание годичного и суточного движений вызывает неравномерность движения частей земного шара. |
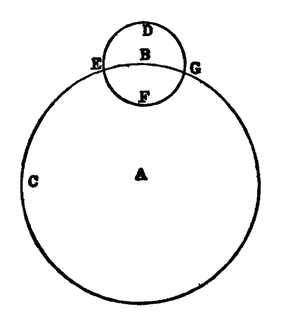 тому, каким оно было раньше, в D. Кроме того, в то время как части Е, так сказать, опускаются к F, части G поднимаются к D. При наличии такой противоположности движений у частей земной поверхности, во время движения вокруг собственного центра, из сочетания суточного движения с годовым необходимо должны получиться для отдельных частей земной поверхности абсолютные движения, в одних местах значительно ускоренные, в других — соответственно замедленные. Это очевидно, если рассмотреть часть около точки D, абсолютное движение которой будет весьма быстрым, как рождающееся из двух движений, совершаемых в одну и ту же сторону, а именно влево; первое из них есть часть годового движения, общего всем частям шара, второе — движение той же точки D, перемещающейся влево же суточным обращением, так что в этом случае суточное движение увеличивает и ускоряет движение годовое; обратное этому происходит с противоположной частью F, которая, будучи перемещаема общим годовым движением со всем шаром влево, перемещается суточным обращением вправо, так что суточное движение в конечном счете вычитается из годового; поэтому абсолютное движение, получающееся от сложения обоих движений, окажется здесь значительно замедленным. Далее, у точек Е и G абсолютное движение оказывается равным простому годовому, поскольку суточное совсем или почти совсем не увеличивает и не уменьшает его, не отклоняя ни вправо, ни влево, ни вверх, ни вниз. Поэтому мы приходим к заключению, что, поскольку верно, что движение всего земного шара и каждой из его частей было бы равномерным и единообразным, если бы они двигались только одним движением, будь то простым годовым или одним суточным, постольку же с необходимостью вытекает, что при сложении вместе этих двух движений для частей того же земного шара получатся два неравномерные движения, то ускоренные, то замедленные, в зависимости от того, прибавляется ли суточное обращение к обращению годовому или отнимается от него. Отсюда, если верно (а это совершенно верно и доказано на опыте), что ускорение и замедление движения сосуда заставляют содержащуюся в нем воду двигаться вдоль него взад и вперед и подниматься и опускаться у его краев, то почему не допустить, что такое явление может и даже с необходимостью должно происходить и с морскими водами, заключенными в водоемах, подверженных таким изменениям, в особенности, если эти водоемы простираются в длину с запада на восток, т. е. по тому направлению,
тому, каким оно было раньше, в D. Кроме того, в то время как части Е, так сказать, опускаются к F, части G поднимаются к D. При наличии такой противоположности движений у частей земной поверхности, во время движения вокруг собственного центра, из сочетания суточного движения с годовым необходимо должны получиться для отдельных частей земной поверхности абсолютные движения, в одних местах значительно ускоренные, в других — соответственно замедленные. Это очевидно, если рассмотреть часть около точки D, абсолютное движение которой будет весьма быстрым, как рождающееся из двух движений, совершаемых в одну и ту же сторону, а именно влево; первое из них есть часть годового движения, общего всем частям шара, второе — движение той же точки D, перемещающейся влево же суточным обращением, так что в этом случае суточное движение увеличивает и ускоряет движение годовое; обратное этому происходит с противоположной частью F, которая, будучи перемещаема общим годовым движением со всем шаром влево, перемещается суточным обращением вправо, так что суточное движение в конечном счете вычитается из годового; поэтому абсолютное движение, получающееся от сложения обоих движений, окажется здесь значительно замедленным. Далее, у точек Е и G абсолютное движение оказывается равным простому годовому, поскольку суточное совсем или почти совсем не увеличивает и не уменьшает его, не отклоняя ни вправо, ни влево, ни вверх, ни вниз. Поэтому мы приходим к заключению, что, поскольку верно, что движение всего земного шара и каждой из его частей было бы равномерным и единообразным, если бы они двигались только одним движением, будь то простым годовым или одним суточным, постольку же с необходимостью вытекает, что при сложении вместе этих двух движений для частей того же земного шара получатся два неравномерные движения, то ускоренные, то замедленные, в зависимости от того, прибавляется ли суточное обращение к обращению годовому или отнимается от него. Отсюда, если верно (а это совершенно верно и доказано на опыте), что ускорение и замедление движения сосуда заставляют содержащуюся в нем воду двигаться вдоль него взад и вперед и подниматься и опускаться у его краев, то почему не допустить, что такое явление может и даже с необходимостью должно происходить и с морскими водами, заключенными в водоемах, подверженных таким изменениям, в особенности, если эти водоемы простираются в длину с запада на восток, т. е. по тому направлению,
|
Главная и первоначальная причина приливов и отливов. |
|
Различные обстоятельства, сопровождающие приливы и отливы. Обстоятельство первое: поднявшаяся на одном конце вода сама собой возвращается к равновесию. |
Второе обстоятельство, которое должно быть отмечено, заключается в том, что только что упомянутое чередование движений совершается
|
Чем короче сосуды, тем быстрее совершаются колебания. |
В качестве третьего заслуживающего быть отмеченным пункта, да будет вам известно, что не только большая или меньшая длина сосуда является причиной того, что вода совершает колебания в различные промежутки
|
Большая глубина вызывает и более быстрое колебание воды. |
В-четвертых, заслуживают быть отмеченными и прилежно рассмотренными два явления, происходящие при подобных колебаниях вод: одно — это попеременные подъем и опускание их то у того, то у другого
|
Вода поднимается и опускается на концах сосудов и перемещается в средних частях. |
Пятая особенность должна быть рассмотрена тем более внимательно, что нам невозможно на опыте или в практике воспроизвести это явление. Дело заключается в следующем. В искусственно изготовленных нами сосудах,
|
Особенность движения Земли, которую невозможно воспроизвести искусственно. |
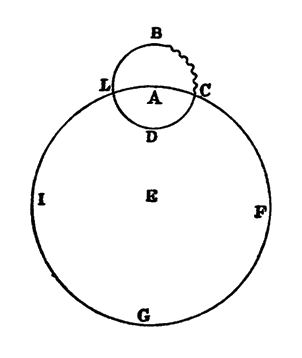 один из концов в силу сложения двух движений — суточного и годового — значительно замедляет свое движение, другой конец оказывается еще причастным быстрейшему движению.
один из концов в силу сложения двух движений — суточного и годового — значительно замедляет свое движение, другой конец оказывается еще причастным быстрейшему движению.
Для лучшего уразумения мы разъясним это сейчас посредством того же чертежа. Представим себе на нем, что поверхность моря занимает в длину, скажем, четверть окружности (дуга ВС); когда части В находятся, как было разъяснено выше, в быстрейшем движении вследствие сложения двух движений — суточного и годового, — имеющих одно и то же направление, тогда части С оказываются в движении замедленном, как лишенные прироста, зависящего от суточного движения. Если мы предположим теперь, что морской залив будет длиной во всю дугу ВС, то мы увидим, что края его будут двигаться в одно и то же время с большой неравномерностью. Наиболее различными были бы скорости движения морской поверхности длиной в полукруг и находящейся в положении дуги BCD, поскольку край В находился бы в быстрейшем движении, D — в движении наиболее медленном, а части около С — в движении среднем. И чем короче будет протяжение этих морей, тем менее они будут подвержены этому странному явлению — обладать в некоторые часы дня в разных частях разными степенями скорости или медленности движения. Таким образом, если, как мы видим на опыте, в первом случае ускорение и замедление, даже в одинаковой мере охватывающие все части водоема, являются причиной движения вперед и назад содержащейся в нем воды, то каких явлений можем мы ожидать в водоемах, столь дивно устроенных, что замедление или ускорение движения распределено между его частями неравномерно? Конечно, мы можем только сказать, что эта явится причиной еще более удивительных и странных перемещений воды. И хотя многим может показаться невозможным, чтобы мы были в силах посредством машин и искусственных сосудов воспроизвести на опыте подобные явления, такая возможность вовсе не исключена; у меня имеется конструкция такого аппарата, на котором можно наглядно наблюдать удивительные действия сложения движений, но для нашей цели достаточно теоретического понимания того, что было сказано7.
Сагредо. — Я со своей стороны очень хорошо понимаю, что это удивительное явление с необходимостью должно происходить в морских заливах, в особенности таких, которые простираются на большое пространство с запада на восток, т. е. в направлении движения земного шара; и так как оно в своем роде таково, что нельзя его себе представить или найти ему пример среди возможных для нас движений, я склонен думать, что от него могут происходить явления, не воспроизводимые путем наших искусственных опытов.
Сальвиати. — После этих разъяснений нам пора перейти к рассмотрению
|
Объяснение особенностей, наблюдающихся в игре прилива и отлива. Двоякого рода причины отсутствия прилива и отлива в малых морях и озерах. |
Я перехожу теперь, во-вторых, к разрешению вопроса, каким образом период приливов и отливов оказывается равным шести часам, если первичный принцип дает толчок к движению воды не иначе, как каждые двенадцать часов, в одном случае создавая максимум скорости, в другом минимум ее. На это следует ответить, что подобное явление
|
Причины, по которым прилив и отлив большей частью чередуются через каждые 6 часов. |
В-третьих, нам нетрудно будет найти причину того, что некоторые
|
Причины, в силу которых многие моря, несмотря на значительную величину, не имеют приливов и отливов. |
В-четвертых, мы поймем без всякого труда, почему приливы и отливы поднимают и опускают воду более всего на концах заливов и менее всего
|
Почему приливы и отливы особенно заметны в концах морских бассейнов и менее всего в средних частях? |
Далее, в-пятых, если мы примем во внимание, что одно и то же количество
|
Почему в проливах течение быстрее, чем на открытых местах? |
Теперь нам следует, в-шестых, для объяснения некоторых загадочных и непонятных явлений, наблюдающихся в этой области, приступить
|
Дело идет о некоторых сокрытых особенностях, наблюдающихся при приливах и отливах. |
Первой и главнейшей из них, как уже мною было рассказано, является определенное ускорение и замедление движения частей Земли, в силу которых воды должны в течение определенного двадцатичетырехчасового {309} времени двигаться на восток и возвращаться обратно на запад. Другая причина зависит от собственной тяжести воды, которая, будучи раз приведена в движение первичной причиной, стремится затем вернуться к равновесию путем повторных колебаний; последние не ограничены одним определенным периодом, но имеют такое же разнообразие периодов, сколько имеется различных длин и глубин у морских бассейнов и заливов; в той мере, в какой движение воды зависит от этого второго принципа, она будет приливать и отливать то в течение часа, то в течение 2, 4, 6, 8, 10 часов и т. д. И вот, если мы начнем теперь первичную причину, у которой имеется устойчивый 12-часовой период, сочетать с какой-либо из вторичных, у которой период был бы, скажем, 5-часовым, то окажется, что в известное время первичная и вторичная причины дают импульс к движению обе в одну сторону; при этом сочетании и, так сказать, дружном сотрудничестве приливы воды будут велики. В другое же время оказывается, что первичный импульс становится до известной степени противодействующим тому, который обусловливает вторичный период; при таком столкновении один из принципов уничтожает то, что должен был дать другой, движение вод ослабевает, и море пребывает в состоянии спокойном и почти неподвижном. В иных случаях, когда оба эти принципа будут не вполне противоположны друг другу, но не будут действовать и в полном согласии, произойдут другие изменения в отношении возрастания и убывания приливов и отливов. Может также случиться, что два моря, достаточно больших и сообщающихся друг с другом посредством узкого пролива, окажутся благодаря смешению принципов движения в таком положении, что у одного будет налицо причина прилива, в то время как у другого причина противоположного движения; в таком случае в канале, посредством которого эти моря сообщаются, возникают необыкновенные волнения, со встречными движениями и опаснейшими водоворотами, о которых столько рассказывают и которые на самом деле наблюдаются. От таких несогласных движений, зависящих не только от различных положений и длин, но в значительной мере и от различных глубин сообщающихся друг с другом морей, в воде возникают различные течения, беспорядочные и трудно определяемые; причины таких движений достаточно смущали и смущают моряков, которые встречаются с ними и не видят ни импульса ветров, ни какого-либо иного значительного изменения в воздухе, которое могло бы явиться их причиной. С этим возмущением воздуха мы должны в иных случаях весьма и весьма считаться и принять его за третью привходящую причину, способную значительно изменить наблюдаемые явления, происходящие от первичных и более существенных причин. Нет сомнения в том, что продолжительные сильные ветры, например с востока, будут удерживать воду, мешая ее отливу; поэтому, если затем в определенные часы придет вторая, а затем и третья волна прилива, воды сильно вздуются; и так воды, поддерживаемые в течение нескольких дней силой ветра, поднимутся значительно выше обычного, причиняя чрезвычайные наводнения.
Мы должны также (и это будет седьмая проблема) обратить внимание на другую причину движения, зависящую от большого скопления вод в реках, вливающихся в моря, не столь обширные. Здесь в каналах или
|
Почему в некоторых узких проливах наблюдается морское течение всегда в одном и том же направлении? |
Вот то, что пока пришло мне в голову сказать вам о причинах первого суточного периода прилива и отлива и о различных его особенностях. Если здесь требуются еще какие-либо пояснения, то можно их сделать, а затем перейти к двум другим периодам — месячному и годовому.
Симпличио. — Мне кажется, нельзя отрицать, что ваше рассуждение представляется весьма правдоподобным, если вести его доказательство, как говорится, ex suppositione, т. е. исходя из предположения, что Земля обладает обоими движениями, приписываемыми ей Коперником; но если такие движения исключить, все останется необоснованным, исключение же такой гипотезы подсказывается нам в достаточной мере ясно самим вашим рассуждением. Исходя из предположения двоякого рода движения Земли, вы объясняете происхождение прилива и отлива; и обратно, впадая в порочный круг, рассматриваете прилив и отлив как
|
Возражение против принятия гипотезы движения Земли для объяснения происхождения приливов и отливов. |
Сальвиати. — На это возражение, на первый взгляд столь веское, я отвечу следующее: правильно, что воздух более тонок и более легок
|
Опровержение возражения против движения земного шара. |
|
Вода способна сохранять приобретенный импульс лучше, чем воздух. |
|
Тела меньшего веса могут быть легче приведены в движение, но менее способны сохранять приобретенное движение. |
|
Скорее можно допустить, что атмосфера приводится в движение неровностями земной поверхности, нежели движением неба. |
То, что сейчас мною сказано, кажется мне достаточно основательным ответом на возражение синьора Симпличио. Но я хочу новым возражением и новым доводом, основанным на одном удивительном опыте, дать ему еще большее удовлетворение, а синьору Сагредо новое подтверждение подвижности земного шара. Я сказал, что воздух, в особенности та его часть, которая не поднимается над вершинами высоких гор, уносится благодаря неровности
|
Подтверждение вращения Земли новым аргументом, почерпнутым из явлений, совершающихся в атмосфере. |
Симпличио. — Это же самое затруднение и я хотел отметить; оно кажется мне весьма веским.
Сальвиати. — Замечание совершенно правильное; таким образом выходит, синьор Симпличио, что, не ощущая в воздухе того, что должно было бы иметь место, если бы земной шар вращался, вы доказываете этим его неподвижность. Но если то, что, как вам кажется, необходимо должно было бы ощущаться, на самом деле на опыте ощущается, примете ли вы это за признак и достаточно веское доказательство в пользу подвижности земного шара?
Симпличио. — В этом случае вы должны обращаться не ко мне одному, ибо, если бы это было так, то причина, от меня скрытая, может быть известна другим.
Сальвиати. — Играя с вами, никогда не имеешь шансов на выигрыш, а всегда только на проигрыш, а потому лучше совсем не играть. Для того чтобы не вводить третьего игрока, я пойду дальше. Мы только что сказали, и я повторяю это с некоторым добавлением, что воздух как тело тонкое и текучее, не соединенное прочно с Землей, повидимому, не имел бы {312} необходимости подчиняться ее движению, если бы неровность земной поверхности не захватывала с собой прилегающую к ней часть, не намного
|
Ближайшая к Земле часть атмосферы, полная испарений, принимает участие в ее движении. |
|
Под тропиками ветер дует постоянно на запад. Путь в Вест-Индию легок, возвращение же трудно. |
|
Ветры с суши производят морские волнения. |
Сагредо. — Хочется и мне напоследок сообщить об одном факте,
|
Другое атмосферное явление, свидетельствующее в пользу движения Земли. |
|
Рейсы в Средиземном море совершаются быстрее в направлении с востока на запад, чем с запада на восток. |
Сальвиати. — Я очень рад, что узнал об этом обстоятельстве, которое дает не малое подтверждение подвижности Земли. И хотя можно было бы сказать, что вся вода Средиземного моря постоянно течет к проливу, так как в океан должны излиться воды стольких впадающих в море рек, все же я не думаю, чтобы такое течение могло быть достаточно сильным, чтобы вызвать столь заметную разницу; это подтверждается и тем, что, как мы видим, у маяка течение воды к востоку не менее сильно, чем обратное течение к западу.
Сагредо. — Я не стремлюсь, как синьор Симпличио, убедить кого-, либо, кроме самого себя. Тем, что было сказано в отношении этой первой части, я удовлетворен, а потому, синьор Сальвиати, если вам угодно продолжать, я готов слушать дальше.
Сальвиати. — Я сделаю то, что вы мне предлагаете, но предварительно мне хотелось бы услышать также и точку зрения синьора Симпличио; из его суждения я могу вывести заключение, чего я с этими своими рассуждениями могу ожидать от школ перипатетиков, если эти рассуждения дойдут и до их ушей.
Симпличио. — Я не хочу, чтобы моя точка зрения заменяла вам суждение других или давала повод строить о нем догадки. Как я уже много раз повторял, я один из самых малых в ряду занимающихся науками этого рода, и то, что придет в голову людям; проникшим в сокровенные тайники философии, не может притти мне, который, как говорится, едва переступил ее порог. Тем не менее, по непосредственному своему впечатлению, скажу, что тем явлениям, о которых вы говорили, и в частности этому последнему, можно дать достаточное объяснение, не прибегая к подвижности Земли, при помощи одной лишь подвижности неба, не вводя ничего нового, кроме обратного тому, что выдвигаете вы.
|
Обратной аргументацией доказывается, что постоянное движение воздуха с востока на запад вызывается движением неба. |
|
Движение воды вызывается движением неба. |
|
Прилив и отлив, вероятно, вызываются суточным движением неба. |
Сальвиати. — Нельзя отрицать, что ваше рассуждение остроумно и кажется весьма правдоподобным; однако, говорю я, оно таково лишь по внешности, а не по существу. Оно распадается на две части — в первой дается объяснение непрерывному движению восточного ветра и подобному же движению воды; во второй — из этого же источника хотят почерпнуть и причину прилива и отлива. Первая часть (как я сказал) имеет некую видимость правдоподобия, но, однако же, гораздо меньшую, чем та, которую
|
Постоянные движения воздуха и воды получают более правдоподобное объяснение при признании движения Земли, нежели ее неподвижности. |
|
Невероятно, чтобы элемент огня мог быть увлечен вогнутостью лунной орбиты. |
|
Приливы и отливы не могут вызываться движением неба. |
Симпличио. — Я ничего не могу возразить ни от своего собственного имени из-за слабости моего разумения, ни от чужого из-за новизны мнения; но, во всяком случае, я думаю, что если бы оно распространилось по школам, то не нашлось бы недостатка в философах, которые сумели бы его опровергнуть.
Сагредо. — Подождем, значит, этого момента, а сами тем временем, если вам угодно, синьор Сальвиати, пойдем дальше.
Сальвиати. — Все, что было до сих пор сказано, относится к суточному периоду прилива и отлива, в отношении которого сначала была показана причина первичная и всеобщая, без которой никакого подобного явления не получалось бы; затем мы перешли к частным явлениям, разнообразным и до некоторой степени беспорядочным, и разобрали причины вторичные и сопутствующие, от коих они зависят. Остаются теперь два других периода — месячный и годовой, которые не привносят ничего нового и отличного в явлениях, уже рассмотренных при суточном периоде, но влияют на них, делая их то большими, то меньшими в различные части лунного месяца и различные времена солнечного года, как если бы и Луна, и Солнце были частичными причинами, производящими и вызывающими такие явления. Но мой рассудок совершенно не может мириться с такой мыслью. Видя, что движение морей есть ощутимое местное движение, совершаемое огромной массой воды, я не могу решиться приписать его свету, умеренному теплу, влиянию скрытых качеств и тому подобным выдумкам, которые tantum abest являются или могут явиться причиной прилива; наоборот, прилив является их причиной, т. е. причиной возникновения этих предположений в головах, более способных к болтовне и тщеславию, чем к изучению и исследованию сокровенных тайн природы. Вместо того, чтобы решиться сказать мудрое, откровенное и скромное слово«не знаю», они позволяют себе изустно и письменно распространять всякие нелепости. Одно лишь наблюдение, что та же самая Луна и то же самое Солнце не производят при помощи своего света, движения, теплоты большой или малой никакого действия на водоемы меньшего размера; что для того, чтобы поднять воду посредством теплоты, нужно довести ее чуть не до кипения и что вообще для нас невозможно искусственно воспроизвести движения прилива и отлива, иначе как посредством движения сосуда, казалось, должно было убедить всякого, что все прочее, {316} приводимое в качестве причины таких действий, является вымыслом, пустым и чуждым истине. Я утверждаю: если верно, что у одного явления имеется лишь одна первичная причина, и между причиной и явлением
|
Изменения явлений указывают на изменения и в причинах. |
|
Подробное разъяснение причин месячного и годового периода приливов и отливов. |
|
Месячные и годичные изменения приливов и отливов могут происходить только от изменения величины прироста или уменьшения годового движения, производимого суточным движением. |
Сагредо. — Я чувствую, точно меня спокойно ведут за руку, и хотя подвигаюсь по дороге гладко и без задержек, но наподобие слепого, ибо не вижу, куда вы меня ведете, и не могу себе представить, где наше странствие должно закончиться.
Сальвиати. — Хотя большая разница существует между моим медленным философствованием и вашим быстрым пониманием, тем не менее в этом частном случае, рассматриваемом нами сейчас, я не буду удивляться тому, что проницательность вашего ума не может победить глубокий мрак, скрывающий тот предел, к которому мы идем. Удивление мое исчезает, когда я вспоминаю, сколько часов, сколько дней и еще более ночей провел я в размышлениях по этому поводу; сколько раз, отчаиваясь дойти до конца, я для собственного утешения старался, подобно несчастному Орландо13, убедить себя, что, может быть, то, что свидетельство стольких заслуживающих доверия людей поставило перед моими глазами, не является правдой. Поэтому не удивляйтесь тому, что на этот раз, вопреки обыкновению, вы не видите цели; если же вы все же будете {317} удивляться, то думаю, что результат, насколько могу судить — довольно неожиданный, заставит вас перестать удивляться.
Сагредо. — Благодарю бога за то, что он воспрепятствовал отчаянию привести вас к концу, постигшему, как передают, несчастного Орландо, или к тому, чем, по рассказам, быть может, не менее легендарным, кончил Аристотель, и не лишил тем меня и других возможности найти познание вещи, столь же сокрытой, сколь и желанной. Прошу вас поэтому как можно скорее утолить мой духовный голод.
Сальвиати. — Я готов удовлетворить вас. В конце концов мы должны были найти, каким образом приращение и ослабление годового движения как следствие земного вращения могут происходить то в большей, то в меньшей пропорции; только такое различие, и не что-либо иное, может считаться причиной месячных и годовых изменений, наблюдаемых в величине приливов и отливов. Я рассмотрю теперь, как эти соотношения
|
Степень усиления или ослабления годового движения вследствие суточного вращения может изменяться трояким способом. |
|
Природа может с величайшей легкостью совершать вещи, постижение которых для нас весьма трудно. |
|
Если бы не изменялось годичное движение, то должны были бы прекратиться месячные изменения. Если бы не изменялось суточное движение, то не существовало бы годичного периода изменений. |
Сагредо. — Значит, месячное изменение приливов и отливов зависит от изменения годового движения Земли? А годовое изменение тех же приливов и отливов происходит от приращения и уменьшения суточного вращения? Тогда я оказываюсь еще более сбитым с толку, без всякой надежды понять, в чем заключается существо этого сплетения, более {318} запутанного, как мне кажется, чем гордиев узел. Я завидую синьору Симпличио, из молчания которого заключаю, что для него все понятно и что он свободен от той смуты, которая царит в моей голове.
Симпличио. — Охотно верю, синьор Сагредо, что вы находитесь в смущении; думается даже, что я знаю причину вашего смущения: оно, по-моему, происходит оттого, что из изложенного недавно синьором Сальвиати часть вы понимаете, а часть нет. Верно и то, что такое смущение мне чуждо, но совсем не по той причине, какую вы предполагаете, т. е. потому, что я будто бы все понял; наоборот, это происходит со мною от противоположного, т. е. оттого, что я ничего не понимаю; смута же происходит среди множества вещей, а не среди отсутствия их.
Сагредо. — Посмотрите-ка, синьор Сальвиати, как после некоторого обуздывания в прошедшие дни синьор Симпличио присмирел и из скакуна превратился в иноходца. Однако, прошу вас, разрешите без промедления для нас обоих эти трудности.
Сальвиати. — Я сделаю все возможное, чтобы победить свойственную мне тяжесть изложения, восполнить которую должна острота вашего понимания. Мы должны отыскать причины двух обстоятельств: первое касается различий, имеющих место у приливов и отливов в течение месячного периода; второе относится к периоду годовому. Сначала побеседуем о месячном периоде, потом рассмотрим и годовой. И все это надо разрешить в соответствии с установленными уже основными положениями и гипотезами, не вводя ради объяснения приливов и отливов ничего нового ни в астрономию, ни во вселенную, и надо показать, что причины всех различных наблюдаемых изменений заключаются в вещах,
|
Бесспорно, справедливо положение, что обращение по малым кругам происходит быстрее, чем по большим; это поясняется двумя примерами. Пример первый. |
|
Пример второй. |
|
Два замечательных свойства маятника и его колебаний. |
 случаях свои колебания с одинаковой частотой, как тогда, когда он движется по дуге в 4 или 6 градусов, так и тогда, когда он должен будет пройти дугу в 160 и более градусов. Это будет видно еще нагляднее, если подвесить два одинаковых груза на двух нитях равной длины и отклонить их затем от перпендикуляра, один на небольшое расстояние, а другой на очень далекое; отпущенные, они будут ходить взад и вперед в одни и те же промежутки времени. Отсюда вытекает решение прекраснейшей задачи.
случаях свои колебания с одинаковой частотой, как тогда, когда он движется по дуге в 4 или 6 градусов, так и тогда, когда он должен будет пройти дугу в 160 и более градусов. Это будет видно еще нагляднее, если подвесить два одинаковых груза на двух нитях равной длины и отклонить их затем от перпендикуляра, один на небольшое расстояние, а другой на очень далекое; отпущенные, они будут ходить взад и вперед в одни и те же промежутки времени. Отсюда вытекает решение прекраснейшей задачи.
|
Удивительная проблема, касающаяся тел, падающих по дуге четверти круга и вдоль любых хорд круга. |
Сагредо. — Постойте, постойте; вы забрасываете меня чудесами и рассеиваете мое внимание по стольким направлениям, что я сомневаюсь, останется ли у меня хотя бы малая часть его свободной для применения к главному предмету нашей беседы, который и сам по себе достаточно {320} темен и труден. Я попрошу вас оказать мне честь и по окончании изысканий причин приливов и отливов почтить своим посещением в другие дни этот дом, столь же ваш, как и мой, чтобы побеседовать о многих других проблемах, которые мы оставили неразрешенными, пожалуй, не менее любопытных и прекрасных, чем те, которые рассматривались нами в прошлые дни и с которыми мы должны сегодня покончить.
Сальвиати. — Готов служить вам; но потребуется устроить нам не одно и не два собрания, если к прочим вопросам, отложенным для отдельного обсуждения, мы захотим присоединить вопросы, касающиеся местного движения как естественно движущихся, так и брошенных тел. Эту тему пространно разработал наш Академик Линчео. Но возвращаюсь к нашему первому положению. После того как мы установили, что у тел, вращаемых движущей силой, пребывающей неизменной, сроки обращения предустановлены и определены, так что невозможно им стать более долгими или более короткими, приведя тому примеры и проделав наглядные и доступные нам опыты, мы можем теперь ту же истину подкрепить наблюдениями над небесными движениями планет, подтверждающими то же правило, а именно, что движущиеся по бо́льшим кругам затрачивают и больше времени на их прохождение. Нагляднейшее подтверждение тому мы имеем в Медицейских планетах, которые в короткие сроки совершают свои обращения вокруг Юпитера. Таким образом, не подлежит сомнению, а наоборот, может считаться вполне твердым и достоверным, что если бы, например, Луна, продолжая быть движимой той же движущей силой, делала постепенно все меньшие и меньшие круги, она приобрела бы тенденцию сокращать сроки своих периодов наподобие того маятника, у которого во время его колебаний мы укорачиваем шнур, т. е. уменьшаем радиус проходимых им окружностей. Знайте же, что то, что сказано мною о Луне в качестве примера, в основном происходит и подтверждается на самом деле16. Припомним то заключение, которое было сделано нами вместе с Коперником относительно невозможности отделить Луну от Земли, вокруг которой она, бесспорно, обращается в течение месяца.
|
Годичное движение Земли по эклиптике неравномерно вследствие движения Луны. |
Сагредо. — Если бы кому-нибудь, кто не имеет никакого понятия о лестнице, показать высокую башню и спросить, хватило ли бы у него духа взобраться на ее вершину, он, думается, ответил бы, безусловно, отрицательно, не понимая, каким другим способом, иначе как взлетев, он мог бы туда попасть. Но если показать ему камень не выше, чем в половину локтя, и спросить, думает ли он, что может подняться на него, то я уверен, он не будет отрицать, что легко поднимется не только один раз, но 10, 20 и 100 раз; поэтому, если показать ему теперь лестницу со ступенями, при помощи которых с легкостью, им самим признанной, он может попасть туда, куда только что, по его словам, невозможно было взобраться, он, думаю, смеясь над самим собой, признался бы в своей недальновидности. Вы, синьор Сальвиати, вели меня с такой постепенностью, что я не без удивления вижу, что почти без всякого труда оказался на такой высоте, подняться на которую представлялось мне невозможным; вместе с тем благодаря темноте лестницы я не замечал, как приблизился и даже достиг вершины, пока, очутившись на воздухе, не узрел обширного моря и просторных полей; и, как подъем на одну ступеньку не требует почти никакого труда, так и переход от одного вашего положения к другому казался таким ясным, что, не встречая ничего или очень мало нового, я думал, что ничего или очень мало что и приобретаю. Тем более возрастает мое удивление перед неожиданным результатом этого рассуждения, которое привело меня к познанию вещей, считавшихся мной непостижимыми. Одно только сомнение у меня остается, от которого я хотел бы избавиться: оно заключается в том, что если движение Земли вместе о движением Луны по зодиаку неравномерно, то неравномерность эту должны были бы заметить и отметить астрономы; не знаю, так ли это. Прошу вас как человека, более меня осведомленного в этих вещах, разрешить мое сомнение и сказать, каково действительное положение вещей.
Сальвиати. — Ваше сомнение весьма основательно, и я, отвечая на ваш вопрос, скажу, что хотя астрономия на протяжении многих веков и сделала большие успехи в исследовании устройства и движения небесных {322}
|
Возможно, что многое в области астрономии еще неизвестно. |
|
Сатурн благодаря медленности своего передвижения и Меркурий вследствие своей редкой видимости последними попадают в область наблюдения. |
|
Особенности путей движения отдельных планет по их орбитам еще не изучены точно. |
Подходя ближе к нашему частному случаю, т. е. к видимому движению Солнца и Луны, скажу, что в нем замечена одна большая неравномерность,
|
Солнце проходит одну половину зодиака на девять дней быстрее, чем другую. |
|
Движение Луны изучается, главным образом, в связи с затмениями. |
|
Приливы и отливы являются изменениями, ничтожными по отношению к величине морей и быстроте земного движения. |
Сагредо. — Я вполне удовлетворен тем, что касается этой части; остается разъяснить, каким образом приращения и уменьшения, происходящие от суточного обращения, становятся то бо́льшими, то меньшими, от какового изменения, как вы нам указали, зависит годовой период возрастания и убывания приливов и отливов.
|
Причины различия в величине ускорений и замедлений, вызываемых в годовом движении суточным вращением Земли. |
Сагредо. — Скорее наоборот, «как я не вижу», потому что пока что я ничего не понимаю.
Сальвиати. — Это я уже предсказывал. Тем не менее попробуем, не удастся ли посредством небольшого чертежа пролить некоторый свет; конечно, лучше было бы пользоваться для примера твердыми телами, чем простыми рисунками, но мы поможем себе перспективой и ракурсами18. Итак, начертим, как и ранее, окружность большой орбиты и представим себе, что точка А на ней является одной из точек солнцестояния, а диаметр АР линией взаимного пересечения колура солнцестояний плоскости большой орбиты или, скажем, эклиптики. Пусть в этой точке А помещается центр земного шара, ось которого CAB, наклонная по отношению к плоскости большой орбиты, лежит в плоскости названного колура, проходящего через обе оси — экватора и эклиптики. Во избежание путаницы мы начертим только круг экватора, обозначив его буквами DGEF, линия взаимного {324} пересечения его и плоскости большой орбиты будет DE, так что половина этого экватора DFE останется наклонной над плоскостью большой орбиты, а другая половина DGE поднимающейся над ней. Представим себе, что обращение этого экватора совершается в последовательности точек D, G, E, F, а движение центра от точки А к Е. Так как, когда центр Земли находится в А, ось СВ (которая перпендикулярна диаметру экватора BE) располагается, как сказано, в колуре солнцестояний, пересекающемся с большой орбитой по диаметру РА, то эта линия РА будет перпендикулярна к той же DE, поскольку колур перпендикулярен к большой орбите; а потому эта линия будет касательной большого круга в точке А. Таким образом, в этом случае движение центра по дуге АЕ, составляющее градус в день, весьма мало отличается от того, которое происходило бы по касательной DAE. И так как благодаря суточному вращению точка D, перемещаясь через G в Е, прибавляет к движению центра,
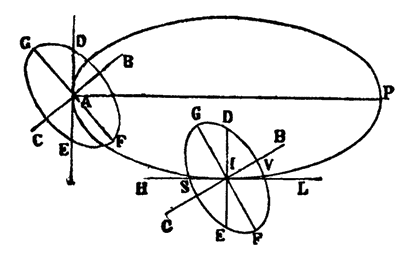 происходящему почти по той же линии DE, величину диаметра DE и, наоборот, настолько же его уменьшает при движении по другой половине круга EFD, то приращения и уменьшения в этом месте, т. е. в пору солнцестояния, будут измеряться полным диаметром DE.
происходящему почти по той же линии DE, величину диаметра DE и, наоборот, настолько же его уменьшает при движении по другой половине круга EFD, то приращения и уменьшения в этом месте, т. е. в пору солнцестояния, будут измеряться полным диаметром DE.
Перейдем теперь к рассмотрению того, будут ли они иметь ту же величину и во время равноденствия. Положим, что центр Земли перенесся в точку I, удаленную на четверть окружности от точки А, и представим себе тот же экватор GEFD, то же пересечение его с большой орбитой по линии DE и ось с тем же наклоном СВ; касательной к большой орбите в точке I будет, однако, уже не BE, а другая линия, которая пересечет ее под прямым углом; пусть это будет линия HIL, по которой начнется движение центра I, движущегося по окружности большой орбиты. При этом положении приращения и уменьшения не измеряются уже более диаметром DE, как раньше, так как такой диаметр не простирается уже по линии годового движения HL, а пересекает его под прямым углом, почему его конечные точки D и Е ничего не привносят и не отнимают. Приращения и уменьшения должны измеряться тем диаметром, который находится в плоскости, перпендикулярной к плоскости большой орбиты и пересекающей ее по линии HL, каковой диаметр будет вместе с тем диаметром GF; и прибавочное, так сказать, движение будет то, которое точка G совершает по половине круга GEF, а убавляющее — остальное, совершаемое по другой половине круга FDG. Но этот диаметр, не совпадая с линией годового движения HL, но пересекая ее, как это можно видеть, в точке I, причем один конец G оказывается выше, а другой ниже плоскости большой орбиты, не определяет приращений и уменьшений всей своей длиной, и величина их должна определяться частью линии HL, которая заключается между перпендикулярами, опущенными на нее из точек G и F, т. е. линиями GS и FV, так что мерой приращений является линия SV, меньшая чем GF или же чем линия DE, которая была мерой приращения и уменьшения в солнцестоянии А. В зависимости от того, в каких других точках квадранта AI будет находиться центр Земли, можно, проводя касательные в этих точках и опуская на них перпендикуляры из концов тех диаметров экватора, которые лежат в плоскостях, перпендикулярных к плоскости большой орбиты и проходящих через соответствующие касательные, получить отрезки этих касательных (уменьшающиеся в сторону равноденствия и увеличивающиеся в сторону солнцестояния), которые и дадут величины приращений и уменьшений. Насколько разнятся самые малые приращения от самых больших, легко понять, {325} ибо между ними такое же различие, как между осью или диаметром сферы и его частью, заключенной между полярными кругами, которая меньше всего диаметра приблизительно на одну двенадцатую часть, причем я имею в виду приращения и уменьшения, происходящие на экваторе; на других параллелях они уменьшаются соответственно уменьшению диаметров последних19.
Вот все, что я могу сказать вам по этому поводу и что может быть доступно нашему человеческому знанию, которое, как вам хорошо известно, приобретается только путем заключений, прочно обоснованных на явлениях постоянных, а таковыми являются три рода периодов прилива и отлива, зависящих от причин неизменных, единых и вечных. Но так как к этим причинам первичным и общим присоединяются затем вторичные и частные, могущие внести множество изменений, и эти вторичные причины частью не поддаются наблюдению и отличаются непостоянством, как, например, изменения ветров, частью же хотя и могут быть постоянны и устойчивы, но все же недоступны наблюдению по своей многообразности, как длины водоемов, различие их простирания в том или другом направлении, а также разнообразие глубин, то кто сможет без продолжительных наблюдений и достоверных сведений дать такое обстоятельное их описание, чтобы оно могло послужить гипотезой и верной предпосылкой для того, кто хотел бы при помощи комбинирования всех этих причин дать полное объяснение всех явлений и, скажу, аномалий и частных различий, могущих иметь место в движениях вод? Я удовольствуюсь сделанным мною указанием на то, что случайные причины, существующие в природе, могут произвести большие изменения; делать обстоятельные наблюдения я предоставляю тем, кто плавает по разным морям. В заключение нашего рассуждения рассмотрю лишь, каким образом точные сроки приливов и отливов могут изменяться не только под влиянием длины и различной глубины заливов, ибо значительные изменения, думается мне, могут происходить от соединения участков моря, разнящихся по величине и положению, или, скажем, направлению; такое явление имеет место как раз здесь в Адриатическом заливе, который гораздо меньше всего остального Средиземного моря и расположен в столь отличном направлении, что в то время как последнее имеет предел, ограждающий его с востока, каковым являются берега Сирии, залив замыкается более с запада; и так как на конце гораздо сильнее приливы и отливы, а здесь весьма велики только подъем и убыль, то весьма вероятно, что время приливов в Венеции совпадает с временем отлива в другом море, которое, будучи гораздо больше и простираясь более прямо с запада на восток, оказывается в известном смысле господствующим над Адриатикой. Поэтому не следует удивляться, если результаты воздействия первичных причин не проявляются в Адриатике в надлежащие сроки, соответствующие периодам, существующим в остальной части Средиземного моря. Но эти уклонения требуют длительных наблюдений, которых я до сего времени не производил; не знаю, смогу ли я произвести их в будущем.
Сагредо. — Мне кажется, вы сделали достаточно много, открыв путь к столь высокому умозрению. Если бы вы не привели нам ничего, кроме первого общего положения, не допускающего, как мне кажется, никаких возражений, то и его одного достаточно для убедительного доказательства того, что если бы водоемы, содержащие морские воды, пребывали в покое, то в соответствии с общим ходом природы невозможно было бы, чтобы в них происходили те движения, которые мы наблюдаем, и что, наоборот, при предположении движения, приписанного Коперником земному шару, исходя из других соображений, подобные явления в морях необходимо должны иметь место. Это одно, если бы не было ничего {326} другого, кажется мне настолько превышающим нелепости, выдвигавшиеся по этому поводу многими другими, что одно воспоминание о них вызывает во мне отвращение. Весьма дивлюсь я, что из людей высокого ума, которых было немало, ни одному не бросилась в глаза несовместимость периодического движения воды и неподвижности содержащего их водоема, несовместимость, которая теперь кажется столь явной.
Сальвиати. — Более следует дивиться тому, что хотя некоторым
|
Для возникновения прилива и отлива недостаточно одного простого движения Земли. |
|
Отвергается мнение математика Селевка. |
|
Кеплер получает мягкий упрек. |
Сагредо. — Я того мнения, что с этими умами произошло то же самое, что приключилось теперь со мной; невозможно сразу понять это сплетение трех периодов — годового, месячного и суточного — и то, каким образом причина их зависит от Солнца и Луны, хотя ни Солнце, ни Луна не имеют никакого отношения к воде. Для полного уразумения этой проблемы мне требуется более продолжительное и упорное напряжение ума, чтобы преодолеть трудность и новизну, до сих пор значительно затемняющие дело; я не теряю, однако, надежды после продолжительного продумывания наедине и в тиши усвоить то, что еще не вполне мною усвоено. Итак, в результате четырехдневной беседы мы имеем важные свидетельства в пользу системы Коперника, из которых следующие три, почерпнутые: первое — из стояния и попятного движения планет и их приближения и удаления по отношению к Земле; второе — из обращения Солнца вокруг самого себя и того, что наблюдается с его пятнами; третье — из морских приливов и отливов, кажутся мне весьма убедительными22.
Сальвиати. — К трем приведенным выше свидетельствам можно
|
Синьор Чезаре Марсили наблюдает изменения меридиана. |
Сагредо. — Не в первый раз слышу я разговор об исключительной учености этого синьора и о том, сколь заботливым покровителем ученых он является. Если то или иное произведение его выходит в свет, можно быть уверенным, что оно является вещью замечательной24.
Сальвиати. — Теперь, когда настала пора положить конец нашим беседам, мне остается просить вас об одном: если при более внимательном рассмотрении изложенных мною вещей вы встретитесь с затруднениями и сомнениями, не вполне разрешенными, то извините меня, приняв во внимание новизну мысли, слабость моего дарования, обширность темы и, наконец, то, что я не претендую и не претендовал на то, чтобы другие признавали за истину фантазию, с которой я не согласен и которую я, скорее, мог бы считать пустой химерой и блистательным парадоксом. Вы, синьор Сагредо, в течение нашей беседы неоднократно с большим одобрением выражали согласие с некоторыми из моих мыслей, что вызывалось, думается, скорее их новизной, нежели достоверностью, а в еще большей степени проистекало из вашей любезности: вы хотели своим согласием доставить мне то удовольствие, которое мы обычно испытываем от одобрения и похвалы всего того, что исходит от нас. И как вы обязали меня своей учтивостью, так порадовал меня своей непосредственностью и синьор Симпличио, а его настойчивость в защите с такой силой и непоколебимостью доктрин своего учителя особенно меня к нему расположила. И как вам, синьор Сагредо, я приношу благодарность за вашу любезную благосклонность, так у синьора Симпличио прошу извинения, если раздосадовал его своей подчас слишком резкой и решительной речью; спешу заверить, что я делал это не со злым умыслом, а только для того, чтобы дать ему новый повод изложить ряд высоких мыслей для моего поучения.
Симпличио. — Вам незачем приносить эти извинения, они совершенно излишни, в особенности по отношению ко мне. Посещая часто кружки и публичные диспуты, я сотню раз был свидетелем того, что спорящие, разгорячась, пререкались так, что не могли удержаться даже от оскорбительных слов, и, казалось, вот-вот готовы были подраться. Что касается наших бесед, в особенности последней, касавшейся причины происхождения морских приливов и отливов, то в них я не все вполне понимаю, но должен признаться, что и на основании того слабого представления, которое я составил по этому вопросу, ваша мысль кажется мне гораздо более остроумной, чем другие гипотезы, о которых мне приходилось слышать. Однако, я все же не могу на этом основании считать ее правильной и доказательной.
Перед моим умственным взором всегда стоит надежнейшее и непоколебимейшее учение, некогда воспринятое мною от особы ученейшей, имеющей высокий духовный сан. Я знаю, что на вопрос, мог ли бог своим бесконечным могуществом и премудростью сообщить элементу воды попеременное движение, которое мы в ней замечаем, иным образом, нежели путем приведения в движение водоемов, вы оба можете дать только один ответ, а именно, что он мог бы и сумел бы сделать это многими способами, даже непостижимыми для нашего ума. А если это так, то я делаю отсюда вывод, что большой дерзостью было бы желать стеснить и ограничить божественное могущество и премудрость единственным человеческим измышлением.
Сальвиати. — Достойное удивления, поистине небесное учение, и в полном согласии с ним находится другое божественное постановление, которое хотя и разрешает нам обсуждать строение мира, но указывает (быть может, для того, чтобы не притупить и не уничтожить деятельность ума человеческого), что нам не дано постигнуть сущность дел рук его. Итак, будем пользоваться дозволенной и угодной богу деятельностью {328} для того, чтобы познавать его величие и исполняться удивлением ему тем большим, чем менее мы чувствуем себя способными проникнуть в бездну его премудрости.
Сагредо. — Это может быть последним выводом из наших четырехдневных рассуждений. После них синьор Сальвиати нуждается в некотором перерыве для отдыха, в котором мы, несмотря на нашу любознательность, не можем ему отказать, однако, при том условии, что позже, когда ему это будет удобно, он удовлетворит наше желание, особенно мое, вернуться к обсуждению в одном или двух собраниях отложенных и записанных мною проблем, как то было уже условлено.
В особенности я горю желанием ознакомиться с элементами новой науки нашего Академика, касающейся местных движений, естественных и насильственных. А пока мы можем, как обычно, прокатиться часок в гондоле, которая нас ждет, и насладиться вечерней прохладой.
(Конец дня четвертого и последнего)
| << | {329} | >> |
По поводу введения новшеств.
Кто может сомневаться в том, что введенные новшества, стремящиеся сделать рабами чужой воли умы, созданные богом свободными, не могут не привести к сильнейшей смуте? И требовать, чтобы люди отказывались от своих собственных суждений и подчинялись суждениям других, и назначать лиц, совершенно невежественных в науке или искусстве, судьями над людьми учеными, наделяя их властью обращаться с последними по своему усмотрению, это такие новшества, которые способны довести до гибели республику и разрушить государство.
Хитроумные комментаторы занимаются толкованием разных незначительных и бессодержательных сочинений (Сакробоско и других) и открывают в них удивительный смысл, наподобие того, как искусный повар делает посредством разных приправ негодную по существу пищу вкусной для того, кто ее пробует.
Многие хвалятся тем, что могут привести большое число авторитетов в подтверждение своего мнения; я же хотел бы, чтобы мои мнения были новыми и составленными мною самостоятельно.
Берегитесь, теологи, желающие сделать из вопроса о движении или покое Солнца и Земли догмат веры; вы подвергаетесь опасности осудить в свое время как еретиков всех тех, кто утверждал, что Земля неподвижна, а Солнце меняет место; говорю в свое время, когда ясно и неопровержимо будет доказано, что Земля движется, а Солнце неподвижно.
Если один круг движется внутри другого, то можно считать движение его совершающимся соответственно движению или делению внешнего круга на основании отношения частей внутреннего круга к обращенным к ним частям круга внешнего, объемлющего; таким образом, можно сказать, что внутренний круг abed движется в порядке частей efgh круга объемлющего, когда обращение происходит от точки d к а и от а к b, каковые точки обращены к дуге hef; нельзя сказать, что это движение противоположно порядку hef на том основании, что движение части bcd будет противоположно hef, ибо bcd обращена к fgh и движение направлено в ту же сторону. Заметьте это, пожалуйста, по отношению к вращению солнечных пятен, которое, к стыду Шейнера, должно совершаться от запада к востоку. {330}
Заметки у Фромондо стр. 10 у знака γ, где он говорит, что узнал об обращении пятен от Кеплера и меня, а не от Анеллеса.
Тем, кого смущает необходимость изменить всю философию, показать, что это не так, что остаются те же учения о душе, о воспроизведении, о метеорах, о животных.
Тех, которые не соглашаются с годовым движением, так как земной шар при этом должен то подниматься, то опускаться, спросить, удовлетворятся ли они, если бы им вовсе не пришлось подниматься. Объяснить, что то же самое можно было бы сказать о корабле, совершающем плавание вокруг Земли. Так как они понимают под движением, которое не поднимается и не опускается, то, которое совершается по кругам, полюс которых находится у нас в зените, обратить их внимание, что все круги имеют полюс на чьем-либо зените и что, мы обитатели Тосканы, не имеем в нашем зените никакой привилегии перед жителями Португалии или Персии; и как движение вокруг земного шара по любому кругу не является ни повышением, ни понижением, так нет их и в движении по небесным кругам и т. д.
Спрашиваю: приливы и т. д. могут ли быть объяснены только одним способом или же многими. Если одним..., то они вызываются движением Земли, ибо вытекают из него..., если многими, то я исследую, какими именно они вызываются...
Дело идет о приобретении, ибо невозможно потерять ни одного сторонника...
Скажи мне Сос.°, что, по-твоему, может скорее случиться — получу ли я пользу от противников или же вред от своих сторонников.
Sol stetit; утверждая (его) движение, подтверждаем всю систему и удлиняем день.
Стояния, приближения (планет), движения пятен, изменения в неподвижных звездах, морские приливы — явления, столь различные и находящие объяснение в движении Земли, являются аргументами, более чем достаточными.
Из того, что части Земли оказывают такое сопротивление удалению их от ее поверхности, нельзя сделать вывода, что весь шар земной сопротивляется перемещению (годовым движениям), как нельзя заключить из сопротивления разъединенных частиц птичьего клея, будто сосуд, наполненный птичьим клеем, труднее переместить, чем если бы он был наполнен водой или чем-либо иным. Если бы это было так, то ванну, наполненную свинцом, было бы в (сто) раз труднее передвигать, чем ванну, наполненную ртутью. Вы не должны думать, синьор Симпличио, будто оттого, что дуга лука оказывает такое сопротивление движению и сгибанию в направлении зарубок, весь арбалет оказывает такое же сопротивление передвижению в этом направлении; также и канат не оказывает большего сопротивления движению в ту или другую сторону вследствие того, что он противится разрыву, если два человека тянут его, один к востоку, другой к западу. Так как частицы Земли повсюду сопротивляются движению к зениту и склонны к движению к надиру, отсюда проистекает то, что весь шар в целом не оказывает никакого сопротивления движению в том или другом направлении. {331}
Симпличио. — Однако, я видел, что сосуд с клеем оказывал сильное сопротивление, когда его хотели поднять.
Сальвиати. — Да, но такое сопротивление совершенно отлично от сопротивления частей разъединению, оно зависит от вязкости, препятствующей движению частей в любом направлении, а не от тяжести, сопротивляющейся движению только вверх. В случае с клеем, сопротивляющимся движению во всех направлениях, оказывается, что сосуд в целом не противится движению в любом направлении; то же происходит и с тяжелыми телами, которые сопротивляются движению во всех направлениях по отношению во всему шару (ибо сопротивляются движению ко всем зенитам), и это приводит к тому, что шар в целом не противится движению в любую сторону:
...о, С, они весьма обязаны твоему полному невежеству: если бы не оно, ты не мог бы скрывать и прикрывать жестокую злобу и беззаконие, протягивая руку помощи, чтобы выбраться из великой религиозной смуты... можешь сказать, что мнение Коперника начинает итти in perniciem и т. д., ибо никто из его сторонников не говорит, что оно противно писанию или вере, как и я этого не говорил.
Время, показываемое часами, приводимыми в действие водой, вероятно, может служить для измерения часов и т. д.
Попутный ветер подгоняет менее быстро движущееся тело, ветер противный — задерживает его; следовательно, воздух, движущийся с одинаковой скоростью, не оказывает никакого действия.
Новая провозглашаемая вами доктрина, которой вы хотите... принудить ум и чувства не понимать и не видеть, сделать движение и покой и т. д. вопросов веры, подвергает святую церковь опасности, которая может когда-нибудь наступить..., когда сочтут еретиками тех, кто считает Землю неподвижной, а Солнце движущимся. Это новшество вносит в религию большую смуту и т. д. Не найдется ни одного астронома или философа (каким бы еретиком он ни был в других отношениях), который подрывал бы веру в священное писание..., объявляя его ложным, потому что там говорится, что Солнце движется и т. д. ..., поощряющее писателей, приспособляющихся к уровню черни и т. д. ..., вы сами создаете почву для ересей, считая без всякого основания, что писание гласит то, что вам угодно, и требуя, чтобы люди знающие отрешались от собственного чувства и неопровержимых доказательств; ...считаете свои суждения настолько превосходящими суждения древних, что в то время как последние почитали людей, сделавших открытия, наравне с богами, вы, как более мудрые, осуждаете их на изгнание из пределов республики.
Части Земли имеют такое стремление к ее центру, что если бы она изменила свое положение, части эти, хотя бы они были даже разъединены с земным шаром в тот момент, когда он приходит в движение, всюду последовали бы за ним; примером тому являются Медицейские звезды, постоянно сопровождающие Юпитер, хотя они и отделены от него. То же самое можно сказать о Луне, принужденной следовать за Землей. Да послужит это поучением для простаков, которые находят непостижимым, как оба эти шара, не будучи связаны друг с другом цепью или посажены оба на одну ось, следуют один за другим, так что ускорение или замедление движения одного заставляет другой двигаться быстрее или медленнее.
Сальвиати. — Я утверждаю, что ничто в природе не движется естественно прямолинейным движением. Поговорим по этому поводу более подробно: движения всех небесных планет круговые: суда, повозки, кони, птицы {332} движутся по круговым линиям по поверхности Земли; движения членов животных все кругообразны; короче, мы вынуждены будем признать, что только gravia deorsum и levia sursum, повидимому, происходят по прямым линиям, но и в этом мы не можем быть уверены, не доказав сперва, что земной шар неподвижен.
Симпличио. — Хотя я не умею привести убедительного аргумента в доказательство такого положения, не исключается, что другой это может сделать.
Сагредо. — Остерегайтесь, чтобы это положение не оказалось ложным, ибо я уверяю вас, что ни вы и никто на свете не сможет привести достаточных доказательств его правильности. Возможно, что я не в силах буду открыть неправильность доказательства, но чтобы оно могло быть правильным, это совершенно исключается.
Симпличио. — Когда я обращаю взор к небу и представляю себе огромность пространства, простирающегося от востока до запада, мне кажется удивительным, что я не могу заметить никакого движения в звездах, пробегающих это пространство в такой краткий срок, как 10—12 часов.
Сальвиати. — Когда вы смотрите на стрелку часов, висящих на той стене, замечаете ли вы ее движение? А ведь она также описывает половину окружности в 12 часов.
Симпличио. — Нет, синьор, но чем является круг с радиусом в 4—6 локтей по сравнению с бесконечной величиной небесной дуги, простирающейся с востока на запад на столько тысяч тысяч миль.
Из двух систем одна является ясной, а другая темной; тот, кто не вовсе слеп, должен уметь различать белое; так скажите же мне прямо, что кажется вам белым?
В теологии я уступаю вам, как уступаю великому герцогу в собирании скульптуры, и все же я имею одну совсем маленькую камею, прекраснее всех, принадлежащих герцогу. Таким же образом в этом единственном специальном вопросе, вопросе о том, что думать об учении Коперника, я полагаю, что имею преимущество над многими, в остальном превосходящими меня своей начитанностью.
Сальвиати. — Ты, Аристотель, устанавливаешь, что простые движения суть те, которые совершаются по простым линиям, и называешь простыми линиями прямую и окружность. Тогда если простота движения зависит от простоты линии, движение по прямой, проходящей через центр, будет простым; таким же будет и движение по прямой, пересекающей круг, но не проходящей через центр. Однако, ты скажешь, что движение по прямой до центра будет противоположно продолжению его по той же прямой за центром, и не будешь больше считать движения, которое ты называл простым в силу того, что оно происходит по простой линии, свойственным простому телу, а будешь утверждать, что по одной и той же прямой происходят противоположные движения.
Для того чтобы простое движение соответствовало простому телу, необходимо наличие такого движения, простота которого зависела бы от чего-то иного, чем простота линий, ибо иначе движение тяжелых тел к центру было бы для них не более характерным и естественным, чем движение от центра.
| << | {333} | >> |
| Коперник считает, что Земля — такой же шар, как и планеты | 24 | |||
| По мнению Аристотеля, в природе необходимо признать существование субстанций небесных (неизменных) и стихийных (изменчивых) | 24 | |||
| Аристотель считает мир совершенным, так как он трехмерен | 24 | |||
| Доказательство Аристотеля в пользу того, что измерений существует только три | 24 | |||
| Тройственное число восхваляется пифагорейцами | 25 | |||
| Ум человеческий причастен божеству, потому что разумеет числа, по мнению Платона | 25 | |||
| Тайны пифагорейских чисел — басня | 26 | |||
| Геометрическое доказательство трехмерности | 26 | |||
| В доказательствах естественных не следует искать точности геометрической | 27 | |||
| Частей вселенной по Аристотелю две: небесная и стихийная — друг другу противоположные | 28 | |||
| Движения местные — трех родов: прямолинейное, круговое и смешанное | 28 | |||
| Движения прямолинейное и круговое — простые, потому что совершаются по простым линиям | 28 | |||
| Определение природы, данное Аристотелем, или неправильно, или несовершенно | 28 | |||
| Спираль, обвивающая цилиндр, может быть названа простой линией | 28 | |||
| Аристотель прилаживает план к мирозданию, а не строит здание по плану | 29 | |||
| Движение прямолинейное — иногда простое, иногда смешанное, по Аристотелю | 29 | |||
| Окружность, по Аристотелю, совершенна, а прямая — несовершенна, и почему | 30 | |||
| В мире, по допущению автора, господствует совершенный порядок | 31 | |||
| Прямолинейное движение не может существовать в хорошо упорядоченном мире | 31 | |||
| Прямолинейное движение по природе бесконечно. Движение прямолинейное невозможно по природе | 31 | |||
| Природа не предпринимает ничего, что не может быть выполнено | 31 | |||
| ||||
| Прямолинейное движение в первичном хаосе | 31 | |||
| Прямолинейное движение пригодно для того, чтобы внести порядок в тела плохо упорядоченные | 31 | |||
| Тела во вселенной движутся сперва прямолинейно, а затем по кругу — по мнению Платона | 31 | |||
| Подвижное тело, находящееся в состоянии покоя, не придет в движение, если у него нет влечения к какому-нибудь особому месту | 32 | |||
| Движущееся тело ускоряет движение, когда оно двигается к тому месту, к которому имеет влечение | 32 | |||
| Движущееся тело, отправляясь от покоя, проходит все степени медленности | 32 | |||
| Покой есть степень бесконечной медленности | 32 | |||
| Движущееся тело приобретает ускорение только тогда, когда движется к назначенному пункту | 32 | |||
| Природа, чтобы довести движущееся тело до некоторой степени скорости, заставляет его двигаться прямолинейно | 32 | |||
| Равномерная скорость присуща круговому движению | 32 | |||
| Между покоем и какой бы то ни было степенью скорости посредствует бесконечное количество степеней меньших скоростей» | 32 | |||
| Природа не сообщает непосредственно определенной степени скорости, хотя могла бы | 32 | |||
| Движущееся тело, отправляясь от состояния покоя, проходит все степени скорости, не задерживаясь ни на одной из них | 33 | |||
| Движущееся тяжелое тело, падая, приобретает импульс, достаточный для того, чтобы вернуть тело на прежнюю высоту | 33 | |||
| Импульсы движущихся тел, приблизившихся к центру, равны | 34 | |||
| На горизонтальной плоскости тело остается без движения | 34 | |||
| Скорость по наклонной плоскости равна скорости по перпендикуляру, но движение по перпендикуляру быстрее движения по наклонной | 34 | |||
| Скорости называются равными тогда, когда пройденные пространства пропорциональны времени | 34 | |||
| Круговое движение не может быть приобретено естественным путем без предшествовавшего прямолинейного движения | 38 | |||
| Круговое движение непрерывно и равномерно | 38 | |||
| Величина орбит и скорости движения планет соответствуют их исхождению из одного места | 38 | |||
| Круговые движения, законченные и определенные, не вносят беспорядка в части вселенной | 39 | |||
| В круговом движении каждая точка окружности — начальная и конечная точка | 40 | |||
| Движение круговое — единственное равномерное | 40 | |||
| Круговое движение продолжается непрерывно | 40 | |||
| Прямолинейное движение при естественных условиях не может быть постоянным | 40 | |||
| Прямолинейное движение предназначено естественным телам для того, чтобы приводить их в совершенный порядок, когда они из него выведены | 40 | |||
| Только покой и круговое движение пригодны для сохранения порядка | 40 | |||
| Чувственный опыт должен быть предпочтен человеческим рассуждениям | 40 | |||
| Кто отрицает чувство, заслуживает, чтобы у него отняли чувство | 40 | |||
| ||||
| Чувство показывает, что тяжелое движется к середине, а легкое — к своду | 40 | |||
| Сомнительно, движутся, ли тяжелые падающие тела прямолинейно | 41 | |||
| Земля сферична вследствие стремления частей к своему целому | 41 | |||
| Более вероятно, что в центре вселенной находится Солнце, а не Земля | 41 | |||
| Прямолинейное движение тяжелых тел, воспринимаемое чувствами | 41 | |||
| Доказательство Аристотеля, что тяжелые тела движутся по направлению к центру вселенной | 42 | |||
| Тяжелые тела движутся к центру Земли per accidens | 42 | |||
| Спрашивать о том, что воспоследовало бы за невозможным, тщетное занятие | 42 | |||
| Тела небесные, по Аристотелю, ни легки, ни тяжелы | 42 | |||
| Аристотель не может ошибаться, потому что он — основоположник логики | 42 | |||
| Паралогизм Аристотеля при доказательстве того, что Земля находится в центре мира | 42 | |||
| Паралогизм Аристотеля вскрывается и с другой стороны | 43 | |||
| Доказывается, что с большим правом можно говорить, что тяжелые тела тяготеют к центру Земли, чем к центру мира | 43 | |||
| Условия, согласно которым небесные тела отличаются от элементарных, зависят от движений, приписанных им Аристотелем | 43 | |||
| Философия может только выиграть от споров и разногласий философов | 44 | |||
| Рассуждение Аристотеля в доказательство нетленности неба | 44 | |||
| По Аристотелю, возникновение и разрушение существуют только при наличии противоположностей | 44 | |||
| Круговому движению никакое другое движение не противоположно | 44 | |||
| Небо — обитель бессмертных богов | 44 | |||
| Неизменность неба воспринимается чувством | 44 | |||
| Доказательство того, что круговое движение не имеет противоположного | 44 | |||
| Гораздо легче удостовериться в том, движется ли Земля, чем в том, обусловлено ли уничтожение противоположностями | 45 | |||
| Простое перемещение частей может представить тела в различных видах | 45 | |||
| Отрицая начала науки, можно поддерживать какой угодно парадокс | 46 | |||
| Небесные тела возникающи и уничтожаемы так, как они невозникающи и неуничтожаемы | 46 | |||
| Своеобразное рассуждение, называемое соритом | 47 | |||
| Среди небесных тел нет противоположностей | 47 | |||
| Противоположности, которые являются причиной разрушения, не пребывают в том самом теле, которое разрушается | 47 | |||
| Небесные тела воздействуют на элементы, но не подвергаются воздействию со стороны элементов | 47 | |||
| Тяжесть и легкость, редкость и плотность — противоположные свойства | 47 | |||
| Звезды бесконечно превосходят по плотности субстанции остального неба | 48 | |||
| Редкость и плотность небесных тел отличны от редкости и плотности элементов (Кремонино) | 48 | |||
| ||||
| Аристотель, видно, преуменьшил перечисление причин того, что элементы возникаемы и уничтожаемы | 48 | |||
| Аристотель и Птоломей считают земной шар неподвижным | 49 | |||
| Более естественно говорить о земном шаре, что он сохраняет покой, чем то, что он прямолинейно движется вниз | 49 | |||
| Больше оснований приписывать прямолинейные движения частям, чем стихиям в целом | 50 | |||
| Перипатетики без всякого основания приписывают стихиям в качестве естественных те движения, которыми они никогда не двигались, и называют противоестественными те, которыми они движутся всегда | 50 | |||
| Чувственный опыт нужно предпочесть человеческим рассуждениям | 50 | |||
| Небо неизменно, так как никогда на нем не было видно изменений | 51 | |||
| Светоносные тела по природе отличаются от темных | 51 | |||
| Средиземное море образовалось в результате разделения Абиле и Кальпе | 52 | |||
| Разрушение звезды столь же невозможно, как и разрушение всего земного шара | 53 | |||
| Аристотель переменил бы мнение, если бы видел новости нашего века | 53 | |||
| Достоверность заключения помогает найти доказательство посредством аналитического метода | 53 | |||
| Пифагор совершил гекатомбу за найденное геометрическое доказательство | 53 | |||
| Новые звезды, появившиеся на небе | 53 | |||
| Пятна, которые появляются и распадаются на лике Солнца | 53 | |||
| Солнечные пятна больше всей Азии и Африки | 54 | |||
| Астрономы, опровергнутые Антитихо | 54 | |||
| Антитихо приспосабливает астрономические наблюдения к своим целям | 54 | |||
| Различные мнения о солнечных пятнах | 54 | |||
| В науках о природе ораторское искусство недействительно | 55 | |||
| Аргумент, который необходимо доказывает, что солнечные пятна возникают и распадаются | 55 | |||
| Движение пятен у окружности Солнца кажется медленным | 55 | |||
| Очертания пятен узки около окружности солнечного диска и почему это так кажется | 55 | |||
| Солнечные пятна не обладают сферической формой; они растянуты, как тонкие слои | 56 | |||
| По Аристотелю, нельзя е определенностью говорить о небе из-за его громадного удаления | 56 | |||
| По Аристотелю, чувство нужно предпочесть рассуждениям | 56 | |||
| В согласии о учением Аристотеля небо скорее можно назвать изменяющимся, чем неизменяющимся | 56 | |||
| Благодаря телескопу мы можем лучше Аристотеля рассуждать о предметах неба | 57 | |||
| Речи Симпличио | 57 | |||
| Перипатетическая философия неизменна | 57 | |||
| Возникаемость и изменчивость — большее совершенство в мировых телах, чем противоположные свойства | 58 | |||
| Земля особенно благородна из-за многих происходящих в ней изменений | 58 | |||
| ||||
| Земля, лишенная изменений, бесполезна и преисполнена праздности | 58 | |||
| Земля более благородна, чем золото и драгоценности | 58 | |||
| Недостаток и избыток придают цену и унижают вещи | 59 | |||
| Неуничтожаемость превозносится только из-за страха смерти | 59 | |||
| Хулящие уничтожаемость заслуживают быть превращенными в статую | 59 | |||
| Небесные тела, устроенные для служения Земле, нуждаются только в движении и в свете | 59 | |||
| У небесных тел нет обоюдного взаимодействия друг с другом | 59 | |||
| Изменчивость не пребывает в земном шаре в целом, а только в некоторых частях | 59 | |||
| Небесные тела изменчивы во внешних частях | 59 | |||
| Движения и изменения, происходящие на Земле, — все для блага человека | 60 | |||
| На Луне отсутствуют рождения, похожие на наши, и она не населена людьми | 60 | |||
| На Луне могут рождаться вещи, отличные от наших | 60 | |||
| Кто не знает стихии воды, тот никогда не сможет представить себе кораблей и рыб | 60 | |||
| На Луне могут быть субстанции, отличные от наших | 60 | |||
| Первое сходство между Луной и Землей — это форма, что доказывается тем, как Луна освещается Солнцем | 61 | |||
| Второе сходство в том, что Луна темна, как и Земля | 61 | |||
| Третье — вещество Луны плотно и гористо, как и у Земли | 61 | |||
| Четвертое — Луна делится на две части, отличающиеся по светлоте и темноте, как и земной шар — на моря и на земную поверхность | 62 | |||
| Поверхность моря покажется издалека темнее, чем поверхность Земли | 62 | |||
| Пятое — изменение фаз Земли подобно изменению фаз | ||||
| Луны и происходит в тот же самый период | 62 | |||
| Вся Земля видит только половину Луны, и только половина Луны видит всю Землю | 63 | |||
| С Земли видно больше половины лунного шара | 63 | |||
| Два пятна на Луне, из наблюдения которых следует, что она обращена в своем движении к центру Земли | 64 | |||
| Шестое — Земля и Луна обоюдно освещаются | 64 | |||
| Свет, отраженный Землей на Луну | 64 | |||
| Вторичный свет признается собственным светом Луны | 65 | |||
| Земля бессильна отражать лучи Солнца | 65 | |||
| По Аристотелю, небесные субстанции непроницаемы | 65 | |||
| Небесная материя — неосязаема | 66 | |||
| Поверхность Луны глаже поверхности зеркала | 66 | |||
| Возвышенности и углубления на Луне — иллюзии, вызванные прозрачностью и непрозрачностью | 66 | |||
| Подробно доказывается, что у Луны шероховатая поверхность | 67 | |||
| Плоские зеркала посылают отражение в одно место, а сферические повсюду | 69 | |||
| Сфера активности у небесных тел больше, чем у элементарных | 69 | |||
| Если бы Луна была подобна сферическому зеркалу, то она была бы невидима | 69 | |||
| ||||
| Излучающее свет тельце звезд кажется в тысячу раз бо́льшим, чем голое | 71 | |||
| Свет, отраженный от шероховатых тел, более всесторонен, чем от гладких, и почему | 71 | |||
| Если бы Луна была гладкой и чистой, то она была бы невидимой | 71 | |||
| Некоторые писатели пишут то, чего не понимают, а потому непонятно то, что они пишут | 72 | |||
| Брильянты выделываются со многими гранями и почему | 72 | |||
| Шлифованное серебро представляется более темным, чем нешлифованное, и почему | 72 | |||
| Более шероховатая поверхность отражает свет сильнее, чем менее шероховатая | 73 | |||
| Перпендикулярные лучи освещают больше, чем косые, и почему | 73 | |||
| Косые лучи освещают меньше и почему | 74 | |||
| Почему перипатетиками признается совершенная сферичность небесных тел | 76 | |||
| Форма не является причиной неуничтожаемости, а только большей продолжительности существования | 76 | |||
| Разрушаемость может быть большей и меньшей, но не неуничтожаемость | 76 | |||
| Совершенство формы оказывает влияние в разрушаемых телах, но не в вечных | 76 | |||
| Если бы сферическая форма сообщала вечность, то все тела были бы вечными | 76 | |||
| Перламутр способен подражать видимым неодинаковостям поверхности Луны | 77 | |||
| Видимым неровностям Луны нельзя подражать при помощи более или менее прозрачной и непрозрачной материи | 77 | |||
| Различные виды Луны доступны подражанию любой непрозрачной материей | 78 | |||
| Различные явления, которыми доказывается гористость Луны | 78 | |||
| Ночью Луна кажется более сияющей, чем днем | 78 | |||
| Луна, видимая днем, подобна облачку | 78 | |||
| Облака способны освещаться Солнцем не меньше Луны | 79 | |||
| Освещенная Солнцем стена по сравнению с Луной блестит не меньше ее | 79 | |||
| Больше освещает третье отражение солнечного света от стены, чем первое от Луны | 79 | |||
| Свет Луны слабее света сумерек | 80 | |||
| Освещенные тела кажутся более светлыми при темном окружении | 80 | |||
| По мнению некоторых вторичный свет Луны порожден Солнцем | 81 | |||
| Одно и то же: мнения ли новы для людей или люди новы для мнений | 82 | |||
| Вторичный свет Луны проявляется в форме кольца, т. е. он ярок у края окружности, а не по середине, и почему | 82 | |||
| Способ наблюдения вторичного света Луны | 82 | |||
| Диск Луны при затмениях Солнца можно видеть только из-за отсутствия света | 83 | |||
| Автор книжки заключений приспосабливает вещи к своим положениям, а не положения к вещам | 83 | |||
| ||||
| Шутка, сыгранная с человеком, желавшим продать секрет того, как можно разговаривать с кем-нибудь на расстоянии тысячи миль | 83 | |||
| Земля может воздействовать светом на небесные тела | 84 | |||
| Сродство между Землей и Луной в зависимости от близости | 85 | |||
| Твердость лунного тела доказывается тем, что оно гористо | 85 | |||
| Отражение света от моря гораздо слабее, чем от Земли | 85 | |||
| Опыт, показывающий, что отражение воды менее светло, чем Отражение земли | 85 | |||
| Вторичный свет Луны ярче перед соединением, чем после него | 85 | |||
| Более темные части Луны — ровные, а более светлые — гористые | 86 | |||
| Вокруг лунных пятен тянутся длинные цепи гор | 86 | |||
| На Луне зарождаются вещи, не подобные нашим, а чрезвычайно отличные, если только там существует зарождение | 86 | |||
| Луна не состоит из земли и воды | 87 | |||
| Положения Солнца, необходимые для наших зарождений, не таковы на Луне | 87 | |||
| Естественный день на Луне длится один месяц | 87 | |||
| На Луне Солнце понижается и повышается с разницей в 10 градусов, а на Земле — в 47 градусов | 87 | |||
| На Луне не бывает дождей | 87 | |||
| Никогда ничего не поняв в совершенстве, некоторые думают, что понимают все | 87 | |||
| Вещание оракула правильно, когда он признает Сократа мудрейшим | 88 | |||
| Божественное знание бесконечное число раз бесконечно | 88 | |||
| Возвышенный гений Буонаротти | 88 | |||
| Человек многое разумеет интенсивно, но мало разумеет экстенсивно | 89 | |||
| Способ познания бога отличен от способа познания у людей | 89 | |||
| Человек идет к познанию путем рассуждения | 89 | |||
| Определения охватывают потенциально все свойства определяемых вещей | 89 | |||
| Бесконечное число свойств, может быть, составляет одно единственное свойство | 89 | |||
| Переходы, которые человеческое рассуждение осуществляет во времени, божественный разум осуществляет мгновенно | 89 | |||
| Удивительная острота гения человеческого | 90 | |||
| Изобретение письма изумительнее всех других изобретений | 90 | |||
ДЕНЬ ВТОРОЙ | ||||
| Комический ответ одного философа в связи с изысканием начала нервов | 92 | |||
| Начало нервов, по Аристотелю и по мнению врачей | 92 | |||
| Что требуется для того, чтобы быть хорошим философом наподобие Аристотеля | 92 | |||
| Остроумное средство научиться философии из любой книги | 93 | |||
| Изобретение подзорной трубы заимствовано у Аристотеля | 93 | |||
| Алхимики видят в вымыслах поэтов указания на секрет делать золото | 93 | |||
| Многие приверженцы Аристотеля унижают его достоинство, всячески стараясь преувеличить его значение | 94 | |||
| ||||
| Космическая история одного ваятеля | 94 | |||
| Бессовестный образ действий одного философа-перипатетика | 95 | |||
| Узость многих приверженцев Аристотеля | 95 | |||
| Чрезмерная приверженность к Аристотелю достойна порицания | 95 | |||
| Тот, кто никогда не философствует, не должен присваивать себе титула философа | 95 | |||
| Движения Земли незаметны для ее обитателей | 96 | |||
| Земле могут принадлежать лишь такие движения, которые кажутся нам присущими всем частям вселенной вообще, кроме Земли | 96 | |||
| Суточное движение, повидимому, есть движение, общее всему миру, за исключением Земли | 96 | |||
| Аристотель и Птоломей оспаривают приписываемое Земле суточное движение | 96 | |||
| Почему суточное движение скорее должно принадлежать одной Земле, чем всему остальному миру | 97 | |||
| Для предметов, захваченных равномерным движением, это последнее как бы не существует и проявляет свое действие только на вещах, не принимающих в нем участия | 97 | |||
| Положение Аристотеля взято им от предшественников, но изменено | 98 | |||
| Первое доказательство того, что суточное движение принадлежит Земле | 98 | |||
| Природа не употребляет многих средств там, где она может обойтись немногими | 98 | |||
| Из суточного движения не возникает никаких изменений в расположении небесных тел относительно друг друга; все изменения имеют отношение только к Земле | 98 | |||
| Второе доказательство суточного движения Земли | 99 | |||
| По Аристотелю не существует противоположностей в круговых движениях | 99 | |||
| Третье подтверждение того же мнения | 99 | |||
| Чем больше орбиты, тем продолжительнее движение по ним | 99 | |||
| Сроки обращения Медицейских звезд | 99 | |||
| 24-часовое движение высшей сферы нарушает порядок сфер низших | 100 | |||
| Четвертое подтверждение. Большая неравномерность движений отдельных постоянных звезд, если их сферы движутся | 100 | |||
| Движения постоянных звезд становятся в разное время то быстрее, то медленнее, если движется звездная сфера | 100 | |||
| Шестое подтверждение | 100 | |||
| Седьмое подтверждение | 101 | |||
| Свободно плавающая, взвешенная в жидкой сфере Земли, повидимому, неспособна к сопротивлению силе суточного движения | 101 | |||
| Одно простое подвижное тело имеет только одно естественное движение; все остальные движения ему сообщены извне | 101 | |||
| Нет движения без движущегося предмета | 101 | |||
| Один единственный опыт или строгое доказательство обращают в ничто соображения, основанные на вероятности | 102 | |||
| Бесконечное могущество, вероятно, проявит себя скорее в большом, нежели в малом | 102 | |||
| В бесконечности нет ни больших, ни меньших частей, хотя бы таковые были неодинаковы | 103 | |||
| ||||
| При аксиоме Frustra fit per plura etc. — прибавка aeque bene излишня | 103 | |||
| Соображения Аристотеля в пользу неподвижности Земли | 103 | |||
| Соображения двоякого рода по вопросу о том, движется ли Земля или нет | 104 | |||
| Основания Птоломея, Тихо и других, помимо Аристотеля | 104 | |||
| Первый аргумент, почерпнутый из движения твердого тела, падающего сверху вниз | 104 | |||
| Подтверждение его примером тела, падающего с вершины корабельной мачты | 105 | |||
| Второй аргумент, почерпнутый из движения тела, подброшенного высоко вверх | 105 | |||
| Третий аргумент, почерпнутый из стрельбы из пушки к востоку и к западу | 105 | |||
| Подтверждение аргумента практикой выстрелов, направленных к югу и северу | 105 | |||
| То же подтверждается практикой выстрелов к востоку и западу | 105 | |||
| Коперниканцы пришли к своему взгляду не вследствие незнания доводов противоположной стороны | 106 | |||
| Христиан Вурстейзен прочел несколько лекций, посвященных учению Коперника; каков был результат их? | 106 | |||
| Коперниканцы ранее придерживались противоположных воззрений; приверженцы Аристотеля и Птоломея никогда ранее не разделяли противного мнения | 106 | |||
| Движение и покой — главнейшие свойства природы | 107 | |||
| Ложное не может быть так хорошо доказуемо, как истинное | 108 | |||
| Для правильных положений всегда находятся многие убедительные аргументы; но не то по отношению к доказательству положений ложных | 108 | |||
| Аристотель опроверг бы доводы противников или изменил бы свое мнение | 108 | |||
| Аргумент, взятый из движения облаков и птиц | 108 | |||
| Аргумент, взятый из опыта с воздухом, который кажется нам при езде дующим нам навстречу | 109 | |||
| Аргумент, почерпнутый из силы отбрасывания и рассеивания, присущего вращательному движению | 109 | |||
| Правда и красота идентичны, так же как ложь и безобразие | 110 | |||
| Возражение на первый довод Аристотеля | 110 | |||
| Насильственное не может быть вечным, а что не может быть вечным, не может быть естественным | 110 | |||
| Два необходимых условия для вечного движения — неограниченность пространства и неразрушаемость тела | 111 | |||
| Прямолинейное движение не может продолжаться вечно и потому не может быть от природы присуще Земле | 111 | |||
| Возражение на второй аргумент | 111 | |||
| Рассуждение Аристотеля против движения Земли несостоятельно с двух сторон | 112 | |||
| Возражение на третий аргумент | 113 | |||
| Возражение на четвертый аргумент | 113 | |||
| Ошибка Аристотеля и Птоломея, которые принимают за известное то, что требуется доказать | 114 | |||
| Аристотель принимает, что огонь движется прямо вверх по своей природе и по кругу — в силу соучастия | 115 | |||
| Различие между падением камня с мачты корабля и падением с высоты башни | 115 | |||
| ||||
| Часть атмосферы ниже высоких гор следует за движением Земли | 116 | |||
| Движение воздуха может увлекать очень легкие вещи, но не тяжелые | 116 | |||
| Камень, падающий с корабельной мачты, всегда попадет в одно и то же место, движется ли корабль или стоит на месте | 117 | |||
| Брошенное тело движется, по Аристотелю, не вложенной в него силой, но средой | 121 | |||
| Действие среды при продолжающемся движении брошенного тела | 122 | |||
| Разные опыты и доводы против принимаемой Аристотелем причины движения брошенного тела | 122 | |||
| Среда не вызывает движения, но препятствует ему | 123 | |||
| Замечательное свойство движения брошенных тел | 124 | |||
| Различные любопытные проблемы, связанные с движением брошенных тел | 126 | |||
| Линия, описываемая свободно падающим телом при предположении вращения Земли около своего центра, вероятно, была бы окружностью круга | 131 | |||
| Тело, падающее с вершины башни, движется по окружности круга | 132 | |||
| Оно движется не больше и не меньше, чем если бы оставалось наверху | 132 | |||
| Оно движется не ускоренным, а равномерным движением | 132 | |||
| Прямолинейного движения, кажется, вовсе не существует в природе | 133 | |||
| Соображения, в силу которых кажется, что дальность выстрела из орудия к западу должна быть больше, чем при выстреле к востоку | 134 | |||
| Опыт с двигающейся повозкой для обнаружения разницы в дальности выстрелов | 134 | |||
| Опровержение аргументов, почерпнутых из рассмотрения стрельбы из пушки на восток и на запад | 135 | |||
| Замечательный пример Сагредо для доказательства того, что общее движение не производит никакого действия | 136 | |||
| Достаточно безвкусные тонкости, заимствованные из некоей энциклопедии и приведенные иронически | 137 | |||
| Возражения против суточного движения, основанные на отвесном пушечном выстреле | 138 | |||
| Опровержение возражения с указанием логической ошибки | 138 | |||
| Другое опровержение того же возражения | 138 | |||
| Брошенные тела продолжают движение по тем же самым прямым линиям, которые они описывали, когда еще находились в соединении с бросающим | 138 | |||
| Поскольку Земля вращается, ядро, проходящее прямой канал пушки, движется не по прямой, а по кривой линии | 139 | |||
| Как стрелки попадают в птиц, летящих по воздуху? | 140 | |||
| Опровержение возражения, основанного на выстрелах из пушки, направленных на юг или на север | 141 | |||
| Разрешение проблемы, возникающей в связи с выстрелами по направлению к востоку и к западу | 142 | |||
| Коперниканцы, идя навстречу противникам, принимают за правильные многие сомнительные утверждения | 142 | |||
| Вычисление величины, на которую при предположении движения Земли должны отклоняться от цели пушечные выстрелы | 142 | |||
| ||||
| Весьма остроумно доказывается, что при предполагаемом движении Земли пушечные выстрелы давали бы не большее отклонение, чем при покое | 143 | |||
| Можно только с большой осторожностью признавать правильными опыты, на которые ссылаются люди, никогда их не производившие | 144 | |||
| Опыт и доводы против движения Земли кажутся нам доказательными, пока мы не уяснили себе дела вполне | 144 | |||
| Великое, завидное счастье тех, кто мнит, что он все знает | 145 | |||
| Опровержение возражения против движения Земли, основанного на полете птиц | 145 | |||
| Опыт, показывающий несостоятельность всех опытов, приводимых против движения Земли | 146 | |||
| Глупость людей, полагающих, что Земля начала вращаться с того времени, как пифагорейцы начали утверждать, что она движется | 148 | |||
| Аристотель и Птоломей, кажется, оспаривают движение Земли перед людьми, думающими, что она сначала находилась в покое и пришла в движение во времена Пифагора | 148 | |||
| Быстрое вращение производит отбрасывание и рассеивание | 149 | |||
| Наше знание, согласно Платону, есть род припоминания | 149 | |||
| Движение брошенного тела может быть только прямолинейным | 150 | |||
| Брошенное тело движется по касательной круга прежнего движения в точке отрыва | 151 | |||
| Тяжелое брошенное тело с самого момента его отрыва от бросающего начинает склоняться вниз | 152 | |||
| Геометрическое доказательство невозможности отбрасывания тел вследствие вращения Земли | 154 | |||
| Сила правды иногда укрепляется нападками на нее | 158 | |||
| И материальная сфера касается материальной плоскости только в одной точке | 158 | |||
| Определение сферы | 159 | |||
| Доказательство одним перипатетиком того, что прямая линия есть кратчайшая | 159 | |||
| Ошибка этого перипатетика, доказывающего ignotum per ignotius | 159 | |||
| Доказательство того, что сфера касается плоскости только в одной точке | 160 | |||
| Почему абстрактная сфера касается абстрактной плоскости в одной точке, а материальная, конкретная — не в одной | 160 | |||
| Абстрактные положения вполне согласуются с конкретными | 161 | |||
| Касание в одной точке не является исключительно особенностью совершенных сфер, а свойственно всем криволинейным фигурам | 161 | |||
| Труднее найти фигуры, которые соприкасались бы частью своих поверхностей, чем соприкасающиеся в одной точке | 161 | |||
| Сферическая фигура легче воспроизводится, чем всякая другая | 162 | |||
| Построение круга, принятое как постулат | 162 | |||
| Круглые тела различной величины могут быть воспроизведены при помощи одного и того же инструмента | 162 | |||
| Неправильные формы трудно воспроизводимы | 162 | |||
| Вопрос о системе мироздания — одна из самых высоких проблем | 163 | |||
| ||||
| Причина отбрасывания не возрастает пропорционально возрастанию скорости, обусловленной увеличением колеса | 164 | |||
| Если существует суточное вращение Земли, то постройки, горы и даже, быть может, весь земной шар разрушились бы, если бы Земля была каким-либо препятствием остановлена | 164 | |||
| Склонность тяжелых тел к движению вниз равняется их сопротивлению к движению вверх | 165 | |||
| Большая скорость возмещает в точности большую тяжесть | 166 | |||
| Другие возражения двух новейших писателей против Коперника | 168 | |||
| Первое возражение современного автора книжки заключений | 168 | |||
| Пушечное ядро, по мнению современного автора книжки Заключений, затратило бы более шести дней, чтобы упасть с лунной сферы до центра Земли | 169 | |||
| Нелепость возражения, основанного на падении тела с лунной сферы | 170 | |||
| Точное вычисление времени падения пушечного ядра с лунной сферы до центра Земли | 170 | |||
| Естественное ускорение движения падающего тела происходит соответственно последовательному ряду нечетных чисел, начиная с единицы | 171 | |||
| Пройденные падающим телом пространства относятся как квадраты времени | 171 | |||
| Вся область знания, касающаяся местного движения, открыта Академиком | 171 | |||
| Ошибка Аристотеля, утверждавшего, что тяжелые тела при падении движутся со скоростью, пропорциональной их весу» | 171 | |||
| Если бы падающее тяжелое тело продолжало в течение равного времени двигаться равномерно со скоростью, им достигнутой, то оно прошло бы пространство, двойное против того, которое прошло, двигаясь ускоряющимся движением | 173 | |||
| Движение качающихся тяжелых тел при устранении препятствий продолжалось бы вечно | 174 | |||
| Если бы земной шар был просверлен насквозь, то тяжелое тело, падающее по такому колодцу, поднялось бы по другую сторону центра на такую же высоту, с которой оно спустилось | 174 | |||
| Ускорение движения свободно падающего тела растет постоянно с мгновения на мгновение | 175 | |||
| В естественных науках математическая строгость не нужна | 176 | |||
| Тело, подвешенное на длинной нити, колеблется медленнее, чем подвешенное на короткой | 176 | |||
| Колебания одного и того же маятника происходят одинаково часто, велики ли эти колебания или малы | 176 | |||
| Причины, задерживающие маятник и приводящие его к состоянию покоя | 177 | |||
| Нить или цепочка, на которой подвешен маятник, при колебаниях сгибается дугой, а не остается прямой | 177 | |||
| Мы не лучше знаем то, что движет тяжелые тела вниз, чем то, что заставляет звезды двигаться по кругу; мы знаем только обычное для этого явления название | 179 | |||
| Сила, которая заставляет брошенные тела подниматься вверх, для них не менее естественна, чем тяжесть, двигающая их вниз | 180 | |||
| Противоположные принципы не могут естественно находиться в одном и том же субъекте | 180 | |||
| ||||
| Естественное движение превращается само собой в такое, которое именуется противоестественным и насильственным | 180 | |||
| Склонность элементарных тел следовать за Землей имеет ограниченную сферу | 181 | |||
| В смешанных движениях мы не замечаем круговой его части, так как сами движемся кругообразно | 184 | |||
| Сначала должны быть налицо тяжелые субстанции, а потом уже центр тяжести | 186 | |||
| Если переместить большую часть тяжелых субстанций в другое место, то оторвавшиеся от них частички пойдут вместе с ними | 186 | |||
| Не исключена возможность, что окружностью маленького, не много раз вращающегося круга можно пройти или описать линию, которая больше какого угодно большого круга | 186 | |||
| Коперниково учение обращает в ничто критерий философии | 187 | |||
| Общее движение — как бы движение несуществующее | 187 | |||
| Аргумент, заимствованный из отвесного падения тел, опровергается иным способом | 188 | |||
| Каким образом замечается движение падающего тела? | 188 | |||
| Движение глаза доказывает нам движение наблюдаемого объекта | 188 | |||
| Опыт, доказывающий, что движение общее не замечается | 188 | |||
| Тонкий вопрос — может ли подзорная труба так же хорошо применяться на вершине мачты, как у ее, подножия | 189 | |||
| Различные происходящие от качки корабля движения | 190 | |||
| Два рода изменений положения трубы вызываются качкой корабля | 190 | |||
| Годовое движение Земли должно было бы вызывать постоянный и весьма сильный ветер | 191 | |||
| Если мы остаемся в соприкосновении с одной и той же частью атмосферы, мы не чувствуем никакого толчка | 191 | |||
| С точки зрения Коперника необходимо отказаться от показания чувственного опыта | 191 | |||
| Наше движение может происходить от внутренних или внешних причин без того, чтобы мы его замечали или чувствовали | 192 | |||
| Движение судна неощутимо для находящихся на нем | 192 | |||
| Движение лодки может быть заметно благодаря чувству зрения и при помощи разумных соображений | 192 | |||
| Движение Земли познается по звездам | 192 | |||
| Аргументы против движения Земли ex rerum natura | 193 | |||
| Три аксиомы, которые принимаются как явно правильные | 193 | |||
| Простое тело, каким является Земля, не может двигаться тремя различными движениями | 193 | |||
| Земля не может выполнять ни одного из приписанных ей Коперником движений | 193 | |||
| Возражения против аргументов, опровергающих движение Земли ex rerum natura | 194 | |||
| Четвертая аксиома против движения Земли | 194 | |||
| Члены животных необходимы для выполнения различных движений | 194 | |||
| Другой аргумент против троякого движения Земли | 194 | |||
| Члены животных не предназначены для того, чтобы производить ими различные движения | 194 | |||
| Движения животных все одного рода | 194 | |||
| ||||
| Концы всех подвижных костей круглы | 194 | |||
| Указания на то, что по необходимости концы костей должны быть круглы, а движения всех животных кругообразны | 194 | |||
| Вторичные движения животных обусловлены первичными | 195 | |||
| Для движения Земли не требуется членов | 195 | |||
| Хотят знать, посредством каких членов земной шар может выполнять три разных движения | 195 | |||
| Один единственный принцип может вызывать многие движения | 195 | |||
| Другое возражение против троякого движения | 195 | |||
| Грубая ошибка противников Коперника | 195 | |||
| Хитроумное и вместе с тем глупое возражение против Коперника | 196 | |||
| Ошибка противника обнаруживается и объясняется тем, что годовое и суточное движения, если они присущи Земле, направлены в одну сторону, а не противоположны друг другу | 196 | |||
| Из другой грубой ошибки вытекает, что противник Коперника мало учился | 196 | |||
| Представляется сомнительным, понял ли противник третье, приписываемое Коперником Земле движение | 196 | |||
| Опровержение того же возражения подобными примерами других небесных тел | 197 | |||
| Движение более отлично от покоя, чем прямолинейное движение от кругового | 197 | |||
| Скорее можно допустить наличие у Земли двух принципов для прямолинейного и кругового движения, нежели одного принципа для движения, а другого для покоя | 198 | |||
| Движения частиц Земли при возвращении к своему целому, возможно, кругообразны | 198 | |||
| Различие движений дает возможность познания разнообразия вещей | 198 | |||
| Природа создала сначала вещи по-своему, а только потом человеческий разум со способностью их понимать | 198 | |||
| Коперник ошибочно приписывает разным вещам одинаковое действие | 198 | |||
| Общие свойства не могут дать познания разнородности предметов | 199 | |||
| Согласованность элементов в одном и том же движении значит не больше и не меньше, чем согласованность в одном и том же состоянии покоя | 199 | |||
| Тела одного и того же рода имеют движения одинакового рода | 199 | |||
| Другой аргумент, также направленный против Коперника | 199 | |||
| Из темноты Земли или световой силы Солнца и неподвижных звезд может быть сделано заключение о движении первой и о неподвижности последних | 200 | |||
| Другое различие между Землей и небесными телами, касающееся чистоты и нечистоты | 200 | |||
| Коперник вносит беспорядок во вселенную Аристотеля | 200 | |||
| Ошибочный вывод автора Антитихо | 200 | |||
| Глупость утверждения, что Земля находится вне неба | 200 | |||
| Аргумент, заимствованный от животных, которые нуждаются в отдыхе, хотя их движения естественны | 201 | |||
| Аргумент Кеплера в пользу Коперника | 201 | |||
| Автор Антитихо представляет возражение против Кеплера | 201 | |||
| ||||
| Быстрота кругового движения возрастает вместе о возрастанием диаметра круга | 201 | |||
| Объяснение истинного смысла слов Кеплера и защита его | 202 | |||
| Большая и малая величины тела обусловливают различие при движении, но не при покое | 202 | |||
| Порядок природы таков, что меньшие пути проходятся в меньшие сроки, большие — в более продолжительные | 202 | |||
| Воображаемый ответ Кеплера со скрытой иронией | 202 | |||
| Животные не уставали бы, если бы их движение происходило так, как происходит движение, приписываемое Земле | 202 | |||
| Причины утомления у животных | 203 | |||
| Движение животных можно назвать скорее насильственным, чем естественным | 203 | |||
| Сила не уменьшается там, где она не встречает противодействия | 203 | |||
| Возражение Киарамонти обращается против него самого | 203 | |||
| Для правильных положений находятся убедительные доказательства, но не для ложных | 203 | |||
| Скорее можно опасаться усталости небесных сфер, нежели усталости земного шара | 204 | |||
ДЕНЬ ТРЕТИЙ | ||||
| Некоторые исходят в своих рассуждениях из готового сложившегося в их уме положения, в которое они верят и к которому затем подгоняют свои выводы | 205 | |||
| Движение воды между отливом и приливом не прерывается покоем | 206 | |||
| Метод Киарамонти для опровержения астрономов и метод Сальвиати, его опровергающий | 208 | |||
| Минимальные и максимальные высоты новой звезды отличаются друг от друга не более, чем высоты полюса, как скоро новая звезда стоит на небесном своде | 209 | |||
| Астрономические инструменты могут легко давать ошибочные показания | 214 | |||
| До сих пор никем не доказано, конечен ли мир или бесконечен | 234 | |||
| Доказательства Аристотеля, приводимые в пользу конечности вселенной, все отпадают, если отрицать ее подвижность | 234 | |||
| Аристотель делает центром вселенной ту точку, вокруг которой вращаются все небесные сферы | 234 | |||
| Спрашивается, какую из двух предпосылок, противоречащих учению Аристотеля, он предпочел бы, если бы был вынужден выбрать одну | 234 | |||
| Объемлющему и объемлемому более подходит вращаться вокруг одного и того же центра, нежели вокруг разных | 235 | |||
| Если центр вселенной совпадает с точкой, вокруг которой движутся планеты, то в нем находится Солнце, а не Земля | 235 | |||
| Наблюдения, из которых можно заключить, что Солнце, а не Земля расположено в центре небесных обращений | 235 | |||
| Смена фаз Венеры доказывает движение ее вокруг Солнца | 235 | |||
| Луна не может отделиться от Земли | 236 | |||
| Годичное движение Земли в соединении с движением других планет вызывает удивительные явления | 236 | |||
| Схема устройству мира на основании явлений | 236 | |||
| ||||
| Венера кажется наибольшей во время вечернего и наименьшей во время утреннего соединения с Солнцем | 237 | |||
| Убедительное доказательство того, что Венера обращается вокруг Солнца | 237 | |||
| Доказательство того, что обращение Меркурия вокруг Солнца происходит внутри орбиты Венеры | 237 | |||
| Марс необходимо включает в свою орбиту и Землю, и Солнце | 237 | |||
| Марс в противостоянии с Солнцем кажется в 60 раз большим, чем в соединении | 237 | |||
| Юпитер и Сатурн также охватывают Землю и Солнце | 237 | |||
| Приближение и удаление трех верхних планет на двойное расстояние до Солнца | 237 | |||
| Различие в видимой величине у Сатурна меньше, чем у Юпитера, а у Юпитера меньше, чем у Марса, и причины этому | 238 | |||
| Орбита Луны обнимает Землю, но не Солнце | 238 | |||
| Вероятное положение постоянных звезд | 238 | |||
| Как можно представить себе сферу вселенной? | 238 | |||
| Покой, годичное и суточное движение должны быть поделены между Солнцем, Землей и небесной сферой | 238 | |||
| При движущейся сфере больше оснований считать неподвижным центр ее, нежели какую-либо другую ее часть | 338 | |||
| Если допустить годичное движение Земли, то ей же нужно приписать и суточное | 238 | |||
| Достаточно самых детских доводов, чтобы заставить глупцов держаться за свое мнение о неподвижности Земли | 239 | |||
| Показывается, сколь неправдоподобным кажемся учение Коперника | 239 | |||
| Разум и логика у Аристарха и Коперника господствуют над показаниями чувственного опыта | 239 | |||
| Марс яростно выступает против системы Коперника | 243 | |||
| Явления, замеченные на Венере, стоят в противоречии с системой Коперника | 243 | |||
| Другое затруднение, создаваемое Венерой для Коперника | 243 | |||
| Венера, по Копернику, или обладает собственным светом, или состоит из прозрачной субстанции | 244 | |||
| Коперник умалчивает о малом изменении видимой величины Венеры и Марса | 244 | |||
| Луна нарушает порядок других планет | 244 | |||
| Ответы на три первые возражения против системы Коперника | 244 | |||
| Причины того, что Венера и Марс изменяют свою видимую величину не в той мере, в какой следовало бы | 244 | |||
| Показания телескопа считаются перипатетиками обманчивыми | 245 | |||
| Причины, по которым светящиеся тела кажутся тем более увеличенными, чем они меньше | 245 | |||
| Площади фигур возрастают в отношении квадратов по сравнению с линейными размерами | 245 | |||
| Чем ярче предметы, тем более увеличенными они кажутся | 246 | |||
| Легко производимый опыт, показывающий увеличение размера звезд вследствие привходящих лучей | 246 | |||
| Юпитер испытывает меньшее увеличение, чем Сатурн | 246 | |||
| Солнце и Луна испытывают только ничтожное увеличение | 246 | |||
| Очевидным опытом доказывается, что у тел более блестящих происходит более сильное излучение, чем у менее блестящих | 246 | |||
| ||||
| Подзорная труба является лучшим средством лишить звезды венца из лучей | 246 | |||
| Вторая причина незначительного видимого прироста величины Венеры | 246 | |||
| Коперник был убежден доводами рассудка вопреки противоречащим показаниям чувственного опыта | 247 | |||
| Меркурий не поддается точным наблюдениям | 247 | |||
| Устранение затруднения, порожденного тем, что Земля обращается вокруг Солнца не одна, но в сопровождении Луны | 247 | |||
| Медицейские звезды являются четырьмя лунами у Юпитера | 247 | |||
| Главная цель астрономии — это давать объяснения явлениям | 248 | |||
| Коперник реформировал астрономию на основании предпосылок Птоломея | 248 | |||
| Что побудило Коперника построить свою систему? | 248 | |||
| Несообразности, присущие системе Птоломея | 248 | |||
| В высокой степени важный аргумент в пользу Коперника — это устранение стояния и попятного движения планет | 249 | |||
| Одно только годичное движение Земли вносит большую неравномерность в видимое движение пяти планет | 249 | |||
| Доказательство неравномерности движения трех верхних планет, обусловливаемое годичным движением Земли | 249 | |||
| Возвратные движения чаще у Сатурна, реже у Юпитера и еще реже у Марса; объяснения этого | 250 | |||
| Доказательства возвратного движения Венеры и Меркурия Аполлонием и Коперником | 250 | |||
| Годичное движение Земли лучше всего объясняет неправильность движения пяти планет | 250 | |||
| Само Солнце свидетельствует о том, что годичное движение присуще Земле | 250 | |||
| Академик Линчео является первым открывшим солнечные пятна, а также все остальные новые небесные явления | 250 | |||
| История продолжительных систематических наблюдений, произведенных Академиком над солнечными пятнами | 250 | |||
| Внезапная мысль, пришедшая в голову Академику Линчео, относительно важности следствий, вытекающих из движения солнечных пятен | 251 | |||
| Удивительные изменения, наблюдаемые в движении пятен, предусмотренные Академиком для случая, если годичное движение свойственно Земле | 252 | |||
| Первая особенность, которую следует отметить в движении солнечных пятен; в дальнейшем будут объяснены и остальные | 252 | |||
| Наблюдаемое в действительности соответствует предсказаниям | 255 | |||
| Хотя годичное движение, приписываемое Земле, вполне соответствует явлениям солнечных пятен, отсюда еще не следует, что из явления солнечных пятен можно сделать обратный вывод о том, что Земле присуще годичное движение | 255 | |||
| Истинные перипатетики будут высмеивать солнечные пятна и касающиеся их явления как иллюзии, относимые к стеклам телескопа | 255 | |||
| Если бы Земля была неподвижна в середине круга зодиака, то Солнцу пришлось бы приписать четыре движения, как будет объяснено далее | 256 | |||
| Иронические возражения против Коперника в одной известной книжке | 258 | |||
| ||||
| Если принять, что годичное движение свойственно Земле, то неподвижные звезды должны быть больше, чем вся земная орбита | 259 | |||
| Аргумент Тихо основан на ложных предпосылках | 259 | |||
| Те, кто не правы в споре, придираются к каждому случайному слову противника | 259 | |||
| Видимое изменение движения планет не заметно на неподвижных звездах | 259 | |||
| Если предположить, что неподвижная звезда шестой величины не больше, чем Солнце, то изменение, значительное для планет, почти не заметно для неподвижных звезд | 259 | |||
| Расстояние до Солнца составляет 1208 полудиаметров Земли | 259 | |||
| Поперечник Солнца равен половине градуса | 260 | |||
| Поперечник неподвижных звезд первой и шестой величины | 260 | |||
| Во сколько раз видимый поперечник Солнца больше видимого поперечника неподвижной звезды? | 260 | |||
| Как велико должно быть расстояние до неподвижной звезды шестой величины в предположении, что такая звезда по величине равна Солнцу | 260 | |||
| Для неподвижных звезд изменение видимого положения, вызываемое перемещением Земли, меньше, чем вызываемое величиной Земли изменение видимого положения Солнца | 260 | |||
| Звезды шестой величины приняты Тихо и автором книжки в десять миллионов раз большими, чем нужно | 260 | |||
| Вычисление размеров неподвижной звезды по отношению к большой орбите | 260 | |||
| Общая ошибка всех астрономов относительно величины звезд | 260 | |||
| Венера уличает астрономов в непростительной ошибке при определении величины звезд | 261 | |||
| Способ измерения видимого диаметра звезды | 261 | |||
| Диаметр неподвижной звезды первой величины не может быть больше пяти секунд | 262 | |||
| Зрачок в глазу расширяется и суживается | 262 | |||
| Как находится расстояние от зрачка до места схождения лучей | 262 | |||
| Астрономы согласны в том, что большая величина орбит является причиной большей медленности обращения | 264 | |||
| При других принятых астрономами предпосылках вычисления показывают, что удаленность неподвижных звезд составляет 10800 полудиаметров земной орбиты | 264 | |||
| Из соотношений с Юпитером и Марсом мы находим, что звездная сфера удалена еще гораздо более | 264 | |||
| Огромные величины и числа не охватываются нашим умом | 265 | |||
| Природа и бог заботятся о людях так, как если бы у них не было других забот | 265 | |||
| Забота бога о роде человеческом на примере Солнца | 265 | |||
| Великая дерзость называть излишним во вселенной то, пользу чего для нас мы не постигаем | 266 | |||
| Только удалив с неба какую-нибудь звезду, можно было бы узнать, как она воздействует на нас | 266 | |||
| Многое на небе может быть невидимо для нас | 266 | |||
| Большое, малое, огромное и т. д. — суть понятия относительные | 266 | |||
| Несостоятельность мнения тех, которые считают звездную сферу слишком обширной по учению Коперника | 266 | |||
| ||||
| Пространство, отведенное для одной неподвижной звезды, много меньше пространства, отведенного для одной планеты | 267 | |||
| Звезда называется малой по отношению к величине окружающего ее пространства | 267 | |||
| Вся звездная сфера с большого расстояния может показаться столь же малой, как одна единственная звезда | 267 | |||
| Возражения в форме вопросов автора книжки | 267 | |||
| Ответы на возражения автора книжки | 267 | |||
| Автор книжки в своих вопросах путается и противоречит сам себе | 267 | |||
| Вопросы автору книжки, которые показывают несостоятельность его вопросов | 267 | |||
| То, что удаленные предметы кажутся маленькими, является следствием несовершенства глаза, как это и доказывается | 268 | |||
| Ни Тихо, ни его приверженцы не пытались посмотреть, существует ли какое-либо явление на небе, говорящее против или в пользу годичного движения | 268 | |||
| Астрономы едва ли отдавали себе отчет о тех небесных явлениях, которые должны были вытекать из годичного движения Земли | 268 | |||
| Кое-чего Коперник не знал из-за отсутствия необходимых инструментов | 268 | |||
| Тихо и другие возражают против годового движения, основываясь на неизменной высоте полюса | 269 | |||
| Движение, поскольку оно общее, как будто не существует | 270 | |||
| Пример, удобный для того, чтобы разъяснить, что высота полюса не должна изменяться в результате годового движения Земли | 270 | |||
| Годичное движение Земли могло бы иметь следствием изменение положения каких-нибудь неподвижных звезд, но не полюса | 271 | |||
| Опровергается неправильное мнение, будто при годовом движении Земли должны происходить большие изменения в высоте неподвижных звезд | 271 | |||
| Прямая линия и окружность бесконечно большого круга — одно и то же | 271 | |||
| Спрашивается, в каких звездах и какие изменения должны были бы наблюдаться в результате годового движения Земли | 272 | |||
| Раз астрономы не определили точно, какие изменения могли бы проистекать из годового движения Земли, то это является признаком того, что они как следует этого не понимали | 272 | |||
| Изменения у неподвижных звезд должны быть у одних бо́льшими, у других меньшими, а у третьих сводиться к нулю | 272 | |||
| Главный аргумент против Коперника — это то, что проявляется на Солнце и на неподвижных звездах | 272 | |||
| Возражения Аристотеля против античных философов, желавших сделать Землю планетой | 273 | |||
| Годичное движение центра Земли по эклиптике и суточное движение Земли вокруг собственного центра | 273 | |||
| Ось Земли всегда параллельна самой себе, описывает цилиндрическую поверхность и наклонна по отношению к большой орбите | 273 | |||
| Земной шар никогда не изменяет наклона и сохраняет его неизменным | 273 | |||
| Неподвижные звезды, находящиеся в плоскости эклиптики, никогда не повышаются и не понижаются вследствие {352} годового движения Земли, а только приближаются или удаляются | 274 | |||
| Соображения против годового движения Земли, вызванные находящимися на эклиптике неподвижными звездами | 274 | |||
| Стояние, поступательное и попятное движение у планет узнаются по их отношению к неподвижным звездам | 275 | |||
| Показания неподвижных звезд, подобные наблюдаемым у планет, как доказательство годового движения Земли | 275 | |||
| Неподвижные звезды вне эклиптики повышаются и понижаются больше или меньше в зависимости от их расстояния от эклиптики | 275 | |||
| Земля приближается к неподвижным звездам эклиптики и удаляется от них на расстояние диаметра большой орбиты | 277 | |||
| Большие изменения происходят с более близкими звездами, чем с более далекими | 277 | |||
| Обзор явлений, наблюдаемых у неподвижных звезд, порождаемых годовым движением Земли | 277 | |||
| Приближение и удаление очень далеких светящихся предметов неуловимо | 278 | |||
| Если бы в неподвижных звездах было заметно какое-нибудь годичное изменение, то против движения Земли нельзя было бы возражать | 278 | |||
| Доказательство того, как мало можно полагаться на астрономические инструменты при точных наблюдениях | 278 | |||
| Недоверие Птоломея к инструменту, изготовленному Архимедом | 279 | |||
| Инструменты Тихо сделаны с большими затратами | 279 | |||
| Какие инструменты требуются для чрезвычайно точных наблюдений? | 279 | |||
| Точное наблюдение вхождения и выхождения Солнца при летнем солнцестоянии | 279 | |||
| Место, подходящее для наблюдения неподвижных звезд, поскольку это касается годового движения Земли | 279 | |||
| Система Коперника представляет трудности для понимания, но не для существования | 280 | |||
| Предпосылки, необходимые для того, чтобы правильно понять следствия, вытекающие из движения Земли | 280 | |||
| Чрезвычайно простой чертеж, представляющий систему Коперника и ее следствия | 281 | |||
| Как происходит в системе Коперника годичное движение Солнца | 281 | |||
| Удивительное явление, происходящее оттого, что ось Земли не наклоняется | 283 | |||
| Аксиомы, обычно принимаемые всеми философами | 284 | |||
| Аристотель упрекает Платона в слишком большом пристрастии к геометрии | 284 | |||
| Перипатетические философы осуждают изучение геометрии | 285 | |||
| Четыре различных движения, приписываемых Земле | 285 | |||
| Движение вниз свойственно не земному шару, а его частям | 285 | |||
| Годичное и суточное движения Земли совместимы | 285 | |||
| Каждое взвешенное и парящее тело, переносимое по окружности какого-либо круга, приобретает движение вокруг самого себя, противоположное первому | 285 | |||
| Опыт, наглядно показывающий, что два противоположные от природы движения могут быть присущи одному и тому же движущемуся телу | 286 | |||
| ||||
| Третье движение, приписываемое Земле, есть, скорее, сохранение неизменяемости положения | 286 | |||
| Удивительная внутренняя сила земного шара — всегда смотреть на одни и те же части неба | 286 | |||
| Земной шар является магнитом | 286 | |||
| Магнетическая философия Вильяма Гильберта | 286 | |||
| Ограниченность заурядных умов | 286 | |||
| Земной шар состоит из разнородной материи | 287 | |||
| Внутренние части земного шара должны быть чрезвычайно прочными | 288 | |||
| Обитаемый нами шар назывался бы «Камнем», а не «Землей», если бы это название было ему дано сначала | 289 | |||
| Ход мыслей Гильберта в его философствовании | 289 | |||
| Многообразные свойства магнита | 289 | |||
| Убедительный аргумент в пользу того, что земной шар является магнитом | 289 | |||
| Магнит в оправе удерживает несравненно больше, чем без оправы | 290 | |||
| Первые наблюдатели и изобретатели достойны особого удивления | 291 | |||
| Истинная причина значительного увеличения силы магнита благодаря оправе | 291 | |||
| Для нового явления должна быть новая причина | 291 | |||
| Доказывается, что железо состоит из частиц более тонких, чистых и теснее расположенных, чем магнит | 292 | |||
| Наглядно показывается нечистота магнита | 292 | |||
| Симпатии и антипатии — термины, употребляемые философами для облегчения понимания причин многих явлений природы | 293 | |||
| Шутливый пример для доказательства несостоятельности некоторых философских рассуждений | 293 | |||
| Три различных естественных движения магнита | 294 | |||
| Аристотель допускает для смешанных тел сложные движения | 294 | |||
| Движение смешанных тел должно быть таким, чтобы оно могло получиться в результате движений простых тел, их составляющих | 295 | |||
| Из двух прямолинейных движений не составляется кругового движения | 295 | |||
| Философы должны признать, что магнит состоит из небесный и элементарных субстанций | 295 | |||
| Ошибка тех, кто называет магнит сложным телом, а земной шар простым | 295 | |||
| Перипатетические рассуждения полны ошибок и противоречий | 295 | |||
| Невероятное свойство, ошибочно допускаемое Гильбертом в магните | 296 | |||
| Вздорное рассуждение некоторых писателей в доказательство того, что элемент воды обладает сферической поверхностью | 296 | |||
ДЕНЬ ЧЕТВЕРТЫЙ | ||||
| Природа как бы в шутку заставляет приливы и отливы свидетельствовать о подвижности Земли | 297 | |||
| Периодичность движения моря и движения Земли подтверждают друг друга | 297 | |||
| ||||
| Наблюдаемые на Земле явления, за исключением периодичности движения морей, недостаточны для доказательства движения или покоя Земли | 297 | |||
| Первое основное положение о невозможности приливов и отливов при неподвижности Земли | 297 | |||
| Изучение явлений приводит к исследованию их причин | 298 | |||
| Троякие периоды изменения — суточные, месячные и годичные | 298 | |||
| Различные обстоятельства, привходящие при суточном движении | 298 | |||
| Объяснение приливов и отливов, даваемое одним современным философом | 299 | |||
| Причина приливов и отливов некиим прелатом приписывается Луне | 299 | |||
| Джироламо Борро и другие перипатетики объясняют прилив и отлив умеренной теплотой Луны | 299 | |||
| Указания на несостоятельность всех приводимых объяснений происхождения приливов и отливов | 299 | |||
| Острова являются признаками неровностей морского дна | 300 | |||
| Два рода поэтически настроенных натур | 300 | |||
| Истина источает такой свет, что он не может остаться незамеченным среди темноты ошибок | 300 | |||
| Аристотель называет чудесными такие явления, причины которых неизвестны | 300 | |||
| Доказательство невозможности естественного объяснения прилива и отлива при признании неподвижности Земли | 301 | |||
| Действительно естественные явления всегда происходят без затруднений | 302 | |||
| Два рода движения сосуда, заставляющие содержащуюся в нем воду подниматься и опускаться | 302 | |||
| Земные водоемы не могут приблизиться к своему центру или удалиться от него | 302 | |||
| Неравномерное поступательное движение сосуда может вызвать перемещение содержащейся в нем воды | 302 | |||
| Части земного шара испытывают при своем движении ускорения и замедления | 303 | |||
| Доказательство того, что части земного шара испытывают ускорения и замедления | 303 | |||
| Части равномерно вращающегося вокруг своего центра круга в разное время производят противоположные движения | 303 | |||
| Сочетание годичного и суточного движений вызывает неравномерность движения частей земного шара | 304 | |||
| Главная и первоначальная причина приливов и отливов | 304 | |||
| Различные обстоятельства, сопровождающие приливы и отливы. Обстоятельство первое: поднявшаяся на одном конце вода сама собой возвращается к равновесию | 305 | |||
| Чем короче сосуды, тем быстрее совершаются колебания | 305 | |||
| Большая глубина вызывает и более быстрое колебание воды | 305 | |||
| Вода поднимается и опускается на концах сосудов и перемещается в средних частях | 305 | |||
| Особенность движения Земли, которую невозможно воспроизвести искусственно | 305 | |||
| Объяснение особенностей, наблюдающихся в игре прилива и отлива | 306 | |||
| Двоякого рода причины отсутствия прилива и отлива в малых морях и озерах | 307 | |||
| ||||
| Причины, по которым прилив и отлив большей частью чередуются через каждые 6 часов | 307 | |||
| Причины, в силу которых многие моря, несмотря на значительную величину, не имеют приливов и отливов | 308 | |||
| Почему приливы и отливы особенно заметны в концах морских бассейнов и менее всего в средних частях? | 308 | |||
| Почему в проливах течение быстрее, чем на открытых местах? | 308 | |||
| Дело идет о некоторых сокрытых особенностях, наблюдающихся при приливах и отливах | 308 | |||
| Почему в некоторых узких проливах наблюдается морское течение всегда в одном и том же направлении? | 309 | |||
| Возражение против принятия гипотезы движения Земли для объяснения происхождения приливов и отливов | 310 | |||
| Опровержение возражения против движения земного шара | 310 | |||
| Вода способна сохранять приобретенный импульс лучше, чем воздух | 311 | |||
| Тела меньшего веса могут быть легче приведены в движение, но менее способны сохранять приобретенное движение | 311 | |||
| Скорее можно допустить, что атмосфера приводится в движение неровностями земной поверхности, нежели движением неба | 311 | |||
| Подтверждение вращения Земли новым аргументом, почерпнутым из явлений, совершающихся в атмосфере | 311 | |||
| Ближайшая к Земле часть атмосферы, полная испарений, принимает участие в ее движении | 312 | |||
| Под тропиками ветер дует постоянно на запад | 312 | |||
| Путь в Вест-Индию легок, возвращение же трудно | 312 | |||
| Ветры с суши производят морские волнения | 312 | |||
| Другое атмосферное явление, свидетельствующее в пользу движения Земли | 312 | |||
| Рейсы в Средиземном море совершаются быстрее в направлении с востока на запад, чем с запада на восток | 313 | |||
| Обратной аргументацией доказывается, что постоянное движение воздуха с востока на запад вызывается движением неба | 313 | |||
| Движение воды вызывается движением неба | 314 | |||
| Прилив и отлив, вероятно, вызываются суточным движением неба | 314 | |||
| Постоянные движения воздуха и воды получают более правдоподобное объяснение при признании движения Земли, нежели ее неподвижности | 314 | |||
| Невероятно, чтобы элемент огня мог быть увлечен вогнутостью лунной орбиты | 314 | |||
| Приливы и отливы не могут вызываться движением неба | 314 | |||
| Изменения явлений указывают на изменения и в причинах | 316 | |||
| Подробное разъяснение причин месячного и годового периода приливов и отливов | 316 | |||
| Месячные и годичные изменения приливов и отливов могут происходить только от изменения величины прироста или уменьшения годового движения, производимого суточным движением | 316 | |||
| Степень усиления или ослабления годового движения вследствие суточного вращения может изменяться трояким способом | 317 | |||
| Природа может с величайшей легкостью совершать вещи, постижение которых для нас весьма трудно | 317 | |||
| Если бы не изменялось годичное движение, то должны были бы прекратиться месячные изменения. Если бы не изменялось {356} суточное движение, то не существовало бы годичного периода изменений | 317 | |||
| Бесспорно, справедливо положение, что обращение по малым кругам происходит быстрее, чем по большим; это поясняется двумя примерами | 318 | |||
| Пример первый | 318 | |||
| Пример второй | 318 | |||
| Два замечательных свойства маятника и его колебаний | 318 | |||
| Удивительная проблема, касающаяся тел, падающих по дуге четверти круга и вдоль любых хорд круга | 319 | |||
| Годичное движение Земли по эклиптике неравномерно вследствие движения Луны | 320 | |||
| Возможно, что многое в области астрономии еще неизвестно | 322 | |||
| Сатурн благодаря медленности своего передвижения и Меркурий вследствие своей редкой видимости последними попадают в область наблюдения | 322 | |||
| Особенности путей движения отдельных планет по их орбитам еще не изучены точно | 322 | |||
| Солнце проходит одну половину зодиака на девять дней быстрее, чем другую | 322 | |||
| Движение Луны изучается, главным образом, в связи с затмениями | 322 | |||
| Приливы и отливы являются изменениями, ничтожными по отношению к величине морей и быстроте земного движения | 322 | |||
| Причины различия в величине ускорений и замедлений, вызываемых в годовом движении суточным вращением Земли | 323 | |||
| Для возникновения прилива и отлива недостаточно одного простого движения Земли | 326 | |||
| Отвергается мнение математика Селевка | 326 | |||
| Кеплер получает мягкий упрек | 326 | |||
| Синьор Чезаре Марсили наблюдает изменения меридиана | 326 | |||
| << | {357} | >> |
1. Диалог Галилея был впервые опубликован в виде отдельной книги на итальянском языке в 1632 г. и выпущен анонимно на латинском языке в 1635 г. В последнее итальянское издание, так называемое «национальное», он вошел в качестве VII его тома (Флоренция, 1897 г.). В конце того же тома помещены заметки Галилея, которые были им собственноручно сделаны при просмотре экземпляра первого издания Диалога, до сих пор хранящегося в библиотеке Падуанской семинарии, и не могли быть разнесены по отдельным местам основного текста; они приводятся в виде особого небольшого дополнения после четвертого дня Диалога.
В 1892 г. появился перевод Диалога на немецкий язык, выполненный Эмилем Штраусом с предыдущего итальянского издания собрания сочинений Галилея, также флорентийского, том I, 1842 г. (Dialog über die beiden hauptsächlichsten Weltsysteme, das Ptolemäische und das Kopernikanische, von Galileo Galilei. Aus dem italienischen übersetzt und erläutert von Emil Strauss, Leipzig, 1892). Эта работа Штрауса заслуживает большого внимания. Поскольку она появилась в печати ранее, чем перевод на немецкий язык Discord Галилея, выполненный А. Эттингеном и опубликованный им в серии Ostwald's Klassiker der exakten Wissenschaften (№№ 11, 24 и 25), Э. Штраус попытался придать ей, как первой переводной на немецкий язык работе, посвященной Галилею, характер монографии, трактующей в предисловии и многочисленных примечаниях не только о Диалоге, но и об общих механических воззрениях Галилея, а также об общих этапах его жизни и деятельности. Примечания Э. Штрауса имеют особую ценность: во-первых, он проявил исключительное трудолюбие и добросовестность в подыскании и цитировании различных работ, на которые имеются указания или ссылки в тексте Диалога, и во-вторых, он советовался с лучшими современными ему знатоками эпохи Галилея — А. Фаваро (Antonio Favaro) и Вольвилем (Е. Wohlwill), с которыми он состоял в оживленной переписке. Это обстоятельство позволило мне широко использовать комментарии Э. Штрауса при составлении своих примечаний к Диалогу, тем более что (при пересмотре и частичном сличении их с первоисточниками мною не было обнаружено никаких неправильностей или неточностей.
Несколько слов о характере наших примечаний к Диалогу. Здесь придется повторить в основном то, что уже было сказано в предисловии к I тому собрания сочинений Галилея, содержащему его Discorsi. Если бы речь шла только о квалифицированных знатоках истории физико-математических наук, то примечания, пожалуй, вообще были бы излишними. Но поскольку мы рассчитываем на более широкий круг советских читателей, в кратких комментариях имеется определенная надобность. К ним я счел необходимым отнести как то, что требует пояснения для лучшего понимания отдельных, отнюдь не бесспорных положений Галилея (частично же и исправления их), так и то, что связано с историей вопроса {358} (цитаты, имена, положения, ссылки и пр.). Касаться в примечаниях общих механических воззрений Галилея я не стал, поскольку основная его работа в этой области — Discorsi — опубликована на русском языке в виде первого тома собрания сочинений Галилея (1934 г.), другая же весьма интересная его работа — I Galeggianti — увидела свет в моей книге: Начала гидростатики. Архимед, Стэвин, Галилей, Паскаль (1932 и 1934 гг.). Примечания к этим двум переводам и использование соответствующей общей историко-критической литературы (в частности, работы Е. Дюринга Критическая история общих принципов механики, 1893 г.) позволяют читателю Диалога легко разобраться в этих специальных вопросах. Там же содержится и толкование иногда применяемых Галилеем своеобразных терминов: «момент» (momento), «импульс» (impeto), «работа» (laboro) и т. д. Равным образом я не стал отмечать в примечаниях и некоторых совершенно незначительных отступлений, допущенных в переводе на русский язык оригинального итальянского текста, поскольку дело касалось не мыслей и положений Галилея, а только изредка применяемых им непривычных для нас оборотов или выражений, т. е. чисто филологической стороны перевода. Так, «шевелюра» звезды мною трактуется как «лучистое окружение», которое иногда можно «остричь», применяя соответствующие методы наблюдения; термин «большая орбита» иногда переводится как «земная орбита», хотя это и не совсем последовательно с точки зрения птоломеевой системы мира; между «элементами» и «стихиями» я рекомендую нашим читателям поставить знак равенства, хотя Галилей и пользуется только первым из этих двух терминов; нам сейчас весьма легко говорить о «морской стихии» и крайне затруднительно — об «элементе» морской воды. Думаю, что это ни в коей мере не умаляет точности перевода, если понимать под последней не столько грамматическую и филологическую правильность интерпретации текста, сколько действительную правдивость передачи сущности рассматриваемых автором явлений и положений. К такому изложению текста Диалога на русском языке меня обязывала, в частности, его высокая художественность, многократно отмечавшаяся исследователями данной эпохи. Соответствующие примечания явились бы несущественными частностями, отвлекающими внимание читателей от основных рассуждений.
Настоящий перевод Диалога выполнен с текста, помещенного в упомянутом выше VII томе собрания сочинений Галилея (Editione Nationale Firenze, 1897), тщательно проверен С. Н. Долговым и проредактирован мною. При этом все опечатки и погрешности, содержавшиеся не только в первом издании Диалога, но и в последующих, приняты нами во внимание, поскольку в нашей работе мы руководствовались весьма внимательно проверенным текстом последнего итальянского издания и указаниями Э. Штрауса.
Общую библиографию, приведенную на стр. 610–611 первого тома собрания сочинений Галилея, необходимо пополнить следующими специальными изданиями, вышедшими у нас в последние годы: М. Я. Выгодский, Галилей и инквизиция, часть I, 1934 г.; З. А. Цейтлин, Политическая сторона инквизиционного процесса Галилея, Мироведение, № 1, январь—февраль 1935 г.; З. А. Цейтлин, Галилей, 1935 г. (серия Жизнь замечательных людей); весьма полезными для читателя явятся также издания общего характера: Ф. Розенбергер, История физики, часть I–II, 1933–1936 гг., и Л. Ольшки, История литературы на новых языках, т. I–III, 1933–1936 гг. Первые из двух упомянутых работ (носящие до некоторой степени дискуссионный характер) особенно интересны, как непосредственно касающиеся Диалога и содержащие в тексте и ссылках богатый документальный материал, по-новому использованный авторами. {359}
2. Discreto переведено как «благоразумный»; в предыдущем издании напечатано просто: Galileo Galilei de Lettore.
3. Четырьмя «принципами Аристотеля» являлись, как известно, форма, материя, движущая причина и цель.
4. Симплиций (лат.), Симпличио (итальян.) — весьма заслуженный комментатор Аристотеля, живший в VI веке.
1. Указание Галилея на то, что Диалог является как бы продолжением предшествующих бесед, является только литературным приемом.
2. «Он» — Аристотель. «Небесная стихия», эфир, пятый элемент (quinta essentia) — противопоставлялись четырем «земным» стихиям или элементам, т. е. огню, воздуху, воде и земле.
3. Ad pleniore scientiam — термин, свойственный школьной логике и применявшийся в отношении дополнительных разъяснений в пользу данного положения, доказательство которому уже дано.
4. Намек на анекдот, содержащийся у Макробия (начало V столетия). В нем повествуется, что некий юноша, желая отделаться от расспросов матери, сказал ей, будто бы римский сенат тайно обсуждал вопрос о том, что лучше: предоставить ли право мужчине иметь двух жен или женщине двух мужей. Молва разнеслась, и женщины города склонились к последнему решению.
5. Аристотель различает три вида изменений: количественное, качественное и местное. Особенность последнего приводит его к различию между земной (или элементарной) и небесной материей. По Аристотелю, всякое тело «стремится» к своему естественному «месту»; отсюда термин «местное движение». Подробнее см. Discorsi, где этот термин может быть прекрасно заменен выражением «падение тел».
6. Огню «присуще» движение от центра, а земле — к центру.
7. Обоснование этого полемического выпада Галилея против Аристотеля дать затруднительно. Э. Штраус справедливо указывает, что в наиболее достоверных текстах трактата «О небе» Аристотель говорит о природе только как о причине движения. Возможно, что Галилей пользовался иными источниками, как это предполагает А. Фаваро.
8. Итальянское mondo, латинское mundus, греческое cosmoz; обозначало первоначально порядок, благолепие.
9. В оценке прямолинейного движения, как противоречащего мировому порядку, Галилей вполне сходится с Коперником, который унаследовал этот взгляд от древних греческих авторов.
10. Это утверждение Галилея показывает, что, составляя свой Диалог, он был еще далек от сознания закона инерции. Анализ роли Галилея в установлении последнего можно найти в общих трудах по истории механики и физики.
11. Этот вопрос Галилей развил впоследствии в своих Discorsi (см. Беседы и математические доказательства, стр. 444–446). Однако, ссылка его на Платона не вполне убедительна, так как последний нигде прямо не упоминает о первичном переходе от прямолинейного движения к круговому. С этим вопросом мы встретимся и в дальнейшем.
12. Под «нашим общим другом» подразумевается Галилей, бывший членом Академии «dei Lincei».
13. На экземпляре первого издания Диалога, находящемся в библиотеке Падуанской семинарии, рукой Галилея сделана следующая {360} приписка: «Пусть любое наитяжелейшее тело движется с любой скоростью и пусть оно встречает на своем пути любое тело, пребывающее в покое, хотя бы самое слабое и обладающее ничтожным сопротивлением; движущееся тело, натолкнувшись на последнее, никогда не сообщит ему непосредственно своей скорости; очевидный показатель этого состоит в том, что можно слышать звук удара, который не был бы слышен или, лучше сказать, вовсе не имел бы места, если бы тело, пребывающее в состоянии покоя, прибретало от столкновения с движущимся телом скорость последнего». Вопросу об ударе тел посвящен шестой день Discorsi. К сожалению, он остался незаконченным и производит впечатление только наброска основных неразработанных идей Галилея (см. Беседы и математические доказательства, стр. 561—606).
14. Это заключение является неожиданным и не вытекающим из предыдущих рассуждений Галилея. Последние доказывают, что переход от состояния покоя к движению не может совершаться со скоростями конечной величины. Однако, из них совсем не следует, что для достижения телами, в частности планетами, равномерного движения по кругу необходимо предварительное равномерно ускоренное движение, как об этом говорится в дальнейшем. На это обстоятельство обратил внимание еще в 1633 г. один из противников Галилея — Антонио Рокко.
15. Последующий обмен мнениями между Симпличио и Сагредо (до вступления Сальвиати), взятый нами в прямые скобки, является вставкой, сделанной Галилеем на Падуанском экземпляре Диалога.
15а. Здесь Галилей почти дословно повторяет мысли Коперника (см. De Revol., Ed. Thoun, p. 23).
16. Приводимые Галилеем латинские термины были в его время столь обычными, что он не счел нужным переводить их на итальянский язык: deorsum значит вниз, sursum — вверх, ad medium— к середине, a medio — от середины, eadem est ratio totius et partium — отношение целого таково же, как и его частей.
17. «С отрицающим аксиомы научные споры невозможны».
18. «По случайному совпадению».
19. Воззрения Галилея на природу комет изложены им, главным образом, в его работе Il Saggiatore; в ней он защищает неправильное положение, относя кометы к «подлунной сфере». Наоборот, Тихо Браге (1546–1601 гг.), основываясь на исчезающе малом параллаксе кометы 1572 г., пришел к совершенно правильному выводу о ее большом расстоянии от Земли; это изложено им во втором томе его Progymnasmata, носящем титул De Mundi Aetherei recentioribus phaenqmeniu liber secundum. Против него выступил Киарамонти, опубликовавший в 1621 г. свою работу Antitycho.
20. Параллаксом называется угол, образуемый двумя прямыми, проведенными от звезды к каким-либо двум точкам на поверхности земного шара; зная этот угол и положение указанных точек, можно вычислить расстояние звезды от Земли. В последующем этот вопрос разбирается весьма подробно, равно, как и следующие вопросы о новых звездах и солнечных пятнах (см. День третий).
21. Э. Штраус указывает, что, несмотря на все старания, ему не удалось установить, откуда взяты Галилеем эти цитируемые им рассуждения.
22. Марк Вельзер, дуумвир Аугсбурга, попросил Галилея в январе 1612 г. высказать свое мнение о трех письмах иезуита-астронома Шейнера, которые были опубликованы под псевдонимом Apelles post tabulam и посвящены вопросу о солнечных пятнах. Ответ Галилея на этот запрос, последующие письма Вельзера и работы Шейнера были изданы в 1613 г. академией dei Lincei под названием Letters intorno alle macchie solari. {361}
23. Апельсиновые и померанцевые деревья были завезены в Европу португальцем Хуаном де-Кастро в 1548 г. и во времена Галилея продолжали возбуждать к себе большой интерес.
24. «Природа ничего не делает напрасно».
25. Так как Луна обладает собственным движением с запада на восток, равным приблизительно 12° в сутки, то одна и та же точка земного шара вернется для нее к видимому своему исходному положению приблизительно через 25 часов.
26. Для объяснения неправильности в видимом движении планет, в том числе и Луны, Птоломей помещал каждую из них на окружность малого круга, по которому она и вращалась, в то время как центр последнего перемещался по большому кругу, за центр которого он принимал Землю. Эти малые круги носят название «эпициклов». По терминологии Коперника и Галилея, Луна не обращается вокруг своей оси; если мы представим себе ее перенесенной на эпицикл и сохраняющей то же отсутствие обращения в отношении ее центра, то с Земли мы в течение лунного месяца должны были бы наблюдать всю ее поверхность; а так как этого нет, то Луне надо приписать обращение вокруг своей оси. В настоящее время мы говорим, что Луна обращается вокруг своей оси в течение одного лунного месяца.
27. Согласно учению пифагорейцев существует тело, противоположное земле, которое они называли aviSwv; некоторые из них отождествляли его с Луной.
28. Речь идет о так называемой либрации Луны, которую Галилей обнаружил, вероятно, не позже, чем в 1630 г. Пятна, которыми он пользовался для наблюдений, получили впоследствии названия на картах луны «Море кризисов» и «Гримальди». «Дракон» — видимый путь Луны.
29. Галилей, так же как и его гениальный предшественник Леонардо-да-Винчи (1452–1519), дает здесь совершенно правильное объяснение так называемому «пепельному» свету Луны. Опровергаемое ниже предположение, что пепельный свет Луны вызывается освещением ее Венерой, исходило от Тихо Браге.
30. Здесь, вероятно, имеется в виду перипатетик Чезаро Кремонини, современник Галилея.
31. См. примечание 21-ое; то же относится к последующей цитате.
32. К вопросу об этом явлении Галилей возвращается в третьем дне Диалога; даваемое ему объяснение является в основном правильным.
33. «Мрак есть отсутствие света».
34. Pietra serena — голубовато-серая разновидность плотного песчаника, применявшаяся во Флоренции для построек.
35. Намек на воззрения одного из современников Галилея — Лодовико делла Коломбе или Юлия Цезаря Ла Галла, вернее, последнего; в своей книге De Phaenomenis in Orba Lunae (1612 г.) последний критиковал взгляды Галилея.
36. Последнее явление наблюдается относительно редко; во времена Галилея оно было отмечено Кеплером для затмений 1601 и 1620 гг., а также Гевелем для затмения 1642 г.
37. Под «книжкой заключений» (libretto di condusioni) Галилей обычно подразумевает весьма слабую работу Лохера, ученика Шейнера, изданную в 1614 г. и озаглавленную Disquisitiones mathematicae de contro-versiis et novitatibus astronomic, которая была защищена автором на публичном диспуте. Клеомед был, вероятно, современником римского императора Августа; его работа Cyclica consideratio meteorum была издана в 1539 г.; Вителлий жил в конце XIII века; его работа вместе с работой арабского ученого Альгазена под заглавием Opticae Thesaurus была издана в 1572 г.; Макробий — латинский грамматик, живший в начале {362} V века; приводимая Галилеем цитата взята из сочинений этого последнего.
38. Смысл этих весьма туманных рассуждений разъясняется последующей их критикой со стороны Сальвиати.
39. Отсюда следует, что диаметр Луны Галилей принимает равным 2000 миль, или около 3000 км; в настоящее время диаметр Луны принимается равным около 3500 км.
40. В первом издании Диалога выступление Симпличио при печатании книги было в основном тексте по ошибке пропущено и отпечатано на отдельном вложенном впоследствии листке. В падуанском экземпляре этого листка не оказалось, и Галилей восстановил его на полях, добавив первую фразу, помещенную нами в кавычках.
41. Эрмизин — особый вид тафты, легкой шелковой ткани, получившей свое название от персидского города Ормуса.
42. Явный выпад против тех приверженцев Аристотеля, которые полагали, что им удалось создать законченную систему знания.
43. Пифагореец Архит из Тарента (430—365 гг. до нашей эры) — замечательный математик, астроном и механик; предание приписывает ему изобретение автомата — летающего голубя.
44. Из этого сравнения как будто можно вывести заключение, что Галилей считал распространение света мгновенным. Однако, его рассуждения и описания опытов, поставленных им с целью определения скорости света, показывают, что он в этом не был убежден (См. Беседы и математические доказательства, ГТТИ, 1934 г., стр. 112—114).
1. Галенисты — последователи знаменитого врача Клавдия Галена (130—200 гг.).
2. «Так он сказал» — выражение, подчеркивающее безусловное признание авторитета.
3. Центон или кентон (лат. cento) — поэма, собранная из различных отрывков.
4. Иоахим, родом из Калабрии, жил во второй половине XII века; его считали обладавшим «пророческим даром» и многократно комментировали и разъясняли его предсказания.
5. Выражение «humor melancholicus» не является специфическим термином алхимии; оно относится, скорее, к определению одного из четырех «темпераментов».
6. Имеется в виду Александр, именуемый Экзегетом, который преподавал философию Аристотеля в Афинах около 200-х годов.
7. Меонийские или лидийские девы-служанки королевы Омфалы, у которой, согласно греческому мифу, Геркулес нес обязанности, обычно выполняющиеся женщинами.
8. Речь идет о годовом движении Земли, разбору которого посвящен третий день Диалога.
9. «Медицейскими звездами» Галилей, как известно, назвал в честь Тосканского великогерцогского дома Медичи спутников Юпитера, открытых им в 1610 г.
10. Часто принималось, что за сферой неподвижных звезд находится еще девятая сфера, лишенная звезд, так называемая «primum mobile». Ей приписывалось суточное движение, тогда как звездной сфере приписывалось движение, вызываемое прецессией, вследствие которой звезды {363} кажутся совершающими в 26000 лет обращение вокруг полюса эклиптики. В дальнейшем этот вопрос разбирается более подробно.
11. Во времена Галилея велись оживленные споры по вопросу о том, какая материя — твердая или жидкая — присуща небесным сферам. В частности, Тихо Браге особенно энергично боролся с воззрением перипатетиков, считавших небо непроницаемым и твердым.
12. «Бесцельно применять много средств там, где достаточно немногих!».
13. Имеется в виду видимое перемещение всех планет с запада на восток.
14. Опровержение движения Земли излагается Птоломеем преимущественно в 4-ой и 6-ой главах его Альмагеста. Возражения Тихо Браге против системы Коперника содержатся, главным образом, в его Epistolae astronomicae (1596 г.). Следует впрочем отметить, что под конец жизни Тихо Браге менее решительно отвергал суточное движение Земли.
15. Христиан Вурстейзен (1544—1588 гг.), родившийся в Базеле (а не в Ростоке, как ошибочно указывает Галилей), историк, теолог и астроном, был одним из первых последователей Коперника; он усиленно пропагандировал его систему в Италии.
16. «Кроме того, все, что движется круговым движением, кажется отстающим и движется больше, чем одним движением, за исключением первой сферы, почему и Земле, находящейся около центра или в центре, необходимо было бы двигаться двумя движениями. А если бы это случилось, необходимы были бы перемещения и сдвиги неподвижных звезд; этого, однако, не наблюдается, и они всегда восходят и заходят в одних и тех же своих местах».
17. Petitio principii (в подлиннике una petizion di principio) этим термином в логике определяется ошибочное доказательство, в котором утверждение подкрепляется положением, зависящим от того же утверждения. Встречающееся далее в тексте выражение: «Ignotum per aeque ignotum» означает: неизвестное посредством также неизвестного.
18. Аристотель признавал, что часть сферы элементов участвует в суточном движении (Метеорология, кн. 1), поскольку в нем участвуют кометы, звездные скопления и пр., относимые Аристотелем именно к этой сфере.
19. Здесь, как и в некоторых других местах, Галилей проводит различие между инерцией при «естественном» и «насильственном» движении, относя к первому круговое движение земного шара. См. также примечание 9-ое к первому дню.
20. «Приобретают силы в пути».
21. «Ничто не производит никаких действий».
22. Речь идет об игре, и до сих пор не забытой в Италии, — «giuoco di palla a corda» (лапта), правила которой напоминают игру в теннис; однако, мяч, перебрасываемый через веревку, имеет диаметр около 20 см. Вторая игра носит название giuoco delle palle (или «boccie»).
23. Этим трактатом является работа Галилея De motu naturaliter accelerate, впоследствии вошедшая почти без изменений в его Discorsi.
24. Чрезвычайно интересно сравнить эти еще весьма несовершенные рассуждения Галилея с тем, что им излагается в достаточно строгой геометрической форме в четвертом дне его Бесед и математических доказательств» (стр. 424 и далее) о движении падающих тел по параболам. Основной причиной этого несовершенства является допущение кругового движения тела, как естественно происходящего вследствие инерции, а также завершение этого движения, совершающегося якобы по дуге окружности, в центре земного шара. {364}
25. В данном случае имеется в виду libretto di conclusioni не Лохера (см. примечание 37-ое к первому дню), а изданная в Риме в 1624 г. Enciclopaedia иезуита Клементи.
26. Последующее рассуждение Сальвиати ошибочно; неправильное представление о круговом движении тела по инерции он распространяет даже на тот случай, когда центром такового является не Земля, а глаз стрелка. Следующее за этим выступление Сагредо значительно сглаживает ошибку.
27. Этот ответ Сальвиати ошибочен: теоретически при вращении Земли и неизменной горизонтальности направления выстрела на восток снаряд попадал бы выше цели, а на запад — ниже цели, тогда как при неподвижности Земли оба снаряда попадали бы в цель. Несколько ниже, как бы сомневаясь в правильности выставленного положения, Галилей устами Сальвиати пытается произвести подсчет возможного отклонения от цели. Этот последний также построен на мало понятных и ошибочных соображениях (исчисление отклонения по кругу с радиусом в пятьсот локтей). Следует также отметить, что помещение пушки под экватором, о котором дальше говорит Сальвиати, не дает никаких преимуществ перипатетикам; наоборот, отклонение должно бы было быть большим при больших широтах. На произведенном подсчете это, однако, не сказывается, так как широта, на которой расположена пушка, в нем никак не учитывается.
28. «Наше знание есть некоторое припоминание».
29. Рассуждения Галилея о сущности центробежной силы представляют собой одно из интереснейших мест Диалога с точки зрения истории развития основных принципов механики, они подвергаются подробному анализу в соответствующих работах. Ошибочность конечных выводов Галилея не умаляет огромного значения метода, примененного им к выяснению этой трудной проблемы механики.
30. Ad destruendum sufficit unum — буквально: «для разрушения достаточно одного», в переносном смысле: «для опровержения утверждения достаточно всего одного обстоятельства, ему противоречащего».
31. Вопрос сформулирован неясно, однако смысл его быстро выясняется в дальнейшем ходе беседы.
32. Каламбур «solle vare» обозначает и подниматься, и возбуждаться.
33. «Третья пропорциональная» X при заданных ВА и С находится из пропорции ВА : С = С : X.
34. Последующее рассуждение Сальвиати замечательно тем, что в нем впервые применен в механике метод изображения зависимости одной переменной величины от другой; отрезки времени откладываются по оси абсцисс, соответствующие скорости — по оси ординат.
35. Положение совершенно правильное, но признать его очевидным затруднительно, и сам Галилей отводит в Discorsi (День третий) большое место его доказательству.
36. Сальвиати принимает здесь полностью утверждение Аристотеля, что скорость падения пропорциональна весу. В последующем наличие такой пропорциональности отвергается. Однако, полную независимость скорости падения от веса Галилей устанавливает только в своих Discorsi (День первый, стр. 143 и далее).
37. Переводя это рассуждение на современный язык, мы сказали бы, что «движение», обусловливаемое центробежной силой, является бесконечно малой величиной второго порядка, тогда как другое — бесконечно малой величиной первого порядка. Это рассуждение, однако, ошибочно, так как оба эти «движения» являются величинами одного и того же порядка; для сравнения надо брать или пространства или скорости, Галилей же оперирует для первого «движения» пространствами, {365} а для второго — скоростями. Самый метод изложения вопроса заслуживает, однако, исключительного внимания.
38. «Сфера касается плоскости в одной точке». По вопросу о приложимости отвлеченных математических выводов к реальным физическим предметам споры велись еще в древности.
39. Доказательство «неизвестного путем еще менее известного».
40. Галилей придавал своей теории отливов и приливов, изложенной в четвертом дне Диалога, настолько большое значение, как доводу в пользу системы Коперника, что первоначально хотел придать настоящему своему труду заглавие Dialogo del flusso e reflusso.
41. Из последующего видно, что Галилей совершенно правильно считал центробежную силу обратно пропорциональной радиусу, но ошибочно принимал ее прямо пропорциональной линейной скорости (а не квадрату последней, как это было впоследствии установлено Гюйгенсом в его Horologium oscillatorium, 1673 г.).
42. Под «книжечкой рассуждений», как и ранее, разумеется работа Лохера; второй книгой является работа упомянутого ранее (примечание 19-ое к первому дню) Киарамонти, озаглавленная De tribus novis stellis, quae annuis 1572, 1600, 1604 comparuere, 1628. Именно этого автора и имеют в виду собеседники, когда переходят к вопросу о новых звездах.
43. Немецкая миля принималась равной 1 : 5400 части экватора.
44. Последующее вычисление производится, конечно, в предположении неизменности ускорения на всем пути от Луны до Земли, тогда как по законам всемирного тяготения, установленным Ньютоном, оно обратно пропорционально квадрату расстояния от центра притяжения.
45. Если отвлечься от сопротивления воздуха, то за пять секунд свободно падающее тело должно пройти около 120 м, или около 200 локтей, т. е. величину, вдвое большую, чем указанная Галилеем. Разницу следует, вероятно, объяснить не столько сопротивлением воздуха, сколько ошибками в определении малых промежутков времени, достаточно трудном в ту эпоху.
46. «Золотое правило» — «regula aurea» — вычисление четвертого члена пропорции по трем данным. Запись чисел при извлечении корней производилась во времена Галилея совершенно иначе, чем сейчас, как это видно из приведенного в тексте вычисления.
47. Попытка обоснования этого ошибочного положения приводится несколько ниже.
48. Представление Галилея о движении тела в шахте, пронизывающей земной шар, правильно, поскольку речь идет о равенстве удаления в ту и другую сторону от центра. Однако, закон этого движения будет отличен от предполагаемого Галилеем вследствие уменьшения силы тяготения, а следовательно, и ускорения движения. (Ср. Ньютон, Математические принципы натуральной философии, книга I, отдел XII).
49. Понять в точности, что представляет собой написанный ряд чисел, довольно трудно. Они не могут обозначать средних скоростей для каждого интервала, так как таковые пропорциональны нечетным числам 1, 3, 5 и т. д. Если же предположить, что они обозначают скорости, достигнутые в конце каждого интервала, то почему число 10 записано дважды? Это могло бы быть лишь в том случае, если бы максимальная скорость достигалась не в конце десятого интервала, а в половине одиннадцатого. Но тогда и в тексте вместо 10 должно было бы стоять 101/2. Далее, если и можно складывать эти числа, то лишь в том случае, когда они представляют собой средние скорости, а не конечные. Если, наконец, поставить в начале ряда чисел нуль, то цифры будут представлять начальные скорости, но тогда последнее число опять не даст наибольшей скорости. {366}
Интервалы |
Скорости |
||
Начальная |
Средняя |
Конечная |
|
1 |
0 |
1 |
2 |
2 |
2 |
3 |
4 |
3 |
4 |
5 |
6 |
4 |
6 |
7 |
8 |
5 |
8 |
9 |
10 |
6 |
10 |
9 |
8 |
7 |
8 |
7 |
6 |
8 |
6 |
5 |
4 |
9 |
4 |
3 |
2 |
10 |
2 |
1 |
0 |
Из этой таблички видно, что сумма средних скоростей дает тот же результат, что и умножение наибольшей скорости на половинное число интервалов. Совершенно ясно, что при переходе от конечных интервалов к бесконечно малым, что Галилей и имел в виду, все эти неточности исчезают.
50. Доказательство, исключительное по своему изяществу. Здесь впервые чисто геометрическое интегрирование, широко применявшееся Архимедом, переносится в область механики путем построения системы координат время — скорость. См. также Беседы и математические доказательства (День третий, стр. 311 и далее).
51. Галилей совершенно правильно установил для математического маятника независимость периода качания маятника от его массы и амплитуды качаний (при небольших размахах) и прямую пропорциональность этого периода корню квадратному из длины маятника (см. Беседы и математические доказательства, День первый, стр. 193 и далее). Это, хотя и не с такой же ясностью, видно из некоторых мест Диалога. Однако, последующее рассуждение о свойствах физических маятников, в котором Галилей пытается доказать, что они не могут быть изохронными, ошибочно.
52. «Годовое движение Земли вынуждает коперниканцев признать суточное ее вращение, иначе одно и то же полушарие Земли постоянно было бы обращено к Солнцу, в то время как противоположное оставалось бы в тени».
53. «А что вращение Земли невозможно, доказываем так».
54. Легенда о влиянии растущей Луны на улиток, раковин, крабов и пр. ведет свое начало с древних времен.
55. «При таком предположении необходимо, чтобы в случае кругового движения Земли все, находящееся в воздухе, и т. д... Так что, если возьмем эти ядра, равные по весу, величине и тяжести, и, поместив их на лунной сфере, дадим им свободно падать, то, если сравним движение вниз с движением круговым (что однако не так, поскольку ядро А и т. д.), они пройдут по меньшей мере (чтобы сделать уступку противникам) шесть дней и за это время шесть раз обернутся вокруг Земли и т. д.».
56. Согласно господствовавшим философским воззрениям многие движения, в том числе и небесных сфер, обусловливались духовными воздействиями. Последние рассматривались и как исходящие от самих движущихся тел («intelligenza informante»), например в случае одушевленных предметов, а по мнению некоторых — и небесных сфер, и как исходящие извне — от ангела («intelligenza assistente»); последнее особенно часто принималось в отношении небесных сфер.
57. «Если от внешнего, то не бог ли его вызывает посредством непрерывного чуда? Или ангел? Или воздух? Ведь и последнему многие приписывают (причину). Но, напротив...»
58. «Встают труднейшие, даже неразрешимые вопросы другого рода. Есть ли этот внутренний принцип акциденция или субстанция: {367} если первая, то какая именно? Ибо до сих пор, кажется, не было известно круговращающегося качества».
59. «И даже, если бы оно было, как могло бы оно обретаться в вещах столь противоположных? В огне, как и в воде? В воздухе, как и в земле? В живом, как и в лишенном жизни?».
60. «Если же второе (а именно, если скажешь, что такой принцип есть субстанция), то это либо материя, либо форма, либо сочетание их; но и этого не позволяет столь различная природа вещей, каковы суть птицы, улитки, камни, стрелы, снег, дым, град, рыбы и т. д., которые, будучи различны по виду и роду, все, однако, двигались бы по природе своей кругообразной, при полном различии их природы и т. д.».
61. «Если бы Земля по воле божией остановилась, то не прекратилось ли бы и остальное вращение? Если да, то неверно, будто она вращается от природы; если нет, то возвращаются первые вопросы, и, конечно, было бы удивительно, что даже при желании не могли бы устремляться чайка на рыбу, жаворонок к своему гнезду, ворон на улитку или на скалу».
62. «Кроме того, как происходит, что эти вещи, столь разнообразные, вращаются только с запада на восток, параллельно экватору? И что всегда они движутся и никогда не покоятся?».
63. «Почему, чем они выше, тем (движутся) быстрее, чем ниже, тем медленнее?».
64. «Почему лежащие ближе к экватору движутся по большему кругу, дальше лежащие — по меньшему кругу?».
65. «Почему тот же шар на экваторе вращался бы весь вокруг центра по наибольшей земной окружности с быстротой невероятной, а у полюса вокруг собственного центра, без кругового пути с величайшей медленностью?».
66. «Почему та же вещь, например свинцовый шар, обойдя однажды Землю по наибольшему кругу, не всюду обходит ее по большому кругу, но, переместившись с экватора, он пойдет по меньшим кругам?».
67. Имеется в виду смещение звезд, вызываемое прецессией и открытое еще Гиппархом (около 160—125 гг. до нашей эры).
68. «Если перемещение по кругу присуще тяжелым и легким телам по природе, то каков'о же совершающееся по прямой линии? Ибо, если оно естественно, то каким образом естественно и то движение, которое совершается по кругу, раз круг специфически отличен от прямой. Если же оно насильственно, то почему пущенная вверх стрела поднимается своим зажженным концом вверх от Земли и не обращается по кругу и т. д.?».
69. «Почему центр падающей сферы описывает под экватором спираль в его плоскости, под другими параллелями описывает спираль по конусу, а у полюса опускается по оси, пробегая линию вращения, начертываемую вокруг цилиндрической поверхности?».
70. «Если бы вся Земля вместе с водой была обращена в ничто, то ни град, ни дождь не ниспадали бы из тучи, но только естественно обращались бы по кругу; и никакой огонь и ничто огненное не поднималось бы вверх, поскольку, по их неправдоподобному мнению, наверху нет никакого огня».
71. «Чему, однако, противоречат опыты и разум».
72. «Камень, помещенный в центре, или поднимется на Землю в какую-нибудь точку, или нет. Если второе,— то неверно, будто части лишь из-за разобщенности с целым движутся к нему. Если первое, — то этому противится всякий разум и опыт, и тяжелые тела не успокаиваются в центре своей тяжести. Так же, если подвешенный камень, будучи предоставлен самому себе, упадет к центру, то разобщается с целым, вопреки {368} Копернику, а если повиснет, то этому воспротивится всякий опыт, поскольку мы видим, что рушатся целые своды».
73. Имя этого неудачного Copernici defensor осталось неизвестным, поскольку оно не указано и автором книжки. Соответствующее место последней, видимо, было понято Галилеем не совсем точно, что и отразилось на выступлении Симпличио. Впоследствии он убедился в своей ошибке и на полях Падуанского экземпляра сделал следующую пометку (после вступления Сальвиати): «Здесь автору книжки приписывается ошибка, в действительности же ошибки там нет».
74. «Не видит, что делает либо годовой круг меньшим, либо земной шар, поистине, гораздо большим». Это положение правильно, так как движение Земли, как колеса, требует именно такого отступления от действительного соотношения земного шара и орбиты.
75. «И во-первых, если принять мнение Коперника, то критерий натуральной философии хотя и не упраздняется совершенно, но все же, как видно, сильно расшатывается».
76. Следующее предложение, заключенное в квадратные скобки, является припиской Галилея, сделанной им на полях Падуанского экземпляра.
77. ... «С Землею движется окружающий воздух, движение же его, хотя и более скорое и быстрое, нежели любой самый быстрый ветер, не ощущается нами, но почитается за полнейший покой, если не привходит другое движение. Что же такое действительный обман чувств, если это не является обманом?».
78. «Кроме того, мы также вращаемся от кругообращения Земли» и т. д.
79. «Из этого мнения вытекает, что необходимо не доверять нашим чувствам, как совершенно обманчивым или тупым при распознавании чувственного, даже ближайшего и различимого; на какую, значит, можем мы рассчитывать истину, которая берет начало от способности, столь обманчивой?».
80. «Из природы вещей».
81. «Представим только, вслед за Коперником, что Земля некоей своей силой и внутренним принципом гонима с запада на восток в плоскости эклиптики, а также обращается, далее, вследствие внутреннего же принципа, вокруг собственного центра с востока на запад, в-третьих, отклоняется собственной склонностью к югу и обратно».
82. Галилей обнаружил вытянутую форму диска Сатурна в июле 1610 г. и приписал ее наличию двух спутников, касающихся с противоположных сторон тела планеты («тройственное строение Сатурна»); однако, через два года он этих спутников у Сатурна не обнаружил, и диск планеты оказался совершенно круглым. Видимо, это наблюдение и позволяет ему говорить здесь об «исчезновении спутников» Сатурна. Правильное объяснение изменения видимой формы Сатурна дал Гюйгенс, установивший в 1656 г. наличие у этой планеты кольца.
83. К вопросу о свойствах магнита Галилей возвращается в конце третьего дня Диалога.
84. «Труднее сверх меры напрягать свойства предмета, чем увеличивать предмет, лишенный свойства. Поэтому ближе к истине Коперник, увеличивающий неподвижную сферу звезд, чем Птоломей, который увеличивает движение ее до беспредельной скорости».
85. Аристарх Самосский — один из значительнейших астрономов всех времен, живший около 270 г. до нашей эры; его можно считать, хотя и условно, единственным действительным предшественником Коперника, поскольку он приписывал Земле и суточное, и годовое движение. {369}
1. Пертика (лат. pertica; итал. perticha) — буквально: жердь, шест — мера длины, равная 10 футам.
2. «В точке поворота назад наступает покой».
3. Галилей действительно был раньше в дружеских отношениях с Киарамонти и с похвалой отзывался о нем в своем «Saggiatore».
4. Среди этих «очень известных людей» в первую очередь надо назвать Кеплера.
5. Далее собеседники переходят к разбору упоминавшейся ранее книги Киарамонти De tribus novis stellis quae annuls 1572, 1600, 1604 comparuera libri tres. Критику взглядов Киарамонти как будто уместнее было бы отнести к первому, а не третьему дню Диалога; исходя из этого, Э. Штраус высказывает предположение, что в то время, когда Галилей писал первый день, он еще не был знаком с работой Киарамонти.
6. В дальнейшем упоминается 13 имен астрономов; однако, двое из них — Пеукер и Шулер — пользовались для вычислений одними и теми же данными. Не совсем правильно утверждение, что все они относили новую звезду к сфере неподвижных звезд: Буш и Урсин придерживались иного взгляда.
7. При изложении вопроса Киарамонти пользовался не работами указанных ниже астрономов, а детальным критическим разбором их, изложенным в Astronomie instauratae Progymnasmata и т. д. (1602 г.) Тихо Браге. Ниже приводятся краткие данные об этих астрономах. Xайнцель поддерживал дружеские отношения с Тихо Браге; он вел наблюдения над новой звездой в окрестностях Аугсбурга, где им был установлен по указаниям Тихо огромный квадрант. Пеукеры, отец и сын, из Виттенберга, оба наблюдали новую звезду, причем первый был связан с Хайнцелем и Ландграфом Вильгельмом IV Гессенским, большим любителем астрономии, сообщавшим результаты своих наблюдений над новой звездой Тихо, а второй — с профессором Шулером, другом своего отца. Xачек — королевский врач в Праге, друг Тихо; в 1574 г. издал небольшую работу о новых звездах. Элиас Камерарий — профессор во Франкфурте на Одере; результаты его наблюдений стали известны Тихо через Хачека. Урсино из Нюрнберга сообщил о своих наблюдениях над новой звездой в своем Prognosticatio anni 1574 г. Муньос — профессор математики в Валенсии; с результатами его наблюдений Тихо познакомился лишь из двух работ Корнелия Гемма, из которых вторая, более подробная, вышла в 1575 г. Буш — художник и любитель астрономии, проживавший в Эрфурте. Рейнгольд, врач по профессии, проживавший в Зальфельде, описал свои наблюдения над новой звездой в своем Prognosticum astrologicum anno 1574 destinatum. Тихо обвиняет его в том, что он использовал наблюдения Ландграфа, не называя его имени, и пользовался высотой полюса в Касселе, хотя находился в то время в Зальфельде или Эрфурте. Мавролик из Мессины (1495–1575 гг.) был одним из первых, обнаруживших новую звезду (8 ноября 1572 г.). Результаты его наблюдений в Progymnasmata не содержатся. Они помещены в основных своих частях в работе Клавия (Christophori Clavii Bambergonsis ex societate Iesu in Spacram Ioannis de Sacro Bosco Commentarius, 3-е изд., 1585 г.); данные, приводимые Галилеем, совпадают с помещенными в этом сочинении. Киарамонти в своей книге воспользовался тем же источником. Необходимо отметить, что у Тихо упоминается еще целый ряд астрономов, занимавшихся новой звездой. Всех их Тихо делит на три группы: не обнаруживших, как и сам Тихо, параллакса и потому относивших явление к области неподвижных звезд; обнаруживших параллакс, но не столь значительный, чтобы новую {370} звезду можно было поместить ближе Луны, и наконец, высказавших по данному вопросу несостоятельные суждения, причем к числу последних он относит и тех, кто считал новую звезду сублунарной.
8. Э. Штраус проделал очень большую и кропотливую работу по сличению с первоисточниками данных, приводимых как в первом, так и в последующих изданиях Диалога, кончая изданием Альбери (1842–1856 гг.), а также проверке соответствующих вычислений. При этом им было обнаружено значительное число опечаток и погрешностей, которые он и отметил в примечаниях к своему переводу. В последнем «национальном» издании, которым мы пользовались, эти недоразумения по большей части оговорены. Как отмечает Э. Штраус, внесение исправлений в исходные цифровые данные не требует изменения текста Диалога, поскольку они лишь незначительно сказываются на конечных численных результатах и совершенно не колеблют выводов.
9. Галилей пользовался для последующих вычислений таблицами синусов, которые Коперник приводит в заключение двенадцатой главы первой книги своих Revolutiones. В них даются синусы углов первого квадранта с пятью знаками при интервалах в 10'. Величина угла ВDС была указана в первых изданиях равной 154°45' вместо требуемой 154°35'; эта ошибка исправлена, однако в последующих вычислениях сохранена величина синуса 42920 вместо требуемой 42657; на конечный результат существенного влияния это не оказывает. Расположение делимого и делителя и вся запись чисел при делении значительно отличаются от принятых в настоящее время. Все приводимые вычисления производятся, как это легко видеть, по формуле:
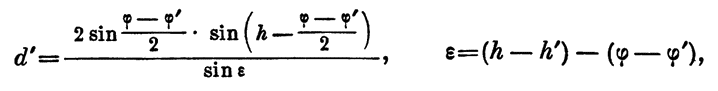
где j — высота полюса для наблюдателя более северного, j' — для наблюдателя более южного; h и h' — кульминационные высоты звезды тех же наблюдателей; d' — расстояние звезды, выраженное в радиусах земного шара.
10. Высоту звезды по Камерарию следовало принять в 24°8', а не 24°28' Это приводит к отрицательному параллаксу. Текст и в этом случае оставлен без изменений.
11. Для синуса угла ВDС вместо 97845 надо взять 97827.
12. Метод исправления вычислений, примененный Галилеем, строго говоря, неточен. Так, в разбираемом случае, сводя параллакс с 4°42'30" к 20', разность в 4°22'30" следовало бы как-то поделить между двумя наблюдателями. Признавая же угол ВDС определенным правильно, Галилей всю ошибку относит за счет наблюдений Мавролика. Подобное же предпочтение северным наблюдателям Галилей оказывает и во всех других разбираемых случаях. Впрочем эта поправка не оказала бы существенного влияния на конечные результаты, так как наблюдения того времени, естественно, не могли претендовать на большую точность.
13. При этих подсчетах Галилей пользуется не теми данными, которые приведены в таблице, а значительно отличающимися от них.
14. Для хорды ошибочно принята величина 4034 вместо 4304, что сказалось на результате.
15. Синус угла ВDС, равного 158°31', следует принять равным 36623 вместо 36643.
16. Знаменателем дроби должно быть число 300000, а не 100000, поэтому вместо ок. 301/2 мы получим ок. 301/5.
17. Тихо Браге определяет расстояние между новой звездой и X Кассиопеи в 1°31'. {371}
18. Галилей, как это явствует из изложения, дает нижний предел удаления звезды. Если мы обозначим через j высоту полюса, h1 и h2 — высоты верхней и нижней кульминации, ω1 и ω2 — расстояние звезды от полюса при верхней и нижней кульминациях, то найдем, что указанный предел вычисляется Галилеем по формуле
e > |
sin(d – φ + ω2) sin(ω2 – ω1) |
, |
где d — прямой угол; но так как ω1 = h1 – φ и ω2 = h2 – φ, то формула принимает вид
e > |
cos h2 sin(2φ – h1 – h2) |
. |
19. Во времена Галилея под «синусом» подразумевали то, что мы называем «линией синуса», поэтому в вычисления надо было вводить отношение последней к соответствующему радиусу (или гипотенузе), который обычно назывался «sinus totus».
20. Явление рефракции было известно еще древним, в частности Птоломею. Однако, и во времена Галилея представление о ней было неправильным. Так, Тихо Браге в Progymnasmata построил свои таблицы рефракции отдельно для Солнца, Луны и звезд, исходя из распространенного мнения, что величина ее зависит от удаленности светила. Кеплер оспаривал это воззрение в своей работе Ad Vitellionem Paralipomena quibus Astronomiae Pars Optica Traditur (1604 г.) и дал свою таблицу рефракции, широко применявшуюся в течение многих лет.
21. Источника описываемой ниже ошибки не отрицал и Тихо, однако при той неточности инструментов, которая имела место в то время, значение ее было совершенно ничтожным.
22. После слов «я к вашим услугам» на стр. 325 Падуанского экземпляра поставлен знак Δ, а после стр. 408, на которой заканчивается третий день, вложено несколько листков, написанных рукой Галилея и содержащих помещаемое ниже добавление, отмеченное в тексте прямыми скобками. Этому добавлению Галилей предпослал следующее указание: «Δ на стр. 325 происходит следующий разговор к знаку Δ».
23. «Недавно видел я себя (свое изображение) у берега, когда в безветрии покоилось море».
24. Утверждение несколько неожиданное. Если обозначить через b ширину колодца, а через h его глубину и предположить для простоты, что он расположен под экватором, то время видимости звезды будет пропорционально углу x, величина которого найдется, очевидно, из уравнения
tg |
x 2 |
= |
b 2h |
. |
25. Здесь Галилей допустил некоторую неточность, так как Коперник сам не занимался нагромождением кругов, чтобы достигнуть желаемой цели, и говорит лишь о других, кои этим занимались. Это явствует из предисловия к его труду, обращенному к папе Павлу III.
26. Аполлоний Пергейский — один из знаменитейших древних геометров, живший приблизительно за два века до нашей эры и создавший законченное учение о конических сечениях.
27. Такими сферами, составленными из десяти кругов, ранее пользовались не только как наглядными или учебными пособиями, но и для наблюдений; в последнем случае они изготовлялись с особой тщательностью. Описание последних, так называемых армиллярных сфер, можно найти в пятой книге Альмагеста Птоломея.
28. Не совсем понятно, почему Галилей упоминает здесь о «нашем меридиане», не имеющем по существу отношения к рассматриваемому {372} движению солнечных пятен, и тем несколько затемняет совершенно ясные рассуждения. Необходимо помнить, далее, что выражения «выше» и «ниже» следует понимать относящимися к плоскости эклиптики, которая изображена на чертеже горизонтальной.
29. Последующие доводы Галилея нельзя признать убедительными. Особое значение он придает «третьему» обстоятельству, а именно, если бы при обращении Солнца вокруг Земли ось его собственного движения, наклонная к эклиптике, была всегда параллельна самой себе, пути пятен, наблюдаемые с Земли, сохранялись бы неизменными. Легко видеть, что этого не случилось бы. Поэтому отпадает и вывод, что Солнцу надо приписать еще одно движение, осложняющее систему, а именно годовое обращение около оси, параллельной оси эклиптики.
30. Помимо суточного движения вокруг своей оси и годового вокруг Солнца Коперник, как известно, приписывал Земле еще третье движение — годовое обращение вокруг оси, перпендикулярной к плоскости эклиптики. Это допущение было необходимо для сохранения параллельности земной оси, поскольку Коперник представлял себе Землю, совершающую обращение около Солнца, как бы жестоко связанной с центром вращения, в каковом случае земная ось должна описывать в пространстве, коническую, а не цилиндрическую поверхность. Между этим «третьим» движением Земли и воображаемым новым движением Солнца Галилей и проводит аналогию.
31. «Таким образом» Землю вместе с Луной и всей нашей сферой стихий Коперник...»
32. Последующие подсчеты требуют некоторых пояснений. Расстояние от Солнца до Земли принималось в то время весьма преуменьшенным: оно равно приблизительно 23000 земных радиусов; вследствие этого и диаметру Солнца приписывалась величина всего в 11 земных радиусов, во столько же раз преуменьшенная, как и расстояние до Солнца, поскольку видимый диаметр солнечного диска принимался в 1/2°? T. е. довольно близким к действительности. Видимый диаметр неподвижных звезд, как известно, не поддается измерению; если бы ближайшая к нам звезда была равна по величине Солнцу, то видимый диаметр ее не превышал бы 0,004". Большой заслугой Галилея является его указание на чрезвычайную преувеличенность видимых размеров звезд, которые им приписывались в эту эпоху. Под выражением «orbe magno» (лат. orbis magnus) — большая орбита — подразумевалась как земная орбита, так и сфера, радиус которой равен расстоянию от Земли до Солнца; в последнем случае мы переводим этот термин также как «большая орбита», выделяя эти слова курсивом, во избежание возможных недоразумений.
33. Альфергани (Al-Fergani или Alfagrano и Alfragan) жил в 800-х годах; Альбатегний (Albategnius или Albattâni) жил с 850 г. по 927 г.; оба, особенно последний, были выдающимися арабскими астрономами; работы их были изданы в 1537 г. Региомонтаном под заглавием: Alfragani rudimenta astronomiae et Albategnii liber de motu Stellarum, et observationibus turn propriis, turn Ptolomaei. Фебит (Thebit) был современником Альбатегния и участником предпринятой арабами обработки сочинений Птоломея (Альмагест). Клавий (Clavius) жил с 1537 г. по 1612 г.; известен своими математическими работами (Opera mathematical 1612); он участвовал также в комиссии по установлению нового (грегорианского) календаря.
34. Если D — диаметр шнура, d — диаметр зрачка, l — расстояние от шнура до зрачка и х — расстояние точки пересечения лучей от глаза, (х + l) = d : D, откуда
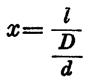
В разбираемом {373} примере D : d = 4 и l = 30, поэтому х = 10, т. е. точка пересечения лучей удалена на 10 локтей от глаза и на 40 локтей от шнура.
35. Ratio eversa — технический термин, обозначавший, что в пропорции неизвестным является третий ее член, а не четвертый, как обычно.
36. В основу этого подсчета положено, что Юпитер в 5 раз, а Марс в 11/2 раза дальше, чем Солнце, время же обращения Юпитера равно 12 и Марса 2 годам.
37. В 6-ой главе III книги своих Revolutiones Коперник приводит для периода прецессии цифру 25816 лет.
38. Если бы наш глаз обладал дополнительной способностью давать увеличение, как телескоп, то «видимые величины» небесных светил, понимая под ними определенные угловые величины, не изменились бы; не изменилось бы поэтому и соотношение между ними. «Большими» мнимые изображения светил, которые дает нам телескоп, казались бы лишь по сравнению с тем, что мы наблюдаем невооруженным глазом.
39. Ad hominem — «против человека»; под этим термином разумеется доказательство, основанное не на доказанных или общепринятых положениях, а на тех, которые считает правильными противник.
40. Галилей имеет в виду Инголи, адвоката из Равенны, пославшего ему в 1616 г. письмо с возражениями против системы Коперника. Галилей ответил ему письмом, опубликованным лишь после его смерти, в котором высказывал те же суждения, что и в Диалоге. Вторым неназванным лицом является Христофор Ротман, математик и астроном.
41. Latitudo ortiva (буквально «широта восхождения») — дуга горизонта между точкой восхождения светила и точкой пересечения горизонта и экватора.
42. Вопреки этому утверждению некоторое видимое смещение звезд на эклиптике, хотя и очень незначительное, должно иметь место: расстояние между двумя смежными звездами должно быть больше, когда Земля всего ближе к ним, и меньше, когда она от них наиболее удалена; поэтому и в отношении этих неподвижных звезд можно было бы говорить о своеобразном «поступательном» и «попятном» движении.
43. Это замечательное предсказание Галилея полностью подтвердилось, когда в 1838 г. Бесселю именно таким образом удалось установить параллакс 61 звезды Лебедя.
44. Под «колурами» (лат. coluri) разумеются два больших круга, проходящих через полюсы и точки солнцестояния и соответственно равноденствия. Первый из них перпендикулярен к плоскости эклиптики, второй наклонен. Оба их Галилей называет «меридианами», разумея под последним термином любой большой круг, проходящий через полюсы. Под «высотой», о которой говорится дальше, следует понимать видимое расстояние звезды от эклиптики.
45. Тихо Браге дал описание выстроенной им обсерватории в своих Epistolae astronomicae, описанию же своих инструментов он посвятил особую работу Astronomiae instrauratae Mechanica (1598).
46. Описываемые ниже наблюдения Галилей (а не Сальвиати) производил, проживая на вилле Беллосгварда близ Флоренции с 1617 г. по 1631 г. Оттуда группа скал Пьетрапана хорошо видна в подзорную трубу. О своих наблюдениях Галилей сообщил Марсили 5 апреля 1631 г.
47. В эпоху Галилея принято было говорить о полюсах не только больших кругов сферы, но и любых ее кругов.
48. См. 30-ое примечание.
49. Этот опыт описывается также в работе Галилея Il Saggiatore.
50. Вильям Гильберт, придворный врач английской королевы Елизаветы, опубликовал свое знаменитое сочинение о магнитах (Guilielmi Gilberti Colcestrensis, Medici Londonensis, De Magnete, {374} Magneticisque Corporibus, Et De Magno Magnete tellure и т. д.); в 1600 г. Галилей чрезвычайно заинтересовался работой Гильберта и уже с 1602 г. ревностно занялся изучением магнитных явлений.
51. Указанное свойство магнитной стрелки было впервые замечено Георгом Гартманом в 1544 г.; Роберт Норман произвел первые измерения ее склонения в 1576 г.; Гильберт подробно разбирает этот вопрос в 5-ой книге своего сочинения. Несколько ниже Галилей приписывает открытие склонения Гильберту, хотя последний прямо называет Нормана. Большую часть опытов Гильберт производил над магнитами сферической формы, которые он называл «малой землей».
52. Устройство оправы для магнитов Гильберт описывает в 17-ой главе 2-ой книги своей работы. На оба полюса магнита он надевал железные «шапки» («cassis terrae»), снабженные крючками и петлями, посредством которых они плотно прижимались к телу магнита. Усиление действия магнита оправой Гильберт объясняет примерно так же, как и Галилей.
53. Для объяснения обращения Земли Гильберт принимал, что свободно парящий магнитный шар может сам по себе притти во вращение. Это воззрение нашло широкое распространение среди физиков, а из только что сказанного Сагредо можно было бы заключить, что и Галилей склонялся к этому взгляду. Но это было бы неправильным: несколько позже Галилей устами Сальвиати решительно высказывается против такого предположения.
54. Oliopotrida или ollapotrida — кушанье, приготовлявшееся сперва в Испании, а затем и других странах, из свинины, баранины, хлеба, чеснока, лука, огурцов, шафрана и т. д.
55. Сферическую астрономию (или просто «сферы», как в то время было принято говорить) обычно излагали, руководствуясь сочинением Иоганна Сакробоско (John Halifax), известного математика и астронома, умершего в 1256 г. Место, которое имеет в виду Галилей, содержится в 1-й главе его Sphaera mundi.
1. Автором первого трактата является архиепископ Марк Антонио де-Доминис, опубликовавший в 1624 г. работу Euripus sive sententia de fluxu et refluxu marts. Второе воззрение принадлежало Джироламо Борро, бывшему профессором медицины и философии в Пизе в тот период, когда Галилей посещал университет; оно изложено в его работе Del flusso et reflusso del mare et de Winondatione del Nilo.
2. Несколько ниже Галилей определяет высоту подъема воды в Венеции при приливе в 5—6 футов, т. е. 11/2 м; эта величина представляется значительно преувеличенной.
3. Под Лидо (Lido) в широком смысле понимается длинная цепь нешироких дюн, отделяющая венецианские лагуны от Адриатического моря.
4. Это воззрение принадлежало Аполлонию Тианскому, неопифагорейцу, жившему во времена Нерона.
5. Фузина расположена на юго-западе от Венеции. «Lizza» значит, собственно, преграда, застава, шлагбаум.
6. Продолжительность колебания стоячей волны (t) для сосуда, длина которого (l) весьма значительна по сравнению с его высотой (h), выражается формулой
t = |
l √gh |
, |
где g — ускорение силы тяжести. Этим подтверждается правильность указаний Галилея. {375}
7. Здесь имеет место противоречие с тем, что Галилей утверждал несколько выше, именно, что это явление нельзя воспроизвести на опыте. В своем Discorso sopra il flusso e reflusso del mare, написанном в 1616 г., Галилей выразился осторожнее, указав на затруднительность, а не невозможность устройства соответствующего аппарата. Из только что приведенной фразы трудно, далее, заключить, идет ли речь о существующей уже «конструкции» или только еще задуманной. Во всяком случае, нам остается совершенно неизвестным, производил ли Галилей когда-нибудь подобные опыты.
8. Так как под островом Сан-Лоренцо подразумевается, бесспорно, Мадагаскар, то, чтобы понять последнюю фразу, приходится допустить, что Галилей считал его расположенным южнее, может быть, против мыса Доброй Надежды, а под «Эфиопским морем» подразумевал южную часть Атлантического океана, соединяющуюся через Магелланов пролив с «Южным морем», т. е. Тихим океаном.
9. Галилей имеет в виду пассаты — постоянные ветры с годичным периодом, дующие между тропиками и вызываемые тем, что более плотный холодный воздух, текущий от полюсов к экватору, лишь постепенно приобретает соответствующую скорость; движение его, направленное с севера и юга, благодаря вращению Земли отклоняется и становится северовосточным для нашего полушария и юго-восточным для южного полушария. Северная граница пассатов, правда, чрезвычайно ослабленных, доходит до 39° широты, т. е. захватывает и Средиземное море. Поэтому последующее указание Сагредо, что здесь господствуют восточные ветры, является правильным.
10. На этом заканчивается первая часть четвертого дня Диалога, представляющая собой в основном переработку упомянутого выше более раннего труда Галилея Discorso sopra il flusso e reflusso del mare (1616 г.); последующие рассуждения являются совершенно новыми.
11. Симпличио излагает взгляды, весьма близкие к высказанным Фрэнсисом Бэконом (Веруламским, 1561—1626 гг.) в его работе De fluxu et refluxu maris.
12. Плутарх (около 45—120 гг.) сообщает, что Селевк (Seleucus) из Вавилонии (около 150 г. до нашей эры) объяснял приливы и отливы одним лишь суточным движением Земли.
13. Галилей был большим почитателем Ариосто (1474—1533 гг.) и его поэму «Неистовый Орланд» (Orlando furioso) знал почти наизусть.
14. Примерное соотношение скоростей годового и суточного движений Земли (3 : 1) Галилей получил, принимая, как и ранее, расстояние от Солнца до Земли равным 1208 земным радиусам (1208 : 365 ≈ 3).
15. Изохронность маятников имеет место, строго говоря, в том случае, когда они движутся по циклоидам, а не дугам круга (см., например, Ньютон, Математические принципы натуральной философии, стр. 210 и далее); для малых амплитуд различие, однако, весьма незначительно. Падение тела по хордам и дуге круга подробно разбирается Галилеем в его Discorsi (см. Беседы и математические доказательства, стр. 405 и далее); приведенные здесь положения совершенно правильны, за исключением того, что кратчайшее время падения совершается не по дуге круга, а по циклоиде — «брахистохроне» (см. там же, стр. 194 и примечание 25-ое, стр. 623).
16. Дальнейшее изложение требует некоторых предварительных пояснений. Прежде всего надо совершенно отвлечься от наличия сил тяготения — понятия, совершенно чуждого Галилею, и рассматривать движение только с точки зрения кинематики. Галилей считает, что Земля неизменно сохраняет свое расстояние от Солнца, а Луна — от Земли, причем скорость движения последней уподобляет скорости колебания маятника {376} (допущение, конечно, произвольное, но в высокой степени остроумное); вследствие этого в полнолуние Луна должна обладать скоростью меньшей, чем средняя; однако, она связана с Землей так же, как два шара маятника, расположенных на одной нити, причем центром качания этого маятника является Солнце, поэтому в полнолуние она будет несколько задерживать движение Земли.
17. Основными предметами в области астрономии, которые в течение чрезвычайно длительного периода преподавались в университетах, были Sphaera и Theoricae planetarum; в последнем излагались особые виды движения каждой из планет. Указание на чрезвычайную сложность движения Марса вызвано, повидимому, знаменитой работой Кеплера Astronomia nova (1609), в которой он опубликовал два первых из установленных им законов обращения планет, выведенных на основе наблюдений, именно — Марса.
18. Для более ясного понимания последующего можно воспользоваться помещаемым ниже чертежом, не содержащим никаких принципиальных
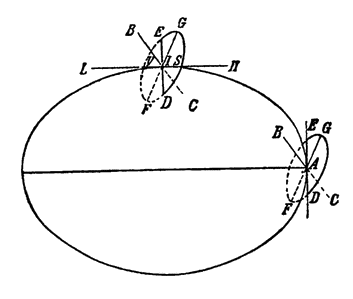 отклонений от помещенного в тексте, но более наглядным (ср. Диалог в переводе Э. Штрауса, стр. 479).
отклонений от помещенного в тексте, но более наглядным (ср. Диалог в переводе Э. Штрауса, стр. 479).
19. Изложенные выводы совершенно правильно и естественно вытекают из основных положений, принятых Галилеем. Однако, уже в его эпоху (и не без основания) указывалось, что приливы и отливы достигают максимальной величины во время равноденствий, а не солнцестояний (в частности, Фр. Бэконом, см. примечание 11-ое), т. е. обратно тому, что следует из теории Галилея. Вообще свои теоретические выводы, касающиеся месячного и годового периода изменений в приливах и отливах, Галилей не сравнивает с практическими данными и не подкрепляет их последними.
20. Возражение Галилея направлено против взглядов уже упомянутого Селевка (см. примечание 12-ое).
21. Как видно из многих мест текста Диалога, Галилею были совершенно чужды идеи воздействия небесных тел друг на друга: всякие qualitas occulta (скрытые или таинственные свойства) вызывали с его стороны решительные возражения, и это было одной из больших его заслуг. Однако, в отношении Кеплера он был неправ. Мысли, изложенные Кеплером во введении к его Astronomia nova, которые, повидимому, Галилей и имеет здесь в виду, весьма глубоки и позволяют считать его до некоторой степени предшественником Ньютона.
22. Среди заметок Галилея, сохраняющихся вместе с Падуанским экземпляром его Диалога, имеется следующее добавление, которое многие итальянские исследователи считают вставкой, относящейся именно к этому месту Диалога:
Сальвиати. — Здесь, синьор Симпличио, вы не сможете избежать признания, что в подтверждение одного из двух мнений не было приведено сколько-нибудь веских оснований, для подтверждения же другого имеются доказательства весьма убедительные. Теперь скажите, какие кажутся вам вескими и какие пустыми?
Симпличио. — Я скажу только: очень может статься, что в пользу точки зрения, которую я считаю истинной, ни Аристотелем, ни Птоломеем не приведено истинного и необходимого доказательства; но это не может умалять достоинства самого дела и заставлять принимать за истину другое мнение, более разукрашенное, нежели доказанное. {377}
Сальвиати. — Так, по крайней мере, согласитесь со мной, что сторонники Коперника опровергли доводы Аристотеля и Птоломея, которые весь свет до сих пор одобрял, считая их доказательными. Вам следовало бы, по крайней мере, оставаться нейтральным до тех пор, пока появятся на свет доказательства более убедительные, чем те, которые до сих пор представлялись. Икоперниканцев, открывших ошибки Аристотеля и Птоломея, не следовало бы высмеивать, ссылаясь лишь на авторитет этих великих мужей, которые хотя и велики, но все же должны были спасовать перед коперниканцами.
23. Чезаре Марсили (Cesare Marslli) прислал Галилею этот трактат из Болоньи 17 марта 1631 г.; в нем он утверждает, что им обнаружено изменение меридиана церкви Петрония в указанном городе. Свидетельство это едва ли можно признать достоверным, принимая во внимание степень точности тех инструментов, которыми астрономы пользовались в XV веке.
24. По прочтении изложенных выше рассуждений Галилея, не содержащих принципиальных ошибок, читателю будет полезно ознакомиться с современным объяснением явления приливов и отливов, ведущим свое начало со времен Ньютона (ср. Ньютон, «Математические принципы натуральной философии, 1937 г., стр. 300 и далее). Влияние притяжения Луны (и Солнца) на воды земного шара в количественном выражении, конечно, чрезвычайно велико по сравнению с тем, что могут вызвать в отношении приливов и отливов суточное и годичное движения Земли. Заключительная часть Диалога, следующая ниже, равно как и введение, возбуждали особое внимание римской цензуры; об этом см. «Предисловие».
25. Ниже приводятся некоторые заметки Галилея, относящиеся к Диалогу и сделанные им на экземпляре первого издания, хранящегося в настоящее время в библиотеке Падуанской семинарии. Те из них, для которых им указано определенное место, уже включены в текст или оговорены в примечаниях, как это видно из предыдущего.
Поэтому здесь содержатся только те пометки, которые не приурочены к определенным местам Диалога или носят общий характер. Очень незначительное число их нами не переведено, так как понять их крайне затруднительно. Так же поступил и Э. Штраус. Оригинальный текст заметок помещен на стр. 540–546 указанного выше VII тома итальянского «национального издания», Флоренция, 1897 г. Многие из них крайне интересны, как характеризующие отношение Галилея к наложенному на него 22 июня 1633 г. «обету молчания».
* Одинаково хорошо.
** Гипотетически.
* По-профессорски.
* «Половина полного возвышения» (meza elevazione) — здесь — угол возвышения 45°. Под «полным возвышением» понимается направление вертикально вверх.
| << | {379} | >> |
ГАЛИЛЕО ГАЛИЛЕЙ
Диалог о двух главнейших системах мира — птолемеевой
и коперниковой
| 3 | ||
| 21 | ||
| 22 | ||
| 24 | ||
| 91 | ||
| 205 | ||
| 297 | ||
Заметки Галилея, относящиеся к Диалогу о двух главнейших системах мира | 329 | |
| 333 | ||
| 357 | ||
| 357 | ||
| 359 | ||
| 362 | ||
| 369 | ||
| 374 | ||
| 378 | ||
Редакторы:
Э. Г. Ананиагивилли и Г. Н. Кольченко
Подписано к печати 21/Х 1947 г.
А 09954. Печати, листов 23,75.
Отпечатано в тип. М-162 и М-138 с матриц
1-й Образцовой типографии треста «Полиграфкнига» ОГИЗа. Москва.