MARK KAC
ENIGMAS
OF CHANCE
An Autobiography

HARPER & ROW, PUBLISHERS, New York
Cambridge, Philadelphia, San Francisco, London
Mexico City, Sao Paulo, Singapore, Sydney
| {iii} |
ENIGMAS OF CHANCE
BOOKS IN THE ALFRED P. SLOAN FOUNDATION SERIES Disturbing the Universe by Freeman Dyson Advice to a Young Scientist by Peter Medawar The Youngest Science by Lewis Thomas Haphazard Reality by Hendrik B. G. Casimir In Search of Mind by Jerome Bruner A Slot Machine, a Broken Test Tube by S. E. Luria Enigmas of Chance by Mark Kac |
| {iv} |
|
THIS BOOK IS PUBLISHED AS PART |
| {v} |
|
MARK KAC ENIGMAS An Autobiography 
HARPER & ROW, PUBLISHERS, New York |
| {vi} |
Grateful acknowledgment is made for permission to reprint:
Brief excerpts from “Mathematics: Trends and Tensions” by Mark Kac originally published in Boston University Journal vol. xxiv, No. 1. Copyright (g 1976 by the Trustees of Boston University. Reprinted by permission.
“Hugo Steinhaus: A Reminiscence and a Tribute” originally appeared in American Mathematical Monthly, June 1974.
ENIGMAS OF CHANCE. Copyright © 1985 by The Estate of Mark Kae. All rights reserved. Printed in the United States of America. No part of this book may be used or reproduced in any manner whatsoever without written permission except in the case of brief quotations embodied in critical articles and reviews. For information address Harper and Row, Publishers, Inc., 10 East 53rd Street, New York, N.Y. 10022. Published simultaneously in Canada by Fitzhenry & Whiteside Limited. Toronto.
FIRST EDITION
Designer: Sidney Feinberg
Library of Congress Cataloging in Publication Data
Kac, Mark.
Enigmas of chance.
(Alfred P. Sloan Foundation series)
1. Kac, Mark. 2. Mathematicians—United States—
Biography. I. Title. II. Series.
QA29.K23A34 1985 510'.92'4 [BJ 84–48605
ISBN 0-06-015433-0
85 86 87 88 89 HC 10 9 8 7 6 5 4 3 2 1
| {vii} |
ix | ||
xi | ||
xiii | ||
xv | ||
1 | ||
1. | 6 | |
2. | 20 | |
3. | 48 | |
4. | 78 | |
5. | 95 | |
6. | 117 | |
7. | 131 | |
150 | ||
157 |
| {viii} |
| {ix} |
The Alfred P. Sloan Foundation has for many years included in its areas of interest the encouragement of a public understanding of science. It is an area in which it is most difficult to spend money effectively. Science in this century has become a complex endeavor. Scientific statements are embedded in a context that may look back over as many as four centuries of cunning experiment and elaborate theory; they are as likely as not to be expressible only in the language of advanced mathematics. The goal of a general public understanding of science, which may have been reasonable a hundred years ago, is perhaps by now chimerical.
Yet an understanding of the scientific enterprise, as distinct from the data and concepts and theories of science itself, is certainly within the grasp of us all. It is, after all, an enterprise conducted by men and women who might be our neighbors, going to and from their workplaces day by day, stimulated by hopes and purposes that are common to all of us, rewarded as most of us are by occasional successes and distressed by occasional setbacks. It is an enterprise with its own rules and customs, but an understanding of that enterprise is accessible to any of us, for it is quintessentially human. And an understanding of the enterprise inevitably brings with it some insights into the nature of its products.
Accordingly, the Sloan Foundation has set out to encourage a representative selection of accomplished and articulate scientists to set down their own accounts of their lives in science. The form those accounts will take has been left in each instance to the author: {x} one may choose an autobiographical approach, another may produce a coherent series of essays, a third may tell the tale of a scientific community of which he was a member. Each author is a man or woman of outstanding accomplishment in his or her field. The word “science” is not construed narrowly: it includes activities in the neighborhood of science such as technology and engineering as well as such disciplines as economics and anthropology as much as it includes physics and chemistry and biology.
The Foundation wishes to express its appreciation of the great and continuing contribution made to the program by its Advison Committee. The Committee has been chaired since the program's inception by Robert Sinsheimer, Chancellor of the University of California, Santa Cruz. Present members of the Committee are Simon Michael Bessie, Co-Publisher, Cornelia and Michael Bessie Books; Howard Hiatt, Professor, School of Medicine, Harvard University; Eric R. Kandel, University Professor, Columbia University College of Physicians and Surgeons and Senior Investigator, Howard Hughes Medical Institute; Daniel Kevles, Professor of History, California Institute of Technology; Robert Merton, University Professor Emeritus, Columbia University; Paul Samuelson, Institute Professor of Economics, Massachusetts Institute of Technology; Stephen White, former Vice President of the Alfred P. Sloan Foundation. Previous members of the Committee were Daniel McFadden, Professor of Economics, Professor Philip Morrison, Professor of Physics, both of the Massachusetts Institute of Technology; Mark Kac (deceased), formerly Professor of Mathematics, University of Southern California; and Frederick E. Terman, Provost Emeritus, Stanford University. The Foundation has been represented by Arthur L. Singer, Jr., and Eric Wanner, and Harper & Row, principal publisher for the program, has been represented first by Winthrop Knowlton and now by Edward L. Burlingame and Sallie Coolidge.
—Albert Rees
President, Alfred P. Sloan Foundation
| {xi} |
Mark Kac was a profoundly American person. A refugee from the flaming ruins of the East, he adopted his country like a parent embracing a child, like a parent who knew that the firmness and stability of institutions will give the child the steadiness and freedom he needs to grow.
Mark Kac was one of the founders of probability theory. But more than a theory, probability was to him a new way to the truth of science, a way which he taught with all the rapture that once possessed the Greeks as they discovered geometry. Throughout his life he remained skeptical of abstraction, of techniques, of axiomatics. Instead, he inspired the first generation of scientists who learned to think probabilistically. He warned them that axioms will change with the whims of time, but an application is forever.
His idea of scientific work was the revealing glance that turns a mystery into the clear light of evidence. In mathematics as in physics, he left a heritage of insights whose depth is concealed by beautiful simplicity. The universal function of independence in statistics and number theory, the stochastic modeling of differential equations, the hidden combinatorial roots of phase transitions, are pioneering achievements that will be hard to match.
Mark Kac's finest success was the encouragement he gave his students, to all of us, too many to mention and to remember. The secret of his success as a teacher was his unerring grasp of the student's innermost failings, as his eyes pierced through the hesitations that every beginner faces, through the fears that a student alone might not extricate himself from his ill-defined aspirations. {xii}
A word of Mark's dropped now and then, a nod, a look of understanding, would let us know that he participated in our doubts. But under the gentle pressure of his conditional indulgence we were brought to the realization that there is always a way ahead. Led by his hand, his students would find the courage to follow the path that he had delicately but firmly drawn.
Now that he is gone, we have lost our critic, our leader, our voice. From now on, his presence will be a flickering light, beckoning from the distance to guide us further throughout the meanders of physics, of probability, of combinatorics, of statistics, ready as ever to disclose new horizons of possibility, of discovery, of confidence and hope.
Gian-Carlo Rota
Words spoken at the Memorial Service for Mark Kac.
University of Southern California, Los Angeles.
January 11, 1985.
| {xiii} |
The autobiography of a mathematician must contain some mathematics. Yet a presentation in popular form of some of the problems and ideas with which I have been involved throughout my life is unfortunately an impossible task.
The compromise I have chosen is, like most compromises, not a happy one. The specialist will justly accuse me of being superficial and incomplete and the lay reader might, also justly, find the material opaque and difficult to penetrate.
My plea to the non-expert reader is to at least skim through the parts of the book which contain formulas. He may gain a glimpse of the excitement the author felt especially in his younger years when concepts he struggled with gradually became clear.
The expert will find much of the material (especially in Chapter 3) so familiar as to be trite. But the expert of today has the advantage of fifty years of progress and education while we in the thirties were complete amateurs. Being amateurs and having no one to follow, however, helped to evolve a point of view which proved enormously useful. The expert will appreciate this and I hope that the layman will.
The Prologue was originally written for Rehovot, the journal of the Weizmann Institute in Israel.° Portions of the Postscript are taken from an earlier essay which appeared in the Boston University Journal.† {xiv}
It is with pleasure and gratitude that I thank all of those who made this book possible. Joel Cohen of the Rockefeller University conceived the idea of the book and followed me patiently with a tape recorder through the corridors of the Rockefeller University. Steve White did so much that I find it impossible to single out any one thing for which to thank him. Let us say that he was there when he was needed. The Sloan Book Committee was always helpful with encouragement and advice.
Dan Kevles spent a good many hours helping me to find some clarity in presenting the mathematical portions, especially the scientific part of Chapter 3, by far the most difficult writing in the book. Bob Merton and Paul Samuelson made a number of specific and valuable suggestions. Dr. Theodore Porter researched the historical facts and offered good advice.
I would like to express my special gratitude to our friend Judith Chodos who gave generously of her time and expertise in assisting us to improve the manuscript.
Thanks are also due to my children, Michael and Deborah, for their ideas and assistance in a variety of ways.
No words can express my gratitude to my wife. Kitty, who worked so patiently and painstakingly with me day by day, page by page for these many months. Her contribution has made it truly “our” book.
September, 1984.
| {xiii} |
|
Toute acte de l'homme, done toute oeuvre—creations et inventions—est autobiographique. —Boris Rybak, from the general introduction |
Creative people live in two worlds. One is the ordinary world which they share with others and in which they are not in any special way set apart from their fellow men. The other is private and it is in this world that the creative acts take place. It is a world with its own passions, elations and despairs, and it is here that, if one is as great as Einstein, one may even hear the voice of God. The two worlds are intimately and intricately connected. Jealousy, the desire for recognition and competitiveness, for example, are part of the ordinary world but they are among the forces which propel one into the second. Similarly, dreams and triumphs in the second have a way of merging with less than lofty thoughts of rewards in the first.
To create a coherent and truthful picture of life in the two disparate and yet interrelated worlds is a nearly impossible task and this may account, at least in part, for the fact that there have until lately been so few autobiographies of scientists. In recent years, however, a number of them have appeared, each with its own way of facing up to the problem of explaining the dual nature of its author's life.
Among these, three have a special appeal for me. I know the authors personally and I had read their autobiographies long before I thought of writing my own.
They are men to whom Fortune has been generous. Each {xvi} possesses an intellect of the highest order, each is superbly well educated and each is endowed with that most elusive of all gifts— creativity. And yet their accounts of their lives present us with such a variety of substance and style that it is difficult to imagine that they are of the same fraternity.
It is not usual to preface one's autobiography with an essay on autobiographies of others. But I venture to do so in the hope that the reader will indulge me and that he will find the topic as absorbing as I do and that it will bring him closer to an understanding of the vast and complex enterprise which is science.
Of the three, Erwin Chargaff's Heraclitean Fire is probably the most interesting and certainly the most puzzling. Though his native tongue is German, Chargaff's English prose at its best is blindingly brilliant, so much so that its very perfection makes it appear somewhat artificial. Stylistic subtleties in which Chargaff delights are more in tune with French than with English. English impresses me as being too earthy and robust to withstand a high density of “frills.” On the other hand, he can be a wonderfully effective stylist, as illustrated by a sentence taken from his 1971 article “Preface to the Grammar of Biology”: “That Pygmies cast giant shadows is proof of how late in the day it has become.”
Chargaff was born in Rumania and educated in Vienna. He received a strict classical education from which he emerged with a firm belief that to be anything, including a scientist, one has first to be an educated man. That meant that one had to know Greek and Latin—well, at least Latin. Greek is clearly Chargaff's great love and he is so thoroughly steeped in it that when he speaks of Aristotle or Heraclitus, one has the impression that they are his colleagues at the Columbia University College of Physicians and Surgeons. The number of quotes in the original Greek is overwhelming and, to those of us who are less erudite, a bit trying. There is, however, no doubt of Chargaff's love of everything connected with ancient Greece or of his deep conviction that a classical education is essential to any kind of intellectual achievement. It was this belief that was shaken and shaken badly in one of the great dramas of modern science.
The story of DNA has been told and retold by expert insiders. Still, a few salient facts might be recalled. In 1944 Oswald Avery, Colin MacLeod and Maclyn McCarty of the then Rockefeller Institute {xvii} for Medical Research published the results of their classic experiment which proved, though at the time perhaps not quite conclusively, that DNA is the carrier of genetic information. Chargaff was one of the very few biochemists who at once accepted the conclusion of the Rockefeller trio. Recognizing the great importance of their discovery, he changed the direction of research in his laboratory toward a thorough and detailed study of DNA. The result was the discovery of the famed “Chargaff rules”: A = T, C = G. A, C, G and T stand for adenine, cytosine, guanine and thymine, the four nucleotides (bases) which are the building blocks of DNA. DNA in different species has different amounts of A, C, G and T, but in all species, from amoeba to man, the number of molecules of A is very nearly equal to the number of molecules of T and the number of molecules of C is very nearly equal to the number of molecules of G. This striking regularity was one of the important clues in arriving at the structure of DNA, the feat accomplished by James D. Watson and Francis H. C. Crick.
In Heraclitean Fire Chargaff recounts briefly his only encounter with Watson and Crick, which occurred in Cambridge, England, in the last days of May 1952. Twenty-six years later, in 1978, when Heraclitean Fire appeared, Chargaff's contempt for the discoverers of the double-helical structure of DNA remained unabated. Of course, the Nobel Prize that Watson and Crick received in 1962 did not help matters and no doubt contributed to the bitterness which permeates Heraclitean Fire. It was not only that Chargaff lost the race for deciphering the structure of DNA (though he would deny ever being in the race) but he lost it to a couple of upstarts who in his view were scientific plumbers. Not only was the “ill-suited pair,” to use Chargaff's words, uneducated (i.e., lacking in a classical education of the European variety) but they appeared to be ignorant even of chemistry, “the most real of exact sciences.” This is what the allusion to “Pygmies” and their “giant shadows” is all about.
After reading Chargaff on Watson and Crick, I reread Watson's The Double Helix. I remember that when it first came out many biologists were extremely critical and even shocked. To them, Watson broke a number of tribal taboos, such as invading someone else's turf. (In biology, unlike physics, one does not build theories based on someone else's data.) Worse yet was to betray the “secret” {xviii} that the motivation for doing science need not always be as lofty as the search for truth but can be as low as crass ambition or, even lower, the desire to beat to the punch a distinguished senior competitor. In this case it was Linus Pauling.
What Chargaff failed to notice, or perhaps chose to overlook, both in 1952 and in 1978, was Watson's apparent obsession with the problem of the structure of DNA. Watson's mannerisms and his breezy, irreverent style are so much of the “ordinary world” variety that one tends to overlook the occasional reference to his dreams of the DNA structure, which are strictly “other world” stuff. Also, if one is obsessed by a problem, one does not put it aside and begin to study chemistry, or what have you, from the ground up. One learns by doing! This is neither a universal nor a recommended way of acquiring knowledge but for some it works. I know; almost everything new in mathematics that I have learned after getting my doctoral degree has been by being forced to learn it in trying to solve a problem.
Most major scientific figures have had teachers who themselves were major scientific figures—a kind of apostolic succession with remarkably few exceptions. Chargaff is one. By his own account, he chose a young, little-known lecturer to supervise his doctoral dissertation because it entailed a smaller outlay of cash for apparatus and chemicals than it would have had he chosen to work with a more famous Herr Professor. Also, unlike most scientists, Chargaff has few scientific heroes. True, Avery is one, but his real hero is not a scientist at all but a remarkable Viennese literary figure, Karl Kraus.
Karl Kraus is almost unknown in America though a book about him was published a few years ago.° I know a little about him because he was also a hero of my teacher, Hugo Steinhaus. I could not read Kraus in the original because my knowledge of German was woefully inadequate for the task. I am heartened that even Chargaff found the going tough when he first came across Die Fackel (The Torch) in 1915 or 1916; but then he was only ten or eleven years old. Die Fackel was Kraus's journal. He was its sole editor and the sole contributor to it. He accepted no advertisements and the journal was supported by subscriptions alone. The readership {xix} was fanatically faithful, and Steinhaus, who before the war was well-to-do, told me that his greatest material loss of the war was a complete set of Die Fackel. I remember the set in his study—a collection of slim red booklets which, to him, contained the quintessence of human wisdom.
Here is Chargaff's tribute to Kraus:
Karl Kraus, the greatest satirical and polemical writer of our times, was a fearless critic of the war and of the society that had given rise to it. He was the deepest influence on my formative years; his ethical teachings and his view of mankind, of language, of poetry have never left my heart. He made me resentful of platitudes, he taught me to take care of words as if they were little children, to weigh the consequences of what I said as if I were testifying under oath.
I can hear in these cadences distant echoes of the Twenty-third Psalm and I can understand that such veneration leaves no room for other heroes.
What makes Chargaff tick as a scientist? In all respects he is unlike any scientist I have known or read about. For example, can you imagine a biologist coming across a paper which provides a deep insight into the nature of heredity and opens new vistas on the understanding of life processes and not trying to contact the authors to find out more? Chargaff, who at once understood and appreciated the significance of the discovery, was a cab ride away from the Rockefeller trio, and, while Avery may already have retired and moved to Tennessee, both McCarty and MacLeod were easily available. And yet, as noted by George Uhlenbeck, my colleague at the Rockefeller University, who is more perceptive than I in such matters, there is not an inkling in the book that Chargaff made any attempt to seek out the principals. Unbelievable! True, Chargaff's code of behavior may have dictated a certain reticence in approaching strangers without having been properly introduced but when the stakes include cracking a major problem who cares about manners? Jim Watson surely didn't, perhaps even with an indifference that goes beyond the absolute limits of what is acceptable. Theoretically, we all have a Jim Watson component that consists of a mix of brashness, impatience, curiosity and, above all, competitiveness. Could it be that Chargaff is devoid of these traits or is it that he tries to hide them behind a façade of poetry? {xx} No, I think not. The poetry is too beautiful and too heartfelt to be merely a façade. I guess he is just out of step with the rest of us.
What more is there to say? One might think that, having been one of the chosen few to unveil one of nature's secrets, he could achieve a measure of peace in this unpeaceful world. But this is not the case. Still, his book is a remarkable piece of literature and it deserves a wider audience than it has apparently received. At its best it is superb. At its worst, well, honi soit qui mal y pense.
Stanislaw Ulam's Adventures of a Mathematician is of a quite different genre. It is anecdotal, even gossipy, and makes no pretense of being profound. Ulam did have an excellent sense of humor. It is not that Chargaff is devoid of a sense of humor, but his brand is of a more biting, satirical kind. Ulam's was simple and direct, as when he told Francoise, who later became his wife, that lie had infinitely many faults but modesty precluded him from enumerating them all. Even better was his reply to a Los Alamos colleague who asked what he, a pure mathematician, was doing on the project. “I supply the much-needed ‘don't know-how,’” replied Ulam.
Like Chargaff's, Ulam's early years were shaped by the cultural vestiges of the Austro-Hungarian Empire. Lwów, where he was born, resembled in so many respects its much more famous sister city that it was called “Little Vienna.” Even during the period between the wars, when it belonged to Poland, the spirit of old Vienna was omnipresent in Lwów. Ulam also had a classical education, but it was less strict than Chargaff's and its effects were less pronounced. Unlike Chargaff, whose preoccupation with questions of style borders on piety, Ulam, who was impatient by nature, paid almost no attention to the quality of his style. And yet he appreciated style; he was an admirer of Anatole France and a connoisseur of his works.
Among mathematicians, who as a rule tend to be loners, Ulam was unique in having worked almost entirely in collaboration with others. Except for his earliest brilliant papers on set theory and on the problem of measure, almost everything he published was joint work with others. The way Stan did mathematics was by talking, a work style which goes back to his young days in Lwów, which were spent largely in coffee houses (mainly in Szkocka, which is Polish for “Scottish Cafe”) endlessly discussing problems, ideas and conjectures. Great stuff came of this highly unorthodox way of doing {xxi} mathematics and Stan, whose nostalgia for the Lwów period permeates much of the book, tried in later life to re-create the intellectual ambience of those early days. To some extent he succeeded: wherever he found himself he talked mathematics day in and day out, throwing out ideas and generating conjectures at a fantastic rate. He had a marvelously fertile mind and a superb intuition but I don't think that he ever did a hard day's work. Things came easily to him and he coasted along with considerable success. Chargaff's hero, Avery, used to say that “an idea wili not work unless you do,” a rule of almost universal applicability. Stan's ideas were an exception; they worked while he watched happily from the sidelines.
For example, it is now generally admitted, though not always gracefully, that Ulam contributed a crucial idea that led to the creation of the H-bomb. But between the idea and the actual weapon lay the work of hundreds of people and untold hours of computing. In this lengthy and laborious process Stan participated only sporadically and tangentially. It was probably just as well, because he was not very good with tedious tasks.
Stan's breadth of interests and achievements was astounding. He had an enviable record in pure mathematics and is the co-discoverer (with Karol Borsuk) of one of the most beautiful theorems in topology. Known to almost every mathematician as the Borsuk-Ularn theorem, it states that if the surface of a sphere in three-dimensional Euclidian space is mapped continuously on a region in the plane, there is at least one pair of antipodal points on the surface of the sphere which maps into the same point in the plane. In more popular terms, at any given time on the surface of the earth there is at least one pair of antipodal points which have the same temperature and barometric pressure. The theorem is, of course, of no earthly use (no joke intended) in meteorology but the fact it expresses is striking.
In addition to his role in the development of the H-bomb, he collaborated with his Los Alamos colleague C. J. Everett on a proposal to use atomic explosions to generate thrust to propel a rocket. The proposal was taken up by General Atomics and Project Orion was born. Freeman Dyson, who suffers from what I call galactic claustrophobia, saw in Ulam's rocket a vehicle that could explore the solar system and even escape from it into farther {xxii} reaches of our galaxy. He went to General Atomics to work on the project and there is a chapter in his book (Saturn by 1970) in which he describes his experiences. The project had to be abandoned mainly because of negotiations between the two major powers which ultimately led to the treaty banning the testing of atomic weapons in the atmosphere.
Another example of Stan's range of interests is related to biology. As mentioned earlier, DNA, the carrier of genetic information, is composed of four nucleotides: A, C, G and T. A DNA chain (or rather half of it, the other half being a complement of the first) can thus be looked upon as a word in a language whose alphabet consists of only four letters. It is an appealing thought that biological proximities of living beings may be related to the “closeness” of their genetic codes. “Closeness” implies a concept of distance and thus what is needed is a way to define a “distance” between words. This may seem strange, for one usualh' associates the concept of distance with points in ordinary space. However, mathematicians long ago extended this concept to objects which are not at all like points in the familiar space in which we live. The Polish School of mathematics went further than any in defining distances between strange objects. To Stan, the true son of the Polish School, the distance between words was duck soup and as soon as he heard of the problem he came up with a definition of a distance, now bearing his name. To be acceptable, the distance must have a number of properties of which the most decisive is the so-called “triangle inequality” to the effect that, given three “points” P, Q and R. the “distance” between P and Q is less than or at most equal to the sum of the distances between P and R and between Q and R. Most importantly, the distance must be related to biological proximity.
The definition of distance and the proof that it is a “good” distance is as far as Stan went. It was Peter Sellers of the Rockefeller University who heard Stan's lecture on his distance and came up with an ingenious algorithm for actually calculating the Ulam distance on a computer. Now the Ulam distance is one of the tools of molecular biology.
The variety of Ulam's interests, combined with the kind of “hit and run” way in which he approached problems, creates the impression of dilettantism, an impression reinforced by reading his book. But Stan was a dilettante only in the strict dictionary sense— {xxiii} i.e., “a person who cultivates an art or branch of knowledge as a pastime.” The pejorative implication of superficiality is not at all justified. True, he was not a “professional” in the sense in which the term is used these days but neither was he an “amateur.” No amateur would hit upon the Borsuk-Ulam theorem or juggle trans-finite cardinals with the ease with which Stan did.
Stan's Adventures are strictly “ordinary world.” One searches for a glimpse of the other world which might have given a hint of how this remarkable brain worked, but in vain. Those of us who knew him are aware of how much more of himself he might have revealed in his book.
Freeman J. Dyson, whose Disturbing the Universe is superbly written, began as a mathematician. As an undergraduate in Cambridge, England, he showed unusual promise. By the time he graduated he had a number of significant accomplishments to his credit and it was naturally expected that he would stay in mathematics and enjoy a brilliant career in this field. He then went to Cornell on a Commonwealth Fund Fellowship and enrolled as a beginning graduate student in physics!
There is a story, perhaps apocryphal, of how Dyson announced his switch. One day in Cambridge he was walking with Harish-Chandra (at that time an assistant to P. A. M. Dirac) and Nicholas Kemmer. At some point Harish-Chandra said: “I am leaving physics for mathematics, I find physics messy, unrigorous, elusive.” To which, purportedly, Dyson replied: “I am leaving mathematics for physics for exactly the same reasons.” And so they both did and were colleagues on the faculty of the Institute for Advanced Study in Princeton, New Jersey, until the death of Harish-Chandra in 1983.
I am aware of the dangers of trying to read another person's mind (for that matter, it is even dangerous to try to read one's own) but I think I understand what lay behind Dyson's change of course. Some years back I asked a very promising student, who majored in mathematics but who had decided to go into physics, what had prompted his decision. His reply was roughly that in mathematics when you discover something you have the feeling that it has always been there. In physics you have a feeling that you are making a real discovery. This is, of course, terribly vague but there is more than a grain of truth in it. If doing mathematics or science is looked {xxiv} upon as a game, then one might say that in mathematics you compete against yourself or other mathematicians; in physics your adversary is nature and the stakes are higher.
Dyson not only became a physicist, he almost at once became a famous one. He achieved this fame by proving that two seemingly quite different approaches to quantum electrodynamics, one associated with the names of Julian Schwinger and Shinichira Tomanaga and the other with that of Richard Feynman, were in fact equivalent. As a result, physicists in the fifties learned the new quantum electrodynamics not from its originators but from Dyson.
Dyson went on to do many other things in physics, none perhaps of the magnitude of his first work but work of highest quality nonetheless. I am familiar with a few of his contributions because they happen to be closely related to some of my own interests and I can vouch that they are all gems. For his work in physics Dyson has received the highest accolades and numerous prizes. Yet his view of himself is rather modest: “I was, and have always remained, a problem solver rather than a creator of ideas. I cannot, as Bohr and Feynman did, sit for years with my whole mind concentrating upon one deep question. I am interested in too many things.”
Indeed, most of his book is not about physics but about the “many things”: disarmament, nuclear engineering, space travel, the “greening of galaxies.” Horace Freeland Judson. in reviewing Disturbing the Universe, calls Dyson “something of a scientific dandy.” The implication is that Dyson might have come up with some spectacular idea in physics had he not frittered away his time on frivolities. I am afraid Mr. Judson doesn't understand scientists. No scientist who believes he has an important idea or is close to one would put it away to do something else for whatever reason. It is precisely because Dyson did not believe he was capable of having an idea of sufficient importance and depth that, being by his own admission a problem solver, he looked for other problems to solve. Keep also in mind that on Dyson's scale of values an idea would have to be “way up there” before he would set aside problem-solving to pursue it.
Years ago at Cornell I knew a graduate student who was a superb pianist. He gave up the piano to pursue a career in applied science, at which he succeeded quite well. I once asked him why he had decided to give up music and he said: “I know how it should {xxv} sound but I cannot quite do it.” Rather than strive to achieve what in his mind was impossible, he chose to devote his life to a different pursuit. I think that something like that must have happened to Dyson. I suspect that at the time he announced that he was leaving mathematics for physics he had in mind a life like that of a virtuoso performer. Somehow he came to the point at which he, too, knew “how it should sound” but believed that he couldn't “do it.”
To move even further into the realm of conjecture, I'd venture a guess that it was the close contact with Feynman while Dyson was still in his formative years as a scientist that, in some sense, clipped his wings. That he was still able to fly so high and so well is a tribute to the magnitude of his talent and to the strength of his character but I cannot quite believe that back in Cambridge, when he decided to become a physicist, he would have been ready to settle for being a problem solver.
Let me elaborate a little. In science, as well as in other fields of human endeavor, there are two kinds of geniuses: the “ordinary” and the “magicians.” An ordinary genius is a fellow that you and I would be just as good as, if we were only many times better. There is no mystery as to how his mind works. Once we understand what he has done, we feel certain that we, too, could have done it. It is different with the magicians. They are, to use mathematical jargon, in the orthogonal complement of where we are and the working of their minds is for all intents and purposes incomprehensible. Even after we understand what they have done, the process by which they have done it is completely dark. They seldom, if ever, have students because they cannot be emulated and it must be terribly frustrating for a brilliant young mind to cope with the mysterious ways in which the magician's mind works. Richard Feynman is a magician of the highest caliber. Hans Bethe, whom Dyson considers to be his teacher, is an “ordinary genius”; so much so that one may gain the erroneous impression that he is not a genius at all. But it was Feynman, only slightly older than Dyson, who captured the young man's imagination. To be a physicist must have meant to him to be like Feynman and this, alas, was impossible. And so Dyson fell back on the source of strength he always had in reserve: the mastery of mathematical technique.
Though I detect here and there slight signs of wistfulness, Dyson's book is upbeat, and in that it is the diametric opposite of {xxvi} Chargaff's. To use a familiar cliche, Dyson lights candles while Chargaff prefers to curse what he perceives to be the darkness. Little as Dyson writes about physics, he does convey the elation he felt when, in trying to reconcile the two different approaches to quantum electrodynamics, he saw the pieces of the puzzle falling into place. It is this feeling of elation, probably the greatest reward creativity can bestow, that is missing from Chargaff's and Ulam's books. It is present, though camouflaged by mannerisms of prose, in Watson's.
Since that summer of 1930 when I rederived Cardano's formulas and tasted the fruits of discovery, I have not wanted to do anything except mathematics or, more accurately, mathematics and its applications to physics. I have never had administrative ambitions and I have always been impatient and frustrated when academic obligations such as teaching or serving on committees have interfered with my working on a problem which happened to interest me at the moment. I am even resentful of the time I spend writing this book though I am compelled to admit that I am beginning to enjoy it. Fortunately, I am “between problems” at the moment but if I get bitten by one, the “ordinary world” preoccupations, including the writing of this book, will be postponed until I return from yet another trip to the other world. Not that the next problem which will infect me is likely to be of great consequence but it ought to be fun to engage in at least one more chase and to lock horns with one more adversary. And who knows? It may turn out to be a winner.
Like Dyson, I, too, am a problem solver, except that the range of problems that interest me is much narrower than his. Though I am interested in many things outside of mathematics, these interests are largely passive. For example, I am interested in the history of science but I wouldn't dream of taking a year off and working seriously at it. One passion is all I can cope with and when I read Heraclitean Fire I marveled that Chargaff could cope with two. But then I came to the conclusion that science, at which he is supremely good and has been supremely successful, is not, after all, his passion. Was it Ulam's? In spite of a lack of conclusive evidence in his book, the answer is almost surely “yes” and although his and my passions were different in many respects, they had much in common. I knew him well and I can vouch for it. {xxvii}
David Sloan, a collaborator of E. O. Lawrence, the inventor of the cyclotron, once said, “When you get a new idea you don't know if it is any good. They all produce the same quickening of feeling.”
In approaching the writing of my autobiography I would like to think that I will be able to impart to the reader some idea of the thrill that is that “quickening” as well as the frustrations and disappointments inherent in the life of a scientist. I hope to give him a glimpse into the making of a scientist as he is influenced by his family, his teachers and collaborators as well as by those intangibles which pertain to his development: the political conditions and social attitudes of his time and the cataclysmic events of history.
Lastly, I must pay tribute to that powerful but capricious lady, Chance, who chose to bestow her beneficence on my personal life even though I spent much of my mathematical life trying to prove that she does not really exist.
| {xiii} |
| {1} |
It was the summer of 1930 in Krzemieniee, Poland. I was sixteen. In September my last year in school would begin and it was time to think about choosing a career. I was quite good in mathematics and physics, so going into engineering seemed a practical and sensible thing to do. “One philosopher in the family is enough” was my mother's way of both stating the problem and suggesting a solution. The “one philosopher in the family” was my father, who held a doctoral degree in philosopliy from the University of Leipzig and another advanced degree in a combination of history and philology from the University of Moscow. Despite these qualifications, anti-Semitism made it impossible for him to find any kind of teaching position other than for a two-year period during which he served as principal of a short-lived Tarbut school. Much later, when my maternal grandfather's textile business, in which my father was a junior partner, failed he earned a precarious living by tutoring. He may have been the only merchant in history who knew Hebrew, Latin, Greek and even some Old Church Slavonic. The latter came in handy because a number of his pupils were students in the local Greek Orthodox Seminary.
This was not the kind of life that my mother envisaged for her son and going into engineering seemed a step in the right direction. In the summer of 1930 my academic future, however, was not uppermost in my mind. I had been stricken by an acute attack of a disease which at irregular intervals afflicts all mathematicians and, for that matter, all scientists: I became obsessed by a problem. The {2} symptoms are familiar and easily recognized, especially by the victims' wives, since they consist of a marked increase in antisocial behavior. Loss of sleep and appetite is also frequent. In my case the symptoms were especially pronounced; so much so, in fact, that my family was beginning to worry.
The problem that infected me with such virulence was actually of little significance and even lesser consequence. It concerned solving cubic equations and the answer had been known since Cardano published it in 1545. What I did not know was how to derive it.
The sages who had designed the mathematics curricula for secondary schools in Poland had stopped at solving quadratic equations. Questions by curious students about cubic and higher-order equations were deflected with answers such as “This is too advanced for you” or “You will learn this when you study higher mathematics,” thereby creating a forbidden-fruit aura about the subject. But I wasn't having any of this and was determined to find out how one goes about solving cubic equations.
I was defeated by the very first line of the section on cubic equations in a book I picked up for my summer reading. The line read something like: “Set x = u + v.” Since I knew that the answer is a sum of two cube roots, setting x = u + v clearly anticipated the form of the answer and this I judged to be grossly unfair.
I come very close here to a subtle point of mathematical pedagogy having to do with the distinction between the strategy of a proof or derivation, which lies largely outside of logic, and the tactics, which are purely deductive, hence logical and formal in character. One might rephrase this by referring to the distinction between motivation and execution. Most mathematical expositions regretfully tend to stress the latter at the expense of the former.°
I was not going to accept a formal derivation without understanding the motivation behind it, and I considered it an affront to be ordered to set x = u + v without so much as a hint as to why I should do such a thing. I asked my father, but he was too preoccupied with the deteriorating business situation to be of much help. I then {3} announced that I was going to find a different derivation which would be more satisfactory. My father's skepticism can best be measured by his offering a reward of five Polish zlotys (in those days a lot of money) if I succeeded.
Throughout my life I have had a number of bouts with the virus of obsession and a number of the problems causing the infection turned out to be of some significance in mathematics and science, but at no time after the summer of 1930 have I worked as hard or as feverishly. I rose early and, hardly taking time out for meals, I spent the day filling reams of paper with formulas before I collapsed into bed late at night. Conversation with me was useless since I replied only in monosyllabic grunts. I stopped seeing friends; I even gave up dating. Devoid of a strategy, I struck out in random directions, often repeating futile attempts and wedging myself into blind alleys.
Then one morning—there they were! Cardano's formulas on the page in front of me. It took the rest of the day and more to pick out the thread of the argument from the mountain of paper. In the end the whole derivation could be condensed into three or four pages. My father glanced at the result of my labors and paid up.
Soon the school year started and I took a neatly written manuscript to my mathematics teacher. He was a kindly man, fond of vodka, who had had an excellent education at the University of St. Petersburg, but who, when I knew him, remembered little of what he had learned and cared less. Still, he studied the manuscript carefully and submitted it for publication on my behalf to the journal Mlody Matematyk (The Young Mathematician). That seemed to be the end of it because the receipt of the manuscript was not acknowledged and for months nothing was heard from distant Warsaw.
Then, early in May 1931, only a few weeks before the final exams were to begin, the news came in a most unexpected way. It was late in the morning and the period scheduled for religious instruction was just about to begin. Since only Roman Catholicism was taught intramurally, the few of us who were not Catholics now had a free hour. The bell had rung; the dim corridors were nearly empty of students. I was a little late and in my hurry to get away I almost collided with a priest as he entered the classroom. It was then that I saw the principal walking toward me. It had to be {4} toward me because religion classes were never visited by the lay authorities, there was nobody but me around and the corridor was a cul-de-sac with nowhere but the classroom to go.
Encounters with the principal seldom, if ever, boded well, but as I searched my mind for anything I might have done to bring the principal out of his office (rather than to be summoned to it, as was customary) something in his demeanor made me reconsider my original decision that I was about to be punished. In fact, something in his manner suggested, no less inexplicably, that I was about to be rewarded! Even before he spoke he managed somehow to convey a measure of respect which no schoolboy, not even one on the eve of graduation, could possibly have expected. The first words he spoke made the situation quite clear. “His Excellency,” he said, “the Counselor of the Ministry of Education, Antoni Marian Rusiecki, who is visiting our institution, would like to see you in his rooms at 2:30 this afternoon.” The scene might have been lifted straight out of Gogol's The Inspector General except that Antoni Marian Rusiecki was “for real” and it took me only a few seconds to recall that “His Excellency the Counselor” was also the chief editor of Mlody Matematyk.
At 2:30 sharp, scrubbed and dressed in my Sunday (or, rather, Saturday) best, I presented myself to Mr. Rusiecki. He was a tall, rather thin man with a small beard and gold-rimmed glasses. He spoke to me as though we were equals.
“We have received your paper and the reason for the delay is that we in the editorial office were all sure your method was known. There are many different derivations of Cardano's formulas, and it was rather likely that you had rediscovered one of them. However, our search of the literature has convinced us that your method is new and therefore we shall publish your note.” And so they did. It appeared a few months after my graduation under the name of Kati because I thought that the German spelling was fancier than the Slavic Kac.
Before my brief visit was over Mr. Rusiecki asked me my plans for the future. I told him that my family thought that I should study engineering. “No,” he said, “you must study mathematics; you clearly have a gift for it.” I followed this advice and it saved my life. In mathematics, as it turned out, I was good enough (and lucky enough) to win a post-doctoral fellowship to go abroad in 1938. {5} The fellowship was endowed by the wealthy, thoroughly assimilated Polish-Jewish family Parnas, and by the terms of the endowment, one of the two yearly awards had to be given to a Jewish applicant. I came to Johns Hopkins University in December of 1938 and the war caught me there. Had I gone into engineering, I would unquestionably have shared the fate of my family and six million others.
A final postscript: A few years ago my friend and one of the younger stars of U.S. mathematics, Gian-Carlo Rota, delivered a lecture at the Rockefeller University on “Umbral Calculus.” It dealt with a novel approach to invariant theory and in the lecture Rota discussed, among others, a remarkable theorem of Sylvester on homogeneous forms in two variables. Almost en passant he said, “I'll now show you how one can use Sylvester's theorem to solve cubic equations.” After only a few words a feeling of deja vu came over me; it was the method that I had discovered in the summer of 1930.
| {6} |
I was born, literally, to the sound of the guns of August, on the sixteenth day of that fateful month of the year 1914. My birth certificate records the date of my birth as August 3 because the tsars, as if to compensate for being centuries behind, decreed that the Julian calendar, which is thirteen days ahead of its Gregorian counterpart, be used throughout their vast and backward empire. Paralleling the ambiguity of the date of my birth is the uncertainty of the name of the town in which I was born. It was in 1914, as it is now, in the Western Ukraine and its name transliterated from the Cyrillic is Kremenetz. Until the end of the eighteenth century, as well as during the years 1919 to 1939, it belonged to Poland and its name was Krzemieniec. In both languages it means City of Flint, a reference to large quantities of flint imbedded in vast deposits of chalk situated at the edge of the city. The linguistic ambiguity in the name of the town found its way into Who's Who in America with Isaac Stern spelling it Kreminiecz while I stick to the correct Polish Krzemieniec.
The town is known to every Pole as the birthplace of one of the two greatest Polish romantic poets, Juliusz Slowacki. Slowacki was the lyric counterpart to the epic Mickiewicz, who is better known through translations. He is a splendid poet but difficult to translate and therefore unknown outside of Poland, except to a few scholars.
At the time of my birth almost all vestiges of Polish culture had been eradicated by the tsars. The town had a predominantly Jewish population; the villages and hamlets surrounding us were almost {7} entirely Ukrainian. The Russians were few but they were the ruling class through their control of the police, the judiciary, the schools, the post office and the bank. They were unbelievably corrupt, and bribery was as crude as it was widespread.
There was hardly a predicament, no matter how serious, that could not be resolved if one had the money and was willing to spend it. I recall a story told by my maternal grandfather about one of his store clerks who was drafted into the Russian army in 1905, during the Russo-Japanese War. After a period of training he was sent by the Trans-Siberia Express to the front. The trip in those days took about two weeks and halfway through the journey the young man, who was somewhat slow-witted, decided that he didn't like the idea of being a combat soldier. At some stop he left the train and after waiting and hiding for a week (there was only one track that the Trans-Siberia Express could use) he boarded a train going back. Some time later, to the horror of my family, he presented himself on my grandfather's doorstep in full uniform, armed with a rifle. Desertion in wartime was, of course, punishable by death, but my grandfather managed to bribe a recruitment officer, who burned all the papers of the deserter. The young man ceased to exist in a legal sense and there was nothing to prove that he had ever existed! Even more remarkable is the fact that no one ever inquired about him and he still worked for my grandfather when I was a child. How he was “resurrected” when the Poles took over in 1921 I don't know.
I was born of the union of two of the richest and most prominent Jewish families in Krzemieniec. My mother's family, the Roichels (a Hebrew word for “peddler”), had lived in Krzemieniec from the early eighteenth century. They were mainly merchants, though my maternal great-grandfather owned a paper mill in a nearby village. My father's family is traceable only to the first half of the nineteenth century, when his grandfather came from Galicia, which was the part of Poland ceded to Austria when Poland was partitioned late in the eighteenth century. My great-grandfather Mordecai's profession was not honorable but it was extremely lucrative; he was a moneylender. He amassed what in those days must have been a sizable fortune and at his death, sometime early in the century, he left every one of his eighty grandchildren enough money to relieve them of any need to work for a living. All of them, with the {8} exception of my father, chose a life of idle leisure until the First World War, when their inheritance was wiped out.
My father used a part of his inherited wealth to gain an education which culminated in his obtaining advanced degrees from the University of Leipzig and the University of Moscow. He was the first Jew from Krzemieniec to receive an advanced degree of any kind, and the road to this achievement was strewn with major obstacles. That he persevered and ultimately succeeded was in no small measure due to the help, sympathy and encouragement he received from his father.
My grandfather Meshilem. after whom I am named, died shortly before my father completed his studies and before my father married and had a family. Thus I never knew my grandfather, but from what I heard, even taking into account that my father was hardly impartial, he must have been a remarkable man.
Born in a ghetto, he somehow managed to catch a glimpse of, and become impressed by, the vast world of intellect outside the narrow confines of the strict Jewish orthodoxy in which he was raised. He obtained a number of lay books, which his father burned. Undeterred, he became one of the early leaders in a movement to liberalize Judaism and was also one of the first Zionists in the Ukraine. He attended one or possibly two early Zionist Congresses in Basel, Switzerland, and was otherwise active in this young movement. It would have pleased him to know that my son Michael is the third-generation holder of a doctoral degree in our family. Perhaps he would have been amused that all three of us obtained our degrees in cities whose names begin with L: Leipzig, Lwów and Los Angeles.
Under the tsars the Jews were by law deprived of many civil rights. (Although they still are, it is now in violation of the law.) They were consigned to live in the “pale”: that is, they needed special permission to live in large cities such as Moscow, St. Petersburg or Kiev. Only a small quota of applicants was admitted to accredited secondary schools and an even smaller one to universities. Without a secondary-school diploma (known as a Certificate of Maturity) one could not gain entry into a university. Even with a diploma there were stiff competitive entrance examinations designed to further discriminate against Jews and other “unwanted elements.” Even foreign universities, which were much more liberal {9} in their admission policies, presupposed a Certificate of Maturity.
One could, of course, always fall back on bribery, and my father's family could easily have afforded a bribe of almost any size. But my father opted for a much harder solution. The law allowed for obtaining a Certificate of Maturity by passing a set of prescribed examinations without attending school. Those who chose this road were called “externs” and they had to face tough, hostile and even sadistic examining boards. The failure rate was appallingly high, and only a handful dared to apply. My father did, but it was not until he was in his twenties that he finally succeeded.
He matriculated in Leipzig in 1907 or 1908 when he was twenty-six and began to study philosophy. The major figure in the philosophy department was Wilhelm Wundt, considered by some the father of modern psychology. My father, however, wanted to write his dissertation on a little-known philosopher of Jewish descent, Solomon Maimon. Maimon came to Germany from a small town in Poland toward the end of the eighteenth century, having left behind him a wife and family. He was befriended and later spurned by Kant, enjoyed a brief rise to prominence and sank into near oblivion after his death in 1800 at the age of forty-eight. His brief life, dedicated to the “search for truth,” was filled with tragedy. His autobiography impressed both Goethe and Schiller, and Goethe even invited him to Weimar.
I do not know how and when my father chose Maimon as a subject for his dissertation. He certainly was not encouraged in this choice by Professor Volkert, who was his thesis advisor. Volkert wanted my father to write about Hegel or Fichte or some other German philosophical celebrity. “Herr Kac,” he would repeatedly say, “warum wohlen Sie iiber Obscuranten schreiben?” (“Why do you want to write about obscure fellows?”) But my father persevered and ultimately won.
I think when my father read Maimon's autobiography he must have been struck by the similarity between Maimon's heroic struggle and, on a much smaller scale, his own. “In the search for truth,” wrote Maimon, “I left my people, my country and my family. It should not therefore be assumed that I shall forsake truth for any lesser motives.” I think that it was Maimon's life that made ray father want to study Maimon's philosophy.
After obtaining his degree and getting married, my father {10} discovered that his Leipzig diploma was not officially recognized in Russia, and that he would have to go through the process of “nostrification.” In plain language, it meant that to be recognized in Russia one would have to find a Russian equivalent of the Leipzig degree. This proved impossible, the official reason being that Russian universities did not grant degrees in philosophy. After considerable bureaucratic haggling, the official verdict was that my father would have to undertake a somewhat abbreviated course of studies leading to a degree administered by the faculty of history and philology. And so, at the age of thirty-two, married and the father of a child, my father enrolled as a student at the University of Moscow.
In the meantime, sometime in 1915, my maternal grandfather packed up the whole family, including my parents and me, and moved farther east to get away from the fighting. We settled in Berdichev, a town singularly lacking in distinction except that Joseph Conrad was born just outside of it, on his family estate, and that it was, around 1780, the home of the famous Zadik Rabbi, Levi-Isaac.
My father, for the most part, was away in Moscow studying, but otherwise life proceeded more or less normally. Then came the Revolution of 1917. It took a little time for the reverberations of this momentous event to reach Berdichev. When they did, there began a period of indescribable horror that lasted for almost four years. First there was a complete breakdown of civilian authoritv. so that the town was in essence without a government. As the tsarist empire disintegrated and its civil servants fled or were killed, Berdichev and its environs became a battleground. The White Army, which somehow held together for a time, fought the newly organized Red Army. A bandit by the name of Petlura organized a sort of Ukrainian Army which fought both the Red and the White Armies and engaged in the looting and massacre of Jews on the side. And there were also many bands that engaged only in looting. Somewhat later the newly reborn Polish State got into a war with the Soviet Union, adding yet another dimension to the chaos. The Four Horsemen traversed the unhappy region repeatedly, leaving a trail of death and destruction. Millions died from famine, cholera, bubonic plague, typhus and an assortment of lesser diseases.
After the rumble of guns the night before, one never knew in {11} the morning who held the town. One of my earliest recollections is of being bundled up during the night and taken to the cellar at the first sound of bombardment. I do not know how we managed to survive. I remember vividly my first acquaintance with real terror. I was playing in the street one day, probably against orders, when I noticed a man approaching from two or three blocks away. He was advancing at a brisk pace, arms swinging. As he neared our block there was a sudden sharp, resounding crack. He dropped to the street where he lay motionless, his arms and legs contorted. It had been quick and neat, not at all gory. I didn't understand what had happened but I sensed violence and tragedy and ran screaming to my mother.
Unbelievable as it appears to me now, it was under these circumstances that I learned to read and first heard, without any understanding, statements of geometrical theorems.
I learned to read almost by myself (in Russian, of course) by means of alphabet blocks. I must have had some help, probably from my mother, She had had considerably more education than most women of her generation; she was well read, knew quite a bit about music and was interested in all sorts of things. She spoke Russian, Yiddish and a little German. As Yiddish was reserved for private conversations with my father, Russian was the language the family spoke at home. In any case, by the time I was five years old or even earlier I read fluently and voraciously. Even before I could read, books were read to me on quieter evenings. One of the first was The Prince and the Pauper by Mark Twain, in Russian translation. I had a phenomenal memory and could recite long poems by Russian poets, mainly Pushkin. Except for an unusual memory, I was not precocious in any respect and somewhat later, to the chagrin of my father, I was inordinately slow learning the multiplication tables.
My father, who by that time had returned from Moscow after receiving his degree, earned a living by tutoring in mathematics, Latin, Greek and history. Since there was no currency of any kind, he was paid in edibles, clothing, odd pieces of gold and silver and other objects that could be used as barter. Barter was the sole basis of the economic system under which we lived.
Students came to our apartment to be tutored and I often sat listening with little or no understanding. For some reason, sentences {12} such as “Through a point outside a straight line there passes one and only one parallel to that line” or “All right angles are equal” made an impression on me and I began to pester my father to have them explained.
In the meantime the chaos around us continued. The new revolutionary regime of Lenin, after getting a tenuous hold on the region, became embroiled in a full-scale war over Poland's eastern frontier. Finally, on March 18, 1921, a peace treaty was signed in Riga between the Soviet Union and Poland. Two of the provisions of this treaty had a decisive effect on our lives. The first was that Krzemieniec reverted to Poland. The second allowed those born within the new boundaries of Poland to return to their birthplaces. My father at once applied for repatriation and late in 1921 we returned home. I promptly fell ill with what was diagnosed as lice typhus. An epidemic of this disease was raging at that time in our part of the country and even as late as 1924 it was still endemic. My mother caught it shortly after my brother was born in 1923 and she was seriously ill for a number of weeks.
As simple arithmetic shows, my brother was nine years younger than I and this difference in our ages was too large to overcome in the early years. When I left home for the University he was eight years old. He was fifteen when I left Poland. I thus hardly knew him and my recollections of him are blurred. He graduated from the Lycee in Krzemieniec and, not having at first done terribly well there, he had to suffer constant comparison with his older brother, which must have been difficult for him. He was, however, a superb athlete and a crack skier. Toward the end of his school years his intellectual interests developed and he became quite a good student. He was never given a chance to show the real stuff he was made of, as his life was cut short at nineteen by the Germans. I often grieve for the relationship we might eventually have had if it had been allowed to us.
We were now citizens of a country we had hardly known existed, whose language was foreign to us and whose re-entry into the family of nations after a century and a half of subjugation was anything but reassuring. The first democratically elected President, the relatively liberal Gabriel Narutowicz, was assassinated by a right-wing fanatic during the inauguration ceremony. His successor, Stanislaw Wojciechowski, was a nonentity, totally subservient to {13} the reactionary majority of the newly elected Parliament. Anti-Semitism, made illegal by the Constitution (imposed on Poland by the Treaty of Versailles), was nonetheless rampant, though it was more subtle than its tsarist predecessor. Plus ca change, plus ca reste la meme chose, at least as far as the Jews of Eastern Europe were concerned. Still, the guns were silent and we enjoyed reasonable prosperity.
When we arrived in Krzemieniec, the school system was not fully operative and my parents decided to educate me at home. They first engaged a French governess to come every day for half a day and teach me French. She was French by birth and had been married to a White Russian officer who was killed during the war. Strict and unbending, she allowed no Russian to be spoken while she was with me. Conjugation of irregular verbs was her obsession and we spent what seemed like an inordinate amount of time reviewing the subjunctive mode of verbs like recevoir and moudre. I hated her but whatever French I know now I owe to her rather than to the assortment of mediocre French teachers I had for six years in school. (One of them was an exception. That teacher, Edmond Semile, was superb and after all these years I recall his reading to us the soliloquy of the High Priest in Racine's Athalie.) My parents also engaged teachers of art and piano but I showed such a marked lack of talent for both that these projects were soon abandoned. Later, after a totally dismal stint as a drummer, I became a passable flutist and played in both the school orchestra and the school band.
Around this time I also had my first introduction to science through reading A Short History of Science by Arabella Buckley and Faraday's wonderful Lectures on the Chemical History of a Candle, both, of course, in Russian translations.
I kept pestering my father about plane geometry. Considering the difficulties I had been having at that time with the multiplication tables, my father felt that trying to teach me geometry would be utterly futile. “He is a bright youngster,” I overheard him say to my mother, “and I am certain he will amount to something, but I don't think he'll ever be a mathematician.”
That was the second time my father's crystal ball was badly clouded. The first time was when, shortly after the 1917 Revolution, he ran into a fellow he had met in Leipzig some years back who {14} was at the time a reasonably high-ranking member of Lenin's first revolutionary government. On the spot my father was offered the job of Assistant Commissar for Education, or something of the sort, and on the spot my father refused. “I didn't think those jokers would last more than two or three weeks,” he later told me.
In spite of his misgivings, Father succumbed and started to give me informal lessons in geometry. In no time I had a firm grasp of the subject and was able to solve quite difficult problems. I learned geometry, as did everyone in those days, by a semi-intuitive approach. The axiomatic structure of the subject was emphasized, but it was not logically complete. Nothing was said about axioms of order, most likely because the authors of the textbooks were themselves unaware of them. The axiomatic system was strictly that of Euclid and if you were asked to drop a perpendicular from the vertex C of an isosceles triangle on its base AB it was considered obvious that the perpendicular will intersect AB in a point D between A and B. In New Math you have to appeal to axioms of order to justify this fact, and emphasis on such logical subtleties makes modern geometry textbooks appear pedantic and dull. What I enjoyed most were challenging problems. Among my father's books there were several collections of especially tough ones taken from competitive entrance examinations to various engineering schools in tsarist Russia. Oh, what a pleasure it was to crack one of those toughies!
I believe it was in September of 1923 that my father became principal of the newly created Tarbut school. Tarbut schools, in contrast to chedariyn or yeshivoth which taught mainly the Talmud, were lay schools in which secular subjects were taught in Hebrew. They lacked accreditation, depended on local communities for support and were not popular with the Polish authorities. As the son of the principal, I was naturally enrolled as a student and attended the school for as long, I believe, as it lasted, which was two years. I remember little of this period except that I learned to speak Hebrew fluently. Unfortunately, this skill did not stay with me because of neglect on my part. I also learned some Polish since, by law, the school was required to teach it.
In the spring of 1925, as it became clear that the Tarbut was going out of existence, the problem of my schooling arose with some urgency. The only accredited school in town was the Lycee {15} of Krzemieniec. It had been a famous school before Poland ceased to exist as an independent nation. The new Polish State decided not only to preserve its fame but to make it a bastion of Polish culture in a region which for a very long time had had almost no connection with anything Polish. The takeover of eastern territories after the Treaty of Riga amounted to colonization by a foreign and not overly friendly power and the Lycee became one of the outposts of this colonization. In particular, though the Poles were a tiny minority in the area, v/ell over ninety percent of the students admitted to the Lycee were Polish, many of them children of officials. Though guaranteed equal rights by the Constitution, neither Ukrainians nor Jews stood much chance of being admitted, all this under the pretext that they had insufficient command of the Polish language.
Late that spring I presented myself for an entrance examination and, to the joy and relief of my family, I was admitted. In the fall, at the age of eleven, I entered the “third class” (roughly equivalent to our seventh grade) and my education began in earnest.
The first year was rather unhappy. My classmates were at least a year older than I, rough, undisciplined and cruel. I was singled out for all sorts of harassment and accused of everything from not cooperating in their system of cheating on exams to being party to the crucifixion of Christ.
A few years ago I received a letter from one of the bullies. I have forgotten his name and had difficulty placing him in the order of events which took place well over fifty years ago. He apologized for his behavior toward me then and for not having recognized that my “values had been more valid” than his. He invited me to visit him on my next visit to Poland and showed signs of genuine contrition. Considering the magnitude of the crimes which have been committed in the meantime, I found this cry of mea culpa coming from my barely remembered early youth both bizarre and touching.
Discipline in the school was strict, the faculty totally Catholic, mostly seriously so. Politically, the preponderant majority were either members of, or sympathetic to, the National Democratic Party, which was at that time the largest party in the Parliament. The National Democratic Party was right-wing, Catholic to the core and openly anti-Semitic. Anti-Semitism was part of the party's {16} charter, which brought it into conflict with the Constitution. To the very end the National Democratic Party fought to revoke the article of the Constitution guaranteeing equal rights to ethnic and religious minorities. Still, I was treated fairly at the school and, on rare occasions, even kindly.
The quality of teaching ranged from mediocre to excellent and the teacher of natural science was actually first rate. He had done original research in geology and was a member of the Polish Geological Survey, and he taught us biology in an exciting and inspiring way. He was one of the few liberals on the faculty. A humane, kind, tolerant man, he was executed together with a number of his colleagues a few days after the Germans captured Krzemieniec in June 1941. His name was Zdislaw Opolski and I owe him much. He taught me the theory of evolution, how cells divide, how one goes about deciphering the history of the planet earth and how flint is formed in deposits of chalk.
Toward the end of my first year at the Lycee, during the middle of May 1926, Pilsudski overturned the government by a military coup. The Parliament was dissolved and the President forced to resign. A number of deputies, many of them from the left, were jailed and when things finally settled in the fall. Poland was, in effect, a dictatorship. It was run by the “Colonels.” who were Pilsudski's comrades-in-arms in the Polish Legion, which he had organized early in the war to fight Russia. The trappings of democracy remained. There was a Parliament, though it took two separate elections to get the “right” kind of majority. There was a duly elected President, and the “Colonels” did constitute a government responsible, in principle, to the Parliament. Pilsudski himself refused all posts but remained the sole marshal of the Polish army. Pilsudski was the only national hero of postwar Poland. His Legion was immortalized in songs and legends and it was he who turned the Red Army from the gates of Warsaw in 1920; the “Miracle on the Vistula,” this feat was called. His detractors, and there were many, attributed the “miracle” to General Weygand, who was sent by the French to help the Poles. Considering the sorry and inept performance of Weygand in 1940, I now think better of the official Polish version.
The “Colonels” were, with few exceptions, a crew of nobodies and from the perspective of many years I am astounded that the {17} country could run at all, especially after Pilsudski died in 1935. It may be difficult to believe, but the following episode precipitated a major governmental crisis: When Pilsudski died he was interred in Wawel, the ancient royal palace where the Polish kings, great poets and other notables were buried. The custodian of Wawel was by tradition the Archbishop of Cracow, who at the time was a crusty arch-reactionary, Cardinal Sapieha. For reasons that were never clear to me then and are even less so now, the Cardinal decided to move Pilsudski's mortal remains from the original crypt to another. Upon being informed of this act, the Prime Minister, and with him the entire cabinet, resigned! This happened only two or three years before Hitler invaded Poland and it would seem that the government might have been concerned with more weighty matters than with what could have been a calculated insult to the memory of a great leader on the part of a willful Cardinal.
To go back to the Lycee, the effect of the coup was, surprisingly, the beginning of a liberalizing trend that continued until I graduated and even after. The Lycee was one of a complex of three schools which was elevated to the status of an independent school district. The head of the complex was responsible directly to the Minister of Education. The other two schools of the complex were a normal school, whose function was to train grade-school teachers, and a school of agriculture, whose function was to train agricultural technicians. Somewhat misleadingly, the whole complex was called the Lycee of Krzemieniec, although the school of agriculture was situated a few miles outside the city and only the Lycee awarded the Certificates of Maturity required to enter universities and higher professional schools, such as those of engineering, veterinary medicine and mines.
Unlike other schools in Poland, the Lycee had a sizable campus on whose grounds, in addition to school buildings and an imposing Catholic church, were located student dormitories, faculty housing, administrative offices, a largish concert hall and an excellent library. There were also two playing fields, a large garden and, a real rarity, a tennis court. Funds to run this establishment were amply provided by the central government.
To preside over this mini-realm the new government sent Juliusz Poniatowski. A descendant of one of the old aristocratic Polish families (the last Polish king, Stanislaw August, was a Poniatowski) {18} and a man of great culture and charm, lit' stood out in marked contrast to the primitive colonizers we had come to expect as emissaries from Warsaw . To the overwhelming Ukrainian majority he offered, instead of oppression, a partnership: a partnership not perhaps on optimal terms, hut a partnership nonetheless. An expert agricultural economist ami an educator In instinct and vision, his hope for the Lycee of Krzemieniec was to help create a modus vivrtuli by raising both the economic and the educational levels of the largely illiterate, sullen and hostile indigenous population. Time was of course too short to accomplish anything that ambitious: when the German barbarians came, they tound the Ukrainians of the region enthusiastic partners in the murder and plunder ot Jews and Poles alike.
In my school changes became noticeable almost at once. Teachers were transferred and their replacements were as a rule younger, better trained and, above all. more liberal. Discipline was still strict and Catholicism an ever present force, but neither w as as oppressive as before. Although the school had been co-educational, the sexes had been completely separated. Even the gardens were segregated. All ot this nonsense gradually disappeared: it was actually possible to sit next to a girl in class without being threatened with the fires ot hell. Students were recognized as human beings and were accorded some rights. Among these was the right to address school assemblies. The upperclassmen organized a sort ot news bureau which kept the student population informed about important world events. I was the science reporter and one ot the proudest moments ot my journalistic career was when I announced, in Mav 1930, the discovery of the planet Pluto.°
The best year was the last. What made the difference was the appointment of a new teacher of Polish literature. He was voung, fresh out ot school (in tact, when he came he had not yet received his university degree), full of enthusiasm and the desire to share {19} the beauty of the written word with all who were willing to listen and read. He made the understanding of literature both a pleasure and a revelation; whatever humanistic inclinations I may have, I owe largely to him. His name is Kazimierz Groszynski and he is still alive and well. Whenever I go to Poland I visit him and, though we may live in different worlds, the bonds of friendship formed when I was sixteen and he perhaps twenty-two survive to this day.
Was I well educated? If education is defined as what is lefi after one has forgotten most of what one has learned in school, then I guess the answer is yes. I do wish that I had had Latin. I wish that the Catholic view of what is sinful had not prevented me from being guided through Les Fleurs du Mai instead of that monumental bore Atala. I wish that school mathematics had been more challenging. There was nothing about the mathematics curriculum or the way it was taught that particularly stimulated my interest. I was good at it but it was not until my final year that, on Mr. Rusiecki's advice, I focused on it as a possible life career. I wish that I had understood physics better at the time when that great lady Jadwiga Falkowska taught it to me. This last wish is still with me though I have in the meantime been visiting professor of physics in Leiden and Utrecht.
To the official document testifying that I am “mature to pursue higher studies” there is attached a photograph of me at the age of sixteen. When my wife, Kitty, first saw it, she said, “Ah, this was before you heard the devil speak.” Not quite. In those days so filled with hatred, hypocrisy and bigotry it was difficult not to hear the devil speak. But during my last few years in school his voice was muted and for this I shall be forever grateful.
| {20} |
The University of Lwów, the second oldest in Poland,° was founded in 1661 and named after King John Casimir (Jan Kazimierz, 1648–1668). The city is one hundred miles directly west of Krzemieniec and to reach it by train took a little over five hours. Though situated at the very edge of the Byzantine world, it was in appearance and spirit thoroughly Western, but not without traces of the East left by numerous invasions. Elegant and charming, with lovely parks and tree-lined streets, it was unique in Europe in being the home of the archbishops of the three major branches of Catholicism: the Roman, the Greek and the Armenian. The population was largely Polish with a sizable and politically restless Ukrainian minority. There was also a fairly large Jewish community.
Lwów was in Galicia, which, in its entirety, became an Austrian province after the third and final partition of Poland in 1795, but the benevolent attitude of the Austrian rulers toward religious and ethnic minorities allowed the Poles full cultural autonomy. Lwów thus never really ceased to be a Polish city and the contrast with Krzemieniec, where “Polishness” had to be reimposed almost by force, was striking. Lwów is now in the Soviet Ukraine and I often wonder how much of its Western character remains. The university has been renamed after a little-known regional poet, Ivan Franko.
I am ashamed to admit that I know almost nothing of the history of the University before the beginning of the twentieth century but {21} there is probably little to know. In mathematics and science there is no record of even the slightest distinction. Then suddenly between 1905 and 1913 Lwów became a major center of research in theoretical physics in Europe. The credit for this leap from obscurity to fame belongs solely to Marian Smoluchowski.
Smoluchowski was born and educated in Vienna and by the time he came to Lwów as a lecturer in 1899 he was an established physicist. His greatest work, however, was still ahead of him and most of it was done in Lwów before he moved to Cracow in 1913 as a professor of experimental physics. It was during this brief period that the reality of atoms and molecules was firmly established and the dramatic consequences were analyzed and understood.
It seems strange to us now, but at the turn of the century the atomistic theory of matter was far from being universally accepted and major scientific figures of the time, notably Wilhelm Ostwald and Ernst Mach, were strong and vociferous opponents of it. Mach, in fact, never reconciled himself to the existence of atoms. The demonstration of the “reality” of atoms and molecules was achieved by a brilliant analysis of a nearly forgotten phenomenon discovered in 1827 by the Irish botanist Robert Brown.
Brown, looking through a microscope at small particles suspended in a liquid, observed that they performed a peculiarly erratic motion. Since at first he used plant spores as his particles, it seemed that their motion was a manifestation of life. Soon, however, it was discovered that inanimate particles also performed “Brownian motion” and the mystery deepened. Brown's discovery was almost completely forgotten until 1905, when in two remarkable theoretical papers the idea was set forth that Brownian motion was caused by the particles being kicked around by randomly moving molecules of the surrounding liquid. The idea was not just a shot in the dark or a lucky guess; it had been proposed a number of times earlier only to be discarded because calculable properties of the (possibly hypothetical) molecular motion could not seemingly be reconciled with the few known experimental facts about Brownian motion. The two papers not only resolved satisfactorily these difficulties but made new theoretical predictions capable of being tested experimentally. When these were verified in brilliant experiments by Jean Perrin, the atoms were here to stay!
One of the two historical papers was by Marian Smoluchowski. {22} The other, which appeared somewhat earlier and used an entirely different approach, was by Albert Einstein. It was Smoluchowski's bad luck that he had to share his first great discovery, as well as a number of later ones, including the explanation of the blueness of the sky, with so luminous a figure as Einstein. There is probably no more extreme example of the “Matthew Effect,” a wonderfully apt term invented by Robert Merton to describe the all too common phenomenon that the credit for a discovery made jointly or independently by two investigators of unequal fame is invariably given to the more famous one°:
For whosoever hath, to him shall be given, and he shall have more abundance: but whosoever hath not, from him shall be taken away even that he hath. [Matthew 13:12]
During his lifetime Smoluchowski did not suffer from the Matthew Effect. He was universally recognized as one of the leading theoretical physicists of his day and he received many honors which he richly deserved. But with the passage of time the Matthew Effect took its toll. Few realize today what an important role Marian Smoluchowski played in bringing atoms to life and even fewer that it happened in Lwów.
Many years later I was involved in a slightly embarrassing and somewhat comical episode as an indirect result of Smoluchowski's being a victim of the Matthew Effect. Recently the Polish Academy of Sciences established a number of lectures in memory of famous Polish men and women of science. One of the lectures was in memory of Marian Smoluchowski and in the winter of 1980 I was honored by an invitation to deliver the first Smoluchowski Lecture in Warsaw. With the invitation came a suggestion that although English would be acceptable, the lecture was to be of the popular variety and it would be appreciated if I were to deliver it in Polish. I accepted the invitation and, not without misgivings, agreed to give the lecture in Polish.
Polish is no longer a language with which I am entirely comfortable and, to make matters worse, I was about to leave New York for Utrecht, where, under ordinary circumstances, opportunities for practicing Polish would be non-existent. As it happened, {23} at the Institute of Theoretical Physics of the University of Utrecht, to which I was attached as a visiting professor, there was a young Polish theoretical physicist just freshly arrived from Cracow with whom I could converse in Polish with reasonable frequency.
I always plan and organize my lectures in my head and for many years I have done it in English. Shortly before I was to leave for Warsaw I finally faced up to the problem of translating, in my head again, my English composition into passable Polish. I then realized with consternation that I did not know the Polish version of Matthew 13:12 and I wanted to share the Matthew Effect with my Polish audience. My young Polish friend was of no help. He was a member of the postwar godless generation and anyway the Bible has never figured largely in the Catholic experience. There was, of course, no hope of finding a copy of the Polish Bible in Utrecht and I certainly was not going to attempt a free translation from the King James version into my shaky Polish.
Time was getting short. I dispatched a letter to Groszynski, my former teacher of Polish literature at the Lycee, asking for a copy of the Polish Bible. I had little hope that the letter would reach him in time and left for Warsaw with the problem of the Polish version of Matthew 13:12 unresolved.
I arrived in Warsaw a day before the scheduled lecture and was met at the airport by a group of Academy officials. After shaking hands and exchanging a few words of greeting, I met my problem head on and asked whether I could have a copy of the Polish Bible delivered to my hotel. Not wanting to steal even a small piece of my own, albeit mild, thunder, I gave my hosts no reason for what must have seemed to them a singularly bizarre request. Their faces clearly showed their puzzlement. Still, within an hour I had a copy of Father Dudziak's authorized nineteenth-century translation. Unnecessarily, as it turned out; Groszynski had received my letter and now I had two copies.
The lecture went off very well and the reference to the Matthew Effect was received with pleasure and amusement. The faces of my hosts cleared visibly as they understood the reason for my strange request of the day before. The high point of the lecture came unexpectedly and it had nothing to do with either Smoluchowski or St. Matthew. The chalk which I used during the lecture was singularly brittle, and after a piece broke five times in a few seconds {24} while I was trying to draw a simple diagram, I said with some exasperation: “I wish we had some of the chalk from Krzemieniec.” This offhand remark caused a prolonged round of applause. The loss of Krzemieniec to the Soviet Union was very keenly felt.
The University's second period of glory coincided with the short twenty years of Polish independence after World War I. Throughout its history Poland had a recurring dream of becoming a great power. With Germany on one side and Russia on the other, and with a predilection for choosing leaders who more often than not were either suicidal romantics or plain incompetents, these delusions of grandeur were both pathetic and silly. While the ambition to become a great power in the geopolitical sense was thus doomed to failure, it was realized unexpectedly in an entirely different area. Poland became a world power in mathematics!
To appreciate how miraculous this was, it should be realized that there was almost no tradition in either mathematics or science throughout all of Polish history. Smoluchowski was the first major Polish theoretical scientist since Copernicus, with a barren period of nearly five hundred years between them. Marie Curie was a great physicist but she was Polish by birth and sentiment only; her scientific education and work took place in France. A few other names come to mind, notably Zygmunt Wroblewski and Karol Olszewski, who became widely known for having been the first to liquefy oxygen, nitrogen, air and carbon monoxide in 1883. One should perhaps also mention Jozef Hoene-Wronski (1776–1853) because a simple but useful construct he introduced, which is called the Wronskian, still lives on in all books on differential equations. When I was at the Lycee I had learned about Wronski as a romantic Hegelian whose writings promulgated the popular nineteenth-century Polish tenet that Poland was the Christ of Nations and that the partitions were the Crucifixion. This exotic theory helped to keep alive the hope for the Resurrection which would represent the re-emergence of Poland as a free nation. When at the University I first came across Wronskians, I did not connect them with the murky and barely comprehensible philosopher.
With this as background, how did it come about that during the short and rather turbulent period of independence there flowered in Poland a School of Mathematics which left a permanent mark on {25} one of the most ancient and surely the most abstract of all the intellectual disciplines?
It is easy enough to tell how it all began, for it is a matter of record. There were two branches of the Polish School of Mathematics: one in Warsaw and one in Lwów. The one in Warsaw came first and what makes its story unique is that it was the fulfillment of a plan carefully conceived in 1919 by three brilliant young mathematicians: Zygmunt Janiszewski, the spiritus movens of the plan, Waclaw Sierpinski and Stanislaw Mazurkiewicz. The trio had been thinking of how to place Poland on the mathematical map of the world and it was decided that the most promising tactic would be to concentrate on areas of mathematics which at that time lay on the periphery of the discipline and were not actively pursued in major mathematical centers. Since all three young men had already made significant contributions to set theory and certain aspects of topology, and since competition was almost non-existent in these fields, it was decided to concentrate on them. A journal, Fundamenta Mathematicae, was founded to facilitate publication in the chosen fields of concentration and off they went.° The choice of fields was spectacularly fortunate. Almost at once topology and set theory became extremely popular and the new journal became known all over the world. Soon it expanded to include mathematical logic and, gradually, other fields. Even now it maintains much of its original character but, not surprisingly, it has lost its aura of uniqueness.
The Lwów School owes its existence to a lucky accident. In 1916 Hugo Steinhaus, who received his doctorate in Göttingen in 1911 and was then an up-and-coming mathematician, was walking in a park in Cracow when he overheard a snatch of conversation in which the term “Lebesgue measure” was used. Now standard fare in first-year graduate courses in Real Analysis, Lebesgue measure in 1916 was almost unknown outside of France and even there very few were familiar with the concept. Startled and curious, Steinhaus soon located three young men who were heatedly discussing a problem. One of them was Stefan Banach.
As soon as Steinhaus settled in Lwów, he helped Banach to find {26} a job as an assistant at the Engineering School and he guided the younger man through the early stages of his academic career. Banach's doctoral dissertation, written under the sympathetic tutelage if not the actual supervision of Steinhaus, marked the beginning of the modern period in functional analysis. It turned out to be a most fruitful field which became the hallmark of the Lwów branch of the Polish School of Mathematics. In 1929 the Lwów branch founded its own journal, Studia Mathematica. Like its older sister, Fundamenta, it became internationally acclaimed and it, too, survives to this day.
Banach was the unquestioned superstar of Polish mathematics and his name is known wherever mathematics is taught. In the short fifty-three years of his life (he died in 1945) he succeeded in combining an overwhelming flow of brilliant ideas with a style of high living that few men could sustain. In an obituary of Banach, Steinhaus, who outlived him by twenty-seven years, wrote: “He combined a spark of genius with an inner compulsion which incessantly reminded him of the words of the poet: ‘Il n'y a que la gloire ardente du métier’ (Verlaine). Mathematicians know that their craft and that of the poets share the same mystery.”
I didn't know all of this when I chose the University of Lwów. I chose it because it was close to home and thus afforded, in a number of ways, much-needed savings. The financial situation of my family was precarious and every penny counted. My father had somehow managed to save enough money to support me modestly for my first academic year but after that I was to be on my own.
I arrived in Lwów late in September 1931, a few weeks after my seventeenth birthday. Polish universities have always been graduate or professional schools. There was nothing corresponding to the American undergraduate school. Seventeen seems awfully young to start graduate studies but no special precocity on my part was involved. I was only one year younger than the majority of entering students.
The structure of the University could be traced to medieval times. It was divided into the Faculties of Theology, Law, Medicine and Philosophy but later the Faculty of Philosophy was subdivided into the Faculty of Sciences and the Faculty of Humanities. Except for the Faculty of Medicine, which awarded upon graduation the degree of Doctor of Medicine, all the Faculties had an intermediate {27} degree of Magister. In my Faculty it was Magister of Philosophy, or Mag. Phil. for short. The Doctor of Philosophy degree was the required first step toward an academic career. Theoretically, any holder of the Mag. Phil. degree could, upon presentation of a dissertation containing original research, apply for the Doctor's degree. In practice, however, at least one of the professors would have to be acquainted with the candidate's accomplishments before agreeing to read and approve the dissertation. This meant that the candidate for the Doctor of Philosophy degree (at least in mathematics) would have to have some publications to his credit. In essence, he had to be invited to write a thesis, which often was based on the already published material. This helps to explain why between 1919 and 1939, the period during which Lwów was one of the major mathematical centers of the world, fewer than twenty doctorates were awarded. All but one or two of the recipients of these degrees went on to become well-known mathematicians.
In order to aspire to a professorship, possession of a doctorate was not sufficient. The next rung on the academic ladder was something called “habilitation.” This form of torture has its origins in the early battles between the students and faculties of medieval universities over who should control the appointments and dismissals of professors. Since the students held the purse, they felt that they should have full control, while the faculties insisted that they alone should have the right to decide on their membership. The compromise that was finally reached gave the students the right to choose the professors but only from a list of candidates to whom the faculty had granted veniam legendi—that is, the right to lecture. This arrangement survives to this day, with the State, instead of the students, being the keeper of the purse. Thus the State could abolish a chair, as in fact it has from time to time for economic or political reasons, but it could not take away from the holder of the chair his veniam legendi. He could still lecture on a subject of his choice and his lectures would be duly announced in the University Catalogue; he would just not be paid for them.
Habilitation was the process of obtaining veniam legendi. To begin the process, the candidate's “personal qualifications” had to be considered by the whole faculty. If the vote was favorable, the candidate would be asked to present a kind of super-doctoral dissertation, which was then judged by a committee of specialists. {28} If the dissertation was approved, there remained a public lecture on a topic selected by the faculty from a list submitted by the candidate, and a final vote again of the whole faculty. The crucial step was the first. I am certain that in the Poland of my student days a committee of scientists called upon to pass professional judgment on a dissertation would not be influenced in rendering an opinion by the fact that it was submitted by a Jew, a Socialist, a Freemason or what-have-you.° But in the same Poland some of the same scientists who would not allow their scientific judgment to be affected by their prejudices in open court and in the presence of their colleagues would use the latitude which the vague term “personal qualifications” permitted to practice their bigotry. They would say to themselves something like: “Scientifically, this fellow looks pretty good and he may present a dissertation that, as an ‘honest’ scientist, I would not be able to reject. But he is a Jew and I don't want him to be even a candidate for a professorship. So I will vote against him now because what Professor X has just told us casts doubt on his personal qualifications.” Remarkably, there was always a Professor X who would dig up something seemingly detrimental in the candidate's past, and even more remarkable was the speed with which all doubts vanished if the candidate were to convert to Catholicism. Polish anti-Semitism had always been largely religious. Racial overtones, though possibly ever present, became noticeable only after Hitler came to power in Germany.
Passing habilitation and earning the coveted title of “docent” allowed one to lecture without pay and to get onto a list of candidates when a professorial opening materialized because of a retirement or a death. Each professor would then write a letter in support of his favorite candidate and it was up to the Faculty which had the vacancy and finally up to the Minister of Education to choose one. In Germany, where the system was substantially the same, it became the custom for young docents to marry the daughters of influential professors in order to increase their chances of getting the next available professorial chair. This gave rise to the witticism that in academe talent is passed on from father to son-in-law. {29}
Even for docents of great scientific renown the chances of obtaining a professorship in a reasonable length of time were extremely small. They were nil for docents who were Jewish (the name of the mathematician Juliusz Schauder, an internationally famous Lwów docent who never became a professor, comes to mind). Steinhaus used to say in jest that the United States is a poorer country than Poland because Poland educates superb mathematicians and then has no use for them, while the United States could not afford such a waste.
When one is young, and seventeen is very young, one lives in the present. The future, even the near future, is cloaked in unreality. It is true that in this respect I aged very rapidly and in a few years the future was uppermost in my mind, but on that sunny, cool October morning when I entered the University's “Old Building” to attend my first lecture in “higher mathematics,” all I could think of was: “What is it going to be like?”
It was wonderful! Like most first-year students, I was registered for Theoretical Arithmetic, Proseminar in Algebra, Introduction to Analysis with Differential and Integral Calculus (Analysis I) and Experimental Physics with a compulsory Laboratory.
Attendance at lectures was not required and it was possible to obtain the degree of Mag. Phil. without attending a single one. The requirements for the degree consisted of passing examinations in eight subjects, including one elective, with rigidly prescribed syllabi and a final exam in an area of specialization. A dissertation which did not have to contain original material and a two-year participation in a seminar in one's area of specialization were also required. With few exceptions, courses correlated only weakly with the syllabi. Of the eight prescribed examinations only four were in mathematics (five, if one includes theoretical mechanics and six if the candidate chose logic as his one allowable elective). Experimental physics and philosophy were also required. I mention these details to underscore how different the educational system was from the one we have in this country.
The first lecture I attended was in Theoretical Arithmetic. The course was designed to introduce in a rigorous, axiomatic way the number system. It started with the famed axioms of Giuseppe Peano for non-negative integers and ended with irrational numbers. This was my first encounter with abstract mathematics and I took to it {30} like a duck to water. In fact, I was so good at it that the professor who taught the course, Eustachy Zylinski, asked me to help in preparing lecture notes which were then mimeographed and, I believe, sold. I was so pleased to have been thus singled out that I failed to notice that no remuneration was offered for what had been a considerable amount of work. My name, however, did appear on the title page, though less prominently than the name of the professor, who had done almost no work at all. Concurrently, I attended a proseminar on algebra and number theory. It was very loosely connected with the course in theoretical arithmetic and was under the nominal supervision of Zylinski. It was run, however, by Marceli Stark, a junior assistant at the Mathematical Institute. Next to Steinhaus, it was Stark who influenced me most during my student years. He was young, having obtained his Mag. Phil. degree just a year or two before, exceptionally bright and quick. His knowledge of mathematics was prodigious and he was a truly gifted teacher. The proseminar opened to me a new world and offered an opportunity to test myself on a wide variety of interesting and challenging problems.
Marceli was a perfectionist in everything he did, and because of this he published almost nothing except a few excellent advanced textbooks. After the war he was in charge of all advanced mathematical publications in Poland. The credit for the high regard in which these publications are held throughout the world is solely his. He spent the war in a concentration camp working on problems which came from the German aircraft industry and he found a way to sabotage the German war effort while saving his own life.
Marceli became interested in me because I did very well in the proseminar, and he helped me in many ways. He translated into English, which he knew very well, my first serious mathematical note, “A Trigonometric Series,” which appeared in 1934 in the Journal of the London Mathematical Society.° He literally forced me to learn Lebesgue's theory of measure and integration, against which I had developed an irrational prejudice. Fortunately, this bias lasted only a short time. Lebesgue's theory, I should add, is a cornerstone of mathematical analysis and was the bread and butter of the Lwów School. As I have mentioned, it played a role in Steinhaus's discovery of Banach. {31}
Marceli also helped me in an early crisis of my career. The proseminar had already been in session for a number of weeks when Professor Stanislaw Ruziewicz announced the start of his lectures° on Introduction to Analysis with Differential and Integral Calculus. I had been especially looking forward to this course because I wanted very badly to learn calculus, after having tried repeatedly and unsuccessfully to learn it by myself. The opening words of the first lecture came as a real shock. “Gentlemen,” said the professor, disregarding the female one third of the audience, “I shall assume that you are familiar with the theory of Dedekind cuts.” He then proceeded to define the rather subtle concepts of limit superior and limit inferior of a sequence of real numbers. The name Dedekind (1831–1916) was familiar to me because among my father's books were two of Dedekind's classics: Stetigkeit unci Irrazionalzählen (Continuity and Irrational Numbers), in which the “cuts” are introduced and explained, and the more popular Was sind und was sollen die Zählen (What Are Numbers and What Ought They to Be?). I had looked at them but had found them totally incomprehensible. Now, somehow, I was supposed to know this stuff. I came from one of the best schools in Poland and one which emphasized mathematics and science. Yet the most advanced mathematics I had had was a smattering of analytic geometry. Oh, yes, I knew descriptive geometry, seventeen ways to solve triangles and everything that there is to know about quadratic equations. All was totally useless. At what stage of my education could I have heard of Dedekind cuts? But this is an American question. In prewar Poland nobody gave a hoot about the continuity of the educational process, and the concept of a prerequisite was unknown. The secondary schools certified only that one was mature enough to pursue higher studies, not that one was prepared to do so.
Anyway, nobody was required to take calculus the first year; nobody was required to take calculus at all as long as he could pass the examination. The syllabus included Dedekind cuts and also suggested books to read to prepare for the examination. But I wanted to learn calculus now and I didn't fully understand the system. In distress, I ran to Marceli. He showed surprisingly little {32} sympathy or understanding of my predicament. “But I never heard of Dedekind cuts,” I pleaded. “Then you should read about them,” he said and as the only concession he recommended a book. So I went home and read, and as I read, the beauty of the concept hit me with a force that sent me into a state of euphoria. When, a few days later, I rhapsodized to Marceli about Dedekind cuts—in fact, I acted as if I had discovered them—his only comment was that perhaps I had the makings of a mathematician after all.
Once the Dedekind-cuts crisis was over, all went smoothly and soon I was in full command of the material of the course. So much so, that I passed the examination in Analysis I at the end of my first year, which was quite uncommon. Examinations were held at the end of each trimester except for those in electives, which could be scheduled at the convenience of the student and the examiner. The decisive part of each exam was oral, and only in a few subjects and in the final examination a much less important written exam was also required. Students presenting themselves for examinations were assigned at random to the four professors so as to ensure an equitable distribution of examination fees, a source of considerable additional income for them.
For Analysis I, I drew Steinhaus, who had a reputation for being a tough examiner. He asked me two extremely simple questions and gave me an A. Before he dismissed me, I asked his permission to attend his seminar the next year. Permission was required since it was to be the second year of a two-year cycle. He at once signed an appropriate slip and that was that. It is curious that I drew Zylinski as an examiner four out of five times. The a priori probability of this happening is a little less than 1.5 percent, small enough to cause one to raise one's statistical eyebrows. He was unusually gentle with me, and when I presented myself at his office for the oral exam in Mechanics he looked up from some work he was engaged in and said: “Oh, you. You have an A.” When I said: “But won't you ask me at least one question?” he said: “Very well, what is the Schrodinger equation?” I said: “I don't know,” and then he said: “All right. You still have an A.” The Schrodinger equation is the fundamental equation of (non-relativistic) quantum mechanics, which was not a part of the syllabus, and I am quite certain that Zylinski himself didn't know the Schrodinger equation.
I had very little contact with Professor Ruziewicz after my first {33} year in Lwów but he played a very important part in my life: he helped me to get a government fellowship which enabled me to continue my studies. It came about because Ruziewicz himself conducted the once-a-week, two-hour problem sessions connected with his course in Analysis I. Usually, problem sessions connected with courses were conducted by assistants but for some reason Analysis I was an exception during my first year.
Ruziewicz was very shy and he seldom looked at the audience, which may explain his failure to notice women in his classes. He came in and, with hardly a word, wrote a problem on the blackboard and then sat down and waited for someone to volunteer to come to the blackboard and-attempt a solution. At first the problems were quite easy and the number of volunteers was sufficient to move things along. But as they became increasingly tougher the number of volunteers dwindled and after a while I was the only one left who had the courage to go to the blackboard.
As the academic year was drawing to a close I had to face the problem of financial support for the second year. The government awarded a limited number of fellowships (there was no tuition) and I decided to apply for one. I had very little hope of getting it because the competition was fierce and, apart from anti-Semitism, the chances were slim. To have a chance at all, I needed a strong recommendation. Stark wouldn't do because he was too junior, and I didn't quite trust Zylinski. This left Ruziewicz, and with some reluctance I went to see him. My reluctance was based on the rumor that he was a member of the National Democratic Party and hence particularly anti-Semitic. Still, there was no choice. He received me cordially and without so much as a moment's hesitation wrote a few sentences on the special form I had brought with me. Without putting the form in an envelope, he handed it to me. As soon as I left his office, curiosity won out over good manners and I read what he had written. It was terrific. He wrote that my performance in the problem sessions was on a higher level than he had ever encountered and that mathematically I was “hot stuff.” I literally walked on air to the office which handled such matters and handed in my application for a fellowship with Ruziewicz's recommendation firmly attached to it. Some time later I was notified that I was granted a “half-stipend” fellowship. Most fellowships were half-stipends and only in the rarest cases were full-stipend fellowships {34} awarded. The half-stipend was sixty zlotys (about twelve dollars at the prevailing rate of exchange) per month for ten months. I managed on this paltry allowance only because I spent the three summer months at home and earned a little extra money by tutoring. Life in Poland was quite cheap in those days.
A few more words about Ruziewicz. He was a solid, good mathematician and had a number of valuable contributions to his credit. He was not in the class of Banach or Steinhaus but then, few were. Inexplicably, his chair was abolished by the Ministry of Education in 1935 or 1936 but, having his veniani legendi, he continued to lecture occasionally on set theory. He later got a professorship in the local Business School. He was executed by the Germans late in June 1941, together with one hundred other Polish intellectuals, many of whom were distinguished writers and scholars. Among them were Professor Kazimierz Bartel, a well-known expert in descriptive geometry and the theory of perspective who served several times as Prime Minister in the early thirties, and Tadeusz Zelenski, who translated Moliere into Polish and who, under the pen name Boy, wrote wonderfully witty light verse.
To backtrack a little, early in my first trimester I was caught in a riot against Jewish students organized by Polish Nationalist students. I was in the reading room of the Mathematical Institute when suddenly a large band of young men and women shouting anti-Semitic slogans broke into the room and, before I knew what was happening, I was knocked down. The hooligans disappeared almost as quickly as they had come but they stayed long enough for me to see a number of faces contorted by hatred. I was not hurt but my jacket had to be cleaned. It was a singularly demeaning experience and one which is difficult to forget. Because the universities were autonomous (another vestige of medieval times) they enjoyed the privilege of extraterritoriality, which meant that the police could not enter the university grounds unless summoned by the rector. Not that the police would have been much help: they were notoriously on the side of the offenders. Rectors (they were elected for periods of one year each) in my Lwów days dealt with the problem of riots, whose frequency and intensity was constantly increasing, by closing the University. I estimate that between October 1931, when I first went to Lwów, to November 1938, {35} when I left Poland, the University was closed about one third of the time.
It was, I believe, during the next anti-Jewish riot, in which I was not involved, that Polish Nationalist students attacked a Jewish self-defense group, which resulted in the death of one of the attackers, who was hit by a flying stone. The funeral a few days later would have made one believe that a great national hero had fallen for God and country. It was attended by the Rector Magnificus of the University, who that year was a professor of theology and a priest.
My first academic year saw the advent of the green ribbons which were worn as boutonnieres by students to indicate their adherence and devotion to anti-Semitism. This made it possible to identify the few decent colleagues who refused to wear them.
The anti-Jewish riots of the fall of 1931 were only a beginning. The campaign against the Jews inside and outside of the universities was steadily gaining in intensity. After the death of Pilsudski in 1935 the Polish government, which up until then had tried, albeit not with great vigor, to contain the ever escalating student demands for anti-Jewish legislation, began instead to seek accommodation. The most shameful surrender came in the fall of 1937, when the Minister of Education, a mediocre professor of physical chemistry, ordered the Jewish students to sit on the left side of each classroom. Because of the autonomy of the universities this order, which created what became known as “ghetto benches,” could not become operative without the signatures of the rectors. All but one signed. The exception was Stanislaw Kulczynski, the rector of my university that year. A noted plant scientist and a man of rather conservative political views, he refused to sign and resigned in protest. To the Minister of Education he sent a message which said, in part, that “if one destroys a power plant, it is dark at once; if one destroys a university, it is dark fifty years hence.” The darkness descended much earlier and it brought with it horrors compared to which “ghetto benches” look pale and insignificant, but the courageous act and the moving words of Rector Kulczynski deserve to be remembered.
But I am ahead of my story. I passed the final examinations for the Mag. Phil. degree in March 1935, in record time. The title of {36} my Mag. Phil. thesis was “Some Original Observations Concerning Trigonometric Series and Rademaeher Systems.” If I remember correctly, it consisted of reprints of two notes which had already been published and a few handwritten pages containing a number of remarks on Rademaeher functions.
There is really not much to tell about my second, third and fourth years at the University. I enjoyed Steinhaus's seminar hugely and learned a tremendous amount of mathematics. I had almost no contact with Banach, but I did try to learn something about hyperbolic differential equations by attending, for a trimester, lectures by Schauder. The subject was too difficult for me then and Schauder was not the clearest of lecturers. I read a lot on my own, mainly in the theory of orthogonal series, a subject closely related to Banach's brand of functional analysis and one on which Steinhaus and Docent Stefan Kaczmarz were writing a monograph. I also began to read A. A. Markov's book Wahrscheinlichkeitsrechnung (Calculus of Probability).
I was elected (though not unanimously) to the membership of the local chapter of the Polish Mathematical Society (not a major honor) and began to attend meetings, which were always held on Saturdays at 8:00 p.m. After the meetings almost all of the members adjourned to the famed Szkocka Cafe for a coffee or a beer. Finances permitting, I joined the group. Steinhaus seldom did.
Perhaps one aspect of my formal university education deserves mention. It had to do with my interest in physics. Theoretical physics in Poland after Smoluchowski's death in 1917 went into a state of decline. When I was a student, there were only two theoretical physicists in the country whose reputations extended beyond the boundaries of Poland. One was Wojciech Rubinowicz and the other, Leopold Infeld. Rubinowicz was a professor at the Lwów Polytechnicum (Engineering School) and a former student of the famous Arnold Sommerfeld of Munich. He had to his credit a number of major contributions and enjoyed a sound international reputation. Infeld was a much younger man who became a docent in Lwów just around the time I entered the University. He soon after was awarded one of the much coveted traveling fellowships under a special program set up and generously endowed by the Rockefeller Foundation, and he spent most of his tenure in Cambridge, England, where he collaborated with Max Born. {37}
A man of considerable talent and originality, Infeld never quite made it to the very top of his profession. In his brilliantly written, angry autobiography, Quest,° he blames his failure on the wasted years of his young life, during which, instead of learning and doing physics, he had to eke out a miserable living by teaching in private Jewish secondary schools. In the same autobiography there is also a detailed account of an anti-Semitic intrigue which kept him from obtaining a professorship and coincidentally saved his life. He went to Princeton in 1936 on an invitation from Einstein and later became a professor at the University of Toronto. He left Canada in 1950 as a result of despicable behavior on the part of the Canadian governmentf and returned to Poland, where he almost single-handedly created an excellent school of theoretical physics. During our brief overlap in Lwów, I did attend a seminar on Quantum Mechanics which he conducted but I found the subject extremely difficult. I was also busy with a number of mathematical problems which had a higher priority.
While I was a student, the chair of theoretical physics stood vacant, with Szczepan Szczeniowski occupying it temporarily as acting professor.‡ Szczeniowski, a student of Smoluchowski from Cracow, was an experimental physicist by inclination and training. He was converted into a theoretician just to keep the chair warm until a permanent occupant could be found, and he performed competently.
I went to see him some time in 1934 because I had decided to choose Thermodynamics as my elective. I was at the time becoming interested in probability theory, and the syllabus of thermodynamics included a smattering of kinetic theory, which in a significant way depends on probabilistic concepts. I was told to study an all-time classic, Max Planck's Thermodynamik, and a couple of chapters on kinetic theory in the second volume of Clemens Schaefer's textbook, standard in those days, Einfuhrung in die Theoretische Physik (Introduction to Theoretical Physics). I borrowed the two books from the library and off I went. The oral exam was set for two months hence. {38}
To learn theoretical physics by oneself, without the aid of a course and without anyone to ask for help, is not a simple matter. It certainly was not for me, and for the first time I felt that I did not have the subject I was studying under any kind of control. In those days the distance between a student and a professor, even an acting one, was such that going to Szczeniowski to ask for help was unthinkable. So I sweated in solitude on what I call the outer edge of understanding. Much too soon the dreaded day of the oral was upon me. I could have tried to reschedule the exam but it would only be postponing the disaster. I even toyed with the idea of changing the.elective to logic or astronomy, both of which I was sure I could master in a reasonable time. Some inexplicable suicidal instinct sent me at the appointed time to what I was certain was going to be my academic execution. It wasn't. Quite to the contrary, I emerged with an A after sketching the derivation of the Boltzmann equation (a subject on which many years later I wrote a number of papers) and discussing with feigned assurance different formulations of the Second Law of Thermodynamics. Szczeniowski even complimented me on my performance. “God,” I thought to myself, “how is it possible? I really don't understand the damned thing at all—and here I am being praised for having done so well.” It was many years before I earned that A but earn it I did. In 1972, when Professor Szczeniowski honored me by attending a lecture of mine in Poland on a topic directly related to thermodynamics, I asked him whether he remembered giving me an A in this very subject. When he replied in the affirmative, I said, “Now I deserve it.”
The exact chronology of the events of my life in the period just before and just after my obtaining the Mag. Phil. degree is not entirely clear in my mind, but what I do remember and what is of importance is that it was the period during which my contacts with Steinhaus became more frequent and more personal. I attended his seminar, of course, and I sat in on two of his courses. One was a lovely set of lectures on elementary mathematics from an advanced point of view which was modeled, to some degree, on a Göttingen course by the famous Felix Klein. I am mentioning this particular course because it gives me an opportunity to tell an anecdote which illustrates one of the many facets of Steinhaus's sense of humor. The course had a small attendance and one day only one other student and I were present. Steinhaus went through the lecture {39} without so much as a glance at the depleted audience and at the end I asked him what was the minimal number of listeners to whom he would feel compelled to lecture. “Tres facit collegium” (“Three make a college,” in a loose translation), he replied. The very next time I was the sole survivor. As the professor started to speak I interrupted him by asking, “What about the 'tres facit collegium'?” “God,” he said, “is always present” and continued to lecture. Steinhaus was an avowed atheist, by the way.
Then one day in the spring of 1935 he called me into his office and said: “I have thought of functions which I propose to call stochastically independent which are defined as follows,” and he proceeded to write-down the definition on a piece of paper. “Why don't you think about them and see if anything interesting comes out?” I had no idea of the motivation behind the definition and, frankly, it looked rather strange to me but my respect for Steinhaus was so great that I began to study the strange objects.
There are, roughly speaking, two kinds of mathematical creativity. One, akin to conquering a mountain peak, consists of solving a problem which has remained unsolved for a long time and has commanded the attention of many mathematicians. The other is exploring new territory. What Steinhaus asked me to do belonged to this second category. As it turned out, the mathematical territory I entered that spring and summer was far from having been unexplored but I didn't know it and neither did Steinhaus. During the summer I obtained a number of results and, to my surprise and delight, I began to make contact with portions of Markov's book which only a short time before had been totally obscure to me. Steinhaus's “stochastically independent functions” turned out to be wonderfully concrete models of the mysterious “independent random quantities” (“Unabhängige Zufällge Grosse”) which Markov, as far as I could tell, had failed to define. Now it seemed that probability theory might become a part of the theory of functions of a real variable (the subject of my specialization for the Mag. Phil. degree) and especially of the general theory of orthogonal systems which was at the center of interest of the Lwów School. 1 didn't realize that much of what I had discovered was known under a different guise but it was known to very few and it was terribly far from the main preoccupations of mathematics in those days.
When I communicated to Steinhaus what I had done, he became {40} excited and almost at once made elegant use of one of my results. When I returned to Lwów in the fall of 1935 we began to collaborate. Until the day I left Poland we were inseparable.
After the summer vacation of 1935 I returned to Lwów, no longer a student. I was now Mag. Phil. with good prospects for receiving a doctorate in a reasonable time. Steinhaus took it for granted that I would have no difficulty in preparing an acceptable thesis. He supported my application for a continuation of my fellowship and I did receive it, but with a delay of three months during which I came very close to starvation. When we were finally paid retroactively the fantastic sum of one hundred and eighty zlotys (thirty-six dollars), another successful applicant and I went to a restaurant which was way beyond our means under ordinary circumstances and ordered three dinners each. Our stomachs could not stand such a sudden jump from near-starvation to disgusting gluttony and we both gave up somewhere in the middle of the first dinner. A terrible waste, but it was worth it.
Roughly at that time (the end of 1935 or early in 1936) Steinhaus engaged me as his private assistant. He did not really need an assistant, since he was an extremely capable, efficient and well-organized man. He merely wanted to help me financially and, being a sensitive man, he didn't want to hurt my feelings bv just offering me money. However, after a period during which I was more of a hindrance than a help, I did prove useful in a number of wavs. The most important of these had to do with his project to write an almost wholly pictorial book on mathematics, and a magnificent book it turned out to be! After forty-five years (it was first published in 1938) Mathematical Snapshots, as it is called, has had innumerable editions, has been translated into ten or more languages and has recently been issued as a paperback. As Steinhaus puts it in the introduction, the book was meant to appeal “to the scientist in the child and to the child in the scientist” and in this respect it succeeds magnificently. Much as I would like to, I cannot claim any role in either the conception or the execution of the project. Steinhaus naturally did discuss with me various items connected with the book and I suggested one of the examples but the book is his alone. One of my duties as his assistant was, however, to oversee the photographic work and this led to my only serious romantic involvement on that side of the Atlantic. {41}
Steinhaus wanted to illustrate an ellipse by using the surface of water in a tilted glass and he suggested that we photograph the glass in a woman's hand. One late afternoon, as I was lying on the floor of the photographer's studio arranging some objects we were about to photograph, the door to the studio opened and a slim young woman in a wide-brimmed black fiat came in. As she waved a greeting to the lady photographer, I noticed from my vantage point on the floor that the newcomer's hand was especially eh gant. Here was the opportunity to get tint ellipse photo and I seized it even before we were introduced. “If you will let me borrow your right hand for a few minutes,” I said, “I can promise you immortality.” I kept this promise, for thousands of readers in all parts of the world who bought, borrowed or stole Mathematical Snapshots have admired the elegant hand of Men Dubinski. Those who read this book will know that I also planned to marry the owner of the hand I helped preserve for posterity.
All of this happened at the time when I had resolved to find a way to get out of Poland. With the persistence of Cato, who ended each of his speeches with: “Delenda et Carthago,” I kept repeating to myself, “I've got to get out of Poland.” I knew that it would require every ounce of my energy to achieve the minimal level of scientific visibility necessary to have any chance at all. I was young, not even a Ph.D., with only two or three published notes, while my “competitors” from Hitler's Germany were, in many cases, world-renowned. The last thing I needed was a romantic entanglement. And yet when the moment came and I still had a choice, I took the plunge.
After one of the late-afternoon photographic sessions which Men' attended with some regularity I walked her to her streetcar stop. As we were waiting for the right tram, she said, “Would you like to come home with rue for supper and meet my mother?” I could easily have excused myself, but while the voice of reason told me to say, “I'm sorry, but ...” I heard myself say, “I'd love to.”
She was a tallish girl with wavy brown hair and rather sharp features which softened when she smiled. When I met her she was recovering from an unhappy love affair and at first she was naturally reluctant to let herself in for possibly another disappointment. She knew that I was trying to get out of Poland and that my work came first. As we drew closer, Steinhaus, whose interest in my welfare {42} was almost parental, became concerned lest I get married and lose the freedom I so badly needed in order to escape. I suspect, though I have not a scintilla of evidence, that he communicated his concern to my parents. Still, when I took Meri to Krzemieniec to meet them, they easily passed the test for civilized behavior. There was no warmth but neither was there a sign of hostility. It was difficult to be hostile to Meri—she was terribly nice and lots of fun to be with.
My parents need not have worried. Both Meri and I were sufficiently practical to know that marriage under the circumstances was out of the question and we agreed on the following plan: If and when I reached the United States, I would contact her mother's brother, who was a well-established electrical contractor in New York. I would try to persuade him to give Meri an affidavit of support, without which one could not even try to obtain an entry visa. We would be married as soon as she reached those shores. These were the dreams of our innocence. No hint of the magnitude of the tragedy that was to overtake the world entered our imaginings of the future together.
In spite of the worsening political situation in Poland, the growth of Hitlerism in Germany and ominous news of barbaric purges in the Soviet Union, life went on and it wasn't all bad. With what Steinhaus paid me added to my fellowship, I could afford an occasional foray with Meri into a decent nightclub for an evening of dining and dancing, and I began to visit the Szkocka more frequently after the Saturday-night meetings of the Mathematical Society. My work was going well. At the end of 1936 I had enough material for a respectable, though not really brilliant, doctoral dissertation.
During this period I met Wladyslaw (Wladek) Hetper, who became my closest and best friend. Wladek came from Cracow, where he received his Mag. Phil. degree in mathematics. While still a student he came under the influence of Leon Chwistek, a philosopher and logician who around 1930 came to Lwów from Cracow to become the first occupant of the newly created chair of philosophy in the Faculty of Sciences. Wladek followed him, but with considerable delay.
Chwistek was an extremely interesting man and a distinct maverick. A follower of Bertrand Russell (rumor had it that he was the {43} only one who, except for the authors, had read all three volumes of Principia Mathematica), he attracted attention by improving and simplifying the theory of types which Whitehead and Russell introduced to deal with self-reference paradoxes. In the twenties he had made a number of other notable contributions to logic and sometime in the early thirties he began designing a system of logic that could house all of mathematics without the threatening specter of paradoxes.
As a philosopher, Chwistek was close to the Wiener Kreis (the Vienna Circle), the famous philosophical group in Vienna whose membership included such luminaries as Rudolph Carnap, Kurt Gödel and Moritz Schlick. I remember a lecture on philosophy by Chwistek on the day the news was received that Schlick had been assassinated by a deranged student. After bravely trying to eulogize his friend, Chwistek broke down and cried.
Chwistek professed to being a non-Hegelian Marxist, which to some may appear to be a contradiction in terms but he held Hegel in such contempt (which I acquired from him) that he chose heresy rather than accepting anything that emanated from Hegel's pen or from his hopelessly (according to Chwistek) confused brain. Chwistek's Communist sympathies, Hegel or no Hegel, made him choose to join the retreating Soviet Army in June 1941 and he ultimately reached Moscow. He died of a stroke during a Kremlin banquet which was attended by Stalin.
Chwistek was also a leader of a group of abstract Polish painters and was himself a talented painter. Several of his paintings hang in the modern wing of the National Museum in Warsaw. He left his philosophical credo in the form of a book, Limits of Science (available in English translation). It is probably the most unsystematic and idiosyncratic book ever published, but it is also extremely interesting and even exciting in spots. It contains an intermediate version of “The System” (I do not believe that a final version was ever completed). As far as I can judge, “The System” did not face up fully to Godel's monumental discoveries which came at the time the book was being written. Chwistek married one of Steinhaus's sisters but the two brothers-in-law did not get along—scientifically, at least. I passed the prescribed exam in philosophy (the Polish system took seriously the Phil, in Mag. Phil.) while accompanying Chwistek on his daily noontime walk in one of Lwów's parks. My {44} knowledge and understanding of philosophy was subminimal but Chwistek was the kindest of men and he could not bring himself to flunk me. Instead, he gave me an A. He was also a member of my Ph.D. examining committee, the other two being Steinhaus and Banach.
Chwistek began to develop “The System” while he was still a lecturer in Cracow. He was helped by two brilliant students, Jan Herzberg and Wladyslaw Hetper. Herzberg, whom I met only once, was, if one can believe it, a saintly Communist. A man of unbounded compassion and decency, he could not come to terms with a world which was filled with pain and injustice. Somehow he came to the conclusion that Communism was the antidote and for this conclusion he paid with years spent in Polish jails. In Poland, Communist activities were illegal and the penalties for engaging in them severe.
Wladek Hetper was of exactly the same moral makeup as Jan but he found his answer in religion. Through him I came to reexamine my attitude toward Catholicism and Christianity in general. The history of the Jews after the fall of the Second Temple and during the subsequent diaspora is a history of continual religious persecution, all in the name of Christ, who preached love and forgiveness. If one contemplates the incongruity of the Sermon on the Mount and the Inquisition, one may, I think, be forgiven for looking at Christianity with a jaundiced eye. My own experiences did little to dispel my suspicions and prejudices, which I inherited from my ancestors. Wladek changed all of this. By example he made it evident that an underlying nobility of spirit could be reinforced and maintained by a deep belief in God, independent of the ritualistic mode in which this belief was expressed.
I do not remember how and when we met but we soon took a room together which we shared until the time of my departure. Wladek also had a government fellowship, with a full stipend at that, and he was working for his doctorate. He was four or five years older than I and at the time we met he was recovering from a great personal tragedy: his only brother, a gifted poet, had drowned in the Baltic Sea. There were hints of suicide following an unhappy love affair but I naturally never pressed for details.
Wladek was tall, blond and blue-eyed. He was a superb athlete and as a concession to our friendship he took me cross-country skiing from time to time. Quite frequently and with good humor {45} he had to stop and extricate me from all sorts of situations in which a poor skier like me would find himself. I had a special propensity for falling in such a way that I could neither move nor reach a binding to unfasten one of the skis. Wladek was also a first-class chess player. Only rarely could I beat him and at that time I was reasonably good myself.
One year we lived in a room which was heated by a coal stove and because of the danger of carbon-monoxide poisoning we had to let the fire go out at night before retiring. Polish winters are severe and we often woke up to subfreezing temperatures. We took turns on successive days jumping out of bed and starting the fire and then jumping back in. It took about forty-five minutes before the room achieved a livable temperature and we used this time to play double blindfold chess. It was also during these “warming up” periods that Wladek, who knew the Iliad and the Odyssey as well as most of Ovid and Horace by heart, taught me random snatches from these immortal works. I can still recite the first seven or eight lines of the Iliad.
Late in May 1937 both Wladek and I passed examinations for the doctorate and we arranged to have our degrees conferred on us in a double ceremony. As tradition required, the Rector, the Dean and, of course, the “promoters”—Steinhaus and Chwistek in this case—had to be present at the ceremony, resplendent in their academic gowns. As the “pedel” (a kind of herald), also in a gown, knocked three times on the floor with a staff, the Rector pronounced an ancient oath to which the candidate had to reply, “Spondeo ac policeor” (I promise and I swear). All went fine except that in spite of Steinhaus's repeated tutoring I put the accent in spondeo on the second syllable instead of on the first. Steinhaus cringed and so did my father, who had journeyed from Krzemieniec to attend the ceremony. Wladek's mother had come down from Cracow. Thus on the fifth day of June 1937 my friend Wladyslaw Hetper and I became Doctors of Philosophy.
A few days later I was notified that I had not got the Parnas Foundation foreign fellowship for which I had applied. It was a terrible blow, especially since Steinhaus, who was the University's representative on the board of the Foundation, had believed that my chances were very good. Suddenly I was an unemployed Ph.D. with no immediate prospects. True, I was almost certain to get the {46} fellowship the next year, but what was I to do in the meantime? Chance intervened again in an unexpected way. An insurance company, Feniks, with home offices in Vienna, collapsed and it took an act of the Polish Parliament to arrange for a receivership of the Polish branch. The receiver needed a large number of actuaries to recompute the portfolio prior to an orderly liquidation and I was offered a job. Thus did I come to benefit from the misfortune of thousands of people who lost their life savings. The work was hopelessly boring but the pay was reasonable and, most important, I could be in Lwów with Steinhaus and continue to work in mathematics. Being near Meri was also, needless to say, a commanding attraction.
In due time I was notified that the Parnas Foundation had granted me the fellowship and I began to make preparations for going to the United States. Late in November 1938 I boarded the M/S Pilsudski and sailed to what became my adopted country. I was, at the time, twenty-four years old. Before I went to Gdynia to take the boat, I said goodbye to Meri; the sadness of our parting was eased by my belief that we would soon be together again. My friends threw me a roaring farewell party. I then journeyed the five hours by train to Krzemieniec for what turned out to be my last visit with my parents, my brother and the many other members of my family. The political situation was grave—it had been two months since Munich—but we did not dream of what lay ahead. I was full of hope that I could arrange to stay in the United States permanently and ultimately send for my parents and my brother. They shared this hope and were happy that we might eventually be reunited in a saner world.
In less than a year the world exploded and much of my part of it was consumed by flames. Millions, including my parents and my brother, were murdered by the Germans and many disappeared without a trace in the vastness of the Soviet Union. Wladek Hetper was one of them. In 1939, before the outbreak of the war, he received his venianx legendi. When hostilities started, as a reserve officer he was called to active duty and sent to the Eastern Front. I heard nothing more of him until, long after the war, an article in a London-based Polish literary journal printed excerpts from the diary of a Feliks Lachman who had spent some time with Wladek in a Soviet prisoners' camp in 1940. He wrote a short, moving {47} account of their friendship, which was interrupted by Lachman's sentencing and deportation to Siberia. Wladek, according to this account, was in poor health, which, considering what a superb physical specimen he had been, leads me to conjecture that he was suffering from malnutrition. On a visit to London I contacted Lachman and some time later (April 1974) he sent me an excerpt from his diary:
1940, December, Starobielsk |
The Fourth Dimension |
My acquaintance with Wladek the mathematician lasted for not longer than five weeks. Like the homeless swallow in the Norse saga, he flew into my life out of darkness, and into darkness he went away. I never met him again, neither do I know where his bones lie now. He was thirty-one when I met him, a pessimist, though a deeply religious man. He played chess marvelously and could solve difficult mathematical problems in his memory. We spent many a long and thrilling evening discussing Bertrand Russell, the principles of topology and entertaining one another with physical-mathematical puzzles and intelligence tests. We succeeded in reconstructing Cardano's solution of the cubic equation. And then, head first, we plunged into multi-dimensional worlds.
This was the last glimpse I had of my friend in a cruelly distorted mirror image of our times together in Lwów. We, too, had talked of Russell and topology and had entertained each other with all sorts of puzzles. And cubic equations! Another shadow of the past? I'll never know.
| {20} |
|
Tout le monde y croit (la lois des erreurs) par ce que les mathematicians s'imaginent que c'est un fait d'observation, et les observateurs que c'est un theoreme de mathematiques. —Henri Poincare in the Preface to Thermodynamique |
My mathematical life began with my collaboration with Hugo Steinhaus. That three-year period (from the spring of 1935 to the end of November 1938) which seems so short a time to me today was decisive in my development as a mathematician. Even now echoes of those days persist.
Reminiscing in a memorial issue of a Polish journal about Steinhaus as a teacher in the Lwów period, Marceli Stark commented that when he read my paper “Can One Hear the Shape of a Drum?'”° he could detect Steinhaus's distant influence. Stark was perceptive and knew Steinhaus well. Though Steinhaus might not have put it quite this way, the leitmotif of our collaboration was the search for the meaning of independence. Independence is the central concept of probability theory and few would believe today that understanding what it meant was ever a problem. To most mathematicians, once a concept is defined, it is automatically understood. But such a super-formal view was distasteful to Steinhaus and he felt as I do, to an even greater extent, that accepting it is a sort of cop-out. Our work began at a time when probability theory was emerging from a century of neglect and was slowly gaining acceptance as a respectable branch of pure mathematics. This {49} turnabout came as a result of a book by the great Soviet mathematician A. N. Kolmogorov on foundations of probability theory, published in 1933. It appeared to us awesomely abstract. Even the much more accessible work of Stan Ulam and Zbigniew Lomnicki, who were the first to connect independence with so-called product measures, was not quite what we were searching for.
What was it that we were searching for? To come anywhere close to the answer, it would help to become a little better acquainted with Steinhaus, the mathematician and the man.
Hugo Dyonizy (a name he disliked and seldom used) Steinhaus was born on January 14, 1887, in a town called Jaslo in western Galicia. He came, from a distinguished, thoroughly assimilated Jewish family with strong ties both to the Austrian establishment and to the Polish patriotic movement. An uncle, Ignacy Steinhaus, was a member of the Austrian Parliament, and a cousin, Wladyslaw, the son of Ignacy, was killed at the age of eighteen fighting with Pilsudski's Legion. Steinhaus himself served briefly in the Legion.
Steinhaus received a strict classical education in a Jaslo secondary school, where he excelled in all subjects but especially in Polish, the language he loved and knew to perfection. He spent a year studying philosophy and mathematics at the University of Lwów and then moved to Göttingen, which at the time was the mathematical center of the world. He received his doctoral degree in 1911 under David Hilbert, who was the greatest mathematician of this century.
As an interesting historical footnote, it may be added that while Steinhaus was a student in Göttingen, A. A. Michelson of the Michelson-Morley experiment came for a visit. Michelson was so impressed by Steinhaus that he offered him a job as his mathematical assistant.
For a few years after he received his doctorate Steinhaus was what the Germans call a Privatgelehrte, an untranslatable term describing a person who does scientific or scholarly work without an official affiliation and without pay. At the time lie passed his habilitation in 1917 at the University of Lwów he had a number of major achievements to his credit, including a pioneering paper on methods of summability which was a forerunner of modern functional analysis. He had also published a solution of a problem posed by Sierpinski and a well-known Russian mathematician, Nicolas Lusin, {50} concerning trigonometric series. My first serious mathematical publication, the 1934 note mentioned in Chapter 2, was an outgrowth of this paper. He held briefly two semi-administrative posts and was named extraordinary (associate) professor in 1920 and professor in 1923, both at the University of Lwów.° He remained in Lwów until the summer of 1941, when he went into hiding. He spent most of the war in a small town not far from Cracow under the name of Grzegorz Krochmalny, a deceased forest ranger whose documents were supplied by a friend in the Polish Underground. The Underground saved his life on a number of critical occasions. While in hiding, he taught in a clandestine school, began writing voluminous memoirs (of which only a small part has been published) and, without access to books or periodicals, reconstructed from memory most, if not all, of the mathematics he had ever known.
In 1945 came what he told me was the happiest day in his life: a twenty-four-hour interregnum between the moment the Germans left and the moment the pursuing Russians came in. “It was wonderful,” he said in 1946 when he first visited the United States. “They had left, and they had not yet come.” It sounds better, somehow, in Polish (“Ci odeszli a ci jeszcze nie przyszli”). Shortly thereafter the same rector of the University of Lwów who had resigned in 1937 in protest against the ghetto benches was commissioned by the government to organize the newly established Polish University in Wroclaw (formerly Breslau) and he invited Steinhaus to help in this endeavor. Lwów, the city which for centuries had been quintessentially Polish, became part of the Soviet Ukraine and Breslau, which for an even longer period had been completely Germanized, became part of the new Poland. Thus at the age of fifty-nine Steinhaus began a second university career under physical and psychological handicaps which defy description. By the time of his death in 1972, Wroclaw was a thriving mathematical center, the second he had helped to create in his lifetime.
So much for the bare biographical facts. Behind them lay a many-faceted man with a constantly searching, restless mind, an almost infinite intelligence, an unbending integrity and the highest {51} moral principles. He was in all respects a man of the West. He had full command of German and French and his knowledge of English was only a notch less than perfect. He loved Latin and could not imagine an educated man who did not know it. He was, however, much more tolerant than Chargaff when it came to Greek. His wit was well known in Poland. The most famous example was his response to a document he received from the Polish Academy of Sciences chiding him for not having justified his absence from a meeting of a committee of which he was a member. Replying directly to the president of the Academy, he wrote, “As long as there are members who have not yet justified their presence, I do not have to justify rny absence.”
Posthumously a booklet of his aphorisms in Polish, French and Latin was published but unfortunately they are not easy to translate into English. The only one I am willing to risk is an irreverent rendition of the opening line of the Gospel according to St. John: “In the beginning was the bon mot.”
As a mathematician, Steinhaus's main strengths were his intelligence and an unerring instinct and taste in the choice of problems. In this respect he reminded me of John von Neumann, a mathematician whom he greatly liked and admired.
His bent was toward the concrete and a perusal of his bibliography shows only one paper of a truly abstract nature. It is a famous one, written jointly with Banach in 1927, featuring a fundamental theorem of functional analysis known to all students of this subject as the Banach-Steinhaus theorem. Much later, in the sixties, he ventured briefly into mathematical logic (a subject he claimed he disliked) and proposed, in collaboration with his student Jan My-cielski, an axiom in set theory (called the axiom of determinancy) which is much studied even now. Characteristically, he first thought of the axiom in connection with the seemingly concrete question as to whether certain infinite two-person games admit of winning strategies for either one or the other of the players. For games which must terminate in a finite number of moves this is so,° but for infinite games the situation is much more subtle.
Games always fascinated Steinhaus and he was the first to discuss {52} the concept of strategy and related concepts from the mathematical point of view. He published his considerations in 1925 as a two-page note (in Polish) entitled “Definitions Which Are Needed in the Theories of Games and Pursuit” in a totally inaccessible student publication. Fortunately, it was rescued from obscurity and republished in English in the Naval Logistics Quarterly, vol. 7 (1960), with an introduction by Professor Harold W. Kuhn and a letter from Steinhaus to Commander Harris P. Jones, the publisher of the Quarterly. Steinhaus thus anticipated von Neumann, who a few years later (1928) presented a fully developed Theory of Games which became a lively part of mathematics with important applications in economics.
Steinhaus saw mathematics everywhere around him. “To him,” as I wrote in 1974 in a reminiscence and a tribute,° “mathematics was a mirror of reality and life, in much the same way as poetry is such a mirror, and he liked to play with numbers, sets and curves the way a poet plays with words, phrases and sounds.” He enthusiastically collaborated with physicians, biologists, geologists, economists, engineers and even lawyers. He proposed, for example, a simple method for estimating the probability that a woman in a paternity suit will falsely name a particular man the father of her child. This method is now a part of the legal literature on the subject.
My favorite example of Steinhaus's incisive intelligence is the way he estimated the losses of the German army during World War II. Bear in mind that he was hiding under an assumed name and his only contact with the outside world was a rigidly controlled local news sheet that the Germans used mainly for propaganda purposes. The authorities allowed the news sheet to print each week a fixed number of obituaries of German soldiers who had been killed on the Eastern Front. The obituaries were standardized and read something like this: “Klaus, the son of Heinrich and Elvira Schmidt, fell for the Fuhrer and Fatherland.” As time went on—late in 1942 and throughout 1943—some obituaries began to appear which read “Gerhardt, the second of the sons of . . . ,” and this was information enough to get the desired estimate. A friend to whom I told this {53} story had occasion to tell it to a former high official of the CIA at a luncheon they both attended; the official was quite impressed, as well he might have been.
Steinhaus liked to use statistical arguments even in jest. I remember especially one such occasion. Each week I read Nature in the hope that a position would be advertised which did not require the applicant to be a British subject. Sure enough, one week the Imperial College of Science and Technology in London announced an opening for an assistant lecturer in mathematics at the salary of one hundred and fifty pounds sterling per annum, and being a British subject was not a requirement. The yearly salary, roughly equivalent to seven hundred and fifty dollars, seemed so measly that I could not imagine any self-respecting British subject coveting the job. I went to Steinhaus and asked him whether I should apply. At the time I didn't know a word of English but I was willing to perjure myself by claiming that my English was adequate. “Let us see,” said Steinhaus. “I would estimate your chances of getting the job as being about one in a thousand, and if you multiply this by one hundred and fifty pounds, you get three shillings; this is much more than the cost of mailing the letter, so you should apply.” I did, and the job went to a British subject who after all did covet it.
Since the thirties, when I began to cut my mathematical teeth, mathematics has undergone profound changes, not all of them for the better, but Steinhaus's views remained steadfastly the same until his death. In my reminiscence and tribute I tried to summarize them:
His approach to mathematics was largely visual and only seldom abstract. He liked objects and facts and was suspicious of most generalities and extensions. “A statement about curves is not interesting unless it is already interesting in the case of a circle,” he told me years ago, and this sums up well his fundamental belief that real insights are gained from contemplating the simplest and most elementary things. He deplored the growing professionalization of mathematics, the ever-increasing specialization, the flight from robust reality into the murky clouds of uncontrolled abstraction. He spent a significant portion of his scientific life collaborating with non-mathematicians such as physicians, engineers and oil prospectors without a thought that he might be engaging in a different sort of activity {54} than that which had led him and Banach to formulate the principle of the condensation of singularities.
Mathematics to him was mathematics and he was scornful of labels such as “pure,” “applied,” “concrete,” “useful,” etc. He liked clear, sharp points and was impatient with long-winded discourses. “Wo ist der Witz?” (“Where is the point?”) he liked to ask in an attempt, not always successful, to cut through the fog.
As I have written earlier, our collaboration began in the spring of 1935 when he handed me the definition of “stochastically independent functions” and asked me to study them. It was much later that I learned that it was Marceli Stark who had suggested to Steinhaus that he look after me. It may very well have been that Steinhaus, who generated ideas at a fantastic rate, threw one of them at me without much real thought as to what it might lead to. It might have led nowhere if it weren't for the fortunate accident that I had been struggling with Markov's book. For the stochastically independent functions not only filled in the gaps in my understanding of Markov; they led to the bringing of the still mysterious and neglected probability theory into the mathematical fold. Had we done ten years earlier the work that we did together then, the achievement would have been tremendous. As it was, we succeeded in rediscovering much of what had been done by others. But the point of view, the slant, one might say, was new and different and made it possible to contemplate concepts, methods and techniques of probability theory in parts of mathematics which, in themselves, had nothing to do with it.
The editors, K. Baclawski and M. D. Donsker, write in their introduction to a selection of my papers, that “Using the insights, intuition and techniques of probability theory in other areas” is the “underlying theme” of my work. This is indeed so and the first time this theme was heard was in Lwów during my collaboration with Steinhaus.
The first variation on this theme was also composed during this period and it featured the curve whose equation is
y = |
1 σ√2π |
e–(x – μ)2/2σ2. |
| {55} |
Known as the law of errors or the normal law, it is probably the most ubiquitous of curves and the only one claimed as its own by physical, biological and social sciences. It contains two of the most famous constants in mathematics, e = 2.71828 . . . , the base of natural (Napierian) logarithms, and π = 3.14159 . . . , known to every schoolchild from the formula A = πr2 for the area A of a circle of radius r. Steinhaus, with his predilection for metaphors, used to quote a Polish proverb, “Fortumy kolem sie tocza” (Luck runs in circles), to explain why π, so intimately connected with circles, keeps cropping up in probability theory and statistics, the two disciplines which deal with randomness and luck.
There was hardly, a page in Markov's book which did not feature the normal law and it cast a spell over me from which I have never fully recovered. Adding to the fascination was the impression that somehow the normal law was the key to the mysterious and elusive world of chance phenomena. The myth—and it turned out to be just that—that the appearance of the normal law was an unmistakable symptom of the presence of chance was, and I am afraid still is, widespread. Glib talk about randomness and chance is what I think turned most mathematicians off probability theory.
The normal law made its first appearance in 1718 in a remarkable paper by Abraham de Moivre (1667–1754) which, because it was ahead of its time by a century, was nearly forgotten until Laplace saved it from oblivion in his monumental treatise Theorie Analytique des Probabilites, published in 1812.
Shortly before the appearance of Laplace's work the great German mathematician Carl Friedrich Gauss (1777–1855) introduced the “law of errors” which bears his name.
Gauss devoted much time and effort to astronomy and, in particular, to the calculation of orbits of asteroids. These orbits are approximately elliptical and the problem is to “fit” the “best” ellipse to the astronomical observations of the positions of the asteroids at different times. The difficulty is that all observations and measurements are subject to error. To deal with this difficulty Gauss developed a theory which, with some extensions and improvements, survives to this day.
One usually distinguishes three kinds of error: gross, systematic and “random.” Since it may be hoped that by exercising sufficient caution one can get rid of the first two kinds, there remain only {56} the unavoidable “random” ones. Gauss's theory was designed to deal with these.
To illustrate his theory, let us think of measuring the length of a table with a meter stick. One begins with the assumption that there is a “true length” μ of the table but because of the ever present “random” errors the results of successive measurements will all be different, though clustering around μ. Gauss asked himself what the probability is that a single measurement x will lie between a and b (a being the smaller of the two). Under plausible assumptions he then showed that the answer is the area under the curve of the law of errors with x lying between a and b.
The following graph illustrates this statement:
 |
Graph of the curve y = (1/σ√2π){exp[–(x – μ)2/2σ2]} with the shaded area being equal to the probability that a single measurement x lies between a and b. |
The number a is called standard deviation and it reflects the accuracy of the measuring instrument. The smaller it is, the more accurate the instrument.
Gauss made his law of errors the basis for the so-called method {57} of least squares which has since been used and abused by all who handle empirical data.
Toward the middle of the nineteenth century the curve of the law of errors came into science from an entirely different direction. It turned out to be a nearly universal description of the variability of measurable traits.
Consider, for example, the weights in pounds of boys of a certain age. In a sample of 4451 Canadian nine-year-olds the weights ranged from about 40 pounds to about 119 pounds, and the table below gives the numbers of boys in 5-pound intervals starting with 39.5 pounds as well as these numbers converted into percentages. Thus, for example, there are 103 boys, or 2.31 percent of the sample, whose weights are between 79.5 and 84.5 pounds.
Weight in pounds |
Number of boys |
Number of boys |
39.5–44.5 |
20 |
0.45 |
44.5–49.5 |
146 |
3.28 |
49.5–54.5 |
553 |
12.42 |
54.5–59.5 |
979 |
22.01 |
59.5–64.5 |
1084 |
24.35 |
64.5–69.5 |
807 |
18.13 |
69.5–74.5 |
468 |
10.52 |
74.5–79.5 |
180 |
4.04 |
79.5–84.5 |
103 |
2.31 |
84.5–89.5 |
41 |
0.92 |
89.5–94.5 |
25 |
0.56 |
94.5–99.5 |
21 |
0.47 |
99.5–104.5 |
11 |
0.25 |
104.5–109.5 |
5 |
0.11 |
109.5–114.5 |
5 |
0.11 |
114.5–119.5 |
3 |
0.07 |
Total 4451 |
Total 100% |
It is most convenient to display such a table graphically by proceeding as follows: on the horizontal “weight axis” one marks off 5-pound intervals starting with 39.5 and ending with 119.5. Over each such interval one draws a horizontal bar whose height is equal to the percentage of boys whose weights fall within that
| {58} |
 |
interval. Thus, for example, the height of the horizontal bar over the interval between 79.5 and 84.5 pounds is 2.31. The resulting “staircase” graph (above) is called a histogram. It turns out that the histogram is very well approximated by the normal curve with an appropriate μ and σ.°
The example of the weights of nine-year-olds is one of literally thousands of such examples. The normal curve can be fitted to histograms based on heights of men and women, sizes of skulls, weights of beans, spreads of wings of various insects, etc., etc. Adolphe Quetelet (1796–1874), the Belgian astronomer and statistician, was, I believe, the first to recognize and appreciate the universality of the normal curve and he fitted it to a large collection of data taken from all corners of science. He found that it is applicable even to data from what we now call social sciences and {59} attempted to make it a basis of a new discipline which he proposed to call physique sociale.
As Gauss was calculating orbits of asteroids and Quetelet and others were fitting the normal curves to more and more histograms, another development was taking place. It, too, featured the normal curve. It originated in lowly problems posed by gamblers who not unnaturally were concerned with estimating odds, but in the hands of de Moivre and Pierre Simon, Marquis de Laplace (1749–1827), one of the greatest mathematicians and scientists of all time, it soon flowered into a grand discipline to which de Moivre had already, in 1718, given the exalted name of “Doctrine of Chances.”
Laplace, like de Moivre before him, was concerned with situations in which, as in all ordinary games, the number of possible outcomes is finite and he defined the probability of an event as the ratio of the number of favorable outcomes in which the event can be realized to the total number of outcomes, assuming that the latter can be taken to be equiprobable.
Since one example is better than any number of definitions, let us consider a roll of two dice and ask for the probability of obtaining a 5. There are six possible outcomes of a throw of one die and therefore
36 = 6 × 6
possible outcomes of a throw of two. Now 5 can be obtained in the following four ways:
|
Die 1: 1 2 3 4 Die 2: 4 3 2 1 |
Thus, according to Laplace, the probability of getting 5 is
|
Number of favorable outcomes Total number of outcomes |
= |
4 36 |
= |
1 9 |
. |
or about 11 percent.
Calculating probabilities in Laplace's theory was thus reduced to counting. Counting sounds easy until one gets to large numbers. For example, if we toss a coin 10 times and ask for the probability {60} that exactly 5 heads will show, we have to calculate how many of the 210 = 1024 possible outcomes of the ten tosses will show exactly 5 heads and 5 tails. If one is very patient, one can, after considerable labor, come out with the answer, which is 252; but for 100 tosses the number of possible outcomes is 2100, a staggeringly large number. To count the number of outcomes which contain exactly 50 heads and 50 tails would be utterly impossible. Fortunately, mathematicians have developed methods of what I call “counting without counting” and the answer can be written down as:
|
100! 50!50! |
where 100! is an abbreviation for 1 × 2 × 3 × 4 × · · · × 100 — i.e., the product of integers from 1 to 100 inclusive (similarly 50! = 1 × 2 × 3 × · · · × 50, etc.). This is still useless, for already 8! = 1 × 2 × 3 × · · · × 8 = 40320 and we still have a long way to go before we reach 100 or even 50. Mathematicians have conquered this obstacle, too, by deriving convenient approximate formulas to deal with the difficulty of size. Armed with such weapons, Abraham de Moivre considered (and solved!) the following problem:
If an “honest” coin is tossed n times, one cannot, of course, predict the number Hn of heads that will show. But it is intuitively appealing that the average number of heads should be n/2 and that therefore it is natural to study the distribution of the difference Hn – n/2 between the actual number of heads and the average one. But de Moivre made the crucial observation that Hn – n/2 should also be properly scaled before its distribution becomes simple in the limit of large n. The scaling turned out to be n and de Moivre's final result is that as n approaches infinity the probability that
a < |
Hn – n/2 √n |
< b |
approaches the area under the normal curve
|
√2 √π |
e–2x2 |
| {61} |
between x = a and x = b.
In standard notation:
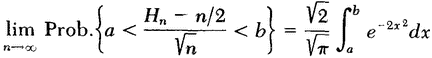
Laplace extended de Moivre's result but soon the whole Doctrine of Chances all but disappeared from the mathematical scene. Not being a historian, I can only guess at the reasons. First, there was a flaw of circularity in Laplace's definition of probability. One may recall from a few pages back that to define probability he needed the “equiprobabihty” of all possible outcomes. This may seem trivial and picayune but the nineteenth century saw the birth of strict and even militant standards of mathematical rigor. By these new standards the foundation of Laplace's great Doctrine were unacceptably shaky. Then there was the extremely special nature of the results. Stripped of its probabilistic interpretation, de Moivre's theorem and its extension by Laplace were simple corollaries of an approximate formula for
n! = 1 × 2 × · · · × n
So why get excited?°
Both objections were soon dealt with but it happened in Bussia and the man who picked up Laplace's barely flickering torch was the great P. L. Chebyshev (1821–1894).
I am not sure how it came about but gradually it was realized that in assigning equal probabilities to all outcomes of tosses of a coin, one is making two quite different assumptions: the first is that the coin is “honest”—i.e., probabilities assigned to heads and tails are both equal to 1/2; the second is that the successive tosses are independent.
Independence of events is not a purely mathematical concept. It can, however, be made plausible that it should be interpreted by the rule of multiplication of probabilities and this leads to the mathematical definition of independence.
Two or more events E1, E2 · · · whose probabilities are somehow {62} known to be p1, p2 . . ., respectively, are said to be independent if the probability that they occur jointly is the product p1 × p2 × · · · There is a hidden subtlety in this definition which is best illustrated by the old chestnut of how to decrease the probability of a bomb being taken aboard an airplane on which you are planning to travel. You merely bring a bomb of your own. The probability of having two bombs on the same plane is p × p = p2 (p being the probability that one bomb is taken aboard). Since p is already small. p2 becomes negligible. The conclusion is so obviously absurd that it calls for a comment. It is true that the probability that two bombs would be brought onto the plane independently of each other is p2. But if one bomb is already on the plane, then, again because of independence, it has no influence on the act of the criminal or the maniac who may decide to bring aboard his own. Thus, given that a bomb is already aboard, the probability that a second one will make an appearance is still p.
Be all this as it may, one can approach de Moivre's theorem in a different way. With each toss of an “honest” coin we associate a symbol X which is 1 if the toss results in heads and 0 if it results in tails. In this way
X1 + X2 + · · · + Xn = Hn
represents the number of heads which show up in n consecutive tosses.
To reflect the assumptions that the coin is honest and the tosses are independent the symbols X1, X2, X3, . . . , whatever they are, must have certain properties. The assumption of “honesty” implies that
|
Prob.{X1 = 1} = Prob.{X1 = 0} = 1/2 Prob.{X2 = 1} = Prob.{X2 = 0} = 1/2 |
etc.
These formulas are mathematical shorthand for the statement that in each toss the probability that the coin will show heads (X = 1) is equal to the probability that it will show tails (X = 0) and that therefore both are equal to 1/2. {63}
Independence of tosses can also be expressed in terms of the symbols X1, X2, X3, . . . , as, for example,
|
Prob.{X1 = 1, X2 = 0, X3 = 1} = = Prob.{X1 = 1} Prob.{X2 = 0} Prob.{X3 = 1} = 1/8 Prob.{X1 = 0, X2 = 0, X3 = 1, X4 = 0, X5 = 1} = = Prob.{X1 = 0} Prob.{X2 = 0} Prob.{X3 = 1} · · Prob.{X4 = 0} Prob.{X5 = 1} = 1/32 |
etc.
These formulas restate the rule of multiplication of probabilities for independent events which in the first case, for example, are that the first toss will show heads, the second tails and the third heads again. Even if we don't know what the X's are, it is possible from the above rules to calculate the probability that
a < |
X1 + X2 + · · · + Xn – n/2 √n |
< b |
which since
X1 + X2 + · · · + Xn = Hn
is the expression we have encountered on page 62.°
What has been accomplished? Actually, a great deal, for this formulation made it clear that the normal law is intimately related to sums of independent quantities.
Even more important, it made possible a vast generalization of the de Moivre-Laplace theory. The X's could be much more {64} general than those related to coin-tossing. All one needs is the knowledge of
Prob.{Xk < α}
for every k = 1, 2, 3, . . . and for every real α and the assumption of independence which means that
|
Prob.{X1 < α1, X2 < α2, · · · Xn < αn} = = Prob.{X1 < α1} Prob.{X2 < α2} · · · Prob.{Xn < αn} |
for every k = 1, 2, 3, . . , and every real α1, α2, α3, . . . Recall that the definition of independence involves multiplication of probabilities.
Under appropriate conditions one could then prove that there are numbers An and Bn such that the probability that
a < |
X1 + X2 + · · · + Xn – An Bn |
< b |
approaches the area under the normal curve
|
√2 √π |
e–2x2 |
between x = a and x = b.
Chebyshev also developed a novel method (known as the method of moments, still in wide use in probability and statistics) to calculate probabilities related to sums of independent quantities but neither he nor his student A. A. Markov (1856–1922), whose book I was reading, defined what the X's were. They and their successors were content to rely upon formal manipulations without worrying too much about what the objects they were manipulating actually were.
Fascinated as I was by the normal law, I was utterly frustrated because I could not accept a formal point of view and although Markov's book appeared to be plain mathematics, it was the kind I could not fully understand. It was as if a curtain had been placed {65} between me and an elusive and mysterious world; a curtain through which I could dimly perceive familiar mathematical objects floating among shapeless blobs. It was tantalizing.
Then came Steinhaus with his definition of “stochastically independent functions” and almost at once the curtain began to rise.
Steinhaus's interest in probability theory went back to 1923, when he wrote a pioneering paper which for the first time gave a rigorous mathematical theory of coin-tossing. The idea, which was already implicitly contained in a remarkable 1909 paper by the French mathematician Emile Borel, was, like so many great ideas, remarkably simple.
To explain it, let me first review a few facts about decimal expansions. The fundamental fact is that every number t between 0 and 1, 0 ⩽ t ⩽ 1, in standard mathematical notation, has a unique non-terminating decimal expansion. (I don't like to be overly pedantic but if I didn't insist on expansions being non-terminating, certain numbers—e.g., 3/100—would have two different expansions, namely .03 and .02999...).
For example,
2/7 = .285714285714...
and because 2/7 is a rational number (i.e., common fraction) the decimal expansion has a periodic structure. For irrational numbers like √2 no such periodicities are present.
The decimal expansion above is an abbreviation of
|
2 10 |
+ |
8 102 |
+ |
5 103 |
+ |
7 104 |
+ |
1 105 |
. . . |
and the fundamental fact about decimal expansions can be stated in full generality as follows:
For every number t between 0 and 1 there exists a unique sequence d1, d2, d3, ... of digits (i.e., each d can assume only values 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) such that
t = |
d1 10 |
+ |
d2 102 |
+ |
d3 103 |
+ . . . |
| {66} |
Since the digits d1, d2, d3 . . . clearly depend on t (are functions of t in mathematical terminology) it is more illuminating to rewrite the above formula in the form
t = |
d1(t) 10 |
+ |
d2(t) 102 |
+ |
d3(t) 103 |
+ . . . |
which emphasizes the fact that d1(t) is the first, d2(t) the second, d3(t) the third etc. digit of t. Going back to our example of t = 2/7, we have d1(2/7) = 2, d2(2/7) = 8 etc.
There is nothing sacred about base 10, and what I have said above is applicable to all bases including the simplest, which is base 2. In this base, instead of ten digits, we have only two—namely, 0 and 1—and the fundamental statement reads now as follows:
For every number t between 0 and 1 there exists a unique sequence of binary digits b1, b2, b3, . . . (each b can assume only the values 0 and 1) such that
t = |
b1 2 |
+ |
b2 22 |
+ |
b3 23 |
+ |
b4 24 |
+ . . . |
The expansion of 2/7 is now
|
2 7 |
= |
0 2 |
+ |
1 22 |
+ |
0 23 |
+ |
0 24 |
+ |
1 25 |
+ |
0 26 |
+ . . . |
so that, for example, b1(2/7) = 0 and b2(2/7) = 1.
Now comes the crucial observation, which we illustrate by two examples.
Consider those numbers t for which b1(t) = 1, b2(t) = 0 and b3(t) = 1—i.e., numbers whose binary expansion begins with
|
1 2 |
+ |
0 22 |
+ |
1 23 |
+ . . . |
| {67} |
The smallest such t is clearly
|
1 2 |
+ |
0 22 |
+ |
1 23 |
= |
5 8 |
The largest is obtained by making all the b's from b4 on as large as possible—i.e., by making them all equal to 1. Thus the largest t, whose first three binary digits are 1, 0, 1, is
|
1 2 |
+ |
0 22 |
+ |
1 23 | + |
1 24 |
+ |
1 25 |
+ |
1 26 |
+ ... = |
6 8 |
I hope I do not insult the reader by reminding him that the sum of the infinite geometric progression
|
1 24 |
+ |
1 25 | + |
1 26 |
+ |
1 27 |
+ ... |
is equal to 1/8.
Finally, the numbers t for which b1(t) = 1, b2(t) = 0 and b3(t) = 1 form the interval (5/8, 6/8) whose length is 1/8.
Let us now consider the numbers t for which b1(t) = 1. These are the numbers whose binary expansions begin with
|
1 2 |
+ . . . |
By the same argument as above we see that the smallest such number is 1/2 and the largest is
|
1 2 |
+ |
1 22 |
+ |
1 23 | + |
1 24 |
+ ... = 1 |
In other words, the numbers t for which b1(t) = 1 is the interval (5/8, 1).
Now a slightly more difficult question—namely, what are the numbers t for which b2(t) = 0? Since nothing has been said about {68} b1, it can be either 0 or 1. In other words, the binary expansions of numbers t for which b2(t) = 0 begin either with
|
0 2 |
+ |
0 22 |
or
|
1 2 |
+ |
0 22 |
Thus the t's for which b2 = 0 consist of two disjoint intervals, the end points of the first being
|
0 2 |
+ |
0 22 |
= 0 |
and
|
0 2 |
+ |
0 22 |
+ |
1 23 | + |
1 24 |
+ ... = |
1 4 |
and the end points of the second being
|
1 2 |
+ |
0 22 |
= |
1 2 |
and
|
1 2 |
+ |
0 22 |
+ |
1 23 | + |
1 24 |
+ ... = |
3 4 |
By this time the reader should be expert in this game, so I'll leave it to him to verify that the numbers t for which b3 = 1 consist of the four non-overlapping intervals (1/8, 1/4), (3/8, 1/2), (5/8, 3/4), (7/8, 1).
If S is a collection of disjoint intervals, let us denote by L{S} the sum of the lengths of these intervals. With this notation our {69} labors of the past couple of pages can now be recorded as follows:
L{b1 = 1, b2 = 0, b3 = 1} = 1/8
L{b1 = 1} = 1/2, L{b2 = 0} = 1/2, L{b3 = 1} = 1/2
and therefore
1/8 |
= L{b1 = 1, b2 = 0, b3 = 1} = |
= L{b1 = 1} L{b2 = 0} L{b3 = 1} = |
|
= 1/2 × 1/2 × 1/2 |
Similarly, unless he has lost his expertise the reader will verify that
1/32 |
= L{b1 = 0, b2 = 0, b3 = 1, b4 = 0, b5 = 1} = |
= L{b1 = 0} L{b2 = 0} L{b3 = 1} L{b4 = 0} L{b5 = 1} |
|
= 1/2 × 1/2 × 1/2 × 1/2 × 1/2 |
These formulas should ring a bell. They are the same as those on page 63 if the b's are replaced by the X's and Prob.{ } by L{ } and therefore all the manipulations on the X's which lead to de Moivre's theorem can be repeated step by step for the b's, obtaining the statement that total length of the t intervals in which
a < |
b1(t) + b2(t) + · · · + bn(t) + n/2 √n |
< b |
approaches as n gets larger and larger the area under the normal curve
|
√2 √π |
e–2x2 |
between x = a and x = b.
Using mathematical notation, we can record this version of de Moivre's theorem in the form
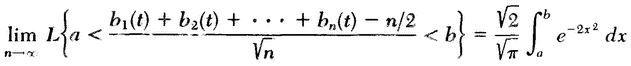
| {70} |
and there are no coins, no chance and no mystery.
The stochastically independent functions which Steinhaus asked me to study were a natural generalization of binary digits and, like binary digits, they were defined on the comfortably familiar interval (0, 1).
We were unaware at the time that considerable progress had been made in clarifying the foundations of probability theory and, in particular, the mysterious X's of Markov's book had been rigorously defined. But the definition was cloaked in abstraction while the stochastically independent functions were quite concrete and even closely related to other objects which had been extensively studied in Lwów and elsewhere.
When in this context I made contact with the normal law I was immensely impressed. I found it difficult to believe that this law, rooted in empirical histograms and games of chance, could be part of ordinary everyday mathematics.
In our third (and last) joint note, “Stir les fonctions independences IV,” the point of view which originated in Steinhaus's 1923 paper, and is called arithmetization of probability theory, yielded something genuinely new and it brought the normal law closer to the mainstream of mathematics.
Here, roughly, was how our thinking went. Time flows from the dim past into the most distant future. That is, from minus to plus infinity. Among the most interesting phenomena are those which repeat in time with perfect regularity, and those are called periodic. Their variability in time is described by so-called periodic functions and of these the most common and best known are cosines.°
It was natural to consider cosines with different frequencies λ1, λ2, λ3, . . . i.e.,
cos λ1t, cos λ2t, cos λ3t. . .
(t, of course, is time) and to inquire whether they could be independent. Once the idea was planted everything went smoothly. We proved that if the frequencies λ1, λ2, λ3, . . . satisfy a certain
| {71} |
 |
Figure 1 |
purely arithmetical condition, then the cosines are indeed independent in the sense that the proportion of time during which simultaneously
cos λ1t < α1, cos λ2t < α2, . . . , cos λnt < αn
is equal to the product of the proportions of times during which separately
cos λ1t < α1, cos λ2t < α2, . . . , cos λnt < αn
Let me illustrate this theorem on the simple example of two cosines. First take the graph of cos λ1t (Figure 1) and consider the time intervals during which the graph lies below the level α1. These are exhibited in Figure 2.
Now do the same to cos λ2t and level α2 (Figures 3 and 4). Finally, exhibit the time intervals during which both cos λ1t < α1 and cos λ2t < α2 (Figure 5).
 |
Figure 2 |
| {72} |
 |
Figure 3 |
Our theorem is then that the proportion of the time during which simultaneously
cos λ1t < α1, cos λ2t < α2
is equal to the product of proportions of time during which cos λ1t < α1 and the proportion of time during which cos λ2t < α2, provided—and it is a crucial proviso—that the ratio λ1/λ2 is irrational!
The irrationality of λ1/λ2 is the special case of the arithmetical
. |
Figure 4 |
 |
Figure 5 |
| {73} |
condition mentioned above. From more than two cosines the condition is a little too technical to burden the reader with. It was first introduced by the famous nineteenth-century German mathematician Leopold Kronecker in what seemed to be a totally unrelated context. The condition is called “linear independence over the field of rationals” and the appearance of the word “independence” may cause some confusion. The fact that the purely arithmetic concept of linear independence happens to be closely related to the concept of stochastical independence is one of those minor miracles that make mathematics fun.
To amuse the reader, we have used the computer to illustrate the theorem. We took the time interval (–150, 150), λ1 = 1, λ2 = √2, α1 = 1/2 and α2 = –1/2. Unfortunately, the computer is incapable of dealing with irrational numbers, so we replaced √2 by its seven-digit approximation 1.4142135.
The proportion of time during which cos t < 1/2 came out to be .668572 and the proportion of time during which cos (1.4142135)t < –1/2 came out to be .337143.
The proportion of time during which both cos t < 1/2 and cos(1.4142135)t < –1/2 turned out to be .225714 while the product of .668572 and .337143 is .225404.
The two numbers are not exactly equal because the interval from –150 to +150 is not the interval from minus infinity to plus infinity and 1.4142135 is not √2. Taking longer and longer intervals and better and better approximations to √2, the agreement would get better and better.
We don't need the computer at all since we have a proof of the theorem, but the exercise is not without interest and pedagogical value.
Finally, we can restate our theorem in its definitive way: if the frequencies X1, X2, X3, . . . satisfy the arithmetic condition of linear independence, the proportions of times during which
cos λ1t < α1, cos λ2t < α2, . . . , cos λnt < αn
behave as if there were probabilities of independent events. Except that in probability theory independence is always posttdated while {74} in our case it is a demonstrable property of ordinary mathematical objects.
At the time we discovered the independence of the cosines, my fascination with the normal law became close to being an obsession. I literally dreamed about it and in my dreams I saw it coming out naturally in contexts close to some kind of physical reality. Independent functions over the interval (0, 1) were too contrived and their abstract counterparts, the independent random variables, even more so. “Could it be,” I thought gloomily, “that the normal law will forever be tied to histograms and games of chance?” Then one morning—it must have been late in the spring of 1936—as I was walking through the park in front of the University's main building I experienced the quickening of feeling which comes with an idea. “God,” I said to myself, “our cosines! Of course—they obey the normal law.” And indeed they do.
It was child's play to verify that it was so, since we had all the machinery to do it—the machinery, by the way, which went back to Chebyshev and Markov (and had been perfected by our contemporary Paul Levy of France) and which Steinhaus and I had rediscovered in the course of our search for the meaning of independence.
This was my discovery of that spring morning: the proportion of time during which the graph of the function
xn(t) = |
cos λ1t + cos λ2t + · · · + cos λnt √n |
stays in the horizontal strip between a and b approaches, as n gets larger and larger, the area under the normal curve
|
√2 √π |
e–2x2 |
between x = a and x = b.
Many years later I noticed an interesting extension of this result. It has to do with Smoluchowski's theory of Brownian motion of a little mirror suspended on a quartz fiber in a vessel containing air. An experiment testing the theory was performed in 1931 by E.
| {75} |
Kappler, who by a simple and ingenious method magnified the angular deflections of the mirror and converted them into linear ones. He was then able to obtain photographic tracings of the motion of the mirror.
One such tracing of 30 seconds' duration is reproduced on the figure above. One cannot fail to be impressed by such an ad oculus demonstration of the existence of molecules, for if it weren't for molecules of air hitting the little mirror, the tracing would have been purely sinusoidal. It is also difficult to escape the feeling that one is in the presence of chance incarnate and the tracing could only have been produced by a random mechanism.
Indeed, Smoluchowski's theory, so completely confirmed by Kappler's experiment, was based on the assumption that the mirror is hit “at random” by the molecules of the air. The theory predicts that the displacement of the mirror is what is called a stationary Gaussian process. Such a process is determined by its so-called covariance function, and this function is also given by the theory in terms of pertinent physical parameters.
Now, if I have this information, I can choose a sequence of numbers λ1, λ2, λ3 · · · and a “scale” α such that
α |
cos λ1t + cos λ2t + · · · + cos λnt √n |
for sufficiently large n will be indistinguishable from Kappler's {76} tracing. Not only will the graph look like Kappler's but when subjected to the same statistical analysis it will yield the same results.
So what is chance?
The crux of the matter was, of course, the independence of the cosines and in this we were partly anticipated by Aurel Wintner. This confluence of ideas and interests was decisive in my choice of Johns Hopkins University, where Wintner was a professor, as the place to spend the tenure of my fellowship.
Wintner was a superbly well-educated and very knowledgeable mathematician. He certainly had all the tools to draw the conclusion about xn(t) following the normal law but he did not do so. Unfortunately, shortly after my arrival in Baltimore our personal relationship deteriorated to the point that we were practically not on speaking terms. Thus I never had a chance to ask him about not taking the small step from independence of the cosines to the normal law.° But then it took me quite some time to realize that spring morning that the normal law followed at once from independence of the cosines—and I had lived and breathed normal law for close to a year. I can only think of one explanation of this blindness: the myth that the normal law is inextricably bound to randomness, whatever randomness is. The theorem that xn(t) defined above obeyed the normal law helped to break the spell which randomness cast on it and even raise serious doubts as to whether randomness is an operationally viable concept.
Once the spell was broken, other possibilities opened up. Before I left Poland I published two more papers featuring the normal law and had completed a third one which became my first paper to appear in the United States. All three belonged to the much-studied subject of so-called gap series and the functions involved were only “almost independent,” allowing for the normal law still to hold without functions (though defined on the interval (0, 1)) being in any way “pathological” or weird as their strictly independent counterparts were.
I was also beginning to think of searching for independence in number theory, the part of mathematics which deals with the most {77} fundamental, elementary and yet mysterious objects—namely, integers. The search proved spectacularly successful and it gave birth to the thriving discipline called probabilistic number theory. This part of the story belongs, however, in the next chapter, for it all happened when I was on this side of the Atlantic.
Even before the climax of our search for the meaning of independence was reached, it became abundantly clear why tout le monde was justified in believing in the “loi des erreurs.” It proved to be both “un fait d'observation” and “une theoreme de mathematiques.”
| {78} |
Late in November 1938, after a stormy crossing, the M/S Pilsudski docked in Hoboken, New Jersey, on a gray and snowy morning. Hoboken did not suggest a propitious entry into the New World, but because the storms at sea had delayed us and we came into New York harbor in the evening, we were rewarded by the unforgettable sight of the gigantic city emerging from below the horizon as its lights were coming on.
I was met by relatives, with whom I spent a week or so before continuing to Baltimore. Much of the time was spent delivering greetings and presents to a sizable colony of immigrants from Krzemieniec. Somehow the relatives of these immigrants, still residing in Krzemieniec, got the idea that there was no good chocolate to be had in the United States, so I was carrying half a suitcase of chocolate bars for the deprived American cousins. At the Customs counter it appeared that I had several bars above the allowable quota. I may have misunderstood but I thought that I had to get rid of some. I recall sharing part of the loot with the Customs officer and we ate chocolate together. A day or two later I had one hell of a time explaining to an immigrant what had become of the bars he didn't get. His family had sent him a letter detailing every item I was carrying for him and some of these were missing! Shades of Sholem Aleichem and life in a shtetl.
My first impressions of New York are blurred. The enormous buildings and seething crowds were numbing; I was too stunned to absorb very much. My kind relatives tried in one week to show me {79} all there was to see in New York; the Krzemieniec colony insisted on getting all the news of their families, whom I had hardly known; and all I wanted was to go to Baltimore and do mathematics. But there was one thing I had to do and wanted to do, and that was to see Meri's uncle.
If my recollection is right, I saw him twice during that week. He was a pleasant, soft-spoken gentleman with an unmistakable resemblance to Meri's mother. I told him that I planned to marry his niece as soon as she came to the United States and that his help was needed in the form of a guarantee of support for her. Without such a guarantee, getting an immigration visa would be hopeless, and even with it, a tremendous effort would be required to get her to the United States. Polish quotas were filled and there were long waiting lists.
He was sympathetic but cautious. I could not blame him for not considering me to be a very good bet. I was young, impecunious and on a temporary visa; I hardly spoke English. Even without these handicaps, prospects were minimal. There were hardly any academic-job openings and better-qualified refugees from Nazi Germany were arriving in ever increasing numbers. The country was still suffering from the Depression. As if all this were not enough, he had had a traumatic experience with a sister whom he had brought over from Poland. She was a very strange lady and she had nearly wrecked his home life. He had finally sent her back. The fact was, he did not want to become involved with Meri. Even if he had agreed to help, it is by no means certain that we could have gotten her out. We had, as it turned out, only nine months—much too short a time for cutting through the immigration bureaucracy in those days.
So there the matter rested. Soon I was caught up in a life in a new and exciting country. Our letters were getting shorter and the intervals between them longer. Soon they stopped altogether. It became clear that the affair was over. Then came the war. Between the end of September 1939 and June 21, 1941, when Hitler sent his hordes eastward, Lwów and Krzemieniec as well were part of the Soviet Union and a modicum of postal communication was possible (I received a number of letters from my parents during this period). I heard that Meri had married a brilliant young physician who was also a highly promising medical researcher whom {80} I had known slightly in my Lwów days. They both died tragically— murdered by the Germans, though I learned this only when the war was over.
Among the few remaining possessions which I brought from Poland is a photograph of Meri wearing the hat that she wore when I first met her. On the back she had written, prophetically as it turned out: “It began with a glass of water and it ended on the ocean.” Oddly, it did not penetrate my consciousness at the time that she felt that things were not going to pan out and yet the message should have been clear.
I arrived in Baltimore during the first week of December 1938 and was met at the station by Professor and Mrs. Wintner and E. R. van Kampen, a young member of the department of mathematics and one of Wintner's collaborators. I was, in fact, startled by how young they all were. Somehow, I had imagined Wintner to be closer to Steinhaus's age, but he was only in his thirties and van Kampen was thirty at most. If any further proof is needed that the world, especially the academic world, is small, it turned out that Mrs. Wintner was the daughter of Otto Holder, a distinguished and well-known German mathematician who in 1913 was on my father's doctoral committee in Leipzig.
The Wintners and van Kampen helped me the very first day to find a tiny apartment (as a footnote to economic history, it might be of interest to record that for a bedroom, a small sitting room and a bath I paid something like fourteen dollars a month) on St. Paul Street, a few blocks from the campus, and I was all set to go. My English was not.
One summer while I was still in Poland—it may have been the summer of 1936—I had made my first attempt to learn English. There was a bitter jest in Europe in those days summarized in the question: “Are you an Aryan or are you taking English lessons?” The message was urgent. Someone recommended a lady in Krzemieniec who purportedly knew English and charged reasonable fees for lessons. The fees were indeed reasonable and the lady may have known English but her ideas as to how to teach it were, to say the least, highly unorthodox. When I went to her as an eager pupil my knowledge of English consisted of exactly one sentence, a motto on a detective story of the tough school I had picked up somewhere: “I like my whiskey strong and my women weak.” {81} Whatever one may think of the sentiment, this motto does not provide one with a firm enough foundation for reading Dickens. And yet my teacher chose A Christmas Carol to get me started. As could have been predicted, we got hopelessly bogged down on Marley's being “dead as a doornail” and after two useless lessons I pleaded financial insolvency and fled.
In the fall of 1937, while I was working as an actuary for Feniks in Lwów, I resumed my English education. This time I got a real pro and his fees were on the unreasonable side. But he was realistic and he chose a textbook entitled An Englishman's Daily Life. It was unimaginably dull and if I were an Englishman I would be tempted to sue the author for libel—no one's daily life could have been so devoid of even the slightest spark. In any case, my finances began to show signs of strain just as we were about to start the chapter “Parts of the Body,” and I quit.
All this time I had kept myself in shape by reading mathematical papers in English and at some point I decided that I could try my hand at writing up two relatively short mathematical notes in English. It took unmitigated gall but I did it and was promptly chastised by no less a mathematician than G. H. Hardy, whom I had asked (in English, God help me!) to present my notes for publication in the Journal of the London Mathematical Society. In a letter dated December 3, 1937, Hardy wrote:
Dear Sir,
I shall be glad to communicate your two notes, which I have now read, to the London Mathematical Society.
It would, however, be much better if you were to rewrite them in French. There are just too many definite linguistic mistakes and even if these are corrected, the English would not read at all naturally. There would be no alternative except of rewriting them completely.
With a red face I rewrote the notes in French and they appeared just before I left for the United States.
Hardy also made a purely mathematical comment about one of the notes. The note was on Fourier integrals, a subject on which Hardy was an acknowledged world expert. I was greatly complimented by his comment that the idea of the note was new to him but was disappointed by his lack of any reaction to the second note. This note featured the normal curve in a context which was certainly {82} familiar to Hardy but I guess it was either too strange or not strange enough to elicit a reaction.
Be all this as it may, it should come as no surprise that my ability to communicate in English was severely limited when I came to Baltimore. The hardest problem was ordering meals, since I invariably got something that didn't even vaguely resemble what I thought I ought to be getting. I finally solved the problem of lunches, which I ate in a drugstore a block from where I lived: I learned to say reliably, “Cream cheese sandwich and coffee.” Unfortunately, the young man who served me would always respond: “On toast?” and all I could do was to smile inanely. The result was satisfactory, since I liked what I got, and my smiles were taken as signs of acquiescence. I looked up “toast” in the somewhat inadequate Polish-English, English-Polish pocket dictionary I carried and it gave just one meaning: “Gentlemen, the King!” Having been logically conditioned, I assumed that “on toast” must be some kind of salutation and I proceeded on this assumption. For a period of about two weeks the following ritual took place at lunch:
I: “Cream cheese sandwich and coffee.”
Waiter: “On toast?”
I (bowing slightly and smiling): “On toast!”
Somehow it dawned on me that something was not quite right and I finally asked van Kampen. He laughed a little longer than I thought was kind, and finally said: “Why didn't you at least once answer in the negative? You would have soon known what ‘on toast’ meant.” “I didn't want to risk being impolite,” I replied and he laughed again.
Many years later, in January of 1956, to be precise, I was reminded of this story under unusual circumstances. I was visiting Cambridge, England, and was invited by a friend to dine in his college. As happens not infrequently on such occasions, I was seated between two rather taciturn gentlemen. The conversation was not progressing smoothly at all. We finally gave up and devoted all our attention to the food and wines. At the conclusion of the meal, those of us at the High Table proceeded to the “Port and Madeira” room, where I was approached by one of my dinner neighbors.
“You are from the States?” he asked.
“Yes,” I said.
“Cornell University?” {83}
“Yes.”
“A mathematician?”
I again gave an affirmative answer.
He raised his glass. “On toast!” he said.
I do not know how this story had traveled to England.
It was around the time that the meaning of “on toast” became clarified that I was asked to give my first lecture in English. It must have been awful; I remember seeing signs of puzzlement on the faces of my audience. Fortunately, American audiences are generally polite and tolerant and English has the remarkable property that it can be mutilated almost beyond recognition and still be understood.
Some years later Hans Bethe told a similar story about a young geneticist friend of his who came to this country in the late thirties and went to Cal Tech, which at the time was the home of the famous Thomas Hunt Morgan and his celebrated school of drosophila genetics. Bethe's friend was also asked to give a talk early in his stay and he noticed that throughout the lecture the audience would at times tense up. When it was all over, a member of the audience took the speaker aside and said: “It was a most interesting lecture and we all enjoyed it very much; but perhaps you should know that in English the result of crossing two species is called a ‘hybrid,’ not a ‘bastard.’” Such are the vicissitudes of learning a language the hard way.
Otherwise, everything went swimmingly. Wintner was pleased with me and wrote to Steinhaus extolling my virtues. Steinhaus, perhaps unwisely, sent this letter to me and I may therefore have missed signs of a change in attitude toward me on the part of Wintner. To this day I do not know the real reasons for the break between us.
Wintner was a very gifted and original mathematician who for some reason did not receive the recognition he deserved. Partly, it was his own fault, for he seemed to have a nearly pathological compulsion to publish and he published much that might better have been left in a drawer. To quote a witticism, which has been wrongly attributed to me, he filled too many “much-needed gaps.” Also his writing style was, I think deliberately, designed to hide rather than to explain ideas. But he had fine ideas in not just one but in several different fields of mathematics. {84}
He was a profoundly unhappy man, or so he appeared to me, and I can guess partly why. It had to do with the disappointment he must have felt when his seminal work on the foundations of Quantum Mechanics was overshadowed by the more definitive and easier-to-understand work of John von Neumann and Marshall H. Stone. As a result, his 1929 book Spektraltheorie der Unendlichen Matrizen (Spectral Theory of Infinite Matrices),° which should have brought him fame, became obsolete before the printer's ink was dry. A pity. The book, in spite of only half solving a major problem and in spite of being written in a peculiarly arcane style, is well worth reading even today. I learned a lot from it.
Although we were not on speaking terms, we managed to coauthor three papers, all with van Kampen as the third co-author, and even one with Paul Erdös as the fourth. I chose only the “quadruple” paper for inclusion in my Selected Papers; the other two filled the aforementioned “much-needed gaps.” Van Kampen, who became a close friend, acted as an intermediary between Wintner and me. I gave him “power of attorney” in all matters connected with our joint work with Wintner and a modicum of peace reigned because of this.
Egbertus Robertus van Kampen, called v.K. by all his friends, was one of the most interesting and colorful mathematicians I have known. Born in Holland, he was a child prodigy, obtaining his doctorate in Leiden in 1929 at the age of nineteen. Anybody familiar with the highly structured Dutch academic system will appreciate how remarkable this was.
Around that time F. D. Murnaghan, the chairman of the mathematics department at Johns Hopkins, was traveling in Europe in search of talent. It was before the great Depression, and academic jobs, though not overly plentiful, were not too difficult to get, especially if you were good. Van Kampen was naturally highly recommended and Murnaghan made him an offer of an associateship, a rank equivalent to that of an assistant professorship, which, as far as I know, existed only at Johns Hopkins. After van Kampen accepted, he applied for a visa only to be told that persons below the age of twenty-one could enter the United States only if accompanied by their parents! The picture of an assistant professor in a {85} major university arriving to assume his duties with his parents in tow seemed too ludicrous even to contemplate, and v.K. was given a leave of absence to await maturity. He spent the time in Delft as an assistant to Professor J. A. Schouten, one of the leading Dutch mathematicians.
Finally, the time came and v.K. arrived in the United States. University professors, clergymen, and those of several other occupations could emigrate outside the national quotas and v.K had one of these highly coveted non-quota visas. There was a story that at the immigration desk he was asked the routine question about his occupation and instead of answering “professor” or “teacher” or even “mathematician,” he answered “topologist” (his justly celebrated doctoral dissertation was about so-called topological groups). The immigration official could not find “topologist” on the list of occupations qualifying for a non-quota visa and he naturally asked what a topologist does. As v.K. tried to explain, the immigration official gained, not unnaturally under the circumstances, the impression that he was dealing with a nut. He detained v.K. for further examination and Johns Hopkins authorities had to step in to extricate him. V.K. never confirmed or denied this story—but it was completely in character. He was a curious combination of brilliance and sophistication on the one hand and childlike naivete on the other.
He was a bachelor and much in demand in certain circles of Baltimore society inside and outside the University. He introduced me to many of his friends, some of whom became my friends, too. As an introduction to America, my ten months in Baltimore were superb. I find it difficult to find words to convey the feeling of decompression, of freedom, of being caught in a sweep of unimagined and unimaginable grandeur. It was a life on a different scale with more of everything—more air to breathe, more things to see, more people to know. And there was the friendliness and warmth from all sides, the ease, the naturalness of social contacts. The contrast to Poland, where the line dividing the Jews from the non-Jews was firmly drawn, defied description. Only once did I hear a comment that even vaguely reminded me that the line might be there after all, and, for all I know, it was made in complete innocence. It happened about two years after I left Baltimore, when around Christmas 1941 I went back there to see v.K., who was in the hospital. I took the opportunity to see a particularly close friend, a {86} lovely lady who had practically adopted me when I came to Johns Hopkins.
“I am getting married, Z.M.,” I told her.
“What's her name?” she asked.
“Kitty,” I said. “Katherine Mayberry.”
“How wonderful,” she exclaimed. “This will make you even more one of us.”
I am recounting this minor episode to underscore how sensitive one becomes after having lived in a country like Poland.
Being a bachelor, v.K. was well off financially and indulged in all sorts of extravagance. He scandalized a number of stuffy characters by buying a Buick, which at the time was a symbol of opulence. To drive a more expensive car than your “superiors” did was a no-no in those days.
He had impressive collections of teas and cheeses, and he made superb cheese omelets. He frequently invited me for a supper consisting of a cheese omelet, French bread, red wine and an exotic tea for a finale. His cheeses were classified as elementary, intermediate and overpowering; his ambition, he joked, was to find a cheese that would walk away from you as you reached for it.
He was a true friend. If it sounds trite, it is because I cannot find better words. He helped me in more ways than I can number and saved my life by lending me money during the most difficult and crucial period.
As I look back on my life I marvel at the improbable assortment of people who, independently of each other, cooperated to keep me from being incinerated in the ovens of Auschwitz or Belsen: Antoni Marian Rusiecki, the Counselor of the Ministry of Education in Warsaw, who gave me a much-needed push to study mathematics; Marceli Stark, who “discovered” me; Hugo Steinhaus, who molded me as a mathematician and lifted me over the line of mathematical visibility and then helped me to get the only fellowship that was available to me and which became my ticket to salvation. And not least, on this side of the Atlantic, Francis Dominick Murnaghan and Egbertus Robertus van Kampen.
In May my visa was close to expiration and I was running out of money. I did have a return ticket (in fact, I still have it) which the American consul in Warsaw had made me buy (I guess to save the cost of deporting me if the need arose) and, much as I hated the {87} idea of returning to Poland, I could not see an alternative. It was at this point that Murnaghan came to the rescue. Out of the blue, he called me to his office and offered to help. “It is too dangerous to go back,” he told me (as if I didn't know it!), “and the war may break out at any moment.” He would try to arrange for an extension of my visa and in the fall, if all else failed, he could promise me a course to teach in night school. I have often thought that if I had gotten my fellowship a year earlier there would have been no compelling reason for Murnaghan to intervene and I would have returned to Poland. Strange, but even not getting the fellowship, which I considered to be a terrible blow at the time, turned out to be a major blessing—enough to make one believe he was born under a lucky star.
I don't remember the details but the extension of the visa came through in record time and I could breathe more easily. What I could not do was eat, for while all of this was happening my money did run out. My family and friends in Poland could probably have scraped up some funds—not much was needed—but there were strict currency restrictions and permits to send hard currency abroad were essentially impossible to get. This problem was solved by van Kampen, who, unasked, offered to lend me money to tide me over the summer months.
The hot, steamy summers in the Baltimore-Washington area have a well-deserved reputation. The summer of 1939 was one of the worst. I had, of course, never experienced anything like it and it was just plain hell. The temperature hardly ever dropped below ninety and the humidity kept pace with it. There was no breeze of any kind and the nights were almost worse than the days because one expected some relief which never came. Everybody who could escaped from this inferno and I was left practically alone. I dragged myself in the morning to Rowland Hall to spend a little time in the library. I did not even think of going up to my cubicle on the top floor; the temperature there was a good ten degrees higher than outside. Air-conditioning was not yet in general use and I often wondered how the government could operate during the summer months.
News from Europe was getting more ominous by the day and the question was no longer whether a war was coming but how long it was likely to last and what kind of war it was going to be. I {88} don't think anyone dreamed of the horror that was to come. In fact, optimistic letters came from Barbara Poniatowski, the only child of Juliusz Poniatowski, the head of the Lycee of Krzemieniec Complex in my schooldays. Barbara was a classmate at the Lycee and remained a friend with whom I kept in reasonably close touch. Gifted, intelligent, compassionate and tolerant of almost everything short of bigotry and injustice, she may have felt that having a just cause was enough to prevail. She believed in the human spirit triumphant over brutal force—one of the noble themes of Polish history, perhaps the noblest.
Barbara's father was at the time the Minister of Agriculture and Agricultural Reform and thus a member of the government. Could it be that the government was so uninformed as not to have at least an inkling of the odds it was facing? Or was it, as were the rest of us, taken in by the myth that Hitler was no match for England and France?
Barbara did not join her parents when, with the rest of the Polish government, they went into exile. Instead, she joined the Underground and was killed during the Warsaw uprising. Her mother died in exile but her father returned to Poland after the war to become a professor of agricultural economics. He did not relish the sterile existence of an exile and he felt he could contribute something positive to his country even though he disapproved of its regime. I saw him a number of times on my visits to Poland—a lonely old man with an unbroken and unbreakable spirit.
The war came as the Baltimore weather became bearable. When in a few days Polish resistance was crushed and the government was forced to flee, it stopped briefly in Krzemieniec on the way to Rumania; for a couple of days my hometown was thus the capital of a dying country.
The morning I read that Krzemieniec was bombed by the Germans I received a telegram. I was sure that it contained news of someone in my family having been killed or wounded. It did not. It was from W. B. Carver of Cornell University offering me an instructorship at the magnificent salary of eighteen hundred dollars a year. A few days later a letter confirmed the offer but it added a discouraging note that the vacancy had occurred because one of the regular members of the department had unexpectedly taken a {89} leave of absence and “therefore there are no prospects for a reappointment.
To go back a few months, in January 1939 I attended my first sectional meeting of the American Mathematical Society, which was held in New York. I gave a ten-minute talk and, luckily for me, Norbert Wiener was in the audience. In the corridor, between sessions, he complimented me on my presentation three different times and each time he also introduced himself to me. The next time I saw him was three months later, in April, when I rode with him, Mrs. Wiener and their two daughters from Baltimore to Princeton. He could not have known much about me, but, as I learned later, he had recommended me to Cornell in the strongest terms. We became good though not close friends and once we even went skiing together in the White Mountains of New Hampshire. That this event actually took place is usually greeted with a measure of disbelief by all who knew either one of us.
Around the time of the January meetings I also met, for the first time, Paul Erdös, who became a lifelong friend with whom I collaborated on two different occasions. The first collaboration took place shortly after we met, under somewhat dramatic circumstances. The story has been told in print twice, but it can stand, I hope, one more repetition.
I have already mentioned that during my last days in Lwów I had begun to think of looking for independence in number theory. The first step was easy. Divisibility by different primes is independent in the following sense. Think of integers divisible by 2—these are 2, 4, 6, 8 . . . i.e., half the integers are even. Integers divisible by 3 are 3, 6, 9, 12 ... or one-third of the integers are divisible by 3. Similarly, one-sixth of all integers are divisible by 6. But for an integer to be divisible by 6 it has to be divisible by both 2 and 3 (and vice versa) and since
|
1 6 |
= |
1 2 |
× |
1 3 |
the rule of multiplication of probabilities comes to mind. This nearly obvious remark can, of course, be extended to any finite number of primes.
The second step was not much harder, but it required being {90} conditioned to think in a certain way and I had been so conditioned by my collaboration with Steinhaus. “Where there is independence there must be the normal law,” I said to myself and proceeded to take the next step. This step was also relatively easy. All I had to do was to introduce a simple little formalism by defining, for p a prime and m a positive integer, the symbol Xp(m) to be 1 if m is divisible by p and 0 if it isn't. Then
X2(m) + X3(m) + X5(m) + . . .
is simply the number of divisors of m which are primes (“prime divisors,” as they are called) and this° function, denoted by ν(m), was a much-studied object in number theory. But the Xp(m) are independent functions analogous in some ways to the cosines of the last chapter and the way seemed open to find out in what sense ν(m) obeyed the normal law. It was not even very difficult to conjecture what the final answer ought to be but in trying to prove it I encountered a hitch. This is not the place to tell precisely what the hitch was except to say that it was related to one of a common variety having to do with the difficulty of justifying the interchange of taking limits. Analysts and number theorists are plagued with this pest and there is no universal cure. Each case requires its own brand of medication.
I knew very little number theory at the time, and I tried to find a proof along purely probabilistic lines but to no avail. In March 1939 I journeyed from Baltimore to Princeton to give a talk. Erdös, who was spending the year at the Institute for Advanced Study, was in the audience but he half-dozed through most of my lecture; the subject matter was too far removed from his interests. Toward the end I described briefly my difficulties with the number of prime divisors. At the mention of number theory Erdös perked up and asked me to explain once again what the difficulty was. Within the next few minutes, even before the lecture was over, he interrupted to announce that he had the solution!
The final result for the number of prime divisors ν(m) is as follows: The proportion (density) of integers m for which
log log m + a√log log m < ν(m) < log log m + b√2 log log m
is given by the area under the normal curve
|
1 √π |
e–x2 |
between x = a and x = b.
The reader, I hope, will forgive my lack of modesty if I say that it is a beautiful theorem. It marked the entry of the normal law, hitherto the property of gamblers, statisticians and observateurs, into number theory and, as I said earlier, it gave birth to a new branch of this ancient discipline.
It took what looks now like a miraculous confluence of circumstances to produce our result. Each of us contributed something which was almost routine in our respective areas of competence and neither of us was familiar with the ingredients which the other had in his possession and which were all essential for success.
It would not have been enough, certainly not in 1939, to bring a number theorist and a probabilist together. It had to be Erdös and me: Erdös because he was almost unique in his knowledge and understanding of the number theoretic method of Viggo Brun, which was the decisive and, I may add, the deepest of the ingredients, and me because I could see independence and the normal law through the eyes of Steinhaus.
We wrote up our result, which appeared in the Proceedings of the National Academy of Sciences a few months later. It took longer to write up a detailed version mainly because I had to assimilate thoroughly Erdös's part of the argument. The paper, entitled “The Gaussian Law of Errors in the Theory of Additive Number Theoretic Functions,” was submitted for publication in December of 1939 when I was at Cornell and it appeared in 1940.
I wish I could report that when it appeared, our paper catapulted us to heights of fame. It didn't. In fact, it was hardly noticed. Perhaps the war had something to do with it. Perhaps it was because the paper was not very well written—my fault since I did the writing. Most likely it was because the subject was a bit esoteric {92} at the time. It did not take off until the fifties. By that time I was doing other things.
Paul Erdös deserves a full-length biography but a few glimpses of this remarkable man will have to do here. Because he is quite eccentric in his behavior and attitudes (he, for example, never in his seventy years has held anything resembling a regular job) one may fail to realize that, apart from being one of the most gifted and original mathematicians of our time, he is also a wonderful human being. Kind, compassionate and generous to a fault, he has nearly all the qualities associated with saintliness, including an uncompromising stance against injustice and evil. Saints are not, however, the easiest people to understand or to be with and Erdös has had his share of difficulties. The most serious and also the most ludicrous was with the United States Immigration Service.
It is one of Erdös's principles that he is against becoming a citizen of a great power. Thus, while he was a permanent resident of the United States he never applied for naturalization. In 1952 he was invited to give a lecture at the International Congress of Mathematicians, which was held that year in Amsterdam, and he applied, as all permanent resident aliens are required to do, for a re-entry permit. Under ordinary circumstances this is a simple, routine matter, but in 1952 nothing was simple or routine and Erdös was called for an interview. After attempting to explain to an official why after more than ten years as a resident he had failed to apply for citizenship, he was refused the re-entry permit on the grounds, I assume, that granting such a permit would not be in the best interests of the United States. This silly and totally unwarranted action of officialdom so enraged Erdös (even saints get angry sometimes) that he left for Europe without a re-entry permit, thus, according to the immigration laws of that period, forsaking the possibility of ever entering the United States again. He, in effect, became a homeless person with a Hungarian passport, which at the time was not an easy document with which to move around the world. Yet Erdös had to move around the world (which he still does and likes doing), for it was nearly impossible for him to establish a permanent or even a semi-permanent domicile. It was a number of years before sanity returned to the United States and it was no longer in the best interests of this country to keep Erdös from occasionally coming for visits. {93}
As a mathematician Erdös is what in other fields is called a “natural.” If a problem can be stated in terms he can understand, though it may belong to a field with which he is not familiar, he is as likely as, or even more likely than, the experts to find a solution. An example of this is his solution of a problem in dimension theory, a part of topology of which in 1939 he knew absolutely nothing. The late Witold Hurewicz and a younger colleague, Henry Wallman, were writing a book on dimension theory which later became an acknowledged classic. They were interested in the unsolved problem of the dimension of the set of rational points in Hilbert space. What all this means is unimportant except that the problem seemed very difficult and that the “natural” conjectures were that the answer is either zero or infinity. Erdös overheard several mathematicians discussing the problem in the commons room of the old Fine Hall at Princeton. “What is the problem?” asked Erdös. Somewhat impatiently he was told what the problem was. “What is dimension?” he asked, betraying complete ignorance of the subject matter. To pacify him, he was given the definition of dimension. In a little more than an hour he came with the answer, which, to everyone's immense surprise, turned out to be “1”!
Most of Erdös's work is in elementary number theory. Don't let “elementary” fool you. Only the statements are elementary; the proofs usually require phenomenal ingenuity, though seldom refined or advanced tools. His bent of mind is combinatorial, which, very roughly, means that he relies on counting and classifying. Even when he deals with transfinite numbers he counts and classifies. Let me hasten to add that counting and classifying are among the most difficult activities in mathematics.
Mathematics is Erdös's life and while he is interested in many things (politics being one of them) they are all secondary; to him the sacred calling is mathematics.
When in 1947 a paper written jointly with my friend A. J. F. Siegert and based on our work during the war at the Radiation Laboratory at MIT appeared in the Journal of Applied Physics, I got a one-sentence postcard from Erdös. It read: “I am praying for your soul.” Thus he was reminding me that I might be straying from the path of true virtue, which, as a matter of fact, I was.
As I was preparing to leave Baltimore an unexpected complication developed. One of the younger members of the department, John {94} Williamson, went with his family to his native Scotland for the summer vacation and was caught there by the outbreak of the war. Murnaghan assumed that Williamson would not be able to return in time for the beginning of the school year and he offered me his job for the academic year.
I had not formally accepted the Cornell offer and staying on for another year in familiar surroundings was tempting. On the other hand, because of my strained relations with Wintner I was eager to get away now that I had an opportunity to do so. True, I had no idea where I would be going. A glance at the map disclosed that Ithaca was situated in the middle of nowhere at the southern tip of a lake with the quaint name of Cayuga. Friends from whom I inquired could only assure me that Cornell had a good football team.
So it finally boiled down to the choice between another year of not speaking to Wintner or the unknown, and I chose the latter—most fortunately, as it turned out, in all respects. For one, Williamson did manage to secure passage and after a harrowing crossing dodging German submarines he and his family showed up in Baltimore just in time for the start of the school year.
And so came the day on which with some sadness I boarded a bus and started my journey into the unknown. As the row houses with their white-painted steps, so characteristic of Baltimore, receded into the distance, I greeted the future with the salutation born months ago of ignorance: “On toast, Ithaca!”
| {95} |
Ithaca, New York, was my home for twenty-two years. I lived there longer than anywhere else. It was there that I met Kitty and it was there that our two children were born. It is now in every sense my hometown, my roots in Krzemieniec having been torn out and brutally destroyed.
I arrived in Ithaca from Baltimore at close to midnight on Sunday, September 24, 1939, to assume my duties as an instructor of mathematics at Cornell University. It was the Sunday that daylight time ended, thereby causing a monumental mix-up in the timetables of the trains and buses. It took fourteen hours with two changes to complete the trip from Baltimore by Greyhound. Neither the bus depot nor the hotel across the street from it, in which I spent half the night (I had to move to a different hotel in self-defense against singularly vicious bedbugs), augured a bright future. “Where the hell am I?” I muttered to myself in Polish as I finally fell asleep.
Morning brought relief and a pleasant surprise. The town looked livable. Still I was skeptical until a city bus deposited me at the top of a long hill. No one had prepared me for the loveliness of the campus that lay spread about me on that sunny morning. The quiet beauty of its walks and lawns was in sharp contrast to a dramatically precipitate gorge on its northern edge. This, together with the distant view of an intensely blue Lake Cayuga, convinced me that, whatever might be in store for me, I would be working in magnificent surroundings. {96}
I had been instructed to go to White Hall and I naturally interpreted this to mean “a building that was white.” This little bit of ignorance delayed me but I soon found it. White Hall is one of the three original buildings, the other two being Morrill and McGraw halls. They stood, as they do today, somewhat sedately side by side overlooking a large quadrangle.
Registration was in progress and I met most of my new colleagues that day. This was my first contact with an almost purely American academic milieu. At Hopkins I had been surrounded by other foreigners: Murnaghan was an Irishman; the other senior professor, Oscar Zariski, came from Eastern Europe and was educated in Italy; Wintner was a Hungarian by birth and German by education; and v.K. was a Dutchman. Williamson, whose job I had nearly taken, was a Scotsman.
At Cornell only a fellow instructor, Fritz Herzog, was not a native American. He was a refugee from Germany who had tried to speed up his process of Americanization by reading the comics. He gave up the struggle when he first came across Popeye the Sailor's “I yam what I yam” and discovered that a yam is a sweet potato. I didn't even try to penetrate the comics, though many years later I came, somewhat grudgingly, to admire Pogo.
Walter Buckingham Carver, who had offered me the job (“without any prospects of a reappointment”), had just retired as chairman and was succeeded by Ralph Palmer Agnew, who became my lifelong friend. During his ten years as chairman, Ag, as he is called by his friends, brought about, at times at considerable personal sacrifice, changes in outlook and attitude which prepared the way for the mathematics department to become one of the leading departments in the country. Ag was a very good mathematician and a superb administrator. By the latter I do not mean that he was universally popular. Quite to the contrary, he was at times severely criticized but he stayed with his convictions and in the end most of his controversial decisions were vindicated.
Coming from a farming family (he was born in the small farming town of, if you can believe it, Poland, Ohio), he had many of the traits associated with this hardy breed and in particular he was absolutely unflappable. When one must preside over mathematicians, who tend to flap more readily than the rest of the human race, this is an invaluable asset. Ag avoided emergencies by anticipating them {97} and acting before they had a chance to arise. After our entry into the war, he foresaw that sooner or later large numbers of soldiers and sailors would be sent to the universities for some kind of technical training and that there was bound to be a tremendous demand for elementary mathematics courses. So very early in the game he began to collect information about faculty members throughout the University who remembered enough of their high-school and college mathematics to be able to teach high-school algebra, plane geometry and possibly a little trigonometry.
Sure enough, six hundred Army recruits arrived in June 1943, to be followed by more than sixteen hundred Navy V-12s including three hundred Marines. The Army contingent came, if I remember correctly, on a Friday, and the following Monday twenty or so as yet unscheduled sections had to be met. They all were, after Ag spent the weekend telephoning his “reserves.” Because of his genius for organization and his foresight, that Monday proceeded in a reasonably well-ordered way instead of being the chaos that one might have expected.
Morris Bishop, in his A History of Cornell, without a hint of Ag's preliminary labors, sums up the situation thus: “Eminent authorities in the classics or philosophy found themselves teaching trigonometry to sailors. Aristotle, for the moment, yielded to Bowditch.”°
There were, of course, problems. I remember one in particular, because it caused us considerable chagrin. One of Ag's “finds,” a big, burly fellow from the music department, decided to meet his class for the first time with a palsy-walsy approach and started by saying something like “Well, fellows, I don't know much about this subject, so I guess we'll have to teach each other.” Fatal. Absolutely fatal. In no time there was a disciplinary problem of major proportions and the only solution was to remove the teacher.
Because of such incidents and the normal turnover of the faculty, Ag had to be constantly on the lookout for prospective teachers. I recall how he hired one of them. I happened to be in his office when a gray-haired but young-looking man came in—seeped in would be a better description, for he was obviously ill at ease. “I was told,” he said, “that you might recommend a book on linear {98} algebra which is slanted toward applications to econometrics.” This was clearly a promising candidate and Ag pounced. “What did you say your name was?” he asked, though the visitor had not introduced himself. “Johnson” (which I use to conceal his real name), answered the visitor. Ag sized him up for about ten seconds and with a certain false heartiness boomed, “Sit down, Johnson.” Before any one of us, least of all poor Johnson, knew it, he was signed up to teach a section of V-12 sailors. As we later discovered, he was a perennial student of independent means who lived a reclusive life and was obsessively shy. When the day came for him to meet his first class, two of us practically had to carry him into the classroom. He turned out to be one of our best and most successful teachers. “Made a man out of him,” was Ag's comment.
My own teaching career began a day or two after registration. My schedule consisted of two sections of college algebra and two sections of trigonometry—twelve contact hours a week. The subject matter of both courses belonged to a secondary-school curriculum. Most universities do not teach such pre-calculus stuff anymore. This was my first introduction to the American undergraduate because at Hopkins most of the undergraduate education was relegated to a small, specially selected faculty group. I had had no contact with this phase of American education. At Cornell graduate education was frosting on the undergraduate cake and at the time the number of graduate students was quite small. All of them were teaching assistants.
My first undergraduates were as nice a bunch of boys and girls as one could hope for, but their preparation had been weak. The deficiency in background became even more noticeable when I began to teach calculus the next term. In all fairness, my English was still not entirely reliable (for example, I used the word “sub-straction,” a literal translation of the French “soustraction,” until a student finally corrected me) and I may have not always been properly understood.
In one of my trigonometry classes I discovered to my great surprise that a few students claimed never to have heard of the Pythagorean theorem. It may have been because of the quaint way in which I pronounced or mispronounced Pythagoras but this obvious explanation did not occur to me. “Did you know,” I addressed the students, “that Pythagoras was so elated when he {99} proved his theorem that he sacrificed a hundred oxen to the Greek gods in gratitude for the inspiration? And that since those days all oxen tremble when a truth is found?” I was quoting a famous line of Heine's. Nobody smiled and from that moment on I relied on more elementary humor.
The department of mathematics was small—there were thirteen of us in residence, with two on leave—and extremely congenial and friendly. There were only three full professors: Ag, who had just been promoted, and the “old-timers,” Walter Buckingham Carver and Wallie Abraham Hurwitz.
Carver came to Cornell in 1907 or thereabouts. He had received his doctoral degree from Johns Hopkins under Frank Morley, the father of the writer Christopher Morley. Carver seems not to have done much original research but he had been throughout his life very active in the Mathematical Association of America, whose primary mission was, and to a large extent still is, collegiate mathematics. Its journal, The American Mathematical Monthly, is unique and is my favorite mathematical publication. In the Association's new quarters in Washington, D.C., there is a room named in memory of Carver.
A superb and dedicated teacher, Carver was an embodiment of all the virtues which in my mind were associated with Americans at the turn of the century. I am not sure how I formed the image of the turn-of-the-century American, nor am I sure to this day that the image had a basis of any kind, but, rightly or wrongly, Carver fitted it. He was fair, tolerant and, though a staunch Republican, a liberal in the best sense of that terribly abused word. It was he who led me to the surprising discovery that the finest liberals are often the wise conservatives. A pity there are so few of them. I would gladly have trusted him with my life, and if I were tried for a crime I would hope for a jury of twelve Carvers—but only if I were innocent.
Carver, his wife, Jean, and their three sons introduced me to football. Early in my Cornell days I was invited to a Saturday luncheon at the Carvers' and one of their sons offered me his ticket to the afternoon football game. After lunch all of us lay down on the floor with a large cardboard on which diagrams of plays were drawn and explained for my benefit. We then adjourned to the stadium. I attended several more games before I got the point but {100} I never really became an aficionado.
Wallie Hurwitz, the other old-timer in the department, was the only Cornell mathematician whose name was familiar to me. A paper he had co-authored with his friend and colleague David C. Gillespie had caught the attention of Banach and his cohorts. Several years younger than Carver, he was the son of Jewish-German immigrants who came to the United States about 1870 and settled in Missouri. His father must have been an enterprising young fellow. For some reason he traveled by mule team as far west as Salt Lake City in the eighties, a trip which in those days must have required considerable stamina. His son Wallie was born in Joplin, Missouri. Wallie may have seen a mule in his lifetime but I am certain he never got near one. An only child and somewhat sickly, he was worried and fussed over by his loving and anxious parents, who had lost their first child. He compensated for this physical weakness with a marked precocity in matters academic. After sailing through the University of Missouri quickly and easily, he went on to Harvard to do graduate work in mathematics. He soon won a Sheldon Traveling Fellowship which took him to Göttingen, where he took his doctoral degree under the great David Hilbert, who had also been the teacher of Steinhaus. Their tenure there overlapped but neither recalled their having met. He came to Cornell in 1912 and remained there throughout his life. He died in 1958 at the age of seventy-one.
In 1914, in collaboration with his friend and fellow instructor Louis Silverman, Wallie wrote two classic papers on certain methods of summability. The authors had the misfortune to have the credit for this achievement taken away from them by a famous German mathematician, Felix Haussdorff, who made the discovery quite independently. Once again, the Matthew Effect. After the death of Gillespie in 1937, Wallie, only fifty-two, gave up active research in mathematics. He taught advanced courses and attended faithfully the weekly meetings of the Oliver Mathematics Club, where he could always be counted on to make a cogent comment or to ask a penetrating question. But he gave up the chase and politely but firmly rejected all the efforts that Ag (who had been his student) and I made to entice him into a collaborative effort. A shame. He had an excellent mind and was very knowledgeable.
Wallie was a genuine eccentric and a campus character. A {101} lifelong bachelor and somewhat frugal in his habits, he was very well-to-do but looked woefully impoverished and neglected. Every two or three years one of his friends drove him to Rochester, New York, where he bought three identical gray three-piece suits at bargain prices. These suits were then worn “in series.” That is, he wore one until it fell apart and then started with the next one. He did not drive a car, though rumor had it that he had once tried to learn this most quintessential of American arts but had given up after wrecking the car and nearly killing himself.
Books and music were central to Wallie's life. His private library held close to three thousand volumes, some of which were very rare. One of his hobbies was represented by an extensive collection of volumes on cryptography. The United States Navy borrowed several of these early in the war, as they could not be found in the Library of Congress. He loved Gilbert and Sullivan and had a fascinating collection of G&S scores, programs, reviews and other memorabilia. Wallie's knowledge of music, especially chamber music, bordered on the expert although he was a less than mediocre performer on the viola.
When he was invited to dinner he invariably brought with him a favorite book which he wanted to share and we were always in for a reading after the meal. My education in English literature was enhanced by exposure to such nearly forgotten minor classics as Daisy Ashford's The Young Visiters or Mr. Salteena's Plan° (written when the author was nine years old) and Edmund Clarehew's Biography for Beginners† and More Biography.‡ On the other hand, I swear that my progress in English was retarded by Wallie's being a compulsive punster.
The stock market held an endless fascination for him and he displayed some wizardry in his dealings there. He was shrewd enough to sell out a short time before the crash and to buy in again at zero when the economy showed signs of an upturn, thus acquiring a sizable estate. He left it to the University of Missouri, to Harvard and to Cornell.
I owe to Wallie meeting a fellow faculty member, William Strunk, Jr., who later became something of a hero to me for having {102} written that little masterpiece The Elements of Style (The Little Book), which was revised and preserved for posterity by E. B. White.°
Strunk was fond of mathematical puzzles and he frequently called on Wallie for help. One day he came to White Hall, puzzle in hand, but Wallie was too busy to see him and sent him to me. I recall vividly the knock at my office door (it must have been in 1954, when Strunk was Professor Emeritus) followed by the appearance of a figure surely from the nineties: high collar, steel-rimmed glasses and gray hair parted precisely in the middle by a line so straight that it would have cheered Euclid.
“Professor Hurwitz told me that you might be able to help me with a puzzle,” he said and he explained the problem. It had something to do with placing an egg in a champagne glass, which in mathematical terms translates into inscribing an ellipsoid into a cone. It was a singularly dull but rather difficult problem and I thought that working it was a sheer waste of time. Strunk was rather glad to have my disapprobation and this led to a wonderfully satisfying friendship. He regularly sent me postcards with quotations from William Blake directed against mathematics. This was a challenge to me to defend my subject when we next met. Unfortunately, our acquaintance was all too brief—he died not long after our first meeting.
It turned out that we had friends in common with whom we regularly played charades and Strunk was drawn into this maniacal circle. Wallie was a member, too. Strunk was an enthusiastic performer and very good company as well. We loved hearing about an assignment he had had that was very precious to him—several months in Hollywood as the literary advisor to the production of Romeo and Juliet with Norma Shearer and Leslie Howard. I would have given a fortune to have seen him on a Hollywood set!
I never felt that Wallie's peculiarities were deliberate or his mannerisms studied; he was in a sense a descendant of the early “characters” who were very much in evidence at Cornell in its infancy. “Eccentricity,” as Morris Bishop writes in his A History of Cornell, “seems to loom large in the records of the early days.” This in a way detracts from appreciating what a remarkable institution Cornell was from the moment of its inception. {103}
The University owes its existence to the unlikely partnership of a self-made inventor-businessman of humble origins, Ezra Cornell, and the patrician Andrew D. White. White, according to Bishop, was one of the one thousand best-educated men in the United States. He dreamed of a “truly great university.” Writing in August 1862, at the height of the Civil War, to a wealthy reformer and abolitionist of Peterboro, New York, named Gerit Smith, he asked for financial backing and he included a blueprint for his dream:
First, to secure a place where the most highly prized instruction may be afforded to all—regardless of sex or color.
Secondly, to turn the current of mercantile morality which has long swept through this land.
Thirdly, to temper and restrain the current of military passion which is to sweep through the land hereafter.
Fourthly, to afford an asylum for Science—where truth shall be sought for truth's sake, where it shall not be the main purpose of the Faculty to stretch or cut science exactly to fit “Revealed Religion.”
Fifthly, to afford a center and a school for a new Literature—not graceful and indifferent to wrong but earnest—nerved and armed to battle for the right.
Sixthly, to give a chance for instruction in moral philosophy, history and political economy unwarped to suit present abuses in politics and religion.
Seventhly, to secure the rudiments, at least, of a legal training in which Legality shall not crush Humanity.
Eighthly, to modify the existing plan of education in matters of detail where it is in vain to hope improvement from the existing universities.
Ninthly, to afford a nucleus around which liberally-minded men of learning—men scattered throughout the land—comparatively purposeless and powerless—could cluster—making this institution a center from which ideas and men shall go forth to bless the nation during ages.
Although the ideas expressed in this remarkable document are commonplace today, they represented a revolutionary vision at the time. White concluded with the words: “I write in one of the darkest periods of our national history, but I remember that the great University of Leiden was founded when Holland was lying in ruins.”
Gerit Smith withheld his support but a few years later White's letter became the design for Cornell University. Thus, Bishop {104} comments, his book (from which the above material is taken) was written “in Ithaca and not from a Gerit Smith University of Peterboro, New York.”
Conceived in the best tradition of enlightened liberalism (it had, for example, owing to Ezra Cornell's Quakerism, no formal connection with a religious denomination and therefore no school of divinity), the University has remained to a large extent true to its heritage. Of the major universities of America it seems to me to be the most free and the least stuffy. Though it has had its bad moments (not all of the successors of Andrew D. White have shared his vision), on the whole Cornell gets high marks as an institution of higher learning. I found it very difficult to leave and my affection for it remains undiminished by the passage of time.
My career evolved normally, which in those days meant slowly. Two months after I came to Cornell, Ag informed me that I would be reappointed for a period of two years and added that my future would be assured if I “keep up the good work” which meant “keep publishing.” On the strength of this newly gained financial stability (at eighteen hundred dollars a year!) I bought a dilapidated 1934 Pontiac and sub-leased a decent apartment from a fellow instructor. Then I met Kitty, who came to my twenty-seventh birthday party on August 16, 1941, as the date of a young physiology Ph.D. with whom I shared the apartment. For the first time in my life I was truly smitten. This was nothing like the low-keyed affair with Men. For a while the courtship progressed rather awkwardly en trois. There were a number of threesome dates, my roommate being not quite willing to relinquish his precedence as a suitor, until he finally left to study medicine at another university. After that things moved inevitably toward our marriage. It took place in Baltimore on April 4, 1942.
Our happiness during this period was marred by v.K.'s death. I had known for several months that he was terminally ill with a brain tumor and had visited him in the hospital in Baltimore. Yet his death in February 1942 was a great sorrow. He had been alive and well such a short time before that it was difficult to accept the fact that I would never see him again.
Kitty is a native of Ithaca and a first-generation American. Her mother came from London and her father from a small hamlet in {105} County Mayo in Ireland by the name of Knappaugh. County Mayo is a bastion of Catholicism but in Knappaugh there were several Protestant families including the Mayberrys.
Kitty's father died after a lingering illness when she was ten years old and upon graduation from high school (the Depression year of 1934) she had to go to work as a salesgirl in the only local department store. By the time I met her she had risen to advertising manager of the store, though by temperament and inclination she was ill-suited to the world of retail business and thoroughly disliked her job despite being very good at it. She found escape in reading and music and it was the latter that brought us together. She played the violin in a town-and-gown ensemble called the String Sympho-nietta; my aforementioned summer roommate was the concertmaster.
An amusing corollary of Kitty's background is that our children learned from their English grandmother some of the turn-of-the-century London vaudeville songs. I can recall how startled some of our friends were when, in the forties, they were subjected to childish renditions of the nearly forgotten classics such as “Father was Papering the Parlour.” How is that for a melting pot?
In the spring of 1943, after four years as an instructor—a rank which has all but disappeared—I was promoted to assistant professor. At the time of this promotion I had about twenty-five publications. How times have changed!
In October 1943 I became associated with the Radiation Laboratory at MIT as a consultant, though I continued to teach a full schedule (sometimes as many as seventeen hours a week) at Cornell. The Laboratory wanted me full time, but the University, seriously depleted of its teaching personnel by the war, appealed the case and I continued to teach and visit the Laboratory for a few days each month for consultations.
By May 1945 the Radiation Laboratory was beginning to be demobilized and my visits stopped. As the war in Europe came to an end, news of the mass exterminations began to reach this country. Indirectly, I heard that the Jewish population of Krzemieniec had perished, with at most a handful of survivors. The terrible news was being confirmed by independent sources but my attempts to obtain some official information about my family through the Soviet Embassy in Washington proved futile. They either did not know {106} or, for reasons of their own, did not want to tell. Of course, the immediate postwar chaos made the gathering of information about individuals all but impossible.
The meaning of the tragedy for me cannot be captured in words. Language is a human instrument and it is simply not capable of coping with the acts of inhumanity which the Germans invented and perfected. The very scale of the evil is beyond comprehension, let alone description. On my first postwar visit to Poland in 1959 I learned from a colleague who was several years ahead of me at the Lycee that the extermination of the Jews and some non-Jews in Krzemieniec took place in a series of mass executions during 1942 and 1943. He saw my father on the eve of one of these massacres and exchanged a few words with him. Within days he and the rest of my family perished. That was the only news that I had until a few years ago when I attended a scientific conference in Kiev and made contact with a second cousin whom I had last seen in Krzemieniec when she was ten or eleven years old. One of her sisters had married a Ukrainian during the First World War and had moved away from Krzemieniec. Her in-laws, who were local farmers, remained, and they had hidden the youngest sister of their daughter-in-law. After the war the sisters were reunited in Kiev.
A letter to my cousin announcing that I would be in Kiev on certain dates was late in reaching her but she finally came to my hotel on the evening before my departure. We were total strangers but I would have recognized her by her voice, which had changed remarkably little. It must have been difficult for her; it certainly was for me. We chatted somewhat awkwardly about trivia, avoiding carefully the subject that hovered palpably between us. She was clearly relieved when the time came for her to catch the last train to the suburb where she lived. As I walked her to the bus stop she said: “Would you like to know how it was in Krzemieniec?” and before I could reply she continued: “No, it is better if you don't know.”
When I first learned of the tragedy it seemed that life would never be the same but being alive proved stronger than my grief. Much stronger. Gradually, layers of mist were interposed between the present and the past and the grief receded. But it is there and it always will be.
The healing was aided by the acquisition of a family. In October {107} 1943, Michael Benedict was born. The news came as I was teaching a class of Army recruits and an excited departmental secretary rushed into the classroom with: “Mark! The hospital just called. You have a son.” As if responding to a command, my soldiers rose as one man and in military unison shouted: “Congratulations, Dr. Kac!” Not quite a twenty-one-gun salute, but the closest equivalent under the circumstances. In spite of this martial beginning Michael grew up to be a confirmed pacifist.
It is curious that Michael's intellectual interests paralleled those of his paternal grandfather, whom he never knew. He majored in philosophy at Haverford College and then went on to do graduate work in linguistics and he is at present an associate professor of linguistics at the University of Minnesota. From Kitty he inherited considerable musical talent and is an accomplished harpsichordist. However, between the piano, which he studied for something like eight years, and the harpsichord, which he now plays extremely well, he took a detour into rock music. He interrupted his graduate studies at the University of Pennsylvania to join a rock group and for about two years earned a living as an itinerant musician. His group, Mandrake Memorial, made two quite respectable albums and is still remembered by some rock aficionados in the Philadelphia area. He then resumed his graduate work after moving to UCLA, got his doctorate there and rejoined academe.
Linguistics is a strange field full of cliques and fiefdoms, each fiercely attached to its staked-out territory and consumed with enmity toward the others. Michael, as far as I can judge, is outside of this turmoil and whenever I understand what he is trying to do I find it very interesting and sensible. But then, I am his father.
On September 3, 1947, Deborah Katherine joined the human race. As a young child she was enormously lively. A dedicated chandelier acrobat, she demonstrated a physical vigor which was not a recognizable family characteristic and often left her parents amazed and exhausted. In high school she was at first an indifferent student. She did poorly in mathematics (in spite of possessing a definite mathematical ability) and she failed first-year Latin although she loved the subject and wanted badly to learn it. After a summer tutorial she took the exam again, got an A and continued with Latin through quite advanced courses in college, getting near-perfect grades. She has a clear, sharp, well-organized mind. And she has {108} character. Few, if any, would, as she did, continue with a subject she had failed at the first attempt and emerge in every sense victorious. As a longtime teacher I can assure the reader that this takes guts and a desire to learn strong enough to survive adversity. She went to New York University, where she majored in English. She graduated with honors and was elected to Phi Beta Kappa. Quite a recovery from the trials and tribulations she suffered while in high school.
During the relatively brief period of my association with the Laboratory I accumulated a sizable number of problems on which I wanted to continue to work. A year without any formal duties appeared most desirable and I applied for a Guggenheim Fellowship and was awarded one. On July 1, 1946, I went on leave.
Before my leave started, Ag told me that upon my return I would be promoted to an associate professorship. To the outside world, however, my situation at Cornell must have appeared to be lacking in stability. Here I was with over thirty publications to my credit, still an assistant professor and going on leave. Keep in mind that in the years immediately following the end of the war universities across the land entered a period of feverish expansion to compensate for the lean Depression years and the dislocations caused by the war. With returning veterans and the GI Bill of Rights, enrollments were skyrocketing, deficits were replaced by surpluses and continuing growth and prosperity were predicted for the foreseeable future.
Department chairmen roamed the meetings of professional societies, which were turning into auctions of academic talent. No wonder that, given these circumstances, I looked like a good catch. Indeed, a number of hunters began to stalk me.
As a result of several job offers I was promoted twice while still on leave and started the academic year 1947–1948 as a full professor at more than double the salary I had earned the previous year. Thus in one year I was more than compensated for having been kept an instructor for four.
My year and a half at the Radiation Laboratory marked the beginning of a shift in my mathematical interests. Until early 1944 I had stuck close to the problematics which were traceable to my collaboration with Steinhaus and only then went off in different directions. Still, as late as December 1948, when I was invited to {109} give an hour-long address at the annual meeting of the Mathematical Society, I chose as my topic “Probability Methods in Some Problems of Analysis and Number Theory,” which was a review of results obtained while I was already in the United States but whose origins went back to the Lwów period. It was to be my swan song in the search for the meaning of independence but “on revient toujours a ses premieres amours.” I returned to my first love twice. I chose it as the topic for a series of popular lectures and then expanded them into a course for honor students at Haverford College in the spring of 1958. The Haverford lectures were published as a Carus Monograph under the title Statistical Independence in Probability, Analysis and Number Theory and it was dedicated to Steinhaus. This was the real swan song, except that now and then I use some of the material for a popular lecture entitled “When Is Random Random?”
The Radiation Laboratory at MIT was organized to promote research and development in radar. Except for Los Alamos, it was the largest and most important wartime research laboratory and its influence on the postwar development of electronic art and industry in this country is immeasurable. It consisted of a number of divisions which in turn were subdivided into groups. The theory group of the Fundamental Research Division was headed by G. E. Uhlenbeck.
George Eugene Uhlenbeck is one of the leading theoretical physicists of this century. Known primarily as the co-discoverer, with his friend and fellow student S. A. Goudsmit, of electron spin, he has made numerous other important contributions to physics. He has had a lifelong active interest in statistical physics and his influence on this fascinating field has been profound and lasting. As the head of the theory group George had to oversee a large number of projects dealing with radar design and operation but his own research activities and those of a small subgroup around him were concerned with the problem of detectability of weak signals, which turns out to belong naturally to statistical physics.
The main obstacle to detectability is the ever present “noise.” “Noise” can be of external origin (for example, electrical activity in the atmosphere) and this kind is relatively easy to deal with. Much more serious is the internal noise in the receiver itself. The internal noise is caused mainly by the thermal “random” motion of electrons in resistors (the Johnson noise) and nothing short of {110} cooling the receiver to absolute zero can eliminate it.
Radar operates on the principle of echo. A signal is sent out and if it hits an object it is reflected. The reflected signal is then received with a time delay which makes it possible to calculate the distance from the reflecting object. The reflected signal is displayed on an oscilloscope. If it is strong enough, it is easily distinguished from the background noise. But if the reflecting object is far away, the returning signal (the echo) arrives much attenuated and often it is not at all easy to spot it.
The understanding of the statistical properties of noise (and noise plus signal) was clearly of great importance and a body of theory had to be developed and assimilated. Today the theory of random noise is a chapter (and a relatively small one) of a much more general theory of stochastic processes, or random functions as they are still occasionally called.
The theory suffers from a slight case of schizophrenia because it is shared, in an uneasy partnership, by the mathematicians on the one hand and by the physicists and communication engineers on the other. In 1943 the mathematical theory was in its infancy and it was beset by subtleties which the physicists were not inclined to take seriously. The mathematicians looked for rigorous, unambiguous concepts and definitions; the physicists wanted formulas and numbers. There was a story going around the Laboratory of an exchange between Sam Goudsmit, who preceded George Uhlenbeck as the head of the theory group, and Norbert Wiener, who was a consultant. “You can keep your Hilbert space,” Sam reportedly told Norbert, “I want the answer in volts.”
Parenthetically, I may add that 1 did not meet Sam until long after the war. By the time I came to the Radiation Laboratory in October 1943 he had vanished, as had a number of scientists in those days. He emerged toward the end of the war as the scientific chief of the famed “Alsos” mission, which followed the American Army into Germany to find out how far the Germans had gone toward building an A-bomb. The story of the mission is beautifully told in Sam's book Alsos°; the Germans, by the way, hadn't made even a respectable beginning.
My introduction to stochastic processes was by the way of “noise” and therefore from the physics end of the subject. It was {111} some time before I understood and appreciated some of the purely mathematical subtleties of the subject but even today I am not interested in many of them. They belong to the foundations of the subject and I am more concerned with the superstructure. I have often claimed that if a subject is robust it should be insensitive to its foundations, and therefore too great an emphasis on the latter tends to produce a misleading slant. Concern about foundations should come, if at all, after one has a firm intuitive grasp of the subject.
I profited greatly from my association with the Laboratory. To begin with, my scientific outlook was widened by my being brought face to face with, problems which, if I am allowed yet another metaphor, were God-given and not just man-made. True, even in the “purest” parts of mathematics the distinction between the two kinds of problem can be detected; the great Henri Poincare put it by saying that there are problems “qui se posent” and problems “qu'on se pose.” But the demarcation line between the problems which come from the “real world” and those which are invented by the human mind is much more sharply drawn. Unless, of course, you are of the philosophical persuasion which denies the existence of the external world except as reflected in the workings of the human mind.
Most important, however, was my close contact with George Uhlenbeck. George is blessed with an unusual clarity of thought and expression which, combined with an uncompromisingly critical attitude, makes him an ideal teacher. His knowledge of physics is as broad as his understanding of it is deep. To this day, in his eighty-fourth year, he tolerates no nonsense or sloppiness. In his younger days he would interrupt a colloquium speaker in an attempt to steer him into an acceptable mode of presentation. “Not so fast,” he would say. “First the assumption; then the assertion.” He pronounced “first” with the Dutch accent which made it sound like “feerst” and somehow more emphatic. If, as it frequently happened, George's attempts at extracting clarity failed, his comment about the culprit speaker would invariably be: “He should have been spanked when he was young.”
I was on occasion “spanked” by the Master while I was still young enough to learn. If I am a reasonably clear lecturer, it is in no small measure due to these spankings. Steinhaus also deserves a {112} good deal of credit, for he taught me to assume that the audience is completely ignorant of the subject. “Nobody ever knows anything” is the way he put it. Between this assumption and the principle “feerst the assumption, then the assertion” one can, with practice, become a more than passable lecturer.
As I left the Laboratory in April 1945, I entered a new phase of my scientific life. It is a little difficult to sort out accurately the sequence of events that led to the change in my interests and preoccupations, but my experience in the Radiation Laboratory certainly played a decisive role. For one thing, I learned from George Uhlenbeck much about the theory of Brownian motion, especially of the work of Smoluchowski. My work (mainly in collaboration with Arnold Siegert) on noise in radar provided me with a firm intuitive grasp of stochastic processes and I began to perceive, albeit dimly, new worlds to conquer.
While I was still in Lwów I heard that Norbert Wiener had developed an approach to the theory of Brownian motion and once when I had to see Banach on some matter of business I found him reading a paper of Wiener's on this very subject. I had a look at some of Wiener's work on Brownian motion but found it extremely difficult to follow and there the matter rested.
Uhlenbeck's attitude to Wieners work was brutally pragmatic and it is summarized at the end of footnote 9 in his paper (written jointly with Ming Chen Wong) “On the Theory of Brownian Motion II”°:
The authors are aware of the fact that in the mathematical literature, especially in papers by N. Wiener, J. L. Doob and others [cf. for instance Doob (Annals of Mathematics 43, 351 {1942}) also for further references], the notion of a random (or stochastic) process has been defined in a much more refined way. This allows [us], for instance, to determine in certain cases the probability that the random function y(t) is of bounded variation or continuous or differentiable, etc. However it seems to us that these investigations have not helped in the solution of problems of direct physical interest and we will therefore not try to give an account of them.†
I prefer concrete things and I don't like to learn more about abstract stuff than I absolutely have to. The footnote represented a sort of papal dispensation relieving me from the need to learn {113} things I didn't particularly want to learn.
Fortunately, I did not take full advantage of the dispensation and I soon became intimately involved with Wiener's way of looking at Brownian motion. An important role in my “conversion” was played by William T. (Ted) Martin, who was the chairman of the mathematics department at Syracuse University. He and Robert H. Cameron, who was then at MIT, were engaged in an ambitious program of extending Wiener's early ideas.
Ted and I saw each other regularly and we often discussed his joint work with Cameron. I did not fully understand what they were after because of my ignorance of Wiener's work but one of their results caught my attention because of its close similarity to a result which Siegert and I had obtained in our studies of noise in receivers with so-called square-law rectifiers.
I quickly familiarized myself with the fundamentals of Wiener's theory (though at the time a number of subtleties still escaped me) and, applying the method of Siegert and myself, rederived the Cameron-Martin result. Wiener's theory was concerned with the x-component, x(t), of the displacement of a free Brownian particle. This is one of the simplest (and most fundamental) of all stochastic processes and because of its special nature the Cameron-Martin result led to a differential equation of a type known as the Sturm-Liouville equation. The Sturm-Liouville equations are ubiquitous in classical mathematical physics and their appearance in yet another context was unexpected and pleasing. There was clearly more to Wiener's theory than Uhlenbeck's footnote implied and I decided to look into the matter more thoroughly.
I began by solving a problem posed to me by Ted which he and Cameron had found intractable. Wiener's theory, though probabilistic in origin and nature, can be presented in a way which requires no familiarity with probabilistic concepts or terminology. To Bob and Ted, neither of whom was familiar with probability theory (few were in those days), Wiener's theory was a theory of measure and integration in the space of continuous functions, which, in fact, was the way in which Wiener first presented it.
At the peril of being ejected from the mathematical community for not adhering to standards of rigor and precision, I'll attempt a brief explanation of the mysterious words in the last sentence. I cannot, of course, hope for complete understanding on the part of {114} the reader but I may succeed in creating an illusion of it.
The problem of measure—that is, how to assign areas to plane figures or volumes to solids—goes back to the Greeks. It provided a strong motivation for the development of integral calculus and it culminated in the work of Henri Lebesgue (1875–1941) in the early days of our century.
Taking the Euclidian plane as an example, one can very roughly illustrate the procedure as follows: One starts with a collection of “elementary” figures (sets) whose measures (areas in our example) are postulated. In plane geometry the elementary figures are rectangles and their areas are taken to be, as every schoolchild knows, products of their bases and heights. A non-elementary figure is “approximated” in a certain well-defined sense by rectangles and this ultimately yields an unambiguous (unique) number which is taken to be the plane measure of the figure. I shudder as I reread what I have just written, for I have left out all the subtleties and difficulties, of which there are many. Still, I have told the truth and nothing but the truth.
It turns out that this scheme can be vastly generalized. Wiener, in fact, showed how to assign measures to large collections of subsets of the set of all possible paths a Brownian particle can follow, starting from some origin. In this he was guided by the Einstein-Smoluchowski theory which suggested what the elementary-figures (analogues of rectangles) ought to be and what measures (analogues of areas) are to be assigned to them. Once we have the measure, we can introduce the integral, following Lebesgue, and we end up with a kind of integral calculus over the set of Brownian paths.
I solved the problem posed to me by Ted Martin by reducing it to a problem in probability theory. I shall illustrate the method on a closely related problem which is more natural than the original one.
Suppose I toss an honest coin n times, the successive tosses being independent. Suppose furthermore that I win a dollar on heads and lose a dollar on tails. What is the distribution of the proportion of time during which I am ahead (in the limit as n approaches infinity)?
In other words, if Nn denotes the number of times during the {115} first n tosses that I am ahead, what is the limit as n approaches infinity of the probability that
|
Nn n |
< a (a ⩽ 1)? |
It turns out that the answer is equal to the (Wiener) measure of a certain set of Brownian paths—namely, the set of paths which spend less time than a above the t axis.
What is of interest and importance is that one can replace coin tossing by much more general games as long as the tosses are independent and the distribution of the gain in a single toss satisfies certain mild conditions (in particular, the mean of each gain must be zero and the so-called variance must be one).
What I have just said embodies a principle which became known as the invariance principle. A number of special cases have been proved by Erdös and myself but the first general setting was found by Monroe Donsker in his doctoral dissertation at the University of Minnesota. This was the beginning of a close friendship and scientific association which continues to this day.
The invariance principle is now textbook stuff. It has also been extended and generalized beyond recognition. A recent book on the subject is outside my comprehension—not that I have made a serious effort to penetrate it.
The invariance principle made it possible to prove a number of novel theorems in probability theory and to calculate a class of Wiener integrals, but its applicability was limited and I had a vague feeling that I was missing the crux of the matter. I was missing it, though without knowing it I came awfully close to what later became known as the Feynman-Kac formula, which was the crux.
In its various guises the F-K formula is ubiquitous throughout much of quantum physics on the one hand and probability theory on the other. It is probably safe to say that I am better and more widely known for being the K in the F-K formula than for anything else I have done during my scientific career.
But first a little history. At the end of the war Hans Bethe returned to Cornell from Los Alamos and brought with him a group of brilliant young experimental and theoretical physicists. Among {116} them was Richard Feynman, who, to no one's surprise, went on to become a leading physicist of our day. It must have been in the spring of 1947 that Feynman gave a talk at the Cornell Physics Colloquium based on some material from his 1942 Princeton Ph.D. dissertation, which had not yet been published.
A fundamental concept of quantum mechanics is a quantity called the propagator, and the standard way of finding it (in the non-relativistic case) is by solving the Schrodinger equation. Feynman found another way based on what became known as the Feynman path integral or “the sum over histories,” which Dyson alludes to in his book Disturbing the Universe.
During his lecture Feynman sketched the derivation of his formula and I was struck by the similarity of his steps to those I had encountered in my work. In a few days I had my version of the formula, although it took some time to complete a rigorous proof.
My formula connected solutions of certain differential equations closely related to the Schrodinger equation with Wiener integrals.
It is only fair to say that I had Wiener's shoulders to stand on. Feynman, as in everything else he has done, stood on his own, a trick of intellectual contortion that he alone is capable of.
I find Feynman's formula to be very beautiful. It connects the quantum mechanical propagator, which is a twentieth-century concept, with the classical mechanics of Newton and Lagrange in a uniquely compelling way.
My own formula is more prosaic but it, too, spans two centuries: the differential equation my formula solves is nineteenth-century, while the Wiener integral is a creation of the twentieth. It turned out that many properties of the solution which were difficult and even opaque from the nineteenth-century point of view became simple and transparent when looked upon from the point of view of the twentieth. The formula and its many close and distant relatives have proven to be useful and sometimes powerful tools in a variety of problems. I got tremendous mileage out of them and so did many others. Hardly a month passes without someone discovering yet another application. Remarkable and, of course, highly gratifying.
| {117} |
The invariance principle, limit theorems and calculations of Wiener integrals were not the only topics which occupied me in the immediate postwar period. There were actually many others but only two will be singled out here because both belong to statistical physics, which was becoming the center of my scientific interests.
The first was the Ehrenfest “dog-flea” model (the reason for this picturesque name will become clear). This model was first introduced in 1906 (though a more definitive version appeared in 1907°) by Paul and Tatiana Ehrenfest to clarify certain logical difficulties which beset Ludwig Boltzmann's attempts to derive the Second Law of Thermodynamics from the laws of mechanics.
Boltzmann's attempts, stretching over a period of nearly forty years, to persuade his opponents of the fundamental soundness of his work is one of the most interesting and dramatic chapters in the history of science. The debate, always vigorous and at times acrimonious, contributed to Boltzmann's bitterness.† His suicide in 1906 has been frequently (though probably erroneously) attributed to an accumulation of disappointments.
What were the issues that could engender such emotions and what was the role of the “dog-flea” model?
The following example illustrates the pertinent points. Suppose {118} that two isolated pieces of matter (bodies) of unequal temperatures are brought in thermal contact (i.e., allowed to exchange heat). Then the Second Law of Thermodynamics decrees that the heat will flow unidirectionally from the hotter to the colder body, and that at no time can the flow be reversed. “At no time” meant never, and the Second Law took “never” with utmost seriousness.
Now, let us assume the atomistic point of view; that is, consider matter as composed of particles acting upon each other with forces and subject to the laws of mechanics. Can one reconcile this mechanistic view with the uncompromising never of the Second Law?
From the point of view of logic the answer is a resounding no. For the laws of mechanics are time reversible—i.e., two observers using the same instruments, except for clocks running in opposite directions, will give identical descriptions of mechanistic phenomena, while the Second Law has “an arrow of time” built into it and one of the above observers would report a flow of heat from the colder to the hotter body, which is a strict taboo.
The dilemma was thus clear. Either the Second Law or the atomistic theory had to go. But Boltzmann was not ready to accept such a drastic resolution and he proposed to save the day by interpreting the Second Law statistically. Maxwell had already suggested that the Second Law be so interpreted (the famed Maxwell's demon was invented to emphasize this point) but this departure from thermodynamics did not create a detectable stir— possibly because the suggestion was contained in a letter to Maxwell's friend Peter Guthrie Taite and was not widely known. Boltzmann was in the middle of an open and heated polemic with opponents who refused to concede that even the statistical interpretation could cure the underlying incompatibility between the approach to equilibrium (equalization of temperatures in our example) and time reversal.
The Ehrenfest model made it clear that the incompatibility was illusory. Here is Ehrenfest's own description of the model:
Suppose we have N balls (one hundred for example). They are numbered consecutively from 1 to N so that they can be individually distinguished. They are at some moment distributed between two urns so that urn A contains P balls (90 for example) and urn B has Q = N – P balls (therefore 10). But it is not known which individual balls are located in A and which in B. We also have, in a bag, N lottery tickets numbered from 1 to N. {119} Every ten seconds a ticket is drawn, its number is announced, it is returned to the bag and the tickets are thoroughly mixed. Then another is chosen, announced, etc. Every time a number is announced, the ball that bears this number jumps out of the urn in which it happens to be located and into the other urn, and it stays there until its number is drawn once again. Notice: it is always more likely that the ball just summoned will be found in the fuller urn than in the emptier one. As long, therefore, as urn A is still much fuller than urn B, most of the subsequent lottery drawings will produce an emptying out of urn A into urn B and only rarely will urn A receive a ball from urn B.°
The reader will now understand the name “dog-flea” model. The urns are the dogs and the balls are the fleas. The latter prefer less crowded surroundings and choose to jump from the more infested dog onto the less infested one.
Let us now see how the model resolves the conflict between the approach to equilibrium and time reversal.
First, as long as there are many more balls in urn A (e.g., 80) one will observe the emptying of A. One can calculate easily the average excess of the number of balls in A over the equilibrium value 50 after s drawings, obtaining
30(1 – |
1 50 |
)s |
which is of the same exponential form as the actual law of cooling. On the other hand, if at some instant the number of balls in A is 80, then, as can be calculated, the probability that at the previous instant it was 79 is 80/100, which is exactly the same as the probability that it will be 79 at the next instant. If this seems paradoxical, consider the extreme case of all 100 balls in box A. It is a certainty that in the previous instant there were 99 balls in A and it is just as certain that there will be 99 balls in A in the subsequent instant. All this is a clear indication of the symmetry between the past and the future, and the dilemma is thus resolved. The price one pays for introducing the statistical element is that the “never” of the Second Law becomes “well, hardly ever.”
The model played an important part in the history of statistical physics. When Ehrenfest gave a lecture on the model in Göttingen, he caught the attention of the great Felix Klein, who invited the {120} young and barely known Paul Ehrenfest to write an article for the prestigious Encyclopedia of the Mathematical Sciences (of which Klein was editor-in-chief) on conceptual foundations of statistical mechanics. The article, which appeared in 1911, is an all-time classic and it attracted the attention of H. A. Lorentz, who a year later recommended Ehrenfest as his successor to the chair of theoretical physics in Leiden.
George Uhlenbeck was a student of Ehrenfest and from his student days he had been interested in the “dog-flea” model. Ehrenfest derived only the most elementary properties of his model. These were sufficient to vindicate Boltzmann's views, at least as far as their logical consistency was concerned, but a complete mathematical discussion of the model was lacking. In particular, there was no formula for P(m/n; s), the probability that if one starts with m balls in urn A there will be n balls in this urn after s drawings. Uhlenbeck mentioned this problem to me and urged me to try to solve it. I was already familiar with the model since it was described in one of the chapters in Clemens Schaefer's textbook, which I had read for my exam in thermodynamics, but I hadn't appreciated its significance. Steinhaus and I had actually tried our hands at the model but hadn't got very far. Now I was ready to try again.
George, who keeps wonderfully orderly notebooks, loaned me the one which contained his abortive attempt to soke the problem. It ended with an intractable differential equation which I checked. but I was unable to proceed any further.
In the fall of 1946 George asked for his notebook back. I mailed it to him and this proved to be an unexpected blessing. One evening I decided to take one more look at the problem.
Without going into technicalities, let me say that there are two seemingly equivalent ways of seeking the solution.° George tried one and ran into a cul-de-sac. Not having his notes to guide me, I accidentally chose the second and it worked. In a couple of hours I had the complete solution. Sheer serendipity!
Finding the solution of the Ehrenfest model was a source of great pleasure in spite of the accidental nature of the discovery and the relatively minor scientific significance of the result. It was a {121} footnote to our understanding of the statistical nature of the Second Law, but to be even a footnote to so great and so dramatic a development was immensely satisfying.
Actually, my solution generated considerable further work and the “dog-flea” model keeps cropping up from time to time in unexpected contexts. I published my solution in an expository paper, “Random Walk and the Theory of Brownian Motion,” which won me my first Chauvenet Prize of the Mathematical Association of America for “a noteworthy exposition.” It was in 1949 and the cash award was fifty dollars. Twenty years later I received a second Chauvenet Prize for a paper entitled “Can One Hear the Shape of a Drum?”° The magnitude of the inflation in the intervening years is reflected in the size of the prize, which this time was five hundred dollars!
As if all this were not enough, I became involved with the problem of phase transitions, an involvement which to this day continues with unabated passion.
Phase transitions are abrupt, discontinuous changes in the state of matter caused by gradual changes of physical parameters. Melting is a phase transition and so is the liquefaction of a gas. In the latter case, when a gas is cooled below a certain temperature (known as the critical temperature) and subjected to a gradually increasing pressure, it becomes a liquid.
Less well known but equally dramatic and puzzling are phase transitions associated with magnetism. At room temperature an ordinary piece of iron shows no magnetic properties. If put in an external magnetic field, it will become magnetized but it will lose this property as the external field is removed. If, however, the same piece of iron is cooled below a certain temperature (known as the Curie temperature after Pierre Curie, who discovered the phenomenon), then it will retain the magnetization even after the field is removed! The field gets “frozen in” as it were.
To explain phase transitions from “first principles” on the basis of statistical mechanics is still a largely unsolved problem. It continues to fascinate physicists and since it can be stated in purely mathematical terms it has also attracted the attention of mathematicians.
Because of the inherent complexity of matter one is compelled {122} to work with simplified models which, one hopes, capture the qualitative and even some quantitative features of their counterparts in nature.
The most celebrated class of models proposed for the purpose of understanding magnetic phase transitions is the Ising models. Introduced in 1925 by Ernst Ising, they are still vigorously studied today and the literature on them is staggering.
The models envisage magnetic material as a lattice of points with a little magnet situated at each lattice point. In the Ising picture each of the little magnets can be described by a symbol σ which can be either +1 or —1. With each configuration of σ's one associates an expression called the interaction energy, and once this is given, the rules of statistical mechanics tell us how to calculate various pertinent quantities. These quantities should then be studied in the limit of infinitely large lattices.
The lattices can be of any dimensionality but the most realistic case is that of three dimensions. The one-dimensional case is easy but it exhibits no phase transition. The three-dimensional case does exhibit a phase transition but exact calculation of its properties has proved hopelessly difficult. The two-dimensional case for so-called nearest-neighbor interactions was solved explicitly by Lars Onsager in 1944. Onsager's solution, a veritable tour de force of mathematical ingenuity and inventiveness, uncovered a number of surprising features and started a series of investigations which continue to this day.
The solution was difficult to understand and George Uhlenbeck urged me to try to simplify it. “Make it human” was the way he put it. Well, I tried and soon it became clear that it was a most difficult assignment. I then reached for a time-honored tactic used by mathematicians: if you cannot solve the real problem, change it into one you can solve. Instead of the σ's being plus or minus ones, I took them to be Gaussian (i.e., distributed continuously according to the normal distribution). With this modification the problem became solvable and the answer even looked a little bit like Onsager's. But instead of exhibiting a phase transition, the model ceased to make sense for low enough temperatures, leading to infinite answers which were, of course, unacceptable on physical grounds.
I then tried yet another modification and allowed the σ's to {123} assume any values subject only to the constraint that the sum of the squares of the σ's over the points of the lattice = the number of the points of the lattice.
The motivation for this condition is very simple. Since in the Ising case σ = ±1, we have σ2 = 1 and hence automatically the sum of the squares of the σ2 over the points of the lattice is equal to the number of the points of the lattice.
Now one could be sure that the answers would be finite b'it the calculations, even after a promising first reduction, looked prohibitively difficult. I remember asking Feynman for help. He succeeded in solving the problem in the one-dimensional case but the more interesting higher-dimensional cases remained beyond reach.
Then in December 1947 George Uhlenbeck invited me to Ann Arbor to give a lecture on the subject. It was an evening lecture and the dinner which preceded it featured a nearly lethal mixture of Dutch gin and several wines. Details are therefore hazy in my mind but I do remember that Ted Berlin, who was in the audience, questioned me closely after the lecture about a number of details. Ted, although he received his doctorate in chemistry, had fallen under George's influence and had become a physicist. I had met him a number of times on my visits to Ann Arbor and we had had many discussions from which I profited greatly. I was glad that he had become interested in the model but was completely unprepared for what was to come. In a couple of weeks—it couldn't have been much longer—I got a letter from Ted outlining the complete solution in one, two and three dimensions!
To say that I was impressed would be understating it. I was stunned and elated. The method Ted used, called the method of steepest descent, is a powerful but delicate instrument. Mathematicians shy away from using it, for in general it is difficult to justify rigorously. Physicists are less squeamish and more optimistic. They also have an intuition which makes it possible for them to spot wrong answers and reach for the right ones. They believe with Einstein that “The Lord is subtle but He is not malicious.” In any case, the result was that in two dimensions there is no phase transition but there is one in three, and while the model has many non-physical features it is qualitatively quite realistic—or, to use a favorite expression of Norbert Wiener, “it is not manifestly absurd.” The model, known as the spherical model, generated a tremendous {124} literature and the flood has yet to become a trickle. Considering the ad hoc manner in which it was conceived, it has shown remarkable vitality.
I spent the academic year 1951–1952, my sabbatical, at the Institute for Advanced Study at Princeton.
The Institute was founded in 1930 to provide a domicile for a group of the most distinguished mathematicians and physicists in the world (later a group of historians of equal distinction was added) and to provide the opportunity for brilliant young post-doctoral fellows to spend a year or two doing research free from financial and other worries. The Institute also provided supplemental stipends to senior faculty members from all over America who chose to spend sabbatical years there and an illustrious company of foreign visitors was always in residence.
The original faculty, which included Einstein, Weyl, von Neumann and Gbdel, to mention just a few of the names best known to the general public, soon made the new Institute the world center of mathematics and to this day it maintains a commanding leadership.
Abraham Flexner (1866–1959) was the first director of the Institute and with unerring instinct he chose to make the young institution a center of post-doctoral education. That the United States is today a major mathematical force is in no small measure due to Flexner's vision.
At the end of the Second World War, J. Robert Oppenheimer (1904–1967) became the director and he attracted a brilliant group of young physicists, two of whom went on to win the Nobel Prize.°
Oppenheimer's tenure was not a happy one, not only because of the personal tragedy caused by the infamous hearings. There was, for one, a growing friction between the director and the mathematicians over matters of priorities. I believe that the chief cause was that the original raison d'etre for the Institute was gradually being lost. It was still a wonderful place to be but in the meantime American mathematics and physics had matured and there were many good places to spend a post-doctoral year. The uniqueness was gone as the original members retired or died and their successors, though absolutely first-rate, were not quite of the caliber of the founding fathers.
My year at the Institute was pleasant and productive. It was a {125} transition period between the “old” and the “new” Institute but it was still more like the old. The only source of friction, as far as I could ascertain from general gossip, was the opposition of some mathematicians to von Neumann's famous project—building a digital computer. Sounds silly in retrospect.
Getting to know von Neumann better was one of the delights of my stay in Princeton. Apart from being one of the greatest mathematicians of our century, he was a wonderful companion. Endowed with an incomparable sense of humor, he was full of stories and jokes, some of which Stan Ulam fortunately preserved for posterity in his Adventures of a Mathematician.
At the Institute I met John C. Ward, one of the most versatile and original theoretical physicists of his generation. I had an idea of how to simplify Onsager's solution of the Ising model and it turned out that John had the same idea. We joined forces and, owing to a crucial observation of John's, we succeeded in rederiving Onsager's result. Our success was in large measure due to knowing the answer; we were, in fact, guided by this knowledge. But our solution turned out to be incomplete, for we had not taken into account a large class of terms. These terms had to cancel since already without them the answer agreed with that of Onsager, but the reason for the cancellation turned out to be quite subtle and it took several years and the efforts of several people before the gap in the derivation was filled. Even Feynman got into the act. He attended two lectures I gave at Cal Tech in November 1952 and came up with the clearest and sharpest formulation of what was needed to fill the gap. The only time I have ever seen Feynman take notes was during these two lectures. Usually, he is miles ahead of the speaker but following combinatorial arguments is difficult for all mortals.
During my year in Princeton I also met for the first time C. N. Yang and T. D. Lee. They were engaged in writing two papers on the general theory of phase transitions which justly became classics on the subject. I kibitzed them a little and learned a lot.
Back in Ithaca, life went on as before. I was actually glad to go back to the more organized life which academic chores such as teaching and serving on committees provide. Being free from all duties can be quite disconcerting. In research, ideas don't come with great frequency and there are long quiescent periods between {126} bursts of feverish activity. During such periods it is good to have an excuse for not being productive. In a university environment, excuses abound. The students are pestering you, the dean keeps calling, there are too many committee meetings, etc., etc., etc. But at a place like the Institute for Advanced Study all such excuses are removed and if no startling revelation is forthcoming one tends to get depressed. I was rather fortunate that working with John Ward and looking over the shoulders of Yang and Lee kept me from having morbid thoughts about the waning of my mathematical powers.
I like teaching and in general I prefer to teach undergraduate courses. Of the more advanced courses, I regularly taught Mathematical Methods of Physics, which was required of all first-year graduate students of physics. The course was also open to the better undergraduates and many availed themselves of the opportunity. One year the course included Steve Weinberg and Shelly Glashow, who went on to share the 1979 Nobel Prize in physics with Abdul Salam. They were both seniors at the time.
During my years at Cornell I “spawned” seventeen Ph.D.s. Two of them have been recently elected to the National Academy of Sciences—a pretty good average. Most graduate students in science and engineering picked mathematics as one of two required “minor” subjects. I was such a popular choice for membership on doctoral committees that one year I ended up serving on sixty-five of them! Served me right for not keeping count.
There were innumerable stories about me as an examiner, most of them pure invention. The most famous one happens to be true and it is perhaps worth recording. The candidate shall remain anonymous. He was not terribly good—in mathematics at least. After he had failed to answer a couple of questions, I asked him a really simple one, which was to describe the behavior of the function 1/z in the complex plane. “The function is analytic, sir, in the whole plane except at z = 0, where it has a singularity,” he answered and it was perfectly correct. “What is the singularity called?” I continued. The student stopped in his tracks. “Look at me,” I said. “What am I?” His face lit up. “A simple Pole, sir,” which is in fact the correct answer.
American students are not used to oral exams and the first experience can be traumatic. I remember one case of a student {127} whom I knew quite well and who was quite good. After the first question elicited only a dull stare into infinity, it became clear that continuing the examination would be a punishment. In an attempt to snap the poor fellow out of his catatonic state, I asked, “What is your name?” “My name, sir?” he replied. “What is my name?” And then it hit him how ludicrous it all was. I cannot say that he recovered completely but at least a semblance of an intelligent conversation became possible.
For the academic year 1955–1956 I was awarded a research grant and we decided to spend the year abroad. We wanted the children to learn French, so we chose Geneva because of its central location and because it was difficult to find suitable housing in Paris.
Foreigners who come to Switzerland are expected to send their children to private schools but this presented a problem for us. The famed International School would not at that time enroll students in its French Division unless they were already proficient in French. To put our children in an English-speaking environment would have defeated our purpose, so we decided on public school. This was not kindly received. Finally, after our landlord, who was a high official at the UN, applied a little pressure in the right places, the children were admitted to a public school within easy walking distance from where we lived.
This turned out to be something of a mixed blessing. Having students who did not speak the language puts an added strain on overworked teachers and at no time were we allowed to forget that our children were a burden to them. To handle problems caused by having in class a child who in a sense is a mute requires imagination and compassion. It was, unfortunately, precisely those qualities which the Swiss teachers we came in contact with seemed to lack completely. Michaels teacher had enough sense to leave him alone for three months until by some inexplicable process he “soaked up” the language. But the succession of women to whose tender mercies we entrusted the eight-year-old Deborah were individually and collectively a menace to youthful humanity. Time after time I had to compose, in my limited French, letters invariably addressed to “Chere Madame” (though the “madames” changed during the year) trying, mostly without success, to explain that what was being done to my child was cruel, unusual and totally undeserved punishment. {128}
Tolerance for misbehavior in this school was remarkable. The “crime” was to make an error—be it in giving a wrong answer to a question in arithmetic or, worse yet, to blot a copy book with ink. The children were required to use dip pens, something Deborah had barely seen in her life. Seeing the children around her having their hair and ears pulled as a punishment for minor blots kept Deborah, who was drowning in ink, in a constant state of terror for them and for herself. She entreated us to cut her hair so that there would be no way to get a hold on it. In fairness to all, she never was actually physically punished for this. It was simply added to the growing list of ineptitudes which kept her in a continued state of disfavor and disgrace. Reluctantly deciding that this project had been a failure, we offered to withdraw her from school but she insisted on sticking it out and, to her credit, she did.
Michael fared much better. He was, of course, four years older, and his reading and writing in one language were firmly set before he was forced to deal with another. He learned French easily and to this day he speaks it well with, of course, a Geneva accent which is quite musical and pleasant. That year marked the beginning of the interest in languages which led to his becoming a professional linguist.
The Swiss experience, where a departure from routine was treated as a damned nuisance, was in sharp contrast to an experience we had shortly after returning to Ithaca in the summer of 1956.
I had brought with me from Europe to Cornell two graduate students who wanted to work with me. One was from Belgium. His father was killed by the Germans and his widowed mother and younger brother lived in Brussels. Tragically and unexpectedly, his mother died shortly after he, the older son, reached Ithaca, leaving him as the sole guardian of his young brother. We obtained the necessary visa for the boy to come to the United States and arranged for him to be admitted to Ithaca High School. He arrived just in time for the fall registration and I went with him and his brother to help with the formalities.
We were assigned to a guidance counselor (who I learned later had been one of Kitty's high-school English teachers some years before) and we joined the line of waiting registrants. By the time our turn came it was almost the end of the day and I am sure that the counselor was anxious to get home, kick off her shoes and relax {129} with a drink. Instead she was confronted with a bereaved, bewildered boy who had just come to a strange country and spoke not a word of English. A damned nuisance? Not at all. The complex problems of fitting the young man into the system made her day. It was a challenge after hour after hour of making out and approving routine schedules of ordinary students. “Let's see,” she said, “he is ready for third-year Latin, but I'll put him in the second year to make it easy for him and give him more time to learn English.” And so on, until a schedule was completed. “Be sure to come and see me if things don't work out” were her parting words. They did work out. From that day on I have told this story whenever the American educational system,is criticized as being inferior to its European (and especially Swiss) counterpart. Perhaps the comparison is not entirely fair, as the Ithaca High School was one of the best, if not the best, in the state. But I am convinced that the attitude shown there reflected a general one in the United States—that children are human beings and are to be dealt with as such.
A final comment on the Swiss education of our children: In Michael's class the students had to study world geography. The textbook, unsurprisingly entitled Geographie Mondiale, reflected a rather unexpected view of the world. Half the book was on “La Republique et le Canton de Geneve”; half of the remaining half was on “La Suisse” and what was left covered the rest of the world. The United States was allotted about two pages, which, like everything else, had to be memorized. Now, dear reader, would you not think that, having a native in the classroom, it would occur to the teacher to ask about life in that strange and distant land? Especially since the aforementioned native spoke fluent French by that time and could correct some of the wrong and obsolete things that the textbook was full of? But, oh, no. The principle that children should be seen and not heard could not be violated.
When we returned to Ithaca the Superintendent of Public Schools, who happened to be our neighbor, was teaching a Cornell Summer School course in comparative educational systems. Being aware that Michael had just been subjected to the Swiss system, he extended an invitation to him to address his class of teachers. Michael began his remarks by saying that the most striking difference between the American and the Swiss systems is that in Switzerland a twelve-year-old boy would never be invited to address a group of {130} teachers. To the Swiss it was unthinkable that one can learn from children. And yet the great psychologist Jean Piaget, who championed the idea that the most original philosophers are children, was Swiss and lived and taught in Geneva.
Scientifically, my year in Geneva was not particularly memorable. I finished a few things and began a few. Mainly, I traveled and lectured. I gave a cycle of lectures in Brussels and another cycle in Paris, both, God help me, in French. I also gave a large number of single lectures all over Europe. I made many friends and I discovered that while Europe was awfully nice, I could live only in America.
The only new thing which was conceived and published while I was abroad was a short note, “Some Remarks on the Use of Probability in Classical Statistical Mechanics.” It featured a model (sometimes called “Kac's ring model”) which is my second footnote to our understanding of the statistical nature of the Second Law. It is a nice footnote even if it is immodest of me to say so.
| {117} |
Late in the fall of 1959 I received a letter from George Uhlenbeck. The gist of it was that Sam Goudsmit had approached him, on behalf of Detlev W. Bronk, to inquire whether he (George), Ted Berlin and I would be interested in joining the faculty of the Rockefeller Institute in New York. If our reactions were favorable, detailed negotiations could begin. George sounded skeptical (“It seems a little crazy,” he wrote) but dutifully passed on Sam's inquiry to Ted and me. Ted responded with immediate enthusiasm. As a professor of physics at the Johns Hopkins University he knew Bronk, who had been president of the school from 1948 to 1953. The two men liked and admired each other.
Bronk left Hopkins in 1953 to assume the presidency of the Rockefeller Institute for Medical Research and was given a broad mandate by the trustees to transform the institution into a graduate university in science. Bringing in a group in mathematics and physics was high on Bronk's list of priorities and he sought advice from Sam Goudsmit, who was a longtime friend.
Founded in 1901 by John D. Rockefeller, Sr., the Rockefeller Institute for Medical Research was one of the most famous of its kind in the world. Some of the great discoveries in biology and medicine were made within its walls, including the first cancer-causing virus (by Peyton Rous), the M, N and P blood factors (by Karl Landsteiner, the discoverer of blood groups) and the proof that DNA is the carrier of genetic information (by Oswald Avery, Colin MacLeod and Maclyn MacCarty). At the height of its fame in {132} the late forties, the Institute stood at a crossroads, owing in part to the impending retirement of its director, the distinguished neuro-physiologist Herbert Gasser.
Bronk, who was a member of the Institute's Board of Scientific Directors, was appointed chairman of the special subcommittee to seek Gasser's successor and to propose new policies and directions. In the end Bronk was persuaded to accept the presidency of the Institute and to implement the recommendations of his subcommittee that the Institute become a graduate university of science.
Thus in 1953 the second era in the history of the Rockefeller Institute began. The first students (or Graduate Fellows, as they were called) came in 1955 and the first degrees were awarded in 1959. In 1965 the name was changed to the Rockefeller University.
I had heard, of course, of the Rockefeller Institute for Medical Research and I think I knew that it was the model for the McGurk Institute in Sinclair Lewis's Arrowsmith. But that was about all I knew and I was not aware until I received George's letter that the Institute was in the process of undergoing a profound change.
My attitude toward Sam's suggestion was about halfway between George's skepticism and Ted's enthusiasm. I had just declined an attractive offer from another institution and while offers are flattering they are also unsettling. To go through the ritual of the academic dance so soon again was not a welcome prospect. Yet the opportunity to participate in a novel experiment with two of my closest friends and scientific associates was obviously tempting.
With Sam acting as intermediary, there began a somewhat protracted three-pronged negotiation. The result was that the three of us accepted an offer to join the faculty of the Rockefeller Institute (the “for Medical Research” was dropped to underscore the change in the nature of the institution). George and Ted moved to New York in January of 1961 and I followed in July of the same year.
The first year was idyllic. We were a part of an exciting, lively scientific enterprise and no one could have wished for better conditions in which to do research and teach. Whatever doubts we may have had before making the move vanished in the glow which surrounded us. But in November 1962 tragedy struck and all but shattered our newfound joy. Returning to New York on a train from Washington, Ted, the youngest member of our group, was seized by a heart attack. Feeling ill but apparently not realizing {133} what was wrong, he left the train in Baltimore and managed to get to a hotel room, where he phoned friends for help. He died before they could reach him.
Our sense of personal as well as professional loss was overwhelming. For a while we were literally paralyzed, but practicalities had to be faced. Ted had brought with him from Johns Hopkins a gifted post-doctoral fellow and he had been involved in a number of tutorials. Irreplaceable as Ted was, finding a successor was urgent. We were lucky to have with us as a short-term visitor E. D. G. (Eddie) Cohen from the University of Amsterdam. Eddie was a natural successor to Ted. Three years earlier he had spent six months with George at the University of Michigan and another six months with Ted at Johns Hopkins. His scientific interests meshed perfectly with ours and it took only a few minutes to persuade Det to offer him the position. Several months elapsed before the immigration formalities could be ironed out but eventually the problems were dealt with successfully and he arrived in the United States with his family to begin a new life. Eddie is still at the Rockefeller doing excellent work.
Soon a small but excellent group in high-energy theoretical physics was added under the leadership of Abraham Pais, a disciple of George's and yet another Dutchman. Then came a distinguished group in behavioral sciences and another in philosophy. In mathematics we expanded by appointing the renowned logician Hao Wong from Harvard and two young rising stars, Henry P. McKean and Gian-Carlo Rota from MIT. We had sufficient funds to bring visitors from all over the world and we provided an intellectual domicile for the great Hans Rademacher after his retirement from the University of Pennsylvania and to that master of ars combinatoria John Riordan after he retired from the Bell Telephone Laboratories. In short, things were humming.
No one was more pleased by the growth and expansion of the institution than its president. Det's long-cherished dream of a graduate university which would also be “a community of scientific scholars” was coming true. A unique experiment in the history of American education was on its way to becoming a spectacular success.
Detlev Wolf Bronk, the man with the dream, was one of the most remarkable contemporary figures in America. That he is hardly {134} known to the general public is a sad indication that more than one hundred and twenty years after Andrew D. White wrote his letter to Gerit Smith we still have not succeeded in turning “the spirit of mercantile morality.”
Bronk's long and distinguished service as president of the National Research Council and the National Academy of Sciences, his chairmanship of the National Science Board and his membership (under three presidents) in the President's Science Advisory Committee (PSAC) are sufficient proof of his deep dedication to the concept of science in the service of the nation and of mankind.
Most important, there was Bronk's deep conviction that science is a great adventure of the human mind, that it is indivisible and that it is a part of the humanistic tradition on which our civilization rests.
In recommending to the trustees the appointment of Ludwig Edelstein in 1961 as professor at the Institute, Bronk stated: “It is only of incidental significance that he is a distinguished historian of biology and medicine. It is of deep significance that he is a great humanist; as a community of scientists we have suffered too long from the lack of association with scholars such as he who is versed in the origins of modern science and the influence of science on ideas and habits of man.” One must go back to Andrew D. White to find a university president of such eloquence.
I liked Det from the moment I met him. He had great charm and at the age of almost sixty-five there was a certain boyishness about him which Kitty and I found singularly engaging. He once surprised Kitty enormously by remarking to her that he was usually ill at ease with young people but that he enjoyed our children because he found them easy to talk to and comfortable to be with. This from a man whose life was devoted to the education of young men and women!
He could be as hard as nails. His temper was legendary and he was not above throwing a tantrum. He made me angry only once. It was early in my Rockefeller days and I don't remember what the whole thing was about except that I had heard, secondhand, that Det criticized—unjustly, I thought—something that I had done or, more likely, failed to do. I was indignant. Since Det was temporarily out of town (as he often was) I went to Frank Brink and asked him to convey to Det my intention of resigning. A couple of hours later {135} I got a phone call from Mabel Bright, the great lady who, as Det's administrative assistant, managed with wit and tact the complicated activities of her mercurial and ubiquitous boss. “Dr. Bronk is back. Could you have a drink with him in the bar at 5:30 today?” she asked Still fuming, I accepted. I was a minute or two late and Det had already ordered his customary Manhattan. My equally customary Martini came almost at once and before we had taken two sips I was charmed out of my wrath.
Truly indicative of the nature of our relationship was the following episode. Since Det abhorred the departmental structure of universities, he kept the old Institute structure in which, with a few exceptions, each professor was the head of a laboratory, which was the administrative unit. Thus each professor negotiated the budget of his laboratory directly with the president. Once, after the budgets were all in and approved, I went to Det with a request for an additional appointment. He approved at once. Somewhat startled by the speed with which the matter had been handled, I asked, “What would you do if I asked for something quite unreasonable?” “But you wouldn't,” he replied and, to the best of my knowledge, I never did.
Det's educational ideas were strongly influenced by two men— Daniel Coit Gilman (1831–1908) and Abraham Flexner. Gilman was the first president of Johns Hopkins University and he had tried to make it a purely graduate university. Although it soon became necessary to add an undergraduate component to the institution, graduate education and research emerged as the main objectives of the new university. The example of Hopkins was soon followed, in part at least, by many leading universities which, albeit belatedly, recognized the central role of graduate education and research.
Abraham Flexner (whose older brother Simon was the first director of the Rockefeller Institute for Medical Research) was the first president of the Institute for Advanced Study and a longtime critic of American medical education and of higher education in general. To him, much of the undergraduate education was wasteful and inefficient, especially for the gifted. He admired Gilman, espoused his ideas and wrote a biography of him.°
As president of Hopkins, Det went back to Gilman's ideas and {136} was guided by them. In his last annual Hopkins report he wrote that he believed that “research, as the basis of thought and as a prelude to action, was essential to modern life” and he wanted “little emphasis on pedestrian instruction” and no “distinction between faculty, graduate and undergraduate students.”
In the same report he states: “The growth of knowledge and the increase of information regarding man and nature require specialisation. But understanding requires comprehension of many related fields of learning. Unless creative scholars and students learn in universities which stress the unity of knowledge and scholarly endeavor, universities fail to provide the intellectual leadership sorely needed in our complex civilization.”
At the Rockefeller, Det finally had an unrestrained opportunity to build his ideal university. Though the following excerpt is from the 1967–1968 catalogue, it describes perfectly the university as I found it in 1961.
The purpose of this University is to further natural science and its applications for the improvement of human welfare.
The University is not an aggregate of departments dealing with specialized fields of science. It is a community of scientific scholars who are free to follow their interests in any field of scholarship.
The students are few, and the faculty are many. This enables close association between the two, they live and work as junior and senior colleagues.
Students must be capable of self-directed study. Although main courses are offered, teaching is done primarily in seminars, in tutorial conferences and in faculty research laboratories. There is thus considerable freedom for the active process of independent learning.
It is clear that the students would have to be quite unusual to survive and grow in such an environment. It may seem strange, but unrestrained freedom can be a heavy burden and lack of pressure the worst pressure of all. It is therefore not surprising that there were failures, some even tragic, but the overall record was that of spectacular success. Of the one hundred and twenty-five students who received their doctorates from Det's hands, two went on to win Nobel Prizes, many adorn the membership of the National Academy of Sciences and almost all occupy distinguished positions in leading universities and medical schools.
In the early years Det depended on his wide acquaintanceship {137} in academic circles to bring promising candidates to his attention. To the last day of his presidency he interviewed personally every candidate for admission. He undertook this task with utmost seriousness and I know of several occasions when he left meetings of important government committees in Washington to catch a shuttle to New York to meet with a prospective student.
One of the requirements for a Ph.D. was a public presentation, in a popular form, of the candidate's doctoral dissertation; to the best of my knowledge, Det attended every one. With his manifold time-consuming obligations in Washington and elsewhere, the affairs of the University were uppermost on his mind. During the years I knew him the University was his life. It was as if he had staked his immortality on the success of his grand experiment.
Eventually, the “mercantile forces” dimmed the luster and thwarted the dream, but the “Bronkian era” is still cherished in the memory of those who were a part of it. On May 29, 1968, at Det's retirement dinner, Gerald M. Edelman, one of the members of the second graduating class (1960) and a future Nobelist (1972), paid tribute to Det. A paragraph from this moving speech is worth recording.
Let me say at the outset what I think is original, precious and remarkable about this University as Dr. Bronk has conceived it. It is best said, I think, by borrowing a phrase from a famous historical work, The Civilization of the Renaissance in Italy by Jakob Burekhardt. Part One of that book speaks of the State as a work of art. In the Renaissance this was a new fact in history—the State as the outcome of reflections and calculation, the State as a work of art. In the present age of overwhelming bureaucracy and specialism in multiversities, it is the idea of the university as a work of art which Dr. Bronk has espoused and reinvented.
When I left Cornell to join the Rockefeller Institute many of my friends were frankly puzzled. New York City has two major mathematics departments, one at Columbia and one at New York University (The Courant Institute of Mathematical Sciences). There are two more within fifty miles, at Princeton and at Yale. Why another? Furthermore, our size precluded us from offering the variety of courses and seminars which are required these days for mathematics Ph.Ds. But the proliferation of specialized courses tended to isolate mathematics from other sciences at other institutions. {138} At the Rockefeller we had an opportunity to bring mathematics back into its traditional partnership with physics and perhaps even to open lines of communication with biology. One could even dream of educating “bilingual” scientists, as fluent in the language of mathematics and the exact sciences as in the quite different language of biology, in which the rules are few and the exceptions many.
When I first visited the Rockefeller during our negotiations I was impressed, as are all first-time visitors, by the physical beauty of the campus. It is an oasis in the city with superbly landscaped grounds transversed with marble-chip walks; the Alexandrian school transplanted to our century. “How exciting.” I thought, in a romantic glow, “to once again, after all these centuries, teach while walking in the gardens!” Well, it didn't last. Romantic dreams seldom do.
First my younger colleagues, Rota and McKean, found the smallness uncongenial. Not being as strongly tied to physics as I was, they felt isolated. They left for larger institutions where there were more mathematicians to talk to or to stay away from. We tried to compensate for these losses by making a major appointment in mathematical physics in the person of James A. Glim and by attracting from Harvard Joel Cohen, who is one of the truly “bilingual” scientists and a Renaissance man to boot. But the prospects for even modest growth were, for all intents and purposes, nil.
All this happened after Det's retirement. His successor, Frederick Seitz, a noted theoretical physicist, was at the time of his appointment president of the National Academy of Sciences just as Det had been when he succeeded Herbert Gasser. But the times were different and although Fred committed the University to a new program in experimental high-energy physics and was very helpful in keeping mathematics afloat, the rising deficits soon forced him to institute drastic economies.
For three years (1971–1974) I served as the faculty representative on the Board of Trustees and I can vouch for the painful reality of the deficits. Skyrocketing oil prices alone added almost a million dollars to the heating bill. The administration judged the situation to be critical and called for Draconian measures. {139}
The rapidity with which we went from riches to rags was unsettling and the morale of the faculty plummeted. Faced with a shrinking pie, it was only natural for some of the faculty to put at least part of the blame on Det's so-called “extravagance” in expanding the institution by adding “peripheral” areas of research and graduate study. The community of scientific scholars began to show signs of strain.
Fred tried to maintain the integrity of Det's idea. When the first unmistakable signs of an impending financial crisis appeared in 1970, he received a letter from one of the most distinguished members of the faculty, a world-renowned biochemist, who argued that perhaps contracting to the old bio-medical core might help solve the financial problem. Fred sent me a copy of this letter. Soon after, I visited a leading West Coast institution, where I was invited to join the faculty. I was greatly tempted by this invitation, as my faith in the future of the Rockefeller had been somewhat shaken by my colleagues letter. I went to Fred to discuss the matter, prepared to resign. Somewhat to my surprise, Fred used every argument at his disposal to persuade me to stay. He minimized the significance of the letter and reassured me in a number of ways. I had known Fred for many years and I trusted him completely. I decided to stay.
Several years later the financial situation worsened to such a degree that something like panic set in. One of the results was the dissolution of the philosophy group, which was not done skillfully, thus bringing the University some adverse publicity. Under Fred's successor there was further shrinkage. A distinguished group in psychology was the victim this time.
By the time I left the Rockefeller in 1981 after twenty happy, productive years all signs indicated that, except for the presence of students, the institution was moving in the direction of becoming again primarily an institute for bio-medical research.
When I left I was four years away from the compulsory retirement age. The Bronkian Camelot was long since gone. Kitty and I were getting tired of the Eastern winters and I found commuting from Scarsdale an ever growing aggravation. Our daughter and her two children lived on the West Coast. To make things even easier, the University of Southern California expressed interest in my joining {140} its faculty to help build up its mathematics department. And so we emigrated to California.
When I went to the Rockefeller in 1961 I was almost forty-seven years old, an age at which one is theoretically way past one's mathematical prime. By and large it is true, for mathematics and, even more, physics are young men's games. And yet some of what I consider to be my best work was done during my years at the Rockefeller when I was by accepted reckoning an old man.
My most favorite “old age” discovery has to do with the phenomenon of condensation. As mentioned in the last chapter, all gases if cooled below a certain critical temperature liquefy if subjected to a sufficiently high pressure. That so universal a phenomenon cannot even now be explained from “first principles”—that is, from the basic tenets of statistical mechanics—is remarkable.
The first stab at a theory of condensation was made by the Dutch physicist Johannes Diderick van der Waals in his Leiden doctoral dissertation, published in 1873.
Every high-school student who has taken an elementary physics course knows the equation of state
p = |
kT υ |
for an ideal gas (the Boyle-Charles law). Here p is the pressure, υ the specific volume (that is, volume per molecule) and T the absolute temperature; k is an absolute constant known as the Boltzmann constant.
An ideal gas does not liquefy, but van der Waals argued that the equation of state of a real gas should be the form
|
kT υ |
= |
1 υ – δ |
– |
ν υ2 |
where δ is related to the non-zero size of the molecules and ν to the attractive force between them (if δ = 0 and ν = 0 one obtains the ideal-gas law above).
For sufficiently large T the graph p/kT versus υ is a smooth decreasing curve.
| {141} |
But below a certain temperature the graph has a wiggle
and the appearance of this wiggle was interpreted as the onset of condensation (that is, liquefaction).
Unfortunately, the wiggle is inconsistent with the laws of thermodynamics and therefore van der Waals's theory could not be right. {142}
Maxwell remedied the situation with his equal-area rule, which called for replacing the graph above with the one in which the wiggle was replaced by a horizontal line drawn in such a way that the shaded areas were equal.
But Maxwell's argument was ad hoc and the problem remained whether or not statistical mechanics alone is sufficient to derive the van der Waals isotherm with the Maxwell rule. In other words, was the van der Waals equation, as modified by the Maxwell rule, an inspired empirical formula or was it in some sense a consequence of the universally accepted principles of statistical mechanics?
That it is the latter was demonstrated conclusively in the first of a series of three papers written jointly with George Uhlenbeck and Per Christian Hemmer, our first “post-doc” at the Rockefeller (now a professor of theoretical physics at the Norwegian Technical University in Trondheim).
In our three papers we discussed in great detail a special one-dimensional model which I had introduced a few years earlier. I learned later that Feynman had introduced the same model but his treatment was different from mine. Because of the special nature of the model we were able to go much further than the derivation {143} of the van der Waals equation with the Maxwell rule.°
Mathematically, our discussion concerned properties of an integral equation from my earlier paper. That these purely mathematical properties reflected a piece of physical reality left me in a state of awe. From the physics course of my Lycee days as well as from my university course in experimental physics I was familiar with the isotherm with the horizontal piece. It was, as far as I could recall, presented to us as an empirical fact. Now the dimly remembered picture was extractable from an integral equation! Could nature know so much mathematics?
My second favorite “old age” contribution was of an entirely different kind.
The Mathematical Association of America had been given a grant to record on film or video tape a number of lectures by or interviews with contemporary mathematicians. I was invited to participate and I chose to have a lecture of mine filmed. The title of the lecture, “Can One Hear the Shape of a Drum?” (I get only half credit for this title, the other half justly belongs to Lipman Bers), caught on beyond all expectations. There is now hardly a mathematician who hasn't heard of the title even though he may not have seen the film or read the “script” on which it was based.
The origins of the lecture as well as the title are worth recording. To honor the memory of H. A. Lorentz, one of the greatest physicists of all times, the University of Leiden established a chair in his name to be occupied by visitors from different countries. In the spring of 1963 I had the honor of being the “Lorentz Professor” and Kitty and I spent two delightful months in Holland. At the end of my visit I was asked, as was every Lorentz Professor before me, {144} to deliver a semi-popular lecture at the famous Colloquium established by Ehrenfest and named after him. Ehrenfest, as may be recalled, was Lorentz's successor in the chair of theoretical physics in Leiden. In considering on what subject to lecture, the thought came to me that by picking an appropriate topic and choosing an appropriate title I might, albeit in a small way, honor the memories of both men.
I was lucky because a problem on which I had worked for some time was ideal for the kind of lecture which was expected of me and, most importantly, it originated in a lecture which Lorentz had given in Gottfngen in 1910.
Ehrenfest was fond of using questions as titles of his scientific papers (“In What Way Does It Become Manifest in the Fundamental Laws of Physics That Space Has Three Dimensions?” comes to mind) and in his honor I chose to change what would have been a precise but dull title into a provocative question. Thus “Can One Hear the Shape of a Drum?”
As an amusing footnote I may add that the announcements of my lecture, sent out all over Holland, contained a misprint in the title and came out to be “Can One Hear the Shape of a Dream?” In spite of my pleas to let things stand, corrections were mailed out, thus depriving me of what might have been a perplexed audience of psychoanalysts.
A To go back to the actual lecture, let me first plead guilty to a poetic license. The “drum” of the title is really a tambourine. This is a membrane held fixed along its perimeter. Unlike strings, which have a very simple structure of overtones—their frequencies being merely multiples of the fundamental—membranes exhibit much richer and more complex harmonic patterns. A natural question arises as to whether the knowledge of all the overtones determines the shape of the membrane. The answer is still not known (and I suspect it is in the negative) but some of the geometrical information about the membrane can be obtained.
In his Göttingen lecture of 1910 Lorentz conjectured that the overtones determine the area of the membrane and challenged the mathematicians present to provide a proof (actually, Lorentz dealt with the three-dimensional case of electromagnetic vibrations but the mathematical problematics are essentially the same as for the membrane).
There is a story that Hilbert, who attended the lecture, predicted {145} that the conjecture would not be proved in his lifetime. He was wrong by quite a bit, for in less than two years his own brilliant student Hermann Weyl provided a proof, thereby opening a new and important chapter in mathematical analysis.
Many years later (1936) a Swedish mathematician, A. Pleijel, went an important step further and showed that the length of the boundary of the membrane can also be determined from the overtones.
In 1952 I had given a simpler proof of Weyl's theorem based on an entirely different principle. It so happens that the squares of the overtone frequencies come up also in the problem of diffusion, which physically , is quite unrelated to the theory of vibrations whence Lorentz's conjecture came. But looking at Lorentz's problem from the point of view of diffusion theory provided an insight which led to simplifications and extensions. In particular, Pleijel's result could also be derived in a more transparent way.
Upon returning home, I went a step further and it is this step that opened new vistas. Using my method, I made it plausible, though I couldn't provide a proof,° that if the membrane has holes their number can also be calculated from the overtones. The number of holes is related simply to a number called connectivity, and connectivity is a topological concept. Connections between topological and analytic concepts are always exciting and the “drum” found itself in the center of feverish activity. A friend writing from Oxford—it must have been in the early seventies—concluded his letter with the words “the sound of the drum is deafening.”
To return briefly to my lecture at the Ehrenfest Colloquium— mention should be made of a ceremonial going back to the earliest days of the Colloquium. Each visiting lecturer had to sign his name, together with the date of his lectures, on a whitewashed wall under the blackboard. When the Institute for Theoretical Physics was moved, that part of the wall was cut out and moved to the new building, thus preserving this quaint tradition. The signatures read like Who's Who in the world of physics, and when my turn came to sign I was briefly tempted to use the space between Einstein and Becquerel (which would have just accommodated my name). Good manners, if not a natural modesty, dictated that I find less illustrious company.
Looking over my bibliography from the Rockefeller period, I {146} am surprised and pleased at how active I was. True, much of the work was an elaboration of ideas conceived in earlier times but here and there I found ventures into new territory. Nothing striking but not bad either—certainly not for an old man.
The Rockefeller years were also the years when the rewards of recognition began to come in (elections to academies, invitations to deliver prestigious lectures, an occasional prize, an honorary degree here and there).
Strange thing, this recognition. I recall my father telling me about a teacher of mathematics he had had in a school in Odessa which he attended briefly. The teacher, V. F. Kagan, was internationally known for having given a simplified solution of one of Hilbert's famous problems and for many other important contributions to geometry. He applied to the University of Odessa, a miserable provincial school of no distinction at all, for a Doctor's degree, which in Russia was then, as it is now, a very high degree. As part of the requirement Kagan had to defend a dissertation and on the day of the examination he met my father. Somehow in the course of a brief conversation he asked, rhetorically no doubt: “Why do I seek their recognition? There is no one on the committee who can possibly understand what I have written.”
This is an extreme example but it does make one stop and think as to what it is all about. The fact is that when recognition comes, whatever the source, it brings with it pleasure. And when it fails to come, a degree of bitterness may be generated that can be destructive. That is the way we are and there is no use pretending that it is otherwise.
Obviously, one of the most rewarding and pleasant signs of recognition is to be invited to spend some time in an interesting and intellectually stimulating place.
Besides being the Lorentz Professor in Leiden (Spring 1963), I was most fortunate to be Visiting Professor (Kramers Chair) in Utrecht (Spring 1980), Nordita visitor in Trondheim (Fall 1968), Fermi Lecturer at the Scuola Normale Superiore in Pisa (Spring 1980) and Visiting Lecturer at Oxford University and Visiting Fellow at Brasenose College (Spring term 1969).
Of these various honors the one that touched me most came from Cornell. As part of its centennial celebration in 1965 the University created special Andrew D. White Professorships-at-Large. {147} The tenure of each professor was limited to seven years and the duties consisted of visiting the campus for varying periods of time during which technical lectures, informal discussions and debates with the local faculty and students were organized. It was a splendid idea and it helped bring to the University a variety of creative and gifted people.
I was among the first seven elected and our group included, among others, Barbara McClintock and the late Raymond Aron. Being a professor-at-large gave Kitty and me lots of opportunities to maintain our ties with old friends and colleagues in Ithaca. I enjoyed my none-too-arduous duties, especially the public disputations with the philosopher Max Black, who is a superb debater.
I had heard and read so much about the Cambridge and Oxford colleges that the prospect of a firsthand experience looked singularly enticing.
It began on the day I received an official letter from Brasenose College notifying me of my election to a visiting fellowship and including a form to be filled out so that I could be granted a temporary M.A. degree. The latter was an absolute necessity, for otherwise I would not be entitled to a gown, without which I could not dine in College. The form was somewhat quaint and I found it impossible to answer some of the queries. “Give name of parent or guardian” was the toughest. I finally answered that my parents were dead and that the only person who could even remotely qualify as my guardian was my wife, Katherine Mayberry Kac. Well, the College secretary, who turned out to be a lady although I had consistently addressed her as “Dear Sir,” grasped the situation and waived the requirement of my having to name a guardian.
On the evening of the day the Brasenose letter arrived, our daughter and her fiance, who were both seniors at NYU and both majoring in English, came out to dine with us in Scarsdale. After greeting them I said: “I have just been notified of having been elected Visiting Fellow of a college whose name rings only a faint bell in my memory—Brasenose.” “Brasenose College!” exclaimed Deborah and Peter in unison. “The college of Walter Pater!” Now, the name Walter Pater rang no bell at all, and the children, with the mixture of scorn and pity which the young reserve for their ignorant and feeble-minded elders, gave me a lecture on Pater. They were taking a course in the literature of the transition period {148} in which the name Pater loomed large, especially since the professor who taught the course was an expert on Pater. “He tried to limit his audience,” the children quoted their teacher, “and succeeded beyond his wildest dreams.” He certainly had as far as I was concerned. It was the surprise of my life when I learned that George Uhlenbeck, born and educated in Holland, had read Marius the Epicurean and thought it to be a fine piece of literature.
Well, it turned out that at Brasenose Pater was not much of a presence. His portrait was hanging behind a blackboard in a room adjoining the hall in which the Fellows and their guests had pre-dinner sherry. Most of his papers and manuscripts had somehow become the property of Warden Sparrow of All Souls.
Later, when Deborah and Peter visited us at Oxford, they vowed to do all they could to restore Pater to his rightful place. They found his much-neglected grave in a local cemetery and they pestered my Brasenose colleagues on every possible occasion about the shabby treatment Pater was receiving at their hands. I cannot swear that it was through their efforts but when I visited Brasenose a year later Pater's portrait had been moved from the obscure place it had occupied to the common room.
The education system at Oxford is, of course, totally elitist, though less so than before the Second World War. It is also extremely good, and I would venture a guess that for the chosen few it is the best in the world. Only at the Rockefeller would a student get a comparable degree of individual attention.
The University is the institution that appoints professors and lecturers, offers courses, runs laboratories, controls requirements for degrees and is solely endowed with the power to grant them. Colleges are independent of the University and their role is to tutor their students so they can pass the prescribed examinations leading to a degree. The tutors, with few exceptions, are Fellows, whose selection is a jealously guarded prerogative of the colleges.
In principle and in actual fact, there are thus two separate faculties, one chosen by the University and the other by the colleges. It does not take much imagination to detect possible sources of friction inherent in this system, and friction indeed there is aplenty. There is no need to go into detail but I can assure the reader that the lot of a young University lecturer who cannot find a college affiliation is not a happy one—financially and socially. {149} Neither is the lot of a young Fellow happy even if he also holds a University appointment. The tutorial load is so heavy that it seriously interferes with the possibility of doing independent research, especially in fields like mathematics and science. For some the system may be lethal.
It is superb for undergraduates, who get a fantastically good education, and for professorial Fellows. They have no tutorial obligations and have free room (if they are unmarried) and board. Visiting Fellows, like myself, have all the advantages of professorial Fellows and even fewer responsibilities. I enjoyed my two months in Oxford hugely, but now and then I felt that I had been transported to a different era.
A day or two before we were to sail for home I went to dinner at College to say goodbye to my fellow Fellows. The term was over and only about ten of them were still in town. We dined in one of the small dining rooms and I was seated next to one of the most senior Fellows, a charming, somewhat old-fashioned man whose specialty was ancient history. Making idle conversation (you get good at this art, dining at High Table), I asked him how he saw the future of the world. Somewhat to my surprise, he foresaw the rise of emerging nations (the term “Third World” had not yet been invented) at the expense of the declining Western World. I should have left it at that but I went on to ask him whether he could foresee a leader who might counteract this trend. “Perhaps one,” he answered. “Prince Charles.” To this day I do not know if he was pulling my leg.
There is not much more to tell about my Rockefeller years. They were mostly happy years even when the character of the institution began to change. When I left, more in sorrow than in anger, though I will not deny some anger, the University, as far as I could tell, was headed in the direction of becoming mainly a research institute in the bio-medical sciences. The students are still there and therein may lie the hope for the future. As long as there are young, lively, questioning, irreverent minds they will provide a counterforce to the specialization and intellectual isolation which research institutes tend to engender.
In any case, it was fun while it lasted.
| {150} |
Mathematics is an ancient discipline. For as long as we can reliably reach into the past, we find its development intimately connected with the development of the whole of our civilization. For as long as we have a record of man's curiosity and his quest for understanding, we find mathematics cultivated and cherished, practiced and taught. Throughout the ages it has stood as an ultimate in rational thought and as a monument to man's desire to probe the workings of his own mind.
You will not find much confirmation of this heroic view in what I have written about my own work. Nor, very likely, would any of my contemporaries do much better. There are too many of us and we do too many different things. And yet, though composed of many parts, mathematics retains a remarkable degree of cohesive-ness. Perhaps this is so because these many parts influence and enrich each other in mysterious ways—or, to borrow a Faustian phrase from Hermann Weyl, “Im Dunkeln Befruchten.” But being cohesive does not mean that mathematics is monolithic. It is more like a kaleidoscope in which the pieces stay the same while the patterns are infinite in their variety. Since this is my autobiography, I have naturally tried to let the reader catch a glimpse of the patterns that appeared when I shook the kaleidoscope. The remaining few pages will tell something about the kaleidoscope itself.
The urge to understand and to create mathematics has always been remarkable, considering that those who have devoted their lives to the service of this aloof and elusive mistress could expect {151} neither great material rewards nor widespread fame. To illustrate the kind of passion that mathematics could engender, let us go back to the Greeks. They left us two great areas of unsolved problems. The first was concerned with Euclid's Fifth Postulate, and the second with whether or not certain constructions (notably, the trisecting of an angle, the doubling of a cube and the squaring of a circle) could be performed by the sole use of a compass and an unmarked ruler.
The problem of the Fifth Postulate is purely logical. The Greeks felt uneasy about the necessity of assuming that through a point outside a given straight line one can pass one, and only one, parallel to the line. It seemed that this nearly self-evident statement could be logically derived from the remaining axioms, which were considered to be more self-evident.
The problem of geometric constructions may appear even more strange. The Greeks and their successors were well aware that the constructions could be performed with ease to any desired degree of accuracy. They were also aware that by allowing a wider range of instruments the construction could be performed exactly. But they insisted on using the compass and the unmarked ruler as the sole instruments! It took nearly eighteen centuries of prodigiously futile and anonymous efforts before the impossibility of the task was magnificently demonstrated during the past century.
It took almost as long to settle the problem of the Fifth Postulate. Again, the pages of history are strewn with assaults on this seemingly invincible fortress. The magnificent obsession that pushed mathematics forward can be dramatized no better than by the life of the seventeenth-century monk Saccheri, who, in the austerity of his medieval cell, labored so hard to prove the Fifth Postulate that he anticipated by more than a century many propositions of non-Euclidian geometry. Yet, like many before him and many after him, he died not knowing that his search was in vain, and was in vain because the laws of logic decreed that it had to be in vain. Not until the early nineteenth century did N. I. Lobachewsky and J. Bolyai demonstrate that a consistent system of geometry can be constructed in which all of Euclid's axioms are satisfied but which states that through a point outside a line there are infinitely main parallels to it.
Perhaps if one thinks of Saccheri and others like him, one may {152} forgive the pride with which the great nineteenth-century mathematician C. F. Jacobi declared that mathematics is practiced “pour la gloire de l'esprit humain.”
The pursuit of truth for its own sake was not the only force that lay behind the development and progress of mathematics. Mathematics, as we all know, has helped man to reach for the stars and explore the innermost secrets of the atom. Some of the greatest mathematical discoveries, calculus being the most notable among them, were brought about by man's quest for an understanding of the world about him. Even geometry, for ages the main source of intellectual purity, originated no doubt in astronomy and geodesy. Because of the dichotomy of sources of inspiration, mathematics has played the roles of both queen and handmaiden of science. This dual role has proved to be a source of great strength. It has permitted a healthy cross-fertilization of ideas, and it lias helped mathematics to steer a straight course between the dead ends of extreme pragmatism and empty and useless abstraction.
But the great advantages resulting from the duality of roles have often been neither recognized nor acclaimed. Quite the contrary . At various stages of our long and proud history the extreme “purists” in our midst have tried to free mathematics from its dual role. Witness the following quote from Plutarch's “Life of Marcellus”:
These machines he [Archimedes] had designed and contrived, not as matters of any importance, but as mere amusements in geometry; in compliance with King Hiero's desire and request, some little time before, that he should reduce to practice some part of his admirable speculation in science, and by accommodating the theoretic truth to sensation and ordinary use, bring it more within the appreciation of the people in general. Eudoxus and Archytas had been the first originators of this far-famed and highly prized art of mechanics, which they employed as an elegant illustration of geometrical truths and as a means of sustaining experimentally, to the satisfaction of the senses, conclusions too intricate for proof by words and diagrams. As, for example, to solve the problem, so often required in constructing geometrical figures, given the two extremes, to find the two mean lines of a proportion, both these mathematicians had recourse to the aid of instruments, adapting to their purpose certain curves and sections of lines. But what with Plato's indignation at it, and his invectives against it as mere corruption and annihilation of the one good {153} in geometry, which was thus shamefully turning its back upon the unem-bodied objects of pure intelligence to recur to sensation, and to ask help (not to be obtained without base supervisions and deprivation) from matter; so it was that mechanics came to be separated from geometry, and, repudiated and neglected by philosophers, took its place as a military art.
The followers of Plato are still with us, as are the tensions within our discipline. By its nature and by its historical heritage, mathematics lives on the interplay of ideas. The progress of mathematics and its vigor depend on the abstract helping the concrete and on the concrete feeding the abstract. To isolate mathematics and to divide it means in the long run to starve it and perhaps even destroy it.
There are those among us who urge division and separation. Like Plato centuries before, they see in applications of mathematics “mere corruption and annihilation of the one good in geometry” and they want mathematics to return to “the unembodied objects of pure intelligence.” And our extreme pragmatists preach division on opposite grounds.
The two great streams of mathematical creativity are a tribute to the universality of human genius. Each carries its own dreams and its own passions. Together they generate new dreams and new passions. Apart, both may die—one in a kind of unembodied sterility of medieval scholasticism and the other as a part of military art.
Is the view tenable that the two streams of mathematical creativity are distinguishable because one is concerned only with “unembodied objects of pure intelligence” while the other seeks inspiration “(not to be obtained without base supervisions and deprivation) from matter”?
An emphatic “yes” comes from Bertrand Russell who in an essay, “Mathematics and the Metaphysicians,” wrote:
Pure mathematics consists entirely of assertions to the effect that, if such and such a proposition is true of anything, then such and such another proposition is true of that thing. It is essential not to discuss whether the first proposition is really true, and not mention what the anything is, of which it is supposed to be true. Both these points would belong to applied mathematics. We start, in pure mathematics, from certain rules of inference, by which we can infer that if one proposition is true then so is some other proposition. These rules of inference constitute the major part of the {154} principles of formal logic. We then take any hypothesis that seems amusing, and deduce its consequences. If our hypothesis is about anything, and not about some one or more particular things then our deductions constitute mathematics. Thus mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true. People who have been puzzled by the beginnings of mathematics, will, I hope, find comfort in this definition, and will probably agree that it is accurate.
Even after one discounts the epater-le-bourgeois aspect of Russell's passage, there emerges a dull and rather miserable picture of mathematics. And yet the picture is not wholly wrong. It is just hopelessly incomplete and one-sided.
Let us see why. When you studied elementary geometry, the chances are you learned it the old-fashioned way, the way that prevailed before New Math went wild on strict axiomatics. The old-fashioned way was partly intuitive and partly rigorous—that is, dependent on axioms. You dealt with points, straight lines, triangles, right angles, congruences and all sorts of such things. But has it occurred to you that you didn't really know what a point is or what a straight line is? The very old-fashioned texts on plane geometry, following Euclid, defined points as entities that had no length or width and straight lines as entities that had length but not width. Such definitions are sheer nonsense. So Russell is right when he says that in mathematics “we never know what we are talking about.” But how can we do anything with objects when we don't know what these objects are? Ah! because the axioms allow us to combine terms we don't understand into “true” statements provided that the axioms themselves were “true” statements. So Russell is again right.
The only useful conclusion from all of this is that geometry is teachable to a blind person and even to a computer. The axiomatics must be absolutely tight, then, for any reliance on a diagram or any other sensory aid is out. Euclid's own axiomatics were far from foolproof. He skipped a whole group of axioms called axioms of order (which deal with the concept of a point on a line lying between two other points on that line) and was rather cavalier about other axioms. The first complete axiomatization of geometry was given as late as 1899 by David Hilbert. Great as this feat was, some {155} may feel it was the death knell of a beautiful subject that would now be relegated to a computer.
The discovery by Bolyai and Lobachewsky of a non-Euclidian geometry did more than merely topple Euclid's geometry from the pedestal of absolutism that it had occupied for centuries. It gradually led to the view of pure mathematics as described by Russell and, in part at least, accepted by many mathematicians today.
E. T. Bell in his Development of Mathematics° writes:
To the abstract algebra of 1830 and the hold creation of Lobachewsky and Bolyai can be traced directly the current (1940) estimate of mathematics as an arbitrary creation† of mathematicians. In precisely the same way as a novelist invents characters, dialogues and situations of which he is both author and master, the mathematician devises at will the postulates upon which he bases his mathematical systems.
If this sounds familiar, it should. It is a paraphrase of Russell's “we then take any hypothesis that seems amusing and deduce its consequences.”
On a number of occasions, both in print and in lectures, I have referred to a wartime cartoon depicting two chemists surveying ruefully a small pile of sand surrounded by an impressively complicated apparatus. The caption read: “Nobody really wanted a dehydrated elephant but it is nice to see what can be done.” Russell's view of pure mathematics constitutes a most liberal license for creating dehydrated elephants and I am happy to report that this license has not been used indiscriminately.
There surely must be more cogent reasons than being merely amusing for this or that system to deserve investigation and study. For one, there are esthetic reasons, and here I am reminded of something Balthazaar van der Pol, a great Dutch scientist and engineer who was also a fine musician, remarked to me about the music of Bach. “It is great,” he said, “because it is inevitable and yet surprising.” I have often thought about this lovely epigram in connection with mathematics and am convinced that, with some caution, it is applicable. The inevitability is, in many cases, provided by logic alone, but the element of surprise must come from an {156} insight outside the rigid confines of logic.
Saccheri started from the same negation of the Fifth Postulate as did Lobachewsky and Bolyai—that is, that there is a whole angle of parallels to a line through a point not on it—and with impeccable logic he proceeded to derive the same conclusions as they later did. But Saccheri was convinced that the Fifth Postulate was correct, and he was thus searching for a contradiction. Lobachewsky and Bolyai became convinced, on the basis of roughly the same evidence, that they would never reach a contradiction and they boldly announced that there is a new geometry just as internally consistent as that of Euclid. At the time this enormously surprising conclusion was reached, it could not be proved in a way which would satisfy modern standards of rigor. But only a few decades later an Italian mathematician, E. Beltrami (1835–1900), showed that there is a surface (so-called pseudosphere) whose points and geodesies (lines of shortest distance) satisfy the Bolyai-Lobachewsky geometry. Thus an exercise in logic became a part of reality.
If mathematics is indeed an arbitrary creation of mathematicians, it may be condemned to proliferating “dehydrated elephants” ad infinitum. Are there safeguards against such a terrible fate? Here I am afraid we shall not find much agreement. Most mathematicians insist that no safeguards are needed: that tradition will guarantee the survival of the fittest, and that many “amusing hypotheses” will share the fate of the dinosaurs and become extinct. Perhaps. I would prefer to play it a little safer and listen to the voices of nature to guide us in the choice of what is “amusing” and what is not.
On one thing I am sure we shall all agree. Creativity in mathematics, a vast and fascinating subject in itself, is, fortunately, not a matter of merely taking “any hypothesis that seems amusing” and deducing its consequences. If it were, it could never generate the kind of fire, despair and triumph that shine through the beautiful letters between Bolyai the elder and his son.
In urging his son to abandon the struggle with the Fifth Postulate, the father, himself a noted and respected mathematician, wrote: “I have traveled past all the reefs of the infernal Dead Sea and have always come back with a broken mast and a torn sail.”
To which, some time later, came a reply in triumph and elation: “Out of nothing I have created a new and wonderful world!”
° “How I Became a Mathematician,” Rehovot, vol. 9, no. 2 (1981/82).
† “Mathematics: Trends and Tensions.” Boston University Journal, vol. xxiv, no. 1 (1976) pp. 59-65.
° Frank Field, The Last Days of Mankind: Karl Kraus and His Vienna (Macmillan, 1967).
° In the recent excellent book The Mathematical Experience by Philip Davis and Reuben Hersh (Birkhauser, 1980) this issue is discussed with much wit and wisdom in the section “The Classic Classroom Crises of Understanding and Pedagogy” (pp. 274–284), which describes a student near-revolt caused by the seemingly innocent statement by the teacher: “Now consider r(0) = p(0) – q(0).”
° There is a little sequel to this story. In late December of 1964 I was at the New Mexico State University in Las Cruces and a friend asked me whether I would be interested in meeting Cly de Tombaugh. The name didn't ring a bell until I was told that he was the discos ever ot Pluto Polish oithograpln follows a consistent if, from the standpoint of an English speaker, somewhat bizarre set of rules. For example, Shakespeare is spelled Szekspir and Chopin, Szopen. I will leave it to the imagination ot the reader as to how simple Tombaugh became mutilated in the process of Polonization. It's a long way from Krzemieniec to Las Cruces, New Mexico!
° The oldest is the University of Cracow, founded in 1364, the Alma Mater of Copernicus.
° Robert Merton, “The Matthew Effect in Science.” Science, vol. 159 (January 5, 1968) pp. 56-63.
° Janiszewski did not live to see the first volume of Fundamenta. He died in 1920 at the age of thirty-two during the epidemic of the Spanish flu.
° Intellectual corruption on this level exists today in the Soviet Union, where excellent dissertations in mathematics are routinely rejected by certifying committees solely because the authors are Jews.
° Journal of the London Mathematical Society, vol. IX (1934).
° With the exception of Steinhaus, whose punctuality was proverbial and who respected the official beginning of the academic year, professors chose the starting dates of their lectures more or less at random.
° Doubleday, Doran, 1941.
† Leopold Infeld, Why I Left Canada (McGill-Queens Press, Montreal, 1978).
‡ Just after I finished my studies Rubinowicz was given the chair. This was one in a sequence of moves designed to eliminate Infeld from contention but Rubinowicz was completely innocent and played no part in this sordid affair.
° American Mathematical Monthly, vol. 73 (1966), pp. 1-23.
° To the best of my knowledge, Steinhaus was the only professor of Jewish origin in Poland who had not converted to Catholicism. His international reputation combined with his own and his family's ties to the Polish patriotic movement were probably responsible for his being able to break through the anti-Semitic barrier. A few years later he might not have made it.
° If, for example, chess is augmented by the rule that if white does not win by. say, the fiftieth move, black is declared the winner, then there is a winning strategy for either white or black.
° “Hugo Steinhaus: A Reminiscence and a Tribute,” American Mathematical Monthly, vol. 81, no. 6 (June-July 1974), pp. 572-581.
° Different scales are used on the horizontal and vertical axes to bring out more clearly the fit. I am skipping these and other details as I am interested in giving only the flavor of the subject and not in attempting a mini-course on descriptive statistics.
° There is historical evidence that another reason for the neglect of Laplace's theory was that it lacked “serious” applications.
° We also need the axiom of additivity, which states that if events E1, E2, E3 . . . are mutually exclusive—i.e., the occurrence of one precludes the occurrence of any other one—then one has Prob.E1 or E2 or E3 or · · · >{E1 or E2 or E3 or · · · } = Prob.E1>{E1} + Prob.E2>{E2} + Prob.E3>{E3} + · · · Since it is not my purpose here to write a textbook on probability theory, I am glossing over a number of important and subtle points. I hope that the expert will forgive me and the layman will still get the essence of the subject.
° Lest the reader be surprised that I have failed to mention sines, let him be reminded
sin t = cos(1/2π — t)
and that therefore sines are expressible in terms of cosines.
° Wintner did have a “thing” about statistics, which he considered to be a lowly creation not worthy of admission into the sacred halls of mathematics. He may have identified the normal law so much with statistics that he just didn't think about it.
° Aurel Wintner, Spektraltheorie der Unendlichen Matrizen (S. Hirzel, Leipzig, 1929).
° For example, if m = 60, its prime divisors are 2, 3 and 5 and therefore ν(60) = 3. One also verifies easily that, e.g., ν(4) = 1, ν(40) = 2, etc. {91}
° Nathaniel Bowditch (1773–1838), Useful Tables from the American Practical Navigator.
° The Young Visiters or Mr. Salteena's Plan, with a foreword by J. M. Barrie (Doubleday, 1919).
† Biography for Beginners (Laurie, London, 1905).
‡ More Biography (Methuen, London, 1929).
° William Strunk, Jr., and E. B. White, The Elements of Style (Macmillan, 1959).
° Samuel Goudsmit, Alsos (H. Schuman, 1947).
° Review of Modern Physics, vol. 17 (April-July 1945).
† Emphasis mine.
° P. and T. Ehrenfest, “Uber zwei bekannte Einwdnde gegen das Boltzmann H-Theorem,” Physikalische Zeitschrift, vol. 8 (1907), pp. 311–314.
† In the preface to the second volume of his Vorlesungen uber Gastheorie, published in 1898, Boltzmann writes: “I am conscious of being only an individual struggling wearily against the stream of time.”
° This translation is taken from M. J. Klein's excellent biography, Paul Ehrenfest (North Holland, 1970). See in particular pp. 115–116.
° Mathematically, the problem is reduced to diagonalizing a matrix and this in turn requires finding its right and its left eigenvectors. George started with the right and got nowhere; I started with the left and everything miraculously fell into place.
° American Mathematical Monthly, vol. 73 (1966), pp. 1–23.
° T. D. Lee and C. N. Yang.
° Daniel Coit Gilman: Creator of the American Type of University (Harcourt, Brace).
° Following cur work but using quite different methods, this was accomplished in the more realistic three-dimensional case first by N. G. van Kanipen and then by J. L. Lebowitz and O. Penrose. In the three-dimensional case the term
|
1 υ – δ |
is wrong and its exact form not known. Thus, strictly speaking, the van der Waals original equation is valid only in the one-dimensional case. It should also be stressed that it became clear that the van der Waals theory could only be rigorously true if the attractive forces between the molecules were weak and long-ranged. When the nature of the intermolecular forces became better understood it turned out that they could not be of the kind that would lead to the van der Waals equation of state. It is remarkable that in spite of this the van der Waals theory is qualitatively excellent, except very near the critical point.
° A proof was given shortly after by I. M. Singer and Henry McKean.
° McGraw-Hill, 1940.
† Emphasis mine.
| {157} |
Adventures of a Mathematician (Ulam), xx, xxiii, xxvi, 125
Alsos (Goudsmit), 110
American Mathematical Monthly, The, 48n, 52n, 99, 121n
American Mathematical Society, 89
Amsterdam, University of, 133
Annals of Mathematics, 112
anti-Semitism:
in post-revolutionary Russia, 13, 15–16, 28n
in pre-revolutionary Russia, 8–9
Archytas, 152
Aron, Raymond, 147
Arrowsmith (Lewis), 132
Ashford, Daisy, 101
atomic theory, proof of, 21–22
Avery, Oswald, xvi, xviii, xix, xxi, 131
axiom of additivity, 63n
axiom of determinancy, 51
Baclawski, K., 54
Banach, Stefan, 25–26, 36, 51, 100, 112
Banach-Steinhaus theorem, 51
Bartel, Kazimierz, 34
Becquerel, Antoine Henri, 145
Bell, E. T., 155
Bell Telephone Laboratories, 133
Beltrami, E., 156
Bers, Lipman, 143
Biography for Beginners (Clarehew), 101
Black, Max, 147
Bohr, Niels, xxiv
Boltzmann, Ludwig, 117–118, 120
Boltzmann constant, 140
Boltzmann equation, 38
Borel, Emile, 65
Born, Max, 36
Borsuk-Ulam theorem, xxi, xxiii
Boston University Journal, xiii
Bowditch, Nathaniel, 97n
Boyle-Charles law, 140
Brasenose College, 146, 147–148
Bright, Mabel, 135
Brink, Frank, 134
Kac's relationship with, 134–135
as Rockefeller University president, 131–134, 136–137
Brown, Robert, 21
Brownian motion:
discovery of, 21
theories of, 21–22, 74–75, 112
Brun, Viggo, 91
Buckley, Arabella, 13
Burckhardt, Jakob, 137
Cambridge University, xxiii, 147
Cameron, Robert H., 113
“Can One Hear the Shape of a Drum?” (Kac), 48, 121, 143, 144
Cardano, Geronimo, 2
Cardano's formulas, xxvi, 2–4, 47
Carnap, Rudolph, 43 {158}
Carver, Walter Buckingham, 88, 99
DNA studied by, xvii
Greek loved by, xvi
Chargaff rules, xvii
Chauvenet Prize, 121
Christmas Carol, A (Dickens), 81
Chwistek, Leon:
as painter, 43
Civilization of the Renaissance in Italy, The (Burckhardt), 137
Clarehew, Edmund, 101
Cohen, E. D. G. (Eddie), 133
Cohen, Joel, 138
Columbia University, 137
Columbia University College of Physicians and Surgeons, xvi
Commonwealth Fund Fellowship, xxiii
Kac's studies of, 140, 142–143
Maxwell's studies of, 142
van der Waals's studies of, 140–143
Conrad, Joseph, 10
Kac's teaching at, 88, 95–96, 104–105, 108, 125–127
researchers associated with, xxiii, 100, 115
Courant Institute of Mathematical Sciences, 137
Cracow, University of, 20n, 21, 37
Crick, Francis H. C., xvii
cubic equations:
Curie, Pierre, 121
Curie temperature, 121
Daniel Coit Gilman (Bronk), 135n
Davis, Philip, 2n
Dedekind, Julius Wilhelm Richard, 31
“Definitions Which Are Needed in the Theories of Games and Pursuit” (Kac), 52
de Moivre, Abraham, 55, 59–61, 69
de Moivre-Laplace theory, 63
Development of Mathematics (Bell), 155
Dickens, Charles, 81
Dirac, P. A. M., xxiii
Disturbing the Universe (Dyson), xxiii–xxvi, 116
Doob, J. L., 112
Double Helix, The (Watson), xvii–xviii, xxvi
Dubinski, Meri, 41–42, 46, 79–80
Dyson, Freeman J., 116
as mathematician, xxiii
mentors of, xxv
as problem-solver, xxiv
Edelman, Gerald M., 137
Edelstein, Ludwig, 134
Ehrenfest, Paul, 117, 119, 144
Ehrenfest, Tatiana, 117
Ehrenfest “dog-flea” model, 118–121
in history of physics, 119–120
Second Law of Thermodynamics and, 117–118, 121
Einführung in die Theoretische Physik (Schaefer), 37, 120
Einstein, Albert, xv, 22, 37, 123, 124, 145
Einstein-Smoluchowski theory, 114
Elements of Style, The (Strunk and White), 102
Encyclopedia of the Mathematical Sciences, 120
equal-area rule, 142
Erdös, Paul:
Kac's collaboration with, 84, 89–91, 115
as mathematician, 93
personality of, 92
Eudoxus, 152
Everett, C. J., xxi
Fackel, Die (Kraus), xviii–xix
Falkowska, Jadwiga, 19
Faraday, Michael, 13
Feynman, Richard, xxiv, xxv, 116, 123, 125, 142
Feynman-Kac formula, 115
Field, Frank, xviiin
Flexner, Abraham, 124, 135 {159}
Flexner, Simon, 135
France, Anatole, xx
Franko, Ivan, 20
Fundamenta Mathematicae, 25, 26
Gasser, Herbert, 132
Gauss, Carl Friedrich, 55–56, 59
“Gaussian Law of Errors in the Theory of Additive Number Theoretic Functions, The” (Kac), 91
Gilbert, Sir William, 101
Gillespie, David C, 100
Gilman, Daniel Coit, 135
Glashow, Shelly, 126
Glim, James A., 138
Gogol, Nikolai, 4
Göttingen, University of, 49, 100, 119, 144
Goudsmit, Samuel A., 109–110, 131–132
Groszynski, Kazimierz, 19
Guggenheim Fellowship, 108
Hardy, G. H., 81
Harvard University, 100, 101, 133, 138
Haussdorff, Felix, 100
Hemmer, Per Christian, 142
Heraclitean Fire (Chargaff), xvi–xviii, xx, xxvi
Hersh, Reuben, 2n
Herzberg, Jan, 44
Herzog, Fritz, 96
Hetper, Wladyslaw (Wladek):
Kac's friendship with, 42, 44–45
Hilbert, David, 49, 100, 144–145, 154
History of Cornell, A (Bishop), 97, 102
Holder, Otto, 80
Howard, Leslie, 102
“Hugo Steinhaus” (Kac), 52n
Hurewicz, Witold, 93
Hurwitz, Wallie Abraham, 99, 100–102
independence:
mathematical definition of, 61–64
Institute for Advanced Study, Princeton, N.J.:
history of, 124
researchers associated with, xxiii, 90, 124, 135
International Congress of Mathematicians, 92
invariance principle, 115
Ising, Ernst, 122
Jacobi, C. F., 152
Janiszewski, Zygmunt, 25
Johns Hopkins University:
Kac's choice of, 76
Kac's studies at, 5, 80, 82–94
researchers associated with, 80, 84, 99, 131, 133, 135
Jones, Harris P., 52
Journal of Applied Physics, 93
Journal of the London Mathematical Society, 30, 81
Judson, Horace Freeland, xxiv
Kac, Deborah Katherine:
Kac, Katherine (Kitty) Mayberry, 86, 95, 147
Kac's marriage to, 104
musical talent of, 107
Kac, Mark:
academic achievements of, 32, 35, 38, 45
brother of, 12
Brownian motion studied by, 112–116
Cardano's formulas derived by, 3–4
condensation studied by, 140, 142–143
at Cornell University, 88, 95–96, 104–105, 108, 125–127, 146–147
cubic equations studied by, 2–5
education as viewed by, 128–129
Ehrenfest model studied by, 120–121
English-language problems of, 80–83
father of, 1, 8–10, 11, 13–14, 105–106
fellowships awarded to, 4–5, 34–35, 40, 46, 108 {160}
Kac, Mark (cont.)
financial problems of, 26, 33–34, 40, 87
friends of, 42, 45–47, 84–86, 89, 96
Hetper's association with, 42, 44–45
independence of cosines studied by, 70–75
at Institute for Advanced Study, 124–125
at Johns Hopkins University, 5, 80, 82–94
mathematics chosen by, 1–6, 12, 13
mathematics as viewed by, 150–156
membrane overtones studied by, 144–145
normal law studied by, 64–65, 74–76
number theory studied by, 89–92
at Oxford University, 146, 147–149
phase transitions studied by, 122–124
at Rockefeller University, 131–133, 137–143, 145, 149
romances of, 41–42, 46, 79, 104
Steinhaus's collaboration with, 40–42, 48–49, 54, 70, 120
stochastically independent functions
at University of Leiden, 19, 143–145, 146
University of Lwów chosen by, 26
Kac, Meshilem (grandfather), 8
Kac, Michael Benedict:
birth of, 107
intellectual interests of, 107
Kac, Mordecai (great-grandfather), 7
Kaczmarz, Stefan, 36
Kagan, V. F., 146
Kant, Immanuel, 9
Kemmer, Nicholas, xxiii
Klein, M. J., 119n
Kolmogorov, A. N., 49
Kronecker, Leopold, 73
Krzemieniec (Kreminiecz), 24
after the Russian Revolution, 12–13, 15
before the Russian Revolution, 6–7
school system of, 13, 14–15, 17
Kuhn, Harold W., 52
Kulczynski, Stanislaw, 35
Lagrange, Joseph Louis, 116
Landsteiner, Karl, 131
Laplace, Pierre Simon, Marquis de, 55, 59
Last Days of Mankind (Field), xviiin
law of errors, see normal law
Lawrence, E. O., xxvii
Lebesgue, Henri, 114
Lebowitz, J. L., 143n
Lectures on the Chemical History of a Candle (Faraday), 13
Leiden, University of, 103
Kac's teaching at, 19, 143–145, 146
scientists associated with, 120, 140
Leipzig, University of, 1, 7, 8
Lenin, V. I., 12
Lewis, Sinclair, 132
“Life of Marcellus” (Plutarch), 152–153
Limits of Science (Chwistek), 43
Lobachewsky, N. I., 151, 155, 156
Lomnicki, Zbigniew, 49
Lusin, Nicolas, 49
Lwów, University of:
McCarty, Maclyn, xvi, xix, 131
McClintock, Barbara, 147
Mach, Ernst, 21
McKean, Henry P., 133, 138, 145n
Maimon, Solomon, 9
Marius the Epicurean (Pater), 148
Markov, A. A., 36, 39, 54, 64, 70, 74
Martin, William T. (Ted), 113
Massachusetts Institute of Technology, 113, 133
Mathematical Association of America, 99, 121, 143
Mathematical Experience, The (Davis and Hersh), 2n
Mathematical Snapshots (Steinhaus), 40–41
“Mathematicians and the Metaphysicians” (Russell), 153–154 {161}
in ancient Greece, 151
axiomatics in, 154
creativity in, 156
non-Euclidean geometry and, 155, 156
“Matthew Effect in Science, The” (Merton), 22n
Maxwell, James Clerk, 118, 142
Mazurkiewicz, Stanislaw, 25
Merton, Robert, 22
Michelson, A. A., 49
Michelson-Morley experiment, 49
Michigan, University of, 133
Mickiewicz, Adam, 6
Minnesota, University of, 107, 115
Missouri, University of, 100, 101
Moliere, 34
More Biography (Clarehew), 101
Morgan, Thomas Hunt, 83
Morley, Christopher, 99
Morley, Frank, 99
Moscow, University of, 1, 7, 10
Murnaghan, F. D., 84, 86–87, 96
Mycielski, Jan, 51
Narutowicz, Gabriel, 12
National Academy of Sciences, 126, 134, 136
National Research Council, 134
National Science Board, 134
Nature, 53
Naval Logistics Quarterly, 52
New Mexico State University in Las Cruces, 18n
Newton, Sir Isaac, 116
independence of cosines and, 74–76
Kac's studies of, 64–65, 74–76
stochastically independent functions and, 64–65, 70
sums of independent quantities in, 63–64
Norwegian Technical University, 142, 146
Odessa, University of, 146
Oliver Mathematics Club, 100
Olszewski, Karol, 24
Opolski, Zdislaw, 16
Oppenheimer, J. Robert, 124
Ostwald, Wilhelm, 21
Oxford University, 146, 148–149
Pais, Abraham, 133
Paul Ehrenfest (Klein), 119n
Pauling, Linus, xviii
Peano, Giuseppe, 29
Pennsylvania, University of, 133
Penrose, O., 143n
Perrin, Jean, 21
physics:
Ehrenfest “dog-flea” model and, 119–120
Kac's interest in, 36–38, 117, 121, 130,143
in Poland, 36
Physikalische Zeitschrift, 117
Pilsudski, Josef, 16–17, 35, 49
Planck, Max, 37
Pleijel, A., 145
Pol, Balthazaar van der, 155
Poland:
ambitions for greatness of, 24
anti-semitism in, 28, 33, 34–35, 50
educational system in, 26–27, 29, 31–32
independence of, 24
Polish Academy of Sciences, 22
Polish Mathematical Society, 36
Poniatowski, Barbara, 88
“Preface to the Grammar of Biology” (Chargaff), xvi
President's Science Advisory Committee, 134
Prince and the Pauper, The (Twain), 11
Principia Mathematica (Whitehead and Russell), 43
probability theory, 39
arithmetization of, 70
Feynman-Kac formula and, 115 {162}
independence in, 48, 61–64, 73
in variance principle in, 115
normal law in, see normal law
stochastically independent functions and, 54, 70
Proceedings of the National Academy of Sciences, 91
Pythagorean theorem, 98
Quest (Infeld), 37
Quetelet, Adolphe, 58
Rademacher, Hans, 133
Radiation Laboratory, MIT:
Kac's association with, 93, 105, 111–112
“Random Walk and the Theory of Brownian Motion” (Kac), 121
Rehovot, xiii
Review of Modern Physics, 112
Riordan, John, 133
Rockefeller, John D., Sr., 131
Rockefeller Foundation, 36
Rockefeller Institute, see Rockefeller University
Rockefeller University:
financial problems of, 138–139
Kac's appointment to, 131–133, 137–143, 145, 149
organization of, 136
researchers associated with, xvi–xvii, xix, xxii, 5
Roichel family, 7
Rous, Peyton, 131
Rusiecki, Antoni Marian, 4, 19, 86
Russell, Bertrand, 42–43, 47, 153–155
Russia:
anti-semitism in, 8–9, 13, 15–16, 28n
during Russo-Japanese War, 7
as Kac's teacher, 31
life of, 34
Rybak, Boris, xv
St. Petersburg, University of, 3
Salam, Abdul, 126
Sapieha, Cardinal (Archbishop of Cracow), 17
Saturn by 1970 (Dyson), xxii
Schlick, Moritz, 43
Schouten, J. A., 85
Schwinger, Julian, xxiv
Science, 22n
Second Law of Thermodynamics, 117–118, 121, 130
Seitz, Frederick, 138
Sellers, Peter, xxii
Semile, Edmond, 13
Shearer, Norma, 102
Sheldon Traveling Fellowship, 100
Short History of Science, A (Buckley), 13
Silverman, Louis, 100
Singer, I. M., 145n
Sloan, David, xxvii
Slowacki, Juliusz, 6
Smoluchowski, Marian, 37
Brownian motion studied by, 21–22, 74–75,112
“Some Remarks on the Use of Probability in Classical Statistical Mechanics” (Kac), 130
Sommerfeld, Arnold, 36
Southern California, University of, 139
Spektraltheorie der Unendlichen Matrizen (Wintner), 84
standard deviation, 56
Stark, Marceli, 48
Kac influenced by, 30
as mathematician, 30
Steinhaus, Hugo Dyonizy, xviii–xix, 29, 30, 83
Kac's collaboration with, 40–42, 48–49, 54, 70, 120
as Kac's teacher, 32, 36, 38–40, 45, 86, 111–112
at Polish University in Wroclaw, 50
probability theory studied by, 65, 70
sense of humor in, 38–39, 51, 53
Steinhaus, Ignacy, 49
Steinhaus, Wladyslaw, 49
Stern, Isaac, 6
Stetigkeit und Irrazionalzählen (Dedekind), 31
stochastically independent functions:
concreteness of, 70
Kac's studies of, 39, 54, 70–75
probability theory and, 54, 70
Steinhaus's proposal of, 39, 54, 65
Stone, Marshall H., 84
Studia Mathematica, 26
Sturm-Liouville equations, 113
Sullivan, Sir Arthur, 101
Sylvester, Joseph, 5
Syracuse University, 113
Szczeniowski, Szczepan, 37, 38
Taite, Peter Guthrie, 118
Théorie Analytique des Probabilités (Laplace), 55
Thermodynamik (Planck), 37
Thermodynamique (Poincare), 48
Tomanaga, Shinichira, xxiv
Tombaugh, Clyde, 18n
Toronto, University of, 37
triangle inequality, xxii
“Trigonometric Series, A” (Kac), 30
Twain, Mark, 11
“Über zwei bekannte Einwände gegen das Boltzmann H-Theorem” (Ehrenfest and Ehrenfest), 117n
Uhlenbeck, George Eugene, xix, 110, 123, 133, 148
Brownian motion studied by, 112
condensation studied by, 142
Ehrenfest model interesting to, 120
radar studied by, 109
at Radiation Laboratory, 109–110
at Rockefeller University, 131–132
Ulam, Stanislaw, xx–xxiii, 125
biology interesting to, xxii
as mathematician, xx, xxii–xxiii, 48
Ulam distance, xxii
Useful Tables from the American Practical Navigator (Bowditch), 97
Utrecht, University of, 19, 23, 146
van Kampen, Egbertus Robertus, 80, 96
death of, 104
as mathematician, 84
van Kampen, N. G., 143n
von Neumann, John, 51, 52, 84, 124, 125
Vorlesungen über Gastheorie (Boltzmann), 117n
Waals, Johannes Diderick van der, 140
Wahrscheinlichkeitsrechnung (Markov), 36, 64, 70
Wallman, Henry, 93
Was sind und was sollen die Zählen (Dedekind), 31
Watson, James D., xvii–xviii, xix, xxvi
Weinberg, Steve, 126
Weizmann Institute, xiii
Weygand, Maxime, 16
White, Andrew D., 103–104, 134
Whitehead, Alfred North, 43
Who's Who in America, 6
Why I Left Canada (Infeld), 37n
Wiener, Norbert, 89, 110, 112–116, 123
Wintner, Aurel, 76, 80, 83–84, 96
Wojciechowski, Stanislaw, 12–13
Wong, Hao, 133
Wong, Ming Chen, 112
Wroblewski, Zygmunt, 24
Wronski, Jozef Hoene, 24
Wundt, Wilhelm, 9
Yale University, 137
Young Visiters or Mr. Salteena's Plan, The (Ashford), 101
Zariski, Oscar, 96
Zelenski, Tadeusz, 34