In the account of the life and discoveries of Galileo, we have endeavoured to inculcate the safety and fruitfulness of the method followed by that great reformer in his search after physical truth. As his success furnishes the best instance of the value of the inductive process, so the failures and blunders of his adversaries supply equally good examples of the dangers and the barrenness of the opposite course. The history of John Kepler might, at the first view, suggest conclusions somewhat inconsistent with this remark. Every one who is but moderately acquainted with astronomy is familiar with the discoveries which that science owes to him; the manner in which he made them is, perhaps, not so generally known. This extraordinary man pursued, almost invariably, the hypothetical method. His life was passed in speculating on the results of a few principles assumed by him, from very precarious analogies, as the causes of the phenomena actually observed in Nature. We nevertheless find that he did, in spite of this unphilosophical method, arrive at discoveries which have served as guides to some of the most valuable truths of modern science.
The difficulty will disappear if we attend more closely to the details of Kepler's investigations. We shall perceive that to an unusual degree of rashness in the formation of his systems, he added a quality very rarely possessed by philosophers of the hypothetical school. One of the greatest intellectual vices of the latter was a wilful blindness to the discrepancy of facts from their creed, a perverse and obstinate resistance to physical evidence, leading not unfrequently to an attempt at disguising the truth. From this besetting sin of the school, which from an intellectual fault often degenerated into a moral one, Kepler was absolutely free. Scheme after scheme, resting originally upon little beyond his own glowing imagination, but examined and endeared by the ceaseless labour of years, was unhesitatingly sacrificed, as soon as its insufficiency became indisputable, to make room for others as little deserving support. The history of philosophy affords no more remarkable instance of sincere uncompromising love of truth. To this virtue he owed his great discoveries: it must be attributed to his unhappy method that he made no more.
In considering this opinion upon the real nature of Kepler's title to fame, it ought not to be forgotten that he has exposed himself at a disadvantage on which certainly very few philosophers would venture. His singular candour allowed him to comment upon his own errors with the same freedom as if scrutinizing the work of a stranger; careless whether the impression on his readers were favourable or otherwise to himself, provided it was instructive. Few writers have spoken so much, and so freely of themselves, as Kepler. He records, on almost every occasion, the train of thought by which he was led to each of the discoveries that eventually repaid his perseverance; and he has thus given us “a most curious and interesting view of the workings of a mind of great, though eccentric power.” “In what follows,” says he (when introducing a long string of suppositions, of which he had already discovered the fallacy), “let the reader pardon my credulity, whilst working out all these matters by my own ingenuity. For it is my opinion that the occasions by which men have acquired a knowledge of celestial phenomena are not less admirable than the discoveries themselves.” Agreeing altogether with this opinion in its widest application, we have not scrupled, in the following sketch, to introduce at some length an account even of Kepler's erroneous speculations; they are in themselves very amusing, and will have the additional utility of proving the dangerous tendency of his method; they will show by how many absurd theories, and how {2} many years of wasted labour, his real discoveries and services to science lie surrounded.
John Kepler was born (as we are assured by his earliest biographer Hantsch) in long. 29°7', lat. 48°54', on the 21st day of December, 1571. On this spot stands the imperial city of Weil, in the duchy of Wirtemberg. His parents were Henry Kepler and Catherine Guldenmann, both of noble, though decayed families. Henry Kepler, at the time of his marriage, was a petty officer in the Duke of Wirtemberg's service; and a few years after the birth of his eldest son John, he joined the army then serving in the Netherlands. His wife followed him, leaving their son, then in his fifth year, at Leonberg, under the care of his grandfather. He was a seven months child, very weak and sickly; and after recovering with difficulty from a severe attack of small-pox, he was sent to school in 1577. Henry Kepler's limited income was still farther reduced on his return into Germany, the following year, in consequence of the absconding of one of his acquaintance, for whom he had incautiously become surety. His circumstances were so much narrowed by this misfortune, that he was obliged to sell his house, and nearly all that he possessed, and for several years he supported his family by keeping a tavern at Elmendingen. This occasioned great interruption to young Kepler's education; he was taken from school, and employed in menial services till his twelfth year, when he was again placed in the school at Elmendingen. In the following year he was again seized with a violent illness, so that his life was almost despaired of. In 1586, he was admitted into the monastic school of Maulbronn, where the cost of his education was defrayed by the Duke of Wirtemberg. This school was one of those established on the suppression of the monasteries at the Reformation, and the usual course of education followed there required that the students, after remaining a year in the superior classes, should offer themselves for examination at the collate of Tubingen for the degree of bachelor: they then returned to their school with the title of veterans; and after completing the studies taught there, they were admitted as resident students at Tubingen, proceeded in about a year to the degree of master, and were then allowed to commence their course of theology. The three years of Kepler's life following his admission to Maulbronn, were marked by periodical returns of several of the disorders which had well nigh proved fatal to him in his childhood. During the same time disagreements arose between his parents, in consequence of which his father quitted his home, and soon after died abroad. After his father's departure, his mother also quarrelled with her relations, having been treated, says Hantsch, “with a degree of barbarity by her husband and brother-in-law that was hardly exceeded even by her own perverseness:” one of his brothers died, and the family-affairs were in the greatest confusion. Notwithstanding these disadvantages, Kepler took his degree of master in August 1591, attaining the second place in the annual examination. The first name on the list was John Hippolytus Brentius.
Whilst he was thus engaged at Tubingen, the astronomical lectureship at Gratz, the chief town of Styria, became vacant by the death of George Stadt, and the situation was offered to Kepler. Of this first occasion of turning his thoughts towards astronomy, he has himself given the following account: “As soon as I was of an age to feel the charms of philosophy, I embraced every part of it with intense desire, but paid no especial regard to astronomy, I had indeed capacity enough for it, and learned without difficulty the geometrical and astronomical theorems occurring in the usual course of the school, being well grounded in figures, numbers, and proportions. But those were compulsory studies—there was nothing to show a particular turn for astronomy. I was educated at the expense of the Duke of Wirtemberg, and when I saw such of my companions as the duke selected to send abroad shrink in various ways from their employments, out of fondness for home, I, who was more callous, had early made up my mind to go with the utmost readiness whithersoever I might be sent. The first offering itself was an astronomical post, which I was in fact forced to accept by the authority of my tutors; not that I was alarmed, in the manner I had condemned in others, by the remoteness of the situation, but by the unexpected and contemptible nature of the office, and by the slightness of my information in this branch of philosophy. I entered on it, therefore, better furnished with talent than knowledge: with many protestations that I was {3} not abandoning my claim to be provided for in some other more brilliant profession. What progress I made in the first two years of my studies, may be seen in my ‘Mysterium Cosmographicum;’ and the encouragement given me by my tutor, Mästlin, to take up the science of astronomy, may be read in the same book, and in his letter which is prefixed to the ‘Narrative of Rheticus.’ I looked on that discovery as of the highest importance, and still more so, because I saw how greatly it was approved by Mästlin.”
The nature of the singular work to which Kepler thus refers with so much complacency, will be best shown by quoting some of the most remarkable parts of it, and especially the preface, in which he briefly details some of the theories he successively examined and rejected, before detecting (as he imagined he had here done) the tree cause of the number and order of the heavenly bodies. The other branches of philosophy with which he occupied himself in his younger years, were those treated by Scaliger in his ‘Exoteric Exercises,’ to the study of which book Kepler attributed the formation of many of his opinions; and he tells us that he devoted much time “to the examination of the nature of heaven, of souls, of genii, of the elements, of the essence of fire, of the cause of fountains, the ebb and flow of the tide, the shape of the continents, and inland seas, and things of this sort.” He also says, that by his first success with the heavens, his hopes were greatly inflamed of discovering similar analogies in the rest of the visible world, and for this reason, named his book merely a Prodromus; or Forerunner, meaning, at some future period, to subjoin the Aftercomer, or Sequel. But this intention was never fulfilled; either his imagination failed him, or, what is more likely, the laborious calculations in which his astronomical theories engaged him, left him little time for turning his attention to objects unconnected with his first pursuit.
It is seldom that we are admitted to trace the progress of thought in those who have distinguished themselves by talent and originality; and although the whole of the following speculations begin and end in error, yet they are so characteristic, and exhibit such an extraordinary picture of the extravagances into which Kepler's lively imagination was continually hurrying him, that we cannot refrain from citing nearly the whole preface. From it, better than from any enumeration of peculiarities, the reader will at once apprehend the nature of his disposition.
“When I was attending the celebrated Mästlin, six years ago, at Tubingen, I was disturbed by the manifold inconveniences of the common theory of the universe, and so delighted with Copernicus, whom Mästlin was frequently in the habit of quoting with great respect, that I not only often defended his propositions in the physical disputations of the candidates, but also wrote a correct essay on the primary motion, maintaining, that it is caused by the rotation of the earth. And I was then at that point that I attributed to the earth the motion of the sun on physical (or, if you will, on metaphysical) grounds, as Copernicus had done for mathematical reasons. And, by this practice, I came by degrees, partly from Mästlin's instructions, and partly from my own efforts, to understand the superior mathematical convenience of the system of Copernicus beyond Ptolemy's. This labour might have been spared me, by Joachim Rhetieus, who has shortly and clearly explained everything in his first Narrative. While incidentally engaged in these labours, in the intermission of my theology, it happened conveniently that I succeeded George Stadt in his situation at Gratz, where the nature of my office connected me more closely with these studies. Everything I had learned from Mästlin, or had acquired of myself, was there of great service to me in explaining the first elements of astronomy. And, as in Virgil, ‘Fama mobilitate viget, viresque acquirit eun-do,’ so it was with me, that the diligent thought on these things was the occasion of still further thinking; until, at last, in the year 1595, when I had some intermission of my lectures allowed me, I brooded with the whole energy of my mind on this subject. There were three things in particular, of which I pertinaciously sought the causes why they are not other than they are: the number, the size, and the motion of the orbits. I attempted the thing at first with numbers, and considered whether one of the orbits might be double, triple, quadruple, or any other multiple of the others, and how much, according to Copernicus, each differed from the rest. I spent a great deal of time in that labour, as if it were mere sport, but could find no equality either in the proportions or {4} the differences, and I gained nothing from this beyond imprinting deeply in my memory the distances as assigned by Copernicus; unless, perhaps, reader, this record of my various attempts may force your assent, backwards and forwards, as the waves of the sea; until tired at length, you will willingly repose yourself, as in a safe haven, on the reasons explained in this book. However, I was comforted in some degree, and my hopes of success were supported as well by other reasons which will follow presently, as by observing that the motions in every case seemed to be connected with the distances, and that where there was a great gap between the orbits, there was the same between the motions. And I reasoned, that if God had adapted motions to the orbits in some relation to the distances, it was probable that he had also arrayed the distances themselves in relation to something else.
“Finding no success by this method, I tried another, of singular audacity. I inserted a new planet between Mars and Jupiter, and another between Venus and Mercury, both of which I supposed invisible, perhaps on account of their smallness, and I attributed to each a certain period of revolution.* I thought that I could thus contrive some equality of proportions, increasing between every two, from the sun to the fixed stars. For instance, the Earth is nearer Venus in parts of the terrestrial orbit, than Mars is to the Earth in parts of the orbit of Mars. But not even the interposition of a new planet sufficed for the enormous gap between Mars and Jupiter; for the proportion of Jupiter to the new planet was still greater than that of Saturn to Jupiter. And although, by this supposition, I got some sort of a proportion, yet there was no reasonable conclusion, no certain determination of the number of the planets either towards the fixed stars, till we should get as far as them, nor ever towards the Sun, because the division in this proportion of the residuary space within Mercury might be continued without end. Nor could I form any conjecture, from the mobility of particular numbers, why, among an infinite number, so few should be moveable. The opinion advanced by Rheticus in his Narrative is improbable, where he reasons from the sanctity of the number six to the number of the six moveable heavens; for he who is inquiring of the frame of the world itself, must not derive reasons from these numbers, which have gained importance from things of later date.
“I sought again, in another way, whether the distance of every planet is not as the residuum of a sine; and its motion as the residuum of the sine of the complement in the same quadrant.

“Conceive the square AB to be constructed, whose side AC is equal to the semidiameter of the universe. From the angle B opposite to A the place of the sun, or centre of the world, describe the quadrant DG with the radius BC. Then in AC, the true radius of the world, let the sun, fixed stars, and planets be marked at their respective distances, and from these points draw lines parallel to BC, meeting the quadrant. I imagined the moving force acting on each of the planets to be in the proportion of these parallels. In the line of the sun is infinity, because AB is touched, and not cut, by the quadrant: therefore the moving force is infinite in the sun, as deriving no motion except from its own act. In Mercury the infinite line is cut off at K, and therefore at this point the motion is comparable with the others. In the fixed stars the line is altogether lost, and compressed into a mere point C; therefore at that point there is no moving force. This was the theorem, which was to be tried by {5} calculation; but if any one will reflect that two things were wanting to me, first, that I did not know the size of the Sinus Totus, that is, the radius of the proposed quadrant; secondly, that the energies of the motions were not thus expressed otherwise than in relation one to another; whoever, I say, well considers this, will doubt, not without reason, as to the progress I was likely to make in this difficult course. And yet, with unremitting labour, and an infinite reciprocation of sines and arcs, I did get so far as to be convinced that this theory could not hold.
“Almost the whole summer was lost in these annoying labours; at last, by a trifling accident, I lighted more nearly on the truth. I looked on it as an interposition of Providence, that I should obtain by chance, what I had failed to discover with my utmost exertions; and I believed this the more, because I prayed constantly that I might succeed, if Copernicus had really spoken the truth. It happened on the 9th or 19th* day of July, in the year 1595, that, having occasion to show, in my lecture-room, the passages of the great conjunctions through eight signs, and how they pass gradually from one trine aspect to another, I inscribed in a circle

a great number of triangles, or quasitriangles, so that the end of one was made the beginning of another, in this manner a smaller circle was shadowed out by the points in which the lines crossed each other.
“The radius of a circle inscribed in a triangle is half the radius of that described about it; therefore the proportion between these two circles struck the eye as almost identical with that between Saturn and Jupiter, and the triangle is the first figure, just as Saturn and Jupiter are the first planets. On the spot I tried the second distance between Jupiter and Mars with a square, the third with a pentagon, the fourth with a hexagon. And as the eye again cried out against the second distance between Jupiter and Mars, I combined the square with a triangle and a pentagon. There would be no end of mentioning every trial. The failure of this fruitless attempt was the beginning of the last fortunate one; for I reflected, that in this way I should never reach the sun, if I wished to observe the same rule throughout; nor should I have any reason why there were six, rather than twenty or a hundred moveable orbits. And yet figures pleased me, as being quantities, and as having existed before the heavens; for quantity was created with matter, and the heavens afterwards. But if (this was the current of my thoughts), in relation to the quantity and proportion of the six orbits, as Copernicus has determined them among the infinite other figures, five only could be found having peculiar properties above the rest, my business would be done. And then again it struck me, what have plane figures to do among solid orbits? Solid bodies ought rather to be introduced. This, reader, is the invention and the whole substance of this little work; for if any one, though but moderately skilled in geometry, should hear these words hinted, the five regular solids will directly occur to him with the proportions of their circumscribed and inscribed spheres: he has immediately before his eyes that scholium of Euclid to the 18th proposition of his 13th Book, in which it is proved to be impossible that there should be, or be imagined, more than five regular bodies. “What is worthy of admiration (since I had then no proof of any prerogatives of the bodies with regard to their order) is, that employing a conjecture which was far from being subtle, derived from the distances of the planets, I should at once attain my end so happily in arranging them, that I was not able to change anything afterwards with the utmost exercise of my reasoning powers. In memory of the event, I write down here for you the sentence, just as it fell from me, and in the words in which it was that moment conceived:—The Earth is the {6} circle, the measurer of all; round it describe a dodecahedron, the circle including this will be Mars. Round Mars describe a tetrahedron, the circle including this will be Jupiter. Describe a cube round Jupiter, the circle including this will be Saturn. Now, inscribe in the Earth an icosaedron, the circle inscribed in it will be Venus. Inscribe an octaedron in Venus, the circle inscribed in it will be Mercury. This is the reason of the number of the planets.
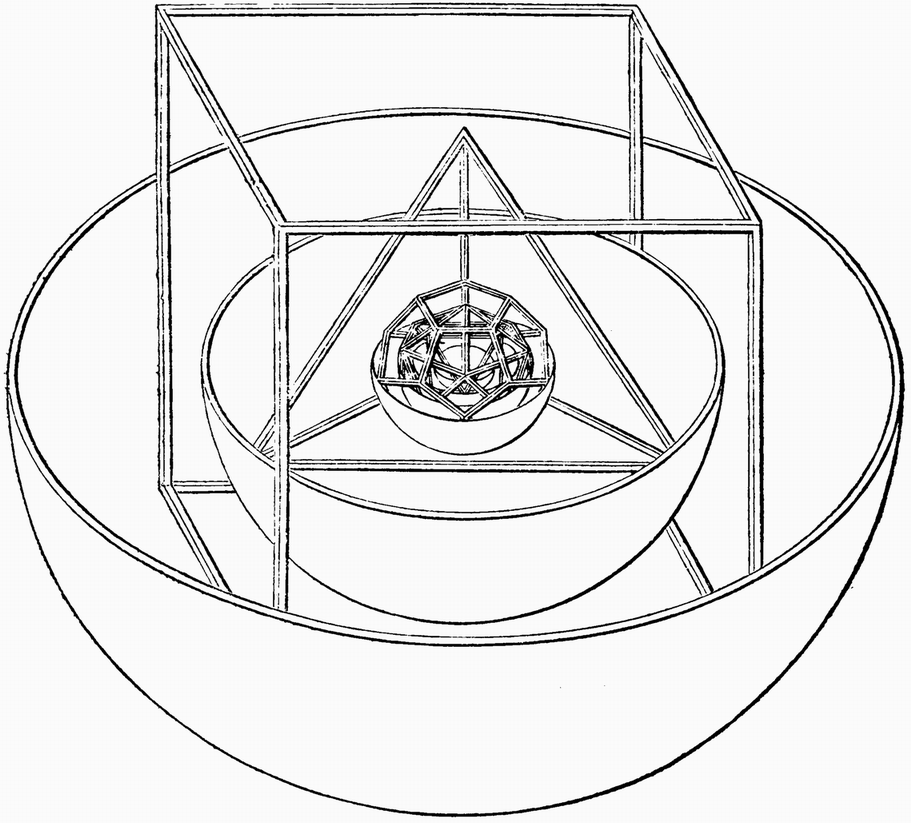
“This was the cause, and such the success, of my labour: now read my propositions in this book. The intense pleasure I have received from this discovery never can be told in words. I regretted no more the time wasted; I tired of no labour; I shunned no toil of reckoning; days and nights I spent in calculations, until I could see whether this opinion would agree with the orbits of Copernicus, or whether my joy was to vanish into air. I willingly subjoin that sentiment of Archytas, as given by Cicero: ‘If I could mount up into heaven, and thoroughly perceive the nature of the world, and beauty of the stars, that admiration would be without a charm for me, unless I had some one like you, reader, candid, attentive, and eager for knowledge, to whom to describe it.’ If you acknowledge this feeling, and are candid, you will refrain from blame, such as not without cause I anticipate; but if, leaving that to itself, you fear lest these things be not ascertained, and that I have shouted triumph before victory, at least approach these pages, and learn the matter in consideration: you will not find, as just now, new and unknown planets interposed; that boldness of mine is not approved, but those old ones very little loosened, and so furnished by the interposition (however absurd you may think it) of rectilinear figures, that in future you may give a reason to the rustics when they ask for the hooks which keep the skies from falling.— Farewell.”
In the third chapter Kepler mentions, that a thickness must be allowed to {7} each orb sufficient to include the greatest and least distance of the planet from the sun. The form and result of his comparison with the real distances are as follows:—
Book V.
If the |
ì |
Saturn |
ü |
be taken at |
ì |
Jupiter = 577 |
ü |
According to |
ì |
635 Ch. 9 |
It will he observed, that Kepler's results were far from being entirely satisfactory; but he seems to have flattered himself, that the differences might be attributed to erroneous measurements. Indeed, the science of observation was then so much in its infancy, that such an assertion might be made without incurring much risk of decisive refutation.
Kepler next endeavoured to determine why the regular solids followed in this rather than any other order; and his imagination soon created a variety of essential distinctions between the cube, pyramid, and dodecahedron, belonging to the superior planets, and the other two.
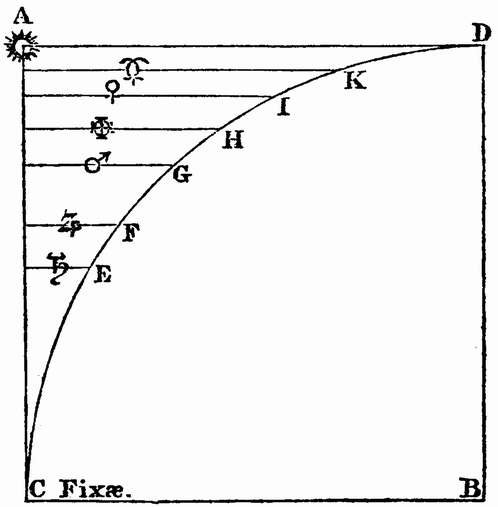
The next question examined in the book, is the reason why the zodiac is divided into 360 degrees; and on this subject, he soon becomes enveloped in a variety of subtle considerations, (not very intelligible in the original, and still more difficult to explain shortly to others unacquainted with it,) in relation to the divisions of the musical scale; the origin of which he identifies with his five favourite solids. The twentieth chapter is appropriated to a more interesting inquiry, containing the first traces of his finally successful researches into the proportion between the distances of the planets, and the times of their motions round the sun. He begins with the generally admitted fact, that the more distant planets move more slowly; but in order to show that the proportion, whatever it may be, is not the simple one of the distances, he exhibits the following little Table:—
♄ |
||||||
D.Scr. |
♃ |
|||||
♄ |
10759.12 |
D.Scr. |
♂ |
|||
♃ |
6159 |
4332.37 |
D.Scr. |
♁ |
||
♂ |
1785 |
1282 |
686.59 |
D.Scr. |
♀ |
|
♁ |
1174 |
843 |
452 |
365.15 |
D.Scr. |
☿ |
♀ |
844 |
606 |
325 |
262.30 |
224.42 |
D.Scr. |
☿ |
434 |
312 |
167 |
135 |
115 |
87.58 |
At the head of each vertical column is placed the real time (in days and sexagesimal parts) of the revolution of the planet placed above it, and underneath the days due to the other inferior planets, if they observed the proportion of distance. Hence it appears that this proportion in every case gives a time greater than the truth; as for instance, if the earth's rate of revolution were to Jupiter's in the proportion of their distances, the second column shows that the time of her period would be 843 instead of 3651/4 days; so of the rest. His next attempt was to compare them by two by two, in which he found that he arrived at a proportion something like the proportion of the distances, although as yet far from obtaining it exactly. This process amounts to taking the quotients obtained by dividing the period of each planet by the period of the one next beyond.
For if |
ì |
|
ü |
be successively |
ì |
|
But if the distance of each planet in |
ì |
|
From this table he argued that to make the proportions agree, we must assume one of two things, “either that the moving intelligences of the planets are weakest in those which are farthest from the Sun, or that there is one moving intelligence in the Sun, the common centre forcing them all round, but those most violently which are nearest, and that it languishes in some sort, and grows weaker at the most distant, because of the remoteness and the attenuation of the virtue.”
We stop here to insert a note added by Kepler to the later editions, and shall take advantage of the same interruption to warn the reader not to confound this notion of Kepler with the theory of a gravitating force towards the Sun, in the sense in which we now use those words. According to our theory, the effect of the presence of the Sun upon the planet is to pull it towards the {8} centre in a straight line, and the effect of the motion thus produced combined with the motion of the planet, which if undisturbed would be in a straight line inclined to the direction of the radius, is, that it describes a curve round the Sun. Kepler considered his planets as perfectly quiet and unwilling to move when left alone; and that this virtue supposed by him to proceed in every direction out of the Sun, swept them round, just as the sails of a windmill would carry round anything which became entangled in them. In other parts of his works Kepler mentions having speculated on a real attractive force in the centre; but as he knew that the planets are not always at the same distance from the Sun, and conceived erroneously, that to remove them from their least to their greatest distance a repulsive force must be supposed alternating with an attractive one, he laid aside this notion as improbable. In a note he acknowledges that when he wrote the passage just quoted, imbued as he then was with Scaliger's notions on moving intelligences, he literally believed “that each planet was moved by a living spirit, but afterwards came to look on the moving cause as a corporeal though immaterial substance, something in the nature of light which is observed to diminish similarly at increased distances.” He then proceeds as follows in the original text. “Let us then assume, as is very probable, that motion is dispensed by the sun in the same manner as light. The proportion in which light emanating from a centre is diminished, is taught by optical writers: for there is the same quantity of light, or of the solar rays, in the small circles as in the large; and therefore, as it is more condensed in the former, more attenuated in the latter, a measure of the attenuation may be derived from the proportion of the circles themselves, both in the case of light and of the moving virtue. Therefore, by how much the orbit of Venus is greater than that of Mercury, in the same proportion will the motion of the latter be stronger, or more hurried, or more swift, or more powerful, or by whatever other word you like to express the fact, than that of the former. But a larger orbit would require a proportionably longer time of revolution, even though the moving force were the same. Hence it follows that the one cause of a greater distance of the planet from the Sun, produces a double effect in increasing the period, and conversely the increase of the periods will be double the difference of the distances. Therefore, half the increment added to the shorter period ought to give the true proportion of the distances, so that the sum should represent the distance of the superior planet, on the same scale on which the shorter period represents the distance of the inferior one. For instance, the period of Mercury is nearly 88 days; that of Venus is 2242/3, the difference is 1362/3: half of this is 681/3, which, added to 88, gives 1561/3. The mean distance of Venus ought, therefore, to be, in proportion to that of Mercury, as 1561/3 to 88. If this be done with all the planets, we get the following results, taking successively, as before, the distance of each planet at 1000.
The distance in |
ü |
|
But accord- |
ì |
|
As you see, we have now got nearer the truth.”
Finding that this theory of the rate of diminution would not bring him quite close to the result he desired to find, Kepler immediately imagined another. This latter occasioned him a great deal of perplexity, and affords another of the frequently recurring instances of the waste of time and ingenuity occasioned by his impetuous and precipitate temperament. Assuming the distance. of any planet, as for instance of Mars, to be the unit of space, and the virtue at that distance to be the unit of force, he supposed that as many particles as the virtue at the Earth gained upon that of Mars, so many particles of distance did the Earth lose. He endeavoured to determine the respective positions of the planets upon this theory, by the rules of false position, but was much astonished at finding the same exactly as on his former hypothesis. The fact was, as he himself discovered, although not until after several years, that he had become confused in his calculation; and when half through the process, had retraced, his steps so as of course to arrive again at the numbers from which he started, and which he had taken from his former results. This was the real secret of the identity of the two methods; and if, when he had taken the distance of Mars at 1000, instead of assuming the distance of the earth at 694, as he did, he had taken any other number, and operated upon it in the same manner, he would {9} have had the same reason for relying on the accuracy of his supposition. As it was, the result utterly confounded him; and he was obliged to leave it with the remark, that “the two theories are thus proved to be the same in fact, and only different in form; although how that can possibly be, I have never to this day been able to understand.”—His perplexity was very reasonable; they are by no means the same; it was only his method of juggling with the figures which seemed to connect them.
Notwithstanding all its faults, the genius and unwearied perseverance displayed by Kepler in this book, immediately ranked him among astronomers of the first class; and he received the most flattering encomiums from many of the most celebrated; among others, from Galileo and Tycho Brahe, whose opinion he invited upon his performance. Galileo contented himself with praising in general terms the ingenuity and good faith which appeared so conspicuously in it. Tycho Brahe entered into a more detailed criticism of the work, and, as Kepler shrewdly remarked, showed how highly he thought of it by advising him to try to adapt something of the same kind to the Tychonic system. Kepler also sent a copy of his book to the imperial astronomer, Raimar, with a complimentary letter, in which he exalted him above all other astronomers of the age. Raimar had surreptitiously acquired a notion of Tycho Brahe's theory, and published it as his own; and Tycho, in his letter, complained of Kepler's extravagant flattery. This drew a long apologetical reply from Kepler, in which he attributed the admiration he had expressed of Raimar to his own want of information at that time, having since met with many things in Euclid and Regiomontanus, which he then believed original in Raimar. With this explanation, Tycho professed himself perfectly satisfied.
The publication of this extraordinary book, early as it occurs in the history of Kepler's life, was yet preceded by his marriage. He had contemplated this step so early as 1592; but that suit having been broken off, he paid his addresses, in 1596, to Barbara, Muller von Muhleckh. This lady was already a widow for the second time, although two years younger than Kepler himself. On occasion of this affiance he was required to prove the nobility of his family, and the delay consequent upon the inquiry postponed the marriage till the following year. He soon became involved in difficulties in consequence of this inconsiderate engagement; his wife's fortune was less than he had been led to expect, and he became embroiled on that account with her relations. Still more serious inconvenience resulted to him from the troubled state in which the province of Styria was at that time, arising out of the disputes in Bohemia and the two great religious parties into which the empire was now divided, the one headed by Rodolph, the feeble minded emperor,—the other by Malthias, his ambitious and enterprising brother.
In the year following his marriage, he thought it prudent, on account of some opinions he had unadvisedly promulgated, (of what nature does not very distinctly appear,) to withdraw himself from Gratz into Hungary. Thence he transmitted several short treatises to his friend Zehentmaier, at Tubingen—“On the Magnet,” “On the Cause of the Obliquity of the Ecliptic,” and “On the Divine Wisdom, as shown in the Creation.” Little is known of these works beyond the notice taken of them in Zehentmaier's answers. Kepler has himself told us, that his magnetic philosophy was built upon the investigations of Gilbert, of whom he always justly spoke with the greatest respect. About the same time a more violent persecution had driven Tycho Brahe from his observatory of Uraniburg, in the little island of Hueen, at the entrance of the Baltic. This had been bestowed on him by the munificence of Frederick I of Denmark, who liberally furnished him with every means of prosecuting his astronomical observations. After Frederick's death, Tycho found himself unable to withstand the party which had constantly opposed him, and was forced, at a great loss and much inconvenience, to quit his favourite island. On the invitation of the emperor, Rudolph II, he then betook himself, after a short stay at Hamburg, to the castle of Benach, near Prague, which was assigned to him with an annual pension of three thousand florins, a truly munificent provision in those times and that country. {10}
Kepler had been eager to see Tycho Brahe since the latter had intimated that his observations had led him to a more accurate determination of the excentricities of the orbits of the planets. By help of this, Kepler hoped that his theory might be made to accord more nearly with the truth; and on learning that Tycho was in Bohemia, he immediately set out to visit him, and arrived at Prague in January, 1600. From thence he wrote a second letter to Tycho, not having received the answer to his former apology, again excusing himself for the part he had appeared to take with Raimar against him. Tycho replied immediately in the kindest manner, and begged he would repair to him directly: —“Come not as a stranger, but as a very welcome friend; come and share in my observations with such instruments as I have with me, and as a dearly beloved associate.” During his stay of three or four months at Benach, it was settled that Tycho should apply to the emperor, to procure him the situation of assistant in the observatory. Kepler then returned to Gratz, having previously received an intimation, that he might do so in safety. The plan, as it had been arranged between them was, that a letter should be procured from the emperor to the states of Styria, requesting that Kepler might join Tycho Brahe for two years, and retain his salary during that time: a hundred florins were to be added annually, by the emperor, on account of the greater dearness of living at Prague. But before everything was concluded, Kepler finally threw up his situation at Gratz, in consequence of new dissensions. Fearing that this would utterly put an end to his hopes of connecting himself with Tycho, he determined to revive his claims on the patronage of the Duke of Wirtemberg. With this view he entered into correspondence with Mästlin and some of his other friends at Tubingen, intending to prosecute his medical studies, and offer himself for the professorship of medicine in that university. He was dissuaded from this scheme by the pressing instances of Tycho, who undertook to exert himself in procuring a permanent settlement for him from the emperor, and assured him, even if that attempt should fail, that the language he had used when formerly inviting him to visit him at Hamburg, should not be forgotten, in consequence of this encouragement,” Kepler abandoned his former scheme, and travelled again with his wife to Prague. He was detained along time on the road by violent illness, and his money became entirely exhausted. On this he wrote complainingly to Tycho, that he was unable without assistance to travel even the short distance which still separated them, far less to await much longer the fulfilment of the promises held out to him.
By his subsequent admissions, it appears that for a considerable time he lived entirely on Tycho's bounty, and by way of return, he wrote an essay against Raimar, and against a Scotchman named Liddell, professor at Rostoch and Helmstadt, who, like Raimar, had appropriated to himself the credit of the Tychonic system. Kepler never adopted this theory, and indeed, as the question merely regarded priority of invention, there could be no occasion, in the discussion, for an examination of its principles.
This was followed by a transaction, not much to Kepler's credit, who in the course of the following year, and during a second absence from Prague, fancied that he had some reason to complain of Tycho's behaviour, and wrote him a violent letter, tilled with reproaches and insults. Tycho appears to have behaved in this affair with great moderation: professing to be himself occupied with the marriage of his daughter, he gave the care of replying to Kepler's charges, to Ericksen, one of his assistants, who, in a very kind and temperate letter, pointed out to him the ingratitude of his behaviour, and the groundlessness of his dissatisfaction. His principal complaint seems to have been, that Tycho had not sufficiently supplied his wife with money during his absence. Ericksen's letter produced an immediate and entire change in Kepler's temper, and it is only from the humble recantation which he instantaneously offered that we learn the extent of his previous violence. “Most noble Tycho,” these are the words of his letter, “how shall I enumerate or rightly estimate your benefits conferred on me! For two months you have liberally and gratuilously maintained me, and my whole family; you have provided for all my wishes; you have done me every possible kindness; you have communicated to me everything you hold most dear; no one, by word or deed, has intentionally injured me in any thing: in short, {11} not to your children, your wife, or yourself have you shown more indulgence than to me. This being so, as I am anxious to put upon record, I cannot reflect without consternation that I should have been so given up by God to my own intemperance, as to shut my eyes on all these benefits; that, instead of modest and respectful gratitude, I should indulge for three weeks in continual moroseness towards all your family, in head-long passion, and the utmost insolence towards yourself, who possess so many claims on my veneration from your noble family, your extraordinary learning, and distinguished reputation. Whatever I have said or written against the person, the fame, the honour, and the learning of your excellency; or whatever, in any other way, I have injuriously spoken or written, (if they admit no other more favourable interpretation,) as to my grief I have spoken and written many things, and more than I can remember; all and everything I recant, and freely and honestly declare and profess to be groundless, false, and incapable of proof.” Hoffmann, the president of the states of Styria, who had taken Kepler to Prague on his first visit, exerted himself to perfect the reconciliation, and this hasty quarrel was entirely passed over.
On Kepler's return to Prague, in September, 1601, he was presented to the Emperor by Tycho, and honoured with the title of Imperial Mathematician, on condition of assisting Tycho in his calculations. Kepler desired nothing more than this condition, since Tycho was at that time probably the only person in the world who possessed observations sufficient for the reform which he now began to meditate in the theory of astronomy. Rudolph appears to have valued both Tycho Brahe and Kepler as astrologers rather than astronomers; but although unable to appreciate rightly the importance of the task they undertook, of compiling a new set of astronomical tables founded upon Tycho's observations, yet his vanity was flattered with the prospect of his name being connected with such a work, and he made liberal promises to defray the expense of the new Rudolphine Tables. Tycho's principal assistant at this time was Longomontanus, who altered his name to this form, according to the prevalent fashion of giving to every name a Latin termination. Lomborg or Longbierg was the name, not of his family, but of the village in Denmark, where he was born, just as Muller was seldom called by any other name than Regiomontanus, from his native town Konigsberg, as George Joachim Rheticus was so surnamed from Rhetia, the country of the Grisons, and as Kepler himself was sometimes called Leonmontanus, from Leonberg, where he passed his infancy. It was agreed between Longomontanus and Kepler, that in discussing Tycho's observations, the former should apply himself especially to the Moon, and the latter to Mars, on which planet, owing to its favourable position, Tycho was then particularly engaged. The nature of these labours will be explained when we come to speak of the celebrated book “On the Motions of Mars.”
This arrangement was disturbed by the return of Longomontanus into Denmark, where he had been offered an astronomical professorship, and still more by the sudden death of Tycho Brahe himself in the following October. Kepler attended him during his illness, and after his death undertook to arrange some of his writings. But, in consequence of a misunderstanding between him and Tycho's family, the manuscripts were taken out of his hands; and when, soon afterwards, the book appeared, Kepler complained heavily that they had published, without his consent or knowledge, the notes and interlineations added by him for his own private guidance whilst preparing it for publication.
On Tycho's death, Kepler succeeded him as principal mathematician to the emperor; but although he was thus nominally provided with a liberal salary, it was almost always in arrear. The pecuniary embarrassments in which he constantly found himself involved, drove him to the resource of gaining a livelihood by casting nativities. His peculiar temperament rendered him not averse from such speculations, and he enjoyed considerable reputation in this line, and received ample remuneration for his predictions. But although he did not scruple, when consulted, to avail himself in this manner of the credulity of his contemporaries, he passed over few occasions in his works of protesting against the futility of this particular genethliac astrology. His own astrological creed was in a different strain, more singular, but not less extravagant. We shall defer entering into any details concerning it, till we come to treat of his book on Harmonics, in which, he has collected and {12} recapitulated the substance of his scattered opinions on this strange subject.
His next works deserving notice are those published on occasion of the new star which shone out with great splendour in 1604, in the constellation Cassiopeia*. Immediately on its appearance, Kepler wrote a short account of it in German; marked with all the oddity which characterises most of his productions. We shall see enough of his astronomical calculations when we come to his book on Mars; the following passage will probably be found more amusing.
After comparing this star with that of 1572, and mentioning that many persons who had seen it maintained this to be the brighter of the two, since it was nearly twice the size of its nearest neighbour, Jupiter, he proceeds as follows: — “Yonder one chose for its appearance a time no way remarkable, and came into the world quite unexpectedly, like an enemy storming a town, and breaking into the market-place before the citizens are aware of his approach; but ours has come exactly in the year of which astrologers have written so much about the fiery trigon that happens in it†; just in the month in which (according to Cyprian) Mars comes up to a very perfect conjunction with the other two superior planets; just in the day when Mars has joined Jupiter, and just in the place where this conjunction has taken place. Therefore the apparition of this star is not like a secret hostile irruption, as was that one of 1572, but the spectacle of a public triumph, or the entry of a mighty potentate; when the couriers ride in some time before, to prepare his lodgings, and the crowd of young urchins begin to think the time over-long to wait: then roll in, one after another, the ammunition, and money, and baggage waggons, and presently the trampling of horse, and the rush of people from every side to the streets and windows; and when the crowd have gazed with their jaws all agape at the troops of knights; then at last, the trumpeters, and archers, and lackeys, so distinguish the person of the monarch, that there is no occasion to point him out, but every one cries out of his own accord—‘Here we have him!’—What it may portend is hard to determine, and thus much only is certain, that it comes to tell mankind either nothing at all, or high and weighty news, quite beyond human sense and understanding. It will have an important influence on political and social relations; not indeed by its own nature, but, as it were, accidentally through the disposition of mankind. First, it portends to the book-sellers great disturbances, and tolerable gains; for almost every Theologus, Philosophicus, Medicus, and Mathematicus, or whoever else, having no laborious occupation intrusted to him, seeks his pleasure in studiis, will make particular remarks upon it, and will wish to bring these remarks to the light. Just so will others, learned and unlearned, wish to know its meaning, and they will buy the authors who profess to tell them. I mention these things merely by way of example, because, although thus much can be easily predicted without great skill, yet may it happen just as easily, and in the same manner, that the vulgar, or whoever else is of easy faith, or it may be, crazy, may wish to exalt himself into a great prophet; or it may even happen that some powerful lord, who has good foundation and beginning of great dignities, will be cheered on by this phenomenon to venture on some new scheme, just as if God had set up this star in the darkness merely to enlighten them.”
It would hardly be supposed, from the tenor of this last passage, that the writer of it was not a determined enemy to astrological predictions of every description. In 1602 he had published a disputation, not now easily met with, “On the Principles of Astrology,” in which it seems that he treated the professed astrologers with great severity. The essence of this book is probably contained in the second treatise on the new star, which he published in 1606*. In this volume he inveighs repeatedly against the vanity and worthlessness of ordinary astrology, declaring at the same time, that the professors of that art know that this judgment is pronounced by one well acquainted with its principles. “For if the vulgar are to pronounce who is the best astrologer, my reputation is known to be of the highest order; if they {13} prefer the judgment of the learned, they are already condemned. Whether they stand with me in the eyes of the populace, or I fall with them before the learned, in both cases I am in their ranks; I am on a level with them; I cannot be renounced.”
The theory which Kepler proposed to substitute is intimated shortly in the following passage: “I maintain that the colours and aspects, and conjunctions of the planets, are impressed on the natures or faculties of sublunary things, and when they occur, that these are excited as well in forming as in moving the body over whose motion they preside. Now let no one conceive a prejudice that I am anxiously seeking to mend the deplorable and hopeless cause of astrology by far-fetched subtilties and miserable quibbling. I do not value it sufficiently, nor have I ever shunned having astrologers for my enemies. But a most unfailing experience (as far as can be hoped in natural phenomena) of the excitement of sublunary natures by the conjunctions and aspects of the planets, has instructed and compelled my unwilling belief.”
After exhausting other topics suggested by this new star, he examines the different opinions on the cause of its appearance. Among others he mentions the Epicurean notion, that it was a fortuitous concourse of atoms, whose appearance in this form was merely one of the infinite number of ways in which, since the beginning of time, they have been combined. Having descanted for some time on this opinion, and declared himself altogether hostile to it, Kepler proceeds as follows:—“When I was a youth, with plenty of idle time on my hands, I was much taken with the vanity, of which some grown men are not ashamed, of making anagrams, by transposing the letters of my name, written in Greek, so as to make another sentence: out of IoannhV KiplhroV I made Sirhnon kaphloV*; in Latin, out of Joannes Keplerus came Serpens in akuleo†. But not being satisfied with the meaning of these words, and being unable to make another, I trusted the thing to chance, and taking cut of a pack of playing cards as many as there were letters in the name, I wrote one upon each, and then began to shuffle them, and at each shuffle to read them in the order they came, to see if any meaning came of it. Now, may all the Epicurean gods and goddesses confound this same chance, which, although I spent a good deal of time over it, never showed me anything like sense even from a distance*. So I gave up my cards to the Epicurean eternity, to be carried away into infinity, and, it is said, they are still flying about there, in the utmost confusion among the atoms, and have never yet come to any meaning. I will tell these disputants, my opponents, not my own opinion, but my wife's. Yesterday, when weary with writing, and my mind quite dusty with considering these atoms, I was called to supper, and a salad I had asked for was set before me. It seems then, said I aloud, that if pewter dishes, leaves of lettuce, grains of salt, drops of water, vinegar, and oil, and slices of egg, had been flying about in the air from all eternity, it might at last happen by chance that there would come a salad. Yes, says my wife, but not so nice and well dressed as this of mine is.”
During several years Kepler remained, as he himself forcibly expressed it, begging his bread from the emperor at Prague, and the splendour of his nominal income served only to increase his irritation, at the real neglect under which he nevertheless persevered in his labours. His family was increasing, and he had little wherewith to support them beyond the uncertain proceeds of his writings and nativities. His salary was charged partly on the states of Silesia, partly on the imperial treasury; but it was in vain that repeated orders were procured for the payment of the arrears due to him. The resources of the empire were drained by the constant demands of an engrossing war, and Kepler had not sufficient influence to enforce his claims against those who thought even the smallest sum bestowed upon him ill spent, in fostering profitless speculations. In consequence of this niggardliness, Kepler was forced to postpone the publication of the Rudolphine Tables, which he was engaged in constructing from his own and Tycho Brahe's observations, and applied himself to other works of a less costly description. Among these may be {14} mentioned a “Treatise on Comets,” written on occasion of one which appeared in 1607: in this he suggests that they are planets moving in straight lines. The book published in 1804, which he entitles “A Supplement to Vitellion,” may be considered as containing the first reasonable and consistent theory of optics, especially in that branch of it usually termed dioptrics, which relates to the theory of vision through transparent substances. In it was first explained the true use of the different parts of the eye, to the knowledge of which Baptista Porta had already approached very nearly, though he stopped short of the accurate truth. Kepler remarked the identity of the mechanism in the eye with that beautiful invention of Porta's, the camera obscura; showing, that the light which falls from external objects on the eye is refracted through a transparent substance, called, from its form and composition, the crystalline lens, and makes a picture on the fine net-work of nerves, called the retina, which lies at the back of the eye. The manner in which the existence of this coloured picture on the retina causes to the individual the sensation of sight, belongs to a theory not purely physical; and beyond this point Kepler did not attempt to go.
The direction into which rays of light (as they are usually called) are bent or refracted in passing through the air and other transparent substances or mediums, is discussed in this treatise at great length. Tycho Brahe had been the first astronomer who recognized the necessity of making some allowance on this account in the observed heights of the stars. A long controversy arose on this subject between Tycho Brahe and Rothman,” the astronomer at Hesse Cassel, a man of unquestionable talent, but of odd and eccentric habits. Neither was altogether in the right, although Tycho had the advantage in the argument. He failed however to establish the true law of refraction, and Kepler has devoted a chapter to an examination of the same question. It is marked by precisely the same qualities as those appearing so conspicuously in his astronomical writings:—great ingenuity; wonderful perseverance; bad philosophy. That this may not be taken solely upon assertion, some samples of it are subjoined. The writings of the authors of this period are little read or known at the present day; and it is only by copious extracts that any accurate notion can be formed of the nature and value of their labours. The following tedious specimen of Kepler's mode of examining physical phenomena is advisedly selected to contrast with his astronomical researches: though the luck and consequently the fame that attended his divination were widely different on the two occasions, the method pursued was the same. After commenting on the points of difference between Rothman and Tycho Brahe, Kepler proceeds to enumerate his own endeavours to discover the law of refraction.
“I did not leave untried whether, by assuming a horizontal refraction according to the density of the medium, the rest would correspond with the sines of the distances from the vertical direction, but calculation proved that it was not so: and indeed there was no occasion to have tried it, for thus the refractions would increase according to the same law in all mediums, which is contradicted by experiment.
“The same kind of objection may be brought against the cause of refraction alleged by Alhazen and Vitellion. They say that the light seeks to be compensated for the loss sustained at the oblique impact; so that in proportion as it is enfeebled by striking against the denser medium, in the same degree does it restore its energy by approaching the perpendicular, that it may strike the bottom of the denser medium with greater force; for those impacts are most forcible which are direct. And they add some subtle notions, I know not what, how the motion of obliquely incident light is compounded of a motion perpendicular and a motion parallel to the dense surface, and that this compound motion is not destroyed, but only retarded by meeting the denser medium.
“I tried another way of measuring the refraction, which should include the density of the medium and the incidence:
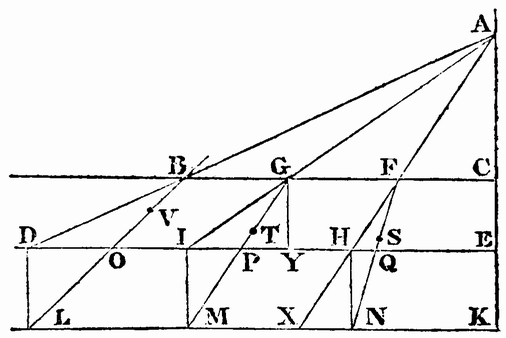
for, since a denser medium is the cause of refraction, it seems to be the same thing as if we were to prolong the depth of the medium in which the rays are {15} refracted into as much space as would be filled by the denser medium under the force of the rarer one.
“Let A be the place of the light, BC the surface of the denser medium, DE its bottom. Let AB, AG, AF be rays falling obliquely, which would arrive at D, I, H, if the medium were uniform. But because it is denser, suppose the bottom to be depressed to KL, determined by this that there is as much of the denser matter contained in the space DC as of the rarer in LC: and thus, on the sinking of the whole bottom DE, the points D, I, H, E will descend vertically to L, M, N, K. Join the points B L, GM, FN, cutting DE in O, P, Q; the retracted rays will be ABO, AGP, AFQ.”—“This method is refuted by experiment; it gives the refractions near the perpendicular AC too great in respect of those near the horizon. Whoever has leisure may verify this, either by calculation or compasses. It may be added that the reasoning; itself is not very sure-footed, and, whilst seeking to measure other things, scarcely takes in and comprehends itself.” This reflection must not be mistaken for the dawn of suspicion that his examination of philosophical questions began not altogether at the right end: it is merely an acknowledgment that he had not yet contrived a theory with which he was quite satisfied before it was disproved by experiment.
After some experience of Kepler's miraculous good fortune in seizing truths across the wildest and most absurd theories, it is not easy to keep clear of the opposite feeling of surprise whenever any of his extravagancies fail to discover to him some beautiful law of nature. But we must follow him as he plunges deeper in this unsuccessful inquiry; and the reader must remember, in order fully to appreciate this method of philosophizing, that it is almost certain that Kepler laboured upon every one of the gratuitous suppositions that he makes, until positive experiment satisfied him of their incorrectness.
“I go on to other methods. Since density is clearly connected with the cause of the refractions, and refraction itself seems a kind of compression of light, as it were, towards the perpendicular, it occurred to me to examine whether there was the same proportion between the mediums in respect of density and the parts of the bottom illuminated by the light, when let into a vessel, first empty, and afterwards filled with water. This mode branches out into many: for the proportion may be imagined, either in the straight lines, as if “one should say that the line EQ, illuminated by refraction, is to EH illuminated directly, as the density of the one medium is to that of the other—Or another may suppose the proportion to be between FC and FH—Or it may be conceived to exist among surfaces, or so that some power of EQ should be to some power of EH in this proportion, or the circles or similar figures described on them. In this manner the proportion of EQ to EP would be double that of EH to EI—Or the proportion may be conceived existing among the solidities of the pyramidal frustums FHEC, FQEC—Or, since the proportion of the mediums involves a threefold consideration, since they have density in length, breadth, and thickness, I proceeded also to examine the cubic proportions among the lines EQ, EH.
“I also considered other lines. From any of the points of refraction as G, let a perpendicular GY be dropped upon the bottom. It may become a question whether possibly the triangle IGY, that is, the base IY, is divided by the refracted ray GP, in the proportion of the densities of the mediums.
“I have put all these methods hew together, because the same remark disproves them all. For, in whatever manner, whether as line, plane, or pyramid, EI observes a given proportion to EP, or the abbreviated line YI to YP, namely, the proportion of the mediums, it is sure that EI, the tangent of the distance of the point A from the vertex, will become infinite, and will, therefore make EP or YP, also infinite. Therefore, IGP, the angle ‘of refraction, will be entirely lost; and, as it approaches the horizon, will gradually become less and less, which is contrary to experiment.
“I tried again whether the images are equally removed from their points of refraction, and whether the ratio of the densities measures the least distance. For instance, supposing E to be the image, C the surface of the water, K the bottom, and CE to CK in the proportion of the densities of the mediums. Now, let F, G, B, be three other points of refraction and images at S, T, V, and let CE be equal to FS, GT, and BV. But according to this rule an image E would still be somewhat raised in the perpendicular AK, which is contrary to experiment, not to mention other {16} contradictions. Thirdly, whether the proportion of the mediums holds between FH and FX, supposing H to be the place of the image? Not at all. For so, CE would be in the same proportion to CK, so that the height of the image would always be the same, which we have just refuted. Fourthly, whether the raising of the image at E is to the raising at H, as CE to FH? Not in the least; for so the images either would never begin to be raised, or, having once begun, would at last be infinitely raised, because FH at last becomes infinite. Fifthly, whether tins images rise in proportion to the sines of the inclinations? Not at all; for so the proportion of ascent would be the same in all mediums. Sixthly, are then the images raised at first, and in perpendicular radiation, according to the proportion of the mediums, and do they subsequently rise more and more according to the sines of the inclinations? For so the proportion would be compound, and would become different in different mediums. There is nothing in it: for the calculation disagreed with experiment. And generally it is in vain to have regard to the image or the place of the image, for that very reason, that it is imaginary. For there is no connexion between the density of the medium or any real quality or refraction of the light, and an accident of vision, by sn error of which the image happens.
“Up to this point, therefore, I had followed a nearly blind mode of inquiry, and had trusted to good fortune; but now I opened the other eye, and hit upon a sure method, for I pondered the fact, that the image of a thing seen under water approaches closely to the true ratio of the refraction, and almost measures it; that it is low if the thing is viewed directly from above; that by degrees it rises as the eye passes towards the horizon of the water. Yet, on the other hand, the reason alleged above, proves that the measure is not to be sought in the image, because the image is not a thing actually existing, but arises from a deception of vision which is purely accidental. By a comparison of these conflicting arguments, it occurred to me at length, to seek the causes themselves of the existence of the image under water, and in these causes the measure of the refractions. This opinion was strengthened in me by seeing that opticians had not rightly pointed out the cause of the image which appears both in mirrors and in water. And this was the origin of that labour which I undertook in the third chapter. Nor, indeed, was that labour trifling, whilst limiting down false opinions of all sorts among the principles, in a matter rendered so intricate by the false traditions of optical writers; whilst striking out half a dozen different paths, and beginning anew the whole business. How often did it happen that a rash confidence made me look upon that which I sought with such ardour, as at length discovered!
“At length I cut this worse than Gordian knot of catoptrics by analogy alone, by considering what happens in mirrors, and what must happen analogically in water. In mirrors, the image appears at a distance from the real place of the object, not being itself material, but produced solely by reflection at the polished surface. Whence it followed in water also, that the images rise ani approach the surface, not according to the law of the greater or less density in the water, as the view is less or more oblique, but solely because of the refraction of the ray of light passing from the object to the eye. On which assumption, it is plain that every attempt I had hitherto made to measure refractions by the image, and its elevation, must fall to the ground. And this lie-came more evident when I discovered the true reason why the image is in the same perpendicular line with the object both in mirrors and in dense mediums. When 1 had succeeded thus far by analogy in this most difficult investigation, as to the place of the image, I began to follow out the analogy further, led on by the strong desire of measuring refraction. For 1 wished to get hold of some measure of some sort, no matter how blindly, having no fear but that so soon as the measure should be accurately known, the cause would plainly appear. I went to work as follows. In convex mirrors the image is diminished, and just so in rarer mediums; in denser mediums it is magnified, as in concave mirrors. In convex mirrors the central parts of the image approach, and recede in concave farther than towards the circumference; the same thing happens in different mediums, so that in water the bottom appears depressed, and the surrounding parts elevated. Hence it appears that a denser medium corresponds with a concave reflecting surface, and a rarer one with a convex one: it was clear, at the same time, that the plane surface of the {17} water affects a property of curvature. I was, therefore, to excogitate causes consistent with its having this effect of curvature, and to see if a reason could be given, why the parts of the water surrounding the incident perpendicular should represent a greater density than the parts just under the perpendicular. And so the thing came round again to my former attempts, which being refuted by reason and experiment, I was forced to abandon the search after a cause. I then proceeded to measurements.”
Kepler then endeavoured to connect his measurements of different quantities of refraction with the conic sections, and was tolerably well pleased with some of his results. They were however not entirely satisfactory, on which he breaks off with the following sentence: “Now, reader, you and I have been detained sufficiently long whilst I have been attempting to collect into one faggot the measure of different refractions: I acknowledge that the cause cannot be connected with this mode of measurement: for what is there in common between refractions made at the plane surfaces of transparent mediums, and mixtilinear conic sections? Wherefore, quod Deus bene voriat, we will now have had enough of the causes of this measure; and although, even now, we are perhaps erring something from the truth, yet it is better, by working on, to show our industry, than our laziness by neglect.”
Notwithstanding the great length of this extract, we must add the concluding paragraph of the Chapter, directed, as we are told in the margin, against the “Tychonomasticks:”—
“I know how many blind men at this day dispute about colours, and how they long for some one to give some assistance by argument to their rash insults of Tycho, and attacks upon this whole matter of refractions; who, if they had kept to themselves their puerile errors and naked ignorance, might have escaped censure; for that may happen to many great men. But since they venture forth publicly, and with thick books and sounding titles, lay baits for the applause of the unwary, (for now-a-days there is more danger from the abundance of bad books, than heretofore, from the lack of good ones,) therefore let them know that a time is set for them publicly to amend their own errors. If they longer delay doing this, it shall be open, either to me or any other, to do to these unhappy meddlers in geometry as they have taken upon themselves to do with respect to men of the highest reputation. And although this labour will be despicable, from the vile nature of the follies against which it will be directed, yet so much more necessary than that which they have undertaken against others, as he is a greater public nuisance, who endeavours to slander good and necessary inventions, than he who fancies he has found what is impossible to discover. Meanwhile, let them cease to plume themselves on the silence which is another word for their own obscurity.”
Although Kepler failed, as we have seen, to detect the true law of refraction (which was discovered some years later by Willibrord Snell, a Flemish mathematician,) there are many things well deserving notice in his investigations. He remarked, that the quantity of refraction would alter, if the height of the atmosphere should vary; and also, that it would be different at different temperatures. Both these sources of variation are now constantly taken into account, the barometer and thermometer giving exact indications of these changes. There is also a very curious passage in one of his letters to Bregger, written in 1605, on the subject of the colours in the rainbow. It is in these words:— “Since every one sees a different rainbow, it is possible that some one may see a rainbow in the very place of my sight. In this case, the medium is coloured at the place of my vision, to which the solar ray comes to me through water, rain, or aqueous vapours. For the rainbow is seen when the sun is shining between rain, that is to say, when the sun also is visible. Why then do I not see the sun green, yellow, red, and blue, if vision takes place according to the mode of illumination? I will say something for you to attack or examine. The sun's rays are not coloured, except with a definite quantity of refraction. Whether you are in the optical chamber, or standing opposite glass globes, or walking in the morning dew, everywhere it is obvious that a certain and definite angle is observed, under which, when seen in dew, in glass, in water, the sun's splendour appears coloured, and under no other angle. There is no colouring by mere reflexion, without the refraction of a denser medium.” How closely does Kepler appear, in this passage, to approach the discovery which forms not the least part of Newton's fame!
We also find in this work a defence of the opinion that the planets are luminous {18} of themselves; on the ground that the inferior planets would, on the contrary supposition, display phases like those of the moon when passing between us and the sun. The use of the telescope was not then known; and, when some years later the form of the disk of the planets was more clearly defined with their assistance, Kepler had the satisfaction of finding his assertions verified by the discoveries of Galileo, that these changes do actually take place. In another of his speculations, connected with the same subject, he was less fortunate. In 1607 a black spot appeared on the face of sun, such as may almost always be seen with the assistance of the telescope, although they are seldom large enough to be visible to the unassisted eye. Kepler saw it for a short time, and mistook it for the planet Mercury, and with his usual precipitancy hastened to publish an account of his observation of this rare phenomenon. A few years later, Galileo discovered with his glasses, a great number of similar spots; and Kepler immediately retracted the opinion announced in his treatise, and acknowledged his belief that previous accounts of the same occurrence which he had seen in old authors, and which he had found great difficulty in reconciling with his more accurate knowledge of the motions of Mercury, were to be referred to a like mistake. On this occasion of the invention of the telescope, Kepler's candour and real love of truth appeared in a most favourable light. Disregarding entirely the disagreeable necessity, in consequence of the discoveries of this new instrument, of retracting several opinions which he had maintained with considerable warmth, he ranged himself at once on the side of Galileo, in opposition to the bitter and determined hostility evinced by most of those whose theories were endangered by the new views thus offered of the heavens. Kepler's quarrel with his pupil, Horky, on this account, has been mentioned in the “Life of Galileo;” and this is only a selected instance from the numerous occasions on which he espoused the same unpopular side of the argument. He published a dissertation to accompany Galileo's “Intelligencer of the Stars,” in which he warmly expressed his admiration of that illustrious inquirer into nature. His conduct in this respect was the more remarkable, as some of his most intimate friends had taken a very opposite view of Galileo's merit, and seem to have laboured much to disturb their mutual regard; Mästlin especially, Kepler's early instructor, seldom mentioned to him the name of Galileo, without some contemptuous expression of dislike. These statements have rather disturbed the chronological order of the account of Kepler's works. We now return to the year, 1609, in which he published his great and extraordinary book, “On the Motions of Mars;” a work which holds the intermediate place, and is in truth the connecting link, between the discoveries of Copernicus and Newton.
Kepler had begun to labour upon these commentaries from the moment. when he first made Tycho's acquaintance; and it is on this work that his reputation should be made mainly to rest. It is marked in many places with his characteristic precipitancy, and indeed one of the most important discoveries announced in it (famous among astronomers by the name of the Equable Description of Areas) was blundered upon by a lucky compensation of errors, of the nature of which Kepler remained ignorant to the very last. Yet there is more of the inductive method in this than in any of his other publications; and the unwearied perseverance with which he exhausted years in hunting down his often renewed theories, till at length he seemed to arrive at the true one, almost by having previously disproved every other, excites a feeling of astonishment nearly approaching to awe. It is wonderful how he contrived to retain his vivacity and creative fancy amongst the clouds of figures which he conjured up round him; for the slightest hint or shade of probability was sufficient to plunge him into the midst of the most laborious computations. He was by no means an accurate calculator, according to the following character which he has given of himself;—“Something of these delays must be attributed to my own temper, for non omnia possumus omnes, and I am totally unable to observe any order; what I do suddenly, I do confusedly, and if I produce any thing well arranged, it has been done ten times over. Sometimes an error of calculation committed by hurry, delays me a great length of time. I could indeed publish an infinity of things, for though my reading is confined, my imagination is abundant, but I grow dissatisfied with such confusion: I get disgusted and out of humour, and either throw them away, or put them aside to {19} be looked at again; or, in other words, to be written again, for that is generally the end of it. I entreat you, my friends, not to condemn me for ever to grind in the mill of mathematical calculations: allow me some time for philosophical speculations, my only delight.”
He was very seldom able to afford the expense of maintaining an assistant, and was forced to go through most of the drudgery of his calculations by himself; and the most confirmed and merest arithmetician could not have toiled more doggedly than Kepler did in the work of which we are about to speak.
In order that the language of his astronomy may be understood, it is necessary to mention briefly some of the older theories. When it had been discovered that the planets did not move regularly round the earth, which was supposed to be fixed in the centre of the world, a mechanism was contrived by which it was thought that the apparent irregularity could be represented, and yet the principle of uniform motion, which was adhered to with superstitious reverence, might be preserved. This, in its simplest form, consisted in supposing the planet to move uniformly in a small circle, called an epicycle, the centre of which moved with an equal angular motion in the opposite direction round the earth*. The circle Dd, described by D, the centre of the epicycle, was called the deferent. For instance, if the planet was supposed to be at A when the centre of the epicycle was at D, its
position, when the centre of the epicycle had removed to d, would be at p, found by drawing dp parallel to DA. Thus, the angle adp, measuring the motion of the planet in its epicycle, would be equal to DEd, the angle described by the centre of the epicycle in the deferent. The angle pEd between Ep, the direction in which a planet so moving would be seen from the earth, supposed to be at E, and Ed the direction in which it would have been seen had it been moving in the centre of the deferent, was called the equation of the orbit, the word equation, in the language of astronomy, signifying what must be added or taken from an irregularly varying quantity to make it vary uniformly.
As the accuracy of observations increased, minor irregularities were discovered, which were attempted to be accounted for by making a second deferent of the epicycle, and making the centre of a second epicycle revolve in the circumference of the first, and so on, or else by supposing the revolution in the epicycle not to be completed in exactly the time in which its centre is carried round the deferent. Hipparchus was the first to make a remark by which the geometrical representation of these inequalities was considerably simplified. In fact, if EC be taken equal to pd, Cd will be a parallelogram, and consequently Cp equal to Ed, so that the machinery of the first deferent and epicycle amounts to supposing that the planet revolves uniformly in a circle round the point C, not coincident with the place of the earth. This was consequently called the excentric theory, in opposition to the former or concentric one, and was received as a great improvement. As the point d is not represented by this construction, the equation to the orbit was measured by the angle CpE, which is equal to pEd. It is not necessary to give any account of the manner in which the old astronomers determined the magnitudes and positions of these orbits, either in the concentric, or excentric theory, the present object being little more than to explain the meaning of the terms it will be necessary to use in describing Kepler's investigations.
To explain the irregularities observed in the other planets, it became necessary to introduce another hypothesis, in adopting which the severity of the principle of uniform motion was somewhat relaxed. The machinery consisted partly of an excentric deferent round E, the earth, and on it an epicycle, in which the planet revolved uniformly; but the centre of the epicycle, instead of revolving uniformly round C, the centre of the deferent, {20}
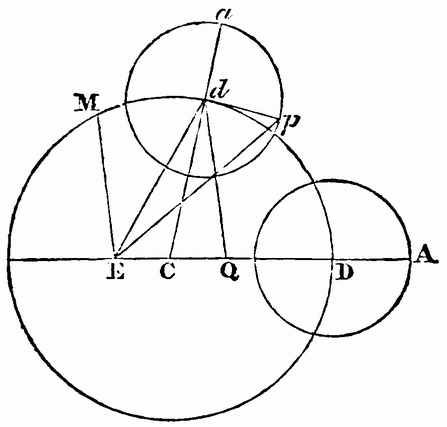
as it had hitherto been made to do, was supposed to move in its circumference with an uniform angular motion round a third point, Q; the necessary effect of which supposition was, that the linear motion of the centre of the epicycle ceased to be uniform. There were thus three points to be considered within the deferent: E, the place of the earth; C, the centre of the deferent, and sometimes called the centre of the orbit; and Q, called the centre of the equant, because, if any circle were described round Q, the planet would appear to a spectator at Q, to be moving equably in it. It was long uncertain what situation should be assigned to the centre of the equant, so as best to represent the irregularities to a spectator on the earth, until Ptolemy decided on placing it (in every case but that of Mercury, the observations on which were very doubtful) so that C, the centre of the orbit, lay just half way in the straight line, joining Q, the centre of equable motion, and E, the place of the earth. This is the famous principle, known by the name of the bisection of the excentricity. The first equation required for the planet's motion was thus supposed to be due to the displacement of E, the earth, from Q, the centre of uniform motion, which was called the excentricity of the equant: it might be represented by the angle dEM, drawing EM parallel to Qd; for clearly M would have been the place of the centre of the epicycle at the end of a time proportional to Dd, had it moved with an equable angular motion round E instead of Q. This angle dEM, or its equal EdQ, was called the equation of the centre (i. e. of the centre of the epicycle); and is clearly greater than if EQ, the excentricity of the equant, had been no greater than EC, called the excentricity of the orbit. The second equation was measured by the angle subtended at E by d, the centre of the epicycle, and p the planet's place in its circumference: it was called indifferently the equation of the orbit, or of the argument. In order to account for the apparent stations and retrogradations of the planets, it became necessary to suppose that many revolutions in the latter were completed during one of the former. The variations of latitude of the planets were exhibited by supposing not only that the planes of their deferents were oblique to the plane of the ecliptic and that the plane of the epicycle was also oblique to that of the deferent, but that the inclination of the two latter was continually changing, although Kepler doubts whether this latter complication was admitted by Ptolemy. In the inferior planets, it was even thought necessary to give to the plane of the epicycle two oscillatory motions on axes at right angles to each other.
The astronomers at this period were much struck with a remarkable connexion between the revolutions of the superior planets in their epicycles, and the apparent motion of the sun; for when in conjunction with the sun, as seen from the earth, they were always found to be in the apogee, or point of greatest distance from the earth, of their epicycle; and when in opposition to the Sun, they were as regularly in the perigee, or point of nearest approach of the epicycle. This correspondence between two phenomena, which, according to the old astronomy, were entirely unconnected, was very perplexing, and it seems to have been one of the facts which led Copernicus to substitute the theory of the earth's motion round the sun.
As time wore on, the superstructure of excentrics and epicycles, which had been strained into representing the appearances of the heavens at a particular moment, grew out of shape, and the natural consequence of such an artificial system was, that it became next to impossible to foresee what ruin might be produced in a remote part of it by any attempt to repair the derangements and refit the parts to the changes, as they began to be remarked in any particular point. In the ninth century of our era, Ptolemy's tables were already useless, and all those that were contrived with unceasing toil to supply their place, rapidly became as unserviceable as they. Still the triumph of genius was seen in the veneration that continued to be paid to the assumptions of Ptolemy and Hipparchus; and even when the great reformer, Copernicus, {21} appeared, he did not for a long time intend to do more than slightly modify their principles. That which he found difficult in the Ptolemaic system, was none of the inconveniences by which, since the establishment of the new system, it has become common to demonstrate the inferiority of the old one; it was the displacement of the centre of the equant from the centre of the orbit that principally indisposed him against it, and led him to endeavour to represent the appearances by some other combinations of really uniform circular motions. There was an old system, called the Egyptian, according to which Saturn, Jupiter, Mars, and the Sun circulated round the earth, the sun carrying with it, as two moons or satellites, the other two planets, Venus and Mercury. This system had never entirely lost credit: it had been maintained in the fifth century by Martianus Capella*, and indeed it was almost sanctioned, though not formally taught, by Ptolemy himself, when he made the mean motion of the sun the same as that of the centres of the epicycles of both these planets. The remark which had also been made by the old astronomers, of the connexion between the motion of the sun and the revolutions of the superior planets in their epicycles, led him straight to the expectation that he might, perhaps, produce the uniformity he sought by extending the Egyptian system to these also, and this appears to have been the shape in which his reform was originally projected. It was already allowed that the centre of the orbits of all the planets was not coincident with the earth, but removed from it by the space EC. This first change merely made EC the same for all the planets, and equal to the mean distance of the earth from the sun. This system afterwards acquired great celebrity through its adoption by Tycho Brahe, who believed it originated with himself. It might perhaps have been at this period of his researches, that Coperniens was struck with the passages in the Latin and Greek authors, to which he refers as testifying the existence of an old belief in the motion of the earth round the sun. He immediately recognised how much this alteration would further his principles of uniformity, by referring all the planetary motions to one centre, and did not hesitate to embrace it. The idea of explaining the daily and principal apparent motions of the heavenly bodies by the revolution of the earth on its axis, would be the concluding change, and became almost a necessary consequence of his previous improvements, as it was manifestly at variance with his principles to give to all the planets and starry worlds a rapid daily motion round the centre of the earth, now that the latter was removed from its former supposed post in the centre of the universe, and was itself carried with an annual motion round another fixed point.
The reader would, however, form an inaccurate notion of the system of Copernicus, if he supposed that it comprised no more than the theory that each planet, including the earth among them, revolved in a simple circular orbit round the sun. Copernicus was too well acquainted with the motions of the heavenly bodies, not to be aware that such orbits would not accurately represent them; the motion he attributed to the earth round the sun, was at first merely intended to account for those which were called the second inequalities of the planets, according to which they appear one while to move forwards, then backwards, and at intermediate periods, stationary, and which thenceforward were also called the optical equations, as being merely an optical illusion. With regard to what were called the first inequalities, or physical equations, arising from a real inequality of motion, he still retained the machinery of the deferent and epicycle; and all the alteration he attempted in the orbits of the superior planets was an extension of the concentric theory to supply the place of the equant, which he considered the blot of the system. His theory for this purpose is shown in the accompanying diagram, where S represents the sun,
Dd, the deferent or mean orbit of the {22} planet, on which revolves the centre of the great epicycle, whose radius, DF, was taken at 3/4 of Ptolemy's excentricity of the equant; and round the circumference of this revolved, in the opposite direction, the centre of the little epicycle, whose radius, FP, was made equal to the remaining 1/4 of the excentricity of the equant.
The planet P revolved in the circumference of the little epicycle, in the same direction with the centre of the great epicycle in the circumference of the deferent, but with a double angular velocity. The planet was supposed to be in the perigee of the little epicycle, when its centre was in the apogee of the greater; and whilst, for instance, D moved equably though the angle DSd, F moved through hdf = DSd, and P through rfp = 2DSd.
It is easy to show that this construction gives nearly the same result as Ptolemy's; for the deferent and great epicycle have been already shown exactly equivalent to an excentric circle round S, and indeed Copernicus latterly so represented it: the effect of his construction, as given above, may therefore be reproduced in the following simpler form, in which only the smaller epicycle is retained:
In this construction, the place of the planet is found at the end of any time proportional to Ff, by drawing fr parallel to SF, and taking rfp = 2Fof. Hence it is plain, if we take OQ, equal to FP, (already assumed equal to 1/4 of Ptolemy's excentricity of the equant,) since SO is equal to 1/4 of the same, that SQ is the whole of Ptolemy's excentricity of the equant; and therefore, that Q is the position of the centre of his equant. It is also plain if we join Qp, since rfp = 2Fof, and oQ = fp, that pQ is parallel to fo, and, therefore, pQP is proportional to the time; so that the planet moves uniformly about the same point Q, as in Ptolemy's theory; and if we bisect SQ in C, which is the position of the centre of Ptolemy's deferent, the planet will, according to Copernicus, move very nearly, though not exactly, in the same circle, whose radius is CP, as that given by the simple excentric theory.
The explanation offered by Copernicus, of the motions of the inferior planets, differed again in form from that of the others. He here introduced what was called a hypocycle, which, in fact, was nothing but a deferent not including the sun, round which the centre of the orbit revolved. An epicycle in addition to the hypocycle was introduced into Mercury's orbit. In this epicycle he was not supposed to revolve, but to librate, or move up and down in its diameter. Copernicus had recourse to this complication to satisfy an erroneous assertion of Ptolemy with regard to some of Mercury's inequalities. He also retained the oscillatory motions ascribed by Ptolemy to the planes of the epicycles, in order to explain the unequal latitudes observed at the same distance from the nodes, or intersections of the orbit of the planet with the ecliptic. Into this intricacy, also, he was led by placing too much confidence in Ptolemy's observations, which he was unable to satisfy by an unvarying obliquity. Other very important errors, such as his belief that the line of nodes always coincided with the line of apsides, or places of greatest and least distance from the central body, (whereas, at that time, in the case of Mars, for instance, they were nearly 90° asunder,) prevented him from accurately representing many of the celestial phenomena.
These brief details may serve to show that the adoption or rejection of the theory of Copernicus was not altogether so simple a question as sometimes it may have been considered. It is, however, not a little remarkable, while it is strongly illustrative of the spirit of the times, that these very intricacies, with which Kepler's theories have enabled us to dispense, were the only parts of the system of Copernicus that were at first received with approbation. His theory of Mercury, especially, was considered a masterpiece of subtle invention. Owing to his dread of the unfavourable judgment be anticipated on the main principles of his system, his work remained unpublished during forty years, and was at last given to the world only just in time to allow Copernicus to receive the first copy of it a few hours before his death.
| {23} |
We may now proceed to examine Kepler's innovations, but it would be doing injustice to one of the brightest points of his character, not to preface them by his own animated exhortation to his readers. “If any one be too dull to comprehend the science of astronomy, or too feeble-minded to believe in Copernicus without prejudice to his piety, my advice to such a one is, that he should quit the astronomical schools, and condemning, if he has a mind, any or all of the theories of philosophers, let him look to his own affairs, and leaving this worldly travail, let him go home and plough his fields: and as often as he lifts up to this goodly heaven those eyes with which alone he is able to see, let him pour out his heart in praises and thanksgiving to God the Creator; and let him not fear but he is offering a worship not less acceptable than his to whom God has granted to see yet more clearly with the eyes of his mind, and who both can and will praise his God for what he has so discovered.”
Kepler did not by any means underrate the importance of his labours, as is sufficiently shewn by the sort of colloquial motto which he prefixed to his work. It consists in the first instance of an extract from the writings of the celebrated and unfortunate Peter Ramus. This distinguished philosopher was professor of mathematics in Paris, and in the passage in question, after calling on his contemporaries to turn their thoughts towards the establishment of a system of Astronomy unassisted by any hypothesis, he promised as an additional inducement to vacate his own chair in favour of any one who should succeed in this object. Ramus perished in the massacre of St. Bartholomew, and Kepler apostrophizes him as follows:—“It is well, Ramus, that you have forfeited your pledge, by quitting your life and professorship together: for if you still held it, I would certainly claim it as of right belonging to me on account of this work, as I could convince you even with your own logic.” It was rather bold in Kepler to assert his claim to a reward held out for a theory resting on no hypothesis, by light of a work filled with hypotheses of the most startling description; but of the vast importance of this book there can be no doubt; and throughout the many wild and eccentric ideas to which we are introduced in the course of it, it is fit always to bear in mind that they form part of a “work which is almost the basis of modern Astronomy.”
The introduction contains a curious criticism of the commonly-received theory of gravity, accompanied with a declaration of Kepler's own opinions on the same subject. Some of the most remarkable passages in it have been already quoted in the life of Galileo; but, nevertheless, they are too important to Kepler's reputation to be omitted here, containing as they do a distinct and positive enunciation of the law of universal gravitation. It does not appear, however, that Kepler estimated rightly the importance of the theory here traced out by him, since on every other occasion he advocated principles with which it is scarcely reconcileable. The discussion is introduced in the following terms:—
“The motion of heavy bodies hinders many from believing that the earth is moved by an animal motion, or rather a magnetic one. Let such consider the following propositions. A mathematical point, whether the centre of the universe or not, has no power, either effectively or objectively, to move heavy bodies to approach it. Let physicians prove if they can, that such power can be possessed by a point, which neither is a body, nor is conceived unless by relation alone. It is impossible that the form* of a stone should, by moving its own body, seek a mathematical point, or in other words, the centre of the universe, without regard of the body in which that point exists. Let physicians prove if they can, that natural things have any sympathy with that which is nothing. Neither do heavy bodies tend to the centre of the universe by reason that they are avoiding the extremities of the round universe; for their distance from the centre is insensible, in proportion to their distance from the extremities of the universe. And what reason could there be for this hatred? How strong, how wise must those heavy bodies be, to be able to escape so carefully from an enemy lying on all sides of {24} them: what activity in the extremities of the world to press their enemy so closely! Neither are heavy bodies driven into the centre by the whirling of the first moveable, as happens in revolving water. For if we assume such a motion, either it would not be continued down to us, or otherwise we should feel it, and be carried away with it, and the earth also with us; nay, rather, we should be hurried away first, and the earth would follow; all which conclusions are allowed by our opponents to be absurd. It is therefore plain that the vulgar theory of gravity is erroneous.
The true theory of gravity is founded on the following axioms:—Every corporeal substance, so far forth as it is corporeal, has a natural fitness for resting; in every place where it may be situated by itself beyond the sphere of influence of a body cognate with it. Gravity is a mutual affection between cognate bodies towards union or conjunction (similar in kind to the magnetic virtue), so that the earth attracts a stone much rather than the stone seeks the earth. Heavy bodies (if we begin by assuming the earth to be in the centre of the world) are not carried to the centre of the world in its quality of centre of the world, but as to the centre of a cognate round body, namely, the earth; so that wheresoever the earth may be placed, or whithersoever it may be carried by its animal faculty, heavy bodies will always be carried towards it. If the earth were not round, heavy bodies would not tend from every side in a straight line towards the centre of the earth, but to different points from different sides. If two stones were placed in any part of the world near each other, and beyond the sphere of influence of a third cognate body, these stones, like two magnetic needles, would come together in the intermediate point, each approaching the other by a space proportional to the comparative mass of the other. If the moon and earth were not retained in their orbits by their animal force or some other equivalent, the earth would mount to the moon by a fifty-fourth part of their distance, and the moon fall towards the earth through the other fifty-three parts and they would there meet; assuming however that the substance of both is of the same density. If the earth should cease to attract its waters to itself, all the waters of the sea would be raised and would flow to the body of the moon. The sphere of the attractive virtue which is in the moon extends as far as the earth, and entices up the waters; but as the moon flies rapidly across the zenith, and the waters cannot follow so quickly; a flow of the ocean is occasioned in the torrid zone towards the westward. If the attractive virtue of the moon extends as far as the earth, it follows with greater reason that the attractive virtue of the earth extends as far as the moon, and much farther; and in short, nothing which consists of earthly substance any how constituted, although thrown up to any height, can ever escape the powerful operation of this attractive virtue. Nothing which consists of corporeal matter is absolutely light, but that is comparatively lighter which is rarer, either by its own nature, or by accidental heat. And it is not to be thought that light bodies are escaping to the surface of the universe while they are carried upwards, or that they are not attracted by the earth. They are attracted, but in a less degree, and so are driven outwards by the heavy bodies; which being done, they stop, and are kept by the earth in their own place. But although the attractive virtue of the earth extends upwards, as has been said, so very far, yet if any stone should be at a distance great enough to become sensible, compared with the earth's diameter, it is true that on the motion of the earth such a stone would not follow altogether; its own force of resistance would be combined with the attractive force of the earth, and thus it would extricate itself in some degree from the motion of the earth.”
Who, after perusing such passages in the works of an author, whose writings were in the hands of every student of astronomy, can believe that Newton waited for the fall of an apple to set him thinking for the first time on the theory which has immortalised his name? An apple may have fallen, and Newton may have seen it; but such speculations as those which it is asserted to have been the cause of originating in him had been long familiar to the thoughts of every one in Europe pretending to the name of natural philosopher.
As Kepler always professed to have derived his notion of a magnetic attraction among the planetary bodies from the writings of Gilbert, it may be worth while to insert here an extract from the “New Philosophy” of that author, to show in what form he presented a similar theory of the tides, which affords the {25} most striking illustration of that attraction. This work was not published till the middle of the seventeenth century, but a knowledge of its contents may, in several instances, be traced back to the period in which it was written:—
“There are two primary causes of the motion of the seas—the moon, and the diurnal revolution. The moon does not act on the seas by its rays or its light. How then? Certainly by the common effort of the bodies, and (to explain it by something similar) by their magnetic attraction. It should be known, in the first place, that the whole quantity of water is not contained in the sea and rivers, but that the mass of earth (I mean this globe) contains moisture and spirit much deeper even than the sea. The moon draws this out by sympathy, so that they burst forth on the arrival of the moon, in consequence of the attraction of that star; and for the same reason, the quicksands which are in the sea open themselves more, and perspire their moisture and spirits during the flow of the tide, and the whirlpools in the sea disgorge copious waters; and as the star retires, they devour the same again, and attract the spirits and moisture of the terrestrial globe. Hence the moon attracts, not so much the sea as the subterranean spirits and humours; and the interposed earth has no more power of resistance than a table or any other dense body has to resist the force of a magnet. The sea rises from the greatest depths, in consequence of the ascending humours and spirits; and when it is raised up, it necessarily flows on to the shores, and from the shores it enters the rivers.”*
This passage sets in the strongest light one of the most notorious errors of the older philosophy, to which Kepler himself was remarkably addicted. If Gilbert had asserted, in direct terms, that the moon attracted the water, it is certain that the notion would have been stigmatized (as it was for a long time in Newton's hands) as arbitrary, occult, and unphilosophical: the idea of these subterranean humours was likely to be treated with much more indulgence. A simple statement, that when the moon was over the water the latter had a tendency to rise towards it, was thought to convey no instruction; but the assertion that the moon draws out subterranean spirits by sympathy, carried with it a more imposing appearance of theory. The farther removed these humours were from common experience, the easier it became to discuss them in vague and general language; and those who called themselves philosophers could endure to hear attributes bestowed on these fictitious elements which revolted their imaginations when applied to things of whose reality at least some evidence existed.
It is not necessary to dwell upon the system of Tycho Brahe, which was identical, as we have said, with one rejected by Copernicus, and consisted in making the sun revolve about the earth, carrying with it all the other planets revolving about him. Tycho went so far as to deny the rotation of the earth to explain the vicissitudes of day and night, but even his favourite assistant Longomontanus differed from him in this part of his theory. The great merit of Tycho Brahe, and the service he rendered to astronomy, was entirely independent of any theory; consisting in the vast accumulation of observations made by him during a residence of fifteen years at Uraniburg, with the assistance of instruments, and with a degree of care, very far superior to anything known before his time in practical astronomy. Kepler is careful repeatedly to remind us that without Tycho's observations he could have done nothing. The degree of reliance that might be placed on the results obtained by observers who acknowledged their inferiority to Tycho Brahe, may be gathered from an incidental remark of Kepler to Longomontanus. He had been examining Tycho's registers, and had occasionally found a difference amounting sometimes to 4’ in the right ascensions of the same planet, deduced from different stars on the same night. Longomontanus could not deny the fact, but declared that it was impossible to be always correct within such limits. The reader should never lose sight of this uncertainty in the observations, when endeavouring to estimate the difficulty of finding a theory that would properly represent them.
When Kepler first joined Tycho Brahe at Prague, he found him and Longomontanus very busily engaged in correcting the theory of Mars, and accordingly it was this planet to which he also first directed his attention. They had formed a catalogue of the mean oppositions of Mars during twenty years, and had discovered a position of the equant, which (as they said) represented them with tolerable {26} exactness. On the other hand, they were much embarrassed by the unexpected difficulties they met in applying a system which seemed on the one hand so accurate, to the determination of the latitudes, with which it could in no way be made to agree. Kepler had already suspected the cause of this imperfection, and was confirmed in the view he took of their theory, when, on a more careful examination, he found that they overrated the accuracy even of their longitudes. The errors in these, instead of amounting as they said, nearly to 2', rose sometimes above 21'. In fact they had reasoned ill on their own principles, and even if the foundations of their theory had been correctly laid, could not have arrived at true results. But Kepler had satisfied himself of the contrary, and the following diagram shews the nature of the first alteration he introduced, not perhaps so celebrated as some of his later discoveries, but at least of equal consequence to astronomy, which could never have been extricated from the confusion into which it had fallen, till this important change had been effected. The practice of Tycho Brahe, indeed of all astronomers till the time of Kepler, had been to fix the position of the planet's orbit and equant from observations on its mean oppositions, that is to say, on the times when it was precisely six signs or half a circle distant from the mean place of the sun. In the annexed figure, let S represent the sun, C the centre of the earth's orbit, Tt.
Tycho Brahe's practice amounted to this, that if Q were supposed the place of the centre of the planet's equant, the centre of Pp its orbit was taken in QC, and not in QS, as Kepler suggested that it ought to be taken. The consequence of this erroneous practice was, that the observations were deprived of the character for which oppositions were selected, of being entirely free from the second inequalities. It followed therefore that as part of the second inequalities were made conducive towards fixing the relative position of the orbit and equant, to which they did not naturally belong, there was an additional perplexity in accounting for the remainder of them by the size and motion of the epicycle. As the line of nodes of every planet was also made to pass through C instead of S, there could not fail to be corresponding errors in the latitudes. It would only be in the rare case of an opposition of the planet in the line CS, that the time of its taking place would be the same, whether O, the centre of the orbit, was placed in CQ or SQ. Every other opposition would involve an error, so much the greater as it was observed at a greater distance from the line CS.
It was long however before Tycho Brahe could be made to acquiesce in the propriety of the proposed alteration; and, in order to remove his doubts as to the possibility that a method could be erroneous which, as he still thought, had given him such accurate longitudes, Kepler undertook the ungrateful labour of the first part of his “Commentaries.” He there shewed, in the three systems of Copernicus, Tycho Brahe, and Ptolemy, and in both the concentric and excentric theories, that though a false position were given to the orbit, the longitudes of a planet might be so represented, by a proper position of the centre of the equant, as never to err in oppositions above 5’ from those given by observation; though the second inequalities and the latitudes would thereby be very greatly deranged.
The change Kepler introduced, of observing apparent instead of mean oppositions, made it necessary to be very accurate in his reductions of the planet's place to the ecliptic; and in order to be able to do this, a previous knowledge of the parallax of Mars became indispensable. His next labour was therefore directed to this point; and finding that the assistants to whom Tycho Brahe had previously committed this labour had performed it in a negligent and imperfect manner, he began afresh with Tycho's original observations. Having satisfied himself as to the probable limits of his errors in the parallax on which he finally fixed, he proceeded to determine the inclination of the orbit and {27} the position of the line of nodes. In all these operations his talent for astronomical inquiries appeared pre-eminent in a variety of new methods by which he combined and availed himself of the observations; but it must be sufficient merely to mention this fact, without entering into any detail. One important result may be mentioned, at which he arrived in the course of them, the constancy of the inclination of the planet's orbit, which naturally strengthened him in his new theory.
Having gone through these preliminary inquiries, he came at last to fix the proportions of the orbit; and, in doing so, he determined, in the first instance, not to assume, as Ptolemy appeared to have done arbitrarily, the bisection of the excentricity, but to investigate its proportion alone with the other elements of the orbit, which resolution involved him in much more laborious calculations. After he had gone overall the steps of his theory no less than seventy times—an appalling labour, especially if we remember that logarithms were not then invented—his final result was, that in 1587, on the 6th of March, at 7h23', the longitude of the aphelion of Mars was 4s28°48'55"; that the planet's mean longitude was 6s0°51'35''; that if the semidiameter of the orbit was taken at 100000, the excentricity was 11332; and the excentricity of the equant 18564. He fixed the radius of the greater epicycle at 14988, and that of the smaller at 3628.
When he came to compare the longitudes as given by this, which he afterwards called the vicarious theory, with the observations at opposition, the result seemed to promise him the most brilliant success. His greatest error did not exceed 2'; but, notwithstanding these flattering anticipations, he soon found by a comparison of longitudes out of opposition and of latitudes, that it was yet far from being so complete as he had imagined, and to his infinite vexation he soon found that the labour of four years, which he had expended on this theory, must be considered almost entirely fruitless. Even his favourite principle of dividing the excentricity in a different ratio from Ptolemy, was found to lead him into greater error than if he had retained the old bisection. By restoring that, he made his latitudes more accurate, but produced a corresponding change for the worse in his longitudes; and although the errors of 8', to which they now amounted, would probably have been disregarded by former theorists, Kepler could not remain satisfied till they were accounted for. Accordingly he found himself forced to the conclusion that one of the two principles on which this theory rested must be erroneous; either the orbit of the planet is not a perfect circle, or there is no fixed point within it round which it moves with an uniform angular motion. He had once before admitted the possibility of the former of these facts, conceiving it possible that the motion of the planets is not at all curvilinear, but that they move in polygons round the sun, a notion to which he probably inclined in consequence of his favourite harmonics and geometrical figures.
In consequence of the failure of a theory conducted with such care in all its practical details, Kepler determined that his next trial should be of an entirely different complexion. Instead of first satisfying the first inequalities of the planet, and then endeavouring to account for the second inequalities, he resolved to reverse the process, or, in other words, to ascertain as accurately as possible what part of the planet's apparent motion should be referred solely to the optical illusion produced by the motion of the earth, before proceeding to any inquiry of the real inequality of the planet's proper motion. It had been hitherto taken for granted, that the earth moved equably round the centre of its orbit; but Kepler, on resuming the consideration of it, recurred to an opinion he had entertained very early in his astronomical career (rather from his conviction of the existence of general laws, than that he had then felt the want of such a supposition), that it required an equant distinct from its orbit no less than the other planets. He now saw, that if this were admitted, the changes it would everywhere introduce in the optical part of the planet's irregularities might perhaps relieve him from the perplexity in which the vicarious theory had involved him. Accordingly he applied himself with renewed assiduity to the examination of this important question, and the result of his calculations (founded principally on observations of Mars’ parallax) soon satisfied him not only that the earth's orbit does require such an equant, but that its centre is placed according to the general law of the bisection of the excentricity which be had previously found {28} indispensable in the other planets. This was an innovation of the first magnitude, and accordingly Kepler did not venture to proceed farther in his theory, till by evidence of the most varied and satisfactory nature, he had established it beyond the possibility of cavil.
It may be here remarked, that this principle of the bisection of the eccentricity, so familiar to the Ptolemaic astronomers, is identical with the theory afterwards known by the name of the simple elliptic hypothesis, advocated by Seth Ward and others. That hypothesis consisted in supposing the sun to be placed in one focus of the elliptic orbit of the planet, whose angular motion was uniform round the other focus. In Ptolemaic phraseology, that other focus was the centre of the equant, and it is well known that the centre of the ellipse lies in the middle point between the two foci.
It was at this period also, that Kepler first ventured upon the new method of representing inequalities which terminated in one of his most celebrated discoveries. We have already seen, in the account of the “Mysterium Cosmographicum,” that he was speculating, even at that time, on the effects of a whirling force exerted by the sun on the planets with diminished energy at increased distances, and on the proportion observed between the distances of the planets from the sun, and their periods of revolution. He seems even then to have believed in the possibility of discovering a relation between the times and distances in different planets. Another analogous consequence of his theory of the radiation of the whirling force would be, that if the same planet should recede to a greater distance from the central body, it would be acted on by a diminished energy of revolution, and consequently, a relation might be found between the velocity at any point of its orbit, and its distance at that point from the sun. Hence he expected to derive a more direct and natural method of calculating the inequalities, than from the imaginary equant. But these ingenious ideas had been checked in the outset by the erroneous belief which Kepler, in common with other astronomers, then entertained of the coincidence of the earth's equant with its orbit; in other words, by the belief that the earth's linear motion was uniform, though it was known not to remain constantly at the same distance from the sun. As soon as this prejudice was removed, his former ideas recurred to him with increased force, and he set himself diligently to consider what relation could be found between the velocity and distance of a planet from the sun. The method he adopted in the beginning of this inquiry was to assume as approximately correct Ptolemy's doctrine of the bisection of the excentricity, and to investigate some simple relation nearly representing the same effect.
In the annexed figure, S is the place of the sun, C the centre of the planet's
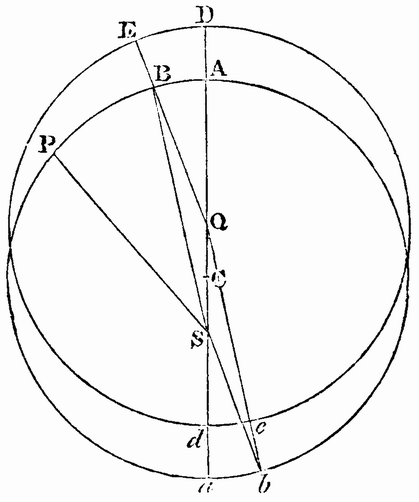
orbit ABab, Q the centre of the equant represented by the equal circle DEde, AB, ab, two equal small arcs described by the planet at the apsides of its orbit: then, according to Ptolemy's principles, the arc DE of the equant would be proportional to the time of passing along AB, on the same scale on which de would represent the time of passing through the equal arc ab.
QD:QA::DE:AB, nearly; and because QS is bisected in C, QA, CA or QD, and SA, are in arithmetical proportion: and, therefore, since an arithmetical mean, when the difference is small, does not differ much from a geometrical mean, QD : QA :: SA : QD, nearly. Therefore, DE : AB :: SA : QD, nearly, and in the same manner de : ab :: Sa : Qd nearly; and therefore DE : de :: SA : Sa nearly. Therefore at the apsides, the times of passing over equal spaces, on Ptolemy's theory, are nearly as the distances from the sun, and Kepler, with his usual hastiness, immediately concluded that this was the accurate and general law, and that the errors of the old theory arose solely from having departed from it.
It followed immediately from this assumption, that after leaving the point A, the time in which the planet would {29} arrive at any point P of its orbit would be proportional to, and might be represented by, the sums of all the lines that could be drawn from S to the arc AP, on the same scale that the whole period of revolution would be denoted by the sum of all the lines drawn to every point of the orbit. Kepler's first attempt to verify this supposition approximately, was made by dividing the whole circumference of the orbit into 360 equal parts, and calculating the distances at every one of the points of division. Then supposing the planet to move uniformly, and to remain at the same distance from the sun during the time of passing each one of these divisions, (a supposition which manifestly would not differ much from the former one, and would coincide with it more nearly, the greater was the number of divisions taken) he proceeded to add together these calculated distances, and hoped to find that the time of arriving at any one of the divisions bore the same ratio to the whole period, as the sum of the corresponding set of distances did to the sum of the whole 360.
This theory was erroneous; but by almost miraculous good fortune, he was led by it in the following manner to the true measure. The discovery was a consequence of the tediousness of his first method, which required, in order to know the time of arriving at any point, that the circle should be subdivided, until one of the points of division fell exactly upon the given place. Kepler therefore endeavoured to discover some shorter method of representing these sums of the distances. The idea then occurred to him of employing for that purpose the area inclosed between the two distances, SA, SP, and the arc AP, in imitation of the manner in which he remembered that Archimedes had found the area of the circle, by dividing it into an infinite number of small triangles by lines drawn from the centre. He hoped therefore to find, that the time of passing from A to P bore nearly the same ratio to the whole period of revolution that the area ASP bore to the whole circle.
This last proportion is in fact accurately observed in the revolution of one body round another, in consequence of an attractive force in the central body. Newton afterwards proved this, grounding his demonstration upon laws of motion altogether irreconcileable with Kepler's opinions; and it is impossible not to admire Kepler's singular good fortune in arriving at this correct result in spite, or rather through the means, of his erroneous principles. It is true that the labour which he bestowed unsparingly upon every one of his successive guesses, joined with his admirable candour, generally preserved him from long retaining a theory altogether at variance with observations; and if any relation subsisted between the times and distances which could any way be expressed by any of the geometrical quantities under consideration, he could scarcely have failed—it might be twenty years earlier or twenty years later,—to light upon it at last, having once put his indefatigable fancy upon this scent. But in order to prevent an over-estimate of his merit in detecting this beautiful law of nature, let us for a moment reflect what might have been his fate had he endeavoured in the same manner, and with the same perseverance, to discover a relation, where, in reality, none existed. Let us take for example the inclinations or the excentricities of the planetary orbits, among which no relation has yet been discovered; and if any exists, it is probably of too complicated a nature to be hit at a venture. If Kepler had exerted his ingenuity in this direction, he might have wasted his life in fruitless labour, and whatever reputation he might have left behind him as an industrious calculator, it would have been very far inferior to that which has procured for him the proud title of the “Legislator of the Heavens,”
However this may be, the immediate consequence of thus lighting upon the real law observed by the earth in its passage round the sun was, that he found himself in possession of a much more accurate method of representing its inequalities than had been reached by any of his predecessors; and with renewed hopes he again attacked the planet Mars, whose path he was now able to consider undistorted by the illusions arising out of the motion of the earth. Had the path of Mars been accurately circular, or even as nearly approaching a circle as that of the earth, the method he chose of determining its position and size by means of three distances carefully calculated from his observed parallaxes, would have given a satisfactory result; but finding, as he soon did, that almost every set of three distances led him to a different result, he began to suspect another error in the long-received {30} opinion, that the orbits of the planets must consist of a combination of circles; he therefore determined, in the first instance, to fix the distances of the planet at the apsides without any reference to the form of the intermediate orbit. Half the difference between these would, of course, be the excentricity of the orbit; and as this quantity came out very nearly the same as had been determined on the vicarious theory, it seemed clear that the error of that theory, whatever it might be, did not lie in these elements.
Kepler also found that in the case of this planet likewise, the times of describing equal arcs at the apsides were proportional to its distances from the sun, and he naturally expected that the method of areas would measure the planet's motion with as much accuracy as he had found in the case of the earth. This hope was disappointed: when he calculated the motion of the planet by this method, he obtained places too much advanced when near the apsides, and too little advanced at the mean distances. He did not, on that account, immediately reject the opinion of circular orbits, but was rather inclined to suspect the principle of measurement, at which he felt that he had arrived in rather a precarious manner. He was fully sensible that his areas did not accurately represent the sums of any distances except those measured from the centre of the circle; and for some time he abandoned the hope of being able to use this substitution, which he always considered merely as an approximate representation of the true measure, the sum of the distances. But on examination he found that the errors of this substitution were nearly insensible, and those it did in fact produce, were in the contrary direction of the errors he was at this time combating. As soon as he had satisfied himself of this, he ventured once more on the supposition, which by this time had, in his eyes, almost acquired the force of demonstration, that the orbits of the planets are not circular, but of an oval form, retiring within the circle at the mean distances, and coinciding with it at the apsides.
This notion was not altogether new; it had been suggested in the case of Mercury, by Purbach, in his “Theories of the Planets.” In the edition of this work published by Reinhold, the pupil of Copernicus, we read the following passage. “Sixthly, it appears from what has been said, that the centre of Mercury's epicycle, by reason of the motions above mentioned, does not, as is the case with the other planets, describe the circumference of a circular deferent, but rather the periphery of a figure resembling a plane oval.” To this is added the following note by Reinhold. “The centre of the Moon's epicycle describes a path of a lenticular shape; Mercury's on the contrary is egg-shaped, the big end lying towards his apogee, and the little end towards his perigee*.” The excentricity of Mercury's orbit is, in fact, much greater than that of any of the other planets, and the merit of making this first step cannot reasonably be withheld from Purbach and his commentator, although they did not pursue the inquiry so far as Kepler found himself in a condition to do.
Before proceeding to the consideration of the particular oval which Kepler fixed upon in the first instance, it will be necessary, in order to render intelligible the source of many of his doubts and difficulties, to make known something more of his theory of the moving force by which he supposed the planets to be carried round in their orbits. In conformity with the plan hitherto pursued, this shall be done as much as possible in his own words.
“It is one of the commonest axioms in natural philosophy, that if two things always happen together and in the same manner, and admit the same measure, either the one is the cause of the other, or both are the effect of a common cause. In the present case, the increase or languor of motion invariably corresponds with an approach to or departure from the centre of the universe. Therefore, either the languor is the cause of the departure of the star, or the departure of the languor, or both have a common cause. But no one can be of opinion that there is a concurrence of any third thing to be a common cause of these two effects, and in the following chapters it will be made clear that there is no occasion to imagine any such third thing, since the two are of themselves sufficient. Now, it is not agreeable to the nature of things that activity or languor in linear motion should be the cause of distance from the centre. For, distance from the centre is conceived anteriorly to linear motion. In fact linear motion cannot exist without {31} distance from the centre, since it requires space for its accomplishment, but distance from the centre can be conceived without motion. Therefore distance is the cause of the activity of motion, and a greater or less distance of a greater or less delay. And since distance is of the kind of relative quantities, whose essence consists in boundaries, (for there is no efficacy in relation per se without regard to bounds,) it follows that the cause of the varying activity of motion rests in one of the boundaries. But the body of the planet neither becomes heavier by receding, nor lighter by approaching. Besides, it would perhaps be absurd on the very mention of it, that an animal force residing in the moveable body of the planet for the purpose of moving it, should exert and relax itself so often without weariness or decay. It remains, therefore, that the cause of this activity and languor resides at the other boundary, that is, in the very centre of the world, from which the distances are computed. — Let us continue our investigation of this moving virtue which resides in the sun, and we shall presently recognize its very close analogy to light. And although this moving virtue cannot be identical with the light of the sun, let others look to it whether the light is employed as a sort of instrument, or vehicle, to convey the moving virtue. There are these seeming contradictions:—first, light is obstructed by opaque bodies, for which reason if the moving virtue travelled on the light, darkness would be followed by a stoppage of the moveable bodies. Again, light flows out in right lines spherically, the moving virtue in right lines also, but cylindrically: that is, it turns in one direction only, from west to east; not in the opposite direction, not towards the poles, &c. But perhaps we shall be able presently to reply to these objections. In conclusion, since there is as much virtue in a large and remote circle as in a narrow and close one, nothing of the virtue perishes in the passage from its source, nothing is scattered between the source and the moveable. Therefore the efflux, like that of light, is not material, and is unlike that of odours, which are accompanied by a loss of substance, unlike heat from a raging furnace, unlike every other emanation by which mediums are filled. It remains, therefore, that as light which illuminates all earthly things, is the immaterial species of that fire which is in the body of the sun, so this virtue, embracing and moving all the planetary bodies, is the immaterial species of that virtue which resides in the sun itself, of incalculable energy, and so the primary act of all mundane motion.—I should like to know who ever said that there was anything material in light!—Guided by our notion of the efflux of this species (or archetype), let us contemplate the more intimate nature of the source itself. For it seems as if something divine were latent in the body of the sun, and comparable to our own soul, whence that species emanates which drives round the planets; just as from the mind of a slinger the species of motion sticks to the stones, and carries them forward, even after he who cast them has drawn back his hand. But to those who wish to proceed soberly, reflections differing a little from these will be offered.”
Our readers will, perhaps, be satisfied with the assurance, that these sober considerations will not enable them to form a much more accurate notion of Kepler's meaning than the passages already cited. We shall therefore proceed to the various opinions he entertained on the motion of the planets.
He considered it as established by his theory, that the centre E of the planet's epicycle (see fig. p. 33.) moved round the circumference of the deferent Dd, according to the law of the planet's distances; the point remaining to be settled was the motion of the planet in the epicycle. If it were made to move according to the same law, so that when the centre of the epicycle reached E, the planet should be at F, taking the angle BEF equal to BSA, it has been shewn (p. 19) that the path of F would still be a circle, excentric from Dd by DA the radius of the epicycle.
But Kepler fancied that he saw many sound reasons why this could not be the true law of motion in the epicycle, on which reasons be relied much more firmly than on the indisputable fact, which he mentions as a collateral proof, that it was contradicted by the observations. Some of these reasons are subjoined: “In the beginning of the work it has been declared to be most absurd, that a planet (even though we suppose it endowed with mind) should form any notion of a centre, and a distance from it, if there be no body in that centre to serve for a distinguishing mark. And although you should say, that the planet {32} has respect to the sun, and knows beforehand, and remembers the order in which the distances from the sun are comprised, so as to make a perfect excentric; in the first place, this is rather far-fetched, and requires, in any mind, means for connecting the effect of an accurately circular path with the sign of an increasing and diminishing diameter of the sun. But there are no such means, except the position of the centre of the excentric at a given distance from the sun; and I have already said, that this is beyond the power of a mere mind. I do not deny that a centre may be imagined, and a circle round it; but this I do say, if the circle exists only in imagination, with no external sign or division, that it is not possible that the path of a moveable body should be really ordered round it in an exact circle. Besides, if the planet chooses from memory its just distances from the sun, so as exactly to form a circle, it must also take from the same source, as if out of the Prussian or Alphonsine tables, equal excentric arcs, to be described in unequal times, and to be described by a force extraneous from the sun; and thus would have, from its memory, a foreknowledge of what effects a virtue, senseless and extraneous from the sun, was about to produce: all these consequences are absurd.”
“It is therefore more agreeable to reason that the planet takes no thought, either of the excentric or epicycle; but that the work which it accomplishes, or joins in effecting, is a libratory path in the diameter Bb of the epicycle, in the direction towards the sun. The law is now to be discovered, according to which the planet arrives at the proper distances in any time. And indeed in this inquiry, it is easier to say what the law is not than what it is.”—Here, according to his custom, Kepler enumerates several laws of motion by which the planet might choose to regulate its energies, each of which is successively condemned. Only one of them is here mentioned, as a specimen of the rest. “What then if we were to say this? Although the motions of the planet are not epicyclical, perhaps the libration is so arranged that the distances from the sun are equal to what they would have been in a real epicyclical motion.—This leads to more incredible consequences than the former suppositions, and yet in the dearth of better opinions, let us for the present content ourselves with this. The greater number of absurd conclusions it will be found to involve, the more ready will a physician be, when we come to the fifty-second chapter, to admit what the observations testify, that the path of the planet is not circular.”
The first oval path on which Kepler was induced to fix, by these and many other similar considerations, was in the first instance very different from the true elliptical form. Most authors would have thought it unnecessary to detain their readers with a theory which they had once entertained and rejected; but Kepler's work was written on a different plan. He thus introduces an explanation of his first oval. “As soon as I was thus taught by Brahe's very accurate observations that the orbit of a planet is not circular, but more compressed at the sides, on the instant I thought that I understood the natural cause of this deflection. But the old proverb was verified in my case;—the more haste the less speed.—For having violently laboured in the 39th chapter, in consequence of my inability to find a sufficiently probable cause why the orbit of the planet should be a perfect circle, (some absurdities always remaining with respect to that virtue which resides in the body of the planet,) and having now discovered from the observations, that the orbit is not a perfect circle, I felt furiously inclined to believe that if the theory which had been recognized its absurd, when employed in the 39th chapter for the purpose of fabricating a circle, were modulated into a more probable form, it would produce an accurate orbit agreeing with the observations. If I had entered on this course a little more warily, I might have detected the truth immediately. But, being blinded by my eagerness, and not sufficiently regardful of every part of the 39th chapter, and clinging to my first opinion, which offered itself to me with a wonderful show of probability, on account of the equable motion in the epicycle, I got entangled in new perplexities, with which we shall now have to struggle in this 45th chapter and the following ones as far as the 50th chapter.”
In this theory, Kepler supposed that whilst the centre of the epicycle was moving round a circular deferent, according to the law of the planets’ distances (or areas) the planet itself moved equably in the epicycle, with the mean angular velocity of its centre in the deferent. In consequence of this supposition, since {33}
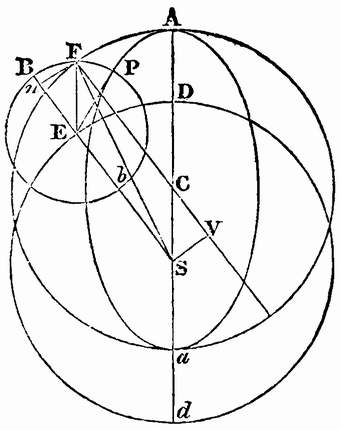
at D, when the planet is at A the aphelion, the motion in the deferent is less than the mean motion, the planet will have advanced through an angle BEP greater than BEF or BSA, through which the centre of the epicycle has moved; and consequently, the path will lie everywhere within the circle Aa, except at the apsides. Here was a new train of laborious calculations to undergo for the purpose of drawing the curve APa according to this law, and of measuring the area of any part of it. After a variety of fruitless attempts, for this curve is one of singular complexity, he was reduced, as a last resource, to suppose it insensibly different from an ellipse on the same principal axes, as an approximate means of estimating its area. Not content even with the results so obtained, and not being able to see very clearly what might be the effect of his alteration in substituting the ellipse for the oval, and in other simplifications introduced by him, he had courage enough to obtain the sums of the 360 distances by direct calculation, as he had done in the old circular theory.
In the preface to his book he had spoken of his labours under the allegory of a war carried on by him against the planet; and when exulting in the early prospects of success this calculation seemed to offer, he did not omit once more to warn his readers, in his peculiar strain, that this exultation was premature.
“Allow me, gentle reader, to enjoy so splendid a triumph for one little day (I mean through the five next chapters), meantime be all rumours suppressed of new rebellion, that our preparations may not perish, yielding us no delight. Hereafter if anything shall come to pass, we will go through it in its own time and season; now let us be merry, as then we will be bold and vigorous.” At the time foretold, that is to say, at the end of the five merry chapters, the bad news could no longer be kept a secret. It is announced in the following bulletin:— “While thus triumphing over Mars, and preparing for him, as for one altogether vanquished, tabular prisons, and equated eccentric fetters, it is buzzed here and there that the victory is vain, and that the war is raging anew as violently as before. For the enemy, left at home a despised captive, has burst all the chains of the equations, and broken forth of the prisons of the tables. For no method of geometrically administering the theory of the 45th chapter was able to come near the accuracy of approximation of the vicarious theory of the 16th chapter, which gave me true equations derived from false principles. Skirmishers, disposed all round the circuit of the excentric, (I mean the true distances,) routed my forces of physical causes levied out of the 45th chapter, and shaking off the yoke, regained their liberty. And now there was little to prevent the fugitive enemy from effecting a junction with his rebellious supporters, and reducing me to despair, had I not suddenly sent into the field a reserve of new physical reasonings on the rout and dispersion of the veterans, and diligently followed, without allowing him the slightest respite, in the direction in which he had broken out.”
In plainer terms, Kepler found, after this labour was completed, that the errors in longitude he was still subject to were precisely of an opposite nature to those he had found with the circle; instead of being too quick at the apsides, the planet was now too slow there, and too much accelerated in the mean distances; and the distances obtained from direct observation were everywhere greater, except at the apsides, than those furnished by this oval theory. It was in the course of these tedious investigations that he established, still more satisfactorily than he had before done, that the inclinations of the planets’ orbits are invariable, and that the lines of their nodes pass through the centre of the Sun, and not, as before his time had been supposed, through the centre of the ecliptic.
When Kepler found with certainty that this oval from which be expected so much would not satisfy the observations, his vexation was extreme, not merely from the mortification of finding a theory confuted on which he had spent {34} such excessive labour, for he was accustomed to disappointments of that kind, but principally from many anxious and fruitless speculations as to the real physical causes why the planet did not move in the supposed epicycle, that being the point of view, as has been already shewn, from which he always preferred to begin his inquiries. One part of the reasoning by which he reconciled himself to the failure exhibits much too curious a view of the state of his mind to he passed over in silence. The argument is founded on the difficulty which he met with, as abovementioned, in calculating the proportions of the oval path he had imagined. “In order that you may see the cause of the impracticability of this method which we have just gone through, consider on what foundations it rests. The planet is supposed to move equably in the epicycle, and to be carried by the Sun unequably in the proportion of the distances. But by this method it is impossible to be known how much of the oval path corresponds to any given time, although the distance at that part is known, unless we first know the length of the whole oval. But the length of the oval cannot be known, except from the law of the entry of the planet within the sides of the circle. But neither can the law of this entry be known before we know how much of the oval path corresponds to any given time. Here you see that there is a petitio principii; and in my operations I was assuming that of which I was in search, namely the length of the oval. This is at least not the fault of my understanding, but it is also most alien to the primary Ordainer of the planetary courses: I have never yet found so ungeometrical a contrivance in his other works. Therefore we must either hit upon some other method of reducing the theory of the 45th chapter to calculation; or if that cannot be done, the theory itself, suspected on account of this petitio principii, will totter.” Whilst his mind was thus occupied, one of those extraordinary accidents which it has been said never occur but to those capable of deriving advantage from them (but which, in fact, are never noticed when they occur to any one else), fortunately put him once more upon the right path. Half the extreme breadth between the oval and the circle nearly represented the errors of his distances at the mean point, and he found that this half was 429 parts of a radius, consisting of 100000 parts; and happening to advert to the greatest optical inequality of Mars, which amounts to about 5°18', it struck him that 429 was precisely the excess of the secant of 5°18’ above the radius taken at 100000. This was a ray of light, and, to use his own words, it roused him as out of sleep. In short, this single observation was enough to produce conviction in his singularly constituted mind, that instead of the distances SF, he should everywhere substitute FV, determined by drawing SV perpendicular on the line FC, since the excess of SF above FV is manifestly that of the secant above the radius in the optical equation SFC at that point. It is still more extraordinary that a substitution made for such a reason should have the luck, as is again the case, to be the right one. This substitution in fact amounted to supposing that the planet, instead of being at the distance SP or SF, was at Sn; or, in other words, that instead of revolving in the circumference, it librated in the diameter of the epicycle, which was to him an additional recommendation. Upon this new supposition a fresh set of distances was rapidly calculated, and to Kepler's inexpressible joy, they were found to agree with the observations within the limits of the errors to which the latter were necessarily subject. Notwithstanding this success, he had to undergo, before arriving at the successful termination of his labours, one more disappointment. Although the distance corresponding to a time from the aphelion represented approximately by the area ASF, was thus found to be accurately represented by the line Sn, there was still an error with regard to the direction in which that distance was to be measured. Kepler's first idea was to set it off in the direction SF, but this he found to lead to inaccurate longitudes;
| {35} |
and it was not until after much perplexity, driving him, as he tells us, “almost to insanity,” that he satisfied himself that the distance SQ equal to FV ought to be taken terminating in Fm, the line from F perpendicular to Aa, the line of apsides, and that the curve so traced out by Q would be an accurate ellipse.
He then found to his equal gratification and amazement, a small part of which he endeavoured to express by a triumphant figure on the side of his diagram, that the error he had committed in taking the area ASF to represent the sums of the distances SF, was exactly counterbalanced; for this area does accurately represent the sums of the distances FV or SQ. This compensation, which seemed to Kepler the greatest confirmation of his theory, is altogether accidental and immaterial, resulting from the relation between the ellipse and circle. If the laws of planetary attraction had chanced to have been any other than those which cause them to describe ellipses, this last singular confirmation of an erroneous theory could not have taken place, and Kepler would have been forced either to abandon the theory of the areas, which even then would have continued to measure and define their motions, or to renounce the physical opinions from which he professed to have deduced it as an approximative truth.
These are two of the three celebrated theorems called Kepler's laws: the first is, that the planets move in ellipses round the sun, placed in the focus; the second, that the time of describing any arc is proportional in the same orbit to the area included between the arc and the two bounding distances from the sun. The third will be mentioned on another occasion, as it was not discovered till twelve years later. On the establishment of these two theorems, it became important to discover a method of measuring such elliptic areas, but this is a problem which cannot be accurately solved. Kepler, in offering it to the attention of geometricians, stated his belief that its solution was unattainable by direct processes, on account of the incommensurability of the arc and sine, on which the measurement of the two parts AQm, SQm depends. “This,” says he in conclusion, “this is my belief, and whoever shall shew my mistake, and point out the true solution,
Is erit mihi magnus Apollonius.”
When presenting this celebrated book to the emperor, Kepler gave notice that he contemplated a farther attack upon Mars's relations, father Jupiter, brother Mercury, and the rest; and promised that he would be successful, provided the emperor would not forget the sinews of war, and order him to be furnished anew with means for recruiting his army. The death of his unhappy patron, the Emperor Rodolph, which happened in 1612, barely in time to save him from the last disgrace of deposition from the Imperial throne, seemed to put additional difficulties in the way of Kepler's receiving the arrears so unjustly denied to him; but on the accession of Rodolph's brother, Matthias, he was again named to his post of Imperial Mathematician, and had also a permanent professorship assigned to him in the University of Linz. He quitted Prague without much regret, where he had struggled against poverty during eleven years. Whatever disinclination he might feel to depart, arose from his unwillingness to loosen still more the hold he yet retained upon the wreck of Tycho Brahe's instruments and observations. Tengnagel, son-in-law of Tycho, had abandoned astronomy for a political career, and the other members of his family, who were principally females, suffered the costly instruments to lie neglected and forgotten, although they had obstructed with the utmost jealousy Kepler's attempts to continue their utility. The only two instruments Kepler possessed of his own property, were “An iron sextant of 21/2 feet diameter, and a brass azimuthal quadrant, of 31/2 feet diameter, both divided into minutes of a degree.” These were the gift of his friend and patron, Hloffman, the President of Styria, and with these he made all the observations which he added to those of Tycho Brahe. His constitution was not favourable to these studies, his health being always delicate, and suffering much from exposure to the night air; his eyes also were very weak, as he mentions himself in several places. In the summary of his character which he drew up when proposing to become Tycho Brahe's assistant, he describes himself as follows:—“For observations {36} my sight is dull; for mechanical operations my hand is awkward; in politics and domestic matters my nature is troublesome and choleric; my constitution will not allow me, even when in good health, to remain a long time sedentary (particularly for an extraordinary time after dinner); I most rise often and walk about, and in different seasons am forced to make corresponding changes in my diet.”
The year preceding his departure to Linz was denounced by him as pregnant with misfortune and misery. “In the fust place I could get no money from the court, and my wife, who had for a long time been suffering under low spirits and despondency, was taken violently ill towards the end of 1610, with the Hungarian fever, epilepsy, and phrenitis. She was scarcely convalescent when all my three children were at once attacked with small-pox. Leopold with his army occupied the town beyond the river, just as I lost the dearest of my sons, him whose nativity you will find in my book on the new star. The town on this side of the river where I lived was harassed by the Bohemian troops, whose new levies were insubordinate and insolent: to complete the whole, the Austrian army brought the plague with them into the city. I went into Austria, and endeavoured to procure the situation which I now hold. Returning in June, I found my wife in a decline from her grief at the death of her son, and on the eve of an infectious fever; and I lost her also, within eleven days after my return. Then came fresh annoyance, of course, and her fortune was to he divided with my step-sisters. The Emperor Rudolph would not agree to my departure; vain hopes were given me of being paid from Saxony; my tune and money were wasted together, till on the death of the emperor, in 1612, I was named again by his successor, and suffered to depart to Linz. These, methinks, were reasons enough why I should have overlooked not only your letters, but even astronomy itself.”
Kepler's first marriage had not been a happy one; but the necessity in which he felt himself of providing some one to take charge of his two surviving children, of whom the eldest, Susanna, was born in 1602, and Louis in 1607, determined him on entering a second time into the married state. The account he has left us of the various negotiations which preceded his final choice, does not, in any point, belie the oddity of his character. His friends seem to have received a general commission to look out for a suitable match, and in a long and most amusing letter to the Baron Strahlendorf, we are made acquainted with the pretensions and qualifications of no less than eleven ladies among whom his inclinations wavered.
The first on the list was a widow, an intimate friend of his first wife's, and who, on many accounts, appeared a most eligible match. “At first she seemed favourably inclined to the proposal; it is certain that she took time to consider it, but at last she very quietly excused herself.” It must have been from a recollection of this lady's good qualities that Kepler was induced to make his offer; for we learn rather unexpectedly, after being informed of her decision, that when he soon afterwards paid his respects to her, it was for the first time that he had seen her during the last six years; and he found, to his great relief, that “there was no single pleasing point about her.” The truth seems to be that he was nettled by her answer, and he is at greater pains than appear necessary, considering this last discovery, to determine why she would not accept his offered hand. Among other reasons he suggested her children, among whom were two marriageable daughters; and it is diverting afterwards to find them also in the catalogue which Kepler appeared to be making of all his female acquaintance. He seems to have been much perplexed in attempting to reconcile his astrological theory with the fact of his having taken so much trouble about a negotiation not destined to succeed. “Have the stars exercised any influence here? For just about this time the direction of the Mid-Heaven is in hot opposition to Mars, and the passage of Saturn, through the ascending point of the zodiac, in the scheme of my nativity, will happen again next November and December. But if these are the causes, how do they act? Is that explanation the true one which I have elsewhere given? For I can never think of handing over to the stars the office of deities to produce effects. Let us therefore suppose it accounted for by the stars, that at this season I am violent in my temper and attentions, in rashness of belief, in a shew of pititul tender-heartedness; in catching at reputation by new and paradoxical notions, and the {37} singularity of my actions; in busily inquiring into, and weighing and discussing, various reasons; in the uneasiness of my mind with respect to my choice. I thank God that that did not happen which might have happened; that this marriage did not take place: now for the others.” Of these others, one was too old, another in bad health, another too proud of her birth and quarterings; a fourth had learned nothing but shewy accomplishments, “not at all suitable to the sort of life she would have to lead with me.” Another grew impatient, and married a more decided admirer, whilst he was hesitating. “The mischief (says he) in all these attachments was, that whilst I was delaying, comparing, and balancing conflicting reasons, every day saw me inflamed with a new passion.” By the time he reached the eighth, he found his match in this respect. “Fortune at length has avenged herself on my doubtful inclinations. At first she was quite complying, and her friends also: presently, whether she did or did not consent, not only I, but she herself did not know. After the lapse of a few days, came a renewed promise, which however had to be confirmed a third time; and four days after that, she again repented her confirmation, and begged to be excused from it. Upon this I gave her up, and this time all my counsellors were of one opinion.” This was the longest courtship in the list, having lasted three whole months; and quite disheartened by its bad success, Kepler's next attempt was of a more timid complexion. His advances to No. 9, were made by confiding to her the whole story of his recent disappointment, prudently determining to be guided in his behaviour, by observing whether the treatment he had experienced met with a proper degree of sympathy. Apparently the experiment did not succeed; and almost reduced to despair, Kepler betook himself to the advice of a friend, who had for some time past complained that she was not consulted in this difficult negotiation. When she produced No. 10, and the first visit was paid, the report upon her was as follows:—“She has, undoubtedly, a good fortune, is of good family, and of economical habits; but her physiognomy is most horribly ugly; she would be stared at in the streets, not to mention the striking disproportion in our figures, I am lank, lean, and spare; she is short and thick: in a family notorious for fatness she is considered superfluously fat.” The only objection to No. 11 seems to have been her excessive youth; and when this treaty was broken of on that account, Kepler turned his back upon all his advisers, and chose for himself one who had figured as No. 5 in the list, to whom he professes to have felt attached throughout, but from whom the representations of his friends had hitherto detained him, probably on account of her humble station.
The following is Kepler's summary of her character. “Her name is Susanna, the daughter of John Reuthinger and Barbara, citizens of the town of Eferdingen; the father was by trade a cabinet-maker, but both her parents are dead. She has received an education well worth the largest dowry, by favour of the Lady of Stahrenberg, the strictness of whose household is famous throughout the province. Her person and manners are suitable to mine; no pride, no extravagance; she can hear to work; she has a tolerable knowledge how to manage a family; middle-aged, and of a disposition and capability to acquire what she still wants. Her I shall marry by favour of the noble baron of Stahrenberg at twelve o'clock on the 30th of next October, with all Eferdingen assembled to meet us, and we shall eat the marriage-dinner at Maurice's at the Golden Lion.”
Hantsch has made an absurd mistake with regard to this marriage, in stating that the bride was only twelve years old. Kustner and other biographers have been content to repeat the same assertion without any comment, notwithstanding its evident improbability. The origin of the blunder is to be found in Kepler's correspondence with Bernegger, to whom, speaking of his wife, he says “She has been educated for twelve years by the Lady of Stahrenberg.” This is by no means a single instance of carelessness in Hantsch; Kustner has pointed out others of great inconsequence. It was owing to this marriage, that Kepler took occasion to write his new method of gauging, for as he tells us in his own peculiar style “last November I brought home a new wife, and as the whole course of Danube was then covered with the produce of the Austrian vineyards, to be sold at a reasonable rate, I purchased a few casks, thinking it my duty as a good husband and a father of a family, to see that my household was well provided with drink.” When the seller came to ascertain the quantity, Kepler objected to his method {38} of gauging, for he allowed no difference, whatever might he the proportion of the bulging parts. The reflections to which this incident gave rise, terminated in the publication of the above-mentioned treatise, which claims a place among the earliest specimens of what is now called the modern analysis. In it he extended several properties of plane figures to segments of cones and cylinders, from the consideration that “these solids are incorporated circles,” and, therefore, that those properties are true of the whole which belong to each component part. That the book might end as oddly as it began, Kepler concluded it with a parody of Catullus:
|
“Et cum pocula mjlle mensi erimus Conturbubimus illa, ne sciamus,” |
His new residence at Linz was not long undisturbed. He quarrelled there, as he had done in the early part of his life at Gratz, with the Roman Catholic party, and was excommunicated. “Judge,” says he to Peter Hoffman, “how far I can assist you, in a place where the priest and school-inspector have combined to brand me with the public stigma of heresy, because in every question 1 take that side which seems to me to be consonant with the word of God.” The particular dogma which occasioned his excommunication, was connected with the doctrine of transubstantiation. He published his creed in a copy of Latin verses, preserved by his biographer Hantsch.
Before this occurrence, Kepler had been called to the diet at Ratisbon to give his opinion on the propriety of adopting the Gregorian reformation of the calendar, and he published a short essay, pointing out the respective convenience of doing so, or of altering the old Julian Calendar in some other manner. Notwithstanding the readiness of the diet to avail themselves of his talents for the settlement of a difficult question, the arrears of his salary were not paid much more regularly than they had been in Rodolph's time, and he was driven to provide himself with money by the publication of his almanac, of which necessity he heavily and justly complained. “In order to pay the expense of the Ephemeris for these two years, I have also written a vile prophesying almanac, which is scarcely more respectable than begging; unless it be because it saves the emperor's credit, who abandons me entirely; and with all his frequent and recent orders in council, would suffer me to perish with hunger.” Kepler published this Ephemeris annually till 1620; ten years later he added those belonging to the years from 1620 to 1628.
In 1617 Kepler was invited into Italy, to succeed Magini as Professor of Mathematics at Bologna. The offer tempted him; but, after mature consideration, he rejected it, on grounds which he thus explained to Roffini:—“By birth and spirit I am a German, imbued with German principles, and bound by such family ties, that even if the emperor should consent, I could not, without the greatest difficulty, remove my dwelling-place from Germany into Italy. And although the glory of holding so distinguished a situation among the venerable professors of Bologna stimulates me, and there appears great likelihood of notably increasing my fortune, as well from the great concourse to the public lectures, as from private tuition; yet, on the other hand, that period of my life is past which was once excited by novelty, or which might promise itself a long enjoyment of these advantages. Besides, from a boy up to my present years, living a German among Germans, I am accustomed to a degree of freedom in my speech and manners, which, if persevered in on my removal to Bologna, seems likely to draw upon me, if not danger, at least notoriety, and might expose me to suspicion and party malice. Notwithstanding this answer, I have yet hopes that your most honourable invitation will be of service to me, and may make the imperial treasurer more ready than he has hitherto been to fulfil his master's intentions towards me. In that ease I shall the sooner be able to publish the Rudolphine Tables and the Ephemerides, of which you had the scheme so many years back; and in this manner you and your advisers may have no reason to regret this invitation, though for the present it seems fruitless.”
In 1619, the Emperor Matthias died, and was succeeded by Ferdinand III, who retained Kepler in the post he had filled under his two predecessors on the imperial throne. Kästner, in his “History of Mathematics,” has corrected a gross error of Hantsch, in asserting that Kepler prognosticated Matthias's death. The letter to which Hantsch refers, in support of his statement, does indeed mention the emperor's death, but merely as a notorious event, for the purpose of recalling a date to the memory of his correspondent.
| {39} |
The “Cosmographical Mystery” was written, as has been already mentioned, when Kepler was only twenty-six, and the wildness of its theories might be considered as due merely to the vivacity of a young man; but as if purposely to shew that his maturer age did not renounce the creations of his youthful fancy, he reprinted the “Mystery” in 1619, nearly at the same time when he published his celebrated work on Harmonics; and the extravagance of the latter publication does not at all lose in comparison with its predecessor. It is dedicated to James I of England, and divided into five books: “The first, Geometrical, on the origin and demonstration of the laws of the figures which produce harmonious proportions;—the second, Architectonical, on figurate geometry, and the congruence of plane and solid regular figures;—the third, properly Harmonic, on the derivation of musical proportions from figures, and on the nature and distinction of things relating to song, in opposition to the old theories;— the fourth, Metaphysical, Psychological, and Astrological, on the mental essence of harmonies, and of their kinds in the world, especially on the harmony of rays emanating on the earth from the heavenly bodies, and on their effect in nature, and on the sublunary and human soul;—the fifth, Astronomical and Metaphysical, on the very exquisite harmonies of the celestial motions, and the origin of the excentricities in harmonious proportions.”
The two first books are almost strictly, as Kepler styles them, geometrical, relating in great measure to the inscription of regular polygons in a circle. The following passage is curious, presenting an analogous idea to that contained in one of the extracts already given from the Commentaries on Mars. “The heptagon, and all other polygons and stars beyond it, which have a prime number of sides, and all other figures derived from them, cannot be inscribed geometrically in a circle; although their sides have a necessary magnitude, it is equally a matter of necessity that we remain ignorant of it. This is a question of great importance, for on this account is it that the heptagon, and other figures of this kind, have not been employed by God in the adornment of the world, as the other intelligible figures are employed which have been already explained.” Kepler then introduces the algebraical equation, on the solution of which this problem depends, and makes a remark which is curious at this period of the history of algebra—that the root of an equation which cannot be accurately found, may yet be found within any degree of approximation by an expert calculator. In conclusion he again remarks that “the side of the heptagon has no place among scientific existences, since its formal description is impossible, and therefore it cannot be known by the human mind, since the possibility of description precedes the possibility of knowledge; nor is it known even by the simple eternal act of an omniscient mind, because its nature belongs to things which cannot be known. And yet this scientific nonentity has some scientific properties, for if a heptagon were described in a circle, the proportion of its sides would have analogous proportions.”
The third book is a treatise on music, in the confined and ordinary sense in which we now use that word, and apparently a sober and rational one, at least as nearly so as Kepler could be trusted to write on a subject so dangerous to his discretion. All the extravagance of the work seems reserved for the fourth book, the title of which already conveys some notion of the nature of its contents. In this book he has collected the substance of the astrological opinions scattered through his other works. We shall content ourselves with merely citing his own words, without any attempt to explain the difference between the astrology which he believed, and that which he contemptuously rejected. The distinctive line seems very finely drawn, and as both one and the other are now discarded by all who enjoy the full use of their reasoning powers, if is not of much consequence that it should be accurately traced.
It is to be observed, that he does not in this treatise modify or recant anything of his earlier opinions, but refers to the favourable judgment of his contemporary philosophers as a reason for embodying them in a regular form. “Since many very celebrated professors of philosophy and medicine are of opinion {40} that I have created a new and most true philosophy, this tender plant, like all novelties, ought to be carefully nursed and cherished, so that it may strike root in the minds of philosophers, and not be choked by the excessive humours of vain sophistications, or washed away by the torrents of vulgar prejudices, or frozen by the chill of public neglect; and if I succeed in guarding it from these dangers, I have no fear that it will be crushed by the storms of calumny, or parched by the sun of sterling criticism.”
One thing is very remarkable in Kepler's creed, that he whose candour is so indisputable in every other part of his conduct, professed to have been forced to adopt his astrological opinions from direct and positive observation.—“It is now more than twenty years since I began to maintain opinions like these on the predominant nature of the elements, which, adopting the common name, I call sublunary, I have been driven to this not by studying or admiring Plato, but singly and solely by observing seasons, and noting the aspects by which they are produced. I have seen the state of the atmosphere almost uniformly disturbed as often as the planets are in conjunction, or in the other configurations so celebrated among astrologers. I have noticed its tranquil state, either when there are none or few such aspects, or when they are transitory and of short duration. I have not formed an opinion on this matter without good grounds, like the common herd of prophesiers, who describe the operations of the stars as if they were a sort of deities, the lords of heaven and earth, and producing everything at their pleasure. They never trouble themselves to consider what means the stars have of working any effects among us on the earth, whilst they remain in the sky, and send down nothing to us which is obvious to the senses except rays of light. This is the principal source of the filthy astrological superstitions of that vulgar and childish race of dreamers, the prognosticates.”
The real manner in which the configurations of the stars operate, according to Kepler, is as follows:—“Like one who listens to a sweet melodious song, and by the gladness of his countenance, by his voice, and by the beating of his hand or foot attuned to the music, gives token that he perceives and approves the harmony: just so does sublunary nature, with the notable and evident emotion of the bowels of the earth, bear like witness to the same feelings, especially at those times when the rays of the planets form harmonious configurations on the earth.”—“I have been confirmed in this theory by that which might have deterred others; I mean, by observing that the emotions do not agree nicely with the instants of the configurations; but the earth sometimes appears lazy and obstinate, and at another time (after important and long-continued configurations) she becomes exasperated, and gives way to her passion, even without the continuation of aspects. For in fact the earth is not an animal like a dog, ready at every nod; but more like a bull, or an elephant, slow to become angry, and so much the more furious when incensed.”
This singular doctrine must not be mistaken for one of Kepler's favourite allegories; he actually and literally professed to believe that the earth was an enormous living animal; and he has enumerated, with a particularity of details into which we forbear to follow him, the analogies he recognized between its habits and those of men and other animals. A few samples of these may speak for the rest. “If any one who has climbed the peaks of the highest mountains throw a stone down their very deep clefts, a sound is heard from them; or if he throw it into one of the mountain lakes, which beyond doubt are bottomless, a storm will immediately arise, just as when you thrust a straw into the ear or nose of a ticklish animal, it shakes its head, or runs shuddering away. What so like breathing, especially of those fish who draw water into their mouths and spout it out again through their gills, as that wonderful tide! For although it is so regulated according to the course of the moon, that, in the preface to my ‘Commentaries on Mars,’ I have mentioned it as probable that the waters are attracted by the moon as iron is by the loadstone; yet, if any one uphold that the earth regulates its breathing according to the motion of the sun and moon, as animals have daily and nightly alternations of sleep and waking, I shall not think his philosophy unworthy of being listened to; especially if any flexible parts should be discovered in the depths of the earth to supply the functions of lungs or gills.”
From the next extract, we must leave the reader to learn as well as he may, {41} how much Kepler did, and how much he did not believe on the subject of genethliac astrology.—“Hence it is that human spirits, at the time of celestial aspects, are particularly urged to complete the matters which they have in hand. What the goad is to the ox, what the spur or the rowel is to the horse, to the soldier the bell and trumpet, an animated speech to an audience, to a crowd of rustics a performance on the fife and bagpipes, that to all, and especially in the aggregate, is a heavenly configuration of suitable planets; so that every single one is excited in his thoughts and actions, and all become more ready to unite and associate their efforts. For instance, in war you may see that tumults, battles, fights, invasions, assaults, attacks, and panic fears, generally happen at the time of the aspects of Mars and Mercury, Mars and Jupiter, Mars and the Sun, Mars and Saturn, &c. In epidemic diseases, a greater number of persons are attacked at the times of the powerful aspects, they suffer more severely, or even die, owing to the failure of nature in her strife with the disease, which strife (and not the deaih) is occasioned by the aspect. It is not the sky which does all these things immediately, but the faculty of the vital soul, associating its operation with the celestial harmonies, is the principal agent in this so-called influence of the heavens. Indeed this word influence has so fascinated some philosophers that they prefer raving with the senseless vulgar, to learning the truth with me. This essential property is the principal foundation of that admirable genethliac art. For when anything begins to have its being when that is working harmonies, the sensible harmony of the rays of the planets has peculiar influence on it. This then is the cause why those who are born under a season of many aspects among the planets, generally turn out busy and industrious, whether they accustom themselves from childhood to amass wealth, or are born or chosen to direct public affairs, or finally, have given their attention to study. If any one think that I might be taken as an instance of this last class, I do not grudge him the knowledge of my nativity. I am not checked by the reproach of boastfulness, notwithstanding those who, by speech or conduct, condemn as folly all kinds of writing on this subject; the idiots, the half-learned, the inventors of titles and trappings, to throw dust in the eyes of the people, and those whom Picus calls the plebeian theologians: among the true lovers of wisdom, I easily clear myself of this imputation, by the advantage of my reader; for there is no one whose nativity or whose internal disposition and temper I can learn so well as I know my own. Well then, Jupiter nearest the nonagesimal had passed by four degrees the trine of Saturn; the Sun and Venus, in conjunction, were moving from the latter towards the former, nearly in sextiles with both: they were also removing from quadratures with Mars, to which Mercury was closely approaching: the moon drew near the trine of the same planet, close to the Bull's Eye, even in latitude. The 25th degree of Gemini was rising, and the 22d of Aquarius culminating. That there was this triple configuration on that day—namely, the sextile of Saturn and the Sun, the sextile of Mars and Jupiter, the quadrature of Mercury and Mars, is proved by the change of weather; for, after a frost of some days, that very day became warmer, there was a thaw and a fall of rain.*”
“I do not wish this single instance to be taken as a defence and proof of all the aphorisms of astrologers, nor do I attribute to the heavens the government of human affairs: what a vast interval still separates these philosophical observations from that folly or madness as it should rather be called. For, following up this example, I knew a lady†, born under nearly the same aspects, whose disposition, indeed, was exceedingly restless, but who not only makes no progress in literature (that is not strange in a woman), but troubles her whole family, and is the cause to herself of deplorable misery. What, in my case, assisted the aspects was—firstly, the fancy of my mother when pregnant with me, a great admirer of her mother-in-law, my grandmother, who had some knowledge of medicine, my grandfather a profession; a second cause is, that I {42} was born a male, and not a female, for astrologers have sought in vain to distinguish sexes in the sky; thirdly, I derive from my mother a habit of body, more fit for study than other kinds of life; fourthly, my parents’ fortune was not large, and there was no landed property to which I might succeed and become attached; fifthly, there were the schools, and the liberality of the magistracy towards such boys as were apt for learning. But now if I am to speak of the result of my studies, what I pray can I find in the sky, even remotely alluding to it. The learned confess that several not despicable branches of philosophy have been newly extricated or amended or brought to perfection by me: but here my constellations were, not Mercury from the east, in the angle of the seventh, and in quadratures with Mars, but Copernicus, but Tycho Brahe, without whose books of observations everything now set by me in the clearest light must have remained buried in darkness; not Saturn predominating Mercury, but my Lords the Emperors Rodolph and Matthias; not Capricorn, the house of Saturn, but Upper Austria, the home of the Emperor, and the ready and unexampled bounty of his nobles to my petition. Here is that corner, not the western one of the horoscope, but on the Earth, whither, by permission of my imperial master, I have betaken myself from a too uneasy court; and whence, during these years of my life, which now tends towards its setting, emanate these Harmonies, and the other matters on which I am engaged.”
“However, it may be owing to Jupiter's ascendancy that I take greater delight in the application of geometry to physics, than in that abstract pursuit which partakes of the dryness of Saturn; and it is perhaps the gibbous moon, in the bright constellation of the Bull's forehead, which fills my mind with fantastic images.”
The most remarkable thing contained in the 5th Book, is the announcement of the celebrated law connecting the mean distances of the planets with the periods of their revolution about the Sun. This law is expressed in mathematical language, by saying that the squares of the times vary as the cubes of the distances*. Kepler's rapture on detecting it was unbounded, as may be seen from the exulling rhapsody with which he announced it. “What I prophecied two-and-twenfy years ago, as soon as I discovered the five solids among the heavenly orbits — what I firmly believed long before I had seen Ptolemy's ‘Harmonics’—what I had promised my friends in the title of this book, which I named before I was sure of my discovery—what, sixteen years ago, I urged as a thing to be sought—that for which I joined Tycho Brahe, for which I settled in Prague, for which I have devoted the best part of my life to astronomical contemplations, at length I have brought to light, and have recognized its truth beyond my most sanguine expectations. Great as is the absolute nature of Harmonics with all its details, as set forth in my third book, it is all found among the celestial motions, not indeed in the manner which I imagined, (that is not the least part of my delight,) but in another very different, and yet most perfect and excellent. It is now eighteen months since I got the first glimpse of light, three months since the dawn, very few days since the unveiled sun, most admirable to gaze on, burst out upon me. Nothing holds me; I will indulge in my sacred fury; I will triumph over mankind by the honest confession, that I have stolen the golden vases of the Egyptians*, to build up a tabernacle for my God far away from the confines of Egypt. If you forgive me, I rejoice; if you are angry, 1 can bear it: the die is cast, the book is written; to be read either now or by posterity, I care not which: it may well wait a century for a reader, as God has waited six thousand years for an observer.”
He has told, with his usual particularity, the manner and precise moment of the discovery. “Another part of my ‘Cosmographical Mystery,’ suspended twenty-two years ago, because it was then undetermined, is completed and introduced here, after I had discovered the true intervals of the orbits, by means of Brahe's observations, and had spent the continuous toil of a long time in investigating the true proportion of the periodic times to the orbits,
|
Sera quidem respexit inertem, Respexit tamen, et longo pass tempore venit. |
If you would know the precise moment, the first idea came across me on the 8th March of this year, 1618; but chancing {43} to make a mistake in the calculation, I rejected it as false. I returned again to it with new force on the 15th May, and it has dissipated the darkness of my mind by such an agreement between this idea and my seventeen years’ labour on Brahe's observations, that at first I thought I must be dreaming, and had taken my result for granted in my first assumptions. But the fact is perfect, the fact is certain, that the proportion existing between the periodic times of any two planets is exactly the sesquiplicate proportion of the mean distances of the orbits.”
There is high authority for not attempting over anxiously to understand the rest of the work. Delambre sums it up as follows:—“In the music of the celestial bodies it appears that Saturn and Jupiter take the bass, Mars the tenor, the Earth and Venus the counter-tenor, and Mercury the treble.” If the patience of this indefatigable historian gave way, as he confesses, in the perusal, any further notice of it here may be well excused. Kepler became engaged, in consequence of this publication, in an angry controversy with the eccentric Robert Fludd, who was at least Kepler's match in wild extravagance and mysticism, if far inferior to him in genius. It is diverting to hear each reproaching the other with obscurity.
In the “Epitome of the Copernican Astronomy,” which Kepler published, about the same time, we find the manner in which he endeavoured to deduce the beautiful law of periodic times, from his principles of motion and radiation of whirling forces. This work is in fact a summary of all his astronomical opinions, drawn up in a popular style in the form of question and answer. We find there a singular argument against believing, as some did, that each planet is carried round by an angel, for in that case, says Kepler, “the orbits would be perfectly circular; but the elliptic form, which we find in them, rather smacks of the nature of the lever and material necessity.”
The investigation of the relation between the periodic times and distances of the planets is introduced by a query whether or not they are to be considered heavy. The answer is given in the following terms:—“Although none of the celestial globes are heavy, in the sense in which we say on earth that a stone is heavy, nor light as fire is light with us, yet life they, by reason of their materiality, a natural inability to move from place to place: they have a natural inertness or quietude, in consequence of which they remain still in every situation where they are placed alone.”
“P. Is it then the sun, which by its turning carries round the planets? How can the sun do this, having no hands to seize the planet at so great a distance, and force it round along with itself?— Its bodily virtue, sent forth in straight lines into the whole space of the world, serves instead of hands; and this virtue, being a corporeal species, turns with the body of the sun like a very rapid vortex, and travels over the whole of that space which it fills as quickly as the sun revolves in its very confined space round the centre.
“P. Explain what this virtue is, and belonging to what class of things?— As there are two bodies, the mover and the moved, so are there two powers by which the motion is obtained. The one is passive, and rather belonging to matter, namely, the resemblance of the body of the planet to the body of the sun in its corporeal form, and so that part of the planetary body is friendly, the opposite part hostile to the sun. The other power is active, and bearing more relation to form, namely, the body of the sun has a power of attracting the planet by its friendly part, of repelling it by the hostile part, and finally, of retaining it if it be placed so that neither the one nor the other be turned directly towards the sun.
“P. How can it be that the whole body of the planet should be like or cognate to the body of the sun, and yet part of the planet friendly, part hostile to the sun? —Just as when one magnet attracts another, the bodies are cognate; but attraction takes place only on one side, repulsion on the other.
“P. Whence, then, arises that difference of opposite parts in the same body? —In magnets the diversity arises from the situation of the parts with respect to the whole. In the heavens the matter is a little differently arranged, for the sun does not, like the magnet, possess only on one side, but in all the parts of its substance, this active and energetic faculty of attracting, repelling, or retaining the planet. So that it is probable that the centre of the solar body corresponds to one extremity or pole of the magnet, and its whole surface to the other pole.
“P. If this were so, all the planets {44} would be restored* in the same time with the sun?—True, if this were all: but it has been said already that, besides this carrying power of the sun, there is also in the planets a natural inertness to motion, which causes that, by reason of their material substance, they are inclined to remain each in its place. The carrying power of the sun, and the impotence or material inertness of the planet, are thus in opposition. Each shares the victory; the sun moves the planet from its place, although in some degree it escapes from the chains with which it was held by the sun, and so is taken hold of successively by every part of this circular virtue, or, is it may be called, solar circumference, namely, by the parts which follow those from which it has just extricated itself.
“P. But how does one planet extricate itself more than another from this violence?—First, because the virtue emanating from the sun has the same degree of weakness at different distances, as the distances or the width of the circles described on these distances†. This is the principal reason. Secondly, the cause is partly in the greater or less inertness or resistance of the planetary globes, which reduces the proportions to one-half; but of this more hereafter.
“P. How can it be that the virtue emanating from the sun becomes weaker at a greater distance? What is there to hurt or weaken it? — Because that virtue is corporeal, and partaking of quantity, which can be spread out and rarefied. Then, since there is as much virtue diffused in the vast orb of Saturn as is collected in the very narrow one of Mercury, it is very rare and therefore weak in Saturn's orbit, very dense and therefore powerful at Mercury.
"P. You said, in the beginning of this inquiry into motion, that the periodic times of the planets are exactly in the sesquiplicate proportion of their orbits or circles: pray what is the cause of this? —Four causes concur for lengthening the periodic time. First, the length of the path; secondly, the weight or quantity of matter to be carried; thirdly, the degree of strength of the moving virtue; fourthly, the bulk or space into which is spread out the matter to be moved. The circular paths of the planets are in the simple ratio of the distances; the weights or quantities of matter in different planets are in the subduplicate ratio of the same distances, as has been already proved; so that with every increase of distance, a planet has more matter, and therefore is moved more slowly, and accumulates more time in its revolution, requiring already as it did more time by reason of the length of the way. The third and fourth causes compensate each other in a comparison of different planets: the simple and subduplicate proportion compound the sesquiplicate proportion, which therefore is the ratio of the periodic times.”
Three of the four suppositions here made by Kepler to explain the beautiful law he had detected, are now indisputably known to be false. Neither the weights nor the sizes of the different planets observe the proportions assigned by him, nor is the force by which they are retained in their orbits in any respect similar in its effects to those attributed by him to it. The wonder which might naturally be felt that he should nevertheless reach the desired conclusion, will be considerably abated on examining the mode in which he arrived at and satisfied himself of the truth of these three suppositions. It has been already mentioned that his notions on the existence of a whirling force emanating from the sun, and decreasing in energy at increased distances, are altogether inconsistent with all the experiments and observations we are able to collect. His reason for asserting that the sizes of the different planets are proportional to their distances from the sun, was simply because he chose to take for granted that either their solidities, surfaces, or diameters, must necessarily be in that proportion, and of the three, the solidities appeared to him least liable to objection. The last element of his precarious reasoning rested upon equally groundless assumptions. Taking as a principle, that where there is a number of different things they must be different in every respect, he declared that it was quite unreasonable to suppose all the planets of the same density. He thought it indisputable that they must be rarer as they were farther from the sun, “and yet not in the proportion of their distances, for thus we should sin against the law of variety in another way, and make the quantity of matter (according to what he had just said of their bulk) the name in {45} all. But if we assume the ratio of the quantities of matter to be half that of the distances, we shall observe the best mean of all; for thus Saturn will be half as heavy again as Jupiter, and Jupiter half again as dense as Saturn. And the strongest argument of all is, that unless we assume this proportion of the densities, the law of the periodic times will not answer.” This is the proof alluded to, and it is clear that by such reasoning any required result might be deduced from any given principles.
It may not be uninstructive to subjoin a sketch of the manner in which Newton established the same celebrated results, starting from principles of motion diametrically opposed to Kepler's, and it need scarcely be added, reasoning upon them in a manner not less different. For this purpose, a very few prefatory remarks will be found sufficient.
The different motions seen in nature are best analysed and classified by supposing that every body in motion, if left to itself, will continue to move forward at the same rate in a straight line, and by considering all the observed deviations from this manner of moving, as exceptions and disturbances occasioned by some external cause. To this supposed cause is generally given the name of Force, and it is said to be the first law of motion, that, unless acted on by some force, every body at rest remains at rest, and every body in motion proceeds uniformly in a straight line. Many employ this language, without perceiving that it involves a definition of force, on the admission of which, it is reduced to a truism. We see common instances of force in a blow, or a pull from the end of a string fastened to the body: we shall also have occasion presently to mention some forces where no visible connexion exists between the moving body and that towards which the motion takes place, and from which the force is said to proceed.
A second law of motion, founded upon experiment, is this: if a body have motion communicated to it in two directions, by one of which motions alone it would have passed through a given space in a given time, as for instance, through BC’ in one second, and by the other alone through any other space Bc in the same time, it will, when both are given to it, at the same instant, pass in the same time (in the present instance in one second) through BC the diagonal of the parallelogram of which BC’ and Bc are sides.
Let a body, acted upon by no force, be moving along the line AE; that
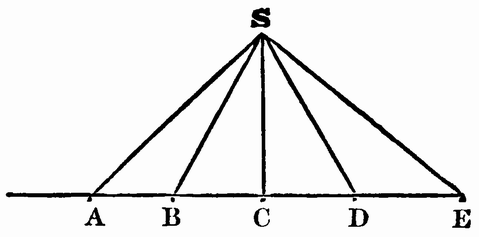
means, according to what has been said, let it pass over the equal straight lines AB, BC, CD, DE, &c, in equal times. If we take any point S not in the line AE, and join AS, BS, &c, the triangles ASB, BSC, &c. are also equal, having a common altitude and standing on equal bases, so that if a string were conceived reaching from S to the moving body (being lengthened or shortened in each position to suit its distance from S), this string, as the body moved along AE, would sweep over equal triangular areas in equal times. Let us now examine how far these
conclusions will be altered if the body from time to time is forced towards S. We will suppose it moving uniformly from A to B as before, no matter for the present how it got to A, or into the direction AB. If left to itself it would, in an equal time (say 1") go through BC in the same straight line with and equal to AB. But just as it reaches B, and is beginning to move along BC, let it be suddenly pulled towards S with a motion which, had it been at rest, would have carried it in the same time, 1", through any other space Bc. According to the second law of motion, its direction during this 1", in consequence of the two motions combined, will be along BC, the diagonal of the parallelogram of which BC', Bc, are sides. In {46} this case, as this figure is drawn, BC, though passed in the same time, is longer than AB; that is to say, the body is moving quicker than at first. How is it with the triangular areas, supposed as before to he swept by a string constantly stretched between S and the body? It will soon be seen that these still remain equal, notwithstanding the change of direction, and increased swiftness. For since CC’ is parallel to Bc, the triangles SCB, SC'B arc equal, being on the same base SB, and between the same parallels SB, CC', and SC'B is equal to SBA as before, therefore SCB, SBA are equal. The body is now moving uniformly (though quicker than along AB) along BC. As before, it would in a time equal to the time of passing along BC, go through an equal space CD’ in the same straight line. But if at C it has a second pull towards S, strong enough to carry it to d in the same time, its direction will change a second time to CD, the diagonal of the parallelogram, whose sides are CD', Cd; and the circumstances being exactly similar to those at the first pull, it is shewn in the same manner that the triangular area SDC = SCB = SBA.
Thus it appears, that in consequence of these intermitting pulls towards S, the body may be moving round, sometimes faster, sometimes slower, but that the triangles formed by any of the straight portions of its path (which are all described in equal times), and the lines joining S to the ends of that portion, are all equal. The path it will take depends of course, in other respects, upon the frequency and strength of the different pulls, and it might happen, if they were duly proportionate, that when at H, and moving off in the direction HA', the pull Ha might be such as just to carry the body back to A, the point from which it started, and with such a motion, that after one pull more, Ab, at A, it might move along AB as it did at first. If this were so, the body would continue to move round in the same polygonal path, alternately approaching and receding from S, as long as the same pulls were repeated in the same order, and at the same intervals.
It seems almost unnecessary to remark, that the same equality which subsists between any two of these triangular areas subsists also between an equal number of them, from whatever part of the path taken; so that, for instance, the four paths AB, BC, CD, DE, corresponding to the four areas ASB, BSC, CSD, DSE, that is, to the area ABCDES, are passed in the same time as the four EF, FG, GH, HA, corresponding to the equal area EFGHAS. Hence it may be seen, if the whole time of revolution from A round to A again be called a year, that in half a year the body will have got to E, which in the present figure is more than half way round, and so of any other periods.
The more frequently the pulls are supposed to recur, the more frequently will the body change its direction; and if the pull were supposed constantly exerted in the direction towards S, the body would move in a curve round S, for no three successive positions of it could be in a straight line. Those who are not familiar with the methods of measuring curvilinear spaces must here be contented to observe, that the law holds, however close the pulls are brought together, and however closely the polygon is consequently made to resemble a curve: they may, if they please, consider the minute portions into which the curve is so divided, as differing insensibly from little rectilinear triangles, any equal number of which, according to what has been said above, wherever taken in the curve, would be swept in equal times. The theorem admits, in this case also, a rigorous proof; but it is not easy to make it entirely satisfactory, without entering into explanations which would detain us too long from our principal subject.
The proportion in which the pull is strong or weak at different distances from the central spot, is called “the law of the central or centripetal force,” and it may be observed, that after assuming the laws of motion, our investigations cease to have anything hypothetical or experimental in them; and that if we wish, according to these principles of motion, to determine the law of force necessary to make a body move in a curve of any required form, or conversely to discover the form of the curve described, in consequence of any assumed law of force, the inquiry is purely geometrical, depending upon the nature and properties of geometrical quantities only. This distinction between what is hypothetical, and what necessary truth, ought never to be lost sight of.
As the object of the present treatise is not to teach geometry, we shall {47} describe, in very general terms, the manner in which Newton, who was the first who systematically extended the laws of motion to the heavenly bodies, identified their results with the two remaining laws of Kepler. His “Principles of Natural Philosophy” contain general propositions with regard to any law of centripetal force, but that which he supposed to be the true one in our system, is expressed in mathematical language, by saying that the centripetal force varies inversely as the square of the distance, which means, that if the force at any distance be taken for the unit of force, at half that distance, it is two times twice, or four times as strong; at one-third the distance, three times thrice, or nine times as strong, and so for other distances. He shewed the probability of this law in the first instance by comparing the motion of the moon with that of heavy bodies at the surface of the
 earth. Taking LP to represent part of the moon's orbit described in one minute, the line PM between the orbit and the tangent at L would shew the space through which the central force at the earth (assuming the above principles of motion to be correct) would draw the moon. From the known distance and motion of the moon, this line PM is found to be about sixteen feet. The distance of the moon is about sixty times the radius of the earth, and therefore if the law of the central force in this instance were such as has been supposed, the force at the earth's surface would be 60 times 60, or 3600 times stronger, and at the earth's surface, the central force would make a body fall through 3600 times 16 feet in one minute. Galileo had already taught that the spaces through which a body would be made to fall, by the constant action of the same unvarying force, would be proportional to the squares of the times during which the force was exerted, and therefore according to these laws, a body at the earth's surface ought (since there are sixty seconds in a minute) to fall through 16 feet in one second, which was precisely the space previously established by numerous experiments.
earth. Taking LP to represent part of the moon's orbit described in one minute, the line PM between the orbit and the tangent at L would shew the space through which the central force at the earth (assuming the above principles of motion to be correct) would draw the moon. From the known distance and motion of the moon, this line PM is found to be about sixteen feet. The distance of the moon is about sixty times the radius of the earth, and therefore if the law of the central force in this instance were such as has been supposed, the force at the earth's surface would be 60 times 60, or 3600 times stronger, and at the earth's surface, the central force would make a body fall through 3600 times 16 feet in one minute. Galileo had already taught that the spaces through which a body would be made to fall, by the constant action of the same unvarying force, would be proportional to the squares of the times during which the force was exerted, and therefore according to these laws, a body at the earth's surface ought (since there are sixty seconds in a minute) to fall through 16 feet in one second, which was precisely the space previously established by numerous experiments.
With this confirmation of the supposition, Newton proceeded to the purely geometrical calculation of the law of centripetal* force necessary to make a moving body describe an ellipse round its focus, which Kepler's observations had established to be the form of the orbits of the planets round the sun. The result of the inquiry shewed that this curve required the same law of the force, varying inversely as the square of the distance, which therefore of course received additional confirmation. His method of doing this may, perhaps, be understood by referring to the last figure but one, in which Cd, for instance, representing the space fallen from any point C towards S, in a given time, and the area CSD being proportional to the corresponding time, the space through which the body would have fallen at C in any other time (which would be greater, by Galileo's law, in proportion to the squares of the times), might be represented by a quantity varying directly as Cd, and inversely in the duplicate proportion of the triangular area CSD, that is to say, proportional to Cd/(SC × Dk)2, if Dk be drawn from D perpendicular on SC. If this polygon represent an ellipse, so that CD represents a small arc of the curve, of which S is the focus, it is found by the nature of that curve, that Cd/(Dk)2 is the same at all points of the curve, so that the law of variation of the force in the same ellipse is represented solely by 1/(DC)2. If Cd, &c are drawn so that Cd/(Dk)2 is not the same at every point, the curve ceases to be an ellipse whose focus is at S, as Newton has shewn in the same work.
The line to which (Dk)2/Cd is found to be equal, is one drawn through the focus at right angles to the longest axis of the ellipse till it meets the curve;—this line is called the lotus rectum, and is a third proportional to the two principal axes.
Kepler's third law follows as an immediate consequence of this determination; for, according to what has been already shown, the time of revolution round the whole ellipse, or, as it is {48} commonly called, the periodic time, bears the same ratio to the unit of time as the whole area of the ellipse does to the area described in that unit. The area of the whole ellipse is proportional in different ellipses to the rectangle contained by the two principal axes, and the area described in an unit of time is proportional to SC x Dk, that is to say, is in the subduplicate ratio of SC2 × Dk2 or Dk2/Cd, when the force varies inversely as the square of the distance SC; and in the ellipse, as we have said already, this is equal to a third proportional to the principal axes: consequently the periodic times in different ellipses, which are proportional to the whole areas of the ellipses directly, and the areas described in the unit of time inversely, are in the compound ratio of the rectangle of the axes directly, and subduplicatly as a third proportional to the axes inversely; that is to say, the squares of these times are proportional to the cubes of the longest axes, which is Kepler's law.
Kepler's “Epitome,” almost immediately on its appearance, enjoyed the honour of being placed by the side of the work of Copernicus, on the list of books prohibited by the congregation of the index at Rome. He was considerably alarmed on receiving this intelligence, anticipating that it might occasion difficulties in publishing his future writings. His words to Remus, who had communicated the news to him, are as follows:— “I learn from your letter, for the first time, that my book is prohibited at Rome and Florence. I particularly beg of you, to send me the exact words of the censure, and that you will inform me whether that censure would be a snare for the author, if he were caught in Italy, or whether, if taken, he would be enjoined a recantation. It is also of consequence for me to know whether there is any chance of the same censure being extended into Austria. For if this be so, not only shall I never again find a printer there, but also the copies which the bookseller has left in Austria at my desire will be endangered, and the ultimate loss will fall upon me. It will amount to giving me to understand, that I must cease to profess Astronomy, after I have grown old in the belief of these opinions, having been hitherto gainsayed by no one,—and, in short, I must give up Austria itself, if room is no longer to be left in it for philosophical liberty.” He was, however, tranquillized, in a great degree, by the reply of his friend, who told him that “the book is only prohibited as contrary to the decree pronounced by the holy office two years ago. This has been partly occasioned by a Neapolitan monk (Foscarini), who was spreading these notions by publishing them in Italian, whence were arising dangerous consequences and opinions: and besides, Galileo was at the same time pleading his cause at Rome with too much violence. Copernicus has been corrected in the same manner for some lines, at least in the beginning of his first book. But by obtaining a permission, they may be read (and, as I suppose, this “Epitome” also) by the learned and skilful in this science, both at Rome and throughout all Italy. There is therefore no ground for your alarm, either in Italy or Austria: only keep yourself within bounds, and put a guard upon your own passions.”
We shall not dwell upon Kepler's different works on comets, beyond mentioning that they were divided, on the plan of many of his other publications, into three parts, Astronomical, Physical, and Astrological. He maintained that comets move in straight lines, with a varying degree of velocity. Later theories have shewn that they obey the same laws of motion as the planets, differing from them only in the extreme excentricity of their orbits. In the second book, which contains the Physiology of Comets, there is a passing remark that comets come out from the remotest parts of ether, as whales and monsters from the depth of the sea; and the suggestion is thrown out that perhaps comets are something of the nature of silkworms, and are wasted and consumed in spinning their own tails.
Among his other laborious employments, Kepler yet found time to calculate tables of logarithms, he having been one of the first in Germany to appreciate the full importance of the facilities they afford to the numerical calculator. In 1618 he wrote to his friend Schickhard: “There is a Scottish Baron (whose name has escaped my memory), who has made a famous contrivance, by which {49} all need of multiplication and division is applied by mere addition and subtraction; and he does it without sines. But even he wants a table of tangents*, and the variety, frequency, and difficulty of the additions and subtractions, in some cases, is greater than the labour of multiplying and dividing.”
Kepler dedicated his “Ephemeris” for 1620 to the author of this celebrated invention, Baron Napier, of Merchistoun; and in 1624, published what he called “Chilias Logarithmorum,” containing the Napierian logarithms of the quotients of 100,000 divided by the first ten numbers, then proceeding by the quotients of every ten to 100, and by hundreds to 100,000. In the supplement published the following year, is a curious notice of the manner in which this subtle contrivance was at first received: “In the year 1621, when I had gone into Upper Austria, and had conferred everywhere with those skilled in mathematics, on the subject of Napier's logarithms, I found that those whose prudence had increased, and whose readiness had diminished, through age, were hesitating whether to adopt this new sort of numbers, instead of a table of sines; because they said it was disgraceful to a professor of mathematics to exult like a child at some compendious method of working, and meanwhile to admit a form of calculation, resting on no legitimate proof, and which at some time might entangle us in error, when we least feared it. They complained that Napier's demonstration rested on a fiction of geometrical motion, too loose and slippery for a sound method of reasonable demonstration to be founded on it†. “This led me forthwith to conceive the germ of a legitimate demonstration, which during that same winter I attempted, without reference to lines or motion, or flow, or any other which I may call sensible quality.”
“Now to answer the question; what is the use of logarithms? Exactly what ten years ago was announced by their author, Napier, and which may be told in these words.—Wheresoever in common arithmetic, and in the Rule of Three, come two numbers to be multiplied together, there the sum of the logarithms is to be taken; where one number is to be divided by another, the difference; and the number corresponding to this sum or difference, as the case may be, will be the required product or quotient. This, I say, it the use of logarithms. But in the same work in which I gave the demonstration of the principles, I could not satisfy the unfledged arithmetical chickens, greedy of facilities, and gaping with their beaks wide open, at the mention of this use, as if to bolt down every particular gobbet, till they are crammed with my precepticles.”
The year 1622 was marked by the catastrophe of a singular adventure which befell Kepler's mother, Catharine, then nearly seventy years old, and by which he had been greatly harassed and annoyed during several years. From her youth she had been noted for a rude and passionate temper, which on the present occasion involved her in serious difficulties. One of her female acquaintance, whose manner of life had been by no means unblemished, was attacked after a miscarriage by violent headaches, and Catharine, who had often taken occasion to sneer at her notorious reputation, was accused with having produced these consequences, by the administration of poisonous potions. She repelled the charge with violence, and instituted an action of scandal against this person, but was unlucky (according to Kepler's statement) in the choice of a young doctor, whom she employed as her advocate. Considering the suit to be very instructive, he delayed its termination during five years, until the judge before whom it was tried was displaced. He was succeeded by another, already indisposed against Catharine Kepler, who on some occasion had taunted him with his sudden accession to wealth from a very inferior situation. Her opponent. aware of this advantage, turned the {50} tables on her, and in her turn became the accuser. The end of the matter was, that in July, 1620, Catharine was imprisoned, and condemned to the torture. Kepler was then at Linz, but as soon as he learned his mother's danger, hurried to the scene of trial. He found the charges against her supported only by evidence which never could have been listened to, if her own intemperate conduet had not given advantage to her adversaries. He arrived in time to save her from the question, but she was not finally acquitted and released from prison till November in the following year. Kepler then returned to Linz, leaving behind him his mother, whose spirit seemed in no degree broken by the unexpected turn in the course of her litigation. She immediately commenced a new action for costs and damages against the same antagonist, but this was stopped by her death, in April 1622, in her seventy-fifth year. In 1620 Kepler was visited by Sir Henry Wotton, the English ambassador at Venice, who finding him, as indeed he might have been found at every period of his life, oppressed by pecuniary difficulties, urged him to go over to England, where he assured him of a welcome and honourable reception; but Kepler could not resolve upon the proposed journey, although in his letters he often returned to the consideration of it. In one of them, dated a year later, he says, “The fires of civil war are raging in Germany—they who are opposed to the honour of the empire are getting the upper hand—everything in my neighbourhood seems abandoned to flame and destruction. Shall I then cross the sea, whither Wotton invites me? I, a German? a lover of firm land? who dread the confinement of an island? who presage its dangers, and must drag along with me my little wife and flock of children? Besides my son Louis, now thirteen years old, I have a marriageable daughter, a two-year old son by my second marriage, an infant daughter, and its mother but just recovering from her confinement.” Six years later, he says again,—“As soon as the Rudolphine Tables are published, my desire will be to find a place where I can lecture on them to a considerable assembly; if possible, in Germany; if not, why then in Italy, France, the Netherlands, or England, provided the salary is adequate for a traveller.” In the same year in which he received this invitation an affront was put upon Kepler by his early patrons, the States of Styria, who ordered all the copies of his “'Calendar,” for 1624, to be publicly burnt. Kepler declares that the reason of this was, that he had given precedence in the title-page to the States of Upper Ens, in whose service he then was, above Styria. As this happened during his absence in Wirtemberg, it was immediately coupled by rumour with his hasty departure from Linz: it was said that he had incurred the Emperor's displeasure, and that a large sum was set upon his head. At this period Matthias had been succeeded by Ferdinand III, who still continued to Kepler his barren title of imperial mathematician.
In 1624 Kepler went to Vienna, in the hopes of getting money to complete the Rudolphine Tables, but was obliged to be satisfied with the sum of 6000 florins and with recommendatory letters to the States of Suabia, from whom he also collected some money due to the emperor. On his return he revisited the University of Tubingen, where he found his old preceptor, Mästlin, still alive, but almost worn out with old age. Mästlin had well deserved the regard Kepler always appears to have entertained for hirn; he had treated him with great liberality whilst at the University, where he refused to receive any remuneration for his instruction. Kepler took every opportunity of shewing his gratitude; even whilst he was struggling with poverty he contrived to send his old master a handsome silver cup, in acknowledging the receipt of which Mästlin says,—“Your mother had taken it into her head that you owed me two hundred florins, and had brought fifteen florins and a chandelier towards reducing the debt, which I advised her to send to you. I asked her to stay to dinner, which she refused: however, we handselled your cup, as you know she is of a thirsty temperament.”
The publication of the Rudolphine Tables, which Kepler always had so much at heart, was again delayed, notwithstanding the recent grant, by the disturbances arising out of the two parties into which the Reformation had divided the whole of Germany. Kepler's library was sealed up by desire of the Jesuits, and nothing but his connexion with the Imperial Court secured to him his own personal indemnity. Then followed a popular insurrection, and the {51} pesantry blockaded Linz, so that it was not until 1827 that these celebrated tables finally made their appearance, the earliest calculated on the supposition that the planets move in elliptic orbits. Ptolemy's tables had been succeeded by the “Alphonsine,” so called from Alphonso, King of Castile, who, in the thirteenth century, was an enlightened patron of astronomy. After the discoveries of Copernicus, these again made way for the Prussian, or Prutenic tables, calculated by his pupils Reinhold and Rheticus. These remained in use till the observations of Tycho Brahe showed their insufficiency, and Kepler's new theories enabled him to improve upon them. The necessary types for these tables were cast at Kepler's own expense. They are divided into four parts, the first and third containing a variety of logarithmic and other tables, for the purpose of facilitating astronomical calculations. In the second are tables of the elements of the sun, moon, and planets. The fourth gives the places of 1000 stars as determined by Tycho, and also at the end his table of refractions, which appears to have been different for the sun, moon, and stars. Tycho Brahe assumed the horizontal refraction of the sun to be 7'30", of the moon 8', and of the other stars 3'. He considered all refraction of the atmosphere to be insensible above 45° of altitude, and even at half that altitude in the case of the fixed stars. A more detailed account of these tables is here obviously unsuitable: it will be sufficient to say merely, that if Kepler had done nothing in the course of his whole life but construct these, he would have well earned the title of a most useful and indefatigable calculator.
Some copies of these tables have prefixed to them a very remarkable map, divided by hour lines, the object of which is thus explained:—
“The use of this nautical map is, that if at a given hour the place of the moon is known by its edge being observed to touch any known star, or the edges of the sun, or the shadow of the earth; and if that place shall (if necessary) be reduced from apparent to real by clearing it of parallax; and if the hour at Uraniburg be computed by the Rudolphine tables, when the moon occupied that true place, the difference will snow the observer's meridian, whether the picture of the shores be accurate or not, for by this means it may come to be corrected.”
This is probably one of the earliest announcements of the method of determining longitudes by occultations; the imperfect theory of the moon long remained a principal obstacle to its introduction in practice. Another interesting passage connected with the same object may be introduced here. In a letter to his friend Cruger, dated in 1616, Kepler says: “You propose a method of observing the distances of places by sun-dials and automata. It is good, but needs a very accurate practice, and confidence in those who have the care of the clocks. Let there be only one clock, and let it be transported; and in both places let meridian lines be drawn with which the clock may be compared when brought. The only doubt remaining is, whether a greater error is likely from the unequal tension in the automaton, and from its motion, which varies with the state of the air, or from actually measuring the distances. For if we trust the latter, we can easily determine the longitudes by observing the differences of the height of the pole.”
In an Appendix to the Rudolphine Tables, or, as Kepler calls it, “an alms doled out to the nativity casters,” he has shown how they may use his tables for their astrological predictions. Everything in his hands became an allegory; and on this occasion he says, —“Astronomy is the daughter of Astrology, and this modern Astrology, again, is the daughter of Astronomy, bearing something of the lineaments of her grandmother; and, as I have already said, this foolish daughter, Astrology, supports her wise but needy mother, Astronomy, from the profits of a profession not generally considered creditable.”
Soon after the publication of these tables, the Grand Duke of Tuscany sent him a golden chain; and if we remember the high credit in which Galileo stood at this time in Florence, it does not seem too much to attribute this honourable mark of approbation to his representation of the value of Kepler's services to astronomy. This was soon followed by a new and final change in his fortunes. He received permission from the emperor to attach himself to the celebrated Duke of Friedland, Albert Wallenstein, one of the most remarkable men in the history of that time. {52} Wallenstein was a firm believer in astrology, and the reception Kepler experienced by him was probably due, in great measure, to his reputation in that art. However that may be, Kepler found in him a more munificent patron than any one of his three emperors; but he was not destined long to enjoy the appearance of better fortune. Almost the last work which he published was a commentary on the letter addressed, by the missionary Terrentio, from China, to the Jesuits at Ingolstadt. The object of this communication was to obtain from Europe means for carrying into effect a projected scheme for improving the Chinese calendar. In this essay Kepler maintains the opinion, which has been discussed with so much warmth in more modern times, that the pretended ancient observations of the Chinese were obtained by computing them backwards from a much more recent date. Wallenstein furnished him with an assistant for his calculations, and with a printing press; and through his influence nominated him to the professorship in the University of Rostoch, in the Duchy of Mecklenburg. His claims on the imperial treasury, which amounted at this time to 8000 crowns, and which Ferdinand would gladly have transferred to the charge of Wallenstein, still remained unsatisfied. Kepler made a last attempt to obtain them at Ratisbon, where the imperial meeting was held, but without success. The fatigue and vexation occasioned by his fruitless journey brought on a fever, which unexpectedly put an end to his life, in the early part of November, 1630, in his fifty-ninth year. His old master, Mästlin, survived him for about a year, dying at the age of eighty-one.
Kepler left behind him two children by his first wife, Susanna and Louis; and three sons and two daughters, Sebald, Cordelia, Friedman, Hildebert, and Anna Maria, by his widow. Susanna married, a few months before her father's death, a physician named Jacob Bartsch, the same who latterly assisted Kepler in preparing his “Ephemeris.” He died very shortly after Kepler himself. Louis studied medicine, and died in 1663, whilst practising as a physician at Konigsberg. The other children died young.
Upon Kepler's death the Duke of Friedland caused an inventory to be taken of his effects, when it appeared that new 24,000 florins were due to him, chiefly on account of his salary from the emperor. His daughter Susanna, Bartsch's widow, managed to obtain a part of these arrears by refusing to give up Tycho Brahe's observations till her claims were satisfied. The widow and younger children were left in very straightened circumstances, which induced Louis, Kepler's eldest son, to print, for their relief, one of his father's works, which had been left by him unpublished. It was not without much reluctance, in consequence of a superstitious feeling which he did not attempt to conceal or deny. Kepler himself, and his son-in-law, Bartsch, had been employed in preparing it for publication at the time of their respective deaths; and Louis confessed that he did not approach the task without apprehension that he was incurring some risk of a similar fate. This little rhapsody is entitled a “Dream on Lunar Astronomy;” and was inintended to illustrate the appearances which would present themselves to an astronomer living upon the moon.
The narrative in the dream is put into the mouth of a personage, named Duracoto, the son of an Icelandic enchantress, of the name of Fiolxhildis. Kepler tells us that he chose the last name from an old map of Europe in his house, in which Iceland was called Fiolx: Duracoto seemed to him analogous to the names he found in the history of Scotland, the neighbouring country. Fiolxhildis was in the habit of selling winds to mariners, and used to collect herbs to use in her incantations on the sides of Mount Hecla, on the Eve of St. John. Duracoto cut open one of his mother's bags, in punishment of which she sold him to some traders, who brought him to Denmark, where he became acquainted with Tycho Brahe. On his return to Iceland, Fiolxhildis received him kindly, and was delighted with the progress he had made in astronomy. She then informed him of the existence of certain spirits, or demons, from whom, although no traveller herself, she acquired a knowledge of other countries, and especially of a very remarkable country, called Livania. Duracoto requesting further information, the necessary ceremonies were performed for invoking the demon; Duracoto and his mother enveloped their heads in their clothing, and presently “the screaking of a harsh dissonant voice began to speak {53} in the Icelandic tongue.” The island of Livania is situated in the depths of ether, at the distance of about 250000 miles; the road thence or thither is very seldom open, and even when it is passable, mankind find the journey a most difficult and dangerous one. The demon describes the method employed by his fellow spirits to convey such travellers as are thought fit for the undertaking: “We bring no sedentary people into our company, no corpulent or delicate persons; but we pick out those who waste their life in the continual use of post-horses, or who sail frequently to the Indies; who are accustomed to live upon biscuit, garlic, dried fish, and such abominable feeding. Those withered old hags are exactly fit for us, of whom the story is familiar that they travel immense distances by night on goats, and forks, and old petticoats. The Germans do not suit us at all; but we do not reject the dry Spaniards.” This extract will probably be sufficient to show the style of the work. The inhabitants of Livania are represented to be divided into two classes, the Privolvans and Subvolvans, by whom are meant those supposed to live in the hemisphere facing the earth, which is called the Volva, and those on the opposite half of the moon: but there is nothing very striking in the account given of the various phenomena as respects these two classes. In some notes which were added some time after the book was first written, are some odd insights into Kepler's method of composing. Fiolxhildis had been made to invoke the daemon with twenty-one characters; Kepler declares, in a note, that he cannot remember why he fixed on this number, “except because that is the number of letters in Astronomia Copernicana, or because there are twenty-one combinations of the planets, two together, or because there are twenty-one different throws upon two dice.” The dream is abruptly terminated by a storm, in which, says Kepler, “I suddenly waked; the Demon, Duracoto, and Fiolxhildis were gone, and instead of their covered heads, I found myself rolled up among the blankets.”
Besides this trifle, Kepler left behind him a vast mass of unpublished writings, which came at last into the hands of his biographer, Hantsch. In 1714, Hantsch issued a prospectus for publishing them by subscription, in twenty-two folio volumes. The plan met no encouragement, and nothing was published but a single folio volume of letters to and from Kepler, which seem to have furnished the principal materials for the memoir prefixed to them. After various unavailing attempts to interest different learned bodies in their appearance, the manuscripts were purchased for the library at St. Petersburg, where Euler, Lexell, and Kraft, undertook to examine them, and select the most interesting parts for publication. The result of this examination does not appear.
Kepler's body was buried in St. Peter's churchyard at Ratisbon, and a simple inscription was placed on his tombstone. This appears to have been destroyed not long after, in the course of the wars which still desolated the country. In 1786, a proposal was made to erect a marble monument to his memory, but nothing was done, Kästner, on whose authority it is mentioned, says upon this, rather bitterly, that it matters little whether or not Germany, having almost refused him bread during his life, should, a century and it half after his death, offer him a stone.
Delambre mentions, in his History of Astronomy, that this design was resumed in 1803 by the Prince Bishop of Constance, and that a monument has been erected in the Botanical Garden at Ratisbon, near the place of his interment. It is built in the form of a temple, surmounted by a sphere; in the centre is placed a bust of Kepler, in Carrara marble. Delambre does not mention the original of the bust; but says it is not unlike the figure engraved in the frontispiece of the Rudolphine Tables. That frontispiece consists of a portico of ten pillars, supporting a cupola covered with astronomical emblems. Copernicus, Tycho Brahe, Ptolemy, Hipparchus, and other astronomers, are seen among them. In one of the compartments of the common pedestal is a plan of the observatory at Uraniburg; in another, a printing press; in a third is the figure of a man, meant for Kepler, seated at a table. He is identified by the titles of his works, which are round him; but the whole is so small as to convey very little idea of his figure or countenance. The only portrait known of Kepler was given by him to his assistant Gringallet, who presented it to Bernegger; and it was placed by the latter in the library at Strasburg. Hantsch had a copy taken for the purpose of engraving it, but died before it was {54} completed. A portrait of Kepler is engraved in the seventh part of Boissard's Bibliotheca Chaleographica. It is not known whence this was taken, but it may, perhaps, be a copy of that which was engraved by desire of Bernegger in 1620. The likeness is said not to have been well preserved. “His heart and genius,” says Kästner, “are faithfully depicted in his writings; and that may console us, if we cannot entirely trust his portrait.” In the preceding pages, it has been endeavoured to select such passages from his writings as might throw the greatest light on his character, with a subordinate reference only to the importance of the subjects treated. In conclusion, it may be well to support the opinion which has been ventured on the real nature of his triumphs, and on the danger of attempting to follow his method in the pursuit of truth, by the judgment pronounced by Delambre, as well on his failures as on his success. “Considering these matters in another point of view, it is not impossible to convince ourselves that Kepler may have been always the same. Ardent, restless, burning to distinguish himself by his discoveries, he attempted everything; and having once obtained a glimpse of one, no labour was too hard for him in following or verifying it. All his attempts had not the same success, and, in fact, that was impossible. Those which have failed seem to us only fanciful; those which have been more fortunate appear sublime. When in search of that which really existed, he has somelimes found it; when he devoted himself to the pursuit of a chimera, he could not but fail; but even there he unfolded the same qualities, and that obstinate perseverance that must triumph over all difficulties but those which are insurmountable*.”
List of Kepler's published Works.
Ein Calender . . | Gratz, | 1594 |
Prodromus Dissertat. Cosmograph. | Tubingae, | 1596, 4to. |
De fundamentis Astrologiae . | Pragae, | 1602, 4to. |
Paralipomena ad Vitellionem . . | Francofurti, | 1604, 4to. |
Epislola de Soils deliquio | 1605 | |
De stellii nova . | Pragae, | 1616, 4to. |
Vom Koinclen . . . | Halle, | 1608, 4to. |
Antwort an Röslin . | Pragae, | 1609, 4to. |
Astronomia Nova . . . | Pragae, | 1609, fol. |
Tertius interveniens . . | Frankfurt, | 1610, 4to. |
Dissertatio cum Nuncio Sidereo | Francofurti, | 1610, 4to. |
Slrena, seu De nive sexangula . | Frankfurt, | 1611, 4to. |
Dioptrica . . . . | Francofurti, | 1611, 4to. |
Vom Geburls Jahre des Heylandes | Strasburg, | 1613, 4to. |
Respons. ad epist S. Calvisili | Francofurti, | 1614, 4to. |
Eclogae Chronicae . . . | Frankfurt, | 1615, 4to. |
Nova Slereometria . . . | Lincii, | 1615, 4to. |
Ephemerides 1G17—1620 | Lincii, | 1616, 4to. |
Epitomes Astron. Copern. Libri i. ii. iii. | Lentiis, | 1618, 8vo. |
De Cometia . . . . | Aug. Vindelic. | 1619, 4to. |
Harmonice Mundi . . | Lincii, | 1619, fol. |
Kanones Pueriles . . . | Ulmae, | 1620 |
Epitomes Astron. Copern. Liber iv. . | Lentiis, | 1622, 8vo. |
Epitomes Astron. Copern. Libri v. vi. vii. | Francofurti, | 1622, 8vo. |
Discurs von der grossen Conjunction | Linz, | 1623, 4to. |
Chilias Logarithmorum . | Marpurgi, | 1624, fol. |
Supplementum | Lentiis, | 1625, 4to. |
Hyperaspistes . . | Francofurti, | 1625, 8vo. |
Tabulae Rudolphinae . . . | Ulmae, | 1627, fol. |
Resp. ad epist. J. Bartschii | Sagani, | 1629, 4to. |
De anni 1631 plitenomeois . . | Liptae, | 1629, 4to. |
Terrenlii epistolium cum commentatiuncula | Sagani, | 1630, 4to. |
Ephemerides . . . . | Sagani, | 1630, 4to. |
Somnium | Francofurti, | 1634, 4to. |
Tabulae manuales | Argentorati, | 1700, 12mo. |
• The following scrupulous note added by Kepler In 1621 to a subsequent edition of this work, deserves to be quoted. It shows how entirely superior he was to the paltriness of attempting to appropriate the discoveries of others, of which many of his contemporaries had exhibited instances even on slighter pretences than this passage might have afforded him. The note is as follows: “Not circulating round Jupiter like the Medicrean stars. Be not deceived, I never had them in my thoughts, but, like the other primary planets, including the sun in the centre of the system within their orbits.”
• This inconvenient made of dating was neccesary before the new or Gregorian style was universally adopted.
* See Life of Galiileo, p. 16.
+ The fiery trigon ocean about once in every 800 years, when Saturn, Jupiter, and Mars are in the three fiery signs, Aries, Leo, and Sagittarius.
* The copy of this work in the British Museum is Kepler's presentation copy to our James I. On the blank leaf, opposite the title-page, is the following inscription, apparently in the author's handwriting:—“Regi philosophianti, phlilosophus serviens, Platoni Diogenes, Britannias tenenti, Pragae stipem mendicans ab Alexandre, e dolio conductitio, hoc suum philosophema misit et commendavit.”
• The tapster of the Sirens.
† A serpent in his sting.
• In one of his anonymous writings Kepler has anagrammatized his name, Joannes Keplerus, in a variety of other forms, probably selected from tlte luckiest of his shuffles:—“Kleopas Herennius, Helenor Kapuensis, Raspinus Enkeleo, Kanones Pueriles.”
• By “the opposite direction” is meant, that while the motion in the circumference of one circle appeared, as veiwed from its centre, to be from left to right, the other, viewed from its center, appeared from right to left. This must be understood whenever these or similar expressions are repeated.
• Venus Mercuriusque, licet ortus occasusque quotidianos ostendunt, tamen corum circull terras omnio non ambiont, sed circa solem laxlore ambitu circulantur. Denique circulorum surcum centron in sole constituunt.—De Noptiis Philologiae et Mercurii. Vicentiss, 1499.
• It is not very easy to carry the understanding aright among these Aristotelian ideas. Many at the present day might think they understood better what is meant, if for “form” had been written “nature.”
* De mundo nostro sublunari, Philosophia Nova. Amsterdam, 1651.
* Theoricae novae planetarum, G. Purbachii, Parisus, 1553.
* This mode of verifying configurations, though something of the boldest, was by no means unusual. On a former occasion Kepler, wishing to cast the nativity of his friend Zehentmaier, and being unable to procure more accurate information than that he was born about three o'clock in the afternoon of the 21st of October, 1751, supplied the deficiency by a record of fevers and accidents at known periods of his life, from which he deduced a more exact horoscope.
† Kepler probably meant his own mother, whose horoscope he in many places declared to be nearly the same as his own.
* See Preliminary Treatise, p. 13.
• An allusion to the Harmonics of Ptolemy.
• This is a word borrowed from the Ptolemaic astronomy, according to which the sun and planets are hurried from their places by the daily motion of the primum mobile, and by their own peculiar motion seek to regain or be restored to their former places.
† In other parts of his works Kepler assumes the diminution to be proportional to the circles themselves, not to the diameters.
• In many curves, as in the circle and ellipse there is a point to which the name of centre is given, on account of peculiar properties belonging to it: but the term “centripetal force” always refers to the place towards which the force is directed, whether or not situated in the centre of the curve.
• The meaning of this pasiage is not very clear: Kepler evidently had seen and used logarithms at the time of writing this letter; yet there is nothing in the method to justify this expression.—“At tamen opus est ipsi Tangentium canone.”
† This was the objection originally made to Hewton's “Fluxions,” and in fact, Napier's idea of logarithms is identical with that method of conceiving quantities. This may be seen at once from a few of his definitions,
1 Def. A line is said to increase uniformly, when the point by which it is described passes through equal intervals, in equal times.
2 Def. A line is said to diminish to a shorter one proportionally when the point passing along it cuts off in equal times segments proportional to the remainder. 3 Def. The logarithm of any sine is the number most nearly denoting the line, which has increased uniformly, whilst the radius has diminished to that sine, proportionally, the initial velocity being the same in both motions. (Mirifici logarithmorum canonis descriptio, Edinburgi 1614.) This last definition contains what we should now call the differential equation between a number and a logarithm of its reciprocal.
* Histoire del'Astronomie Moderne, Paris, 1821.