

| {i} |
Atom and Void
| {iii} |
|
Atom and Void ESSAYS ON SCIENCE J. Robert Oppenheimer PRINCETON UNIVERSITY PRESS PRINCETON, NEW JERSEY |
| {iv} |
Published by Princeton University Press, 41 William Street,
Princeton, New Jersey 08540
Copyright © 1989 by Princeton University Press
All Rights Reserved
Library of Congress Cataloging-in-Publication Data
Oppenheimer, J. Robert, 1904-1967
Atom and void : essays on science and community / J. Robert Oppenheimer.—1st Princeton science library ed. print, p. cm.—(Princeton science library) Rev. ed. of: Science and the common understanding. 1954 ISBN 0-691-08547-1 (alk. paper) ISBN 0-691-02434-0 (pbk. : alk. paper) 1. Science—Philosophy. 2. Science—Social aspects. I. Oppenheimer, J. Robert, 1904-1967. Science and the common understanding. II. Title. III. Series. Q175.065 1989 501—dc20 89-10413 First Princeton Science Library edition printing, 1989
10 9 8 7 6 5 4 3 2 1
10 9 8 7 6 5 4 3 2 1, pbk.
The preface to this volume is © 1989 by Freeman J. Dyson. The first six essays were adapted from the 1953 Reith Lectures sponsored by the British Broadcasting Corporation. They are © 1953, 1954, by J. Robert Oppenheimer, and originally published by Simon & Schuster, Inc., in Science and the Common Understanding. They are reprinted here by arrangement with Simon & Schuster, Inc. [The seventh essay, “The Open Mind,” is © 1955 by J. Robert Oppenheimer; it appeared in The Open Mind, published by Simon & Schuster in 1955, and is reprinted by arrangement with Simon & Schuster.] The last three essays are edited transcripts of lectures delivered in 1962 under the title The Flying Trapeze: Three Crises for Physicists, and commissioned by the Whidden Lecture Series of McMaster University. The transcriptions are © 1964 by Oxford University Press, and are reprinted by permission of McMaster University, with the approval of Oxford University Press.
Princeton University Press books are printed on acid-free paper, and meet the guidelines for permanence and durability of the Committee on Production Guidelines for Book Longevity of the Council on Library Resources
Printed in the United States of America by Princeton University Press, Princeton, New Jersey
| {v} |
vii | |
3 | |
16 | |
28 | |
40 | |
52 | |
64 | |
76 | |
85 | |
113 | |
133 | |
143 | |
154 | |
157 |
| {vii} |
by Freeman J. Dyson
When Robert Oppenheimer went to England in 1953 to deliver the Reith lectures, the lectures that make up the first half of this book, millions of listeners were baffled and disappointed. He was then, after Einstein, the second most famous living scientist. He had been a prime mover, first in the building of atomic bombs, second in the effort to establish an international control of nuclear energy, and third in the political struggles that raged around the building of hydrogen bombs. In 1953 the public already knew that he was involved in secret disputes which were to break out into the open with the denial of his security clearances a few months later.
The listeners in England expected hot news. They expected dramatic statements about the great events and great issues of the day. They expected a personal message from the man who in those days was widely proclaimed to be the conscience of humanity. Instead, they got these lectures. They got a scholarly and impersonal discussion of the history of science. They got a rarified and philosophical view of the mysteries of quantum mechanics. They got a picture of the human predicament as it might be seen by an observer at an immense distance in space and time, totally detached from day-to-day events and practical details. Barely a word about the bomb. No answers to any of the urgent political questions of the 1950s. No glimpse of that inner world of action and power in which Oppenheimer had been living for the previous ten years. No wonder the listeners were scornful. One of my English friends who heard the lectures compared Oppenheimer unkindly with the poet Bunthorne in the Gilbert and Sullivan operetta Patience: {viii}
You walk down Piccadilly
With a poppy or a lily
In your medieval hand—
And everyone will say,
As you walk your mystic way,
If this young man expresses himself
In terms too deep for me,
Why, what a very singularly deep young man
This deep young man must be.
Now, thirty-five years later, we can see that Oppenheimer chose his subject-matter wisely. He knew that any discussion of current events that attempted to be up-to-date would soon be out-of-date. He had no wish to give lectures that would cause a political sensation today and be obsolete tomorrow. He wanted to speak to the ages, to say something of permanent value. As a result, these lectures have stood well the test of time. They are as pertinent to our situation in 1989 as they were in 1953. The English listeners’ loss is our gain. We can now see that Oppenheimer's sense of history, his awareness of the long past and the long future, are the most important part of his legacy to mankind. In these lectures, and especially in the quotations assembled in the appendix at the end, his sense of history shines like a beacon, guiding our footsteps into the unknown for centuries to come.
When he came to give the Whidden lectures in Canada, the lectures that make up the second half of this book, less was expected of him. Nine years after the Reith lectures and eight years after his fall from power, he had become a respected elder statesman of science, no longer a worker of miracles. Nobody expected political thunderbolts. He spoke, as before, quietly, mostly about the history of science. But he allowed himself, in the last lecture, to unbend a little, to tell some personal stories about his involvement with the bomb and its consequences. His listeners were grateful for that last lecture, and we may be grateful too.
To end this preface I would like to put on record a description of Robert Oppenheimer written by Lansing {ix} Hammond in a letter to me in 1979. Hammond was in charge of programs and placements for the Commonwealth Fund Fellows, young Britons (of which I was one) who came to America to study at American universities with Fund support. I wrote back, “It is sad that in the official memorials to Robert there was never anything said or written that gave such a fine impression of Robert in action. I hope there may still be a chance sometime to make your story public.” Hammond died a few years later and this preface gives me the chance that he missed.
“I'd just received copies of the application papers—60 of them—for the 1949 awards. Among them were four or five in that, to me, shadowy borderline realm between theoretical physics and mathematics. I was in Princeton for a couple of days, asking for help on all sides. Summoning all the courage I could muster, I made an appointment to see Robert Oppenheimer the next morning, leaving the relevant papers with his secretary. I was greeted graciously, asked just enough questions about my academic background to put me at ease. One early comment amazed me: ‘You got your doctorate at Yale in eighteenth-century English literature—Age of Johnson. Was Tinker or Pottle your supervisor?’ How did he know that?
“Then we got down to business. In less than ten minutes I had enough facts to support trying to persuade candidate Z that Berkeley was more likely to satisfy his particular interests than Harvard; he would fare well at the Institute; would be welcome; but Berkeley was really the best choice. I was scribbling notes as fast as I could; occasionally a proper name produced wrinkles on my forehead. Oppenheimer would flash me an understanding grin and spell out the name for me: ‘That may save you some time and trouble.’
“As I was gathering up my papers, feeling I'd already taken up too much of the great man's time, he asked gently: ‘If you have a few minutes you can spare, I'd be interested in looking at some of your applications in other fields, to see what this year's group of young Britons are {x} interested in pursuing over here? I took him at his word, and was completely overwhelmed by what ensued: ‘Umm—indigenous American music—Roy Harris is just the person for him, he'll take an interest in his program. Roy was at Stanford last year but he's just moved to Pea-body Teachers College in Nashville. Social psychology, he gives Michigan as first choice—umm—he wants a general, overall experience. At Michigan he's likely to be put on a team and would learn a lot about one aspect. I'd suggest looking into Vanderbilt; smaller numbers; he'd have a better opportunity of getting what he wants.’ (The candidate was persuaded to try Vanderbilt for one term, with the option of transferring to Michigan if he wasn't satisfied. He spent two years at Vanderbilt, with profit and enthusiasm.) ‘Symbolic logic, that's Harvard, Princeton, Chicago or Berkeley; Let's see where he wants to put the emphasis. Ha! Your field, Eighteenth-century English Lit. Yale is an obvious choice, but don't rule out Bate at Harvard, he's a youngster but a person to be reckoned with.’ (My field, and I'd not yet even heard of Bate, but I took pains, the next time I was in Cambridge, to meet and talk with him.) We spent at least an hour, thumbing through all of the 60 applications. Robert Oppenheimer knew what he was talking about. He pleaded ignorance of about two or three esoteric programs. Every positive comment or recommendation was right on target. And so, when it finally came time to leave, I couldn't resist saying that if I could only bribe him, once a year, to repeat what he'd just done, it would save me months of sweating. He really grinned at that. ‘That wouldn't be fair to you, Dr. Hammond. It would take away the satisfaction and excitement of talking with lots of other people and finding out for yourself.’ I left, walking on air, head abuzz, most of my problems solved. Never before, never since have I talked with such a man. No suggestion of trying to impress. No need to. Robert Oppenheimer's was just genuine interest in all fields of the intellect; a fantastically up-to-date knowledge of what was going on in U.S. graduate schools and research {xi} centers; an intuitive understanding of where a given person with definite interests would best fit in; and taking pleasure in being of help to someone who badly needed it.” The Robert Oppenheimer that Hammond saw that morning in 1949 was the same Robert Oppenheimer who had mastered every detail of the bomb project at Los Alamos five years earlier, and had fitted the most appropriate task to each scientist and engineer in his army of subordinates. He was equally at home in the world of literature and the world of science, in the eighteenth century and the twentieth. His listeners in 1953 were surprised to hear a voice from the eighteenth century discussing the discoveries of the twentieth. Readers of this book need not be surprised to find that the continuity of human experience over the centuries is its central theme, defining both the style and the substance of Oppenheimer's discourse.
The Institute for Advanced Study
Princeton, New Jersey
April 1989
| {2} |
Atom and Void
| {3} |
Science has changed the conditions of man's life. It has changed its material conditions; by changing them it has altered our labor and our rest, our power, and the limits of that power, as men and as communities of men, the means and instruments as well as the substance of our learning, the terms and the form in which decisions of right and wrong come before us. It has altered the communities in which we live and cherish, learn and act. It has brought an acute and pervasive sense of change itself into our own life's span. The ideas of science have changed the way men think of themselves and of the world.
The description of these changes is not simple; it is rich in opportunity for error. As for the great material changes which science and practical art have made possible—machines, for instance, or power, the preservation of life, the urbanization of populations, new instruments of war, new means of communication and information—these are but part of the materials for the analysis of political economy and the wisdom and the insight of history. These are strands in the tangled affairs of men, and their evaluation is no more likely to be final and exhaustive than in any other part of history.
As for the more direct effects of discovery in science on the way men think about things which are not themselves part of science, the historian of ideas has a similar problem. Noting what in actual fact men have said about what they thought, who it was that thought it, and why he thought it, one finds, as in all history, that the contingent and the {4} unpredictable, the peculiar greatnesses and blindnesses of individual men play a determining part. One even finds the science of great scientists taken in the name of those scientists for views and attitudes wholly foreign and sometimes wholly repugnant to them. Both Einstein and Newton created syntheses and insight so compelling and so grand that they induced in professional philosophers a great stir of not always convenient readjustment. Yet the belief in physical progress, the bright gaiety, and the relative indifference to religion characteristic of the enlightenment, were as foreign to Newton's character and preoccupation as could be; this did not keep the men of the enlightenment from regarding Newton as their patron and prophet. The philosophers and popularizers who have mistaken relativity for the doctrine of relativism have construed Einstein's great works as reducing the objectivity, firmness, and consonance to law of the physical world, whereas it is clear that Einstein has seen in his theories of relativity only a further confirmation of Spinoza's view that it is man's highest function to know and to understand the objective world and its laws.
Often the very fact that the words of science are the same as those of our common life and tongue can be more misleading than enlightening, more frustrating to understanding than recognizably technical jargon. For the words of science—relativity, if you will, or atom, or mutation, or action—have been given a refinement, a precision, and in the end a wholly altered meaning.
Thus we may well be cautious if we inquire as to whether there are direct connections, and if so of what sort, between the truths that science uncovers and the way men think about things in general—their metaphysics—their ideas about what is real and what is primary; their episte-mology—their understanding of what makes human knowledge; their ethics—their ways of thinking, talking, judging, and acting in human problems of right and wrong, of good and evil. {5}
These relations, the relations between scientific findings and man's general views, are indeed deep, intimate, and subtle. If I did not believe that, I should hardly be addressing these lectures to an attempt to elucidate what there is new in atomic physics that is relevant, helpful, and inspiring for men to know; but the relations are not, I think, relations of logical necessity. This is because science itself is, if not an unmetaphysical, at least a non-metaphysical activity. It takes common sense for granted as well as most of what has gone before in the specialized sciences. And where it adds, alters, or upsets, it does so on the basis of an uncritical acceptance of a great deal else. Thus, to the irritation of many, the assertions of science tend to keep away from the use of words like “real” and “ultimate.” The special circumstances of the discovery of scientific truth are never very far from our minds when we expound it, and they act as a protecting sheath against their unlimited and universal acceptance. A few illustrations may make this clearer.
We have discovered atoms. In many ways they act like the atoms of the atomists. They are the stuff of which matter is made; their constellation and motion account for much—in fact, for most of the ordinarily observable properties of matter. But neither they nor the smaller, less composite particles of which they are made are either permanent, unchanging, or unchangeable. They do not act like objects of fixed form and infinite hardness. Such findings may be persuasive in discouraging the view that the world is made of fixed, immutable, infinitely hard little spheres and other shapes; but such findings are not in the nature of things conclusive, for one may always hold that the true atoms, the immutable, hard atoms, have so far eluded physical discovery, but that they are nevertheless there, and only when they are found will physics be dealing with the ultimate reality. Beyond that, one can hold that, although they may never be found by physical experiment, {6} they are the underlying reality in terms of which all else, including the world of physics, is to be understood.
Or, again, we may have discovered that as the nervous impulses pass from the retina of the eye toward the brain itself their geometric disposition resembles less and less that of the object seen. This may complicate or qualify the view that the idea is a geometric replica of the object of vision. It cannot and need not wholly exorcise it.
The scientist may be aware that, whatever his findings, and indeed whatever his field of study, his search for truth is based on communication with other people, on agreement as to results of observation and experiment, and on talking in a common tongue about the instruments and apparatus and objects and procedures which he and others use. He may be aware of the fact that he has learned almost everything he knows from the books and the deeds and talk of other people; and, in so far as these experiences are vivid to him and he is a thoughtful man, he may be hesitant to think that only his own consciousness is real and all else illusion. But that view, too, is not by logic exorcised; from time to time it may rule his spirit.
Although any science gives countless examples of the interrelation of general law and changing phenomena, and although the progress of science has much to do with the enrichment of these relations, knowledge of science and practice of it and interest in it neither compel nor deny the belief that the changing phenomena of the actual world are illusion, that only the unchanging and permanent ideas are real.
If, in the atomic world, we have learned—-as we have learned—that events are not causally determined by a strict, efficient, or formal cause; if we have learned to live with this and yet to recognize that for all of the common experience with ordinary bodies and ordinary happenings this atomic lack of causality is of no consequence and no moment, neither the one finding nor the other ensures that men when they think of the world at large are bound to a causal or a non-causal way of thinking. {7}
These many examples show that there can indeed be conflict between the findings of science and what a philosopher or a school of philosophy has said in great particular about some part of experience now accessible to science. But they also show that, if there are relationships between what the sciences reveal about the world and how men think about those parts of it either not yet or never to be explored by science, these are not relationships of logical necessity; they are not relationships which are absolute and compelling, and they are not of such a character that the unity and coherence of an intellectual community can be based wholly upon it.
But if these examples indicate, as we should indeed expect from the nature and conditions of scientific inquiry, that what science finds does not and cannot uniquely determine what men think of as real and as important, they must show as well that there is a kind of relevance—a relevance which will appear different to different men and which will be responsive to many influences outside the work of science. This relevance is a kind of analogy, often of great depth and scope, in which views which have been created or substantiated in some scientific enterprise are similar to those which might be held with regard to metaphysical, epistemological, political, or ethical problems. The success of a critical and sceptical approach in science may encourage a sceptical approach in politics or in ethics; the discovery of an immensely successful theory of great scope may encourage the quest for a simplified view of human institutions. The example of rapid progress in understanding may lead men to conclude that the root of evil is ignorance and that ignorance can be ended.
All these things have happened and all surely will happen again. This means that, if we are to take heart from any beneficent influence that science may have for the common understanding, we need to do so both with modesty and with a full awareness that these relationships are not inevitably and inexorably for man's good.
It is my thesis that generally the new things we have {8} learned in science, and specifically what we have learned in atomic physics, do provide us with valid and relevant and greatly needed analogies to human problems lying outside the present domain of science or its present borderlands. Before I talk of what is new I shall need to sketch, with perhaps an exaggerated simplicity and contrast, the state of knowledge and belief to which these correctives may apply. In doing this, we may have in mind that the general notions about human understanding and community which are illustrated by discoveries in atomic physics are not in the nature of things wholly unfamiliar, wholly unheard of, or new. Even in our own culture they have a history, and in Buddhist and Hindu thought a more considerable and central place. What we shall find is an exemplification, an encouragement, and a refinement of old wisdom. We shall not need to debate whether, so altered, it is old or new.
There are, then, two sketches that I would like to draw of the background for the altered experience of this century. One is the picture of the physical world that began to take shape in the years between Descartes’ birth and Newton's death, that persisted through the eighteenth century, and with immense enrichments and extensions still was the basic picture at the beginning of our own.
The second sketch has to do with the methods, the hopes, the program, and the style which seventeenth- and eighteenth-century science induced in men of learning and in men of affairs, with some of the special traits of that period of enlightenment which we recognize today as so deep in our tradition, as both so necessary to us and so inadequate.
More than one great revolution had ended and had been almost forgotten as the seventeenth century drew its picture of the physical world. A centuries-long struggle to decide whether it were rest or uniform motion that was the normal state of an undisturbed body no longer troubled men's minds: the great clarity, so foreign to everyday experience, that motion, as long as it was uniform, needed no {9} ause and no explaining was Newton's first law. The less deep but far more turbulent Copernican revolution was history: the earth revolved about the sun. The physical world was matter in motion: the motion was to be understood in terms of the impetus or momentum of the bodies which would change only for cause, and of the force that was acting upon it to cause that change. This force was immediate and proximate. It produced a tendency for the impetus to change, and every course could be analyzed in terms of the forces deviating bodies from their uniform motions. The physical world was a world of differential law, a world connecting forces and motions at one point and at one instant with those at an infinitely near point in space and point of time; so that the whole course of the physical world could be broken down into finer and finer instants, and in each the cause of change assigned by a knowledge of forces.
Of these forces themselves the greatest in cosmic affairs—that which governed the planets in the heavens and the fall of projectiles on earth—had been found by Newton in the general law of gravity. Was this, too, something that spread from place to place, that was affected only instant by instant, point by point; or was it a property given as a whole, an interaction somehow ordained to exist between bodies remote from one another? Newton was never to answer this question; but he, and even more than he, Huygens, studying the propagation of light, were laying the foundations for a definite view—a view in which the void of the atomists would lose much of its emptiness and take on properties from the bodies which inhabited it, which in turn would affect bodies far away.
It was not until the nineteenth century and Faraday that the full richness of space began to be understood: how it could be the seat not only of gravitational forces produced by the mass of material particles but of electric and magnetic forces produced by their charges. Even in Newton's day it was clear that there were very strong forces at work in lending to material objects their solidity. Newton wrote: {10}
It seems probable to me, that God in the Beginning form'd Matter in solid, massy, hard, impenetrable, moveable Particles, of such Sizes and Figures, and with such other Properties and in such Proportion to Space, as most conduced to the End for which he formed them; and that these primitive Particles being Solids, are incomparably harder than any porous Bodies compounded of them; even so very hard, as never to wear or break in pieces; no ordinary Power being able to divide what God himself made one in the first Creation.
Newton saw that what held atoms together and made matter must be forces of inordinate strength, and he never considered their existence without a sense of mystery and awe. He did not know, nor do we today know, in what subtle way these forces might or might not be related to the forces of gravity.
But for many of his contemporaries and successors these questions appeared less pressing than the confidence that, once given the forces, the course of nature could be foretold and that, where the laws of gravity could be found, other forces would yield to observation and analysis. It is only in this century that we have begun to come to grips with other instances of antinomy, the apparent irreconcilability between the differential description of nature, point by point, instant to instant, and the total unique law and event. It is only in this century that we have had to recognize how unexpected and unfamiliar that relation between bodies and the atoms on the one hand, and that space full of light and electricity and gravitational forces on the other, could prove to be.
For the eighteenth century the world was a giant mechanism. It was a causal world, whether or not gravity and the other forces acting on bodies inhered in them by their nature or by God's will or that they, too, grew, through laws as rigorous as the laws of motion, from the properties induced in space by the bodies in it. All that happened had its full, complete, immediate, efficient cause. The great machine had a determinate course. A knowledge of its present and therefore its future for all time was, in principle, {11} man's to obtain, and perhaps in practice as well. These objects with which the world was filled—the heavenly bodies, the impenetrable atoms and all things composed of them—were found by observation and by experiment; but it would have occurred to no one that their existence and their properties could be qualified or affected by the observations that told of them. The giant machine was not only causal and determinate; it was objective in the sense that no human act or intervention qualified its behavior.
A physical world so pictured could not but sharpen the great gulf between the object and the idea. It would do much to bring about that long, critical, and, in its later phase, irrational and mystical, view of the relations between the knower and the known that started with Locke and is perhaps even today not fully or happily ended.
It is, of course, clear that many developments in science that were to flower in the eighteenth and nineteenth centuries would soon moderate and complicate the harsh basic picture of the giant machine and of the vast gulf between it and the knowing human mind that thought about it and analyzed its properties. This is true of the great development of statistics, which in the end made room for human ignorance as an explicit factor in estimating the behavior of physical forces. It is true of chemistry, whose phenomena, whatever their ultimate description, looked so very little like the result of matter in motion. It is even more true of the biological sciences, where matter in motion, ever evident and inevitable, appears both at first sight and upon deeper analysis only marginally relevant to what makes biological forms interesting.
But with all of this, and with varying degrees of agreement and reservation, there was the belief that in the end all nature would be reduced to physics, to the giant machine. Despite all the richness of what men have learned about the world of nature, of matter and of space, of change and of life, we carry with us today an image of the giant machine as a sign of what the objective world is really like. {12}
This view of the Newtonian world is oversimplified; perhaps any view of what men made of their new sciences, their new powers, and their new hopes will be simplified to the point of distortion. Science for the eighteenth century was not a finished undertaking; and, if men were overwhelmed with what they had learned, they were easily reminded of how much was still missing. A rational understanding of the world was not an understanding for one generation or one man, as it is alleged that it at one time appeared to be to Descartes. The immense discoveries of the recent past made it impossible to hold the view that all that was really worth knowing had long been known—a view that is a sort of parody, in any case, of the Renaissance.
This was a long journey on which men were embarked, the journey of discovery; they would need their wits and their resources and their forbearance if they were to get on with it. But it was a job in which progress was inevitable, and in which the style and success of physical science would tend to set the style for all undertakings of man's reason. What there is of direct borrowing from Newtonian physics for chemistry, psychology, or politics is mostly crude and sterile. What there is in eighteenth-century political and economic theory that derives from Newtonian methodology is hard for even an earnest reader to find. The absence of experiment and the inapplicability of Newtonian methods of mathematical analysis make that inevitable. These were not what physical science meant to the enlightenment.
It meant a style of thought, a habit of success, and an understanding of community quite typical for the age. These are to be found best in the learned communities that grew up in Europe and later in America—in the Royal Society and in the far more ambitious, far more revolutionary, far more programmatic French Academy. These communities were infused by a confidence in the power of reason and by a sense of improvement constant and almost inevitable in the condition of man's knowledge, and therefore {13} of his actions and his life. They rest on a consensus of men, often seeing with their own eyes the crucial experiment that was to test or to confirm a theory; on the common experience of criticism and analysis; on the widespread use of mathematical methods with all the assurance of objectivity and precision that they give us. These were communities banded together for the promotion of knowledge—critical, rapacious to correct error, yet tolerant from knowing that error is an inevitable step in acquiring new knowledge. These were communities proud of their broad, non-sectarian, international membership, proud of their style and their wit, and with a wonderful sense of new freedom. One may recapture some sense of these communities from the writings of the time. The first history of the Royal Society is not truly a history but an apology, written when the society was only a few years old, explaining it, defending it against its critics. Bishop Sprat has this to say:
Their Purpose is, in short, to make faithful Records of all the Works of Nature, or Art, which can come within their Reach; that so the present Age, and Posterity, may be able to put a Mark on the Errors, which have been strengthened by long Prescription; to restore the Truths, that have lain neglected; to push on those, which are already known, to more various Uses; and to make the way more passable, to what remains unreveal'd. This is the Compass of their Design . . .
They have tried to put it into a Condition of perpetual Increasing, by settling an inviolable Correspondence between the Hand and the Brain. They have studied, to make it not only an Enterprise of one Season, or of some lucky Opportunity; but a Business of Time; a steady, a lasting, a popular, an uninterrupted Work . . .
It is to be noted, that they have freely admitted Men of different Religions, Countries, and Professions of Life. This they were oblig'd to do, or else they would come far short of the Largeness of their own Declarations. For they openly profess, not to lay the Foundation of an English, Scotch, Irish, Popish, or Protestant Philosophy; but a Philosophy of Mankind. {14}
Reading this today, we can hardly escape a haunting sense of its timeliness and a certain nostalgia at how little the texture of our life conforms to these agreeable and noble ideals. We cannot perhaps wholly forget how much these communities owed to the long centuries of Christian life and Christian tradition; how much that they then took for granted in their inquiries and thoughts, in their whole style, derived from a way of life and a history which they were about to change beyond all recognition; and how deeply this, their program, could alter the very men and the very minds to whom their program would in time become entrusted.
These, however, were not reflections to darken much the eighteenth century or to cast real shadows on that great path of light, that renewed hope of men for a growing and growingly rational comprehension of their world and of themselves. At the very end of the century in another land largely nourished and fathered by the enlightenment, a gentleman and patriot wrote a letter. He wrote in answer to a young friend inquiring about his present course of study. He wrote in the last days of the Directorate, when the course of history was diverging in alarming and immense ways from that charted by the men of the French Academy. He wrote it about two years before he was to assume the Presidency of the United States, there for over a century to raise more firmly than ever before the standard of man's freedom, his progress, and his rational nature.
I am among those who think well of the human character generally. I consider man as formed for society, and endowed by nature with those dispositions which fit him for society. I believe also, with Condorcet, as mentioned in your letter, that his mind is perfectible to a degree of which we cannot as yet form any conception . . . science can never be retrograde; what is once acquired of real knowledge can never be lost. To preserve the freedom of the human mind then and freedom of the press, every spirit should be ready to devote himself to martyrdom; {15} for as long as we may think, as we will, and speak as we think, the condition of man will proceed in improvement. The generation which is going off the stage has deserved well of mankind for the struggles it has made, and for having arrested that course of despotism which had overwhelmed the world for thousands and thousands of years. If there seems to be danger that the ground they have gained will be lost again, that danger comes from the generation your contemporary. But that the enthusiasm which characterises youth should lift its parracide hands against freedom and science would be such a monstrous phaenomenon as I cannot place among possible things in this age and country.
The writer of the letter was Thomas Jefferson.
| {16} |
It is inherent in the very notion of culture and of tradition that there is a cumulative aspect to human life. The past underlies the present, qualifies and moderates it, in some ways limits it and in some ways enriches it. We understand Shakespeare better for having read Chaucer, and Milton for having read Shakespeare. We appreciate Trevelyan more for knowing Thucydides. We see Cezanne with better eyes for having looked also at Vermeer, and understand much more in Locke for knowing Aristotle, St. Matthew for knowing Job. But in actual fact we rather seldom bring a knowledge of the earlier to our first acquaintance with the later; and if it is true that Job throws light on Matthew, it is also true that Matthew throws light on Job. We can understand a great deal of what is written today, knowing little explicitly of what has been written in the past. We can and do know a great deal of what Shakespeare means and intends without any knowledge of those earlier men who altered and educated his sensibility.
The cumulative character of science is very different and very much more essential. It is one of the reasons for the great difficulty of understanding any science in which one has not largely become an expert—the science of which Hobbes wrote: “Of that nature, as none can understand it to be, but such as in good measure have attayned it.”
There are at least two reasons for this: one has to do with the relation of later discoveries in science to earlier, and the other with the use that is made of earlier work in science as an instrument of progress. When we find out {17} something new about the natural world this does not supersede what we knew before; it transcends it, and the transcendence takes place because we are in a new domain of experience, often made accessible only by the full use of prior knowledge. The work of Huygens and Fresnel on the wave properties of light is as necessary today as it ever was, although we know that there are properties of light which are left out in their account and their experience, properties which, in the context of atomic happenings, are decisive. Newton's law of gravitation and his equations of motion apply to and underlie immense realms of physical experience and are not made wrong by the fact that in other and still vaster spheres they must be replaced by the broader laws of Einstein. The chemical theory of valency has been explained, elucidated, and, to some small degree, extended by an understanding, in terms of the behavior of electrons and nuclei, of what goes on in chemical bonding; but the chemical theory of valency is not superseded and will presumably be used as long as man's interest in chemistry continues. The foundations of solid fact and the laws which describe it persevere through the whole course of science, to be refined and adapted to new contexts but never to be ignored or cast out.
But this is only a part of the story. It is a recurring experience of scientific progress that what was yesterday an object of study, of interest in its own right, becomes today something to be taken for granted, something understood and reliable, something known and familiar—a tool for further research and discovery. Sometimes the new instrument which is used to extend experience is a natural phenomenon, only barely qualified or controlled by the experimenter. We are familiar with the use of calcite crystals to produce two separate beams of polarized light. We know that the cosmic rays are both an object of investigation in themselves and a tool of hitherto unparalleled power for probing the properties and transmutations of primordial matter here on earth and in the laboratory. Sometimes past knowledge is embodied not in a natural {18} phenomenon but in an invention, or in elaborate pyramids of invention, a new technology.
There are many well known and major examples of technological development during the last war which have added to the instruments of the investigator of the physical and biological world. We may recall two. Microwave radar—the generation, control, and detection of electromagnetic waves of relatively very short length—played a heroic part in the Battle of Britain. In the years since, it has provided powerful new means of investigating atomic, molecular, and even nuclear problems from which in actual fact subtle discoveries have been made about the laws of interaction of electrons and protons and neutrons.
The nuclear reactor embodies in its technology very recently acquired understanding of the fission processes in uranium and of the behavior of neutrons in their collisions with atomic nuclei; it is now an important tool whose controlled and well-understood radiations are telling us about properties of matter hitherto barely accessible. Artificially radioactive substances made in great profusion by atomic reactors enable us to follow the course of individual atoms in chemical and biological changes. In biology especially they may be an addition to our instrumental facilities and techniques comparable in importance with the microscope itself.
It is an oversimplification to say that technologies based upon recently discovered natural phenomena are taken as wholly for granted and as wholly known, but this is essentially the truth. They are added to the experimenter as a good tool is added to the artisan; as the pencil in the writer's hand ceases to be an object in itself and becomes almost a part of the writer; or as a horse under a good horseman becomes for the time being not an animal to be cared for and thought about but a part of the entity “horseman.” Thus what has been learned and invented in science becomes an addition to the scientist, a new mode of perception, a new mode of his action. {19}
There are some cautions to be added to this. No experimenter takes his equipment quite so much for granted that he fails to check whether in fact it is performing as it is supposed to perform; but the notion of how it is supposed to perform is for him in general a fixed thing not calling for further inquiry. This may be true even when the invention is a sample of practical art rather than a sample of true understanding. The photographic plate has served as an instrument of science for decades, during which its behavior was only very incompletely understood. Any machine can get out of order, and in a laboratory most machines do. The horse is shod and bridled and fed before he can become part of the horseman. Nevertheless we use what we have learned to go further. A perpetual doubting and a perpetual questioning of the truth of what we have learned is not the temper of science. If Einstein was led to ask not “What is a clock?” but “How, over great distances and with great precision, do we synchronize clocks?” that is not an illustration of the scepticism of science; it exemplifies rather the critical reason creating a new synthesis from paradoxes, anomalies, and bewilderments, which experiments carried on with new precision and in a new context brought into being.
All this means that science is cumulative in a quite special sense. We cannot really know what a contemporary experiment means unless we understand what the instruments and the knowledge are that are involved in its design. This is one reason why the growing edge of science seems so inaccessible to common experience. Its findings are defined in terms of objects and laws and ideas which were the science of its predecessors. This is why the student spends many long years learning the facts and arts which, in the acts of science, he will use and take for granted—why this long tunnel, at the end of which is the light of discovery, is so discouraging for the layman to enter, be he an artist, scholar, or man of affairs.
This conversion of an object of study into an instrument has its classic exemplification in Rutherford and the {20} α-particle. This is a trail we will follow for some time. It will lead us to the heart of atomic physics. The α-particle, emitted by many naturally radioactive substances, identical with the nucleus of helium, was indeed a strong right arm for Rutherford and all his school in probing the atomic world. Rutherford's early works had been largely devoted to writing the wonderful natural history of the radioactive families—those which start with spontaneous changes in the heavy elements uranium and thorium. Part of the natural history was to discover the genetic relations between the various radioactive substances, some of them growing as a result of the decay of others and in turn giving rise to daughter products by further transmutation.
The natural history involves a chemical identification of the radioactive substances, the determination of the rapidity of their decay and of the alternative modes of decay, which some of them exhibit. It involves the recognition of three fundamentally different kinds of radiation, all of which appear at one stage or another in these family histories. This identification, which we shall meet again in later contexts, means learning some of the basic properties of the particles emitted. This identification, as we shall shortly see, is made possible by the fact that even a single such particle has readily detectable effects.
These properties include the mass of the particle and its electric charge. These have usually been found in the first instance by studying their behavior in large-scale electric and magnetic fields and applying Newton's laws to analyze their motion. These same methods give one a measure of the velocity or energy with which the particles are emitted, and of the loss of this energy as the particles pass through matter. Sometimes, at a later stage, the products of an atomic or nuclear disintegration can be more thoroughly studied. They may have more subtle electromagnetic properties than charge, such as a small magnetic moment. They may have structure or size. But the basic identifications can all be made in terms of the response of the radiations to familiar, large-scale, experimentally controllable situations {21} like the classical electric and magnetic fields of our laboratory courses.
The α-particle of the naturally radioactive substances became for the middle years of Rutherford's life the sharpest experimental tool; it was to be supplemented and to some extent superseded only when artificially accelerated nuclei became available during the nine teen-thirties. The essential features of the experiments that have told us most about atoms and nuclei and the ingredients of matter are two: one has to do with structure, and the other with scale.
The structure of the experiment involves three parts: a probe, which is an object meant to explore or disturb matter in its natural state, typically with some degree of violence. This was the role of the α-particle. The second element is the target, which is some form of matter, whether pure or of controllable and manageable complications; and the third is the detector, which identifies and describes the objects emerging from the disturbance, whether they be the altered or the unaltered probe, or something knocked out of the target, or created in the collision, or something appearing long after the collision as evidence of a rearrangement of the collision products consequent upon the disturbance. This is not a universal pattern—this probe-target-detector assembly. The collision is not the only way of learning about atomic systems; but almost all of what we have learned has derived at least in part from such experiments and can be elucidated in terms of them.
As to scale, it is the scale that determines the possibility of detection. The events that are so studied—the collisions, transmutations—can typically be studied event by event, atom by atom. The reason for this lies in two circumstances: one is that in nuclear transformations, and even more so in transformations induced by cosmic rays and superaccelerators, the energy characteristic of a single atomic process is enormous compared to the chemical energies, and is sufficient to produce recognizable physical and chemical changes in hundreds of thousands or even millions of atoms. {22}
The second circumstance lies in the art that has been devoted toward exploiting these energies in systems of detection. The detectors for Rutherford's experiments are by now familiar. One is the scintillation screen, where an α-particle creates a flash of light easily visible through a microscope at the point where it hits the screen. Another is the beautiful cloud chamber of C.T.R. Wilson, which is, according to legend, an outcome of the inventor's interest in the mist and clouds and rain of his native Scotland. In this cloud chamber the track of a charged particle is marked by the occurrence of innumerable small yet readily visible droplets of water or other liquid close to where the particles passed. A third is the counter, in which the electrical disturbance produced in a gas by the passage of a charged particle gives rise to a substantial electrical discharge, which can be amplified and analyzed by electronic circuitry.
These detectors have been supplemented by many, many others; and the precision and power of electronic amplification and analysis have been developed into a great art. The detector of atomic physics still characteristically is designed to take advantage of the very great energy involved in the changes of a single atom, and of the power to amplify this energy almost at will to make it accessible. The clicking counters and flashing lights and occasionally even the ringing bells of a modern nuclear laboratory make the doings of individual atoms very vivid and immediate, and make the subtle atoms of Epicurus or of Newton seem very private and remote.
Rutherford and his probing α-particles and detectors are old history, dating back roughly some forty years. They are basic alike to atomic and nuclear physics, basic as a foundation for the great revolution in science which it is my principal purpose to describe, and for the further developments at the very forefront of contemporary discovery that have us today perplexed and bemused. With his α-particles, obtained from natural radioactivity, Rutherford {23} discovered the atomic nucleus and the nuclear model of the atom; with some help from other evidence he discovered the mass and the charge of the various atomic nuclei and thus rationalized Mendelyeev's table of the elements. With the α-particles, he was able to touch nuclear matter itself and measure its dimensions. He showed that it could be transmuted; he identified at least some of its ingredients.
For the most part, α-particles when they pass through a bit of matter are not very much deflected or changed in direction; they are gradually slowed down; but occasionally a particle will change its direction of motion very greatly. It will be scattered through a large angle; it will act as though some great force had disturbed it, as though it had hit something quite small and quite hard. The law describing these deflections is Rutherford's law; and to it he gave a simple meaning: there are forces acting on the α-particles; they are not unfamiliar to physics. They are the electric repulsion between the charge of the atomic nucleus and the charge of the α-particle—the same force which manifests itself when two positively charged pith balls push each other apart in an elementary demonstration. The balls repel each other because the two charges are similar; and the repulsion is described by Coulomb's law—very much the same law as Newton's law of gravitation. The repulsion is inversely proportional to the square of the separation of the charges. The charge of the atomic nucleus is a multiple of that of the proton—the nucleus of hydrogen. The multiple is the atomic number, which determines the number of electrons in the atom, and almost all the chemical properties of the element, and the position in the periodic table of that element. The mass of the nucleus is almost the whole mass of the atom as expressed by its atomic weight. This charge and mass is concentrated in a small volume. Everywhere outside it, the α-particle feels only the electric field.
By using α-particles fast enough to overcome the electric repulsion, and using light elements for which the charge and therefore the repulsion are not too great, Rutherford {24} found that occasionally α-particles penetrated to a different domain entirely, where very strong forces, not electric forces, deflected them. In this way he found the dimensions of the nucleus itself: roughly one part in 10,000 of the dimensions of the atom as a whole. This characterized the nucleus as a region of incredibly high density, of many millions of tons per cubic inch. Rutherford discovered even more: he was able to show that when fast α-particles penetrated nuclear matter things other than α-particles emerged from the melee. In experiments undertaken during the First World War, and justified by Rutherford as of greater importance than any contribution he could then make to the prosecution of that war, Rutherford for the first time induced by human action the transmutation of an atomic nucleus, knocking out of the nucleus of nitrogen a nucleus of hydrogen, or proton, and starting a chain of events which led, among many things, to man's release of atomic energy, to what may some day be judged the most compelling argument of all for putting an end to war itself.
The story went on from there. Before we revert to the nuclear model of the atom and how oddly different its properties are from any we can understand on the basis of Newtonian physics, we may follow sketchily and partially this course of discovery with probe, target, and detector that Rutherford initiated and that has continued until the present day. Twenty years ago, using the same α-particles as probes, Chadwick managed to identify another survivor of the disturbance, another ingredient of the nucleus, the neutron, which has roughly the proton's mass but no charge, and thus to lay the foundations for an elementary view of nuclear composition. The nucleus is made up of neutrons and protons—enough protons to account for its charge, the atomic number; enough neutrons to account for the excess of its atomic weight over its atomic number—held together in their tiny volume by strong forces wholly dissimilar from those of electricity and magnetism, {25} whose description even today is a far from completely solved problem.
Chadwick's neutrons, in their turn, became probes, inducing nuclear transmutations very copiously, because they were not kept away from nuclei by the positive nuclear charge. Their use led, in the years just before the war, to Hahn's discovery that, when uranium was transmuted by being hit by neutrons, among the products was barium, a large half of the original nucleus, but only about half— and thus to nuclear fission.
Even this was only the beginning. In the very energetic particles of cosmic radiation, in the nuclei accelerated by giant modern accelerators to energies a hundredfold those of Rutherford's α-particles, we have found new probes to elicit new phenomena; the story of sub-nuclear matter began to unfold and ramify. A whole new family of hitherto unknown, and, for the most part, unrecognized and unexpected objects began to emerge from the nuclear encounters. The first of these were the various mesons, some charged and some uncharged, about ten times lighter than the proton and some hundreds of times heavier than the electron. In the last years there have appeared in increasing variety objects heavier than the mesons, other objects heavier even than protons, whose names are still being changed, from month to month, by solemn conferences. Physicists call them vaguely, and rather helplessly, “the new particles.” They are without exception unstable, as in the neutron. They disintegrate after a time which varies from one millionth to less than a billionth of a second into other lighter components. Some of these components are in turn unfamiliar to physics and are themselves in turn unstable. We do not know how to give a clear meaning to this question. We do not know why they have the mass and charge that they do; why they and just they exist; why they disintegrate as they do; why in most cases they last as long as they do, or anything much about them. They are the greatest puzzle in today's physics. {26}
But all this is now; and these were not the puzzles of Rutherford's day. To these we shall turn in the next lectures. They become manifest when we try to deduce and describe the properties of Rutherford's atom in terms of Newtonian mechanics. This attempted description failed. The atoms of nature are radically, dramatically, unlike atoms, composed as Rutherford found of electrons and small nuclei, subject to the forces Rutherford discovered and described, and moving according to Newton's laws. The failure of this classical description turned out to be a major clue, one of the few major clues, in the atomic story. We learned, before the story was finished, that more than Newtonian mechanics would have to be modified if we were to understand and describe our experience with atomic systems. We would have to alter our ideas on very fundamental points, on causality, for instance, and even on the nature of the objectivity of parts of the physical world. We were to be reminded, in a quite unexpected way, of the nature and limitations, as well as the power, of human knowledge itself. It is largely for this reason that the story of atomic discovery has appeared to me so full of instruction for us all, for layman as well as specialist. For it has recalled to us traits of old wisdom that we can well take to heart in human affairs.
Before these great changes could be completed, and the strange situation elucidated, many new ideas and methods of description were to be introduced. We learned words new for us, like “quantum,” and “state,” words like “correspondence” and “complementarity,” words with a new meaning for physics. Of these the word “correspondence” came to stand for the conservative and traditional traits of the new physics, that bound it to the physics of the past; whereas “complementarity” described, as we shall come to see, those new features, unknown to the physics of Newton, that have broadened and humanized our whole understanding of the natural world.
Time and experience have clarified, refined, and enriched our understanding of these notions. Physics has {27} changed since then. It will change even more. But what we have learned so far, we have learned well. If it is radical and unfamiliar and a lesson that we are not likely to forget, we think that the future will be only more radical and not less, only more strange and not more familiar, and that it will have its own new insights for the inquiring human spirit.
| {28} |
Our understanding of atomic physics, of what we call the quantum theory of atomic systems, had its origins at the turn of the century and its great synthesis and resolutions in the nineteen-twenties. It was a heroic time. It was not the doing of any one man; it involved the collaboration of scores of scientists from many different lands, though from first to last the deeply creative and subtle and critical spirit of Niels Bohr guided, restrained, deepened, and finally transmuted the enterprise. It was a period of patient work in the laboratory, of crucial experiments and daring action, of many false starts and many untenable conjectures. It was a time of earnest correspondence and hurried conferences, of debate, criticism, and brilliant mathematical improvisation.
For those who participated, it was a time of creation; there was terror as well as exaltation in their new insight. It will probably not be recorded very completely as history. As history, its recreation would call for an art as high as the story of Oedipus or the story of Cromwell, yet in a realm of action so remote from our common experience that it is unlikely to be known to any poet or any historian. In other ways, there will be such times again. Most of us are convinced that today, in our present probings in the subatomic and sub-nuclear world, we are laying the groundwork for another such time for us and for our sons. The great growth of physics, the vast and increasingly complicated laboratories of the mid-twentieth century, the increasing sophistication of mathematical analysis, have altered many of the conditions of this new period of crisis. We do not think that they will have altered its heroic and creative character. {29}
When quantum theory was first taught in the universities and institutes, it was taught by those who had participated, or had been engaged spectators, in its discovery. Some of the excitement and wonder of the discoverer was in their teaching; now, after two or three decades, it is taught not by the creators but by those who have learned from others who have learned from those creators. It is taught not as history, not as a great adventure in human understanding, but as a piece of knowledge, as a set of techniques, as a scientific discipline to be used by the student in understanding and exploring new phenomena in the vast work of the advance of science, or its application to invention and to practical ends. It has become not a subject of curiosity and an object of study but an instrument of the scientist to be taken for granted by him, to be used by him, to be taught to him as a mode of action, as we teach our children to spell and to add.
What we must attempt to do in these talks is wholly different. This is no school to learn the arts of atomic physics. Even those prior arts—the experimental tools, the mathematical powers, the theories, inventions, instruments, and techniques which defined the problems of atomic physics, which established the paradoxes, described the phenomena, and underlay the need for synthesis—are not known to us of our own experience. We must talk of our subject not as a community of specialized scientists but as men concerned with understanding, through analogy, description, and an act of confidence and trust, what other people have done and thought and found. So men listen to accounts of soldiers returning from a campaign of unparalleled hardship and heroism, or of explorers from the high Himalayas, or of tales of deep illness, or of a mystic's communion with his God. Such stories tell little of what the teller has to tell. They are the threads which bind us in community and make us more than separate men.
Here, then, we have our atoms. Their ingredients have been made manifest by Rutherford and his α-particles, as {30} have the forces that act between the ingredients, and by probing with electrons and with light as well as with α-particles. There is the nucleus, with almost the whole of the atom's mass and almost none of its size, and with a charge which is measured by the atomic number, equal to the number of electrons that surround the nucleus in the normal atom. We have the simple laws of attraction and repulsion, familiar from the large-scale, everyday experience with electricity. Unlike charges attract and like repel; and the forces, like Newton's, decrease inversely with the square of their separation.
In Rutherford's day it seemed reasonable, as it no longer entirely does today in facing our modern physics, to subdivide the problem of atomic structure into three questions: what are the ingredients of the atom; what are the forces, and the laws of force, acting between these ingredients; how in response to those forces do the ingredients move? We know that even in atomic problems this division is not completely rigorous; but the refinements are minor and have largely proved tractable. They consist of taking into account the effect of the motion of the particles themselves on the forces between them and, in some cases, the distortion of the properties of particles, very small itself in the atomic structures, by the presence of other particles and the forces that they exert. It is surely not wholly true of the nucleus that these distortions are small; and in the strange objects which emerge so readily when nuclei undergo violent collisions we have persuasive, if indirect, evidence for that.
The atom, then, has a massive charged nucleus; the atom as a whole is neutral and 10,000 to 100,000 times as far across as its tiny nuclear core. The rest of the atom is composed of electrons and electric fields—electrons that are the universal ingredients of matter, the determinants of almost all its chemical properties and of most of its familiar physical properties as well. There will be as many electrons in the atom as the atomic number, the nuclear charge; this makes the atom as a whole neutral. There will {31} be one electron in hydrogen and thirteen in aluminum and ninety-two in uranium. These are the ingredients; and the laws of force, complex only in the last refinements, are basically simple. The electron feels an attractive Coulomb force exerted by the nucleus, attractive since the electron and nucleus are oppositely charged, and once again falling off with distance in the same way as gravitational forces according to Newton's law. For hydrogen, this means a simple situation: two bodies with a force between them identical in structure with that which the sun exerts on the planets; two bodies small enough compared to the atom's size so that they almost never touch, and the properties of their contact can have little influence. The law of forces has been verified not only by probing with particles, by which it was originally discovered, but by probing with electrons themselves, in the first instances by the beta rays of naturally radioactive substances. For other atoms there is in addition the electrical repulsion between the several electrons, balancing to some extent the nuclear attraction. And there is, further, the well-known mathematical complication of describing quantitatively the behavior of a system with many particles.
But with hydrogen this should not be so. Here we have essentially a single light body moving in a simple and well-known force. The description of this system should be a perfect example of Newtonian dynamics, and should, in its refinements, be intelligible in terms of all that the nineteenth century had discovered about the behavior of charged particles in motion and the electromagnetic radiation produced when they are accelerated.
But it did not turn out that way. To what appeared to be the simplest questions, we will tend to give either no answer or an answer which will at first sight be reminiscent more of a strange catechism than of the straightforward affirmatives of physical science. If we ask, for instance, whether the position of the electron remains the same, we must say “no”; if we ask whether the electron's position {32} changes with time, we must say “no”; if we ask whether the electron is at rest, we must say “no”; if we ask whether it is in motion, we must say “no.” The Buddha has given such answers when interrogated as to the conditions of a man's self after his death; but they are not familiar answers for the tradition of seventeenth- and eighteenth-century science.
Let us review, then, what a hydrogen atom should be like if we could apply Newton's laws and the whole classical picture of matter in motion to the simple model. The electron is held to its nucleus as the earth is to the sun, or as is Venus. It should revolve in an ellipse, as Kepler found and Newton explained. The size of the ellipse could be varied from atom to atom as the orbits of the planets are different, depending on how it was formed and what its history, and so should the shape of the orbits, whether they are narrow or round. There should be no fixed size for a hydrogen atom and no fixed properties; and when we disturb one by one of our probings, or when it is disturbed in nature, we would not expect it to return to a size and shape at all similar to that from which it started. This is not all—there are more recondite points. When a charge moves in anything but a straight line, it should send out electromagnetic radiation. This is what we see in every radio antenna. As far as our model goes, this radiation should in time sap the energy of the electron to make up for the energy that has been sent out in the form of light waves; and the ellipses on which the electron moves should get smaller and smaller as it gets nearer to its attractive sun and loses its energy. For a system about the size of the hydrogen atom as we know it in nature, a few hundredths of a millionth of an inch across, this process should go very rapidly; and the atom should become far, far smaller than atomic dimensions in very much less than a millionth of a second. The color of the light that the electron radiates should be determined by the period of its revolution; it too should be random, differing from orbit to orbit, differing from time to time as the orbits shrink and alter. This is the picture {33} which classical physics—Newtonian physics—predicts for the hydrogen atom, if Rutherford's model is right.
It could hardly be further from the truth. By all we know, hydrogen atoms if undisturbed are all identical. They are the same size and each has the same properties as any other, whatever its history, provided only that it has had a chance to recover from any disturbance. They last indefinitely. We think of them, rightly, as completely stable and unchanging. When they are undisturbed, they do not radiate light or any other electromagnetic radiation, as indeed they could not if they are to remain unaltered. When they are disturbed, they sometimes do radiate, but the color of the light that they emit is not random and continuous but falls in the sharp lines of the hydrogen spectrum. The very stability, extent, and definiteness is not at all understandable on the basis of classical physics; and indeed on the basis of classical physics there is no length that we can define in terms of the masses and charges of the ingredients of the atom, and that is even roughly of the actual dimensions of the atom.
In other respects, too, the atomic system shows a peculiar lack of continuity wholly at variance with the properties of Newtonian dynamics. If we probe atoms with a stream of electrons, for instance, the electrons will typically lose some of their initial energy, but these losses are not random in amount. They correspond to definite, well-defined energy gaps, characteristic for the atom in question, reproducible and not too hard to measure. When an atom is irradiated by light, an electron will be ejected, if and only if the energy of that light exceeds a certain minimum known as the photo-electric threshold. Indeed, it was this discovery which led Einstein in the early years of the century to a finding about light almost equally revolutionary for our understanding of light and for our understanding of atomic systems. This finding, to be more precise, is that as one alters the frequency of the light that shines on a body, the energy of the electrons ejected increases linearly with the frequency; linearly—that means proportionally. {34} The constant of proportionality, which connects energy with frequency, is the new symbol of the atomic domain. It is called Planck's constant, or the quantum of action, and it gives a measure of energy in terms of frequency. It is the heraldic symbol over the gateway to the new world; and it led Einstein to the bold, though at the time hardly comprehensible, conclusion that light, which we know as an electromagnetic disturbance of rapidly changing electrical fields, which we know as a continuous phenomenon propagating from point to point and from time to time like a wave, is also and is nevertheless corpuscular, consisting of packets of energy determined by the frequency of the light and by Planck's constant. When a material system absorbs light, it absorbs such a packet, or quantum, of energy, neither less nor more; and the discontinuous nature of the energy exchanges between an atom and an electron is paralleled by the discontinuous nature of the energy exchanged when radiation is absorbed or emitted.
We shall have to come back more than once to light as waves, and light as quanta; but how radical a problem of understanding this presents can be seen at once from all of classical optics, from the work of Huygens and its mathematical elaboration by Fresnel, and even more completely from its electromagnetic interpretation by Maxwell. We know that light waves interfere. We know, that is, that if there are two sources of light, the intensity of the light to be found at some other place will not necessarily be just composed of the sum of that which comes from the two sources; it may be more and it may be less. We know from unnumbered attempts how to calculate, and how to calculate correctly, what the interference of the sources will turn out to be. If we have light impinging on a screen which is opaque and there are two holes in the screen, not too large and not too far apart in the terms of the wave length, the wavelets that come from one of the holes will be added to those that come from the other. Where two crests of these wavelets coincide, we shall have more light than the sum of the two. Where a crest and a trough coincide, we shall have {35} less; and so we observe and understand and predict and are quite confident of these phenomena of interference.
Try for a moment to describe this in the terms of the passage of particles of quanta. If one of those quanta which characterize both the emission of light at the source and its detection—let us say, by the eye or by the photographic plate or photocell on the far side of the screen—if a quantum passes through one of the holes, how can the presence of the other hole through which it did not pass affect its destiny? How can there be any science or any prediction if the state of affairs remote from the trajectory of the quantum can determine its behavior? Just this question and our slow answer to it will start us on the unravelling of the physics of the atomic world.
The first great step, taken long before the crisis of quantum theory, was to find a way of describing atomic behavior, not forgetting the mechanics and electrodynamics of the past, but knowing that one had here to do with something new and different, and necessarily postponing the question of the connection of that which is new with the old laws. This is Bohr's first theory. It has given us the symbol of the atomic world: the nucleus and a series of circles and ellipses represent in a pictorial way the states of the atom. We use it today, though we know in far more detail and far more completely what Bohr knew when he proposed it, that it could be at best a temporary and partial analogy. This was Bohr's first postulate: that in every atom there were stationary states whose stability and uniqueness could not be understood in terms of classical dynamics. The lowest one, the one with the least energy, the ground state, is truly stable. Unless we disturb it, it will last unaltered. The others are called excited states, and they may be excited by collision or radiation or other disturbance. They, too, are stable in a sense incomprehensible in terms of Newton's theory. Their stability is not absolute though. Just as these states could be reached by transition induced by collision or disturbance, so an atom may return to states of lower {36} energy, whether by further collision or spontaneously. In these spontaneous changes it gives out that radiation which is the analog of the radiation which in classical theory would make all motion unstable. In simple cases, the energy of these stationary states and some of the properties such as their shape are identical with or similar to the energy of some of the properties of Newtonian orbits. But this stops being true when we go even from hydrogen to helium, with its two electrons. It is only partially true in hydrogen; and the rules which Bohr laid down for determining the character of the orbits that would correspond to stationary states, the so-called quantum conditions, were from the first recognized by him as incomplete and provisional. We know now that the states are in fact nothing like orbits at all; that the element of change with time, which is inherent in an orbit, is missing from these states; and that in fact the very notion of an orbit can be applied to the motion of matter only when the stationary state is not defined, and that a stationary state can exist only when there is no possibility of describing an orbit at all.
That was the first rule. And what is the second? The second rule is that an atom can change only by passing from state to state; that its energy changes by the difference in energy between the states; and that, when this exchange of energy occurs in the absorption, emission, or scattering of light, the frequency of the light will be related to the energy by the relation of Einstein and of Planck. The energy will be the frequency multiplied by the quantum of action; thus atomic spectra directly reveal energy differences between states, and by this the whole field of spectroscopy becomes evidence for the location and the properties of atomic states, and we begin to learn what properties of these states are like those of classical orbits and what are unlike.
But what are we to think of the transitions themselves? Do they take place suddenly? Are they very quick motions, executed in going from one orbit to another? Are they causally determined? Can we say, that is, when an atom will {37} pass from one of its states to another as we disturb it; and can we find what it is that determines that time? To all these questions, the answer would turn out to be “no.” What we learned to ask was what determined not the moment of the transition but the probability of the transition. What we needed to understand was not the state of affairs during the transition but the impossibility of visualizing the transition—an even more radical impossibility than with the states themselves—in terms of the motion of matter. We learned to accept, as we later learned to understand, that the behavior of an atomic system is not predictable in detail; that of a large number of atomic systems with the same history, in, let us say, the same state, statistical prediction was possible as to how they would act if they were let alone and how they would respond to intervention; but that nowhere in our battery of experimental probings would we find one to say what one individual atom would in fact do. We saw in the very heart of the physical world an end of that complete causality which had seemed so inherent a feature of Newtonian physics.
How could all this be and yet leave the largely familiar world intact as we knew it? Large bodies are, of course, made up of atoms. How could causality for bullets and machines and planets come out of acausal atomic behavior? How could trajectories, orbits, velocities, accelerations, and positions re-emerge from this strange talk of states, transitions, and probabilities? For what was true yesterday would be true still, and new knowledge could not make old knowledge false. Is there a possible unity between the two worlds and what is its nature?
This is the problem of correspondence. Whatever the laws which determine the behavior of light or of electrons in atoms or other parts of the atomic world, as we come closer and closer to the familiar ground of large-scale experience, these laws must conform more and more closely to those we know to be true. This is what we call the principle of correspondence. In its formulation the key is the {38} quantum of action, whose finiteness characterizes the new features of atomic physics. And so the physicist says that, where actions are large compared to the quantum of action, the classical laws of Newton and Maxwell will hold. What this tends to mean in practice is that when mass and distances are big compared to those of the electron and the atom's size, classical theory will be right. Where energies are large and times long compared to atomic energies and times, we shall not need to correct Newton. Where this is so, the statistical laws of atomic physics will lead to probabilities more and more like certitudes, and the acausal features of atomic theory will be of no moment, and in fact lost in the lack of precision with which questions about large events will naturally be put.
In Bohr's hands and those of the members of his school, this correspondence principle was to prove a powerful tool. It did not say what the laws of atomic physics were, but it said something about them. They must in this sense be harmonious with, and ultimately reducible to, those of large-scale physics. And when to this principle was added the growing conviction that the laws of atomic physics must deal not with the Newtonian position, velocity, and acceleration that characterized a particle but with the observable features of atoms—the energies and properties of stationary states, the probabilities of transitions between these states—the groundwork was laid for the discovery of quantum mechanics.
The principle of correspondence—this requirement that the new laws of atomic mechanics should merge with those of Newtonian mechanics for large bodies and events—thus had great value as an instrument of discovery. Beyond that, it illustrates the essential elements of the relation of new discovery and old knowledge in science; the old knowledge, as the very means for coming upon the new, must in its old realm be left intact; only when we have left that realm can it be transcended.
A discovery in science, or a new theory, even when it appears most unitary and most all-embracing, deals with {39} some immediate element of novelty or paradox within the framework of far vaster, unanalyzed, unarticulated reserves of knowledge, experience, faith, and presupposition. Our progress is narrow; it takes a vast world unchallenged and for granted.
This is one reason why, however great the novelty or scope of new discovery, we neither can, nor need, rebuild the house of the mind very rapidly. This is one reason why science, for all its revolutions, is conservative. This is why we will have to accept the fact that no one of us really will ever know very much. This is why we shall have to find comfort in the fact that, taken together, we know more and more.
| {40} |
In exploring the atomic world, we have traveled to a new country, strange for those who have lived in the familiar world of Newtonian physics, strange even to Newton's own view of wonder and pre-vision. “God in the Beginning,” he wrote, “form'd Matter in solid, massy, hard, impenetrable, movable Particles. . . .”
We have our atoms; we are trying to understand them. We have the simplest of the atoms, hydrogen, with a single proton for its nucleus and a single electron to make it up. But the ingredients do not follow Newton's laws of motion. Atoms of hydrogen appear to be all alike; they have a fixed size; they are stable and not transitory; the light that they emit is not what an electron circling in ever smaller ellipses would radiate. They have a stability that does not derive from Newtonian mechanics. When they are disturbed by light or electrons or other matter, they take up energy in definite quanta characteristic for the atom. They are described in terms of states—states that are not orbits, though they have some of the properties of some special orbits. The states are stable, or almost stable. Transition between them, occasioned by disturbance, or occurring spontaneously with the emission of light, occurs by chance. We do not know the cause of the individual transition but only, at best, their probable distribution in time; nor do we have, in terms of space and time and trajectory, any picture whatever of what these transitions may be. These acausal atoms compose the familiar world of large bodies, orbits, and Newton's laws. The laws that describe atomic behavior, the stationary states and transitions, reduce by correspondence, when applied to large systems, to Newton's laws. {41} The discovery of these laws by Heisenberg could itself have led to all we now know of quantum theory, but it was supplemented as a matter of history by new discoveries in related fields which make the task of understanding and exposition simpler and more direct. Yet even these are both unfamiliar and abstract; I fear that no exposition can be wholly without difficulty.
Our problem has to do with the so-called duality of wave and particle. On the one hand we have light, described in detail as a continuous electromagnetic wave with electric and magnetic fields, changing with a frequency that determines the light's color, and with an amplitude that determines its intensity. The waves of light differ from radio waves only in one respect: their wave length is much shorter. They differ obviously from the waves we see on water, which are the more or less regular displacement of matter. But when we talk here of waves, in this account of wave-particle duality, as we shall have to, it will mean something quite abstract, something common to light, radio, and water waves.
It will mean a state of affairs distributed in space and propagating with time, sometimes a harmonic like a pure note of sound and sometimes irregular like noise. It will mean that these disturbances in general add, so that two crests reinforce, and a crest and a trough tend to cancel. It will mean that the sum of two effects may not be greater than either, but smaller, as the phases of crest and trough indicate. It will mean that, if we leave more than one alternative for a particle or for light to go from one place to another, the chance of arriving may be greater than the sum of the chances or smaller than the sum of the chances, because of this interference of the waves that represent the alternatives.
When we deal with light, we deal with such waves; but we also deal, as Einstein discovered, with something sharp, discrete, and discontinuous—the light quantum. Whenever light acts on matter, or is produced by it, we find packets of defined energy and impulse, related to their {42} frequency and their wave number by the universal proportionality of the quantum of action. How were these quanta to be thought of? Were they guided by the waves? Were they the waves? Were the waves an illusion, after all?
This turned out to be a universal quandary. De Broglie suggested and later Davison found that there were waves associated with electrons. Specifically Davison's experiment showed that electrons, too, when they are scattered by the regular disturbance of a natural crystal, exhibit the same signs of interference, the same unmistakable signature of the superposition of waves as light and as X-rays; and later experiments showed that this is true of all the other particles as well—protons, neutrons, and the atoms themselves. It would be true of large objects also were it not that their wave length is small, because of smallness of Planck's constant, and becomes completely insignificant compared with their dimensions and with any practical possibility of determining their location and outline.
All the questions which puzzled men about the relations of Einstein's quanta and Maxwell's waves were thus to be equally sharp and equally troublesome for the wave and particle properties of matter. The resolution of these questions is the heart of atomic theory. They were brought to the point of crisis by another great discovery—Schroedinger's discovery of his wave equation.
In its original, bold form this was the discovery of a simple law for the propagation of electron waves—a natural generalization of the connection between wave number and impulse, between energy and frequency, a generalization nevertheless adequate to describe the gross features of atomic systems and most of the familiar properties of matter. This equation had many sorts of solutions. Some were stationary, unchanging in time, with a frequency and energy that corresponded to the stationary states of atoms. This same equation had other solutions of a very different kind, representing the trajectory of an electron as it might be seen crossing the Wilson cloud chamber. It had still other solutions, compounded by addition of several {43} stationary states with their several proper frequencies. These were not stationary but varied in time with frequencies corresponding to the spectrum of atoms and molecules.
But what were these waves? What did they describe? How were they related to the ways in which we observe and study atomic systems, to Rutherford's probings, to the collisions and disturbances of atoms? Schroedinger understood that in some sense the world of classical physics would emerge from his equation, whenever the wave lengths were small enough; then the trajectories for bodies and planets would be like the geometric paths of light, the rays of optics. But what would the waves mean when this was not the case?
It would have been no answer to this question to attempt to interpret the waves as an essentially mechanical disturbance in some underlying mechanical medium; for the questions which needed answering had to do with the problems of stationary states, and the behavior of electrons, and not with a sub-stratum inaccessible to observation. Nor was such a path followed. The discouraging outcome of an analogous attempt with electromagnetic waves was conclusive. It did not seem reasonable, nor in fact has it ever proved possible, at a time when the very foundations of classical mechanics were being altered, to reinterpret this revolution in classical mechanical terms.
There was another false start. It was at one time suggested that the waves, as they spread and moved, in some sense represented the changing shape, extension, and flow of the electron itself; when the disturbance grew larger the electron grew larger; when the wave moved faster the electron moved faster. But to this interpretation there was an insuperable obstacle. Whenever we looked for the position of the particle, looked not directly with the eye, but with the natural extension of looking with a microscope, we did not find it spread out; we never found part of it in the place where we were looking. Either it was there or it was not there—the whole or none of it. Whenever we tried to measure the velocity of an electron or its impulse, we never {44} found that part of it was moving with one speed and part with another; there was always one electron, one velocity, one answer to an experimental inquiry. The spreading of the waves in space thus did not mean that the electron itself spread; it meant that the probability or likelihood of our finding the electron, when we look for it, spread as the wave does.
And thus it was that these waves were recognized as describing a state of affairs, as summarizing information we had about the electron, as very much more abstract waves indeed than we had hitherto encountered in physics. Their interpretation was statistical as well as abstract: where a disturbance was large, there we were likely to find the electron if we looked for it; where it was small, unlikely. If the disturbance had ripples in which a certain wave length was prominent, a measurement of the momentum would be likely to give us a value corresponding to that wave length. This clearly is qualitative talk. Quantitative rules for assigning a wave function to describe the outcome of an observation—or of other certain forms of knowledge, such as that of an atom in its state of lowest energy— needed to be, could be, and were developed; and they are a part of quantum theory. Their exposition presupposes some mathematical talk and calls at least for a blackboard. Similarly, the simple rules which relate the magnitude or properties of a wave function to the expectations that it implies for one or another observation are a rigorous and necessary part of the theory. But with these bonds to tie the wave to our knowledge and to interpret it for our prediction, the basis of the new physics has been laid.
It is a statistical physics, as indeed might have been expected from the statistical features of atomic transitions. Its predictions are in the form of assertions of probability and only rarely and specially in the form of certitudes. With this in mind, let us look again at our problem of interference, and of the two holes. {45}
Let us think of an opaque screen with two holes in it. Let us think of light, if we will; or, better still, let us think of electrons of a given velocity and therefore a given wave length and direction. We can do two experiments with a source of electrons. In one, each hole in turn will be open for a little, while the other is closed; in the other, both holes will be open together. If we register the electrons on the far side of the screen, for instance, with a photographic plate, we see that the two patterns are radically different. In the one case, we have a transmission through each of the holes separately, with the characteristic diffraction pattern for that wave length and for holes of that diameter. These patterns are just added to one another on the photographic film. But if both holes are open at the same time, something else happens. The waves that come through one interfere with those that come through the other; spots that were blackened before are now untouched and new spots appear where the electrons do arrive.
If we try to think of this in terms of following the electrons through one or the other of the holes, we cannot understand how it can make any difference whether that hole through which the electron did not pass is open or shut; yet it does. If we argue that the effect can be traced to the interaction of electrons passing through the two holes, we can disprove this by noting that the pattern is not affected by reducing the number of electrons to the point where there almost never are two passing through the two holes at the same time. What we are observing is something characteristic of the behavior of single particles, not of the interaction of several.
We are thus led to say that in this experiment a knowledge of which hole the electron passed through is in principle inaccessible to us, that it is just the possibility of its passing through one or the other that leads to the characteristic new interference phenomena, the new light spots and the new dark spots on the photographic film. We conclude that, if we should make provision for registering {46} through which hole the electron went, such as looking for it or observing the small push that it gives to the screen as it passes through, we would destroy the interference effects. We would then have the same result as if we had in fact opened and shut the holes successively.
We see the connection between these conclusions and the description of the state of affairs by a wave held in qualitative terms, rather closely paralleling the arguments that were made quantitative in the uncertainty principle of Heisenberg.
For we note that, if we were sure that the electron passed through one of the holes, the wave field would have to be restricted to that region; and that, if this were true, it would have to be composed not of a single wave length, or approximately a single one, but of waves of enough different wave lengths so that they can reinforce each other at one hole and vanish at the other; and we know that such waves have lost the coherent quality necessary for interference. A little more generally, the waves of a single wave length will correspond to an electron of a definite velocity or impulse, but in an ill-defined or undefined position; the waves that are localized to represent a definition of position will be broadly scattered in wave length and represent an undefined velocity or impulse. This complementary restriction on the degree to which a wave field can represent both a well-defined position and a well-defined impulse is universal; it is measured by the quantum of action. It holds not only for electrons but for the more complicated waves that describe complex systems, for atoms and nuclei and more composite bits of matter and more elementary ones. And the very fact that no wave field can give that complete definition of the position and velocity of an object which was taken for granted in classical physics is also a description of the limitation on the observations which in the real world we shall manage to make. It represents the fact that, when we study a system, making an experiment or an observation on it, we may—and in general we will, if we have prior knowledge before the {47} experiment—be losing in whole or in part that prior knowledge. The experiment itself—that is, the physical interactions between the system and the equipment that we are using to study it—will not only alter what we previously knew, but will in general alter it in a way which cannot be followed without invalidating the measurement or observation we have undertaken.
To cite but one example: if in the problem of the two holes we try to detect which hole the electron has passed through by noticing the push that it gives to the screen at that point, we shall have to leave a part of the screen free to respond to the push; and by this we lose all certitude as to where that part of the screen was when that electron passed through it. Many complex and detailed studies have been made of how this limitation of knowledge occurs in an experiment; but since the principle of complementarity, and the general adequacy of a wave field to describe a state of affairs, underlies the description of both the object and the instrument of observation, these examples only illustrate and make vivid what must generally be true: the universal limitation, in contrast to classical physics, of the extent to which all aspects of a physical system can be defined for the same system in the same instance.
In observing atomic systems, in observing a system where the finiteness of the quantum of action plays an important part, we have a wide range of choice in the kind of probe, the kind of experiment, the kind of experimental equipment we wish to make. To any of these, if it is a good experiment, there will be a meaningful answer which tells us what the state of affairs is. From this, and from the wave field which represents it, we can then make statistical predictions of what will happen in a subsequent experiment. The potentialities of measurement are varied. We can do one thing or another; there are no inherent limits on the choice of actions on the part of the observer.
This is a very different view of reality from Newton's giant machine. It is not causal; there is no complete causal determination of the future on the basis of available knowledge {48} of the present. The application of the laws of quantum theory restricts, but does not in general define, the outcome of an experiment. This means that every observation on a system reveals some new knowledge as to what its state is that did not exist before, and could not by analysis and mathematical computation have been obtained. It means that every intervention to make a measurement, to study what is going on in the atomic world, creates, despite all the universal order of this world, a new, a unique, not fully predictable, situation.
Even in a brief account other points need to be mentioned. We have almost lost the concept of equations of motion, having discovered that the very terms in which they are formulated—position, velocity, acceleration, and force— are not simultaneously applicable and do not, taken together, correspond to things that we know about the electron with enough accuracy to be meaningful for an atomic system. Instead, what we can have is a knowledge of the state, summarizing for us what we have found by observation; and the analogue of the equation of motion must tell us how, in response to forces acting within the system or upon it, this state will change with time. This, it turns out, is just what Schroedinger's equation does. And once again this equation, when applied to the familiar contexts of massive bodies and great distances, where the quantum of action is in fact negligibly small, will describe for us waves so reasonably concentrated in space, so little dispersed about their average wave length, that the Newtonian orbit reappears in its unaltered, classical path.
But this condition—this emergence of an orbit—is a long way from the wave that describes the normal state of an atom. State and orbit, like position and impulse, are complementary notions; where one applies, the other cannot be defined, and for a full description we must be able to use now one, now the other, depending on the observation and the questions that we put.
When we speak here of observer and object, of instrument or probe, and system to be probed, we are not talking {49} of the mind of man. We are talking of a division between the object of study and the means used to study it. That division can be made in more than one way. We may regard the α-particles that Rutherford used as an instrument, and their response as a measure of the state of affairs. We may regard the α-particle as a part of the system we are studying, and the slits that define its path or the fields that deflect it and the screens that detect it as the instrument. But whichever we do, the observation will always be transformed into some large-scale happening— some flash of light, some triggering of a circuit, some pointing of a pointer on the dial of an instrument—which is well defined and familiar and unambiguous, and where the question of our freedom to do one or another observation on it no longer is relevant. The atomic world has not lost its objective quality; but it attains this by means of those interlockings with experiment which we use to define one or another of its properties and to measure them.
It needs to be clear that what is described here is not an expression of mood or preference or taste; it is an exact, beautiful, quantitative, immensely versatile, and immensely successful science. It is what students learn when they prepare themselves for further researches in physics, or what engineers learn whose engineering involves a knowledge of the solid state of physical materials, or what chemists learn if they wish to understand the subtler features of chemical bonding or chemical kinetics, or astronomers if they wish to know what things are like in the interior of the stars. One could go much farther in describing this discipline, even without mathematics; but the words would before long become cumbersome and unfamiliar and almost a misinterpretation of what in mathematical terms can be said with beauty and simplicity.
Even some of the more paradoxical features of quantum theory turn out to be related to practical matters of real importance. One of the earliest to be noted and the oddest is this: if, in familiar life, we roll a ball up a hill and it does not have enough vigor to get over the top, it will roll back {50} on the same side; it will not get through the hill. But if we bombard such a hill with α-particles or electrons they may have a small chance of getting through, even when they cannot get over. This has a close analogy with the fact that very small objects do not cast sharp shadows in a beam of light. Light because of its wave nature bends around them. It corresponds to the fact that when we let electrons or other particles of definite energy encounter a barrier, neither the kinetic nor the potential energy alone can be completely well defined; and indeed, were we to try to detect the electron just as it passes through the hill, we should need an experiment that could give the electron enough energy to be quite legitimately on top of the hill. This penetration of barriers is not without importance. It accounts for the fact that the α-particles that Rutherford used could sometimes, after millions of years, escape from the nuclei through a high hill where electrostatic repulsion had imprisoned them. It accounts for the fact that in the sun and other stars nuclei having only very moderate energy occasionally come into contact and react. Thus the stars light the heavens, and the sun warms and nourishes the earth.
Another consequence of the wave-like character of all matter is that, when particles with very low velocity and very long wave length bombard other particles of matter, they may interact far more often than if these interactions were limited to their coming in contact. The very lack of definition of their relative position makes interaction possible, in some cases over distances characterized not by their dimensions but by their wave length. This is the circumstance which, among many others, enables the rare Uranium-235, as it occurs in natural uranium, to catch up enough of the neutrons which fly about to sustain a chain reaction in an atomic reactor.
There are even some odd things about the identity and the identifiability of the electrons themselves. That they are all similar we know. Their inherent properties, their charge, their mass when at rest, are the same. We wish that {51} we understood this better; some day, no doubt, we shall; but we know that it is true. But if classical physics were the whole story, we could still, if we wished, always identify an electron, and know that it was the same as the one we had seen before. We could follow it, not, it is true, without trouble, but without paradox, without inconsistency, from where we first found it through its collisions and interactions and deflections and changes by keeping in touch with its trajectory. If it hit another electron, we would know which it was that came out in one direction and which in another. In fact this is not really true, except in those special instances where the collision is of such low energy that the two electrons can be described by waves which never overlap at the same place at the same time. As soon as that is no longer the case, we lose in principle all ability to tell one electron from another; and in atomic physics, where the electrons of an atom, and even the electrons of neighboring atoms, are not well defined in position and can often occupy the same volume, we have no way of identifying the individual particle. This, too, has consequences. When two electrons collide, the wave that represents one of them and the wave that represents the other may, and do, interfere; and this gives rise to novel effects and new forms for the interactions produced by their electric repulsion. It is responsible for the permanent magnetism of magnets. It is responsible for the bonding of organic chemistry and for the very existence in any form that we can readily imagine of living matter and of life itself.
These examples are not given to perplex and bemuse. They are rather illustrations of how even the most paradoxical and unexpected consequences of the new mechanics, of wave-particle duality, and of complementarity are involved in an understanding of important and familiar features of the natural world, and of how massive is the system of understanding and knowledge of which they are a part.
| {52} |
A century after Newton, in 1784, the progress of that century was celebrated in an anonymous memorial lodged in the ball of the tower of St. Margaret's church at Gotha, to be found by men of future times. It read:
“Our days have been the happiest time of the eighteenth century. . . . Hatred born of dogma and the compulsion of conscience sink away; love of man and freedom of thought gain the upper hand. The arts and sciences blossom, and our vision into the workshop of nature goes deep. Artisans approach artists in perfection; useful skills flower at all levels. Here you have a faithful portrait of our time. ... Do the same for those who come after you and rejoice!”
Transience is the backdrop for the play of human progress, for the improvement of man, the growth of his knowledge, the increase of his power, his corruption and his partial redemption. Our civilizations perish; the carved stone, the written word, the heroic act fade into a memory of memory and in the end are gone. The day will come when our race is gone; this house, this earth in which we live will one day be unht for human habitation, as the sun ages and alters.
Yet no man, be he agnostic or Buddhist or Christian, thinks wholly in these terms. His acts, his thoughts, what he sees of the world around him—the falling of a leaf or a child's joke or the rise of the moon—are part of history; but they are not only part of history; they are a part of becoming and of process but not only that: they partake also of the world outside of time; they partake of the light of eternity. {53}
These two ways of thinking, the way of time and history and the way of eternity and of timelessness, are both part of man's effort to comprehend the world in which he lives. Neither is comprehended in the other nor reducible to it. They are, as we have learned to say in physics, complementary views, each supplementing the other, neither telling the whole story. Let us return to this.
First, we had best review and extend somewhat this account of the complementarity of the physicists. In its simplest form it is that an electron must sometimes be considered as a wave, and sometimes as a particle—a wave, that is, with the continuous propagation and characteristic interference that we learn to understand in the optics laboratory, or as a particle, a thing with well-defined location at any time, discrete and individual and atomic. There is this same duality for all matter and for light. In a little subtler form this complementarity means that there are situations in which the position of an atomic object can be measured and defined and thought about without contradiction; and other situations in which this is not so, but in which other qualities, such as the energy or the impulse of the system, are defined and meaningful. The more nearly appropriate the first way of thinking is to a situation, the more wholly inappropriate the second, so that there are in fact no atomic situations in which both impulse and position will be defined well enough to permit the sort of prediction with which Newtonian mechanics has familiarized us.
It is not only that when we have made an observation on a system and determined, let us say, its position, we do not know its impulse. That is true, but more than that is true. We could say that we know the position of that system and that it may have any one of a number of different impulses. If we try on that basis to predict its behavior as a sort of average behavior of all objects which have the measured position and which have different and unmeasured impulses, and work out the average answer according to {54} Newton's laws, we get a result that is wholly at variance with what we find in nature. This is because of the peculiar property, which has no analogue in the mechanics of large objects, of interference between waves representing the consequences of assuming one impulse and those of assuming another. We are not, that is, allowed to suppose that position and velocity are attributes of an atomic system, some of which we know and others of which we might know but do not. We have to recognize that the attempt to discover these unknown attributes would lose for us the known; that we have a choice, a disjunction; and that this corresponds to the different ways we can go about observing our atom or experimenting with it.
We have a state of affairs completely defined by the nature of the observation and by its outcome—the nature determining what properties of the system will be well defined in the state and what poorly. The outcome then is the determination of the well-defined quantities by measurement. This state thus is a summary, symbolic and uncomfortably abstract for general exposition, of what sort of observation we have made and what we have found through it. It codifies those characteristics of the experimental arrangement which are reliable, in the sense that the equipment we use records something that we know about atomic systems. It describes also those characteristics that are indeterminate, in the sense that they may not only have been disturbed or altered, but that their disturbance cannot be registered or controlled without the loss, in the experiment, of all ability to measure what was supposed to be measured.
This state, this description of the atom, is not the only way of talking about it. It is the only way appropriate to the information we have and the means that we have used to obtain it. It is the full account of this information; and if the experiment was properly and scrupulously done it tells us all that we can find out. It is not all that we could have found out had we chosen a different experiment. It is all that we could find out having chosen this. {55}
This state is objective. We can calculate its properties, reproduce it with similar atoms on another occasion, verify its properties and its ways of change with time. There is no element of the arbitrary or subjective. Once we have done our experiment and its result is recorded and the atom disengaged, we know its meaning and its outcome; we can then forget the details of how we got our information.
But, although the state of the system is objective, a mechanical picture of how it was brought into being is not generally possible. There is a most vivid example of this, made famous by the prominent part it played in the debates between Einstein and Bohr as to the meaning and adequacy of atomic theory. It can be put rather simply. Let us suppose that we have two objects; one of them may be an electron or an atom, and it will be the one we wish to study. The other may be a relatively large piece of matter—a screen with a hole through it, or any other body; but it should be heavy so that its motion will be unimportant compared to that of the electron. Let us suppose that we by measurement know the impulse or momentum of both of these objects, and have them collide. Let the electron go through the hole, or bounce off the other body. If, after the collision, we measure the impulse of the heavy body, we will then know that of the electron because, as Newton's third law teaches us, the sum of the impulses is not altered by the collision. In that case we would have a state of the electron of well-defined impulse, as precisely defined as we had made the precision of our measurements. If, on the other hand, we observed the position of the heavy body, we would know where the light one had been at the moment of the collision, and so would have a quite different description of its state, one in which its position and not its impulse had been well defined—or, in the language of waves, a spherical wave with its center at the point of collision, and not a plane wave with its direction and wave length corresponding to the momentum.
We have thus the option of realizing one or the other of two wholly dissimilar states for the electron, by a choice of {56} what we observe about the heavy body with which it once was in interaction. We are not, in any meaningful sense, physically altering or qualifying the electron; we are defining a part of, although in this case a late part of, the experimental procedure, the very nature of the experiment itself. If we exercise neither option, if we let the heavy body go with unmeasured momentum and undefined position, then we know nothing of the electron at all. It has no state, and we are not prepared to make any meaningful predictions of what will become of it or of what we shall find should we again attempt an experiment upon it. The electron cannot be objectified in a manner independent of the means chosen for observing or studying it. The only property we can ascribe to it without such consideration is our total ignorance.
This is a sharp reminder that ways of thinking about things, which seem natural and inevitable and almost appear not to rest on experience so much as on the inherent qualities of thought and nature, do in fact rest on experience; and that there are parts of experience rendered accessible by exploration and experimental refinement where these ways of thought no longer apply.
It is important to remember that, if a very much subtler view of the properties of an electron in an atomic system is necessary to describe the wealth of experience we have had with such systems, it all rests on accepting without revision the traditional accounts of the behavior of large-scale objects. The measurements that we have talked about in such highly abstract form do in fact come down in the end to looking at the position of a pointer, or the reading of time on a watch, or measuring out where on a photographic plate or a phosphorescent screen a flash of light or a patch of darkness occurs. They all rest on reducing the experience with atomic systems to experiment and observation made manifest, unambiguous, and objective in the behavior of large objects, where the precautions and incertitudes of the atomic domain no longer directly apply. So it is that ever-increasing refinements and critical revisions {57} in the way we talk about remote or small or inaccessible parts of the physical world have no direct relevance to the familiar physical world of common experience.
Common sense is not wrong in the view that it is meaningful, appropriate, and necessary to talk about the large objects of our daily experience as though they had a velocity that we knew, and a place that we knew, and all the rest of it. Common sense is wrong only if it insists that what is familiar must reappear in what is unfamiliar. It is wrong only if it leads us to expect that every country that we visit is like the last country we saw. Common sense, as the common heritage from the millennia of common life, may lead us into error if we wholly forget the circumstances to which that common life has been restricted.
Misunderstanding of these relations has led men to wish to draw from new discoveries, and particularly those in the atomic domain, far-reaching consequences for the ordinary affairs of men. Thus it was noted that, since the ultimate laws of atomic behavior are not strictly causal, not strictly determinate, the famous argument of Laplace for a wholly determinate universe could not be maintained. And there were men who believed that they had discovered in the acausal and indeterminate character of atomic events the physical basis for that sense of freedom which characterizes man's behavior in the face of decision and of responsibility.
In a similar light-hearted way it was pointed out that, as the state of an atomic system requires observation for its definition, so the course of psychological phenomena might be irretrievably altered by the very effort to probe them—as a man's thoughts are altered by the fact that he has formulated and spoken them. It is, of course, not the fact that observation may change the state of an atomic system that gives rise to the need for a complementary description; it is the fact that, if the observation is to be meaningful, it will preclude any analysis or control of that change, that is decisive. {58}
But these misapplications of the findings of atomic physics to human affairs do not establish that there are no valid analogies. These analogies will, in the nature of things, be less sharp, less compelling, less ingenious. They will rest upon the fact that complementary modes of thought and complementary descriptions of reality are an old, long-enduring part of our tradition. All that the experience of atomic physics can do in these affairs is to give us a reminder, and a certain reassurance, that these ways of talking and thinking can be factual, appropriate, precise, and free of obscurantism.
There are a number of examples which are illuminated by, and in turn illuminate, the complementarity of atomic theory. Some of them are from quite different parts of human life and some of them from older parts of science. There is one from physics itself which is revealing, both in its analogies and its points of difference. One of the great triumphs of nineteenth-century physics was the kinetic theory of heat—what is called statistical mechanics. This is both an interpretation and a deduction of many of the large-scale properties and tendencies of matter: of the tendency, for instance, of bodies that can exchange heat to come to a common temperature, or of the density of a gas to be uniform throughout a container, or of work to dissipate itself in heat, or quite generally of all of those irreversible processes in nature wherein the entropy of systems increases, and forms become more uniform and less differentiated when left to themselves to develop.
The phenomena we deal with here are defined in terms of temperature and density and pressure and other large-scale properties. The kinetic theory, statistical mechanics, interprets the behavior of these systems in terms of the forces acting on the molecules and of the motion of the molecules that compose them, which are usually quite accurately described by Newton's laws. But it is a statistical theory of this motion, recognizing that in fact we do not in general know, and are not in detail concerned with, the positions and velocities of the molecules themselves, but {59} only with their average behavior. We interpret the temperature of a gas, for instance, in terms of the average kinetic energy of its molecules, and the pressure as the average of the forces exerted by the collision of these molecules on the surface of the container. This description in terms of averages, embodying as part of itself our ignorance of the detailed state of affairs, is thus in some sense complementary to a complete dynamic description in terms of the motion of the individual molecules. In this sense kinetic theory and dynamics are complementary. One applies to a situation in which the individual patterns of molecular behavior are known and studied; the other applies to a situation largely defined by our ignorance of these patterns.
But the analogy to atomic complementarity is only partial, because there is nothing in the classical dynamics which underlies kinetic theory to suggest that the behavior of a gas would be any different if we had performed the immense job of locating and measuring what all the molecules were doing. We might then, it is true, not find it natural to talk about temperature, because we would need no average behavior; we would have an actual one; but we could still define the temperature in terms of the total kinetic energy of the molecules, and we would still find that it tended to equalize between one part of the system and another.
We have therefore a situation in which there are two ways of describing a system, two sets of concepts, two centers of preoccupation. One is appropriate when we are dealing with a very few molecules and want to know what those molecules do; the other appropriate when we have a large mass of matter and only rough and large-scale observations about it.
There is, however, no logical or inherent difficulty within the framework of classical physics, in combining both descriptions for a single system—and classical physics, we repeat, is adequate for most, if not all, of these problems of statistical mechanics. It is not that we cannot do this {60} without violating the laws of physics; it is that it makes no sense to do it, since each description is appropriate to a context quite different from the other. It is clear that, if we insisted on the detailed description of the motion of individual molecules, the notions of probability which turn out to be so essential for our understanding of the irreversible character of physical events in nature would never enter. We should not have the great insight that we now do: namely, that the direction of change in the world is from the less probable to the more, from the more organized to the less, because all we would be talking about would be an incredible number of orbits and trajectories and collisions. It would be a great miracle to us that, out of equations of motion, which to every allowed motion permit a precisely opposite one, we could nevertheless emerge into a world in which there is a trend of change with time which is irreversible, unmistakable, and familiar in all our physical experience.
In considering the relations between the various sciences, there are similar instances of complementary views. In many cases, it is not clear whether this is the sort of complementarity that we have between the statistical and dynamic descriptions of a gas, a contrast of interest and terminology, but not an inherent inapplicability of two ways of talking; or whether on the contrary the situation is in fact more as it is in atomic physics, where the nature of the world is such that the two modes of description cannot be applied at once to the same situation. Every science has its own language. But dictionaries of translation between the languages do exist, and mark an evergrowing understanding and unity of science as a whole. It is not always clear whether the dictionaries will be complete; between physics and chemistry they apparently are. Everything the chemist observes and describes can be talked about in terms of atomic mechanics, and most of it at least can be understood. Yet no one suggests that, in dealing with the complex chemical forms which are of biological interest, the {61} language of atomic physics would be helpful. Rather it would tend to obscure the great regularities of biochemistry, as the dynamic description of a gas would obscure its thermodynamic behavior.
The contrast becomes even more marked when we consider the physico-chemical description of living forms. Here, in spite of the miraculous sharpness of the tools of chemical analysis, of the extensive use not only of the microscope but of the electron microscope to determine fine details of biological structure, in spite of the use of tracers to follow changes on a molecular scale, questions have still been raised as to whether this description can in the nature of things be complete.
The question involves two points: the first having to do with the impossibility of wholly isolating a biological system from its physical environment without killing it; the second with the possibility that a really complete physico-chemical study of the pivotal structures in biological processes—of genes, let us say, in the nuclei of dividing cells—might not be incompatible with the undisturbed course of life itself. It would appear to be the general opinion of biologists that no such limitations will prove decisive; that a complete description of biology will be possible not only in terms of the concepts of biology but in terms reducible to those of physics and chemistry. Certainly it is a large part of the aim and wonder of biological progress to carry this program as far as possible.
Analogous questions appear much sharper, and their answer more uncertain, when we think of the phenomena of consciousness; and, despite all the progress that has been made in the physiology of the sense organs and of the brain, despite our increasing knowledge of these intricate marvels both as to their structure and their functioning, it seems rather unlikely that we shall be able to describe in physico-chemical terms the physiological phenomena which accompany a conscious thought, or sentiment, or will. Today the outcome is uncertain. Whatever the outcome, we know that, should an understanding of {62} the physical correlate of elements of consciousness indeed be available, it will not itself be the appropriate description for the thinking man himself, for the clarification of his thoughts, the resolution of his will, or the delight of his eye and mind at works of beauty. Indeed, an understanding of the complementary nature of conscious life and its physical interpretation appears to me a lasting element in human understanding and a proper formulation of the historic views called psycho-physical parallelism.
For within conscious life, and in its relations with the description of the physical world, there are again many examples. There is the relation between the cognitive and the affective sides of our lives, between knowledge or analysis and emotion or feeling. There is the relation between the aesthetic and the heroic, between feeling and that precursor and definer of action, the ethical commitment; there is the classical relation between the analysis of one's self, the determination of one's motives and purposes, and that freedom of choice, that freedom of decision and action, which are complementary to it.
Whether a physico-chemical description of the material counterpart of consciousness will in fact ever be possible, whether physiological or psychological observation will ever permit with any relevant confidence the prediction of our behavior in moments of decision and in moments of challenge, we may be sure that these analyses and these understandings, even should they exist, will be as irrelevant to the acts of decision and the castings of the will as are the trajectories of molecules to the entropy of a gas. To be touched with awe, or humor, to be moved by beauty, to make a commitment or a determination, to understand some truth—these are complementary modes of the human spirit. All of them are part of man's spiritual life. None can replace the others, and where one is called for the others are in abeyance.
Just as with the α-particles of Rutherford, which were first for him an object of study and then became for him a tool of study, a tool for investigating other objects, so our {63} thoughts and words can be the subject of reflection and analysis; so we can be introspective, critical, and full of doubt. And so, in other times and other contexts, these same words, these same thoughts taken as instruments, are the power of human understanding itself, and the means of our further enlightenment.
The wealth and variety of physics itself, the greater wealth and variety of the natural sciences taken as a whole, the more familiar, yet still strange and far wider wealth of the life of the human spirit, enriched by complementary, not at once compatible ways, irreducible one to the other, have a greater harmony. They are the elements of man's sorrow and his splendor, his frailty and his power, his death, his passing, and his undying deeds.
| {64} |
For some moments during these lectures we have looked together into one of the rooms of the house called “science.” This is a relatively quiet room that we know as quantum theory or atomic theory. The great girders which frame it, the lights and shadows and vast windows—these were the work of a generation our predecessor more than two decades ago. It is not wholly quiet. Young people visit it and study in it and pass on to other chambers; and from time to time someone rearranges a piece of the furniture to make the whole more harmonious; and many, as we have done, peer through its windows or walk through it as sight-seers. It is not so old but that one can hear the sound of the new wings being built nearby, where men walk high in the air to erect new scaffoldings, not unconscious of how far they may fall. All about there are busy workshops where the builders are active, and very near indeed are those of us who, learning more of the primordial structure of matter, hope some day for chambers as fair and lovely as that in which we have spent the years of our youth and our prime.
It is a vast house indeed. It does not appear to have been built upon any plan but to have grown as a great city grows. There is no central chamber, no one corridor from which all others debouch. All about the periphery men are at work studying the vast reaches of space and the state of affairs billions of years ago; studying the intricate and subtle but wonderfully meet mechanisms by which life proliferates, alters, and endures; studying the reach of the mind and its ways of learning; digging deep into the atoms and {65} the atoms within atoms and their unfathomed order. It is a house so vast that none of us know it, and even the most fortunate have seen most rooms only from the outside or by a fleeting passage, as in a king's palace open to visitors. It is a house so vast that there is not and need not be complete concurrence on where its chambers stop and those of the neighboring mansions begin.
It is not arranged in a line nor a square nor a circle nor a pyramid, but with a wonderful randomness suggestive of unending growth and improvisation. Not many people live in the house, relatively speaking—perhaps if we count all its chambers and take residence requirements quite lightly, one tenth of one per cent, of all the people in this world— probably, by any reasonable definition, far fewer. And even those who live here live elsewhere also, live in houses where the rooms are not labelled atomic theory or genetics or the internal constitution of the stars, but quite different names like power and production and evil and beauty and history and children and the word of God.
We go in and out; even the most assiduous of us is not bound to this vast structure. One thing we find throughout the house: there are no locks; there are no shut doors; wherever we go there are the signs and usually the words of welcome. It is an open house, open to all comers.
The discoveries of science, the new rooms in this great house, have changed the way men think of things outside its walls. We have some glimmering now of the depth in time and the vastness in space of the physical world we live in. An awareness of how long our history and how immense our cosmos touches us even in simple earthly deliberations. We have learned from the natural history of the earth and from the story of evolution to have a sense of history, of time and change. We learn to talk of ourselves, and of the nature of the world and its reality as not wholly fixed in a silent quiet moment, but as unfolding with novelty and alteration, decay and new growth. We have understood something of the inner harmony and beauty of strange primitive cultures, and through this see the qualities {66} of our own life in an altered perspective, and recognize its accidents as well as its inherent necessities. We are, I should think, not patriots less but patriots very differently for loving what is ours and understanding a little of the love of others for their lands and ways. We have begun to understand that it is not only in his rational life that man's psyche is intelligible, that even in what may appear to be his least rational actions and sentiments we may discover a new order. We have the beginnings of an understanding of what it is in man, and more in simple organisms, that is truly heritable, and rudimentary clues as to how the inheritance occurs. We know, in surprising detail, what is the physical counterpart of the act of vision and of other modes of perception. Not one of these new ideas and new insights is so little, or has so short a reach in its bearing on the common understanding but that it alone could make a proper theme for “Science and the Common Understanding.” Yet we have been, bearing in mind my limited area of experience, in that one room of the part of the house where physics is, in which I have for some years worked and taught.
In that one room—in that relatively quiet room where we have been together—we have found things quite strange for those who have not been there before, yet reminiscent of what we have seen in other houses and known in other days. We have seen that in the atomic world we have been led by experience to use descriptions and ideas that apply to the large-scale world of matter, to the familiar world of our schoolday physics; ideas like the position of a body and its acceleration and its impulse and the forces acting on it; ideas like wave and interference; ideas like cause and probability. But what is new, what was not anticipated a half-century ago, is that, though to an atomic system there is a potential applicability of one or another of these ideas, in any real situation only some of these ways of description can be actual. This is because we need to take into account not merely the atomic system we are studying, but the means we use in observing it, and the {67} fitness of these experimental means for defining and measuring selected properties of the system. All such ways of observing are needed for the whole experience of the atomic world; all but one are excluded in any actual experience. In the specific instance, there is a proper and consistent way to describe what the experience is; what it implies; what it predicts and thus how to deal with its consequences. But any such specific instance excludes by its existence the application of other ideas, other modes of prediction, other consequences. They are, we say, complementary to one another; atomic theory is in part an account of these descriptions and in part an understanding of the circumstances to which one applies, or another or another.
And so it is with man's life. He may be any of a number of things; he will not be all of them. He may be well versed, he may be a poet, he may be a creator in one or more than one science; he will not be all kinds of man or all kinds of scientist; and he will be lucky if he has a bit of familiarity outside the room in which he works.
So it is with the great antinomies that through the ages have organized and yet disunited man's experience: the antinomy between the ceaseless change and wonderful novelty and the perishing of all earthly things, and the eternity which inheres in every happening; in the antinomy between growth and order, between the spontaneous and changing and irregular and the symmetrical and balanced; in the related antinomy between freedom and necessity; between action, the life of the will, and observation and analysis and the life of reason; between the question “how?” and the questions “why?” and “to what end?”; between the causes that derive from natural law, from unvarying regularities in the natural world, and those other causes that express purposes and define goals and ends.
So it is in the antinomy between the individual and the community; man who is an end in himself and man whose tradition, whose culture, whose works, whose words have {68} meaning in terms of other men and his relations to them. All our experience has shown that we can neither think, nor in any true sense live, without reference to these antinomic modes. We cannot in any sense be both the observers and the actors in any specific instance, or we shall fail properly to be either one or the other; yet we know that our life is built of these two modes, is part free and part inevitable, is part creation and part discipline, is part acceptance and part effort. We have no written rules that assign us to these ways; but we know that only folly and death of the spirit results when we deny one or the other, when we erect one as total and absolute and make the others derivative and secondary. We recognize this when we live as men. We talk to one another; we philosophize; we admire great men and their moments of greatness; we read; we study; we recognize and love in a particular act that happy union of the generally incompatible. With all of this we learn to use some reasonable part of the full register of man's resources.
We are, of course, an ignorant lot; even the best of us knows how to do only a very few things well; and of what is available in knowledge of fact, whether of science or of history, only the smallest part is in any one man's knowing.
The greatest of the changes that science has brought is the acuity of change; the greatest novelty the extent of novelty. Short of rare times of great disaster, civilizations have not known such rapid alteration in the conditions of their life, such rapid flowering of many varied sciences, such rapid changes in the ideas we have about the world and one another. What has been true in the days of a great disaster or great military defeat for one people at one time is true for all of us now, in the sense that our ends have little in common with our beginnings. Within a lifetime what we learned at school has been rendered inadequate by new discoveries and new inventions; the ways that we learn in childhood are only very meagerly adequate to the issues that we must meet in maturity. {69}
In fact, of course, the notion of universal knowledge has always been an illusion; but it is an illusion fostered by the monistic view of the world in which a few great central truths determine in all its wonderful and amazing proliferation everything else that is true. We are not today tempted to search for these keys that unlock the whole of human knowledge and of man's experience. We know that we are ignorant; we are well taught it, and the more surely and deeply we know our own job the better able we are to appreciate the full measure of our pervasive ignorance. We know that these are inherent limits, compounded, no doubt, and exaggerated by that sloth and that complacency without which we would not be men at all.
But knowledge rests on knowledge; what is new is meaningful because it departs slightly from what was known before; this is a world of frontiers, where even the liveliest of actors or observers will be absent most of the time from most of them. Perhaps this sense was not so sharp in the village—that village which we have learned a little about but probably do not understand too well—the village of slow change and isolation and fixed culture which evokes our nostalgia even if not our full comprehension. Perhaps in the villages men were not so lonely; perhaps they found in each other a fixed community, a fixed and only slowly growing store of knowledge—a single world. Even that we may doubt, for there seem to be always in the culture of such times and places vast domains of mystery, if not unknowable, then imperfectly known, endless and open.
As for ourselves in these times of change, of ever-increasing knowledge, of collective power and individual impotence, of heroism and of drudgery, of progress and of tragedy, we too are brothers. And if we, who are the inheritors of two millennia of Christian tradition, understand that for us we have come to be brothers second by being children first, we know that in vast parts of the world where there has been no Christian tradition, and with men who {70} never have been and never may be Christian in faith there is nevertheless a bond of brotherhood. We know this not only because of the almost universal ideal of human brotherhood and human community; we know it at first hand from the more modest, more diverse, more fleeting associations which are the substance of our life. The ideal of brotherhood, the ideal of fraternity in which all men, wicked and virtuous, wretched and fortunate, are banded together has its counterpart in the experience of communities, not ideal, not universal, imperfect, impermanent, as different from the ideal and as reminiscent of it as are the ramified branches of science from the ideal of a unitary, all-encompassing science of the eighteenth century.
Each of us knows from his own life how much even a casual and limited association of men goes beyond him in knowledge, in understanding, in humanity, and in power. Each of us, from a friend or a book or by concerting of the little we know with what others know, has broken the iron circle of his frustration. Each of us has asked help and been given it, and within our measure each of us has offered it. Each of us knows the great new freedom sensed almost as a miracle, that men banded together for some finite purpose experience from the power of their common effort. We are likely to remember the times of the last war, where the common danger brought forth in soldier, in worker, in scientist, and engineer a host of new experiences of the power and the comfort in even bleak undertakings, of common, concerted, co-operative life. Each of us knows how much he has been transcended by the group of which he has been or is a part; each of us has felt the solace of other men's knowledge to stay his own ignorance, of other men's wisdom to stay his folly, of other men's courage to answer his doubts or his weakness.
These are the fluid communities, some of long duration when circumstances favored—like the political party or many a trade union—some fleeting and vivid, encompassing in the time of their duration a moment only of the member's life; and in our world at least they are ramified {71} and improvised, living and dying, growing and falling off almost as a form of life itself. This may be more true of the United States than of any other country. Certainly the bizarre and comical aspects impressed de Tocqueville more than a century ago when he visited our land and commented on the readiness with which men would band together: to improve the planting of a town, or for political reform, or for the pursuit or inter-exchange of knowledge, or just for the sake of banding together, because they liked one another or disliked someone else. Circumstances may have exaggerated the role of the societies, of the fluid and yet intense communities in the United States; yet these form a common pattern for our civilization. It brought men together in the Royal Society and in the French Academy and in the Philosophical Society that Franklin founded, in family, in platoon, on a ship, in the laboratory, in almost everything but a really proper club.
If we err today—and I think we do—it is in expecting too much of knowledge from the individual and too much of synthesis from the community. We tend to think of these communities, no less than of the larger brotherhood of man, as made up of individuals, as composed of them as an atom is of its ingredients. We think similarly of general laws and broad ideas as made up of the instances which illustrate them, and from an observation of which we may have learned them.
Yet this is not the whole. The individual event, the act, goes far beyond the general law. It is a sort of intersection of many generalities, harmonizing them in one instance as they cannot be harmonized in general. And we as men are not only the ingredients of our communities; we are their intersection, making a harmony which does not exist between the communities except as we, the individual men, may create it and reveal it. So much of what we think, our acts, our judgments of beauty and of right and wrong, come to us from our fellow men that what would be left were we to take all this away would be neither recognizable nor human. We are men because we are part of, but not {72} because only part of, communities; and the attempt to understand man's brotherhood in terms only of the individual man is as little likely to describe our world as is the attempt to describe general laws as the summary of their instances. These are indeed two complementary views, neither reducible to the other, no more reducible than is the electron as wave to the electron as particle.
And this is the mitigant of our ignorance. It is true that none of us will know very much; and most of us will see the end of our days without understanding in all its detail and beauty the wonders uncovered even in a single branch of a single science. Most of us will not even know, as a member of any intimate circle, anyone who has such knowledge; but it is also true that, although we are sure not to know everything and rather likely not to know very much, we can know anything that is known to man, and may, with luck and sweat, even find out some things that have not before been known to him. This possibility, which, as a universal condition of man's life is new, represents today a high and determined hope, not yet a reality; it is for us in England and in the United States not wholly remote or unfamiliar. It is one of the manifestations of our belief in equality, that belief which could perhaps better be described as a commitment to unparalleled diversity and un-evenness in the distribution of attainments, knowledge, talent, and power.
This open access to knowledge, these unlocked doors and signs of welcome, are a mark of a freedom as fundamental as any. They give a freedom to resolve difference by converse, and, where converse does not unite, to let tolerance compose diversity. This would appear to be a freedom barely compatible with modern political tyranny. The multitude of communities, the free association for converse or for common purpose, are acts of creation. It is not merely that without them the individual is the poorer; without them a part of human life, not more nor less fundamental than the individual, is foreclosed. It is a cruel and humorless sort of pun that so powerful a present {73} form of modern tyranny should call itself by the very name of a belief in community, by a word “communism” which in other times evoked memories of villages and village inns and of artisans concerting their skills, and of men of learning content with anonymity. But perhaps only a malignant end can follow the systematic belief that all communities are one community; that all truth is one truth; that all experience is compatible with all other; that total knowledge is possible; that all that is potential can exist as actual. This is not man's fate; this is not his path; to force him on it makes him resemble not that divine image of the all-knowing and all-powerful but the helpless, iron-bound prisoner of a dying world. The open society, the unrestricted access to knowledge, the unplanned and uninhibited association of men for its furtherance—these are what may make a vast, complex, ever-growing, ever-changing, ever more specialized and expert technological world nevertheless a world of human community.
So it is with the unity of science—that unity that is far more a unity of comparable dedication than a unity of common total understanding. This heartening phrase, “the unity of science,” often tends to evoke a wholly false picture, a picture of a few basic truths, a few critical techniques, methods, and ideas, from which all discoveries and understanding of science derive; a sort of central exchange, access to which will illuminate the atoms and the galaxies, the genes and the sense organs. The unity of science is based rather on just such a community as I have described. All parts of it are open to all of us, and this is no merely formal invitation. The history of science is rich in example of the fruit-fulness of bringing two sets of techniques, two sets of ideas, developed in separate contexts for the pursuit of new truth, into touch with one another. The sciences fertilize each other; they grow by contact and by common enterprise. Once again, this means that the scientist may profit from learning about any other science; it does not mean that he must learn about them all. It means that the unity {74} is a potential unity, the unity of the things that might be brought together and might throw light one on the other. It is not global or total or hierarchical.
Even in science, and even without visiting the room in its house called atomic theory, we are again and again reminded of the complementary traits in our own life, even in our own professional life. We are nothing without the work of others our predecessors, others our teachers, others our contemporaries. Even when, in the measure of our adequacy and our fullness, new insight and new order are created, we are still nothing without others. Yet we are more.
There is a similar duality in our relations to wider society. For society our work means many things: pleasure, we hope, for those who follow it; instruction for those who perhaps need it; but also and far more widely, it means a common power, a power to achieve that which could not be achieved without knowledge. It means the cure of illness and the alleviation of suffering; it means the easing of labor and the widening of the readily accessible frontiers of experience, of communication, and of instruction. It means, in an earthy way, the power of betterment—that riddled word. We are today anxiously aware that the power to change is not always necessarily good.
As new instruments of war, of newly massive terror, add to the ferocity and totality of warfare, we understand that it is a special mark and problem of our age that man's ever-present preoccupation with improving his lot, with alleviating hunger and poverty and exploitation, must be brought into harmony with the over-riding need to limit and largely to eliminate resort to organized violence between nation and nation. The increasingly expert destruction of man's spirit by the power of police, more wicked if not more awful than the ravages of nature's own hand, is another such power, good only if never to be used.
We regard it as proper and just that the patronage of science by society is in large measure based on the increased power which knowledge gives. If we are anxious {75} that the power so given and so obtained be used with wisdom and with love of humanity, that is an anxiety we share with almost everyone. But we also know how little of the deep new knowledge which has altered the face of the world, which has changed—and increasingly and ever more profoundly must change—man's views of the world, resulted from a quest for practical ends or an interest in exercising the power that knowledge gives. For most of us, in most of those moments when we were most free of corruption, it has been the beauty of the world of nature and the strange and compelling harmony of its order, that has sustained, inspirited, and led us. That also is as it should be. And if the forms in which society provides and exercises its patronage leave these incentives strong and secure, new knowledge will never stop as long as there are men.
We know that our work is rightly both an instrument and an end. A great discovery is a thing of beauty; and our faith—our binding, quiet faith—is that knowledge is good and good in itself. It is also an instrument; it is an instrument for our successors, who will use it to probe elsewhere and more deeply; it is an instrument for technology, for the practical arts, and for man's affairs. So it is with us as scientists; so it is with us as men. We are at once instrument and end, discoverers and teachers, actors and observers. We understand, as we hope others understand, that in this there is a harmony between knowledge in the sense of science, that specialized and general knowledge which it is our purpose to uncover, and the community of man. We, like all men, are among those who bring a little light to the vast unending darkness of man's life and world. For us as for all men, change and eternity, specialization and unity, instrument and final purpose, community and individual man alone, complementary each to the other, both require and define our bonds and our freedom.
| {76} |
A few weeks ago the president of a college in the prairie states came to see me. Clearly, when he tried to look into the future, he did not like what he saw: the grim prospects for the maintenance of peace, for the preservation of freedom, for the flourishing and growth of the humane values of our civilization. He seemed to have in mind that it might be well for people, even in his small college, to try to take some part in turning these prospects to a happier end; but what he said came as rather a shock. He said, “I wonder if you can help me. I have a very peculiar problem. You see, out there, most of the students, and the teachers too, come from the farm. They are used to planting seed, and then waiting for it to grow, and then harvesting it. They believe in time and in nature. It is rather hard to get them to take things into their own hands.” Perhaps, as much as anything, my theme tonight will have to do with enlisting time and nature in the conduct of our international affairs: in the quest for peace and a freer world. This is not meant mystically, for the nature which we must enlist is that of man; and if there is hope in it, that lies not least in man's reason. What elements are there in the conduct of foreign affairs which may be conducive to the exercise of that reason, which may provide a climate for the growth of new experience, new insight and new understanding? How can we recognize such growth, and be sensitive to its hopeful meaning, while there is yet time, through action based on understanding, to direct the outcome?
To such difficult questions one speaks not at all, or very modestly and incompletely. If there are indeed answers to be found, they will be found through many diverse avenues of approach—in the European Recovery Program, in {77} our direct relations with the Soviet states, in the very mechanisms by which our policies are developed and determined. Yet you will not find it inappropriate that we fix attention on one relatively isolated, yet not atypical, area of foreign affairs—on atomic energy. It is an area in which the primary intent of our policy has been totally frustrated. It is an area in which it is commonly recognized that the prospects for success with regard to this primary intent are both dim and remote. It is an area in which it is equally recognized that this failure will force upon us a course of action in some important respects inconsistent with our original purposes. It is an area in which the excellence of our proposals, and a record in which we may and do take pride, have nevertheless not managed quite to quiet the uneasy conscience, nor to close the mind to further trouble.
The history of our policy and our efforts toward international atomic control is public; far more important, it has from the first aroused widespread interest, criticism and understanding, and has been the subject of debates in the Congress and the press, and among our people. There may even be some notion of how, if we had the last years to live over again, we might alter our course in the light of what we have learned, and some rough agreement as to the limits within which alternative courses of action, if adopted at a time when they were still open to us, could have altered the outcome. The past is in one respect a misleading guide to the future: It is far less perplexing.
Certainly there was little to inspire, and nothing to justify, a troubled conscience in the proposals that our government made to the United Nations, as to the form which the international control of atomic energy should take. These proposals, and some detailed means for implementing them, were explored and criticized, elaborated, and recommended for adoption by fourteen of the seventeen member nations who served on the United Nations Atomic Energy Commission. They were rejected as wholly unacceptable, even as a basis for further discussion, by the three {78} Soviet states, whose contributions to policy and to debate have throughout constituted for us a debasingly low standard of comparison.
This September, the Commission made its third, and what it thought its final, report to the General Assembly, meeting in Paris. It recommended to the Assembly that the general outlines of the proposed form of international control be endorsed, that the inadequacy of the Soviet counterproposals be noted, and that the Commission itself be permitted to discontinue its work pending either a satisfactory prior negotiation between the permanent members of the Security Council and Canada, or the finding by the General Assembly that the general political conditions which had in the past obstructed progress had been so far altered that agreement now appeared possible. The Assembly did in fact accept all the recommendations but one. It asked the Commission to continue meeting. In its instructions to the Commission, however, the Assembly failed to provide affirmative indications of what the Commission was to do, or to express any confidence in the success of its further efforts; in fact, one might dismiss this action as no more than an indication of unwillingness on the part of the Assembly to accept as permanent the obvious past failures of the Commission to fulfill its mandate.
Yet we may recognize that more is involved in this action, that we will come to understand in the measure in which the nature and purposes of our own preoccupation with the problem become clearer. In part at least the Assembly asked that this problem of the atom not be let lapse because it touches in a most intimate, if sometimes symbolic, way the profoundest questions of international affairs; because the Assembly wished to reaffirm that these problems could not be dismissed, that these issues could not be lost, whatever the immediate frustrations and however obscure the prospects. The Assembly was in fact asking that we let time and nature, and human reason and good example as a part of that nature, play some part in fulfilling the age-old aspirations of man for preserving the peace. {79}
In any political action, and surely in one as complex and delicate as the international act and commitment made by the United States with regard to atomic energy, far more is always involved than can or should be isolated in a brief analysis. Despite all hysteria, there is some truth to the view that the steps which we took with regard to atomic energy could be understood in terms of the terror of atomic warfare. We have sought to avert this; we have further sought to avert the probable adverse consequences of atomic armament for our own institutions and our freedom. Yet more basic and more general issues are involved, which, though symbolized and rendered critical by the development of atomic energy, are in their nature not confined to it; they pervade almost all the key problems of foreign policy. If we are to seek a clue to the misgivings with which we tend to look at ourselves, we may, I think, find it just in the manner in which we have dealt, in their wider contexts, with these basic themes.
The first has to do with the role of coercion in human affairs; the second with the role of openness. The atomic bomb, born of a way of life, fostered throughout the centuries, in which the role of coercion was perhaps reduced more completely than in any other human activity, and which owed its whole success and its very existence to the possibility of open discussion and free inquiry, appeared in a strange paradox, at once a secret, and an unparalleled instrument of coercion.
These two mutually interdependent ideals, the minimization of coercion and the minimization of secrecy, are, of course, in the nature of things, not absolute; any attempt to erect them as absolute will induce in us that vertigo which warns us that we are near the limits of intelligible definition. But they are very deep in our ethical as well as in our political traditions, and are recorded in earnest, eloquent simplicity in the words of those who founded this nation. They are in fact inseparable from the idea of the dignity of man to which our country, in its beginnings, was dedicated, and which has proved the monitor of our vigor and of our health. These two ideals are closely related, the {80} one pointing toward persuasion as the key to political action, the other to free discussion and knowledge as the essential instrument of persuasion. They are so deep within us that we seldom find it necessary, and perhaps seldom possible, to talk of them. When they are challenged by tyranny abroad or by malpractice at home, we come back to them as the wardens of our public life—as for many of us they are as well wardens of our lives as men.
In foreign affairs, we are not unfamiliar with either the use or the need of power. Yet we are stubbornly distrustful of it. We seem to know, and seem to come back again and again to this knowledge, that the purposes of this country in the field of foreign policy cannot in any real or enduring way be achieved by coercion.
We have a natural sympathy for extending to foreign affairs what we have come to learn so well in our political life at home: that an indispensable, perhaps in some ways the indispensable, element in giving meaning to the dignity of man, and in making possible the taking of decision on the basis of honest conviction, is the openness of men's minds, and the openness of whatever media there are for communion between men, free of restraint, free of repression, and free even of that most pervasive of all restraints, that of status and of hierarchy.
In the days of the founding of this republic, in all of the eighteenth century which was formative for the growth and the explicit formulation of our political ideals, politics and science were of a piece. The hope that this might in some sense again be so, was stirred to new life by the development of atomic energy. In this it has throughout been decisive that openness, openness in the first instance with regard to technical problems and to the actual undertakings underway in various parts of the world, was the one single essential precondition for a measure of security in the atomic age. Here we met in uniquely comprehensible form the alternatives of common understanding, or of the practices of secrecy and of force.
In all this I pretend to be saying nothing new, nothing that has not been known to all thoughtful men since the {81} days of Hiroshima; yet it has seldom come to expression; it has been overlaid with other preoccupations, perhaps equally necessary to the elaboration of an effective international control, but far less decisive in determining whether such a control could exist. It is just because it has not been possible to obtain assent, even in principle, even as an honest statement of intent or purpose, to these basic theses that the deadlock in attempting to establish control has appeared so serious, so refractory, and so enduring.
These words have an intent quite contrary to the creation of a sense of panic or of doom. Yet we need to start with the admission that we see no clear course before us that would persuade the governments of the world to join with us in creating a more and more open world, and thus to establish the foundation on which persuasion might so largely replace coercion in determining human affairs. We ourselves have acknowledged this grim prospect, and responded by adopting some of the very measures that we had hoped might be universally renounced. With misgivings—and there ought to be misgivings—we are rearming, arming atomically, as in other fields. With deep misgivings, we are keeping secret not only those elements of our military plans, but those elements of our technical information and policy, a knowledge of which would render us more subject to enemy coercion and less effective in exercising our own. There are not many men who see an acceptable alternative to this course, although there apparently are some who would regard it as a proof of the shallowness and insincerity of our earlier renunciation of these ways. But whether, among our own people or among our friends abroad or even among those who are not our friends, these measures which we are taking appear excessive, or on the whole insufficient, they must have at least one effect. Inevitably they must appear to commit us to a future of secrecy, and to an immanent threat of war. It is true that one may hear arguments that the mere existence of our power, quite apart from its exercise, may turn the world to the ways of openness and of peace. Yet we have today no clear, no formulated, no in some measure credible account of {82} how this may come about. We have chosen to read, and perhaps we have correctly read, our past as a lesson that a policy of weakness has failed us. But we have not read the future as an intelligible lesson that a policy of strength can save us.
When the time is run, and that future become history, it will be clear how little of it we today foresaw or could foresee. How then can we preserve hope and sensitiveness which could enable us to take advantage of all that it has in store? Our problem is not only to face the somber and the grim elements of the future, but to keep them from obscuring it.
Our recent election has seemed to touch this deep sense of the imponderable in the history of the future, this understanding that we must not preclude the cultivation of any unexpected, hopeful turnings. Immediately after the election people seemed stirred, less even by the outcome itself, than by the element of wonder; they would tend to say things like: “Well, after this perhaps we need not be so sure that there will be a war.” This sense that the future is richer and more complex than our prediction of it, and that wisdom lies in sensitiveness to what is new and hopeful, is perhaps a sign of some maturity in politics.
The problem of doing justice to the implicit, the imponderable, and the unknown is of course not unique to politics. It is always with us in science, it is with us in the most trivial of personal affairs, and it is one of the great problems of writing and of all forms of art. The means by which it is solved is sometimes called style. It is style which complements affirmation with limitation and with humility; it is style which makes it possible to act effectively, but not absolutely; it is style which, in the domain of foreign policy, enables us to find a harmony between the pursuit of ends essential to us, and the regard for the views, the sensibilities, the aspirations of those to whom the problem may appear in another light; it is style which is the deference that action pays to uncertainty; it is above all style through which power defers to reason. {83}
We need to remember that we are a powerful nation.
We need to remember that when the future that we can now foresee deviates so markedly from all that we hope and all that we value, we can, by our example, and by the mode and the style with which we conduct our affairs, let it be apparent that we have not abandoned those hopes nor forsaken those values; we need to do this even while concrete steps, to which we resort to avert more immediate disaster, seem to negate them.
Our past is rich in example. In that other agony, the Civil War, where the foundations of our government were proved and reaffirmed, it was Lincoln who again and again struck true the balance between power and reason. By 1863, the war and the blockade had deepened the attrition of the South. They had also stopped the supplies of cotton to the English mills. Early that year Lincoln wrote a letter to the working men of Manchester. He wrote:
“. . . It is not always in the power of governments to enlarge or restrict the scope of moral results which follow the policies that they may deem it necessary for the public safety from time to time to adopt.
“I have understood well that the duty of self-preservation rests solely with the American people; but I have at the same time been aware that favor or disfavor of foreign nations might have a material influence in enlarging or prolonging the struggle with disloyal men in which the country is engaged. A fair examination of history has served to authorize a belief that the past actions and influences of the United States were generally regarded as having been beneficial toward mankind. I have, therefore, reckoned upon the forbearance of nations . . .”
Fifteen months later, a year before Lincoln's death, the battle had turned. He could say:
“. . . When the war began, three years ago, neither party, nor any man, expected it would last till now. Each looked for the end in some way, long ere today. Neither did any anticipate that domestic slavery would be much affected by the war. But here we are; the war has not ended, and {84} slavery has been much affected—how much needs not now to be recounted . . .
“But we can see the past, though we may not claim to have directed it; and seeing it, in this case, we feel more hopeful and confident for the future . . .”
In such magnanimity even Grant, at Appomattox a year later, looking beyond the bitter slaughter, looking to nature and to time, could speak to Lee: His troops were to keep their horses; they would need them for the spring plowing.
Each of us, recalling our actions in these last critical years, will be able to find more than one instance where, in the formulation or implementation of policy, we have been worthy of this past. Each of us will mourn the opportunities that may seem to him lost, the doors once open and now closed. Not even in critical times can the sense of style, the open mind, be fostered by issuing directives; nor can they rest wholly on soliciting great actions not yet taken, great words not yet spoken. If they were wholly a matter for one man, all could well rest on his wisdom and his sensitiveness—they neither are, nor can, nor should be. The spirit in which our foreign affairs are conducted will in the large reflect the understanding and the desires of our people; and their concrete, detailed administration will necessarily rest in the hands of countless men and women, officials of the government, who constitute the branches of our foreign service, of our State Department, and of the many agencies which now supplement the State Department, at home and abroad. The style, the perceptiveness, the imagination and the openmindedness with which we need to conduct our affairs can only pervade such a complex of organizations, consisting inevitably of men of varied talent, taste and character, if it is a reflection of a deep and widespread public understanding. That is why, despite their sketchiness, it has seemed appropriate to present these views to a group of interested and devoted citizens. It is in our hands to see that the hope of the future is not lost, because we were too sure that we knew the answers, too sure that there was no hope.
| {85} |
This has been a great century in physics, a century of unexpected, profound, and moving discoveries, and of applications that have changed a great deal in the condition of human life. The last years have seen very great progress in the understanding of essential features of life, and I am confident that the years ahead will teach us more than all preceding history of man about how living organisms perform their miraculous functions and about man as a part of nature. We in physics are still engaged in what feels at the moment like a very great intractable struggle to find out the laws of matter, the nature of matter. It is not of that that I want to speak, but of chapters that are to some extent closed, although questions raised by the answers found earlier in the century are still before us, still wide open. I shall, in this and the second lecture, speak of increases in our understanding, changes in our understanding, of the world of nature. In the third lecture I shall speak rather of changes in the human situation brought about by the developments in physics and other sciences.
Our time is marked by the prominence of the sciences. It is marked by very rapid change and very great growth— growth in science, growth in productivity, growth in population, growth in travel, growth in communication. Almost any statistic that you look at shows a sharp curve with a characteristic of doubling in ten or twenty or thirty years. In the case of the sciences, this doubling occurs in about ten years, and there are several quite spectacular figures which mark it. If you think of all those people who devote their lives to studying nature or applying what has been learned in the technical way and call them scientists, then throughout man's history there have been a number of them and of that number about 93 percent are still living {86} today, so rapidly has the number of people so engaged increased. A friend of mine, in Europe, calculated how fast one of our journals of fundamental physics was growing, and established that if the rate of growth were maintained, then next century the volumes would weigh more than the whole earth. I was called on, not very long ago, by the Scientific Secretary of the Soviet Academy of Sciences, who spent a day with me in Princeton. I believe that his is an important political office, and we talked a little bit about the growth of scientific activity, in which he is engaged as an administrator. I asked him how he saw the future beyond the next five-year plan, say fifty years from now. Without thinking he said, ‘Then all of us will be scientists’; the horror of it came over him slowly and he added, ‘No, not quite.’
Still, in talking of this as a scientific age and thinking of this as a time remarkably influenced by science, we need, I think, to bear in mind two cautions. One is that we probably have no very good idea today of the range of problems which will be accessible to science. We do not know how much of human behaviour may yield in one way or another to the characteristically objective and often rather unexpected study that is a science, and we may today live in something of an imbalance between what we know of the physical world, what we are beginning to know of the living world, and what we know of the human world. I, however, am deeply convinced that the scientific knowledge which may be available about men—not much today—will always be, as is our knowledge of the physical world, very very incomplete and partial, and that the sense of having to live and act in response to tradition, good judgement, and wisdom, which we have now, will not ever be alleviated by any development of the sciences.
I think we need secondly to remember that a great part of the present scene arises not from what we have learned, but by its application in technology. This, in turn, rests on an organization of the economy and to a more limited, but still real, extent on our political arrangements. Neither of {87} these derives from, nor is in any tight way related to, the sciences, because, although the growth of knowledge is largely responsive to human needs, it is not fully so. The existence of terrible and intractable diseases does cause a very wide and intensive study of problems that may be related to the diseases. Problems of agricultural productivity, problems of gadgetry, perhaps most of all problems of military importance stimulate the vigour and increase the support for research. Still it is a profound and necessary truth that the deep things in science are not found because they are useful; they are found because it was possible to find them.
Think of the long centuries in which attempts were made to change mercury into gold because that seemed like a very useful thing to do. These efforts failed and we found how to change mercury into gold by doing other things that had quite different intentions. And so I believe that the availability of instruments, the availability of ideas or concepts—not always but often mathematical—are more likely to determine where great changes occur in our picture of the world than are the requirements of man. Ripeness in science is really all, and ripeness is the ability to do new things and to think new thoughts. The whole field is pervaded by this freedom of choice. You don't sit in front of an insoluble problem for ever. You may sit an awfully long time, and it may even be the right thing to do; but in the end you will be guided not by what it would be practically helpful to learn, but by what it is possible to learn.
I think that to those who are far removed from the life of the sciences, this sometimes appears to be irresponsible. It seems as though having made something potentially pestiferous, like nuclear bombs, we ought to go ahead and find something potentially helpful in getting rid of them. Indeed we ought; but instead it is much more likely that our thoughts will turn to things that are easier to do than that, that are more at hand than that. It is not irresponsibility; it is characteristic of the special way in which one does {88} advance so rapidly in knowledge, for often one may quickly make an irreversible accession to knowledge by establishing an error. Having proved that something is not right, you do not go back to it again; you have learned your lesson. Progress, which in moral and human things is a very elusive word applicable, certainly, to some aspects of our life, but not to all, is an inevitable thing in the sciences. Progress is co-extensive with the existence of the scientific world.
Now the first two of these lectures have to do with just such episodes, where previously held, firmly entrenched errors were with considerable shock and very great grandeur corrected—and in such a way that those errors will not be made again. Moreover, this progress in learning about the world of nature has changed rather profoundly not only what we know of nature, but some of the things that we know about ourselves as knowers. It has changed, to use an old phrase that is beloved of Butterfield, the ‘thinking caps’ of men, as did the revolutions of the late middle ages and the seventeenth century. I may be wrong, but I share with my colleagues, or with many of them, a strong conviction that this experience is one which we would gladly extend beyond the range of limited technical communities. The experience of seeing how our thought and our words and our ideas have been confined by the limitation of our experience is one which is salutary and is in a certain sense good for a man's morals as well as good for his pleasure. It seems to us that this is an opening up of the human spirit, avoiding its provincialism and narrowness. You may think of the example of what it has meant to all of us to learn over the last centuries how different other cultures could be from our own and still in some real sense be cultures.
Progress of this kind is possible only because it blends two almost contradictory traits. The one is a great love of adventure, so that you look for new things and for changed circumstances, look far into the sky, look close into matter, do all sorts of things that take you away from the familiar {89} human experience. That lies on the one hand, and on the other is a great adherence to such order and clarity as has already been attained. One may describe the latter as a sense of conservatism about not giving up any understanding that has been achieved, so that even though you are about to rewrite Newton you are very very reluctant to move very far away from Newton, and even though you may realize that everything that has been said before in physics is only very partially true, you will fight very hard to keep that partial truth. You will be strong through the tradition, and you will use the tradition in describing the new experience until that point comes when you simply cannot go on with it and you have to make a great break.
Many of the men who have contributed to the great changes in science have really been very unhappy over what they have been forced to do. Kepler, who loved spheres, discovered ellipses. Planck, with his famous quantum of action, introduced an element of discontinuity into physics, which seemed to him absolutely intolerably strange and ugly. Einstein, who was able to live with the theories of relativity and regretted only very few aspects of them, also contributed to the development of quantum theory; he proposed the idea of light quanta, but never could reconcile himself to the quantum theory logically built up from this basis. And de Broglie, who discovered that there are waves which are associated with material particles, could never reconcile himself to their interpretation as waves which only represented information and not some disturbance in a corporeal medium.
These changes are forced on physicists somewhat reluctantly because we are both traditional and conservative and at the same time a little too adventurous. In our lifetimes we have seen, in a limited area, our beliefs and our experience radically altered—the popular word is revolutionized, but that is not quite right, for they have been deepened and changed, but not completely overthrown. I have the impression that a general awareness of this and a general experience of it may be of some use in dealing with human {90} problems in a time when the world also is changing so very rapidly.
I have in my enterprise tonight and tomorrow very severe limits; one of them is that especially in physics it is often believed that without the mathematical forms one cannot really say what the discoveries are all about. There is a measure of truth in this; the discoveries could probably not have been made without the mathematical forms which give a quick synoptic and luminous way of representing the order that inheres in nature. It is not surprising that mathematics is involved in nature; it is really a requirement of consistency and the one thing that we are all confident of is that nature may be difficult, but she will not be inconsistent. (It is only we who can be that.) But I think that some understanding of the concepts of physics can be conveyed with very limited use of mathematics, and I propose so to restrict myself. You may think of an analogy. It is certainly better to see Hamlet acted, if it is reasonably well acted, than to read it. It was written to be acted, not to be read in a study. Still, if you read it, you have, with good will and imagination and luck, a good deal of feeling for the meaning of the play. It is certainly a very daring enterprise to try to guess from an English translation what Pasternak's novel is like; but you know a good deal more about it reading it in English than not reading it at all. And I hope that you may, if not at my hands at least in some happier future, feel that mathematics, though a help, is not indispensable for some insight into the essentials of what has been found in modern physics.
In the second lecture, I shall be talking about quite profound changes in our idea of causality, in what we think of determinism in the natural world, and most of all of what we mean and may mean by objectivity. These changes were necessary in order to attain the prize of a reasonable understanding of the ordinary properties of matter, those properties which manifest themselves even when you are not attacking matter with the violence which the great accelerators and the cosmic rays make possible. And in this {91} lecture I want to discuss some changes in the ideas of space and time. Both of these themes are variations on the problem of the consistency of what we know about motion in space and about what is in space, about its field or content.
The quantum theory was the work of many people. I think that we would all agree that Niels Bohr was the heart of this brilliant group. On the other hand, the ideas of space and time, though they go back a long way, were revolutionized in this century by one man, and in some aspects at least it is permissible to think that if he hadn't lived, the revolution would not have occurred. He was Einstein.
The first theory of relativity, at least in the Western world, does not date from the twentieth century. It dates from the thirteenth and early fourteenth, from the Paris school of natural philosophers, of whom Buridan and Oresme are the best known. It was certainly one of the great changes in human thought and it is remarkable because, although it is physics, it did not rest on any elaboration of observational or experimental technique but on analysis and on ordinary common-sense knowledge of how things behave. And it was the opening without which the future development of science is hardly thinkable. This was the discovery: in an analysis of the problem of motion, uniform motion—a body moving with constant velocity— was not something for which you could find or needed to find any explanation or cause; uniform motion was a natural state of matter. Of course, this was not the schoolman's view; it was not Aristotle's view, for whom it was obvious that to keep something moving you had to work on it, and the only natural state was one of rest. The new viewpoint was called the theory of impetus, which we would today say was the theory of momentum, namely that the constant impetus of a body was something that needed no explanation and that all you had to explain was change in its impetus, change in its motion, change in its momentum. This, as you know, was also Galileo's view; and we call the transformation of co-ordinates, which emphasizes this causeless {92} character of uniform motion, the Galilean transformation—although without his permission and without any good historical ground. The idea behind this transformation is that because it involves no cause to have uniform motion there will be a similarity in objects which are in motion with respect to each other. There will be no inherent difference between them. There will be an ability to describe one as analogous to the other. This so-called Galilean transformation tells you how from the co-ordinates x of an object that is at rest at a time t, you can derive the co-ordinates, the time, and the velocity as seen in a system in which that same object moves uniformly with a velocity υ.
|
x' = x + υt, t' = t. |
Suppose you have something at rest and it's at the point x and you are looking at it at a time t. Now suppose you move with respect to it with a velocity —υ. Then the co-ordinate of the object will be given by x’, the time won't be changed, and any velocity V that may appear in the original system will appear as a new velocity V in the new system, V = V + υ. This is the Galilean in variance and it's just common sense. It says the particle simply moves along with its coordinate increasing because it is in motion, the time isn't changed by this velocity, and the velocities add. This theory of impetus is, of course, Newton's first law; and Newton's laws of motion, which describe how accelerations are produced by forces, are invariant under this simple transformation. You cannot distinguish one uniform motion from another by the application of Newton's laws; they are relativistic in the sense that relative motion is observable, but absolute motion is not as long as it is uniform, that is with no acceleration.
From the time of Newton up to the end of the last century, physicists built, on the basis of these laws, a magnificently precise and beautiful science involving the celestial mechanics of the solar system, involving incredible problems {93} in the Cambridge Tripos, involving the theory of gases, involving the behaviour of fluids, of elastic vibrations, of sound—indeed a comprehensive system so robust and varied and apparently all-powerful that what was in store for it could hardly be imagined. I think the only record I have seen of any explicit doubt on the subject of the Galilean transformation and of Newtonian mechanics was about a century earlier than the theory of relativity in a paper of Euler. Because of the relative transverse motion between a fixed star and the earth, you see the star at a slightly different angle than the true direction. Euler found that he did not get exactly the same result when he calculated this variation from the point of view of the star and the point of view of the earth. The difference was totally insignificant experimentally and he didn't say anything more about it. He just noted it.
But early in the nineteenth century and increasingly through that century another study in physics was under way, not having to do with the motion of bodies under gravitational forces, but having to do with the domain of light and electromagnetism. It was not necessary—although today it is—to decide whether gravity was an action at a distance in which one body affected another very far away or whether gravity spread from one body to another. And there was at that time and is today no really good experimental way of distinguishing the two. There are, in principle, very good ways and we feel sure that we know the answer, but we have not yet tried it out. However, with electromagnetic forces the situation is quite different. I think you have all seen what happens when you have a simple bar magnet and some iron filings on a piece of paper. The iron filings assume quite regular patterns, following lines which have something like parabolic shapes around the poles of the magnet. Already in the first half of the nineteenth century Faraday knew about this and his vision was that the space surrounding the magnet, although it had no pieces of matter in it, had something which was physically important present in it, and that was {94} a magnetic field: the power to affect a magnet. Of course, the little iron filings act like magnets and are affected and do respond to this field and make it manifest. In the same way if you have an electrically charged rod or ball and if you come into the near-by area with another charged object with the same charge, you will feel it pushed away a little; if you present an opposite charge, you will feel it pulled in a little. And these are things that happen when the two are not in contact: they arise from a property of the space surrounding the electric charge or the magnet. Faraday talked of these lines and tubes of force, of the electric and magnetic potentials—I don't use this term technically—which exist in space, and for him space became animated with these fields. They were things which anyone could measure: one could measure their directions, one could measure their strengths; they were as palpable as the corporeal bodies themselves, but they existed in a vacuum. Indeed, they exist very well in a vacuum, and have nothing to do with the presence of air; they are modified by any matter if it is there, but they are present without any matter. This picture, of course, is beginning to be the famous aether, the empty space that is capable of having properties.
Faraday showed that if you changed the magnetic field rapidly, you would make an electric field and Maxwell discerned theoretically that if you changed the electric field rapidly enough you produce a magnetic field. This effect was later verified; it is much harder to see than Faraday's result, merely because of practical considerations. In fact, Maxwell predicted that, in the absence of any charges and currents, field pulsations of this kind, in which electric and magnetic fields would generate each other, could propagate freely. He calculated the velocity of the pulsations and found that it was a rather well-known velocity—that with which light propagates.
Thus this field of Faraday's is busy. It not only has fields around charges and magnetic poles—magnetic dipoles {95} really—but it transmits electromagnetic waves. It transmits all the waves which feed the television sets and instruct the rockets and give us our wonderful culture over the radio; it transmits light, it transmits heat; it transmits many forms of very high energy radiation—forms of light which are very penetrating, which play a big part in nuclear physics. (The reality of man-generated long wavelength electromagnetic waves was established late in the last century by Hertz.)
This highly peopled space, full of electric and magnetic phenomena, is related to particles in motion in the following way: if I have a charged object it will, of course, respond to gravity (a universal force), but it will also respond to electric fields and if it is in motion it will respond to magnetic fields. It will feel a supplementary push, the electric field pulling it in the direction of the field, and the magnetic field in general pushing it at right-angles to the field, and to its own velocity. The laws of these effects on charges were reasonably well known at the turn of the century, at least for objects that did not move too fast. But what was very troublesome is that Maxwell's account of the propagation of electromagnetic waves of light and the whole basis of his theory and Faraday's intuitive picture of a space filled with fields was not consistent with the Galilean invariance property.
One can see this from a general viewpoint for, if this space is full of electric and magnetic fields, it need not appear at all the same thing when I move with respect to it. More specifically—and this is really the crux of the difficulty—according to Maxwell's theory the velocity of light is something that is fixed by his equations. His result was very close to the observed measure. But if I move with respect to the medium in which these fields are described by Maxwell's equations then I would expect to apply the formula V' = V + υ, that the velocity which I see for the light is the sum of the velocity with which I am moving (or its negative) and the velocity of light in the medium; it {96} might be bigger or it might be smaller, depending on whether I am moving towards the source of light or away from it. This is a view which was indeed prevalent at the turn of the century, and which was shown by many indirect methods and one very direct experiment, one of the great crucial experiments in history, to be simply not so.
Before this experiment, the situation presented at least three alternatives. First, one might say that there is a system—the system in which electric and magnetic fields are described and exist and obey Maxwell's equations—which is unique, and absolute rest has meaning by reference to that system, and anything in motion with reference to it may have different physical behaviour because of this motion. To accept this alternative is to give up the invariance law and to give up the whole idea of relativity, that is the relativity of uniform motion. The second possibility was to say that Maxwell's equations, in spite of their describing such an enormous range of phenomena, may somehow not be right, and this was extremely hard to do after a half-century of success. And the third was to say: ‘There is relativity and Maxwell is right, but the Galilean equations don't describe the transformations of relativity.’ No one could do that until the situation got really desperate.
And it was made desperate by the Michelson-Morley experiment. In preparing for these lectures I looked up Einstein's lectures in 1921 at Princeton; he said of the Michelson-Morley experiment: ‘I assume its results are known to you.’ I thought I should not quite do that because it was done a long time ago. What Michelson did was to measure the time taken by light to move a moderate distance back and forth in the laboratory and to see whether this was the same when parallel to the earth's motion round the sun and perpendicular to it. The expected differences were quite small, and it took a very great technical virtuosity to be able to look for them. But Michelson did the experiment and he did it over and over again. Now, the earth might just possibly be in the preferred rest system of electromagnetic phenomena in January, but then in June {97} it is moving in a very different direction, and with substantial speed; Michelson's sensitivity was enough to have detected very very easily the motion of the earth, by the change in the velocity of light depending on whether the earth was moving with or against or not at all in this luminiferous aether, the seat of electromagnetic phenomena. He got a null result. This was so unexpected that the experiment, with many refinements and variations, was repeated for decades after that as a witness to the traumatic character of this answer.
So we are not allowed to believe that the velocity of light depends on the velocity of the source. We are not really allowed to doubt that Maxwell's equations are true in all co-ordinate systems and we are not really allowed to doubt that the equations of the Galilean transformation are not a good description—they are only an approximate description—of what happens when we observe a system that is in uniform motion with respect to us. At this point three people found the solution, but only one found its full meaning right away, and that was Einstein.
Einstein said: ‘Let us imagine what the situation would be if we could not communicate with a speed greater than a light signal.’ That is pretty fast (3 × 1010 centimetres per second) by ordinary standards; we would not normally notice this limitation. We would not find that our bicycles were getting away from us. But it is a finite velocity, and that makes a very big conceptual change. If you do not have instantaneous communication and if you want to compare information at two different places, you must make allowance for the time it takes for the message to get back and forth. For instance, suppose you want to synchronize two clocks that are a long way apart. (They should be clocks of the same type, perhaps natural clocks which are more or less guaranteed the same—‘atomic clocks’.) A natural way to synchronize them so that they read the same time would be to set the clock at one place half-way between the time at which the signal left the other and the time at which it was received back after reflection. The {98} notion of simultaneity, which intuitively seems to be something that should not depend on any moving around you do, is indeed a valid notion when things are at the same point of space, but is no longer a valid notion over substantial distances and when relative motions at all comparable to the velocity of light come into play.
This means that if it is true that you cannot send signals faster than light, and if it is a physical contradiction to imagine it, then you have this relativity of simultaneity, this velocity dependence of judgements of simultaneity. Also you have other physical effects which are produced for you by the machines that you use for measuring distance and for measuring time. Let me explain that when I say ‘clock’ I mean something that is designed to measure as accurately as possible regular intervals of time, and when I say ‘distance’ I mean something that you measure with a ruler, which has been by remote comparisons calibrated by a standard metre in Paris. The clocks and rulers then are physical objects.
Now, in order to be consistent with the fact that there is a limiting velocity which is not infinite, but is the finite velocity of light (called by everybody c), the Galilean transformation must be abandoned and replaced by a new transformation called the Lorentz transformation, after the first man who wrote it down. This must provide the co-ordinate of a point x and a time t, when I look at it from a system uniformly moving with a velocity –υ.
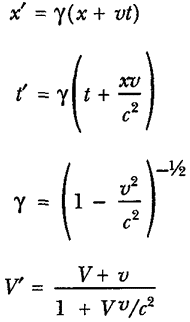
| {99} |
This is a very simple Lorentz transformation; υ is the relative velocity of the two systems, and γ is something which is near one when the velocity υ is small compared to the velocity of light c and which becomes infinite, marking the limit of the applicability of these transformations, as υ approaches c. Moreover, this clearly indicates the limiting character of the velocity of light. You see that it shows that a length interval in one co-ordinate system will appear to be shrunk by the factor 1/γ when examined in a moving co-ordinate system. You see that the time is not told the same in the two co-ordinate systems and that the difference not only has a difference of scale but depends on the positions of the clocks. This is the point about the judgements of simultaneity. And you see further that if you have a process going on which takes a time t as measured in the system where the object is at rest, then if you move at a velocity υ with respect to it, the time will be lengthened, being γt.
To summarize, motion decreases the measurements of length, motion increases the intervals of time, and the two facts together are encompassed in the Lorentz transformation. Further, the formula for the velocity V' indicates that if you add two velocities that are very close to the velocity of light you never get beyond the velocity of light, you just get a little closer to it. This completely consistent system never enables you to talk about or to discuss the properties of relative motion with a velocity greater than that of light, but it does tell you how to talk about real motions in terms of the actual behaviour of actual clocks and rods and atoms and all the rest of physics. These equations give an invariant description of physical phenomena, a description independent of relative uniform motion, one which is as good in one system as in another. This formalism re-expresses the ancient theme of Buridan, that uniform motion requires no cause, but now with this very new wrinkle that couldn't have been anticipated on the basis of ordinary experience, that, because objects cannot be accelerated beyond the velocity of light, the analogue of an infinite velocity is a finite velocity. {100}
From this viewpoint one naturally asks that not only Maxwell's equations of electromagnetism but the equations of motion for charged particles and then also for neutral particles should be invariant, i.e. that they should have the same content, irrespective of the frame of reference in which we describe the phenomena, as long as we are talking only about uniform motion. We do that naturally in talking of ordinary things. If there is a complete symmetry in a problem, so that no direction is singled out, then we certainly would like to talk about it in such a way that that symmetry is preserved in our description; and if there is nothing in space to make one point different from another, we would like to give a description which is as valid in Chicago as it is in Hamilton. And in the same way here we would like a description valid irrespective of the relative velocity of the objects we are talking about and what we ourselves happen to be doing while we are looking at them.
This was done for mechanics and gave at once the rather clear sign that Newton's equations are wrong. This is clear a priori, because if the acceleration is proportional to the force and inversely proportional to the mass, there is no reason why you cannot make velocities bigger than that of light. Something must prevent those forces from being so effective, and what it is, to put it a little oversimply, is that the mass of a body is not in fact constant. Indeed, if the theory of mechanics is to be compatible with the requirement of the constancy of the velocity of light and relativity in this restricted sense—the mass of a body must increase with its velocity in just this way:
m = |
m0 √1 – V²/c² |
. |
Here m0 is the mass of the body at zero speed and m its mass at speed V. This is the origin of much fertile speculation by Einstein, because if the mass of a body increases with its velocity so does its kinetic energy and it will increase in the same way, viz:
ΔT = c2Δm.
| {101} |
The symbol ΔT means the change in kinetic energy and Δm represents the corresponding change in mass.
Because the total energy is really something that is not lost or gained by a system, but is conserved, what is true of kinetic energy must be true of all energy and, therefore, a change of energy and a change of mass go hand in hand and the change in energy is related to the change in mass by the square of the velocity of light. This is something that it would be nice to have a little mathematics or more time to show; but it is a direct and really quite inescapable consequence of the purely kinematic connexions which I have written down as the Lorentz transformation.
Another important point is that these transformations mix up space and time very much more than the Galilean ones. To a limited extent you cannot interchange space and time. They have inherently different character. A watch is a watch and a ruler is a ruler and you cannot use the ruler to measure the time and the clock to measure the co-ordinates. But they do change with relative motion. Of course, you are not restricted to move in a straight line with respect to something you are studying: you can also turn around or you can take another place in space. This whole set of procedures—rotation, translation (moving to another origin, that is another base point), and moving uniformly in some direction—together are a set of operations that are closed and form the Lorentz group. You cannot, with these operations, convert any space-like interval into a time-like interval or any time-like interval into a spacelike one, but you can change the ‘direction’ of a space-like interval and give it some slightly more time-like quality, and you can do the same thing for time-like intervals.
This system, this special theory of relativity, which predicts correctly the behaviour of rods and clocks under motion, became an absolutely all-pervasive feature of physics. We use it literally in almost every branch of nuclear physics and many branches of atomic physics, and in all branches of physics dealing with the fundamental particles. It has been checked and cross-checked and counter-checked in {102} the most numerous ways and it is a very rich part of our heritage. For instance, many of the particles that are produced in the atmosphere by cosmic rays are unstable. They have a natural tendency to come apart into others, to decay. But if they move very fast, their decay rate is slowed down and the rule is simply:
τ' = τ(1 – V2/c2)½ = τ/γ
where τ is the decay rate when the particles are at rest and τ' is the decay rate when they are moving with speed V. This is observed and is a very vivid thing. We have not yet seen people stay young, but we have seen particles stay young by the billions.
There is another point, a little out of chronological order. I have spoken of rotations, translations, and uniform motions as part of the Lorentz group, but there is another part of the Lorentz group that is not so simply connected with these operations. You cannot rotate your right hand into your left. The only way you can get the one to be congruent to the other is with a reflection in a mirror. You may try wiggling your hands about, but it is really not possible to rotate one into the other. One would think that if rotation did not make any physical difference, reflection would not either, that if space were so isotropic that there was no direction singled out in it, then it would not matter if something were right-handed or left-handed. The two arrangements would be equally probable—there is a good deal of this accidental character in human asymmetries. This invariance law was believed for at least thirty years. Many many brilliant examples turned up where you could classify the states of atomic and nuclear systems according to whether they were unaltered by reflection or whether their symbols changed sign under reflection; in both cases you may say that to any allowed motion or phenomenon in physics, the mirror image also is allowed. If you can have something happen with a wheel turning a certain way and an arrow pointing up, then keeping the wheel the same, but reversing the arrow, which is what happens when you {103} hold up a mirror, will also be allowed. Such objects do exist in physics; in fact the neutrino is a very good example of one. It is only a few years ago that some doubt arose as to whether this rule was strictly true—the rule, that is, that to any system found in nature, the mirror image must occur, being compatible with the laws of nature. The doubts were sufficiently anxious and deep that Lee and Yang looked into it and found that no proof of this rule had been really given experimentally in a certain class of very feeble forces and very slow reactions. And so they looked—not they but their friends—and the answer is that nature has, in this special manifestation, a most violent and total prejudice in favour of right-handed and against left-handed arrangements and the other way round in other cases. It is very odd, very unexpected, and possible only because you cannot get from a rotation or a translation to a reflection. What we now more or less believe is that if any configuration is allowed, then if you take its mirror image and replace all the positive charges by negative and vice versa, and let it run backward in time, that will also be allowed. But that is all we are really confident we know.
This theory of relativity has been very much mixed up in all the developments of physics. I would stress that the odd and often seemingly paradoxical things that are embodied in the special theory of relativity are not paradoxes in the sense of being conflicts between different experiments. They do not involve any contradiction on the part of nature; what they do involve is a gross change, a rather sharp change, from what learned people and ordinary people thought throughout the past centuries, thought as long as they had thought about things at all. The simple facts, namely that light travels with a velocity that cannot be added to or subtracted from by moving a source of light, the simple fact that objects do contract when they are in motion, the simple fact that processes are slowed down when they take place in motion, and very much so if they move with velocities comparable to the velocity of light— these are new elements of the natural world and what the {104} theory of relativity has done is to give coherence and meaning to the connexion between them. These contractions of objects and these retardations of events are, of course, reciprocal; and that is a little paradoxical. It is a little hard to think that, if a moving chunk of matter gets flatter and flatter in the direction in which it is moving, and if you happen to be with that chunk of matter, you would get flatter and flatter if you looked at yourself where you originally were. But it is true; and the same kind of thing is true about time; this is the origin of the twin paradox. It is true also that when there are changes in mass, there is in practical terms a corresponding enormously big change of energy, as we know, both to our hope and our caution. We are not sure that in approaching the domain of the very small (and I am here not now talking of ordinary atomic dimensions, but dimensions some million times smaller), we know exactly what it means to say that ‘nothing’ can move faster than light. But we are sure that our doubt is not with moving faster than light; our ambiguity is with ‘nothing’—we do not quite know what that means in this domain.
I come now to a generalization of the theory of relativity, which starts when you begin to think about motions which are not uniform, and goes on to consider the nature of gravity. General relativity has very very few connexions with any other part of physics and, as I said, is something that we might just now be beginning to discover, if Einstein had not done so more than forty years ago. This is partly because, compared to electricity, gravity is a very weak force and really manifests itself only when you are dealing with bodies that are pretty substantial, such as the earth, the sun, and smaller things, but not on an atomic scale. Consequently, it is rather inaccessible to experiment, because the objects you deal with are big and not things you can wiggle around very much. You might think that gravitation should resemble electricity in producing fields which exist in the vacuum, which can be measured, and which propagate with the velocity of light. Something like this is {105} true, but there are two enormous differences. One sign of a difference is that like charges repel each other, like masses attract, and this means the two cannot be really quite the same. Another is that gravitation is a quite universal phenomenon; all bodies follow the same pattern when they are acted on only by gravity: this was Galileo's principle of equivalence. However, if you follow out the attempt, and this has only been done in the last year or so, to make a theory for gravity as much like the theory of electricity and magnetism as you can, you find that, quite apart from the rigorously predictable effects of uniform motion on the measurement of space and time, gravitational fields have much deeper and much more tangled effects on the behaviour of rods and clocks.
If you study this further, you have to come to two conclusions, that in important ways gravitation is a very different thing from electricity and magnetism. First, the rods and clocks are so affected that the space that they measure out, which is always flat if you look in a small region of space in a small interval of time, manifests over bigger regions curvature like the surface of a two-dimensional egg. This curvature may vary from point to point and is itself an expression of the gravitational effects which are in this space. And second, because gravitation, like electro-magnetism, involves potential energy and because gravitation is produced by all mass, and therefore, by all energy, gravitation produces gravitation and gravitational fields are not linear in the sense that if you have two gravitational waves they do not merely superimpose their effects, but they interact. Also, if you have a gravitational wave and a gravitational field around the sun they interact. All of this can be found out in a sort of pedestrian way by making the analogy with electricity and magnetism.
But for Einstein it was entirely different. He came at it from two points. One was the universality of motion in a gravitational field which enabled him to think that this might be a geometric thing. The second was the fact that the principle of relativity, philosophically, ought not to be {106} limited to uniform motion. If there is nothing else around, how can you tell if something is being accelerated or not? You can only tell that by reference to something that is not being accelerated. But we know that accelerated motion differs from uniform motion in that we do not have to be told when we are undergoing it, because we feel it and phenomena do respond to it. Einstein observed that a uniform acceleration is exactly the same thing as a uniform gravitational field in all its physical effects. This is another principle of equivalence. And he, therefore, was led to the idea that the problem of dealing with non-uniform motions and the problem of explaining gravitation were related and indeed identical.
If you are moving in something resembling free space you really cannot tell how fast you are moving unless you refer your motion to something else, to the earth or the sun or the stars. But if you are moving in a jerky way, if you are being made to move faster, being accelerated or slowed down, you can have all the blinds drawn, you cannot know where anything else in the world is, but you still can tell that something is going on and you can measure it. And, therefore, there can be no elementary possibility of talking about general motions, motion on a circle, motion which speeds up and slows down, motion on a bumpy railroad train being relative, because within the moving thing (this railroad car or elevator or rocket) you can tell by the way you feel, and you can look at gauges to measure that you are being pushed, pulled, hauled around, jerked, whatever it is. One could, therefore, say that relative uniform motion is indeed relative and no law of nature must discriminate in favour of one such motion rather than another, but that the elementary fact about accelerated motions is that, at least in the part of the universe where we live, we can tell whether we are being jerked around or not, and such motion is not relative. Nevertheless, Einstein's theory of accelerated motions is called the general theory of relativity; it is a very unfortunate terminology. One might almost say that this should be called the general theory of unrelativity, {107} except for one clue, a very deep clue, that was known before, but was understood and made very prominent by Einstein.
If you are confined to a box from which you cannot look out and in which you can make only internal measurements, and if you feel a uniform acceleration, you cannot tell whether you are being speeded up by some force acting directly on the box, or whether you are feeling a uniform gravitational field. The simplest way to confirm this is to fall freely and notice that when you fall freely there is no gravity and there is no acceleration; you are, in fact, accelerating, and you are, in fact, in a gravitational field, but the two of them cancel. You should not achieve this state by jumping out of the window, but if you ride in airplanes enough it will be done for you. Therefore, Einstein understood that one could deal with a more general class of motion only if one also encompassed the phenomena of gravitation. I should say that this principle, that gravitational fields and accelerations are in large measure equivalent to each other, is often called the equivalence principle. It is closely related to Galileo's principle that if the only forces involved are gravitational, all bodies move in the same way. If Galileo's principle were not so, you would not be able to replace gravitation by an acceleration which clearly is the same for all bodies. In the way Einstein did this, the theory of gravitation and the theory of general motions were indissolubly linked.
But one could go about it in what appears to be a more straightforward way, and, in recent years, this less beautiful approach has been developed. One could say that gravitational forces, like the electromagnetic forces, are long range, in that they fall off slowly with distance, and that this suggests that one make a theory of gravitation, which is a natural analogue of the intuitive pictures of Faraday and the equations of Maxwell which describe electromag-netism, electromagnetic waves, and the fields around magnets and charges. The principal point of difference for which one must allow from the beginning is this: that two {108} like charges repel each other, whereas all masses attract each other. If you do this you get a description which reproduces Newton's theory of gravity if fields are not phenomenally strong—and there may be no strong gravitational fields in the world—and if in addition they don't change rapidly with time so that the finiteness of the limiting velocity (of light) plays no part. In this theory one has both principles of equivalence, both that of Galileo and that of Einstein. And one has some famous physical consequences which also were predicted by Einstein. For instance, both theories predict that when light falls in a gravitational field it turns bluer; it turns from red to blue, as frequency increases, and the wavelength decreases. The most precise and, I think, by far the most beautiful example of this is a recent experiment conducted at Harvard in which light was simply allowed to fall down from the third floor to the basement of the Physics Building. One could see how much bluer it had become: one part in 1014: not very much. Also, as Einstein predicted, and as had been guessed before, light is deflected when it passes through a gravitational field, near the sun, or, for that matter, near a star. And you also find, as I have already mentioned, that a gravitational field induces more gravitational field, unlike the standard case of light.
Finally, and perhaps most importantly, if you develop this analogy between gravitation and electromagnetism, you find one very major and deep difference. This is the point where really to explain where the difference comes in would take not a little, but a lot of scribbling on the blackboard, but to explain what the difference is, I think, does not. I shall use the word ‘space’ to mean both the three-dimensional space that we usually mean and the extension in time which we have learned to see is not sharply and totally separable from spatial intervals, because they get mixed up when you look at things in uniform motion. You find that if you explore space with ordinary rulers and clocks, this real space is not the space of Euclid, it is not the space of the classical geometers, but it has some structure {109} and some distortion built into it. This is not the space you imagine on paper; it is the space which you measure, typically, with rods. Now it is very hard to think, at least for me, about four-dimensional continua, especially when one of them is not a distance but a time, but it is legitimate to think of an ordinary two-dimensional surface and suppose that the four-dimensional affair is just a mathematically similar abstraction—just as easy to discuss mathematically but much harder for people to visualize. Then what we have been saying is that we are not dealing with the analogue of a plane surface, but with the analogue of something curved in a rather peculiar way. Locally, in a small enough region, any curved surface, if it has no ridge in it, is flat and it looks like a plane; but if you move along it for some distance, the inherent distortion of the space becomes clear; for instance, the sum of the angles of a triangle will not be a straight angle and Pythagoras's theorem will not be true, and all sorts of geometrical complications will be induced. When you have a sufficiently vigorous and wild gravitational field, such distortions will occur in the nature of space and time, and can be detected by actual measurement. From this it then follows that if you accept the gravitational analogy of electromagnetism you are led to things that have no parallel in electromagnetism; and, if you have your eyes open, you reach Einstein's theory, or something very like it and close to it.
But Einstein, forty-five years ago, did not do this. He developed his description of gravity on the basis of a few rather general ideas. One is that gravitational forces are determined by matter and express themselves in the geometry of space and time. Now, what are the determining aspects of matter? Not its colour, for example, but those aspects that are most clearly related to its mass, energy, momentum, or impetus and related things which form a unitary description of matter. I should say, in this context, that electricity and magnetism, because they have energy, also contribute to gravitational fields. The second important point is that the inherent properties of the geometry {110} wholly determine the gravitational forces that act on bodies. We use the word ‘inherent’ to stress that we are not concerned with how you describe the geometry in terms of co-ordinates, but with those properties which constitute the structure of space and time. So that you have on the one hand that the inherent geometry is determined by the distribution of matter and, on the other, that the response of matter to gravity is determined entirely by the geometry. In fact, matter moves as nearly in a straight line as the crinkly character of the geometry permits. These are the two basic points of Einstein, but they would not lead to anything very definite. In a way which is quite characteristic of physics and which will recur later in these lectures, Einstein also had in mind limiting situations where he knew the right answer. One was the gravitational theory of Newton, which is right, as I said, when fields do not vary too much with time and when they are not overwhelmingly strong. The other is that space and time, if you look at a sufficiently small region, must be flat, and in such a region must be described by the Lorentz space of special relativity. Those are four elements, we may say four of Einstein's postulates; and the fifth one is the one that nobody can ever translate: the theory must be a simple thing. And here it seems to me we really are faced with the fact that only by inventing the right notation and using the right mathematical ideas can you say whether something is simple or not. With a good deal of fumbling, and many years of unsuccessful trying, many years in which the physical ideas which I have just outlined were clear, Einstein finally came upon a branch of mathematics that other people had made and which gave him the perfect vehicle for writing down how it goes with gravitation and what the general theory of relativity is. And no one today, plodding along to remake this theory along more pedestrian lines, can fail to be overwhelmed by the imagination, the daring, and the beauty of what Einstein did. It is a very different thing to say whether this is a correct theory. {111}
It is, of course, correct in all those particulars which I have talked about, but there is very little experimental evidence about the features of the theory which are peculiar to it, and which have nothing in common with electromagnetic theory, with flat space time, or with Newton's theory. We may be a long time wishing that we knew, but I have never known a physicist who did not think that it was probably a very very good guess indeed. And there is not a shred of evidence against it. We have for space and time not finished with the story. What will come is not my business to try to say, but on two fronts there are wide-open questions.
One is on the scale of the very big, encompassing everything that we see with telescopes and that we hear with radio telescopes. That means more than the distance that light can travel in five or ten billion years, which is about where the present limit lies. We see the universe flying apart; we do not see anything very detailed about its spatial structure. And it is a completely open question, not answered now and conceivably never to be answered, whether the volume of space (I am not now talking of time) is a finite or infinite thing. Einstein thought it was finite, but that was because he thought that everything was steady and static. When we look we see that the motion is the characteristic feature; the further away we look, the faster things are receding from us, and in such a world we have no insight into whether this will stop and there is a finite distance to look or whether it will go on for ever and ever.
Another kind of open question I referred to earlier, and that is that when we get to dimensions so small that they are not of the size of atoms, not even of the size of nuclei, but of the size of those objects of which nuclei and atoms are composed, we cannot really be sure to what extent we can discriminate near-by points in space and time and to what extent the designation of such points is still meaningful. But I will say one thing. Here there is no question of curvature of space because gravity is an utterly negligible {112} force, and we assume that here, too, the velocity of light is a finite limiting velocity imposed on all physical disturbances or signals. From this assumption a great deal can be made to follow, and, so far, nothing that follows from it has shown itself to be in conflict with experience. It is one of the powerful tools of modern-day physics.
| {113} |
The subject of my lecture tonight is really the quantum theory. It has two parallel and even complementary historical origins. One is from the properties of electromagnetic radiation, but from other properties than those which were important for relativity. The other is from an attempt to understand the structure of atoms. I mean by the structure of atoms the atoms of the chemist and the spectroscopist, and not the atoms of the physicist who works with a giant accelerator and who smashes everything that he looks at with his violent collisions. This subject is also interesting but it has been opened up really only in the last decades, and is not understood, whereas the quantum theory was very much a complete theory thirty-five years ago. As to the properties of electromagnetic radiation, I need first of all to come back with a little more than just words to the idea that a changing magnetic field makes an electric one, a changing electric one makes a magnetic one, and that this pumping cycle produces an electromagnetic wave. These waves have certain important, deep, but rather abstract properties, in common with everything else that physicists call waves. A typical electromagnetic wave may have the electric force changing with time periodically, so that it is sometimes positive and sometimes negative, that is, sometimes pointing, let us say, in the positive direction, sometimes in the negative, and going through zero as it changes from one to the other; the magnetic force is doing the same thing at right-angles to the electric force and out of phase with it, so that when the electric force is zero the magnetic force is a maximum, and the whole thing is travelling at right-angles both to the electric force and the magnetic force with the velocity of light. That is one kind of electromagnetic wave and for us it is plenty.
| {114} |
 |
c = υλ |
Such a wave is characterized by three numbers: the wavelength A., the frequency υ, and the velocity. The wavelength is the distance from crest to crest of the wave, that is the distance from one point where the electric field is a maximum to the next point at which it is a maximum. The frequency is the rate at which the electric field changes with time at a given point. The product of these two is the velocity of the wave—for an electromagnetic wave, this is the velocity of light, and we write c = kυ. More generally, we can define in a similar wave the wavelength and frequency for a sound wave, or a water wave, and their product is the velocity of the wave, that is the speed of sound and the speed of progress of the crest of a water wave respectively.
Now the important part of a wave motion, which is true of electromagnetic waves, sound waves, or water waves, and is indeed very easy to observe with water waves, is that if you have two waves more or less in the same part of space and time, they affect each other so that the disturbances add. For example, the electric field that comes from having two electromagnetic waves is the sum of the electric fields of the separate waves; so is the magnetic field. That means that I may have another wave that is added to a given one in such a way that the electric fields add or in such a way that they cancel, depending on how they lie with respect to each other. An important point is that the intensity of light or electromagnetic radiation, the energy it carries, and many of the effects it produces are proportional not to the electric field but to its square. Looking at the diagram, you see that waves can interfere with each other
| {115} |
 |
(a) Two waves cancelling to give zero disturbances |
 |
(b) Two waves adding to give a disturbance larger than either |
both by adding and producing twice the height of the wave and therefore four times the intensity, or destructively, according to the upper curve (a), so that where one wave is big and positive, the other wave is big and negative, and you get zero for an answer. These are the general phenomena of waves which I need to presume, I hope not wholly irresponsibly, that I have told you about, and which we shall be using all evening in our discussion. We must remember that these properties are true of all waves—water waves, sound waves, and all electromagnetic waves, from those that one uses for the longest wave radio transmission through microwaves, through heat, through light, through ultraviolet light, through X-rays, and up to the highest frequencies there can be.
One consequence of this wave property is that light which comes through different paths may interfere and I will give just two examples of that; one of which we will have to return to.
The sketch shows a source S, a diaphragm with very thin slits in it, and out of these slits diverging waves of light. The curved lines represent the crests of these waves: where the crests coincide you will have particularly intense light; where the crest and a trough coincide you will have none at all. You see that the presence of the two slits gives rise to a pattern of brightness and darkness, which either slit alone would not explain and which is characteristic of {116} the wavelength and the separation of the slits. If there were a large number of slits, all spaced the same distance apart, then light would only move in certain directions from this collection of slits, which is called a grating, and these directions are simply related to the ratio of the wavelength and the separation of the slits.
Now, a century of experimentation showed how beautifully the phenomena of the propagation of light—its reflection, its passage through slits, its diffraction from gratings, its dispersion—could be explained in terms of these simple ideas of the interference of waves. There is not to this day the slightest doubt that this is a correct description; it is used every time a radar antenna is designed and any time that one really wants to deal with electromagnetic radiation and its propagation around objects; the light or radio waves from different gaps are brought together and give a resultant intensity depending on the relative phases of the interacting waves. In this case the waves are abstract in the sense that there is no matter moving and, by Chapter I, no aether moving either; but they are concrete in the sense that there are electric and magnetic fields, the ones that Faraday dreamed so much about, which you can measure; every one of these crests corresponds to a measurement of a big electric field at a certain time, and every trough corresponds to a big magnetic field at a certain time. (These measurements would {117} be extremely tedious to do with light, but with long radio waves it is a straight-forward experiment that does not teach you very much, but confirms your sanity.) Now, it was exactly at the turn of the century that this harmonious picture of the nature of electromagnetic radiation received a sharp jolt from which it has never recovered. To explain this, it would be easier to skip history entirely, but I will say how Planck discovered it.
When you have a gas of molecules each molecule has, on the average, about the same energy as every other and this energy is a simple measure of the temperature of the gas. If you have electromagnetic waves in an enclosure you can convince yourself that every wavelength should also have about the same energy as every other, and this energy is equal to the temperature of the matter which forms the enclosure and is emitting the waves. This is, on the face of it, absurd, because the theory of relativity says that there can be no limit on how short wavelengths are since all you have to do to make them shorter is get on a fast train, and they will be shorter. Therefore, there will be an infinite energy content to any piece of space that is allowed to come into thermal equilibrium. Energy would simply drain out of matter and everything would be absolutely cold, because all the energy would go into the electromagnetic field. This, it was known, is not true. In struggling to find out why, Planck had a very great advantage. He knew that, for very low frequencies of the light waves, this rule that all the light waves in the enclosure had the same energy was right. He knew that for very high frequencies something quite different happened, and the energy that a wave had was the energy that would be required if one had to create a quantum of energy given by the expression hν. He introduced the constant h to connect these two regimes which had earlier been studied; it has always since been called Planck's constant. It is, as you see, a constant which, when multiplied by a frequency, gives one an energy, and it will recur; it is the signal, the mark, of atomic physics and is called the quantum of action or Planck's constant. Planck {118} was able to derive a formula which reconciled this behaviour of the equilibrium properties of the enclosed radiation, and also to determine a reasonably accurate value of his constant, but only by employing the technically possible assumption that light was not emitted continuously as a wave should be, but only in energy packets, which correspond to a multiple of the frequency, viz. hν. He did not believe this, and for many many years struggled to get his formula without making this dreadful assumption which contradicted the whole idea of light as a wave. Because here it was being said, not that light was emitted, like radio waves, simply by charges moving around, but that light was emitted in a whole single operation with a unit of energy, and if that amount of energy could not be emitted, nothing happened; if that could be emitted, it happened; if it could happen more than once, it happened more than once. Well, in this very statistical and complex and dark area it was possible to suppose that Planck had made a mistake, and he lived for years in the confident hope that he had made a mistake.
But he was wrong; and a great blow was struck to his hope when, in the same year that Einstein made the special theory of relativity, he made another paper, which was to prove even more mischievous. The second paper is very closely related to Planck's discovery. If you shine light that is not too red on a metal surface, electrons, which are part of the metal, will come out of it. The very odd thing which had been found in the laboratory was that if you shine the light twice as strongly it does not affect the velocity of the electrons; rather, it affects their number. But, of course, if you are thinking of light as an electromagnetic wave and the wave is more intense, you would expect that the electrons would have more work done on them. But not at all. The energy of the electrons is unrelated to the intensity of the light, but very simply related to the frequency of the light and to Planck's constant.
E = hν – B
| {119} |
The light energy hν is the same energy that Planck had introduced five years earlier, E is the energy of the electron as it moves away from the metal and B is not fundamental: it is the work that you have to do to get the electron out of the metal in the first place. This formula has been very accurately and beautifully confirmed. And Einstein said: ‘This clinches it. Obviously there are units of energy in light.’ When light is absorbed by an electron, it happens in multiples of these units hν, and then the energy is simply carried off by the electron and that explains the formula.
But, of course, this did not do away with the century of experiences on wave phenomena. Interferometers and prisms, microscopes and radio waves still studied light in terms of the propagation of waves. On the other hand, here was this discontinuous particle aspect, at least to phenomena in which light was absorbed or emitted, which could not be laughed away. Moreover, this was even confirmed by experiments with very hard light, viz. X-rays. In fact, when they collide with electrons, they act as though they had the energy given by E = hν and a momentum, or impulse, p = h/λ, which is just h, the same constant, divided by the wavelength. Thus one could see that light acted in collision with electrons like a particle with a momentum and an energy related to its frequency and wavelength by these very simple rules, consistent with the rules connecting energy and momentum for an electromagnetic wave, but involving both this constant h, and a discrete transfer of energy and of momentum from light to electron in a collision between the two. This experiment, called the Compton effect, had led to a very serious and critical view as to the dual nature of light by about 1923.
Probably the situation could not have been readily understood had it not also been compounded by another and equally puzzling aspect: this time not directly the behaviour of light, but the behaviour of matter on an atomic scale. Let me remind you that, just before this century, Thomson discovered the universal ingredient of ordinary {120} matter, the negatively charged electron which is very light compared to the atom, some 1/2,000th as heavy or less, and which has the unit of charge which we find uniquely throughout the atomic world. Thomson rightly imagined that the number of electrons in an atom was connected with its chemical properties and its place in the periodic table, so that atomic hydrogen would have one electron, helium two, uranium—92. He knew the atoms were neutral, but he did not know where the neutralizing positive charge was; and his best guess was that it was probably extended over a volume of the order of the size of atoms, that is a sphere l/100th of a millionth of a centimetre in diameter. This was the Thomson model of the atom, and it raised no problems, because it was a rather vague model, and you could not do very much about it. But Thomson was able to show that some regularities, like the occurrence of regular numbers and periods, such as occur in the periodic table, might be expected from such a model. However, this model did not last long, because of the work of Rutherford, which started at McGill, continued at Manchester, and was finally brought to fruition there. Rutherford showed that positive charge of an atom was not spread out over atomic dimensions.
How he did this is itself very beautiful. He had been studying naturally radioactive radiations, coming from uranium, radium, and related heavy elements; he got their family relationships straight and decided which chemical elements were produced by the natural decay of which other elements and which disintegrations followed which; he had distinguished three types of radiation: positively charged and heavy, which were the nuclei of helium and which he called α-particles; negatively charged, and light, which were electrons; and neutral, which were very high frequency light. He did not at first know that α-particles were helium nuclei, but he thought they were, and he became interested in what happened to them, as they passed through matter. They did not do what they would if atoms had a uniform smooth positive charge, and very {121} light electrons located within it, as suggested by the Thomson model.
In that case there could never be a big force to deflect the α-particle, because the smooth charge does not have sufficiently concentrated electricity and the electrons have much too little mass to knock an α-particle around, for it is 7,000 times as heavy. But he found that indeed the α-particles were, not often but regularly, deflected through very big angles indeed, and from this he concluded that the positive charge was concentrated, and that it was concentrated, along with most of the mass of the atom, in a region with dimensions smaller than 1/10,000th of atomic dimensions. And so he discovered the atomic nucleus which has the positive charge which gives the atom its chemical and most of its physical properties.
This was a marvellous story, but it was only the beginning of really very great puzzles. Think of the simplest of all such atoms, the hydrogen atom. It has a proton, one nuclear particle, at the centre with a unit positive charge, and somehow there is an electron associated with this to make up a system which has a well-defined size. The size is standard; unless the hydrogen atom has been through a wringer or been hit over the head, it always is the same. And it emits a certain characteristic batch of colours when you bash it. Not one of these properties could be intelligible on the basis of Newton's ideas about motion and the idea of how charged particles affect each other, because Rutherford had proved that the field around the proton was the electric field. This field is in its form exactly like the gravitational field around the sun: the forces fall off with the inverse square of the distance and they all point towards the proton, for in this case they are attractive, since the electron and proton are oppositely charged. Consequently, it is just the problem of the planetary motions all over again. Now, one obvious thing that we know about planetary motions is they can be more or less anything: any ellipse, in any plane, with any eccentricity, and any size. Therefore, it is most odd that all hydrogen atoms should {122} have the same size and act in the same way. There is no trace in classical physics of any reason why each hydrogen atom should not be of a different size and shape and behaviour than the next or any other.
Furthermore, although I have not gone into this in detail, we know that if we have a charged particle describing a circular or elliptical orbit, it is accelerated, and an accelerated charged particle will make light waves and lose energy. But hydrogen, unless it is bashed, does not do anything of the kind. It can sit for years and centuries quite content without ever changing. It does not lose its energy and the electron does not spiral in and disappear into the nucleus. And finally the laws relating the colours of light that are emitted from such a classical orbit are a little more complicated, but similar in form to the laws determining the sound frequencies produced by a violin string. There will be a fundamental which is connected to the period of revolution of the electron in the orbit and there will be overtones or harmonics, i.e. multiples of this frequency; whereas the observed frequencies for atomic spectra, hydrogen included, are not harmonics or integral multiples of a fundamental frequency, but rather complicated arrangements of differences between numbers which are not harmonically related. To be specific all the observed frequencies can be written as
ν = νi – νj
when νi and νj are two of a sequence of numbers ν1, ν2, ν3, . . . In the case of hydrogen, these numbers had been recognized by Balmer, and in general they characterize the atom in question. In other words, the uniqueness of atom systems (which is harder to prove, but just as true, for an atom with 92 electrons) expressed in the law of the light emitted when they are excited, their stability, and the fact that they are all the same size, had no roots in any then existing piece of physics. This was the very great predicament which caused Bohr to make one of those wild guesses {123} which even his own great caution was unable to keep from looking very revolutionary. Bohr said: ‘For reasons which we don't yet understand, an atom is not characterized by classical orbits, but it is characterized by a set of states which are essentially stationary, which don't change in time.’ Of these the most familiar and important is the one with the lowest energy, the ground state, and that lasts forever, unless the atom is disturbed. These states have different energies and those which have more energy than the ground state may not be stable; a transition may occur from such a state to a lower one spontaneously. We remember that each frequency emitted from a given atomic species can be written as ν = ν1 – ν2, and we may make this into an intelligible equation by multiplying it by h, Planck's constant
hν = hν1 – hν2
Then each term in this equation is an energy, and we could assume that the two quantities, hν1 and hν2, are the energies of two states in the atom, and the quantity hν is the energy of the quantum of light that is emitted in the transition between them. ‘I cannot,’ said Bohr, ‘describe these transitions. They are not motions in any classical sense. They are something new that I don't understand.’ Bohr went on to say: ‘I can give you a rule, in some cases, for I calculated the energies for these states, and this I can do in terms of the properties of the corresponding classical orbits.’ But Bohr did not say, and this turned out not to be true, that these states have anything in common with orbits. For one thing, an orbit is a motion and something changes with time. The stationary state is just what it says: it does not change with time at all.
We have now reached the crisis of quantum theory; but before we get through with this story we will see that we have a vast extension of our idea of intelligibility in science, that we have a vast generalization of what we mean by objective knowledge, and that we have a much better {124} analogue to the human predicament than could possibly have been built on Newtonian physics.
Our crisis arose in two studies which, it turns out, are very closely related. The first was the discovery that, although all electromagnetic waves, including light, are described so perfectly as wave phenomena showing interference and giving diffraction patterns, nevertheless, in their transactions with matter, they have a discrete character, behaving like light quanta, with definite energy and definite momentum, and that they negotiate with matter by giving up this energy, or by taking it from matter or by colliding with matter in an elastic collision. Secondly, we had the problem, created by Rutherford's discovery of the atomic nucleus, of what in the dickens the electrons were doing in the neighbourhood of the nucleus. They were not moving on planetary orbits, they were not radiating, they were not behaving like a small solar system; but they were, for the most part, in stationary states, essentially stable, the lowest one completely stable, as Bohr said. When they moved from one state to another, this was not a motion which could be pictured in space and time; but the energy difference between the energies of the stationary states could appear in a form of radiation, the corresponding light quantum. There were rules which were not precise and not generally applicable and which I shall not write down, that Bohr gave for identifying the energy of these states.
Bohr knew that this was a radical departure and an incomprehensible one and he immediately followed it up with a suggestion very much like that which guided Einstein, namely that this new scheme, which seemed so wild and unfamiliar, must, in some situations, reproduce the world we knew. Those situations were ones in which very highly excited states of the atom were involved, in which many stationary states were involved, and where the discreteness of the stationary state and the finiteness of Planck's constant would not make very much difference. This he called the ‘correspondence principle.’ The new {125} theory must describe the world of Newton and the world of Maxwell when we are away from the discrete elements that characterize the quantum theory. This principle turned out to be a most powerful tool; and by 1925 it had been possible to write down laws not involving any image of motion, not involving any clear connexion with Newton's laws or with particles in orbits, but laws which nevertheless were generalizations of Newtonian mechanics and which directly described the connexion between transitions between atomic states and the properties of the atomic state themselves.
I am glad that it did not stay at that, because this is very hard to explain without mathematics. I think my first paper dealt with a simple problem of a molecule with two atoms by this machinery, but it was very hard to interpret what this was about and very hard to solve problems. The solution which most of us find easiest to explain and which is in fact identical with that which the ‘correspondence principle’ led to, came in a very different way. It came in a wild idea that was very soon generalized and verified, and the wild idea was that there should be a wave associated not just with electromagnetism, but also with every kind of particle in nature, specifically with an electron.
These waves are not electric and magnetic disturbances; what they are I will say in a minute. But the relations which characterize the connexion between the wave properties of light and its energy momentum were preserved, viz:
|
E = hν p = h/λ. |
I have used the same letters, ν and λ for frequency and wavelength, E and p for energy and momentum. This was proposed by de Broglie, who was able to show that one could get a plausible account of the stationary states of the hydrogen atom by the requirement that those states would be realized in which standing waves could be established which were in resonance, that is where the number of wavelengths in the circumference of the Bohr ‘orbit’ would {126} be an integer. This was pretty shaky and it was thoroughly disbelieved—I believe his paper was refused publication. Nevertheless, it was right, and within a year one had found evidence that electrons are indeed in some way wave-like, because they show interference and they diffract just as light does and just as X-rays do.
Also within a year, one found a less sketchy way of describing the relation between the propagation of these waves and the simple forces present in something like a hydrogen atom, where the electron is simply subject to the electric attraction of the proton. This universal wave-particle duality immediately did several things. It explained the existence of stationary states, not as orbits, but as something new with no analogue in classical theory, as things which indeed were steady in time. But they were not static in this sense! If you measured the kinetic energy or the average square momentum of an electron in a stationary state it would not be zero, but it would be the same at any time as it was at any other. It would not change in the course of time. A close connexion between the properties of these waves and Bohr's ‘correspondence principle’ was very quickly set up. But I will not turn to these questions, which are a little mathematical, but rather to the way in which the discovery of the universality of wave-particle duality gave a clue as to the relations between the wave aspects and the particle aspects of light and of all matter. It is also true that a brick is associated with a wave, but it is not a useful thought, because the brick is very much bigger than its wavelength, and we shall never see the interference effects that correspond to macroscopic objects.
The wave-particle duality refers to an individual event and that is a very very striking thing. Let us think again of our two slits. The source may be a light source, or it may be an electron source. The interference acts between the crests of the waves to produce a bright spot in the pattern, or destructively between a crest and a trough to get very little light. This not only describes what happens when you have a lot of light coming from a source, but it describes {127} perfectly well what happens when the light is very faint and you expose a photographic plate for a long time. It describes, in other words, the behaviour of individual quanta of light or individual electrons leaving the source. That fact tells us that the relation of the wave to the finding of the particle is a statistical one: where the wave is strong, we are likely to find the particle, and where the wave, because of destructive interference, is weak, we are unlikely to find it. More than that, the reconciliation of the wave-particle problem involves the following considerations. If you think of this experiment in terms of a light quantum going through one of the slits and being affected by the other slit through which it does not go, you are led to an impossible description of nature, because then things which are not involved in an experiment may affect the outcome. Thus, our presence here tonight may affect the outcome of an experiment in the reactor building a little away; such an idea has no end. The point then is this: in such a set-up you will observe the interference of the light or the electron waves passing through the two slits (or in the more general case, you will get the unidirectional character of light transmitted through a long grating of slits), but you will only do so as long as you leave the experiment as it is with no attempt to find out through which hole the light or the electron passed. Once you arrange to have a {128} little spring in one of the slits, so that when the light is bounced on that slit you notice it, you will have destroyed the interference pattern and you will get only the pattern that you would have if that slit, and that slit alone, were open. How can this be?
It can be because not just the light and the electron, but the slits themselves have the character of being represented by a wave field. Now a wave field, however abstract it may be, has the property that if you want it concentrated in a little region of space you must have different wavelengths present which will reinforce each other in that region of space and cancel outside it. If Δx is a dimension of the region of space, there must be a spread of wavelengths Δλ, such that
Δ(1/λ) ≳ |
1 Δx |
; Δλ ≳ |
λ2 Δx |
; |
the smaller the region in which you wish to confine the disturbance, the larger must be the spread of the wavelengths. But if you look at this formula, and remember that p = h/λ, you will see that there must be a spread of momenta involved. Indeed, the equations show that ΔpΔx ~ h. In words, the spread in momentum multiplied by the spread in position cannot be less than the quantum of action, Planck's constant. This result is true for the light, for the electron, for the slit, and for anything else that you want to study. This provides a completely consistent restriction on how you may and how you may not use the idea of wave and the idea of particle. The restriction is consistent, because it is universal in that every measuring instrument that you use is as limited in its ability to define at the same time both position and momentum as is the object that you are studying.
In actual fact, these waves represent not electric or magnetic fields, but a state of information. They represent what you have learned by an experiment. Suppose, for instance, that you set out to determine that light passed through the upper slit, or to determine that it was monochromatic light emitted from the source. These two {129} complementary measurements are, in fact, mutually exclusive, because by the time that you had detected the passage of the light through the slit, you would have allowed it to collide with a slit in an effective manner, and thereby to destroy your confidence as to its colour (which is essentially its wavelength). The colour would have been changed by the collision. These waves have a well-defined relation to statistical prediction in that, as in the case of light, their square determines the intensity, which in this case is the probability of finding the particle, either light quantum or electron. They also represent in a general way the kind of information which you can obtain about an atomic system, whether it be its momentum, its position, its energy, or any other possible kind of study you may wish to make of it.
In deciding what measurement is possible, we must take into account the fact that not only the system, but everything we can use to observe it with, is subject to the limitation of complementarity, of which this uncertainty relation between the definition of the momentum of a particle and the definition of its position is the most famous and the most fundamental example. If you have an atom, the stationary states are not orbits. To produce orbits you must take a whole mass of stationary states and build up the waves in a suitable manner by adding the waves of stationary states. So an orbit is complementary to a stationary state; you can realize one or the other, but if you do one, the other is foreclosed. It is also the same with a light quantum; you may have a probability wave for a light quantum, and that is what we have been talking about here; but if you want to build up an electromagnetic wave you must have many light quanta and you must superimpose the waves from many light quanta to make a good old-fashioned electromagnetic wave such as we send and receive. We know that there are indeed many quanta in such waves.
The important point is that it is not merely that we do not always know everything that in classical mechanics we thought we could know, like the position and momentum of an object; if that were so, you could say: ‘Well, I know {130} its momentum and I will suppose that it is distributed somehow over different possible positions and I will calculate what I'm interested in and take the average.’ But you must not do that. If you suppose that an object whose momentum you have determined by experiment has a distribution in positions, no matter what the distribution, you will get the wrong answer. It is not that you do not know it; it is that it is not defined. The experiment which gives you the momentum forecloses the possibility of your determining the position. If you welch on it and say, ‘Well, I want to know the position in the first place,’ then you can, but then you lose the knowledge which the earlier experiment had given.
One is thus led to a view that a good, well-designed observation gives information. This will determine a wave field, and this wave field develops in time in a quite causal way. That is, if you know it at one time its future will be also known. From this wave field, by taking its square, you can determine the probability for the outcome of another experiment at the future time. These predictions have been checked and checked and checked, and in some wonderful cases are right to one part in ten billion, or something like that. When you make your new observation to check the prediction you generally, but not always, render the old wave function no longer a reasonable description of the system. You also have wild situations in which you may use one particle to study another and in which, depending on what you do with the test particle, you may produce a state for the other which either has a well defined momentum, or a well-defined position. You cannot do both and you exercise your option by what you do with the observing particle rather than with the observed particle. This gives in a most vivid way a notion of how limited the objectivity of an atomic system is, because apart from a description of what you have done to study its properties, it is not logically possible to assign properties to that atomic system. You cannot say: ‘I think it is in this part of space and maybe it has such and such a velocity. Let me try it {131} out.’ You have to take into account, in order to give it any properties at all, what you have done to observe it or what you know of its history. In other words, you have to take into account the relation of this object to the world of nature, not to you as a human being, but to you as one of the many physicists who are in the game.
This theory is, therefore, one which has forced us to a quite different notion of what we mean by objectivity. All over the world, in France, in Japan, in New Zealand, in communist countries, we talk about atomic physics, and we check each other's experiments. In that sense it is a most objective part of our knowledge, and a most well-verified one. These comparisons are possible because we can tell each other how we have gone about an experiment and what we saw and what we found. Mistakes are made, but they are found very quickly. The objectivity which we see in this is not a characteristic that you can look up in a book, it is not an ontological characteristic of the atom at all. It is a characteristic of the way we can talk with each other about it, of the lack of ambiguity and of the reproducibility and the verifiability of our communication with each other.
Quantum theory is, of course, an acausal theory in the sense that events happen for which no precise cause can be determined or given. A given nucleus disintegrates at three o'clock on the afternoon of a certain day. No one in the world could find out when that would happen until it did happen, but he could give a law saying how many in 100,000 nuclei of the same kind would disintegrate in any interval of time. It is a non-determinist theory. There is no possibility, as there was in Laplace's nightmare, of knowing everything about the world right now—not a very plausible assumption—and therefore knowing all about its future— not a very happy outcome. In every experiment, in atomic physics, you look at something, or have other ways of knowing something about the system; it develops according to laws of wave propagation which are simple and well known; then you look again and you get an answer. Everything about this is quite different from the Newtonian picture. {132} You are free in your choice of what you are going to look at to begin with. You are free in what question you ask later; but the event itself is unique. You can try it again and it will not in general give the same answer, because the connexion between the two experiments is a statistical one, not a necessary one.
| {133} |
I have been discussing the idea of complementarity: that it is impossible to measure precisely two complementary aspects of a physical system. Always when you talk about an atomic system it may be big, it may be a crystal, it may be a nucleus, it may have billions and billions of atoms in it, but always it is a finite part of the world; and in order that you can make an observation of it, you must use the rest of the world for the machinery with which you do it. Especially Bohr has pointed out the analogies between this situation of complementarity and familiar traits in life. He has had, I think, a double purpose: one to illuminate the situation in physics and one to reinforce our interest in complementary aspects of human life.
A favourite one is this. When I write with the chalk it is part of me and I use it without any separation between it and my hand. When I look at it and get interested in what it is and put it under a microscope, it is an object of study. I can do one or the other, but the effective doing of one obviously forecloses the effective doing of the other. I may, as we all have to, make a decision and act or I may think about my motives and my peculiarities and my virtues and my faults and try to decide why I am doing what I am. Each of these has its place in our life, but clearly the one forecloses the other. We may talk, as we increasingly do, about the physical disposition and chemical mechanisms in living objects, but when we talk about living objects we also need to talk about the purpose for which these mechanisms have been developed and have survived. Both methods of description have a valuable part, to give either up is to impoverish our understanding of life; but they are not things that can be done at once without confusion. {134}
There are many other examples. Perhaps one of the deepest, because it is the most familiar, is that we all encounter situations in our life in which we look at the predicament of a man, a friend perhaps, or a son, and see it in the light of what is good for him and of our love for him. We know that others will look at it in the light of what is just and what is proper in society. We know that the good societies, if there are any, the better societies are those in which this conflict and this dichotomy and this element of complementarity is not too terrible. Still, we all know, because of the tragic quality of life, that it will always be there. Those who have lived through the unravelling of the heart of the atomic paradox as it existed twenty-five or thirty years ago believe that one has come to a vision of the physical world with far more room for the human spirit in it than could have been found in the great mechanism of Newton.
Very soon physicists, pleased with what they had found and enormously armed with new theoretical and mathematical methods, turned to other problems—not just atomic physicists, but their colleagues in chemistry, in mathematics, and in other branches of physics. For instance, very soon after the quantum theory was elucidated one began really to make a theory of the electron, the first fundamental particle, other than light, to be studied in detail. And the positron, the counterpart to the electron, which has the same mass, but opposite charge, was discovered, and detailed studies were made of the beautiful processes of materialization and dematerialization, in which a pair of charged particles disappear to give two rays of light (two gamma rays), or in which two gamma rays collide to make a pair. This is as beautiful an example of Einstein's relation between mass and energy as one can ask for. But then we got into another branch of study which in the end involved us as a community in politics in some sense (I mean it in a good sense—the judgement of the good society, not the winning of an election), and in the great questions of national and political power. This, of course, is not {135} unheard of. Archimedes, in Syracuse, had the same troubles, and Hobbes, ten years before Newton's Principia, wrote of them with a dry dispassion. This began to happen very slowly and without anyone seeing it, when, armed with quantum theory and eager to understand, physicists turned their attention not to the behaviour of the atomic electrons around the nucleus, but to the nucleus itself.
This field was very much opened up by two developments. One, which occurred in the same year as the discovery of the positron, was the discovery of the neutron, the neutral ingredient of atomic nuclei. The second was the design and construction of accelerators, machines for giving to charged particles sufficient energy to overcome the electric repulsion of atomic nuclei, and to get at them and break them up and to see what they were made of and how they reacted. By 1939 we knew quite a lot of how nuclei behaved, of what their stationary states were like, of how they reacted when bombarded, and of what kind of products would be produced. Although those were the days of small accelerators, a million times less energetic than those now under study, they were good enough to give a very good insight into the behaviour of atomic nuclei. Rutherford was dead then, in 1939. It was he, who, during the First World War, had produced the first artificial transmutation of nuclei, not with an accelerated particle, but with one of his beloved α-particles. He went to his death rather doubtful that large-scale energy releases could be practically accomplished on earth, although the energy changes were certainly there to be made. We learned more of this when, on the basis of studies of nuclei and of what the astronomers could tell, it was possible to give a convincing and rather detailed account of some of the principal sources of the energy of the sun and of many other stars in terms of nuclear reactions changing nuclei and releasing energy in the hot central regions of these stars.
Nineteen thirty-nine was the year of fission and was also the year of the outbreak of the Second World War; a good many changes had come to all people, but also to physicists. {136} Early in the 1920s up until the very early 1930s scientists from the Soviet Union were welcome and were frequently found in the great centres of learning in Europe and warm collegial relations were formed then between Russians, Englishmen, Germans, Scandinavians, many of which persist to this day. That was changed, too, in the 1930s. During the 1930s very many men of science, like very many other men, either had to leave or in conscience did leave Germany. Many of them came to Canada, many to the United Kingdom, and perhaps most of all to the United States. Some came from Italy as well. By 1939 the Western world was no longer a suburb of the scientific community, but a centre in its own right, and when fission was discovered the first analyses of what nuclei were involved and what prospects there were for its practical use for the release of energy were largely conducted in the United States. I remember that Uhlenbeck, who was still in Holland, thought it his duty to tell his government about this development; the Minister of Finance immediately ordered 50 tons of uranium ore from the Belgian mining company, and remarked: ‘Clever, these physicists.’
Actually it was very largely the refugee scientists in England and in the United States who took the first steps to interest their governments in the making of atomic explosives and who took some steps, very primitive ones, in thinking out how this might be done and what might be involved in it. In fact, we all know that it was a letter from Einstein, written at the suggestion of Szilard, Wigner, and Teller, that first brought the matter to President Roosevelt's attention; in the United Kingdom I think it was Simon and Peierls who played this early part. Bohr remained in Denmark as long as it was humanly possible for him to do so. The governments were busy. They had a war on their hands and certainly any reasonable appraisal would have suggested that radar, probably the proximity fuse, and in principle if not in fact rockets would have very much more to do with the outcome of the war than would the atomic energy undertaking. It started slowly under {137} crazy names like Tube Alloys in the United Kingdom, and Department of Substitute Materials in the United States. When I came into it my predecessor had the title Co-ordinator of Rapid Rupture.
There were really very many questions. Would a bomb work and what sort of a thing would it be, how much material would it need, what kind of energies would it release; would it ignite the atmosphere in nuclear reactions and end us all; could it be used to start fusion reactions? There was also the problem of producing, in industrial processes that had no previous analogue in human history, the very considerable number of pounds of the special materials, uranium and plutonium, of which the first bombs had to be made. By late 1941 an authorization for production was really given. There was an uneasy co-operation between the United Kingdom, Canada, and the United States, later substantially to improve, but never, I think, to become completely free of trouble, especially for our friends from the United Kingdom, though we learned much and gained much from all their help. There was also, of course, very much secrecy.
Late in 1942 we decided that we must get to work on how to make bombs themselves. On July 16th, 1945, early in the morning, the first bomb was exploded. It did a little better than we thought it might. One of the guards said: ‘The long hairs have let it get away from them.’ That day, the President of the United States, the Prime Minister of England, and Stalin were meeting in Potsdam. I believed, because I was told by Dr. Bush, that the President would take the occasion to discuss this development with Stalin, not in order to tell him how to make a bomb, which the President did not know, but to do something that seemed important at the time, to treat the Russians as allies in this undertaking and to start discussing with them how we were going to live with this rather altered situation in the world. It did not come off that way. The President said something, but it is completely unclear whether Stalin understood it or not. No one was present except Stalin's interpreter {138} of the moment and the President, who does not know Russian. But it was a casual word and that was all.
The bombs were used against Japan. That had been foreseen and in principle approved by Roosevelt and Churchill when they met in Canada and again at Hyde Park. It was largely taken for granted; there were questions raised, but I believe there was very little deliberation and even less record of any deliberation there was. And I would like synoptically, briefly, on the basis of my memory of the time and of talk with many historians who have grappled with it, to tell you what little I think about this. I think first of all that we do not know and at the moment cannot know whether a political effort to end the war in the Far East could have been successful. The Japanese Government was deeply divided and stalemated in favour of war. The dissident part of the Government had made an overture through Moscow to the West. Moscow did nothing about it until Potsdam. Stalin told Truman about it. Stalin did not seem interested, Truman did not seem interested, and nothing happened. This was at the very time when the test bomb was successful and a couple of weeks before the bombing of Japan. The actual military plans at that time for the subjugation of Japan and the end of the war were clearly much more terrible in every way and for everyone concerned than the use of the bombs. There is no question about that; and these plans were discussed with us; they would have involved, it was thought, a half a million or a million casualties on the Allied side and twice that number on the Japanese side. Nevertheless, my own feeling is that if the bombs were to be used there could have been more effective warning and much less wanton killing than took place actually in the heat of battle and the confusion of the campaign. That is about all that I am clear about in hindsight. That, and one other thing: I am very glad that the bomb was not kept secret. I am glad that all of us knew, as a few of us already did, what was up and what readjustments in human life and in political institutions would be called for. Those are the days when we all drank one toast only: ‘No more wars.’ {139}
When the war was over, the great men of physics spoke quite simply and eloquently, Einstein in advocacy of world government and Bohr, first to Roosevelt and to Churchill and to General Marshall and then finally quite openly, when nobody else listened but the public, of the need to work for a world which was completely open. He had in mind that we had some very great secrets and that we ought to be willing to relinquish them in exchange for the disappearance of secrecy from all countries and particularly from the secret-ridden communist societies. Stimson, who resigned as Secretary of War in September 1945, wrote: ‘Mankind will not be able to live with the riven atom, without some government of the whole.’ Among many reports that we in our innumerable commissions produced, I remember two. One of them, which remains, I think, to this day Top Secret, ended roughly: ‘If this weapon does not persuade men of the need for international collaboration and the need to put an end to war, nothing that comes out of a laboratory ever will.’ The other said: ‘If there is to be any international action for the control of atomic energy there must be an international community of knowledge and of understanding.’
All of this was very deep and genuine and I think most of our community, and many other people also, believed it desirable. It was not exactly what Stalin wanted. And it really was not anything to which any government became very clearly or deeply or fully committed. In the absence of a practical way of getting there, the most that could be done was to put forward some tentative and not entirely disingenuous suggestions about the control of atomic energy which, if accepted, would have led in the direction of international collaboration and in the direction of a suitable beginning of world order. That is not how it has worked; and I remind you only of two obvious things. We are in an arms race of quite unparalleled deadliness—I think this is not the place to speak about the amount of devilment that is piled up on both sides, or about the precautions and the difficulties of making sure that it does not go off; on the other hand, we have lived sixteen and a half {140} years without a nuclear war. In the balance, between the very great gravity of the risks we face and the obvious restraints that have seen us through this time, I have no counsel except that of sobriety and of some hope.
It may seem wrong to speak of this as an experience of physicists. It certainly is not an intellectual challenge like that out of which the theory of relativity was born or that which gave rise to the solution of the paradoxes of wave-particle duality and the quantum theory. I doubt if there is a certain specific right idea to be had in the field of how to remake the world to live with these armaments and to live with our other commitments and our other hopes. But it is true that we have been marked by our deep implication in this development, by the obvious fact that without physics it could not have happened, and by the heavy weight which has been laid on so many members of this community in counselling their government, in speaking publicly and in trying above all in the early phases to find a healthy direction. I do not think that even our young colleagues, tearing away at the new unsolved problems of fundamental physics, are as free of preoccupation for their relation to the good life and the good society, as we were, long ago, when we were their age.
There have been, as you know, many deep and painful conflicts among technical people, and I think one can pick up the paper almost any day and find examples of learned men calling their colleagues liars. We are torn by conflicts, and this, I think, was not openly and clearly true in 1945 and 1946. The arms race, the Cold War, the obduracy of the political conflict, and the immense and complex and terrifying scope of the technological enterprise are not a climate in which the simple discussion of physical problems finds very much place. But more than that, of course, these are not physical problems and they cannot be settled by the methods of science. The question of what our purpose is on earth, the question of how we may make a government that will represent these purposes, the question of what our own responsibility is, the question of what business it is of {141} ours to think about these things, are not to be solved in any laboratory or settled by any equation or any mathematics. Part of the conflict among technical people is like the conflict among all people: it comes from conflicting assessments of what our antagonist's course may be, what his behaviour will be—a subject rich in mystery, even for the experts. Part of it comes because we are talking about a world in which there is no relevant previous experience. No world has ever faced a possibility of destruction—in a relevant sense annihilation—comparable to that which we face, nor a process of decision-making even remotely like that which is involved in this. Those of you who have been in battle know how tangled, unpredictable, and unamenable to prior planning the course of a battle often turns out to be, even when it was well planned. No one has any experience with warfare in the nuclear age. These are some of the reasons for acrimonious differences as to what fraction of a population may survive if you do this or do that, or what you may trust our antagonists to do and what you must suspect them of doing. In addition, the community of physicists is certainly no more than any other free of evil, free of vanity, or free of their own glory; we must expect rather ugly things to happen and they do.
But I would really think that on a few rather deep points which do not imply the answers to all the questions in which we could rightly be interested, we are as a community really rather clear as to what our duty is. It is, in the first place, to give an honest account of what we all know together, know in the way in which I know about the Lo-rentz contraction and wave-particle duality, know from deep scientific conviction and experience. We think that we should give that information openly whenever that is possible, that we should give it to our governments in secret when the governments ask for it, or, even if the governments do not ask for it, that they should be made aware of it, when we think it essential, as Einstein did in 1939. We all, I think, are aware that it is our duty to distinguish between knowledge in this rather special and proud, but {142} therefore often abstract and irrelevant, sense, and our best guess, our most educated appraisal of proposals which rest on things that in the nature of the case cannot yet be known, like the little cost of some hundred million to build a certain kind of nuclear carrier. We think that it is even more important, and even more essential, to distinguish what we know in the vast regions of science where a great deal is known and more is coming to be known all the time, from all those other things of which we would like to speak and should speak in another context and in another way, those things for which we hope, those things which we value. Finally, I think we believe that whenever we see an opportunity, we have the duty to work for the growth of that international community of knowledge and understanding, of which I spoke earlier, with our colleagues in other lands, with our colleagues in competing, antagonistic, possibly hostile lands, with our colleagues and with others with whom we have any community of interest, any community of professional, of human, or of political concern. We think of these activities as our contribution, not very different from those of anybody else, but with an emphasis conditioned by the experiences of growing, increasing understanding of the natural physical world, in an increasingly tangled, increasingly wonderful and unexpected situation. We think of this as our contribution to the making of a world which is varied and cherishes variety, which is free and cherishes freedom, and which is freely changing to adapt to the inevitable needs of change in the twentieth century and all centuries to come, but a world which, with all its variety, freedom, and change, is without nation states armed for war and above all, a world without war.
| {143} |
All these ‘things being consider'd, it seems probable to me, that God in the Beginning form'd Matter in solid, massy, hard, impenetrable, moveable Particles, of such Sizes and Figures, and with such other Properties, and in such Proportion to Space, as most conduced to the End for which he form'd them; and that these primitive Particles being Solids, are incomparably harder than any porous Bodies compounded of them; even so very hard, as never to wear or break in pieces; no ordinary Power being able to divide what God himself made one in the first Creation. While the Particles continue entire, they may compose Bodies of one and the same Nature and Texture in all Ages: But should they wear away, or break in pieces, the Nature of Things depending on them, would be changed. Water and Earth, composed of old worn Particles and Fragments of Particles, would not be of the same Nature and Texture now, with Water and Earth composed of entire Particles in the Beginning. And therefore, that Nature may be lasting, the Changes of corporeal Things are to be placed only in the various Separations and new Associations and Motions of these permanent Particles; compound Bodies being apt to break, not in the midst of solid Particles, but where those Particles are laid together, and only touch in a few Points. It seems to me farther, that these Particles have not only a Vis inertce, accompanied with such passive Laws of Motion as naturally result from that Force, but also that they are moved by certain active Principles, such as is that of Gravity, and that which causes Fermentation, and the Cohesion of Bodies. These Principles I consider, not as occult Qualities, {144} supposed to result from the specifick Forms of Things, but as general Laws of Nature, by which the Things themselves are form'd; their Truth appearing to us by Phsenomena, though their Causes be not yet discover'd. . . .
|
Sir Isaac Newton, Opticks (New York: Dover Publications, Inc., 1952), Book 3, Part I, Query 31, p. 400. Based on the Fourth Edition, London, 1730. |
I will here, in the first place, contract into few Words, the whole Sum of their Resolutions; which I shall often have occasion to touch upon in Parcels. Their Purpose is, in short, to make faithful Records of all the Works of Nature, or Art, which can come within their Reach; that so the present Age, and Posterity, may be able to put a Mark on the Errors, which have been strengthned by long Prescription; to restore the Truths, that have lain neglected; to push on those, which are already known, to more various Uses; and to make the way more passable, to what remains unreveal'd. This is the Compass of their Design. And to accomplish this, they have endeavour'd, to separate the Knowledge of Nature, from the Colours Rhetorick, the Devices of Fancy, or the delightful Deceit of Fables. They have labor'd to inlarge it, from being confin'd to the Custody of a few, or from Servitude to private Interests. They have striven to preserve it from being overpress'd by a confus'd Heap of vain and useless Particulars; or from being streightned and bound too much up by general Doctrines. They have tried to put it into a Condition of perpetual Increasing; by settling an inviolable Correspondence between the Hand and the Brain. They have studied, to make it not only an Enterprise of one Season, or of some lucky {145} Opportunity; but a Business of Time; a steady, a lasting, a popular, an uninterrupted Work. They have attempted, to free it from the Artifice, and Humors, and Passions of Sects; to render it an Instrument, whereby Mankind may obtain a Dominion over Things, and not only over one another's Judgments: And lastly, they have begun to establish these Reformations in Philosophy, not so much, by any solemnity of Laws, or Ostentation of Ceremonies, as by solid Practice and Examples; not by a glorious Pomp of Words; but by the silent, effectual, and unanswerable Arguments of real Productions.
This will more fully appear, by what I am to say on these four Particulars, which shall make up this Part of my Relation, the Qualifications of their Members; the Manner of their Inquiry; their Weekly Assemblies; and their Way of Registring.
As for what belongs to the Members themselves that are to constitute the Society: It is to be noted, that they have freely admitted Men of different Religions, Countries, and Professions of Life. This they were oblig'd to do, or else they would come far short of the Largeness of their own Declarations. For they openly profess, not to lay the Foundation of an English, Scotch, Irish, Popish, or Protestant Philosophy; but a Philosophy of Mankind.
That the Church of England ought not to be apprehensive of this free Converse of various Judgments, I shall afterwards manifest at large. For the present, I shall frankly assert, that our Doctrine, and Discipline, will be so far from receiving Damage by it; that it were the best Way to make them universally embrac'd, if they were oftner brought to be canvass'd amidst all Sorts of Dissenters. It is dishonorable, to pass a hard Censure on the Religions of all other Countries: It concerns them, to look to the Reasonableness of their Faith; and it is sufficient for us, to be establish'd in the Truth of our own.
|
Thomas Sprat, The History of the Royal Society of London (3rd ed.; London, 1722), pp. 61-63. |
| {146} |
Monticello June 18. 99.
DEAR SIR,
I have to acknolege the reciept of your favor of May 14. in which you mention that you have finished the 6. first books of Euclid, plane trigonometry, surveying and algebra and ask whether I think a further pursuit of that branch of science would be useful to you. There are some propositions in the latter books of Euclid, and some of Archimedes, which are useful, and I have no doubt you have been made acquainted with them. Trigonometry, so far as this, is most valuable to every man, there is scarcely a day in which he will not resort to it for some of the purposes of common life; the science of calculation also is indispensible as far as the extraction of the square and cube roots; Algebra as far as the quadratic equation and the use of logarithms are often of value in ordinary cases: but all beyond these is but a luxury; a delicious luxury indeed; but not to be indulged in by one who is to have a profession to follow for his subsistence. In this light I view the conic sections, curves of the higher orders, perhaps even spherical trigonometry, Algebraical operations beyond the 2d dimension, and fluxions. There are other branches of science however worth the attention of every man: Astronomy, botany, chemistry, natural philosophy, natural history, anatomy. Not indeed to be a proficient in them; but to possess their general principles and outlines, so as that we may be able to amuse and inform ourselves further in any of them as we proceed through life and have occasion for them. Some knowlege of them is necessary for our character as well as comfort. The general elements of astronomy and of natural philosophy are best acquired at an academy where we can have the benefit of the instruments and apparatus usually provided there: but the others {147} may well be acquired from books alone as far as our purposes require. I have indulged myself in these observations to you, because the evidence cannot be unuseful to you of a person who has often had occasion to consider which of his acquisitions in science have been really useful to him in life, and which of them have been merely a matter of luxury.
I am among those who think well of the human character generally. I consider man as formed for society, and endowed by nature with those dispositions which fit him for society. I believe also, with Condorcet, as mentioned in your letter, that his mind is perfectible to a degree of which we cannot as yet form any conception. It is impossible for a man who takes a survey of what is already known, not to see what an immensity in every branch of science yet remains to be discovered, and that too of articles to which our faculties seem adequate. In geometry and calculation we know a great deal. Yet there are some desiderata. In anatomy great progress has been made; but much is still to be acquired. In natural history we possess knowlege; but we want a great deal. In chemistry we are not yet sure of the first elements. Our natural philosophy is in a very infantine state; perhaps for great advances in it, a further progress in chemistry is necessary. Surgery is well advanced; but prodigiously short of what may be. The state of mede-cine is worse than that of total ignorance. Could we divest ourselves of every thing we suppose we know in it, we should start from a higher ground and with fairer prospects. From Hippocrates to Brown we have had nothing but a succession of hypothetical systems each having it's day of vogue, like the fashions and fancies of caps and gowns, and yielding in turn to the next caprice. Yet the human frame, which is to be the subject of suffering and torture under these learned modes, does not change. We have a few medecines, as the bark, opium, mercury, which in a few well defined diseases are of unquestionable virtue: but the residuary list of the materia medica, long as it is, {148} contains but the charlataneries of the art; and of the diseases of doubtful form, physicians have ever had a false knowlege, worse than ignorance. Yet surely the list of unequivocal diseases and remedies is capable of enlargement; and it is still more certain that in the other branches of science, great fields are yet to be explored to which our faculties are equal, and that to an extent of which we cannot fix the limits. I join you therefore in branding as cowardly the idea that the human mind is incapable of further advances. This is precisely the doctrine which the present despots of the earth are inculcating, and their friends here re-echoing; and applying especially to religion and politics; ‘that it is not probable that any thing better will be discovered than what was known to our fathers.’ We are to look backwards then and not forwards for the improvement of science, and to find it amidst feudal barbarisms and the fires of Spital-fields. But thank heaven the American mind is already too much opened, to listen to these impostures; and while the art of printing is left to us, science can never be retrograde; what is once acquired of real knowlege can never be lost. To preserve the freedom of the human mind then and freedom of the press, every spirit should be ready to devote itself to martyrdom; for as long as we may think as we will, and speak as we think, the condition of man will proceed in improvement. The generation which is going off the stage has deserved well of mankind for the struggles it has made, and for having arrested that course of despotism which had overwhelmed the world for thousands and thousands of years. If there seems to be danger that the ground they have gained will be lost again, that danger comes from the generation your cotemporary. But that the enthusiasm which characterises youth should lift it's parracide hands against freedom and science would be such a monstrous phaenomenon as I cannot place among possible things in this age and this country. Your college at least has shewn itself incapable of it; and if the youth of any other place have seemed to rally under other {149} banners it has been from delusions which they will soon dissipate. I shall be happy to hear from you from time to time, and of your progress in study, and to be useful to you in whatever is in my power; being with sincere esteem Dear Sir
Your friend & servt
Th: Jefferson
Scripta Mathematica, I (1932), 88-90.
Good successe is Power; because it maketh reputation of Wisdome, or good fortune; which makes men either feare him, or rely on him.
Affability of men already in power, is encrease of Power; because it gaineth love.
Reputation of Prudence in the conduct of Peace or War, is Power; because to prudent men, we commit the government of our selves, more willingly than to others.
Nobility is Power, not in all places, but onely in those Common-Wealths, where it has Priviledges: for in such priviledges consisteth their Power.
Eloquence is power; because it is seeming Prudence.
Forme is Power; because being a promise of Good, it rec-ommendeth men to the favour of women and strangers.
The Sciences, are small Power; because not eminent; and therefore, not acknowledged in any man; nor are at all, but in a few; and in them, but of a few things. For Science is of that nature, as none can understand it to be, but such as in a good measure have attayned it.
Arts of publique use, as Fortification, making of Engines, and other Instruments of War; because they conferre to Defence, and Victory, are Power: And though the true Mother of them, be Science, namely the Mathematiques; {150} yet, because they are brought into the Light, by the hand of the Artificer, they be esteemed (the Midwife passing with the vulgar for the Mother,) as his issue.
|
Thomas Hobbes, Leviathan, ed. by A. R. Waller (“Cambridge English Classics”; Cambridge: Cambridge University Press, 1904), Part I, Chap. 10, pp. 54-55. |
Unsere Tage füllten den glücklichsten Zeitraum des achtzehnten Jahrhunderts. Kaiser, Könige, Fürsten steigen von ihrer gefürchteten Höhe menschenfreundlich herab, verachten Pracht und Schimmer, werden Väter, Freunde und Vertraute ihres Volks. Die Religion zerreisst das Pfaffengewand und tritt in ihrer Göttlichkeit hervor. Aufklärung geht mit Riesenschritten. Tausende unserer Brüder und Schwestern, die in geheiligter Unthätigkeit lebten, werden dem Staat geschenkt. Glaubenshass und Gewissenszwang sinken dahin; Menschenliebe und Freiheit im Denken gewinnen die Oberhand. Künste und Wissenschaften blühen, und tief dringen unsere Blicke in die Werkstatt der Natur. Handwerker nähern sich gleich den Künstlern der Vollkommenheit, nützliche Kenntnisse Keimen in allen Ständen. Hier habt Ihr eine getreue Schilderung unserer Zeit. Blickt nicht stolz auf uns herab, wenn Ihr höher steht und weiter seht als wir; erkennt vielmehr aus dem gegebenen Gemälde, wie sehr wir mit Muth und Kraft Euren Standort emporhoben und stützten. Thut für Eure Nachkommenschaft ein Gleiches und seid glücklich!
Our days have been the happiest time of the eighteenth century. Emperors, kings and princes step down from their feared heights, {151} and as friends of men scorn pomp and glitter and become fathers, friends and confidants of their people. Religion tears off its popish garb and stands forth in its divinity. Enlightenment advances with giant steps. Thousands of our brothers and sisters who previously spent their lives in holied idleness are given back to the community. Hatred born of dogma and the compulsion of conscience sink away; love of man and freedom of thought gain the upper hand. The arts and sciences blossom, and our vision into the workshop of nature goes deep. Artisans approach artists in perfection; useful skills flower at all levels. Here you have a faithful portrait of our time. Look not proudly down upon us, should you stand higher or see farther than we, but rather recognize from this picture how with courage and strength we raised and supported your standard. Do the same for those who come after you and rejoice!
|
Hermann Hettner, Literaturgeschichte des Achtzehnten Jahrhunderts, Vol. III (Braunschweig: Friederich Vieweg und Sohn, 1879), Book 2, Chap. 1, p. 171. |
DE L'USAGE QUE LES AMÉRICAINS FONT DE
L'ASSOCIATION DANS LA VIE CIVILE
Je ne veux point parler de ces associations politiques à l'aide desquelles les hommes cherchent à se défendre contre l'action despotique d'une majorité ou contre les empiétements du pouvoir royal. J'ai déjà traité ce sujet ailleurs. Il est clair que si chaque citoyen, à mesure qu'il devient individuellement plus faible, et par conséquent plus incapable de préserver isolément sa liberté, n'apprenait pas l'art de s'unir à ses semblables pour la défendre, la tyrannie croîtrait nécessairement avec l'égalité. Il ne s'agit ici que des associations qui se forment dans la vie civile, et dont l'objet n'a rien de politique. {152}
Les associations politiques qui existent aux États-Unis ne forment qu'un détail au milieu de l'immense tableau que l'ensemble des associations y présente.
Les Américains de tous les âges, de toutes les conditions, de tous les esprits, s'unissent sans cesse. Non-seulement ils ont des associations commerciales et industrielles auxquelles tous prennent part, mais ils en ont encore de mille autres espèces: de religieuses, de morales, de graves, de futiles, de fort gênérales et de très-particulières, d'immenses et de fort petites; les Américains s'associent pour donner des fêtes, fonder des séminaires, bâtir des auberges, élever des églises, répandre des livres, envoyer des missionaires aux antipodes; ils créent de cette manière des hôpitaux, des prisons, des écoles. S'agit-il enfin de mettre en lumière une vérité, ou de développer un sentiment par l'appui d'un grand exemple: ils s'associent. Partout où, à la tête d'une entreprise nouvelle, vous voyez en France le gouvernement, et en Angleterre un grand seigneur, comptez que vous apercevrez aux États-Unis une association. J'ai rencontré en Amérique des sortes d'associations dont je confesse que je n'avais pas même l'idée, et j'ai souvent admiré l'art infini avec lequel les habitants des États-Unis parvenaient à fixer un but commun aux efforts d'un grand nombre d'hommes, et à les faire marcher librement.
OF THE USE WHICH THE AMERICANS MAKE OF
PUBLIC ASSOCIATIONS IN CIVIL LIFE
I do not propose to speak of those political associations by the aid of which men endeavor to defend themselves against the despotic action of a majority or against the aggressions of regal power. That subject I have already treated. If each citizen did not learn, in proportion as he individually becomes more feeble and consequently more incapable of preserving his freedom singlehanded, to combine with his fellow citizens for the purpose of defending it, it is clear that tyranny would unavoidably increase together with equality.
Only those associations that are formed in civil life without reference to political objects are here referred to. The political {153} associations that exist in the United States are only a single feature in the midst of the immense assemblage of associations in that country. Americans of all ages, all conditions, and all dispositions constantly form associations. They have not only commercial and manufacturing companies, in which all take part, but associations of a thousand other kinds, religious, moral, serious, futile, general or restricted, enormous or diminutive. The Americans make associations to give entertainments, to found seminaries, to build inns, to construct churches, to diffuse books, to send missionaries to the antipodes; in this manner they found hospitals, prisons, and schools. If it is proposed to inculcate some truth or to foster some feeling by the encouragement of a great example, they form a society. Wherever at the head of some new undertaking you see the government in France, or a man of rank in England, in the United States you will be sure to find an association.
I met with several kinds of associations in America of which I confess I had no previous notion; and I have often admired the extreme skill with which the inhabitants of the United States succeed in proposing a common object for the exertions of a great many men and in inducing them voluntarily to pursue it.
|
Alexis de Tocqueville, De la Démocratie en Amérique, Vol. III (14ieme édition; Paris: Michel Levy Frères, 1864), Deuxième Partie, Chap. 2, p. 175. English translation from Alexis de Tocqueville, Democracy in America, Vol. II (New York: Alfred A. Knopf, 1948), Book 2, Chap. 5, p. 106. |
| {154} |
Chapters Two to Five deal at some length with atomic theory and with some of the experiments that underlie it. With the exception of contemporary work on the “new particles,” there are many admirable technical text books and monographs.
As for Chapter Two, the interested reader may wish to turn to the classic texts of E. R. Rutherford, Radioactive Substances and their Radiations (Cambridge: Cambridge University Press; New York: Putnam; 1913), and to Rutherford, Chadwick, and Ellis, Radiations from Radioactive Substances (Cambridge: Cambridge University Press, 1930). The “new particles” were discussed at a conference held at Bagneres de Bigorre, July, 1953. The record of this conference, issued by the Ecole Poly technique, Paris, gives a most vivid impression of the present state of knowledge, ignorance, and progress. Even for those who do not wish to consult the proceedings of the conference, the comment following the title may be of interest: “Les particules decrites au cours de ce Congres ne sont pas entierement fictives, et toute analogie avec des particules existant dans la nature n'est pas une pure coincidence!”
There are numerous good technical texts on the quantum mechanics, the quantum theory of atoms. In particular I recommend:
P.A.M. Dirac. The Principles of Quantum Mechanics. Oxford: Clarendon Press, 1930.
W. Pauli. “Die Allgemeinen Prinzipien der Wellen-mechanik,” Handbuch der Physik, XXIV (1933), 1, 83.
L. I. Schiff. Quantum Mechanics. New York: McGraw-Hill Book Co., 1949.
Of these, Schiff's text is the most elementary.
No attempt has been made in the lectures to give a full historic account of the contributions made to the development {155} of quantum theory. Where names have been mentioned, it is because they have become generally identified with principles or with theories; but any account of the history of quantum theory should at least mention Born, Dirac, and Pauli, in addition to the names that occur in the text.
As the interpretation of quantum theory, these may serve to guide the reader should he want more detailed, more original, and more substantive accounts of the matters touched on in the lectures:
W. Heisenberg. The Physical Principles of the Quantum Theory. Chicago: University of Chicago Press, 1930.
N. Bohr. Atomic Theory and the Description of Nature. New York: (Cambridge University Press) The Macmillan Co., 1934.
N. Bohr. “On the Notions of Causality and Complementarity,” Diabetica, II (1948), 312.
N. Bohr. “Discussion with Einstein on Epistemological Problems in Atomic Physics,” Albert Einstein, Philosopher-Scientist. Edited by P. A. Schilpp. “Library of Living Philosophers”; Evanston, Illinois, 1949.
W. Pauli. “Die philosophische Bedeutung der Idee der Komplementarität,” Experientia, VI (1950), 72.
| {157} |
The first six essays in this volume are transcriptions of the 1953 Reith lectures, commissioned and broadcast by the British Broadcasting Corporation; these were first published in 1954 by Simon & Schuster under the title Science and the Common Understanding. The seventh essay is adapted from a lecture before a joint session of the Rochester Association for the United Nations and the Rochester Foreign Policy Association in 1948; it was published in this form by Simon & Schuster in The Open Mind, 1955.
The last three essays are edited transcriptions of the Whidden Lecture Series, entitled The Flying Trapeze: Three Crises for Modern Physicists, delivered at McMaster University in 1962. These were originally published by Oxford University Press under the same title.
The editors of the present volume wish to express gratitude for permission to reprint these essays.
We also are grateful to Freeman J. Dyson, Professor of Physics at The Institute for Advanced Study's School of Natural Sciences, not only for the preface he has contributed but also for his decisive endorsement of the breadth of the present selection.
Arthur S. Wightman, Thomas D. Jones Professor of Mathematical Physics and Chairman of Princeton University's Mathematics Department, believed in this project from the start, and gave excellent advice on style and content along the way.
James A. Quitslund, Associate Director of The Institute for Advanced Study, offered help and encouragement as we researched our sources.
The cover design is by Laury A. Egan. The cover illustration, a photograph of Oppenheimer posed with Princeton University's Univac II in 1966, is from the archives of The Institute for Advanced Study.